Площадь поверхности и объем параллелепипеда
Примечание. Это часть урока с задачами по геометрии (раздел теорема стереометрия — параллелепипед). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак «√»Задача
Основание прямоугольного параллелепипеда — ромб. Найдите площадь боковой поверхности параллелепипеда, если площади его диагональных сечений равны P и QРешение.
Площадь первого сечения выразим как
P = hd1 , где
h — высота параллелепипеда
d1 — длина диагонали
Площадь второго сечения выразим как
Q= hd2 , где
h — высота параллелепипеда
d2 — длина диагонали
Соответственно,
d2 = Q / h
Площадь боковой поверхности равна
S = 4ah, где
a — длина стороны ромба
h — высота параллелепипеда
По теореме Пифагора
a = sqrt( ( d1 / 2 )2 + ( d2 / 2 )2 )
a = sqrt( d12 / 4 + d22 / 4 )
a = sqrt( d12 + d22 ) / 2
Тогда
S = 4ah
S = 4h sqrt( d12 + d22 ) / 2
S = 2h sqrt( d12 + d22 )
поскольку
d1 = P / h
d2 = Q / h
то
S = 2h √( ( P / h )2 + ( Q / h )2 )
S = 2h √( P 2 + Q2 ) / h
S = 2 √( P 2 + Q2 )
Ответ
: S = 2 √( P 2 + Q2 )Задача
|
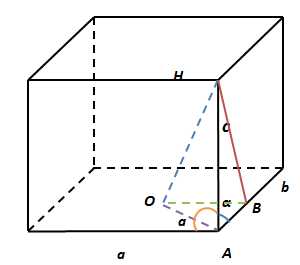
Вычислить объем прямоугольного параллелепипеда, диагональ которого а образует с плоскостью основания угол а, а с боковой гранью – угол β. |
Обчислити об’єм прямокутного паралелепіпеда, діагональ якого а утворює з площиною основи кут а, а з бічною гранню кут β. |
Решение. Рiшення.
|
По условию AC’ = a ∠C’AC = α ∠AC’B = β Тогда AB = a sin β; AC = a cos α; CC´ = a sin α; BC2 = AC2 — AB2 a2cos2α — a2sin2β = a2( cos2α — sin2β ) (cos2α — sin2β > 0 т.к. АС – гипотенуза, а АВ – катет). |
За умовою AC’ = a ∠C’AC = α ∠AC’B = β Тоді V = AB х BC х CC´ ; AB = a sin β; AC = a cos α; CC´ = a sin α; BC2 = AC2 — AB2 a2cos2α — a2sin2β = a2( cos2α — sin2β ) (cos2α — sin2β > 0 т.к. АС – гіпотенуза, а АВ – катет). |

Задача
|
В параллелепипеде длины трех ребер, выходящих из одной вершины, равны |
У паралелепіпеді довжини трьох ребер, що виходять з однієї вершини, дорівнюють а, b, с. Ребра а і b взаємно перпендикулярні, а ребро с утворює з кожним з них кут α. Знайти об’єм паралелепіпеда. |
Решение. Рiшення.
|
Так как углы, образуемые ребром с с ребрами а и b, равны, то треугольник АОВ равнобедренный и прямоугольный, катеты которого АВ=ОВ=с*cosα, а гипотенуза ОА= *c*cosα |
Так як кути, утворені ребром с з ребрами а і b рівні, то трикутник АОВ і прямокутний рівнобедрений, катети якого АВ=ОВ=с*cosα, а гіпотенуза ОА= *c*cosα |
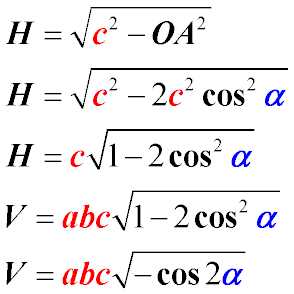 Параллепипед |
Описание курса | Призма с треугольником в основании
Параллепипед |
Описание курса | Призма с треугольником в основании
profmeter.com.ua
Как найти объем и площадь прямоугольного параллелепипеда
То есть если известны длины двух сторон треугольника , которые равны и , а также угол между этими сторонами, то искомая площадь: Формула площади треугольника. Второй способ. Чтобы найти площадь треугольника, нужно сторону умножить на высоту, проведенную к этой стороне (рис.
Объемы фигур. Объем параллелепипеда.
Объем прямоугольного параллелепипеда, формула.
6 граней, а они, в свою очередь, являются параллелограммами.
Параллелепипед, у которого 4 боковые грани — это прямоугольники, является Прямым
Прямой параллелепипед, у которого все 6 граней прямоугольники, является Прямоугольным.
Другими словами, Прямоугольный параллелепипед — это объемная фигура, у которой есть 6 граней, и
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту:
Где, H — высота параллелепипеда,
A – длина параллелепипеда,
B – ширина параллелепипеда,
H — высота прямоугольного параллелепипеда,
Примеры прямоугольного параллелепипеда: спортивный зал, кирпич, картонная коробка или столешница
Длины 3 рёбер прямоугольного параллелепипеда, которые имеют общий конец, называются Измерениями
Прямоугольный параллелепипед с одинаковыми измерениями является кубом. Все 6 граней куба — это
Квадрат длины диагонали прямоугольного параллелепипеда = сумме квадратов 3 его измерений.
Объем прямого параллелепипеда, формула.
Как найти объем параллелепипеда?
Площадь боковой поверхности параллелепипеда, формула:
Площадь полной поверхности, формула
Объем произвольного параллелепипеда.
Объём и соотношения в Наклонном параллелепипеде часто определяются с помощью векторной алгебры.
Чему равен объём параллелепипеда? Объем параллелепипеда равен абсолютной величине смешанного
Произведения трёх векторов, которые определяются 3-мя сторонами параллелепипеда, которые исходят
Из одной вершины.
Соотношение длина сторон параллелепипеда – угол между ними даёт утверждение, что определитель
Грама указанных 3х векторов равен квадрату их смешанного произведения.
Как найти объем и площадь прямоугольного параллелепипеда
Объемы фигур. Объем параллелепипеда.
Объем прямоугольного параллелепипеда, формула.
6 граней, а они, в свою очередь, являются параллелограммами.
Параллелепипед, у которого 4 боковые грани — это прямоугольники, является Прямым
Прямой параллелепипед, у которого все 6 граней прямоугольники, является Прямоугольным.
Другими словами, Прямоугольный параллелепипед — это объемная фигура, у которой есть 6 граней, и
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту:
Где, H — высота параллелепипеда,
A – длина параллелепипеда,
B – ширина параллелепипеда,
H — высота прямоугольного параллелепипеда,
Примеры прямоугольного параллелепипеда: спортивный зал, кирпич, картонная коробка или столешница
Длины 3 рёбер прямоугольного параллелепипеда, которые имеют общий конец, называются Измерениями
Прямоугольный параллелепипед с одинаковыми измерениями является кубом. Все 6 граней куба — это
Квадрат длины диагонали прямоугольного параллелепипеда = сумме квадратов 3 его измерений.
Объем прямого параллелепипеда, формула.
Как найти объем параллелепипеда?
Площадь боковой поверхности параллелепипеда, формула:
Площадь полной поверхности, формула
Объем произвольного параллелепипеда.
Объём и соотношения в Наклонном параллелепипеде часто определяются с помощью векторной алгебры.
Чему равен объём параллелепипеда? Объем параллелепипеда равен абсолютной величине смешанного
Произведения трёх векторов, которые определяются 3-мя сторонами параллелепипеда, которые исходят
Из одной вершины.
Соотношение длина сторон параллелепипеда – угол между ними даёт утверждение, что определитель
Грама указанных 3х векторов равен квадрату их смешанного произведения.
Как найти объем и площадь прямоугольного параллелепипеда
Параллелепипед формулы
Параллелепипед – это многогранник с 6 гранями, каждая из которых является параллелограммом.
Прямоугольный параллелепипед – это параллелепипед, каждая грань которого является прямоугольником.
Любой параллелепипед характеризуется 3 сторонами a, b и c (см. рисунок) и диагональю. Именно эти характеристики используются в Формулах параллелепипеда при вычислении объема и площади.
Диагональ параллелепипеда – это отрезок, соединяющий противоположные вершины параллелепипеда.
Формула диагонали параллелепипеда
Диагональ d прямоугольного параллелепипеда можно получить, зная его стороны:
D 2 = a 2 + b 2 + c 2
Формула площади параллелепипеда
Площадь поверхности прямоугольного параллелепипеда можно получить, зная его стороны:
Формула объема параллелепипеда
Объем прямоугольного параллелепипеда можно вычислить, зная его стороны:
Поделитесь статьей с одноклассниками «ПАРАЛЛЕЛЕПИПЕД формулы объема, площади поверхности».
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.
До экзаменов еще есть время!
Напишите, каких разделов и тем Вам не хватает на сайте, и мы постараемся по возможности их добавить:

poiskvstavropole.ru
Применение формул объема и площади поверхности прямоугольного параллелепипеда для решения практических задач и математического моделирования
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (180,7 кБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цель урока: На практике научиться применять формулы объёма и площади поверхности прямоугольного параллелепипеда.
Инструменты: мультимедийная установка, мел, доска, макеты параллелепипедов.
Ход урока
I. Проверка домашнего задания.
II. Устный опрос.
- Сколько ребер у прямоугольного параллелепипеда? Какой фигурой они являются?
- Сколько граней у прямоугольного параллелепипеда? Какой фигурой они являются?
- Сколько вершин у прямоугольного параллелепипеда? Какой фигурой они являются?
III. Работа по готовым чертежам.
- Что такое a, b и c?
- Как найти площадь боковой грани? Есть ли еще грани с такой же площадью?
- Как найти площадь верхней грани?
- Как найти площадь передней грани?
- Записать на доске формулу для нахождения площади поверхности параллелепипеда.
- Записать формулу для нахождения объёма параллелепипеда.
- В каких единицах измеряется площадь поверхности параллелепипеда, а в каких объём.
IV. Решить задачу по чертежу, изображенному на рисунке.
Найти площадь поверхности и объём прямоугольного параллелепипеда.
Решение.
- 3*4 = 12 (кв. см) – площадь передней поверхности.
- 3*5 = 15 (кв. см) – площадь боковой поверхности.
- 4*5 = 20 (кв. см) – площадь верхней поверхности.
- 2*(12+15+20) = 94 (кв. см) – площадь боковой поверхности параллелепипеда.
Ответ: 94 кв.см.
V. Практическая часть. Раздать параллелепипеды
- Измерить ребра параллелепипеда (длину, высоту и ширину). Записать результаты в тетрадь.
- Найти площадь боковой поверхности параллелепипеда.
- Найти объем параллелепипеда.
- Подписать грань параллелепипеда площадь, которой равна
- Вариант 1 – 14 кв. см
- Вариант 2 – 18 кв. см
- Вариант 3 – 48 кв. см
VI. Письменная работа на доске с фронтальным обсуждением.
Задача.
Найти площадь поверхности и объём прямоугольного параллелепипеда с вырезом.
Решение.
- 2*(4*5+5*5+5*4) = 130 кв. см – площадь поверхности.
- 5*5*4 = 100 куб. см – объём параллелепипеда.
Ответ: 130 кв. см и 100 куб. см.
VII. Задача с практическим содержанием.
Сколько ведер воды по 8 литров каждое, налито в аквариум, изображенный на рисунке.
Мы знаем, что 1 литр = 10 куб.дм.
- 25-5 = 20 (см) – высота налитой воды.
- 20*40*60 = 48000 (куб. см) – объём воды в аквариуме.
48000 куб. см = 48 куб. дм = 48 литров - 48:8 = 6 (вед.) – воды потребуется.
Ответ: 6 ведер.
VIII. Выставление оценок.
IX. Домашнее задание.
10.01.2012
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
основные формулы и примеры задач :: SYL.ru
Часто ученики возмущенно спрашивают: «Как мне в жизни это пригодится?». На любую тему каждого предмета. Не становится исключением и тема про объем параллелепипеда. И вот здесь как раз можно сказать: «Пригодится».
Как, например, узнать, поместится ли в почтовую коробку посылка? Конечно, можно методом проб и ошибок выбрать подходящую. А если такой возможности нет? Тогда на выручку придут вычисления. Зная вместимость коробки, можно рассчитать объем посылки (хотя бы приблизительно) и ответить на поставленный вопрос.
Параллелепипед и его виды
Если дословно перевести его название с древнегреческого, то получится, что это фигура, состоящая из параллельных плоскостей. Существуют такие равносильные определения параллелепипеда:
- призма с основанием в виде параллелограмма;
- многогранник, каждая грань которого — параллелограмм.
Его виды выделяются в зависимости от того, какая фигура лежит в его основании и как направлены боковые ребра. В общем случае говорят о наклонном параллелепипеде, у которого основание и все грани — параллелограммы. Если у предыдущего вида боковые грани станут прямоугольниками, то его нужно будет называть уже прямым. А у прямоугольного и основание тоже имеет углы по 90º.
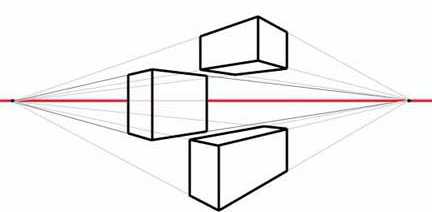
Причем последний в геометрии стараются изображать так, чтобы было заметно, что все ребра параллельны. Здесь, кстати, наблюдается основное отличие математиков от художников. Последним важно передать тело с соблюдением закона перспективы. И в этом случае параллельность ребер совсем незаметна.
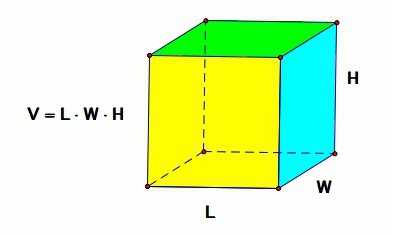
О введенных обозначениях
В приведенных ниже формулах справедливы обозначения, указанные в таблице.
| Величина | Ее обозначение |
| длины ребер основания | а, в |
| длина бокового ребра | с |
| высота | н |
| площадь основания | Sо |
| площадь боковой поверхности | Sб |
| площадь всей поверхности | Sп |
| периметр основания | Ро |
| объем | V |
Формулы для наклонного параллелепипеда
Первая и вторая для площадей:
Третья для того, чтобы вычислить объем параллелепипеда:
Так как основание — параллелограмм, то для расчета его площади нужно будет воспользоваться соответствующими выражениями.
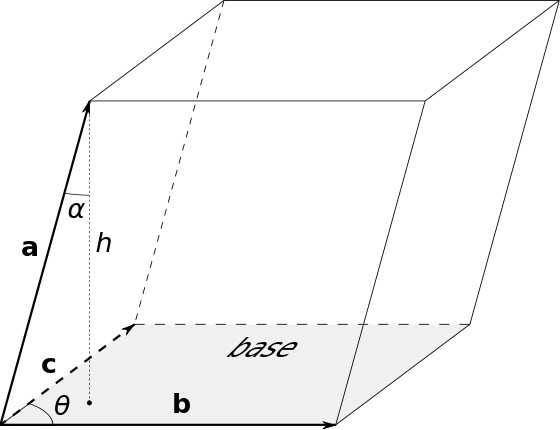
Формулы для прямоугольного параллелепипеда
Аналогично первому пункту — две формулы для площадей:
И еще одна для объема:
Первая задача
Условие. Дан прямоугольный параллелепипед, объем которого требуется найти. Известна диагональ — 18 см — и то, что она образует углы в 30 и 45 градусов с плоскостью боковой грани и боковым ребром соответственно.
Решение. Чтобы ответить на вопрос задачи, потребуется узнать все стороны в трех прямоугольных треугольниках. Они дадут необходимые значения ребер, по которым нужно сосчитать объем.
Сначала нужно выяснить, где находится угол в 30º. Для этого нужно провести диагональ боковой грани из той же вершины, откуда чертилась главная диагональ параллелограмма. Угол между ними и будет тем, что нужен.
Первый треугольник, который даст одно из значений сторон основания, будет следующим. В нем содержатся искомая сторона и две проведенные диагонали. Он прямоугольный. Теперь потребуется воспользоваться отношением противолежащего катета (стороны основания) и гипотенузы (диагонали). Оно равно синусу 30º. То есть неизвестная сторона основания будет определяться как диагональ, умноженная на синус 30º или ½. Пусть она будет обозначена буквой «а».
Это легко сосчитать: а = 18 * ½ = 9 (см).
Вторым будет треугольник, содержащий известную диагональ и ребро, с которым она образует 45º. Он тоже прямоугольный, и можно опять воспользоваться отношением катета к гипотенузе. Другими словами, бокового ребра к диагонали. Оно равно косинусу 45º. То есть «с» вычисляется как произведение диагонали на косинус 45º.
с = 18 * 1/√2 = 9 √2 (см).
В этом же треугольнике требуется найти другой катет. Это необходимо для того, чтобы потом сосчитать третью неизвестную — «в». Пусть она будет обозначена буквой «х». Ее легко вычислить по теореме Пифагора:
х = √(182 — (9√2)2) = 9√2 (см).
Теперь нужно рассмотреть еще один прямоугольный треугольник. Он содержит уже известные стороны «с», «х» и ту, что нужно сосчитать, «в»:
в = √((9√2)2 — 92 = 9 (см).
Все три величины известны. Можно воспользоваться формулой для объема и сосчитать его:
V = 9 * 9 * 9√2 = 729√2 (см3).
Ответ: объем параллелепипеда равен 729√2 см3.
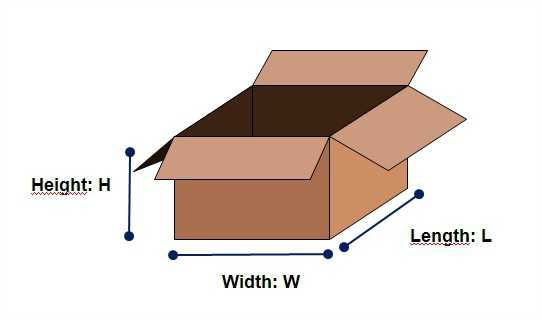
Вторая задача
Условие. Требуется найти объем параллелепипеда. В нем известны стороны параллелограмма, который лежит в основании, 3 и 6 см, а также его острый угол — 45º. Боковое ребро имеет наклон к основанию в 30º и равно 4 см.
Решение. Для ответа на вопрос задачи нужно взять формулу, которая была записана для объема наклонного параллелепипеда. Но в ней неизвестны обе величины.
Площадь основания, то есть параллелограмма, будет определена по формуле, в которой нужно перемножить известные стороны и синус острого угла между ними.
Sо = 3 * 6 sin 45º = 18 * (√2)/2 = 9 √2 (см2).
Вторая неизвестная величина — это высота. Ее можно провести из любой из четырех вершин над основанием. Ее найти можно из прямоугольного треугольника, в котором высота является катетом, а боковое ребро — гипотенузой. При этом угол в 30º лежит напротив неизвестной высоты. Значит, можно воспользоваться отношением катета к гипотенузе.
н = 4 * sin 30º = 4 * 1/2 = 2.
Теперь все значения известны и можно вычислить объем:
V = 9 √2 * 2 = 18 √2 (см3).
Ответ: объем равен 18 √2 см3.
Третья задача
Условие. Найти объем параллелепипеда, если известно, что он прямой. Стороны его основания образуют параллелограмм и равны 2 и 3 см. Острый угол между ними 60º. Меньшая диагональ параллелепипеда равна большей диагонали основания.
Решение. Для того чтобы узнать объем параллелепипеда, воспользуемся формулой с площадью основания и высотой. Обе величины неизвестны, но их несложно вычислить. Первая из них высота.
Поскольку меньшая диагональ параллелепипеда совпадает по размеру с большей основания, то их можно обозначить одной буквой d. Больший угол параллелограмма равен 120º, поскольку с острым он образует 180º. Пусть вторая диагональ основания будет обозначена буквой «х». Теперь для двух диагоналей основания можно записать теоремы косинусов:
d2 = а2 + в2 — 2ав cos 120º,
х2 = а2 + в2 — 2ав cos 60º.
Находить значения без квадратов не имеет смысла, так как потом они будут снова возведены во вторую степень. После подстановки данных получается:
d2 = 22 + 32 — 2 * 2 * 3 cos 120º = 4 + 9 + 12 * ½ = 19,
х2 = а2 + в2 — 2ав cos 60º = 4 + 9 — 12 * ½ = 7.
Теперь высота, она же боковое ребро параллелепипеда, окажется катетом в треугольнике. Гипотенузой будет известная диагональ тела, а вторым катетом — «х». Можно записать Теорему Пифагора:
н2 = d2 — х2 = 19 — 7 = 12.
Отсюда: н = √12 = 2√3 (см).
Теперь вторая неизвестная величина — площадь основания. Ее можно сосчитать по формуле, упомянутой во второй задаче.
Sо = 2 * 3 sin 60º = 6 * √3/2 = 3√3 (см2).
Объединив все в формулу объема, получаем:
V = 3√3 * 2√3 = 18 (см3).
Ответ: V = 18 см3.

Четвертая задача
Условие. Требуется узнать объем параллелепипеда, отвечающего таким условиям: основание — квадрат со стороной 5 см; боковые грани являются ромбами; одна из вершин, находящихся над основанием, равноудалена от всех вершин, лежащих в основании.
Решение. Сначала нужно разобраться с условием. С первым пунктом про квадрат вопросов нет. Второй, про ромбы, дает понять, что параллелепипед наклонный. Причем все его ребра равны 5 см, поскольку стороны у ромба одинаковые. А из третьего становится ясно, что три диагонали, проведенные из нее, равны. Это две, которые лежат на боковых гранях, а последняя внутри параллелепипеда. И эти диагонали равны ребру, то есть тоже имеют длину 5 см.
Для определения объема будет нужна формула, записанная для наклонного параллелепипеда. В ней опять нет известных величин. Однако площадь основания вычислить легко, потому что это квадрат.
Sо = 52 = 25 (см2).
Немного сложнее обстоит дело с высотой. Она будет таковой в трех фигурах: параллелепипеде, четырехугольной пирамиде и равнобедренном треугольнике. Последним обстоятельством и нужно воспользоваться.
Поскольку она высота, то является катетом в прямоугольном треугольнике. Гипотенузой в нем будет известное ребро, а второй катет равен половине диагонали квадрата (высота — она же и медиана). А диагональ основания найти просто:
d = √(2 * 52) = 5√2 (см).
Высоту нужно будет сосчитать как разность второй степени ребра и квадрата половины диагонали и не забыть потом извлечь квадратный корень:
н = √ (52 — (5/2 * √2)2) = √(25 — 25/2) = √(25/2) = 2,5 √2 (см).
Осталось сосчитать объем:
V = 25 * 2,5 √2 = 62,5 √2 (см3).
Ответ: 62,5 √2 (см3).
www.syl.ru
Все тонкости того, как вычислить площадь параллелепипеда :: SYL.ru
Параллелепипед — самая распространенная фигура из тех, что окружают людей. Большинство помещений представляют собой именно его. Особенно важно знать площадь параллелепипеда, хотя бы его боковых граней, во время ремонта. Ведь нужно точно знать, сколько материала приобрести.
Что он собой представляет?
Это призма с четырехугольным основанием. Поэтому у нее четыре боковых грани, которые являются параллелограммами. То есть такое тело имеет всего 6 граней.
Для определения параллелепипеда в пространстве у него определяют площадь и объем. Первая может быть как отдельно для каждой грани, так и для всей поверхности. К тому же выделяют еще и площадь только боковых граней.
Какие существуют виды параллелепипедов?
Наклонный. Такой, у которого боковые грани образуют с основанием угол, отличный от 90 градусов. У него верхний и нижний четырехугольники не лежат друг напротив друга, а сдвинуты.
Прямой. Параллелепипед, боковые грани которого являются прямоугольниками, а в основании лежит фигура с произвольными величинами углов.
Прямоугольный. Частный случай предыдущего вида: в его основании находится прямоугольник.
Куб. Особый тип прямого параллелепипеда, в котором все грани представлены квадратами.
Некоторые математические особенности параллелепипеда
Может возникнуть ситуация, когда они окажутся полезными в том, чтобы найти площадь параллелепипеда.
- Грани, которые лежат напротив друг друга, не только параллельны, но и равны.
- Диагонали параллелепипеда точкой пересечения делятся на равные части.
- Более общий случай, если отрезок соединяет две точки на поверхности тела и проходит через точку пересечения диагоналей, то он делится этой точкой пополам.
- Для прямоугольного параллелепипеда справедливо равенство, в котором в одной его части стоит квадрат диагонали, а в другой — сумма квадратов его высоты, ширины и длины.
Площади прямого параллелепипеда
Если обозначить высоту тела как «н», а периметр основания буквой Рос, то вся боковая поверхность может быть вычислена по формуле:
Sбок = Рос * н
Используя эту формулу и определив площадь основания, можно сосчитать полную площадь:
S = Sбок + 2 * Sос
В последней записи Sос., то есть площадь основания параллелепипеда, может быть вычислена по формуле для параллелограмма. Другими словами, потребуется выражение, в котором нужно перемножить сторону и высоту, опущенную на нее.
Площади прямоугольного параллелепипеда
Принято стандартное обозначение длины, ширины и высоты такого тела буквами «а», «в» и «с» соответственно. Площадь боковой поверхности будет выражаться формулой:
Sбок= 2 * с * (а + в)
Чтобы вычислить полную площадь прямоугольного параллелепипеда, потребуется такое выражение:
S = 2 * (ав + вс + ас)
Если окажется необходимым узнать площадь его основания, то достаточно вспомнить, что это прямоугольник, а значит, достаточно перемножить «а» и «в».
Площади куба
Его боковая поверхность образована четырьмя квадратами. Значит, чтобы ее найти, потребуется воспользоваться известной для квадрата формулой и умножить ее на четыре.
Sбок = 4 * а2
А из-за того, что его основания — такие же квадраты, полная площадь определится по формуле:
S = 6 * а2

Площади наклонного параллелепипеда
Поскольку его грани — это параллелограммы, то нужно узнать площадь каждого из них и потом сложить. К счастью, противолежащие равны. Поэтому вычислять площади нужно только три раза, а потом умножить их на два. Если записать это в виде формулы, то получится следующее:
Sбок = (S1 + S2) * 2,
S = (S1 + S2 + S3) * 2
Здесь S1 и S2 являются площадями двух боковых граней, а S3 — основания.
Задачи по теме
Задание первое. Условие. Необходимо узнать длину диагонали куба, если площадь всей его поверхности равна 200 мм2.
Решение. Начать нужно с получения выражения для искомой величины. Ее квадрат равен трем квадратам стороны куба. Это значит, что диагональ равна «а», умноженной на корень из 3.
Но сторона куба неизвестна. Здесь потребуется воспользоваться тем, что известна площадь всей поверхности. Из формулы получается, что «а» равно квадратному корню из частного S и 6.
Осталось только сосчитать. Ребро куба оказывается равным √ (200/6), что равно 10/ √3 (мм). Тогда диагональ получится равной (10/ √3) * √3 = 10 (мм).
Ответ. Диагональ куба равна 10 мм.
Задание второе. Условие. Необходимо вычислить площадь поверхности куба, если известно, что его объем равен 343 см2.
Решение. Потребуется воспользоваться той же формулой для площади куба. В ней опять неизвестно ребро тела. Но зато дан объем. Из формулы для куба очень просто узнать «а». Оно будет равно кубическому корню из 343. Простой подсчет дает такое значение для ребра: а = 7 см.
Теперь осталось только сосчитать его квадрат и умножить на 6. а2 = 72 = 49, отсюда площадь окажется равной 49 * 6 = 294 (см2).
Ответ. S = 294 см2.
Задание третье. Условие. Дана правильная четырехугольная призма со стороной основания 20 дм. Необходимо найти ее боковое ребро. Известно, что площадь параллелепипеда равна 1760 дм2.
Решение. Начинать рассуждения нужно с формулы для площади всей поверхности тела. Только в ней нужно учесть, что ребра «а» и «в» равны. Это следует из утверждения о том, что призма правильная. Значит, в его основании лежит четырехугольник с равными сторонами. Отсюда а = в = 20 дм.
Учитывая это обстоятельство, формула площади упростится до такой:
S = 2 * (а2 + 2ас).
В ней известно все, кроме искомой величины «с», которая как раз и является боковым ребром параллелепипеда. Чтобы его найти, нужно выполнить преобразования:
- разделить все неравенство на 2;
- потом перенести слагаемые так, чтобы слева оказалось слагаемое 2ас, а справа — деленная на 2 площадь и квадрат «а», причем последнее будет со знаком «-»;
- затем поделить равенство на 2а.
В итоге получится выражение:
с = (S/2 — а2) / (2а)
После подстановки всех известных величин и выполнения действий получается, что боковое ребро равно 12 дм.
Ответ. Боковое ребро «с» равняется 12 дм.
Задание четвертое. Условие. Дан прямоугольный параллелепипед. Одна из его граней имеет площадь, равную 12 см2. Необходимо вычислить длину ребра, которое перпендикулярно этой грани. Дополнительное условие: объем тела равен 60 см3.
Решение. Пусть известна площадь той грани, которая расположена лицом к наблюдателю. Если принять за обозначение стандартные буквы для измерений параллелепипеда, то в основании ребра будут «а» и «в», вертикальное — «с». Исходя из этого, площадь известной грани определится как произведение «а» на «с».
Теперь нужно воспользоваться известным объемом. Его формула для прямоугольного параллелепипеда дает произведение всех трех величин: «а», «в» и «с». То есть известная площадь, умноженная на «в», дает объем. Отсюда получается, что искомое ребро можно вычислить из уравнения:
12 * в = 60.
Элементарный расчет дает результат 5.
Ответ. Искомое ребро равно 5 см.
Задание пятое. Условие. Дан прямой параллелепипед. В его основании лежит параллелограмм со сторонами 6 и 8 см, острый угол между которыми равен 30º. Боковое ребро имеет длину 5 см. Требуется вычислить полную площадь параллелепипеда.
Решение. Это тот случай, когда нужно узнать площади всех граней по отдельности. Или, точнее, трех пар: основание и две боковые.
Поскольку в основании расположен параллелограмм, то его площадь вычисляется как произведение стороны на высоту к ней. Сторона известна, а высота — нет. Ее нужно сосчитать. Для этого потребуется значение острого угла. Высота образует в параллелограмме прямоугольный треугольник. В нем катет равен произведению синуса острого угла, который ему противолежит, на гипотенузу.
Пусть известная сторона параллелограмма — это «а». Тогда высота будет записана как в * sin 30º. Таким образом, площадь основания равна а * в * sin 30º.
С боковыми гранями все проще. Они — прямоугольники. Поэтому их площади — это произведение одной стороны на другую. Первая — а * с, вторая — в * с.
Осталось объединить все в одну формулу и сосчитать:
S = 2 * (а * в * sin 30º + а * с + в * с )
После подстановки всех величин получается, что искомая площадь равна 188 см2.
Ответ. S = 188 см2.
www.syl.ru
Как найти объём параллелепипеда
1. Заполните, пожалуйста размеры рёбер параллелепипеда 2. Для вычисления необходимо знать ширину, высоту и длину 3. Онлайн калькулятор параллелепипеда вычислит объём, моментально решит задачу и напишет решение которое вам останется только переписать!
Формула используемая в нашем калькуляторе найдёт объём прямоугольного параллелепипеда. А если ваш параллелепипед имеет косые грани, вместо длины соответствующего косого ребра — необходимо ввести значение высоты этой части фигуры.
Формула объёма прямоугольного параллелепипеда
L * H * N = V
Чтобы его найти, необходимо знать размеры рёбер: высоту, ширину и длину. По формуле, размеры граней параллелепипеда необходимо перемножить в произвольном порядке.
Объём можно представить в литрах или куб.см., кубических миллиметрах.
Формула площади поверхности параллелепипеда
S1*2 + S2*2 + S3*2 = S
По формуле площади параллелепипеда необходимо найти площади всех сторон параллелепипеда, а затем их сложить. Противоположные стороны, грани, и рёбра параллелепипеда равны между собой, по этому при вычислении площадей можно применять умножение на два.
Основание параллелепипеда
В некоторых случаях бывает известна площадь основания параллелепипеда, тогда для того, что бы найти объём достаточно площадь основания умножить на высоту. ! ВАЖНО ! — это верно, только для прямоугольного параллелепипеда.
Как найти объём параллелепипеда?
Проще всего найти объём введя три известных значения в графы онлайн калькулятора объёма! Затем — нажми на кнопу — получишь результат )!
Калькулятор вычислит объём параллелепипеда abcda1b1c1d1 и распишет решение подробно и с комментариями. Вам останется только переписать строчное решение параллелепипеда себе в тетрадь. Подробное текстовое решение с разъяснениями позволит найти понимание методики решения таких задач и при необходимости снять вопросы, дав развёрнутый и грамотный ответ.
Расчёты объёма и площадь параллелограмма — это элементарная основа для многих технических и бытовых расчётов! Например для расчёта ремонта в комнате, вычисления данных для отопления помещений или их кондиционирования.
Параллелограмм это объёмная геометрическая фигура, имеющая шесть сторон, каждая из сторон при этом параллелограмм. Стороны параллелограмма обычно называются гранями. Если все грани параллелепипеда имеют форму прямоугольника — то это уже прямоугольный параллелограмм! Обозначается эта фигура буквами abcda1b1c1d1.
allcalculators.ru
Площадь параллелепипеда. Формулы и задачи
Формула нахождения полной площади параллелепипеда
Параллелепипед – это четырехугольная призма, в основании имеющая параллелограмм. Существуют готовые формулы для расчета боковой и полной площади поверхности фигуры, для которых необходимы лишь длины трех измерений параллелепипеда.
Как найти площадь боковой поверхности прямоугольного параллелепипеда
Необходимо различать прямоугольный и прямой параллелепипед. Основание прямой фигуры может представлять собой любой параллелограмм. Площадь такой фигуры необходимо вычислять по другим формулам.
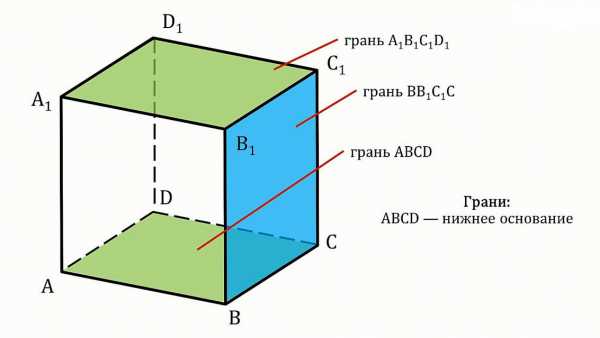
Сумма S боковых граней прямоугольного параллелепипеда вычисляется по простой формуле P*h, где P – периметр и h – высота. На рисунке видно, что у прямоугольного параллелепипеда противоположные грани равны, а высота h совпадает с длиной ребер, перпендикулярных основанию.
Площадь поверхности прямоугольного параллелепипеда
Полная площадь фигуры состоит из боковой и площади 2-х оснований. Как найти площади прямоугольного параллелепипеда:
, где a, b и c – это измерения геометрического тела.
Описанные формулы просты для понимания и полезны при решении множества задач геометрии. Пример типового задания представлен на следующем изображении.

При решении подобного рода задач следует помнить, что основание четырехугольной призмы выбирается произвольно. Если за основание принять грань с измерениями x и 3, то значения Sбок будет иным, а Sполн останется 94 см2.
Площадь поверхности куба
Куб – это прямоугольный параллелепипед, у которого все 3 измерения равны между собой. В связи с этим формулы полной и боковой площади куба отличаются от стандартных.
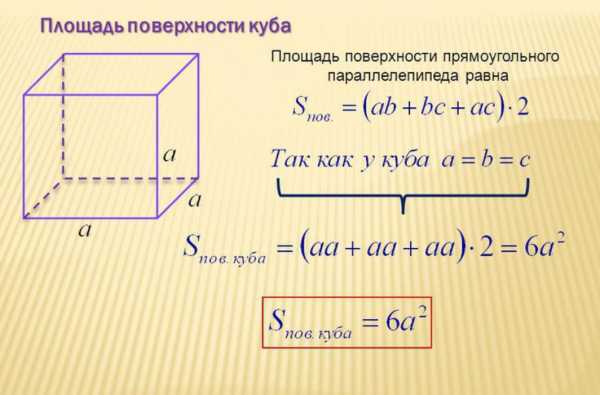
Периметр куба равен 4a, следовательно, Sбок= 4*a*a = 4*a2. Данные выражения не обязательны для заучивания, но значительно ускоряют решение заданий.
Пример решения задачи
Приведенные формулы могут использоваться в ходе поиска диагоналей параллелепипеда.

Для нахождение B1D достаточно применить теорему Пифагора: сумма квадратов катетов равна квадрату гипотенузы.
Похожие статьи
Рекомендуем почитать:
karate-ege.ru
