Транспортировать матрицу: Онлайн калькулятор. Транспонирование матрицы

Транспонирование (Transpose) · Loginom Wiki

Разделы: Алгоритмы Loginom: Куб (визуализатор), Свёртка столбцов (обработчик), Кросс-таблица (обработчик) Транспонирование — в линейной алгебре это операция над матрицами в результате которой матрица поворачивается относительно своей главной диагонали. При этом столбцы исходной матрицы становятся строками результирующей. Операция транспонирования обозначается символом «T», указываемом после обозначения матрицы в верхнем регистре, например AT. Очевидно, что если исходная матрица A имела размер m×n, то транспонированная матрица AT будет размером n×m. Матрица-строка в результате транспонирования преобразуется в матрицу-столбец и наоборот. Несложно увидеть, что ATij=Aji. Например [1234]T=[1324] ⎡⎢⎣123456⎤⎥⎦T=[135246] Таким образом, для получения транспонированной матрицы достаточно каждую строку исходной матрицы записать в виде столбца результирующей, соблюдая порядок следования элементов. Впервые, операция транспонирования была введена британским математиком Артуром Кейли в 1858 году. В линейной алгебре операция транспонирование является промежуточным действием, которое делает удобнее выполнение более сложных матричных преобразования, обладающие собственной логикой. В анализе данных операция транспонирования применяется к таблицам с данными, в результате чего столбцы таблицы становятся строками, а строки — столбцами. Такое преобразование обычно преследует две цели: сделать более удобным визуальный анализ таблиц. Если текущее представление таблицы не соответствует логике анализа, то, возможно, транспонирование поможет улучшить это соответствие. преобразовать набор данных для дальнейшего анализа. Обучающие наборы данных и статистические выборки, использующиеся для построения аналитических моделей (нейронных сетей, деревьев решений, регрессии и т.д.), в столбцах содержат переменные, а в строках — наблюдения. Поэтому если из источниках данных таблица поступает «в перевёрнутом» виде, то для неё необходимо использовать трансформацию в виде транспонирования. Например, исходная таблица может иметь вид: Дата Товар Кол-во продаж 05.02.2019 Обои 75 05.02.2019 Затирка 54 07.02.2019 Обои 21 09.02.2019 Герметик 35 Тогда результатом транспонирования будет таблица вида: Дата Обои Затирка Герметик 05.02.2019 75 05.02.2019 54 07.02.2019 21 09.02.2019 35 Несложно увидеть, что результат транспонирования для таблиц несколько отличается от результатов транспонирования матрицы. Это связано с тем, что между таблицей данных и матрицей в алгебре строгое соответствие вообще говоря, отсутствует: таблица, в отличие от матрицы, не математический объект, а средство визуализации. Поэтому для таблицы результаты транспонирования можно определить так: данные, изначально отображавшиеся в столбцах, будут отображаться в строках, и наоборот. При этом столбцы, где содержатся, скажем, идентификаторы записей или даты, вообще могут не менять своего положения (что в случае транспонирования в алгебре совершенно некорректно). Кроме этого транспонирование является одной из операций, используемых в оперативной аналитической обработке данных для настройки наиболее удобного представления в OLAP-кубах.

Транспонирование матрицы. Онлайн калькулятор

0
AC		+/-	÷
7	8	9	×
4	5	6	—
1	2	3	+
0	00	,	=

При помощи данного калькулятора вы можете легко транспонировать матрицу и получить подробное решение с объяснением

Как транспонировать матрицу

Матрица размерности m × n – это таблица чисел у которой m строк и n столбцов.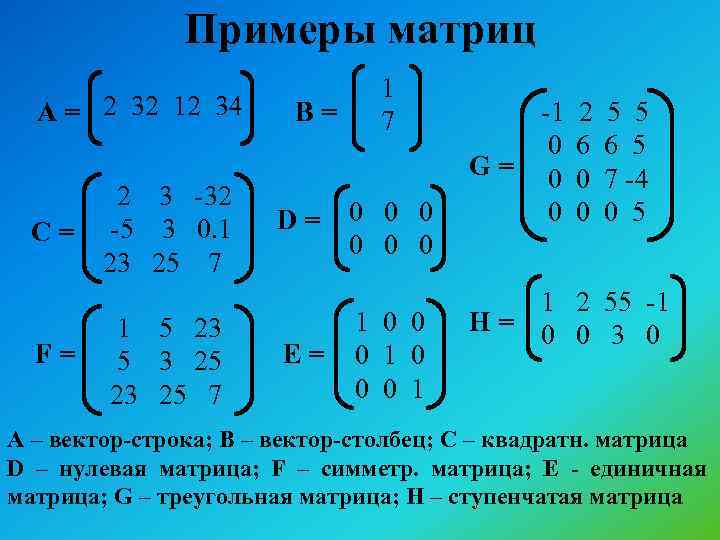 Элементы матрицы обозначаются как a_ij, где i – номер строки, j – номер столбца.

Транспонированная матрица для матрицы A обозначается A^T

Для того чтобы транспонировать матрицу A необходимо каждую строку данной матрицы представить в виде столбца соблюдая порядок.

При транспонировании матрицы A размерности m × n получаем матрицу A^T размерности n × m.

---

Приведем пример, транспонируем матрицу A.

A =	0 6 876 86 7 0 7 0 0

Решение

Как было сказано выше, для того, чтобы получить транспонированную матрицу A^T из исходной матрицы A необходимо каждую строку исходной матрицы A записать в виде столбца в том же порядке.

При транспонировании матрицы A размерности m × n получаем матрицу A^T размерности n × m

	3 × 3
A =	a11 a12 a13 a21 a22 a23 a31 a32 a33	=	0 6 876 86 7 0 7 0 0

A =	a11 a12 a13 a21 a22 a23 a31 a32 a33	где,	a11 = 0 a12 = 6 a13 = 876 a21 = 86 a22 = 7 a23 = 0 a31 = 7 a32 = 0 a33 = 0

Так как A^T_ij = A_ji тогда

	3 × 3
AT =	aT11 = a11 aT12 = a21 aT13 = a31 aT21 = a12 aT22 = a22 aT23 = a32 aT31 = a13 aT32 = a23 aT33 = a33	=	0 86 7 6 7 0 876 0 0

Вам могут также быть полезны следующие сервисы

Калькуляторы линейная алгебра и аналитическая геометрия

Калькулятор сложения и вычитания матриц

Калькулятор умножения матриц

Калькулятор транспонирование матрицы

Калькулятор нахождения определителя (детерминанта) матрицы

Калькулятор нахождения обратной матрицы

Длина отрезка. Онлайн калькулятор расстояния между точками

Онлайн калькулятор нахождения координат вектора по двум точкам

Калькулятор нахождения модуля (длины) вектора

Калькулятор сложения и вычитания векторов

Калькулятор скалярного произведения векторов через длину и косинус угла между векторами

Калькулятор скалярного произведения векторов через координаты

Калькулятор векторного произведения векторов через координаты

Калькулятор смешанного произведения векторов

Калькулятор умножения вектора на число

Калькулятор нахождения угла между векторами

Калькулятор проверки коллинеарности векторов

Калькулятор проверки компланарности векторов

Калькуляторы (Комбинаторика)

Калькулятор нахождения числа перестановок из n элементов

Калькулятор нахождения числа сочетаний из n элементов

Калькулятор нахождения числа размещений из n элементов

Калькуляторы систем счисления

Калькулятор перевода чисел из арабских в римские и из римских в арабские

Калькулятор перевода чисел в различные системы счисления

Калькулятор сложения, вычитания, умножения и деления двоичных чисел

Системы счисления теория

N2 | Двоичная система счисления

N3 | Троичная система счисления

N4 | Четырехичная система счисления

N5 | Пятеричная система счисления

N6 | Шестеричная система счисления

N7 | Семеричная система счисления

N8 | Восьмеричная система счисления

N9 | Девятеричная система счисления

N11 | Одиннадцатиричная система счисления

N12 | Двенадцатеричная система счисления

N13 | Тринадцатеричная система счисления

N14 | Четырнадцатеричная система счисления

N15 | Пятнадцатеричная система счисления

N16 | Шестнадцатеричная система счисления

N17 | Семнадцатеричная система счисления

N18 | Восемнадцатеричная система счисления

N19 | Девятнадцатеричная система счисления

N20 | Двадцатеричная система счисления

N21 | Двадцатиодноричная система счисления

N22 | Двадцатидвухричная система счисления

N23 | Двадцатитрехричная система счисления

N24 | Двадцатичетырехричная система счисления

N25 | Двадцатипятеричная система счисления

N26 | Двадцатишестеричная система счисления

N27 | Двадцатисемеричная система счисления

N28 | Двадцативосьмеричная система счисления

N29 | Двадцатидевятиричная система счисления

N30 | Тридцатиричная система счисления

N31 | Тридцатиодноричная система счисления

N32 | Тридцатидвухричная система счисления

N33 | Тридцатитрехричная система счисления

N34 | Тридцатичетырехричная система счисления

N35 | Тридцатипятиричная система счисления

N36 | Тридцатишестиричная система счисления

Дроби

Калькулятор интервальных повторений

Учим дроби наглядно

Калькулятор сокращения дробей

Калькулятор преобразования неправильной дроби в смешанную

Калькулятор преобразования смешанной дроби в неправильную

Калькулятор сложения, вычитания, умножения и деления дробей

Калькулятор возведения дроби в степень

Калькулятор перевода десятичной дроби в обыкновенную

Калькулятор перевода обыкновенной дроби в десятичную

Калькулятор сравнения дробей

Калькулятор приведения дробей к общему знаменателю

Калькуляторы (тригонометрия)

Калькулятор синуса угла

Калькулятор косинуса угла

Калькулятор тангенса угла

Калькулятор котангенса угла

Калькулятор секанса угла

Калькулятор косеканса угла

Калькулятор арксинуса угла

Калькулятор арккосинуса угла

Калькулятор арктангенса угла

Калькулятор арккотангенса угла

Калькулятор арксеканса угла

Калькулятор арккосеканса угла

Калькулятор нахождения наименьшего угла

Калькулятор определения вида угла

Калькулятор смежных углов

Калькуляторы (Теория чисел)

Калькулятор выражений

Калькулятор упрощения выражений

Калькулятор со скобками

Калькулятор уравнений

Калькулятор суммы

Калькулятор пределов функций

Калькулятор разложения числа на простые множители

Калькулятор НОД и НОК

Калькулятор НОД и НОК по алгоритму Евклида

Калькулятор НОД и НОК для любого количества чисел

Калькулятор делителей числа

Представление многозначных чисел в виде суммы разрядных слагаемых

Калькулятор деления числа в данном отношении

Калькулятор процентов

Калькулятор перевода числа с Е в десятичное

Калькулятор экспоненциальной записи чисел

Калькулятор нахождения факториала числа

Калькулятор нахождения логарифма числа

Калькулятор квадратных уравнений

Калькулятор остатка от деления

Калькулятор корней с решением

Калькулятор нахождения периода десятичной дроби

Калькулятор больших чисел

Калькулятор округления числа

Калькулятор свойств корней и степеней

Калькулятор комплексных чисел

Калькулятор среднего арифметического

Калькулятор арифметической прогрессии

Калькулятор геометрической прогрессии

Калькулятор модуля числа

Калькулятор абсолютной погрешности приближения

Калькулятор абсолютной погрешности

Калькулятор относительной погрешности

Калькуляторы площади геометрических фигур

Площадь квадрата

Площадь прямоугольника

КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ

Генератор Pdf с примерами

Тренажёры решения примеров

Тренажёр таблицы умножения

Тренажер счета для дошкольников

Тренажер счета на внимательность для дошкольников

Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ.

Тренажер решения примеров с разными действиями

Тренажёры решения столбиком

Тренажёр сложения столбиком

Тренажёр вычитания столбиком

Тренажёр умножения столбиком

Тренажёр деления столбиком с остатком

Калькуляторы решения столбиком

Калькулятор сложения, вычитания, умножения и деления столбиком

Калькулятор деления столбиком с остатком

Конвертеры величин

Конвертер единиц длины

Конвертер единиц скорости

Конвертер единиц ускорения

Цифры в текст

Калькуляторы (физика)

Механика

Калькулятор вычисления скорости, времени и расстояния

Калькулятор вычисления ускорения, скорости и перемещения

Калькулятор вычисления времени движения

Калькулятор времени

Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения.

Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния.

Импульс тела. Калькулятор вычисления импульса, массы и скорости

Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы.

Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения

Оптика

Калькулятор отражения и преломления света

Электричество и магнетизм

Калькулятор Закона Ома

Калькулятор Закона Кулона

Калькулятор напряженности E электрического поля

Калькулятор нахождения точечного электрического заряда Q

Калькулятор нахождения силы F действующей на заряд q

Калькулятор вычисления расстояния r от заряда q

Калькулятор вычисления потенциальной энергии W заряда q

Калькулятор вычисления потенциала φ электростатического поля

Калькулятор вычисления электроемкости C проводника и сферы

Конденсаторы

Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе

Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе

Калькулятор вычисления энергии W заряженного конденсатора

Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов

Калькуляторы по астрономии

Вес тела на других планетах

Ускорение свободного падения на планетах Солнечной системы и их спутниках

Генераторы

Генератор примеров по математике

Генератор случайных чисел

Генератор паролей

Транспонирование матрицы — значение, свойства, примеры

Транспонирование матрицы — один из наиболее распространенных методов преобразования матриц в матричных понятиях в линейной алгебре. Транспонирование матрицы получается путем замены строк на столбцы и столбцов на строки для данной матрицы. Это особенно полезно в приложениях, где необходимо получить обратные и сопряженные матрицы.

В этой статье давайте узнаем о транспонировании матрицы, ее определении, свойствах и решенных примерах.

1.	Что такое транспонирование матрицы?
2.	Порядок транспонирования матрицы
3.	Транспонирование квадратной матрицы
4.	Свойства транспонирования матрицы
5.	Транспонирование горизонтальной и вертикальной матрицы
6.	Транспонирование симметричной матрицы
7.	Транспонирование диагональной матрицы
8.	Транспонирование транспонированной матрицы
9.	Определитель транспонирования матрицы
10.	Связь между сопряженной и транспонированной матрицей
11.	Часто задаваемые вопросы о транспонировании матрицы

Что такое транспонирование матрицы?

Транспонирование матрицы получается путем преобразования ее строк в столбцы (или, что то же самое, ее столбцов в строки).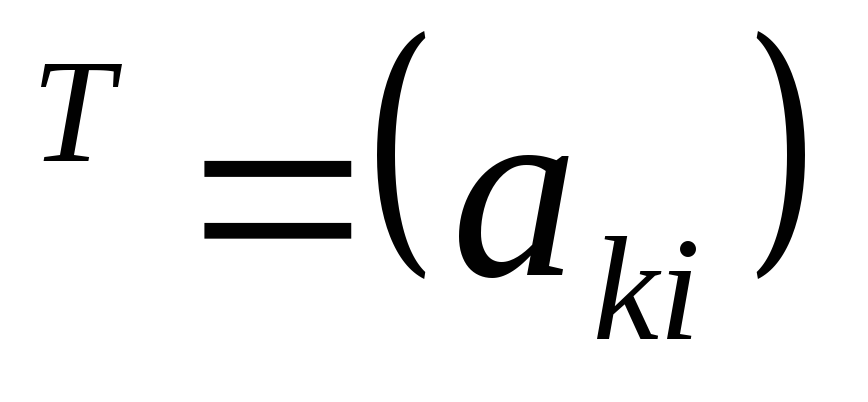 Прямоугольный массив чисел или функций, расположенных в виде строк и столбцов, называется матрицей. Этот массив чисел называется элементами или элементами матрицы.

Здесь для матрицы A элементы первой строки записаны в первый столбец новой матрицы, а элементы второй строки записаны во второй столбец новой матрицы. И эта новая матрица обозначается как A ^T , который представляет собой транспонирование данной матрицы A.

Транспонирование символа матрицы

В линейной алгебре транспонирование матрицы на самом деле является оператором, который переворачивает матрицу по диагонали, переключая строку и столбец индексы матрицы B и создание другой матрицы. Транспонирование матрицы B часто обозначается как B’ или B ^T . Иногда они также обозначаются как B ^tr или Б ^т . Если матрица B имеет порядок m×n, то транспонированная матрица B’ имеет порядок n×m.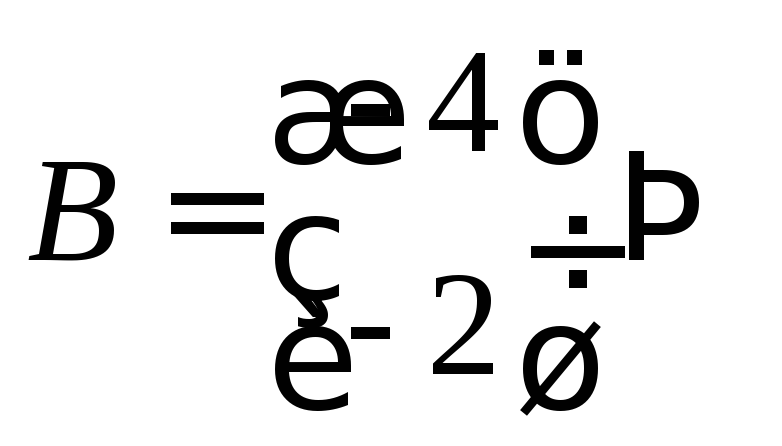

Порядок транспонирования матрицы

Порядок матрицы представляет количество строк и столбцов в данной матрице. Все горизонтальные линии элементов называются строками матрицы, обозначаемой буквой n, а вертикальные линии элементов называются столбцами матрицы, обозначаемой буквой m. Вместе они представляют порядок матрицы, который записывается как n × м. А -й порядок транспонирования данной матрицы записывается как m x n.

Давайте проверим приведенный ниже пример, чтобы лучше понять, как найти транспонирование матрицы.

A = \(\left[\begin{массив}{ll}
-2&5&6\
5 и 2 и 7
\end{array}\right]\)

В приведенном выше примере мы видим, что задана матрица порядка 2 × 3. Элементы первой строки [-2, 5, 6] записаны в первом столбце , а элементы второй строки [5, 2, 7] записываются во второй столбец, чтобы получить транспонированную матрицу. Транспонирование матрицы A равно A ^T и имеет порядок 3 x 2.

A ^T = \(\left[\begin{array}{ll}
-2 и 5\
5 и 2 \\6 и 7
\конец{массив}\справа]\)

Транспонирование квадратной матрицы

Матрица, полученная из данной матрицы B после замены или обращения ее строк в столбцы и столбцов в строки, называется транспонированием матрицы B. Рассмотрим транспонирование квадратных матриц 2 × 2 и 3 × 3.

Транспонирование матрицы 2 × 2

Рассмотрим матрицу 2 × 2 C, после перестановки строк и столбцов результирующая транспонированная матрица C ^T выглядит так:

Таким же образом мы можем найти транспонирование матрицы A как:

\(A=\left[\begin{array}{ll}
1&-2\
3 и -4
\end{array}\right]\)

После перестановки строк и столбцов результирующая транспонированная матрица A ^T выглядит так:

A ^T = \(\left[\begin{array}{ll}
1 и 3 \
-2 и -4
\end{array}\right]\)

Транспонирование матрицы 3 × 3

Рассмотрим матрицу 3 × 3 C:

\(C = \left[\begin{array}{ccc}
c_{11} и c_{12} и c_{13} \\
c_{21} и c_{22} и c_{23} \\
c_{31} и c_{32} и c_{33}
\end{array}\right] \)

После перестановки строк и столбцов результирующая транспонированная матрица C ^T выглядит так:

C ^T = \(\left[\begin{array}{ccc}
c_{11} и c_{21} и c_{31} \\
c_{12} и c_{22} и c_{32} \\
c_{13} и c_{23} и c_{33}
\end{array}\right] \)

Таким же образом мы можем найти транспонирование матрицы A как:

\(A = \left[\begin{array}{ccc}
1&2&-3\
4&-5&6\
7 и 8 и -9
\end{массив}\right] \)

После перестановки строк и столбцов результирующая транспонированная матрица A ^T выглядит так:

A ^T = \(\left[\begin{array}{ccc}
1 и 4 и 7 \
2&-5&8\
-3 и 6 и -9
\конец{массив}\справа] \)

Свойства транспонирования матрицы

Транспонирование матрицы используется в некоторых линейных преобразованиях, поскольку они раскрывают некоторые важные свойства преобразования. Давайте узнаем о некоторых важных свойствах транспонирования матрицы:

• Квадратная матрица B порядка n × n считается ортогональной матрицей только тогда, когда B ^T × B = B × B ^T = I, здесь I — единичная матрица.
• Квадратная матрица B порядка n × n считается симметричной матрицей, если ее транспонирование равно самой себе. т. е. В ^Т = В.
• Квадратная матрица B порядка n × n считается кососимметричной матрицей только тогда, когда ее транспонирование равно ее отрицательному значению. т. е. В ^Т = -Б.
• Транспонирование суммы/разности (B ± C) ^T есть сумма/разность транспонирования матриц B и C, т. е. B ^T ± C ^T = (B ± C) ^T .
• Транспонирование обратимой матрицы B также обратимо, и его инверсия на самом деле является транспонированием обратной исходной матрицы B. Это можно представить как: (B ^T ) ^-1 = (B ^-1 ) ^Т .
• Транспонирование при применении к матрице имеет более высокий приоритет, чем операции умножения и сложения, т. е.
  CB ^T = C(B ^T ) и
  С + Д ^Т = С + (Д ^Т )

Свойство сложения транспонирования матрицы

Рассмотрим две матрицы B и C, транспонирование суммы (B + C) ^T является суммой транспонирования матриц B и C. Это можно представить как ( Б + В) ^Т = Б ^Т + С ^Т . Рассмотрим пример:

B = \(\left[\begin{array}{ll}
2 и 3\
1 и 0
\end{массив}\right]\)

C = \(\left[\begin{массив}{ll}
4&-2\
3 и 5
\end{массив}\right]\)

B + C = \(\left[\begin{массив}{ll}
(2+4) & (3-2) \\
(1+3) и (0+5)
\end{массив}\right]\) = \(\left[\begin{массив}{ll}
6 и 1 \
4 и 5
\end{массив}\right]\)

(B+C) ^T = \(\left[\begin{array}{ll}
6 и 4\
1 и 5
\end{array}\right]\)

Теперь возьмем транспонирование матриц отдельно,

B ^T = \(\left[\begin{array}{ll}
2 и 1 \
3 и 0
\end{массив}\right]\)

C ^T = \(\left[\begin{array}{ll}
4 и 3 \
-2 и 5
\end{массив}\right]\)

B ^T + C ^T =\(\left[\begin{array}{ll}
(2+4) & (1+3) \\
(3-2) и (0+5)
\end{массив}\right]\) = \(\left[\begin{массив}{ll}
6 и 4 \
1 и 5
\end{массив}\right]\)

B ^T + C ^T = \(\left[\begin{array}{ll}
6 и 4 \
1 и 5
\end{array}\right]\)

Из приведенного выше примера видно, что сумма остается одинаковой в обоих случаях. Таким образом, операция транспонирования учитывает сложение.

Транспонирование горизонтальной и вертикальной матрицы

Матрица считается горизонтальной, если количество строк в матрице меньше количества столбцов в этой матрице. И матрица считается вертикальной, когда количество столбцов в матрице меньше, чем количество строк в этой матрице. Рассмотрим горизонтальную матрицу P и вертикальную матрицу Q как:

P = \(\left[\begin{array}{ll}
1 и 2 и 3 \\
4 и 5 и 6
\end{массив}\right]\)

P ^T = \(\left[\begin{массив}{ccc}
1 и 4 \
2 и 5 \
3 и 6
\end{массив}\right] \)

Q = \(\left[\begin{массив}{ccc}
1 и 4 \
2 и 5 \
3 и 6
\end{массив}\right] \)

Q ^T = \(\left[\begin{array}{ll}
1 и 2 и 3 \\
4 и 5 и 6
\end{array}\right]\)

Из приведенных выше двух примеров мы можем видеть, что транспонирование горизонтальной матрицы P приводит к вертикальной матрице P ^T , а транспонирование вертикальной матрицы Q дает горизонтальную матрицу Q ^T .

Транспонирование симметричной матрицы

Квадратная матрица порядка n × n считается симметричной тогда и только тогда, когда она симметрична относительно своей диагонали. Квадратная матрица C размера n x n считается симметричной тогда и только тогда, когда C ^T = C. Рассмотрим две заданные симметричные матрицы A и B:

A = \(\left[\begin{array}{ll}
2&-1\
-1 и 2
\end{массив}\right]\)

A ^T = \(\left[\begin{array}{ll}
2&-1\
-1 и 2
\end{массив}\right]\)

B = \(\left[\begin{массив}{ccc}
2 и 3 и 6 \
3 и 4 и 5 \
6 и 5 и 9
\end{массив}\right] \)

B ^T = \(\left[\begin{array}{ccc}
2 и 3 и 6 \
3 и 4 и 5 \
6 и 5 и 9
\end{array}\right] \)

Из приведенного выше примера видно, что после транспонирования двух матриц A и B они равны своим исходным матрицам, т. Е. A = A ^T и B = В ^Т .

Транспонирование диагональной матрицы

Квадратная матрица порядка n × n считается диагональной матрицей тогда и только тогда, когда все ее элементы, кроме диагональных, равны нулю. Рассмотрим две заданные диагональные матрицы C и D:

C = \(\left[\begin{массив}{ll}
5&0\
0 и -5
\end{массив}\right]\)

C ^T = \(\left[\begin{array}{ll}
5&0\
0 и -5
\end{массив}\right]\)

D = \(\left[\begin{массив}{ccc}
1&0&0\
0 & 2 & 0 \
0 и 0 и 3
\end{массив}\right] \)

D ^T = \(\left[\begin{array}{ccc}
1&0&0\
0 & 2 & 0 \
0 и 0 и 3
\end{array}\right] \)

Из приведенных выше двух примеров видно, что две диагональные матрицы C и D остаются диагональными матрицами даже после применения транспонирования.

Транспонирование транспонированной матрицы

Транспонирование транспонированной матрицы само по себе. т. е. для любой матрицы B (B ^T ) ^T = B. Рассмотрим здесь два примера:

C = \(\left[\begin{array}{ll}
1&-2\
3 и -4
\end{массив}\right]\)

C ^T = \(\left[\begin{array}{ll}
1 и 3 \
-2 и -4
\end{массив}\right]\)

(C ^T ) ^T = \(\left[\begin{array}{ll}
1&-2\
3 и -4
\end{массив}\right]\)

D = \(\left[\begin{массив}{ccc}
1&2&-3\
4&-5&6\
7 и 8 и -9
\end{массив}\right] \)

D ^T = \(\left[\begin{array}{ccc}
1 и 4 и 7 \
2&-5&8\
-3 и 6 и -9
\end{массив}\right] \)

(D ^T ) ^T = \(\left[\begin{array}{ccc}
1&2&-3\
4&-5&6\
7 и 8 и -9
\end{array}\right] \)

Из приведенных выше двух примеров видно, что транспонирование уже транспонированной матрицы дает исходную матрицу.

Определитель транспонирования матрицы

Определитель транспонированной матрицы A равен определителю самой матрицы A.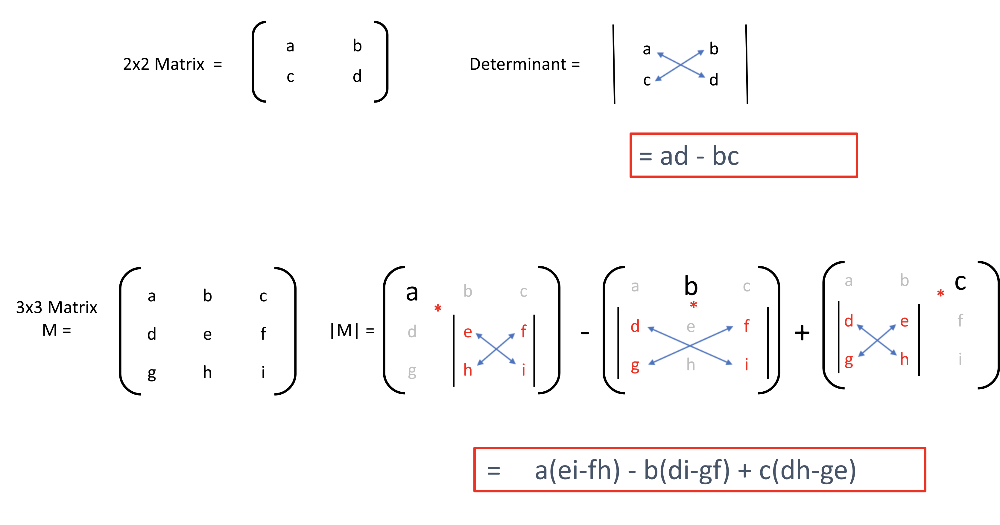 т. е. det A = det A ^T для любой квадратной матрицы A. Для получения дополнительной информации вы можете нажать здесь.

Связь между сопряженной и транспонированной матрицей

Сопряженная квадратная матрица B является транспонированной кофакторной матрицей C исходной B. Связь между сопряженной исходной матрицей B и транспонированной кофакторной матрицей C может быть представлена ​​как adj(B) = ( В) ^Т . Рассмотрим этот пример:

Рассмотрим матрицу 2×2 D:

D = \(\left[\begin{array}{ll}
3 и 6 \
-4 и 8
\end{array}\right]\)

Младшая матрица M может быть представлена ​​как:

\(M=\left[\begin{array}{ll}
8&-4\
6 и 3
\end{array}\right]\)

Матрица кофакторов C может быть представлена ​​как:

\(C=\left[\begin{array}{ll}
8 и 4 \
-6 и 3
\end{array}\right]\)

Транспонирование C ^T матрицы кофакторов может быть показано как:

adj(D) = C ^T = \(\left[\begin{array {ll}
8&-6\
4 и 3
\end{array}\right]\)

Важные замечания по транспонированию матрицы:

• Транспонирование матрицы на самом деле является оператором, который переворачивает матрицу по ее диагонали, меняя местами индексы строк и столбцов матрицы B. и изготовление другой матрицы.
• Транспонирование матрицы B часто обозначается либо B’, либо B ^T . Иногда их также обозначают как B ^tr или B ^t .
• Если матрица B имеет порядок m x n, то транспонированная матрица B’ имеет порядок n x m.

☛ Статьи по теме:

• Калькулятор матриц
• Формула матрицы
• Калькулятор диагональной матрицы
• Калькулятор матрицы транспонирования

Часто задаваемые вопросы о транспонировании матрицы

Что означает транспонирование матрицы?

Транспонирование матрицы — это матрица, полученная после замены или преобразования ее строк в столбцы (или столбцов в строки). Транспонирование B обозначается как B ^T .

Как найти транспонирование матрицы?

Транспонирование любой заданной матрицы можно вычислить, поменяв местами ее строки и столбцы. Рассмотрим матрицу 2 × 2 B:

\(A=\left[\begin{массив}{ll}
1&-2\
3 и 7
\end{array}\right]\)

После перестановки строк и столбцов результирующая транспонированная матрица C ^T выглядит так:

A ^T = \(\left[\begin{array}{ ll}
1 и 3 \
-2 и 7
\end{array}\right]\)

Что такое свойство сложения при транспонировании матрицы?

Согласно аддитивному свойству транспонирования матрицы, для двух матриц B и C транспонирование суммы (B + C) ^T представляет собой сумму транспонирований матриц B и C. Это можно представить как (B + C) ^T = B ^T +C ^T .

Что такое свойство умножения транспонирования матрицы?

Согласно свойству умножения транспонирования матрицы, транспонирование при применении к матрице имеет более высокий приоритет, чем операции умножения и сложения, т. е. CB ^T = C(B ^T ) и C + D ^T = С + (Д ^Т )

Каковы различные свойства транспонирования матрицы?

Вот различные свойства транспонирования матрицы:

• Квадратная матрица B порядка n × n считается ортогональной матрицей, только когда B × B ^T = I, здесь I тождество матрица.
• Квадратная матрица B порядка n × n считается кососимметричной матрицей только тогда, когда она транспонирована B ^T = -B, т. е. равна своей отрицательной.
• Транспонирование разности (B — C) ^T — это разность транспонирования матриц B и C. B ^T — C ^T = (B — C) ^T
• Транспонирование обратимой матрицы B также обратимо, а ее инверсия B ^-1 на самом деле является транспонированием обратной исходной матрицы B. Это можно представить как: (B ^T ) ^-1 = (Б ^-1 ) ^Т .
• Транспонирование при применении к матрице имеет более высокий приоритет, чем операции умножения и сложения, т. е. CB ^T = C(B ^T ) и C + D ^T = C + (D ^T )

Что является определителем транспонирования матрицы?

Определитель транспонированной квадратной матрицы порядка n×n равен определителю матрицы, т.е. |B ^T | = |В|.

Что такое транспонирование квадратной матрицы?

Для любой квадратной матрицы порядка n×n транспонирование применяется к матрице следующим образом. Рассмотрим матрицу 2 × 2 C:

\(C=\left[\begin{массив}{ll}
с_{11} и с_{12} \\
c_{21} и c_{22}
\end{array}\right]\)

После перестановки строк и столбцов результирующая транспонированная матрица C ^T выглядит так:

C ^T = \(\left[\begin{array}{ ll}
с_{11} и с_{21} \\
c_{12} и c_{22}
\end{array}\right]\)

Как найти обратную матрицу методом транспонирования?

Вот шаги, которые нужно выполнить, чтобы вычислить обратную матрицу D с помощью метода транспонирования:

• Найдите определитель |D|. Если |Д| = 0, то обратное не существует. Только если |D| ≠ 0, существует обратное.
• Найдите минорную матрицу M всех элементов матрицы D
• Найдите матрицу кофакторов C всех минорных элементов матрицы M
• Найдите прил D путем транспонирования матрицы кофакторов C
• Затем найдите обратную матрицу D как D ^-1 = (1/|D|) × adj(D)
• Проверьте правильность обратного выражения, проверив его как D × D ^-1 = I, где I — единичная матрица.

Транспонирование матрицы

90 008

arm_status	arm_mat_trans_f16 (const arm_matrix_instance_f16 *pSrc, arm_matrix_instance_f16 *p Dst)
	Транспонирование матрицы с плавающей запятой. Подробнее…
arm_status	arm_mat_trans_f32 (const arm_matrix_instance_f32 *pSrc, arm_matrix_instance_f32 *pDst)
	Транспонирование матрицы с плавающей запятой. Подробнее…
arm_status	arm_mat_trans_f64 (const arm_matrix_instance_f64 *pSrc, arm_matrix_instance_f64 *pDst) 90 010
	Транспонирование матрицы с плавающей запятой. Подробнее…
arm_status	arm_mat_trans_q15 (const arm_matrix_instance_q15 *pSrc, arm_matrix_instance_q15 *pDst)
	Транспонирование матрицы Q15. Подробнее…
arm_status	arm_mat_trans_q31 (const arm_matrix_instance_q31 *pSrc, arm_matrix_instance_q31 *pDst) 90 010
	Транспонирование матрицы Q31. Подробнее…
arm_status	arm_mat_trans_q7 (const arm_matrix_instance_q7 *pSrc, arm_matrix_instance_q7 *pDst)
	Транспонирование матрицы Q7. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт