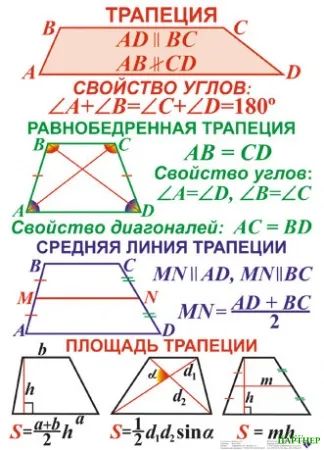
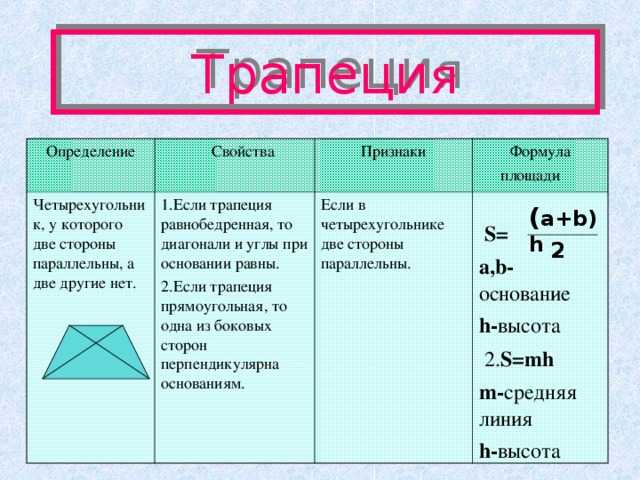
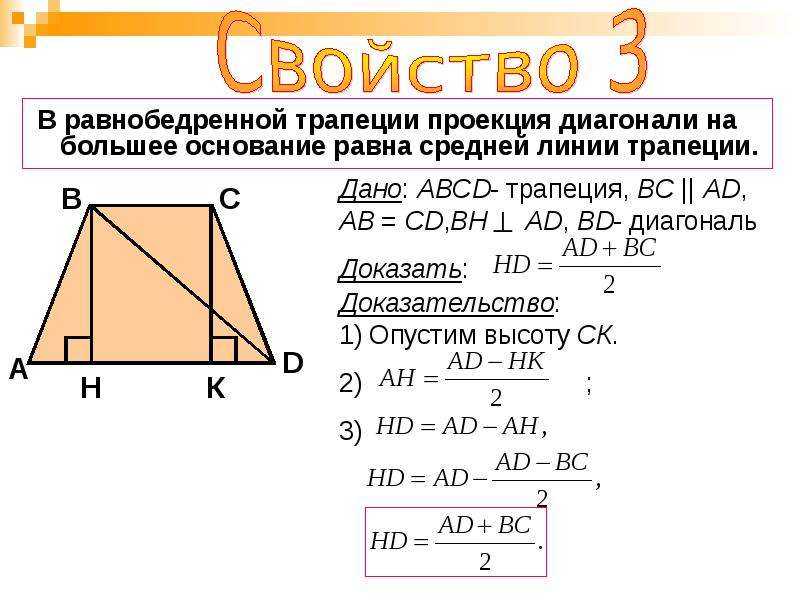
Определение, признаки и свойства произвольной, равнобедренной и прямоугольной трапеции
В курсе геометрии за 8-й класс подразумевается изучение свойств и признаков выпуклых четырёхугольников. К ним относятся параллелограммы, частными случаями которых являются квадраты, прямоугольники и ромбы, и трапеции. И если решение задач на различные вариации параллелограмма чаще всего не вызывает сильных затруднений, то разобраться, какой четырёхугольник называется трапецией, несколько сложнее.
Содержание
Определение и виды
В отличие от других четырёхугольников, изучаемых в школьной программе, трапецией принято называть такую фигуру, две противоположные стороны которой параллельны друг другу, а две другие — нет. Существует и другое определение: это четырёхугольник с парой сторон, которые не равны между собой и параллельны.
Различные виды указаны на рисунке ниже.
На изображении под номером 1 изображена произвольная трапеция. Номером 2 обозначен частный случай — прямоугольная трапеция, одна из сторон которой перпендикулярна её основаниям. Последняя фигура — тоже особый случай: это равнобедренная (равнобокая) трапеция, т. е. четырёхугольник с равными боковыми сторонами.
Номером 2 обозначен частный случай — прямоугольная трапеция, одна из сторон которой перпендикулярна её основаниям. Последняя фигура — тоже особый случай: это равнобедренная (равнобокая) трапеция, т. е. четырёхугольник с равными боковыми сторонами.
Важнейшие свойства и формулы
Для описания свойств четырёхугольника принято выделять определённые элементы. В качестве примера можно рассмотреть произвольную трапецию ABCD.
В её состав входят:
- основания BC и AD — две стороны, параллельные по отношению друг к другу,
- боковые стороны AB и CD — два непараллельных элемента,
- диагонали AC и BD — отрезки, соединяющие противоположные вершины фигуры,
- высота трапеции CH — перпендикулярный основаниям отрезок,
- средняя линия EF — линия, соединяющая середины боковых сторон.
Основные свойства элементов
Чтобы решить задачи по геометрии или доказать какие-либо утверждения, наиболее часто используют свойства, которые связывают различные элементы четырёхугольника. Они формулируются следующим образом:
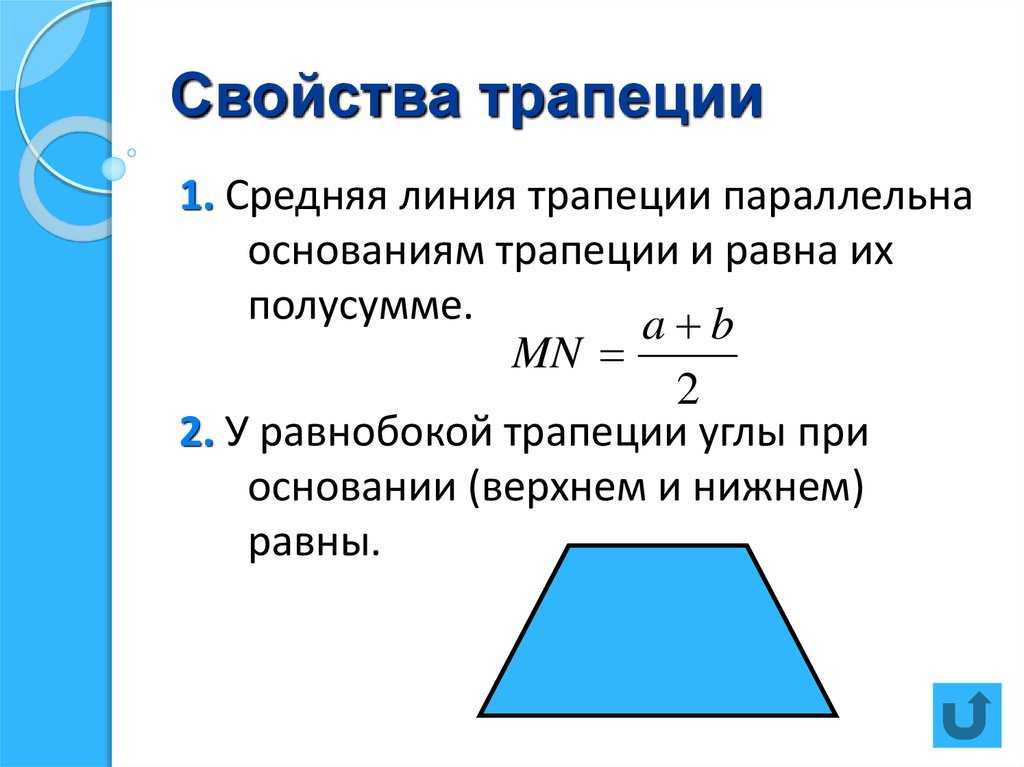
- Средняя линия всегда проходит параллельно обоим основаниям фигуры и численно равна их полусумме: EF = (BC + AD)/2.
- Точка пересечения диагоналей фигуры разделяет их с таким же соотношением длины, с каким относятся основания трапеции: AD : BC = AO : CO = DO : BO.
- Основание можно вычислить, зная длину второго основания и средней линии: BC = 2 · EF — AD, AD = 2 · EF — BC.
- Боковые стороны вычисляются, если известна высота фигуры и синус угла при основании: AB = CH / sinA, CD = CH / sinD.
- Для расчёта высоты необходимо знать, чему равна боковая сторона и прилегающий угол: CH = AB · sinA = CD · sinD.
Кроме того, часто полезно знать и применять следующие утверждения:
- Биссектриса, проведённая из произвольного угла, отделяет на основании отрезок, длина которого равна боковой стороне фигуры.
- При проведении диагоналей образуются 4 треугольника, из них 2 треугольника, образованных основаниями и отрезками диагоналей, обладают подобием, а оставшаяся пара имеет одинаковую площадь.
- Через точку пересечения диагоналей O, середины оснований, а также точку, в которой пересекаются продолжения боковых сторон, можно провести прямую.
Вычисление периметра и площади
Периметр рассчитывается как сумма длин всех четырёх сторон (аналогично любой другой геометрической фигуре):
P = AD + BC + AB + CD.
Есть несколько способов, как можно рассчитать площадь трапеции по формуле. Следует выбрать из них наиболее подходящий вариант, опираясь на то, какие данные известны по условию задачи.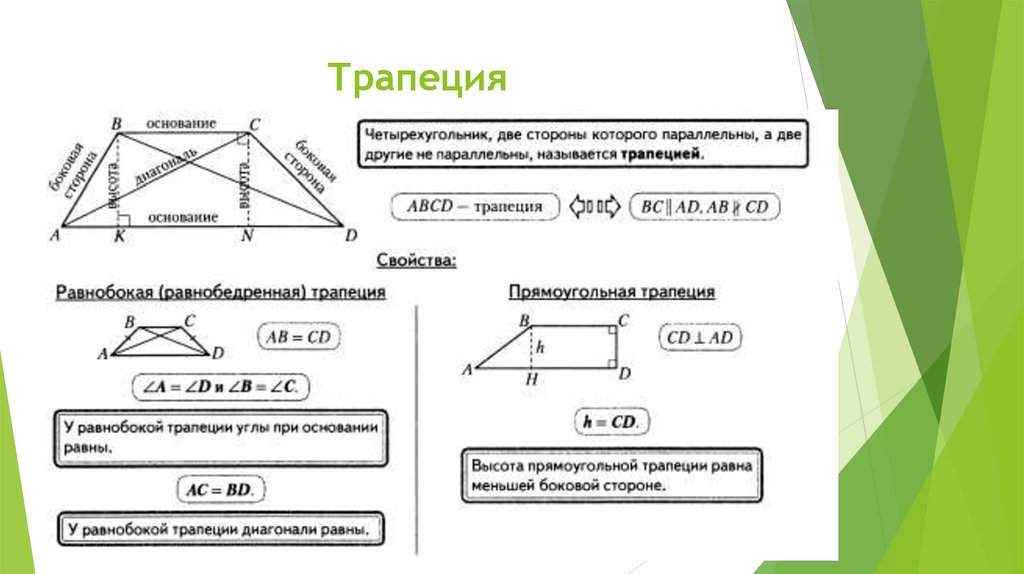
Вписанная и описанная окружность
Окружность возможно описать около трапеции только в том случае, когда боковые стороны четырёхугольника равны.
Чтобы вычислить радиус описанной окружности, необходимо знать длины диагонали, боковой стороны и большего основания. Величина p, используемая в формуле, рассчитывается как полусумма всех вышеперечисленных элементов: p = (a + c + d)/2.
Для вписанной окружности условие будет следующим: сумма оснований должна совпадать с суммой боковых сторон фигуры. Радиус её можно найти через высоту, и он будет равен r = h/2.
Частные случаи
Рассмотрим часто встречаемый случай — равнобокую (равностороннюю) трапецию. Её признаки — равенство боковых сторон или равенство противолежащих углов. К ней применимы все утверждения, которые характерны для произвольной трапеции.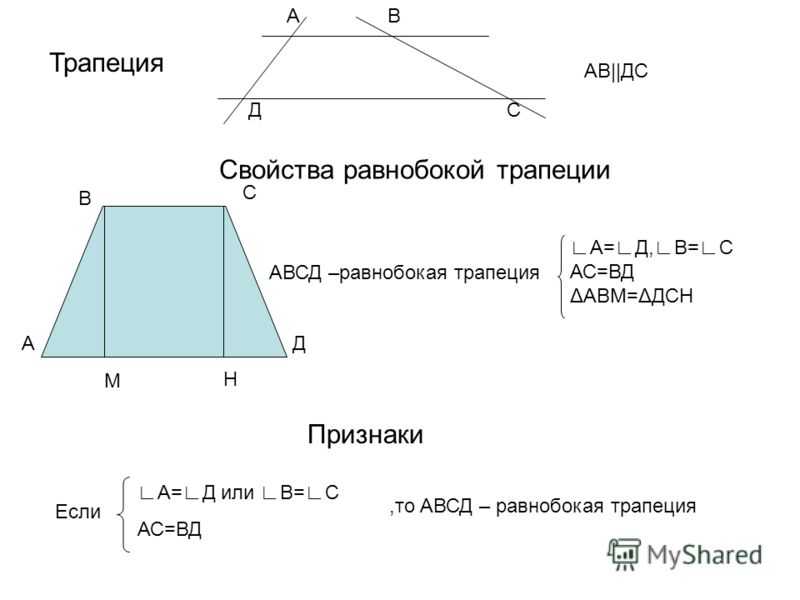 Другие свойства равнобедренной трапеции:
Другие свойства равнобедренной трапеции:
- Прямая, которая проходит через середины оснований фигуры, пересекает их под углом 90 градусов.
- Углы, лежащие при любых основаниях, попарно равны.
- Длины диагоналей совпадают.
- Высота будет равна средней линии, если диагонали проходят перпендикулярно друг к другу.
- Высота, опущенная из вершины к основанию, делит его на 2 отрезка, длина большего вычисляется как половина суммы оснований, а длина меньшего — как половина разности.
Прямоугольная трапеция встречается в задачах не так часто. Её признаки — наличие двух смежных углов, равных 90 градусов, и наличие боковой стороны, перпендикулярной основаниям. Высота в таком четырёхугольнике одновременно является одной из его сторон.
Все рассмотренные свойства и формулы обычно используются для решения планиметрических задач. Однако также их приходится применять в некоторых задачах из курса стереометрии, например, при определении площади поверхности усечённой пирамиды, внешне напоминающей объёмную трапецию.
Трапеция и ее свойства. | Презентация к уроку по геометрии (8 класс) на тему:
Слайд 1
Трапеция и ее свойства. Работу выполнила учитель математики Снегурова А.М. МБОУ СОШ №5 г-к АНАПА. Тот, кто учится самостоятельно, достигнет в семь раз больше того, кому все разъясняется. Артур Гитерман .
Слайд 2
Элементы трапеции Трапеция — четырехугольник, у которого две стороны параллельны, а две стороны не параллельны. Элементы трапеции: Основания трапеции — параллельные стороны Боковые стороны — две другие стороны Средняя линия — отрезок, соединяющий середины боковых сторон. Вторая средняя линия — отрезок, соединяющий середины оснований. Диагонали трапеции – это отрезки, соединяющие противоположные вершины трапеции. Высота трапеции — это расстояние между основаниями .
Слайд 3
a — нижнее основание b — верхнее основание α , β — углы между диагоналями h — высота трапеции m — средняя линия трапеции S — площадь трапеции d 1 , d 2 — диагонали трапеции
Слайд 4
Сумма углов при каждой боковой стороне равна 180 0 ∠1+∠2=180 ∘ ∠3+∠4=180∘
Слайд 5
Биссектриса любого угла отсекает на ее основании (или на ее продолжении)отрезок, равный боковой стороне .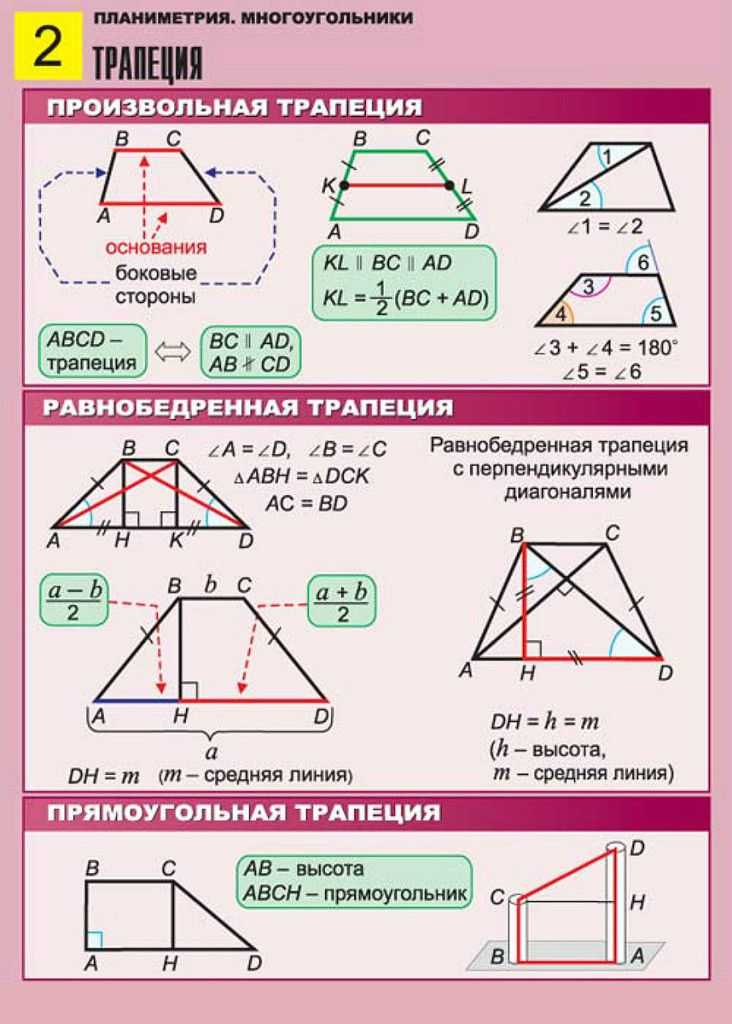 Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом.
Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом.
Слайд 6
Средняя линия трапеции равна полусумме оснований и параллельна им. a b m = =
Слайд 7
Если сумма углов при любом основании трапеции равна 90 градусов, то отрезок, соединяющий середины оснований равен их полуразности : В А С М D K
Слайд 8
Средняя линия
Слайд 9
Линия, проходящая через точку пересечения диагоналей Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен среднему гармоническому длин оснований трапеции (формула Буракова ). MN = M N a b
Слайд 10
Линия, делящая площадь трапеции на равновеликие части
Слайд 11
В трапеции с перпендикулярными диагоналями: FH = S ABCD = h 2 если BF = FC и AH = HD Если провести отрезок, концы которого лежат на основаниях трапеции и проходящий через точку пересечения диагоналей трапеции ,то соотношение составляющих его отрезков от стороны основания до точки пересечения диагоналей будет равно соотношению оснований трапеции. Это справедливо и для диагоналей и для высоты. А площадь такой трапеции равна квадрату высоты : = =
Это справедливо и для диагоналей и для высоты. А площадь такой трапеции равна квадрату высоты : = =
Слайд 12
В равнобедренной трапеции равны не только боковые стороны, но и диагонали: AC = BD h = m Если в равнобедренной трапеции диагонали перпендикулярны, то средняя линия равна высоте трапеции.
Слайд 13
В любой трапеции следующие четыре точки лежат на одной прямой: 1) E – точка пересечения продолжений боковых сторон; 2)F и H – середины оснований; 3) G – точка пересечения диагоналей.
Слайд 14
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований . Таким образом, любая трапеция может быть достроена до треугольника. При этом: Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными. Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Слайд 15
Высота, проведенная из вершины тупого угла в равнобокой трапеции делит большее основание на два отрезка:
Слайд 16
Треугольники, образованные основаниями и диагоналями, подобны. Их коэффициент подобия k равен отношению большего основания к меньшему снованию трапеции.
Их коэффициент подобия k равен отношению большего основания к меньшему снованию трапеции.
Слайд 17
Если в произвольной трапеции сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность: a+b = c+d Диаметр вписанной в трапецию окружности равен высоте трапеции, радиус — половине высоты: d=h или r = Если в трапецию можно вписать окружность, то квадрат высоты равен произведению оснований h 2 = BC · AD h A B C D
Слайд 18
Площадь трапеции равна отношению квадрата радиуса вписанной окружности умноженное на четыре и синуса острого угла между боковой стороной и основанием S = 4r 2 S in α
Слайд 19
В трапецию можно вписать окружность, если: сумма длин боковых сторон равна сумме длин оснований: AB + CD = BC + AD ; трапеция равнобедренная; боковая сторона трапеции видна из центра вписанной окружности под прямым углом.
Слайд 20
Формулы в помощь: * C редняя линия через площадь и высоту: *Высота через площадь и длины оснований: *Высота через площадь и длину средней линии: *Площадь через среднюю линию и высоту S= h·m * В равнобедренной трапеции длина диагонали равна d = где с – боковая сторона, a и b – основания или d = *Длина основания через среднюю линию и другое основание a = 2m — b и b = 2m — a
Слайд 21
Описанная окру́жность многоугольника — окружность , содержащая все вершины многоугольника.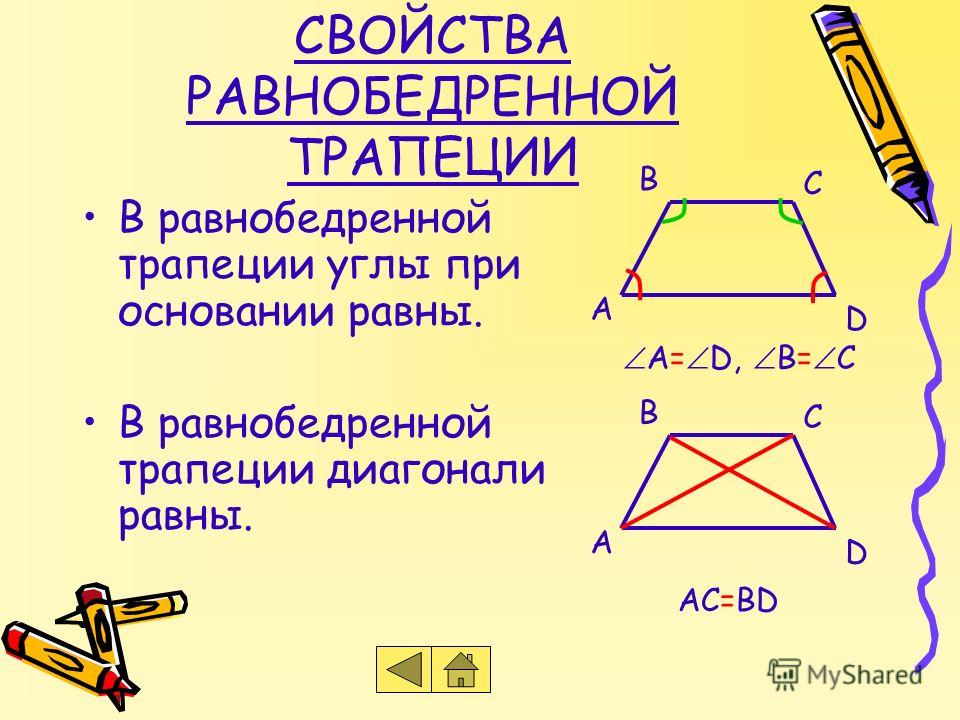 Центром является точка (принято обозначать {O}) пересечения серединных перпендикуляров к сторонам многоугольника . Радиус окружности, описанной около трапеции, можно найти как радиус окружности, описанной около из одного из двух треугольников, на которые трапецию делит ее диагональ. Где находится центр окружности, описанной около трапеции? Это зависит от угла между диагональю трапеции и ее боковой стороной.
Центром является точка (принято обозначать {O}) пересечения серединных перпендикуляров к сторонам многоугольника . Радиус окружности, описанной около трапеции, можно найти как радиус окружности, описанной около из одного из двух треугольников, на которые трапецию делит ее диагональ. Где находится центр окружности, описанной около трапеции? Это зависит от угла между диагональю трапеции и ее боковой стороной.
Слайд 22
Окружность, описанная около трапеции. Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180º. Отсюда следует, что вписать в окружность можно только равнобокую трапецию . Если диагональ трапеции перпендикулярна ее боковой стороне, то центр окружности, описанной около трапеции, лежит на середине ее большего основания. Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания: Радиус описанной окружности — точка пересечения серединных перпендикуляров с сторонам трапеции.
Трапеция — Недвижимость | Формулы | Определение
LearnPracticeDownload
Трапеция — это четырехугольник, в котором одна пара противоположных сторон параллельна.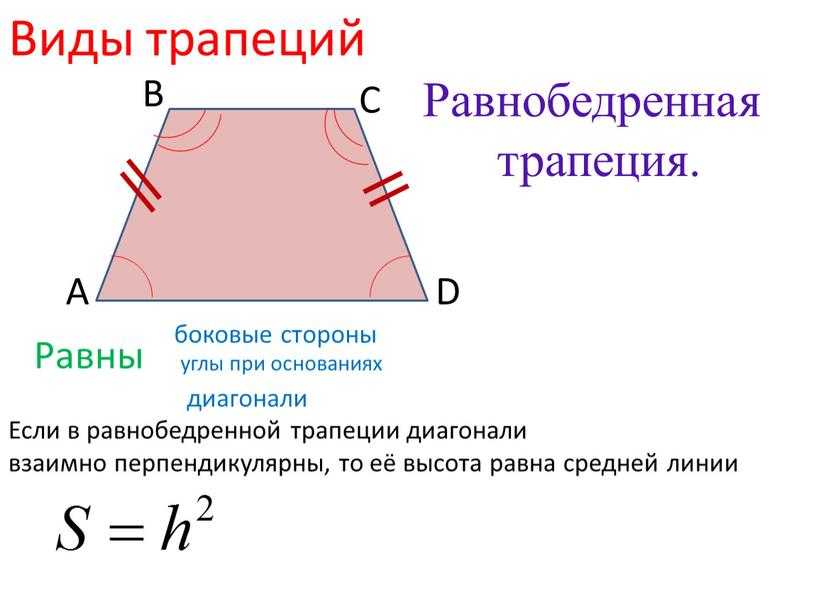 Давайте узнаем больше об определении трапеции, свойствах трапеции, различных типах трапеций, углах трапеции и диагоналях трапеции, а также некоторых примерах трапеций.
Давайте узнаем больше об определении трапеции, свойствах трапеции, различных типах трапеций, углах трапеции и диагоналях трапеции, а также некоторых примерах трапеций.
| 1. | Что такое трапеция в математике? |
| 2. | Типы трапеций |
| 3. | Свойства трапеции |
| 4. | Формулы трапеции |
| 5. | Часто задаваемые вопросы о трапеции |
Что такое трапеция в математике?
Трапеция представляет собой двумерный четырехугольник с одной парой параллельных сторон. Параллельные стороны трапеции называются «основаниями», а непараллельные стороны известны как «ножки» трапеции.
Трапеция Определение
Трапеция представляет собой замкнутую плоскую фигуру с четырьмя сторонами, в которой одна пара противоположных сторон параллельна. Обратите внимание на фигуру трапеции, приведенную ниже, которая показывает трапецию WZYX, в которой WZ параллельна XY, и они являются основаниями, а WX и ZY являются сторонами трапеции.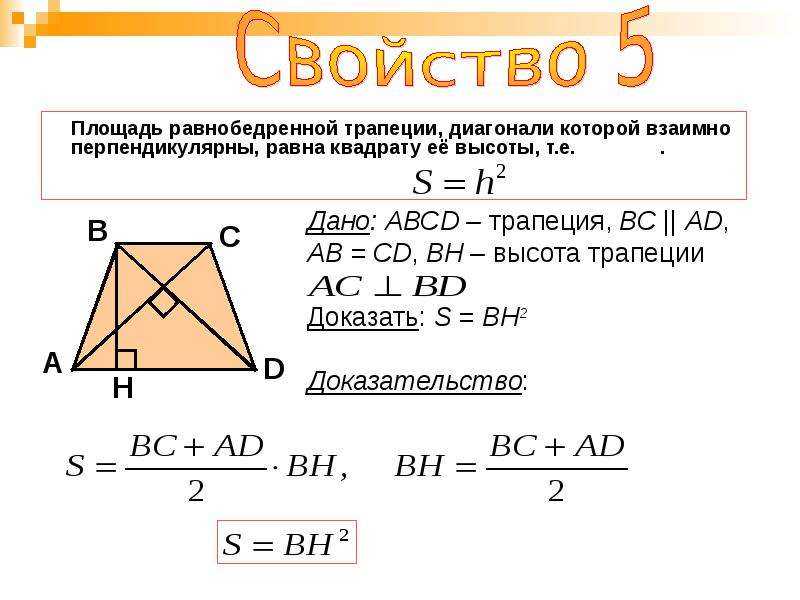
Типы трапеций
Существуют в основном три различных типа трапеций, которые приведены ниже:
- Равнобедренная трапеция
- Лестничная трапеция
- Правая трапеция
Трапеции классифицируются на основе длины ножек или измерения их углов. Определение каждого типа трапеции вместе с ее формой дано ниже.
Свойства трапеции
У каждого четырехугольника есть свои свойства, которые делают его узнаваемым и отличным от остальных. Эти свойства дают больше информации о геометрической конструкции формы. Основные свойства трапеции перечислены ниже:
- Трапеция — это двухмерная фигура.
- Основания трапеции параллельны друг другу.
- Диагонали трапеции всегда пересекаются.
- Сумма смежных внутренних углов равна 180°.
- Сумма всех внутренних углов трапеции всегда равна 360°.
Углы трапеции
В трапеции 4 внутренних угла, сумма которых составляет 360°, а сумма смежных внутренних углов составляет 180°.
Диагонали трапеции
Поскольку трапеция является четырехугольником, у нее 2 диагонали, и обе они пересекаются.
Формулы трапеций
Формулы трапеции в основном связаны с площадью трапеции и периметром трапеции. Возьмем в качестве примера диаграмму трапеции, в которой параллельные стороны обозначены как «a» и «b» соответственно, а высота (высота) обозначена как «h». Обратите внимание на трапецию ABCD, приведенную ниже, чтобы понять формулы трапеции, приведенные после этого.
- Формула, которая используется для нахождения площади трапеции
- Периметр трапеции можно вычислить, сложив длины всех 4-х сторон. Это означает, что формула, которая используется для нахождения периметра трапеции, выражается следующим образом.
 Периметр трапеции = Сумма всех 4 сторон . На этом рисунке это можно записать как Периметр трапеции ABCD = AB + BC + CD + DA.
Периметр трапеции = Сумма всех 4 сторон . На этом рисунке это можно записать как Периметр трапеции ABCD = AB + BC + CD + DA.
☛ Похожие статьи
Проверьте эти интересные статьи, связанные с концепцией формы трапеции в геометрии.
- Четырехугольники
- Трапеция
- Площадь трапеции
- Формула трапеции
- Калькулятор площади трапеции
- Равнобедренная трапеция
Примеры трапеций
Пример 1: Укажите верно или неверно относительно свойств трапеции:
а.) Все квадраты являются трапециями.
б.) Трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна.
Решение:
а.) Верно, что все квадраты являются трапециями, потому что у квадрата противоположные стороны параллельны, поэтому он удовлетворяет этому свойству трапеции.

б.) Верно, трапеция – это четырехугольник, у которого одна пара противоположных сторон параллельна.
Пример 2: Найдите четвертый угол прямой трапеции, если один из заданных углов равен 60°.
Решение: Как мы знаем, в прямой трапеции 2 прямых угла и сумма всех внутренних углов трапеции всегда равна 360°.
Итак, если один из заданных углов равен 60°, пусть недостающий угол равен x°. Четвертый угол можно рассчитать как x° + 90° + 90° + 60° = 360°.
⇒ х° = 360° — (90° + 90° + 60°) = 120°. Следовательно, мера четвертого угла равна 120°.Пример 3: Найдите длину четвертой стороны трапеции, если остальные три стороны имеют размеры 10 единиц, 12 единиц и 7 единиц, а периметр равен 40 единицам.
Решение: Как известно, периметр трапеции равен сумме всех ее сторон. Пусть недостающая длина стороны будет «a». Таким образом, периметр равен 40 = 10 + 12 + 7 + а.

⇒ а = 40 — (10 + 12 + 7) = 11 единиц. Следовательно, длина четвертой стороны равна 11 единицам.
перейти к слайдуперейти к слайдуперейти к слайду
Хотите создать прочную основу в математике?
Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.
Записаться на бесплатный пробный урок
Практические вопросы по трапеции
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о трапеции
Что такое форма трапеции?
Трапеция представляет собой двумерный четырехугольник, имеющий одну пару параллельных сторон. Параллельные стороны трапеции известны как «основания», а непараллельные стороны называются катетами трапеции. Он выглядит как треугольник, который срезан сверху.
Как найти площадь трапеции?
Площадь трапеции можно рассчитать по формуле Площадь трапеции = 1/2 × Сумма параллельных сторон × высота. Это означает, что если мы знаем длину параллельных сторон и высоту, мы можем найти площадь трапеции.
Это означает, что если мы знаем длину параллельных сторон и высоту, мы можем найти площадь трапеции.
Является ли трапеция четырехугольником?
Да, трапеция — четырехугольник. У него четыре стороны, четыре вершины и четыре угла. Сумма всех четырех внутренних углов трапеции равна 360 градусов.
Имеет ли трапеция параллельные стороны?
Да, у трапеции одна пара параллельных сторон. Эти параллельные стороны называются основаниями трапеции.
Может ли трапеция иметь прямой угол?
Да, трапеция может иметь прямой угол. Трапеция с парой прямых углов называется прямой трапецией.
Каковы свойства трапеции?
Характеристики трапеции приведены ниже:
- Трапеция представляет собой двумерную форму и относится к категории четырехугольников.
- В трапеции есть одна пара параллельных сторон, и эти стороны называются основаниями.
- У трапеции 2 диагонали всегда пересекаются.
- Сумма смежных внутренних углов трапеции равна 180°.

- Сумма внутренних углов трапеции всегда равна 360°.
Какая формула площади трапеции?
Формула, которая используется для нахождения площади трапеции, выражается как Площадь трапеции = 1/2 × Сумма параллельных сторон × высота.
Каковы свойства равнобедренной трапеции?
Равнобедренная трапеция – это та, у которой катеты, то есть непараллельные стороны, равны между собой.
В чем разница между трапецией и трапецией?
Трапеция также известна как трапеция. Они относятся к четырехстороннему многоугольнику, имеющему одну пару параллельных сторон и одну пару непараллельных сторон.
Сколько составляют углы трапеции?
В трапеции 4 внутренних угла, сумма которых составляет 360°, а сумма смежных внутренних углов составляет 180°.
Является ли трапеция параллелограммом?
Нет, трапеция не является параллелограммом, потому что у нее только 1 пара параллельных сторон. Тогда как параллелограмм имеет 2 пары параллельных сторон.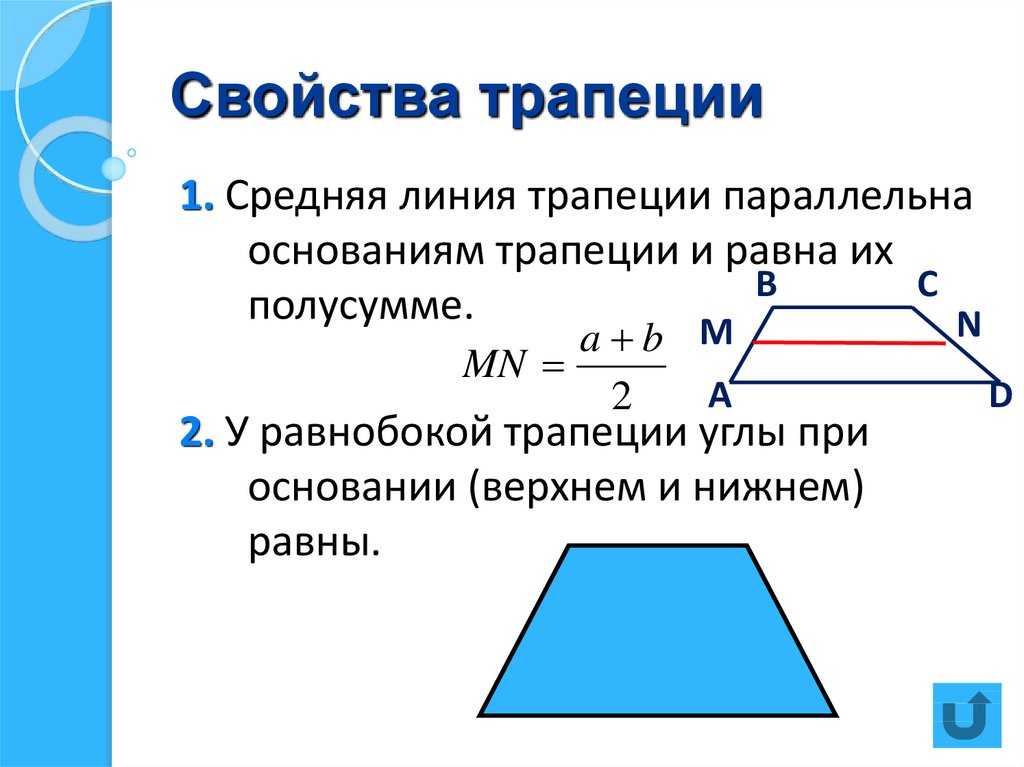
Как выглядит трапеция?
Трапеция выглядит как треугольник, срезанный сверху. Попробуйте нарисовать треугольник и разрезать его горизонтально посередине, и вы увидите форму трапеции на нижнем рисунке, который образовался.
Каковы свойства угла трапеции?
Вот список свойств углов трапеции:
- В трапеции 4 внутренних угла, сумма которых равна 360°.
- Сумма смежных внутренних углов равна 180°.
- Если конкретная трапеция имеет одну пару прямых углов, то она называется прямоугольной трапецией.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочие листы трапеции
Рабочие листы по математике и
наглядный курс
Определение, типы, свойства, формулы, примеры и ответы на часто задаваемые вопросы
Трапеция представляет собой многоугольник с четырьмя сторонами, т. е. четырехугольник. Трапеция — это особый четырехугольник, у которого только одна пара параллельных сторон. Трапеция — это двухмерная фигура, которая выглядит как стол. Трапеция произошла от греческого слова «трапеция», что означает стол.
Трапеция произошла от греческого слова «трапеция», что означает стол.
Трапеция представляет собой двумерный четырехугольник замкнутой формы, имеющий пару параллельных противоположных сторон. Параллельные стороны трапеции называются основаниями, а непараллельные стороны трапеции – катетами. У трапеции четыре стороны и четыре угла. Параллелограмм также называют трапецией с двумя параллельными сторонами.
На приведенном выше рисунке a и b — основания трапеции, а h — высота трапеции.
Types of TrapeziumBased on the sides and the angles, the trapezium is of three types:
- Scalene Trapezium
- Isosceles Trapezium
- Right Trapezium
Isosceles Trapezium
The trapezium которая имеет одинаковую длину катетов, называется равнобедренной трапецией, т.е. у равнобедренной трапеции две непараллельные стороны равны.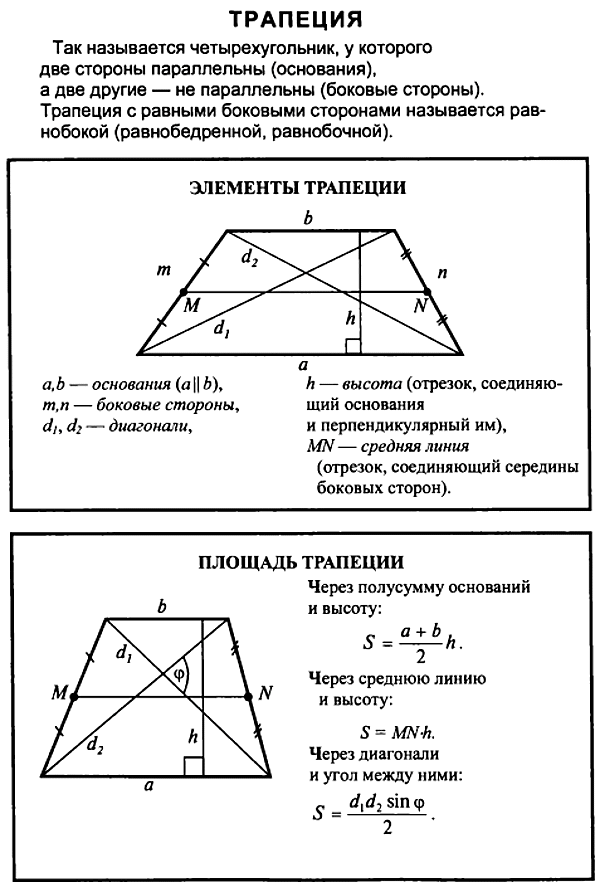
Трапеция, у которой все стороны не равны, называется разносторонней трапецией. В разносторонней трапеции нет двух равных углов.
Трапеция, имеющая пару прямых углов, смежных друг с другом, называется прямой трапецией.
Неправильная трапеция
Трапеция имеет одну пару параллельных сторон, а две другие стороны не параллельны. В правильной трапеции две другие непараллельные стороны равны, а в случае неправильной трапеции две непараллельные противоположные стороны не равны.
Свойства трапеции
- В трапеции основания параллельны друг другу. Пример – Стороны AB и CD параллельны друг другу, как показано на рисунке.
- Смежные внутренние углы трапеции в сумме составляют 180°. Пример – Имеются две пары внутренних углов. Одна пара — это ∠ A и ∠ D, тогда как другая пара — это ∠ B и ∠ C.
 Сумма каждой пары внутренних углов равна 180 ° .
Сумма каждой пары внутренних углов равна 180 ° . - Сумма всех внутренних углов трапеции всегда равна 360°. Пример – На рисунке ∠A+∠D равно 180°, а ∠B+∠C равно 180°. Следовательно, ∠A+∠D +∠B+∠C = 360°.
- Длина обеих диагоналей трапеции одинакова.
- В трапеции обе диагонали пересекаются.
- У трапеции ровно одна пара противоположных сторон параллельна.
Формулы трапеции
Важные формулы трапеции:
- Площадь трапеции = ½ (сумма параллельных сторон) × (расстояние между параллельными сторонами)
- Периметр трапеции = сумма всех четырех сторон соответственно, а его высота равна h.
Теперь площадь трапеции можно вычислить, найдя среднее значение оснований и умножив его результат на высоту.
Отсюда
Площадь трапеции = ((a +b)/2) × h
, где
A
H — это высотаобласть Isosceles Trapezium
Let At Atte Att Atte Att Atta Let At Att Atte Att Att Att Atta Let Att Att Atte Att Atte Att Att At b — длина параллельных сторон трапеции ABCD, где a и b — основания трапеции и a>b.

Теперь, поскольку это равнобедренная трапеция, c — это длина двух непараллельных сторон, а h — высота трапеции.
Npw, AB = a, CD = b, BC = AD = c
В прямоугольном треугольнике, AED
Длина перпендикуляра, h = √(c 2 – (a-b) 2 ) [используя теорему Пифагора]….(1)
Теперь, 90½1 Площадь = 90½1 × сумма параллельных сторон × высота трапеции
= ½ × (a+b) × hс использованием уравнения (1) ) 2 ) (a+b)]
Периметр трапецииПериметр трапеции находится путем вычисления суммы всех ее сторон.
Следовательно,
Периметр трапеции = AB + BC + CD + AD
, где
AB, BC, CD и AD — стороны трапеции.Периметр равнобедренной трапеции
Если в равнобедренной трапеции a и b — длины параллельных сторон, т. е. основания, а c — длина двух равных непараллельных сторон, то периметр определяется как:
Периметр = A+B+2C
, где
A , B — основания
C — равная сторонаразница между трапецией и трапезоидом
в общих терминах, общие термины TRAPEUD и TRAPEODIOD и TRAPEZID и TRAPEZOID
.
 одинаковы, но разница заключается в их стране происхождения.
одинаковы, но разница заключается в их стране происхождения.Трапеция британского происхождения, это четырехсторонний многоугольник и двумерная фигура, у нее ровно одна пара параллельных сторон, противоположных друг другу. В Индии мы следуем британскому английскому языку, поэтому используется слово Trapezium.
Трапеция американского происхождения, это тоже четырехсторонний многоугольник с одной парой параллельных сторон, противоположных друг другу. Параллельные стороны являются основаниями, а две другие непараллельные стороны называются катетами трапеции.
Решенные примеры на трапеции
Пример 1: Найдите четвертую сторону трапеции, если три другие стороны равны 8 см, 12 см и 16 см, а периметр равен 40 см.
Решение:
Периметр равен сумме всех его сторон. Пусть длина неизвестного равна «х» единиц.
Периметр = 40
40 = 8 + 12 + 16 + x
x = 40 – (8 + 12 + 16)
= 4 см
Таким образом, длина неизвестной стороны равна 2 5 9 00004 см
4
Пример 2: Трапеция имеет параллельные стороны длиной 15 см и 11 см и непараллельные стороны длиной 5 см каждая. Вычислите периметр трапеции .
Вычислите периметр трапеции . Решение:
Это равнобедренная трапеция, потому что ясно сказано, что непараллельные стороны по 5 см равны. Согласно равнобедренной трапеции, если две непараллельные стороны трапеции имеют одинаковую длину, то трапеция называется равнобедренной.
Дано, a=15см, b=11см и c=5см 11+10
P = 36 см
Пример 3: Найдите периметр трапеции, стороны которой равны 12 см, 14 см, 16 см и 18 см.
Решение:
Как известно, периметр трапеции определяется суммой всех ее сторон.
P = Сумма всех сторон
P = 12 + 14 + 16 + 18
P = 60 см
Следовательно, периметр трапеции равен 60 см.
Пример 4: Найдите площадь трапеции, у которой сумма параллельных сторон 60 см, а высота 10 см.
Решение:
Дана сумма параллельных сторон 60 см и высота h =10 см
Мы знаем, что
Площадь трапеции, A = 1/2 × Сумма параллельных сторон × расстояние между параллельными сторонами
Подставив данные значения,
A =1/2×60×10
A = 30×10
A = 300 см 2 .

Следовательно, площадь трапеции =300 см 2 .
Часто задаваемые вопросы о трапеции
Вопрос 1: Сколько параллельных сторон у трапеции?
Ответ:
Мы знаем, что трапеция — четырехугольник с одной парой параллельных сторон. Таким образом, трапеция имеет пару параллельных прямых (сторон).
Вопрос 2: Можно ли считать трапецию четырехугольником?
Ответ:
A имеет четыре стороны, четыре вершины и четыре угла. Следовательно, его можно считать четырехугольником, сумма всех четырех внутренних углов трапеции равна 360 градусов.
Вопрос 3: Можно ли квадрат назвать трапецией?
Ответ:
Трапеция — это четырехугольник, у которого только одна пара параллельна, а две другие стороны непараллельны. Но в случае квадрата у него две пары параллельных сторон, следовательно, его нельзя считать трапецией.


 Периметр трапеции = Сумма всех 4 сторон . На этом рисунке это можно записать как Периметр трапеции ABCD = AB + BC + CD + DA.
Периметр трапеции = Сумма всех 4 сторон . На этом рисунке это можно записать как Периметр трапеции ABCD = AB + BC + CD + DA.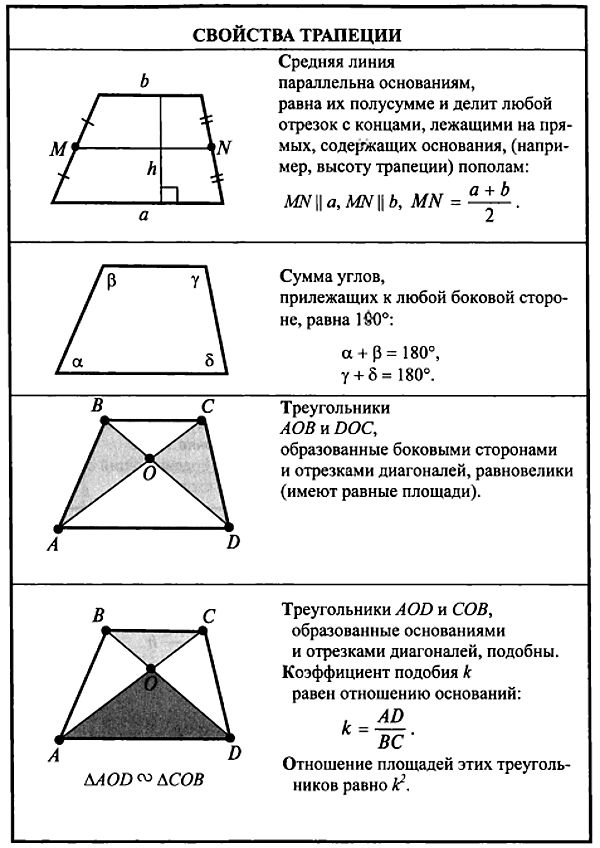

 Сумма каждой пары внутренних углов равна 180 ° .
Сумма каждой пары внутренних углов равна 180 ° .
 одинаковы, но разница заключается в их стране происхождения.
одинаковы, но разница заключается в их стране происхождения.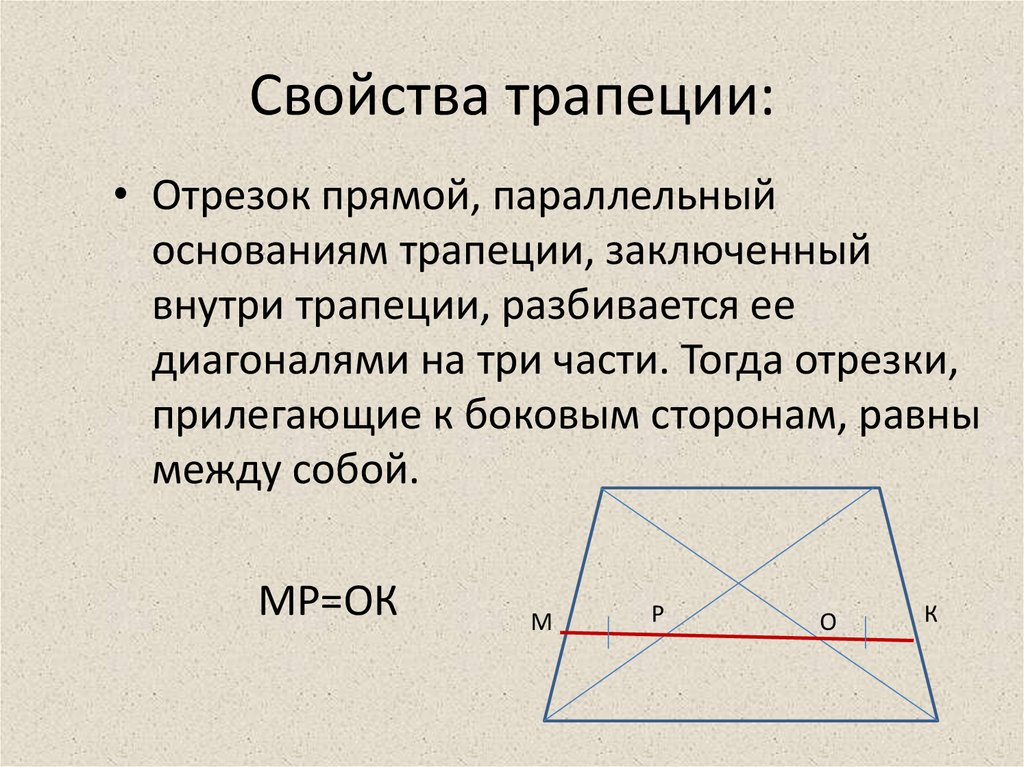 Вычислите периметр трапеции .
Вычислите периметр трапеции .