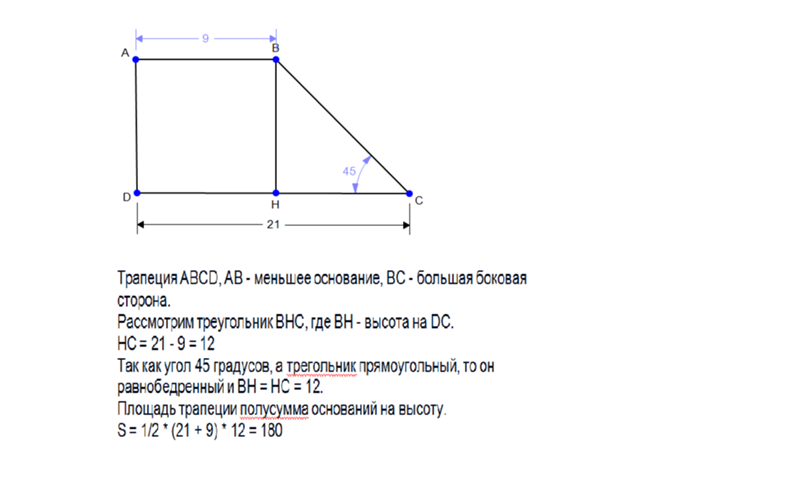
Стороны трапеций найти онлайн, правила, формулы, примеры
Трапеция — это выпуклый четырехугольник с двумя параллельными основами и двумя непараллельными боковыми сторонами.
Иногда фигура определяется как четырёхугольник, у которого пара противолежащих сторон параллельна,
поэтому параллелограмм и прямоугольник являются частными случаями трапеции. Также это
четырехугольник, у которого одна пара противоположных сторон параллельна, а остальные стороны не
равны между собой.
Параллельные стороны называются основами, а остальные боковыми.
Вычисление стороны необходимо для нахождения периметра, площади трапеции, ее диагоналей и других значимых параметров.
- Длина основания через среднию линию и другое известное основание
- Нижнее основание через верхнее основание, высоту и углы при нижнем основании
- Нижнее основание через боковые стороны, верхнее основание и углы при нижнем основании
- Верхнее основание через боковые стороны, нижнее основание и углы при нижнем основании
- Боковую сторону через высоту и угол при нижнем основании
Длина основания через среднюю линию и известное основание
Средняя линия — отрезок, соединяющий середины боковых сторон фигуры. Через её значение
вычисляется одна из основ. Нужно умножить ее на два и вычесть известную:
Через её значение
вычисляется одна из основ. Нужно умножить ее на два и вычесть известную:
a = 2m – b
Средняя линия (m):
ммсмдмм
Изв. основание (b):
ммсмдмм
Цифр после запятой:
012345678910Результат в: ммсмдмм
Например, средняя линия MN равна 6, а основание а – 9. Соответственно, значения, подставленные в формулу, показывают, что b = 2*6 – 9 = 3.
Нижнее основание через верхнее основание, высоту и углы при нижнем основании
Высота h или BK – перпендикуляр, проведенный от одной основы к другой. Высота проводится в любой их точке, но удобнее всего это делать из вершины углов при меньшей основе. Чтобы найти нижнее основание, надо к верхнему прибавить произведение высоты на сумму котангенсов углов при нижнем:
a = b + h*(ctga + ctgb)
Верх. основание (b):
основание (b):
ммсмдмм
Высота (h):
ммсмдмм
Угол (α):
градусырадианыctg
Угол (β):
градусырадианыctg
Цифр после запятой:
012345678910Результат в: ммсмдмм
Дано верхнее основание 10, высота 6 и углы 30 и 45. По формуле а = 10 + 6*(3+1) = 10 + 63 + 6 = 16+63. Для равнобедренного четырёхугольника выведены две формулы. В первой (a = 2S/h – b) основа выражена с помощью формулы площади. Пример: Площадь равнобедренной трапеции ABCD = 18, высота = 6, а AD = 5. Найти BC. BC = 2*18/6 – 5 = 6 – 5 = 1
Второе выражение сформулировано следующим образом: (a = b + 2h*ctga). Высота АН в трапеции ADEF = 10, DE = 4, а DAF = 45 градусам. Найти AF: AF = 4 + 10*2*1 = 24
Верхнее основание через нижнее основание, высоту и углы при нижнем основании
Чтобы найти верхнюю основу, надо из нижней вычесть произведение высоты на сумму котангенсов углов при ней:
b = a – h*(ctg α + ctg β)
Ниж.
ммсмдмм
Высота (h):
ммсмдмм
Угол (α):
градусырадианыctg
Угол (β):
градусырадианыctg
Цифр после запятой:
012345678910Результат в: ммсмдмм
Дана трапеция с нижним основанием 15, высотой 8 и углами в 45 градусов. По формуле а = 15 + 8*(1+1) = 15 + 16 = 31
Формулы для равнобедренного четырёхугольника: b = 2S/h – a и b = a – 2h*ctga.
- Площадь трапеции KLMN = 44, KL=MN, высота равна 8, KN = 5. Найти LM: LM = 44*2/8 – 5 = 6
- Высота трапеции DEFG = 15, DG= 5, а EDG = 45 градусам. Найти EF: EF = 5 + 15*2*1 = 35
Нижнее основание через боковые стороны, верхнее основание и углы при нижнем основании
Для нахождения основы а нужно к основе b прибавить произведение одной и другой стороны и косинусов углов при них
a = b + c * cos α + d * cos β
Верх. 2)/b и a = b +
2c*cosa.
2)/b и a = b +
2c*cosa.
- трапеции ABCD AB = CD = 8, диагональ AC = 12, а BC = 4. Вычислить AD: AD = (12*12 – 8*8)/4 = (144 – 64)/4 = 20
- В трапеции KLMN KL = MN = 4, LM = 7, а LKN равен 30 градусам. Вычислить KN: KN = 7 + 4*2*3/2 = 7 + 43
Верхнее основание через боковые стороны, нижнее основание и углы при нем
Для нахождения основы b нужно из основы а вычесть произведение одной и другой боковой стороны и углов при них
b = a – c * cos α – d * cos β
Ниж. основание (a):
ммсмдмм
Сторона (c):
ммсмдмм
Сторона (d):ммсмдмм
Угол (α):
градусырадианыcos
Угол (β):
градусырадианыcos
Цифр после запятой:
012345678910Результат в: ммсмдмм
Дана трапеция с нижним основанием 27, боковыми сторонами 20 и 14 и углами в 30 и 60 градусов. 2)/a и b = a — 2c*cosa.
2)/a и b = a — 2c*cosa.
- В трапеции DEFG DE и FG = 11, диагональ АС = 13, а EF = 12. Вычислить DG: DG = (13*13 – 11*11)/12= (169 – 121)/12 = 4
- Боковые стороны трапеции BCDE BC и DE = 25, BE = 10, а CBE равен 60 градусам. Вычислить CD: CD = 25 – 10*2*1/2 = 15
Боковая сторона через высоту и угол при нижнем основании
Чтобы найти боковую сторону, надо разделить высоту на синус угла при ней
d = h / sin α
Высота (h):
ммсмдмм
Угол (α):
градусырадианыsin
Цифр после запятой:
012345678910Результат в: ммсмдмм
Дана трапеция с высотой 12 и углами в 30 и 60 градусов. Найти боковые стороны: c = 12/0,5 = 24, d = 12/3/2 = 243
Для прямоугольного типа формулы несколько отличаются.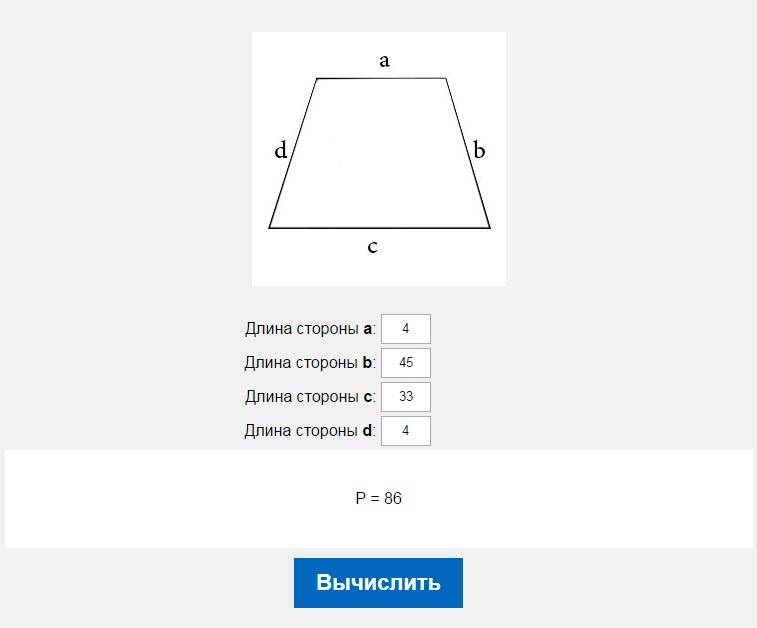 2 – 16*6 =
100 – 96 = 4
2 – 16*6 =
100 – 96 = 4
Виды трапеций
Существуют следующие виды трапеций:
- Равнобедренная трапеция — фигура, у которой боковые стороны и углы при основании равны.
Диагонали также равны. Треугольники, образованные диагоналями и основой, являются
равнобедренными.
 Если диагонали взаимно перпендикулярны, то площадь равна квадрату высоты. Если
разделить обе основы пополам и повести через эти точки линию, то она будет осью геометрической
фигуры. Отрезки, последовательно соединяющие середины смежных сторон, образуют ромб.
Если диагонали взаимно перпендикулярны, то площадь равна квадрату высоты. Если
разделить обе основы пополам и повести через эти точки линию, то она будет осью геометрической
фигуры. Отрезки, последовательно соединяющие середины смежных сторон, образуют ромб. - Прямоугольная трапеция — фигура, у которой одна из боковых сторон перпендикулярна основам и равна высоте. Два угла будут равны 90 градусам, и они всегда принадлежат смежным вершинам, а другие всегда острый и тупой, их сумма всегда будет равна 180 градусам. Каждая диагональ образует с ее меньшей боковой стороной прямоугольный треугольник. А высота, которая проведена из вершины с тупым углом, делит фигуру на две. Одна из них прямоугольник, другая прямоугольный треугольник.
- Разносторонняя трапеция — фигура, боковые стороны которой не равны и углы при основании не
являются прямыми.
 2.
2. - Треугольники ABO и DCO, образованные отрезками диагоналей и боковыми сторонами, имеют одинаковую площадь.
- В трапецию можно вписать окружность, если сумма оснований равняется сумме её боковых сторон.
- Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
- Отрезок, соединяющий середины диагоналей, равняется половине разности основ и лежит на средней линии.
Площадь трапеции — онлайн калькулятор
Чтобы найти площадь трапеции воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Через длины оснований и высоту
Чему равна площадь трапеции, если:
основание a =
основание b =
высота h =
Ответ: S =
 ²
²Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*
Чему равна площадь трапеции если известны основания a и b, а также высота h?
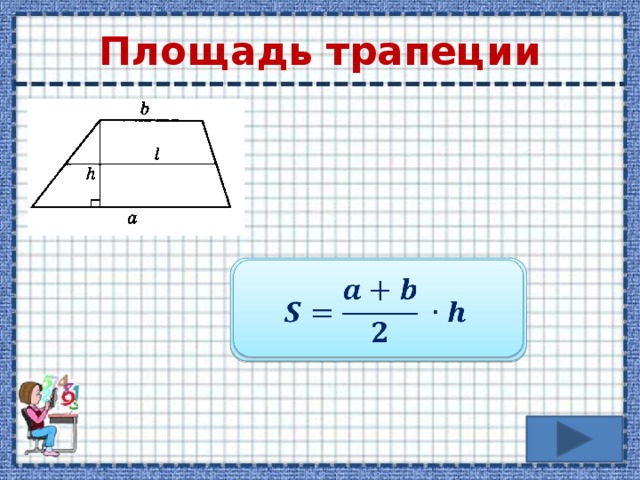
Формула
S = ½ ⋅ (a + b) ⋅ h
Пример
Если у трапеции основание a = 3 см, основание b = 6 см, а высота h = 4 см, то её площадь:
S = ½ ⋅ (3 + 6) ⋅ 4 = 36 / 2 = 18 см²
Через среднюю линию и высоту
Чему равна площадь трапеции, если:
средняя линия m =
высота h =
Ответ: S =
ед.²
Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*
Чему равна площадь трапеции если известны средняя линия m и высота h?
Формула
S = m ⋅ h
Пример
Если у трапеции средняя линия m = 6 см, а высота h = 4 см, то её площадь:
S = 6 ⋅ 4 = 24 см²
Через длины сторон и оснований
Чему равна площадь трапеции, если:
основание a =
основание b =
сторона c = сторона d =
Ответ: S =
ед.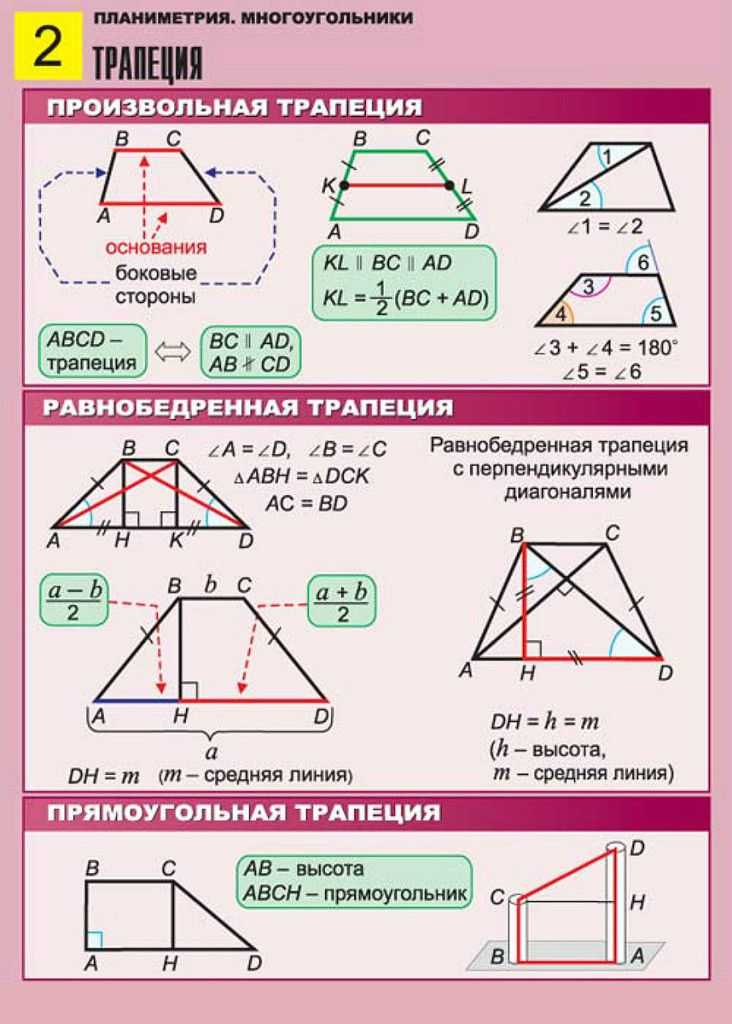 ²
²
Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*
Чему равна площадь трапеции если известны основания a и b, а также стороны c и d?
Формула
Пример
Если у трапеции основание a = 2 см, основание b = 6 см, сторона c = 4 см, а сторона d = 7 см, то её площадь:
S ≈ 13.555 см²
Через диагонали и угол между ними
Чему равна площадь трапеции, если:
диагональ d1 =
диагональ d2 =
угол α =
Ответ: S =
ед.²
Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*
Чему равна площадь трапеции если известны диагонали d1 и d2 и угол между ними α?
Формула
S = ½ ⋅ d1 ⋅ d2 ⋅ sin(α)
Пример
Если у трапеции одна диагональ d1 = 5 см, другая диагональ d2 = 7 см, а угол между ними ∠α = 30°, то её площадь:
S = ½ ⋅ 5 ⋅ 7 ⋅ sin (30) = 17.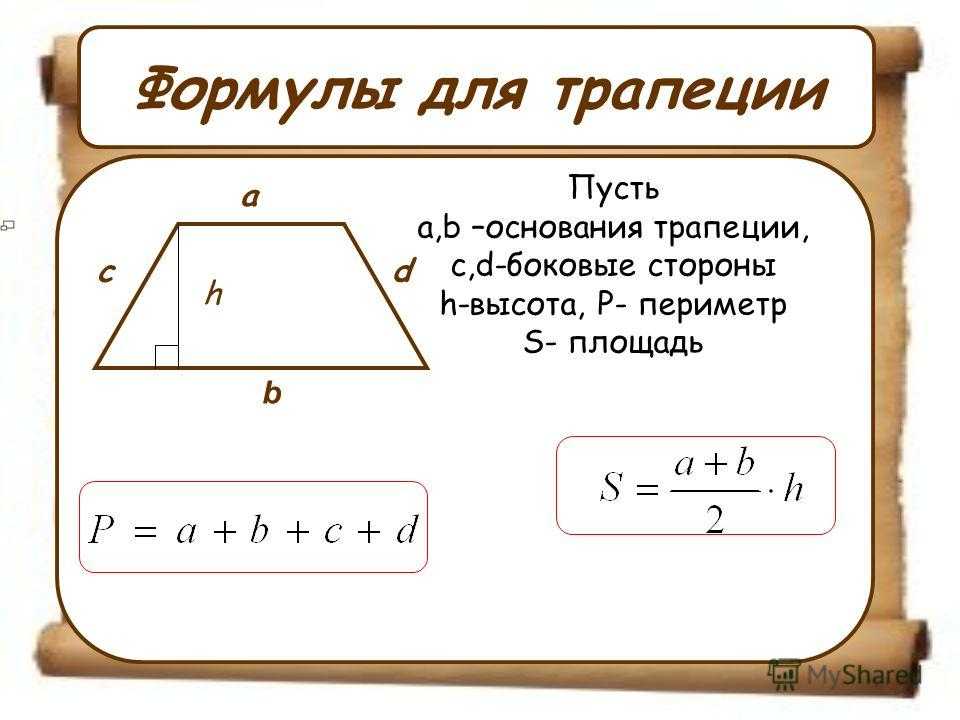 5 ⋅ 0.5= 8.75 см²
5 ⋅ 0.5= 8.75 см²
Площадь равнобедренной трапеции
Через среднюю линию, боковую сторону и угол при основании
Чему равна площадь трапеции, если:
средняя линия m =
сторона c =
угол α =
Ответ: S =
ед.²
Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*
Чему равна площадь равнобедренной трапеции если средняя линия m, боковая сторона с, a угол при основании α?
Формула
S = m ⋅ c ⋅ sin(α)
Пример
Если у равнобедренной трапеции средняя линия m = 6 см, сторона c = 4 см, а угол при основании ∠α = 30°, то её площадь:
S = 6 ⋅ 4 ⋅ sin (30) = 24 ⋅ 0.5 = 12 см²
Через радиус вписанной окружности
Чему равна площадь трапеции, если:
радиус r =
угол α =
Ответ: S =
ед.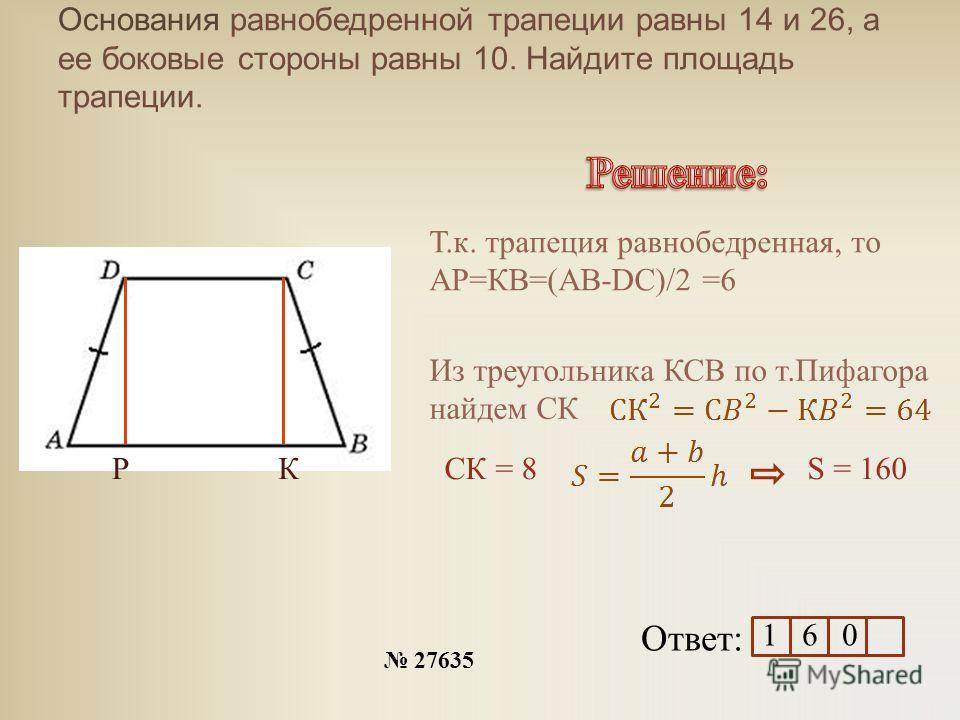 ²
²
Округление ответа: до целогодо десятыхдо сотыхдо тысячныхдо 4 знаковдо 5 знаковдо 6 знаковдо 7 знаковдо 8 знаковдо 9 знаковдо 10 знаковбез округления*
Чему равна площадь равнобедренной трапеции если радиус вписанной окружности r, a угол при основании α?
Формула
S = 4⋅r² ⁄ sin(α)
Пример
Если у равнобедренной трапеции радиус вписанной окружности r = 5 см, а угол при основании ∠α = 30°, то её площадь:
S = 4 ⋅ 5² / sin (30) = 100 / 0.5 = 200 см²
См. также
КАЛЬКУЛЯТОР ТРАПЕЦИЙ
КАЛЬКУЛЯТОР ТРАПЕЦИЙ 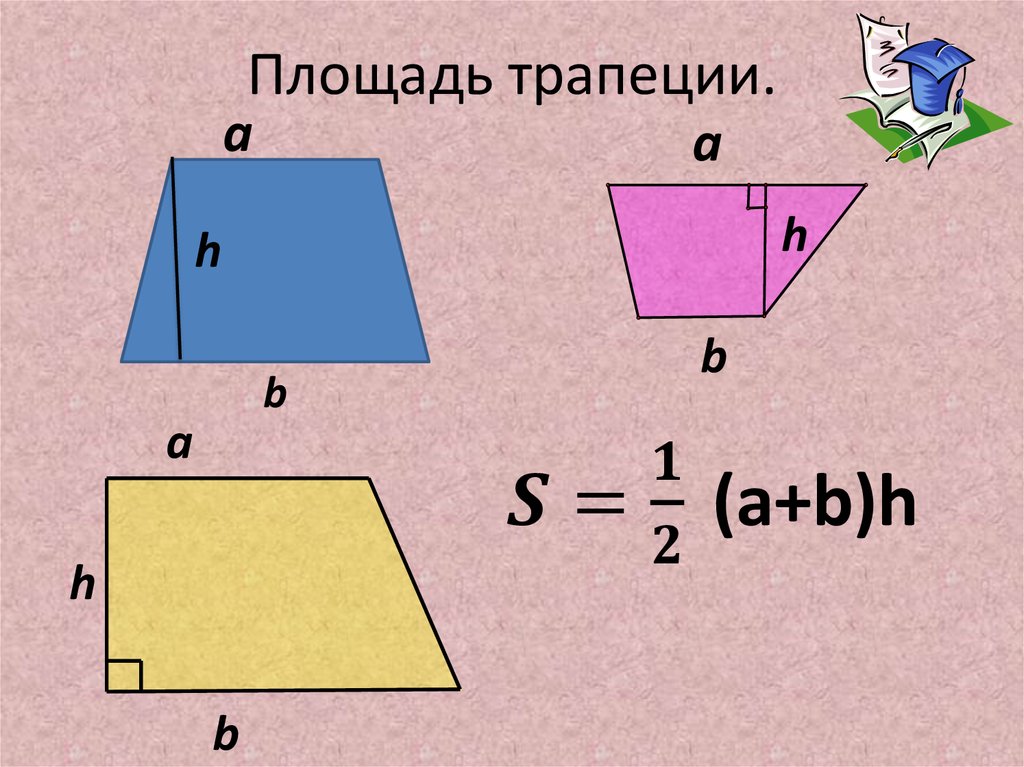 Прямые BC и AD параллельны и называются основаниями. Линии AB и DC являются непараллельными сторонами и называются ответвлениями. Линии AC (или q ) и BD (или p ) называются диагоналями Линия, перпендикулярная линиям AD и BC, называется высотой или высотой. Линия, параллельная линиям AD и BC, проходит через середины линий AB и DC. и называется медиана или средний сегмент . Длина медианы = (Линия AD + Линия BC) ÷ 2 Трапеции имеют 2 пары смежных углов (A и B) и (B и C), которые являются дополнительными (добавить 180°). 
|
| Геометрия | Формы | Контакты и конфиденциальность | Геометрические калькуляторы | Немецкий: Geometriechner, Formen |
| 1DЛиния, дуга окружности, парабола, спираль, кривая Коха
2D Правильные многоугольники: Равносторонний треугольник, квадрат, пятиугольник, шестиугольник, семиугольник, восьмиугольник, многоугольник, десятиугольник, десятиугольник, додекагон, шестиугольник, N-угольник, кольцо многоугольника Другие многоугольники: Круглые формы: Тетраэдр, куб, октаэдр, додекаэдр, икосаэдр рон, усеченный кубооктаэдр, икосододекаэдр, усеченный додекаэдр, усеченный икосаэдр, курносый куб, ромбикосододекаэдр , Усеченный икосододекаэдр, Курносый додекаэдр Каталонские твердые тела: Johnson Solids: Другие многогранники: Круглые формы: | Anzeige Расчеты на трапеции. Форма трапеции: Формулы: Сторона длина, высота, диагонали и периметр имеют одну и ту же единицу измерения (например, метр), площадь имеет эту единицу в квадрате (например, квадратный метр). |

 Если диагонали взаимно перпендикулярны, то площадь равна квадрату высоты. Если
разделить обе основы пополам и повести через эти точки линию, то она будет осью геометрической
фигуры. Отрезки, последовательно соединяющие середины смежных сторон, образуют ромб.
Если диагонали взаимно перпендикулярны, то площадь равна квадрату высоты. Если
разделить обе основы пополам и повести через эти точки линию, то она будет осью геометрической
фигуры. Отрезки, последовательно соединяющие середины смежных сторон, образуют ромб. 2.
2.
 Если да, введите ноль
в поле выше. Это устраняет все форматирование, но это лучше, чем отсутствие
выход вообще.
Если да, введите ноль
в поле выше. Это устраняет все форматирование, но это лучше, чем отсутствие
выход вообще. Спираль, треугольник Рело, циклоида, двойная циклоида, астроида, гипоциклоида, кардиоида, эпициклоида, параболический сегмент, сердце, треугольник, междуговой треугольник, круговой треугольник, междуговой четырехугольник, межокружной четырехугольник, круговой четырехугольник, дуговой многоугольник, коготь, полуинь -Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Многоугольник, Круглый многоугольник, Роза, Шестерня, Овал, Яйцо-профиль, Лемниската, Сквиркл, Круглый квадрат, Дигон, Сферический треугольник
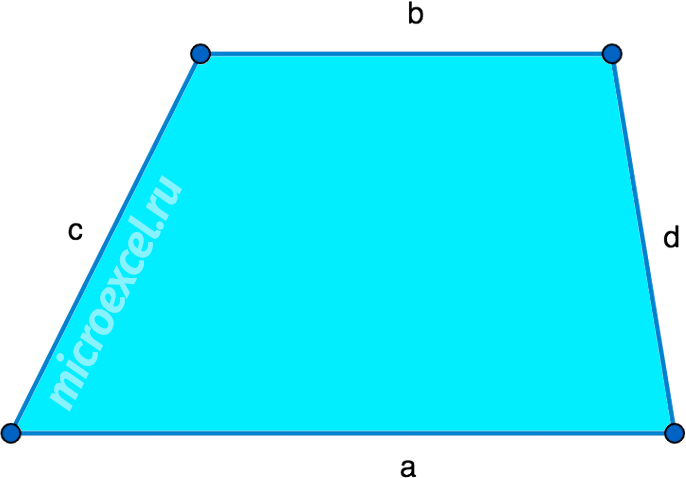
Спираль, треугольник Рело, циклоида, двойная циклоида, астроида, гипоциклоида, кардиоида, эпициклоида, параболический сегмент, сердце, треугольник, междуговой треугольник, круговой треугольник, междуговой четырехугольник, межокружной четырехугольник, круговой четырехугольник, дуговой многоугольник, коготь, полуинь -Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Многоугольник, Круглый многоугольник, Роза, Шестерня, Овал, Яйцо-профиль, Лемниската, Сквиркл, Круглый квадрат, Дигон, Сферический треугольник  Трапеция (или трапеция) – это четырехугольник с двумя параллельными сторонами. Введите три длины сторон и один угол между двумя из этих сторон. Выберите количество знаков после запятой и нажмите «Рассчитать». Пожалуйста, вводите углы в градусах, здесь вы можете конвертировать единицы измерения углов. Здесь можно вычислить только те трапеции, где c не пересекается с a (g1, g2 ≥ 0; α, β ≤ 90°), для остальных см. тупую трапецию.
Трапеция (или трапеция) – это четырехугольник с двумя параллельными сторонами. Введите три длины сторон и один угол между двумя из этих сторон. Выберите количество знаков после запятой и нажмите «Рассчитать». Пожалуйста, вводите углы в градусах, здесь вы можете конвертировать единицы измерения углов. Здесь можно вычислить только те трапеции, где c не пересекается с a (g1, g2 ≥ 0; α, β ≤ 90°), для остальных см. тупую трапецию.