Расчет площади поверхности цилиндра: Площадь поверхности цилиндра формула и калькулятор онлайн

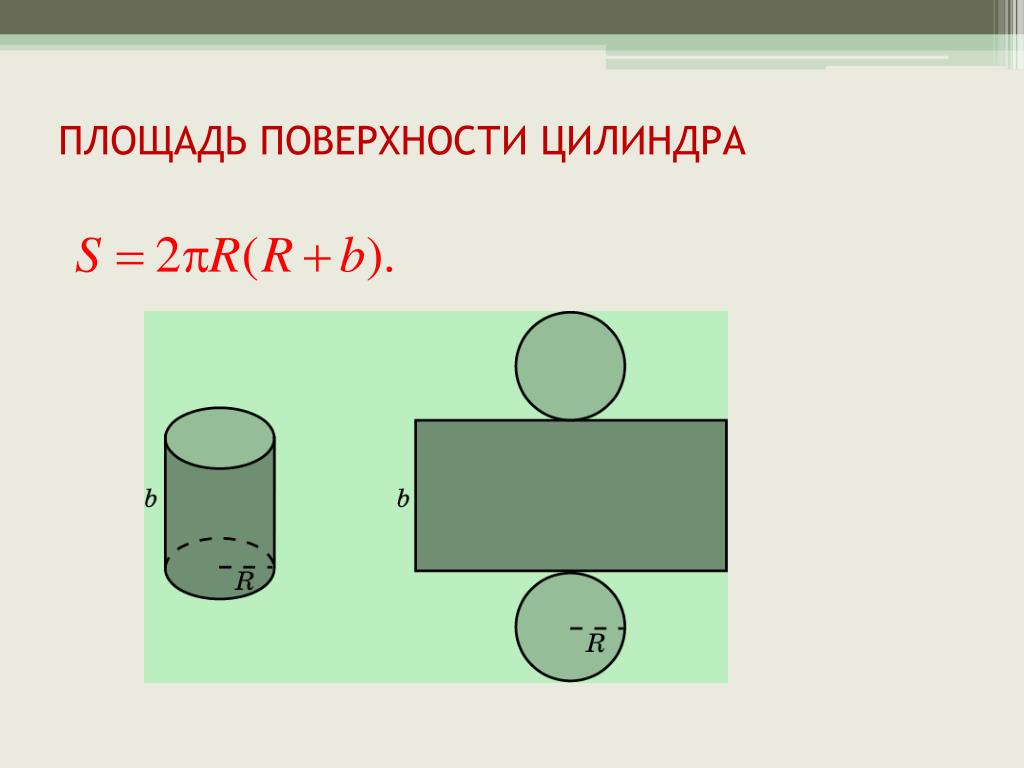
Площадь поверхности цилиндра – формула полной и боковой площади поверхности

4.6

Средняя оценка: 4.6

Всего получено оценок: 9394.

4.6

Средняя оценка: 4.6

Всего получено оценок: 9394.

Цилиндр представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью. В статье поговорим о том, как найти площадь поверхности цилиндра и, применив формулу, решим для примера несколько задач.

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики — более 33 лет.

У цилиндра есть три поверхности: вершина, основание, и боковая поверхность.

Основаниями цилиндра (их два: верхние и нижнее) являются окружности, их легко определить.

Известно, что площадь окружности равна πr². Поэтому, формула площади двух окружностей (двух оснований цилиндра) будет иметь вид πr² + πr² = 2πr².

Боковая поверхность цилиндра

Третья, боковая поверхность цилиндра, является изогнутой стенкой цилиндра. Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).

После полного раскрытия полученной банки мы увидим уже знакомую фигуру (Шаг 3), это прямоугольник. Площадь прямоугольника вычислить легко. Но перед этим вернемся на мгновение к первоначальному цилиндру. Верхнее основание исходного цилиндра является окружностью, а мы знаем, что длина окружности вычисляется по формуле: L = 2πr. На рисунке она отмечена красным цветом.

Когда боковая стенка цилиндра полностью раскрыта, мы видим, что длина окружности становится длиной полученного прямоугольника.

Сторонами этого прямоугольника будут длина окружности(L = 2πr) и высота цилиндра(h). Площадь прямоугольника равна произведению его сторон – S = длина х ширина = L x h = 2πr x h = 2πrh. В результате мы получили формулу для расчета площади боковой поверхности цилиндра.

Формула площади боковой поверхности цилиндра
S_бок. = 2πrh
r – радиус цилиндра, h – высота цилиндра

Площадь полной поверхности цилиндра

Наконец, если мы сложим площадь всех трёх поверхностей, мы получим формулу площади полной поверхности цилиндра. Площадь полной поверхности цилиндра равна площадь верхнего основания цилиндра + площадь нижнего основания цилиндра + площадь боковой поверхности цилиндра или S = πr² + πr² + 2πrh = 2πr² + 2πrh. Иногда это выражение записывается идентичной формулой 2πr (r + h).

Формула площади полной поверхности цилиндра
S = 2πr² + 2πrh = 2πr(r + h)
r – радиус цилиндра, h – высота цилиндра

Примеры расчета площади поверхности цилиндра

Для понимания приведенных формул, попробуем посчитать площадь поверхности цилиндра на примерах.

1. Радиус ос­но­ва­ния цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.

Площадь боковой поверхности рассчитывается по формуле: S_бок. = 2πrh

S_бок. = 2 * 3,14 * 2 * 3

S_бок. = 6,28 * 6

S_бок. = 37,68

Площадь боковой поверхности цилиндра равна 37,68.

2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?

Площадь полной поверхности рассчитывается по формуле: S = 2πr² + 2πrh

S = 2 * 3,14 * 6² + 2 * 3,14 * 6 * 4

S = 2 * 3,14 * 36 + 2 * 3,14 * 24

S = 226,08 + 150,72

S = 376,8

Площадь поверхности цилиндра равна 376,8.

3. Площадь боковой поверхности прямого кругового цилиндра равна 24π, а диаметр основания — 3. Найдите высоту цилиндра.

Из формулы расчета площади боковой поверхности цилиндра Sбок. = 2πrh следует, что высота равна:

h = Sбок./2πr

Значение радиуса получаем из формулы: d = 2r

h = 24π / (2π * 0,5d)

h = 24π / (2π * 0,5 * 3)

h = 12 / 1,5

h = 8

Высота цилиндра равна 8.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Dark Spyro

  5/5

• Татьяна Матвиенко

  5/5

• Юрий Евдокимов

  5/5

• Михаил Чепурной

  5/5

• Дмитрий Новиков

  5/5

• Дилноза Саипова

  4/5

• Darya Simonova

  5/5

• Тамара Иванова

  5/5

• Татьяна Немчинова

  5/5

• Рамиль Сагиров

  5/5

Оценка статьи

4.6

Средняя оценка: 4.6

Всего получено оценок: 9394.

---

А какая ваша оценка?

расчет боковой, полной поверхности цилиндра, формула нахождения

Математика

12. 11.21

6 мин.

Как вычислить площадь поверхности цилиндра — тема данной статьи. В любой математической задаче начать нужно с ввода данных, определить, что известно и чем оперировать в дальнейшем, и лишь затем приступить непосредственно к расчету.

Оглавление:

• Площадь поверхности цилиндра — онлайн калькулятор
• Площадь боковой поверхности цилиндра
• Площадь полной поверхности цилиндра
• Площадь цилиндра — формула через диаметр
• Примеры расчета площади цилиндра
• Заключение

Данное объёмное тело представляет собой геометрическую фигуру цилиндрической формы, ограниченную сверху и снизу двумя параллельными плоскостями. Если приложить немного воображения, то можно заметить, что геометрическое тело образуется вращением прямоугольника вокруг оси, причем осью является одна из его сторон.

Отсюда вытекает, что описываемая кривая сверху и снизу цилиндра будет окружностью, основным показателем которой является радиус или диаметр.

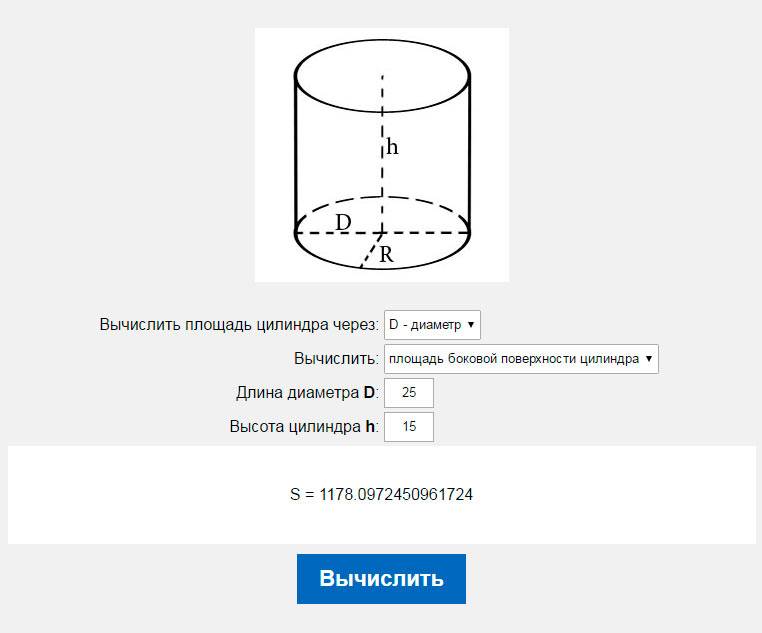
Площадь поверхности цилиндра — онлайн калькулятор

Данная функция окончательно облегчает процесс расчета, и все сводится лишь автоматическому подставлению заданных значений высоты и радиуса (диаметра) основания фигуры. Единственное, что требуется — точно определить данные и не ошибиться при вводе цифр.

Площадь боковой поверхности цилиндра

Сначала нужно представить, как выглядит развертка в двухмерном пространстве.

Это не что иное, как прямоугольник, одна сторона которого равна длине окружности. Формула ее известна с незапамятных времен —2π * r, где r — радиус окружности. Другая сторона прямоугольника равна высоте h. Найти искомое не составит труда.

S_бок = 2π * r * h,

где число π = 3.14.

Площадь полной поверхности цилиндра

Для нахождения полной площади цилиндра нужно к полученной S_бокдобавить площади двух окружностей, верха и низа цилиндра, которые считаются по формуле S_о = 2π * r².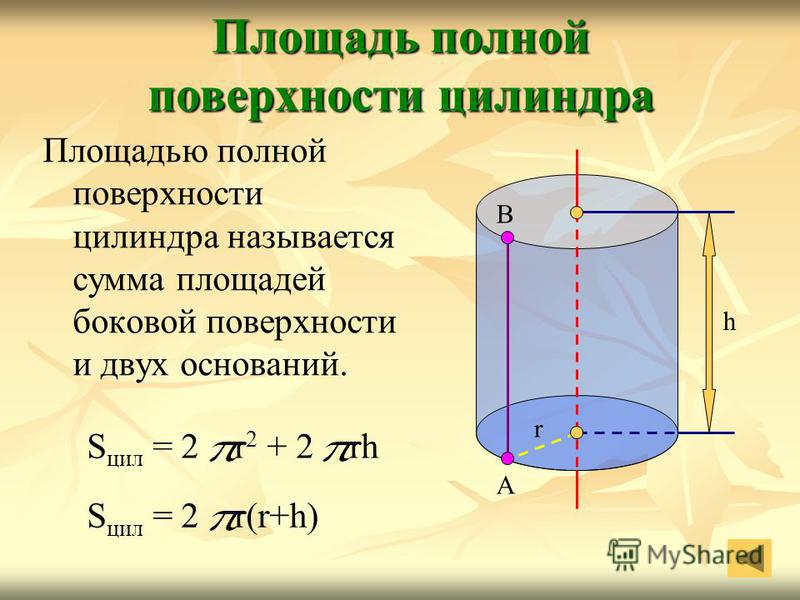

Конечная формула выглядит следующим образом:

S

_пол = 2π * r² + 2π * r * h.

Площадь цилиндра — формула через диаметр

Для облегчения расчетов иногда требуется произвести вычисления через диаметр. Например, имеется кусок полой трубы известного диаметра.

Не утруждая себя лишними расчетами, имеем готовую формулу. На помощь приходит алгебра за 5 класс.

Sпол = 2π * r² + 2π * r * h = 2π * d²/4 + 2π * h * d/2 = π * d²/2 + π * d * h,

Вместо r в полную формулу нужно вставить значение r = d/2.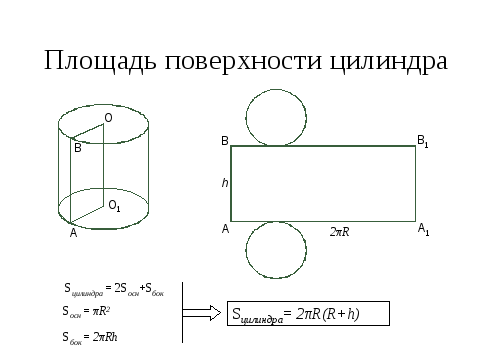

Примеры расчета площади цилиндра

Вооружившись знаниями, приступаем к практике.

Пример 1. Нужно вычислить площадь усеченного куска трубы, то есть цилиндра.

Имеем r = 24 mm, h = 100 mm. Использовать необходимо формулу через радиус:

S_пол = 2 * 3.14 * 24² + 2 * 3.14 * 24 * 100 = 3617,28 + 15072 = 18689,28 (мм²).

Переводим в привычные м² и получаем 0,01868928, приблизительно 0.02 м².

Пример 2. Требуется узнать площадь внутренней поверхности печной асбестовой трубы, стенки которой облицованы огнеупорным кирпичом.

Данные следующие: диаметр 0,2 м; высота 2 м. Используем формулу через диаметр:

S_пол = 3.14 * 0.2²/2 + 3,14 * 0.2 * 2 = 0,0628 + 1.256 = 1.3188 м².

Пример 3. Как узнать, сколько материла нужно для пошива мешка, r = 1 м и высотой 1 м.

Один момент, есть формула:

S_бок

= 2 * 3. 14 * 1 * 1 = 6.28 м².

Заключение

В конце статьи назрел вопрос: а так ли необходимы все эти вычисления и переводы одних значений в другие. Зачем все это нужно и самое главное, для кого? Но не стоит пренебрегать и забывать простые формулы из средней школы.

Мир стоял и будет стоять на элементарных познаниях, из математики, в том числе. И, приступая к какой-нибудь важной работе, никогда не лишне освежить в памяти данные выкладки, применив их на практике с большим эффектом. Точность – вежливость королей.

Не успеваете написать работу?

Заполните форму и узнайте стоимость

Вид работыПоиск информацииДипломнаяВКРМагистерскаяРефератОтчет по практикеВопросыКурсовая теорияКурсовая практикаДругоеКонтрольная работаРезюмеБизнес-планДиплом MBAЭссеЗащитная речьДиссертацияТестыЗадачиДиплом техническийПлан к дипломуКонцепция к дипломуПакет для защитыСтатьиЧасть дипломаМагистерская диссертацияКандидатская диссертация

Контактные данные — строго конфиденциальны!

Указывайте телефон без ошибок! — потребуется для входа в личный кабинет.

* Нажимая на кнопку, вы даёте согласие на обработку персональных данных и соглашаетесь с политикой конфиденциальности

Подтверждение

Ваша заявка принята.

Ей присвоен номер 0000.
Просьба при ответах не изменять тему письма и присвоенный заявке номер.
В ближайшее время мы свяжемся с Вами.

Ошибка оформления заказа

Кажется вы неправильно указали свой EMAIL, без которого мы не сможем ответить вам.
Пожалуйста проверте заполнение формы и при необходимости скорректируйте данные.

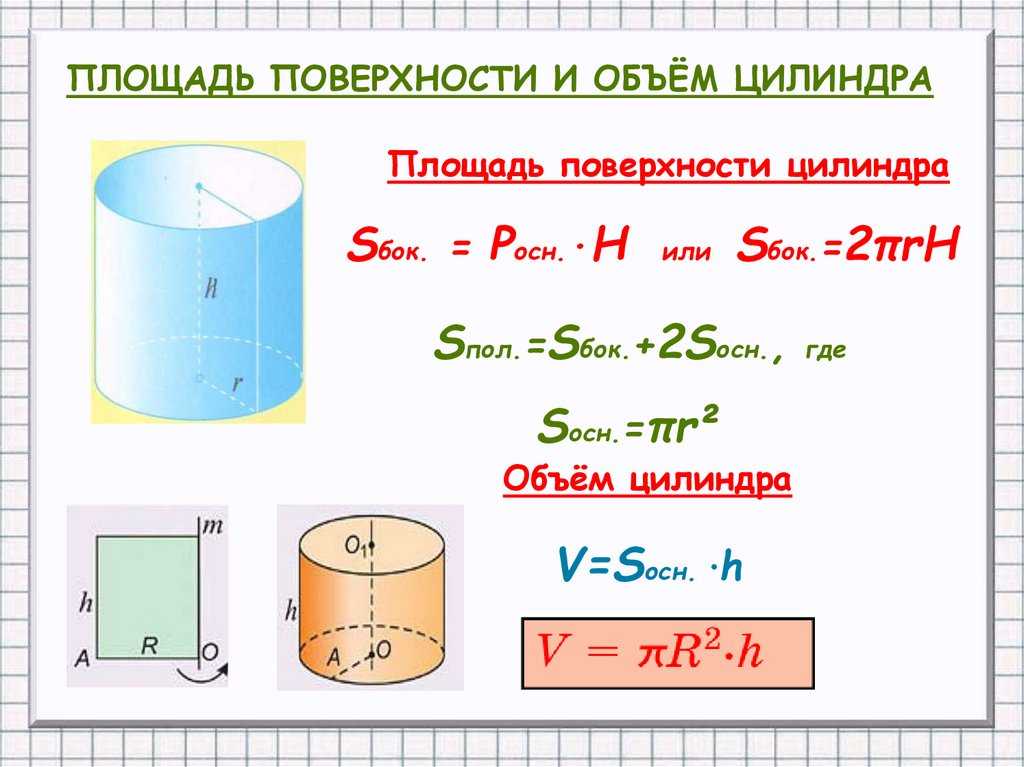
Площадь поверхности цилиндра

Горячая математика

Поскольку цилиндр тесно связана с призма , формулы их площадь поверхности относятся к.

Вспомните формулу площади боковой поверхности призмы. п час а общая площадь поверхности п час + 2 Б . Поскольку основанием цилиндра является окружность, подставляем 2 π р для п и π р 2 для Б где р это радиус основания цилиндра.

Итак, формула для площадь боковой поверхности цилиндра л . С . А . «=» 2 π р час .

Пример 1:

Найдите площадь боковой поверхности цилиндра с радиусом основания 3 дюймов и высотой 9дюймы.

л . С . А . «=» 2 π ( 3 ) ( 9 ) «=» 54 π дюймы 2

≈ 169,64 дюймы 2

Общая формула для общая площадь поверхности цилиндра Т . С . А . «=» 2 π р час + 2 π р 2 .

Пример 2:

Найдите площадь полной поверхности цилиндра с радиусом основания 5 дюймов и высотой 7 дюймы.

Т . С . А . «=» 2 π ( 5 ) ( 7 ) + 2 π ( 5 ) 2 «=» 120 π дюймы 2 ≈ 376,99 дюймы 2

Калькулятор площади поверхности цилиндра.

?

Какова площадь поверхности цилиндра?

Пример расчетов

Часто задаваемые вопросы

Этот калькулятор площади поверхности цилиндра является удобным инструментом, который быстро находит все три типа площадей поверхности:

• Базовая площадь поверхности цилиндра;
• Площадь боковой поверхности цилиндра; и
• Общая площадь поверхности цилиндра.

Цилиндр представляет собой трехмерное тело, состоящее из двух конгруэнтных поверхностей ( оснований ) и одной боковой поверхности . Хотя цилиндры могут принимать разные формы, термин 9Цилиндр 0079 обычно означает правый круговой цилиндр . Наш калькулятор площади поверхности цилиндра предназначен для этого типа цилиндра. Цилиндр прямой , когда одно из его оснований лежит точно над другим основанием, и косой , если нет. Стоит отметить, что основанием цилиндра может быть любая плоская замкнутая поверхность, например, круглый цилиндр имеет круглое основание, а прямоугольный цилиндр имеет прямоугольное основание

Продолжайте читать, если хотите узнать, что такое площадь поверхности цилиндра и как найти площадь поверхности цилиндра. Вы также можете рассчитать другие параметры цилиндра — просто воспользуйтесь нашим правильным калькулятором цилиндров!

Как найти площадь поверхности цилиндра?

Чтобы оценить площадь поверхности цилиндра, вам нужно представить его как сеть . Это как если бы вы открыли цилиндр, как картонную коробку, и расплющили его. Использовать ваше воображение! И что вы получите? Ответ заключается в том, что правильный круговой цилиндр состоит из двух кругов и одного прямоугольника, как вы можете видеть на рисунке ниже.

Следовательно, площадь основания цилиндра равна удвоенной площади круга с радиусом r , а площадь боковой поверхности цилиндра равна площади прямоугольника. Первая сторона этого прямоугольника – высота цилиндра h , а вторая – длина окружности основания, равная 2 × π × r , согласно калькулятору длины окружности.

Какова площадь поверхности цилиндра?

Теперь, когда мы знаем, как найти площадь поверхности цилиндра, давайте выведем соответствующие формулы для площади поверхности прямоугольного цилиндра. Чтобы вычислить площадь базовой поверхности, вам нужно вычислить площадь круга с радиусом р . Но помните, что у каждого цилиндра два основания! Таким образом, вам нужно умножить его на два:

base_area = 2 × π × r²

Оценка площади боковой поверхности еще проще. Поскольку площадь прямоугольника является произведением его сторон, мы можем написать, что:

lateral_area = (2 × π × r) × h ,

, где

• 2 × π × r — длина окружности. опорного круга,
• h высота цилиндра.

Наконец, формула общей площади поверхности цилиндра представляет собой просто сумму площади основания и площади боковой поверхности :

общая_площадь = базовая_площадь + боковая_площадь ,

или общая_площадь = 2 × π × r² + (2 × π × r) × h ,

или общая_площадь = 2 × π × r × (r + h) .

С помощью калькулятора площади поверхности цилиндра вы можете выполнять все расчеты в различных единицах измерения. Если вы хотите узнать больше о преобразовании единиц площади, ознакомьтесь с нашим конвертером площади прямо сейчас!

В расширенном режиме этого калькулятора вы также можете рассчитать объем цилиндра, но у нас также есть специальный инструмент, называемый калькулятором объема цилиндра.

💡 Интересен тот факт, что каждый цилиндр с одинаковой высотой и площадью основания имеет одинаковый объем . Неважно, прямой это цилиндр или косой.

Примеры расчетов

Давайте решим несколько примеров задач с вычислением площади поверхности цилиндра.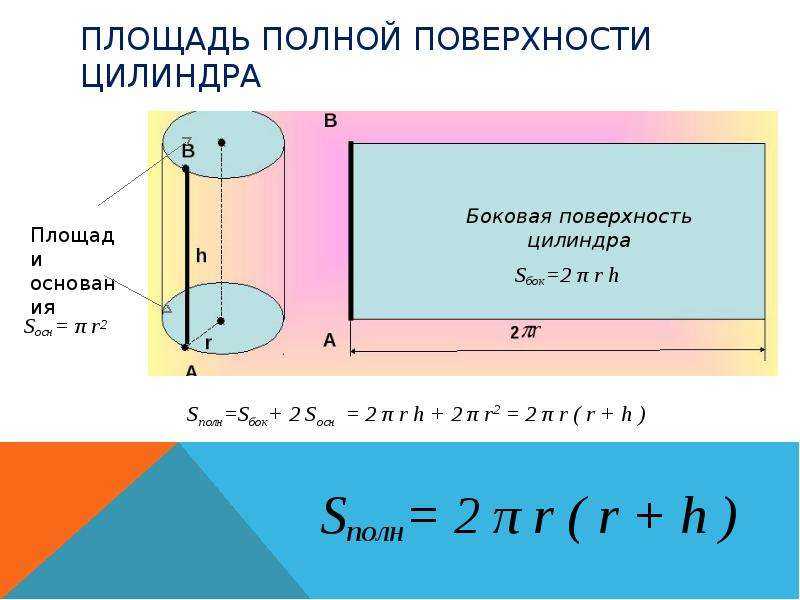

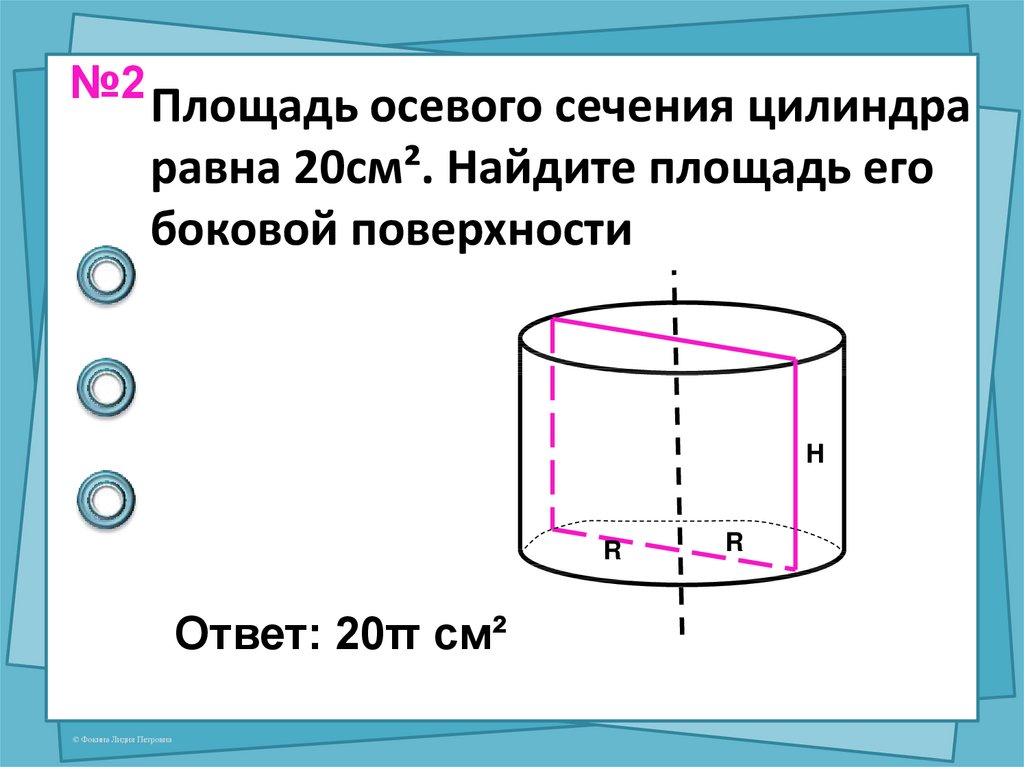
1. Вопрос : Какова площадь поверхности цилиндра с радиусом основания r = 2 см и высотой h = 3 см?

   • Ответ : Площадь основания равна 25,133 см², площадь боковой поверхности равна 37,7 см², а общая площадь поверхности равна 62,83 см².

2. Вопрос : Какова площадь поверхности цилиндра с диаметром основания d = 10 см и высотой h = 5 см?

   • Ответ: Во-первых, вам нужно разделить диаметр на два, чтобы оценить радиус окружности по формуле r = d/2 = 5 см или использовать другой инструмент: вычисление окружности: найти r. Затем введите его вместе с высотой в пустые поля нашего калькулятора. В этой задаче площадь поверхности основания равна 157,08 см², площадь боковой поверхности равна 157,08 см², а площадь полной поверхности равна 314,16 см².

3. Вопрос : Какова высота цилиндра с общей площадью поверхности 200 см² и радиусом r = 2 см?

   • Ответ : Вы можете использовать наш калькулятор площади поверхности цилиндра и в этом случае! Просто введите приведенные выше значения, и вы обнаружите, что высота равна 13,915 см.

Часто задаваемые вопросы

Как найти площадь боковой поверхности цилиндра?

Чтобы найти площадь боковой поверхности цилиндра с радиусом r и высотой h , выполните следующие действия:

1. Вычислите периметр круглого основания, используя C = 2πr .
2. Умножьте это значение на высоту цилиндра, чтобы получить площадь его боковой поверхности, Aₗ = 2πrh .
3. Проверьте свои результаты, используя калькулятор площади поверхности цилиндра!

Как найти радиус по площади поверхности цилиндра?

Чтобы найти радиус , r , цилиндра по его площади поверхности A , необходимо также знать высоту цилиндра , h :

3 высота ч в площадь поверхности уравнения цилиндра, A = 2πr² + 2πrh .
• Сложите всех членов этого уравнения в одну сторону, чтобы получить 2πr² + 2πrh - A = 0 . Обратите внимание, что это квадратное уравнение относительно р .
• Решите это уравнение, используя квадратную формулу, чтобы получить r = (-2πh ± √(4π²h² + 8πA))/4π .

Возьмите только положительный корень этого квадратного уравнения, так как радиус должен быть положительным.

Сколько поверхностей у цилиндра?

Цилиндр имеет три поверхности . К ним относятся две основные круглые поверхности и одна боковая (или изогнутая) поверхность .

Как рассчитать площадь поверхности полого цилиндра?

Для расчета площади поверхности полого цилиндра с внутренним радиусом , rᵢ , внешним радиусом , rₒ , и высотой 06, выполните следующие действия:

1. Рассчитайте площадь поверхности колец сверху и снизу по формуле Aᵣ = 2π(rₒ² — rᵢ²) .

   No related posts.