Треугольник паскаля до 100: Треугольник Паскаля | Онлайн калькулятор

Построение, создание треугольника Паскаля онлайн

Треугольник Паскаля — элегантный математический треугольник, представляющий собой бесконечную таблицу биноминальных коэффициентов. Таблица иллюстрирует скрытые соотношения между числами, которые естественным образом возникают в теории чисел, комбинаторике, теории вероятностей и алгебре.

Суть треугольной последовательности

Число 1 — важное число, а 11? Любопытно, что 11 × 11 = 121, 11 × 11 × 11 = 1331, а 11 × 11 × 11 × 11 = 14641. Если выстроить эти числа сверху вниз и представить их в виде отдельных цифр, то получится интересная формация:

• 1
• 1 1
• 1 2 1
• 1 3 3 1
• 1 4 6 4 1

Эти цифры — первые строки знаменитого треугольника Паскаля. Далее таблица строится по следующему принципу: по краям записываются единицы, а внутри ряда числа формируются путем суммы цифр, расположенных рядом выше слева и справа от искомых. Данная таблица знаменита в математике своей элегантностью, симметрией и неожиданными связями между числами. Связи таблицы с другими математическими сферами превратили треугольник Паскаля в Священный Грааль математики.

История открытия

Считается, что таблица была открыта Блезом Паскалем в 1653 году, однако происхождение формации гораздо древнее. Первое упоминание о бесконечной треугольной таблице встречается в трудах индийских математиков 10-го века, а наиболее полная информация о треугольнике представлена в работе китайского математика Шицзе, опубликованной в 1303 году. Однако и Шизце лишь упомянул о формации, создателем же треугольника Паскаля считается китайский ученый Ян Хуэй, поэтому в Китае таблица биноминальных коэффициентов носит название «треугольник Хуэя».

Удивительные свойства

Симметрия — очевидное свойство треугольника Паскаля. Если из верхней единицы провести вертикальную прямую, то числа справа и слева будут симметричны. Диагонали треугольника также симметричны. Диагонали вообще обладают рядом уникальных свойств. Если первая диагональ, как восточная, так и западная, представляет собой ряд сплошных единиц, то вторая — ряд натуральных чисел, третья — ряд треугольных чисел, а четвертая — тетраэдрических.

• Треугольные числа (1, 3, 6, 10…) — это числа, при помощи которых строятся плоские треугольники. Простыми словами, если в двухмерной игре вы захотите составить треугольник из круглых элементов, то вам понадобится выстроить элементы в количестве, советующему треугольным числам: сначала 6 кругов, потом 3, потом 1.
• Тетраэдрические числа (1, 4, 10, 20…) используются для построения объемных тетраэдров. Проще говоря, если вам понадобится сложить пушечные ядра аккуратной пирамидой, то в основании вам потребуется уложить 20 ядер, на них еще 10, сверху 4 и увенчать пирамиду одним верхним ядром.

Кроме того, если в треугольнике Паскаля четные числа заменить единицами, а нечетные — нулями, то получится треугольник Серпинского — известный фрактал, построенный польским математиком в начале 20 века.

Треугольник Паскаля также имеет удивительную связь с алгеброй. Если мы разложим бином Ньютона вида (1 + x)², то получим 1 + 2x + x². Если же это будет (1 + x)³, то в результате мы получим 1 + 3x + 3x² + x³. Если присмотреться, то биноминальные коэффициенты — это ни что иное как числа из соответствующего ряда треугольника Паскаля.

Построение треугольника Паскаля

Треугольник Паскаля — это бесконечная таблица элементов. При помощи нашего калькулятора вы можете построить таблицу любой размерности, однако не рекомендуется использовать слишком большие числа (n>100), так как столь огромные таблицы не имеют практического применения, а онлайн-калькулятор строит их слишком долго. Помимо элегантных свойств, используемых для решения биноминальных уравнений или построения тетраэдрических последовательностей, таблица Паскаля находит применение в комбинаторике.

Примеры из реальной жизни

Подсчет количества способов

Если на кафедре работают 7 математиков, и троих из них нужно отправить на городскую олимпиаду, то сколькими способами можно это сделать? Это стандартная задача на комбинаторику, в котором важен порядок элементов, то есть вариант «Сидоров, Иванов и Петров» отличается от варианта «Иванов, Петров, Сидоров», хотя выбранная группа математиков одна и та же. Такая ситуация возникает в случае, если преподаватели должны участвовать в разных конкурсах. При «ручном» решении нам пришлось бы использовать стандартные формулы для комбинаторики, однако проще воспользоваться свойствами треугольника Паскаля.

Для ответа на вопрос нам достаточно построить треугольник с n = 10, найти седьмой ряд и третье число в нем. Таким образом, существует 35 способов объединить математиков для поездки на олимпиаду.

Определение вероятности

В корзине лежит 20 шаров, пронумерованных от 1 до 20. Наугад мы берем 3 шара. Какова вероятность, что мы вытащим шары с номерами 5, 12 и 13? Для решения этой задачи нам потребуется построить треугольник Паскаля с n = 20, после чего найти двадцатый ряд и третье число в нем. Вытащить три шара можно 1140 способами. Вероятность наступления нашего события составит 3 из 1140.

Заключение

Треугольник Паскаля — простая таблица, которая таит в себе огромное количество математических тайн. Члены рядов связаны с биноминальными коэффициентами, совершенными числами, числами Фибоначчи, тетраэдрическими и треугольными числами. Используйте наш калькулятор для построения сетки необходимой вам размерности для решения самых разных математических задач.

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Справочник по математике

Алгебра

Формулы сокращенного умножения

      Для того, чтобы получить треугольник Паскаля, перепишем Таблицу 1 из раздела «Формулы сокращенного умножения: степень суммы и степень разности» в следующем виде (Таблица П.):

      Таблица П. – Натуральные степени бинома   x + y

№	Степень	Разложение в сумму одночленов
0	(x + y)0 =	1
1	(x + y)1 =	1x + 1y
2	(x + y)2 =	1x2 + 2xy + 1y2
3	(x + y)3 =	1x3 + 3x2y + 3xy2 + 1y3
4	(x + y)4 =	1x4 + 4x3y + 6x2y2 + 4xy3 + 1y4
5	(x + y)5 =	1x5 + 5x4y + 10x3y2 + 10x2y3 + 5xy4 + 1y5
6	(x + y)6 =	1x6 + 6x5y + 15x4y2 + 20x3y3 + + 15x2y4 + 6xy5 + 1y6
…	…	…

      Теперь, воспользовавшись третьим столбцом Таблицы П. , составим следующую Таблицу — Треугольник Паскаля:

Степень 0: (x + y)0 = Разложение в сумму одночленов: 1

Степень 1: (x + y)1 = Разложение в сумму одночленов: 1x + 1y

Степень 2: (x + y)2 = Разложение в сумму одночленов: 1x2 + 2xy + 1y2

Степень 3: (x + y)3 = Разложение в сумму одночленов: 1x3 + 3x2y + 3xy2 + 1y3

Степень 4: (x + y)4 = Разложение в сумму одночленов: 1x4 + 4x3y + 6x2y2 + + 4xy3 + 1y4

Степень 5: (x + y)5 = Разложение в сумму одночленов: 1x5 + 5x4y + 10x3y2 + + 10x2y3 + 5xy4 + 1y5

Степень 6: (x + y)6 = Разложение в сумму одночленов: 1x6 + 6x5y + 15x4y2 + + 20x3y3 + + 15x2y4 + + 6xy5 + 1y6

…

      Теперь, записыая только коэффициенты разложений степеней бинома в сумму одночленов, получим следующую Таблицу — Треугольник Паскаля:

      Таблица — Треугольник Паскаля

№	Треугольник Паскаля
0	1
1	1     1
2	1     2     1
3	1     3     3     1
4	1     4     6     4     1
5	1     5     10     10     5     1
6	1     6     15     20     15     6     1
…	…

      На всякий случай напомним, что Блез Паскаль – это знаменитый физик и математик, живший во Франции более трех веков назад.

      В треугольнике Паскаля каждая строка соответствует строке с тем же номером в Таблице П. Однако в каждой строке треугольника Паскаля, в отличие от Таблицы П., записаны только коэффициенты разложения в сумму одночленов соответствующей степени бинома   x + y .

      Заполнив сначала строки треугольника Паскаля с номерами   0   и   1,   рассмотрим строки с номерами   2   и далее.

      Основным свойством треугольника Паскаля, позволяющим последовательно, начиная со строки с номером   2,   заполнять его строки, является следующее свойство:

      Каждая из строк, начиная со строки с номером   2,   во-первых, начинается и заканчивается числом   1,   а, во-вторых, между числами   1   стоят числа, каждое из которых равно сумме двух чисел, стоящих над ним в предыдущей строке.

      Действительно, число   2,   стоящее в строке с номером два, равно сумме чисел   1   плюс   1,   стоящих в первой строке. Точно так же, числа   3   и   3,   стоящие в строке с номером три, равны соответственно сумме чисел   1   плюс   2   и сумме чисел   2   плюс   1,   стоящих во второй строке.

      Также и для других строк.

      Таким образом, свойство треугольника Паскаля позволяет, заполнив одну из строк, легко заполнить и следующую за ней, т.е. получить необходимые коэффициенты разложения в сумму одночленов следующей степени бинома   x + y .

      Пример. Написать разложение вида:

(x + y)⁷ .

      Решение. Воспользовавшись строкой треугольника Паскаля с номером   6   и применив основное свойство треугольника Паскаля, получим строку с номером   7:  

6	1    6    15    20    15    6    1
7	1    7    21    35    35    21    7    1

      Следовательно,

(x + y)⁷ = x⁷ + 7x⁶y +
+ 21x⁵y² + 35x⁴y² +
+ 35x³y⁴ +
+ 21x²y⁵ + 7xy⁶ + y⁷ .

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Калькулятор треугольника Паскаля

Создано Maciej Kowalski, кандидатом наук

Рецензировано Bogna Szyk и Jack Bowater

Последнее обновление: 01 февраля 2023 г.

Содержание:

• Что такое треугольник Паскаля ?
• Как пользоваться треугольником Паскаля?
• Модели треугольников Паскаля
• Пример: биномиальное разложение
• Часто задаваемые вопросы

Добро пожаловать в наш калькулятор треугольников Паскаля , где вы узнаете, как использовать треугольник Паскаля и почему вы должны использовать его в первую очередь. Не волнуйся; эта концепция не требует формул площади или расчетов единиц измерения, как в случае с типичным треугольником. Что же такое треугольник Паскаля? Ну, это удобный способ подсчитать количество комбинаций и визуализировать биномиальное расширение . Но прежде чем мы начнем описывать шаблоны треугольников Паскаля, давайте начнем с основ.

Что такое треугольник Паскаля?

Треугольник Паскаля представляет собой таблицу чисел в форме равностороннего треугольника, где k -е число в n -й строке говорит вам сколько существует комбинаций без повторения k элементов из набора n элементы . Он назван в честь французского математика Блеза Паскаля.

💡 Если термин «комбинация» кажется вам редким, проверьте наш калькулятор комбинаций.

(Обратите внимание, что мы следуем соглашению о том, что верхняя строка, та, в которой стоит одна 1, считается нулевой строкой , а первое число в строке, также 1, считается 0-м числом этой строки .) Таким образом, n -я строка в целом подсчитывает все возможные подмножества n -набор элементов. Будь то фильмы для киномарафона, европейские страны, которые стоит посетить этим летом, или продукты из вашего холодильника для завтрашнего ужина, это утверждение о комбинациях всегда остается верным (мы почти уверены, что последнее не совсем то, как работает приготовление пищи, но некоторые из нас должны компенсировать недостаток навыков творчеством ).

Каждое число, показанное в нашем калькуляторе треугольника Паскаля, задается формулой, которую ваш учитель математики называет биномиальным коэффициентом (тот, который известен как nCr в калькуляторе биномиального распределения). Имя не слишком важно, но давайте посмотрим, как выглядит вычисление . Если мы обозначим количество комбинаций k элементов из набора n элементов как C(n,k) , то:

C(n,k) = n! / (k! × (n-k)!) .

Восклицательный знак выше — это то, что математики называют «факториалом», определяемым как произведение всех чисел до включительно n , то есть

n! = n × (n-1) × (n-2) × ... × 2 × 1 .

🔎 Вы можете использовать наш факторный калькулятор, чтобы избежать всех этих сложных умножений.

Как пользоваться треугольником Паскаля?

Скажите, что вы готовите киномарафон для себя и своего партнера. У вас есть список из двадцати ваших любимых фильмов, и ваш партнер сказал вам выбрать три, которые ему могут понравиться. Что ж, это лучшие фильмы из существующих , так что ясно, что они понравятся каждому из них, и не так уж важно, какие из них вы выберете. Кроме того, порядок, в котором вы их смотрите, также не имеет значения. Так сколько вариантов?

Искомое число — третье число в двадцатом ряду, 1140. Магия? Не совсем, просто математика (но опять же, они такие разные?). Действительно, согласно формуле треугольника Паскаля, это число соответствует выражению C(20,3) , которое является количеством троек в наборе из двадцати элементов. Или, в нашем случае, количество способов выбрать три фильма из двадцати .

Треугольники Паскаля

Блез Паскаль сосредоточился на нескольких интересных треугольных свойствах. Действительно, количество комбинаций, которое кодируется отдельными числами в последовательных рядах, уже было известно в его время. Однако треугольник часто вводится с помощью гораздо более простого правила . Обратите внимание, что кроме единиц на дальних концах треугольника, каждое из остальных чисел является суммой двух, стоящих прямо над ним.

Именно это наблюдение (или свойство, если хотите) часто используется для построения треугольника. Используя формулу треугольника Паскаля, мы можем описать это наблюдение:

С(n,k) = C(n-1,k-1) + C(n-1,k) .

В частности, обратите внимание на второе число слева в каждой строке. У каждого из них слева вверху есть единица, а справа вверху — номер строки предыдущей строки . Следовательно, их сумма равна единице плюс номер предыдущей строки (суть нашего калькулятора арифметической последовательности), а результатом является строка, в которой мы находимся.0022 . Заметьте, что в любой строке , если мы читаем последовательные числа слева, мы получим то же самое, что если бы мы читали их справа .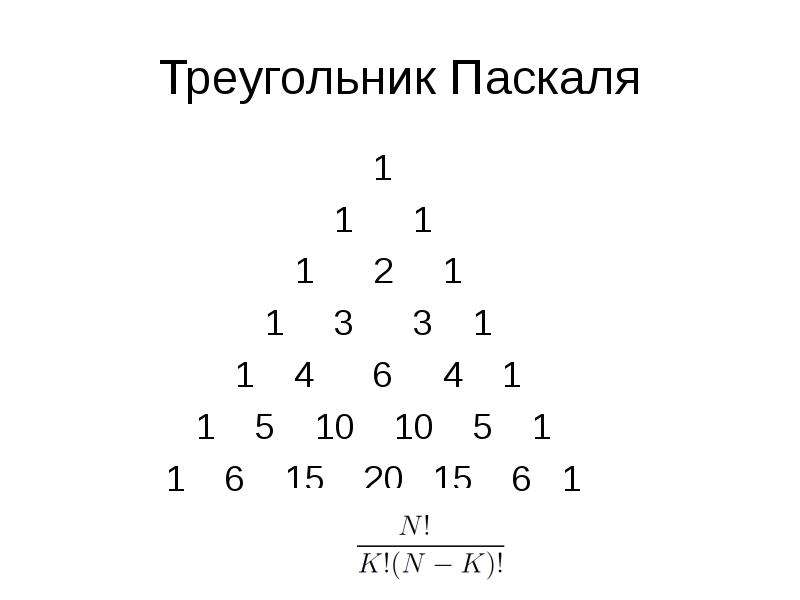 Это снова магия или математика? Что ж, давайте попробуем понять, что здесь происходит.

По определению, число на k -м месте в n -й строке показывает, сколькими способами мы можем выбрать k элементов из набора n элементов. Но что, если вместо этого мы укажем элементы, которые не выбирали? Это может показаться немного расплывчатым, так почему бы нам не показать вам пример?

Вспомним сценарий из второго раздела, где мы хотели выбрать три фильма для просмотра из списка двадцати . Но что, если сложно выбрать три, которые вы хотите увидеть больше всего? Может проще отсеивать по одному те, которые не хочется смотреть ? Конечно, если мы затем вычеркнем семнадцать из них, у нас останется выбор из трех. Это именно то, что мы описали выше — вместо этого мы выбираем семнадцать, которые не хотим смотреть . Это, записанное с использованием обозначений из формулы треугольника Паскаля в первом разделе, будет следующим: k -я точка, считая слева, такая же, как и на k -я при счете справа для любого ряда n .

Пример: биномиальное разложение

Математически говоря, ответ на вопрос « Что такое треугольник Паскаля? » таков: биномиальное разложение . Не волнуйся; мы здесь не для того, чтобы казаться самодовольными, используя какие-то причудливые слова и символы, когда достаточно простого объяснения. Для всеобщего блага мы покажем вам на примере реальной жизни, как ответить на этот вопрос, объясняя, как использовать калькулятор треугольников Паскаля по пути .

Допустим, у вашей собаки будут щенки , и вы знаете, что их будет шесть, но вы не знаете их пола. Если мы пронумеруем щенков в том порядке, в котором они появляются в этом мире, мы можем начать думать о вероятности того, какого пола они будут. Конечно шесть мальчиков менее вероятны, чем, например, два мальчика и четыре девочки . Это потому, что два мальчика могут родиться первыми двумя щенками, или двумя последними, или двумя средними и т. д., и поэтому существует гораздо больше комбинаций, чтобы это произошло.

Итак, самое сложное. Мы попытаемся убедить вас, что щенков можно описать символическим числом (x + y)⁶ . Чтобы увидеть это, свяжите x с «мальчиком» и y с «девочкой». Теперь посмотрите на расширение:

(х + у)⁶ = (х + у) × (х + у) × … × (х + у) .

Как выглядит каждое слагаемое после умножения приведенного выше выражения? Ну, это получается из взятия одного из слагаемых в каждой из круглых скобок, т. е. взятия скобки x или y после скобки. В нашем переводе это означает определение пола каждого из шести щенков по одному . Это означает, что каждое слагаемое вида, скажем, x² × y⁴ , что соответствует двойному выбору x из-за скобок и четыре раза выбирая y , мы получим помет из двух мальчиков и четырех девочек.

Теперь давайте посмотрим на расширение после умножения и реорганизации подобных мономов :

(x + y)⁶ = x⁶ + 6x⁵y + 15x⁴y² + 20x³y³+ 15x²y⁴ + 6xy ⁵ + у⁶ .

Сравните это с шестым уровнем треугольника Паскаля , возвращаемым калькулятором треугольника Паскаля:

1 6 15 20 15 6 1 .

Эти числа соответствуют коэффициентам в расширении выше. Другими словами, шестому (или вообще n-му) уровню треугольника соответствуют коэффициенты (x + y)⁶ (соответственно: в степени n) в их биномиальном разложении . И это, как мы видели в нашем сценарии с собакой, приводит к решению некоторых реальных проблем.

Часто задаваемые вопросы

Как вычислить ряды в треугольнике Паскаля?

Если вы хотите вычислить строку треугольника Паскаля:

1. Начните с записи самой вершины треугольника: нулевая строка содержит один 1 .

2. Тогда первая строка содержит два 1 с.

3. Все остальные строки следуют тому же принципу: запишите 1 в начале и в конце. Каждое из пропущенных чисел представляет собой сумму двух чисел, стоящих прямо над ним (в предыдущей строке).

4. Следуйте этим правилам, пока не получите нужную строку.

Как найти сумму строк в треугольнике Паскаля?

Сумма чисел n -й строки треугольника Паскаля равна 2ⁿ . В самом деле, мы легко проверяем, что последующие суммы равны 1, 2, 4, 8, 16 и т. д. Это следует из того, что множество из n элементов имеет 2ⁿ подмножеств.

Что такое 7-я строка треугольника Паскаля?

Седьмая строка треугольника Паскаля: 1 7 21 35 35 21 7 1 .

Что такое 10-я строка треугольника Паскаля?

Десятая строка треугольника Паскаля: 1 10 45 120 210 252 210 120 45 10 1 .

Maciej Kowalski, PhD кандидат

Посмотреть 8 калькуляторов похожих последовательностей 🔗

Арифметическая последовательность Гипотеза Коллатца Фибоначчи… Еще 5

Построить треугольник Паскаля — Online Math Tools

График Функция

Рисование графиков математических функций.

Нарисовать формулу LaTeX

Создать изображение из выражения LaTeX.

Найти n-ю цифру

Вычислить n-ю цифру числа Эйлера.

Найти n-ю цифру золотого сечения

Вычислить n-ю цифру золотого сечения.

Найти n-ю цифру числа пи

Вычислить n-ю цифру числа пи.

Вычислить сумму e цифр

Найти сумму e цифр.

Вычислить сумму цифр золотого сечения

Найти сумму цифр золотого сечения.

Вычислить сумму пи цифр

Найти сумму пи цифр.

Генерировать цифры Чамперноуна

Генерировать цифры константы Чамперноуна.

Генерация цифр суперзолотого сечения

Генерация цифр константы суперзолотого отношения.

Найти n-ю цифру Чамперноуна

Вычислить n-ю цифру константы Чамперноуна.

Декодирование последовательности «посмотри и скажи»

Выполните обратную операцию над последовательностью «посмотри и скажи».

Генерация P-адических расширений

Вычисление p-адических расширений произвольных чисел.

Создать последовательность панцифровых чисел

Создать список панцифровых чисел.

Создать последовательность номеров Стэнли

Создать список номеров Стэнли.

Создать последовательность номеров звонков

Создать список номеров звонков.

Генерация последовательности номеров Кармайкла

Создание списка номеров Чармичел.

Создать последовательность каталонских номеров

Создайте список каталонских номеров.

Создать последовательность треугольных чисел

Создать список треугольных чисел.

Создать последовательность составных чисел

Создать список составных чисел.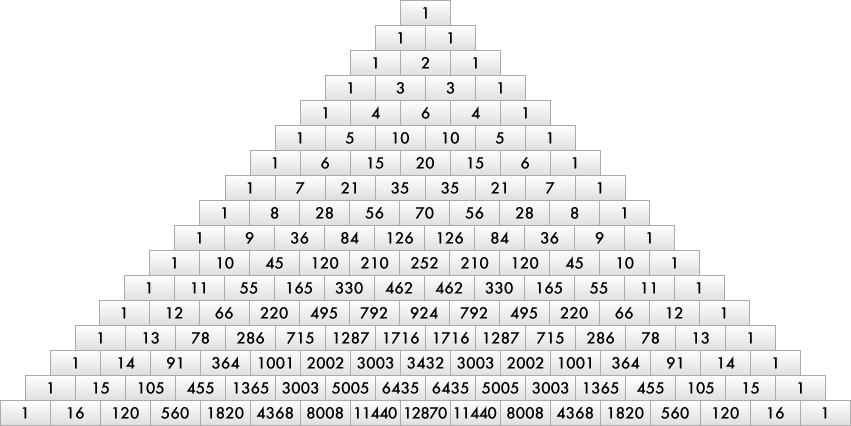

Создать последовательность секущих чисел

Создать список секущих чисел.

Создать последовательность чисел Голомба

Создать список чисел Голомба-Сильвермана.

Создать последовательность чисел Эйлера Тотиент

Создать список фи-чисел Эйлера.

Создать последовательность номеров жонглеров

Создать список номеров жонглеров.

Создать последовательность счастливых номеров

Создать список счастливых номеров.

Создать последовательность номеров Моцкина

Создать список номеров Моцкина.

Создать последовательность номеров Padovan

Создать список номеров Padovan.

Создать последовательность коров Нараяны

Создать список номеров коров Нараяны.

Генерация псевдосовершенной числовой последовательности

Создать список полусовершенных чисел.

Создать последовательность номеров Ulam

Создать список номеров Ulam.

Создать последовательность странных чисел

Создать список странных чисел.

Создать последовательность суперсовершенных чисел

Создать список суперсовершенных чисел.

Продолжить числовую последовательность

Найти закономерность в числовой последовательности и расширить ее.

Разбить число

Найти все разбиения данного целого числа.

Генерировать числа Трибоначчи

Создать список чисел Трибоначчи.

Создание чисел Тетраначчи

Создание списка чисел Тетраначчи.

Создание чисел Пентаначчи

Создание списка чисел Пентаначчи.

Сгенерировать числа n-nacci

Создать список чисел Фибоначчи более высокого порядка.

Создать последовательность номеров разделов

Создать список номеров функций разделов.

Генерировать арифметическую прогрессию

Создать арифметическую последовательность чисел.

Создание геометрической прогрессии

Создание геометрической последовательности чисел.

Создание полиномиальной прогрессии

Создание полиномиальной последовательности чисел.

Создать последовательность натуральных чисел

Создать список натуральных чисел.

Создание степеней двойки

Создание списка чисел степеней двойки.

Создание степеней десяти

Создание списка чисел в степени десятка.

Сортировка матрицы

Сортировка строк или столбцов матрицы.

Зафиксировать матрицу

Установить допустимый диапазон для всех значений матрицы.

Рандомизировать матрицу

Перетасовать все элементы матрицы.

Удалить строки матрицы

Удалить одну или несколько строк данной матрицы.

Удалить столбцы матрицы

Удалить один или несколько столбцов данной матрицы.

Заменить элементы матрицы

Заменить определенные элементы матрицы другими значениями.

Установить определитель матрицы

Создать матрицу с заданным определителем.

Создать матрицу вращения

Создать матрицу вращения из заданного угла.

Декодирование матрицы вращения

Найдите угол по заданной матрице вращения.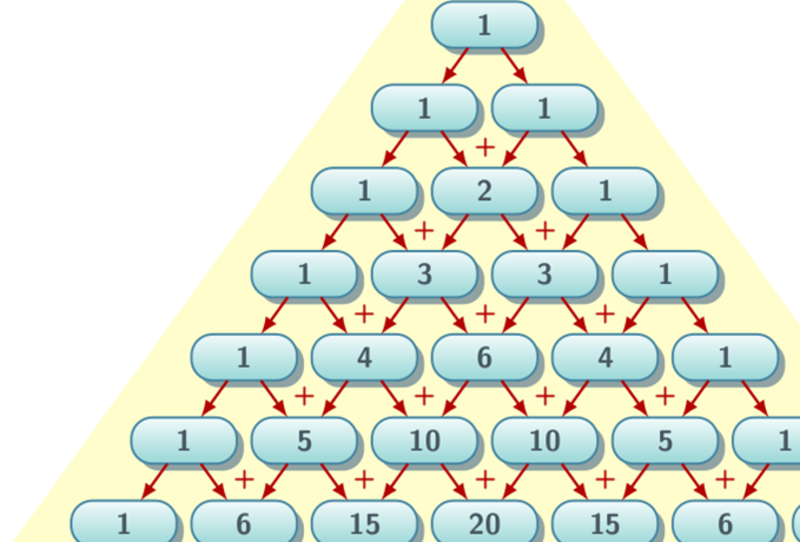

Создание пользовательской матрицы

Создание матрицы с определенными свойствами и элементами.

Создание плотной матрицы

Создание матрицы с очень небольшим количеством нулевых элементов.

Создать разреженную матрицу

Создать матрицу с очень небольшим количеством ненулевых элементов.

Генерация сингулярной матрицы

Генерация вырожденной матрицы с нулевым определителем.

Сгенерировать матрицу нулей

Сгенерировать матрицу со всеми нулями в качестве элементов.

Сгенерировать матрицу единиц

Сгенерировать матрицу со всеми 0 в качестве элементов.

Генерация бинарной матрицы

Генерация матрицы, состоящей из 0 и 1 в качестве элементов.

Создание квадратной матрицы

Создать матрицу с n строками и n столбцами (матрица n×n).

Создание симметричной матрицы

Создание матрицы с симметричными элементами по диагонали.

Создание треугольной матрицы

Создание верхней треугольной или нижней треугольной матрицы.

Сгенерировать диагональную матрицу

Сгенерировать матрицу с элементами, расположенными только по диагонали.

Создание ортогональной матрицы

Создание матрицы с ортогональными строками и столбцами.

Умножить матрицу на скаляр

Умножить все элементы матрицы на число.

Умножение матрицы на вектор

Умножение матрицы на вектор-столбец.

Умножение вектора на матрицу

Умножение вектора-строки на матрицу.

Разбить матрицу на векторы

Создать m или n векторов из матрицы m×n (из строк или столбцов).

Проверить, является ли матрица единственной.

Определить, является ли матрица вырожденной.

Поиск размеров матрицы

Найти количество строк и столбцов матрицы.

Найти матрицу кофакторов

Для заданной матрицы найти ее матрицу кофакторов.

Найдите вспомогательную матрицу

По заданной матрице найдите ее дополнение.

LU Factor a Matrix

Разложить матрицу на LU-факторы.

Найти собственные значения матрицы

Найти собственные значения матрицы.

Найти трассировку матрицы

Найти сумму элементов главной диагонали матрицы.

Найти сумму диагоналей матрицы

Найти сумму всех диагоналей или антидиагоналей матрицы.

Найти сумму строк матрицы

Найти сумму каждой строки матрицы.

Найти сумму столбцов матрицы

Найти сумму каждого столбца матрицы.

Найти сумму элементов матрицы

Найти сумму всех элементов матрицы.

Найти произведение элементов матрицы

Найти произведение всех элементов матрицы.

Украсить матрицу

Украсьте матрицу, аккуратно выровняв все ее столбцы.

Переформатировать матрицу

Преобразовать матрицу одного формата в другой формат.

Визуализация вектора

Нарисуйте двухмерный или трехмерный вектор, чтобы показать его величину и угол.

Сортировка вектора

Сортировка компонентов вектора.

Зафиксировать вектор

Установить допустимый диапазон для всех компонентов вектора.

Рандомизация вектора

Рандомизация порядка компонентов вектора.

Обрезать вектор

Удалить компоненты вектора.

Заменить компоненты вектора

Заменить определенные компоненты вектора другими значениями.

Украсьте вектор

Украсьте вектор и аккуратно выровняйте все его компоненты.

Переформатировать вектор

Преобразование вектора одного формата в другой формат.

Транспонировать вектор

Преобразовать вектор-строку в вектор-столбец.

Дублировать вектор

Создать несколько копий одного и того же вектора.

Увеличение вектора

Увеличение компонентов вектора.

Уменьшение вектора

Увеличение компонентов вектора.

Повернуть вектор

Повернуть вектор на любой угол.

Масштабирование вектора

Уменьшение или увеличение вектора с постоянным коэффициентом.

Вычислить угол вектора

Найти угол между двумя векторами.

Установить угол вектора

Создать пары векторов с заданным углом.

Нормализация вектора

Создать единичный вектор длины один из любого заданного вектора.

Создать случайный вектор

Создать один или несколько случайных векторов любой длины.

Создать пользовательский вектор

Создать пользовательский вектор с определенными компонентами.

Создать плотный вектор

Создать вектор с очень небольшим количеством нулевых компонентов.

Создать разреженный вектор

Создать вектор с большим количеством нулевых компонентов.

Создать нулевой вектор

Создать вектор, все компоненты которого равны нулю.

Создать вектор единиц

Создать вектор, все компоненты которого равны единице.

Создание единичного вектора

Создание одного или нескольких случайных векторов длины один.

Создать противоположные векторы

Создать пары антипараллельных векторов.

Создание параллельных векторов

Создание пар параллельных векторов.

Создание перпендикулярных векторов

Создание пар перпендикулярных векторов.

Создание ортогональных векторов

Создание пар ортогональных векторов.

Создание ортонормированных векторов

Создание пар перпендикулярных единичных векторов длины один.

Найти векторную норму

Вычислить L₁, L₂, L₃, L₄, L₅ и другие векторные нормы.

Найти длину вектора

Вычислить длину вектора.

Установка длины вектора

Создание векторов определенной длины.

Найти скалярное произведение вектора

Вычислить скалярное произведение двух векторов.

Установить скалярное произведение вектора

Найти два вектора с определенным значением скалярного произведения.

Найти векторное произведение

Вычислить векторное произведение двух векторов.

Задать перекрестное произведение векторов

Найти два вектора с заданным значением перекрестного произведения.

Найти скалярное тройное произведение

Вычислить смешанное произведение трех векторов.

Поиск векторного тройного произведения

Рассчитать векторное тройное произведение (задняя часть кабины).

Найти скалярное четверное произведение

Вычислить скалярное четверное произведение четырех векторов.

Найти четверное произведение векторов

Вычислить векторное произведение четырех векторов.

Смешать векторы

Смешать компоненты нескольких векторов.

Объединение векторов

Объединение двух или более векторов.

Добавить векторы

Найти сумму двух или более векторов.

Умножить векторы

Умножить два или более векторов.

Умножить вектор на константу

Умножить все компоненты вектора на скалярное значение.

Найти сумму компонентов вектора

Найти сумму всех компонентов вектора.

Найти произведение компонентов вектора

Найти произведение всех компонентов вектора.

Найти размеры вектора

Найти количество компонентов в векторе.

Вычислить синус

Вычислить синус угла.

Визуализация синуса

Нарисуйте функцию синуса.

Вычислить арксинус

Вычислить арксинус угла.

Визуализация арксинуса

Нарисуйте функцию арксинуса.

Вычислить косинус

Вычислить косинус угла.

Визуализация косинуса

Нарисуйте функцию косинуса.

Вычислить арккосинус

Вычислить арккосинус угла.

Визуализация арккосинуса

Нарисуйте функцию арккосинуса.

Вычислить тангенс

Вычислить тангенс угла.

Визуализация касательной

Нарисуйте функцию касательной.

Вычислить котангенс

Вычислить котангенс угла.

Визуализация котангенса

Нарисуйте функцию котангенса.

Вычислить косеканс

Вычислить косеканс угла.

Визуализация косеканса

Нарисуйте функцию косеканса.

Вычислить секанс

Вычислить секанс угла.

Визуализация секущей

Нарисуйте функцию секанса.

Рисование всех тригонометрических функций

Визуализация всех тригонометрических функций одновременно.

Рисование архимедовой спирали

Создание архимедовой спирали.

Рисование спирали Эйлера

Создание кривой спирали Корню (полиномиальной спирали).

Рисование спирали Фибоначчи

Создание кривой спирали Фибоначчи.

Рисование спирали Теодора

Создание спирали квадратного корня.

Нарисовать спираль Ферма

Создать кривую в виде параболической спирали.

Рисование прямоугольников Фибоначчи

Создание рисунка прямоугольников Фибоначчи.

Нарисуйте головку семени Фибоначчи

Создайте головку цветка Фибоначчи.

Нарисовать фрактал Падована

Создать фрактал равнобуквенных треугольников Падована.

Нарисуйте аполлонову прокладку

Создайте фрактал аполлоновой прокладки.

Нарисовать фрактал Мандельброта

Создать фрактал Мандельброта.

Нарисовать фрактал Джулии

Создать фрактал Джулии.

Нарисовать фрактал Рози

Создать фрактал Рози.

Нарисовать кривую фрактала Бланманже

Создать фрактал Бланманже.

Рисование функции Вейерштрасса

Создание фрактала Вейерштрасса.

Нарисовать кривую Минковского в виде вопросительного знака

Создать фрактал Минковского в виде вопросительного знака.

Нарисуйте функцию Тома

Создайте функцию Тома (также известную как функция попкорна или капли дождя).

Нарисовать функцию Дирихле

Создать функцию Дирихле.

Нарисуйте рог Гавриила

Нарисуйте геометрическую фигуру с бесконечной площадью поверхности и конечным объемом.

Преобразование слов в числа

Преобразование чисел из английского текста в реальные цифры.

Преобразование чисел в слова

Преобразование чисел в письменный текст на английском языке.

Преобразование десятичной записи в научную запись

Преобразование чисел, записанных в десятичной форме, в научную форму.

Преобразование научной записи в десятичную

Преобразование чисел, записанных в научной форме, в десятичную форму.

Округление чисел вверх

Применение операции ceil к числам.

Округление чисел в меньшую сторону

Применить операцию пола к числам.

Анализ чисел

Подсчитайте, сколько раз встречается каждое число.

Преобразование числа в виде суммы

Создайте сумму, которая в сумме равна заданному числу.

Переписать число как продукт

Создайте продукт, который умножается до заданного числа.

Создать таблицу умножения

Нарисовать таблицу умножения n×m.

Создать таблицу сложения

Нарисовать таблицу сложения n×m.

Создать таблицу делений

Нарисовать таблицу делений n×m.

Создание модульной арифметической таблицы

Нарисуйте модульную арифметическую таблицу размера n×m для любого модуля.