Интегрирование по частям. Вторая часть.
Высшая математика » Неопределённые интегралы » Интегрирование по частям » Вторая часть.
Первая часть
Вторая часть
В этой части мы продолжим тему интегрирования по частям в неопределённом интеграле, начатую здесь. Вновь нам будут нужны таблица неопределенных интегралов и таблица производных. Перед прочтением данной страницы рекомендую ознакомиться с предыдущей частью, ибо там были даны полные пояснения к каждому примеру. Здесь же будут затронуты интегралы, которые не подпадают под стандартные правила, указаные в первой части, но, тем не менее, берутся с помощью интегрирования по частям. Мы будем использовать ту же формулу, что и ранее:
$$ \begin{equation} \int u \; dv=u\cdot v-\int v\; du \end{equation} $$
Также рассмотрим интегралы, при вычислении которых получается уравнение относительно исходного интеграла.
Пример №7
Найти $\int\cos\ln x\;dx$.
Решение
Метод решения данного примера аналогичен применённому в предыдущем примере №6:
$$ \int\cos\ln x\;dx=\left | \begin{aligned} & u=\cos\ln x; \; du=-\frac{\sin\ln x}{x}dx.\\ & dv=dx; \; v=x. \end{aligned} \right| =x\cdot \cos\ln x+\int x\cdot\frac{\sin\ln x}{x}dx=\\ =x\cdot \cos\ln x+\int \sin\ln x dx=\left | \begin{aligned} & u=\sin\ln x; \; du=\frac{\cos\ln x}{x}dx.\\ & dv=dx; \; v=x. \end{aligned} \right|=\\ =x\cdot \cos\ln x+x\cdot\sin\ln x-\int x\cdot\frac{\cos\ln{x}}{x}dx =x\cdot \cos\ln x+x\cdot\sin\ln x-\int \cos\ln x \;dx $$
Итак, мы получили уравнение с искомым интегралом:
$$ \int\cos\ln x\;dx=x\cdot \cos\ln x+x\cdot\sin\ln x-\int \cos\ln x \;dx $$
Перенося $\int \cos\ln x \;dx$ из правой части в левую, будем иметь:
$$
2\int\cos\ln x\;dx=x\cdot \cos\ln x+x\cdot\sin\ln x+2C. $$
$$
Деля обе части последнего равенства на $2$, получим:
$$ \int\cos\ln x\;dx=\frac{1}{2}x\cdot \cos\ln x+\frac{1}{2}x\cdot\sin\ln x+C=\frac{x}{2}\cdot (\cos\ln x+\sin\ln x)+C. $$
Ответ: $\int\cos\ln x\;dx=\frac{x}{2}\cdot (\cos\ln x+\sin\ln x)+C$.
Полагаю, что у читателя тут не обойдётся без вопроса, который я изложу ниже.
Вопрос №1
Постойте, тут что-то не сходится. Откуда вообще взялась константа $C$? У нас было равенство
$$ \int\cos\ln x\;dx=x\cdot \cos\ln x+x\cdot\sin\ln x-\int \cos\ln x \;dx. $$
Если перенести $\int \cos\ln x \;dx$ в левую часть, то никакой константы не возникнет, а будет вот что:
$$ 2\int\cos\ln x\;dx=x\cdot \cos\ln x+x\cdot\sin\ln x. $$
Тут вообще нет константы! Как же она возникла в изложенном выше решении?
Ответ
Для того, чтобы разобраться с «внезапно возникшей» контантой, нужно вспомнить, что такое неопределённый интеграл.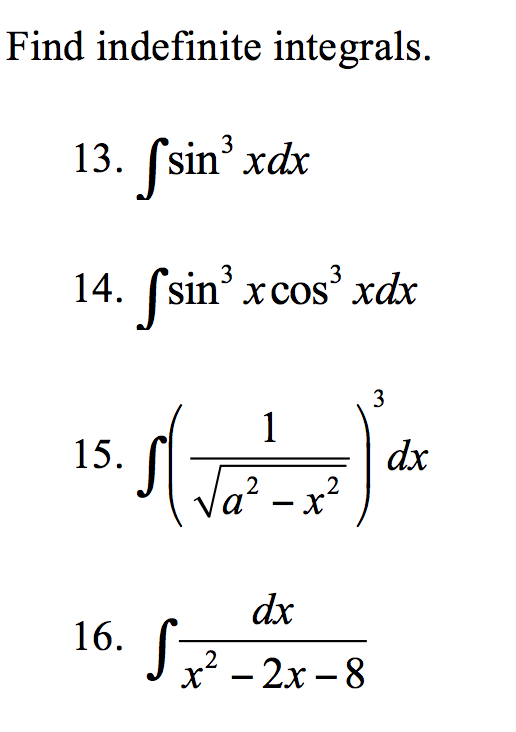 3{x}}+\frac{3\tg{x}}{8\cos{x}}+\frac{3}{8}\ln\left|\tg\left(\frac{\pi}{4}+\frac{x}{2}\right)\right|+C
$$
3{x}}+\frac{3\tg{x}}{8\cos{x}}+\frac{3}{8}\ln\left|\tg\left(\frac{\pi}{4}+\frac{x}{2}\right)\right|+C
$$
Ответ:
Первая часть
Вторая часть
Вернуться к списку тем
Задать вопрос на форуме
Записаться на занятия
Онлайн-занятия по высшей математике
Интеграл от sin 3x — Формула, доказательство
Интеграл от sin 3x определяется выражением (-1/3) cos 3x + C. Интеграл от sin 3x называется антипроизводной от sin 3x, так как интегрирование является обратным дифференцирование процесса. Sin 3x — важная тригонометрическая формула, которая используется для решения различных задач по тригонометрии. Интеграл от sin 3x можно вычислить методом подстановки и по формуле sin 3x.
В этой статье мы вычислим интеграл от sin 3x, докажем его методом подстановки и формулой sin 3x и определим определенный интеграл от sin 3x, используя разные пределы.
1. | Что такое интеграл от Sin 3x? |
| 2. | Интеграл греха 3x Формула |
| 3. | Интеграл от Sin 3x с использованием метода подстановки |
| 4. | Интеграл от Sin 3x с использованием формулы Sin 3x |
| 5. | Определенный интеграл от греха 3x |
| 6. | FAQ по Integral of Sin 3x |
Что такое интеграл от Sin 3x?
Интеграл от sin 3x можно вычислить, используя формулу для интеграла от sin ax, которая задается как ∫sin (ax) dx = (-1/a) cos ax + C. Математически интеграл от sin 3x записывается как ∫sin 3x dx = (-1/3) cos 3x + C, где C — постоянная интегрирования, dx означает, что интегрирование sin 3x производится по x, ∫ — символ интегрирования. Интеграл от sin 3x также можно вычислить с помощью метода подстановки и формулы sin 3x.
Интеграл греха 3x Формула
Формула Sin 3x задается как sin 3x = 3 sin x — 4 sin 3 x, а формула интеграла от sin 3x определяется как ∫sin 3x dx = (-1/3) cos 3x + C, где C — постоянная интегрирования.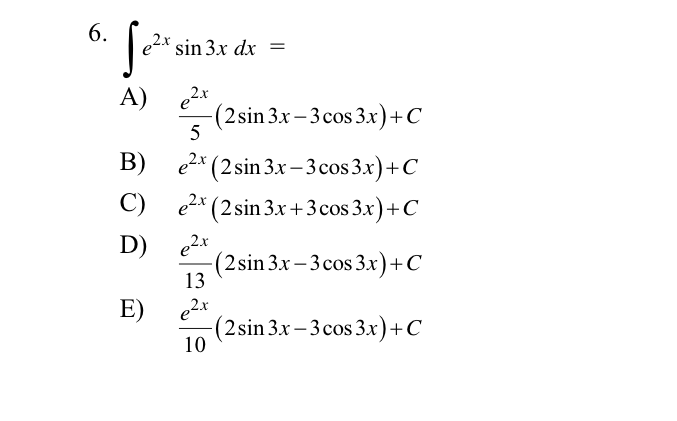
Интеграл от Sin 3x с использованием метода подстановки
Теперь мы знаем, что интеграл от sin 3x равен (-1/3) cos 3x + C, где C — постоянная интегрирования. Докажем это методом подстановки. Будем использовать следующие формулы интегрирования и дифференцирования:
- ∫sin x dx = -cos x + C
- d(ax)/dx = а
Предположим, что 3x = u, тогда, продифференцировав 3x = u по x, мы получим 3dx = du ⇒ dx = (1/3)du. Используя приведенные выше формулы, мы имеем
∫sin 3x dx = ∫sin u (du/3)
⇒ ∫sin 3x dx = (1/3) ∫sin u du
⇒ ∫sin 3x dx = (1/ 3) (-cos u + C) [Поскольку ∫sin x dx = -cos x + C]
⇒ ∫sin 3x dx = (-1/3) cos u + C/3
⇒ ∫sin 3x dx = (-1/3) cos 3x + K, где K = C/3
Таким образом, мы получили интеграл от sin 3x методом подстановки.
Интеграл Sin 3x с использованием формулы Sin 3x
Мы знаем, что формула sin 3x выглядит так: sin 3x = 3 sin x — 4 sin 3 x.
- cos 2 x + sin 2 x = 1 ⇒ sin 2 x = 1 — cos 2 x
- ∫sin x dx = -cos x dx
∫sin 3 х dx = ∫sin х. sin 2 x dx
= ∫sin x.(1 — cos 2 x) dx
= ∫sin x dx — ∫sin x. cos 2 x dx — (1)
= I 1 — I 2 , где I 1 = ∫sin x dx и I 2 = ∫sin x. 2 x dx
Теперь I 1 = ∫sin x dx = -cos x + C 1 , где C 1 – постоянная интегрирования —- (2)
Для I 2 = ∫sinx. cos 2 x dx, предположим, что cos x = u ⇒ -sin x dx = du ⇒ sin x dx = -du
I 2 = ∫sin x. cos 2 x dx
cos 2 x dx
= ∫u 2 (-du)
= — ∫u 2 du
= — u 3 9 01 /13 + C 2 90 0131 2 есть постоянная интегрирования
= (-1/3) cos 3 x + C 2 —- (3)
Подставить значения из (2) и (3) в (1),
∫sin 3 x dx = (-cos x + C 1 ) — ((-1/3) cos 3 x + C 2 )
= -cos x + (1/3) cos 3 x + C 1 — C 2
= -cos x + (1/3) cos 3 x + C, где C = C 1 — C 2
⇒ 09 09 09 09 09 0 x dx = -cos x + (1/3) cos 3 x + C — (4)
Теперь, когда мы получили интеграл от sin 3 x, мы будем использовать эту формулу вместе с некоторыми другими формулами для получения интеграла от sin 3x:
- ∫sin x дх = -cos х дх
- ∫sin 3 x dx = -cos x + (1/3) cos 3 x + C
- sin 3x = 3 sin x — 4 sin 3 x
- cos 3x = 4 cos 3 x — 3 cos x
Используя приведенные выше формулы, мы имеем
∫sin 3x dx = ∫(3 sin x — 4 sin 3 x) dx
= 3 ∫sin x dx — 4 ∫sin 3 x dx
= 3(-cos x) — 4(-cos x + (1/3) cos 3 x) + C, где C — постоянная интегрирования
= -3 cos x + 4 cos x — (4/3)cos 3 x + C
= cos x — (4/3)cos 3 x + C
= (1/3)(3cos x — 4cos 3 x + 3C)
= (1/3)(-cos 3x + 3C) [Потому что cos 3x = 4cos 3 x — 3 cos x]
= (-1/3) cos 3x + C
Следовательно, мы получили интегрирование sin 3x по формуле sin 3x.
Следовательно, значение определенного интегрирования sin 3x в пределах от 0 до π/2 равно 1/3.
Важные замечания по интегралу от sin 3x
- Самый простой способ определить интеграл от sin 3x — использовать формулу ∫sin (ax) dx = (-1/a) cos ax + C.
- Интеграл от sin 3x равен (-1/3) cos 3x + C, а интеграл от куба sin x равен ∫sin 3 x dx -cos x + (1/3) cos 3 x + C.
Связанные темы
- Интеграл тангенса 2x
- Кос 3x
- Грех 3x
FAQ по Integral of Sin 3x
Что такое интеграл от Sin 3x в тригонометрии?
В тригонометрии интеграл от sin 3x записывается как ∫sin 3x dx = (-1/3) cos 3x + C, где C — постоянная интегрирования.