Как найти периметр основания треугольника. Как найти периметр треугольника если известны не все стороны
Как найти периметр треугольника? Таким вопросом задавался каждый из нас, учась в школе. Попробуем вспомнить все, что мы знаем об этой удивительной фигуре, а также ответить на заданный вопрос.
Ответ на вопрос о том, как найти периметр треугольника, обычно является довольно-таки простым — требуется всего-лишь выполнить процедуру сложения длин всех его сторон. Однако есть ещё несколько простых методов искомой величины.
Советы
В том случае, если радиус (r) окружности, которая вписана в треугольник, и его площадь (S) известны, то ответить на вопрос о том, как найти периметр треугольника, довольно просто. Для этого вам необходимо воспользоваться обычной формулой:
Если известны два угла, допустим, α и β, которые прилегают к стороне, и сама длина стороны, то периметр можно найти с помощью весьма и весьма популярной формулы, которая имеет вид:
sinβ∙а/(sin(180° — β — α)) + sinα∙а/(sin(180° — β — α)) + а
Если вы знаете длины смежных сторон и угол β, находящийся между ними, то для того, чтобы найти периметр, требуется воспользоваться теоремой косинусов.
P = b + a + √(b2 + a2 — 2∙b∙а∙cosβ),
где b2 и а2 являются квадратами длин смежных сторон. Подкоренное выражение — это длина третьей стороны, которая неизвестна, выраженная посредством теоремы косинусов.
Если вы не знаете, как найти периметр равнобедренного треугольника, то здесь, на самом деле, нет ничего сложного. Вычислите его по формуле:
где b — основание треугольника, а — его боковые стороны.
Для нахождения периметра правильного треугольника следует воспользоваться простейшей формулой:
где а — длина стороны.
Как найти периметр треугольника, если известны только радиусы окружностей, которые описаны около него или вписаны в него? Если треугольник является равносторонним, то тогда следует применить формулу:
P = 3R√3 = 6r√3,
где R и r являются радиусами описанной и вписанной окружности соответственно.
Если треугольник является равнобедренным, то для него применима формула:
P=2R (sinβ + 2sinα),
где α — это угол, который лежит у основания, а β — угол, который противолежит основанию.
Зачастую для решения математических задач требуется глубочайший анализ и специфическое умение находить и выводить требуемые формулы, а это, как многим известно, довольно непростая работа. Хотя некоторые задачи можно решить всего лишь с помощью одной-единственной формулы.
Давайте рассмотрим формулы, которые являются базовыми для ответа на вопрос о том, как найти периметр треугольника, по отношению к самым разнообразным типам треугольников.
Безусловно, главное правило для нахождения периметра треугольника — это данное утверждение: для нахождения периметра треугольника требуется сложить длины всех его сторон по соответствующей формуле:
где b, a и с — это длины сторон треугольника, а Р — периметр треугольника.
Есть несколько частных случаев данной формулы. Допустим, ваша задача формулируется следующим образом: «как найти периметр прямоугольного треугольника?» В таком случае вам следует воспользоваться следующей формулой:
P = b + a + √(b2 + a2)
В этой формуле b и а являются непосредственными длинами катетов прямоугольного треугольника. Несложно догадаться, что вместо стороны с (гипотенузы) используется выражение, полученное по теореме великого ученного древности — Пифагора.
Несложно догадаться, что вместо стороны с (гипотенузы) используется выражение, полученное по теореме великого ученного древности — Пифагора.
Если требуется решить задачу, где треугольники являются подобными, то логично было бы воспользоваться данным утверждением: отношение периметров соответствует коэффициенту подобия. Допустим, у вас есть два подобных треугольника — ΔABC и ΔA1B1C1. Тогда для нахождения коэффициента подобия необходимо разделить периметр ΔABC на периметр ΔA1B1C1.
В заключение можно отметить, что периметр треугольника можно найти при помощи самых различных методик, в зависимости от тех исходных данных, которые у вас имеются. Необходимо добавить, что существуют некоторые частные случаи для прямоугольных треугольников.
Периметр — это величина, подразумевающая длину всех сторон плоской (двумерной) геометрической фигуры. Для разных геометрических фигур существуют разные способы нахождения периметра.
В данной статье вы узнаете как находить периметр фигуры разными способами, в зависимости от известных его граней.
Вконтакте
Возможные методы:
- известны все три стороны равнобедренного или любого другого треугольника;
- как найти периметр прямоугольного треугольника при двух известных его гранях;
- известны две грани и угол, который расположен между ними (формула косинусов) без средней линии и высоты.
Первый метод: известны все стороны фигуры
Как находить периметра треугольника, когда известны все три грани , необходимо использовать следующую формулу: P = a + b + c, где a,b,c — известные длины всех сторон треугольника, P — периметр фигуры.
Например, известны три стороны фигуры: a = 24 см, b = 24 см, c = 24 см. Это правильная равнобедренная фигура, чтобы вычислить периметр пользуемся формулой: P = 24 + 24 + 24 = 72 см.
Данная формула подходит к любому треугольнику , необходимо просто знать длины всех его сторон. Если хотя бы одна из них неизвестна, необходимо воспользоваться другими способами, о которых мы поговорим ниже.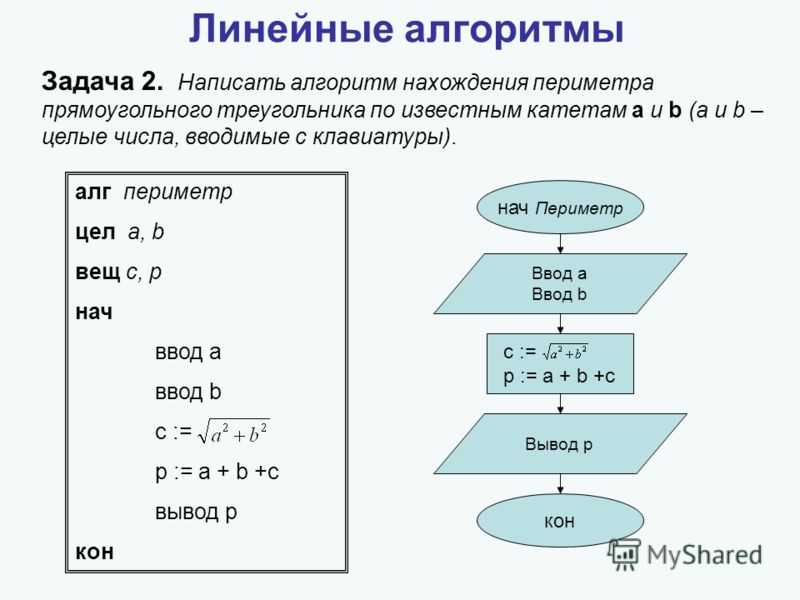 2 — (2 * a * b * cos(C)), где a,b,c — стандартно длины граней, а A,B и С — это углы, которые лежат напротив соответствующих граней треугольника. То есть, A — угол, противолежащий стороне a и так далее.
2 — (2 * a * b * cos(C)), где a,b,c — стандартно длины граней, а A,B и С — это углы, которые лежат напротив соответствующих граней треугольника. То есть, A — угол, противолежащий стороне a и так далее.
Представим, что описан треугольник, стороны а и б которого составляют 100 см и 120 см соответственно, а угол, лежащий между ними, составляет 97 градусов. То есть а = 100 см, б = 120 см, C = 97 градусов.
Все, что нужно сделать в данном случае — это подставить все известные значения в теорему косинусов. Длины известных граней возводятся в квадрат, после чего известные стороны перемножаются между друг другом и на два и умножаются на косинус угла между ними. Далее, необходимо сложить квадраты граней и отнять от них второе полученное значение. Из итоговой величины извлекается квадратный корень — это будет третья, неизвестная до этого сторона.
После того как все три грани фигуры известны, осталось воспользоваться уже полюбившейся нам стандартной формулой поиска периметра описываемой фигуры из первого метода.
Периметр фигуры – сумма длин всех ее сторон. Соответственно, дабы обнаружить периметр
Инструкция
1. Если все три стороны треугольника теснее даны в условии задачи, легко сложите их. Тогда периметр будет равен: P = a + b + c.
2. Пускай даны две стороны a, b и угол между ними?. Тогда третью сторону дозволено обнаружить по теореме косинусов: c? = a? + b? – 2 a b cos(?). Помните, что длина стороны может быть только позитивной.
3. Частный случай теоремы косинусов – теорема Пифагора, которая применима для прямоугольных треугольников. Угол? в данном случае равен 90°. Косинус прямого угла обращается в единицу. Тогда c? = a? + b?.
4. Если в условии дана только одна из сторон, но при этом вестимы углы треугольника, две другие стороны дозволено обнаружить по теореме синусов.
5. Выходит, пускай дана сторона a, угол? между a и b, ? между a и c. 3-й угол? между сторонами b и c легко обнаружить из теоремы о сумме углов треугольника: ? = 180° – ? – ?. По теореме синусов, a / sin(?) = b / sin(?) = c / sin(?) = 2 R, где R – радиус окружности, описанной около треугольника. Дабы обнаружить сторону b, дозволено выразить ее из этого равенства через углы и сторону a: b = a sin(?) / sin(?). Подобно выражается и сторона c: c = a sin(?) / sin(?). Если, скажем, дан радиус описанной окружности, но не дана длина ни одной из сторон, задачу также допустимо решить.
6. Если в задаче дана площадь фигуры, нужно записать формулу для площади треугольника через стороны. Выбор формулы зависит от того, что еще знаменито. Если, помимо площади, заданы две стороны, поможет использование формулы Герона. Площадь дозволено выразить также через две стороны и синус угла между ними: S = 1/2 a b sin(?), где? – угол между сторонами a и b.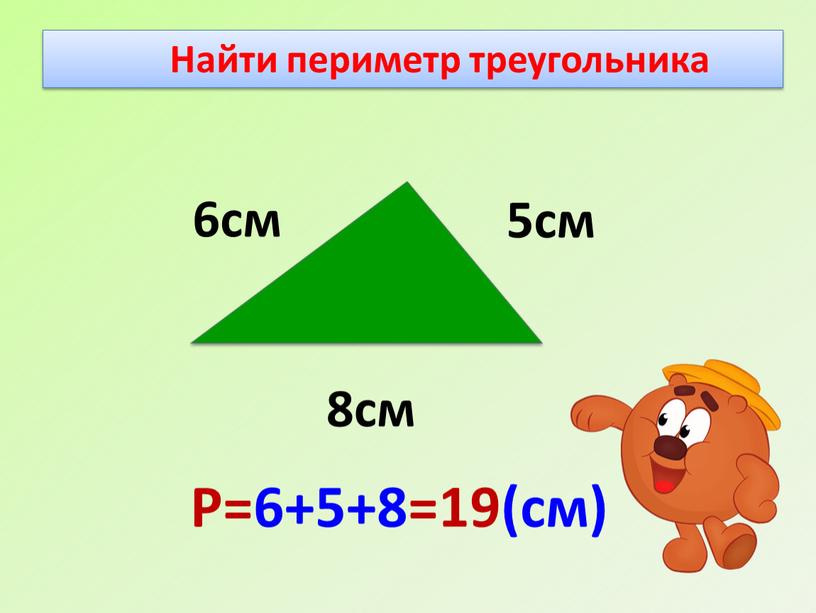
7. В некоторых задачах может быть задана площадь и радиус окружности, вписанной в треугольник. В таком случае выручит формула r = S / p, где r – радиус вписанной окружности, S – площадь, p – полупериметр треугольника. Полупериметр из этой формулы выразить легко: p = S / r. Осталось обнаружить периметр: P = 2 p.
Треугольник – это многоугольник, имеющий три стороны и три угла. Как же вычислить его периметр?
Инструкция
1. Периметр треугольника – это сумма длин всех его 3 сторон.Обозначим стороны треугольника а, b, c. Периметр в математических формулах обозначается латинской буквой Р. Значит, исходя из правила, Р = а + b + cДопустим, наши стороны треугольника имеют такие длины: а = 3 см, b = 4 см, с = 5 смЧтобы обнаружить периметр данного треугольника – необходимо сложить длины всех его сторон.Т.е. Р = 3 + 4 + 5Р = 12 смНе трудная задача, чай правда?
Видео по теме
Видео по теме
Как найти периметр треугольника? Таким вопросом задавался каждый из нас, учась в школе.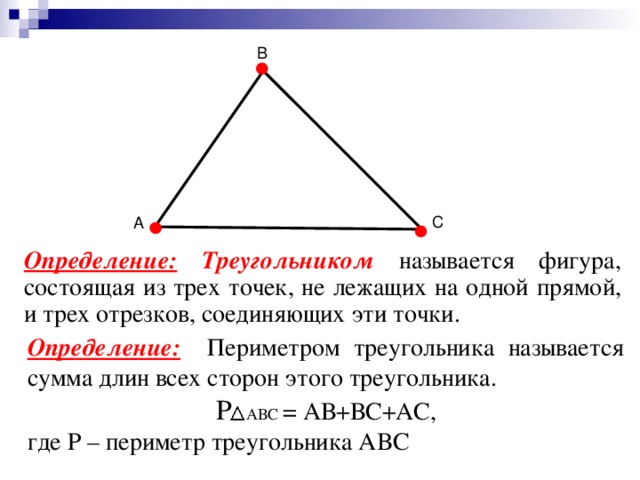 Попробуем вспомнить все, что мы знаем об этой удивительной фигуре, а также ответить на заданный вопрос.
Попробуем вспомнить все, что мы знаем об этой удивительной фигуре, а также ответить на заданный вопрос.
Ответ на вопрос о том, как найти периметр треугольника, обычно является довольно-таки простым — требуется всего-лишь выполнить процедуру сложения длин всех его сторон. Однако есть ещё несколько простых методов искомой величины.
В том случае, если радиус (r) окружности, которая вписана в треугольник, и его площадь (S) известны, то ответить на вопрос о том, как найти периметр треугольника, довольно просто. Для этого вам необходимо воспользоваться обычной формулой:
Если известны два угла, допустим, α и β, которые прилегают к стороне, и сама длина стороны, то периметр можно найти с помощью весьма и весьма популярной формулы, которая имеет вид:
sinβ∙а/(sin(180° — β — α)) + sinα∙а/(sin(180° — β — α)) + а
Если вы знаете длины смежных сторон и угол β, находящийся между ними, то для того, чтобы найти периметр, требуется воспользоваться Периметр вычисляется по формуле:
P = b + a + √(b2 + a2 — 2∙b∙а∙cosβ),
где b2 и а2 являются квадратами длин смежных сторон. Подкоренное выражение — это длина третьей стороны, которая неизвестна, выраженная посредством теоремы косинусов.
Подкоренное выражение — это длина третьей стороны, которая неизвестна, выраженная посредством теоремы косинусов.
Если вы не знаете, как найти периметр то здесь, на самом деле, нет ничего сложного. Вычислите его по формуле:
где b — основание треугольника, а — его боковые стороны.
Для нахождения периметра правильного треугольника следует воспользоваться простейшей формулой:
где а — длина стороны.
Как найти периметр треугольника, если известны только радиусы окружностей, которые описаны около него или вписаны в него? Если треугольник является равносторонним, то тогда следует применить формулу:
P = 3R√3 = 6r√3,
где R и r являются радиусами описанной и вписанной окружности соответственно.
Если треугольник является равнобедренным, то для него применима формула:
P=2R (sinβ + 2sinα),
где α — это угол, который лежит у основания, а β — угол, который противолежит основанию.
Зачастую для решения математических задач требуется глубочайший анализ и специфическое умение находить и выводить требуемые формулы, а это, как многим известно, довольно непростая работа. Хотя некоторые задачи можно решить всего лишь с помощью одной-единственной формулы.
Хотя некоторые задачи можно решить всего лишь с помощью одной-единственной формулы.
Давайте рассмотрим формулы, которые являются базовыми для ответа на вопрос о том, как найти периметр треугольника, по отношению к самым разнообразным типам треугольников.
Безусловно, главное правило для нахождения периметра треугольника — это данное утверждение: для нахождения периметра треугольника требуется сложить длины всех его сторон по соответствующей формуле:
где b, a и с — это длины сторон треугольника, а Р — периметр треугольника.
Есть несколько частных случаев данной формулы. Допустим, ваша задача формулируется следующим образом: «как найти периметр прямоугольного треугольника?» В таком случае вам следует воспользоваться следующей формулой:
P = b + a + √(b2 + a2)
В этой формуле b и а являются непосредственными длинами катетов прямоугольного треугольника. Несложно догадаться, что вместо стороны с (гипотенузы) используется выражение, полученное по теореме великого ученного древности — Пифагора.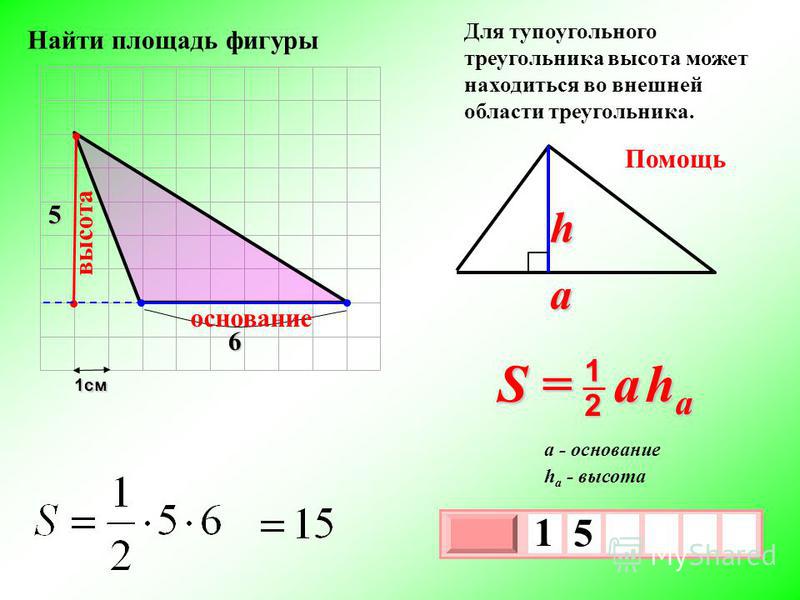
Если требуется решить задачу, где треугольники являются подобными, то логично было бы воспользоваться данным утверждением: отношение периметров соответствует коэффициенту подобия. Допустим, у вас есть два подобных треугольника — ΔABC и ΔA1B1C1. Тогда для нахождения коэффициента подобия необходимо разделить периметр ΔABC на периметр ΔA1B1C1.
В заключение можно отметить, что периметр треугольника можно найти при помощи самых различных методик, в зависимости от тех исходных данных, которые у вас имеются. Необходимо добавить, что существуют некоторые частные случаи для прямоугольных треугольников.
Как найти периметр треугольника
Можете призвать на помощь Яндекс. Впишите в поисковую строку:
периметр треугольника
Яндекс вам предложит вот такой вот интерфейс, куда нужно будет просто подставить значения.
Периметр — это сумма длин всех сторон любого многоугольника. Потому, не задумываясь над тем, какая перед вами геометрическая фигура, смело измеряйте линейкой длину всех сторон и суммируйте. Вот и получите периметр.
Если мы говорим об основах геометрии, то периметр это сумма всех сторон треугольника: Р=а+b+с.
Однако, если речь идт о более сложных геометрических и тригонометрических задачах, когда нам даны определнные данные, то есть несколько других формул, для вычисления периметра треугольника:
Если известны радиус вписанной в треугольник окружности и его площадь, то периметр вычисляется по формуле: P=2S/r.
Если известны два угла, например, amp;#945; и amp;#946;, прилежащих к одной стороне, и длина этой стороны, то формула для периметра следующая: Р=а+sinamp;#945;amp;#8729;а/(sin(180-amp;#945;-amp;#946;)) + sinamp;#946;amp;#8729;а/(sin(180-amp;#945;-amp;#946;)).
Если есть длины смежных сторон и угол amp;#946; между ними, то периметр вычисляется при помощи формулы теоремы косинусов: P=a+b+amp;#8730;(а2+b2-2amp;#8729;aamp;#8729;bamp;#8729;cosamp;#946;), где а2 и b2 квадраты длин смежных сторон. Выражение под корнем длина третьей неизвестной стороны, выраженная через теорему косинусов.
Периметр равнобедренного треугольника имеет следующий вид P=2a+b, где а боковые стороны, а b его основание.
Периметр правильного треугольника: P=3a.
Формула периметра для равностороннего треугольник, если известен радиус вписанной в него окружности P=6ramp;#8730;3, или радиус описанной около него окружности Р=3Ramp;#8730;3, где r и R соответственно радиусы вписанной или описанной окружности.
Для равнобедренного треугольника есть формула: P=2R(2sinamp;#945;+sinamp;#946;), где amp;#945; угол при основании, amp;#946; угол, противолежащий основанию.
Смотря на то, что вам известно из постановки задачи.
Самый простой вариант — сложить длины всех сторон.
В равностороннем треугольнике — длина стороны умножается на три.
По формуле P=2S/r, если известны S — площадь и r — радиус вписанной окружности.
Так же есть формулы для нахождения площади треугольника, если известны его углы.
Если треугольник равносторонний, то чтобы найти его периметр нужно длину одной стороны умножить на три. А если треугольник разносторонний, тогда чтобы найти его периметр нужно сложить длины всех его сторон.
Чтобы найти периметр равностороннего треугольника, нужно длину одной стороны умножить на три.
Чтобы найти периметр равнобедренного треугольника, нужно взять длину одной из равных по длине сторон, умножить на два и прибавить длину основания.
Взять в руки линейку, измерить каждую сторону треугольника (если он равносторонний, то можно измерить только одну) и сложить длины его сторон. В случае равностороннего треугольника длину его стороны умножаем на 3.
В уме, в столбик, на калькуляторе — как сможете, в завсисмости от математических способностей и наличия-отсутствия калькулятора.
Найти периметр треугольника , если известна длина каждой из его сторон, просто нужно сложить длины сторон и получим периметр: (P=a+b+c ).
Еще проще найти периметр равностороннего треугольника нужно просто умножить длину его стороны на 3: (P=3a) .
Но чаще потребность в расчете периметра возникает тогда, когда известна длина не всех его сторон.
Поэтому, если известна одна сторона треугольника c и прилегающие к ней углы, то формула расчета периметра будет выглядеть так:
Периметр треугольника находится просто.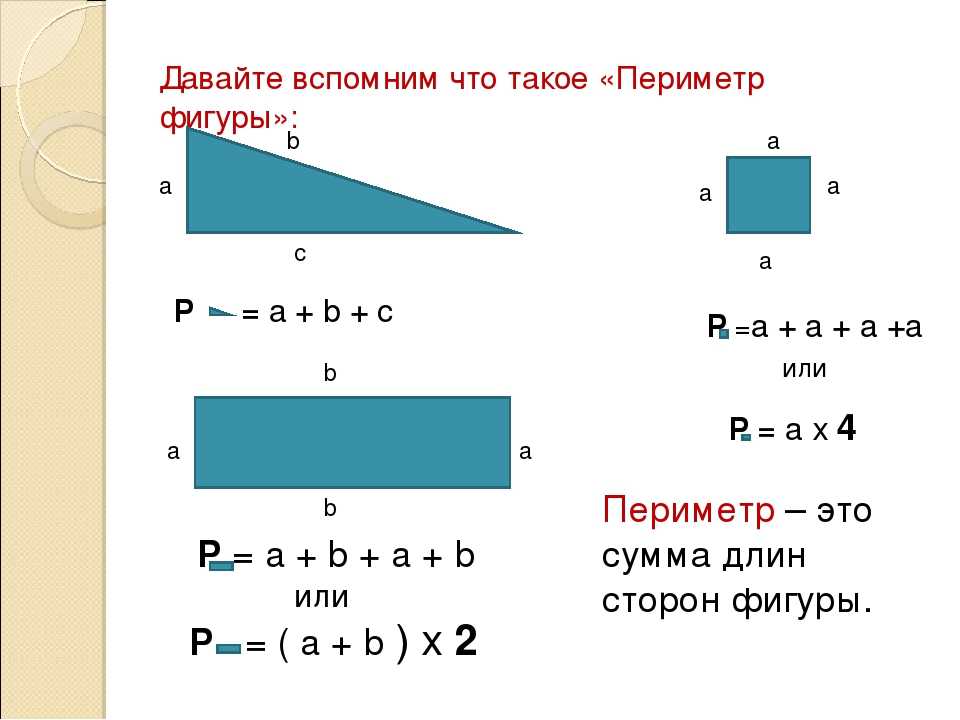 Периметр это длина трх сторон треугольника. Надо сложить первую сторону, вторую сторону и третью сторону — общая длина трх сторон и будет периметром треугольника .
Периметр это длина трх сторон треугольника. Надо сложить первую сторону, вторую сторону и третью сторону — общая длина трх сторон и будет периметром треугольника .
Периметр — это сума длин сторон. Надо просуммировать длины всех сторон треугольника. Или я что-то неправильно поняла? Какие исходные данные задачи?
Чтобы найти периметр треугольника, Вам необходимо сложить длины всех трех его сторон. Если треугольник равнобедренный, то можно длину одного ребра умножить на 2 и прибавить длину основания, таким образом получится периметр равнобедренного треугольника.
Периметр треугольника с прямым углом. Как найти периметр треугольника если известны не все стороны. Полезное видео: задачи на периметр труегольника
Периметр – это величина, подразумевающая длину всех сторон плоской (двумерной) геометрической фигуры. Для разных геометрических фигур существуют разные способы нахождения периметра.
В данной статье вы узнаете как находить периметр фигуры разными способами, в зависимости от известных его граней.
Возможные методы:
- известны все три стороны равнобедренного или любого другого треугольника;
- как найти периметр прямоугольного треугольника при двух известных его гранях;
- известны две грани и угол, который расположен между ними (формула косинусов) без средней линии и высоты.
Первый метод: известны все стороны фигуры
Как находить периметра треугольника, когда известны все три грани , необходимо использовать следующую формулу: P = a + b + c, где a,b,c – известные длины всех сторон треугольника, P – периметр фигуры.
Например, известны три стороны фигуры: a = 24 см, b = 24 см, c = 24 см. Это правильная равнобедренная фигура, чтобы вычислить периметр пользуемся формулой: P = 24 + 24 + 24 = 72 см.
Данная формула подходит к любому треугольнику , необходимо просто знать длины всех его сторон. Если хотя бы одна из них неизвестна, необходимо воспользоваться другими способами, о которых мы поговорим ниже.
Еще один пример: a = 15 см, б = 13 см, c = 17 см. 2 – (2 * a * b * cos(C)), где a,b,c – стандартно длины граней, а A,B и С – это углы, которые лежат напротив соответствующих граней треугольника. То есть, A – угол, противолежащий стороне a и так далее.
2 – (2 * a * b * cos(C)), где a,b,c – стандартно длины граней, а A,B и С – это углы, которые лежат напротив соответствующих граней треугольника. То есть, A – угол, противолежащий стороне a и так далее.
Представим, что описан треугольник, стороны а и б которого составляют 100 см и 120 см соответственно, а угол, лежащий между ними, составляет 97 градусов. То есть а = 100 см, б = 120 см, C = 97 градусов.
Все, что нужно сделать в данном случае – это подставить все известные значения в теорему косинусов. Длины известных граней возводятся в квадрат, после чего известные стороны перемножаются между друг другом и на два и умножаются на косинус угла между ними. Далее, необходимо сложить квадраты граней и отнять от них второе полученное значение. Из итоговой величины извлекается квадратный корень – это будет третья, неизвестная до этого сторона.
После того как все три грани фигуры известны, осталось воспользоваться уже полюбившейся нам стандартной формулой поиска периметра описываемой фигуры из первого метода.
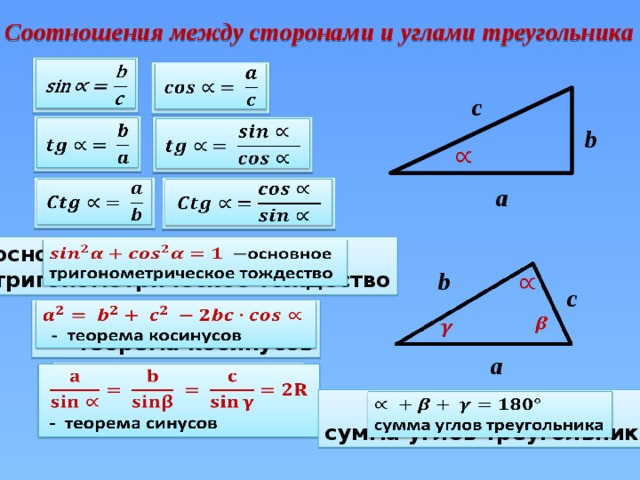
Прямоугольный треугольник — простая, но крайне важная для математики фигура. Знание о его свойствах и умение оперировать основными параметрами прямоугольного треугольника позволит вам справиться как со школьными, так и с реальными задачами.
Геометрия прямоугольного треугольника
Геометрически треугольник — это три точки, не лежащие на одной прямой, которые соединены между собой отрезками. Прямоугольный треугольник — фигура, две стороны которой образуют прямой угол. Эти стороны называются катетами треугольника, а третья, самая длинная сторона, носит название гипотенузы. Соотношение квадратов катетов и гипотенузы устанавливает теорема Пифагора — одна из фундаментальных теорем евклидовой геометрии.
Соотношения гипотенузы и катетов также положили основу для целого раздела математики — тригонометрии. Изначально синусы и косинусы определялись как функции углов прямоугольного треугольника, но в современном значении тригонометрические функции расширены на всю числовую ось. Сегодня тригонометрия используется во многих областях человеческой деятельности: от астрономии и океанографии до анализа финансовых рынков и разработки компьютерных игр.
Сегодня тригонометрия используется во многих областях человеческой деятельности: от астрономии и океанографии до анализа финансовых рынков и разработки компьютерных игр.
Прямоугольный треугольник в реальности
Непосредственно прямоугольный треугольник встречается в реальности на каждом углу, как в прямом, так и в переносном смысле. Форму прямоугольного треугольника имеют грани тетраэдров и призм, которые в реальности превращаются в детали машин, керамическую плитку или скаты крыш. Угольник — чертежный инструмент, с которым человек впервые встречается на уроке геометрии, имеет форму именно прямоугольного треугольника и используется в проектировании, строительстве и столярном деле.
Периметр треугольника
Периметр — это численная оценка длин всех сторон плоской геометрической фигуры. Периметр n-угольника находится как сумма длин n сторон. Для определения периметра прямоугольного треугольника используется простая формула:
a и b – катеты, c – гипотенуза.
Вычисляя периметр треугольника вручную, вам пришлось бы измерять все три стороны, проводить дополнительные тригонометрические операции или вычисления по теореме Пифагора. Используя онлайн-калькулятор вам достаточно узнать следующие пары переменных:
Используя онлайн-калькулятор вам достаточно узнать следующие пары переменных:
- два катета;
- катет и угол;
- гипотенуза и угол.
В школьных задачах или на практике вам будут заданы исходные данные, поэтому калькулятор позволяет найти периметр, зная разные пары параметров. Кроме того, инструмент автоматически рассчитывает все остальные атрибуты прямоугольного треугольника, то есть длины всех сторон и величины всех углов. Рассмотрим пару примеров.
Примеры из жизни
Школьная задача
Пусть в школьной задаче вам задан прямоугольный треугольник с длиной катета равным 5 см и прилежащим углом, величина которого составляет 60 градусов. Требуется найти периметр геометрической фигуры. Онлайн-калькулятор сопровождается рисунком, на котором изображены стороны и углы прямоугольного треугольника. Мы видим, что если катет a = 5 см, то его прилежащий угол — это угол бета. Это важный момент, так как если вы используете для расчетов угол альфа, то результат будет неверным. Вбиваем эти данные в форму и получаем ответ в виде:
Вбиваем эти данные в форму и получаем ответ в виде:
Помимо непосредственно периметра, наша программа также определила величину противолежащего угла, а также длину второго катета и гипотенузы.
Обустройство клумбы
Допустим, вы хотите сделать ограду для клумбы, которая имеет форму прямоугольного треугольника. Для этого вам необходимо узнать периметр фигуры. Конечно, в реальности вы можете просто замерить все три стороны, но легко упростить себе задачу и измерить только два катета. Пусть они имеют длину 8 и 15 метров. Вбиваем эти данные в форму калькулятора и получаем ответ:
Итак, вам понадобится закупить материалы для обустройства 40 метров ограды. Наш калькулятор также подсчитал длину гипотенузы — 17 метров. Числа 8, 15 и 17 составляют пифагорову тройку — натуральные числа, которые удовлетворяют условиям теоремы Пифагора.
Заключение
Прямоугольные треугольники получили широкое распространение в повседневности, поэтому определение площади или периметра геометрической фигуры наверняка пригодится вам при решении школьных задач или бытовых вопросов.
Прямоугольный треугольник — это частный вид произвольного треугольника. Как и любой другой треугольник он имеет три стороны, но один из его углов обязательно должен составлять 90 градусов. Ка только вы определили, что заданный треугольник является прямоугольным, можно приступить к нахождению его основных величин. Одной из характеристик прямоугольного треугольника является его периметр. Нахождению периметра прямоугольного треугольника посвящено много задач по геометрии. Перед тем как мы рассмотрим основные способы нахождения периметра прямоугольного треугольника, хотелось бы напомнить, что периметр любой геометрической фигуры на плоскости равен сумме длин все ее сторон. Для все видов треугольников данное утверждение можно записать в виде следующего выражения:
где P — периметр треугольника;
a, b, c — стороны треугольника.
В прямоугольном треугольнике, как уже было сказано выше присутствует отличительная особенность в виде одного из углов, составляющего 90 градусов. Две стороны треугольника, прилегающие к данному углу называют катетами. Противоположную прямому углу сторону принято называть гипотенузой.
Противоположную прямому углу сторону принято называть гипотенузой.
Необычные свойства прямоугольного треугольника было открыто Пифагором, который обнаружил, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов, что может быть записано в виде выражения:
Прямоугольный треугольник — это частный вид произвольного треугольника. Как и любой другой треугольник он имеет три стороны, но один из его углов обязательно должен составлять 90 градусов. Ка только вы определили, что заданный треугольник является прямоугольным, можно приступить к нахождению его основных величин. Одной из характеристик прямоугольного треугольника является его периметр. Нахождению периметра прямоугольного треугольника посвящено много задач по геометрии.
Где P — периметр треугольника;
A, b, c — стороны треугольника.
Исходя из теоремы Пифагора появилась возможность определять периметр прямоугольного треугольника по его двум любым сторонам известной длины. Если известны длины катетов, то периметр треугольника определяется через нахождение величины гипотенузы по формуле:
Если известен только один из катетов и длина гипотенузы, то периметр треугольника определяется через нахождение величины недостающего катета по формуле:
Если в прямоугольном треугольнике известна только длина гипотенузы с и один из прилегающих к ней острых углов α, то периметр треугольника в данном случае может быть определен по формуле:
В том случае, когда условиями задачи задана длина катета a и величина противолежащего ему острого угла α, то периметр прямоугольного треугольника в данном случае вычисляется по формуле:
Если же задан катет a с прилежащим к нему углом β, то периметр треугольника может быть рассчитан на основе выражения:
P = a + b + c, где, допустим,
P = v(a2 + b2) + a + b, или
P = v(c2 – b2) + b + с.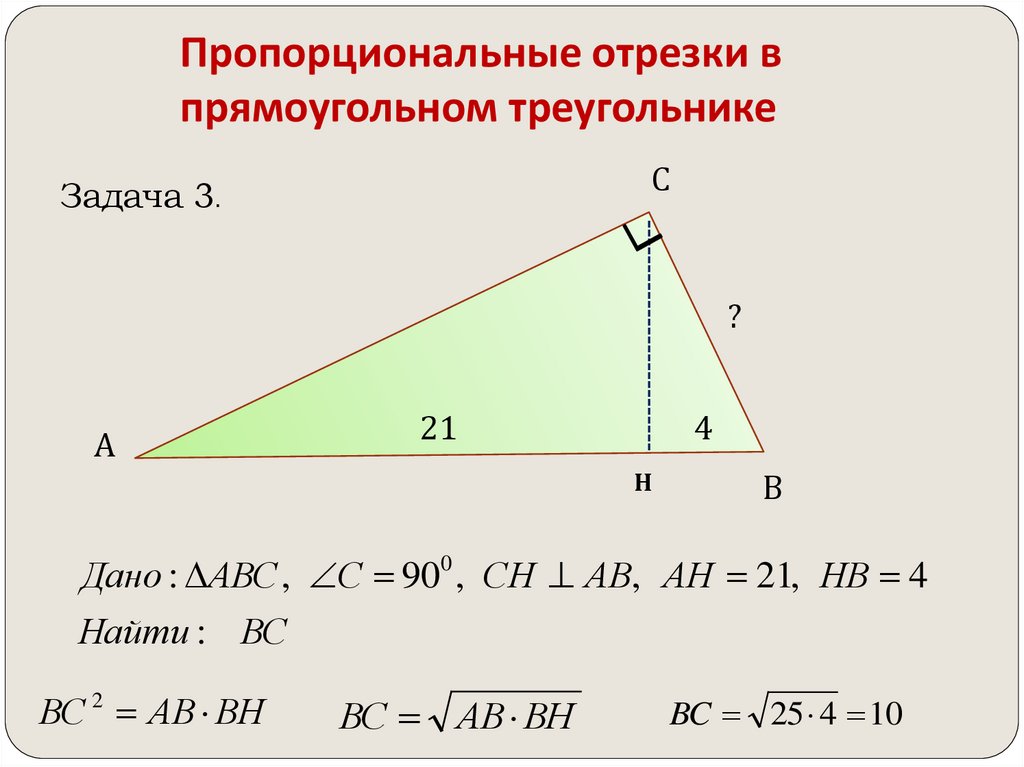
P = (1 + sin? + cos?)*с.
P = a*(1/tg? + 1/sin? + 1)
P = a*(1/сtg? + 1/cos? + 1)
Другие новости по теме:
Как найти периметр прямоугольного треугольника
Прямоугольным треугольником считается такой треугольник, один из углов которого равен 90 градусам, а два других являются острыми углами. Расчет периметра такого треугольника будет зависим от количества известных о нем данных.
В зависимости от случая, знание двух из трех сторон треугольника, а также одного из его острых углов.
Спонсор размещения P&G Статьи по теме «Как найти периметр прямоугольного треугольника» Как найти площадь поверхности пирамиды Как найти периметр если известна площадь Как найти периметр равностороннего треугольника
Способ 1.Если известны все три стороны треугольника, то, независимо от того, прямоугольный ли треугольник или нет, его периметр будет рассчитан так:
P = a + b + c, где, допустим,
Способ 2. Если в прямоугольнике известны только 2 стороны, то, используя теорему Пифагора, периметр этого треугольника можно рассчитать по формуле:
P = v(a2 + b2) + a + b, или
P = v(c2 – b2) + b + с.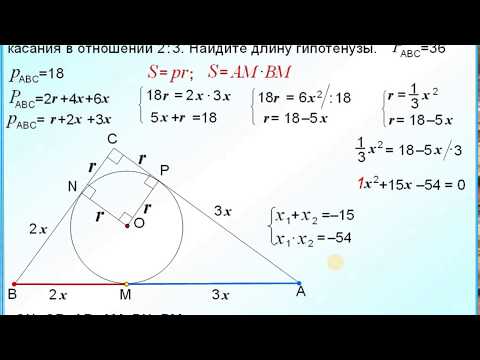
Способ 3. Пусть в прямоугольном треугольнике даны гипотенуза c и острый угол?, то найти периметр можно будет таким образом:
P = (1 + sin? + cos?)*с.
Способ 4. Дано, что в прямоугольном треугольнике длина одного из катета равна a, а напротив него лежит острый угол?. Тогда расчет периметра этого треугольника будет вестись по формуле:
P = a*(1/tg? + 1/sin? + 1)
Способ 5. Пускай нам известен катет a и прилежащий к нему угол?, тогда периметр будет рассчитан так:
P = a*(1/сtg? + 1/cos? + 1)
Другие новости по теме:
Площадь и периметр — основные числовые характеристики любых геометрических фигур. Нахождение этих величин упрощается благодаря общепринятым формулам, согласно которым можно также вычислить одно через другое с минимумом или полным отсутствием дополнительных начальных данных. Спонсор размещения P&G
Равносторонний треугольник наряду с квадратом является, пожалуй, самой простой и симметричной фигурой в планиметрии. Разумеется, все соотношения, справедливые для обычного треугольника, верны также и для равностороннего. Однако для правильного треугольника все формулы становятся намного проще. Вам
Однако для правильного треугольника все формулы становятся намного проще. Вам
Периметр треугольника, как и любой другой плоской геометрической фигуры, составляет сумма длин ограничивающих его отрезков. Поэтому, чтобы вычислить длину периметра, надо знать длины его сторон. Но в силу того, что длины сторон в геометрических фигурах связаны определенными соотношениями с
Прямоугольным считается такой треугольник, у которого один из углов прямой. Сторона треугольника, расположенная напротив прямого угла, называется гипотенузой, а две другие стороны — катетами. Чтобы найти длины сторон прямоугольного треугольника, можно воспользоваться несколькими способами. Спонсор
Периметр любой геометрической фигуры, в том числе треугольника, равен совокупной длине границ этой фигуры. Он обозначается заглавной латинской буквой P и легко находится методом сложения длин всех сторон данной фигуры. Спонсор размещения P&G Статьи по теме «Как вычислить периметр треугольника»
Треугольник — это многоугольник, имеющий три стороны и три угла. Как же вычислить его периметр? Спонсор размещения P&G Статьи по теме «Как находить периметр треугольника» Как найти периметр треугольника, заданного координатами своих вершин Как найти площадь треугольника Как найти длину и ширину
Как же вычислить его периметр? Спонсор размещения P&G Статьи по теме «Как находить периметр треугольника» Как найти периметр треугольника, заданного координатами своих вершин Как найти площадь треугольника Как найти длину и ширину
Гипотенуза – самая длинная сторона прямоугольного треугольника. Она расположена противоположно прямому углу. Способ нахождения гипотенузы прямоугольного треугольника зависит от того, какими исходными данными вы обладаете. Спонсор размещения P&G Статьи по теме «Как найти гипотенузу треугольника» Как
Прямоугольный треугольник характеризуется определенными соотношениями между углами и сторонами. Зная значения одних из них, можно вычислять другие. Для этого используются формулы, основанные, в свою очередь, на аксиомах и теоремах геометрии. Спонсор размещения P&G Статьи по теме «Как определить
Казалось бы, что может быть проще, чем вычисление площади и периметра треугольника – измерил стороны, поставил цифры в формулу – и все. Если вы так считаете, значит, забыли, что для этих целей существует не две простенькие формулы, а гораздо больше – для каждого вида треугольника – своя. Вам
Вам
Периметр треугольника – сумма длин его сторон. Найти периметр треугольника часто требуется как в задачах начальной геометрии, так и в более трудных заданиях. При их решении недостающие величины находят из других данных. Основные зависимости периметра треугольника от его других измерений отражены в
Прямоугольным треугольником считается такой треугольник, один из углов которого равен 90 градусам, а два других являются острыми углами. Расчет периметра такого треугольника будет зависим от числа знаменитых о нем данных.
Вам понадобится
- В зависимости от случая, умение 2-х из 3 сторон треугольника, а также одного из его острых углов.
Инструкция
1. Метод 1.Если знамениты все три стороны треугольника , то, самостоятельно от того, прямоугольный ли треугольник либо нет, его периметр будет рассчитан так:P = a + b + c, где, возможен,c – гипотенуза;a и b – катеты.
2. Метод 2. Если в прямоугольнике вестимы только 2 стороны, то, применяя теорему Пифагора, периметр этого треугольника дозволено рассчитать по формуле:P = v(a2 + b2) + a + b, илиP = v(c2 – b2) + b + с.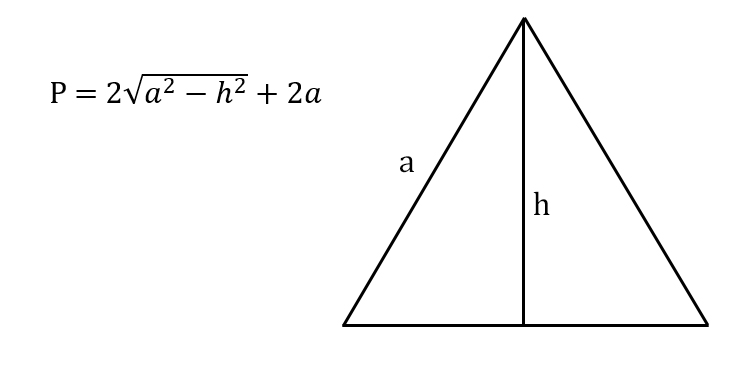
3. Метод 3. Пускай в прямоугольном треугольнике даны гипотенуза c и острый угол?, то обнаружить периметр дозволено будет таким образом:P = (1 + sin ? + cos ?)*с.
4. Метод 4. Дано, что в прямоугольном треугольнике длина одного из катета равна a, а наоборот него лежит острый угол?. Тогда расчет периметра этого треугольника будет вестись по формуле:P = a*(1/tg ? + 1/sin ? + 1)
5. Метод 5. Пускай нам вестим катет a и прилежащий к нему угол?, тогда периметр будет рассчитан так:P = a*(1/сtg ? + 1/cos ? + 1)
Видео по теме
Одной из базовых геометрических фигур является треугольник. Он образуется при пересечении трех отрезков прямых. Данные отрезки прямых формируют стороны фигуры, а точки их пересечения называются вершинами. Каждый школьник, изучающий курс геометрии, обязан уметь находить периметр этой фигуры. Полученное умение будет полезным для многих и во взрослой жизни, к примеру, пригодится студенту, инженеру, строителю,
Существуют разные способы найти периметр треугольника.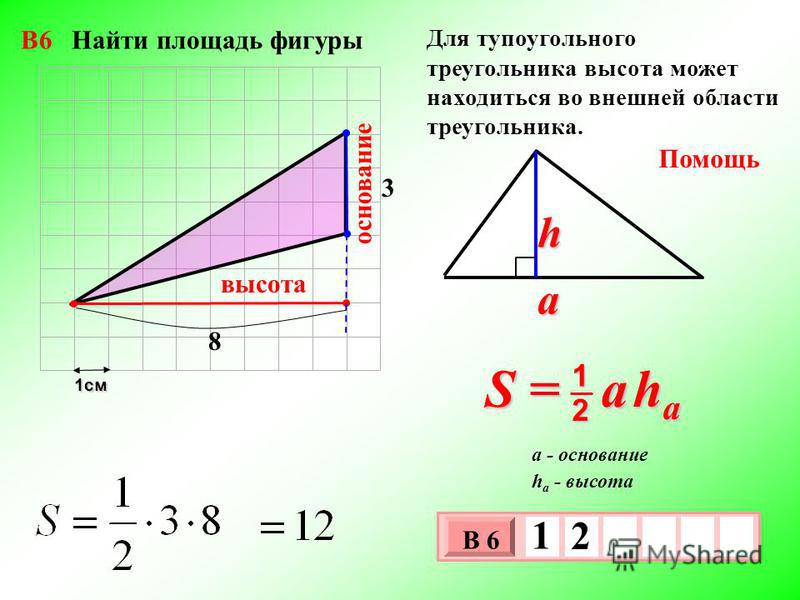 Выбор необходимой для вас формулы зависит от имеющихся исходных данных. Чтобы записать данную величину в математической терминологии используют специальное обозначение – Р. Рассмотрим, что такое периметр, основные способы его расчета для треугольных фигур разных видов.
Выбор необходимой для вас формулы зависит от имеющихся исходных данных. Чтобы записать данную величину в математической терминологии используют специальное обозначение – Р. Рассмотрим, что такое периметр, основные способы его расчета для треугольных фигур разных видов.
Самым простым способом найти периметр фигуры, если есть данные всех сторон. В этом случае используется следующая формула:
Буквой «P» обозначается сама величина периметра. В свою очередь «a», «b» и «c» – это длины сторон.
Зная размер трех величин, достаточно будет получить их сумму, которая и является периметром.
Альтернативный вариант
В математических задачах все данные длины редко бывают известны. В таких случаях рекомендуется воспользоваться альтернативным способом поиска нужной величины. Когда в условиях указана длина двух прямых, а также угол, находящийся между ними, расчет производится через поиск третьей. Для поиска этого числа необходимо добыть квадратный корень по формуле:
.
Периметр по двум сторонам
Для расчета периметра не обязательно знать все данные геометрической фигуры. Рассмотрим способы расчета по двум сторонам.
Равнобедренный треугольник
Равнобедренным называется такой треугольник, не меньше двух сторон которого имеют одинаковую длину. Они называются боковыми, а третья сторона – основанием. Равные прямые образовывают вершинный угол. Особенностью в равнобедренном треугольникеявляется наличие одной оси симметрии. Ось – вертикальная линия, выходящая из вершинного угла и заканчивающаяся посредине основания. По своей сути ось симметрии включает в себя такие понятия:
- биссектриса вершинного угла;
- медиана к основанию;
- высота треугольника;
- срединный перпендикуляр.
Чтобы определить периметр равнобедренного вида треугольной фигуры, воспользуйтесь формулой.
В данном случае вам необходимо знать только две величины: основание и длину одной стороны. Обозначение «2а» подразумевает умножение длины боковой стороны на 2. К полученной цифре нужно добавить величину основания – «b».
К полученной цифре нужно добавить величину основания – «b».
В исключительном случае, когда длина основания равнобедренного треугольника равна его боковой прямой, можно воспользоваться более простым способом. Он выражается в следующей формуле:
Для получения результата достаточно умножить это число на три. Эта формула используется для того, чтобы найти периметр правильного треугольника.
Полезное видео: задачи на периметр труегольника
Треугольник прямоугольный
Главным отличием прямоугольного треугольника от других геометрических фигур этой категории является наличие угла 90°. По этому признаку и определяется вид фигуры. Прежде, чем определить, как найти периметр прямоугольного треугольника, стоит заметить, что данная величина для любой плоской геометрической фигуры составляет сумму всех сторон. Так и в этом случае самый простой способ узнать результат – суммировать три величины.
В научной терминологии те стороны, которые прилегают к прямому углу, имеют название «катеты», а противоположная к углу 90º – гипотенуза. Особенности этой фигуры исследовались еще древнегреческим ученым Пифагором. Согласно с теоремой Пифагора, квадрат гипотенузы равен сумме квадратов катетов.
Особенности этой фигуры исследовались еще древнегреческим ученым Пифагором. Согласно с теоремой Пифагора, квадрат гипотенузы равен сумме квадратов катетов.
.
На основании данной теоремы выведена еще одна формула, объясняющая, как найти периметр треугольника по двум известным сторонам. Рассчитать периметр при указанной длине катетов можно, используя следующий способ.
.
Чтобы узнать периметр, имея информацию о размере одного катета и гипотенузы, нужно определить длину второй гипотенузы. С этой целью используют такие формулы:
.
Также периметр описанного вида фигуры определяется и без данных о размерах катетов.
Вам потребуется знать длину гипотенузы, а также угол, прилегающий к ней. Зная длину одного из катетов, если имеется угол, прилегающий к нему, периметр фигуры рассчитывают по формуле:
.
Расчет через высоту
Рассчитать периметр таких категорий, как равнобедренные и прямоугольные треугольники, можно через показатель их средней линии. Как известно, высота треугольника разделяет его основание пополам. Таким образом, она образует две прямоугольных фигуры. Далее, нужный показатель вычисляется при помощи теоремы Пифагора. Формула будет иметь следующий вид:
Как известно, высота треугольника разделяет его основание пополам. Таким образом, она образует две прямоугольных фигуры. Далее, нужный показатель вычисляется при помощи теоремы Пифагора. Формула будет иметь следующий вид:
.
Если известна высота и половина основания, используя этот способ, вы получите нужное число без поиска остальных данных о фигуре.
Полезное видео: нахождение периметра треугольника
Читайте также…
- Девять самых крутых животных из «Звёздных войн Маленькие зверьки из звездных войн
- Черное Солнце — символ-оберег для Ведающих Черное солнце star wars
- Пример из двух зол выбирают меньшее
- Неизвестная трехпалая раса
Периметр прямоугольного треугольника: онлайн калькулятор, формулы, примеры решений
Фигура
{$ main. figures[data.figure] $}
figures[data.figure] $}
Рассчитываем {$ main.types[data.type] $}
Радиусили диаметр
Стороныили диагонали
Введите 2 величины
Сторона A
Сторона B
Диагонали
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.angles[data.angle] $}
Введите 3 величины
Сторона A
Сторона B
Сторона C
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.angles[data.angle] $}
Угол γ{$ main.angles[data.angle] $}
Введите 2 величины
Сторона A
Сторона B
Сторона C
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.angles[data.angle] $}
Введите 2 величины
Сторона
Высота
Диагональ 1
Диагональ 2
Угол α{$ main.angles[data.angle] $}
Угол β{$ main. angles[data.angle] $}
angles[data.angle] $}
Введите 3 величины
Сторона A
Сторона B
Высота ha
Высота hb
Диагональ 1
Диагональ 2
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.angles[data.angle] $}
Введите 3 величины
Основание A
Основание C
Высота H
Дополните боковые стороны для поиска периметра
Сторона B
Сторона D
Введите 1 величину
Сторона A
Радиус описанной окружности (R)
Радиус вписанной окружности (r)
Количество сторон многоугольника
Введите 1 величину
Сторона A
Радиус описанной окружности (R)
Радиус вписанной окружности (r)
Введите 1 величину
Сторона A = радиусу описанной окружности (R)
Радиус вписанной окружности (r)
Результат расчёта
- Периметр: {$ result.p|number:4 $} type == ‘area'»>Площать: {$ result.s|number:4 $}
Прямоугольный треугольник — простая, но крайне важная для математики фигура. Знание о его свойствах и умение оперировать основными параметрами прямоугольного треугольника позволит вам справиться как со школьными, так и с реальными задачами.
Геометрия прямоугольного треугольника
Геометрически треугольник — это три точки, не лежащие на одной прямой, которые соединены между собой отрезками. Прямоугольный треугольник — фигура, две стороны которой образуют прямой угол. Эти стороны называются катетами треугольника, а третья, самая длинная сторона, носит название гипотенузы. Соотношение квадратов катетов и гипотенузы устанавливает теорема Пифагора — одна из фундаментальных теорем евклидовой геометрии.
Соотношения гипотенузы и катетов также положили основу для целого раздела математики — тригонометрии. Изначально синусы и косинусы определялись как функции углов прямоугольного треугольника, но в современном значении тригонометрические функции расширены на всю числовую ось. Сегодня тригонометрия используется во многих областях человеческой деятельности: от астрономии и океанографии до анализа финансовых рынков и разработки компьютерных игр.
Сегодня тригонометрия используется во многих областях человеческой деятельности: от астрономии и океанографии до анализа финансовых рынков и разработки компьютерных игр.
Прямоугольный треугольник в реальности
Непосредственно прямоугольный треугольник встречается в реальности на каждом углу, как в прямом, так и в переносном смысле. Форму прямоугольного треугольника имеют грани тетраэдров и призм, которые в реальности превращаются в детали машин, керамическую плитку или скаты крыш. Угольник — чертежный инструмент, с которым человек впервые встречается на уроке геометрии, имеет форму именно прямоугольного треугольника и используется в проектировании, строительстве и столярном деле.
Периметр треугольника
Периметр — это численная оценка длин всех сторон плоской геометрической фигуры. Периметр n-угольника находится как сумма длин n сторон. Для определения периметра прямоугольного треугольника используется простая формула:
P = a + b + c,
a и b – катеты, c – гипотенуза.
Вычисляя периметр треугольника вручную, вам пришлось бы измерять все три стороны, проводить дополнительные тригонометрические операции или вычисления по теореме Пифагора. Используя онлайн-калькулятор вам достаточно узнать следующие пары переменных:
- два катета;
- катет и угол;
- гипотенуза и угол.
В школьных задачах или на практике вам будут заданы исходные данные, поэтому калькулятор позволяет найти периметр, зная разные пары параметров. Кроме того, инструмент автоматически рассчитывает все остальные атрибуты прямоугольного треугольника, то есть длины всех сторон и величины всех углов. Рассмотрим пару примеров.
Примеры из жизни
Школьная задача
Пусть в школьной задаче вам задан прямоугольный треугольник с длиной катета равным 5 см и прилежащим углом, величина которого составляет 60 градусов. Требуется найти периметр геометрической фигуры. Онлайн-калькулятор сопровождается рисунком, на котором изображены стороны и углы прямоугольного треугольника. Мы видим, что если катет a = 5 см, то его прилежащий угол — это угол бета. Это важный момент, так как если вы используете для расчетов угол альфа, то результат будет неверным. Вбиваем эти данные в форму и получаем ответ в виде:
Мы видим, что если катет a = 5 см, то его прилежащий угол — это угол бета. Это важный момент, так как если вы используете для расчетов угол альфа, то результат будет неверным. Вбиваем эти данные в форму и получаем ответ в виде:
P = 23,66
Помимо непосредственно периметра, наша программа также определила величину противолежащего угла, а также длину второго катета и гипотенузы.
Обустройство клумбы
Допустим, вы хотите сделать ограду для клумбы, которая имеет форму прямоугольного треугольника. Для этого вам необходимо узнать периметр фигуры. Конечно, в реальности вы можете просто замерить все три стороны, но легко упростить себе задачу и измерить только два катета. Пусть они имеют длину 8 и 15 метров. Вбиваем эти данные в форму калькулятора и получаем ответ:
P = 40
Итак, вам понадобится закупить материалы для обустройства 40 метров ограды. Наш калькулятор также подсчитал длину гипотенузы — 17 метров. Числа 8, 15 и 17 составляют пифагорову тройку — натуральные числа, которые удовлетворяют условиям теоремы Пифагора.
Заключение
Прямоугольные треугольники получили широкое распространение в повседневности, поэтому определение площади или периметра геометрической фигуры наверняка пригодится вам при решении школьных задач или бытовых вопросов.
Как найти периметр треугольника если известны не все стороны. Как найти периметр треугольника если известны не все стороны Как найти периметр треугольника с прямым углом
Прямоугольным треугольником считается такой треугольник, один из углов которого равен 90 градусам, а два других являются острыми углами. Расчет периметра такого треугольника будет зависим от количества известных о нем данных.
Вам понадобится
- В зависимости от случая, знание двух из трех сторон треугольника, а также одного из его острых углов.
Инструкция
- Способ 1.Если известны все три стороны треугольника , то, независимо от того, прямоугольный ли треугольник или нет, его периметр будет рассчитан так:
P = a + b + c, где, допустим,
c — гипотенуза;
a и b — катеты.
- Способ 2. Если в прямоугольнике известны только 2 стороны, то, используя теорему Пифагора, периметр этого треугольника можно рассчитать по формуле:
P = v(a2 + b2) + a + b, или
P = v(c2 – b2) + b + с. - Способ 3. Пусть в прямоугольном треугольнике даны гипотенуза c и острый угол?, то найти периметр можно будет таким образом:
P = (1 + sin ? + cos ?)*с. - Способ 4. Дано, что в прямоугольном треугольнике длина одного из катета равна a, а напротив него лежит острый угол?. Тогда расчет периметра этого треугольника будет вестись по формуле:
P = a*(1/tg ? + 1/sin ? + 1) - Способ 5. Пускай нам известен катет a и прилежащий к нему угол?, тогда периметр будет рассчитан так:
P = a*(1/сtg ? + 1/cos ? + 1)
Периметром треугольника , как в прочем и любой фигуры, называется сумма длин всех сторон. Довольно часто это значение помогает найти площадь или используется для расчета других параметров фигуры.
Формула периметра треугольника выглядит так:
Пример расчета периметра треугольника. Пусть дан треугольник со сторонами a
= 4см, b
= 6 см, c
= 7 см. подставим данные в формулу: см
Пусть дан треугольник со сторонами a
= 4см, b
= 6 см, c
= 7 см. подставим данные в формулу: см
Формула расчета периметра равнобедренного треугольника будет выглядеть так:
Формула расчета периметра равностороннего треугольника :
Пример расчета периметра равностороннего треугольника. Когда все стороны фигуры равны, то их можно просто умножить на три. Допустим, дан правильный треугольник со стороной 5 см в таком случае: см
В общем, когда все стороны даны, найти периметр довольно просто. В остальных же ситуациях требуется найти размер недостающей стороны. В прямоугольном треугольнике можно найти третью сторону по теореме Пифагора . К примеру, если известны длины катетов, то можно найти гипотенузу по формуле:
Рассмотрим пример расчета периметра равнобедренного треугольника при условии, что мы знаем длину катетов в прямоугольном равнобедренном треугольнике.
Дан треугольник с катетами a
=b
=5 см. Найти периметр. Для начала найдем недостающую сторону с
. см
см
Теперь посчитаем периметр: см
Периметр прямоугольного равнобедренного треугольника будет равен 17 см.
В случае, когда известна гипотенуза и длина одного катета, можно найти недостающий по формуле:
Если в прямом треугольнике известна гипотенуза и один из острых углов, то недостающая сторона находится по формуле.
Одной из базовых геометрических фигур является треугольник. Он образуется при пересечении трех отрезков прямых. Данные отрезки прямых формируют стороны фигуры, а точки их пересечения называются вершинами. Каждый школьник, изучающий курс геометрии, обязан уметь находить периметр этой фигуры. Полученное умение будет полезным для многих и во взрослой жизни, к примеру, пригодится студенту, инженеру, строителю,
Существуют разные способы найти периметр треугольника. Выбор необходимой для вас формулы зависит от имеющихся исходных данных. Чтобы записать данную величину в математической терминологии используют специальное обозначение – Р. Рассмотрим, что такое периметр, основные способы его расчета для треугольных фигур разных видов.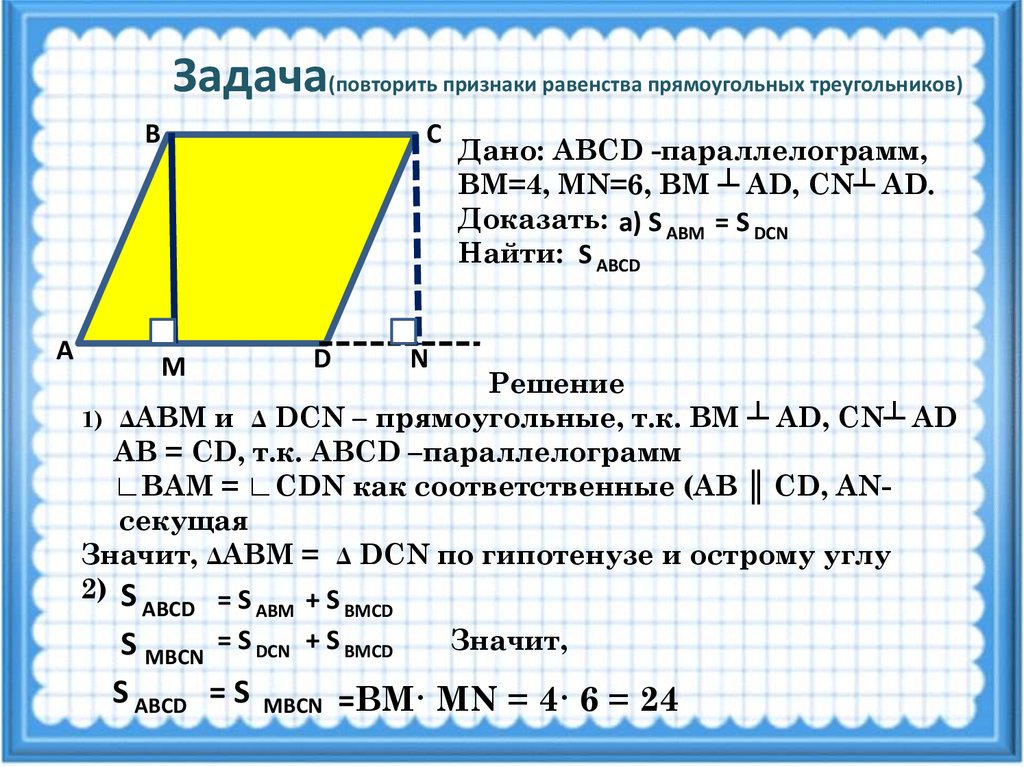
Самым простым способом найти периметр фигуры, если есть данные всех сторон. В этом случае используется следующая формула:
Буквой «P» обозначается сама величина периметра. В свою очередь «a», «b» и «c» – это длины сторон.
Зная размер трех величин, достаточно будет получить их сумму, которая и является периметром.
Альтернативный вариант
В математических задачах все данные длины редко бывают известны. В таких случаях рекомендуется воспользоваться альтернативным способом поиска нужной величины. Когда в условиях указана длина двух прямых, а также угол, находящийся между ними, расчет производится через поиск третьей. Для поиска этого числа необходимо добыть квадратный корень по формуле:
.
Периметр по двум сторонам
Для расчета периметра не обязательно знать все данные геометрической фигуры. Рассмотрим способы расчета по двум сторонам.
Равнобедренный треугольник
Равнобедренным называется такой треугольник, не меньше двух сторон которого имеют одинаковую длину. Они называются боковыми, а третья сторона – основанием. Равные прямые образовывают вершинный угол. Особенностью в равнобедренном треугольникеявляется наличие одной оси симметрии. Ось – вертикальная линия, выходящая из вершинного угла и заканчивающаяся посредине основания. По своей сути ось симметрии включает в себя такие понятия:
Они называются боковыми, а третья сторона – основанием. Равные прямые образовывают вершинный угол. Особенностью в равнобедренном треугольникеявляется наличие одной оси симметрии. Ось – вертикальная линия, выходящая из вершинного угла и заканчивающаяся посредине основания. По своей сути ось симметрии включает в себя такие понятия:
- биссектриса вершинного угла;
- медиана к основанию;
- высота треугольника;
- срединный перпендикуляр.
Чтобы определить периметр равнобедренного вида треугольной фигуры, воспользуйтесь формулой.
В данном случае вам необходимо знать только две величины: основание и длину одной стороны. Обозначение «2а» подразумевает умножение длины боковой стороны на 2. К полученной цифре нужно добавить величину основания – «b».
В исключительном случае, когда длина основания равнобедренного треугольника равна его боковой прямой, можно воспользоваться более простым способом. Он выражается в следующей формуле:
Для получения результата достаточно умножить это число на три. Эта формула используется для того, чтобы найти периметр правильного треугольника.
Эта формула используется для того, чтобы найти периметр правильного треугольника.
Полезное видео: задачи на периметр труегольника
Треугольник прямоугольный
Главным отличием прямоугольного треугольника от других геометрических фигур этой категории является наличие угла 90°. По этому признаку и определяется вид фигуры. Прежде, чем определить, как найти периметр прямоугольного треугольника, стоит заметить, что данная величина для любой плоской геометрической фигуры составляет сумму всех сторон. Так и в этом случае самый простой способ узнать результат – суммировать три величины.
В научной терминологии те стороны, которые прилегают к прямому углу, имеют название «катеты», а противоположная к углу 90º – гипотенуза. Особенности этой фигуры исследовались еще древнегреческим ученым Пифагором. Согласно с теоремой Пифагора, квадрат гипотенузы равен сумме квадратов катетов.
.
На основании данной теоремы выведена еще одна формула, объясняющая, как найти периметр треугольника по двум известным сторонам. Рассчитать периметр при указанной длине катетов можно, используя следующий способ.
Рассчитать периметр при указанной длине катетов можно, используя следующий способ.
.
Чтобы узнать периметр, имея информацию о размере одного катета и гипотенузы, нужно определить длину второй гипотенузы. С этой целью используют такие формулы:
.
Также периметр описанного вида фигуры определяется и без данных о размерах катетов.
Вам потребуется знать длину гипотенузы, а также угол, прилегающий к ней. Зная длину одного из катетов, если имеется угол, прилегающий к нему, периметр фигуры рассчитывают по формуле:
.
Расчет через высоту
Рассчитать периметр таких категорий, как равнобедренные и прямоугольные треугольники, можно через показатель их средней линии. Как известно, высота треугольника разделяет его основание пополам. Таким образом, она образует две прямоугольных фигуры. Далее, нужный показатель вычисляется при помощи теоремы Пифагора. Формула будет иметь следующий вид:
.
Если известна высота и половина основания, используя этот способ, вы получите нужное число без поиска остальных данных о фигуре.
Полезное видео: нахождение периметра треугольника
Прямоугольный треугольник — простая, но крайне важная для математики фигура. Знание о его свойствах и умение оперировать основными параметрами прямоугольного треугольника позволит вам справиться как со школьными, так и с реальными задачами.
Геометрия прямоугольного треугольника
Геометрически треугольник — это три точки, не лежащие на одной прямой, которые соединены между собой отрезками. Прямоугольный треугольник — фигура, две стороны которой образуют прямой угол. Эти стороны называются катетами треугольника, а третья, самая длинная сторона, носит название гипотенузы. Соотношение квадратов катетов и гипотенузы устанавливает теорема Пифагора — одна из фундаментальных теорем евклидовой геометрии.
Соотношения гипотенузы и катетов также положили основу для целого раздела математики — тригонометрии. Изначально синусы и косинусы определялись как функции углов прямоугольного треугольника, но в современном значении тригонометрические функции расширены на всю числовую ось. Сегодня тригонометрия используется во многих областях человеческой деятельности: от астрономии и океанографии до анализа финансовых рынков и разработки компьютерных игр.
Сегодня тригонометрия используется во многих областях человеческой деятельности: от астрономии и океанографии до анализа финансовых рынков и разработки компьютерных игр.
Прямоугольный треугольник в реальности
Непосредственно прямоугольный треугольник встречается в реальности на каждом углу, как в прямом, так и в переносном смысле. Форму прямоугольного треугольника имеют грани тетраэдров и призм, которые в реальности превращаются в детали машин, керамическую плитку или скаты крыш. Угольник — чертежный инструмент, с которым человек впервые встречается на уроке геометрии, имеет форму именно прямоугольного треугольника и используется в проектировании, строительстве и столярном деле.
Периметр треугольника
Периметр — это численная оценка длин всех сторон плоской геометрической фигуры. Периметр n-угольника находится как сумма длин n сторон. Для определения периметра прямоугольного треугольника используется простая формула:
a и b – катеты, c – гипотенуза.
Вычисляя периметр треугольника вручную, вам пришлось бы измерять все три стороны, проводить дополнительные тригонометрические операции или вычисления по теореме Пифагора. Используя онлайн-калькулятор вам достаточно узнать следующие пары переменных:
Используя онлайн-калькулятор вам достаточно узнать следующие пары переменных:
- два катета;
- катет и угол;
- гипотенуза и угол.
В школьных задачах или на практике вам будут заданы исходные данные, поэтому калькулятор позволяет найти периметр, зная разные пары параметров. Кроме того, инструмент автоматически рассчитывает все остальные атрибуты прямоугольного треугольника, то есть длины всех сторон и величины всех углов. Рассмотрим пару примеров.
Примеры из жизни
Школьная задача
Пусть в школьной задаче вам задан прямоугольный треугольник с длиной катета равным 5 см и прилежащим углом, величина которого составляет 60 градусов. Требуется найти периметр геометрической фигуры. Онлайн-калькулятор сопровождается рисунком, на котором изображены стороны и углы прямоугольного треугольника. Мы видим, что если катет a = 5 см, то его прилежащий угол — это угол бета. Это важный момент, так как если вы используете для расчетов угол альфа, то результат будет неверным. Вбиваем эти данные в форму и получаем ответ в виде:
Вбиваем эти данные в форму и получаем ответ в виде:
Помимо непосредственно периметра, наша программа также определила величину противолежащего угла, а также длину второго катета и гипотенузы.
Обустройство клумбы
Допустим, вы хотите сделать ограду для клумбы, которая имеет форму прямоугольного треугольника. Для этого вам необходимо узнать периметр фигуры. Конечно, в реальности вы можете просто замерить все три стороны, но легко упростить себе задачу и измерить только два катета. Пусть они имеют длину 8 и 15 метров. Вбиваем эти данные в форму калькулятора и получаем ответ:
Итак, вам понадобится закупить материалы для обустройства 40 метров ограды. Наш калькулятор также подсчитал длину гипотенузы — 17 метров. Числа 8, 15 и 17 составляют пифагорову тройку — натуральные числа, которые удовлетворяют условиям теоремы Пифагора.
Заключение
Прямоугольные треугольники получили широкое распространение в повседневности, поэтому определение площади или периметра геометрической фигуры наверняка пригодится вам при решении школьных задач или бытовых вопросов.
теорема Пифагора и формула косинусов в зависимости от известных сторон
Периметр — это величина, подразумевающая длину всех сторон плоской (двумерной) геометрической фигуры. Для разных геометрических фигур существуют разные способы нахождения периметра.
В данной статье вы узнаете как находить периметр фигуры разными способами, в зависимости от известных его граней.
…
Оглавление:
- Первый метод: известны все стороны фигуры
- Второй метод: прямоугольный треугольник и две известные его стороны
- Третий метод: по двум граням и углу между ними
Возможные методы:
- известны все три стороны равнобедренного или любого другого треугольника;
- как найти периметр прямоугольного треугольника при двух известных его гранях;
- известны две грани и угол, который расположен между ними (формула косинусов) без средней линии и высоты.
Это интересно: что микроэкономика изучает, кратко об основателях и основах науки.
Первый метод: известны все стороны фигуры
Как находить периметра треугольника, когда известны все три грани, необходимо использовать следующую формулу: P = a + b + c, где a,b,c — известные длины всех сторон треугольника, P — периметр фигуры.
Например, известны три стороны фигуры: a = 24 см, b = 24 см, c = 24 см. Это правильная равнобедренная фигура, чтобы вычислить периметр пользуемся формулой: P = 24 + 24 + 24 = 72 см.
Данная формула подходит к любому треугольнику, необходимо просто знать длины всех его сторон. Если хотя бы одна из них неизвестна, необходимо воспользоваться другими способами, о которых мы поговорим ниже.
Еще один пример: a = 15 см, б = 13 см, c = 17 см. Вычисляем периметр: P = 15 + 13 + 17 = 45 см.
Очень важно помечать единицу измерения в полученном ответе. В наших примерах длины сторон указаны в сантиметрах (см), однако, существуют разные задачи, в условиях которых присутствуют другие единицы измерения. 2 — (2 * a * b * cos(C)), где a,b,c — стандартно длины граней, а A,B и С — это углы, которые лежат напротив соответствующих граней треугольника. То есть, A — угол, противолежащий стороне a и так далее.
2 — (2 * a * b * cos(C)), где a,b,c — стандартно длины граней, а A,B и С — это углы, которые лежат напротив соответствующих граней треугольника. То есть, A — угол, противолежащий стороне a и так далее.
Представим, что описан треугольник, стороны а и б которого составляют 100 см и 120 см соответственно, а угол, лежащий между ними, составляет 97 градусов. То есть а = 100 см, б = 120 см, C = 97 градусов.
Все, что нужно сделать в данном случае — это подставить все известные значения в теорему косинусов. Длины известных граней возводятся в квадрат, после чего известные стороны перемножаются между друг другом и на два и умножаются на косинус угла между ними. Далее, необходимо сложить квадраты граней и отнять от них второе полученное значение. Из итоговой величины извлекается квадратный корень — это будет третья, неизвестная до этого сторона.
После того как все три грани фигуры известны, осталось воспользоваться уже полюбившейся нам стандартной формулой поиска периметра описываемой фигуры из первого метода.
Задача решена.
решение задачи по 2 сторонам, средней линии и известной высоте
Одной из базовых геометрических фигур является треугольник. Он образуется при пересечении трех отрезков прямых. Данные отрезки прямых формируют стороны фигуры, а точки их пересечения называются вершинами. Каждый школьник, изучающий курс геометрии, обязан уметь находить периметр этой фигуры. Полученное умение будет полезным для многих и во взрослой жизни, к примеру, пригодится студенту, инженеру, строителю, дизайнеру.
Существуют разные способы найти периметр треугольника. Выбор необходимой для вас формулы зависит от имеющихся исходных данных. Чтобы записать данную величину в математической терминологии используют специальное обозначение – Р. Рассмотрим, что такое периметр, основные способы его расчета для треугольных фигур разных видов.
Оглавление
- Классическая формула
- Альтернативный вариант
- Периметр по двум сторонам
- Равнобедренный треугольник
- Полезное видео: задачи на периметр труегольника
- Треугольник прямоугольный
- Расчет через высоту
- Полезное видео: нахождение периметра треугольника
Классическая формула
Самым простым способом найти периметр фигуры, если есть данные всех сторон. В этом случае используется следующая формула:
В этом случае используется следующая формула:
P = a + b + c.
Буквой «P» обозначается сама величина периметра. В свою очередь «a», «b» и «c» – это длины сторон.
Зная размер трех величин, достаточно будет получить их сумму, которая и является периметром.
Это интересно! Что значит вертикально и как выглядит вертикальная линия
Альтернативный вариант
В математических задачах все данные длины редко бывают известны. В таких случаях рекомендуется воспользоваться альтернативным способом поиска нужной величины. Когда в условиях указана длина двух прямых, а также угол, находящийся между ними, расчет производится через поиск третьей. Для поиска этого числа необходимо добыть квадратный корень по формуле:
.
Далее рассчитывайте Р по такой формуле:
.
Периметр по двум сторонам
Для расчета периметра не обязательно знать все данные геометрической фигуры. Рассмотрим способы расчета по двум сторонам.
Это интересно! Основы геометрии: что это такое биссектриса треугольника
Равнобедренный треугольник
Равнобедренным называется такой треугольник, не меньше двух сторон которого имеют одинаковую длину. Они называются боковыми, а третья сторона – основанием. Равные прямые образовывают вершинный угол. Особенностью в равнобедренном треугольнике является наличие одной оси симметрии. Ось – вертикальная линия, выходящая из вершинного угла и заканчивающаяся посредине основания. По своей сути ось симметрии включает в себя такие понятия:
- биссектриса вершинного угла;
- медиана к основанию;
- высота треугольника;
- срединный перпендикуляр.
Чтобы определить периметр равнобедренного вида треугольной фигуры, воспользуйтесь формулой.
P = 2a + b.
В данном случае вам необходимо знать только две величины: основание и длину одной стороны. Обозначение «2а» подразумевает умножение длины боковой стороны на 2. К полученной цифре нужно добавить величину основания – «b».
К полученной цифре нужно добавить величину основания – «b».
В исключительном случае, когда длина основания равнобедренного треугольника равна его боковой прямой, можно воспользоваться более простым способом. Он выражается в следующей формуле:
P = 3a.
Для получения результата достаточно умножить это число на три. Эта формула используется для того, чтобы найти периметр правильного треугольника.
Это интересно! Изучаем символы: как обозначается в математике площадь
Полезное видео: задачи на периметр труегольника
Треугольник прямоугольный
Главным отличием прямоугольного треугольника от других геометрических фигур этой категории является наличие угла 90°. По этому признаку и определяется вид фигуры. Прежде, чем определить, как найти периметр прямоугольного треугольника, стоит заметить, что данная величина для любой плоской геометрической фигуры составляет сумму всех сторон. Так и в этом случае самый простой способ узнать результат – суммировать три величины.
Так и в этом случае самый простой способ узнать результат – суммировать три величины.
В научной терминологии те стороны, которые прилегают к прямому углу, имеют название «катеты», а противоположная к углу 90º – гипотенуза. Особенности этой фигуры исследовались еще древнегреческим ученым Пифагором. Согласно с теоремой Пифагора, квадрат гипотенузы равен сумме квадратов катетов.
.
На основании данной теоремы выведена еще одна формула, объясняющая, как найти периметр треугольника по двум известным сторонам. Рассчитать периметр при указанной длине катетов можно, используя следующий способ.
.
Чтобы узнать периметр, имея информацию о размере одного катета и гипотенузы, нужно определить длину второй гипотенузы. С этой целью используют такие формулы:
.
Также периметр описанного вида фигуры определяется и без данных о размерах катетов.
.
Вам потребуется знать длину гипотенузы, а также угол, прилегающий к ней. Зная длину одного из катетов, если имеется угол, прилегающий к нему, периметр фигуры рассчитывают по формуле:
.
Это интересно! Как найти и чему будет равна длина окружности
Расчет через высоту
Рассчитать периметр таких категорий, как равнобедренные и прямоугольные треугольники, можно через показатель их средней линии. Как известно, высота треугольника разделяет его основание пополам. Таким образом, она образует две прямоугольных фигуры. Далее, нужный показатель вычисляется при помощи теоремы Пифагора. Формула будет иметь следующий вид:
.
Если известна высота и половина основания, используя этот способ, вы получите нужное число без поиска остальных данных о фигуре.
Полезное видео: нахождение периметра треугольника
Что такое площадь и периметр треугольника? Определение, примеры
Треугольник
Треугольник – это трехсторонняя замкнутая фигура. Это одна из основных фигур в геометрии, которая имеет 3 стороны и 3 вершины.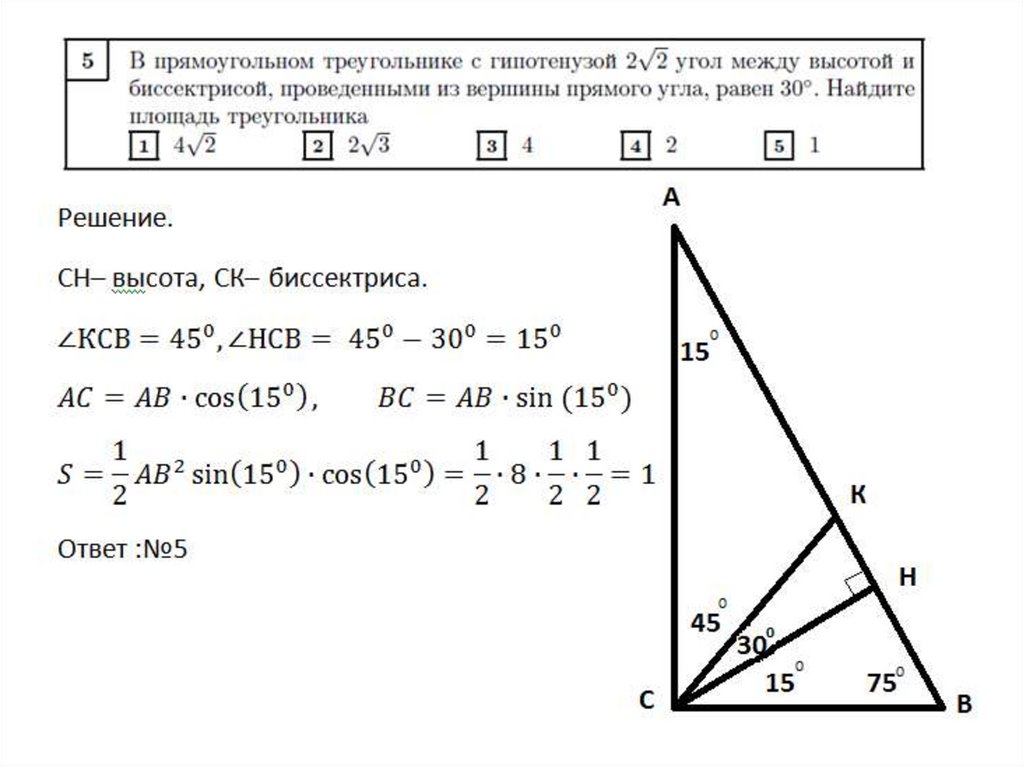 Треугольник можно классифицировать как равносторонний, равнобедренный или разносторонний в зависимости от длины его сторон.
Треугольник можно классифицировать как равносторонний, равнобедренный или разносторонний в зависимости от длины его сторон.
Что такое периметр треугольника?
Периметр полигона — это общая длина границы. Для треугольника мы можем найти его, сложив длины трех его сторон.
Итак, если треугольник ABC. Найдем периметр треугольника ABC, сложив длины всех трех сторон.
Периметр △ABC = AB + BC + CA = a + b + c
Давайте разберемся в этом на примере из реальной жизни.
Предположим, у нас есть треугольный парк. Нам нужно найти длину забора, необходимого для покрытия парка. Как мы это находим?
Длину ограждения, необходимого для треугольного парка, можно найти, найдя периметр треугольника.
Возьмем другой пример.
Сервировочный поднос, как показано, образует равносторонний треугольник, то есть треугольник с тремя равными сторонами. Пусть каждая сторона будет 20 см в длину.
Чтобы найти общую длину декоративного шнурка, который нужно наклеить на внешние края, нужно найти периметр треугольника. Поскольку все три стороны треугольника имеют одинаковую длину, мы можем найти периметр, умножив длину каждой стороны на 3.
Поскольку все три стороны треугольника имеют одинаковую длину, мы можем найти периметр, умножив длину каждой стороны на 3.
20 + 20 + 20 = 3 × 20 = 60 см.
Итак, мы видим, что периметр равностороннего треугольника в 3 раза больше длины каждой стороны.
Какова площадь треугольника?
Площадь двумерной фигуры — это пространство, занимаемое фигурой. Эту площадь можно найти, разделив фигуру на единичные квадраты и определив количество единичных квадратов в фигуре, поскольку каждый единичный квадрат занимает одну квадратную единицу площади.
Рассмотрим прямоугольник длиной 4 см и шириной 3 см. Его можно заполнить 3 строками и 4 столбцами единичных квадратов, поэтому площадь равна 3 умножить на 4 или 12 квадратных сантиметров. То есть площадь прямоугольника равна произведению его длины на ширину.
Прямоугольник можно разделить на два равных треугольника.
Итак, площадь каждого треугольника равна половине площади прямоугольника. Это 12 × l × w, где l — длина прямоугольника, а w — ширина прямоугольника.
Рассмотрим разносторонний треугольник △ABC. Обратите внимание: чтобы записать площадь треугольника как половину площади прямоугольника, нам нужно, чтобы высота была перпендикулярна основанию. Итак, проведите перпендикуляр из вершины в противоположную сторону.
Здесь BD — перпендикуляр, проведенный из вершины B на противоположную сторону AC.
Таким образом, площадь треугольника равна половине произведения его основания на высоту.
Площадь треугольника = ½ × основание × высота.
Интересные факты
- Треугольник — это простейший многоугольник с тремя сторонами. Все остальные многоугольники имеют более трех сторон.
- Слово «периметр» происходит от греческих слов, означающих «вокруг меры».
- Площадь A равностороннего треугольника со стороной s см можно рассчитать по формуле A=34×s2. Значение 3 составляет около 1,73. Таким образом, приблизительное значение становится равным A = 0,4325 с2.
Решенные примеры
- Стороны треугольника имеют следующие длины:
10 см, 14 см и 12 см
Найдите периметр треугольника.
Раствор. Мы знаем, что периметр треугольника равен сумме всех его сторон. Следовательно,
периметра = 10 см + 14 см + 12 см = 36 см.
- У равностороннего треугольника одна сторона имеет длину 6 см. Найдите периметр треугольника.
Раствор. Поскольку все стороны равностороннего треугольника равны по длине, его периметр можно рассчитать следующим образом:
Периметр = 6 см + 6 см + 6 см = 18 см
- Периметр треугольника равен 25 см. Две его стороны равны 4 см и 10 см. Найдите длину третьей стороны.
Раствор. Периметр — это сумма всех сторон. Мы можем найти третью сторону, вычитая размеры двух других сторон из заданного периметра.
Длина третьей стороны = 25 см – (4 см + 10 см) = 11 см
- Высота треугольника 4 см, а его основание 5 см. Найдите его площадь.

Раствор. Мы знаем, что площадь треугольника равна 12 x основание x высота. Следовательно,
Площадь = 12 × 4 × 5 = 10 см кв. 6 см + 4 см = 13 см
9 см
13 см
12 см
16 см
Правильный ответ: 9 см
Периметр = 3 см + 3 см + 3 см = 9 см
6 см
5 см
3 СМ.
4 см
Правильный ответ: 6 см
Длина третьей стороны = 15 см — 5 см — 4 см = 6 см
9 см
11 см составляет: 11 см
4 см + 4 см + 3 см = 11 см.
24 см кв.
44 см кв.
12 см кв.
16 см кв.
Правильный ответ: 24 кв. см
Площадь = $\frac{1}{2}\times 8\times 6$ = 24 см²
Часто задаваемые вопросы
Какова формула периметра треугольника?
Формула периметра треугольника представляет собой сумму длин всех сторон треугольника. Например, если длины сторон треугольника равны 3 см, 4 см и 5 см, то периметр треугольника будет равен 3 + 4 + 5 = 12 см.
Увеличивается ли площадь по мере увеличения периметра?
Увеличение периметра фигуры всегда увеличивает площадь фигуры.
Чему равен периметр равнобедренного треугольника?
Периметр равнобедренного треугольника равен 2 х сторона + основание.
Как определить площадь треугольника?
Площадь треугольника — это пространство, занимаемое внутри его границы. Его можно рассчитать как половину произведения его основания и высоты.
В чем сходство между периметром и площадью?
Площадь и периметр определяют размер фигуры.
Периметр треугольника – формула, определение, примеры
Периметр треугольника определяется как общая длина его границы. Треугольник представляет собой многоугольник с 3 сторонами, и его можно разделить на различные типы в зависимости от размера его сторон и углов. Существуют различные формулы и методы для расчета периметра треугольника в зависимости от типа треугольника.
| 1. | Каков периметр треугольника? |
| 2. | Периметр треугольника Формула |
| 3. | Как найти периметр треугольника? |
| 4. | Часто задаваемые вопросы о периметре треугольника |
Каков периметр треугольника?
Периметр треугольника означает сумму всех трех сторон. Слово «периметр» представляет собой сочетание двух греческих слов: «пери», что означает «вокруг», и «метрон», что означает «мера». Общее расстояние вокруг любой 2D-формы определяется как ее периметр. Поскольку периметр дает длину границы формы, он выражается в линейных единицах.
Пример периметра треугольника из реальной жизни: Представьте, что нам нужно огородить треугольный парк, показанный ниже. Теперь, чтобы узнать размеры забора, складываем длины трех сторон парка. Эта длина или расстояние от границы треугольника называется периметром треугольника.
Периметр треугольника Формула
Чтобы вычислить периметр треугольника, мы просто складываем длины данных сторон. Основная формула, используемая для вычисления периметра треугольника:
Периметр = сумма трех сторон
Давайте разберемся в этой формуле с различными типами треугольников.
Периметр разностороннего треугольника
Если треугольник имеет все три стороны разной длины, то это разносторонний треугольник. Периметр разностороннего треугольника можно вычислить, найдя сумму всех неравных сторон. Формула периметра разностороннего треугольника: Периметр = a + b + c, где «a», «b» и «c» — три разные стороны.
Периметр равнобедренного треугольника
Если у треугольника две стороны одинаковой длины, то это равнобедренный треугольник. Периметр равнобедренного треугольника можно вычислить, найдя сумму равных и неравных сторон. Формула периметра равнобедренного треугольника: Периметр равнобедренного треугольника = 2a + b единиц.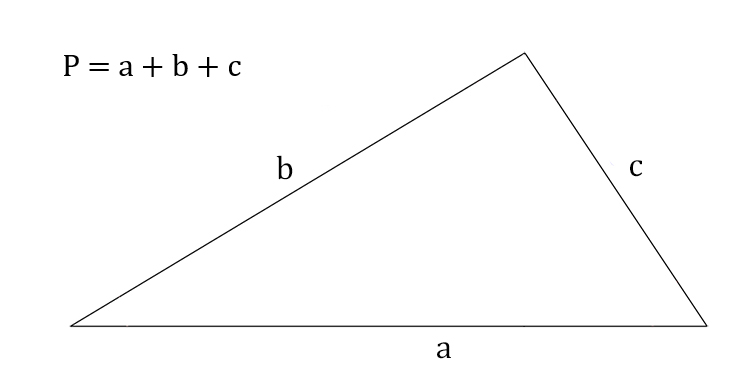
где
- а = стороны равной длины
- б = третья сторона
Периметр равностороннего треугольника
У равностороннего треугольника все стороны равны. Формула периметра равностороннего треугольника:
.
Периметр равностороннего треугольника = (3 × а) единиц.
где «а» = длина каждой стороны треугольника.
Периметр прямоугольного треугольника
Треугольник, один из углов которого равен 90°, называется прямоугольным треугольником или прямоугольным треугольником. Периметр прямоугольного треугольника можно вычислить, сложив данные стороны. Формула для вычисления периметра прямоугольного треугольника:
Периметр прямоугольного треугольника, P = a + b + c единиц.
Поскольку это прямоугольный треугольник, мы можем использовать теорему Пифагора, если какая-либо сторона этого треугольника неизвестна. Теорема Пифагора гласит, что квадрат гипотенузы равен сумме квадратов двух других сторон. Ссылаясь на приведенный выше рисунок:
Ссылаясь на приведенный выше рисунок:
- a = Перпендикулярно
- б = база
- c = Гипотенуза прямоугольного треугольника
Отсюда по теореме Пифагора c 2 = a 2 + b 2 . В этом случае периметр прямоугольного треугольника также можно записать как: P = a + b + √(a 2 + b 2 ). Это потому, что c 2 = a 2 + b 2 , следовательно, c = √(a 2 + b 2 ).
Периметр равнобедренного прямоугольного треугольника
Прямоугольный треугольник с двумя равными сторонами и двумя равными углами называется равнобедренным прямоугольным треугольником. Периметр равнобедренного прямоугольного треугольника можно вычислить, сложив данные стороны.
Формула для расчета периметра равнобедренного прямоугольного треугольника: P = 2l + h, где l — длина двух равных катетов или сторон треугольника, а h — гипотенуза.
Еще один интересный момент, который следует отметить здесь, заключается в том, что, используя теорему Пифагора, мы знаем, что h = √(l 2 + l 2 ) = √2 × l или l = h/√2 единиц. Следовательно, периметр равнобедренного прямоугольного треугольника также можно записать в виде: P = 2l + (√2)l = (2 + √2)l единиц.
Следовательно, периметр равнобедренного прямоугольного треугольника также можно записать в виде: P = 2l + (√2)l = (2 + √2)l единиц.
Кроме того, P = 2(h/√2) + h = (√2 × h) + h единиц.
Как найти периметр треугольника?
Периметр треугольника можно рассчитать, выполнив следующие шаги:
- Шаг 1: Запишите измерения всех сторон треугольника и убедитесь, что все стороны должны иметь одинаковую единицу измерения.
- Шаг 2: Вычислите сумму всех сторон.
- Шаг 3: Дайте ответ вместе с устройством.
Давайте посмотрим, как найти периметр треугольника на примере.
Пример: Найдите периметр △ABC, имеющего следующие размеры: AB = 6 дюймов, BC = 8 дюймов, AC = 10 дюймов.
Решение:
Шаг 1: Проверьте, известны ли все три стороны треугольника.
AB = 6 дюймов, BC = 8 дюймов, AC = 10 дюймов
Шаг 2: Используйте соответствующую формулу и сложите стороны, чтобы получить периметр. Поскольку это разносторонний треугольник, мы используем формулу Периметр = a + b + c. Запишите периметр вместе с его единицами измерения.
Поскольку это разносторонний треугольник, мы используем формулу Периметр = a + b + c. Запишите периметр вместе с его единицами измерения.
Периметр треугольника ABC = 6 + 8 + 10 = 24 дюйма.
Темы, связанные с периметром треугольника
Ознакомьтесь с некоторыми интересными статьями, связанными с периметром треугольника.
- Площадь треугольника
- Площадь и периметр треугольников Рабочие листы
- Калькулятор периметра треугольника
Периметр треугольника Примеры
Пример 1: Найдите периметр прямоугольного треугольника PQR с гипотенузой PR и сторонами PQ = 4 дюйма и QR = 3 дюйма.
Решение:
Дано, PQ = 4 дюйма, QR = 3 дюйма, PR = ?
Чтобы вычислить периметр треугольника, нам нужно знать все три стороны.
Длину гипотенузы (PR) рассчитаем по теореме Пифагора.
PR² = PQ² + QR²
PR² = 4² + 3²
PR² = 16 + 9
Следовательно, PR = √25 дюймов
PR = 5 дюймов.

Теперь мы можем вычислить периметр треугольника.
Периметр треугольника PQR = сумма трех сторон
= 3 + 4 + 5 = 12
Следовательно, периметр равен 12 дюймам.
Пример 2: Найдите длину недостающей стороны треугольного дорожного знака, периметр которого равен 48 дюймам, а две стороны по 17 дюймов каждая.
Решение:
Пусть длина недостающей стороны равна b.
Дано, периметр = 48 дюймов
Длина двух равных сторон = 17 дюймов каждая
Периметр треугольника = сумма длин трех сторон
48 = 17 + 17 + b
48 = 34 + b
b = 14
Следовательно, b = 14 дюймов
Ответ: Длина недостающей стороны = 14 дюймов.
Пример 3: Периметр прямоугольного провода равен 297 дюймов. Та же проволока сгибается в форме равностороннего треугольника. Найдите длину каждой из его сторон.
Решение:
Мы знаем, что периметр прямоугольника = общая длина провода
Длина используемого провода = периметр образованного треугольника
Периметр равностороннего треугольника = 3 × a
297 = 3 × a
a = 99
Ответ: Длина каждой стороны треугольника = 99 дюймов
перейти к слайдуперейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по периметру треугольника
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о периметре треугольника
Что такое периметр треугольника в математике?
Периметр треугольника определяется как общая длина его границы. Это сумма всех трех сторон треугольника.
Какая формула периметра треугольника?
Периметр треугольника можно вычислить, просто сложив длины всех сторон. Основная формула для вычисления периметра треугольника со сторонами «a», «b» и «c» — это a + b + c.
Как найти периметр треугольника с тремя равными сторонами?
Чтобы вычислить периметр треугольника с тремя равными сторонами, мы складываем длины всех сторон или умножаем длину любой стороны на 3. Такой треугольник называется равносторонним треугольником. Формула для расчета периметра равностороннего треугольника: 3а, где а — длина каждой стороны.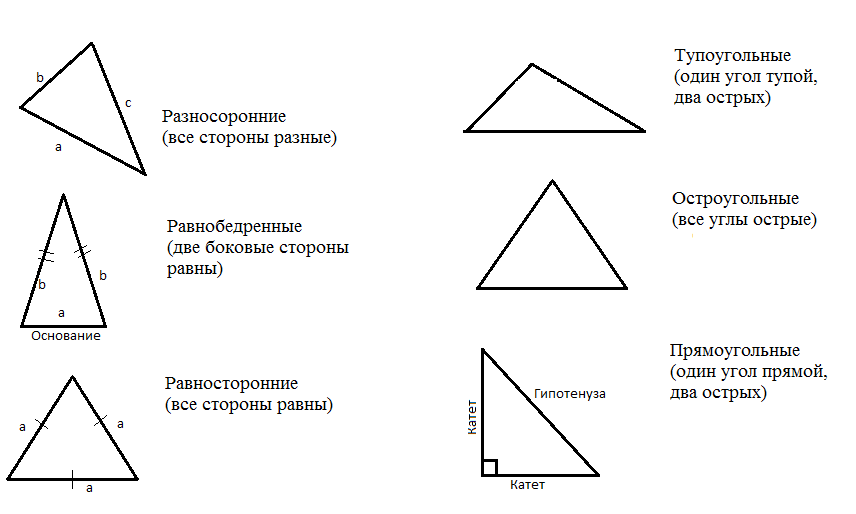
Может ли треугольник иметь одинаковую площадь и периметр?
Треугольник может иметь одинаковый периметр и площадь только в некоторых особых случаях. Эти фигуры, имеющие одинаковый периметр и площадь, называются равными фигурами. Таким образом, треугольник с равными периметром и площадью называется равнобедренным треугольником.
Как найти третью сторону и периметр прямоугольного треугольника по двум сторонам?
Третью сторону прямоугольного треугольника можно вычислить, используя меру двух других сторон, применяя теорему Пифагора. По теореме Пифагора для любого прямоугольного треугольника со сторонами «а», «b» и «с»
в 2 = а 2 + б 2
где
- а = Перпендикуляр
- б = база
- c = Гипотенуза прямоугольного треугольника
Периметр прямоугольного треугольника рассчитывается по формуле: P = a + b + c единиц.
Как найти периметр треугольника с координатами?
Если известны координаты треугольника, то длины всех его сторон можно вычислить по формуле расстояния.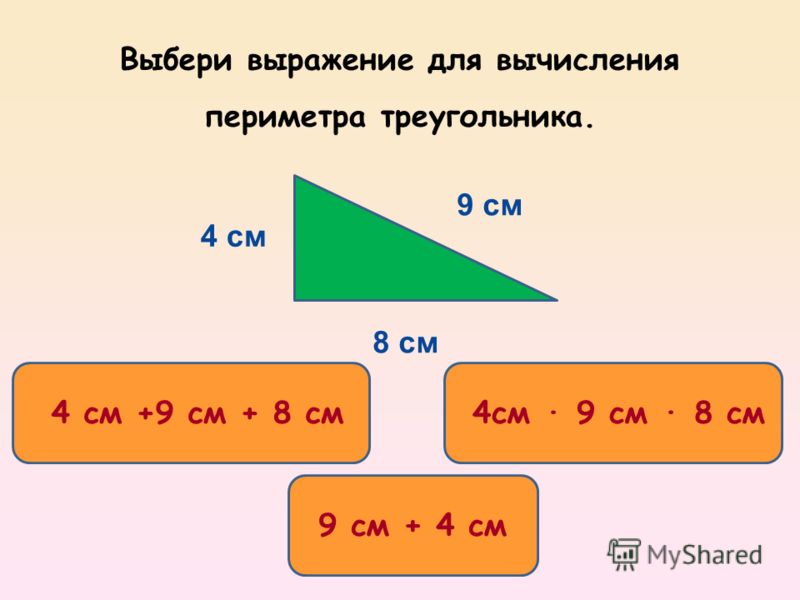 Как только эти длины получены, мы можем просто сложить их, чтобы найти периметр данного треугольника.
Как только эти длины получены, мы можем просто сложить их, чтобы найти периметр данного треугольника.
Как найти периметр треугольника с двумя равными сторонами?
Чтобы вычислить периметр треугольника с двумя равными сторонами, мы находим сумму длин всех сторон. Такой треугольник называется равнобедренным. Формула для вычисления периметра равнобедренного треугольника: 2a + b, где «a» — длина одной из равных сторон, а «b» — длина третьей стороны.
3.4: Треугольники, прямоугольники и теорема Пифагора
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 15139
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Решать приложения, используя свойства треугольников
- Используйте теорему Пифагора
- Решение приложений с использованием свойств прямоугольника
Будьте готовы
Прежде чем начать, пройдите этот тест на готовность.
- Упрощение: \(12(6h)\).
Если вы пропустили эту проблему, просмотрите упражнение 1.10.1. - Длина прямоугольника в три раза меньше ширины. Пусть w представляет ширину. Запишите выражение для длины прямоугольника.
Если вы пропустили эту проблему, просмотрите упражнение 1.3.43. - Решите: \(A=\frac{1}{2}bh\) для b при A=260 и h=52.
Если вы пропустили эту проблему, просмотрите упражнение 2.6.10. - Упрощение: \(\sqrt{144}\).
Если вы пропустили эту проблему, просмотрите упражнение 1.9.10.
Решайте приложения, используя свойства треугольников
В этом разделе мы будем использовать некоторые распространенные геометрические формулы. Мы адаптируем нашу стратегию решения задач, чтобы мы могли решать геометрические задачи. Геометрическая формула назовет переменные и даст нам уравнение для решения. Кроме того, поскольку все эти приложения будут включать в себя те или иные формы, большинство людей считают полезным нарисовать фигуру и пометить ее с помощью заданной информации. Мы включим это в первый шаг стратегии решения задач для геометрических приложений.
Мы включим это в первый шаг стратегии решения задач для геометрических приложений.
РЕШЕНИЕ ГЕОМЕТРИЧЕСКИХ ПРИЛОЖЕНИЙ
- Прочтите задачу и убедитесь, что все слова и идеи поняты. Нарисуйте рисунок и подпишите его с помощью данной информации.
- Определите , что мы ищем.
- Пометьте то, что мы ищем, выбрав переменную для ее представления.
- Переведите в уравнение, написав соответствующую формулу или модель для данной ситуации. Замените предоставленную информацию.
- Решите уравнение, используя хорошие методы алгебры.
- Проверьте ответ, подставив его обратно в уравнение, решенное на шаге 5, и убедившись, что он имеет смысл в контексте задачи.
- Ответьте на вопрос полным предложением.
Мы начнем приложения по геометрии с изучения свойств треугольников.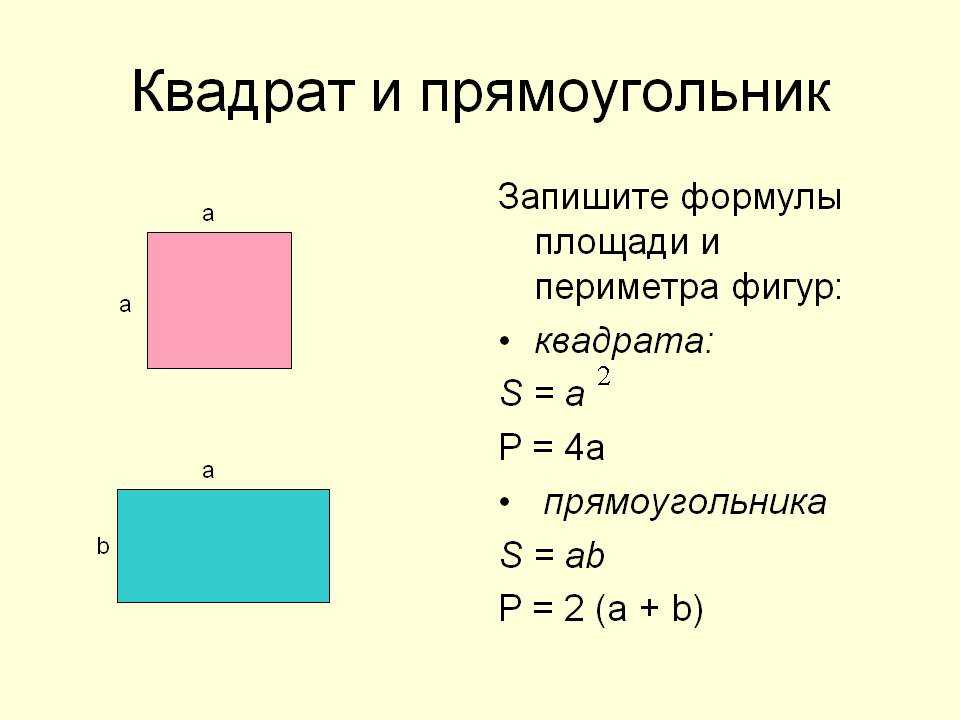 Давайте рассмотрим некоторые основные факты о треугольниках. Треугольники имеют три стороны и три внутренних угла. Обычно каждая сторона помечается строчной буквой, соответствующей прописной букве противоположной вершины. 9{\circ}\]
Давайте рассмотрим некоторые основные факты о треугольниках. Треугольники имеют три стороны и три внутренних угла. Обычно каждая сторона помечается строчной буквой, соответствующей прописной букве противоположной вершины. 9{\circ}\]
- Сумма углов треугольника равна 180°.
Периметр:
\[P = a + b + c\]
- Периметр равен сумме длин сторон треугольника.
Площадь:
\(A = \frac{1}{2}bh, b = \text{основание}, h = \text{высота}\)
- Площадь треугольника равна одной- половина основания умноженная на высоту.
Пример \(\PageIndex{1}\)
Два угла треугольника равны 55 и 82 градусам. Найдите величину третьего угла.
Решение
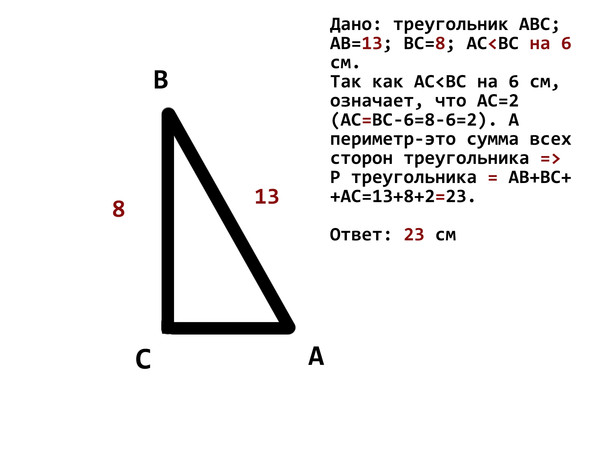 Прочтите задачу. Нарисуйте рисунок и подпишите его с помощью данной информации.
Прочтите задачу. Нарисуйте рисунок и подпишите его с помощью данной информации.\(\begin{array} {rll} {55 + 82 + 43} &{\stackrel{?}{=}} &{180} \\ {180} &{=} &{180\checkmark} \ конец{массив}\)
Попробуйте \(\PageIndex{1}\)
Два угла треугольника равны 31 и 128 градусам.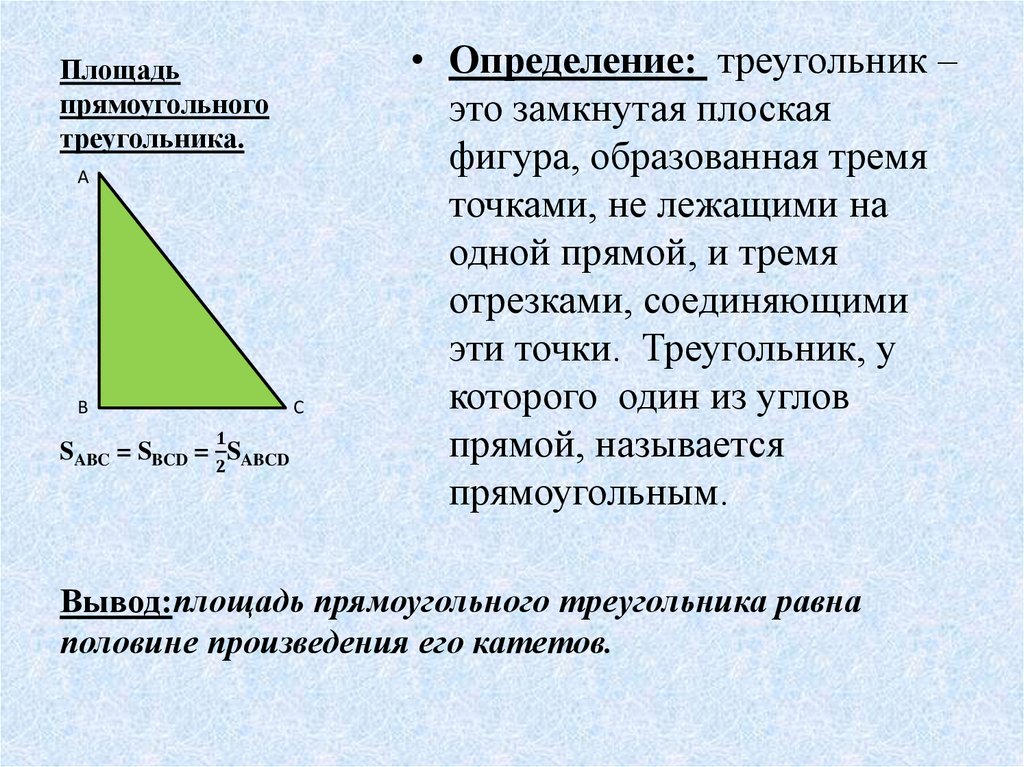 Найдите величину третьего угла.
Найдите величину третьего угла.
- Ответить
21 градус
Попробуйте \(\PageIndex{2}\)
Два угла треугольника равны 49и 75 градусов. Найдите величину третьего угла.
- Ответить
56 градусов
Пример \(\PageIndex{2}\)
Периметр треугольного сада составляет 24 фута. Длины двух сторон четыре фута и девять футов. Какой длины третья сторона?
Решение
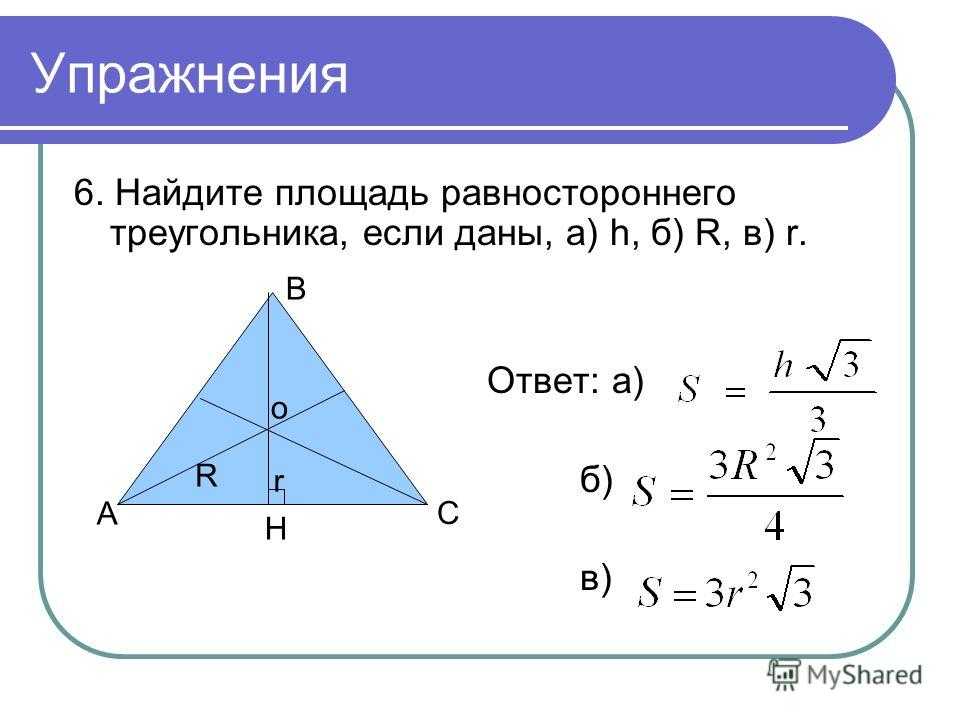 Имя. Выберите переменную для ее представления.
Имя. Выберите переменную для ее представления.\(\begin{array} {rll} {P} &{=} &{a + b +c} \\ {24} &{\stackrel{?}{=}} &{4 + 9+11 } \\ {24} &{=} &{24\checkmark} \end{массив}\)
Попробуйте \(\PageIndex{3}\)
Периметр треугольного сада составляет 48 футов. Длины двух сторон 18 футов и 22 фута. Какой длины третья сторона?
Какой длины третья сторона?
- Ответить
8 футов
Попробуйте \(\PageIndex{4}\)
Длина двух сторон треугольного окна составляет семь футов и пять футов. Периметр 18 футов. Какой длины третья сторона? 9{2}\)
\(12 = h\)
 Проверка.
Проверка. \(\begin{array} {rll} {A} &{=} &{\frac{1}{2}bh} \\ {90} &{\stackrel{?}{=}} &{\ frac{1}{2}\cdot 15\cdot 12} \\ {90} &{=} &{90\checkmark} \end{массив}\)
Попробуйте \(\PageIndex{5}\)
Площадь треугольной картины составляет 126 квадратных дюймов. База 18 дюймов. Какова высота?
- Ответить
14 дюймов
Попробуйте \(\PageIndex{6}\)
Треугольная дверь палатки имеет площадь 15 квадратных футов. Высота пять футов. Что такое база?
- Ответить
6 футов
Свойства треугольника, которые мы использовали до сих пор, применимы ко всем треугольникам. Теперь мы рассмотрим один конкретный тип треугольника — прямоугольный треугольник.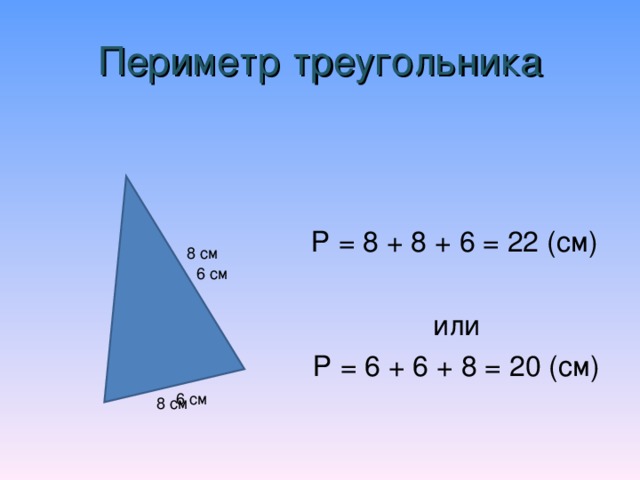 Прямоугольный треугольник имеет один угол 90°, который мы обычно отмечаем маленьким квадратом в углу.
Прямоугольный треугольник имеет один угол 90°, который мы обычно отмечаем маленьким квадратом в углу.
Определение: ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Прямоугольный треугольник имеет один угол 90°, вершина которого часто обозначается квадратом.
Пример \(\PageIndex{4}\)
Один угол прямоугольного треугольника равен 28°. Чему равен третий угол?
Решение
 Переведите.
Переведите. \(\begin{array} {rll} {180} &{\stackrel{?}{=}} &{90+28+62} \\ {180} &{=} &{180\checkmark} \ конец{массив}\)
Попробуйте \(\PageIndex{7}\)
Один угол прямоугольного треугольника равен 56°. Чему равен другой малый угол?
- Ответить
34°
Попробуйте \(\PageIndex{8}\)
Один угол прямоугольного треугольника равен 45°. Чему равен другой малый угол?
Чему равен другой малый угол?
- Ответить
45°
В примерах, которые мы видели до сих пор, мы могли нарисовать фигуру и подписать ее сразу после прочтения задачи. В следующем примере нам нужно будет определить один угол через другой. Мы будем ждать рисования фигуры, пока не напишем выражения для всех искомых углов.
Пример \(\PageIndex{5}\)
Размер одного угла прямоугольного треугольника на 20 градусов больше, чем размер наименьшего угла. Найдите меры всех трех углов.
Решение
 Определите , что вы ищете.
Определите , что вы ищете.Подставить в формулу.
\(\begin{align*} 2a + 110 &= 180 \\[3pt]
2a &= 70 \\[3pt]
a &= 35 \text{первый угол}\\[3pt]
a &+ 20 \text{второй угол}\\[3pt]
{\color{red}{35}} &+ 20 = 55 \end{align*}\)
А третий угол равен 90.
\(\begin{array} {rll} {35 + 55 + 90} &{\stackrel{?}{=}} &{180} \\ {180} &{=} &{180\checkmark} \ конец{массив}\)
 Ответьте на вопрос.
Ответьте на вопрос.Попробуйте \(\PageIndex{9}\)
Размер одного угла прямоугольного треугольника на 50° больше, чем размер наименьшего угла. Найдите меры всех трех углов.
- Ответить
20°,70°,90°
Попробуйте \(\PageIndex{10}\)
Размер одного угла прямоугольного треугольника на 30° больше, чем размер наименьшего угла. Найдите меры всех трех углов.
- Ответить
30°,60°,90°
Использование теоремы Пифагора
Мы узнали, как соотносятся меры углов треугольника. Теперь мы узнаем, как длины сторон связаны друг с другом. Важное свойство, описывающее соотношение между длинами трех сторон прямоугольного треугольника, называется 9.0062 Теорема Пифагора .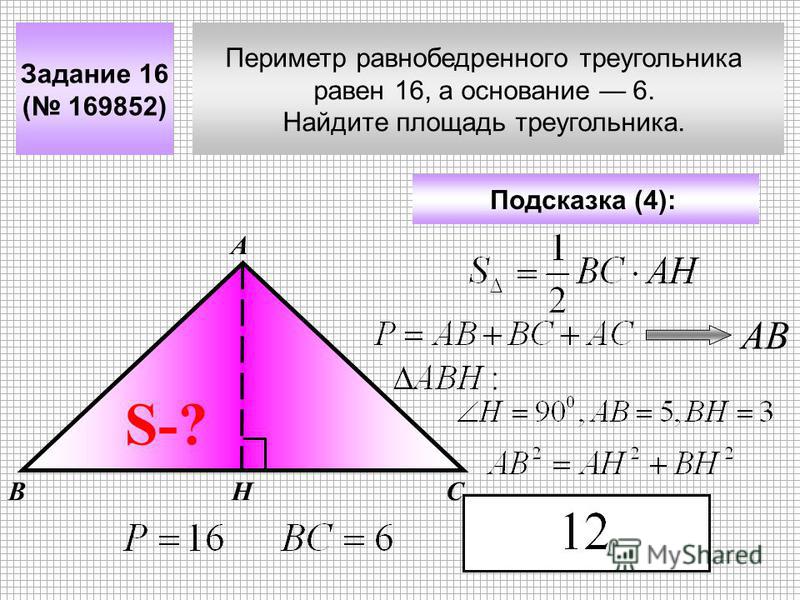 Эта теорема использовалась во всем мире с древних времен. Он назван в честь греческого философа и математика Пифагора, жившего около 500 г. до н.э.
Эта теорема использовалась во всем мире с древних времен. Он назван в честь греческого философа и математика Пифагора, жившего около 500 г. до н.э.
Прежде чем мы сформулируем теорему Пифагора, нам нужно ввести некоторые термины для сторон треугольника. Помните, что прямоугольный треугольник имеет угол 90°, отмеченный маленьким квадратом в углу. Сторона треугольника, противоположная углу 90°90°, называется гипотенузой , а каждая из остальных сторон называется 9{2}\).
Поскольку теорема Пифагора содержит переменные, которые возводятся в квадрат, для определения длины стороны прямоугольного треугольника нам придется использовать квадратные корни.
Пример \(\PageIndex{6}\)
Используйте теорему Пифагора, чтобы найти длину гипотенузы, показанной ниже.
Решение
 Step 7. Answer the question: The length of the hypotenuse is 5.»>
Step 7. Answer the question: The length of the hypotenuse is 5.»>Этикетка сбоку c на рис.
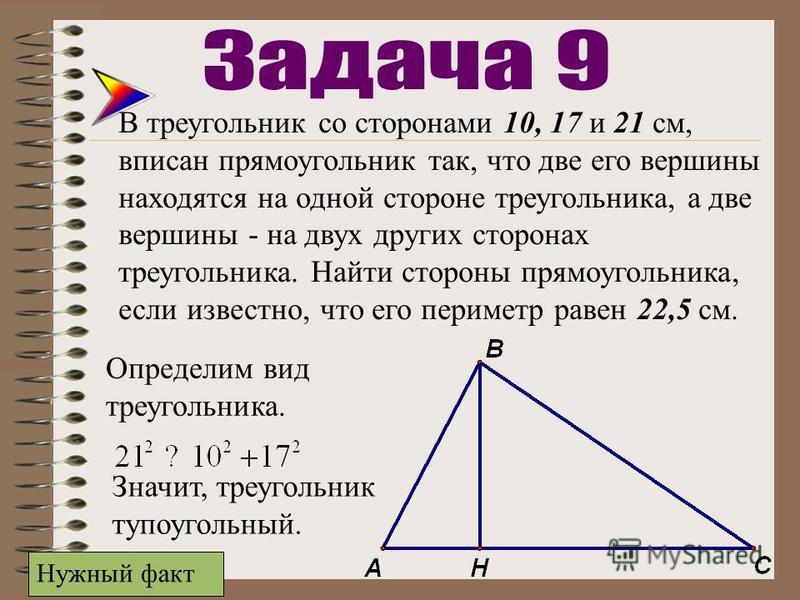
Попробуйте \(\PageIndex{11}\)
Используйте теорему Пифагора, чтобы найти длину гипотенузы в треугольнике, показанном ниже.
- Ответить
с=10
Попробуйте \(\PageIndex{12}\)
Используйте теорему Пифагора, чтобы найти длину гипотенузы в треугольнике, показанном ниже.
- Ответить
с=13
Пример \(\PageIndex{7}\)
Используйте теорему Пифагора, чтобы найти длину ноги, показанной ниже.
Решение
 Step 7. Answer the question: The length of the leg is 12.»>
Step 7. Answer the question: The length of the leg is 12.»>Попробуйте \(\PageIndex{13}\)
Используйте теорему Пифагора, чтобы найти длину катета в треугольнике, показанном ниже.
- Ответить
8
Попробуйте \(\PageIndex{14}\)
Используйте теорему Пифагора, чтобы найти длину катета в треугольнике, показанном ниже.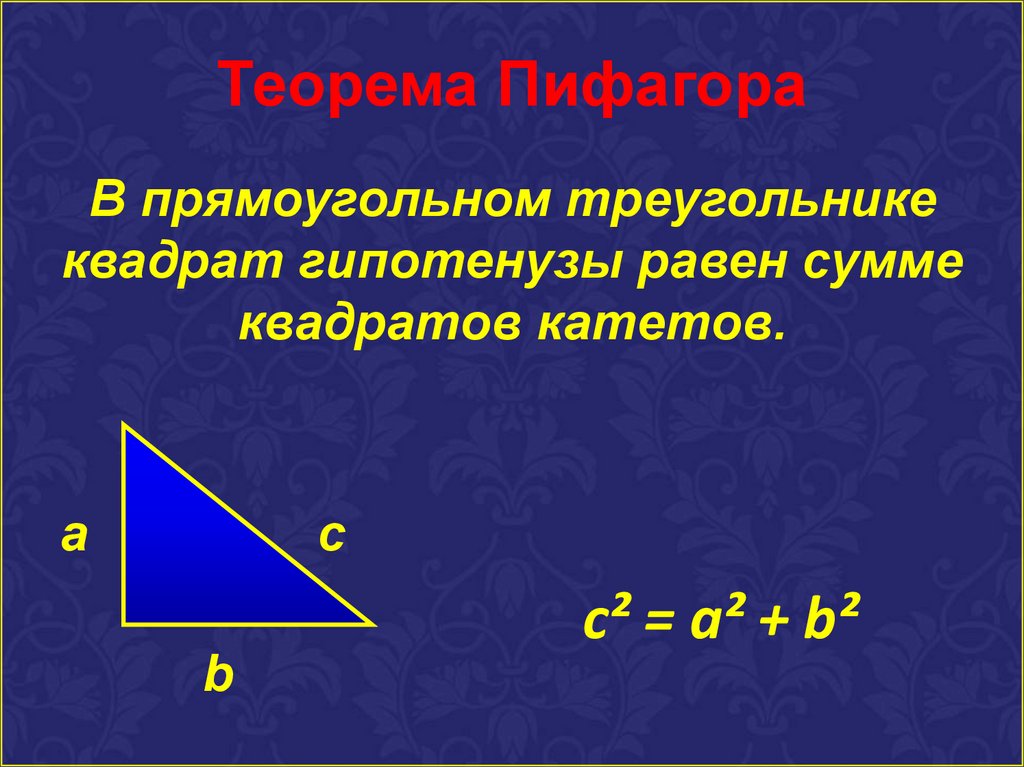 {2} \text{ Да.}} &{} \\\\ {\textbf{Шаг 7. Ответьте на вопрос.}} &{\text{Кельвен должен скрепить каждую часть}} \ \ {} &{\ text{дерево приблизительно 7,1 дюйма f из угла.}} \end{array}\)
{2} \text{ Да.}} &{} \\\\ {\textbf{Шаг 7. Ответьте на вопрос.}} &{\text{Кельвен должен скрепить каждую часть}} \ \ {} &{\ text{дерево приблизительно 7,1 дюйма f из угла.}} \end{array}\)
Попробуйте \(\PageIndex{15}\)
Джон устанавливает основание 13-футовой лестницы в пяти футах от стены своего дома, как показано ниже. Насколько далеко вверх по стене поднимается лестница?
- Ответить
12 футов
Попробуйте \(\PageIndex{16}\)
Рэнди хочет прикрепить 17-футовую гирлянду к вершине 15-футовой мачты своего парусника, как показано ниже. На каком расстоянии от основания мачты он должен прикрепить конец световой нити?
- Ответить
8 футов
Решайте приложения, используя свойства прямоугольника
Возможно, вы уже знакомы со свойствами прямоугольников. Прямоугольники имеют четыре стороны и четыре прямых (90°) угла. Противоположные стороны прямоугольника имеют одинаковую длину. Мы ссылаемся на одну сторону прямоугольника как на длину \(L\), а на соседнюю сторону как на ширину \(W\).
Противоположные стороны прямоугольника имеют одинаковую длину. Мы ссылаемся на одну сторону прямоугольника как на длину \(L\), а на соседнюю сторону как на ширину \(W\).
Расстояние вокруг этого прямоугольника равно \(L+W+L+W\) или \(2L+2W\). это периметр , \(P\), прямоугольника.
\[P=2L+2W\]
Как насчет площади прямоугольника? Представьте себе прямоугольный ковер размером 2 фута в длину и 3 фута в ширину. Его площадь составляет 6 квадратных метров. На рисунке шесть квадратов.
\[\begin{array} {l} {A=6} \\ {A=2\cdot3} \\ {A=L\cdot W} \end{array}\]
Площадь длина умножается на ширину. Формула площади прямоугольника:
\[A=LW.\]
СВОЙСТВА ПРЯМОУГОЛЬНИКОВ
Прямоугольники имеют четыре стороны и четыре прямых угла (90°).
Длины противоположных сторон равны.
Периметр прямоугольника равен сумме удвоенной длины и удвоенной ширины.
\[P=2L+2W\]
Площадь прямоугольника равна произведению длины на ширину.
\[A=L·W\]
Пример \(\PageIndex{9}\)
Длина прямоугольника 32 метра, а ширина 20 метров. Что такое периметр?
Решение
Нарисуйте фигуру и подпишите ее с помощью данной информации.

\(Р = 104\)
\(\begin{array} {rcl} {P} &{\stackrel{?}{=}} &{104} \\ {20+32+20+32} &{\stackrel{?}{= }} &{104} \\ {104} &{=} &{104\checkmark} \end{массив}\)
Попробуйте \(\PageIndex{17}\)
Длина прямоугольника 120 ярдов, а ширина 50 ярдов. Что такое периметр?
- Ответить
340 ярдов
Попробуйте \(\PageIndex{18}\)
Длина прямоугольника 62 фута, а ширина 48 футов. Что такое периметр?
- Ответить
220 футов
Пример \(\PageIndex{10}\)
Площадь прямоугольной комнаты составляет 168 квадратных футов. Длина 14 футов. Какова ширина?
Длина 14 футов. Какова ширина?
Решение
Нарисуйте фигуру и подпишите ее с помощью данной информации.
\(\frac{168}{14} = \frac{14W}{14}\)
\(12 = Вт\)
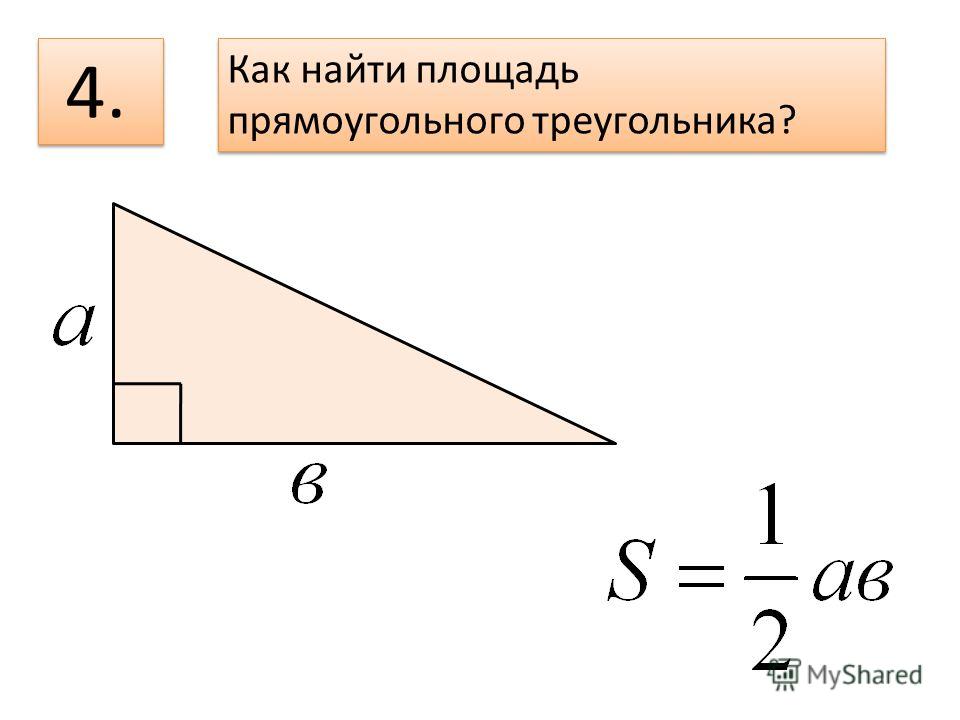 Проверка.
Проверка.
\(\begin{array} {rcl} {A} &{=} &{LW} \\ {168} &{\stackrel{?}{=}} &{14\cdot 12} \\ { 168} &{=} &{168\checkmark} \end{массив}\)
Попробуйте \(\PageIndex{19}\)
Площадь прямоугольника составляет 598 квадратных футов. Длина 23 метра. Какова ширина?
- Ответить
26 футов
Попробуйте \(\PageIndex{20}\)
Ширина прямоугольника 21 метр. Площадь 609квадратные метры. Какова длина?
- Ответить
29 метров
Пример \(\PageIndex{11}\)
Найдите длину прямоугольника с периметром 50 дюймов и шириной 10 дюймов.
Решение
 Step 7. Answer the question: The length is 15.»>
Step 7. Answer the question: The length is 15.»>Нарисуйте фигуру и подпишите ее с помощью данной информации.
\(\begin{array} {rcl} {P} &{=} &{50} \\ {15+10+15+10} &{\stackrel{?}{=}} &{50} \\ {50} &{=} &{50\checkmark} \end{массив}\)
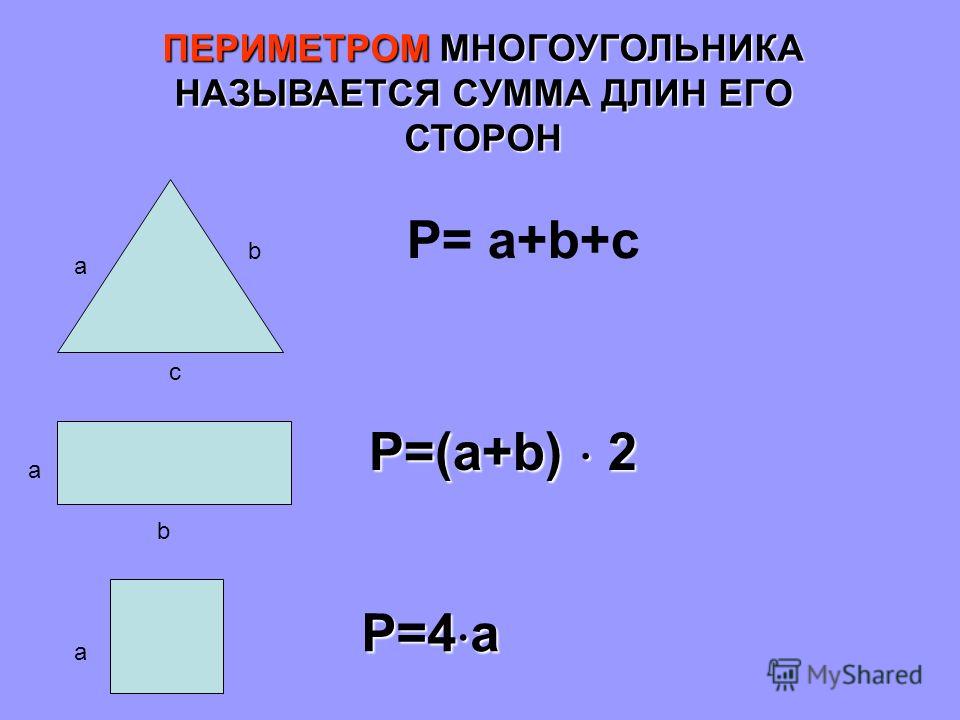 Ответьте на вопрос.
Ответьте на вопрос.Попробуйте \(\PageIndex{21}\)
Найдите длину прямоугольника с периметром 80 и шириной 25.
- Ответ
15
Попробуйте \(\PageIndex{22}\)
Найдите длину прямоугольника с периметром 30 и шириной 6.
- Ответ
9
Мы решали задачи, в которых были заданы длина или ширина, а также периметр или площадь; теперь мы научимся решать задачи, в которых ширина определяется через длину. Мы будем ждать, чтобы нарисовать фигуру, пока не напишем выражение для ширины, чтобы мы могли пометить одну сторону этим выражением.
Пример \(\PageIndex{12}\)
Ширина прямоугольника на два фута меньше его длины. Периметр 52 метра. Найдите длину и ширину.
Решение
 Hence, 14 equals L. The length is 14. Now we need to find the width. The width is L minus 2, which gives us 14 minus 2. Hence the width is 12. Step 6. Check. Since 14 plus 12 plus 14 plus 12 equals 52, this works! Below this, we have a rectangle with length 14 ft and width 12 ft. Step 7. Answer the question: The length is 14 feet, and the width is 12 feet.»>
Hence, 14 equals L. The length is 14. Now we need to find the width. The width is L minus 2, which gives us 14 minus 2. Hence the width is 12. Step 6. Check. Since 14 plus 12 plus 14 plus 12 equals 52, this works! Below this, we have a rectangle with length 14 ft and width 12 ft. Step 7. Answer the question: The length is 14 feet, and the width is 12 feet.»>Поскольку ширина определяется через длину, мы принимаем \(L=\) длину. Ширина на два фута меньше длины, поэтому пусть \(L-2\) ширина.
\(P=52\) футов
 Формула периметра прямоугольника связывает всю информацию.
Формула периметра прямоугольника связывает всю информацию.\(14=L\)
Длина 14 футов.
Ширина 12 футов.
Поскольку \(14+12+14+12=52\), это работает!
 Ответьте на вопрос.
Ответьте на вопрос.Попробуйте \(\PageIndex{23}\)
Ширина прямоугольника на семь метров меньше его длины. Периметр 58 метров. Найдите длину и ширину.
- Ответить
18 метров, 11 метров
Попробуйте \(\PageIndex{24}\)
Длина прямоугольника на восемь футов больше его ширины. Периметр 60 футов. Найдите длину и ширину.
- Ответить
19 футов, 11 футов
Пример \(\PageIndex{13}\)
Длина прямоугольника на четыре сантиметра больше его ширины более чем в два раза. Периметр 32 сантиметра. Найдите длину и ширину.
Решение
 Below this, we have 32 equals 32. Step 7. Answer the question: The length is 12 cm, and the width is 4 cm.»>
Below this, we have 32 equals 32. Step 7. Answer the question: The length is 12 cm, and the width is 4 cm.»>
12
Длина 12 см.
\(\begin{array} {rcl} {P} &{=} &{2L + 2W} \\ {32} &{\stackrel{?}{=}} &{2\cdot 12 + 2 \cdot 4} \\ {32} &{=} &{32\checkmark} \end{массив}\)
Попробуйте \(\PageIndex{25}\)
Длина прямоугольника в восемь раз больше его ширины. Периметр равен 64. Найдите длину и ширину.
- Ответить
24, 8
Попробуйте \(\PageIndex{26}\)
Ширина прямоугольника в шесть раз меньше его длины. Периметр равен 18. Найдите длину и ширину.
- Ответить
5, 4
Пример \(\PageIndex{14}\)
Периметр прямоугольного бассейна составляет 150 футов. Длина на 15 футов больше ширины.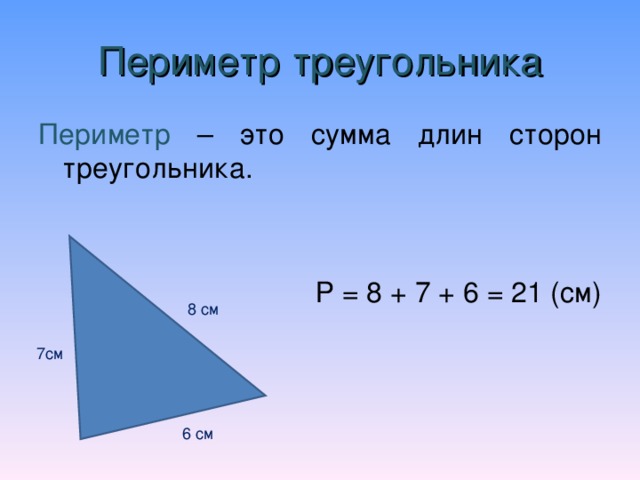 Найдите длину и ширину.
Найдите длину и ширину.
Решение
Нарисуйте фигуру и подпишите ее с помощью данной информации.
\(P=150\) футов
Выберите переменную для представления ширины.
Длина на 15 футов больше ширины.
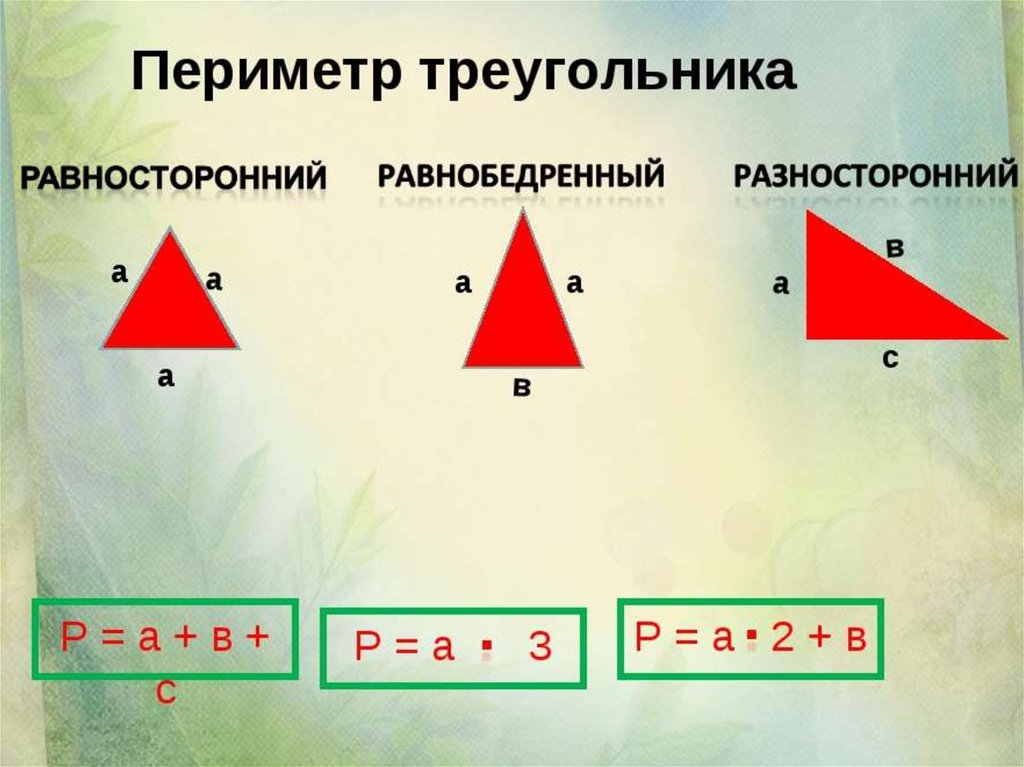
\(\begin{array} {rcl} {P} &{=} &{2L + 2W} \\ {150} &{\stackrel{?}{=}} &{2(45) + 2( 30)} \\ {150} &{=} &{150\checkmark} \end{массив}\)
Попробуйте \(\PageIndex{27}\)
Периметр прямоугольного бассейна составляет 200 футов. Длина на 40 футов больше ширины. Найдите длину и ширину.
- Ответить
70 футов, 30 футов
Попробуйте \(\PageIndex{28}\)
Длина прямоугольного сада на 30 ярдов больше ширины. Периметр 300 метров. Найдите длину и ширину.
Периметр 300 метров. Найдите длину и ширину.
- Ответить
90 ярдов, 60 ярдов
Ключевые концепции
- Стратегия решения задач для приложений геометрии
- Прочтите проблему и сделайте так, чтобы все слова и идеи были поняты. Нарисуйте рисунок и подпишите его с помощью данной информации.
- Определите , что мы ищем.
- Назовите то, что мы ищем, выбрав переменную для ее представления.
- Переведите в уравнение, написав соответствующую формулу или модель для данной ситуации. Замените предоставленную информацию.
- Решите уравнение, используя хорошие методы алгебры.
- Проверьте ответ в задаче и убедитесь, что он имеет смысл.
- Ответьте на вопрос полным предложением.

- Свойства треугольника для △ABC 9{2}\) где \(с\) — длина гипотенузы, а \(а\) и \(b\) — длины катетов.
- Свойства прямоугольников
- Прямоугольники имеют четыре стороны и четыре прямых угла (90°).
- Длины противоположных сторон равны.
- Периметр прямоугольника равен сумме удвоенной длины и удвоенной ширины: \(P=2L+2W\).
- Площадь прямоугольника равна произведению длины на ширину: \(A=LW\).
Эта страница под названием 3.4: Треугольники, прямоугольники и теорема Пифагора распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Показать страницу Содержание
- нет
- Теги
- Теорема Пифагора
- Прямоугольники
- прямоугольных треугольников
- источник@https://openstax.
 org/details/books/elementary-алгебра-2e
org/details/books/elementary-алгебра-2e - источник@https://openstax.org/details/books/intermediate-алгебра-2e
- треугольников
Калькулятор периметра 📐 — рассчитайте периметр квадрата, прямоугольника, треугольника, круга, параллелограмма, трапеции, эллипса…
Быстрая навигация:
- Как рассчитать периметр любой фигуры?
- Периметр квадратной
- Периметра прямоугольника
- Периметр треугольника
- Окружность круга
- Периметр параллелограммы
- Периметра
- Окружно AN -AN -AL -AL -ALSERIPSE). сектор
- Периметр восьмиугольника
- Где полезен калькулятор периметра?
Существуют разные правила вычисления периметра различных геометрических фигур. Наш калькулятор периметра поддерживает множество основных фигур, и ниже вы можете прочитать подробности о каждой из них, включая формулу расчета периметра.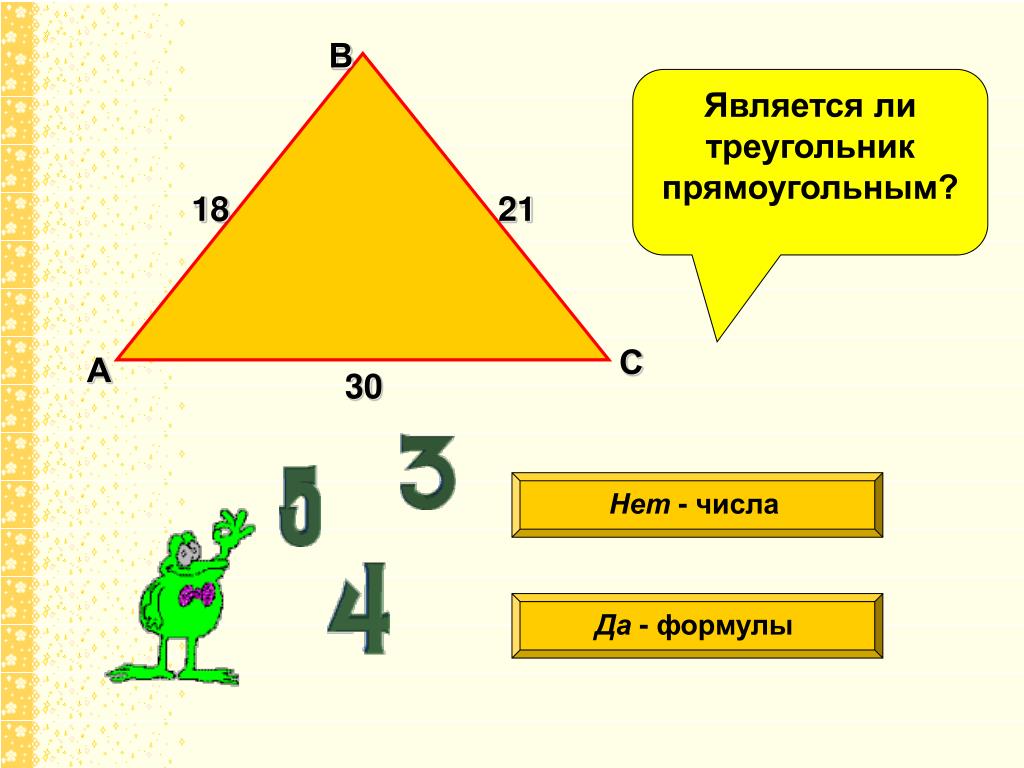 При выполнении расчетов не забывайте проводить каждое измерение в одних и тех же единицах или преобразовывать их в одни и те же единицы, чтобы получить достоверные результаты.
При выполнении расчетов не забывайте проводить каждое измерение в одних и тех же единицах или преобразовывать их в одни и те же единицы, чтобы получить достоверные результаты.
Формула для периметра квадрата: сторона x 4 , как показано на рисунке ниже:
Это самая простая форма для расчета, так как вам нужно выполнить только одно измерение. . Для этого даже калькулятор не нужен. Однако он также редко встречается в практических вопросах.
Периметр прямоугольника
Формула периметра прямоугольника: (ширина + высота) x 2 , как показано на рисунке ниже:
Для прямоугольника нужны два измерения — ширина и длина. Убедитесь, что оба значения указаны в одних и тех же единицах измерения, или при необходимости преобразуйте одно из них. Из-за простоты формы измерения легко выполнить, а калькулятор периметра упрощает расчет только при больших числах.
Формула периметра треугольника: сторона а + сторона b + сторона с , но есть много правил, по которым его можно вычислить. Визуал на рисунке ниже:
Наш калькулятор периметра также поддерживает следующие правила: SAS (сторона, угол, сторона), SSA (сторона, сторона, угол), ASA (угол, сторона, угол), а также правило гипотенузы и стороны для прямоугольных треугольников. .
Окружность круга
Формула для длины окружности 2 x π x радиус , но диаметр окружности d = 2 x r, поэтому другой способ записать это 2 x π x (диаметр / 2) . Визуал на рисунке ниже:
Во многих практических ситуациях легче точно измерить диаметр, чем радиус. Кроме того, во многих инженерных схемах по умолчанию указывается диаметр окружности, а не радиус.
Периметр параллелограммаФормула для периметра параллелограмма (ширина + высота) x 2 , как показано на рисунке ниже:
Периметр параллелограмма рассчитывается по той же формуле, что и прямоугольник, так как у обеих фигур противоположные стороны равны по длине.
Периметр трапеции
Формула периметра трапеции: основание 1 + основание 2 + сторона a + сторона b , как показано на рисунке ниже:
трапеция, так как это более сложная форма, у которой все стороны могут иметь разную длину.
Окружность эллипса (овала)Единой формулы для длины окружности эллипса не существует, так как ее точное вычисление на удивление сложно. Мы используем точный способ его вычисления, который приводит к точному вычислению после бесконечного числа вычислений. Если количество вычислений меньше бесконечности, возникает небольшая ошибка. Он быстро сходится к истинному значению, поэтому мы делаем только несколько шагов.
Сначала калькулятор вычисляет h = (большой радиус — малый радиус) 2 / (большой радиус + малый радиус) 2 . Затем он вычисляет периметр как равный π x (большой радиус + малый радиус) x (1 + h * 0,25 + h 2 * (1/64) + h 3 * (1/256) + h 4 * (25/16384) + h 5 * (49/65536) + h 6 * (441/1048576) .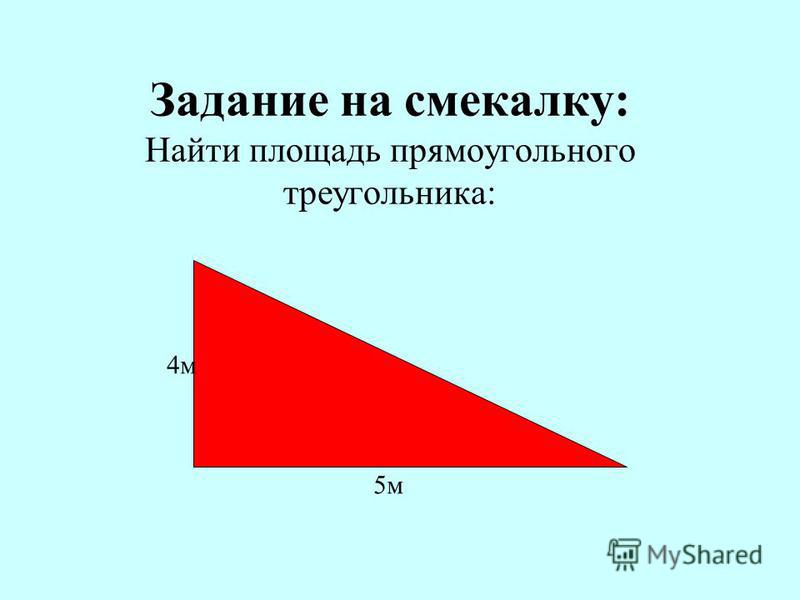 0003
0003
Формула для периметра сектора: 2 x радиус + радиус x угол x (π / 360) . Визуально на рисунке ниже:
Сектор — это просто часть круга, поэтому формула похожа. Дополнительная сложность возникает из-за необходимости вычислять, какая часть круга приходится на сектор.
Периметр восьмиугольникаФормула для периметра правильного восьмиугольника: стороны x 8 , как показано на рисунке ниже:
Это одна из самых простых фигур для расчета периметра — требуется только одно измерение, а простое умножение на восемь — это все, что нужно сделать. Правильные восьмиугольники можно встретить в технике, садово-парковом искусстве, архитектуре.
Где полезен калькулятор периметра?
Помимо очевидных задач на уроках геометрии или домашних заданий, калькулятор периметра может иметь множество практических применений. Например, в спорте — вы можете решить, что вам нужно ходить или бегать по 10 км в день, чтобы оставаться в хорошей физической форме. Однако что делать, если поблизости нет хороших трасс? Вы можете просто выбрать большое здание или любой прямоугольный квартал или набор кварталов, рассчитать их периметр, а затем разделить на него 10 км, чтобы определить, сколько кругов вам нужно сделать.
Однако что делать, если поблизости нет хороших трасс? Вы можете просто выбрать большое здание или любой прямоугольный квартал или набор кварталов, рассчитать их периметр, а затем разделить на него 10 км, чтобы определить, сколько кругов вам нужно сделать.
Калькулятор также может быть полезен в различных проектах «сделай сам» дома или в саду, в том числе в таких вещах, как украшение дома, рукоделие и т. д. Работа в области машиностроения и некоторых ремесел часто заканчивается необходимостью расчета периметра.
Периметр прямоугольника. Определение с примерами решения
Прямоугольник – это четырехугольник (четырехсторонний многоугольник), у которого противоположные стороны равны и параллельны друг другу, а все четыре вершины равны 90 градусам. Поскольку противоположные стороны прямоугольника равны и параллельны, он также известен как параллелограмм. Прямоугольник определяется его длиной и шириной, которые являются различными размерами, что отличает его от квадрата.
Ниже приведены характеристики прямоугольника:
- У него четыре стороны и четыре вершины
- Две противоположные пары сторон параллельны и равны.
- Каждая вершина находится под углом 90 градусов.
- Диагонали являются биссектрисами друг друга.
- Прямоугольный параллелограмм.
- Сумма всех внутренних углов равна 360 градусов
Как найти периметр прямоугольника?
Периметр прямоугольника определяется как общее расстояние, пройденное внешней границей прямоугольника. Измеряется в единицах длины. Формула периметра:
Периметр, P = 2 (длина + ширина)
Периметр прямоугольника можно считать одной из важных формул прямоугольника. Это общее расстояние, пройденное прямоугольником вокруг его внешней стороны. Периметр дает длину фигуры.
Периметр прямоугольника равен сумме его сторон. Все расстояние вокруг сторон любого объекта рассчитывается по формулам периметра. Поскольку противоположные стороны прямоугольника равны, периметр равен удвоенной длине и удвоенной ширине прямоугольника, что обозначается буквой «P».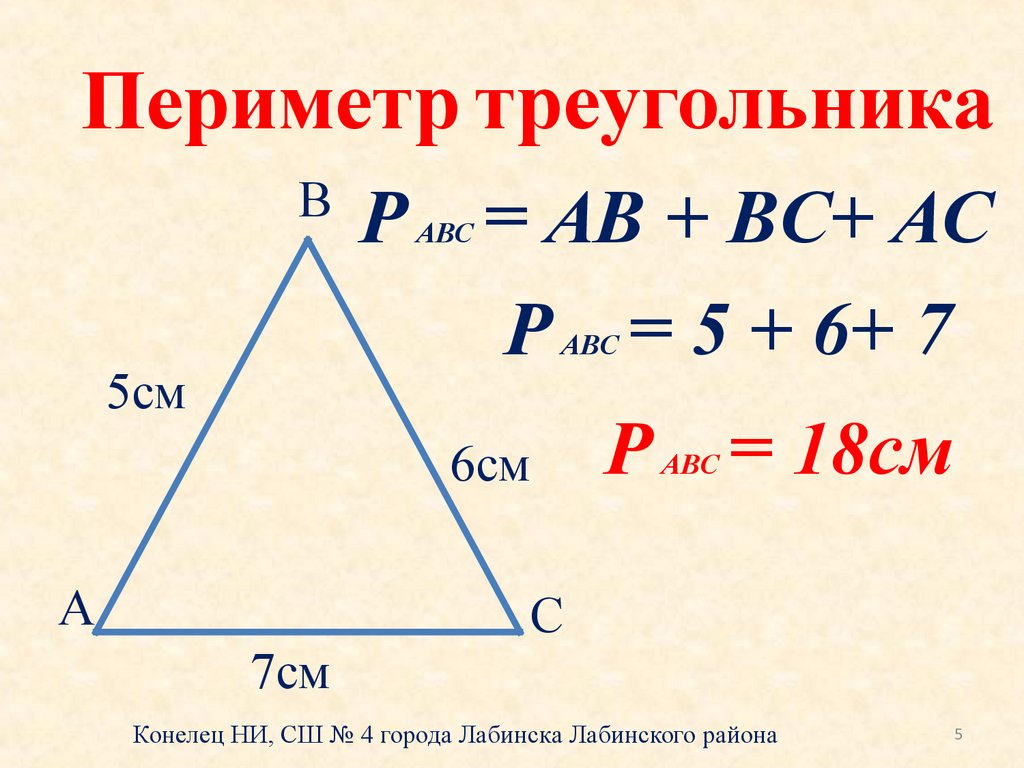
Периметр прямоугольника, согласно определению периметра, равен P = 2(a+b) единицам
где,
«a» — длина прямоугольника
«b» — ширина прямоугольник
Периметр прямоугольника (производное)
Так как периметр равен сумме сторон многоугольника. В результате периметр (P) прямоугольника равен: —
P = сумма всех четырех сторон
P = a + b + a + b (противоположные стороны прямоугольника равны)
P = 2(a + b)
где
«a» — длина прямоугольника
«b» — ширина прямоугольника
Следовательно,
Периметр прямоугольника = 2(длина + Ширина) квадратные единицы
Периметр прямоугольника Задачи
В. Найдите периметр прямоугольника с длиной и шириной 20 см и 12 см соответственно.
- Мы знаем, что периметр прямоугольника = 2(a + b)
где,
«a» — длина прямоугольника
«b» — ширина прямоугольника
∴ P = 2(20+12) = 2(32) = 64 см
Q. Что такое периметр прямоугольника длиной 12 м с основанием шириной 4 м ?
Что такое периметр прямоугольника длиной 12 м с основанием шириной 4 м ?
- Мы знаем, что Периметр прямоугольника = 2(a + b)
где
«a» — длина прямоугольника
«b» — ширина прямоугольника
∴ P = 2(12+4) = 2(16) = 32 м
В. Какова длина прямоугольного поля с периметром 120 см и шириной 50 см?
- Мы знаем, что Периметр прямоугольника = 2(a + b)
где
«a» — длина прямоугольника
«b» — ширина прямоугольника
Пусть P периметр,
∴ P = 2(a+b)
Или 120 = 2(a+50)
120/2 = a+50
a = 60-50
a = 10 см
5
5
Следовательно, длина прямоугольного поля равна 10 см.
В. Прямоугольный двор имеет длину 53 м и периметр 136 м. Определить его ширину.
- P = 136 м (периметр двора)
L = 53 м (длина двора)
Пусть B будет шириной двора.
Мы знаем, что Периметр, P = 2(длина + ширина)
Следовательно,
136= 2(53 + ширина)
53 + B = 68
W = 68 – 53 = 15 м
5
45
5
5
5
5
5 , ширина двора 15м
В.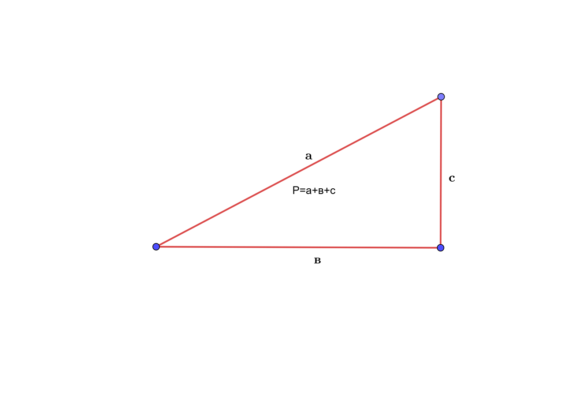 Сад имеет длину 120 дюймов и ширину 85 дюймов. Сколько забора потребуется, чтобы окружить его?
Сад имеет длину 120 дюймов и ширину 85 дюймов. Сколько забора потребуется, чтобы окружить его?
- Чтобы определить, сколько забора потребуется для границы сада, рассчитаем периметр сада по формуле периметра прямоугольника. (Поскольку забор построен на границе сада)
Дано:
Длина (L) = 120 дюймов
Ширина (B) = 85 дюймов
Периметр прямоугольника равен 2(l + w). Когда мы подставляем числа длины и ширины в этот расчет, мы получаем периметр = 2 (l + w) = 2 (120 + 85) = 2 × 205 = 410 дюймов.
Нам понадобится 410 дюймов кружева, чтобы обернуть простыню.
В. Плитка шоколада состоит из квадратов одинакового размера со стороной 1 дюйм. Определить периметр прямоугольной плитки шоколада.
- Каждый маленький квадрат имеет один дюйм со всех сторон.
Следовательно, если мы посчитаем и сложим стороны квадратов по длине стержня, мы получим 6 дюймов как длину (L).
Квадраты по ширине стержня имеют стороны, сумма сторон которых составляет до 2 дюймов.
В результате длина бруска 6 дюймов, а ширина 2 дюйма.
Периметр=2(l + w) = 2 (6 + 2) = 2×8 = 16 дюймов
В результате периметр равен 16 дюймам.
Связь между прямоугольником и квадратом
Квадрат — это четырехугольник, все стороны которого равны и параллельны друг другу, а все четыре вершины равны 90 градусам. Единственная разница между ним и прямоугольником заключается в том, что смежные стороны также равны в дополнение к противоположным сторонам, в результате чего получается квадрат с одинаковой длиной и шириной.
Следовательно, Метод вычисления периметра прямоугольника отличается от формулы вычисления периметра квадрата:-
Формула вычисления периметра прямоугольника
Периметр прямоугольника = 2(a + b),
, где «a» – длина
, а b – ширина.
Периметр квадрата формула, с другой стороны, определяется как
Периметр квадрата = 4s,
, где «s» — длина стороны.
Формула периметра прямоугольника отличается от формулы квадрата. Это потому, что равны только противоположные стороны прямоугольника. С другой стороны, все стороны квадрата имеют одинаковую длину.
Это потому, что равны только противоположные стороны прямоугольника. С другой стороны, все стороны квадрата имеют одинаковую длину.
В результате мы можем переписать формулу для вычисления периметра прямоугольника в квадрат следующим образом:
Периметр прямоугольника = 2(a + b),
, где «а» обозначает длину
и «b» обозначает ширину.
Как мы знаем, у квадрата все стороны равны, a=b=s (стороны квадрата),
Периметр прямоугольника = 2(a + b) = 2(s + s) = 2 x 2s = 4s
Периметр фигуры — это расстояние вокруг ее краев. Расстояние, которое потребуется, чтобы обойти фигуру один раз вдоль ее края. В качестве альтернативы периметр фигуры можно определить как сумму длин всех ее сторон.
Прямоугольник – это четырехсторонний многоугольник (четырехугольник), у которого противоположные стороны одинаковой длины, а внутренние углы равны 90 градусов. Поскольку противоположные стороны имеют одинаковую длину, мы суммируем длины двух соседних сторон и умножаем на 2.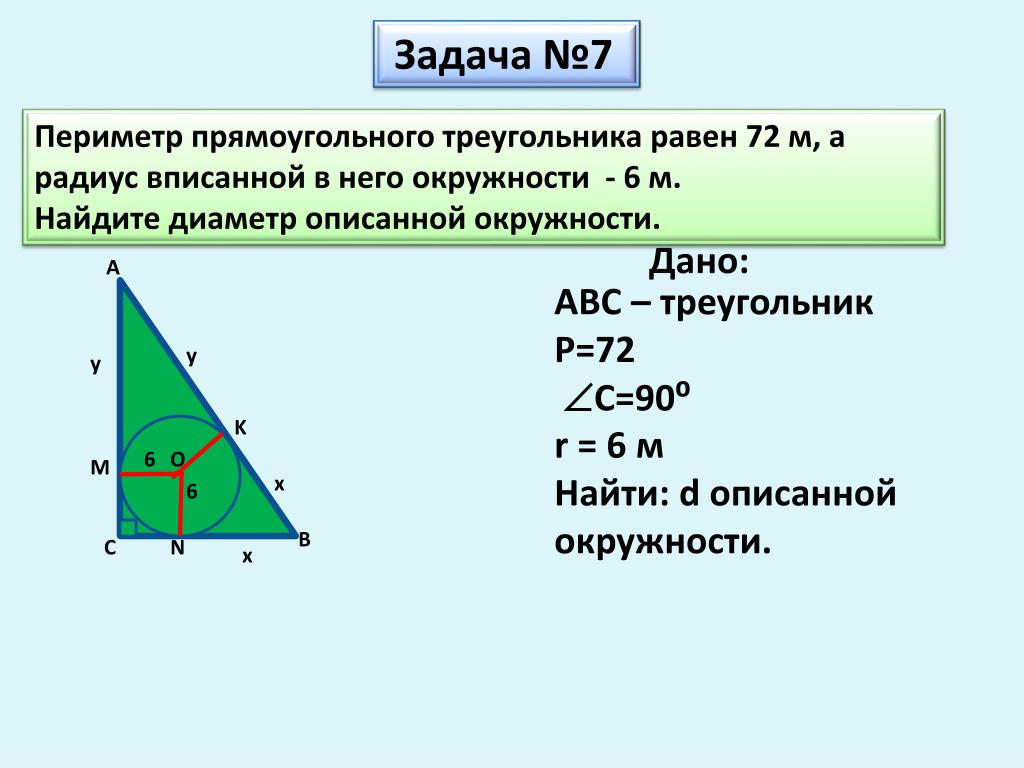 Периметр прямоугольника рассчитывается как 2(a + b), где a и b — длина и ширина прямоугольника соответственно.
Периметр прямоугольника рассчитывается как 2(a + b), где a и b — длина и ширина прямоугольника соответственно.
Формула периметра прямоугольника отличается от формулы квадрата. Это потому, что равны только противоположные стороны прямоугольника. С другой стороны, стороны квадрата имеют одинаковую длину.
Часто задаваемые вопросы
Q1. Что такое Периметр?
Линия или граница, окружающая фигуру, называется ее периметром. Его также можно описать как длину контура фигуры. Самая простая формула для вычисления периметра – это сумма длин всех сторон.
Q2. Что такое периметр прямоугольника?
Периметр прямоугольника определяется как все расстояние, пройденное внешней границей прямоугольника. Измеряется в единицах длины. Формула периметра выглядит следующим образом:
Периметр прямоугольника = 2 (длина + ширина)
Периметр прямоугольника равен сумме его сторон. Формулы периметра используются для вычисления общего расстояния вокруг сторон любого объекта. Поскольку противоположные стороны прямоугольника равны, периметр равен удвоенной длине прямоугольника плюс удвоенной его ширине.
Поскольку противоположные стороны прямоугольника равны, периметр равен удвоенной длине прямоугольника плюс удвоенной его ширине.
Q3. Каковы отличительные признаки прямоугольника?
Прямоугольник имеет четыре стороны и четыре вершины, из которых две противоположные стороны параллельны и равны, а каждая вершина образует 9Угол 0 градусов. Диагонали прямоугольника являются биссектрисами друг друга. Мы также можем назвать прямоугольник прямоугольным параллелограммом.
Q4. Чему равна сумма всех внутренних углов прямоугольника?
Сумма всех внутренних углов прямоугольника равна 360 градусов.
Q5. В чем разница между прямоугольником и квадратом? Как это влияет на их формулы Периметра?
Квадрат определяется как четырехсторонний многоугольник (четырехугольник), все стороны которого равны и параллельны друг другу, а все четыре вершины равны 90 градусов. Единственное отличие здесь от прямоугольника состоит в том, что соседние стороны также равны, помимо того, что они противоположны; следовательно, длина и ширина квадрата равны.
Формула периметра прямоугольника отличается от формулы квадрата. Это потому, что равны только противоположные стороны прямоугольника. С другой стороны, стороны квадрата имеют одинаковую длину.
В результате мы можем преобразовать формулу периметра прямоугольника в квадрат следующим образом:
Периметр прямоугольника = 2(a + b), где «a» представляет длину, а «b» представляет ширину.
Теперь все стороны квадрата равны, a=b=s (стороны квадрата),
Следовательно, периметр прямоугольника = 2(a + b) = 2(s + s) = 2 x 2s = 4s
Часто задаваемые вопросы
1. Что такое периметр треугольника в математике?
Ответ. Периметр треугольника — это расстояние вокруг всей фигуры. Обычно он измеряется в метрах, а его формула рассчитывается путем сложения длин каждой стороны треугольника.
2. Какая формула периметра треугольника?
Ответ. Периметр треугольника — это расстояние вокруг внешней стороны треугольника.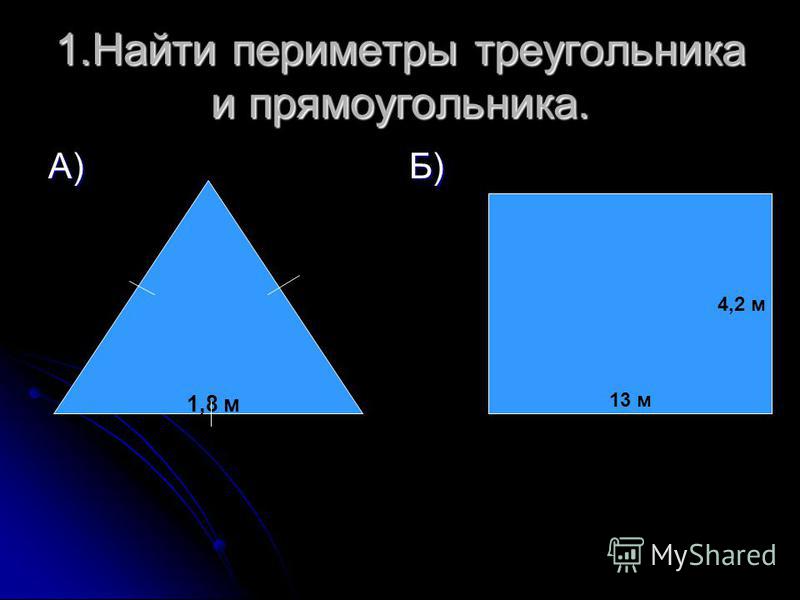 Формула для вычисления периметра: Периметр = (2 a + 2 b + 2*c).
Формула для вычисления периметра: Периметр = (2 a + 2 b + 2*c).
3. Как найти периметр треугольника с тремя равными сторонами?
Ответ. Чтобы найти периметр треугольника с тремя равными сторонами, вам понадобится специальная формула.
Во-первых, вы должны выяснить каждую из трех сторон. Например, предположим, что у вашего треугольника длины сторон равны 1 единице, 2 единицам и 3 единицам. Теперь вы можете использовать это уравнение:
Периметр=2(сумма всех трех сторон)
4.Как найти периметр треугольника с координатами?
Ответ. Периметр треугольника — это расстояние вокруг его внешней стороны. Это то, что вы получите, если сложите все стороны. Формула для нахождения периметра выглядит следующим образом:
P = сумма(a, b, c)
5. Как найти периметр треугольника с двумя равными сторонами?
Ответ. Периметр треугольника с двумя равными сторонами можно найти по формуле:
периметр = 2 * длина стороны + длина стороны + длина стороны
Например, если у нас есть треугольник с двумя равными сторонами, каждая из которых имеет длину 10 дюймов, мы найдем периметр треугольника, умножив 20 на 2, а затем добавить 20 к этому результату.
Периметр: что это такое и как его найти на каждом многоугольнике
Сегодня мы научимся вычислять периметры геометрических фигур. Но сначала начнем с определения.
Что такое периметр?
Периметр — это то, что мы называем длиной контура геометрической фигуры.
Таким образом, периметр является мерой длины, поэтому он выражается в сантиметрах, дюймах и футах, как правило, в линейных единицах.
Вы можете ознакомиться с наиболее распространенными типами многоугольников здесь или посмотреть следующее видео.
Видео: научиться вычислять периметры
История Евы и сада в ее школе поможет вам лучше понять концепцию периметра. Это видео одного из наших интерактивных уроков. Он больше не интерактивный, но у вас есть преимущество в том, что вы можете смотреть его столько раз, сколько необходимо, и делиться им с другими. Если вы хотите получить доступ к реальным интерактивным учебникам, зарегистрируйтесь в Smartick, онлайн-методе обучения математике для детей в возрасте от 4 до 14 лет.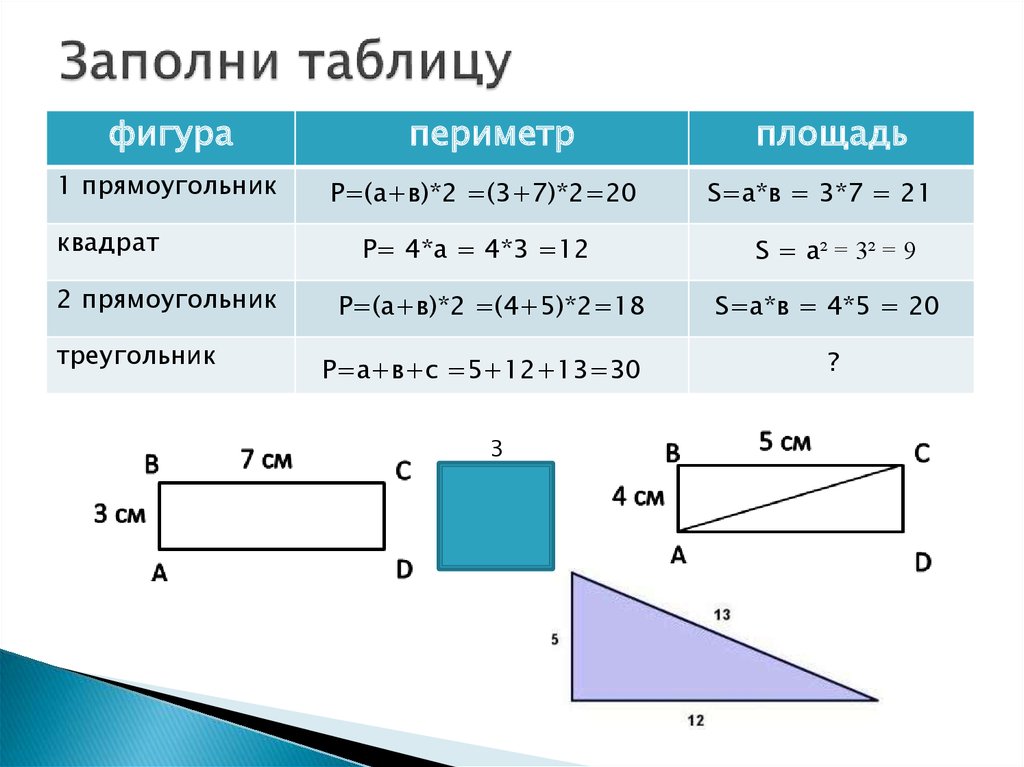
Как найти периметр
Давайте рассмотрим первую стратегию расчета периметра. Неважно, сколько сторон у многоугольника.
Периметр геометрической фигуры всегда можно вычислить, прибавив длину каждой из ее сторон.
Чтобы вычислить периметр, нужно сложить длины его сторон: 17см + 15см + 11см = 43смВы можете использовать эту стратегию для вычисления периметра любого многоугольника.
Как найти периметр многоугольника с примерами
Теперь, когда вы знаете, что такое периметр и как его вычислить для любого многоугольника, мы рассмотрим, как вычислить периметр для каждой из следующих геометрических фигур:
Как найти периметр квадрата
Особенностью квадрата является то, что у него четыре равные стороны .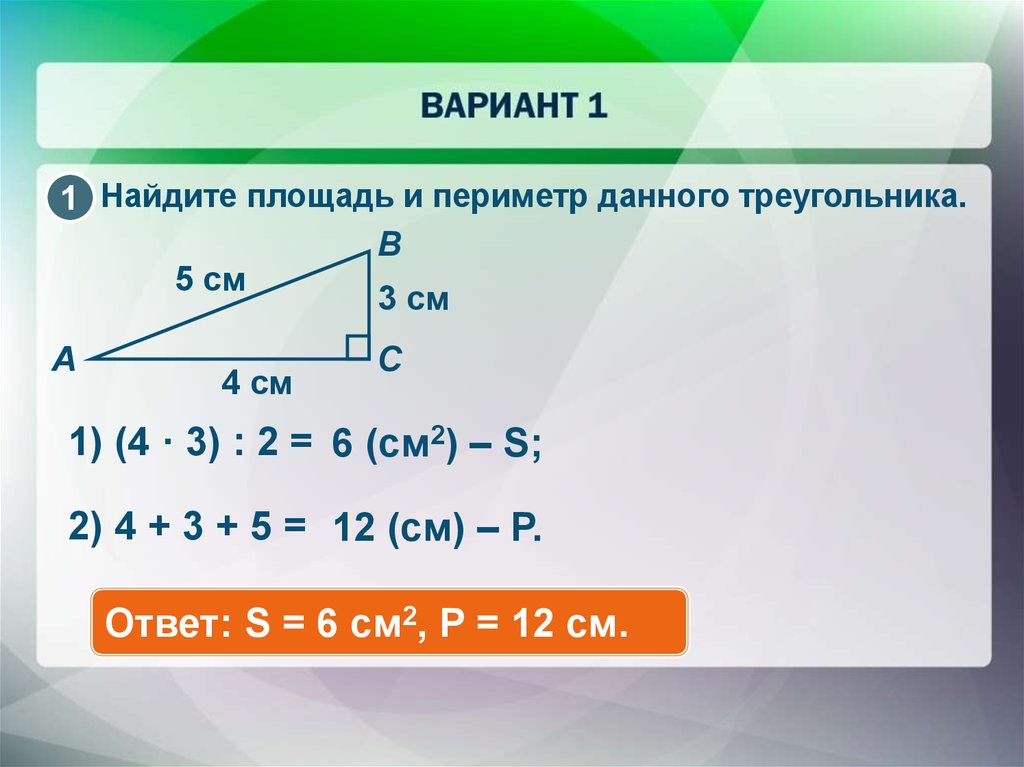 Мы можем воспользоваться этим, упростив наши расчеты.
Мы можем воспользоваться этим, упростив наши расчеты.
Вы можете вычислить периметр этого квадрата, сложив длины четырех сторон.
Периметр = 6 см + 6 см + 6 см + 6 см = 24 см
Так как четыре стороны равны, умножение длины одной стороны на четыре даст вам тот же результат.
Периметр = 4 x 6 см = 24 см
Итак, вы открыли правило, которое поможет вам с любым квадратом.
Периметр квадрата = 4 x длина одной стороны
Как найти периметр прямоугольника
В каждом прямоугольнике противоположные стороны равны друг другу. Его стороны равны два на два .
Чтобы вычислить периметр прямоугольника в примере, вы можете добавить длину его сторон, две стороны по 6 см и две стороны по 4 см.
Периметр = 6см + 4см + 6см + 4см = 20см
Вы можете умножить сумму основания и высоты на два и получить тот же результат, потому что все прямоугольники повторяют длину своих сторон два раза.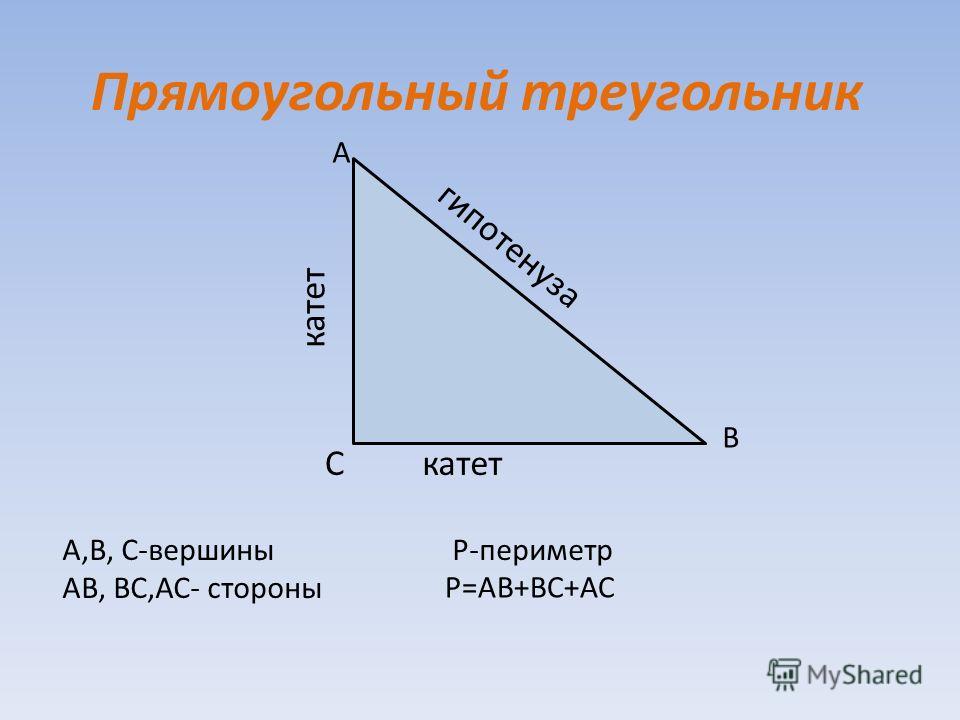
Периметр = 2x (6 см + 4 см) = 20 см
Итак, у вас есть подход к любому прямоугольнику.
Периметр прямоугольника = 2 x (основание + высота). Все они имеют одинаковую длину.
Каждая сторона имеет длину 7 см, и вы можете рассчитать длину ее контура следующим образом.
Периметр = 7 см + 7 см + 7 см = 21 см
Или есть более простой способ. Поскольку три стороны одинаковы, вы можете умножить одну сторону на 3, и результат не изменится.
Периметр = 3 x 7 см = 21 см
И это поможет вам с любым равносторонним треугольником.
Периметр равностороннего треугольника = 3 x длина одной стороны
Равнобедренные треугольники
Равнобедренные треугольники имеют две равные стороны и одну различную .
Чтобы освежить память о различных типах треугольников, взгляните на этот пост о геометрических фигурах.
Учитывая, что две стороны равны, а одна различна, нам просто нужно умножить длину повторяющейся стороны на два, а затем добавить длину другой стороны.
Периметр = 5 см x 2 + 6 см = 16 см
Итак, для любого равнобедренного треугольника:
Периметр равнобедренного треугольника = длина повторной стороны x 2 + длина другой стороны
Как найти периметр равнобедренного треугольника a Ромб
Ромб имеет четыре равные стороны . Но не все его углы равны, а только углы, лежащие друг против друга .
Поскольку четыре стороны равны , мы можем умножить длину одной стороны на четыре , чтобы получить периметр.
Периметр = 4 x 5 см = 20 см
Это правило применимо и к квадратам, поскольку они также имеют четыре равные стороны.
Периметр ромба = 4 x длина одной стороны
Как найти периметр трапеции
Равнобедренная трапеция
Периметр равнобедренных трапеций вычисляется особым образом. Они имеют две противоположные стороны, равные , а другие две стороны , известные как основания (верхнее и нижнее), параллельны, но имеют разную длину .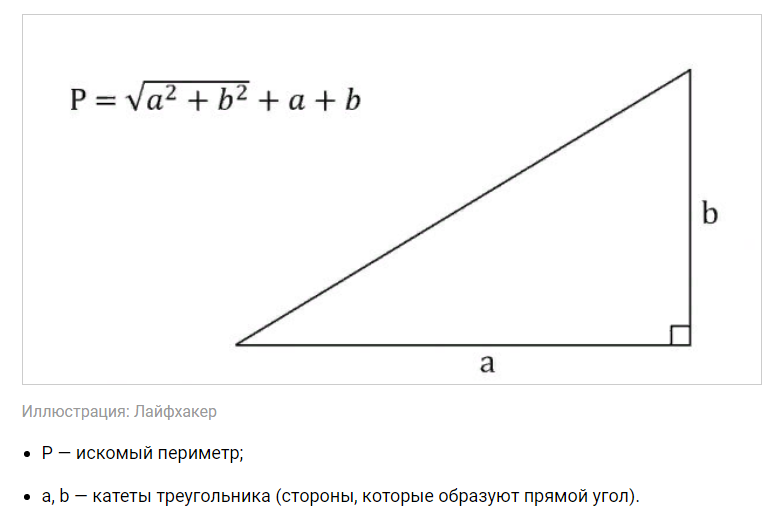
В этом случае нам нужно умножить длину одной из противоположных сторон на два и сложить длины двух оснований.
Периметр = 5 см x 2 + 12 см + 6 см = 28 см
Чтобы вычислить периметр любой равнобедренной трапеции:
Периметр равнобедренной трапеции = длина противоположной стороны x 2 + длина верхнего основания + длина нижнего основания
Как найти периметр ступенчатого многоугольника
Ступенчатые полигоны имеют очень своеобразную характеристику. Сумма длин сторон, параллельных основанию, равна длине основания. И то же самое относится к сумме длин сторон, параллельных высоте, которые измеряют ту же длину, что и высота.
Итак, для вычисления периметра любого ступенчатого многоугольника мы можем использовать ту же формулу, что и для прямоугольников, потому что мы можем приблизиться к сумме длин горизонтальной и вертикальной сторон, как если бы они были равны длине основание и высота. Длина основания и высота как бы повторяются.
Периметр = 2x (6 см + 8 см) = 28 см
Правило работает для любого ступенчатого многоугольника этого типа:
Периметр разностороннего многоугольника = 2 x (основание + высота)
Как найти периметр любого правильного многоугольника
Отличительной особенностью правильных многоугольников является то, что все их стороны имеют одинаковую длину .
Поскольку у пятиугольника пять равных сторон, чтобы найти его периметр, нужно умножить длину одной стороны на пять.
Периметр пятиугольника = 5 x длина одной стороны
А у шестиугольника, который имеет шесть равных сторон, вы можете умножить одну сторону на шесть.
Периметр шестиугольника = 6 x длина одной стороны
Из этих правил мы можем извлечь правило для вычисления периметра любого правильного многоугольника простым способом.
Умножьте количество сторон многоугольника на длину одной из сторон.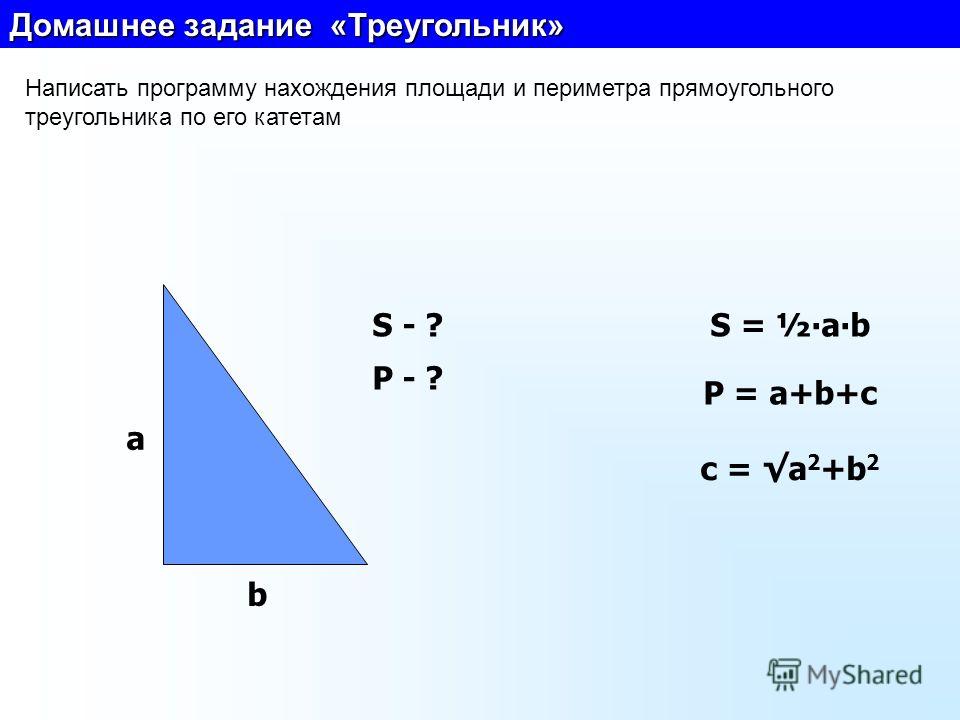
Периметр правильного многоугольника = количество сторон x длина одной стороны
Как вычислить периметр круга
Чтобы вычислить периметр круга, первое, что вам нужно знать, это то, что периметр круга равен длине его окружности .
Чтобы рассчитать длину окружности, необходимо умножить диаметр окружности на число Пи:
- Периметр круга равен произведению числа Пи на диаметр (d): Периметр круга = π x d
- Вы также можете умножить 2 на число Пи на радиус (r): Периметр круга = 2,π x r, потому что диаметр всегда вдвое больше радиуса.
Формулы, которые мы только что видели, используют число Пи, символом которого является π, и происходит от числа, представляющего отношение между длиной окружности и ее диаметром (d), π = периметр окружности/d. Имеет бесконечное количество десятичных знаков, но в школе его обычно округляют до сотых: π ≃ 3,14.
Если вы хотите узнать больше о периметрах, геометрии и других темах начальной математики, войдите в Smartick и попробуйте его бесплатно.


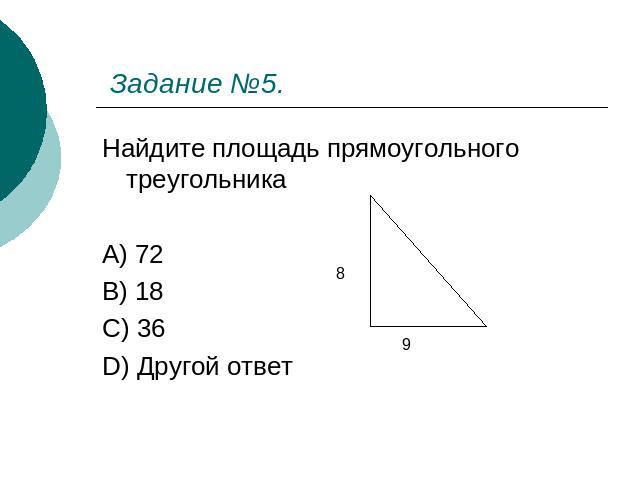



 org/details/books/elementary-алгебра-2e
org/details/books/elementary-алгебра-2e