Решение задач — урок 3 — ГЕОМЕТРИЯ — Уроки для 8 классов — конспекты уроков — План урока — Конспект урока — Планы уроков
Урок № 10
Тема. Решение задач
Цель: обобщить и систематизировать знания учащихся относительно определений, свойств и признаков разновидностей параллелограмма; усовершенствовать умения учащихся применять изученные утверждение во время построения правильных рассуждений для решения типовых задач.
Тип урока: обобщение и систематизация знаний.
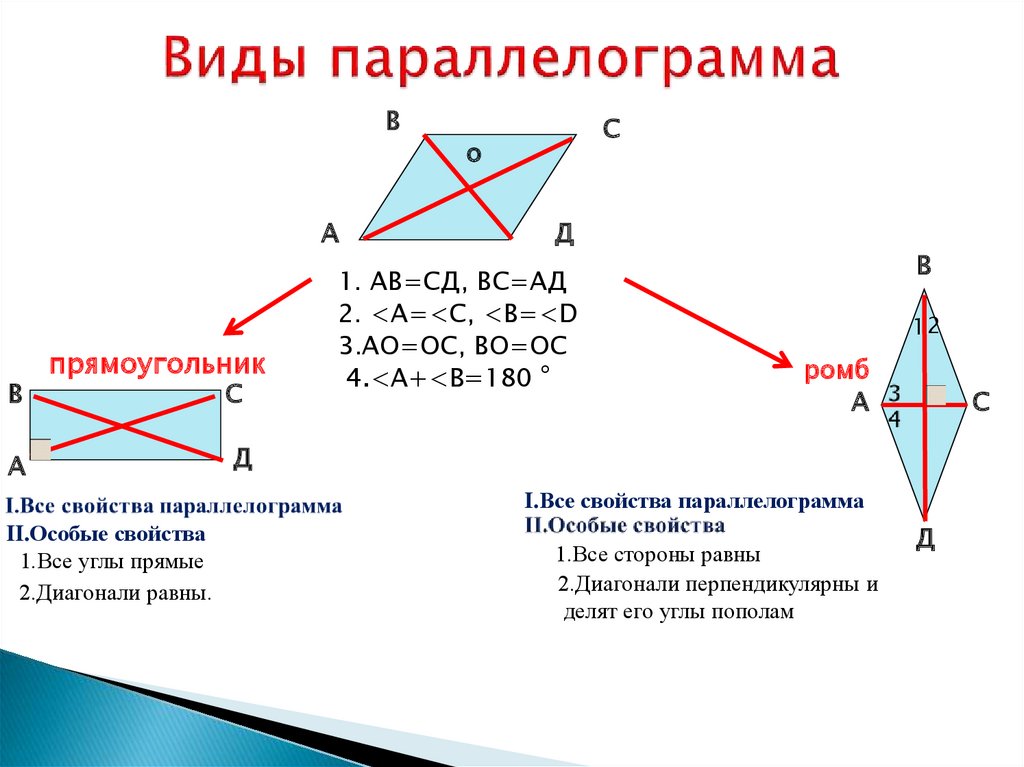
Наглядность и оборудование: конспекты «Параллелограмм», «Ромб. Квадрат».
Ход урока
I. Организационный этан
II. Проверка домашней работы
Самостоятельная работа
Вариант 1
1. Является ромбом любой квадрат?
2. Правильно, что существует прямоугольник, который не является параллелограммом?
3.
Три углы параллелограмма равны. Определите вид параллелограмма.
4. Как с помощью транспортира за наименьшего количества измерений проверить, является ромбом данный параллелограмм?
Вариант 2
1. Является прямоугольником любой квадрат?
2. Правильно, что существует ромб, который не является параллелограммом?
3. Три стороны параллелограмма равны. Определите вид параллелограмма.
4. Как с помощью транспортира за наименьшего количества измерений проверить, является прямоугольником данный параллелограмм?
Вариант 3
1. Существует ли четырехугольник с перпендикулярными диагоналями, который не является ромбом?
2. Правильно, что ни один прямоугольник не является ромбом?
3. Определите вид четырехугольника, у которого есть две пары равных противоположных углов и ни один из них не острый.
4. Как с помощью только циркуля проверить, является ли четырехугольник квадратом?
Вариант 4
1.
Существует ли четырехугольник с равными диагоналями, который не является прямоугольником?
2. Правильно, что ни один ромб не является прямоугольником?
3. Определите вид четырехугольника, у которого две стороны параллельны и равны третьей стороне.
4. Как с помощью только циркуля проверить, является ли четырехугольник прямоугольником?
Поскольку письменные задания домашней работы соответствовали по содержанию и уровню сложности письменным заданием классной работы, проверку этих заданий учитель осуществляет в сжатой форме (проговаривается, какое утверждение было использовано, а также ответ).
III. Формулировка цели и задач урока
Цель урока непосредственно вытекает из темы урока. Поскольку на предыдущих двух уроках было изучено достаточно большой объем теоретического материала, а также рассмотрены лишь случаи прямого применения изученных утверждений, то на этом уроке логично было бы систематизировать утверждение и освоить приемы, а также сформировать устойчивые умения (навыки) с применение приобретенных знаний.
IV. Актуализация опорных знаний
Поскольку одна из целей урока — систематизация знаний учащихся об изученных определений, свойств и признаков прямоугольника, ромба и квадрата, то для достижения этой цели надо восстановить в памяти учащихся названы утверждение. Для этого целесообразно решить устно задачи.
Выполнение устных упражнений
1. В четырехугольнике точка пересечения диагоналей делит их на четыре равные отрезки. Какого вида этот четырехугольник?
2. Найдите в прямоугольнике (рис. 1) все равны между собой углы.
3. АВ — диаметр круга, в который вписан четырехугольник ADBC, причем AD=BC (рис. 2). Докажите, что ADBC — прямоугольник.
4. ABCD — ромб (рис. 3). Определите угол х.
5. ABCD — параллелограмм, CM = CK (рис. 4). Докажите, что ABCD — ромб.
V.
Обобщение и систематизация знаний
Выполнение устных упражнений
1. Верны ли утверждения?
1) Если в четырехугольнике диагонали не перпендикулярны, то этот четырехугольник не ромб.
2) Если в паралелограмі диагонали неровные, то он не может быть прямоугольником.
2. Верны ли утверждения?
1) Каждый квадрат является прямоугольником.
2) Существует ромб, который является прямоугольником.
4) Существует квадрат, который не является ромбом.
3. Чем отличается квадрат от ромба, не являющегося квадратом? Какие общие свойства имеют эти фигуры?
После выполнения устных упражнений учащиеся презентуют схемы, которые они составили дома.
Далее проводится обсуждение, коррекция и обобщение полученных результатов. Таким образом формируется представление учащихся о соотношения между изученными понятиями «четырехугольник», «параллелограмм», «прямоугольник», «ромб», «квадрат», которое может быть изображено в виде схемы.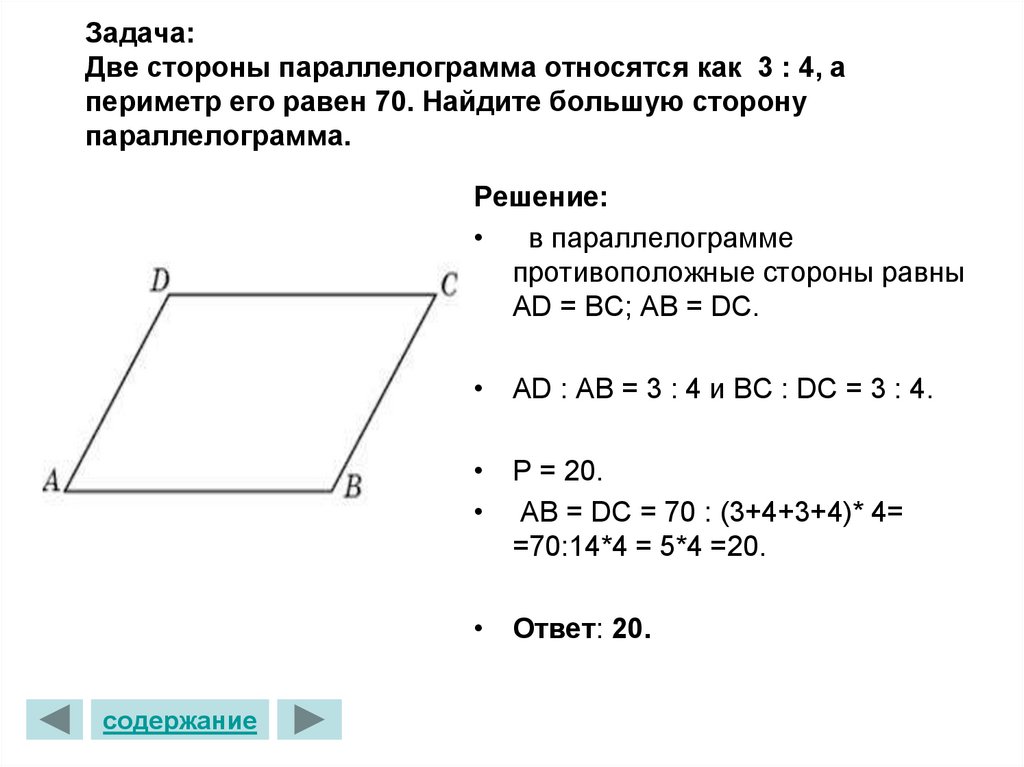
После выполненной работы по сборке схемы следует провести работу с чтения этой схемы, а именно обсудить ряд вопросов следующего содержания:
1. Как доказать, что данный четырехугольник является прямоугольником?
2. Как доказать, что данный четырехугольник является ромбом?
3. Как доказать, что данный четырехугольник является квадратом?
4. Как доказать, что данный параллелограмм является прямоугольником?
5. Как доказать, что данный параллелограмм является ромбом?
6. Как доказать, что данный параллелограмм является квадратом?
7. Дан прямоугольник. Какие равенства выполняются для его элементов?
8. Дан ромб. Какие равенства выполняются для элементов этого ромба?
9. Дан квадрат. Какие равенства выполняются для элементов этого квадрата?
Ответы на эти вопросы фактически общими схемами для решения типовых задач на вычисления и доказательства в теме «Прямоугольник.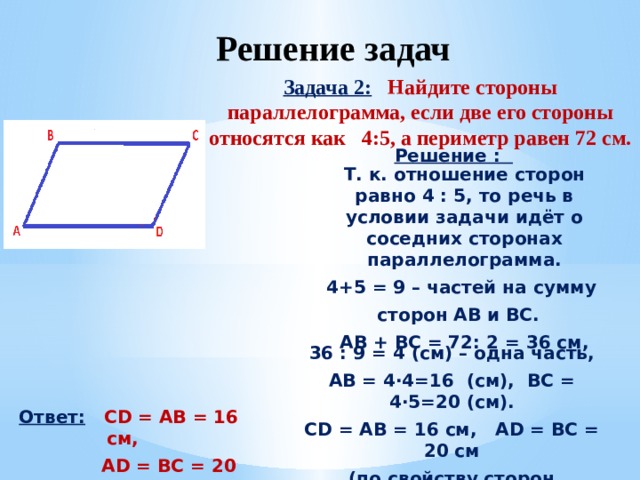
Ромб. Квадрат».
VI. Применение умений и навыков
На этом этапе урока проводится работа по формированию у учащихся умений использовать схему и следствия из нее для решения задач достаточного уровня сложности на доказательство и вычисление с использованием определений, свойств и признаков прямоугольника, ромба и квадрата.
Выполнение письменных упражнений
1. Диагонали параллелограмма образуют углы с одной из его сторон. Докажите, что данный параллелограмм — прямоугольник.
2. Точка пересечения диагоналей прямоугольника расположена от большей стороны на 5 см ближе, чем от меньшей стороны. Найдите стороны прямоугольника, если его периметр равен 44 см.
3. В паралелограмі ABCD биссектрисы углов А и В пересекают стороны ВС и AD в точках Е и F соответственно. Докажите, что ABEF — ромб.
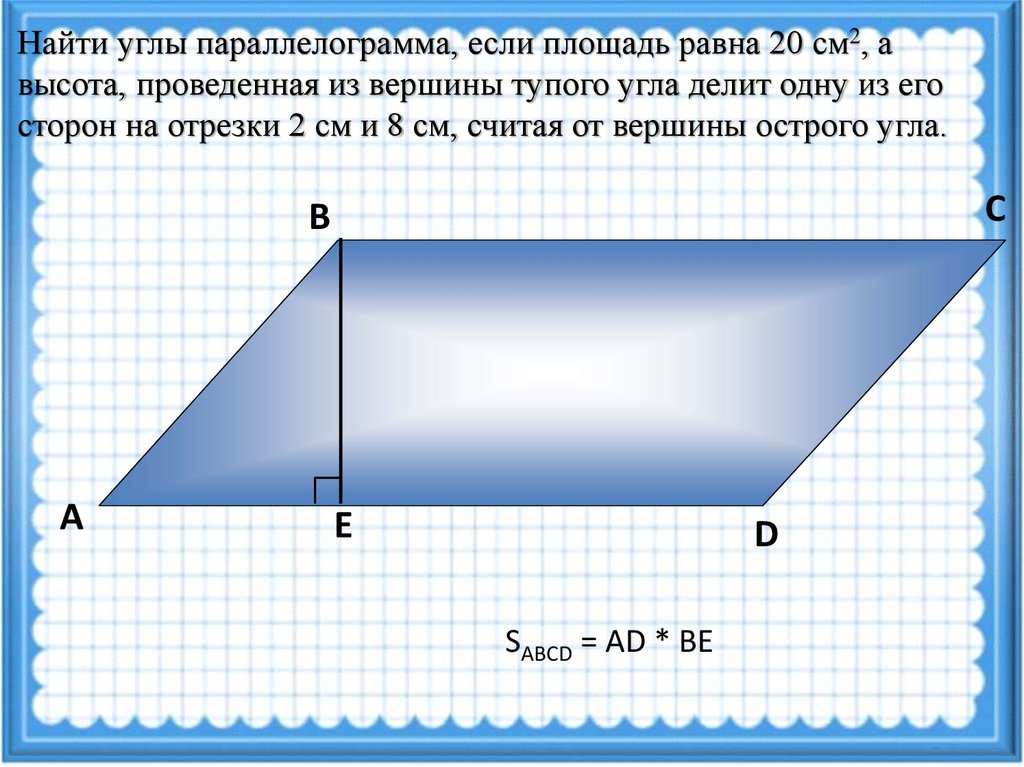
4. Высота, проведенная из вершины тупого угла ромба, делит его сторону пополам. Найдите:
а) углы ромба;
б) сторону ромба, если его меньшая диагональ равна 16 см.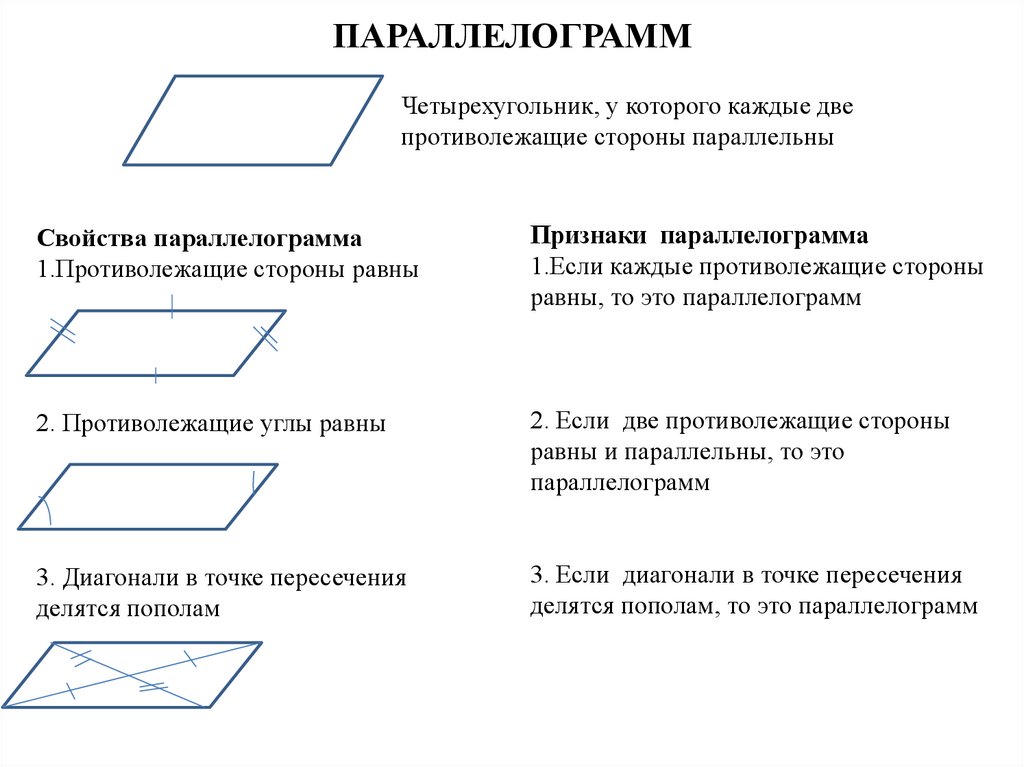
5. Докажите, что прямоугольник, диагонали которого перпендикулярны, является квадратом.
6. На диагонали АС квадрата ABCD отмечены точки К и М так, что АК = СМ (рис. 5). Докажите, что BMDK — ромб.
@ При наличии времени и за счет построения схематического рисунка и записи только плана решения, количество задач для письменного решения может быть увеличена. Во время решения задач учитель формирует у учащихся умение действовать по схеме.
После проведения анализа условия задачи учащиеся составляют соответствующий логическую цепочку, который поможет решить задачу.
Такие умственные действия (выделение вопросов задачи; определение вида вопросу; определение вида утверждение, что должно быть использовано для поиска ответа на вопрос, а дальше — составление логической цепочки с использованием данных задачи) должны предшествовать записям в тетрадях учащихся.
Формирование умения выполнять такие мыслительные действия — одна из главных целей изучения геометрии.
VII. Итоги урока
Для проверки усвоения учащимися основного содержания урока учитель может предложить учащимся решить устное задание: по соответствующим готовым рисунком (рис. 6 а, б) составьте задачу, чтобы она розв’язувалась с использованием:
а) свойства прямоугольника;
б) признаки прямоугольника.
VIII. Домашнее задание
Повторить теоретические сведения по теме «Параллелограмм и его виды».
Выполнить домашнюю самостоятельную работу.
Домашняя самостоятельная работа
Вариант 1
1. Угол между диагональю и стороной ромба равен 20°. Найдите углы ромба.
2. Диагональ делит угол прямоугольника в отношении 1 : 8. Найдите тупой угол, который образуется при пересечении диагоналей прямоугольника.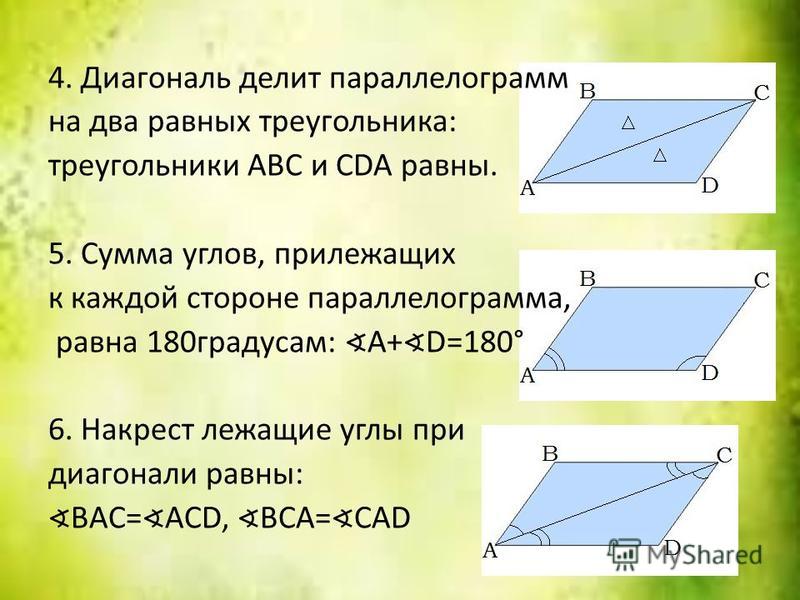
3. Докажите, что прямоугольник является квадратом, когда две соседние стороны образуют с диагональю равные углы.
4. Постройте ромб по высоте и периметру.
Вариант 2
1. Угол ромба равен 140°. Найдите угол между противоположным к этому угла диагональю и стороной ромба.
2. Диагональ делит угол прямоугольника на два угла, один из которых на 10° больше другого. Найдите угол между диагоналями прямоугольника.
3. Докажите, что параллелограмм является ромбом, если две соседние стороны образуют с диагональю равные углы.
4. Постройте ромб с острым углом и высотой.
Параллелограмм (часть 2)
Задача
На диагонали МР прямоугольника МNРQ отложены равные отрезки МА и РВ. Докажите, что АNBQ параллелограмм.
Решение.
Четырехугольник является параллелограммом, если его противоположные стороны попарно равны. Докажем это.
Исходя из условия задачи треугольники MAN и PBQ равны.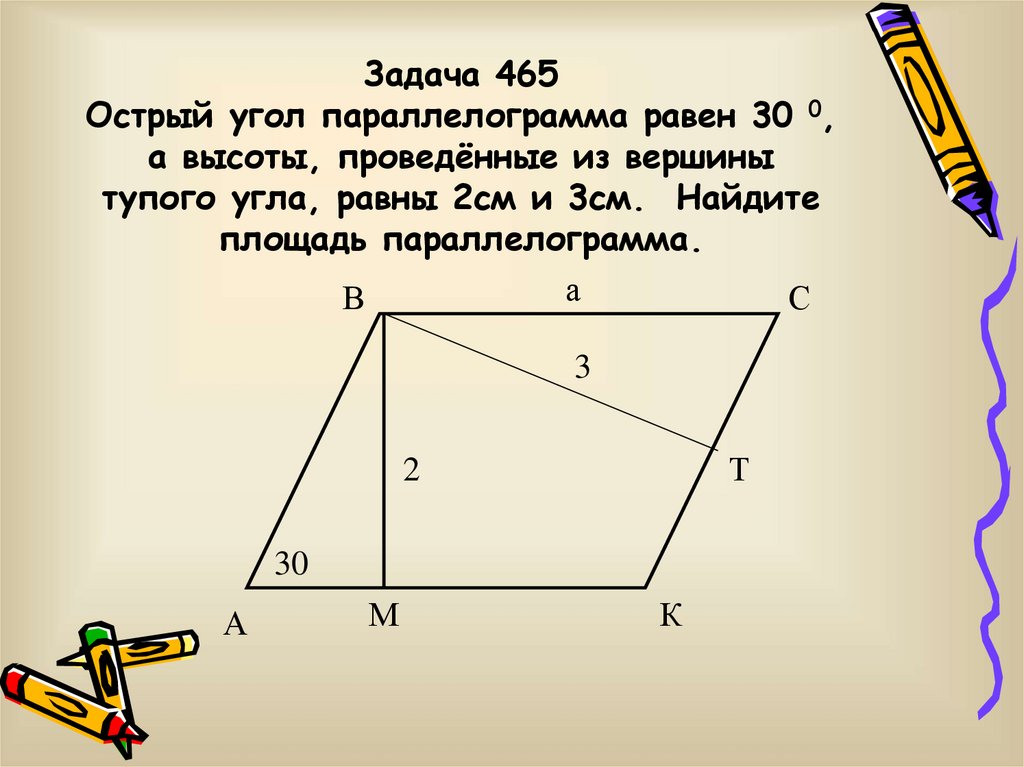
Так как PB = AM по условию задачи, PQ = NM как противоположные стороны прямоугольника, а углы BPQ и NMA равны, как внутренние накрест лежащие для параллельных прямых NP и MQ и секущей MP.
Аналогично доказывается равенство треугольников NBP и QAM.
Поскольку описанные треугольники равны, то NA = BQ, NB = BQ.
Таким образом, поскольку противолежащие стороны равны, то АNBQ параллелограмм.
Задача
В параллелограмме ABCD диагональ BD = 6 см и образует со сторонами AD и DC углы по 60 градусов. Определите углы и периметр параллелограмма ABCD.Дополнительно: определите вид четырехугольника ABMD, где точка M — середина DC, определите углы четырехугольника ABMD.
Решение.
Поскольку нам дана величина угла ADB (диагональ параллелограмма образует со сторонами AD и DC углы по 60 градусов), то величина угла DBC также равна 60 градусов, поскольку противоположные стороны параллелограмма параллельны, соответственно диагональ является секущей для двух параллельных прямых AD и BC, а для любой секущей внутренние накрест лежащие углы равны.
Таким образом, в треугольнике BCD нам известны два угла из трех, и они оба равны 60 градусов. Соответственно, поскольку сумма углов треугольника равна 180 градусов, то угол BCD также равен 60 градусам, из чего следует, что треугольник BCD — равносторонний.
Поскольку треугольник BCD — равносторонний, то BC = CD = BD = 6 см.
Таким образом, поскольку противолежащие стороны параллелограмма равны, периметр его равен 24 см. Параллелограмм является ромбом.
Дополнительно:
Поскольку точка М лежит на стороне CD, то AB и MD — параллельны, следовательно, ABMD — трапеция.
Угол DAB трапеции равен 60 градусов, исходя из решения, изложенного выше, как угол параллелограмма.
Угол ADM равен 120 градусов, так как по условию диагональ BD образует со сторонами AD и DC углы по 60 градусов, а ADM равен сумме данных углов.
Поскольку по условию точка M — середина DC, CM = MD. Значит BM — медиана треугольника DBC.
Как указано выше, треугольник DBC — равносторонний, а в равностороннем треугольнике медиана является, одновременно, биссектрисой и высотой. Значит, угол DBM равен половине угла DBC и равен 60 / 2 = 30 градусов. Откуда угол ABM = 60 + 30 = 90 градусов. Поскольку BM — высота, то BMD равен также 90 градусов.
Исходя из сказанного, ABMD — прямоугольная трапеция.
Ответ: 24 см. 60º, 90º, 90º, 120º — прямоугольная трапеция.
0
Параллелограмм. Задачи про площадь и стороны | Описание курса | Площадь параллелограмма
геометрия — Ромб Идентификация: 3 равные стороны + 2 параллельные стороны?
Задавать вопрос
спросил
Изменено 1 год, 7 месяцев назад
Просмотрено 65 раз
$\begingroup$
Ромб Идентификация: 3 равные стороны + 2 параллельные стороны?
Контекст:
Я буду краток.
У меня был вопрос, и в нем мне нужно было что-то доказать — это ромб. Теперь, очевидно, мы можем сделать:
Параллелограмм + Смежные равные стороны Доказательство.
Диагонали сходятся под прямым углом.
Диагонали делят пополам обе пары противоположных углов.
Однако в данном случае я доказал, что 3 стороны равны (включая 2 параллельные стороны) и 2 стороны параллельны. Честно говоря, я мог бы пойти дальше, чтобы доказать, что два других параллельны, но я этого не сделал (рассмотрите это как тренировочный тест, когда я бы предпочел не возвращаться и не менять ответы после проверки 🙂
Вопрос:
Достаточно ли этого? Доказывает ли, что 3 стороны равны, а 2 параллельные стороны равны, 4-я сторона равна и, таким образом, доказывает, что это ромб?
- геометрия
- решение-проверка
$\endgroup$
6
$\begingroup$
Хорошо — так что благодаря помощи @user я теперь понимаю — я думаю.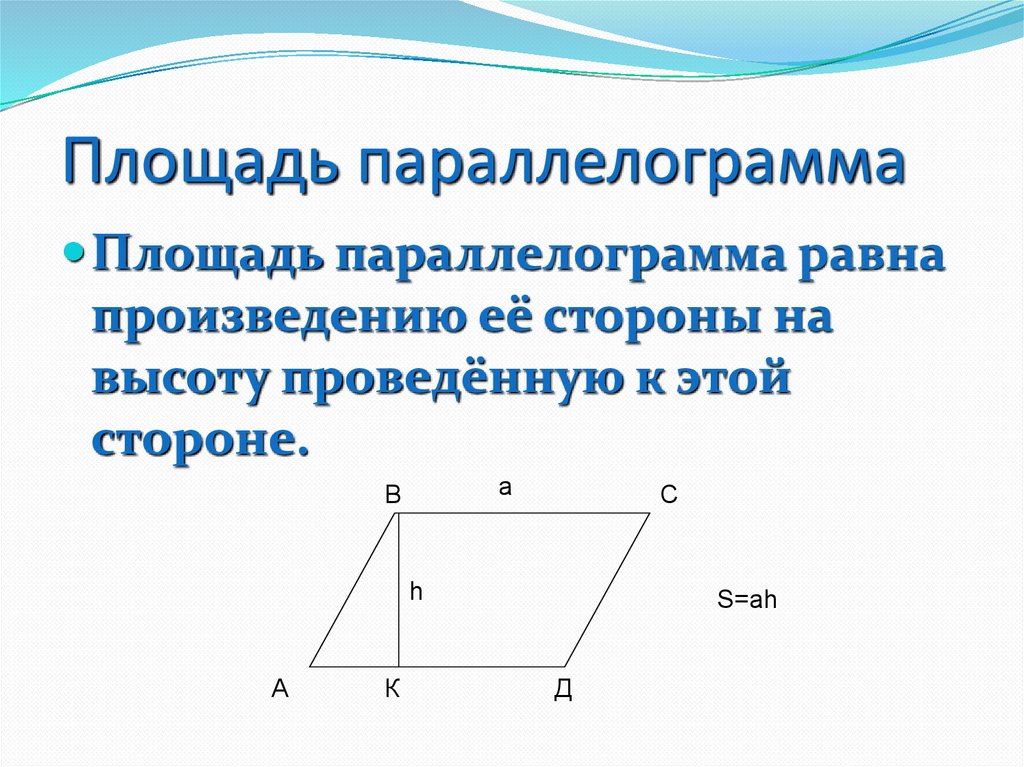
Поскольку я показал, что две параллельные стороны также равны, вся фигура становится параллелограммом. Тогда, поскольку 3-я сторона смежна и равна, это параллелограмм с равными соседними сторонами —> это ромб.
$\endgroup$
$\begingroup$
Если вы можете доказать, что три стороны равны, а две из них параллельны, тогда да. Это потому, что четырехугольник с двумя равными и параллельными сторонами является параллелограммом, и вы также знаете, что две соседние стороны этого параллелограмма равны, поэтому он должен быть ромбом.
Однако, если есть три равные стороны, одна из которых параллельна четвертой стороне, то может получиться равнобедренная трапеция (например, фигура, состоящая из трех сложенных равносторонних треугольников).
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Разница между ромбом и параллелограммом (со сравнительной таблицей)
Последнее обновление by Surbhi S
В геометрии есть много типов четырехугольника, т. е. параллелограмм, ромб, квадрат, прямоугольник, трапеция и воздушный змей, которые имеют общие характеристики, из-за которых люди сталкиваются с проблемами в понимании этих цифр. Ромб можно назвать наклонным квадратом, у которого смежные стороны равны. Напротив, параллелограмм представляет собой наклонный прямоугольник с двумя наборами параллельных противоположных сторон.
Основное различие между ромбом и параллелограммом заключается в их свойствах, т.е. все стороны ромба имеют одинаковую длину, а параллелограмм – это прямолинейная фигура, противоположные стороны которой параллельны.
Содержание: Ромб против параллелограмма
- Сравнительная таблица
- Определение
- Ключевые отличия
- Заключение
Сравнительная таблица
| Основание для сравнения | Ромб | Параллелограмм |
|---|---|---|
| Значение | Ромбом называется плоская четырехгранная фигура, все стороны которой конгруэнтны. | Параллелограмм представляет собой четырехстороннюю плоскую фигуру, противоположные стороны которой параллельны друг другу. |
| Равные стороны | Все четыре стороны имеют одинаковую длину. | Противоположные стороны имеют одинаковую длину. |
| Диагонали | Диагонали делятся пополам под прямым углом, образуя разносторонний треугольник. | Диагонали делят друг друга пополам, образуя два конгруэнтных треугольника. |
| Площадь | (pq)/2, где p и q — диагонали | bh, где b = основание и h = высота |
| Периметр | 4 a, где a = сторона | 2 (a+b), где a = сторона, b = основание |
Определение ромба
Четырехугольник, длины сторон которого равны, называется ромбом. Он имеет плоскую форму и четыре стороны; при этом обращенные стороны параллельны друг другу (см. рисунок ниже).
Противоположные углы ромба равны, т.
е. имеют один и тот же градус. Его диагонали пересекаются друг с другом под углом 90 градусов (прямой угол), следовательно, перпендикулярны друг другу и образуют два равносторонних треугольника. Его смежные стороны дополнительные, а значит, сумма их мер равна 180 градусам. Он также известен как равносторонний параллелограмм.
Определение параллелограмма
Параллелограмм, как следует из его названия, представляет собой плоскую фигуру, имеющую четыре стороны, множество противоположных сторон которых параллельны и конгруэнтны (см. рисунок ниже).
Мера его противолежащих углов равна, а последовательные углы являются дополнительными, т.е. сумма их мер равна 180 градусам. Его диагонали делят друг друга пополам, образуя два конгруэнтных треугольника.
Ключевые различия между ромбом и параллелограммом
Разницу между ромбом и параллелограммом можно ясно изобразить на следующих основаниях:
- Мы определяем ромб как четырехугольник плоской формы, у которого длины всех сторон равны.
Параллелограмм – это четырехсторонняя плоская фигура, у которой противоположные стороны параллельны друг другу. - Все стороны ромба равны по длине, а у параллелограмма равны только противоположные стороны.
- Диагонали ромба делятся пополам под прямым углом, образуя два разносторонних треугольника. В отличие от параллелограмма, диагонали которого пересекаются пополам, образуя два конгруэнтных треугольника.
- Математическая формула площади ромба: (pq)/2, где p и q — диагонали. И наоборот, площадь параллелограмма можно вычислить, умножив основание и высоту.
- Периметр ромба можно рассчитать по следующей формуле – 4 а, где а = сторона ромба. Напротив, периметр параллелограмма можно рассчитать, добавив основание и высоту и умножив сумму на 2.
Параллелограмм – это четырехсторонняя плоская фигура, у которой противоположные стороны параллельны друг другу.Заключение
И параллелограмм, и ромб – четырехугольники, у которых обращенные стороны параллельны, противолежащие углы равны, сумма внутренних углов равна 360 градусов. Сам по себе ромб представляет собой особый вид параллелограмма.