Математический анализ. (Виленкин)
Математический анализ. (Виленкин)
ОглавлениеПРЕДИСЛОВИЕ ДЛЯ УЧИТЕЛЯВВЕДЕНИЕ 2. Числовые множества. 3. Пустое множество. 4. Подмножество. 5. Пересечение множеств. 6. Сложение множеств. 7. Разбиение множеств.  8. Вычитание множеств. 9. Отображение множеств. 10. Краткие исторические сведения. Глава I. МНОГОЧЛЕНЫ ОТ ОДНОГО ПЕРЕМЕННОГО § 1. Тождественные преобразования многочленов 2. Целые рациональные выражения и функции. 3. Степень с натуральным показателем и ее свойства. 4. Многочлены. 5. Умножение многочленов. 6. Числовые кольца и поля. 7. Кольцо многочленов над данным числовым полем. 8. Бином Ньютона. § 2. Деление многочленов. Корни многочленов 2. Теорема Безу. Схема Горнера. 3. Корни многочлена. 4. Интерполяционные формулы. 5. Кратные корни. 6. Многочлены второй степени. 7. Многочлены с целыми коэффициентами. 8. Краткие исторические сведения. Глава II. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА § 1. Общая теория уравнений 2. Область допустимых значений. 3. Уравнения. 4. Совокупности уравнений. 5. Преобразования уравнений. 6. Теоремы о равносильности уравнений. § 2. Уравнения с одним неизвестным 2.  Метод разложения на множители.3. Метод введения нового неизвестного. 4. Биквадратные уравнения. 5. Возвратные уравнения 3-й и 4-й степеней. § 3. Функциональные неравенства 2. Равносильные неравенства. 3. Доказательство неравенств. 4. Линейные неравенства. 5. Решение неравенств второй степени. 6. Решение алгебраических неравенств высших степеней. 7. Краткие исторические сведения. Глава III. ОБОБЩЕНИЕ ПОНЯТИЯ СТЕПЕНИ. ИРРАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ § 1. Степени с целым показателем 2. Степень с нулевым показателем. 3. Степень с целым отрицательным показателем. § 2. Корни. Степени с рациональными показателями 2. Степени с рациональными показателями. 3. Свойства степеней с рациональными показателями. § 3. Иррациональные алгебраические выражения 2. Одночленные иррациональные выражения. 4. Извлечение корня из произведения и степени. 5. Вынесение алгебраических выражений из-под корня и внесение их под корень.  6. Возведение корня в степень. 7. Извлечение корня из корня. 8. Подобные корни. 9. Сложение и вычитание корней. 10. Уничтожение иррациональности в знаменателе или в числителе алгебраической дроби. 11. Преобразование выражений вида … 12. Смешанные задачи на преобразование иррациональных выражений. § 4. Иррациональные уравнения и неравенства 2. Сведение иррациональных уравнений к рациональным. 3. Уединение радикала. 4. Введение нового неизвестного. 5. Особые случаи решения иррациональных уравнений. 6. Иррациональные неравенства. 7. Краткие историчесие сведения. Глава IV. МНОГОЧЛЕНЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. СИСТЕМЫ УРАВНЕНИЙ И НЕРАВЕНСТВ § 1. Системы алгебраических уравнений 2. Системы уравнений. 3. Геометрический смысл решений уравнений и систем уравнений с двумя неизвестными. 4. Совокупность уравнений. 5. Равносильные системы уравнений. 6. Метод подстановки. 7. Метод алгебраического сложения уравнений. 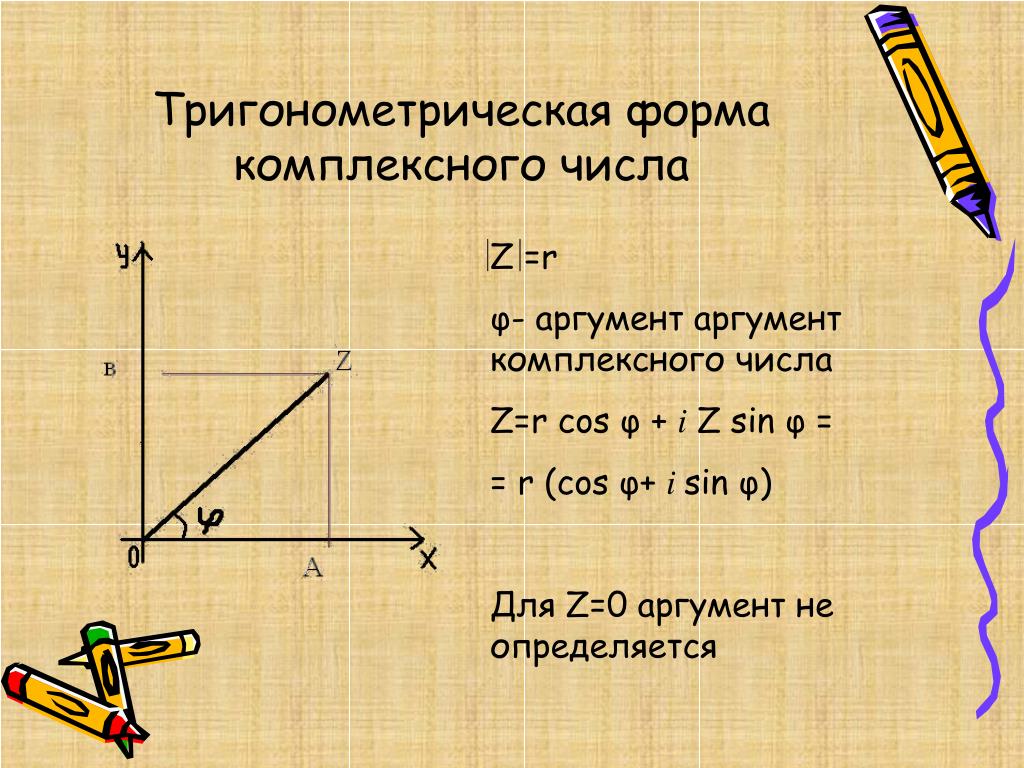 8. Метод введения новых неизвестных. 9. Системы однородных уравнений. 10. Геометрическая интерпретация решения систем двух уравнений с двумя неизвестными. § 2. Системы линейных уравнений 2. Теоремы о равносильности систем линейных уравнений. 3. Пример решения системы линейных уравнений методом Гаусса. 4. Метод Гаусса (приведение системы к обобщенно-треугольному виду). 5. Решение обобщенно-треугольной системы линейных уравнений. 6. Системы однородных линейных уравнений. § 3. Симметрические многочлены и их приложения к решению систем уравнений 3. Основная теорема о симметрических многочленах от двух переменных. 4. Системы симметрических алгебраических уравнений. 5. Применение симметрических многочленов к решению иррациональных уравнений. § 4. Неравенства с многими переменными 2. Среднее арифметическое и среднее геометрическое трех чисел. 3. Неравенство Коши (двумерный вариант). 4. Задачи на наибольшие и наименьшие значения.  § 5. Решение неравенств 2. Неравенства с двумя переменными. 3. Задание областей неравенствами и системами неравенств. 4. Понятие о линейном программировании. 5. Краткие исторические сведения. Глава V. КОМПЛЕКСНЫЕ ЧИСЛА § 1. Комплексные числа в алгебраической форме 2. Комплексные числа. 3. Сложение комплексных чисел; умножение на действительные числа. 4. Умножение комплексных чисел. 5. Квадратные уравнения с действительными коэффициентами. 6. Деление комплексных чисел. 7. Сопряженные комплексные числа. 8. Извлечение квадратных корней из комплексных чисел. § 2. Тригонометрическая форма комплексных чисел 2. Полярная система координат. 3. Тригонометрическая форма комплексного числа. 4. Умножение и деление комплексных чисел в тригонометрической форме. 5. Возведение комплексных чисел в степень. Формула Муавра. 6. Извлечение корня из комплексного числа. 7. Функции комплексного переменного и преобразования комплексной плоскости.  § 3. Некоторые виды алгебраических уравнений 2. Двучленные уравнения. 3. Корни из единицы и построение правильных многоугольников. 4. Трехчленные уравнения. § 4. Основная теорема алгебры многочленов и ее следствия 2. Многочлены с действительными коэффициентами. 3. Разложение на множители многочленов с действительными коэффициентами. Глава VI. ЦЕПНЫЕ ДРОБИ § 1. Конечные цепные дроби 2. Пример цепной дроби. 3. Определение цепной дроби. 4. Представление рациональных чисел в виде конечной цепной дроби. 5. Подходящие дроби. 6. Свойства подходящих дробей. 8. Подходящие дроби и календарь. 9. Приближение цепной дроби подходящими дробями. § 2. Бесконечные цепные дроби 2. Подходящие дроби и наилучшие приближения иррациональных чисел рациональными. 3. Цепные дроби как вычислительный инструмент. 4. Краткие исторические сведения. Глава VII. КОМБИНАТОРИКА § 1. Комбинаторные задачи § 2.  Комбинаторные задачи. Продолжение§ 3. Определения и формулы § 4. Соединения с повторениями § 5. Комбинаторные задачи. Окончание § 6. Бином Ньютона и его обобщения § 7. Краткие исторические сведения Глава VIII. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ § 2. Сложные вероятности. Теоремы сложения и умножения. Условные вероятности § 3. Примеры вычисления вероятностей § 4. Полная вероятность. Формула Байеса § 5. Повторение испытаний § 6. Примеры вычисления вероятностей. Окончание § 7. Краткие исторические сведения |
10.1.3 Тригонометрическая форма комплексного числа.
С геометрической интерпретацией связана и еще одна форма записи комплексных чисел, называемая тригонометрической формой их записи.
Соединим
точку (x, y)
с началом координат отрезком прямой.
Длина этого отрезка r называется модулем комплексного
числа z и
обозначается | z |
или mod(z).
Угол , который этот отрезок образует с осью
Из рисунка ясно, что имеют место соотношения
,
или наоборот
.
Теперь мы можем записать или окончательно
.
Эта форма и получила название комплексного числа в тригонометрической форме.
Операции над комплексными числами в тригонометрической форме.
Пусть имеются два комплексных числа и .
Умножение.
Легко вывести, что
,
то есть при перемножении комплексных чисел их модули перемножаются, а аргументы – складываются.
Деление.
Можно вывести, что
,
то есть при делении комплексных чисел их модули делятся, а аргументы – вычитаются.
Возведение в степень.
Пусть . Тогда имеет место формула
,
то есть
при возведении в степень модуль возводится
в эту степень, а аргумент – умножается
на нее.
Извлечение корня.
Пусть снова . Тогда имеет место формула
,
с . Таким образом, корень n-й степени из комплексного числа имеет ровно n различных значений.
10.1.4 Формула Эйлера. Показательная форма комплексного числа.
Одна из важнейших формул математического анализа – формула Эйлера – имеет вид
.
С учетом тригонометрической формы комплексного числа его теперь можно представить в виде
,
или, с учетом того, что аргумент определяется с точностью до 2,
.
Эта форма записи помогает, например, определить логарифм комплексного числа
.
10.2 Функция комплексной переменной
Представим себе, что есть две плоскости комплексной переменной, одна – плоскость комплексной переменной , другая – плоскость комплексной переменной (см. рис. 10.2).
Правило,
которое каждой точке z из
некоторой области G ставит
в соответствие точку w,
называется функцией комплексной
переменной и обозначается
.
Рис. 10.2 К определению функции комплексной переменной
Подчеркнем, что и аргумент z и значение функции w – комплексные переменные. Так как и , то задание сводится фактически к заданию двух функций и от двух переменных x и y, то есть .
Основные понятия теории функций – предел функции, непрерывность функции и соответствующие им теоремы переносятся на функции комплексной переменной. Отличия начинаются в понятии производной.
Пусть задана функция . Говорят что у существует производная в точке z, если существует
.
Определение. Если имеет производную в каждой точке области G, то она называется аналитической в области G.
Выясним
геометрический смысл производной.
Рассмотрим на плоскости z бесконечно
малый отрезок, соединяющий точки z и z.
Тогда длина этого отрезка есть |z|,
а arg z есть
угол, который этот отрезок образует с
осью OX (см.
рис. 10.3).
Аналогично, на плоскости w бесконечно малый отрезок, соединяющий точки w и w. Тогда длина этого отрезка есть |w|, а arg w есть угол, который этот отрезок образует с осью OU.
Рис. 10.3 Геометрический смысл производной от функции комплексной переменной
А теперь вспомним, что , , так что . Тогда получим
.
Отсюда
.
Отношение есть отношение длин отрезков и . Таким образом, есть коэффициент растяжения бесконечно малого отрезка при его отображении с плоскости z на плоскость w.
Далее, так как
,
то есть угол поворота бесконечно малого отрезка при его отображении с плоскости z на плоскость w. Заметим, что этот угол поворота не зависит от , то есть от направления отрезка .
Видео с вопросами: Нахождение тригонометрической формы корней комплексных чисел
Стенограмма видео
Найдите кубические корни из 64, давая
Ваши ответы в тригонометрической форме.
Этот вопрос фактически задает нам решить уравнение 𝑧 в кубе равно 64. Метод решения этого очень аналогично методу, который мы использовали бы для решения уравнения 𝑧 в кубе, равно один. Мы говорим, что уравнение 𝑧 к 𝑛-я степень равна единице имеет корни, которые называются 𝑛-ми корнями из единицы. Они в тригонометрической форме 𝑧 равно cos два 𝜋𝑘 над 𝑛 плюс 𝑖 sin два 𝜋𝑘 над 𝑛, где 𝑘 равно ноль, один, два и так далее до 𝑛 минус один.
Начнем с того, что перепишем наше уравнение
поскольку 𝑧 в кубе равно 64, умноженным на единицу. Далее найдем кубический корень из
обе части нашего уравнения. Напомним, что корень 𝑛-й степени
Произведение двух действительных чисел 𝑎 и 𝑏 равно произведению корня 𝑛-й степени
эти числа. Итак, мы пишем кубический корень из 64.
умножить на единицу как кубический корень из 64, умноженный на кубический корень из единицы.
Ну, кубический корень из 64 равен четырем.
и кубический корень из единицы, другими словами, кубические корни из единицы, задаются как cos
двух 𝑘𝜋 больше трех плюс 𝑖 грех двух 𝑘𝜋 больше трех, где 𝑘 имеет нулевые значения,
один и два.
Чтобы найти наши три корня, мы
теперь пусть 𝑘 равно нулю, единице и двум. Когда 𝑘 равно нулю, корень,
который мы будем называть 𝑧 меньше единицы, равен четырем, умноженным на косинус нуля плюс 𝑖
грех нуля. Кос нуля равен единице и
грех нуля равен нулю. Это означает, что 𝑧 sub один
просто равно четырем. Когда 𝑘 равно единице, наша вторая
корень 𝑧 меньше двух равно четырем, умноженным на cos два 𝜋 больше трех плюс 𝑖 грех два
𝜋 больше трех. На этом этапе мы могли оценить
cos of two 𝜋 больше трех и sin of two 𝜋 больше трех. Однако, как говорит нам вопрос
чтобы дать наши ответы в тригонометрической форме, мы оставим это как есть.
Наконец, когда 𝑘 равно двум,
наш третий корень 𝑧 меньше трех равен четырем, умноженным на cos четыре 𝜋 больше трех
плюс 𝑖 грех четыре 𝜋 больше трех.
На данном этапе мы можем подумать, что у нас есть три корня. Однако напомним, что главное значение аргумента 𝜃 должно быть больше отрицательного 𝜋 и меньше или равно 𝜋. Это не относится к четырем 𝜋 более три. К счастью, добавляя или вычитая кратно двум 𝜋 из нашего аргумента, мы можем получить тот, который находится внутри диапазона за основную стоимость. Четыре 𝜋 больше трех минус два 𝜋 равно равно отрицательным двум 𝜋 больше трех, что действительно больше отрицательного 𝜋. Поэтому мы можем переписать третий корень 𝑧 меньше три как четыре умножить на косинус минус два 𝜋 больше трех плюс 𝑖 грех минус два 𝜋 больше трех.
Теперь у нас есть три кубических корня из
64 по мере необходимости.
Их четыре, четыре умножить на
потому что два 𝜋 на три плюс 𝑖 грех два 𝜋 на три и четыре умножить на cos
минус два 𝜋 больше трех плюс 𝑖 грех минус два 𝜋 больше трех.
Все о тригонометрической форме
Умножение комплексных чисел сложнее, чем простое сложение. Мы начнем с рассмотрения тригонометрической (или полярной) формы комплексного числа, чтобы лучше понять произведение. Эта тригонометрическая форма связывает алгебру и тригонометрию и может использоваться для быстрого и удобного вычисления степеней и корней комплексных чисел.
Тригонометрическая форма комплексного числа
Комплексное число в тригонометрической форме. Тригонометрическая форма комплексного числа: z = a + bi.
z = r(cosc+i sinc), где r = |a + bi| — модуль z, а tanc = b/a
. Пусть z = (x + i y) — комплексное число.
(r, c) — полярная форма.
R=√x2+y2
C= arc tan(y/x)
r ( cosc+ isinc) = тригонометрическая форма
Тригонометрическая форма =r(cosc+isinc)
Если z=a+bi равно комплексное число.
Пусть r будет величиной z (то есть расстоянием между z и началом координат) и углом, который z образует с положительной действительной осью в этом случае.
Запишите a и b через r и используйте тригонометрию прямоугольного треугольника.
Объясните, почему z можно записать как
z=r(cos(θ)+isin(θ)).
Мы говорим, что z выражено в тригонометрической форме, когда мы записываем его в виде
Вещественное число r является модулем или нормой, а угол называется аргументом комплексного числа z.
Приведенные выше круговые функции, иногда называемые тригонометрическими функциями, можно просто описать как функции угла треугольника. Это означает, что мы доказываем, что эти тригонометрические функции определяют отношения между углами и сторонами треугольника. Синус, косинус, тангенс, котангенс, секанс и косеканс являются основными тригонометрическими функциями. Читайте также о тригонометрических тождествах.
Тождества формул котангенса, секанса и косеканса
Существует несколько тригонометрических формул и тождеств, которые обозначают отношения между функциями и помогают в определении углов треугольника. Все эти тригонометрические функции вместе с их формулами подробно представлены здесь, чтобы помочь читателям их понять.
Синус, косинус и тангенс являются наиболее широко используемыми тригонометрическими функциями в современной математике. Косеканс, секанс и котангенс являются их обратными величинами, которые используются реже. Каждая из этих шести тригонометрических функций имеет обратную функцию, а также аналог гиперболической функции.
В первых определениях тригонометрических функций, связанных с прямоугольными треугольниками, определяются только острые углы. Геометрические определения, использующие обычный единичный круг (т. е. круг с радиусом в 1 единицу), часто используются для расширения функций синуса и косинуса до функций, областью определения которых является вся действительная линия; тогда областью определения остальных функций является действительная линия с удаленными отдельными точками.
Комплексные числа — это те, которые записываются как a+ib, где a,b — действительные числа, а I — мнимое число, известное как «йота». (-1) — это значение i. Например, 2+3i — комплексное число, потому что 2 — действительное число (Re), а 3i — мнимое число (Im).
Комплексное число — это число, состоящее из действительных и мнимых чисел.
К комплексным числам относятся следующие:
Буквы I или j, эквивалентные -1, обычно используются для обозначения мнимых чисел. В результате квадрат мнимого числа имеет отрицательное значение.
Поскольку I = -1, i2 = -1.
Эти числа чаще всего используются для иллюстрации периодических движений, таких как морские волны.
Комплексное число — это компонент системы счисления, который включает в себя действительные числа и особый элемент, обозначенный I, иногда известный как мнимая единица, и который подчиняется уравнению i2 = 1. Кроме того, каждое комплексное число может быть записано как a + bi , где a и b — действительные значения.
Рене Декарт назвал меня мнимым числом, поскольку никакое действительное число не может удовлетворять следующему уравнению. Действительная часть комплексного числа a+bi называется действительной частью, а мнимая часть – мнимой частью. Несмотря на исторический ярлык «мнимых», комплексные числа считаются «реальными» в математических науках.
Преобразовать в тригонометрическую форму
1. Преобразовать 8i в тригонометрическую форму:
Это тригонометрическая форма комплексного числа, где | г | — модуль, а — угол, образованный на комплексной плоскости.
Z=a+ib = |z|cosc+isinc
Расстояние от начала координат на комплексной плоскости является модулем комплексного числа.
| г | = √a2 + b2, где z = a + bi
Подставьте правильные числа вместо a = 0 и b = 8.
Z=√82
Z=8
Найти |z|
Арктангенс значения комплексного компонента над вещественной частью представляет собой угол точки на комплексной плоскости.
C= arc(-8/0)
Поскольку аргумент не определен и b неизвестно,
C= 3π/2
Подставим значение c = 3π/2 и |z|=8
8 (cos3π/2+isin3π\2)
Вопрос 2. -4+4i
Нам понадобится r и для записи числа в тригонометрической форме.
г =√16+16
r= 4√2
Tan c = 4/-4=-1
C= 3π/4
Квадрат II требует угла, таким образом (мы можем увидеть это, изобразив комплексное число
=-4+ 4i= 4√2(cos3π/2+isin3π/2)
Тригонометрическая формула комплексного числа
Комплексное число определяется как уравнение вида z= a+ib, где a и b — действительные числа Re z = a обозначает действительную часть, а Im z = ib обозначает мнимую часть
Комплексное число в тригонометрической форме Тригонометрическая форма комплексного числа z = a + bi z = r(cos + I sin), где r = |a + bi| — модуль z, а tan = b.