Нормальное распределение против стандартного нормального распределения: разница
Нормальное распределение является наиболее часто используемым в статистике распределением вероятностей.
Он имеет следующие свойства:
- Симметричный
- колоколообразный
- Среднее и медиана равны; оба расположены в центре распределения
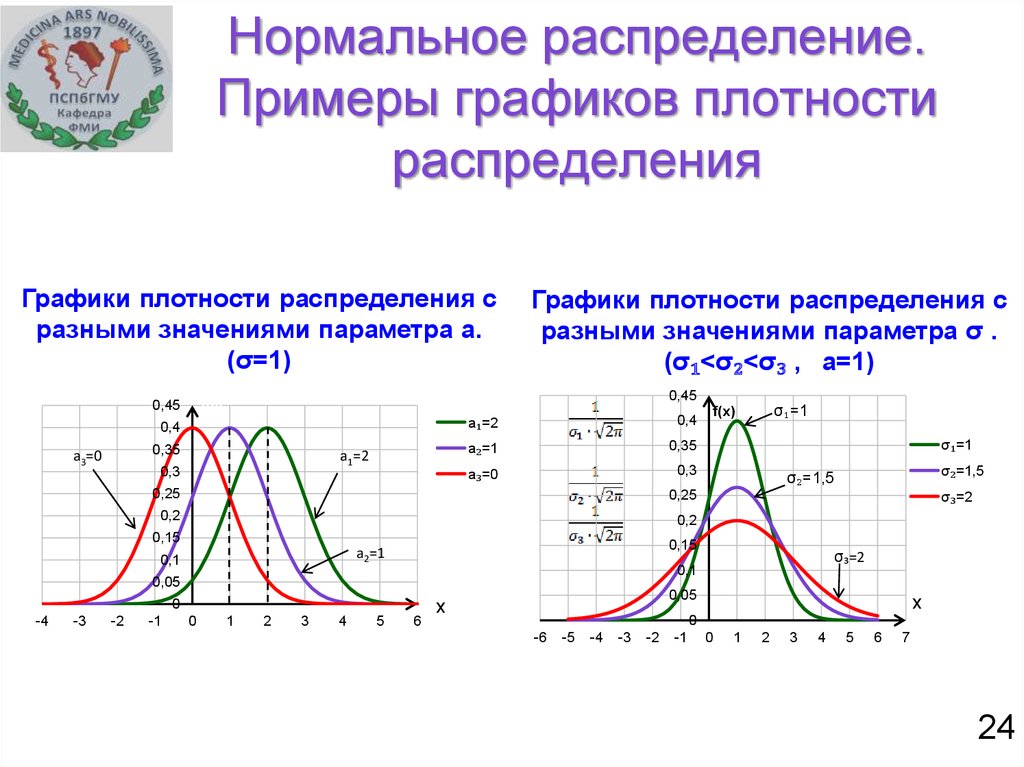
Среднее значение нормального распределения определяет его местоположение, а стандартное отклонение определяет его разброс.
Например, на следующем графике показаны три нормальных распределения с разными средними значениями и стандартными отклонениями:
Стандартное нормальное распределение — это особый тип нормального распределения, где среднее значение равно 0, а стандартное отклонение равно 1.
На следующем графике показано стандартное нормальное распределение:
Как преобразовать нормальное распределение в стандартное нормальное распределениеЛюбое нормальное распределение можно преобразовать в стандартное нормальное распределение путем преобразования значений данных в z-показатели по следующей формуле:
z = (x – μ) / σ
куда:
- x: индивидуальное значение данных
- μ: среднее значение распределения
- σ: стандартное отклонение распределения
Например, предположим, что у нас есть следующий набор данных со средним значением 6 и стандартным отклонением 2,152:
Мы можем преобразовать каждое отдельное значение данных в z-оценку, вычтя 6 из каждого значения и разделив на 2,152:
Z-показатель говорит нам, сколько стандартных отклонений каждая точка данных находится от среднего значения. Например, первое значение данных «3» лежит на 1,39 стандартных отклонения ниже среднего.
Например, первое значение данных «3» лежит на 1,39 стандартных отклонения ниже среднего.
Среднее значение этого распределения z-показателей имеет среднее значение, равное нулю, и стандартное отклонение, равное единице.
Как использовать стандартное нормальное распределениеСтандартное нормальное распределение обладает следующими свойствами:
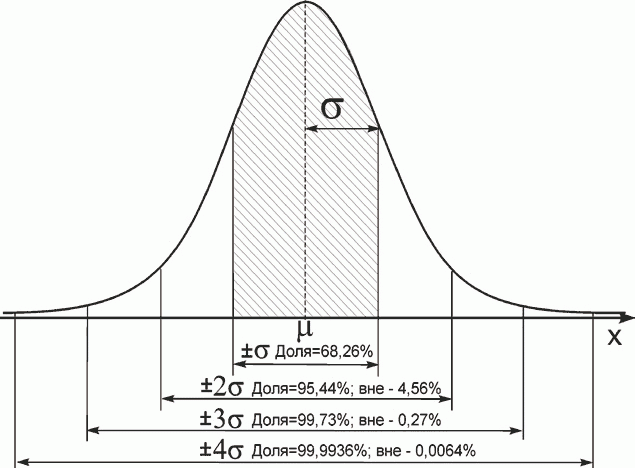
- Около 68% данных находятся в пределах одного стандартного отклонения от среднего
- Около 95% данных находятся в пределах двух стандартных отклонений от среднего
- Около 99,7% данных находятся в пределах трех стандартных отклонений от среднего значения.
Это известно как эмпирическое правило и используется для понимания распределения значений в наборе данных.
Например, предположим, что высота растений в определенном саду нормально распределена со средним значением 47,4 дюйма и стандартным отклонением 2,4 дюйма.
Согласно эмпирическому правилу, какой процент растений имеет высоту менее 54,6 дюймов?
Эмпирическое правило гласит, что для заданного набора данных с нормальным распределением 99,7% значений данных находятся в пределах трех стандартных отклонений от среднего.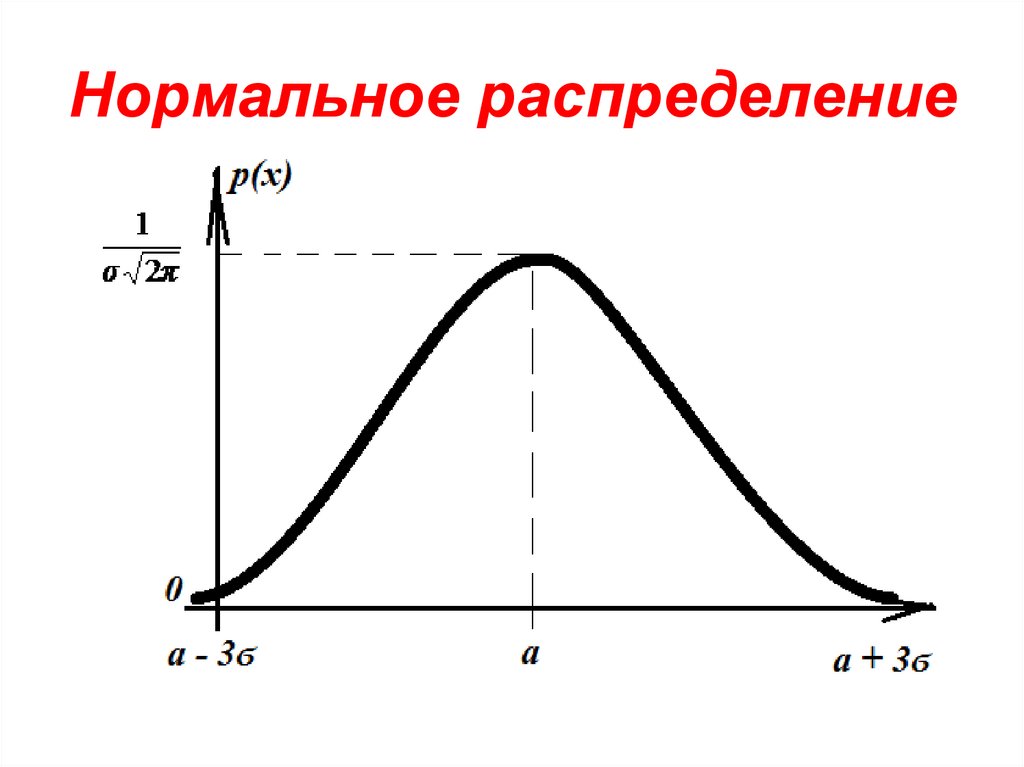 Это означает, что 49,85% значений находятся между средним значением и тремя стандартными отклонениями выше среднего.
Это означает, что 49,85% значений находятся между средним значением и тремя стандартными отклонениями выше среднего.
В этом примере 54,6 находится на три стандартных отклонения выше среднего. Поскольку мы знаем, что 50 % значений данных находятся ниже среднего значения в нормальном распределении, в общей сложности 50 % + 49,85 % = 99,85 % значений попадают ниже 54,6.
Таким образом, 99,85% растений имеют высоту менее 54,6 дюймов.
Дополнительные ресурсыЭмпирические проблемы практики правил
Калькулятор эмпирических правил
Как применить эмпирическое правило в Excel
Функция НОРМ.СТ.РАСП — Служба поддержки Майкрософт
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Возвращает стандартное нормальное интегральное распределение. Это распределение имеет среднее, равное нулю, и стандартное отклонение, равное единице.
Это распределение имеет среднее, равное нулю, и стандартное отклонение, равное единице.
Данная функция используется вместо таблицы площадей стандартной нормальной кривой.
Синтаксис — стандартное нормальное распределение
НОРМ.СТ.РАСП(z;интегральная)
Аргументы функции НОРМ.СТ.РАСП описаны ниже.
-
Z Обязательный. Значение, для которого строится распределение.
-
Интегральная Обязательный. Логическое значение, определяющее форму функции. Если аргумент «интегральная» имеет значение ИСТИНА, функция НОРМ.СТ.РАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается весовая функция распределения.

Замечания
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Формула |
Описание |
Результат |
|
=НОРМ.СТ.РАСП(1,333333;ИСТИНА) |
Нормальное интегральное распределения для числа 1,333333 |
0,908788726 |
|
=НОРМ. |
Нормальное распределение вероятности для числа 1,333333 |
0,164010148 |
Стандартное нормальное распределение | Введение в статистику
Результаты обучения
- Распознавание стандартного нормального распределения вероятностей и его правильное применение
Стандартное нормальное распределение является нормальным распределением стандартизированных значений, называемых z -показатели . Показатель z измеряется в единицах стандартного отклонения . Например, если среднее значение нормального распределения равно пяти, а стандартное отклонение равно двум, значение 11 будет на три стандартных отклонения выше (или правее) среднего значения.
x = μ + ( z )( σ ) = 5 + (3)(2) = 11
Число z равно трем.
Среднее стандартного нормального распределения равно нулю, а стандартное отклонение равно единице. Преобразование [латекс]\displaystyle{z}=\frac{{x — \mu}}{{\sigma}}[/latex] дает распределение Z ~ N(0, 1). Значение x получено из нормального распределения со средним значением μ и стандартным отклонением σ .
В следующих двух видеороликах дается описание того, что означает наличие набора данных с «нормальным» распределением.
Если X является нормально распределенной случайной величиной и X ~ N(μ, σ) , то z -score равен:
90}\008 [latex] \frac{{x — \mu}}{{\sigma}}[/latex] Показатель z показывает, на сколько стандартных отклонений значение x выше (справа) или ниже (слева от) среднего, μ . Значения x , превышающие среднее значение, имеют положительное значение z -оценки, а значения x , которые меньше среднего, имеют отрицательные z -оценки. Если x равно среднему значению, то x имеет нулевую оценку z .
Значения x , превышающие среднее значение, имеют положительное значение z -оценки, а значения x , которые меньше среднего, имеют отрицательные z -оценки. Если x равно среднему значению, то x имеет нулевую оценку z .
Пример
Предположим, X ~ N(5, 6) . Это говорит о том, что x является нормально распределенной случайной величиной со средним значением μ = 5 и стандартным отклонением σ = 6. Предположим, что x = 17. Тогда:
[латекс]\displaystyle{z}=\frac {{x — \mu}}{{\sigma}}[/latex]= [латекс]\displaystyle{z}=\frac{{17-5}}{{6}}={2}[/latex]
Это означает, что x = 17 равно двум стандартным отклонениям (2 σ ) выше или правее среднего значения μ = 5.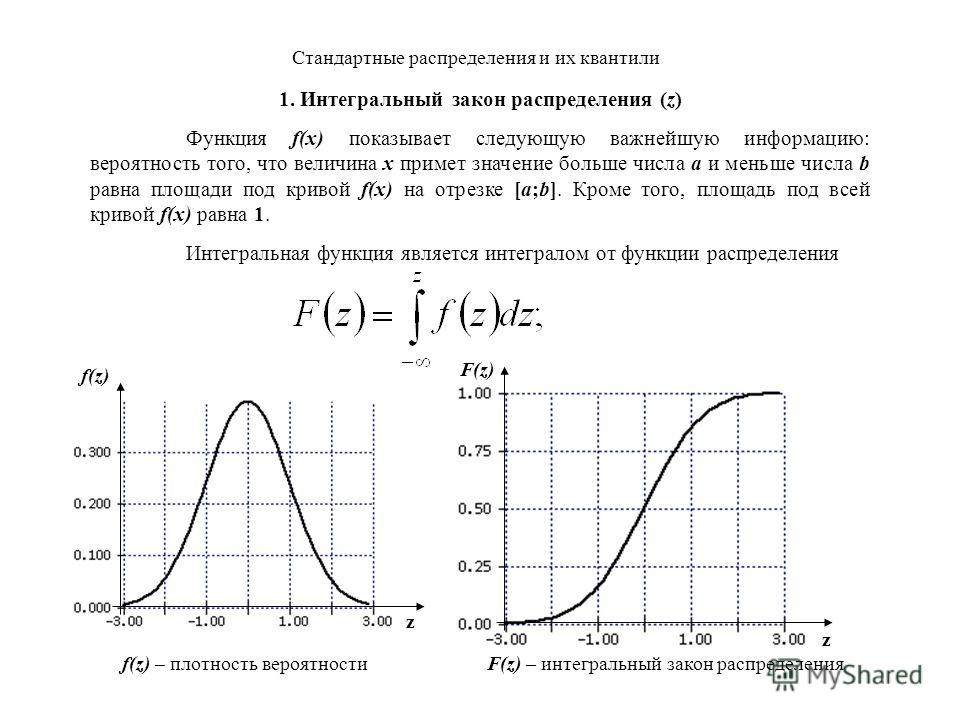 Стандартное отклонение равно σ = 6.
Стандартное отклонение равно σ = 6.
Обратите внимание, что . {{x — \mu}}{{\sigma}}[/latex] = [латекс]\displaystyle {z}=\frac{{1-5}}{{6}} = -{0,67}[/latex ]
(округлено до двух знаков после запятой)
Это означает, что x = 1 равно 0,67 стандартного отклонения (–0,67 σ ) ниже или левее среднего значения μ = 5. Обратите внимание, что: 5 + (–0,67)(6) приблизительно равно единице (имеет вид μ + (–0,67)σ = 1)
Суммируя, когда z положительно, x выше или правее μ и когда z отрицательно, x находится слева от 9 или ниже0012 мк . Или, когда z положительно, x больше µ , а когда z отрицательно, x меньше µ .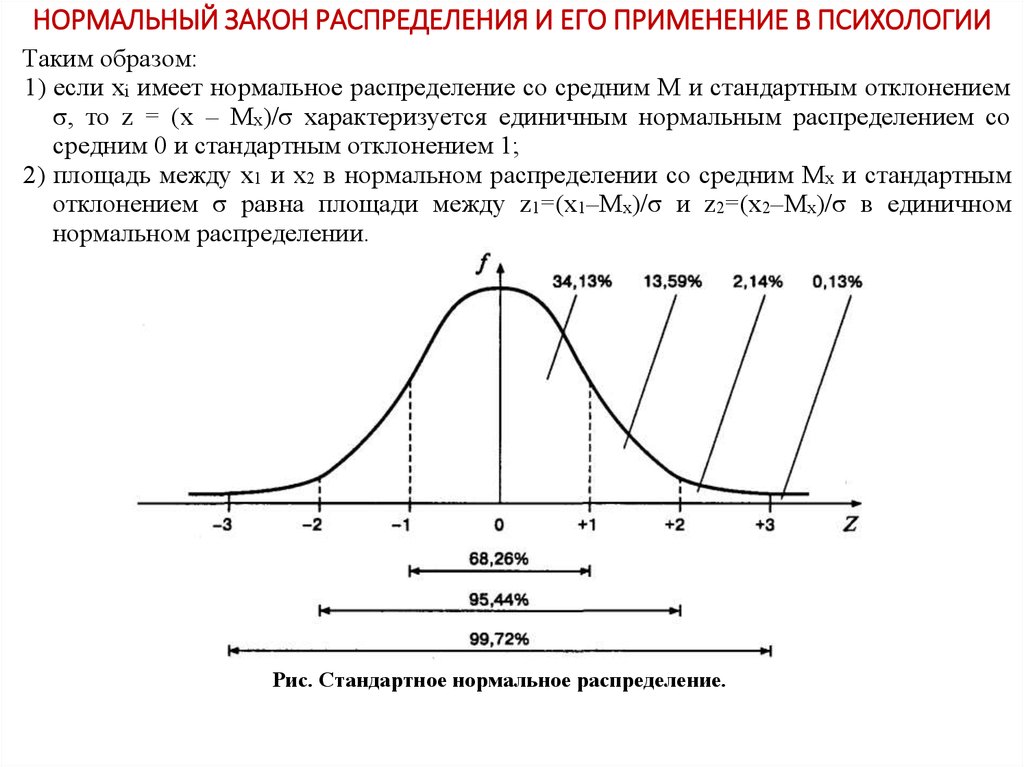
попробуйте
Чему равно z -оценка x , когда x = 1 и X ~ N (12,3)?
[латекс]\displaystyle {z}=\frac{{1-12}}{{3}} = -{3.67} [/latex]
Пример
Некоторые врачи считают, что человек может потерять в среднем пять фунтов за месяц, сократив потребление жиров и регулярно занимаясь физическими упражнениями. Предположим, что потеря веса имеет нормальное распределение. Пусть X = количество веса, потерянного (в фунтах) человеком за месяц. Используйте стандартное отклонение в два фунта. X ~ N (5, 2).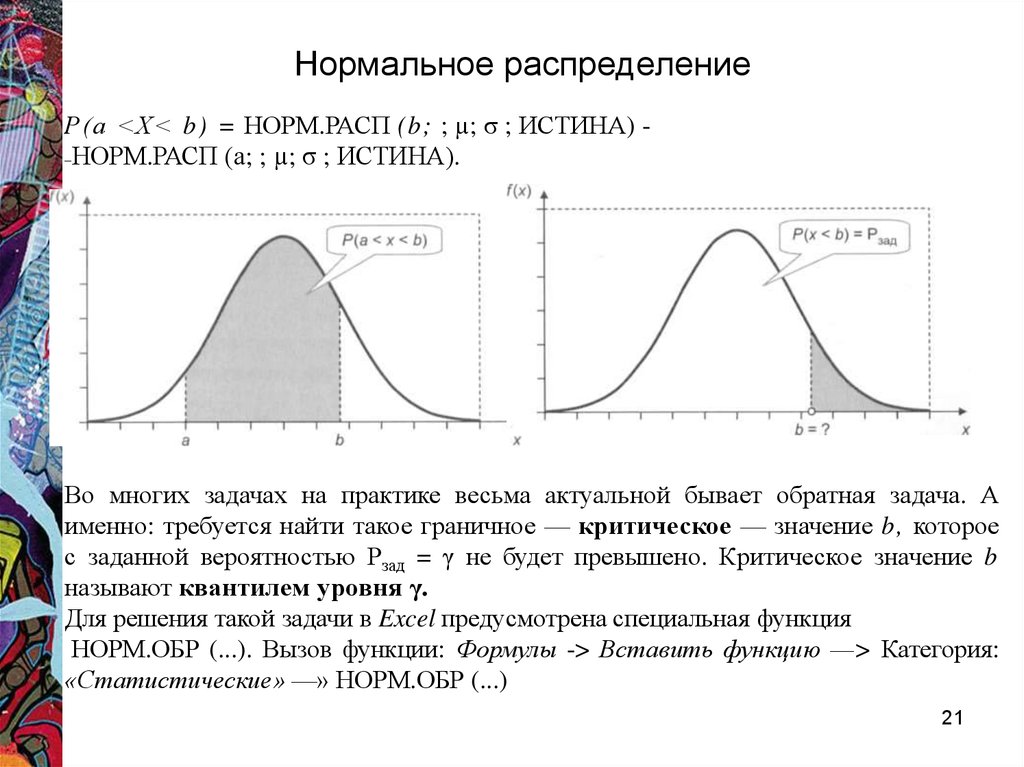 Заполнить бланки.
Заполнить бланки.
- Предположим, человек похудел на десять фунтов за месяц. Результат z , когда x = 10 фунтов, составляет z = 2,5 (проверьте). Эта z -оценка говорит вам, что x = 10 является ________ стандартным отклонением от ________ (вправо или влево) среднего _____ (Что такое среднее значение?).
- Предположим, человек набрал три фунта (отрицательная потеря веса). Тогда z = __________. Это z -оценка говорит вам, что x = –3 составляет ________ стандартных отклонений от __________ (вправо или влево) среднего значения.
Решение:
- Этот результат z говорит вам, что x = 10 составляет 2,5 стандартных отклонений от правильного среднего пяти .

- z = –4. это z -score говорит вам, что x = -3 составляет 4 стандартных отклонений от слева от среднего.
Предположим, что случайные величины X и Y имеют следующие нормальные распределения: X ~ N (5, 6) и Y ~ N (2, 1). Если x = 17, то z = 2. (Это было показано ранее.) Если y = 4, чему равно z ? [латекс]\displaystyle {z}=\frac{{y — \mu}}{{\sigma}} = \frac{{4-2}}{{1}}[/latex].
Оценка z для y = 4 равна z = 2. Это означает, что четыре равно z = 2 стандартных отклонения справа от среднего. Следовательно, x = 17 и y = 4 являются двумя (из их собственных ) стандартными отклонениями справа от их соответствующих средних значений.
Это означает, что четыре равно z = 2 стандартных отклонения справа от среднего. Следовательно, x = 17 и y = 4 являются двумя (из их собственных ) стандартными отклонениями справа от их соответствующих средних значений.
Оценка z позволяет нам сравнивать данные, масштабированные по-разному. Чтобы понять концепцию, предположим, что X ~ N (5, 6) представляет прибавку в весе для одной группы людей, пытающихся набрать вес за шестинедельный период, а Y ~ N (2, 1) измеряет такое же увеличение веса для второй группы людей. Отрицательная прибавка в весе была бы потерей веса. Поскольку x = 17 и y = 4 являются двумя стандартными отклонениями справа от их средних значений, они представляют одинаковую стандартизированную прибавку в весе относительно их средних значений
Попробуйте
Заполните пробелы.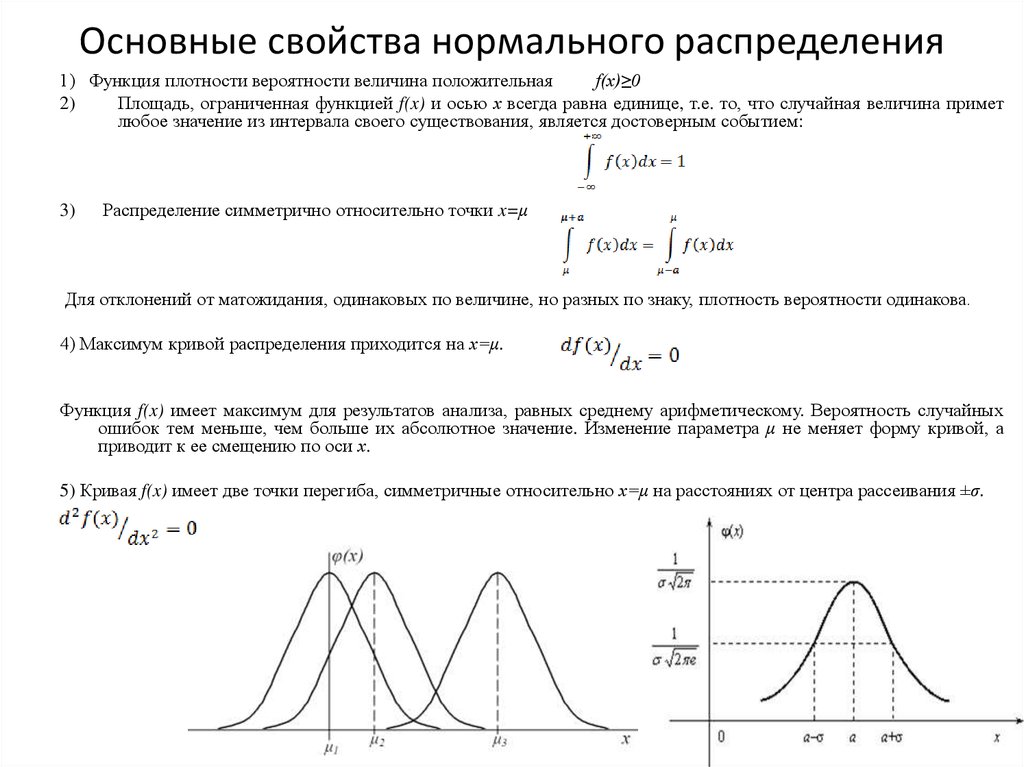
Джером набирает в среднем 16 очков за игру со стандартным отклонением в четыре очка. Х ~ Н (16,4). Предположим, Джером набирает десять очков в игре. Оценка z , когда x = 10, составляет -1,5. Эта оценка говорит вам, что x = 10 составляет _____ стандартных отклонений от ______ (вправо или влево) от среднего ______ (Что такое среднее значение?).
1,5, слева, 16
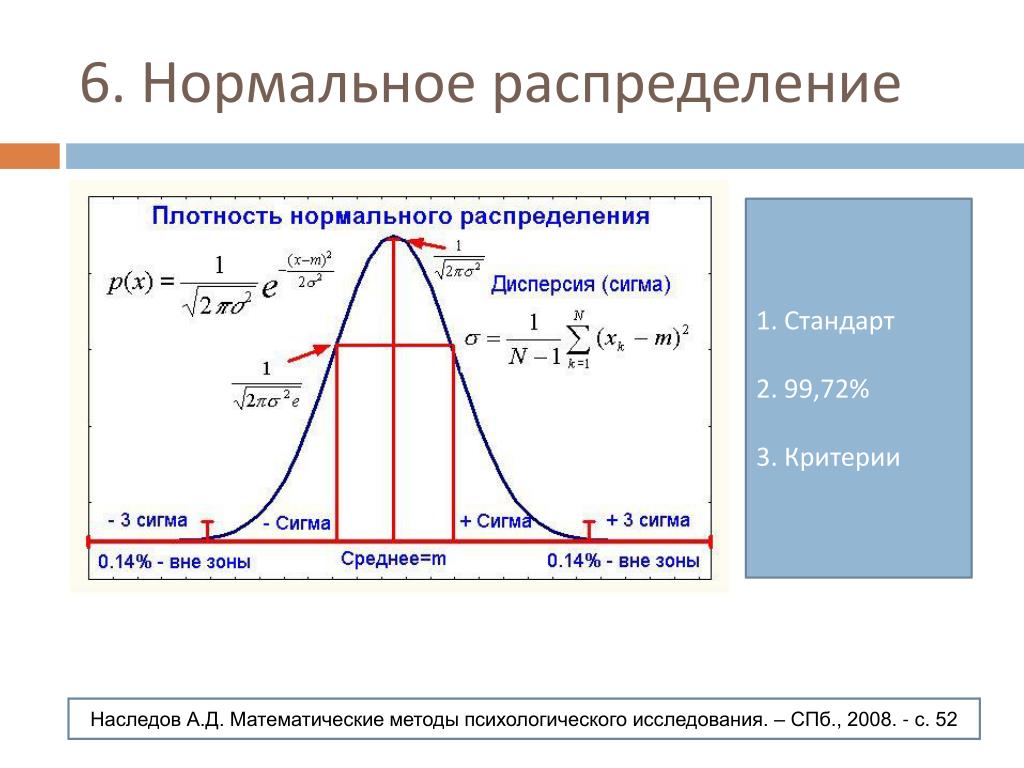
Эмпирическое правило
Если X является случайной величиной и имеет нормальное распределение со средним значением µ и стандартное отклонение σ , то эмпирическое правило говорит следующее:
- (в пределах одного стандартного отклонения от среднего).
- Около 95% значений

- Около 99,7% из 9Значения 0012 x лежат между –3 σ и +3 σ от среднего µ (в пределах трех стандартных отклонений от среднего). Обратите внимание, что почти все значения x лежат в пределах трех стандартных отклонений от среднего.
- z -баллы для +1 σ и –1 σ составляют +1 и –1 соответственно.
- z -баллы для +2 σ и –2 σ составляют +2 и –2 соответственно.
- з -баллы для +3 σ и –3 σ равны +3 и –3 соответственно.
Эмпирическое правило также известно как правило 68-95-99,7.
Пример
Средний рост мужчин в возрасте от 15 до 18 лет из Чили с 2009 по 2010 год составлял 170 см со стандартным отклонением 6,28 см.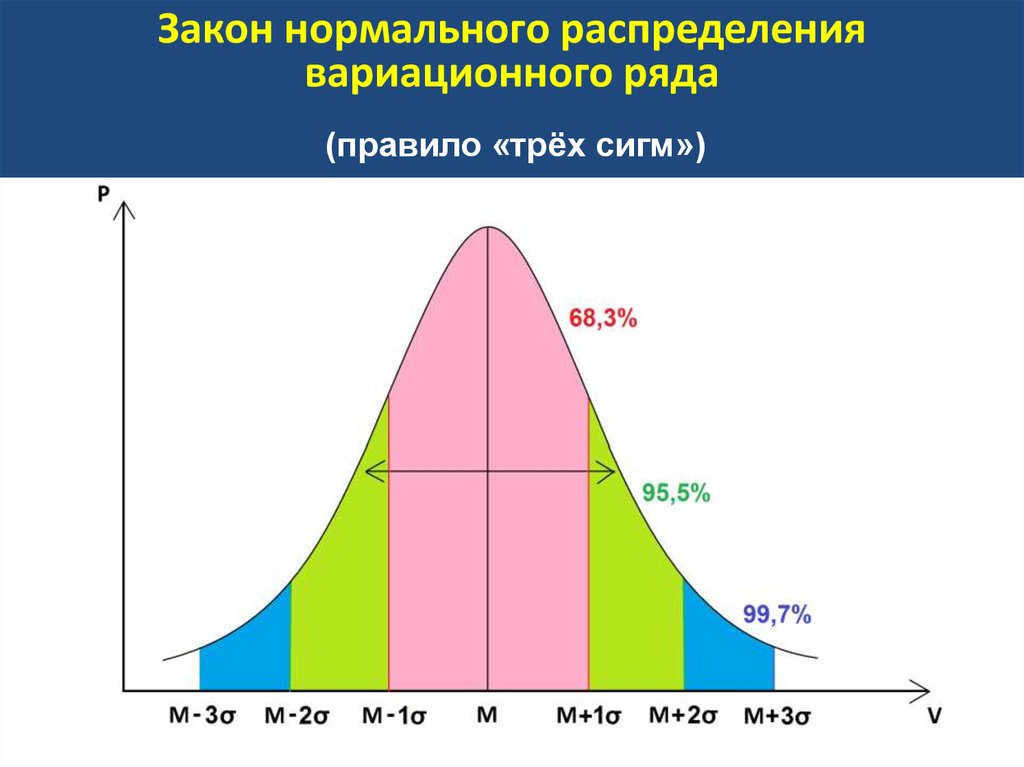 Известно, что рост мужчин подчиняется нормальному распределению. Пусть X = рост мужчины 15-18 лет из Чили в 2009-2010 гг. Тогда X ~ N (170, 6,28).
Известно, что рост мужчин подчиняется нормальному распределению. Пусть X = рост мужчины 15-18 лет из Чили в 2009-2010 гг. Тогда X ~ N (170, 6,28).
а. Предположим, что мужчина в возрасте от 15 до 18 лет из Чили имел рост 168 см с 2009 по 2010 год. Результат z , когда x = 168 см, составляет z = _______. Это z -оценка говорит вам, что x = 168 является ________ стандартным отклонением от ________ (вправо или влево) среднего _____ (Что такое среднее значение?).
б. Предположим, что рост мужчины в возрасте от 15 до 18 лет из Чили с 2009 по 2010 год имеет z -значение z = 1,27. Какой рост у мужчины? z -счет ( z = 1,27) говорит вам, что рост мужчины составляет ________ стандартных отклонений от __________ (вправо или влево) от среднего.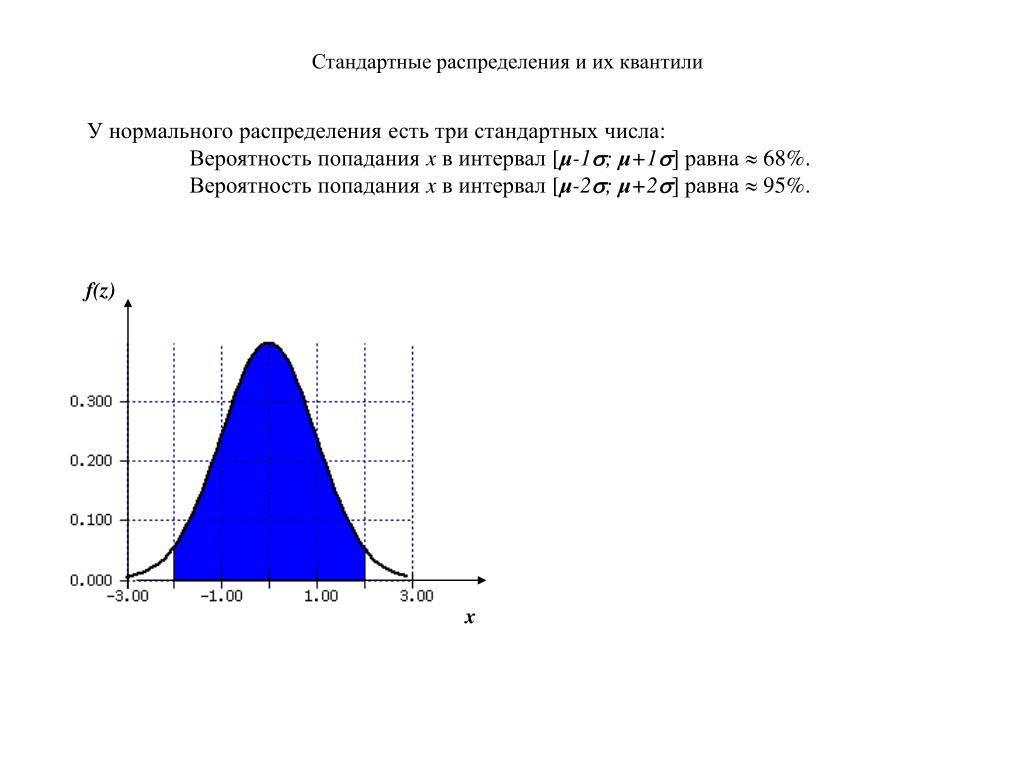
Решение:
а. –0,32, 0,32, левый, 170
б. 177,98, 1,27, справа
попробовать
Используйте информацию из примера 3, чтобы ответить на следующие вопросы.
- Предположим, что мужчина в возрасте от 15 до 18 лет из Чили имел рост 176 см в период с 2009 по 2010 год.0013 = 176 см равно z = _______. Это z -значение говорит вам, что x = 176 см — это ________ стандартных отклонений от ________ (вправо или влево) от среднего _____ (Что такое среднее?).
- Предположим, что рост мужчины в возрасте от 15 до 18 лет из Чили с 2009 по 2010 год имеет z -значение z = –2. Какой рост у мужчины? z -счет ( z = –2) говорит вам, что рост мужчины составляет ________ стандартных отклонений от __________ (вправо или влево) от среднего.

Решите уравнение [латекс]\displaystyle{z}=\frac{{x — \mu}}{{\sigma}}[/latex] относительно x. x = μ + (z)(σ) для x . x = μ + ( z )( σ )
- z<=[латекс]\displaystyle\frac{{176-170}}{{0,96}}[/latex], это z -score говорит вам, что x = 176 см — это 0,96 стандартного отклонения вправо от среднего значения 170 см.
- X = 157,44 см. Результат z ( z = –2) говорит о том, что рост мужчины находится на два стандартных отклонения левее среднего значения.
Пример
С 1984 по 1985 год средний рост чилийских юношей в возрасте от 15 до 18 лет составлял 172,36 см, а стандартное отклонение — 6,34 см. Пусть Y = рост мужчин в возрасте от 15 до 18 лет с 1984 по 1985 год. Тогда Y ~ N (172,36, 6,34).
Тогда Y ~ N (172,36, 6,34).
Средний рост мужчин в возрасте от 15 до 18 лет из Чили с 2009 по 2010 год составлял 170 см со стандартным отклонением 6,28 см. Известно, что рост мужчин подчиняется нормальному распределению. Пусть X = рост мужчины в возрасте от 15 до 18 лет из Чили в 2009-2010 гг. Тогда X ~ N (170, 6,28).
Найдите z -значения для x = 160,58 см и y = 162,85 см. Интерпретируйте каждый z -счет. Что вы можете сказать о х = 160,58 см и у = 162,85 см?
Решение:
Результат z для x = 160,58 равен z = –1,5.
z — оценка для y = 162,85 равна z = –1,5. Оба x = 160,58 и y = 162,85 отклоняются на одинаковое количество стандартных отклонений от соответствующих средних значений и в одном и том же направлении.
попробовать
В 2012 г. экзамен SAT сдали 1 664 479 учащихся. Распределение баллов в вербальной части SAT имело среднее значение µ = 496 и стандартное отклонение σ = 114. Пусть X = оценка вербальной части экзамена SAT в 2012 году. Тогда Х ~ Н (496, 114).
Найдите z -показателей для x 1 = 325 и x 2 = 366,21. Интерпретируйте каждый z -счет. Что вы можете сказать о х 1 = 325 и х 2 = 366,21?
Что вы можете сказать о х 1 = 325 и х 2 = 366,21?
Результат z для x 1 = 325 равен z 1 = –1,14.
Результат z для x 2 = 366,21 равен z 2 = –1,14.
Ученик 2 набрал ближе к среднему значению, чем Ученик 1, и, поскольку они оба получили отрицательные z -баллы, студент 2 получил лучший балл.
Пример
Предположим, что x имеет нормальное распределение со средним значением 50 и стандартным отклонением 6. –6 и 1 σ = (1)(6) = 6 от среднего 50. Значения 50 – 6 = 44 и 50 + 6 = 56 находятся в пределах одного стандартного отклонения от среднего 50. z -оценки составляют –1 и +1 для 44 и 56 соответственно.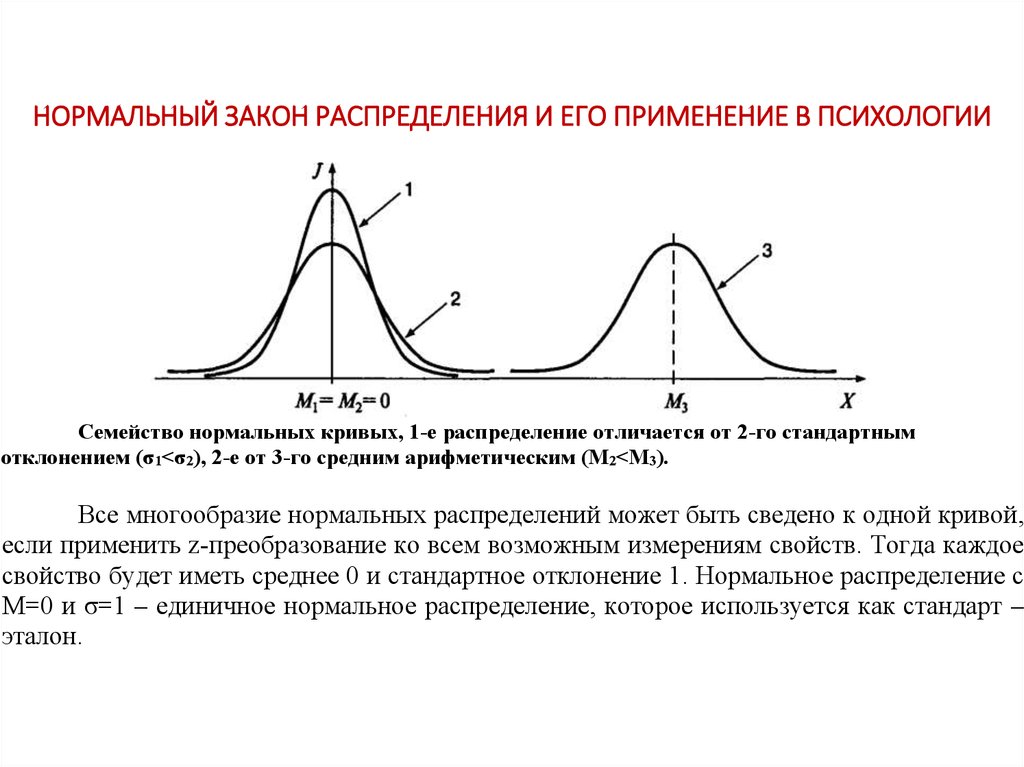
попробуйте
Предположим, что X имеет нормальное распределение со средним значением 25 и стандартным отклонением пять. Между какими значениями x лежит 68% значений?
Решение:
Между 20 и 30.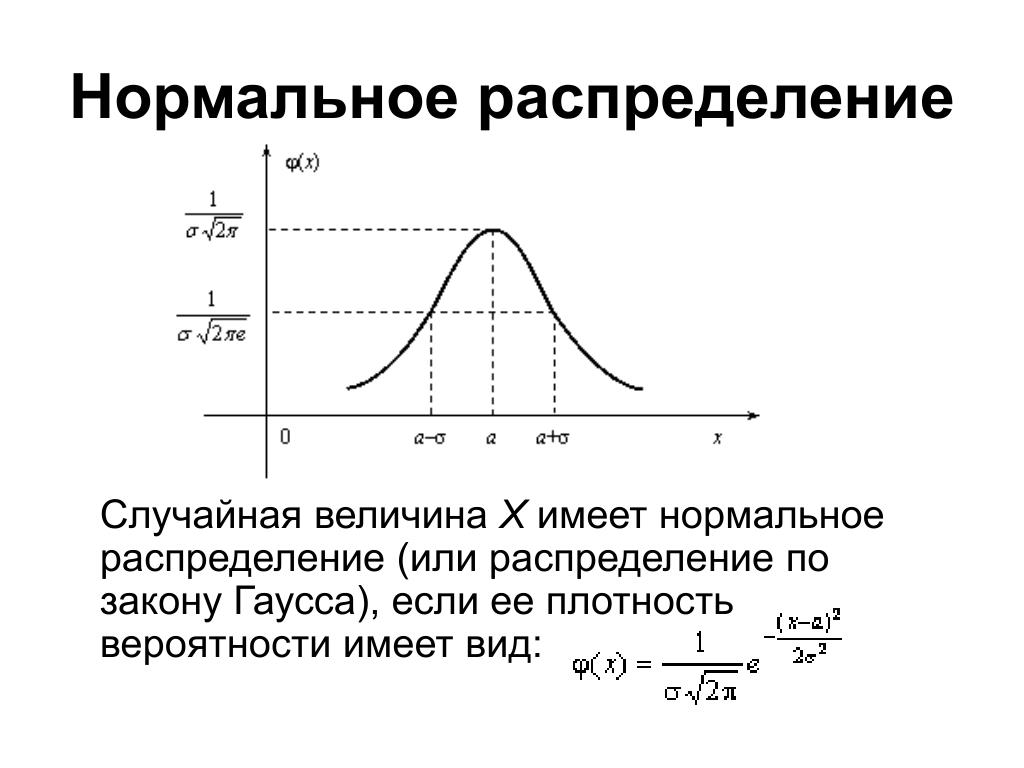
Пример
С 1984 по 1985 год средний рост чилийских мужчин в возрасте от 15 до 18 лет составлял 172,36 см, а стандартное отклонение — 6,34 см. Пусть Y = рост мужчин в возрасте от 15 до 18 лет в период с 1984 по 1985 год. Затем Y ~ N (172,36, 6,34).
- Около 68% значений и лежат между какими двумя значениями? Эти значения ________________. z -оценки равны ________________ соответственно.
- Около 95% значений и лежат между какими двумя значениями? Эти значения ________________. Баллы z равны ________________ соответственно.
- Около 99,7% значений и лежат между двумя 0,7% значений между 153,34 и 191,38. Оценки z равны –3 и 3.
- Около 68% значений и лежат между какими двумя значениями? Эти значения ________________.
 z -оценки равны ________________ соответственно.
z -оценки равны ________________ соответственно.
- Около 68% значений и лежат между какими двумя значениями? Эти значения ________________.
попробуйте
Баллы на вступительном экзамене в колледж имеют приблизительное нормальное распределение со средним значением µ = 52 балла и стандартным отклонением σ = 11 баллов.
.7% значений лежат между 153,34 и 191,38. z -оценки равны –3 и 3.
- Около 68% значений y лежат между какими двумя значениями? Эти значения ________________. z -оценки равны ________________ соответственно.
- Около 95% значений и лежат между какими двумя значениями? Эти значения ________________. z -оценки равны ________________ соответственно.
- Около 99,7% значений и лежат между какими двумя значениями? Эти значения ________________.
 z -оценки равны ________________ соответственно.
z -оценки равны ________________ соответственно.
Решение:
- Около 68% значений лежат между значениями 41 и 63. z -оценки равны –1 и 1 соответственно.
- Около 95% значений лежат между значениями 30 и 74. z -показатели равны –2 и 2 соответственно.
- Около 99,7% значений лежат между значениями 19и 85. Оценки z равны –3 и 3 соответственно.
Ссылки
«Артериальное давление у мужчин и женщин». StatCruch, 2013. Доступно на сайте http://www.statcrunch.com/5.0/viewreport.php?reportid=11960 (по состоянию на 14 мая 2013 г.).
«Использование эпидемиологических инструментов среди населения, пострадавшего от конфликта: открытые образовательные ресурсы для политиков: расчет z-показателей». Лондонская школа гигиены и тропической медицины, 2009 г. Доступно на сайте http://conflict.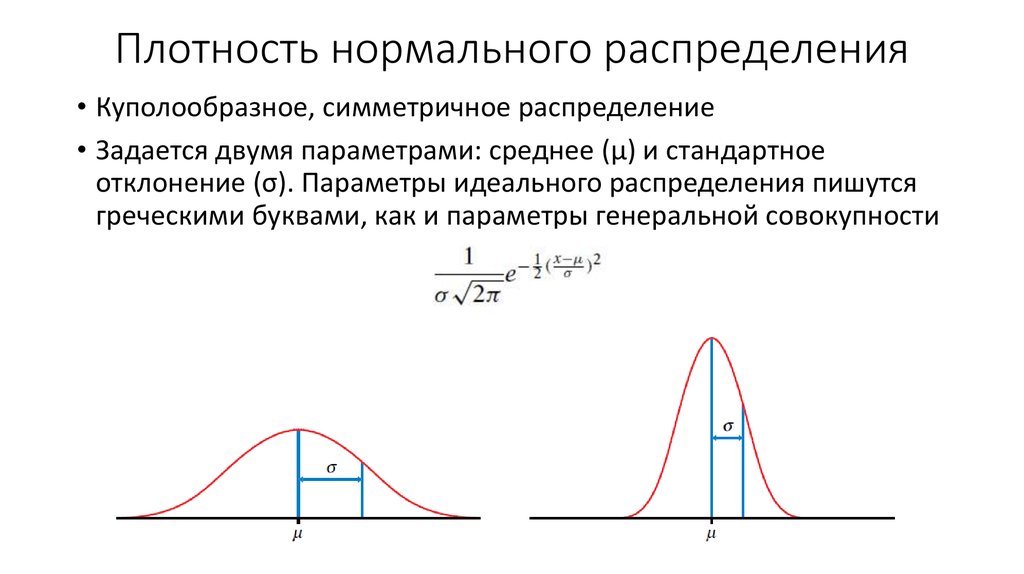 lshtm.ac.uk/page_125.htm (по состоянию на 14 мая 2013 г.).
lshtm.ac.uk/page_125.htm (по состоянию на 14 мая 2013 г.).
«Общий профиль группы старшеклассников за 2012 г.». CollegeBoard, 2012. Доступно на сайте http://media.collegeboard.com/digitalServices/pdf/research/TotalGroup-2012.pdf (по состоянию на 14 мая 2013 г.).
«Дайджест статистики образования: средний балл ACT и стандартные отклонения по полу и расе/этнической принадлежности, а также процент участников теста ACT, по выбранным сводным диапазонам баллов и запланированным областям обучения: выбранные годы, с 1995 по 2009 год». Национальный центр статистики образования. Доступно в Интернете по адресу http://nces.ed.gov/programs/digest/d09./tables/dt09_147.asp (по состоянию на 14 мая 2013 г.).
Данные из San Jose Mercury News .
Данные из Мирового альманаха и Книги фактов .
«Список стадионов по вместимости». Википедия. Доступно в Интернете по адресу https://en.wikipedia.org/wiki/List_of_stadiums_by_capacity (по состоянию на 14 мая 2013 г. ).
).
Данные Национальной баскетбольной ассоциации. Доступно на сайте www.nba.com (по состоянию на 14 мая 2013 г.).
A z -оценка является стандартизированным значением. Его распределение стандартно нормальное, Z ~ N (0, 1). Среднее значение z -значений равно нулю, а стандартное отклонение равно единице. Если z является z -оценкой для значения x из нормального распределения N ( µ , σ ), то z показывает выше, сколько стандартных отклонений x чем) или ниже (меньше) µ .
Z ~ N (0, 1)
z = стандартизированное значение ( z -оценка)
среднее = 0; standard deviation = 1
To find the K th percentile of X when the z -scores is known:
k = μ + ( z ) σ
z -score:[latex]\displaystyle{z}=\frac{{x — \mu}}{{\sigma}}[/latex]
Z = случайная величина для z -scores
Z ~ N (0, 1)
Что такое нормальное распределение и стандартное отклонение в статистике
Данные, которые вы хотите проанализировать, могут иметь любое распределение, а графики распределения вероятностей могут принимать очень четкие и узнаваемые формы.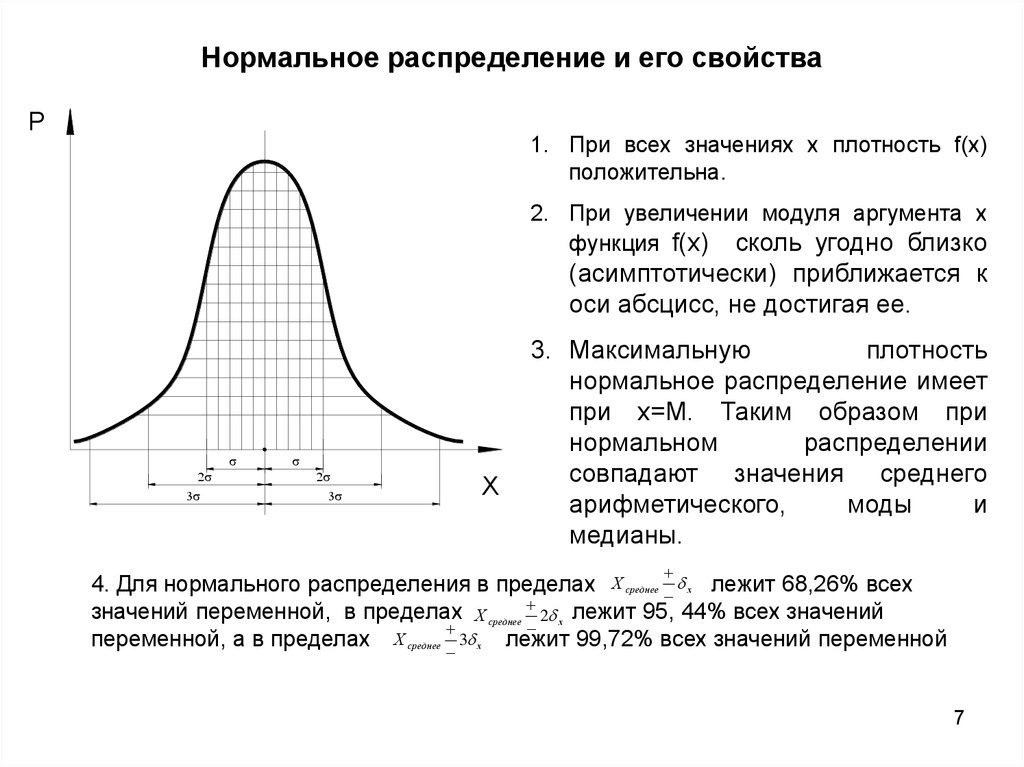 Распознавание этих графиков и распределений может помочь вам найти определенные характеристики ваших данных и выполнить с ними определенные вычисления.
Распознавание этих графиков и распределений может помочь вам найти определенные характеристики ваших данных и выполнить с ними определенные вычисления.
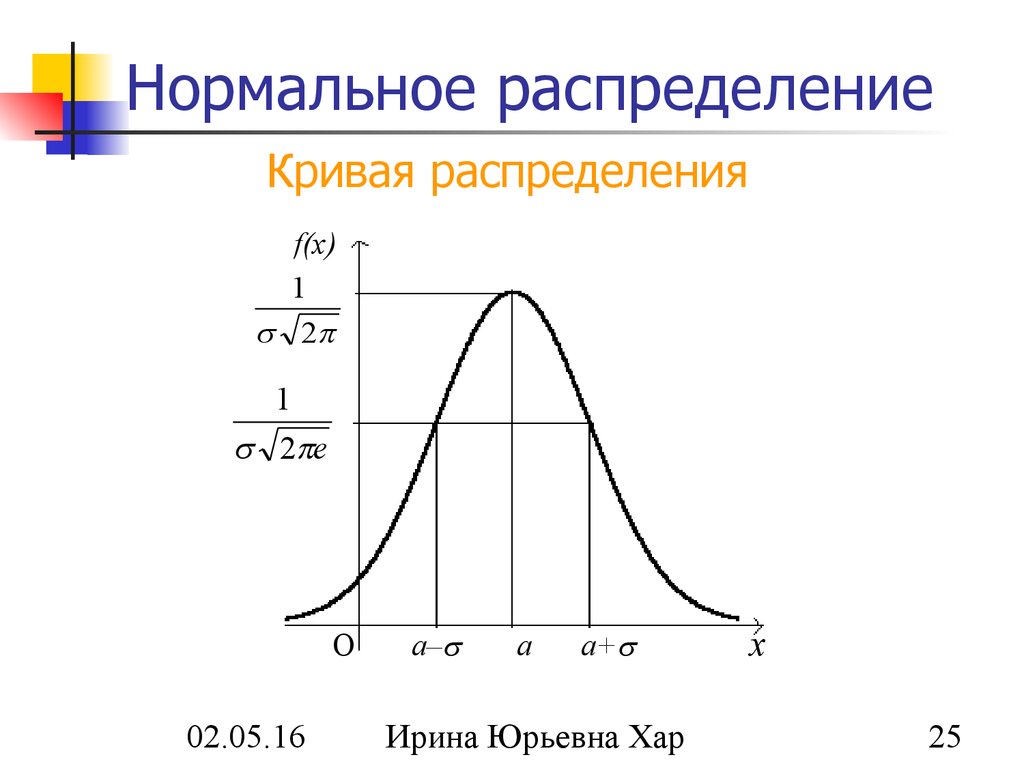
Что такое нормальное распределение?
Нормальное распределение — это непрерывное распределение вероятностей с функцией плотности вероятности, которая дает вам симметричную кривую нормального распределения. Проще говоря, это график функции вероятности переменной, в которой максимальные данные сосредоточены вокруг одной точки, а несколько точек симметрично сужаются к двум противоположным концам.
В этом определении нормального распределения вы изучите следующие термины:
- Непрерывное распределение вероятностей: Распределение вероятностей, при котором случайная величина X может принимать любое заданное значение, например количество осадков. Вы можете записать количество осадков, полученных в определенное время, как 9 дюймов. Но это не точное значение. Фактическое значение может быть 9,001234 дюйма или бесконечное количество других чисел.
 В этом случае нет определенного способа нанести точку, и вместо этого вы используете непрерывное значение.
В этом случае нет определенного способа нанести точку, и вместо этого вы используете непрерывное значение. - Функция плотности вероятности: выражение, используемое для определения диапазона значений, которые может принимать непрерывная случайная величина.
Нормальное распределение имеет распределение вероятностей, центрированное вокруг среднего значения. Это означает, что распределение имеет больше данных вокруг среднего значения. Распределение данных уменьшается по мере удаления от центра. Полученная кривая симметрична относительно среднего значения и образует колоколообразную форму распределения. Рассмотрим приведенный ниже график, который показывает вероятностное распределение роста в классе:
Рисунок 1: Нормальное распределение
На приведенном выше графике видно, что распределение в основном соответствует среднему или среднему значению всех высот. Помимо этого, большинство данных находится около среднего значения.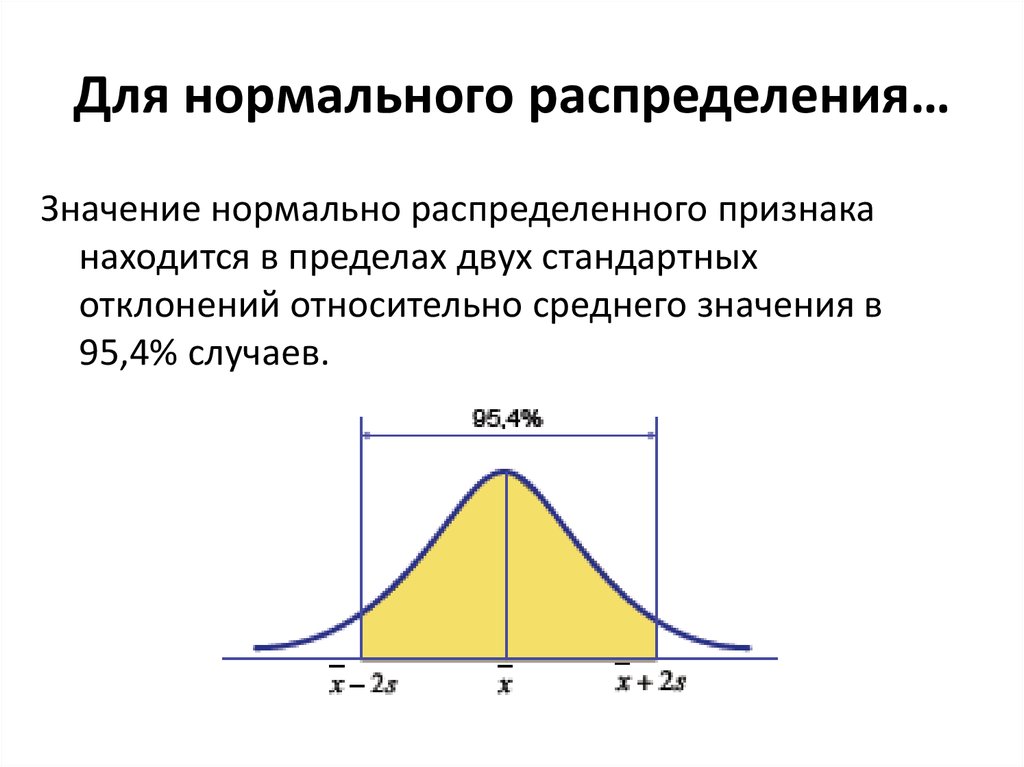 По мере удаления плотность вероятности также уменьшается. Такая кривая называется кривой Белла, и она является общей чертой нормального распределения.
По мере удаления плотность вероятности также уменьшается. Такая кривая называется кривой Белла, и она является общей чертой нормального распределения.
Что такое стандартное отклонение?
Стандартное отклонение — это мера того, насколько значения в ваших данных отличаются друг от друга или насколько разбросаны ваши данные.
Стандартное отклонение измеряет, насколько далеко друг от друга находятся точки данных в ваших наблюдениях. Вы можете рассчитать его, вычитая каждую точку данных из среднего значения, а затем находя квадрат среднего значения разностей; это называется дисперсией. Квадратный корень из дисперсии дает вам стандартное отклонение.
Подобно тому, как среднее значение говорит вам, где центрируются данные, стандартное отклонение дает вам ширину вашей кривой нормального распределения. Он говорит вам, насколько узкой или широкой является кривая нормального распределения. Рассмотрим пример доходов в сельской и городской местности.
Рисунок 2: Стандартное отклонение
В сельской местности, скажем, в фермерском поселке, большинство людей занимаются одной и той же профессией – земледелием.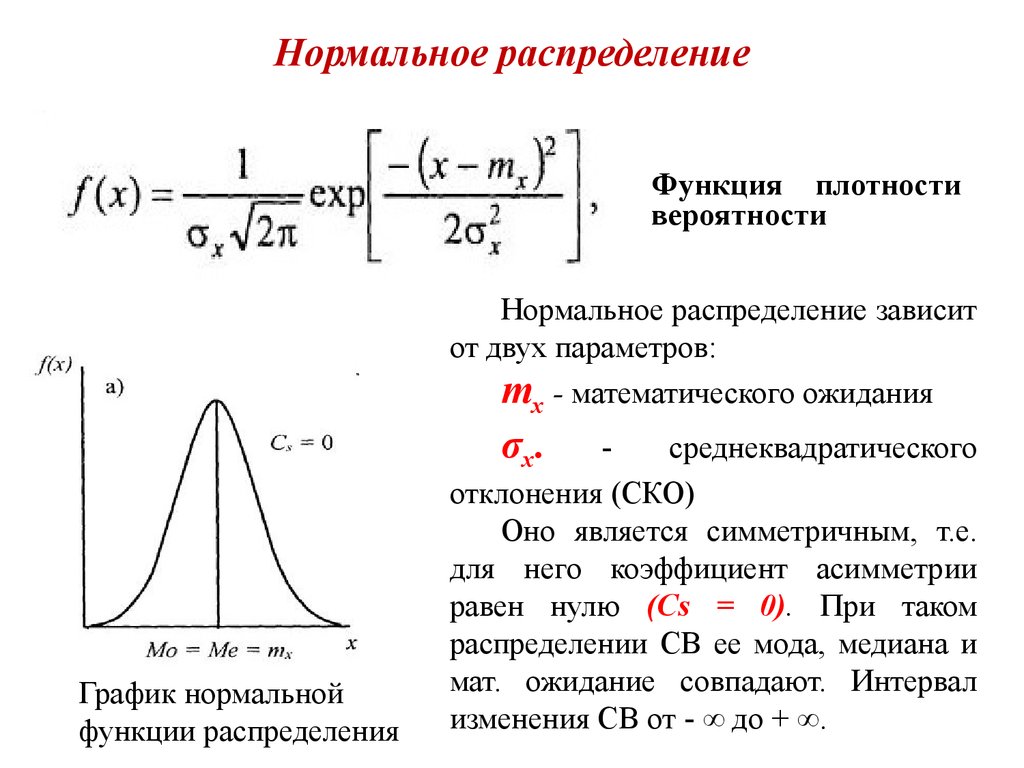 Все они зарабатывают более или менее одинаково, причем заминдар зарабатывает больше всех. Большинство людей здесь получают одинаковый средний доход, о чем свидетельствует высокий пик среднего значения. В наших данных нет большого отклонения. Следовательно, кривая относительно узкая.
Все они зарабатывают более или менее одинаково, причем заминдар зарабатывает больше всех. Большинство людей здесь получают одинаковый средний доход, о чем свидетельствует высокий пик среднего значения. В наших данных нет большого отклонения. Следовательно, кривая относительно узкая.
В городском городе население больше. Есть также больше людей, выполняющих разные работы, которые оплачиваются на очень разном уровне. Некоторые люди могут быть бизнесменами, а другие могут даже не иметь фиксированного дохода. Это приводит к большему разбросу данных, и, следовательно, кривая становится более разбросанной или имеет более высокое стандартное отклонение.
Теперь разберем стандартное отклонение на примере.
Рассмотрим пример роста собак, приведенный ниже:
Рисунок 3: Высота собаки
Сначала вы найдете среднее или среднее значение всех этих значений, сложив их все и разделив полученную сумму на количество точек данных.
Рисунок 4: Средняя высота
Это означает, что средний рост собаки составляет 394 мм. Теперь вычтите все точки данных из среднего значения.
Теперь вычтите все точки данных из среднего значения.
Рисунок 5: Разница между ростом и средним значением
Отрицательные значения означают, что значение находится ниже среднего, а положительные значения говорят о том, что точка данных находится выше среднего. Значение 0 означает, что точка данных совпадает со средним значением. Теперь давайте возведем каждое значение в квадрат и найдем их среднее значение, чтобы получить дисперсию.
Рисунок 6: Стандартное отклонение данных о росте собак
Нахождение квадратного корня из дисперсии дает вам стандартное отклонение. В данном случае это 147 мм. Это означает, что кривая скорее высокая, чем широкая, имеет небольшой разброс и является узкой. В данных не так много отклонений.
Что такое стандартное нормальное распределение?
Стандартное нормальное распределение — это тип нормального распределения со средним значением 0 и стандартным отклонением 1. Это означает, что центр нормального распределения находится в 0, а интервалы увеличиваются на 1.
Среднее значение и стандартное отклонение в нормальном распределении не фиксированы. Они могут принимать любое значение. Однако при стандартизации нормального распределения среднее значение и стандартное отклонение остаются фиксированными и одинаковыми для всех стандартных нормальных распределений. Рассмотрим приведенный ниже пример весов учеников в классе:
Рисунок 7: Стандартное нормальное распределение
Отображает фактический вес учащихся над осью x. Но из графика видно, что точки данных отличаются на 5 баллов. Найдя среднее значение, вы получите его как 50, поэтому вы можете принять это как 0-ю точку. Остальные точки расположены на одинаковом расстоянии друг от друга и при стандартизации отличаются на 1, поэтому вы можете переписать шкалу так, чтобы центрировать ее вокруг 0 и увеличивать на 1. Точки выше среднего попадают в положительные значения, а ниже среднего — в отрицательные. .
Когда вы стандартизируете свои данные, вычисление вероятностей на вашем графике становится проще. Вы также можете легко сравнивать разные графики друг с другом, так как все они имеют одинаковый масштаб. Некоторые характеристики стандартного нормального распределения приведены ниже:
Вы также можете легко сравнивать разные графики друг с другом, так как все они имеют одинаковый масштаб. Некоторые характеристики стандартного нормального распределения приведены ниже:
Рисунок 8: Характеристики стандартного нормального распределения
Что такое Z-показатель?
Z-оценка используется, чтобы сообщить вам, насколько далеко от среднего находится точка данных. Вы вычисляете его, используя среднее значение и стандартное отклонение, поэтому также можно сказать, что Z-показатель — это то, на сколько стандартных отклонений ниже среднего значение данных.
Z-оценка используется для стандартизации вашего нормального распределения. Используя z-оценку, вы можете преобразовать каждую точку данных в значение с точки зрения среднего значения и стандартного отклонения, эффективно преобразовав график в уменьшенную версию. Z-оценка показывает, насколько далеко каждая точка данных от среднего значения в шагах стандартного отклонения. Итак, со средним значением и стандартным отклонением вы можете нанести все точки на наш график.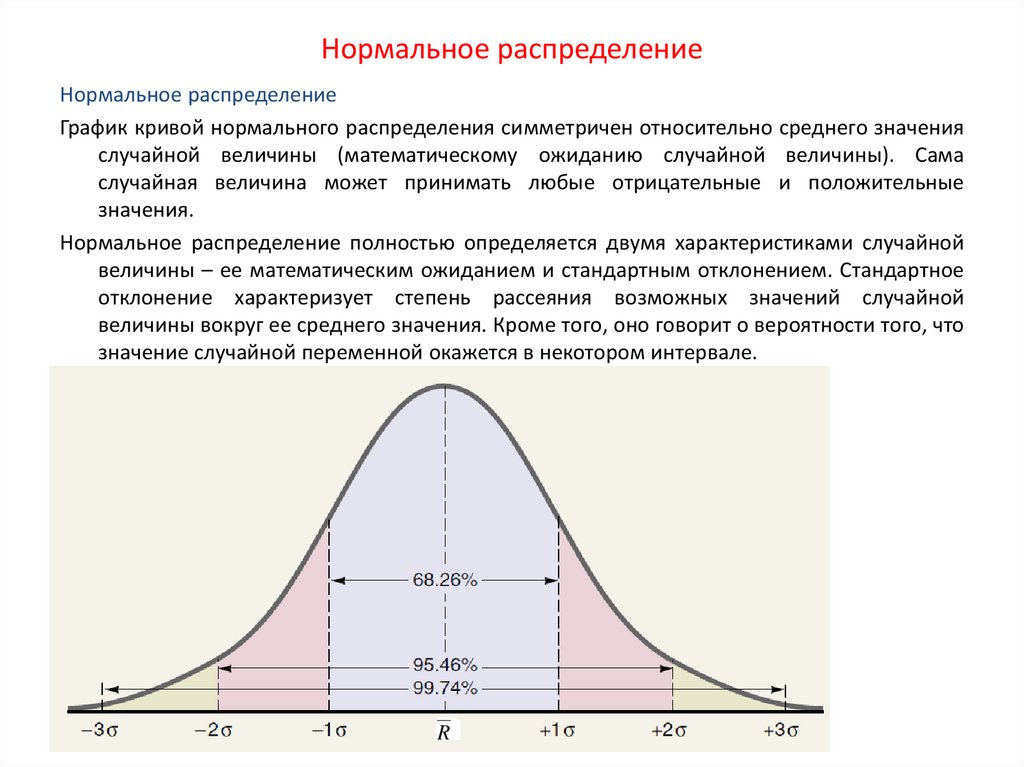
Z-оценка определяется как:
Рисунок 9: Z-показатель
Давайте представим каждую точку данных как «x», тогда формула для z-показателя станет следующей:
Рисунок 10: Формула Z-показателя
Теперь разберемся с z-показателем на примере. Ниже приводится сводная информация о ежедневном времени в пути человека, который едет с работы. Значения указаны в минутах. Рассчитайте среднее значение, стандартное отклонение и Z-показатель.
Рисунок 11: Время в пути
Среднее значение — это среднее всех значений:
Рисунок 12: Среднее время в пути
Теперь вычтите среднее из каждой точки данных и найдите дисперсию и стандартное отклонение.
Рисунок 13: Различное время в пути
Рисунок 14: Разница во времени в пути
Рисунок 15: Стандартное отклонение времени в пути
Z-показатель сообщает нам, где находится точка данных относительно других точек. Z-оценка покажет вам, насколько далеко от среднего находится точка в шагах вашего стандартного отклонения. Теперь вычислите z-оценку для каждой точки:
Z-оценка покажет вам, насколько далеко от среднего находится точка в шагах вашего стандартного отклонения. Теперь вычислите z-оценку для каждой точки:
Рисунок 16: Z-показатель времени в пути
Отрицательные значения говорят о том, что точка находится ниже среднего значения, а положительные значения означают, что точка находится выше среднего значения. Умножение каждого значения на стандартное отклонение даст разницу между средним значением и точкой данных.
В целом, он стандартизировал каждое значение. Вы можете построить новый график со средним значением в центре.
Мечтаете о карьере в области аналитики данных? Посетите учебный курс по аналитике данных и пройдите сертификацию уже сегодня.
Заключение
В этом учебнике «Все, что вам нужно знать о нормальном распределении» вы рассмотрели нормальное распределение и то, как его распознать. Затем вы посмотрели на стандартное отклонение и поняли важность стандартизации нашего нормального распределения.

 СТ.РАСП(1,333333;ЛОЖЬ)
СТ.РАСП(1,333333;ЛОЖЬ)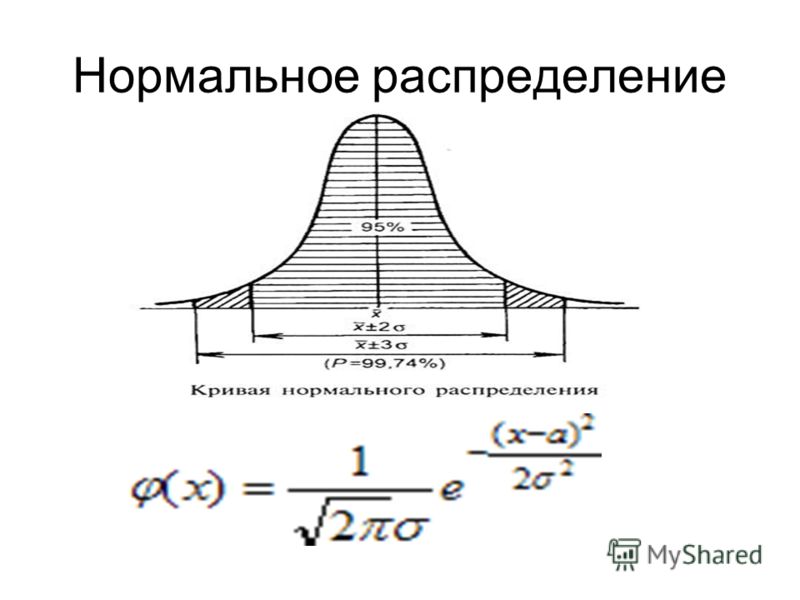
 z -оценки равны ________________ соответственно.
z -оценки равны ________________ соответственно.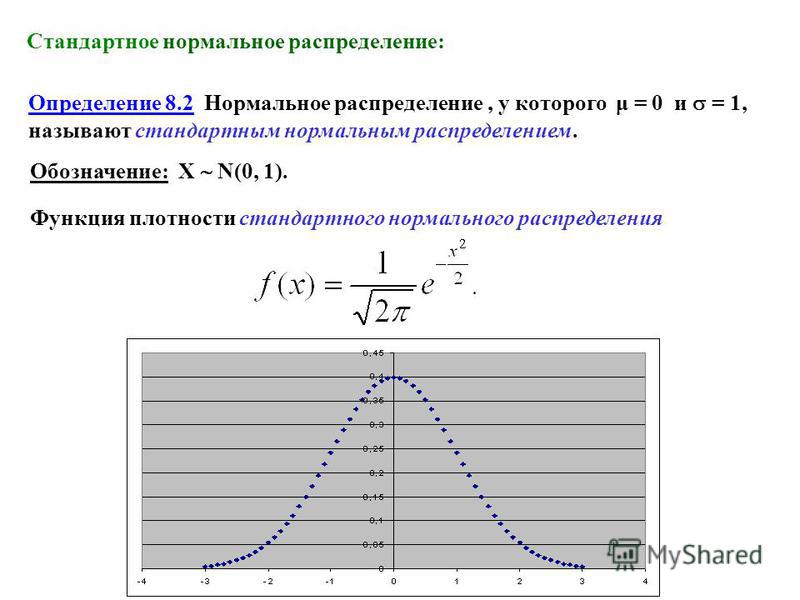 z -оценки равны ________________ соответственно.
z -оценки равны ________________ соответственно.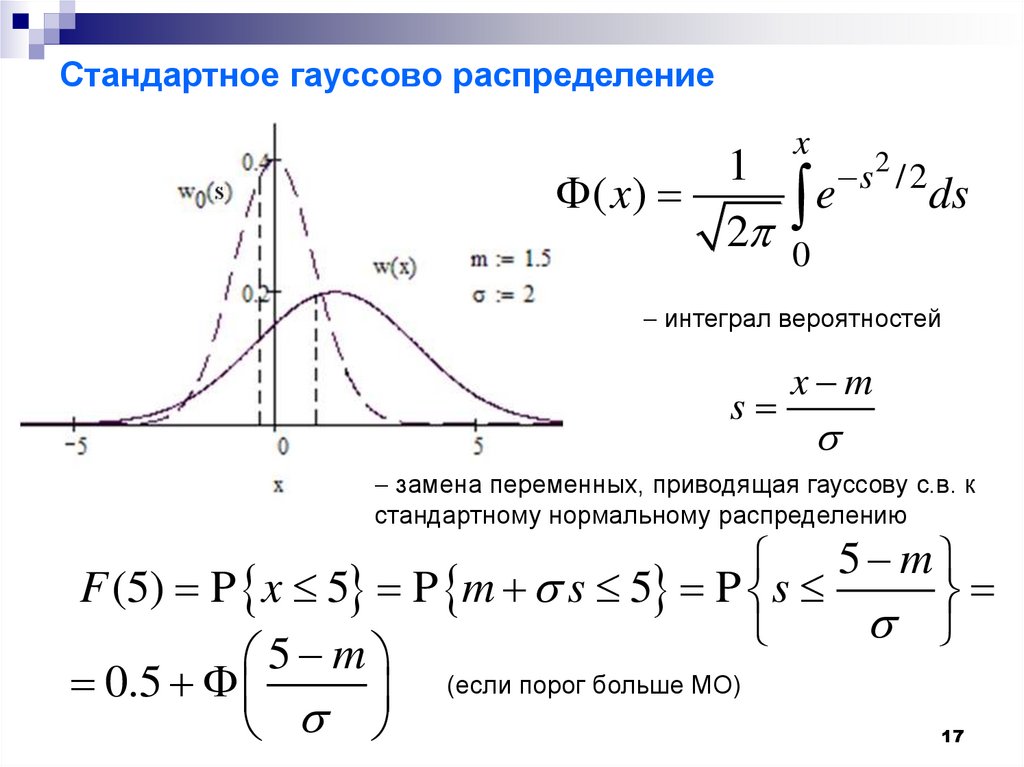 В этом случае нет определенного способа нанести точку, и вместо этого вы используете непрерывное значение.
В этом случае нет определенного способа нанести точку, и вместо этого вы используете непрерывное значение.