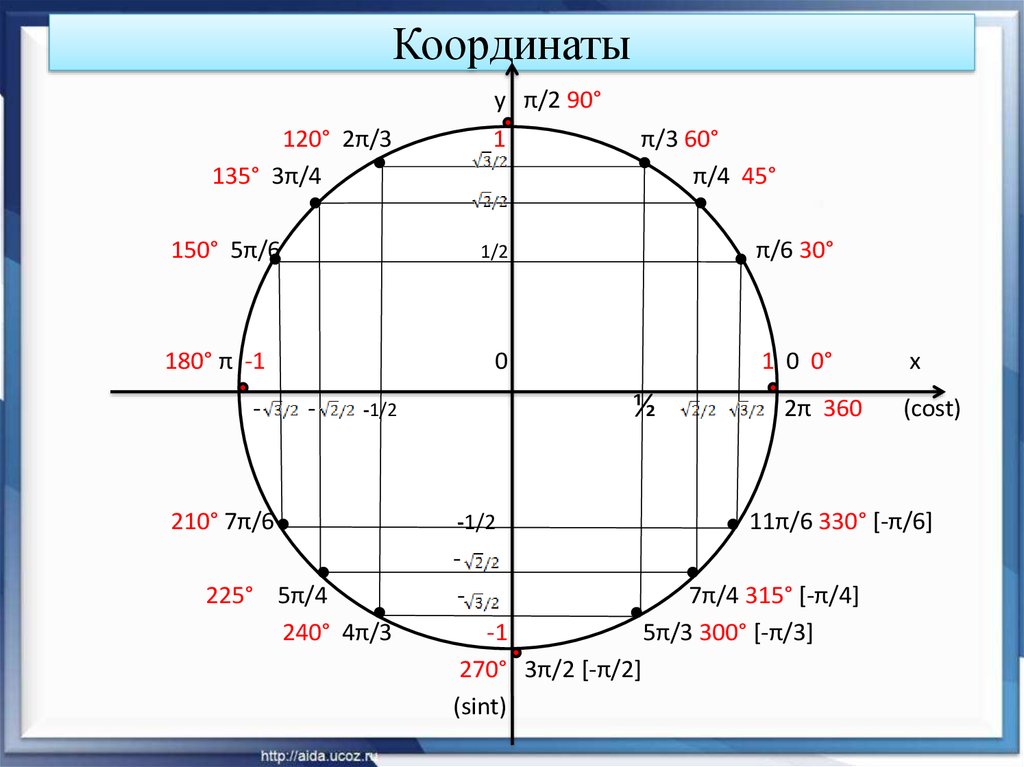
градусная и радианная мера угла, интервалы и отрезки, свойства точки
- Понятие тригонометрии
- Числовая окружность
- Градусная и радианная мера угла
- Свойства точки на числовой окружности
- Интервалы и отрезки на числовой окружности
- Примеры
п.1. Понятие тригонометрии
Тригонометрия – это раздел математики, в котором изучаются тригонометрические функции и их использование.
Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов. Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., — спроектирован с использованием тригонометрии.
п.2. Числовая окружность
Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.
| Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0). Точка с координатами (1;0) является началом отсчета, ей соответствует угол, равный 0. Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным; по часовой стрелке – отрицательным. |
Например:
Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90°, –120°, –180°. |
п.3. Градусная и радианная мера угла
Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).
В целом, более обоснованной и естественной для измерения углов является радианная мера.
Радианной мерой угла называется отношение длины дуги окружности, заключенной между сторонами угла и центром в вершине угла, к радиусу этой окружности.
От радиуса окружности это отношение не зависит.
Например:
Найдем радианную меру прямого угла ∠AOB=90°.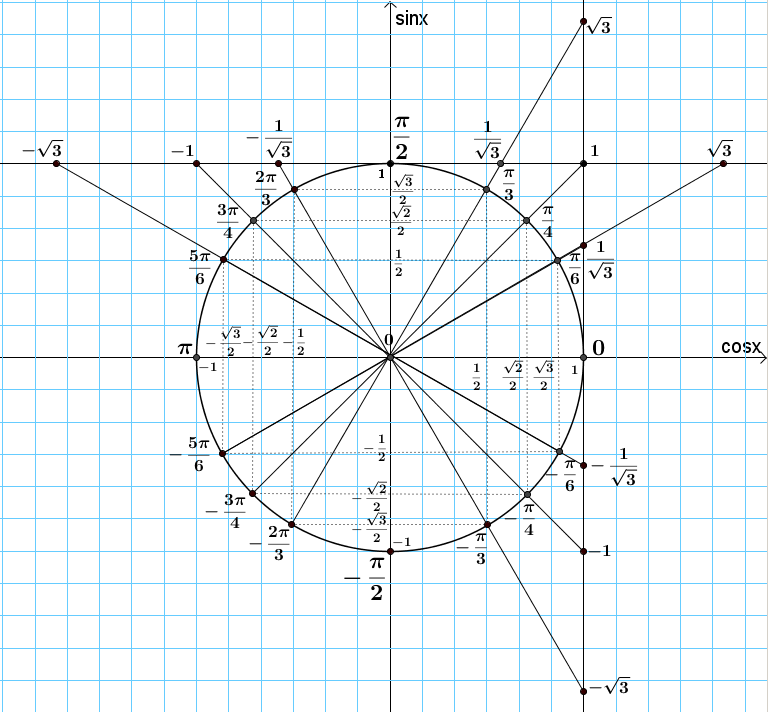 {\circ} $$ {\circ} $$
п.4. Свойства точки на числовой окружностиПостроим числовую окружность. Обозначим O(0;0), A(1;0)
Например:
Каждой точке M(t) на числовой окружности соответствует бесконечное множество действительных чисел t с точностью до полного периода 2π: Например:
п. 5. Интервалы и отрезки на числовой окружности 5. Интервалы и отрезки на числовой окружностиКаждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг. Например:
п. {\circ}\\ \frac{17\pi}{6}=\frac{18-1}{6}\pi=3\pi-\frac{\pi}{6}\rightarrow \pi-\frac{\pi}{6}=\frac{5\pi}{6}\\ \frac{27\pi}{4}=\frac{28-1}{4}\pi=7\pi-\frac{\pi}{4}\rightarrow \pi-\frac{\pi}{4}=\frac{3\pi}{4} \end{gather*} {\circ}\\ \frac{17\pi}{6}=\frac{18-1}{6}\pi=3\pi-\frac{\pi}{6}\rightarrow \pi-\frac{\pi}{6}=\frac{5\pi}{6}\\ \frac{27\pi}{4}=\frac{28-1}{4}\pi=7\pi-\frac{\pi}{4}\rightarrow \pi-\frac{\pi}{4}=\frac{3\pi}{4} \end{gather*} | ||||||||||||||||||||||||||||||||||||||||||
Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.
| Сравниваем каждое число с границами четвертей: \begin{gather*} 0,\ \ \frac\pi2\approx\frac{3,14}{2}=1,57,\ \ \pi\approx 3,14\\ 3\pi\ \ 3\cdot 3,14\\ \frac{3\pi}{2}\approx \frac{3\cdot 3,14}{2}=4,71,\ \ 2\pi\approx 6,28 \end{gather*} |
\(\frac\pi2\lt 2\lt \pi \Rightarrow \) угол 2 радиана находится во 2-й четверти
\(\pi\lt 4\lt \frac{3\pi}{2} \Rightarrow \) угол 4 радиана находится в 3-й четверти
\(\frac{3\pi}{2}\lt 5\lt 2\pi \Rightarrow \) угол 5 радиана находится в 4-й четверти
\(7\gt 2\pi\), отнимаем полный оборот: \(0\lt 7-2\pi\lt \frac\pi2\Rightarrow\) угол 7 радиан находится в 1-й четверти.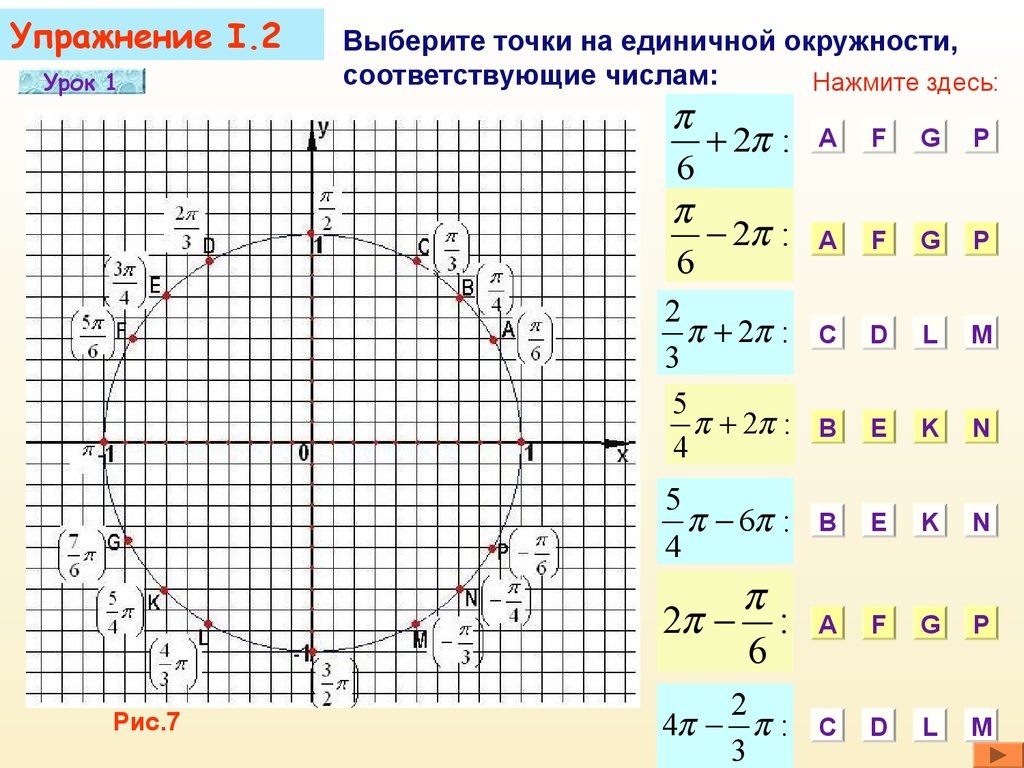
Пример 5. Изобразите на числовой окружности множество точек \((k\in\mathbb{Z})\), запишите количество полученных базовых точек.
| $$ \frac{\pi k}{2} $$ | $$ -\frac{\pi}{4}+2\pi k $$ |
Четыре базовых точки, через каждые 90° | Две базовых точки, через каждые 180° |
| $$ \frac{\pi}{3}+\frac{2\pi k}{3} $$ | $$ -\frac{\pi k}{5} $$ |
Три базовых точки, через каждые 120° | Пять базовых точек, через каждые 72° |
Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.
| $$ \left[0;\ \frac{\pi}{3}\right] $$ | $$ \left(-\frac{\pi}{4};\ \pi\right] $$ |
| $$ \left[\frac\pi2;\ \frac{5\pi}{4}\right) $$ | $$ (1;\ 3) $$ |
| \begin{gather*} 1\ \text{рад}=\frac{180^{\circ}}{\pi}\approx 57,3^{\circ}\\ 3\ \text{рад}=\frac{180^{\circ}}{\pi}\cdot 3\approx 171,9^{\circ} \end{gather*} |
Единичная окружность в тригонометрии
Поможем понять и полюбить математику
Начать учиться
Единичная окружность — идеальный инструмент для тригонометрии. В этой статье узнаем больше про этот вид окружности и возможных с ней действиях.
В этой статье узнаем больше про этот вид окружности и возможных с ней действиях.
Единичная окружность в тригонометрии
При изучении тригонометрии используют единичную окружность. Сейчас узнаем, какую окружность называют единичной и дадим определение.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.
Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.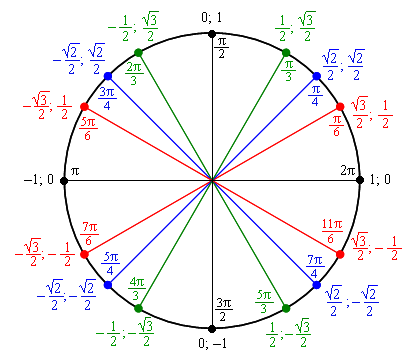
Поясним, как единичная окружность связана с тригонометрией.
В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.
Угол принято считать против часовой стрелки между положительным направлением оси OX и лучом OA.
Величины углов не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании.
Все углы, которые принадлежат одной четверти, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
Если угол находится в первой четверти, все тригонометрические функции имеют положительные значения.
Для угла во второй четверти синус положителен, косинус, тангенс и котангенс — отрицательны.

В третьей четверти синус и косинус отрицательны, а тангенс и котангенс — положительны.
В четвертой четверти синус отрицателен, косинус положителен, тангенс и котангенс — отрицательны.
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:
Радиан — одна из мер для определения величины угла.
Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.
Число радиан для полной окружности — 360 градусов.
Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.
Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.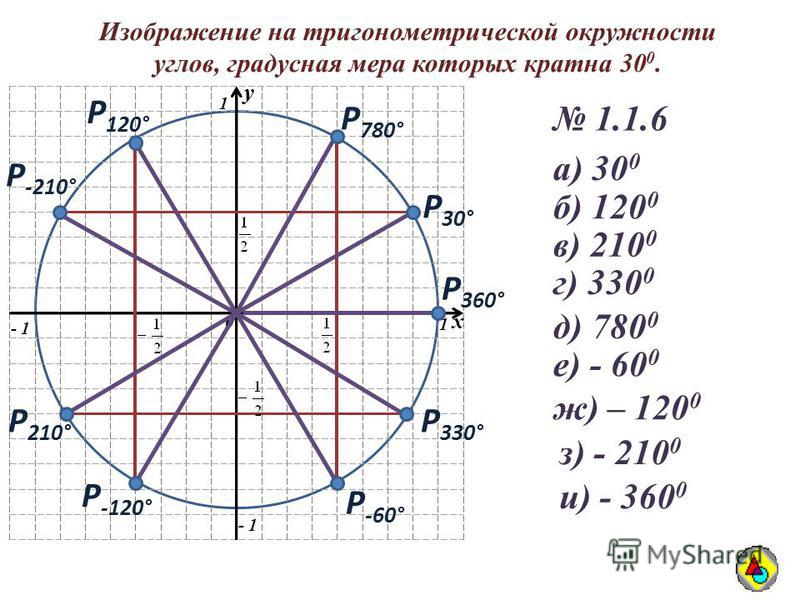
Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
2π радиан = 360°
1 радиан = (360/2π) градусов = (180/π) градусов
360° = 2π радиан
1° = (2π/360) радиан = (π/180) радиан
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Для чего можно использовать единичную окружность
определить синус, косинус, тангенс и котангенс угла
найти значения тригонометрических функций для некоторых значений числового и углового аргумента
вывести основные формулы тригонометрии
применить формулы приведения
найти области определения и области значений тригонометрических функций
определить периодичность тригонометрических функций
определить четность и нечетность тригонометрических функций
определить промежутки возрастания и убывания тригонометрических функций
определить промежутки знакопостоянства тригонометрических функций
применить радианное измерение углов
найти значения обратных тригонометрических функций
решить простейшие тригонометрические уравнения
решить простейшие тригонометрические неравенства.

Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
143.3K
Раскрытие скобок
К следующей статье
109.2K
Действительные числа
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Круговые функции
График уравнения x 2 + y 2 = 1 представляет собой окружность в прямоугольной системе координат. Этот график называется окружностью единиц , имеет центр в начале координат и радиус 1 единицу.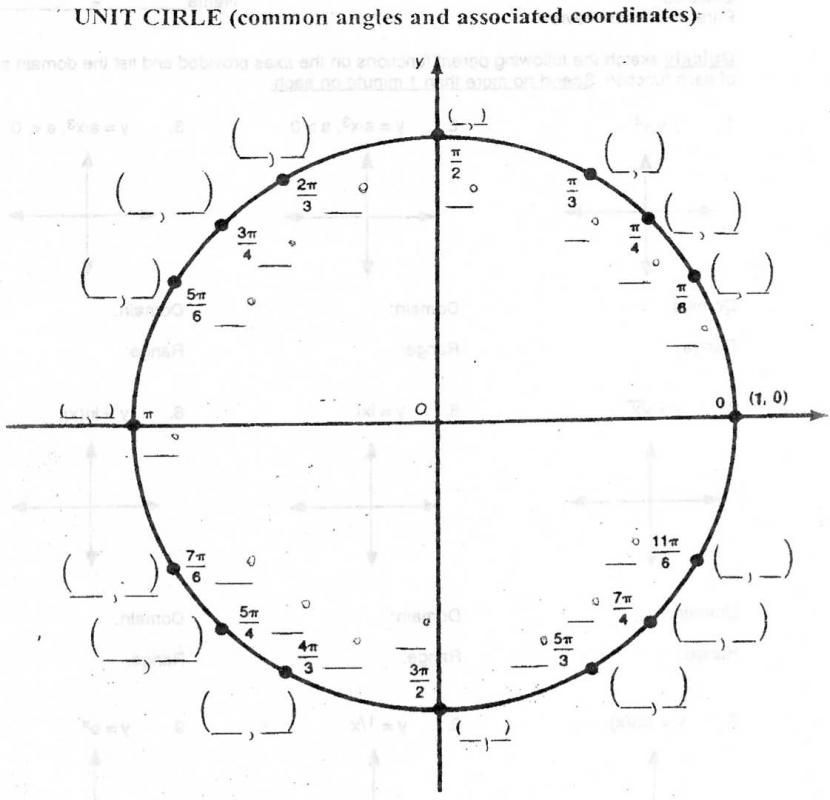 Тригонометрические функции определяются таким образом, что их доменов представляют собой наборы углов , а их диапазоны представляют собой наборы действительных чисел. Круговые функции определены таким образом, что их домены являются наборами чисел , которые соответствуют мерам (в радианах) углов аналогичных тригонометрических функций. Диапазоны этих круговых функций, как и их аналогичные тригонометрические функции, представляют собой наборы действительных чисел. Эти функции называются круговыми, потому что радианные меры углов определяются длинами дуг окружностей. В частности, тригонометрические функции, определенные с помощью единичного круга, ведут непосредственно к этим круговым функциям.
Тригонометрические функции определяются таким образом, что их доменов представляют собой наборы углов , а их диапазоны представляют собой наборы действительных чисел. Круговые функции определены таким образом, что их домены являются наборами чисел , которые соответствуют мерам (в радианах) углов аналогичных тригонометрических функций. Диапазоны этих круговых функций, как и их аналогичные тригонометрические функции, представляют собой наборы действительных чисел. Эти функции называются круговыми, потому что радианные меры углов определяются длинами дуг окружностей. В частности, тригонометрические функции, определенные с помощью единичного круга, ведут непосредственно к этим круговым функциям.
Начните с единичного круга x 2 + y 2 = 1 показано на рисунке . Точка A (1,0) расположена на пересечении единичной окружности и оси x . Пусть q — любое действительное число. Начните с точки A и измерьте | q | единиц по единичной окружности против часовой стрелки, если q > 0, и по часовой стрелке, если q < 0, заканчивая точкой P ( x, y ). Определите синус и косинус числа 9.0021 q как координаты точки P . Другие круговые функции (тангенс, котангенс, секанс и косеканс) могут быть определены через синус и косинус.
Начните с точки A и измерьте | q | единиц по единичной окружности против часовой стрелки, если q > 0, и по часовой стрелке, если q < 0, заканчивая точкой P ( x, y ). Определите синус и косинус числа 9.0021 q как координаты точки P . Другие круговые функции (тангенс, котангенс, секанс и косеканс) могут быть определены через синус и косинус.
Рисунок 1
Ссылка на окружность единицы измерения.
Sin q и cos q существуют для каждого действительного числа q , потому что (cos q , sin q ) являются координатами точки P , расположенной на единичной окружности, что соответствует дуге длины | q |. Поскольку эта длина дуги может быть положительной (против часовой стрелки) или отрицательной (по часовой стрелке), домен каждой из этих круговых функций представляет собой набор действительных чисел. Диапазон более ограничен. Косинус и синус — это абсцисса и ордината точки, которая движется по единичной окружности, и они варьируются от −1 до 1. Таким образом, диапазон каждой из этих функций представляет собой набор действительных чисел
Диапазон более ограничен. Косинус и синус — это абсцисса и ордината точки, которая движется по единичной окружности, и они варьируются от −1 до 1. Таким образом, диапазон каждой из этих функций представляет собой набор действительных чисел
Рисунок 2
Диапазон значений триггерных функций.
Пример 1: Какие значения x в области функции синуса между −2π и 2π имеют значение диапазона, равное 1 (рис. 3 )?
Рисунок 3
Чертеж для примера 1.
Значение диапазона sin x равно 1, если точка P имеет координаты (0, 1). Это происходит, когда х = π/2 и х = -3π/2.
Пример 2: Какие значения x в области функции косинуса между −2π и 2π имеют значение диапазона −1 (рис. 4 )?
Рисунок 4
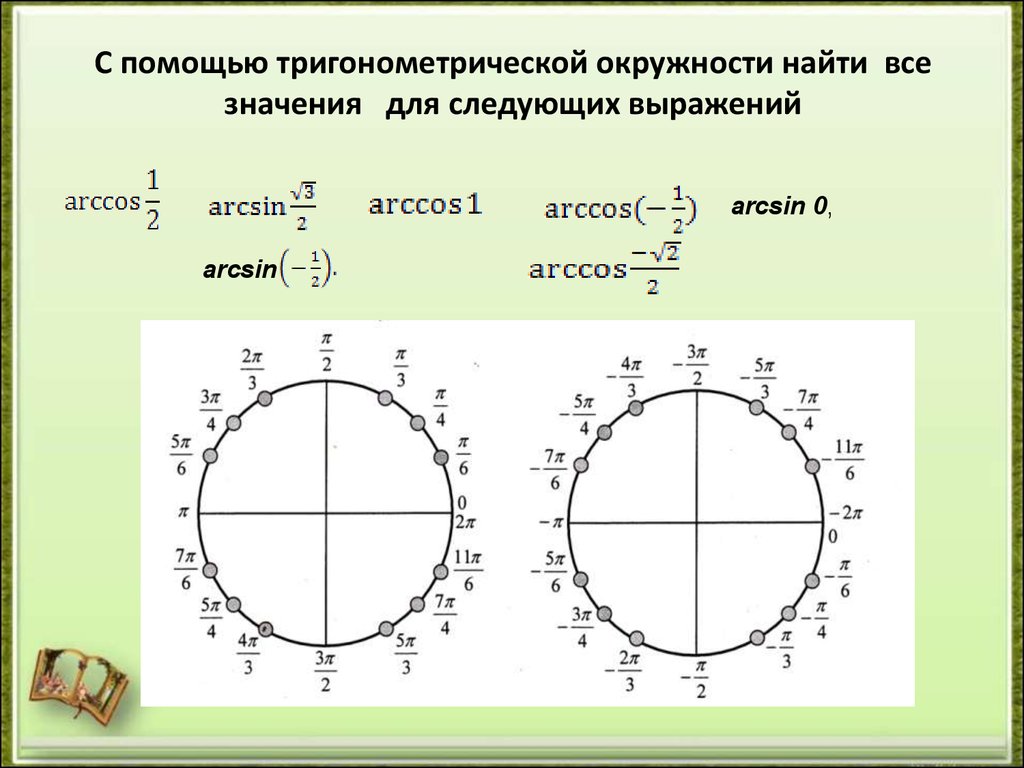
Значение диапазона cos x равно −1, когда точка P (cos x , sin x ) имеет координаты (−1, 0). Это происходит, когда x = π и x = −π.
Пример 3: Точка P находится на единичной окружности. Длина дуги от точки A (1,0) до точки P составляет q единиц. Каковы значения шести круговых функций q ?
Значения синуса и косинуса следуют из определений и являются координатами точки P . Остальные четыре функции получены с использованием синуса и косинуса.
Знак каждой из шести круговых функций (см. Таблицу 1) зависит от длины дуги q . Обратите внимание, что четыре интервала для q непосредственно соответствуют четырем квадрантам для тригонометрических функций.
Определение единичной окружности тригонометрических функций, триг. функции
Единичная окружность
Прежде чем узнать, что такое единичная окружность, полезно вспомнить, что такое числовая линия. Числовая линия — это прямая бесконечная линия с началом и единичной длиной. (OE – единая длина, O – начало координат)
Числовая линия — это прямая бесконечная линия с началом и единичной длиной. (OE – единая длина, O – начало координат)
Что произойдет, если мы обернем нашу бесконечную линию вокруг окружности радиусом 1?
Каждая точка числовой прямой окажется на нашей окружности. Каждой точке на нашей числовой прямой соответствует ровно одна точка на окружности. Этот круг называется единичным кругом. Единичная окружность — это окружность с радиусом 1. Важно, чтобы радиус этой окружности был равен 1.
Как вы знаете, у вас есть положительные и отрицательные числа на вашей числовой прямой. Положительные числа (вверх от начала координат на картинке) воспроизводятся в положительной математической ориентации (против часовой стрелки), а отрицательные (вниз от начала координат) воспроизводятся в отрицательной математической ориентации (по часовой стрелке).
Давайте вспомним, что такое радианы. 1 радиан – это часть окружности, длина дуги которой равна радиусу.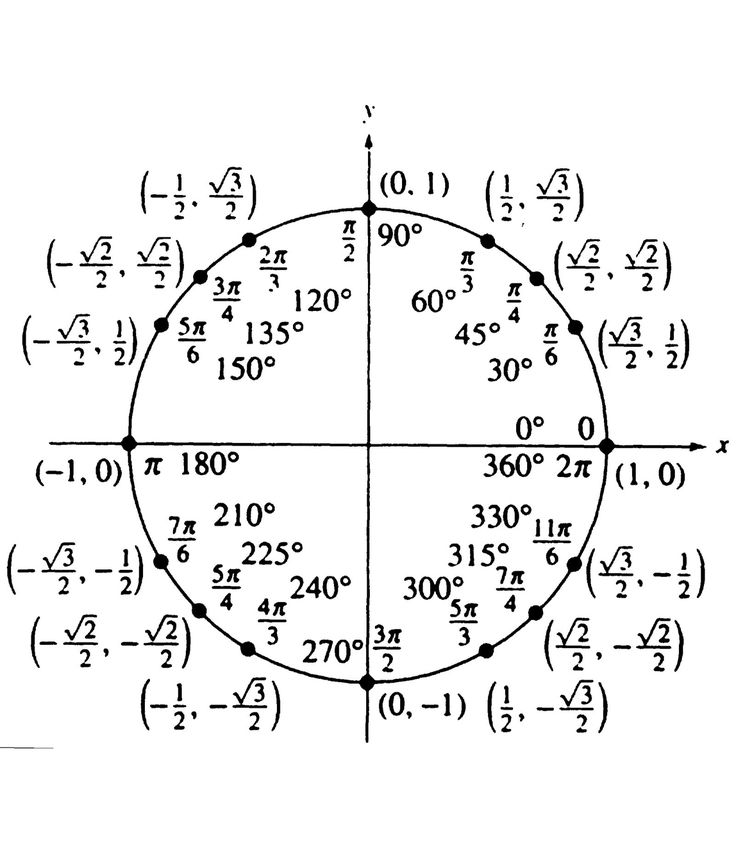 Одна целая окружность имеет $ 2 \pi$ радиан; одна половина круга имеет $\pi$ радиан и так далее.
Одна целая окружность имеет $ 2 \pi$ радиан; одна половина круга имеет $\pi$ радиан и так далее.
Теперь, когда мы это вспомнили, давайте посмотрим на нашу картинку. Вы оборачиваете бесконечную линию вокруг круга. В какой-то момент вы начнете свой второй круг вокруг него, а когда вы снова завернете его, вы начнете третий и так до бесконечности. Это означает, что бесконечно много точек с числовой прямой попадут в одни и те же места на единичной окружности.
Единица окружности радианы
Если ваша числовая линия отмечена радианами, она будет выглядеть так:
Во-первых, у вас есть обычная единичная окружность. В одной четверти круга $\frac{\pi}{2}$, в одной половине $\pi$, в трех четвертях $\frac{3 \pi}{2}$, а в одной целой $2 \пи$.
Что теперь, когда вы начнете следующий круг?
Вы снова в нуле, но теперь с 2π линии вокруг круга. Если вы добавите еще один $\frac{\pi}{2}$, это приведет вас к точке, где находится «старый» $\frac{\pi}{2}$, но теперь это значение будет $2\pi + \frac{\pi}{2} = \frac{5 \pi}{2}$.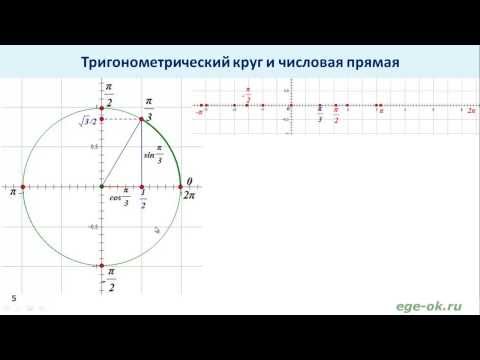 Если вы продолжите и добавите еще $\frac{\pi}{2}$, вы окажетесь в точке, где лежит «старое» π. Теперь эта точка будет равна $\frac{5 \pi}{2} + \frac{\pi}{2} = 3 \pi$. И ты продолжаешь в том же духе. 9{\circ}$ и так далее.
Если вы продолжите и добавите еще $\frac{\pi}{2}$, вы окажетесь в точке, где лежит «старое» π. Теперь эта точка будет равна $\frac{5 \pi}{2} + \frac{\pi}{2} = 3 \pi$. И ты продолжаешь в том же духе. 9{\circ}$ и так далее.
Разделив радианы на все меньшие и меньшие части, мы можем определить меру каждого угла.
Чаще всего используются углы 0, $\frac{\pi}{6}$, $\frac{\pi}{3}$, $\frac{\pi}{2}$ и так далее.
Вы видите здесь закономерность? Если вы наблюдаете только за первым и вторым квадрантом, вы заметите, что линии, перпендикулярные оси Y, которые проходят через $\frac{\pi}{3}$ и $\frac{2 \pi}{3}$, обрезаются. равные части оси Y. То же самое относится к $\frac{3 \pi}{4}$ и $\frac{\pi}{4}$, а также к $\frac{5 \pi}{6}$ и $\frac{\ пи{6}$.
Если вы посмотрите на первый и четвертый квадранты, вы заметите, что линии, перпендикулярные оси x $\frac{\pi}{6}$ и $\frac{11 \pi}{6}$, пересекаются от равной длины оси x, и так далее с другими углами. Это может помочь вам в их рисовании.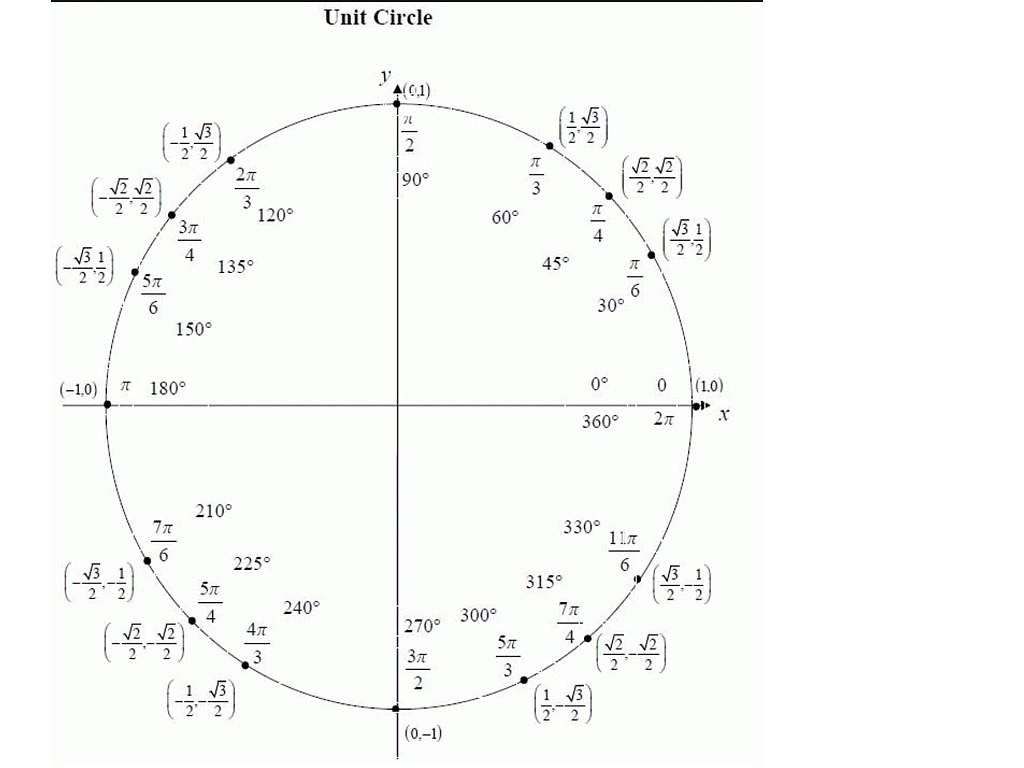 Например, если вы получили задание нарисовать $\frac{5\pi}{6}$, вы можете просто нарисовать $\frac{\pi}{6}$ и перевести его во второй квадрант. Используя этот способ, вам нужно будет только запомнить углы в первом квадранте и перевести их.
Например, если вы получили задание нарисовать $\frac{5\pi}{6}$, вы можете просто нарисовать $\frac{\pi}{6}$ и перевести его во второй квадрант. Используя этот способ, вам нужно будет только запомнить углы в первом квадранте и перевести их.
Пример 1 : Найдите следующие углы на единичной окружности
Если у вас есть дробь, значение которой больше двух, это означает, что вы начинаете новый «круг» по кругу. Когда вы имеете дело с такими значениями, вы должны применить процесс нахождения правильной меры угла. Это означает, что вы должны найти угол, который подходит для заданного угла, но на первом круге. Вы делаете это, вычитая с числом, кратным 2π.
Допустим, у вас есть $\frac{5 \pi}{2}$. $\frac{5\pi}{2}$ больше $2\pi$ на $\frac{\pi}{2}$. Это означает, что вы закончите первый круг и окажетесь в $\frac{\pi}{2}$.
Пример 2 : Найдите следующие углы на единичной окружности перед нашими значениями мы начинаем смотреть с нуля, но в противоположном направлении. Весь круг равен $2\pi$, а это означает, что $ -\frac{\pi}{4}$ будет иметь то же значение, что и $ 2 \pi – \frac{\pi}{4} = \frac{7 \pi}{4}$, $-\pi$ как $\pi$ и $-2 \pi$ как 0,
Весь круг равен $2\pi$, а это означает, что $ -\frac{\pi}{4}$ будет иметь то же значение, что и $ 2 \pi – \frac{\pi}{4} = \frac{7 \pi}{4}$, $-\pi$ как $\pi$ и $-2 \pi$ как 0,
Базовая тригонометрия
Триггерная единичная окружность
Для каждой точки нашей единичной окружности мы хотим знать точную длину от начала координат до ее проекции на оси x и y.
Синус и косинус
Длина от начала координат до проекции точки на ось x называется косинусом , а длина от начала координат до проекции точки на ось y называется синусоидой .
Функции синуса и косинуса — это функции, область определения которых представляет собой целое множество действительных чисел и область значений [-1, 1]. Их область значений — это множество действительных чисел между [-1, 1], потому что мы имеем дело с точками на единичной окружности, радиус которой равен 1,9.0019
Как найти угол, значения синуса и косинуса которого вам известны? Это очень просто. Если у вас есть значение синуса по умолчанию, сначала вы должны найти это значение на оси Y и провести параллельную линию от оси X через эту точку. Вы получите две точки на вашей единичной линии, которые вы соедините с началом координат. Два угла, одно плечо которых — эти линии, а второе — ось x, будут углами, которые вы ищете.
Если у вас есть значение синуса по умолчанию, сначала вы должны найти это значение на оси Y и провести параллельную линию от оси X через эту точку. Вы получите две точки на вашей единичной линии, которые вы соедините с началом координат. Два угла, одно плечо которых — эти линии, а второе — ось x, будут углами, которые вы ищете.
Если вам дано значение косинуса угла, вы просто найдете это значение по оси x, проведете параллельную линию от оси y через эту точку, соедините точки, которые вы получили на единичной окружности, и соедините их с началом координат. Два угла, одно плечо которых — эти линии, а второе — ось x, будут углами, которые вы ищете.
Пример 3 : Найдите углы,
которых $ sin(x) = 5$
d) $ cos(x) = 1$
Решение:
а)
б)
в) $ sin(x) = 5$. Где бы вы нарисовали свою пятёрку? Если бы вы следовали этим шагам, они вывели бы вас куда-то за пределы единичного круга. И где бы вы ни проводили параллели, ни одна из них не пересекает единичную окружность. Это из-за кодомена синуса и косинуса. Помните, что их значения могут быть только [-1,1].
Это из-за кодомена синуса и косинуса. Помните, что их значения могут быть только [-1,1].
d) Это просто. $ cos(x) = 1$. Это значение находится точно на числовой прямой и равно 0.
Тангенс и котангенс
Две другие очень важные тригонометрические функции называются тангенсом и котангенсом .
Это производные функции, но их не менее важно помнить.
Чтобы получить значение тангенса, сначала мы нарисуем линию, параллельную оси y, которая проходит через точку (1, 0).
Чтобы получить значение котангенса, сначала мы нарисуем линию, параллельную оси x, которая проходит через точку (0, 1).
Затем мы проводим линию от начала координат до точки на единичной линии, значение которой мы ищем.
Получим два пересечения: одно с линией, перпендикулярной оси x, и второе с линией, перпендикулярной оси y.
Величина касательной в заданной нами точке равна длине от пересечения с прямой, перпендикулярной оси x и оси y.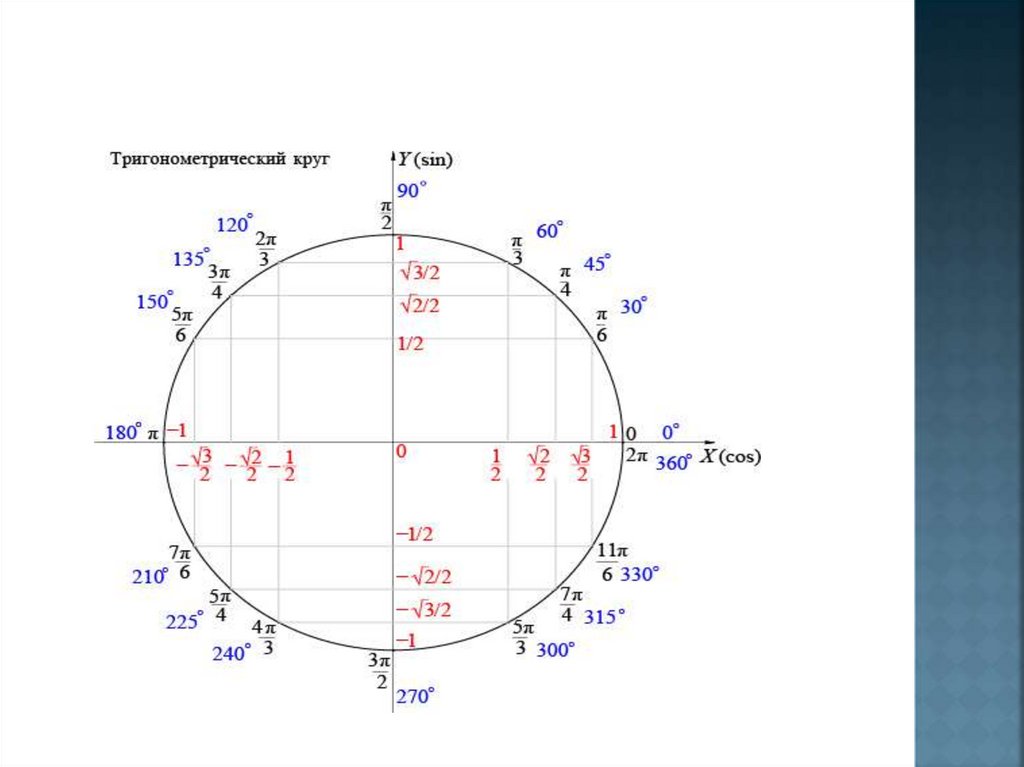 9{-1}(a)}$ — значение функции арккотангенса, обратной функции ограниченной функции котангенса.
9{-1}(a)}$ — значение функции арккотангенса, обратной функции ограниченной функции котангенса.
Теперь мы видим, что решение данного уравнения: $x=\arccot( \frac{1}{2})$ + $k \pi , k \in \mathbf{Z}$.
Пример 5: Вычислите тангенс 60°.
Решение:
Поскольку мы знаем, что $tan(x) = \frac {sin(x)}{cos(x)}$, нам нужно знать только значения $sin(60°)$ и $ cos(60°)$.
Если мы посмотрим на единичный круг, то увидим, что $sin(60°)= \frac{\sqrt{3}}{2}$ и $cos(60°)= \frac{1}{2} $.
Теперь имеем:
$$tan(x) = \frac {sin(60°)}{cos(60°)} = \frac {\frac {\sqrt{3}}{2}}{\ frac{1}{2}}$$
$$=\frac{2 \cdot \sqrt{3}}{2}$$
$$=\sqrt{3}.$$
Тригонометрические функции специальные углы
Специальные углы — это углы, которые имеют относительно простые значения. Следующую таблицу очень важно запомнить. Рассмотрим синус, косинус, тангенс и котангенс:
Этот урок может показаться немного сложным для запоминания, но на самом деле это не так.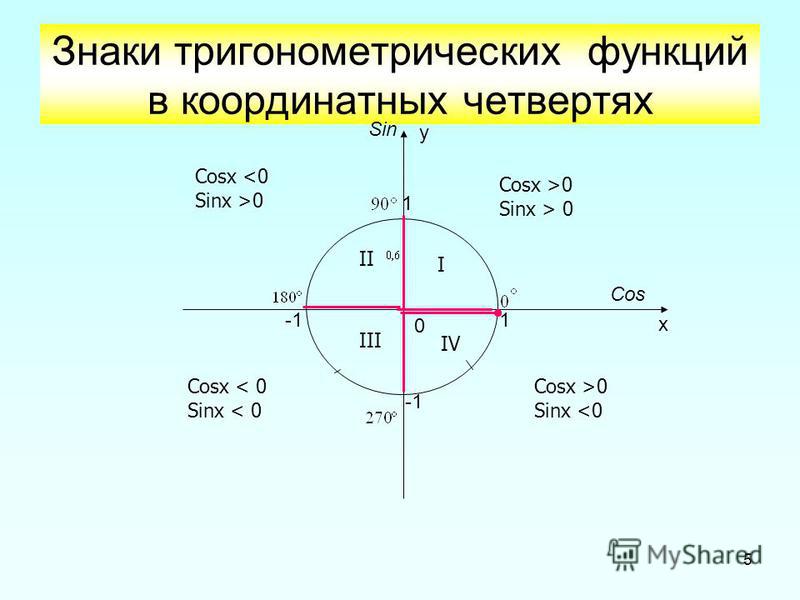

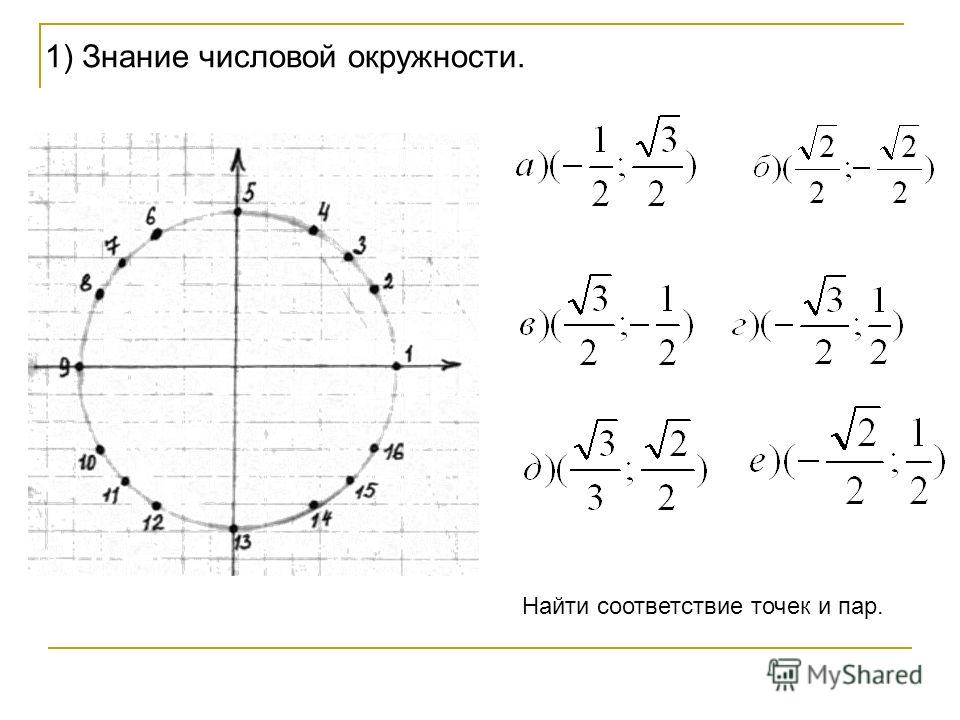 Точка M — искомая.
Точка M — искомая.