Тригонометрические функции | это… Что такое Тригонометрические функции?
Запрос «sin» перенаправляется сюда; см. также другие значения.
Запрос «sec» перенаправляется сюда; см. также другие значения.
Запрос «Синус» перенаправляется сюда; см. также другие значения.
Рис. 1
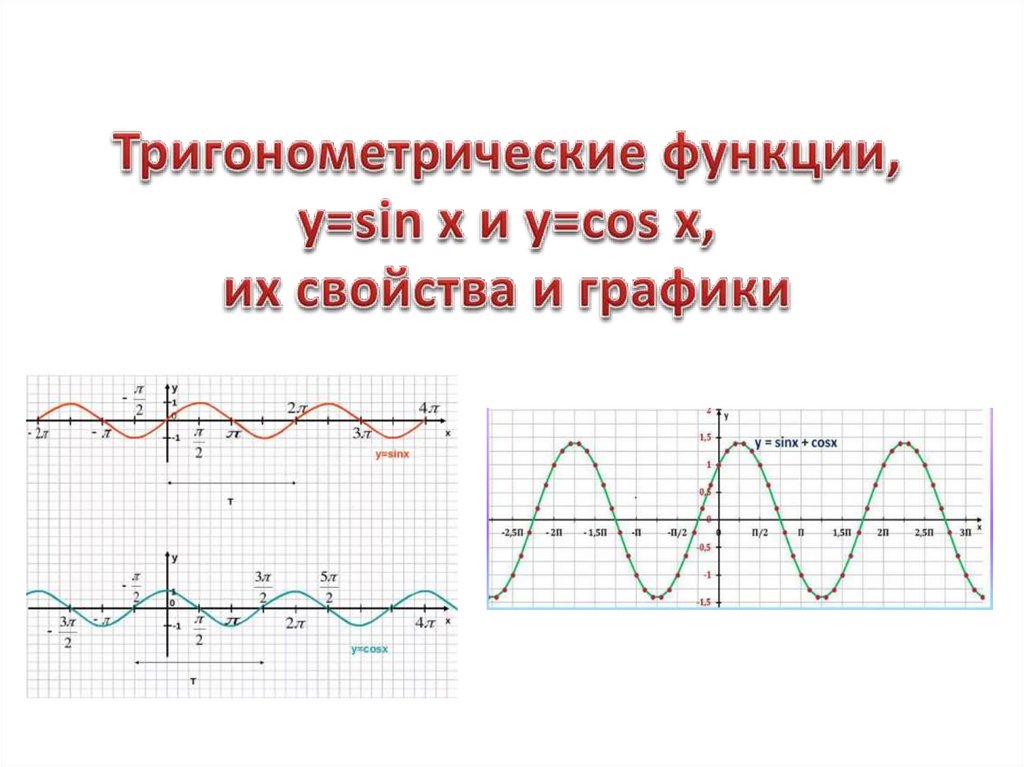
Графики тригонометрических функций: синуса косинуса тангенса котангенса секанса косеканса
Тригонометри́ческие фу́нкции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости сторон этих треугольников от острых углов при гипотенузе (или, что эквивалентно, зависимость хорд и высот от центрального угла в круге). Эти функции нашли широчайшее применение в самых разных областях науки. Впоследствии определение тригонометрических функций было расширено, их аргументом теперь может быть произвольное вещественное или даже комплексное число. Наука, изучающая свойства тригонометрических функций, называется тригонометрией.
К тригонометрическим функциям относятся:
- прямые тригонометрические функции
- синус (sin x)
- косинус (cos x)
- производные тригонометрические функции
- тангенс (tg x)
- котангенс (ctg x)
- другие тригонометрические функции
- секанс (sec x)
- косеканс (cosec x)
В западной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x.
Кроме этих шести, существуют также некоторые редко используемые тригонометрические функции (версинус и т.д.), а также обратные тригонометрические функции (арксинус, арккосинус и т. д.), рассматриваемые в отдельных статьях.
Синус и косинус вещественного аргумента являются периодическими непрерывными и неограниченно дифференцируемыми вещественнозначными функциями. Остальные четыре функции на вещественной оси также вещественнозначные, периодические и неограниченно дифференцируемые на области определения, но не непрерывные.
Содержание
|
Способы определения
Геометрическое определение
Рис. 2
Определение тригонометрических функций
Обычно тригонометрические функции определяются геометрически. Пусть нам дана декартова система координат на плоскости, и построена окружность радиуса R с центром в начале координат O. Измерим углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим xB, ординату обозначим yB (см. рисунок).
рисунок).
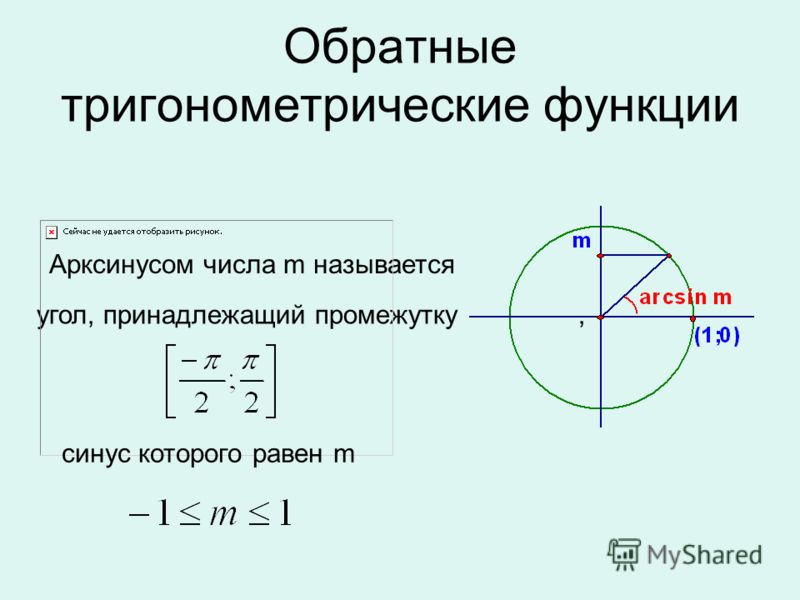
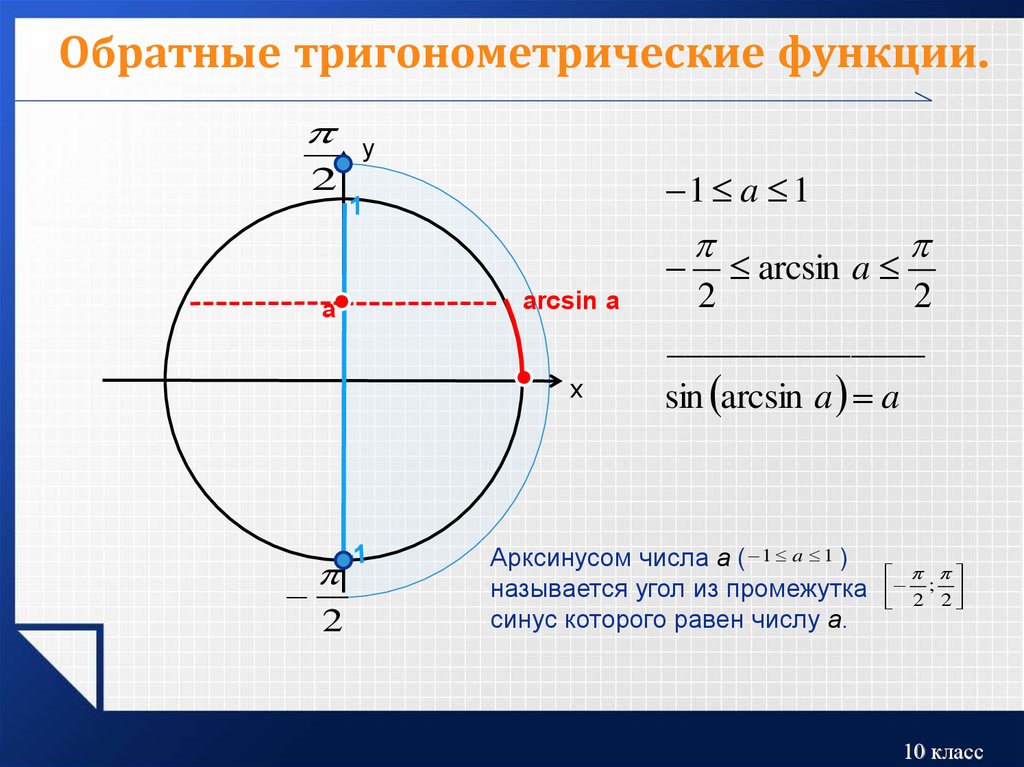
- Синусом называется отношение
- Косинусом называется отношение
- Тангенс определяется как
- Котангенс определяется как
- Секанс определяется как
- Косеканс определяется как
Рис. 3
Численные значения тригонометрических функций угла в тригонометрической окружности с радиусом, равным единице
Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате
Если α — вещественное число, то синусом α в математическом анализе называется синус угла, радианная мера которого равна α, аналогично для прочих тригонометрических функций.
Определение тригонометрических функций для острых углов
Рис. 4
4
Тригонометрические функции острого угла
Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α. Тогда:
- Синусом угла α называется отношение AB/OB (отношение противолежащего катета к гипотенузе).
- Косинусом угла α называется отношение ОА/OB (отношение прилежащего катета к гипотенузе).
- Тангенсом угла α называется отношение AB/OA (отношение противолежащего катета к прилежащему).
- Котангенсом угла α называется отношение ОА/AB (отношение прилежащего катета к противолежащему).
- Секансом угла α называется отношение ОB/OA (отношение гипотенузы к прилежащему катету).
- Косекансом угла α называется отношение ОB/AB (отношение гипотенузы к противолежащему катету).
Построив систему координат с началом в точке O, направлением оси абсцисс вдоль OA и в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее.
Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см.: Теорема синусов, Теорема косинусов).
Определение тригонометрических функций как решений дифференциальных уравнений
Функции косинус и синус можно определить как чётное (косинус) и нечётное (синус) решение дифференциального уравнения
с начальными условиями , то есть как функций одной переменной, вторая производная которых равна самой функции, взятой со знаком минус:
Определение тригонометрических функций как решений функциональных уравнений
Функции косинус и синус можно определить как непрерывные решения (f и g соответственно) системы функциональных уравнений:
Определение тригонометрических функций через ряды
Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде степенны́х рядов:
Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде степенны́х рядов:
Пользуясь этими формулами, а также уравнениями и можно найти разложения в ряд Тейлора и других тригонометрических функций:
где
- — числа Бернулли,
- — числа Эйлера.
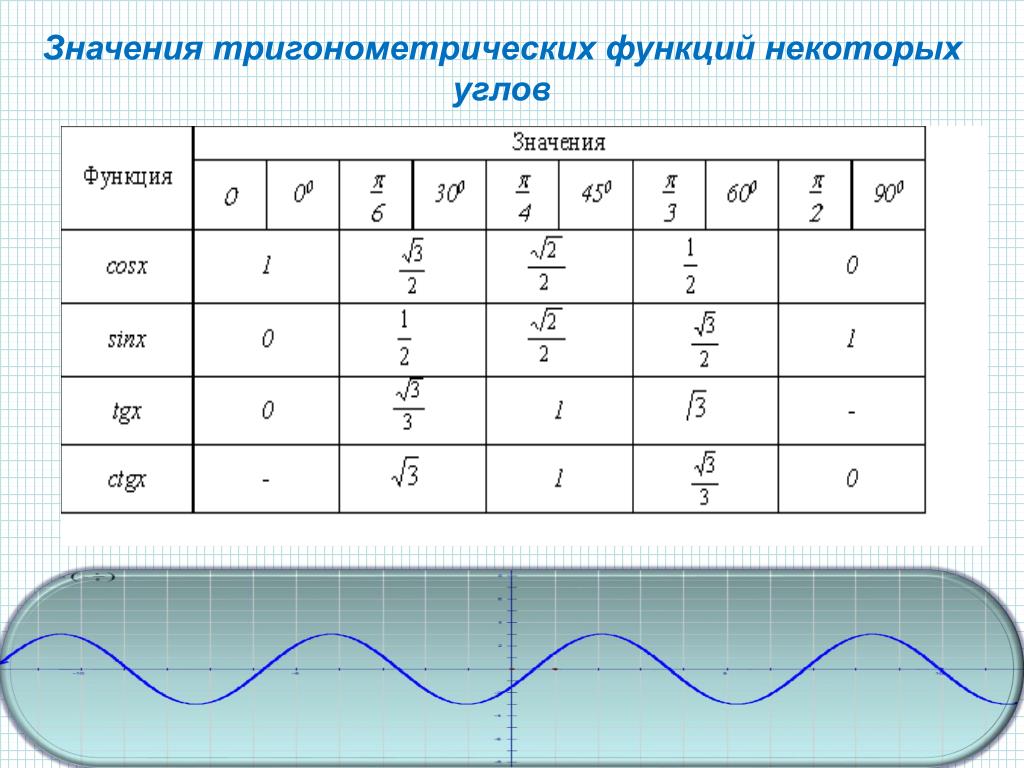
Значения тригонометрических функций для некоторых углов
Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице. («∞» означает, что функция в указанной точке не определена, а в её окрестности стремится к бесконечности).
| 0°(0 рад) | 30° (π/6) | 45° (π/4) | 60° (π/3) | 90° (π/2) | 180° (π) | 270° (3π/2) | 360° (2π) | |
|---|---|---|---|---|---|---|---|---|
Значения косинуса и синуса на окружности.
Значения тригонометрических функций нестандартных углов
Значения тригонометрических функций прочих углов
Свойства тригонометрических функций
Простейшие тождества
Основная статья: Тригонометрические тождества
Поскольку синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α, то, согласно уравнению единичной окружности или теореме Пифагора, имеем:
Это соотношение называется основным тригонометрическим тождеством.
Деля это уравнение на квадрат косинуса и синуса соответственно имеем далее:
Непрерывность
Синус и косинус — непрерывные функции. Тангенс и секанс имеют точки разрыва котангенс и косеканс —
Чётность
Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:
Периодичность
Функции — периодические с периодом 2π, функции и — c периодом π.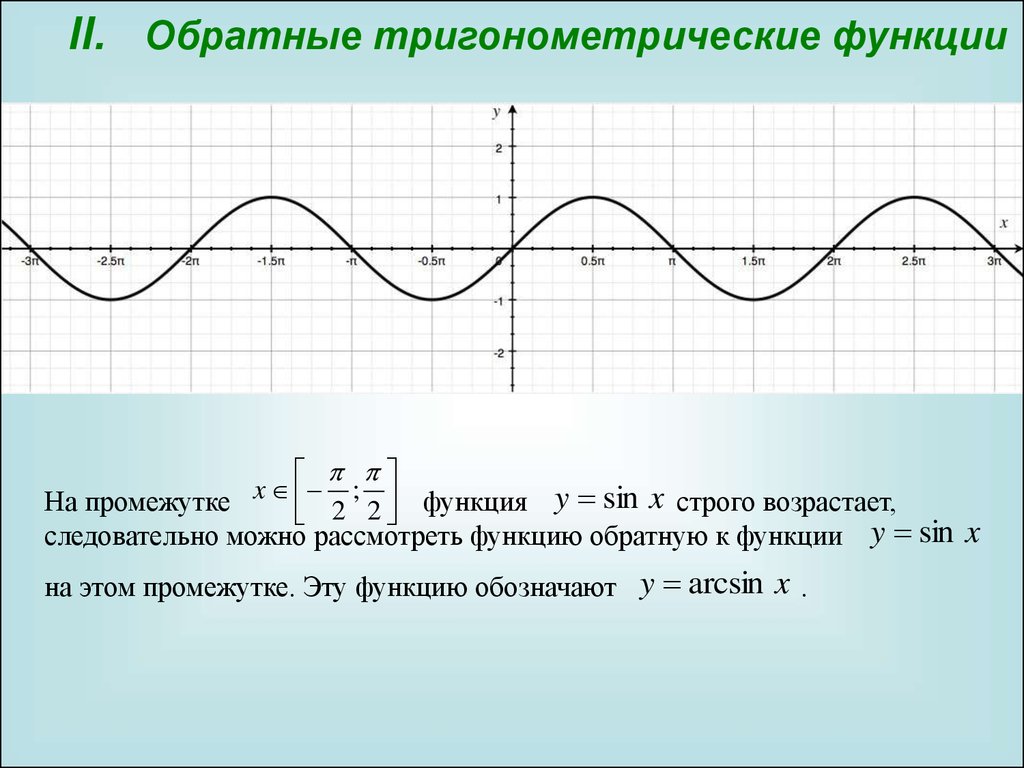
Формулы приведения
Формулами приведения называются формулы следующего вида:
Здесь f — любая тригонометрическая функция, g — соответствующая ей кофункция (то есть косинус для синуса, синус для косинуса, тангенс для котангенса, котангенс для тангенса, секанс для косеканса и косеканс для секанса), n — целое число. Перед полученной функцией ставится тот знак, который имеет исходная функция в заданной координатной четверти при условии, что угол α острый, например:
Некоторые формулы приведения:
Формулы сложения
Значения тригонометрических функций суммы и разности двух углов:
Аналогичные формулы для суммы трёх углов:
Формулы для кратных углов
Формулы двойного угла:
Формулы тройного угла:
Прочие формулы для кратных углов:
- следует из формулы дополнения и формулы Гаусса для Гамма-функции
Формулы половинного угла:
Произведения
Формулы для произведений функций двух углов:
Аналогичные формулы для произведений синусов и косинусов трёх углов:
Формулы для произведений тангенсов и котангенсов трёх углов можно получить, поделив правые и левые части соответствующих равенств, представленных выше.
Степени
Суммы
Для функций от аргумента существует представление:
где угол находится из соотношений:
Однопараметрическое представление
Все тригонометрические функции можно выразить через тангенс половинного угла.
Производные и интегралы
Все тригонометрические функции непрерывно и неограниченно дифференцируемы на всей области определения:
Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:
См. также: Список интегралов от тригонометрических функций
Тригонометрические функции комплексного аргумента
Определение
Формула Эйлера:
позволяет определить тригонометрические функции от комплексных аргументов через экспоненту или (с помощью рядов) как аналитическое продолжение их вещественных аналогов:
- где
Соответственно, для вещественного x,
Комплексные синус и косинус тесно связаны с гиперболическими функциями:
Большинство перечисленных выше свойств тригонометрических функций сохраняются и в комплексном случае.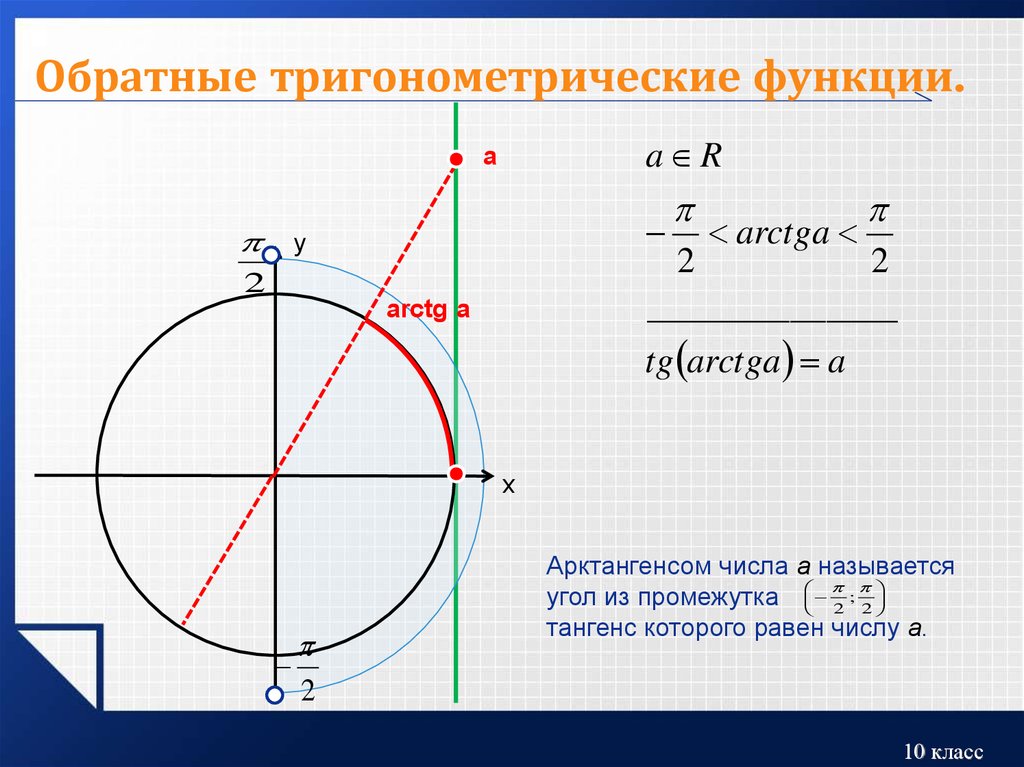 Некоторые дополнительные свойства:
Некоторые дополнительные свойства:
- комплексные синус и косинус, в отличие от вещественных, могут принимать сколь угодно большие по модулю значения;
- все нули комплексных синуса и косинуса лежат на вещественной оси.
Комплексные графики
На следующих графиках изображена комплексная плоскость, а значения функций выделены цветом. Яркость отражает абсолютное значение (чёрный — ноль). Цвет изменяется от аргумента и угла согласно карте.
История названий
Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива», то есть половина хорды), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
Современные краткие обозначения sin и cos введены Уильямом Отредом и закреплены в трудах Эйлера.
Термины «тангенс» (от лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583).
Сам термин тригонометрические функции введён Клюгелем в 1770 году.
См. также
- Гиперболические функции
- Интегральный синус
- Интегральный косинус
- Обратные тригонометрические функции
- Решение треугольников
- Синус-верзус
- Сферическая тригонометрия
- Функция Гудермана
- Четырёхзначные математические таблицы (Таблицы Брадиса)
- Эллиптические функции
Литература
- Бронштейн И.
 Н., Семендяев К. А. Прямолинейная тригонометрия // Справочник по математике. — Изд. 7-е, стереотипное. — М.: Государственное издательство технико-теоретической литературы, 1967. — С. 179—184.
Н., Семендяев К. А. Прямолинейная тригонометрия // Справочник по математике. — Изд. 7-е, стереотипное. — М.: Государственное издательство технико-теоретической литературы, 1967. — С. 179—184. - Г. Б. Двайт Тригонометрические функции // Таблицы интегралов и другие математические формулы. — 4-е изд. — М.: Наука, 1973. — С. 70—102.
Ссылки
- GonioLab — прояснённая единичная окружность, тригонометрические и гиперболические функции (Java Web Start)
- Weisstein, Eric W. Тригонометрические функции (англ.) на сайте Wolfram MathWorld.
- Онлайн калькулятор: вычисление значений тригонометрических функций
- Интерактивная карта значений тригонометрических функций
Тригонометрические функции | это… Что такое Тригонометрические функции?
Запрос «sin» перенаправляется сюда; см. также другие значения.
Запрос «sec» перенаправляется сюда; см. также другие значения.
Запрос «Синус» перенаправляется сюда; см.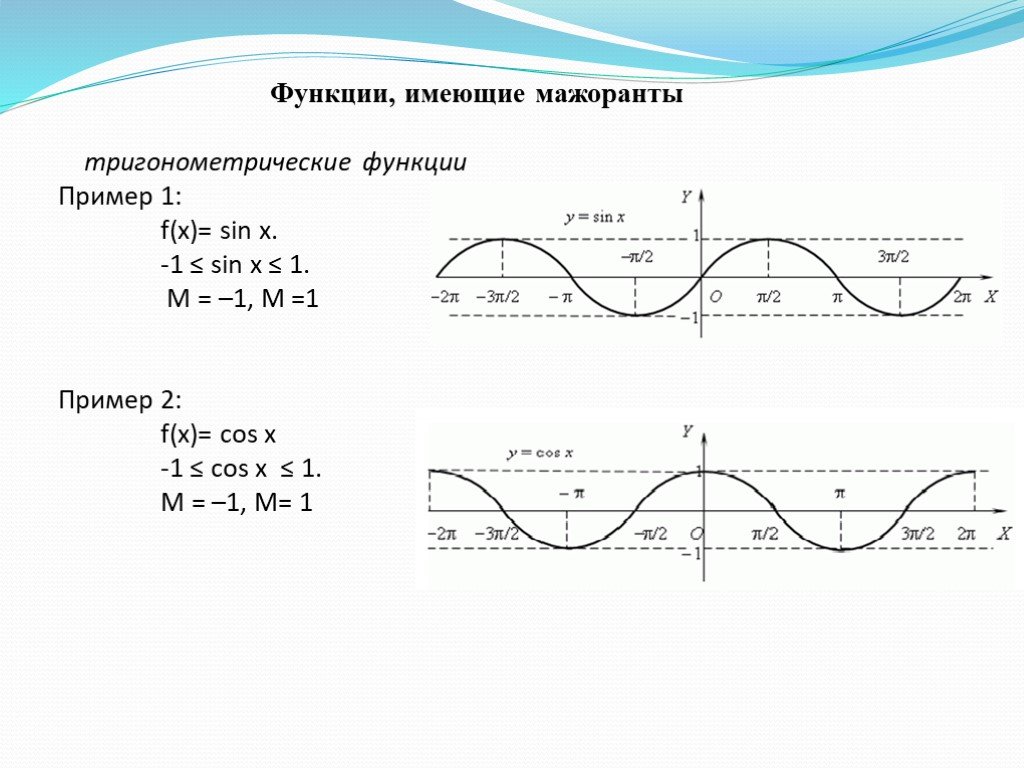 также другие значения.
также другие значения.
Рис. 1
Графики тригонометрических функций: синуса косинуса тангенса котангенса секанса косеканса
Тригонометри́ческие фу́нкции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости сторон этих треугольников от острых углов при гипотенузе (или, что эквивалентно, зависимость хорд и высот от центрального угла в круге). Эти функции нашли широчайшее применение в самых разных областях науки. Впоследствии определение тригонометрических функций было расширено, их аргументом теперь может быть произвольное вещественное или даже комплексное число. Наука, изучающая свойства тригонометрических функций, называется тригонометрией.
К тригонометрическим функциям относятся:
- прямые тригонометрические функции
- синус (sin x)
- косинус (cos x)
- производные тригонометрические функции
- тангенс (tg x)
- котангенс (ctg x)
- другие тригонометрические функции
- секанс (sec x)
- косеканс (cosec x)
В западной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x.
Кроме этих шести, существуют также некоторые редко используемые тригонометрические функции (версинус и т.д.), а также обратные тригонометрические функции (арксинус, арккосинус и т. д.), рассматриваемые в отдельных статьях.
Синус и косинус вещественного аргумента являются периодическими непрерывными и неограниченно дифференцируемыми вещественнозначными функциями. Остальные четыре функции на вещественной оси также вещественнозначные, периодические и неограниченно дифференцируемые на области определения, но не непрерывные. Тангенс и секанс имеют разрывы второго рода в точках ±πn + π/2, а котангенс и косеканс — в точках ±πn.
Содержание
|
Способы определения
Геометрическое определение
Рис. 2
Определение тригонометрических функций
Обычно тригонометрические функции определяются геометрически. Пусть нам дана декартова система координат на плоскости, и построена окружность радиуса R с центром в начале координат O. Измерим углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим xB, ординату обозначим yB (см. рисунок).
Пусть нам дана декартова система координат на плоскости, и построена окружность радиуса R с центром в начале координат O. Измерим углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим xB, ординату обозначим yB (см. рисунок).
- Синусом называется отношение
- Косинусом называется отношение
- Тангенс определяется как
- Котангенс определяется как
- Секанс определяется как
- Косеканс определяется как
Рис. 3
Численные значения тригонометрических функций угла в тригонометрической окружности с радиусом, равным единице
Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате yB, а косинус — абсциссе xB. На рисунке 3 показаны величины тригонометрических функций для единичной окружности.
На рисунке 3 показаны величины тригонометрических функций для единичной окружности.
Если α — вещественное число, то синусом α в математическом анализе называется синус угла, радианная мера которого равна α, аналогично для прочих тригонометрических функций.
Определение тригонометрических функций для острых углов
Рис. 4
Тригонометрические функции острого угла
Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α. Тогда:
- Синусом угла α называется отношение AB/OB (отношение противолежащего катета к гипотенузе).
- Косинусом угла α называется отношение ОА/OB (отношение прилежащего катета к гипотенузе).
- Тангенсом угла α называется отношение AB/OA (отношение противолежащего катета к прилежащему).
- Котангенсом угла α называется отношение ОА/AB (отношение прилежащего катета к противолежащему).

- Секансом угла α называется отношение ОB/OA (отношение гипотенузы к прилежащему катету).
- Косекансом угла α называется отношение ОB/AB (отношение гипотенузы к противолежащему катету).
Построив систему координат с началом в точке O, направлением оси абсцисс вдоль OA и в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее.
Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см.: Теорема синусов, Теорема косинусов).
Определение тригонометрических функций как решений дифференциальных уравнений
Функции косинус и синус можно определить как чётное (косинус) и нечётное (синус) решение дифференциального уравнения
с начальными условиями , то есть как функций одной переменной, вторая производная которых равна самой функции, взятой со знаком минус:
Определение тригонометрических функций как решений функциональных уравнений
Функции косинус и синус можно определить как непрерывные решения (f и g соответственно) системы функциональных уравнений:
Определение тригонометрических функций через ряды
Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу.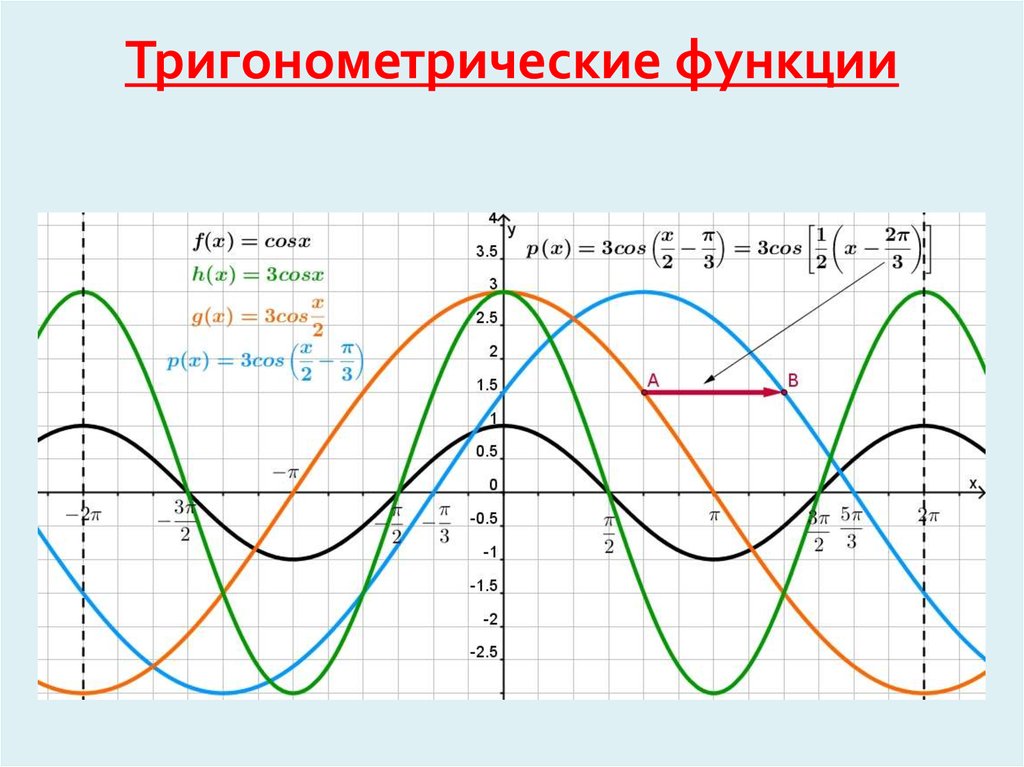 Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде степенны́х рядов:
Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде степенны́х рядов:
Пользуясь этими формулами, а также уравнениями и можно найти разложения в ряд Тейлора и других тригонометрических функций:
где
- — числа Бернулли,
- — числа Эйлера.
Значения тригонометрических функций для некоторых углов
Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице. («∞» означает, что функция в указанной точке не определена, а в её окрестности стремится к бесконечности).
| 0°(0 рад) | 30° (π/6) | 45° (π/4) | 60° (π/3) | 90° (π/2) | 180° (π) | 270° (3π/2) | 360° (2π) | |
|---|---|---|---|---|---|---|---|---|
Значения косинуса и синуса на окружности.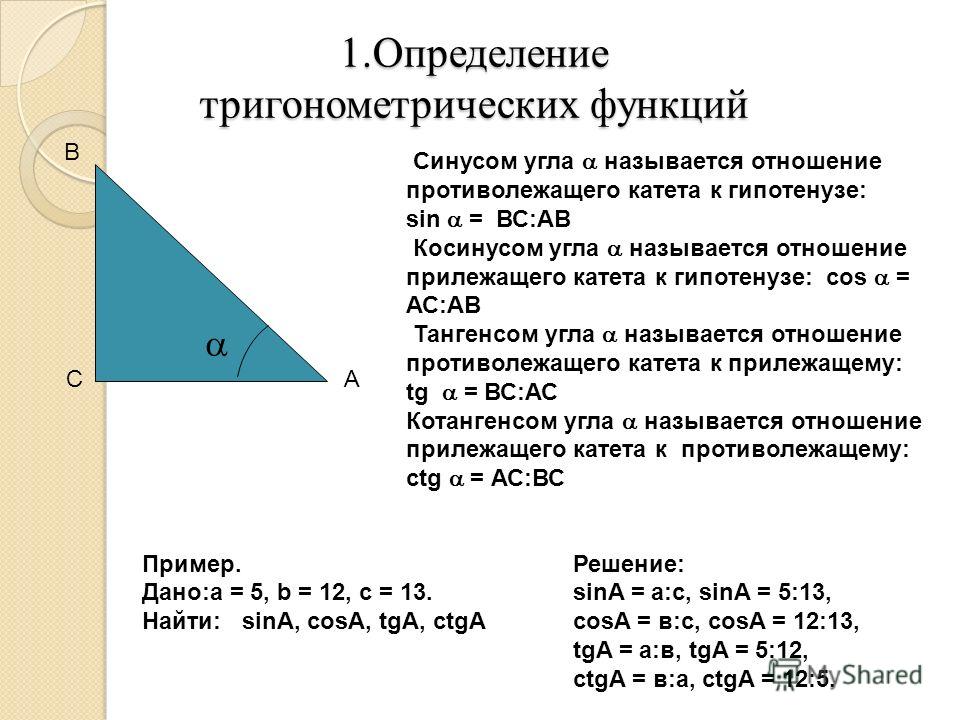
Значения тригонометрических функций нестандартных углов
Значения тригонометрических функций прочих углов
Свойства тригонометрических функций
Простейшие тождества
Основная статья: Тригонометрические тождества
Поскольку синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α, то, согласно уравнению единичной окружности или теореме Пифагора, имеем:
Это соотношение называется основным тригонометрическим тождеством.
Деля это уравнение на квадрат косинуса и синуса соответственно имеем далее:
Непрерывность
Синус и косинус — непрерывные функции. Тангенс и секанс имеют точки разрыва котангенс и косеканс —
Чётность
Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:
Периодичность
Функции — периодические с периодом 2π, функции и — c периодом π.
Формулы приведения
Формулами приведения называются формулы следующего вида:
Здесь f — любая тригонометрическая функция, g — соответствующая ей кофункция (то есть косинус для синуса, синус для косинуса, тангенс для котангенса, котангенс для тангенса, секанс для косеканса и косеканс для секанса), n — целое число. Перед полученной функцией ставится тот знак, который имеет исходная функция в заданной координатной четверти при условии, что угол α острый, например:
Некоторые формулы приведения:
Формулы сложения
Значения тригонометрических функций суммы и разности двух углов:
Аналогичные формулы для суммы трёх углов:
Формулы для кратных углов
Формулы двойного угла:
Формулы тройного угла:
Прочие формулы для кратных углов:
- следует из формулы дополнения и формулы Гаусса для Гамма-функции
Формулы половинного угла:
Произведения
Формулы для произведений функций двух углов:
Аналогичные формулы для произведений синусов и косинусов трёх углов:
Формулы для произведений тангенсов и котангенсов трёх углов можно получить, поделив правые и левые части соответствующих равенств, представленных выше.
Степени
Суммы
Для функций от аргумента существует представление:
где угол находится из соотношений:
Однопараметрическое представление
Все тригонометрические функции можно выразить через тангенс половинного угла.
Производные и интегралы
Все тригонометрические функции непрерывно и неограниченно дифференцируемы на всей области определения:
Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:
См. также: Список интегралов от тригонометрических функций
Тригонометрические функции комплексного аргумента
Определение
Формула Эйлера:
позволяет определить тригонометрические функции от комплексных аргументов через экспоненту или (с помощью рядов) как аналитическое продолжение их вещественных аналогов:
- где
Соответственно, для вещественного x,
Комплексные синус и косинус тесно связаны с гиперболическими функциями:
Большинство перечисленных выше свойств тригонометрических функций сохраняются и в комплексном случае. Некоторые дополнительные свойства:
Некоторые дополнительные свойства:
- комплексные синус и косинус, в отличие от вещественных, могут принимать сколь угодно большие по модулю значения;
- все нули комплексных синуса и косинуса лежат на вещественной оси.
Комплексные графики
На следующих графиках изображена комплексная плоскость, а значения функций выделены цветом. Яркость отражает абсолютное значение (чёрный — ноль). Цвет изменяется от аргумента и угла согласно карте.
История названий
Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива», то есть половина хорды), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба».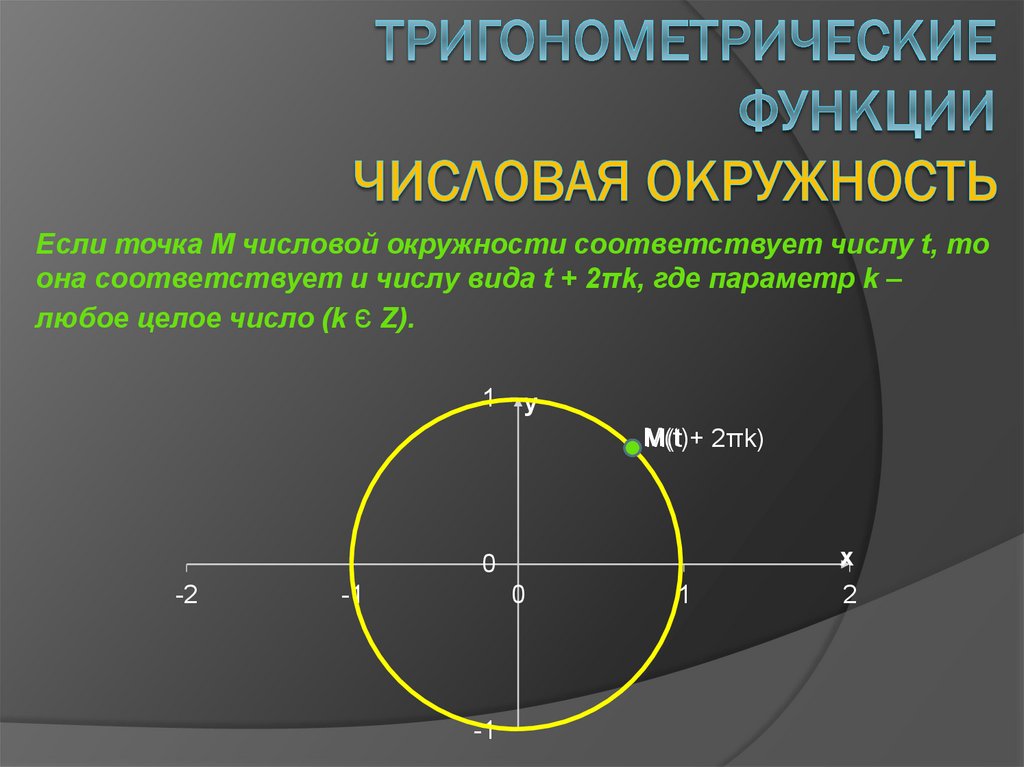 Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
Современные краткие обозначения sin и cos введены Уильямом Отредом и закреплены в трудах Эйлера.
Термины «тангенс» (от лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583).
Сам термин тригонометрические функции введён Клюгелем в 1770 году.
См. также
- Гиперболические функции
- Интегральный синус
- Интегральный косинус
- Обратные тригонометрические функции
- Решение треугольников
- Синус-верзус
- Сферическая тригонометрия
- Функция Гудермана
- Четырёхзначные математические таблицы (Таблицы Брадиса)
- Эллиптические функции
Литература
- Бронштейн И.
 Н., Семендяев К. А. Прямолинейная тригонометрия // Справочник по математике. — Изд. 7-е, стереотипное. — М.: Государственное издательство технико-теоретической литературы, 1967. — С. 179—184.
Н., Семендяев К. А. Прямолинейная тригонометрия // Справочник по математике. — Изд. 7-е, стереотипное. — М.: Государственное издательство технико-теоретической литературы, 1967. — С. 179—184. - Г. Б. Двайт Тригонометрические функции // Таблицы интегралов и другие математические формулы. — 4-е изд. — М.: Наука, 1973. — С. 70—102.
Ссылки
- GonioLab — прояснённая единичная окружность, тригонометрические и гиперболические функции (Java Web Start)
- Weisstein, Eric W. Тригонометрические функции (англ.) на сайте Wolfram MathWorld.
- Онлайн калькулятор: вычисление значений тригонометрических функций
- Интерактивная карта значений тригонометрических функций
1.3: Тригонометрические функции — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2479
- Гилберт Странг и Эдвин «Джед» Герман
- ОпенСтакс
Цели обучения
- Преобразование угловых единиц из градусов в радианы.

- Распознавать треугольные и круговые определения основных тригонометрических функций.
- Запишите основные тригонометрические тождества.
- Определите графики и периоды тригонометрических функций.
- Опишите сдвиг графика синуса или косинуса из уравнения функции.
Тригонометрические функции используются для моделирования многих явлений, включая звуковые волны, колебания струн, переменный электрический ток и движение маятников. На самом деле почти любое повторяющееся или циклическое движение можно смоделировать с помощью некоторой комбинации тригонометрических функций. В этом разделе мы определим шесть основных тригонометрических функций и рассмотрим некоторые основные тождества, включающие эти функции.
Радиан Измерение
Чтобы использовать тригонометрические функции, мы сначала должны понять, как измерять углы. Хотя мы можем использовать как радианы, так и градусы, радиан являются более естественным измерением, потому что они связаны непосредственно с единичной окружностью, окружностью с радиусом 1. Радианная мера угла определяется следующим образом. Для заданного угла \(θ\) пусть \(s\) будет длиной соответствующей дуги на единичной окружности (рис. \(\PageIndex{1}\)). Мы говорим, что угол, соответствующий дуге длины 1, имеет радианную меру 1,9.0046 Рисунок \(\PageIndex{1}\): Мерой угла \(θ\) в радианах является длина дуги \(s\) соответствующей дуги на единичной окружности.
Радианная мера угла определяется следующим образом. Для заданного угла \(θ\) пусть \(s\) будет длиной соответствующей дуги на единичной окружности (рис. \(\PageIndex{1}\)). Мы говорим, что угол, соответствующий дуге длины 1, имеет радианную меру 1,9.0046 Рисунок \(\PageIndex{1}\): Мерой угла \(θ\) в радианах является длина дуги \(s\) соответствующей дуги на единичной окружности.
Так как угол \(360°\) соответствует окружности окружности или дуге длиной \(2π\), мы заключаем, что угол с градусной мерой \(360°\) имеет радианную меру из \(2π\). Точно так же мы видим, что \(180°\) эквивалентно \(\pi\) радианам. В таблице \(\PageIndex{1}\) показано соотношение между обычными значениями в градусах и радианах.
| Градусов | радиан | градусов | радиан |
|---|---|---|---|
| 0 | 0 | 120 | \(2π/3\) |
| 30 | \(π/6\) | 135 | \(3π/4\) |
| 45 | \(π/4\) | 150 | \(5π/6\) |
| 60 | \(π/3\) | 180 | \(π\) |
| 90 | \(π/2\) |
Преобразование радианов в градусы
- Выразите \(225°\) в радианах.

- Выразите \(5π/3\) рад в градусах.
Решение
Используйте тот факт, что \(180\)° эквивалентно \(\pi\) радианам, как коэффициент преобразования (Таблица \(\PageIndex{1}\)):
\[ 1=\dfrac{π \,\mathrm{rad}}{180°}=\dfrac{180°}{π \,\mathrm{rad}}. \nonumber \]
- \(225°=225°⋅\left(\dfrac{π}{180°}\right)=\left(\dfrac{5π}{4}\right)\) рад
- \(\dfrac{5π}{3}\) рад = \(\dfrac{5π}{3}\)⋅\(\dfrac{180°}{π}\)=\(300\)°
Упражнение \(\PageIndex{1}\)
- Выразите \(210°\) в радианах.
- Выразите \(11π/6\) рад в градусах.
- Подсказка
\(π\) радиан равно 180°
- Ответить
- \(7π/6\)
- 330°
Шесть основных тригонометрических функций
Тригонометрические функции позволяют нам использовать угловые измерения в радианах или градусах для нахождения координат точки на любой окружности — не только на единичной окружности — или для нахождения угла по заданной точке на круг.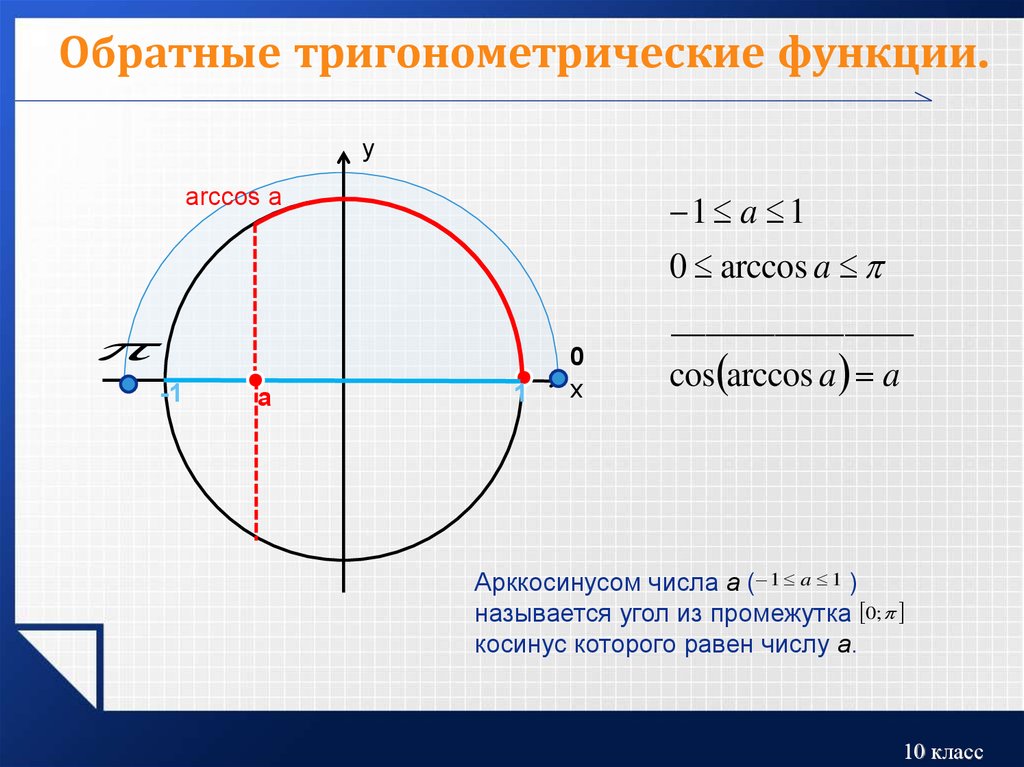 Они также определяют отношения между сторонами и углами треугольника.
Они также определяют отношения между сторонами и углами треугольника.
Чтобы определить тригонометрические функции, сначала рассмотрим единичную окружность с центром в начале координат и точку \(P=(x,y)\) на единичной окружности. Пусть \(θ\) — угол с начальной стороной, лежащей вдоль положительной оси \(x\), и с конечной стороной, являющейся отрезком \(OP\). Говорят, что угол в этом положении находится в стандартном положении (рисунок \(\PageIndex{2}\)). Затем мы можем определить значения шести тригонометрических функций для \(θ\) в терминах координат \(x\) и \(y\).
Рисунок \(\PageIndex{2}\): Угол \(θ\) находится в стандартном положении. Значения тригонометрических функций для \(0\) определяются через координаты \(х\) и \(у\).Определение: тригонометрические функции
Пусть \(P=(x,y)\) — точка на единичной окружности с центром в начале координат \(O\). Пусть \(θ\) — угол с начальной стороной вдоль положительной оси \(x\) и конечной стороной, заданной отрезком \(OP\). Тогда тригонометрические функции определяются как
Тогда тригонометрические функции определяются как
| \(\sin θ=y\) | \(\csc θ=\dfrac{1}{y}\) |
| \(\cos θ=x\) | \(\сек θ=\dfrac{1}{x}\) |
| \(\tan θ=\dfrac{y}{x}\) | \(\cot θ=\dfrac{x}{y}\) |
Если \(x=0, \sec θ\) и \(\tan θ\) не определены. Если \(y=0\), то \(\cot θ\) и \(\csc θ\) не определены.
Мы видим, что для точки \(P=(x,y)\) на окружности радиуса \(r\) с соответствующим углом \(θ\) координаты \(x\) и \( y\) удовлетворяют
\[\begin{align} \cos θ &=\dfrac{x}{r} \\ x &=r\cos θ \end{align} \nonumber \]
и
\[\begin{align} \sin θ &=\dfrac{y}{r} \\ y &=r\sin θ. \end{align} \nonumber \]
Значения других тригонометрических функций могут быть выражены через \(x,y\) и \(r\) (рис. \(\PageIndex{3}\)) .
Рисунок \(\PageIndex{3}\): Для точки \(P=(x,y)\) на окружности радиуса \(r\) координаты \(x\) и \(y\) удовлетворяют \(x=r\cos θ\) и \(y=r\sin θ\).
В таблице \(\PageIndex{2}\) показаны значения синуса и косинуса больших углов в первом квадранте. Из этой таблицы мы можем определить значения синуса и косинуса при соответствующих углах в других квадрантах. Значения других тригонометрических функций легко вычисляются по значениям \(\sin θ\) и \(\cos θ.\)
| \(θ\) θ | \(\sinθ\) | \(\cos θ\) |
|---|---|---|
| 0 | 0 | 1 |
| \(\dfrac{π}{6}\) | \(\dfrac{1}{2}\) | \(\dfrac{\sqrt{3}}{2}\) |
| \(\dfrac{π}{4}\) | \(\dfrac{\sqrt{2}}{2}\) | \(\dfrac{\sqrt{2}}{2}\) |
| \(\dfrac{π}{3}\) | \(\dfrac{\sqrt{3}}{2}\) | \(\dfrac{1}{2}\) |
| \(\dfrac{π}{2}\) | 1 | 0 |
Пример \(\PageIndex{2}\): вычисление тригонометрических функций
Оцените каждое из следующих выражений.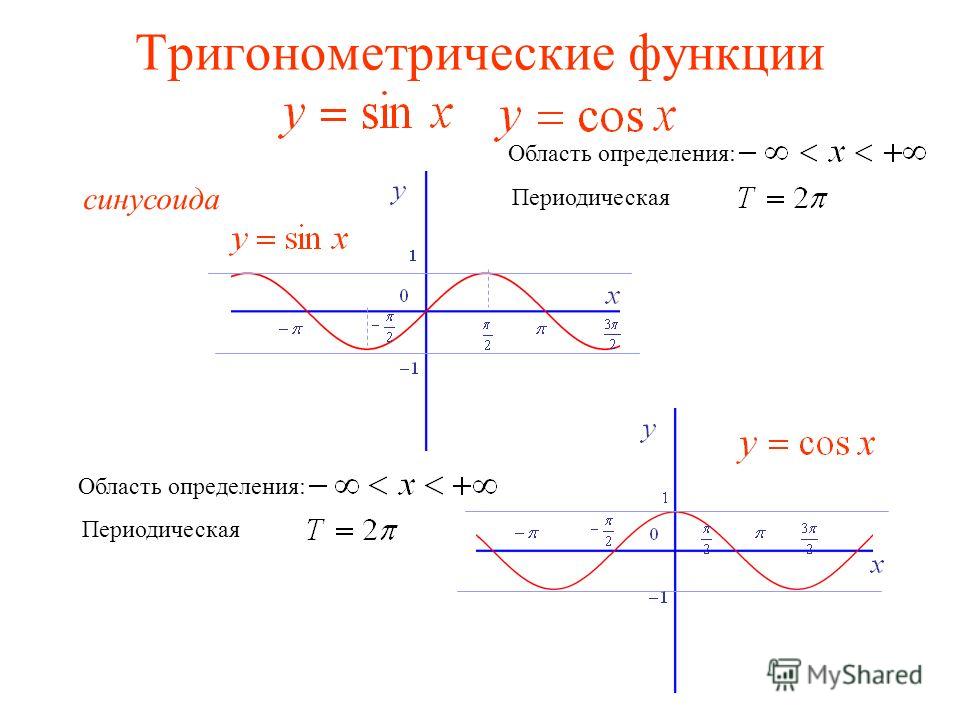
- \(\sin\left(\dfrac{2π}{3}\right)\)
- \(\cos\влево(-\dfrac{5π}{6}\вправо)\)
- \(\тангенс \влево(\dfrac{15π}{4}\вправо)\)
Решение :
а) На единичной окружности угол \(θ=\dfrac{2π}{3}\) соответствует точке \(\left(−\dfrac{1}{2}, \dfrac{\sqrt{3}}{2}\right)\). Следовательно,
\[ \sin \left(\dfrac{2π}{3}\right)=y=\left(\dfrac{\sqrt{3}}{2}\right). \номер\]
b) Угол \(θ=−\dfrac{5π}{6}\) соответствует обороту в отрицательном направлении, как показано. Следовательно,
\[\cos \left(−\dfrac{5π}{6}\right)=x=-\dfrac{\sqrt{3}}{2}. \nonumber \]
c) Угол \(θ\)=\(\dfrac{15π}{4}\)=\(2π\)+\(\dfrac{7π}{4}\). Следовательно, этот угол соответствует более чем одному обороту, как показано. Зная тот факт, что угол \(\dfrac{7π}{4}\) соответствует точке \((\dfrac{\sqrt{2}}{2},-\dfrac{\sqrt{2}}{ 2})\), можно сделать вывод, что
\[\tan \left(\dfrac{15π}{4}\right)=\dfrac{y}{x}=−1. \nonumber \]
\nonumber \]
Упражнение \(\PageIndex{2}\)
Вычислить \(\cos(3π/4)\) и \(\sin(−π/6)\).
- Подсказка
Посмотрите на углы единичной окружности.
- Ответить
\[\cos(3π/4) = −\sqrt{2}/2\номер \]
\[ \sin(-π/6) =-1/2 \не число \]
Как упоминалось ранее, отношения длин сторон прямоугольного треугольника могут быть выражены через тригонометрические функции, вычисленные для любого из острых углов треугольника. Пусть \(0\) — один из острых углов. Пусть \(А\) — длина соседнего катета, \(О\) — длина противоположного катета, а \(Н\) — длина гипотенузы. Вписывая треугольник в окружность радиуса \(H\), как показано на рисунке \(\PageIndex{4}\), мы видим, что \(A,H\) и \(O\) удовлетворяют следующим соотношениям с \(θ\):
| \(\sin θ=\dfrac{O}{H}\) | \(\csc θ=\dfrac{H}{O}\) |
| \(\cos θ=\dfrac{A}{H}\) | \(\сек θ=\dfrac{H}{A}\) |
| \(\tan θ=\dfrac{O}{A}\) | \(\cot θ=\dfrac{A}{O}\) |
Пример \(\PageIndex{3}\): Строительство деревянного пандуса
Деревянный пандус должен быть построен так, чтобы один конец был на земле, а другой конец находился наверху короткой лестницы. Если вершина лестницы находится в \(4\) футах от земли, а угол между землей и пандусом должен быть \(10\)°, какой длины должен быть пандус?
Решение
Пусть \(x\) обозначает длину пандуса. На следующем изображении мы видим, что \(x\) должно удовлетворять уравнению \(\sin(10°)=4/x\). Решая это уравнение относительно \(x\), мы видим, что \(x=4/\sin(10°)\)≈\(23,035\) футов
Упражнение \(\PageIndex{3}\)
Маляр хочет прислонить \(20\)-футовую лестницу к дому. Если угол между основанием лестницы и землей должен быть \(60\)°, на каком расстоянии от дома она должна расположить основание лестницы?
- Подсказка
Нарисуйте прямоугольный треугольник с гипотенузой 20.
- Ответить
10 футов
Тригонометрические тождества
Тригонометрическое тождество — это уравнение, включающее тригонометрические функции, которое истинно для всех углов \(θ\), для которых определены функции. Мы можем использовать тождества, чтобы решить или упростить уравнения. Далее перечислены основные тригонометрические тождества.
Мы можем использовать тождества, чтобы решить или упростить уравнения. Далее перечислены основные тригонометрические тождества.
Тригонометрические тождества
Взаимные тождества
\[\tan θ=\dfrac{\sin θ}{\cos θ} \nonumber \]
\[\cot θ=\dfrac{\cos θ}{ \sin θ} \номер\] 92θ \end{align} \nonumber \]
Пример \(\PageIndex{4}\): Решение тригонометрических уравнений
Для каждого из следующих уравнений используйте тригонометрическое тождество, чтобы найти все решения.
- \(1+\cos(2θ)=\cosθ\)
- \(\sin(2θ)=\tan θ\)
Решение
а) Используя формулу двойного угла для \(\cos(2θ)\), мы видим, что \(θ\) является решением
\[1+\cos(2θ)= \cos θ \nonumber \]
тогда и только тогда, когда 92θ−\cosθ=0. \nonumber \]
Чтобы решить это уравнение, важно отметить, что нам нужно разложить левую часть на множители, а не делить обе части уравнения на \(\cos θ\). Проблема с делением на \(\cos θ\) заключается в том, что возможно, что \(\cos θ\) равно нулю. На самом деле, если бы мы разделили обе части уравнения на \(\cos θ\), мы бы упустили некоторые решения исходного уравнения. Разлагая на множители левую часть уравнения, мы видим, что \(0\) является решением этого уравнения тогда и только тогда, когда
Проблема с делением на \(\cos θ\) заключается в том, что возможно, что \(\cos θ\) равно нулю. На самом деле, если бы мы разделили обе части уравнения на \(\cos θ\), мы бы упустили некоторые решения исходного уравнения. Разлагая на множители левую часть уравнения, мы видим, что \(0\) является решением этого уравнения тогда и только тогда, когда
\[\cos θ(2\cos θ−1)=0. \nonumber \]
Поскольку \(\cos θ=0\), когда
\[θ=\dfrac{π}{2},\dfrac{π}{2}±π,\dfrac{π}{2 }±2π,…, \nonumber \]
и \(\cos θ=1/2\), когда
\[θ=\dfrac{π}{3},\dfrac{π}{3}±2π ,…\mathrm{or}\ θ=−\dfrac{π}{3},−\dfrac{π}{3}±2π,…, \nonumber \]
заключаем, что множество решений этого уравнения равно
\[θ=\dfrac{π}{2}+nπ,\;θ=\dfrac{π}{3}+2nπ \nonumber \]
и
\[θ=−\dfrac{π {3}+2nπ,\;n=0,±1,±2,….\номер \] 92θ−\sinθ=0. \nonumber \]
Однако здесь нужно быть немного осторожным. Даже если \(θ\) удовлетворяет этому новому уравнению, оно может не удовлетворять исходному уравнению, потому что для удовлетворения исходному уравнению нам нужно было бы иметь возможность разделить обе части уравнения на \(\cos θ\). Однако, если \(\cos θ=0\), мы не можем разделить обе части уравнения на \(\cos θ\). Поэтому не исключено, что мы придем к посторонним решениям. Итак, в конце важно проверить наличие посторонних решений. Возвращаясь к уравнению, важно, чтобы мы факторизовали \(\sin θ\) из обоих членов в левой части вместо того, чтобы делить обе части уравнения на \(\sin θ\). Факторизируя левую часть уравнения, мы можем переписать это уравнение как 92θ=1/2\). Решениями первого уравнения являются \(θ=0,±π,±2π,….\). Решениями второго уравнения являются \(θ=π/4,(π/4)±(π/2), (π/4)±π,….\) После проверки на наличие посторонних решений множество решений уравнения равно
Однако, если \(\cos θ=0\), мы не можем разделить обе части уравнения на \(\cos θ\). Поэтому не исключено, что мы придем к посторонним решениям. Итак, в конце важно проверить наличие посторонних решений. Возвращаясь к уравнению, важно, чтобы мы факторизовали \(\sin θ\) из обоих членов в левой части вместо того, чтобы делить обе части уравнения на \(\sin θ\). Факторизируя левую часть уравнения, мы можем переписать это уравнение как 92θ=1/2\). Решениями первого уравнения являются \(θ=0,±π,±2π,….\). Решениями второго уравнения являются \(θ=π/4,(π/4)±(π/2), (π/4)±π,….\) После проверки на наличие посторонних решений множество решений уравнения равно
\[θ=nπ \nonumber \]
и
\[θ=\dfrac{π }{4}+\dfrac{nπ}{2} \nonumber \]
с \(n=0,±1,±2,….\)
Упражнение \(\PageIndex{4}\)
Найти все решения уравнения \(\cos(2θ)=\sin θ.\)
- Подсказка 920\).
Графики и периоды тригонометрических функций
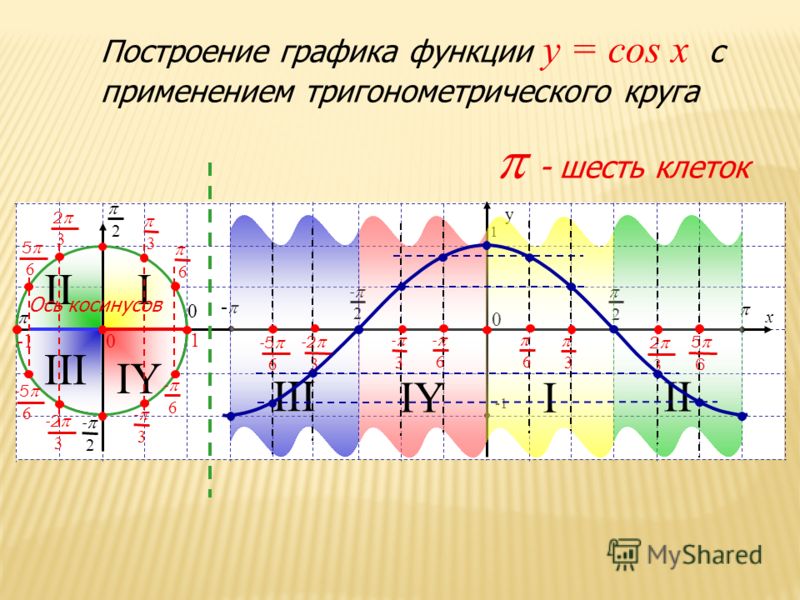
Мы видели, что при движении по единичной окружности значения тригонометрических функций повторяются. Мы можем видеть эту закономерность на графиках функций. Пусть \(P=(x,y)\) — точка на единичной окружности, а \(θ\) — соответствующий угол . Поскольку угол \(θ\) и \(θ+2π\) соответствуют одной и той же точке \(P\), значения тригонометрических функций в точках \(θ\) и в точках \(θ+2π\) равны такой же. Следовательно, тригонометрические функции равны периодические функции . Период функции \(f\) определяется как наименьшее положительное значение \(p\), такое что \(f(x+p)=f(x)\) для всех значений \(x\) в домен \(f\). Функции синуса, косинуса, секанса и косеканса имеют период \(2π\). Поскольку функции тангенса и котангенса повторяются на интервале длины \(π\), их период равен \(π\) (рис. \(\PageIndex{5}\)).
Мы можем видеть эту закономерность на графиках функций. Пусть \(P=(x,y)\) — точка на единичной окружности, а \(θ\) — соответствующий угол . Поскольку угол \(θ\) и \(θ+2π\) соответствуют одной и той же точке \(P\), значения тригонометрических функций в точках \(θ\) и в точках \(θ+2π\) равны такой же. Следовательно, тригонометрические функции равны периодические функции . Период функции \(f\) определяется как наименьшее положительное значение \(p\), такое что \(f(x+p)=f(x)\) для всех значений \(x\) в домен \(f\). Функции синуса, косинуса, секанса и косеканса имеют период \(2π\). Поскольку функции тангенса и котангенса повторяются на интервале длины \(π\), их период равен \(π\) (рис. \(\PageIndex{5}\)).
Как и в случае с алгебраическими функциями, мы можем применять преобразования к тригонометрическим функциям. В частности, рассмотрим следующую функцию:
\[f(x)=A\sin(B(x−α))+C. \nonumber \]
\nonumber \]
На рисунке \(\PageIndex{6}\) константа \(α\) вызывает сдвиг по горизонтали или фазе. Множитель \(B\) изменяет период. Эта преобразованная синусоидальная функция будет иметь период \(2π/|B|\). Множитель \(A\) приводит к вертикальному растяжению с коэффициентом \(|A|\). Мы говорим, что \(|A|\) — это «амплитуда \(f\)». Константа \(C\) вызывает сдвиг по вертикали.
Рисунок \(\PageIndex{6}\): График функции общего синуса.Обратите внимание на рисунок \(\PageIndex{6}\), что график \(y=\cos x\) является графиком \(y=\sin x\), сдвинутым влево \(π/2\) единицы. Следовательно, мы можем написать
\[\cos x=\sin(x+π/2). \nonumber \]
Точно так же мы можем рассматривать график \(y=\sin x\) как график \(y=\cos x\), сдвинутый вправо на \(π/2\) единиц, и заявить, что \(\sin x=\cos(x−π/2).\)
Смещенная синусоида возникает естественным образом при построении графика количества часов дневного света в данном месте в зависимости от дня года. Например, предположим, что город сообщает, что 21 июня — самый длинный день в году с 15,7 часами, а 21 декабря — самый короткий день в году с 8,3 часами. Можно показать, что функция
Можно показать, что функция
\[h(t)=3,7\sin \left(\dfrac{2π}{365}(x−80,5)\right)+12 \nonumber \]
— модель количества часов дневного света \ (h\) в зависимости от дня года \(t\) (рис. \(\PageIndex{7}\)).
Рисунок \(\PageIndex{7}\): Продолжительность светового дня в зависимости от дня в году можно смоделировать с помощью смещенной синусоиды.Пример \(\PageIndex{6}\): набросок графика преобразованной синусоиды
Набросок графика \(f(x)=3\sin(2(x−\frac{π}{4}) )+1.\)
Решение
Этот график представляет собой фазовый сдвиг \(y=\sin (x)\) вправо на \(π/4\) единиц, за которым следует горизонтальное сжатие в 2 раза, вертикальное растяжение в 3 раза, а затем вертикальное смещение на 1 единицу. Период \(f\) равен \(π\).
Упражнение \(\PageIndex{6}\)
Опишите связь между графиком \(f(x)=3\sin(4x)−5\) и графиком \(y=\sin (Икс)\).
- Подсказка
График \(f\) можно нарисовать, используя график \(y=\sin(x)\) и последовательность из трех преобразований.

- Ответить
Чтобы построить график \(f(x)=3\sin(4x)−5\), график \(y=\sin(x)\) необходимо сжать по горизонтали в 4 раза, а затем растянуть по вертикали на в 3 раза, затем сдвинут вниз на 5 единиц. Функция \(f\) будет иметь период \(π/2\) и амплитуду 3,
.
Ключевые понятия
- Радианная мера определяется таким образом, что угол, связанный с дугой длины 1 на единичной окружности, имеет радианную меру 1. Угол с градусной мерой \(180\)° имеет радианную меру \(\pi\ ) рад.
- Для острых углов \(θ\) значения тригонометрических функций определяются как отношения двух сторон прямоугольного треугольника, у которого один из острых углов равен \(θ\).
- Для общего угла \(θ\) пусть \((x,y)\) — точка на окружности радиуса \(r\), соответствующая этому углу \(θ\). Тригонометрические функции можно записать в виде соотношений, включающих \(x\), \(y\) и \(r\).
- Тригонометрические функции являются периодическими.
 Функции синуса, косинуса, секанса и косеканса имеют период \(2π\). Функции тангенса и котангенса имеют период \(π\).
Функции синуса, косинуса, секанса и косеканса имеют период \(2π\). Функции тангенса и котангенса имеют период \(π\).
Ключевые уравнения
- Функция обобщенного синуса
\(f(x)=A \sin(B(x−α))+C\)
Глоссарий
- периодическая функция
- функция является периодической, если она повторяется по мере того, как значения \(x\) перемещаются слева направо
- радиан
- для дуги окружности длиной \(s\) на окружности радиуса 1, радианная мера соответствующего угла \(θ\) равна \(s\)
- тригонометрические функции
- функции угла, определяемые как отношения длин сторон прямоугольного треугольника
- тригонометрическое тождество
- уравнение, включающее тригонометрические функции, верное для всех углов \(θ\), для которых определены функции в уравнении
Эта страница под названием 1.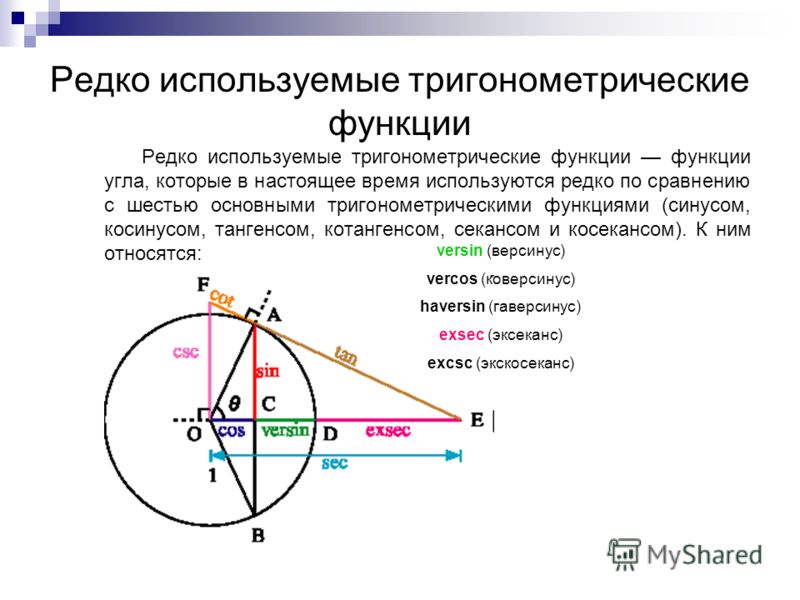 3: Тригонометрические функции распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Странгом и Эдвином «Джедом» Херманом (OpenStax) через исходный контент, который был отредактирован для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
3: Тригонометрические функции распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Странгом и Эдвином «Джедом» Херманом (OpenStax) через исходный контент, который был отредактирован для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать страницу TOC
- нет
- Теги
- автор @ Эдвин «Джед» Герман
- автор@Гилберт Странг
- периодическая функция
- Радиан
- источник@https://openstax.
 org/details/books/calculus-volume-1
org/details/books/calculus-volume-1 - тригонометрические функции
- тригонометрическая идентичность
- единичный круг
Тригонометрические функции
Тригонометрические функцииПонимание математики по Питер Альфельд, кафедра математики, Университет Юты
Первоначально тригонометрические функции были определены в
контекст прямоугольного треугольника. Более общее определение может
быть задано в терминах единичного круга. Используя этот подход
также позволяет не зацикливаться на представлении о том, что эти функции
определяются только для углов до 90 градусов.
Итак, рассмотрим угол t с вершиной в начала координат, причем начальная сторона является положительной частью горизонтальная ось, а крайняя сторона пересекает окружность радиуса 1 с центром в начале координат в точке (х(т),у(т)) . Теперь, это глоток! Это проиллюстрировано, однако, и, надеюсь, ясно, в этом картина:
Ясно, что координаты x и y равны определяется однозначно углом t .
Существуют три основные тригонометрические функции: синус, косинус и тангенс. Они сокращаются до . sin, cos, tan и определяются:
Обратные величины этих функций также были заданы
имена, они называются косеканс, секанс и
котангенс, соответственно, (сокращенно csc, sec, cot ).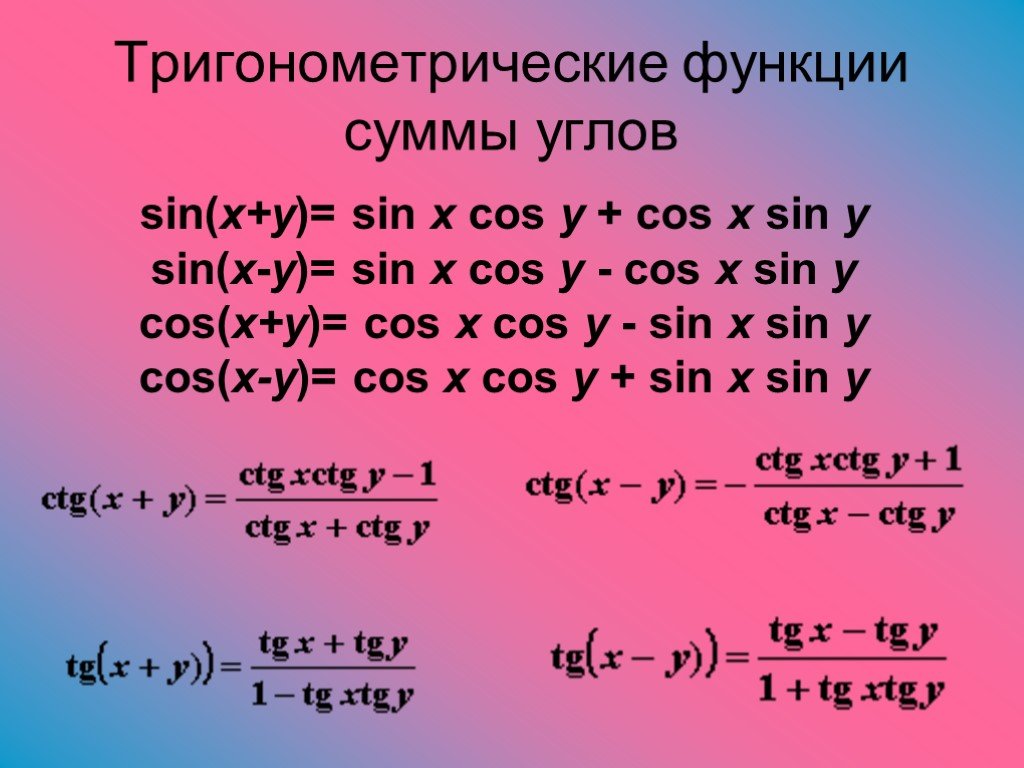 Таким образом
Таким образом
Только первые три имеют значение, остальные всегда могут быть заменены обратными числами sin , cos и загар по мере необходимости. Действительно, у большинства калькуляторов есть ключи только для этих трех функций.
Предупреждение : Ваш калькулятор, вероятно, имеет ключи помечен
Это ключи для триггерных функций , обратных , а не их взаимность! Верно. у большинства калькуляторов есть только ключи для первых трех функций.
Полезно понять, как графики функций относятся к их формулам. В качестве примера рассмотрим:
Это масштабированная и сдвинутая синусоидальная кривая . Конкретно,
Конкретно,
- a — положительное действительное число, амплитуда , т. е. максимальное значение функции.
- f — действительное число, частота функция, т. е. количество циклов на единицу интервал. (Обратное значение частоты равно период или периодичность .)
- p — сдвиг времени , положительное значение из p сдвигает график p единиц к оставил.
Щелкните в любом месте следующего списка, чтобы увидеть графики
такие и подобные функции. Для каждого примера вы увидите
страница с графиком и
Клен
команда, которая его сгенерировала. Вы можете вырезать и вставить это
команду в свой собственный сеанс Maple, если хотите.
Вы можете вырезать и вставить это
команду в свой собственный сеанс Maple, если хотите.
- синусов на основе графиков.
- у = грех(т), базовая функция синуса .
- у = 2*sin(t), удвоенная амплитуда.
- у = грех(2*т), удвоенная частота.
- у = грех(т+2), сдвиг времени -2.
- у = грех(2*Pi*t), частота = 1.

- Графики на основе косинусов
- у = cos(t), базовый косинус .
- у = 2*cos(t), удвоенная амплитуда.
- у = cos(2*t), удвоенная частота.
- у = cos(t+2), сдвиг времени -2.
- у = cos(2*Pi*t), частота = 1.


 9 Степени
9 Степени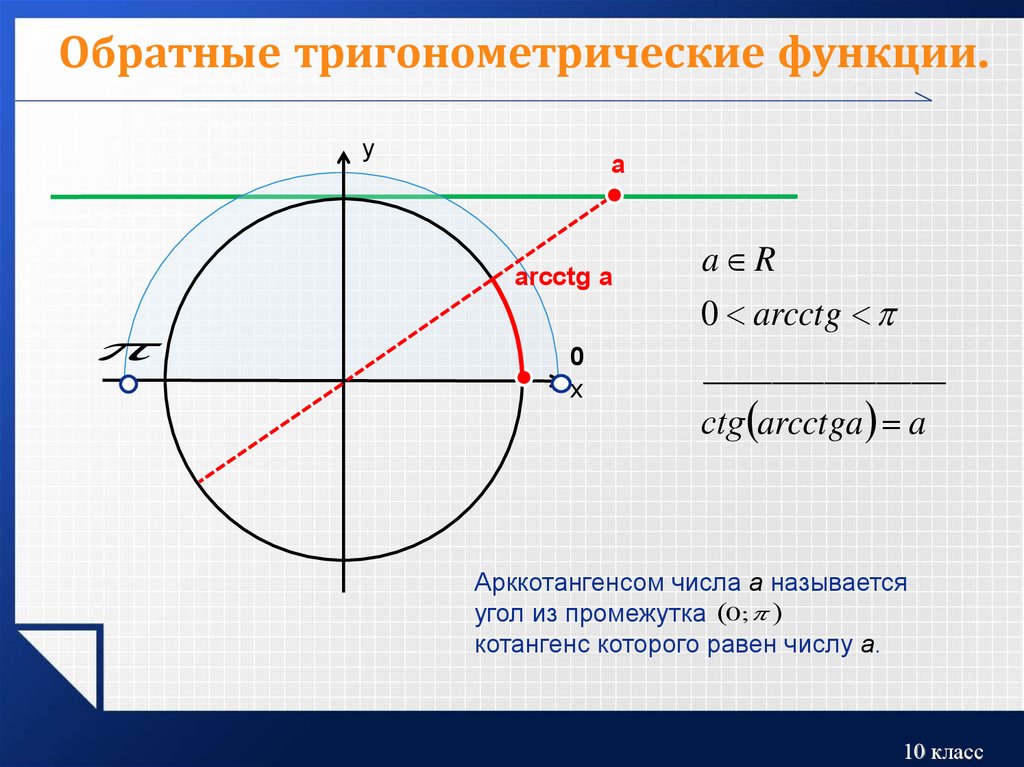 Н., Семендяев К. А. Прямолинейная тригонометрия // Справочник по математике. — Изд. 7-е, стереотипное. — М.: Государственное издательство технико-теоретической литературы, 1967. — С. 179—184.
Н., Семендяев К. А. Прямолинейная тригонометрия // Справочник по математике. — Изд. 7-е, стереотипное. — М.: Государственное издательство технико-теоретической литературы, 1967. — С. 179—184.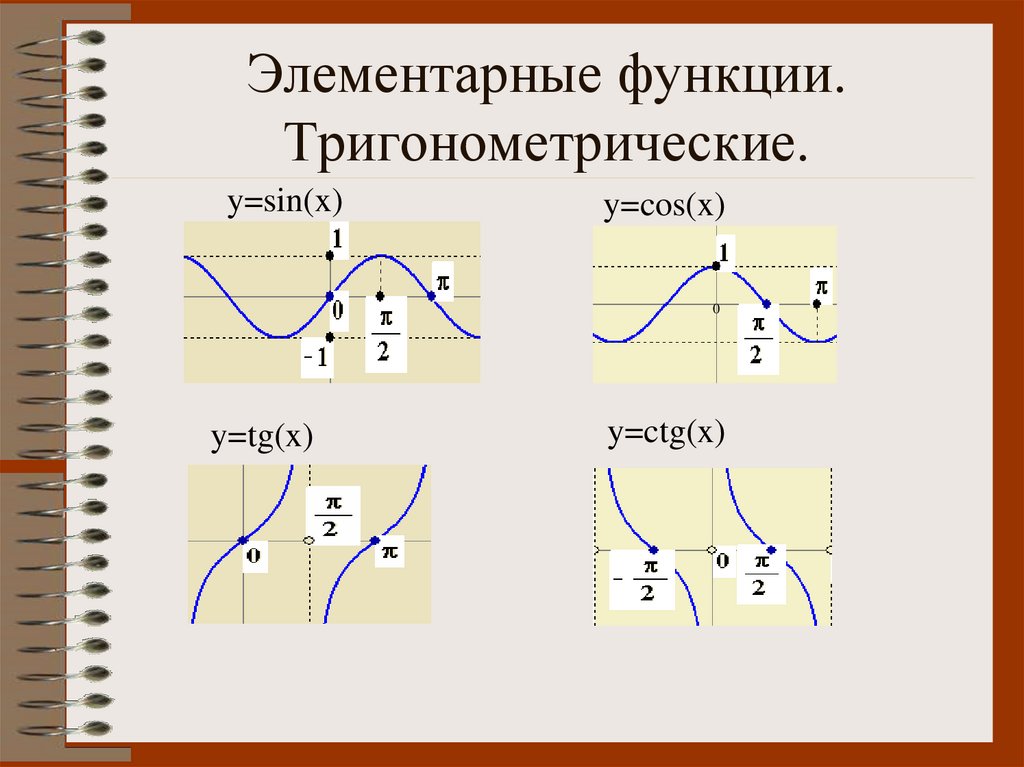 4 Определение тригонометрических функций через ряды
4 Определение тригонометрических функций через ряды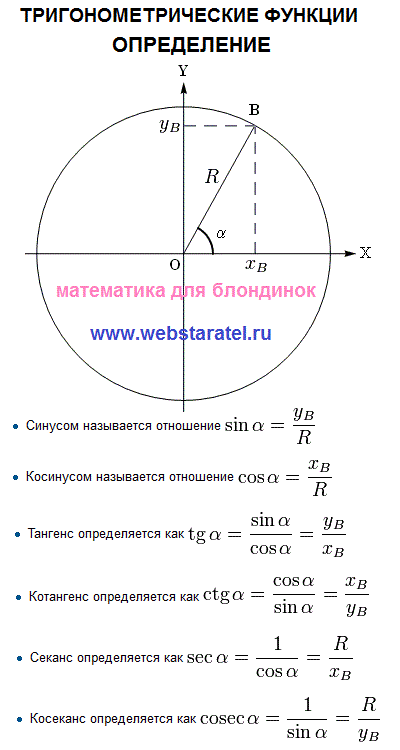
 Н., Семендяев К. А. Прямолинейная тригонометрия // Справочник по математике. — Изд. 7-е, стереотипное. — М.: Государственное издательство технико-теоретической литературы, 1967. — С. 179—184.
Н., Семендяев К. А. Прямолинейная тригонометрия // Справочник по математике. — Изд. 7-е, стереотипное. — М.: Государственное издательство технико-теоретической литературы, 1967. — С. 179—184.

 Функции синуса, косинуса, секанса и косеканса имеют период \(2π\). Функции тангенса и котангенса имеют период \(π\).
Функции синуса, косинуса, секанса и косеканса имеют период \(2π\). Функции тангенса и котангенса имеют период \(π\).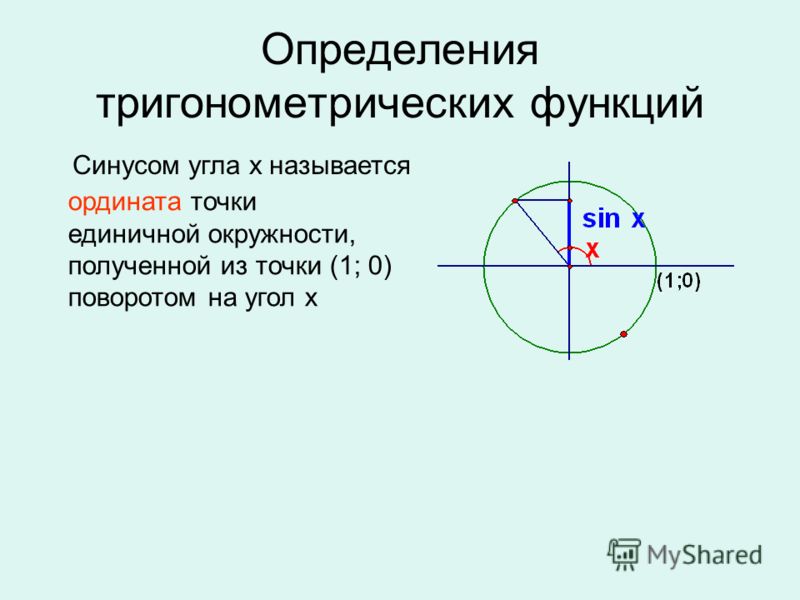 org/details/books/calculus-volume-1
org/details/books/calculus-volume-1