Тригонометрические интегралы: Интегрирование тригонометрических функций.

{-1/2}}{-1/2}+C=-\frac{2}{\sqrt{tg x}}+C=-2\sqrt{ctg x}+C.$$

Ответ: $-{2}{\sqrt{ctg x}}+C.$

 {jumi[*4]} 

6.214. $\int\cos\frac{x}{2}\cos\frac{x}{3}.$

Решение. 

$$\int\cos\frac{x}{2}\cos\frac{x}{3}=\int\frac{1}{2}\left(\cos\left(\frac{1}{2}-\frac{1}{3}\right)x+\cos\left(\frac{1}{2}+\frac{1}{3}\right)x\right)\,dx=$$ $$=\frac{1}{2}\int\left(\cos\frac{1}{6}x+\cos\frac{5}{6}x\right)\,dx=\frac{6}{2}\sin\frac{1}{6}x+\frac{6}{10}\sin\frac{5}{6}x+C=$$ $$=3\sin\frac{x}{6}+0,6\sin\frac{5x}{6}+C.$$ 

Ответ: $3\sin\frac{x}{6}+0,6\sin\frac{5x}{6}+C.$

 

6.215. $\int\sin \frac{x}{3}\cos\frac{2x}{3}\,dx.$

Решение. 

$$\int\sin\frac{x}{3}\cos\frac{2x}{3}=\int\frac{1}{2}\left(\sin\left(\frac{1}{3}-\frac{2}{3}\right)x+\sin\left(\frac{1}{3}+\frac{2}{3}\right)x\right)\,dx=$$ $$=\frac{1}{2}\int\left(\sin\frac{-x}{3}+\sin x\right)\,dx=\frac{3}{2}\cos\frac{1}{3}x-\frac{1}{2}\cos x+C.

3 x\,dx.$

 

 

 

5. Интегралы от тригонометрических функций.

Подставим все в формулу интегрирования по частям и приведем интеграл к табличному, тогда будем иметь:

Методы не применяются для интегрирования функций вида

; ; ; ;

; , т.е. от тригонометрических функций,

умноженных на многочлен. Такие интегралы интегрируются по частям.

При нахождении интегралов от тригонометрических функций используется ряд методов:

Использование тригонометрических формул Понижение степени подынтегральной функции Метод замены переменной Универсальная тригонометрическая подстановка

При работе с тригонометрическими функциями следует помнить, что:

Косинус – это четная функция, то есть , минус исчезает без всяких последствий.

Синус – функция нечетная: – здесь минус, наоборот – не пропадает, а выносится.

Использование тригонометрических формул

Пример34

Найти интеграл.

Используем формулу: и метод подведения под знак дифференциала

Пример 35

Найти интеграл

Для упрощения подынтегральной функции воспользуемся тригонометрическими функциями. Затем с помощью свойств интеграла приведем данный интеграл к табличному виду.

Пример 36

Найти интеграл.

Используем формулу: и метод подведения под знак дифференциала.

Пример 37

Найти интеграл.

Используем формулу:

Пример 38

Найти неопределенный интеграл

Используем формулы преобразования произведения функций сначала для произведения , а затем для произведения синусов в каждом из интегралов :

В результате искомый интеграл будет равен

Понижение степени подынтегральной функции

Данный приём используют, когда в подынтегральных функциях присутствуют синусы и косинусы в чётных степенях. Для понижения степени используют

тригонометрические формулы , и , причем последняя формула чаще используется в обратном

направлении:

Интеграл вида ʃ sinn (x) cosm (x), где n и m – чётные числа, решается методом

понижения степени подынтегральной функции.

Пример 39

Найти интеграл

∫cos2xdx = ∫1+cos2x2	dx =		21	∫(1 + cos2x)dx = 21 x + 21 sin2x + C
Используем формулу:
Пример 40
Найти интеграл		dx =		21 ∫(1 −cos3x)dx = 21 x −31 sin3x + C
∫sin2 23 xdx = ∫1−cos3x2
Используем формулу:

Пример 41

Найти интеграл

Выражаем sin4 x как (sin2 x)2 и применяем формулу

Используем формулу

В третьем слагаемом снова понижаем степень с помощью формулы .

Пример 42

Найти интеграл

Метод замены переменной

Данный приём используют, когда в подынтегральных функциях присутствуют синусы и косинусы в нечётных степенях.

Общие рекомендации :

1.за t нужно обозначить функцию, которая находится в знаменателе.

2.за t нужно обозначить ту функцию, которая, является более сложной.

3.Если в подынтегральной функции одна из тригонометрических функций (синус или косинус) находится в нечетной степени, то нужно от нечетной степени «откусить» одну функцию, а за t – обозначить другую функцию

Интеграл вида ʃ sinn (x) cosm (x), где n или m – нечётные числа, решается методом замены переменной

Пример 43

Найти интеграл

Проведем замену:

Примечание: здесь можно было сделать замену , но гораздо выгоднее обозначить за весь знаменатель.

Пример 44

Найти интеграл Проводим замену

Пример 45

Найти интеграл Проведем замену:

Пример 46

Найти интеграл

Представляем cos3 x dx как cos2 x cos x dx, а cos2x выражаем через синус с помощью основного тригонометрического тождества:

Делаем замену:

Пример 47

Найти интеграл Преобразуем подынтегральное выражение:

Проведем замену:

Пример 48

Найти интеграл Проведем замену:

Пример 49

Найти неопределенный интеграл Для вычисления исходного интеграла введем замену , тогда

Подставляя это в искомый интеграл, получим

Сделаем обратную замену

Пример 50

Найти неопределенный интеграл Преобразуем подынтегральную функцию, используя основное тригонометрическое тождество

Введем замену , тогда исходный интеграл примет вид

Сделаем обратную замену и окончательно получим

Пример 51

Найти неопределенный интеграл Преобразуем подынтегральную функцию, используя вначале формулу для синуса двойного угла:

а затем, формулу для понижения степени

Универсальная тригонометрическая подстановка

Универсальная тригонометрическая подстановка – это частый случай метода замены переменной. Её можно попробовать применить, когда «не знаешь, что делать». Интегралами, где нужно применить универсальную тригонометрическую подстановку, являются интегралы вида:

, , , и т.д.

Указанная замена позволяет свести интеграл от тригонометрической функции к интегралу от рациональной функции.

При этом следует учесть, что из равенства получаем:

;

Обратите внимание, что аргумент под тангенсом должен быть в два раза меньше, чем под синусом и косинусом, т.е., в общем виде, если присутствуют функции вида:

sin(kx), cos(kx), делается подстановка tg(kx/2) = t. Еще раз, при sin2x ‒ tg(2x/2), при sin3x ‒ tg(3x/2) и т.д.

Пример 52

Найти неопределенный интеграл Воспользуемся универсальной тригонометрической подстановкой:

Пример 53

Найти неопределенный интеграл Для решения данного интеграла сделаем упрощенную тригонометрическую замену, положив что

выразим из равенства

то есть Подставим все в искомый интеграл

Сделаем обратную замену

Пример 54

Найти неопределенный интеграл Преобразуем подынтегральную функцию следующим образом:

Для нахождения первого интеграла будем использовать универсальную тригонометрическую замену

Тогда первый интеграл преобразуется следующим образом

Разложим подынтегральную функцию полученного интеграла на элементарные дроби:

Приведем к общему знаменателю дроби в правой части равенства и приравниваем числители:

Приравнивая коэффициенты при соответствующих степенях, получим такую систему для нахождения и

Тогда подынтегральная функция имеет следующее разложение на простые дроби

а соответствующий интеграл равен

Делаем обратную замену

Окончательно искомый интеграл равен:

Пример 55

Найти неопределенный интеграл. Перед применением универсальной тригонометрической подстановки необходимо понизить степени в знаменателе при помощи формул

,

Универсальная тригонометрическая подстановка:

Применение универсальной тригонометрической подстановки часто приводит к длинным и трудоемким вычислениям. Поэтому на практике универсальной тригонометрической подстановки стараются избегать (если возможно).

В ряде случаев целесообразно свести подынтегральное выражение, содержащее sinn(α) и cosm(α), к tg(α) и ее производной 1/cos2(α) т.е. произвести замену:

. Для этого можно воспользоваться формулами

; .

Метод работает, если сумма показателей степеней n+m ‒ целое четное отрицательное число .

Пример56

Найти неопределенный интеграл

Пример57

Найти неопределенный интеграл

Замена tgх =t (чтобы не запутаться)

Пример58

Найти неопределенный интеграл

Пример59

Найти неопределенный интеграл

Пример60

Найти неопределенный интеграл

Пример61

Интеграл из примера55

=

=

=

4 2 − 5 2

(4 2 − 5 2 ) 2

(4 2 − 5) 2

( )

=

2

1

2

1

1

2 − √5

=

4 2 − 5

=

= 4 2 − 5 =

2

(2 )2 − (√5)2

= 2

2√5

2 + √5 + =

= 4√1

5 22 +−√√55 +

Решение значительно быстрее и проще.

6.Интегралы от дробей

Суть методов решения интегралов от дроби сводится к преобразованию дроби в сумму элементарных дробей табличного вида:

1.

2.

3.

4.

5.

6.

Для преобразования дроби используется комплекс приемов, основными из которых будут выделение полного квадрата, подстановка, разложение на множители, с дальнейшим преобразованием в сумму элементарных дробей.

Для решения интегралов от дроби можно придерживаться следующего алгоритма:

Определяем тип подынтегрального выражения.
1.	Для простейших дробей вида				применяется способ подведения функции
под знак дифференциала с дальнейшим интегрированием с помощью таблицы.
				( + )
		( + )		( + )−+		,
∫( + ) = ∫( + )			=	−+		+

Примеры:

2. Для дробей вида

,

,

,

(коэффициенты

a и c не равны нулю) также применяется способ подведения функции под знак дифференциала с дальнейшим интегрированием с помощью таблицы. (Формулы 2 — 6, см. выше).

Примеры:

3. Для дробей вида	сначала представляем
интеграл в виде суммы:

Первый интеграл берем методом подведения под знак дифференциала:

В интегралах вида	выделяем в знаменателе полный квадрат и приводим
выражение к табличному виду.
В ряде случаев, неразложимый многочлен					целесообразно представить в
	необходимо вынести коэффициент за знак интеграла,
виде полного квадрата (перед этим		(		+ + )
поделив все выражение на ) по формуле:

и свести интеграл к виду:

,

или

Пример62

Найти неопределенный интеграл Квадратный трехчлен, который стоит в знаменателе подынтегральной функции, не

раскладывается на множители . Поэтому для нахождения данного интеграла выделим в знаменателе полный квадрат.

Пример63

Найти неопределенный интеграл . Для начала вынесем двойкуиз под знака радикала:

т.е. вида

В подкоренном выражении выделяем полный квадрат:

Поэтому

Пример64

4. Для дробей вида

используют метод интегрирования по частям n раз, каждый раз понижая степень знаменателя и применяя предыдущие способы. Вычисления получаются очень длинные и долгие. Или пользуемся рекуррентными формулами.

5. Дроби( ) , у которых многочлены и в числителе и в знаменателе,

( ) , где Pn(x) и Pm(x) многочлены степени n и m соответственно, перед

собственно взятием интеграла необходимо разложить на множители, а затем, преобразовать в сумму элементарных дробей.

Определяем что дробь правильная. Правильной называется дробь, у которой степень числителя меньше степени знаменателя. Если дробь неправильная, то выделяем целую часть, с оставшейся частью работаем как с правильной дробью.

Раскладываем знаменатель правильной дроби на множители и преобразуем дробь в сумму элементарных дробей.

Для преобразования дроби в сумму элементарных дробей в большинстве случаев используют метод неопределенных коэффициентов.

Метод неопределенных коэффициентов.

т.е.
	Любую дробь вида		( + )( + )( + )		можно представить в виде
				2+ +
	2 + +
( + )( + )( + ) =			+ + + + + ,

+ ++ + +

где A, B, C неизвестные коэффициенты.

Приводим правую часть уравнения к общему знаменателю:

+

=

( + )( + ) + ( + )( + ) ( + )( + )

,

+

+Тогда

+

( + )( + )( + )

+

2

+ +

( + )( + ) + ( + )( + ) + ( + )( + )

( + )( + )( + )

( + )( + )( + )

2

+ + = ( + )( + ) + ( + )( + ) ( + )( + )

Если дроби равны= и равны их знаменатели, то должны быть равны и их числители,

:

+ + =

= 2

Раскрываем скобки

( + ) + + 2 +

( + ) + =

+

( + ) + + 2 +

= ( + + )

+

( + + + + + ) + ( + + )

= + +

Приравниваем коэффициенты в выражениях:

= ( + )

+ ( + ) + ( + )

= + +

Решая систему уравнений, находим неизвестные коэффициенты A, B, C и раскладываем

2

+ +

дробь на сумму элементарных дробей:

+

( + )( + )( + )

+

+

он приравнивается к

(

+ + )

квадратный.

многочлен вида:

Если в знаменателе встречается=

+неразложимый+

( + )(

+

1 + )

2

+

12

, где

— неразложимый квадратный многочлен (D<0), то

( + )(

сумме дробей по формуле:

+ + )

+

(

+ + )

Если в знаменателе2

встречаются=

+кратные2

множители.

вида:

1

,

1

2

1

2

( 1+ )

то они раскладываются по формуле:

( + ) =

+

2 + +

+ ( + ) +

( + )2

+ +

( + )

Пример65

Найти неопределенный интеграл Преобразуем подынтегральную функцию, расписав знаменатель согласно формуле сокращенного умножения для суммы кубов:

Тогда интеграл примет вид:

Далее разложим подынтегральную функцию на простые дроби с неопределенными коэффициентами. В нашем случае имеет место следующее разложение:

Найдем неопределенные коэффициенты, для этого приведем к общему знаменателю дроби в правой части равенства, а затем приравняем соответствующие числители

Далее приравняем коэффициенты при соответствующих степенях

Подставим, выраженные через , коэффициенты и во второе уравнение системы:

, тогда , а Таким образом, искомый интеграл будет равен:

1	1		(2 − 1) − 3
= 3	| + 1| − 6		2 − + 1			=
1	1			2 − 1			−3			=
= 3	| + 1| − 6		2		− + 1 −		6	2 − + 1
1	1	|		2		1
= 3	| + 1| − 6				− + 1| + 2		2 − + 1

Квадратный трехчлен, стоящий в знаменателе последнего интеграла, не раскладывается на

множители				1				1		2						. Поэтому для его нахождения выделим в
															1
знаменателе полный квадрат:
	3 + 1		= = 3		| + 1| − 6				|		− + 1| +				2 2 − + 1 =
1		| + 1| −			1	|	2			1						+ 3 =
= 3					6		2	− + 1| + 2				( − 1)2
1		| + 1| −			1	|				1		1		2			4
= 3					6			− + 1| + 2				3		3			+ =
1		| + 1| −			1	|	2				1		4	2		4
= 3					6			− + 1| + √3					√3 +

Пример66

Найти неопределенный интеграл Дробь является правильной

Раскладываем знаменатель на множители, используя формулу сокращенного умножения

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:

Приводим дробь к общему знаменателю:

Составим и решим систему:

Пример67

Найти неопределенный интеграл Данная дробь является неправильной.

Основной метод решения интеграла с неправильной дробно-рациональной функцией – это

деление числителя на знаменатель.

Сначала рисуем «заготовку» для деления:

ВСЕ недостающие степени (и (или) свободные члены) без пропусков записываем в ОБОИХ многочленах с нулевыми коэффициентами

Теперь маленькая задачка, на какой множитель нужно умножить , чтобы получить ? Очевидно, что на :

Далее умножаем сначала на , потом – на , потом – на , потом – на 0 и записываем результаты слева:

Проводим черточку и производим вычитание (из верха вычитаем низ):

Старшая степень остатка равна двум, старшая степень делителя

– больше, она равна трём, значит, больше разделить не удастся. Если бы

изначально унас был в числителе многочлен пятой степени, то алгоритм деления увеличился бы на один шаг.

Итак, у нас получилась целая часть плюс остаток:

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:

6. Неопределенные интегралы иррациональных функций вида находятся методом подстановки.

В зависимости от рациональных чисел m, n и p вводят следующие новые переменные:

1.

Если p — целое число, то принимают

, где N — общий знаменатель чисел m и n.

2.

— целое число, то

, где N — знаменатель числа p.

Если +

знаменатель

+ p

— целое число, то вводят новую переменную

, где N —

3.

Если

+

числа .

привести к виду:

±

,

−

которые можно

Очень часто в вычислениях встречаются дроби вида

+ −

+

+ =

+

= +

− + = − +

+ −

−

−

− =

−

= −

+ − = − −

+ − = −1 + − = − −

+ −

−

− =

−

= −

+ − = + −

Пример68

Найти неопределенный интеграл

То есть, m = -1, n = 1, p = 1/2. Так как — целое число, то вводим новую

переменную (N = 2 – знаменатель числа p). Выражаем х через z:

Выполняем подстановку в исходный интеграл:

Пример 69

Найти неопределенный интеграл Проведем замену: . Навешиваем дифференциалы на обе части:

Вот почему дифференциалы нужно именно НАВЕШИВАТЬ на обе части и добросовестно

раскрывать эти дифференциалы. Немало чайников здесь формально напишет и допустит ошибку.

Пример70

Найти неопределенный интеграл

Проведем замену: Навешиваем дифференциалы на обе части:

С числителем разобрались. Что делать с в знаменателе? Берем нашу замену и выражаем из неё: Если , то

Пример71

Найти неопределенный интеграл Задача состоит в следующем: провести удачную замену, чтобы сразу избавиться от ВСЕХ корней.

Когда даны разные корни удобно придерживаться следующей схемы решения. Сначала выписываем на черновике подынтегральную функцию, при этом все корни представляем в

виде : . Нас будут интересовать знаменатели степеней.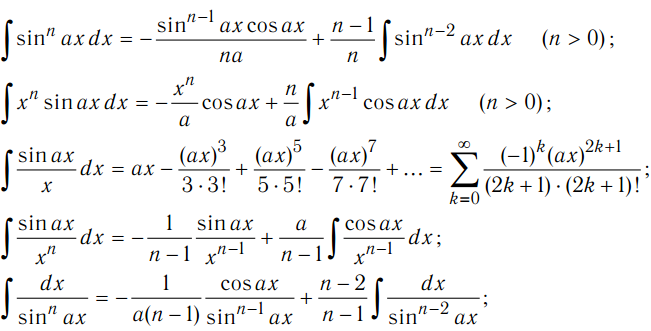 Записываем эти знаменатели: 2, 3, 3.

Теперь нужно найти наименьшее общее кратное чисел 2, 3, 3 – такое число, чтобы оно делилось и на 2 и на 3 (в данном случае), кроме того, это число должно быть как можно меньше.

Очевидно, что наименьшим общим кратным является число 6. Оно делится и на 2 и на 3, кроме того, меньше шестерки ничего не придумать.

Замена в рассматриваемом интеграле будет следующей: Оформляем решение:

Проведем замену:

19. Интегрирование тригонометрических функций. Общие замечания о методах интегрирования

I. Интегралы типа , где т и п — целые числа.

А) Одно из чисел т или П — нечетно. В этом случае интегралы сводятся к интегралам от рациональных функций.

Метод интегрирования ясен из приведенных примеров.

Пример 1.

Замечая, что , сделаем замену переменной: Это дает и, следовательно, так как получим

Пример 2.

Умножив числитель и знаменатель Подынтегрального выражения на получим

. Положим тогда

Б) Оба ПоказатЕЛя т и N — четныЕ нЕОтрицатЕЛьные числа (в частности, одно из них может быть равным нулю). Заменяя и по формулам:

МЫ ДОбьемся того, что произведение заменится СумМой Произведений такого же вида, но с меньшими показателями СТепеней; метод интегрирования ясен из следующих примеров:

Пример 1.

Пример 2.

II. Интегралы типа

ЭТи интегралы вычисляются методом разложения на основании следующих тригонометрических тождеств:

Пример 1.

Пример 2.

III. Интегралы типа

Рассмотрим интегралы типа

Где R — рациональная функция своих аргументов и . Такие интегралы называются Тригонометрическими. Например, интегралы

Будут тригонометрическими интегралами, так как Подынтегральные функции являются рациональными функциями аргументов и . Наоборот, интеграл не является тригонометрическим, так как под интегралом стоит функция, не рацИОнальная относительно и . Покажем, что всякий тригонометрический интеграл можно свести к интегралу от рациональной функции. Для этого вместо Х введем новую переменную Z, связанную с переменной Х соотношением

Тогда и выразятся рационально через Z. В самом деле, применяя формулы, известные из тригонометрии, имеем:

Аналогично,

Наконец, учитывая, что найдем , ДифференЦируя, получим .

Таким образом, если положить , то

(17)

Формулы (17) показывают, что , и Dx рационально выражаются через Z, поэтому

Последний интеграл является интегралом от рациональной функции переменного Z и может быть найден методами, рассмотренными ранее.

Приведем примеры.

Пример 1. Полагая и применяя формулы (17), имеем:

Пример 2. Полагая находим

Заметим, что интеграл можно вычислить, если воспользоваться результатами предыдущего примера. В самом деле,

Хотя ответы по форме получились различными, однако, ЛЕгко показать, что

Пример 3.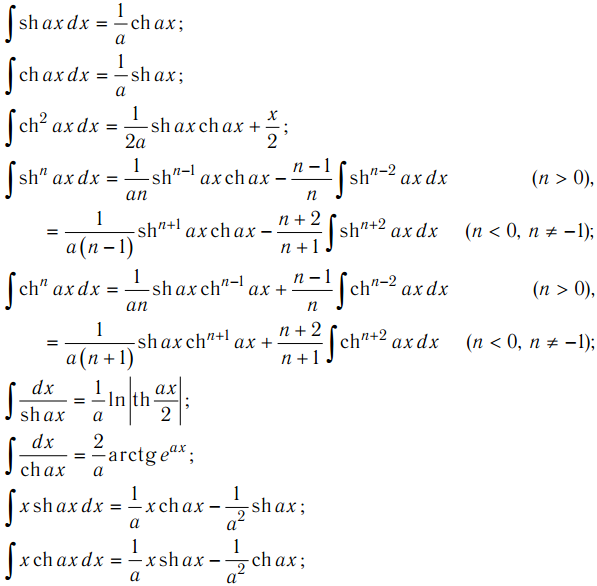 Применим указанную выше замену переменной, положив . Тогда, согласно формулам (17), наш интеграл преобразуется следующим образом:

Разложим дробь на сумму простейших дробей:

Следовательно,

Подстановкой интегралы всегда приводятся к. интегралам от рациональных функций. Однако это ведет порой к слишком громоздким вычислениям. В некоторых случаях эти вычисления можно упростить. Так, например, если где Т И N целые числа, то удобнее пользоваться методами, изложенными в П. I.

Укажем еще на один частный случай функции , при котором применение другой подстановки значительно сокращает вычисления.

IV. ИнтЕГралы от функций, рационально зависящих от

Эти интегралы сводятся к интегралам от рациональной дроби, если СДелать замену переменной .

При этом и, следовательно,

Подынтегральное выражение в последнем интеграле является рациональной функцией от Z.

Приведем пример:

Замечание. Такой же подстановкой берется интеграл , если и входят только в четных степенях. Это следует из того, что и выражаются рационально через

Пример:

делая замену получим:

Мы разобрали наиболее важные методы интегрирования, охвАТывающие довольно обширный класс элементарных функций. Однако следует заметить, что на практике не всегда следует действовать по трафарету.

Так, например, интеграл можно было бы взять обычным методом интегрирования рационАЛьных функций, разложив Подынтегральную функцию в сумму простейших дробей:

Однако при внимательном рассмотрении Подынтегральной функции мы замечаем, что числитель является производной знаменателя. Поэтому

ИскуССтво вычисления интегралов приобретается практикой при решении достаточно большого количества примеров.

Так как нахождение новых интегралов очень часто сводится к ранее известным, то для оБЛегчения можно рекомендовать пользование таблицами интегралов.

В заключение напомним, что далеко не всякий интеграл От Непрерывной элементарной функции может быть взят в элементарных функциях. Иначе говоря, хотя первообразная и существует в силу теоремы существования, но она не может быть выражена с помощью конечного числа алгебраических действий и суперпозиций, проведенных над элементарными ФункЦиями.

При изучении различных методов Интегрирования мы уже всТРечались с такими интегралами. Ранее, например, было указано, что функции , , не интегрируются в элементарных функциях.

Часто бывает важно изучить свойства тех функций, которые являются первообразными от некотОРых элементарных функций, но сами не выражаются через элементарные функции. Рассмотрим несколько примеров таких функций.

Пример 1. Та первообразная от функции , которая удовлетворяет дополнительному условию: ее значение при Х = 0 равно нулю — называется интегральным синусом и обозначается si Х.

Таким образом,

или

Где под si Х подразумевается та первообразная, которая удовлетворяет условию si 0 = 0.

Пример 2. Интегральным косинусом называется та первообразная от , которая удовлетворяет условию

Пример 3. Большое значение в различных приложениях имеет первообразная Ф(Х) от функции удовлетворяющая дополнительному условию Ф (0) = 0. Эта функция встречается, в частностИ, в теории вероятностей и называется интегралом вероятности. Ее график представлен на рис. 1.

Пример 4. Эллиптическими интегралами 1-го и 2-го рода называются такие первообразные от функций:

где

Которые обращаются в нуль при

Эти функции встречаются при вычислении длины дуги эллипса, откуда и происходит их название (эллиптические интегралы).

Все эти функции, а также многие другие функции, получаются подобным образом, хорошо изучены и для них составлены подробные таблицы, помогающие практически использовать эти функции.

< Предыдущая		Следующая >

7.2: Тригонометрические интегралы — Математика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

10771

• OpenStax
• OpenStax

Цели обучения

• Решить задачи интегрирования, связанные с произведениями и степенями \(\sin x\) и \(\cos x\).
• Решить задачи интегрирования с произведениями и степенями \(\tan x\) и \(\sec x\).
• Используйте формулы приведения для решения тригонометрических интегралов.

В этом разделе мы рассмотрим, как интегрировать различные произведения тригонометрических функций. Эти интегралы называются тригонометрическими интегралами . Они являются важной частью метода интеграции, называемого тригонометрическая замена , которая представлена ​​в разделе Тригонометрическая замена. Этот метод позволяет нам преобразовывать алгебраические выражения, которые мы не можем интегрировать, в выражения, содержащие тригонометрические функции, которые мы можем интегрировать с помощью методов, описанных в этом разделе. Кроме того, эти типы интегралов часто появляются, когда мы позже изучаем полярные, цилиндрические и сферические системы координат. Начнем наше исследование с произведений \(\sin x\) и \(\cos x.\) 92(3x)\,dx = \frac{1}{2}x+\frac{1}{12}\sin(6x)+C\)

В некоторых областях физики, таких как квантовая механика, обработка сигналов и вычисление рядов Фурье, часто необходимо интегрировать произведения, включающие \(sin(ax), sin(bx), cos(ax),\ ) и \(cos(bx). \) Эти интегралы оцениваются путем применения тригонометрических тождеств, как указано в следующем правиле.

Правило: интегрирование произведений синусов и косинусов различных углов (bx),\) используйте замены

\[\sin(ax)\sin(bx)=\frac{1}{2}\cos((a−b)x)−\frac{1}{2}\cos((a+b) x) \nonumber \]

\[\sin(ax)\cos(bx)=\frac{1}{2}\sin((a−b)x)+\frac{1}{2}\sin ((a+b)x) \nonumber \]

\[\cos(ax)\cos(bx)=\frac{1}{2}\cos((a−b)x)+\frac{1 }{2}\cos((a+b)x) \nonumber \]

Эти формулы могут быть получены из формул суммы углов для синуса и косинуса.

Пример \(\PageIndex{6}\): оценка \(∫\sin(ax)\cos(bx)\,dx\)

оценка \(\displaystyle ∫\sin(5x)\cos(3x) \,дх.\)

Решение. Примените тождество \(\sin(5x)\cos(3x)=\frac{1}{2}\sin(2x)+\frac{1}{2}\sin(8x).\) Таким образом,

\(\displaystyle ∫\sin(5x)\cos(3x)\,dx=∫\frac{1}{2}\sin(2x)+\frac{1}{2}\sin(8x )\,dx=-\frac{1}{4}\cos(2x)−\frac{1}{16}\cos(8x)+C.\)

Упражнение \(\PageIndex{6}\)

Вычислить \(\displaystyle ∫\cos(6x)\cos(5x)\,dx. \)

Подсказка

Замените \(\cos(6x)\cos(5x)=\frac{1}{2}\cos x+\frac{1}{2}\cos(11x).\)

93x\)

Основные понятия

Интегралы тригонометрических функций можно вычислять с помощью различных стратегий. Эти стратегии включают

1. Применение тригонометрических тождеств для перезаписи интеграла, чтобы его можно было вычислить с помощью \(u\)-подстановки
2. Использование интегрирования по частям
3. Применение тригонометрических тождеств для преобразования произведений синусов и косинусов с различными аргументами в виде суммы отдельных функций синуса и косинуса
4. Применение формул сокращения

Ключевые уравнения

Для интеграции произведений, включающих \(\sin(ax), \,\sin(bx), \,\cos(ax),\) и \(\cos(bx),\), используйте замены .

• Синусоидальные продукты

\(\sin(ax)\sin(bx)=\frac{1}{2}\cos((a−b)x)−\frac{1}{2}\cos((a+b) x)\)

• Произведения синуса и косинуса

\(\sin(ax)\cos(bx)=\frac{1}{2}\sin((a−b)x)+\frac{1}{2}\sin((a+b) х)\)

9{n−2}x\,dx\)

Глоссарий

формула уменьшения мощности

правило, позволяющее заменить интеграл от степени тригонометрической функции на интеграл меньшей степени

тригонометрический интеграл

интеграл, включающий степени и произведения тригонометрических функций

---

Эта страница под названием 7. 2: Тригонометрические интегралы распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована OpenStax.

1. Наверх
• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   4,0

   Показать страницу TOC

   нет

   Включено

   да

2. Теги

   1. расчет: да
   2. формула снижения мощности
   3. тригонометрический интеграл

3.

2 Тригонометрические интегралы. Расчет, том 2

Цели обучения

• 3.2.1 Решите проблемы интеграции, связанные с продуктами и возможностями sinxsinx и cosx.cosx.
• 3.2.2 Решите проблемы интеграции, связанные с продуктами и возможностями tanxtanx и secx.secx.
• 3.2.3 Используйте формулы приведения для решения тригонометрических интегралов.

В этом разделе мы рассмотрим, как интегрировать различные произведения тригонометрических функций. Эти интегралы называются тригонометрическими интегралами. Они являются важной частью метода интеграции, называемого тригонометрическая замена , которая представлена ​​в разделе Тригонометрическая замена. Этот метод позволяет нам преобразовывать алгебраические выражения, которые мы не можем интегрировать, в выражения, содержащие тригонометрические функции, которые мы можем интегрировать с помощью методов, описанных в этом разделе. Кроме того, эти типы интегралов часто появляются, когда мы позже изучаем полярные, цилиндрические и сферические системы координат. Начнем наше исследование с произведений sinxsinx и cosx.cosx.

Интегрирование произведений и мощностей sin

x и cos x

Ключевая идея стратегии, используемой для интегрирования комбинаций произведений и степеней sinxsinx и cosxcosx, заключается в переписывании этих выражений как сумм и разностей интегралов вида ∫sinjxcosxdx∫sinjxcosxdx или ∫cosjxsinxdx.∫cosjxsinxdx. Переписав эти интегралы, мы вычисляем их с помощью u -подстановки. Прежде чем подробно описать общий процесс, давайте рассмотрим следующие примеры.

Пример 3,8

Интегрирование ∫cosjxsinxdx∫cosjxsinxdx

Вычисление ∫cos3xsinxdx.∫cos3xsinxdx.

Решение

Используйте uu-подстановку и пусть u=cosx.u=cosx. В этом случае du=-sinxdx.du=-sinxdx. Таким образом,

∫cos3xsinxdx=-∫u3du=-14u4+C=-14cos4x+C. ∫cos3xsinxdx=-∫u3du=-14u4+C=-14cos4x+C.

Контрольно-пропускной пункт 3,5

Оценить ∫sin4xcosxdx.∫sin4xcosxdx.

Пример 3,9

Предварительный пример: интегрирование ∫cosjxsinkxdx∫cosjxsinkxdx Где

k Нечетный

Вычислить ∫cos2xsin3xdx.∫cos2xsin3xdx.

Решение

Чтобы преобразовать этот интеграл в интегралы вида ∫cosjxsinxdx,∫cosjxsinxdx, перепишите sin3x=sin2xsinxsin3x=sin2xsinx и сделайте замену sin2x=1−cos2x.sin2x=1−cos2x. Таким образом,

∫cos2xsin3xdx=∫cos2x(1−cos2x)sinxdxLetu=cosx;thendu=−sinxdx.=−∫u2(1−u2)du=∫(u4−u2)du=15u5−13u3+C=15cos5x− 13cos3x+C.∫cos2xsin3xdx=∫cos2x(1−cos2x)sinxdxLetu=cosx;тогдаdu=−sinxdx.=−∫u2(1−u2)du=∫(u4−u2)du=15u5−13u3+C=15cos5x− 13cos3x+С.

Контрольно-пропускной пункт 3,6

Оценить ∫cos3xsin2xdx.∫cos3xsin2xdx.

В следующем примере мы видим стратегию, которую необходимо применять, когда имеются только четные степени sinxsinx и cosx. cosx. Для интегралов этого типа тождества

sin2x=12−12cos(2x)=1−cos(2x)2sin2x=12−12cos(2x)=1−cos(2x)2

и

cos2x=12+12cos(2x)=1+cos(2x)2cos2x=12+12cos(2x)=1+cos(2x)2

бесценны. Эти тождества иногда называют уменьшающих мощность тождеств , и они могут быть получены из тождества двойного угла cos(2x)=cos2x-sin2xcos(2x)=cos2x-sin2x и пифагорейского тождества cos2x+sin2x=1.cos2x+sin2x=1.

Пример 3.10

Интегрирование четной степени sinxsinx

Вычислить ∫sin2xdx.∫sin2xdx.

Решение

Чтобы вычислить этот интеграл, воспользуемся тригонометрическим тождеством sin2x=12−12cos(2x).sin2x=12−12cos(2x). Таким образом,

∫sin2xdx=∫(12−12cos(2x))dx=12x−14sin(2x)+C.∫sin2xdx=∫(12−12cos(2x))dx=12x−14sin(2x)+C.

Контрольно-пропускной пункт 3,7

Оценить ∫cos2xdx.∫cos2xdx.

Общий процесс интеграции продуктов степеней sinxsinx и cosxcosx резюмируется в следующем наборе рекомендаций.

Стратегия решения проблем

Стратегия решения проблем: объединение продуктов и возможностей sin

x и cos x

Чтобы интегрировать ∫cosjxsinkxdx∫cosjxsinkxdx, используйте следующие стратегии:

1. Если kk нечетно, перепишите sinkx=sink-1xsinxsinkx=sink-1xsinx и используйте тождество sin2x=1-cos2xsin2x=1-cos2x для перезаписи sink-1xsink 1x с точки зрения cosx.cosx. Интегрируйте с помощью замены u=cosx.u=cosx. Эта замена делает du=-sinxdx.du=-sinxdx.
2. Если jj нечетное, перепишите cosjx=cosj-1xcosxcosjx=cosj-1xcosx и используйте тождество cos2x=1-sin2xcos2x=1-sin2x, чтобы переписать cosj-1xcosj-1x в терминах sinx.sinx. Интегрируйте с помощью замены u=sinx.u=sinx. Эта замена делает du=cosxdx.du=cosxdx. ( Примечание : Если и jj, и kk нечетны, можно использовать либо стратегию 1, либо стратегию 2.)
3. Если и jj, и kk четные, используйте sin2x=(1/2)−(1/2)cos(2x)sin2x=(1/2)−(1/2)cos(2x) и cos2x=(1/ 2)+(1/2)cos(2x). cos2x=(1/2)+(1/2)cos(2x). После применения этих формул упростите и при необходимости повторно примените стратегии с 1 по 3.

Пример 3.11

Интегрирование ∫cosjxsinkxdx∫cosjxsinkxdx, где

k — нечетное

Вычислить ∫cos8xsin5xdx.∫cos8xsin5xdx.

Решение

Поскольку степень sinxsinx нечетна, используйте стратегию 1. Таким образом, .=∫u8(1−u2)2(−du)Letu=cosxanddu=−sinxdx.=∫(−u8+2u10−u12)duExpand.=−19u9+211u11−113u13+CEВычислить интеграл.=−19cos9x+211cos11x -113cos13x+c.substitutuuteu = cosx.∫cos8xsin5xdx = ∫cos8xsin4xsinxdxbreak offsinx. = ∫cos8x (sin2x) 2sinxdxrewritesin4x = (sin2x) 2. = ∫cos8x (1 -cosxriteritesin4x = (sin2x) 2. = ∫cos8x (1 -cos1xiin24x = (sin2x) 2. = ∫cos8x (1 -cos -in. 1−u2)2(−du)Letu=cosxanddu=−sinxdx.=∫(−u8+2u10−u12)duExpand.=−19u9+211u11−113u13+CEВычислить интеграл.=−19cos9x+211cos11x−113cos13x+C. Замена=cosx.

Пример 3.

12

Интегрирование ∫cosjxsinkxdx∫cosjxsinkxdx, где

k и j — четные

Вычислить ∫sin4xdx.∫sin4xdx.

Решение

Поскольку степень sinxsinx четна (k=4)(k=4), а степень cosxcosx четна (j=0),(j=0), мы должны использовать стратегию 3. Таким образом,

∫sin4xdx= ∫(sin2x)2dxRewritesin4x=(sin2x)2.=∫(12−12cos(2x))2dxSubstitutesin2x=12−12cos(2x).=∫(14−12cos(2x)+14cos2(2x))dxExpand(12−12cos (2x))2.=∫(14−12cos(2x)+14(12+12cos(4x))dx.∫sin4xdx=∫(sin2x)2dxRewritesin4x=(sin2x)2.=∫(12−12cos(2x) )2dxSubstitutesin2x=12−12cos(2x).=∫(14−12cos(2x)+14cos2(2x))dxExpand(12−12cos(2x))2.=∫(14−12cos(2x)+14(12+) 12cos(4x))dx

Поскольку cos2(2x)cos2(2x) имеет четную степень, подставим cos2(2x)=12+12cos(4x):cos2(2x)=12+12cos(4x):

=∫(38−12cos( 2x)+18cos(4x))dxSimplify.=38x−14sin(2x)+132sin(4x)+CEВычисление интеграла.=∫(38−12cos(2x)+18cos(4x))dxSimplify. =38x−14sin(2x) )+132sin(4x)+CEВычисление интеграла.

Контрольно-пропускной пункт 3,8

Оценить ∫cos3xdx.∫cos3xdx.

Контрольно-пропускной пункт 3,9

Вычислить ∫cos2(3x)dx.∫cos2(3x)dx.

В некоторых областях физики, таких как квантовая механика, обработка сигналов и вычисление рядов Фурье, часто необходимо интегрировать продукты, которые включают sin(ax),sin(ax),sin(bx),sin(bx) ,cos(ax),cos(ax) и cos(bx).cos(bx). Эти интегралы оцениваются путем применения тригонометрических тождеств, как указано в следующем правиле.

Правило: Интегрирование произведений синусов и косинусов разных углов

Чтобы интегрировать продукты, содержащие sin(ax),sin(ax),sin(bx),sin(bx),cos(ax),cos(ax) и cos(bx),cos(bx), используйте замены

sin(ax)sin(bx)=12cos((a−b)x)−12cos((a+b)x)sin(ax)sin(bx)=12cos((a−b)x)−12cos ((a+b)x)

(3.3)

sin(ax)cos(bx)=12sin((a−b)x)+12sin((a+b)x)sin(ax)cos(bx )=12sin((a−b)x)+12sin((a+b)x)

(3. 4)

cos(ax)cos(bx)=12cos((a−b)x)+12cos(( a+b)x)cos(ax)cos(bx)=12cos((a−b)x)+12cos((a+b)x)

(3,5)

Эти формулы могут быть получены из формул суммы углов для синуса и косинуса.

Пример 3.13

Вычисление ∫sin(ax)cos(bx)dx∫sin(ax)cos(bx)dx

Вычисление ∫sin(5x)cos(3x)dx.∫sin(5x)cos(3x)dx.

Решение

Применить тождество sin(5x)cos(3x)=12sin(2x)+12cos(8x).sin(5x)cos(3x)=12sin(2x)+12cos(8x). Таким образом,

∫sin(5x)cos(3x)dx=∫12sin(2x)dx+∫12sin(8x)dx=−14cos(2x)−116cos(8x)+C.∫sin(5x)cos(3x) dx=∫12sin(2x)dx+∫12sin(8x)dx=−14cos(2x)−116cos(8x)+C.

Контрольно-пропускной пункт 3.10

Вычислить ∫cos(6x)cos(5x)dx.∫cos(6x)cos(5x)dx.

Интеграция продуктов и возможностей tan

x и sec x

Прежде чем обсуждать интегрирование произведений и степеней tanxtanx и secx,secx, полезно вспомнить интегралы, включающие tanxtanx и secxsecx, которые мы уже изучили:

1. ∫sec2xdx=tanx+C∫sec2xdx=tanx+C
2. ∫secxtanxdx=secx+C∫secxtanxdx=secx+C
3. ∫tanxdx=ln|secx|+C∫tanxdx=ln|secx|+C
4. ∫secxdx=ln|secx+tanx|+C. ∫secxdx=ln|secx+tanx|+C.

Для большинства интегралов произведений и степеней tanxtanx и secx,secx мы перепишем выражение, которое хотим интегрировать, как сумму или разность интегралов вида ∫tanjxsec2xdx∫tanjxsec2xdx или ∫secjxtanxdx.∫secjxtanxdx. Как мы видим в следующем примере, мы можем вычислить эти новые интегралы, используя u -подстановку.

Пример 3.14

Оценка ∫secjxtanxdx∫secjxtanxdx

Оценка ∫sec5xtanxdx.∫sec5xtanxdx.

Решение

Начните с перезаписи sec5xtanxsec5xtanx как sec4xsecxtanx.sec4xsecxtanx.

. интеграл.=15u5+CSubstitutesecx=u.=15sec5x+C

СМИ

Вы можете прочитать интересную информацию на этом веб-сайте, чтобы узнать об общем интеграле с участием секущей.

Контрольно-пропускной пункт 3.11

Оценка ∫tan5xsec2xdx.∫tan5xsec2xdx.

Теперь мы рассмотрим различные стратегии интеграции продуктов и возможностей secxsecx и tanx. tanx.

Стратегия решения проблем

Стратегия решения проблем: интеграция ∫tankxsecjxdx∫tankxsecjxdx

Чтобы интегрировать ∫tankxsecjxdx,∫tankxsecjxdx, используйте следующие стратегии:

1. 2xsec2x и используйте sec2x=tan2x+1sec2x=tan2x+1, чтобы переписать secj-2xsecj-2x в терминах tanx.tanx. Пусть u=tanxu=tanx и du=sec2xdx.du=sec2xdx.
2. Если kk нечетно и j≥1,j≥1, перепишите tankxsecjx=tank-1xsecj-1xsecxtanxtankxsecjx=tank-1xsecj-1xsecxtanx и используйте tan2x=sec2x-1tan2x=sec2x-1, чтобы переписать tank-1xtank-1x в терминах secx .secx. Пусть u=secxu=secx и du=secxtanxdx.du=secxtanxdx. ( Примечание : если jj четно, а kk нечетно, то можно использовать либо стратегию 1, либо стратегию 2.)
3. Если kk нечетное, где k≥3k≥3 и j=0,j=0, переписать tankx=tank-2xtan2x=tank-2x(sec2x-1)=tank-2xsec2x-tank-2x.tankx=tank-2xtan2x= бак-2x(sec2x-1)=бак-2xsec2x-бак-2x. Может оказаться необходимым повторить этот процесс для термина tank-2xtank-2x.
4. Если kk четное, а jj нечетное, то используйте tan2x=sec2x-1tan2x=sec2x-1, чтобы выразить tankxtankx через secx.secx. Используйте интегрирование по частям для интегрирования нечетных степеней secx.secx.

Пример 3.15

Интегрирование ∫tankxsecjxdx∫tankxsecjxdx, когда jj четно

Вычислить ∫tan6xsec4xdx.∫tan6xsec4xdx.

Решение

Поскольку мощность secxsecx четная, перепишите sec4x=sec2xsec2xsec4x=sec2xsec2x и используйте sec2x=tan2x+1sec2x=tan2x+1, чтобы переписать первый sec2xsec2x в терминах tanx.tanx. Таким образом,

∫tan6xsec4xdx=∫tan6x(tan2x+1)sec2xdxLetu=tanxanddu=sec2xdx.=∫u6(u2+1)duРасширить.=∫(u8+u6)duВычислить интеграл.=19u9+17u7+CПодставить tanx=u.=19tan9x +17tan7x+C.∫tan6xsec4xdx=∫tan6x(tan2x+1)sec2xdxLetu=tanxanddu=sec2xdx.=∫u6(u2+1)duExpand.=∫(u8+u6)duВычислите интеграл.=19u9+17u7+CSsubstitutetanx=u .=19tan9x+17tan7x+C.

Пример 3.

16

Интегрирование ∫tankxsecjxdx∫tankxsecjxdx, когда kk нечетно

Вычислить ∫tan5xsec3xdx.∫tan5xsec3xdx.

Решение

Поскольку питание на tanxtanx нечетное, начните с перезаписи tan5xsec3x=tan4xsec2xsecxtanx.tan5xsec3x=tan4xsec2xsecxtanx. Таким образом,

tan5xsec3x=tan4xsec2xsecxtanx.Writetan4x=(tan2x)2.∫tan5xsec3xdx=∫(tan2x)2sec2xsecxtanxdxUsetan2x=sec2x−1.=∫(sec2x−1)2sec2xsecxtanxdxLetu=exp.2xanddu=secxtanxdx.=∫ =∫(u6−2u4+u2)duIntegrate.=17u7−25u5+13u3+CSubstitutesecx=u.=17sec7x−25sec5x+13sec3x+C.tan5xsec3x=tan4xsec2xsecxtanx.Writetan4x=(tan2x)2.∫tan5xsec3xdx=∫(tan5xsec3xdx)2secxxsecxtan2xd =sec2x−1.=∫(sec2x−1)2sec2xsecxtanxdxLetu=secxanddu=secxtanxdx.=∫(u2−1)2u2duExpand.=∫(u6−2u4+u2)duIntegrate.=17u7−25u5+13u3+CSubstitutesecx=u.= 17сек7x−25сек5x+13сек3x+C.

Пример 3.17

Интегрирование ∫tankxdx∫tankxdx, где kk — нечетное, а k≥3k≥3

Вычислить ∫tan3xdx. ∫tan3xdx.

Решение

Начните с перезаписи tan3x=tanxtan2x=tanx(sec2x-1)=tanxsec2x-tanx.tan3x=tanxtan2x=tanx(sec2x-1)=tanxsec2x-tanx. Таким образом,

∫tan3xdx=∫(tanxsec2x−tanx)dx=∫tanxsec2xdx−∫tanxdx=12tan2x−ln|secx|+C.∫tan3xdx=∫(tanxsec2x−tanx)dx=∫tanxsec2xdx−∫tanxdx=12tan2x−ln |секх|+С.

Для первого интеграла используйте замену u=tanx.u=tanx. Для второго интеграла используйте формулу.

Пример 3.18

Интеграция ∫sec3xdx∫sec3xdx

Интеграция ∫sec3xdx.∫sec3xdx.

Решение

Этот интеграл требует интегрирования по частям. Для начала пусть u=secxu=secx и dv=sec2xdx.dv=sec2xdx. Эти варианты делают du=secxtanxdu=secxtanx и v=tanx.v=tanx. Таким образом,

∫sec3xdx=secxtanx−∫tanxsecxtanxdx=secxtanx−∫tan2xsecxdxSimplify.=secxtanx−∫(sec2x−1)secxdxSubstitutetan2x=sec2x−1.=secxtanx+∫secxdx−∫sec3xdx+lxRewrite.=secxtanx|nxdx+lx ∫sec3xdx. Evaluate∫secxdx.∫sec3xdx=secxtanx-∫tanxsecxtanxdx=secxtanx-∫tan2xsecxdxSimplify.=secxtanx-∫(sec2x-1)secxdxSubstitutetan2x=sec2x-1.=secxtanx+nsecxdx-∫l+sec3xsecxxПерезаписать. tanx|−∫sec3xdx.Вычислить∫secxdx.

Теперь у нас есть

∫sec3xdx=secxtanx+ln|secx+tanx|−∫sec3xdx.∫sec3xdx=secxtanx+ln|secx+tanx|−∫sec3xdx.

Поскольку интеграл ∫sec3xdx∫sec3xdx снова появился в правой части, мы можем найти ∫sec3xdx∫sec3xdx, прибавив его к обеим частям. При этом мы получаем

2∫sec3xdx=secxtanx+ln|secx+tanx|.2∫sec3xdx=secxtanx+ln|secx+tanx|.

Разделив на 2, получим

∫sec3xdx=12secxtanx+12ln|secx+tanx|+C.∫sec3xdx=12secxtanx+12ln|secx+tanx|+C.

Контрольно-пропускной пункт 3.12

Оценка ∫tan3xsec7xdx.∫tan3xsec7xdx.

Формулы приведения

Вычисление ∫secnxdx∫secnxdx для значений nn, где nn нечетно, требует интегрирования по частям. Кроме того, мы также должны знать значение ∫secn-2xdx∫secn-2xdx, чтобы вычислить ∫secnxdx. ∫secnxdx. Вычисление ∫tannxdx∫tannxdx также требует возможности интегрирования ∫tann-2xdx.∫tann-2xdx. Чтобы упростить процесс, мы можем вывести и применить следующие формулы снижения мощности. Эти правила позволяют нам заменить интеграл степени secxsecx или tanxtanx интегралом меньшей степени secxsecx или tanx.tanx.

Правило: формулы приведения для ∫secnxdx∫secnxdx и ∫tannxdx∫tannxdx

-2xdx

(3.6)

∫tannxdx=1n-1tann-1x-∫tann-2xdx∫tannxdx=1n-1tann-1x-∫tann-2xdx

(3.7)

Первое правило снижения мощности может быть проверено путем интегрирования по частям. Второе можно проверить, следуя описанной стратегии интегрирования нечетных степеней tanx.tanx.

Пример 3.19

Пересмотр ∫sec3xdx∫sec3xdx

Применить формулу сокращения для вычисления ∫sec3xdx.∫sec3xdx.

Решение

Применяя первую формулу приведения, получаем С.

Пример 3.20

Использование формулы приведения

Вычисление ∫tan4xdx.∫tan4xdx.

Решение

Применяя формулу приведения к ∫tan4xdx∫tan4xdx, получаем

∫tan4xdx=13tan3x−∫tan2xdx=13tan3x−(tanx−∫tan0xdx)Применим формулу приведения к ∫tan2xdx.=13tan3x−tanx+∫1dxSimplify.=13tan x+C.Evaluate∫1dx.∫tan4xdx=13tan3x-∫tan2xdx=13tan3x-(tanx-∫tan0xdx)Применить формулу приведения к ∫tan2xdx.=13tan3x-tanx+∫1dxSimplify.=13tan3x-tanx+x+C.Evaluate∫ 1дкс.

Контрольно-пропускной пункт 3.13

Примените формулу приведения к ∫sec5xdx.∫sec5xdx.

Раздел 3.2 Упражнения

Заполните пропуск, чтобы сделать утверждение верным.

69.

sin2x+_______=1sin2x+_______=1

70.

sec2x−1=_______sec2x−1=_______

Используйте тождество, чтобы уменьшить степень тригонометрической функции до тригонометрической функции, возведенной в первую степень.

71.

sin2x=_______sin2x=_______

72.

cos2x=_______cos2x=_______

Оцените каждый из следующих интегралов на и — замещение.

73.

∫sin3xcosxdx∫sin3xcosxdx

74.

∫cosxsinxdx∫cosxsinxdx

75.

∫tan5(2x)sec2(2x)dx∫tan5(2x)sec2(2x)dx

76.

∫sin7(2x)cos(2x)dx∫sin7(2x)cos(2x)dx

77.

∫tan(x2)sec2(x2)dx∫tan(x2)sec2(x2)dx

78.

∫tan2xsec2xdx∫tan2xsec2xdx

Вычислите следующие интегралы, используя рекомендации по интегрированию степеней тригонометрических функций. Используйте CAS для проверки решений. ( Примечание : Некоторые задачи можно решить с помощью изученных ранее методов интегрирования. )

79.

∫sin3xdx∫sin3xdx

80.

∫cos3xdx∫cos3xdx

81.

∫sinxcosxdx∫sinxcosxdx

82.

∫cos5xdx∫cos5xdx

83.

∫sin5xcos2xdx∫sin5xcos2xdx

84.

∫sin3xcos3xdx∫sin3xcos3xdx

85.

∫sinxcosxdx∫sinxcosxdx

86.

∫sinxcos3xdx∫sinxcos3xdx

87.

∫secxtanxdx∫secxtanxdx

88.

∫tan(5x)dx∫tan(5x)dx

89.

∫tan2xsecxdx∫tan2xsecxdx

90.

∫tanxsec3xdx∫tanxsec3xdx

91.

∫sec4xdx∫sec4xdx

92.

∫cotxdx∫cotxdx

93.

∫cscxdx∫cscxdx

94.

∫tan3xsecxdx∫tan3xsecxdx

Для следующих упражнений найдите общую формулу для интегралов.

95.

∫sin2axcosaxdx∫sin2axcosaxdx

96.

∫sinaxcosaxdx.∫sinaxcosaxdx.

Используйте формулы двойного угла для вычисления следующих интегралов.

97.

∫0πsin2xdx∫0πsin2xdx

98.

∫0πsin4xdx∫0πsin4xdx

99.

∫cos23xdx∫cos23xdx

100.

∫sin2xcos2xdx∫sin2xcos2xdx

101.

∫sin2xdx+∫cos2xdx∫sin2xdx+∫cos2xdx

102.

∫sin2xcos2(2x)dx∫sin2xcos2(2x)dx

Для следующих упражнений оцените определенные интегралы. По возможности выражайте ответы в точной форме.

103.

∫02πcosxsin2xdx∫02πcosxsin2xdx

104.

∫0πsin3xsin5xdx∫0πsin3xsin5xdx

105.

∫0πcos(99x)sin(101x)dx∫0πcos(99x) грех (101x) дх

106.

∫−ππcos2(3x)dx∫−ππcos2(3x)dx

107.

∫02πsinxsin(2x)sin(3x)dx∫02πsinxsin(2x)sin(3x)dx

108.

∫04πcos(x/2)sin(x/2)dx∫04πcos(x/2)sin(x/2)dx

109.

∫π/6π/3cos3xsinxdx∫π/6π/3cos3xsinxdx (Округлите этот ответ до трех знаков после запятой.)

110.

∫−π/3π/3sec2x−1dx∫−π/3π/3sec2x−1dx

111.

∫0π/21−cos(2x)dx∫0π/21−cos(2x)dx

112.

Найдите площадь области, ограниченной графиками уравнений y=sinx,y=sin3x,x=0,andx=π2.y=sinx,y=sin3x,x=0,x=π2.

113.

Найдите площадь области, ограниченной графиками уравнений y=cos2x,y=sin2x,x=−π4,andx=π4.y=cos2x,y=sin2x,x=−π4,x=π4.

114.

Частица движется прямолинейно с функцией скорости v(t)=sin(ωt)cos2(ωt).v(t)=sin(ωt)cos2(ωt). Найдите его функцию положения x=f(t)x=f(t), если f(0)=0.f(0)=0.

115.

Найдите среднее значение функции f(x)=sin2xcos3xf(x)=sin2xcos3x на интервале [−π,π].[−π,π].

Для следующих упражнений решите дифференциальные уравнения.

116.

dydx=sin2x.dydx=sin2x. Кривая проходит через точку (0,0).(0,0).

117.

dydθ=sin4(πθ)dydθ=sin4(πθ)

118.

Найдите длину кривой y=ln(cscx),π4≤x≤π2.y=ln(cscx),π4≤x≤π2.

119.

Найдите длину кривой y=ln(sinx),π3≤x≤π2.y=ln(sinx),π3≤x≤π2.

120.

Найдите объем, образованный вращением кривой y=cos(3x)y=cos(3x) вокруг оси x , 0≤x≤π36,0≤x≤π36.

Используйте эту информацию для следующих упражнений: Внутренний продукт двух функций f и g над [a,b][a,b] определяется формулой f(x)·g(x)=〈f, g〉=∫abf·gdx.f(x)·g(x)=〈f,g〉=∫abf·gdx. Две отдельные функции f и g называются ортогональными, если 〈f,g〉=0.〈f,g〉=0.

121.

Покажите, что {sin(2x),cos(3x)}{sin(2x),cos(3x)} ортогональны на интервале [−π,π].[−π,π].

122.

Вычислить ∫−ππsin(mx)cos(nx)dx. ∫−ππsin(mx)cos(nx)dx.

123.

Интегрировать y′=tanxsec4x.y′=tanxsec4x.

Для каждой пары интегралов определите, какой из них сложнее вычислить. Объясните свои рассуждения.

124.

∫sin456xcosxdx∫sin456xcosxdx или ∫sin2xcos2xdx∫sin2xcos2xdx

125.

∫tan350xsec2xdx∫tan350xsec2xdx или ∫tan350xsecxdx∫tan350xsecxdx

Тригонометрические интегралы — предметный тест GRE: математика

• Войти
• Биографии репетитора
• Подготовка к тесту

  СРЕДНЯЯ ШКОЛА

  • ACT Репетиторство
  • SAT Репетиторство
  • Репетиторство PSAT
  • ASPIRE Репетиторство
  • ШСАТ Репетиторство
  • Репетиторство STAAR

  ВЫСШАЯ ШКОЛА

  • Репетиторство MCAT
  • Репетиторство GRE
  • Репетиторство по LSAT
  • Репетиторство по GMAT

  K-8

  • Репетиторство AIMS
  • Репетиторство по HSPT
  • Репетиторство ISEE
  • Репетиторство ISAT
  • Репетиторство по SSAT
  • Репетиторство STAAR

  Поиск 50+ тестов

• Академическое обучение

  репетиторство по математике

  • Алгебра
  • Исчисление
  • Элементарная математика
  • Геометрия
  • Предварительный расчет
  • Статистика
  • Тригонометрия

  репетиторство по естественным наукам

  • Анатомия
  • Биология
  • Химия
  • Физика
  • Физиология

  иностранные языки

  • французский
  • немецкий
  • Латинский
  • Китайский диалект
  • Испанский

  начальное обучение

  • Чтение
  • Акустика
  • Элементарная математика

  прочие

  • Бухгалтерский учет
  • Информатика
  • Экономика
  • Английский
  • Финансы
  • История
  • Письмо
  • Лето

  Поиск по 350+ темам

• О
  • Обзор видео
  • Процесс выбора наставника
  • Онлайн-репетиторство
  • Мобильное обучение
  • Мгновенное обучение
  • Как мы работаем
  • Наша гарантия
  • Влияние репетиторства
  • Обзоры и отзывы
  • Освещение в СМИ
  • О преподавателях университета

Звоните прямо сейчас, чтобы записаться на обучение:

(888) 888-0446

Все предметные тесты GRE: математические ресурсы

2 диагностических теста 148 практических тестов Вопрос дня Карточки Обучение по концепции

Предметный тест GRE: помощь по математике » Расчет » Производные и интегралы » Интегралы » Тригонометрические интегралы

Проинтегрируйте следующее.

Возможные ответы:

Правильный ответ:

Объяснение:

Мы можем интегрировать функцию, используя подстановку, где  так .

Просто сосредоточьтесь на интеграции  sine сейчас: 

Последний шаг — повторно вставить замену:

 

Сообщить об ошибке

Интегрируйте следующее.

Возможные ответы:

Правильный ответ:

Объяснение:

Мы можем интегрировать с помощью подстановки:

и так

Теперь мы можем просто сосредоточиться на интегрировании косинуса :

После завершения интеграции мы можем снова вставить нашу замену:

Сообщить об ошибке

Вычислить следующий интеграл.

Возможные ответы:

Правильный ответ:

Объяснение:

Повторный вызов:  Идентичность

Интеграл можно переписать как 

. Из-за приведенного выше тождества триггера мы можем переписать его по-другому:

Теперь мы можем интегрировать с помощью замены где   и 

               

Наконец, мы повторно вставляем нашу замену:

Сообщить об ошибке

Вычислить следующий интеграл.

Возможные ответы:

Правильный ответ:

Объяснение:

Вспомнить : Тождество триггера

Мы можем переписать интеграл, используя приведенное выше тождество, как

Теперь мы можем решить интеграл, используя замену и

Возможные ответы:

Производное не может быть найдено

Правильный ответ:

Правильный ответ:

. Правильный ответ:

9696

.Пояснение:

Это один из тригонометрических интегралов, который необходимо запомнить.

 

Other common trig derivatives that should be memorized are:

 

 

Report an Error

Evaluate: 

Possible Answers:

Correct answer:

Объяснение:

1) 1/2 является константой, поэтому выводится вперед.

2) Интеграл от cos(x) равен sin(x) по определению.

3) Запись пределов для оценки: 

4) Использование единичного круга,    и .

5)Упрощение:  

Сообщить об ошибке

Уведомление об авторских правах

Посмотреть репетиторов

Alexia
Сертифицированный репетитор

Колумбийский университет биохимии, бакалавр.

No related posts.