Тригонометрические косинус уравнения: Арккосинус и уравнение cos x = a — урок. Алгебра, 10 класс.

Понятие о тригонометрическом уравнении. Простейшие тригонометрические уравнения. — Сайт Александра Бабаева

Содержание

1. Понятие о тригонометрическом уравнении.
2. Простейшие тригонометрические уравнения.
3. Таблица решений простейших тригонометрических уравнений.
4. Ограничения тригонометрических уравнений.

Понятие о тригонометрическом уравнении.

Определение.

Уравнение называется тригонометрическим, если в нём содержится любая тригонометрическая функция.

Например, уравнения $\sin{x} — 1 = 0$, $1-2\cos{x}=4$ и $\sqrt{3}\sin{x}-2\cos{x}=0$ тригонометрические, а $2-x=0$ — нет.

В силу того, что тригонометрическая функция периодична, тригонометрические уравнения имеют множество решений или не имеют их вообще.

Определение.

Под решением тригонометрического уравнения понимается такой набор чисел $x$, который при подстановке в уравнение обращает его в тождество.

Существуют 2 основных способа решения тригонометрических уравнений:

• графический способ, который заключается в том, что строятся графики левой и правой части уравнения и ищутся точки их пересечения;
• аналитический способ, суть которого заключается в применении специальных формул.

Простейшие тригонометрические уравнения.

Определение.

Под простейшими тригонометрическими уравнениями мы будем понимать тригонометрические уравнения, в левую часть которых входит только либо синус, либо косинус, а в правую — одно из чисел: $-1; \ 0; \ 1$.

Решим несколько простейших тригонометрических уравнений.

1. $\sin{x} = 1$

Начертим два графика: $y=\sin{x}$ и $y=1$

Видим, что количество точек пересечения достаточно велико, а, значит, необходимо выявить закономерность. Так как тригонометрические функции являются периодическими, то все точки, попавшие на 1-ый положительный период, будут периодически повторятся. Рассмотрим решения, попавшие на 1-ый период:

Это только одна точка: $\frac{\pi}{2}$. Периодом синуса является $2\pi$, так что получаем ответ:

$x = \frac{\pi}{2} + 2\pi n, \ n \in \mathbb{Z}$.

2. $\cos{x} = 0$

Начертим два графика: $y=\cos{x}$ и $y=0$

Видим, что количество точек пересечения достаточно велико, а, значит, необходимо выявить закономерность. Так как тригонометрические функции являются периодическими, то все точки, попавшие на 1-ый положительный период, будут периодически повторятся. Рассмотрим решения, попавшие на 1-ый период:

Видим, что получается 2 решения, попадающих «на период»: $x_{1}=\frac{\pi}{2}$ и $x_{2}=\frac{3\pi}{2}$.

Замечание.

Две точки решения получаются только у функций синус и косинус. Так как тангенс и котангенс монотонные (и на периоде в том числе), то они имеют лишь только одну точку пересечения с прямой $y=a$.

Получены два решения:

\(\left\{ \begin{array}{c} x_{1} = \frac{\pi}{2} + 2\pi n, \\ x_{2} = \frac{3\pi}{2} + 2\pi n, \end{array} \right. \)

которые можно попытаться объединить в одно.

Замечание.

Не все решения можно объединить в одно. Если это невозможно, то в ответ выписываются 2 решения.

Проверим расстояние между всеми точками (обычно достаточно проверить расстояние между 4 точками), чтобы убедиться, что объединение возможно. Несложно увидеть, что в нашем случае оно всегда равно $\pi$. Тогда наши решения объединяются в одно и мы получаем ответ:

$x = \frac{\pi}{2} + \pi n, \ n \in \mathbb{Z}$

Таблица решений простейших тригонометрических уравнений.

Уравнение	$f(x) = \sin{x}$	$f(x) = \cos{x}$
$f(x)=1$	$x = \frac{\pi}{2} + 2\pi n$	$x =2\pi n$
$f(x)=0$	$x = \pi n$	$x = \frac{\pi}{2} + \pi n$
$f(x)=-1$	$x = — \frac{\pi}{2} + 2\pi n$	$x = \pi + 2\pi n$

Ограничения тригонометрических уравнений.

Очевидно, что тригонометрические функции $\tg$ и $\ctg$ в силу неограниченности по области значений и монотонности всегда имеют одно решение для любого $a$.

А для тригонометрических функций $\sin$ и $\cos$ справедливы следующие утверждения.

Утверждение

Если $|a| > 1$, то не существует  решений тригонометрического уравнения $\sin{x} = a$ или $\cos{x} = a$.

Действительно, так как область значения тригонометрических функций $\sin$ и $\cos$ является отрезком $[-1;1]$, то любая прямая, лежащая выше прямой $y=1$ и ниже прямой $y = -1$, не будет пересекать график тригонометрических функций.

Утверждение

Если $|a| = 1$, то тригонометрические уравнения $\sin{x} = a$ или $\cos{x} = a$ имеют ровно одно решение на полуинтервале $[0;2\pi)$ (далее, периоде).

Действительно, прямая $y=1$ и прямая $y = -1$ пересекают графики тригонометрических функций ровно в одной точке.

Утверждение

Если $|a| < 1$, то тригонометрические уравнения $\sin{x} = a$ или $\cos{x} = a$ имеют ровно два решения на периоде.

Действительно, прямая $y=a$ пересекает графики тригонометрических функций ровно в двух точках.

Информация о записи:

08 марта 2018 в 21:58:51

08 декабря 2018 в 19:10:51

Алгебра, Тригонометрические уравнения и неравенства

тригонометрические уравнения, тригонометрические функции, уравнения

Понятие о тригонометрическом уравнении. Простейшие тригонометрические уравнения.

**/ ?>

Лекция по тригонометрии №5

Тригонометрические уравнения, их виды и методы решения

Великий физик, математик и политик А. Эйнштейн заметил: «Мне приходится делить время между политикой и уравнениями. Однако, уравнения гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно, ведь они основа всех наук». Действительно, самые разные процессы описываются с помощью тригонометрических уравнений, в том числе и биологические, например, слух, зрение, восприятие ультрафиолета, передача возбуждения по нервной ткани, работа сердца и мозга, прием и воспроизведение звука и т. д. Сегодня на уроке мы продолжим разговор про тригонометрические уравнения, вспомним про то, что уже знаем и научимся определять и решать уравнения нового типа. Тригонометрия традиционно включается в материалы экзаменов, конкурсов, олимпиад. В связи с этим очень важно научиться решать тригонометрические уравнения, распознавать их виды и правильно определять методы их решения. С этого и начнем. (Стадия вызова)

1. Вопросы по домашнему заданию. Какие способы решения тригонометрических уравнений вы использовали в №199, №200(Проверка у доски, в это время математический диктант)

2 . Математический диктант на знание теоретического материала по предыдущему тригонометрическому теоретическому материалу:

3. На доске написан набор тригонометрических уравнений. Учащимся предлагается прочитав уравнение, определить способ его решения.

№	Уравнение	Способ решения
	cos (4х – 2) = -1 /2;	формула общего вида решения тригонометрических уравнений
	cos2х – 2cos х = 0;	вынесение за скобку общего множителя
	cos2х– sin2х = 1;	основные тр-кие формулы
	3sin2х – 5sin х – 2 = 0;	сводимое к квадратному
	2sin х – 3cos х = 0;	?
	(tg х— √3)(2sin + 1) = 0;	равенство нулю произведения
	sinх=0	с помощью единичного круга
	3sin²х+sinх cos х= 2cos²х.	?
	3sin²х+sinх cos х — 2cos²х = 4	?

Учащиеся называют уравнение и обозначают способ его решения. В результате остаются три уравнения, для которых не подходит ни один из известных студентам способов решения: 2sin х – 3cos х = 0; 3sin²х+sinх cos х=2cos²х; 3sin²х+sinх cos х — 2cos²х = 4

Два первых уравнения в математике называются однородными, а третье – неоднородным, для каждого есть свой способ решения они нам пока не известны но уметь их решать очень важно.

Тригонометрические уравнения, их виды и методы решения

Пятое, восьмое и девятое уравнения решить известными способами не удалось. Что можно сказать о них?

1. Уравнение вида аsin x + bcos x = 0, где а≠0, b≠0 называют однородным тригонометрическим уравнением первой степени;

2. Уравнение вида аsin²х + bsin х cos х + c cos² x = 0 где a 0, b0, с 0 называют однородным тригонометрическим уравнением второй степени.

Вообще, однородным относительно sin х и cos х называется уравнение вида а₀sinⁿ х + а₁sin^n-1хcos х+…+а_n-1 sin хcos ^n-1 х+а_ncosⁿх=0, где а₀, а₁, …а_{n– действительные числа. Сумма степеней синуса и косинуса в каждом слагаемом левой части одинакова и равна числу n, называемом показателем однородности.}

Отличительные признаки однородных уравнений: а) все одночлены имеют одинаковую степень, б) свободный член равен нулю, в) в уравнении присутствуют степени с двумя различными основаниями.

Примеры: — однородное уравнение первой степени; — однородное уравнение второй степени.

При делении уравнения аsin x + bcos x = 0, где а≠0, b≠0 на cos x ≠ 0 корни этого уравнения не теряются.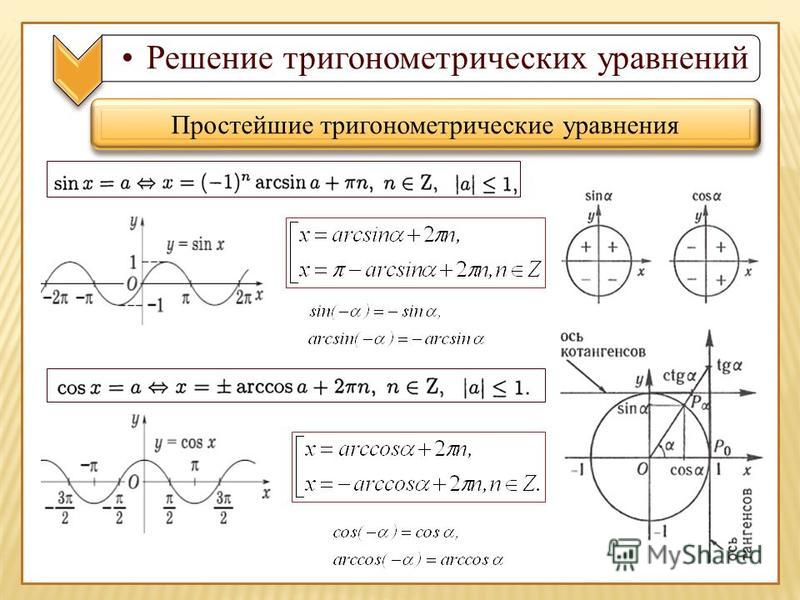 При делении уравнения аsin²х + bsin х cos х + c cos² x = 0, где a 0, b0, с 0 на cos²x ≠ 0 корни этого уравнения так же не теряются.

Следовательно, основной способ решения однородных уравнений заключается в делении на старшую степень синуса или косинуса.

Рассмотрим тригонометрическое уравнение второй степени. И предположим обратное. Пусть cosх равен нулю, но тогда в уравнении аsin²х + bsin х cos х + c cos² x = 0 и sinх будет равен нулю, но sinх и cosх одновременно не могут равняться 0, согласно основному тригонометрическому тождеству. Аналогичная ситуация и для однородного тригонометрического уравнения первой степени. Значит, при делении потери корней не происходит, а, следовательно, делить можно.

1. Нужно найти среди уравнений однородные, определить их вид и указать способ решения.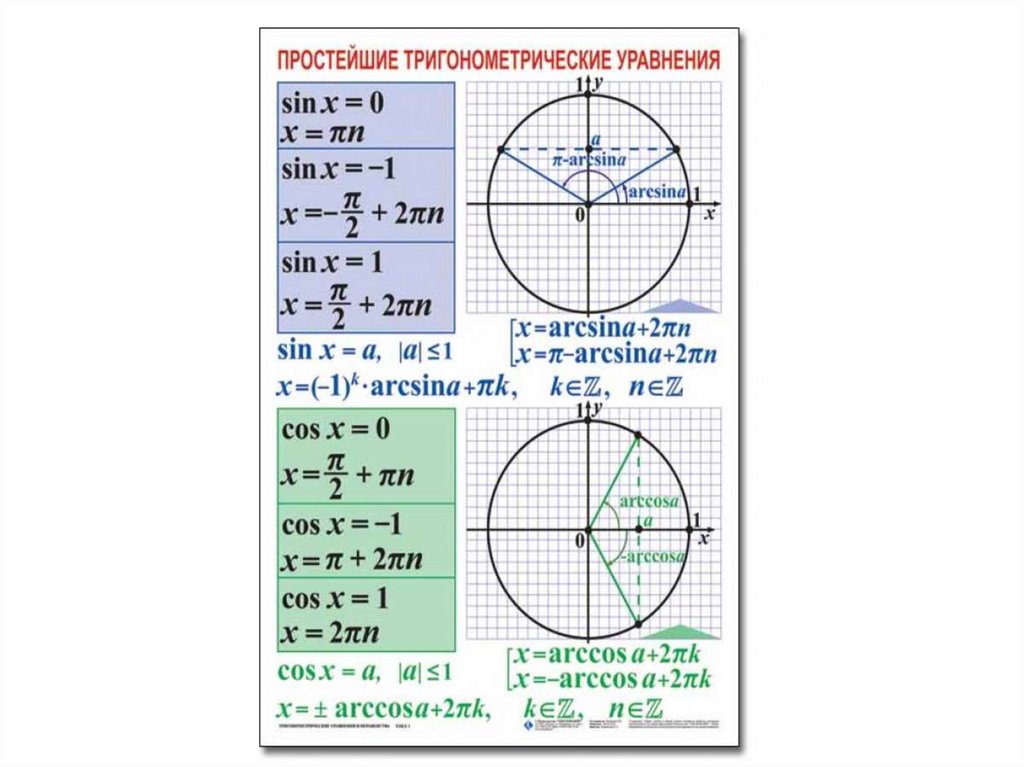

1. sinx = 2cosx – однородное первой степени

2. √3sin3x – cos3x = 0 – однородное первой степени

3. sin²x – 2sinx – 3 = 0 –сводимое к квадратному

4. 2cos²x + 3sin²x + 2cosx = 0 – сводимое к квадратному

5. 6sin²x – cos²x – 5sinxcosx = 0 – однородное второй степени

2. Вернемся к нашим нерешенным уравнениям и попробуем решить их.

1. 2sin х – 3cos х = 0;

2. 3sin²х+sinх cos х=2cos²х.

3. Решите другие однородные тригонометрические уравнения:

1. 3sin² х — 5sin х cos х + 2 cos²х=0

2. sin³ х — sin² х cos х — 4sin х cos² х + 4 cos³х=0

3. 4sin х cos х + 6 cos²х=1(рассмотреть два способа решения)

4. sin^{х+ cosх=√2}

Неоднородные уравнения вида

аsin x + bcos x = k и

аsin²х + bsin х cos х + ccos² x = k решаются приведением к однородному виду путем замены:

k = k*1 = k*(sin²x+cos²x) = k* sin²x + k*cos²x и последующим переносом этих слагаемых в левую часть равенства. Таким образом после приведения подобных слагаемых мы получаем однородное уравнение второй степени, имеющее вид:

(b – k)sin²х + bsin х cos х + (c – k) cos² x = 0,

которое стандартно решается уже разобранным способом.

Итак теперь мы можем решить последнее оставшееся в таблице уравнение и еще одно, очень похожее на него, сделаем это у доски.

1. 3sin²х + sinх cos х — 2cos²х = 4

2. 3sin² х — 5sin х cos х + 2 cos²х = 5

Сегодня вы познакомились с последней темой раздела «Тригонометрия». На следующем занятии будет проводиться итоговое повторение и контрольная работа. Поэтому на дом, кроме теоретических вопросов, рассмотренных по сегодняшней теме, нужно повторить всю теорию раздела и решить следующие уравнения:

3. 5sin² x + 3sin x · cos x – 4 = 0.

4. tg² x + 3tg x – 4 = 0.

5. 2 cos(3x – π/4) = -√2

6. Кластер «Тригонометрические уравнения»

Закрепление изученного материала

Пример 1. Найдите корни уравнения   принадлежащие промежутку 

Решение. Используем вторую формулу на рисунке. Здесь и далее полагаем   (на всякий случай, эта запись означает, что числа   и   принадлежат множеству целых чисел):

 

Арккосинус   есть число, заключенное в интервале от   до  , косинус которого равен  .

Арксинус  есть число, заключенное в интервале от   до  , косинус которого равен  .

Другими словами, нам нужно подобрать такое число из промежутка   косинус которого был бы равен   Это число   Используя это, получаем:  

Задача для самостоятельного решения №1.  

Найдите корни уравнения   принадлежащие промежутку 

Пример 2. Найдите корни уравнения

   принадлежащие промежутку 

Решение. Подобные уравнения решаются один весьма интересным, на мой взгляд, способом. Разделим обе части на  , уравнение тогда примет вид:

Подберем такое число, синус которого равен   а косинус равен   Например, пусть это будет число  . С учетом этого перепишем уравнение в виде:   

Присмотревшись, слева от знака равенства усматриваем разложение косинуса разности   и   Это и есть ключ к решению. Имеем:

  

  

Осуществляем отбор решений, входящих в промежуток  :

1)         

2)         

Задача для самостоятельного решения №2.

 Найдите корни уравнения   принадлежащие промежутку 

Решение тригонометрических уравнений методом замены переменной

Пример 3.  Дано уравнение 

а) Решите уравнение.

б) Укажите корни, принадлежащие отрезке 

Р ешение. Сразу оговорим ограничения, накладываемые на переменную   в этом уравнении:   Откуда взялось это ограничение? Правильно, функция   не существует при этих значениях   Используем замену переменной:   Тогда уравнение принимает вид:

  

Переходим к обратной замене:

Осуществляем отбор решений. Проведем его на этот раз с использованием единичной окружности.

Отбор корней с помощью единичной окружности. Из рисунка видно, что в интересующий нас промежуток входят только два значения из этих серий:   Обратите внимание на один существенный момент. На рисунке точки   и   принадлежат оси тангенсов, а точки       и   — единичной окружности. Очень важно понимать, зачем это нужно для решения данной задачи.Ответ: 

Задача для самостоятельного решения №3.

 Дано уравнение 

a) Решите уравнение.

б) Укажите корни, принадлежащие отрезку 

Ответ:

Решение тригонометрических уравнений методом разложения на множители

Пример 4. Дано уравнение   

a) Решите уравнение.

б ) Укажите корни, принадлежащие отрезку 

Решение. Равносильными преобразования приводим

уравнение к виду:

 

 

  

Осуществляем отбор решений с помощью единичной окружности.

Отбор решений с помощью единичной окружности

Из рисунка видно, что в интересующий нас промежуток входят только два значения из всех этих серий: 

Задача для самостоятельного решения №4. 

Дано уравнение

 

а) Решите уравнение.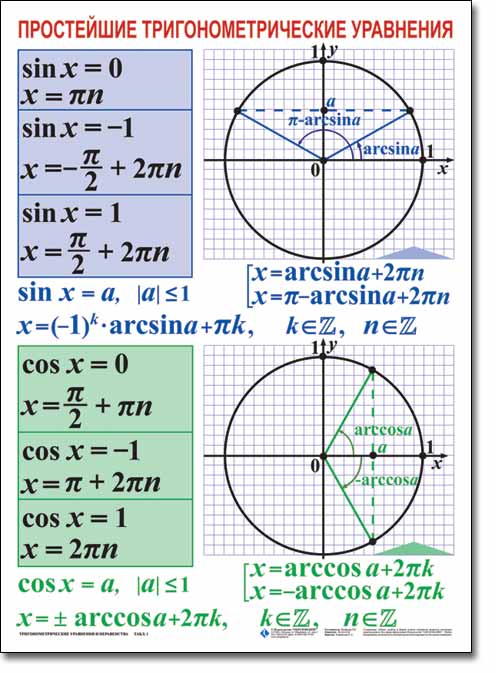

б) Укажите корни, принадлежащие отрезку 

Комбинированные уравнения

При решении уравнений этого типа важно обращать внимание на область допустимых значений входящих в него переменных. Именно поэтому составители вариантов ЕГЭ не просят учеников осуществлять отбор решений из полученных серий ответов. Решение этих уравнений само собой подразумевает выполнение данной математической операции.

Пример 5. Решите уравнение:   

Решение. Данное уравнение эквивалентно следующей системе:

  

Писать, что   нет никакой необходимости, поскольку по условию это выражение равно выражению   которое, в свою очередь, больше или равно нулю.

Решаем первое уравнение системы:

  

  

  

  

Нужно, чтобы   поразмыслив, понимаем, что поэтому из полученной серии ответов нам подходят только Ответ: 

Задача для самостоятельного решения №5.

 Решите уравнение: 

Пример 6. Решите уравнение:

 

Решение. Данное уравение равносильно системе:

  

  

  

Тригонометрическая функция синус положительна в первой и второй координатной четвертях, поэтому из полученных серий выбираем только эту: 

Раз уж мы с этим столкнулись, не лишним будет повторить, какие знаки принимают тригонометрические функций в различных координатных четвертях:

Знаки функций, входящих в тригонометрические уравнения, по координатным четвертям

Ответ: 

Задача для самостоятельного решения №6. 

Решите уравнение:

 

Показать ответ

Пример 7. Решите уравнение:   

Решение.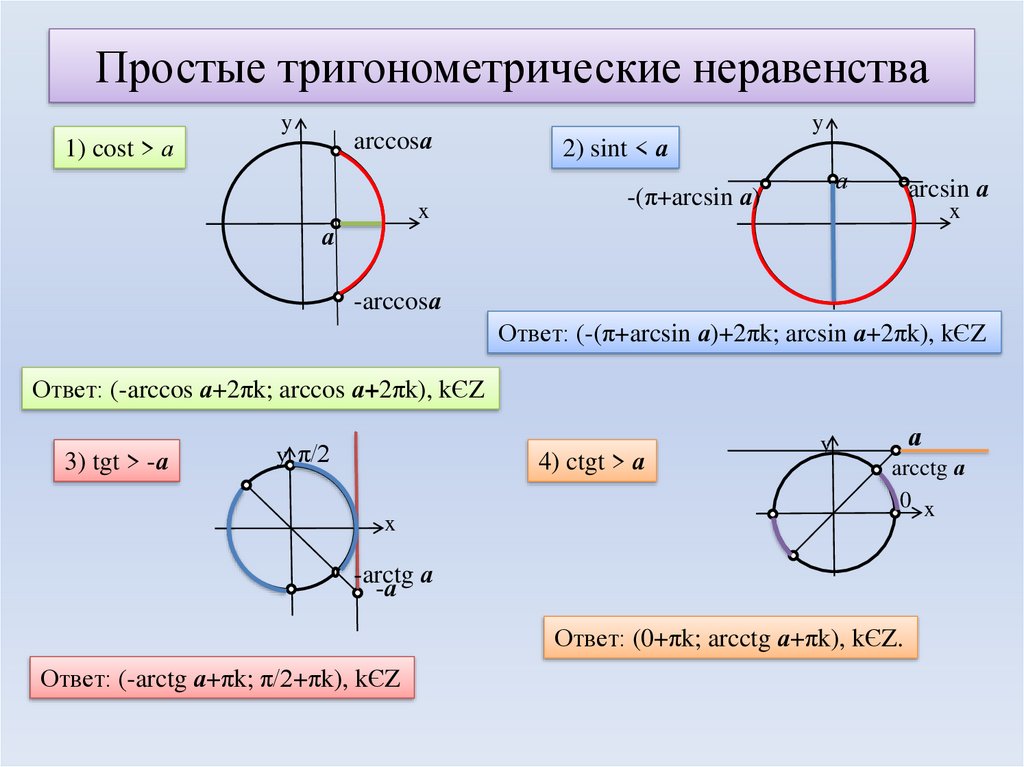  

Область допустимых значения уравнения определяется условием:   то есть

   

Разобьем решение на два случая:

1) Пусть   тогда уравнение принимает вид:

  

  

Последнее равенство неверно, поэтому в данном случае решений у уравнения не будет.

2) Пусть   тогда уравнение принимает вид:

  

  

Условию   удовлетворяет только последняя серия.

Ответ: 

Внеаудиторная самостоятельная работа

Задача для самостоятельного решения №7. 

Решите уравнение: 

Настройка тригонометрических уравнений — тригонометрия

Все ресурсы по тригонометрии

6 диагностических тестов 155 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 Следующая →

Тригонометрия Помощь » Тригонометрические уравнения » Понимание тригонометрических уравнений » Настройка тригонометрических уравнений

Треугольник имеет стороны , ,  длин , ,  соответственно. Угол, противолежащий каждой стороне, называется , , , соответственно. Синус какого угла и косинус другого угла дадут

В ответе сначала укажите синус, а затем косинус.

Возможные ответы:

Правильный ответ:

Объяснение:

Это фигура, описываемая в задаче, и поскольку синус противоположен гипотенузе, а косинус примыкает к гипотенузе, синус  и косинус  дадут правильный ответ.

Сообщить об ошибке

Решить уравнение над доменом  (ответ в градусах).

Возможные ответы:

Правильный ответ:

Объяснение:

Переставьте алгебраически так, чтобы

.

В интервале от 0 до 360 градусов sinx = 1, когда x равен 90 градусам.

Сообщить об ошибке

Решить каждое уравнение в домене  (ответ в градусах).

Возможные ответы:

Правильный ответ:

Объяснение:

Сначала подумайте о значениях углов, для которых . (Это эквивалент приема арктана.)

.

Углы, для которых это верно, составляют 45 градусов и 225 градусов.

Приравняем x-15 к этим двум углам и найдем x, что даст нам 60 и 240. 

Сообщить об ошибке

Решите каждое уравнение в области  (ответ в градусах).

Возможные ответы:

Правильный ответ:

Объяснение:

Измените уравнение так, чтобы

 .

Вспомните углы в интервале от 0 до 360 градусов, для которых sec равно 2.

Это 60 и 300 градусов.

Приравняйте x+7 к этим величинам угла, а затем найдите, что x равно 53 и 293. 

Сообщите об ошибке

Решите каждое уравнение на интервале  

Возможные ответы:

Правильный ответ:

Объяснение:

Измените уравнение так, чтобы

 .

Возьмем квадрат с обеими сторонами и вспомним меры угла, для которого

.

Эти меры в интервале

.

Сообщить об ошибке

Решить каждое уравнение на интервале

Возможные ответы:

Правильный ответ:

Объяснение:

Перестройте уравнение так, чтобы

.

Возьмите квадрат с обеими сторонами и найдите углы, для которых

.

Эти два угла равны  и .

Сообщить об ошибке

Решить  с помощью тригонометрических соотношений.

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти x, сначала составьте тригонометрическое уравнение, используя информацию, представленную на диаграмме. Даны длины двух сторон: гипотенуза, x, и сторона, противоположная заданному углу, 6. Мы можем составить наше уравнение следующим образом:

Синус равен , поэтому мы можем подставить его в:

перекрестное умножение дает нам .

Сообщить об ошибке

Решить  с помощью тригонометрических соотношений.

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти x, сначала составьте тригонометрическое уравнение, используя информацию, представленную на диаграмме.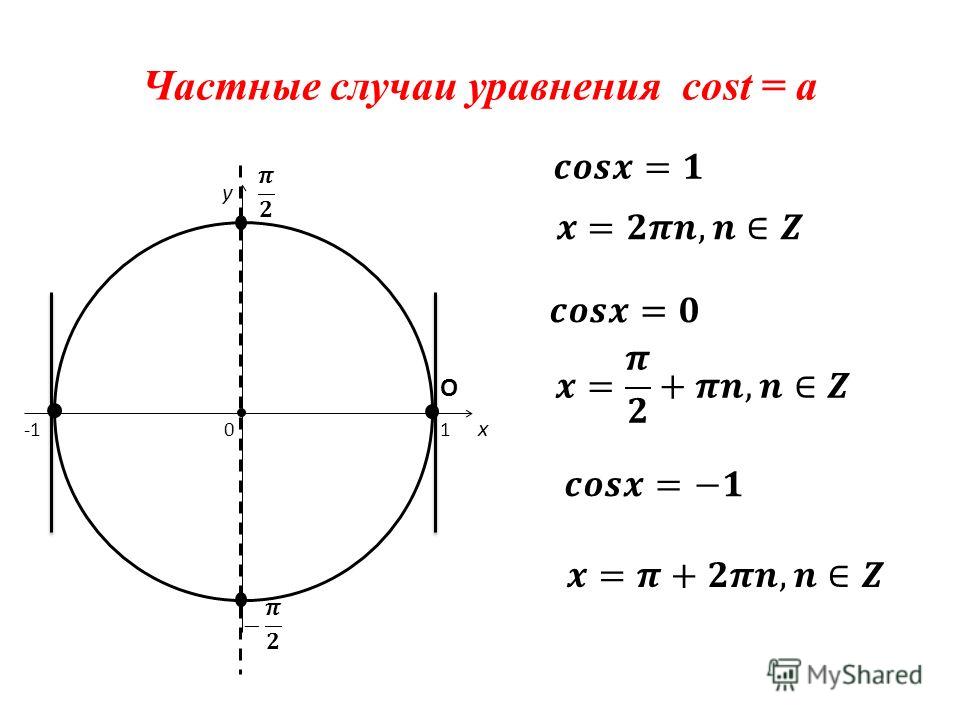 Даны две длины сторон: x, сторона, противоположная углу, и 3, сторона, прилегающая к углу. Это означает, что мы будем использовать касательную. Составьте уравнение следующим образом:

Мы не можем просто узнать тангенс, используя единичную окружность, но мы можем легко вычислить его, используя синус и косинус. Тангенс можно вычислить как синус над косинусом.

Синус равен , а косинус равен . Найдите The Tangent, разделив:

Теперь мы можем заменить это значение в исходное уравнение, которое мы настроили:

Умножьте обе стороны на 3

Отчет о ошибке

для использования TriGomonametric отношения.

Возможные ответы:

Правильный ответ:

Объяснение:

Начните с установки тригонометрического соотношения с использованием заданных углов и сторон.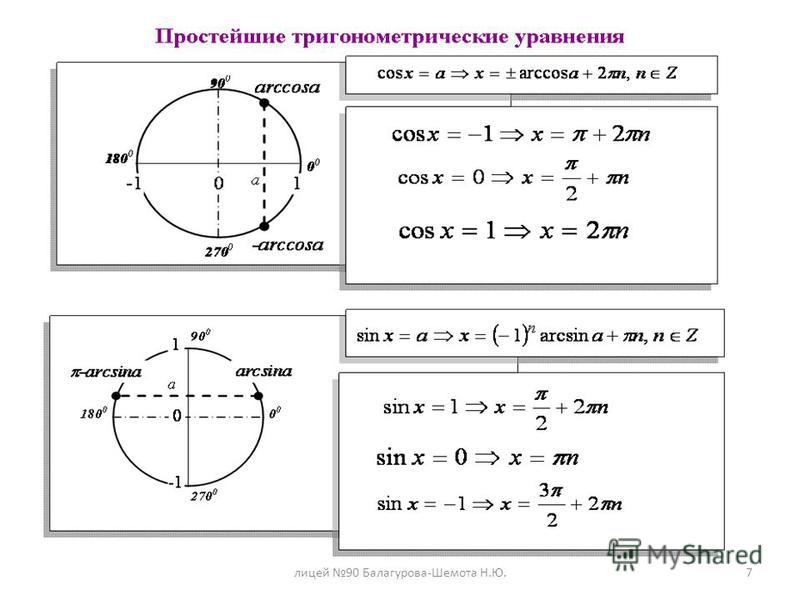 У нас есть длина стороны, прилегающая к углу, 1, и гипотенуза, x, поэтому мы будем использовать косинус:

Косинус равен , так что теперь наше уравнение составляет:

. x должен быть равен 2.

Сообщить об ошибке

Какая из этих синусоидальных функций удовлетворяет следующим критериям?

• Диапазон
• Период
• -перехват

Возможные ответы:

Правильный ответ:

Объяснение:

Исследуя уравнение этой формы:

Мы можем найти , ,  и используя данные подсказки:

• потому что диапазон указывает на амплитуду .
• потому что это середина между  и .
• потому что период не отличается от стандартного.
• . Комбинированный факт, что и (в середине периода) указывает на то, что функция косинуса будет работать — только ответ должен быть задан как функция синуса. Однако, к счастью, мы можем использовать связанное со сдвигом свойство .

В общем, как только мы это осознаем, мы увидим, что
соответствует нашим критериям.

Сообщить об ошибке

← Предыдущая 1 2 Следующая →

Уведомление об авторских правах

Все ресурсы по тригонометрии

6 Диагностические тесты 155 практических тестов Вопрос дня Карточки Учитесь по концепции

4.2: Тригонометрические уравнения — Математика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

7119

• Тед Сандстром и Стивен Шликер
• Государственный университет Гранд-Вэлли через ScholarWorks @ Государственный университет Гранд-Вэлли

Основные вопросы

Следующие вопросы предназначены для того, чтобы направлять наше изучение материала в этом разделе. Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.

• Что такое тригонометрическое уравнение?
• Что значит решить тригонометрическое уравнение?
• Чем тригонометрическое уравнение отличается от тригонометрического тождества?

Мы уже научились решать некоторые типы тригонометрических уравнений. В разделе 2.6 мы узнали, как использовать обратные тригонометрические функции для решения тригонометрических уравнений.

Начало деятельности

Вернитесь к методу из раздела 2.6, чтобы найти все решения уравнения \(\sin(x) = 0,4\).

Тригонометрические уравнения

Когда луч света из точки \(P\) отражается от поверхности в точке \(R\) и освещает точку \(Q\), как показано слева на рис. 4.1, свет создает два углы \(\alpha\) и \(\beta\) с перпендикуляром к поверхности. Угол \(\альфа\) называется угол падения , а угол \(\beta\) называется углом отражения . Закон отражения гласит, что когда свет отражается от поверхности, угол падения равен углу отражения. Что произойдет, если свет пройдет через одну среду (скажем, воздух) из точки \(P\), отклонится в другую среду (скажем, воду) и попадет в точку \(Q\)? Подумайте о том, что произойдет, если вы посмотрите на предмет в стакане с водой. См. рис. 4.1 справа. Снова свет образует два угла \(\alpha\) и \(\beta\) с перпендикуляром к поверхности. Угол \(\альфа\) называется угол падения , а угол \(\бета\) называется углом преломления . Если свет переходит из воздуха в воду, закон преломления гласит, что \[\dfrac{\sin(\alpha)}{\sin(\beta)} = \dfrac{c_{a}}{c_{w}}\ ]

Рисунок \(\PageIndex{1}\): Отражение и преломление.

где \(c_{a}\) — скорость света в воздухе и \(c_{w}\) — скорость света в воде. Отношение \(\dfrac{c_{a}}{c_{w}}\) скорости света в воздухе к скорости света в воде можно рассчитать экспериментально. На практике скорость света в каждой среде сравнивают со скоростью света в вакууме. Отношение скорости света в вакууме к скорости света в воде составляет примерно 1,33. Это называется показателем преломления воды. Показатель преломления воздуха очень близок к 1, поэтому отношение \(\dfrac{c_{a}}{c_{w}}\) близко к 1,33. Обычно мы можем измерить угол падения, поэтому закон преломления может сказать нам, каков угол преломления, решая уравнение (6).

Тригонометрические уравнения возникают в различных ситуациях, таких как закон преломления, и в различных дисциплинах, включая физику, химию и инженерию. По мере разработки тригонометрических тождеств в этой главе мы также будем использовать их для решения тригонометрических уравнений.

Напомним, что уравнение (6) является условным уравнением, поскольку оно не верно для всех допустимых значений переменной. Решить условное уравнение означает найти все значения переменных, которые делают два выражения по обе стороны уравнения равными друг другу.

Уравнения линейного типа

В разделе 2. 6 показано, как решать тригонометрические уравнения, которые можно свести к линейным уравнениям. Мы рассмотрим эту идею в нашем первом примере.

Пример \(\PageIndex{1}\): (Решение уравнения линейного типа)

Рассмотрим уравнение \[2\sin(x) = 1.\]

Мы хотим найти все значения \(x \), которые удовлетворяют этому уравнению. Обратите внимание, что это уравнение очень похоже на линейное уравнение \(2y = 1\) с \(\sin(x)\) вместо \(y\). Таким образом, это тригонометрическое уравнение имеет линейный тип, и мы говорим, что оно линейно относительно \(\sin(x)\). Мы знаем, как решить \(2y = 1\), мы просто делим обе части уравнения на 2, чтобы получить \(y = \dfrac{1}{2}\). Мы можем применить ту же алгебраическую операцию к \(2\sin(x) = 1\), чтобы получить уравнение \[\sin(x) = \dfrac{1}{2}.\] 9{-1}(\dfrac{1}{2}) = \dfrac{\pi}{6}\).

Напомним, однако, это не единственное решение. Первая задача состоит в том, чтобы найти все решения за один полный период синусоидальной функции. Мы можем использовать интервал с \(0 \leq x \leq 2\pi\), но мы часто используем интервал \(-\pi \leq x \leq \pi\). В данном случае это не имеет значения, так как функция синуса положительна во втором квадранте. Используя \(\dfrac{\pi}{6}\) в качестве опорного угла, мы видим, что \(x = \pi — \dfrac{\pi}{6} = \dfrac{5\pi}{6}\ ) является еще одним решением этого уравнения. (Используйте калькулятор, чтобы проверить это.)
Теперь мы используем тот факт, что синусоидальная функция является периодом с периодом \(2\pi\), чтобы написать формулы, которые можно использовать для получения всех решений уравнения \(2\sin(x) = 1\).

Таким образом, углы в первом квадранте равны \(\dfrac{\pi}{6} + k(2\pi)\). а углы во втором квадранте равны \(\dfrac{5\pi}{6} + k(2\pi)\), где \(k\) — целое число. Таким образом, для решений уравнения \(2\sin(x) = 1\) мы пишем \(x = \dfrac{\pi}{6} + k(2\pi)\) или \(x = \ dfrac{5\pi}{6} + k(2\pi)\), где \(k\) — целое число.

Мы всегда можем проверить наши решения, построив обе части уравнения, чтобы увидеть, где пересекаются два выражения. На рис. 4.2 показаны графики \(y = 2\sin(x)\) и \(y = 1\) на интервале \([-2\pi, 3\pi]\). Мы видим, что точки пересечения этих двух кривых совпадают с решениями, которые мы нашли для этого уравнения.

Упражнение \(\PageIndex{1}\)

Найдите точные значения всех решений уравнения \(4\cos(x) = 2\sqrt{2}\). Сделайте это, сначала найдя все решения за один полный период функции косинуса и

Рисунок \(\PageIndex{2}\): Графики \(y = 2\sin(x)\) и \(y = 1\)

затем с использованием свойства периодичности для записи формул, которые могут использоваться для получения всех решений уравнения. Нарисуйте соответствующие графики, чтобы проиллюстрировать ваши решения.

Ответить

Разделим обе части уравнения \(4\cos(x) = 2\sqrt{2}\), чтобы получить \(\cos(x) = \dfrac{\sqrt{2}}{2}\). Итак, \[x = \dfrac{\pi}{4} + k(2\pi)\] или \[x = \dfrac{7\pi}{4} + k(2\pi)\]
, где \(k\) — целое число.

Решение уравнения с использованием обратной функции

При решении уравнения \(2\sin(x) = 1\) мы использовали тот факт, что нам известно, что \(\sin(\dfrac{\pi}{6 }) = \dfrac{1}{2}\).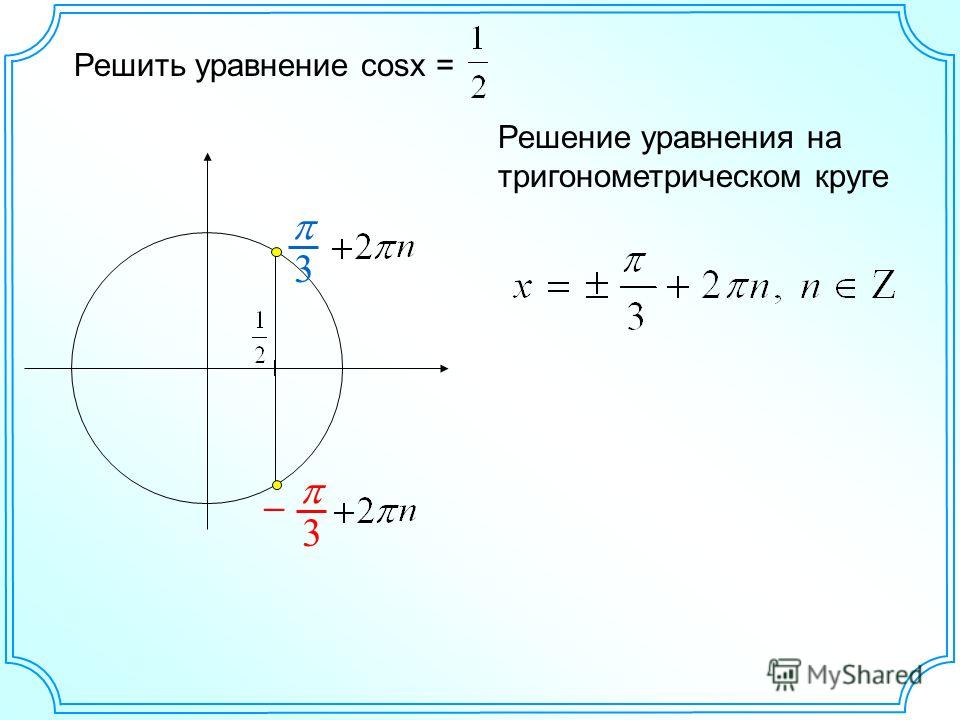 Когда мы не можем использовать одну из общих дуг, мы используем более общий метод использования обратной тригонометрической функции. Это то, что мы сделали в разделе 2.6. См. «Стратегия решения тригонометрической функции» на стр. 158. Мы проиллюстрируем эту стратегию уравнением \(\cos(x) = 0,7\). Начнем с применения функции арккосинуса к обеим частям этого уравнения, чтобы получить 9{-1}(0.7)\]

Это дает единственное решение уравнения, которое находится в интервале \([0, \pi]\). Прежде чем использовать свойство периодичности, нам нужно определить другие решения уравнения за один полный период функции косинуса. Мы можем использовать интервал \([0, 2\pi]\), но проще использовать интервал \([-\pi, \pi]\). Одной из причин этого является следующее так называемое «отрицательное тождество дуги», указанное на странице 82.

\[\cos(-x) = \cos(x)\] для каждого действительного числа \(x\).

9{-1}(0.7) + k(2\pi)\), где \(k\) — некоторое целое число.

Примечание

Примечание. Начальное задание для этого раздела имело уравнение \(\sin(x) = 0,4\). Решениями этого уравнения являются
\(x = \arcsin(0.4) + k(2\pi)\) и \(x = (\pi — \arcsin(0.4)) + k(2\pi)\), где \(k\) — некоторое целое число.

Мы можем записать решения в приближенной форме как \(x = 0,41152 + k(2\pi)\) и \(x = 2,73008 + k(2\pi)\), где \(k\) — целое число.

Упражнение \(\PageIndex{2}\)

9{2}(х — 4\sin(x) = -3)\). Нарисуйте соответствующие графики, чтобы проиллюстрировать ваши решения.

Ответить

Запишем уравнение в виде \(\sin(x) — 4\sin(x) + 3 = 0\) и разложим правую часть, чтобы получить \((\sin(x) — 3)(\sin(x) — 1) = 0\). Итак, мы видим, что \(\sin(x) — 3 = 0\) или \(\sin(x) — 1 = 0\). Однако уравнение \(\sin(x) — 3 = 0\) эквивалентно \(\sin(x) = 3\), и это уравнение не имеет решения. Мы пишем \(\sin(x) — 1 = 0\) как \(\sin(x) = 1\), так что решений

\[х = \dfrac{\pi}{2} + 2\pi k\]

, где \(k\) — целое число.

Резюме

В этом разделе мы изучили следующие важные концепции и идеи:

Тригонометрическое уравнение — это условное уравнение, включающее тригонометрические функции. Если возможно записать уравнение в виде

\(\text{«некоторая тригонометрическая функция от } x \text{«} = \text{число}\)

, мы можем использовать следующую стратегию для решения уравнения уравнение:

• Найти все решения уравнения в пределах одного периода функции. Это часто делается с помощью свойств тригонометрической функции. Довольно часто в течение одного периода будет два решения.
• Используйте период функции, чтобы выразить формулы для всех решений, добавляя целые числа, кратные периоду, к каждому решению, найденному на первом шаге. Например, если функция имеет период \(2\pi\), а \(x_{1}\) и \(x_{2}\) являются единственными двумя решениями в полном периоде, то мы должны написать решения уравнения в виде \[x = x_{1} + k(2\pi), x = x_{2} + k(2\pi)\], где \(k\) — целое число:

Иногда мы можем использовать тригонометрические тождества, чтобы переписать данное уравнение в виде уравнения (1).