Тригонометрические половинного угла формулы: Формулы половинного угла: доказательства (вывод) и примеры

Содержание

основные формулы, шпаргалка, таблица для ЕГЭ

Тригонометрические формулы необходимо знать, чтобы сдать ЕГЭ. Мы собрали основные формулы в одну таблицу, с помощью которой вам будет легко готовиться к экзамену

Тригонометрические формулы для 10 класса по алгебре. Фото: shutterstock.com

Игорь Геращенко Автор КП

Содержание

Основные тригонометрические формулы
Формулы сложения
Формулы двойного угла
Формулы тройного угла
Формулы понижения степени
Таблица с тригонометрическими формулами

История тригонометрии насчитывает более 2 000 лет.

Уже в Древнем Египте, Вавилоне и Китае появились зачатки этой науки. Древнегреческие математики рассматривали ее как часть астрономии. В «Началах» Евклида речь идет уже не только о плоской тригонометрии, но и о сферической.

В последующие годы значительный вклад в науку о соотношениях между углами и сторонами внесли Николай Коперник, Иоганн Кеплер, Исаак Ньютон, Леонард Эйлер, Николай Лобачевский и другие ученые. Если раньше тригонометрия использовалась, в основном, в астрономии, архитектуре и геодезии, то в настоящее время практически нет таких естественных и технических наук, где бы эта дисциплина не нашла своего применения.

Основные тригонометрические формулы

Тригонометрические формулы устанавливают соотношения между основными тригонометрическими функциями: синусом, косинусом, тангенсом и котангенсом. Связей между ними достаточно много, этим и объясняется многообразие тригонометрических формул.

Существуют формулы сложения, двойного угла, тройного угла, формулы понижения степени и целый ряд других.

Шпаргалка для ЕГЭ

Задания по тригонометрии всегда вызывают большие затруднения у учащихся, сдающих ЕГЭ. На ЕГЭ по математике выносятся следующие тригонометрические задания: базовый уровень (задание 7), профильный уровень (задания 4 и 12).

Мы собрали основные тригонометрические формулы, которые помогут при решении задач на ЕГЭ.

Формулы сложения

Тригонометрические формулы сложения показывают то, как тригонометрические функции суммы или разности двух углов находят свое выражение через тригонометрические функции этих углов. Данные формулы являются базой для вывода формул двойного и тройного угла, а также понижения степени.

Скачать формулы сложения

Формулы двойного угла

Формулы двойного угла выражают синус, косинус, тангенс и котангенс угла 2α через тригонометрические функции угла. Данные формулы следуют из формул сложения. Формулы двойного угла используются преимущественно для преобразования тригонометрических выражений.

Скачать формулы двойного угла

Формулы тройного угла

По аналогии с формулами двойного угла мы можем получить формулы тройного угла. Для этого опять-таки используются формулы сложения, а также формулы двойного угла.

Скачать формулы тройного угла

Формулы понижения степени

Тригонометрические формулы понижения степени дают возможность понизить степени тригонометрических функций до первой. Эти формулы помогают переходить от натуральных степеней тригонометрических функций к синусам и косинусам в первой степени, но кратных углов.

Скачать формулы понижения степени

Таблица с тригонометрическими формулами

Чтобы сделать процесс запоминания тригонометрических формул более простым и доступным, мы занесли основные тригонометрические формулы в одну таблицу. Если ее всегда держать перед глазами, постоянно ею пользоваться, то на ЕГЭ не возникнет проблем с выполнением заданий по тригонометрии.

Скачать таблицу с тригонометрическими формулами

Онлайн урок формулы двойного аргумента.

org/ListItem»>Альфашкола
Уроки по математике
Тригонометрия
Формулы двойного аргумента.

В уроке по теме «Тригонометрия это«, 9 и 10 класс, алгебра и геометрия. В тригонометрии изучают основные (синус, косинус, тангенс, котангенс) и обратные (арксинус, арккосинус, арктангенс, арккотангенс) тригонометрические функции, находят их значения для различных тригонометрических углов, выраженных в градусах или радианах. Доказываются основные формулы тригонометрии: тригонометрические тождества, формулы приведения, удвоения аргумента или двойного угла, половинного угла, формулы сложения аргументов, понижения степени.

Составляется таблица значений тригонометрических функций и определяются знаки тригонометрических функций. Смежные понятия: тригонометрическая окружность или круг, теорема синусов, теорема косинусов. В результате уроков происходит построение графиков тригонометрических функций: синусоида и косинусоида, тангенсоида.

Отзывы:

Камо Аркадьевич, добрый день, пишет Вам Екатерина — мама Миши, Вы ему помогаете подготовиться к ОГЭ и подтянуть свои знания по математике. Хотела выразить признательность Вам, поблагодарить за то, что Вам удалось влюбить в математику моего ребенка и мотивировать его на дальнейшее изучение математики в школе и институте, ему тяжело давалась алгебра и геометрия, очень большая нагрузка в школе, учитель экспериментирует в обучении, программа Математическая вертикаль сложная, многие дети не справляются, переходят в другие классы, Вы наша огромная помощь в познании математики, Миша мне говорит, что все, что он знает и может по математике, только благодаря Вам, у Вас отлично получается изложить материал, научить Мишу, Спасибо Вам большое, надеюсь на дальнейшее сотрудничество.

Преподаватель объясняет все доступным и понятным языком. спасибо большое

СПАСИБО! Хороший учитель!

Похожие уроки

Тестирование. 5 класс

Задача 14 (С2). Стереометрия. Сечение многогранников

Проверь себя. Класс 4. Часть 5 (п)

The law of sines.

тригонометрия — Теоретическое значение формул половинного угла

В отличие от законов синусов, косинусов и тангенсов, которые очень хорошо известны, формулы половинного угла кажутся (хотя они робко появляются в математической литературе) не пользуются такая же популярность. Таким образом, хотя закону синусов, косинусов и тангенсов и их применениям посвящены целые главы, в Википедии нет даже статьи о формулах половинного угла. Возможно, сейчас вы представляете себе эту версию формул половинного угла 9.2 {\ frac {\ alpha} {2}} = \ frac {s (sa)} {bc}, \ tag {1} \ label {1} $ $

, где $ a $, $ b $ и $ c$ — стороны треугольника, $\alpha$ — угол, противолежащий стороне $a$, $s$ — полупериметр. Я нашел самую дальнюю ссылку на эти формулы в беседе, опубликованной в Интернете между Конвеем и Дойлом, где Конвей использует их для доказательства формулы Герона, а позже утверждает, что взял ее из продолжения Кейси.

Я обнаружил \eqref{1} самостоятельно, пытаясь доказать закон косинусов от противного. Когда я понял, что они известны, я попытался их обобщить, и у меня получилось вот это 9.2 {\ frac {\ alpha} {2}} = \ frac {(sb) (sc)} {ad + bc}, \ tag {2} \ label {2} $ $

, где $ a $, $ b $, $c$ и $d$ — стороны вписанного четырехугольника, $s$ — полупериметр и $\angle{DAB}=\alpha$.

До того, как я обнаружил разговор между Конвеем и Дойлом, я был взволнован тем, что нашел оригинальное доказательство формулы Герона с помощью \eqref{1}. Когда я нашел \eqref{2}, я подумал, что аналогичными рассуждениями смогу доказать формулу Брахмагупты. Значит это было. Но на форуме по геометрии кто-то сослался на древнегреческую книгу, содержащую \eqref{2}. Затем я отправил доказательство формулы Брахмагупты Мартину Йозефссону, который направил меня к книге Кейси 9.2{\frac{\alpha}{2}}=(sb)(sc),\tag{3}\label{3}$$

, где $a$, $b$, $c$ и $d$ — стороны общего четырехугольника, $s$ — полупериметр, $\angle{DAB}=\alpha$ и $\angle{BCD}=\gamma$. Удивительно, но $(3)$ также обобщает тождество Пифагора. Взгляните на GeoDom — обобщение пифагорейского тригонометрического тождества.

Известно, что формула Бретшнайдера является обобщением формул Герона и Брахмагупты. Естественно, я задался вопросом, смогу ли я обобщить доказательство Кейси формулы Брахмагупты, используя \eqref{3}, и таким образом вывести формулу Бретшнайдера. И я сделал это. Я отправил свои формулы в \eqref{3} и свое доказательство формулы Бретшнайдера Йозефссону (среди многих других математиков), и он сказал мне следующее:

«Мне нравится ваша статья, особенно то, как вы помещаете эти важные формулы в единую структуру.
Я не могу сказать, что видел тождества (4) и (5) где-то еще раньше.»

Где тождества (4) и (5) — это тождества в \eqref{3} в этом посте.

А потом он сказал:

«Несмотря на то, что об этих формулах уже много написано, идеи доказательства формулы Бретшнейдера и площади бицентрического четырехугольника, насколько мне известно, новы. Надеюсь, вы опубликуете свою статью.»

Я решил написать статью об этих формулах под названием «Две идентичности и их последствия» , которая была опубликована в MATINF.

За почти три года изучения возможных применений \eqref{1}, \eqref{2}, \eqref{3} я обнаружил следующее:

Использование \eqref{1}, \eqref{2} мы также можем вывести (большинство доказательств вы можете увидеть на ГеоДом — Доказательства и приложения двух известных формул, содержащих синус, косинус и полупериметр треугольника):

Закон косинусов
Закон синусов
Закон касательных
Теорема Стюарта
Формулы сложных углов
Формула Моллвейде
Товар $AI\cdot{BI}\cdot{CI}$
Формула длины биссектрисы
Формулы Махавиры
Лемма Зелиха
Неравенство треугольника Эйлера
Неравенство Юна (Йозефссона)

Другие безымянные тождества и неравенства:

$\tan{\frac{\alpha}{2}}\tan{\frac{\beta}{2}}+\tan{\frac{\alpha}{2}}\tan{\frac{ \gamma}{2}}+\tan{\frac{\beta}{2}}\tan{\frac{\gamma}{2}}=1$
$r=4R\sin{\frac{\alpha}{2}}\sin{\frac{\beta}{2}}\sin{\frac{\gamma}{2}}$
$ s = 4R \ cos {\ frac {\ alpha} {2}} \ cos {\ frac {\ beta} {2}} \ cos {\ frac {\ gamma} {2}} $
$\sin{\frac{\alpha}{2}}\sin{\frac{\beta}{2}}\sin{\frac{\gamma}{2}}\le\frac{1}{8 }$
Треугольник с $\tan{\frac{\alpha}{2}}=\frac{a}{b+c}$ (см.
решение Граубнера)
Я мог бы продолжать и продолжать…

Формулы \eqref{1}, \eqref{2}, \eqref{3} объясняют развитие Герона-Брахмагупты-Бретшнайдера лучше, чем где-либо еще. Это заставило меня задуматься о том, что произойдет, если я аналогичным образом применю формулы половинного угла к формулам, в которых половинные углы явно фигурируют, таким как формула Моллвейда (скорее, Ньютона) или закон касательных. Вот как возникли эти два обобщения:

Обобщение формулы Моллвейде (скорее, Ньютона)
Обобщение закона касательных

На вопрос Мартина Йозефссона об оригинальности этих обобщений он ответил:

«Насколько я помню, я не видел ни одного из них, по крайней мере, в современных книгах или газетах, и даже если некоторые из них можно найти в старом тексте, они, по крайней мере, малоизвестны, и заслуживают широкой известности».

Кроме доказательства формулы Бретшнайдера, я не нашел других приложений для \eqref{3}.

Интересно, что половинные углы встречаются везде: от теорем об углах окружности до метода подстановки Вейерштрасса в интегральном исчислении. Даже когда Виет выводил свою формулу для $\pi$ с помощью бесконечного произведения, он начал с записи $\sin{x}=2\sin{\frac12x}\cos{\frac12x}$.

Отредактированный вопрос: Разве тот факт, что мы можем вывести все вышеупомянутые классические теоремы из \eqref{1}, не делает \eqref{1} фундаментальным для евклидовой геометрии? Есть ли другие аспекты, которые следует учитывать? Если да, то какие это будут аспекты?

Полугол калькулятор

, созданный Maciej Kowalski, кандидат PhD

. Обзор Стивена Вудлинга

Последний : Использование калькулятора половинных углов

Добро пожаловать в Omni калькулятор половинных углов , где мы изучим тождеств половинных углов . Формулы двойного угла позволяют легко найти функции удвоенного угла. Здесь мы хотели бы сделать то же самое, но вместо того, чтобы умножать угол на два, разделим на . На самом деле, основным инструментом для нахождения формул половинного угла sin, cos и tan являются тождества, уменьшающие степень .

Но не будем забегать вперед! В следующих разделах более чем достаточно времени, чтобы пройтись по ним медленно и подробно .

Мы надеемся, что вы готовы и полностью проснулись, потому что пора начинать !

Тригонометрические функции

Треугольники простейшие геометрические объекты мы можем построить. У них три стороны, три угла и , вот и все, что у них есть . Возможно, у нас не может быть многоугольника с двумя сторонами, не говоря уже об одной. Итак, поскольку треугольники так просты, их должно быть довольно просто понять , верно?

В каком-то смысле это действительно так . Например, есть несколько способов найти площадь треугольника. Хотя не все они красивы (взгляните, например, на калькулятор формул Герона), бывают случаи, когда каждый может быть полезен .

Кроме того, как простейшие многоугольники, треугольников были досконально изучены с древних времен (помните Пифагора?). Что ж, он был не первым и не последним, кто посвятил им свою жизнь.) Ведь мы можем разделить каждый многоугольник на треугольники (например, проведя несколько диагоналей), поэтому, если мы понимаем основной объект, мы должен быть в состоянии понять всех остальных.

Тригонометрия может быть самым полезным инструментом в исследованиях треугольников. Идея заключается в том, чтобы связать длины сторон с внутренними углами. Ведь легко заметить, что если у вас есть треугольник и увеличить один из его углов, то стороны должны измениться соответственно . Оказывается, что « соответственно » можно преобразовать в несколько очень хороших функций. Проверьте калькулятор тригонометрических функций, чтобы узнать больше!

Есть только один верный способ начать разговор о тригонометрических функциях — прямоугольные треугольники (каламбур).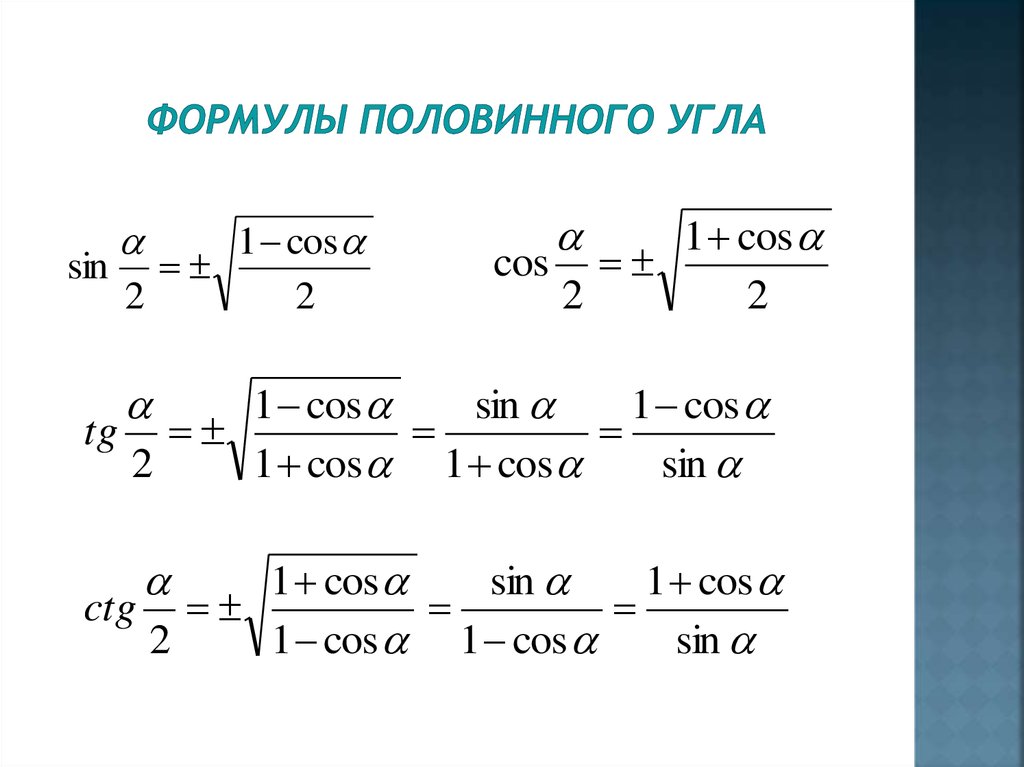 С точки зрения угла это простой случай: мы знаем, что один угол должен быть равен 90 градусов, так что у нас остается только два, чтобы беспокоиться о . Определим тригонометрические функции по приведенным ниже формулам:

Обратите внимание, что мы (и калькулятор тождеств половинного угла) ограничиваемся изучением синуса, косинуса и тангенса, так как остальные не так распространены в приложениях и учебниках.

Однако у приведенных выше определений есть один существенный недостаток: угол α должен быть между 0 и 90 градусов (или между 0 и π/2 радиан) просто потому, что это прямоугольный треугольник. Тем не менее, мы можем распространить определения на любое реальное значение (даже отрицательное), переведя все это в двухмерную плоскость.

Пусть A = (x, y) — точка на плоскости, и обозначим через α угол, идущий против часовой стрелки от положительной половины горизонтальной оси и отрезка, соединяющего (0, 0) и А . (Обратите внимание, как мы сказали, что α идет от одной линии к другой, а не что это между ними. Из-за этого мы часто называем α направленным углом .)

Ясно, что такие угол может быть больше 90 градусов. Еще лучше — может быть больше полного 360 градусов : он может сделать один полный круг, а от 360 вверх начать свой второй круг. Кроме того, поскольку мы определили α , чтобы быть направленным, , теперь мы можем получить отрицательные углы , просто пойдя в другую сторону, то есть по часовой стрелке, а не против часовой стрелки.

Для таких углов мы расширяем определения тригонометрических функций выше , заменяя в формулах выше a вместо y , b вместо x , и c √ вместо ) (расстояние от (0, 0) до A ).

Хорошо, мы надеемся, что нам удалось убедить вас, что полезны тригонометрические функции . Чтобы подружиться с ними, может потребоваться неделя или две, но этот момент обязательно наступит. Однако, прежде чем это произойдет, давайте упомянем некоторые приятные личности, которые их используют. Излишне говорить, что мы сосредоточимся на формулах tan, sin и cos половинного угла .

Тождества половинного треугольника

В тригонометрии, как только мы познакомимся с функциями, следующим шагом будет изучение отношений между ними . Оказывается, что, скажем, синус не только описывает отношение сторон треугольника, но и связан с косинусом соотношением 9.0118 красивые и полезные формулы .

Изучение тригонометрических тождеств и уравнений легко может занять целую книгу или две. В качестве небольшого поощрения углубиться в тему упомянем два, которые довольно часто появляются при работе с треугольниками : закон синусов и закон косинусов.

Мы, однако, собрались здесь сегодня, чтобы изучить полуугловые тождества . А чтобы понять, откуда они берутся, воспользуемся так называемыми формулами снижения мощности 92 {\ влево (х \ вправо)} = \ frac {1 — \ cos {\ влево (2x \ вправо)}} {1 + \ cos {\ влево (2x \ вправо)}} sin2(x)=21−cos(2x)cos2(x)=21+cos(2x)tan2(x)=1+cos(2x)1−cos(2x)

Внимательный глаз заметит, что в каждой формуле справа у нас вдвое больше угла, чем слева . Если быть точным, тот, что слева, это половина того, что справа . А это именно то, что нам нужно!

Сначала возьмем верхнюю формулу. Мы перепишем его с углом x2\frac{x}{2}2x слева и с xxx справа (обратите внимание, что это обозначение должно сохранять только соотношение, что 92 {\ left (\ frac {x} {2} \ right)} = \ frac {1 — \ cos {x}} {2} / \ sqrt {} \\ [5pt] \sin{\left(\frac{x}{2}\right)} = \pm \sqrt{\frac{1 — \cos{x}}{2}}sin2(2x)=21−cosx/

sin(2x)=±21−cosx

Обратите внимание, что нам нужен знак ±\pm± из-за свойств четного показателя. В практических расчетах знак зависит от того, в каком квадранте плоскости мы находимся в с нашим углом.

Формула полуугла cos получается аналогично: frac{x}{2}\right)} = \frac{1 + \cos{x}}{2} / \sqrt{} \\[5pt] \cos{\left(\frac{x}{2}\right)} = \pm \sqrt{\frac{1 + \cos{x}}{2}}cos2(2x)=21+cosx/ 92 {\ left (\ frac {x} {2} \ right)} = \ frac {1 — \ cos {x}} {1 + \ cos {x}} / \ sqrt {} \\ [5pt] \tan{\left(\frac{x}{2}\right)} = \pm \sqrt{\frac{1 — \cos{x}}{1 + \cos{x}}}tan2(2x) =1+cosx1−cosx/

tan(2x)=±1+cosx1−cosx

Кроме того, мы можем получить две другие формулы полуугла тангенса (которые также перечислены в калькулятор формулы половинного угла), которые имеют то преимущество, что не имеют знака ±\pm±. Они исходят из использования тождеств двойного угла вместе с тангенсом ⁡(x)=sin⁡(x)cos⁡(x)\tan\left(x\right) = \frac{\sin\left(x\right) )}{\cos\left(x\right)}tan(x)=cos(x)sin(x) формула и тождество Пифагора sin⁡2(x)+cos⁡2(x)=1\sin ^2\влево(х\вправо) + \cos^2\влево(х\вправо) = 1sin2(x)+cos2(x)=1.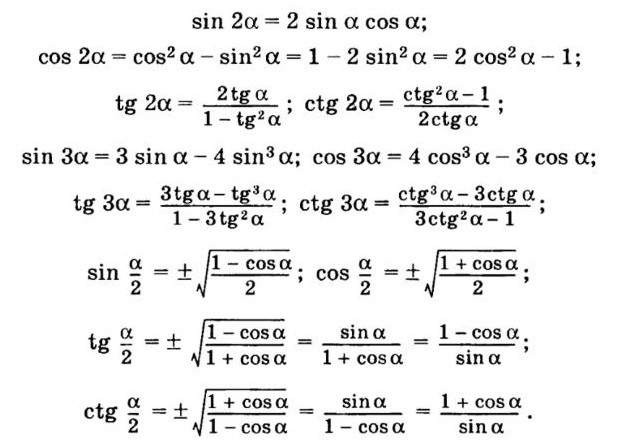 2{ \frac{x}{2}}} \\ [10pt] & = \ frac {\ sin {\ frac {x} {2}}} {\ cos {\ frac {x} {2}}} \\ [10pt] &=\tan{ \frac{x}{2}} \end{align*}1+cosxsinx=1+cos(2⋅2x)sin(2⋅2x)=1+(cos22x−sin22x)2sin2xcos2x=sin22x+cos22x +cos22x−sin22x2sin2xcos2x=2cos22x2sin2xcos2x=cos2xsin2x=tan2x

И на этом мы объявляем конец теории для этой статьи. После всего этого времени, потраченного на чтение формул, , пришло время для некоторых числовых примеров , и это то, чему посвящен следующий раздел!

Пример: Использование калькулятора половинного угла

Наконец-то сбылась ваша самая большая мечта — вы купили себе маленькую хижину в горах ! Ну, это еще не совсем хижина, пока это всего лишь участок земли , на котором вы будете строить, но это, безусловно, начало. И после консультации с нашим калькулятором временной стоимости денег вы решили, что это лучшая форма инвестиций.

Вы подняли социальное дистанцирование на новый уровень и выбрали район вдали от цивилизации . К сожалению, это означает, что даже до того, как вы позволите бригаде заложить бетонный фундамент, вы должны удостовериться, что техника сможет туда безопасно добраться . В частности, необходимо подготовить устойчивый подъезд , хотя бы гравийный. Придет время апгрейдить его до асфальта, а пока придется делать .

Есть одно место, которое требует особого внимания — 30 -уклон, который является серьезным препятствием для более тяжелой строительной техники. Тем не менее, команда говорит вам, что , если бы вы только могли сгладить его вдвое, тогда все должно быть в порядке .

Подождите, кто-нибудь упоминал, что делит угол пополам? Теперь это должно быть проще простого для вычислителя половинного угла !

Для получения точных данных о том, что, где и как следует выравнивать, необходимо выполнить некоторые расчеты относительно уклона . По этой причине вы можете перейти к нашему калькулятору уклона, где мы подробно объяснили это. Чтобы найти градиент склона, было бы полезно знать тригонометрические функции угла , с которым вы имеете дело. (В конце концов, мы можем думать о наклоне как о гипотенузе большого прямоугольного треугольника.) Конечно, мы могли бы просто поискать данные в Google, но , что интересного в этом ? Ответ: забава заключается в использовании калькулятора тождеств половинного угла !

Давайте разберем это на простое пошаговое решение/инструкцию .

Мы знаем, что наклон находится под углом 30 градусов, и мы хотели бы уменьшите его вдвое по сравнению с . Для нахождения тригонометрических функций в этом случае достаточно ввести в вычислитель половинного угла данные, с которых мы начинаем .
В поле « Угол » мы вводим 30 градусов, и как только мы это сделаем, инструмент выдаст ответ , как для полного угла, так и для половинного.
Обратите внимание, что 30 — это частный случай прямоугольного треугольника, поэтому калькулятор половинного угла покажет вам точные значения тригонометрических функций до того, как мы их округлим, т. е. в виде дроби с квадратными корнями.

Кстати, давайте теперь посмотрим , как использовать тождества триггера половинного угла, чтобы найти ответ вручную . Так что хватайте лист бумаги, и давайте приступим к делу !

Прежде всего, начнем с очевидного : половина 30 градусов это 15 градусов. Это означает, что наш полуугол находится в первом квадранте (потому что это между 0 и 90 градусов). Это далее переводит в синус, косинус и тангенс, являющиеся положительными . Поэтому для формул половинного угла sin, cos и тангенса мы будем использовать тождества с +++, где у нас был знак ±\pm±.

Начнем с синуса . Напомним, что cos⁡(30°)=32\cos\left(30\степень\right) = \frac{\sqrt{3}}{2}cos(30°)=23, поэтому:

sin⁡ (15°)=1−cos⁡(30°)2=1−322=2−34≈0,26\мал. \начать{выравнивать*} \sin\left( 15 \степень \справа) &= \sqrt{\frac{1 — \cos\left( 30 \степень \справа)}{2}} \\[10pt] &= \sqrt{\frac{1 — \frac{\sqrt{3}}{2}}{2}} \\[10pt] &= \sqrt{\frac{2 — \sqrt{3}}{4}} \\[10pt] & \ приблизительно 0,26 \end{align*}sin(15°)=21−cos(30°)

=21−23

=42−3

≈0,26

Далее, формула половинного угла 51°s дает: 2 )=1+cos⁡(30°)2=1+322=2+34≈0,97\мал. \начать{выравнивать*} \cos\left( 15 \степень \справа) &= \sqrt{\frac{1 + \cos\left( 30 \степень \справа)}{2}} \\[10pt] &= \sqrt{\frac{1 + \frac{\sqrt{3}}{2}}{2}} \\[10pt] &= \sqrt{\frac{2 + \sqrt{3}}{4}} \\[10pt] & \ приблизительно 0,97 \end{align*}cos(15°)=21+cos(30°)

=21+23 90,97 cos⁡(30°)1+cos⁡(30°)=1−321+32=2−32+3≈0,27\small \начать{выравнивать*} \tan\left( 15 \степень \справа) &= \sqrt{\frac{1 — \cos\left( 30 \степень \справа)}{1 + \cos\left( 30 \степень \справа)}} \ \[10pt] &= \ sqrt {\ frac {1 — \ frac {\ sqrt {3}} {2}} {1 + \ frac {\ sqrt {3}} {2}}} \\ [10pt] &= \sqrt{\frac{2 — \sqrt{3}}{2 + \sqrt{3}}} \\[10pt] & \ приблизительно 0,27 \end{align*}tan(15°)=1+cos(30°)1−cos(30°)

=1+23

1−23

=2+3

2−3

≈0,27