Тригонометрическое неравенство и красивые примеры сложных задач
Анна Малкова (опыт преподавания математики 26 лет, автор книг для подготовки к ЕГЭ по математике).
Привет, дорогие друзья!
Все привыкли к тригонометрическим уравнениям, но иногда нам встречаются тригонометрические неравенства, и мы помним, что в ЕГЭ у нас есть задание № 15 «Неравенства». И неравенства там бывают самые разные: и показательные, и логарифмические, и алгебраические, и степенные, и даже тригонометрические. Причем тригонометрические неравенства я встречала и в сборниках задач ЕГЭ под редакцией Ященко, и даже в вариантах тренировочных работ ЕГЭ, которые старшеклассники пишут в течение учебного года.
У меня есть для вас замечательное тригонометрическое неравенство .
Оно такое короткое, такое безобидное, такое, на первый взгляд, милое, но на его примере я смогу показать, как вообще решаются тригонометрические неравенства. Это вам может пригодиться и в задаче 15, и в задаче с параметрами, и даже иногда в первой части, под № 10 есть задача с практическим содержанием, и там тоже встречаются тригонометрические неравенства. Кроме того, я покажу на примере этой задачи одну классную, абсолютно нетривиальную замену переменной, которая вам может помочь в задаче с параметрами и в олимпиадных задачах, а заодно и повторим, как решать иррациональные неравенства, то есть с корнями, а это тоже полезно.
Давайте начнем с самого простого, с области допустимых значений. Она здесь такая:
Обратите внимание, я могу оставить эту систему в таком виде, а могу сразу ее дорешать. Нарисую тригонометрический круг и отмечу те точки, где синус и косинус неотрицательны. Они находятся в первой четверти, от до + , где принадлежит множеству целых чисел.
И ведь в самом деле, подходят углы только первой четверти, потому что синус неотрицательный для углов из первой и второй четверти, а косинус неотрицательный для углов из первой и четвертой четверти, а и то и другое только в первой четверти.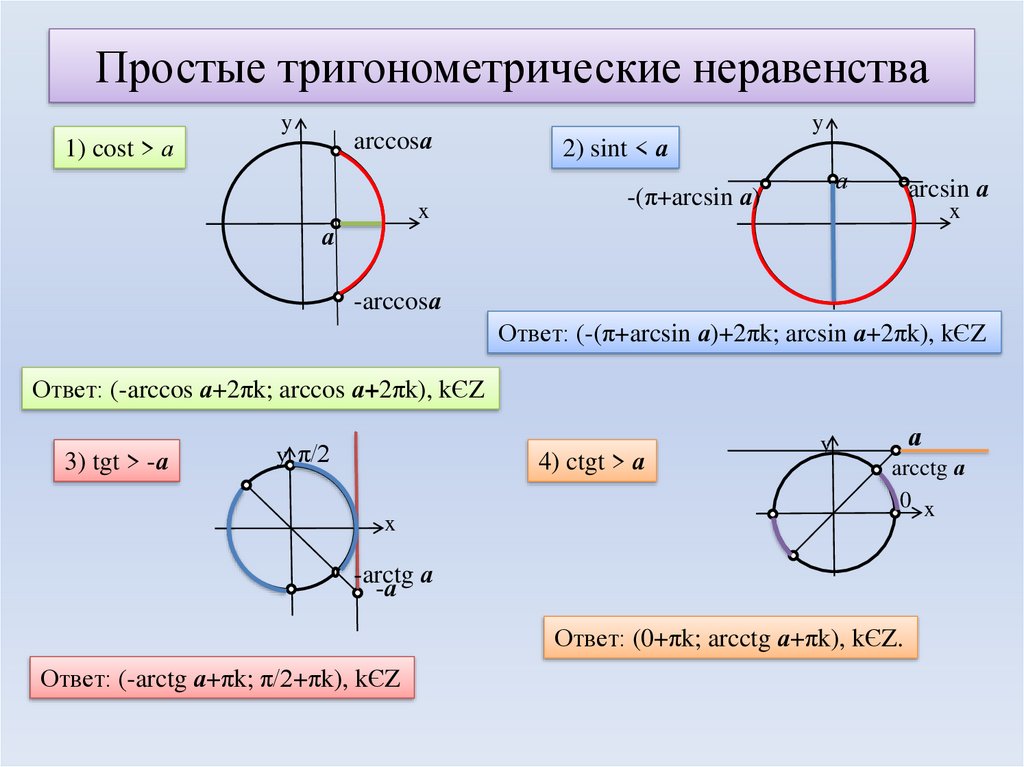
ОДЗ мы записали, что же нам еще сделать?
Слева у нас сумма корней, а корни квадратной величины неотрицательные, значит, левая часть неотрицательная. И правая часть у нас тоже неотрицательная, значит, мы можем возвести обе части этого неравенства в квадрат, конечно, при условиях, что синус х и косинус х больше или равны 0. Мы имеем право возводить в квадрат, когда обе части неотрицательны.
Получаем .
Вы, конечно, узнали формулу .
Здесь же запишу, что и . Получаем
Теперь смотрим на первое неравенство и видим сумму синуса и косинуса и их произведение под корнем. И сейчас я покажу ту самую замену, о которой я говорила вначале.
Если у нас в уравнении или в неравенстве есть только сумма синуса и косинуса, а также произведение синуса и косинуса, а также всевозможные , или , , то мы можем сделать замену .
Эта замена, возможно, поможет вам в олимпиадных задачах и, возможно, в задаче 18, если там встретится тригонометрия, и вы захотите его решать аналитически.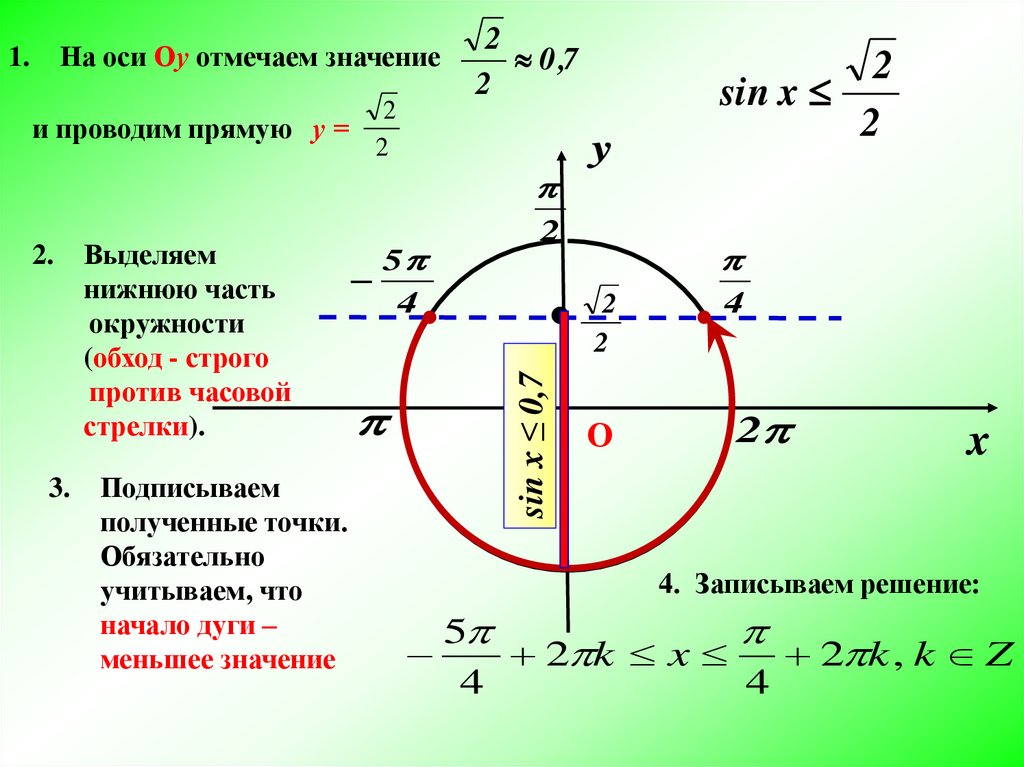 С минусом можно сделать точно так же.
С минусом можно сделать точно так же.
А все остальное мы будем выражать через эту новую переменную t. Давайте так и сделаем.
— замена. И тогда все остальное выразим через эту t. Сейчас покажу, как это сделать.
Если , а мы сказали, что при этом и , то в этом уравнении можно обе части возвести в квадрат, тогда у нас .
.
Получается
Значит, первое неравенство примет вид: .
Давайте уединим корень .
У нас получилось стандартное иррациональное неравенство, про которое вам обещали, что на ЕГЭ 2021-го года их не будет. Но о том, что не будет тригонометрических неравенств, ничего не сказали.
Что же с этим делать? Конечно, хочется возвести обе части в квадрат, но мы знаем, что возводить обе части неравенства в квадрат можно только тогда, когда обе эти части неотрицательные. Если , мы можем возвести обе части в квадрат.
Получаем .
Обратите внимание, что при этом я могу не писать, что , потому что она уже больше, квадрат какого-то неотрицательного выражения больше неотрицательного выражения.
Но это еще не все. Есть второй случай, когда , ведь у нас тоже такое может быть. Тогда в квадрат возводить мы не можем. Но тогда неравенство просто будет выполняться, потому что слева корень, величина неотрицательная, а справа минус. И неравенство выполняется, когда t принадлежит области допустимых значений, когда .
Решаем полученную совокупность
Давайте для первой системы второе неравенство решим методом интервалов
Значит, мы получаем, что
.
Вернемся к переменной t.
Пронумеруем наши два неравенства и будем решать их по порядку
.
1 случай: ; .
Что-то здесь странное, ведь мы же знаем, что
а у нас даже сумма меньше -3. Такого не может быть.
Поскольку у меня
а я могу складывать неравенства с одинаковым знаком, отсюда следует, что .
Мы получаем, что у нашего неравенства нет решений.
— нет решений. Остался второй случай: .
Когда вам попадаются такие уравнения или неравенства, где есть сумма синуса и косинуса, равная какому-то числу, мы знаем, как их решать. Воспользуемся методом введения дополнительного угла. Я об этом уже рассказывала на онлайн-курсе, также об этом можно почитать на нашем сайте в материалах по математике. В простейшем случае, как сейчас у нас, этот метод дается в учебнике алгебры.
Воспользуемся методом введения дополнительного угла. Я об этом уже рассказывала на онлайн-курсе, также об этом можно почитать на нашем сайте в материалах по математике. В простейшем случае, как сейчас у нас, этот метод дается в учебнике алгебры.
Умножаем левую и правую части этого неравенства на корень из 2/2, потому что это .
И у нас получается ; .
Узнаем формулу .
Сворачиваем по формуле и получаем .
Точно не нужно это тригонометрическое неравенство решать в уме, даже простейшие тригонометрические неравенства решать в уме не надо. Надо нарисовать тригонометрический круг.
Пусть у меня угол . И я решаю простейшее тригонометрическое неравенство .
Отмечаем на тригонометрическом круге на оси косинусов и точки, у которых такой косинус. В первой четверти будет угол или и все углы, которые отличаются от на целое число полных кругов. А в четвертой четверти это . А косинус у нас больше, чем
Осталось записать решение для угла , который , .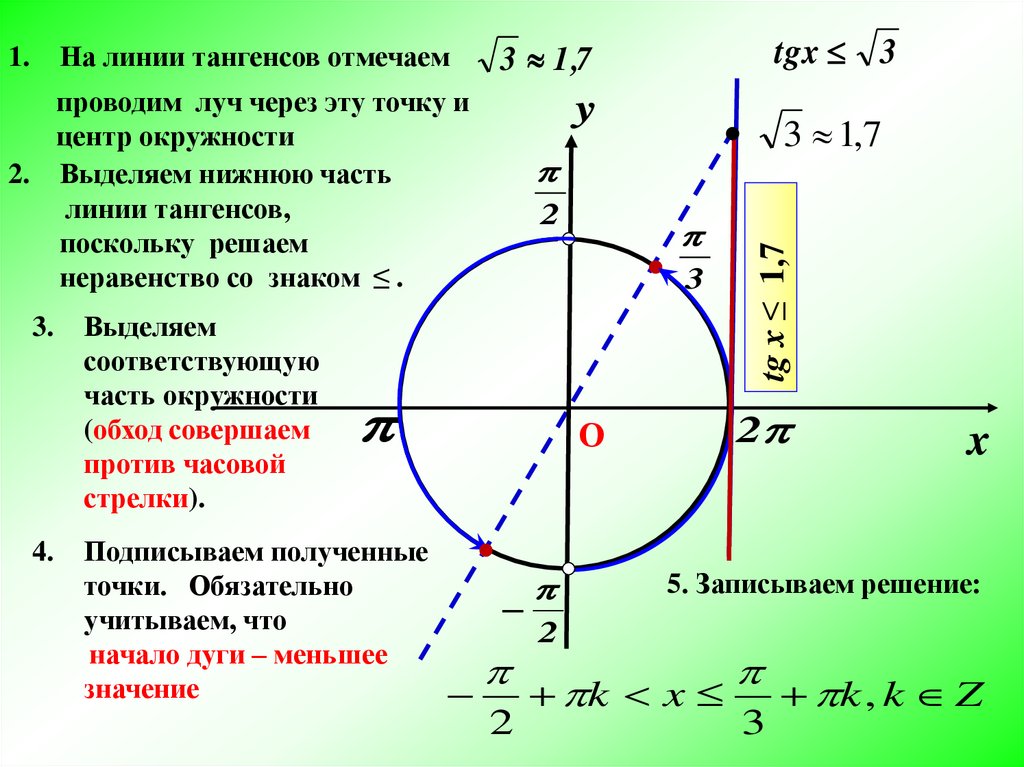
И последним действием мы находим х.
Значит, х – это углы из первой четверти, не включая точки, лежащие на осях. И для всех этих углов выполняется условие и . Мы решили это непростое тригонометрическое неравенство.
Мы сделали очень нетривиальную замену переменной, решили получившееся иррациональное неравенство, вспомнили, как решать тригономитрические неравенства с помощью единичной окружности. Но оказывается, есть более сложные неравенства, которые можно сделать с помощью не тригонометрических, а обратных тригонометрических функций. Если вы хотите неравенства с обратными тригонометрическими функциями и заодно повторить, что такое арксинус и арккосинус, — ставьте лайки и подписывайтесь на мой канал!
Все видео по математике
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Тригонометрическое неравенство и красивые примеры сложных задач» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Публикация обновлена: 06.01.2023
Простейшие тригонометрические уравнения и неравенства. Подведение итогов
Личный кабинет
8 800 551-50-78 (бесплатно)
Онлайн подготовка к ЕГЭ-2023 по профильной математике
Подготовьтесь к ЕГЭ на 80+ баллов. Смотрите видео, читайте теорию, занимайтесь на онлайн-тренажерах
1С:Репетитор
8 800 551-50-78
Личный кабинет
1С:Репетитор – подготовка к ЕГЭ по математике
© ООО «1С-Софт» | ЧОУ ДПО «1С-ОБРАЗОВАНИЕ» | 2016–2022
8 800 551-50-78
Связаться с нами:
Главная
Блог
Простейшие тригонометрические уравнения и неравенства. Подведение итогов
Подведение итогов
Сегодня мы подводим итоги раздела, посвященного решению простейших тригонометрических уравнений и неравенств.
Давайте повторим определения и свойства обратных тригонометрических функций: арксинуса, арккосинуса, арктангенса и арккотангенса:
Запомнить, как строится на тригонометрическом круге множество решений простейшего уравнения, поможет интерактивная модель. Обратите внимание на особые случаи, когда решение уравнения можно записать, используя значения табличных углов.
Тригонометрические уравнения
Посмотрите разбор решения нескольких типов простых тригонометрических уравнений, включая простой случай сведения к квадратному, в этом плейлисте:
С помощью интерактивной модели можно увидеть, как множество решений простейшего тригонометрического неравенства изменяется в динамике на круге и на графике соответствующей функции.
Тригонометрические неравенства
Повторяем задачи к разделу. Напомним, что тренажеры с пошаговым решением и задачи для самостоятельной работы ждут подписчиков в Библиотеке.
| Условие | Ответ |
| Решить уравнение sinπ-3x=12 |
x=-1kπ12+πk3,k∈Z |
| Решить уравнение cosx4-5π4=12 |
x1=19π3+8πk,x2=11π3+8πk,k∈Z |
| Решить уравнение tgx2+3π2=1 |
x=3π2+2πk,k∈Z |
| Решить неравенство cosπ+x2<12 |
-4π3+4πk<x<4π3+4πk,k∈Z |
| Решить неравенство tgx-π2>-2 |
arcctg2+πk<x<π+πk,k∈Z |
Начать тренировку
Мы научились решать простейшие тригонометрические уравнения и неравенства. 2(x) \leq 1$$
что верно только для некоторого $x$. 92$$
2(x) \leq 1$$
что верно только для некоторого $x$. 92$$
Возведение в квадрат сохраняет неравенство только в том случае, если обе части неравенства неотрицательны и принадлежат части области, где функция квадрата строго растет.
$\endgroup$
$\begingroup$
Возведение в квадрат не сохраняет неравенство, так как это функция 2-к-1 над $\mathbb{R}$, следовательно, немонотонная. Имейте в виду, что монотонно убывающая функция перевернула бы неравенство, все равно было бы действительное неравенство, указывающее на противоположный путь. 92 $
$\endgroup$
Тригонометрические неравенства: задачи с решениями
Решите тригонометрическое неравенство: $8\left\vert \tan x\right\vert -1
$-\arctan \left( 8\right) +k\pi
$-\arctan \left( \frac{1}{8}\right) +k\pi
$-\arctan \left( \frac{1}{4}\right) +k\pi
$-8\arctan \left( 1\right) +k\pi
Задача 6
Если $x\in (0,2\pi ]$ , решить $\frac{\cos x}{1-\sin 2x}
$\left( 0,\pi \right) -\frac{\pi }{2}$
$\left( \frac{\pi }{2},\frac{3\pi }{2}\right) $
$\left( \frac{\pi }{3},\frac{3 \pi }{4}\right) -\frac{\pi }{4}$
$\left( \frac{\pi }{2},\frac{3\pi }{2}\right) — \frac{5\pi }{4}$
Задача 7
Решить $\sin \left( x-\frac{\pi }{3}\right) >\sin x$, если $0\leq x\leq 2\pi $
$x\in \left( \frac{\pi }{3},\frac{2\pi }{3}\right) $
$x\in \left( \frac{2 \pi }{3},\frac{5\pi }{3}\right) $
$x\in \left( \frac{\pi }{4}, \frac{5\pi }{4} \справа) $
$x\in \left( \pi ,2\pi \right) $
Задача 8
Учитывая неравенство $p\sin x-q\cos x>\frac{r}{2}$ с решением $x \в
\left( \frac{\pi }{3},\pi \right) $.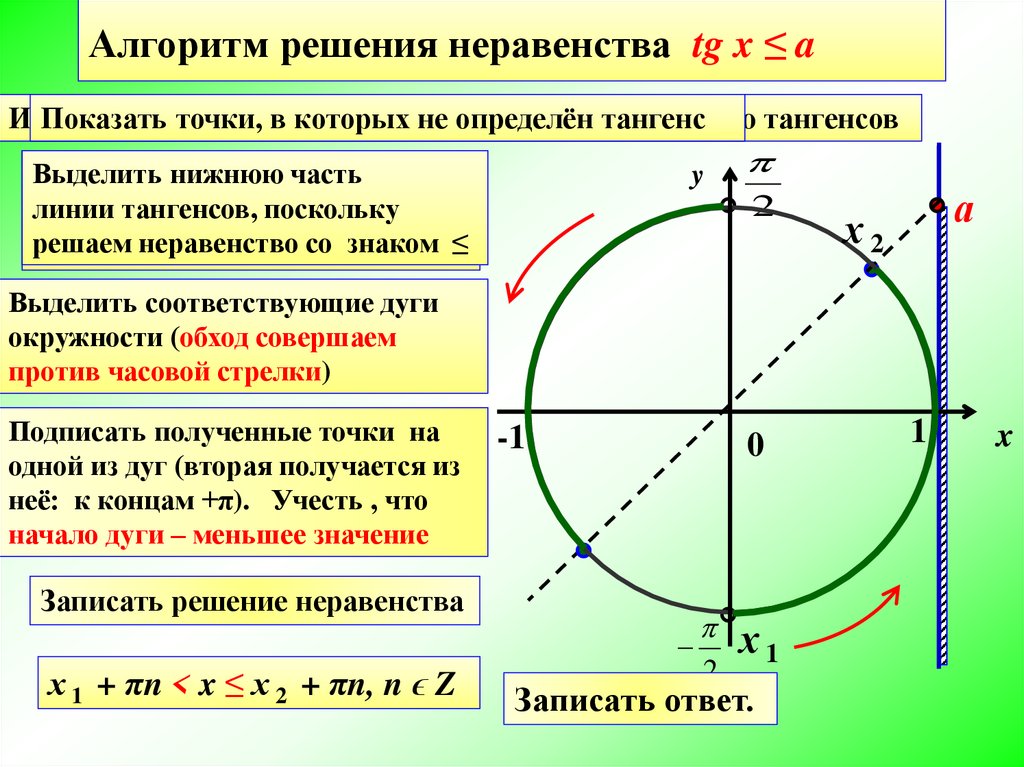
Если $\left( p,q\right) $ — точка, принадлежащая окружности с радиус $r$ и центр $\left( 0,0\right) $,
определить $\frac{p}{q}$
$\frac{p}{q}=1$
$\frac {p}{q}=\frac{1}{2}$
$\frac{p}{q}=2$
$\frac{p}{q}=\sqrt{3}$
Задача 9
Решить: $\sin x\geq \frac{1}{2}$; задано $n\in \mathbb{Z}$
$\left[ \frac{\pi} {6}+2n\pi ;\frac{5\pi} {6}+2n\pi \right]$
$\left[ \frac{\pi }{6}+2n\pi ;\left( 2n+1\right) \pi \right] $
$\left[ 2n\pi ;\frac{\pi } {6}+2n\pi \right]$
$\left[ \frac{\pi }{2};\pi \right] \cup \left[ \frac{\pi }{6};\pi \ right] $
Задача 10
Решить: $\cos x\geq \frac{\sqrt{2}}{2}$; $0\leq x\leq 2\pi $
$\left[ \frac{\pi }{4};\frac{\pi }{2}\right]$
$\влево[0; \frac{\pi }{4} \right]$
$\left[ \frac{7\pi }{4};2\pi \right]$
$\left[ 0;\frac{\pi }{4}\right] \cup \left[ \frac{7\pi }{4};2\pi \right]$
Задача 11
Определить все значения $x$ такие, что:
$\ sin (2x)>6\cos x$, учитывая $n\in \mathbb{Z}$
$x\in \left( n\pi +\frac{\pi }{3};n\pi +\ frac{2\pi }{3}\right)$
$x\in \left( 2n\pi +\frac{\pi }{2};2n\pi +\frac{3\pi }{2} \right)$
$x\in \left( 2n\pi +\frac{\pi }{3};2n\pi +\frac{2\pi }{3}\right) $
$x\in \left( n\pi +\frac{\pi }{2};n\pi +\frac{2\pi }{3}\right) $
Задача 12
Решите неравенство : $\tan x\geq 1$
$\left[ \frac{\pi }{4}+n\pi ;\frac{\pi }{2}+n\pi \right]$
$\ влево [ \frac{3\pi }{4}+n\pi ;\frac{\pi }{2}+n\pi \right] $
$\left[ \frac{3\pi }{4} +n\pi ;\frac{5\pi }{2}+n\pi \right] $
$\left[ \frac{\pi }{4}+n\pi ;\frac{5\pi } {2}+n\pi \right] $
Задача 13
Для каких значений $x$ ($0\leq x\leq 2\pi $) есть $\sin x>\cos x$?
$0
$0
$\frac{\pi }{4}
$0
Задача 14
Найдите все значения $x$, если $x\in (0;2\pi)$ удовлетворяют следующее тригонометрическое неравенство.
