Тригонометрия формулы тригонометрия 10 класс тригонометрия: Основные тригонометрические формулы — Математика 10 класс — Школьная математика — Каталог статей

Содержание

УРОК ПО ТЕМЕ «тРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ»

ОТКРЫТЫЙ УРОК ПО МАТЕМАТИКЕ

Тема: «Мир тригонометрии»

«УЧИТЬСЯ МОЖНО ТОЛЬКО ВЕСЕЛО… ЧТОБЫ ПЕРЕВАРИВАТЬ ЗНАНИЯ, НАДО ПОГЛОЩАТЬ ИХ С АППЕТИТОМ»

АНАТОЛЬ ФРАНС

Цель: Повторить и систематизировать изученный материал.

Задачи:

· Образовательная: обобщить и систематизировать знания учащихся по теме; продолжить формирование умений и навыков по применению тригонометрических формул;

проконтролировать степень усвоения знаний, умений и навыков по теме, формирования навыков самообучения и самоорганизации.

· Развивающая: совершенствовать, развивать умения и навыки по решению задач на применение тригонометрических формул; развивать умения и навыки в работе с тестами; продолжить работу по развитию логического мышления, математической речи и памяти.

· Воспитательная: продолжить формирование навыков эстетического оформления записей в тетради; приучать к умению общаться и выслушивать других; воспитание сознательной дисциплины; развитие творческой самостоятельности и инициативы; стимулировать мотивацию и интерес к изучению тригонометрии.

Тип урока: урок обобщения и систематизации знаний.

Образовательные технологии: модульная педагогическая технология, применение принципа планирования совместной деятельности учителя и обучающегося.

Методы обучения: частично-поисковый, тестовая проверка уровня знаний, организация и осуществление мыслительной деятельности, проблемно-поисковый, практический (исследовательский), демонстрационный, объяснительно — наглядный, проблемный.

Организационные формы общения: индивидуальная, групповая, коллективная.

Материально-техническое оснащение: мультимедийное оборудование (слайды – презентации), компьютеры (тесты), учебники.

План урока:

1. Организационный момент (2 мин.)

2. Актуализация опорных знаний (5мин)

Блиц-опрос на знание тригонометрических формул и тождеств.

3. Закрепление знаний и умений (5-7 мин)

Работа с учебниками (№45 (а,б), №46 (а,в), стр 35 Учебник. Алгебра и начала анализа. 10 класс. Алимов.)

Самостоятельная работа обучающего характера в форме теста, с последующей проверкой (10-15 мин)

5. Это интересно. (История зарождения тригонометрии) (5 мин)

6. Презентация «Тригонометрические тождества и формулы» (6 мин)

7. Домашнее задание: «Алгебра и начала анализа» Алимов. стр.72 (1-5) (1 мин)

8. Рефлексия. Оценка самого себя. (3-5 мин)

9. Итог урока (1-2 мин)

1. Организационный момент.

Французский писатель Анатоль Франс однажды заметил: «Учиться можно только весело… Чтобы переварить знания, надо поглощать их с аппетитом». Давайте будем следовать этому совету писателя, будем активны, внимательны, всё будем делать с удовольствием и большим желанием

Тема сегодняшнего урока «Мир тригонометрии». Повторяем, обобщаем, приводим в систему изученные виды, типы, методы и приёмы решения используя тригонометрические формулы.

Перед вами задача – показать свои знания и умения при использовании тригонометрических формул.

2. Блиц-опрос (по формулам в форме математического диктанта).

(Слайд 3)

3. Закрепление знаний и умений. Работа с учебником. № 45(а, б), №46 (а, в) (Слайд 4)

4. Самостоятельная работа обучающего характера в форме теста, с последующей проверкой на уроке. (Слайд 5)

Проверка самостоятельной работы (проверка теста проводится на уроке, оценки выставляются выборочно). (Слайд 6)

5. Это интересно. (Слайд 7-10)

Зарождение тригонометрии относится к глубокой древности. Еще задолго до новой эры вавилонские ученые умели предсказывать солнечные и лунные затмения. Это позволяет сделать вывод о том, что им были известны простейшие сведения из тригонометрии. Само название “тригонометрия” греческого происхождения, обозначающее “измерение треугольников”. Одним из основоположников тригонометрии считается древнегреческий астроном Гиппарх, живший во 2 веке до нашей эры. Гиппарх является автором первых тригонометрических таблиц.

Тригонометрия в ладони

Значения синусов и косинусов углов “находятся” на вашей ладони. Протяните руку и разведите как можно сильнее пальцы, так как показано на слайде. Сейчас мы измерим углы между вашими пальцами. (Возьмем два прямоугольных треугольника с углами 30°и 45° и приложим вершину нужного угла к бугру Луны на ладони.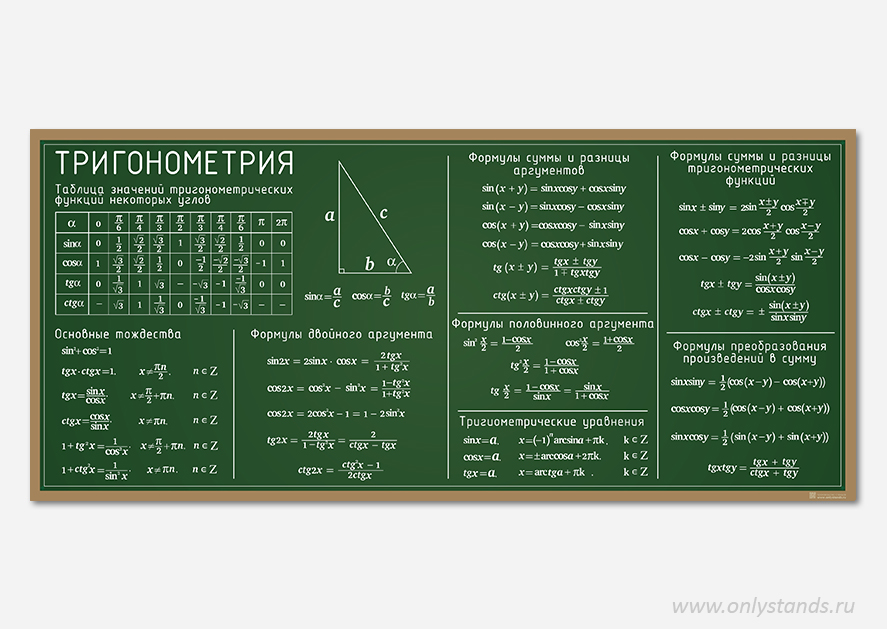 Бугор Луны находится на пересечении продолжений мизинца и большого пальца. Одну сторону угла совмещаем с мизинцем, а другую сторону — с одним из остальных пальцев)

Смотрите, я прикладываю угол в 30°; оказывается, это угол

— между мизинцем и безымянным пальцем;

— между мизинцем и средним пальцем — 45°;

— между мизинцем и указательным пальцем — 60°;

— между мизинцем и большим пальцем — 90°;

И это у всех людей без исключения.

Если пальцы считать лучами, исходящими из бугра Луны на ладони, то, если совместить (сжать) пальцы с мизинцем, угол между лучами будет равен 0°, то есть можно считать, что направление мизинца соответствует началу отсчета углов, то есть 0°, а поэтому введем нумерацию пальцев:

№0 — Мизинец

№1 — Безымянный

№2 — Средний

№3 -Указательный

№4 — Большой

№0 Мизинец 0°

№1 Безымянный 30°

№2 Средний 45°

№3 Указательный 60°

№4 Большой 90°

n — номер пальца

Значения синуса и косинуса угла по “ладони” приведено в таблице.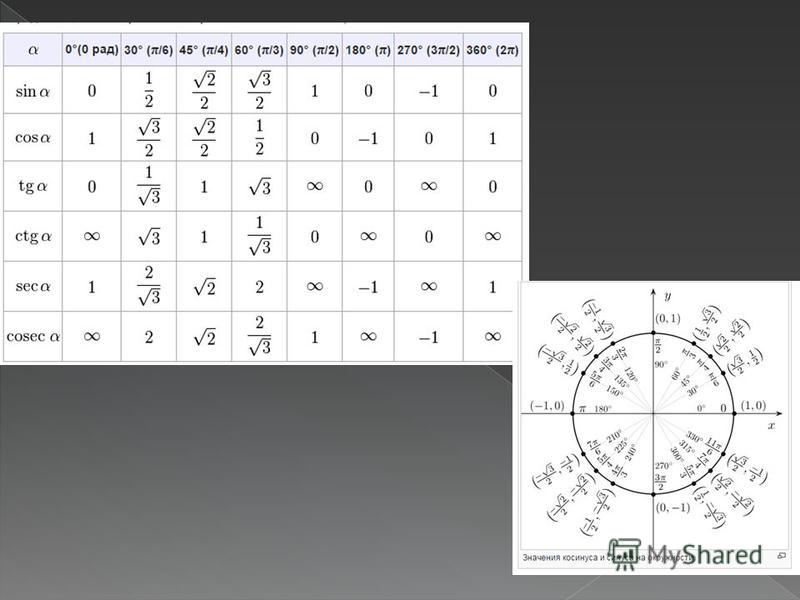

Примечание. Для определения косинуса угла отсчет пальцев происходит от большого пальца руки. [6]

Значения синуса

№ пальца	Угол
0	0
1	30°
2	45°
3	60°
4	90°

Значения косинуса

№ пальца	Угол
4	0°
3	30°
2	45°
1	60°
0	90°

6. Работа студентов. Презентация «Тригонометрические тождества и формулы».

7. Домашнее задание. (Cлайд 11)

“Проверь себя”, стр. 72

8. Рефлексия. (Слайд 12)

Оценка самого себя

1) На уроке мне было интересно:

а) да в) нет с) затрудняюсь ответить

2) Я присутствовал в хорошем настроении:

а) да в) нет с) затрудняюсь ответить

3) На уроке я больше люблю работать:

а) самостоятельно

в) с помощью преподавателя

с) с помощью друга

4) Мне нравится выполнять задания:

а) творческие и интересные

в) сложные и оригинальные

с) простые и понятные

5) Большую часть времени на уроке:

а) активно работаю в) думаю о своем

с) жду окончания урока

6) Темп работы на уроке был для меня:

а) нормальным

в) слишком быстрым

с) слишком медленным

9. Итоги урока (выставление оценок)

Спасибо, урок окончен! (Cлайд 13)

Используемая литература

1. Алимов Ш.А., Колягин Ю.М. и др. Алгебра и начала анализа: учебник для общеобразовательных учреждений. – 16-е изд. – М.: Просвещение, 2010.

2. Абылкасымова А. Е., Шойнбеков К. Д. и др. Алгебра и начала анализа: учебник для 10 кл. Издательство «Мектеп», 2010.

3. Макеева А.В. Карточки по тригонометрии. 10-11 классы: Дидактический материал для учителя — ОАО “Издательство “Лицей”, Саратов, 2002.

4. Изучение алгебры и начал анализа 10-11: Методические рекомендации к учеб.; кн. для учителя / Н.Е.Федорова, М.В. Ткачева. – М.: Просвещение, 2007.

5. Дидактические материалы по алгебре и началам анализа для 10 класс/М.И. Шабунин, М.В. Ткачева и др. -2-е изд. — М.: Просвещение, 2007.

6. Решетников Н.Н. Материалы курса “Тригонометрия в школе” лекции 1-8. – М.: Педагогический университет “Первое сентября”, 2006

1. Организационный момент.

Тема сегодняшнего урока «Мир тригонометрии». (Слайд 1)

Цель урока: повторить, обобщить, привести в систему изученные виды, типы, методы и приёмы решения используя тригонометрические формулы, подготовиться к контрольной работе. (Слайд 2)

Перед вами задача – показать свои знания и умения при использовании тригонометрических формул.

Мир тригонометрии — это основные тригонометрические тождества.(Слайд 3)

Давайте их повторим:

Задания:

1. записать на доске основные тригонометрические формулы

Основные тригонометрические тождества.

1. ; ;

4. и

2. расставить знаки функций по четвертям

3. записать формулы сложения

Формулы сложения.

4. записать формулы суммы и разности синусов и косинусов

Формулы суммы и разности одноименных тригонометрических функций.

6. Записать формулы двойного угла

2. ; ;

Задания: устные упражнения (Слайд 4 )

Упростить выражение: (слайд 5)

Определить знак выражения: (слайд 6)

Блиц-опрос (по формулам в форме математического диктанта) по вариантам. (Слайды 7 — 8)

Закрепление знаний и умений (Слайд 9)

Проверочный тест

Это интересно:

Тригонометрия в ладони

Смотрите, я прикладываю угол в 30°; оказывается, это угол

— между мизинцем и безымянным пальцем;

— между мизинцем и средним пальцем — 45°;

— между мизинцем и указательным пальцем — 60°;

— между мизинцем и большим пальцем — 90°;

И это у всех людей без исключения.

№0 — Мизинец

№1 — Безымянный

№2 — Средний

№3 -Указательный

№4 — Большой

№0 Мизинец 0°

№1 Безымянный 30°

№2 Средний 45°

№3 Указательный 60°

№4 Большой 90°

n — номер пальца

Значения синуса и косинуса угла по “ладони” приведено в таблице.

Примечание. Для определения косинуса угла отсчет пальцев происходит от большого пальца руки. [6]

Значения синуса

№ пальца	Угол
0	0
1	30°
2	45°
3	60°
4	90°

Значения косинуса

№ пальца	Угол
4	0°
3	30°
2	45°
1	60°
0	90°

Тригонометрические формулы.

10 класс — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Тригонометрические формулы

Урок-зачет разработан
учителем математики ВК
МБОУ СОШ №9
Азаровой О.Е.

2. Цель урока

Повторить и систематизировать
изученный материал по теме :
«Тригорометрические формулы»

3. Задачи урока

Повторить определение синуса, косинуса,
тангенса, котангенса числа α;
Повторить формулы приведения, формулы
двойного угла, формулы сложения;
Повторить основное тригонометрическое
тождество и формулы, выражающие связь
между тангенсом и косинусом, между
котангенсом и синусом.

Научить применять полученные знания при
решении задач.

4. Блиц-опрос

Синусом угла α называется _____
точки, полученной поворотом
точки______ вокруг начала
координат на угол α
tg α =
sin2 α +cos2 α=
1+ tg2 α=
sin(-α)=
tg (-α) =
cos (α+β)=
sin (α-β)=
sin 2α=
sin(π- α)=
cos ( 2 + α)=
Косинусом угла α называется
_____ точки, полученной
поворотом точки______ вокруг
начала координат на угол α
ctg α=
tg α∙ ctg α=
1+ ctg2 α=
cos (-α)=
ctg (-α) =
cos (α-β)=
sin (α+β)=
cos 2α=
cos(π- α)=
sin (
2
+ α)=

5. Блиц-опрос

Синусом угла α называется
ордината точки, полученной
поворотом точки (1;0) вокруг
начала координат на угол α
tg α = sin
cos
α +cos2 α = 1
1
1+ tg2 α = cos α
sin2
2
sin(-α) = — sin α
tg (-α) = -tg α
cos (α+β) = cosα cosβ – sinα sinβ
sin (α-β) = sinα cosβ — cosα sinβ
sin 2α = 2sin αcos α
tg tg
tg (α+β) = 1 — tg tg
sin(π- α) =sin α
cos ( 2 + α) = -sinα
Косинусом угла α называется
абсцисса точки, полученной
поворотом точки (1;0) вокруг
начала координат на угол α
cos
ctg α= sin
tg α∙ ctg α = 1
1
1+ ctg2 α= sin
2
α
cos (-α) = cos α
ctg (-α) = -ctg α
cos (α-β)=cosα cosβ +sinα sinβ
sin (α+β)= sinα cosβ + cosα sinβ
cos 2α=cos2 α-sin2 α
2tg
tg 2α= 1 — tg 2
cos(π- α)= — cos α
sin ( + α)=-cos α
2

6.

Оценка«5» — 11
«4» — 9 – 10
«3» — 6 – 8
«2» — 0 – 5

7. Закрепление знаний и умений

№546
1) дано:
найти:
3
sin ;
3 2
cos
ОТВЕТ:
3) дано:
найти:
2
cos
3
tg 2 2 ;0
sin
ОТВЕТ: sin 2 2
3
2
Упростить выражение
1. 2 sin( ) cos 2 cos( ) sin( )
2
2
Ответ: -2
2.
(1 tg( )) (1 tg( )) cos
Ответ:
2
cos 2
№557
Упростить выражение
cos
sin
ОТВЕТ:
sin
cos
4 sin 2
1 cos 4
*
cos
вариант 1
вариант 2
Найдите значение
— 3cos1200+4cos1800
1)
а) -2,5;
2)
б) 5,5;
Дано:
в) -4,75;
3)
31
20
г) -5,5.
3
sin ;
5 2
;б) 1 ;
в)
20
2)
cos tg
Найдите значение:
а)
1)
1;
20
г)
б) -1,5;
Дано:
4 3
cos ;
2
5 2
а)
1 (1 sin ) (1 sin )
tg cos
4)
а) -3,5;
;г) sin
.
Упростите выражение:
в)
sin sin
2
2
;г)
2 sin sin
;
2 sin sin
г) 6,5.

sin ctg
11
11
14
14
1
; б)
; в)
; г) 1
15
15
15
15
3)
Упростите выражение:
4)
Упростите выражение:
ctg sin
1 (sin cos ) 2
1
1
а) 2 cos ; б)
2 cos ;в) 2 sin ;г) 2 sin
sin( ) sin( )
cos( ) cos( )
а) 2 cos cos ;б)
в) -0,5;
Найдите значение:
31 .
20
Упростите выражение:
а) cos ;б) sin 2 ;в) cos
Найдите значение:-3sin120 0-4sin180 0
а)
2 cos sin
в)
sin 2 ;
; б)
г)
2 cos
;
2 sin cos .

11. Проверка

1 вариант
1.
2.
3.
4.
г)
б)
г)
б)
2 вариант
1.
2.
3.
4.
б)
в)
г)
а)

12. Это интересно

Тригонометрия в ладони

13. Зарождение тригонометрии относится к глубокой древности. Само название «тригонометрия» греческого происхождения, обозначающее

«измерение треугольников».
Одним из основоположников
тригонометрии считается
древнегреческий астроном Гиппарх,
живший во 2 веке до нашей эры.

Гиппарх (Hípparchos) (около 180—190
до н. э., Никея, — 125 до н. э., Родос),
древнегреческий учёный.
Гиппарх является автором первых
тригонометрических таблиц и
одним
из
основоположников
астрономии.
№0 Мизинец
№1 Безымянный
№2 Средний
№3 Указательный
№4 Большой
00
300
450
600
900
n
sin α =
2
Значение синуса
№ пальца
Угол α
0
0
sin 0 0
0
0
2
1
30
sin 30 0
1
1
2
2
2
45
sin 450
3
60
4
90
sin 60 0
sin 90 0
2
2
3
2
4
1
2
Значение косинуса
№ пальца
Угол α
4
0
3
30
2
45
1
60
0
90
cos 0 0
4
1
2
cos 30 0
3
2
cos 45
0
cos 60 0
cos 90 0
2
2
1
1
2
2
0
0
2

17. Домашнее задание

Проверь себя
стр. 166
Спасибо, урок
окончен!!!
Спасибо за урок!

English Русский Правила

Тригонометрические формулы для класса 10

Слово «тригонометрия» происходит от греческого слова «тригонон», что означает «треугольник», и «метрон», что относится к термину «мера». Это латинское производное 16 века. Это понятие тригонометрии было дано греческим математиком Гиппархом. Согласно Виктору Кацу в «Истории математики (3-е издание)», тригонометрия была разработана в первую очередь из потребностей греческих и индийских астрономов.

Тригонометрия — важнейшее понятие математики. Он имеет дело со сторонами и углами прямоугольного треугольника. Он играет наиболее важную роль почти во всех областях, будь то авиация, физика, криминология, военная наука, морская биология, разработка звуковых волн, спутниковая навигация, медицинская визуализация и т. д. Тригонометрия используется для нахождения углов или сторон правой стороны. угловой треугольник.

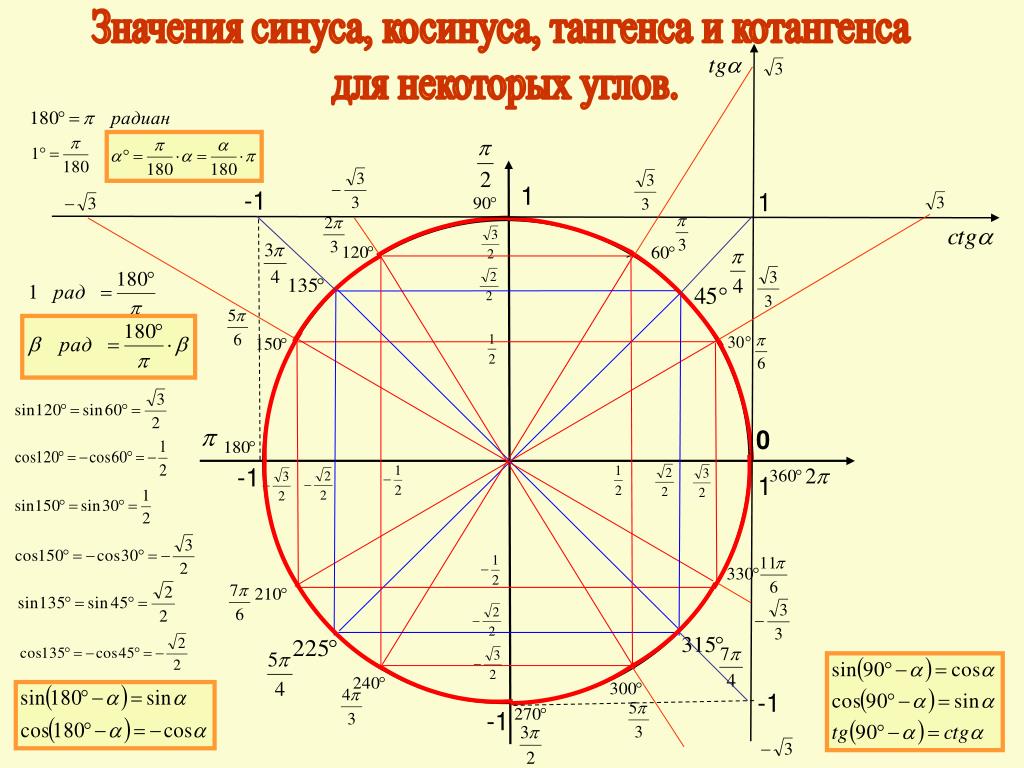
Прямоугольный треугольник:

Здесь на рисунке показан прямоугольный треугольник, имеющий гипотенузу (наибольшая сторона), основание (прилежащая сторона), высоту (противоположная сторона) и угол Ө.

Этот треугольник имеет большое значение, потому что если кто-то попытается найти прямое расстояние и угол, то это можно легко найти, используя это.

Основными функциями тригонометрии являются синус, косинус и тангенс. Остальные три функции косеканс, секанс и котангенс являются обратными величинами синуса, косинуса и тангенса соответственно.

Тригонометрические соотношения:

Три основных тригонометрических соотношения:

\[sin\theta= \frac{\textrm{Противоположная сторона}}{\textrm{Сторона гипотенузы}}\]

\[cos\theta= \frac{\textrm{Смежная сторона}}{\textrm{Сторона гипотенузы}}\]

\[tan\theta= \frac{\textrm{Противоположная сторона}}{\textrm{Смежная сторона}}\]

Обратные отношения выше:

\[sec\theta=\frac{1}{cos\theta}= \frac{\textrm{Сторона гипотенузы}}{\textrm{Смежная сторона}}\]

\[cosec\theta=\frac{1}{sin\theta}= \frac{\textrm{Сторона гипотенузы}}{\textrm{Противоположная сторона}}\]

\[cot\theta=\frac{1 }{tan\theta }= \frac{\textrm{Смежная сторона}}{\textrm{Противоположная сторона}}\]

Ниже приведены соотношения между тригонометрическими тождествами:

\[tan\theta =\frac{sin \theta }{cos\theta }\]

\[cot\theta =\frac{cos\theta }{sin\theta }\]

Тригонометрические углы:

В тригонометрии существует пять углов.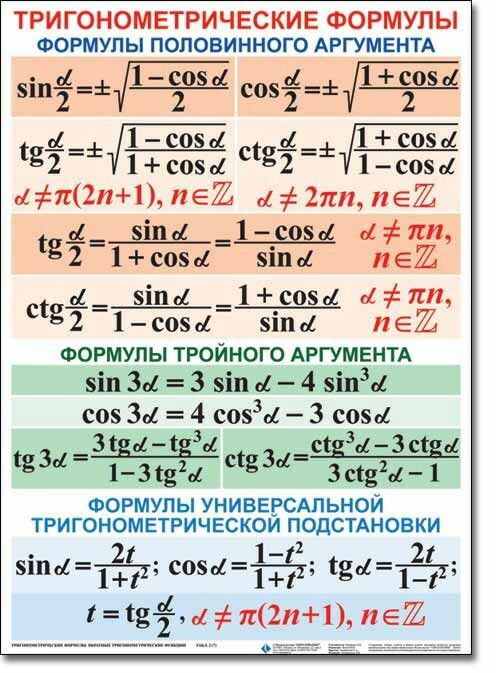 Можно найти и другие углы, но это основные. Эти углы равны 00, 300, 450, 600, 900 . The table for the same is given below:

977 9006. 92\theta -1}{2cot\theta }\]

2. Тождества суммы и разности:

Для двух углов u и v тождества, связанные с суммой и разностью этих двух углов, следующие:

\[sin(u+v)=sin(u)cos(v)+cos(u)sin(v)\]
\[cos(u+v)=cos(u)cos(v) -sin(u)sin(v)\]
\[tan(u+v)=\frac{tan(u)+tan(v)}{1-tan(u)tan(v)}\ ]
\[sin(u-v)=sin(u)cos(v)-cos(u)sin(v)\]
\[cos(u-v)=cos(u)cos(v) +sin(u)sin(v)\]
\[tan(u-v)=\frac{tan(u)-tan(v)}{1+tan(u)tan(v)}\]

3. Формулы приведения:

углы любых других квадрантов можно привести к эквивалентному углу первого квадранта. Это можно сделать, изменив знаки и тригонометрические соотношения. Формулы приведения для того же:

Первый квадрант

\[sin(90-\theta)=cos\theta \]
\[cos(90-\theta)=sin\theta \]
\[загар(90-\theta)=cot\theta \]
\[csc(90-\theta)=sec\theta \]
\[sec(90-\theta)=csc\theta \]
\[cot(90-\theta)=tan\theta \]

Второй квадрант

\[sin(180-\theta)=sin\theta \]
(180-\theta)=-cos\theta \]
\[tan(180-\theta)=-tan\theta \]
\[csc(180-\theta)=csc\theta \]
\[сек(180-\тета)=-сек\тета \]
\[cot(180-\theta)=-cot\theta \]

Третий квадрант

\[sin(180+\theta)=-sin\theta \] 9 9025
\[cos(180+\theta)=-cos\theta \]
\[tan(180+\theta)=tan\theta \]
\[csc(180+\theta)=- csc\theta \]
\[sec(180+\theta)=-sec\theta \]
\[cot(180+\theta)=cot\theta \]

Четвертый квадрант

\[sin(360-\theta)=-sin\theta \]
\[cos(360-\theta)=cos\theta \]
\[tan(360-\) theta)=-tan\theta \]
\[csc(360-\theta)=-csc\theta \]
\[sec(360-\theta)=sec\theta \]
\[cot(360-\theta)=-cot\theta \]

Конгруэнтные треугольники:

Два треугольника конгруэнтны, если они наложены друг на друга. Термин «конгруэнтность» определяет объект и его зеркальное отражение.

Два треугольника должны быть конгруэнтными, если они имеют одинаковую длину сторон и одинаковую меру углов. Таким образом, они могут накладываться друг на друга. Конгруэнтность может быть представлена символом.

\[\cong\]

Правила соответствия:

1. SSS(Side-Side-Side)

Если два треугольника имеют эквивалентные соответствующие стороны, то эти два треугольника будут конгруэнтны по правилу SSS.

Например,

\[\textrm{AC=PR}\]

\[\textrm{BC=QR}\]

\[\textrm{AB=PQ}\]

В приведенных выше двух треугольниках ABC и PQR изображения будут загружены в ближайшее время.

Здесь треугольники ABC и PQR равны по правилу SSS, потому что соответствующие стороны этих двух треугольников эквивалентны.

Таким образом,

\[\Delta \textrm{ABC}\cong \Delta \textrm{PQR}\]

2. SAS (сторона-угол-сторона)

Если два треугольника имеют эквивалентные две соответствующие стороны и также углы, образованные этими соответствующими сторонами, равны, то эти треугольники будут конгруэнтными по правилу SAS.

Например,

В приведенных выше двух треугольниках ABC и PQR изображения будут загружены в ближайшее время.

Здесь треугольники ABC и PQR конгруэнтны по правилу SAS, потому что соответствующие две стороны и углы, образованные этими сторонами, равны.

Таким образом,

3. ASA (Angle-Side-Angle)

Если два треугольника имеют эквивалентные два соответствующих угла, а также стороны между этими соответствующими углами равны, то эти треугольники будут конгруэнтными по правилу ASA.

Например,

В приведенных выше двух треугольниках ABC и PQR изображения будут загружены в ближайшее время.

\[\textrm{AB=PQ}\]

\[\textrm{AC=PR}\]

\[\угол A=\угол P\]

Здесь треугольники ABC и PQR равны по правилу ASA, потому что соответствующие два угла и стороны между этими углами равны.

Таким образом,

\[\Delta ABC\cong \Delta PQR\]

4. RHS (прямой угол-гипотенуза-сторона)

Если гипотенузы и соответствующие стороны двух прямоугольных треугольников эквивалентны, то эти два прямоугольных треугольника будут конгруэнтны по правилу RHS.

Например,

В двух вышеприведенных треугольниках XYZ и RST скоро будут загружены изображения.

\[\textrm{XZ=RT}\]

\[\textrm{YZ=ST}\]

Здесь треугольники XYZ и RST равны по правилу RHS, так как гипотенузы XZ и RT и соответствующие стороны YZ и ST прямоугольных треугольников эквивалентны.

Таким образом,

\[\Delta XYZ\cong \Delta RST\]

Подобные треугольники

Два треугольника будут подобны, если у них одинаковые углы и разные длины сторон. Сходство двух треугольников обозначается символом ~.

Таким образом, два треугольника должны быть подобны, если они имеют равные соответствующие углы и стороны пропорциональны.

Например,

В приведенных выше двух треугольниках ABC и XYZ изображения будут загружены в ближайшее время.

\[\угол A=\угол X,\угол B=\угол Y\textrm{и} \угол C=\угол Z\]

\[\frac{AB}{XY}=\frac{BC }{YZ}=\frac{AC}{XZ}\]

Правила подобия:

1. AAA (Angle-Angle-Angle)

Два треугольника будут подобны по правилу AAA, если у них равны соответствующие углы . Например,

В приведенных выше двух треугольниках ABC и DEF,

\[\угол A=\угол D,\угол B=\угол E \textrm{и} \угол C=\угол F\]

Здесь треугольники ABC и DEF подобны по правилу AAA, потому что соответствующие углы этих двух треугольников равны.

Таким образом,

\[\Delta ABC\sim \Delta DEF\]

2. SSS (Side-Side-Side)

Два треугольника будут подобны по правилу SSS, если соответствующие стороны треугольников находятся в пропорция. Например,

В приведенных выше двух треугольниках ABC и DEF скоро будут загружены изображения.

Здесь треугольники ABC и DEF подобны по правилу SSS, потому что соответствующие стороны этих двух треугольников пропорциональны.

3. SAS (Side-Angle-Side)

Два треугольника будут подобны по правилу SAS, если две соответствующие стороны пропорциональны и углы между этими соответствующими сторонами равны.

Например,

В двух приведенных выше треугольниках LMN и QRS изображения будут загружены в ближайшее время.

\[\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}\]

\[\frac{12}{6}=\frac{16} {8}=\frac{18}{9}\]

\[2=2=2\]

Здесь треугольники LMN и QRS подобны по правилу SAS, потому что две соответствующие стороны этих двух треугольников находятся в пропорция и углы между этими двумя соответствующими сторонами равны.

Таким образом,

\[\Delta ABC\sim \Delta DEF\]

Теоремы подобия

Если два треугольника подобны, то отношение их площадей должно быть пропорционально квадратам отношения их стороны. 92\]

Закон синуса:

Если A, B и C расположены под углом, а a, b и c являются сторонами треугольника, то:

(Изображение будет загружено в ближайшее время)

Список всего Тригонометрические формулы для класса 10

Тригонометрия — это один из основных разделов математики, который имеет дело с функциями углов, а также с тем, как они вычисляются и используются для других измерений. Тригонометрия представлена учащимся в 10 классе CBSE. Учащимся всегда рекомендуется бегло говорить и тщательно отвечать на эти вопросы, поскольку они очень важны с точки зрения экзамена. Тригонометрия имеет вес 12 баллов на экзамене 10-й доски.

Шесть функций тригонометрии:

Синус
Косинус
Касательная
Котангенс
Секанс
Косеканс

Тригонометрия играет наиболее важную роль почти во всех областях, будь то авиация, физика, криминология, военная наука, морская биология, разработка звуковых волн, спутниковая навигация, медицинская визуализация и т. д.

Список тригонометрических формул класса 10

Для нахождения углов или сторон прямоугольного треугольника используется тригонометрия.

Тригонометрические формулы основаны на трех сторонах прямоугольного треугольника, имеющих гипотенуз (самая длинная сторона), основание (прилежащая сторона), высота (противоположная сторона) и угол θ.

Если применить теорему Пифагора для прямоугольного треугольника, то получим:

( Перпендикуляр) ² + (Base) ² = (Hypotenuse) ² ⇒ (P) ² + (B) ² = (H ) ²

Основные тригонометрические формулы

sin A — Перпендикуляр/гипотенуза
cos A — основание/гипотенуза
желтовато-коричневый A — Перпендикулярно/основание
Детская кроватка A — Основание/Перпендикуляр
cosec A — гипотенуза/перпендикуляр

Тригнометрический стол

Angles

300

450

600

900

SIN ө

1/2

1/√2

√3/2

9002 1

√3/2

9002 19000 2 9000 2 9000 2 9000 2 9000 2 9006.

a0003

Cos Ө

√3/2

1/√2

1/2

Tan Ө

1/√3

√3

∞

Cosec Ө

∞

√2

2/√3

Sec Ө

2/√3

√2

∞

Cot Ө

∞

√3

1/√3

Угол	0°	30°	45°	60°	90°
Синθ	0	1/2	1/√2	√3/2	0
Cosθ	1	√3/2	1/√2	1/2	1
Танθ	0	1/√3	1	√3	0
Кот θ	Не определено	√3	1	1/√3	Не определено
Секθ	1	2/√3	√2	2	1
Косекθ	Не определено	2	√2	2/√3	Не определено

Связь между тригонометрическими отношениями

tanA — sinA/cosA
КОТА — КОЗА/СИНА
cosecA — 1/sinA
секА — 1/КоСА

Тригонометрические знаковые функции

sin(-θ) = −sin θ
, потому что (-θ) = потому что θ
тангенс (-θ) = -тангенс θ
cosec(−θ) = −cosec θ
сек(-θ) = сек θ
детская кроватка (-θ) = — детская кроватка θ

Тригонометрические тождества

sin ² A + cos ² A = 1
рыжевато-коричневый ² A + 1 = сек. ² A
детская кроватка ² A + 1 = cosec ² A

Периодические тождества

sin(2nπ + θ) = sinθ
потому что (2nπ + θ) = cosθ
тангенс (2nπ + θ) = тангенс θ
раскладушка (2nπ + θ) = раскладушка θ
сек(2nπ + θ) = секθ
cosec(2nπ + θ) = cosecθ

Дополнительные отношения

Квадрант I

sin(π/2−θ) = cosθ
потому что (π/2−θ) = sinθ
тангенс(π/2−θ) = cotθ
раскладушка (π/2−θ) = tanθ
сек(π/2−θ) = cosecθ
cosec(π/2−θ) = secθ

Квадрант II

sin(π−θ) = sinθ
cos(π−θ) = -cosθ
тангенс (π−θ) = -тангенс
раскладушка (π−θ) = — раскладушка θ
сек(π−θ) = -секθ
cosec(π−θ) = cosecθ

Квадрант III

sin(π+ θ) = – sinθ
cos(π+ θ) = – cosθ
тангенс (π + θ) = тангенс θ
детская кроватка (π + θ) = детская кроватка θ
сек(π+θ) = -секθ
cosec(π+ θ) = -cosecθ

Квадрант IV

sin(2π− θ) = – sinθ
cos(2π− θ) = cosθ
тангенс (2π− θ) = – тангенс θ
раскладушка (2π− θ) = – раскладушка θ
сек (2π− θ) = секθ
cosec(2π− θ) = -cosecθ

Сумма и разность двух углов

sin (A + B) = sin A. cos B + cos A.sin B
sin (A − B) = sin A.cos B – cos A.sin B
cos (A + B) = cos A.cos B – sin A.sin B
cos (A – B) = cos A.cos B + sin A.sin B
tan(A+B) = [(tan A + tan B)/(1 – tan A.tan B)]
tan(A-B) = [(tan A – tan B)/(1 + tan A.tan B)]

Формулы двойного угла

sin2A = 2sinA.cosA = [2tanA + (1+tan ² A)]
cos2A = cos ² A–sin ² A = 1–2sin ² A = 2cos ² A–1= [(1-tan ² A)/(1+tan ^{3 A) )]}
tan2A = (2 tanA)/(1-tan ² A)

Формулы тройного угла

sin3A = 3sinA – 4sin ³ А
cos3A = 4cos ³ A – 3cosA
tan3A = [3tanA–tan ³ A]/[1−3tan ² A]

Некоторые другие тригонометрические формулы:

sin(90° – θ) = cosθ
cos(90° – θ) = sinθ
tan(90° – θ) = cotθ
кроватка(90° – θ) = tanθ
сек(90° – θ) = cosecθ
cosec(90° – θ) = secθ
sin ² θ + cos ² θ = 1
sec2θ = 1 + tan2θ для 0° ≤ θ < 90°
Cosec2θ = 1 + cot2θ для 0° ≤ θ ≤ 90°

Как с помощью CREST Champs подготовиться к экзамену CBSE по математике в 10 классе?

Формулы играют важную роль в получении хороших результатов на экзамене CBSE по математике класса 10 .

УРОК ПО ТЕМЕ «тРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ»

Тригонометрические формулы.

1. Тригонометрические формулы

2. Цель урока

3. Задачи урока

4. Блиц-опрос

5. Блиц-опрос

6.

7. Закрепление знаний и умений

11. Проверка

12. Это интересно

13. Зарождение тригонометрии относится к глубокой древности. Само название «тригонометрия» греческого происхождения, обозначающее

17. Домашнее задание

Тригонометрические формулы для класса 10

Прямоугольный треугольник:

Тригонометрические соотношения:

Ниже приведены соотношения между тригонометрическими тождествами:

Тригонометрические углы:

Конгруэнтные треугольники:

Правила соответствия:

Подобные треугольники

Правила подобия:

Теоремы подобия

Закон синуса:

Список всего Тригонометрические формулы для класса 10

Добавить комментарий Отменить ответ