Y x 8 график: Mathway | Популярные задачи

23-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

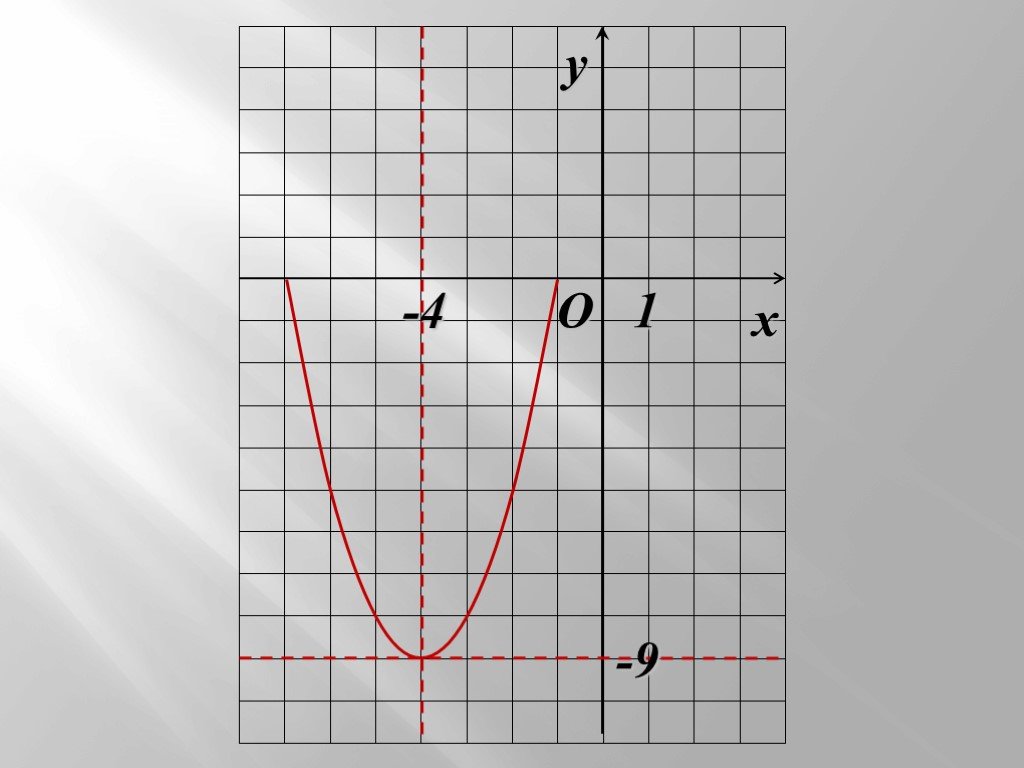
Решение линейных уравнений с помощью графика

Основные понятия

• Решение системы с помощью графика
• График системы уравнений с единственным решением
• График a2 решения 90 системы уравнений без с бесконечным множеством решений

Решение системы линейных уравнений с помощью графика  

1. …………………. . состоит из двух или более линейных уравнений, использующих одни и те же переменные.

2. ………… системы линейных уравнений — это любая упорядоченная пара, которая составляет все уравнения в системе

3. Линии пересекаются в одной точке. Тогда в системе есть ………. решение.

4. Линии не пересекаются; они параллельны. Эта система имеет ………… решение.

5. Линии пересекаются в каждой точке; это одна и та же линия. Эта система имеет бесконечно …….. решений.

6. Наклон и точка пересечения –2x + y=5 равны …………… 

• Сравните с наклоном и точкой пересечения для решений и у=3х+5………….
9. Сколько решений для y=3x+4 и y=4+3x………… 
10. Нарисуйте систему уравнений, чтобы найти решение. x+4y=8 и 3x+4y=0

Ответы:  

1. Система линейных уравнений
2. Solution 
3. One solution 
4. No solution 
5. Many solutions  
6. y=2x+5 
7. One solution 
8. No solution 
9. Infinitely solutions 
10. Не знаю. Хорошо, давайте рисовать, чтобы найти решения.
Исследуй!  

Бет и Данте проходят мимо библиотеки, возвращаясь домой по разным прямым дорожкам.

Модель с математикой

Точка на графике представляет расположение библиотеки. Нарисуйте и подпишите линии на графике, чтобы показать все возможные пути к библиотеке.

Решение:  

B. Напишите систему уравнений, представляющую пути, пройденные Бет и Данте.

Система уравнений

1. -x-2y=-8 и 5x-2y=4
2. -x-y=-5 и x-y=-1

Бет и Данте могут выбирать бесконечные пути на выбор библиотека домой.

Сосредоточьтесь на математических рассуждениях. Что представляет точка пересечения линий в ситуации?

Точка пересечения их путей называется решением уравнений.

На этом уроке мы можем рисовать графики для поиска решений системы уравнений.

Системы уравнений: Набор уравнений называется системой уравнений. Решения должны удовлетворять каждому уравнению системы.

Системы линейных уравнений:  

Решением системы уравнений является упорядоченная пара, удовлетворяющая всем уравнениям системы.

Система линейных уравнений может иметь:

1. Точно одно решение
2. NO Solutions
3. Не бесконечно.
   1. По наклону и форме пересечения
   2. Графиком
   3. Подстановкой
   4. Исключением

   Графическим методом решения линейных уравнений с двумя переменными:  

   Чтобы решить систему двух уравнений с двумя переменными графически, мы рисуем каждое уравнение.

   Шаг 2:  

   Чтобы построить уравнение вручную, сначала преобразуйте его в форму y= mx+b, решив уравнение для y.

   Шаг 3:                

   Начните задавать значения x как 0, 1, 2 и т. д. и найдите соответствующие значения y или наоборот. То есть найти упорядоченные пары, удовлетворяющие каждому из уравнений.

   Шаг 4:    

   Нанесите упорядоченные пары и нарисуйте графики обоих уравнений на одной оси. Определите точку, где пересекаются обе линии.

   Шаг 5:    

   Координаты точки или точек пересечения графиков являются решением или решениями системы уравнений.

   Основной вопрос: Как график системы линейных уравнений представляет ее решение?

   Пример 1:  

   Ли выбирает новый план сотовой связи. Как Ли может использовать графики системы линейных уравнений, чтобы определить, когда тарифные планы телефонов стоят одинаково? Какой план выбрать Ли? Объяснять.

   Решение:  

   Модель с математикой: Вы можете использовать графики системы линейных уравнений для сравнения стоимости каждого плана.

   Шаг 1  

   Напишите систему уравнений. Пусть x = количество минут, используемых каждый месяц.

   Пусть y = общая ежемесячная стоимость плана.

   Общая ежемесячная стоимость плана = стоимость затрат на минуты+неограниченные данные, использованные

   . для уравнений

   • y = 0,20x+75

   Если x=-20, то y=0,20 X (-20) +75 = -4+75=71. Найди координаты методом проб и ошибок.

   Шаг 3:  

   • y = 0,25x+70

   Если x=-40, то y=0,25 X 60 +70 =-40 +70 = 60 ….. Точно так же мы можем найти координаты.

   Граф системы.

   Точка пересечения (100, 95) является решением системы.

   Линии пересекаются, значит, у этой системы уравнений есть одно решение.

   Решите систему, построив график 

   Нарисуйте график системы.

   Точка пересечения (100, 95) является решением системы.

   Линии пересекаются, значит, у этой системы уравнений есть одно решение.

   Если Ли использует 100 минут в месяц, оба плана будут стоить 95 долларов. Она могла выбрать любой план.

    Если Ли использует менее 100 минут, она должна выбрать компанию Б. Если Ли использует более 100 минут, она должна выбрать компанию А. 

   Пример 2  

   Решите систему. y = x – 4 и 2x – 2y = – 2. Нарисуйте уравнения системы, чтобы найти решение.

   Решение:  

   Шаг 1:   Запишите наклон – отрезок заданных уравнений

   y = x – 4.

   Рассуждение: что вы можете сказать о наклонах и y-перехватах уравнений?

   Шаг 2: Сначала запишите форму наклона-пересечения данного уравнения.

   2x – 2y = – 2

   х – у = -1

   – у= – 1 – х

   у = х + 1

   Если х=0, то у = 0 + 1 = 1 система уравнений без решения

   Шаг 3:  

   Нарисуйте, используя координаты системы уравнений.

   Линии параллельны. Нет точки пересечения.

   То есть прямые не пересекаются; они параллельны.

   Эта система не имеет решений.

   Пример 3  

   Решите систему. y =

   1212

   x+3 – 3x + 6y = 18. Нарисуйте уравнения системы, чтобы найти решение.

   Решение:  

   Шаг 1: Это уравнение имеет форму пересечения наклона.

   Шаг 2:  

   Каждая точка (x, y) на линии представляет собой решение.

   Прямые одинаковые, поэтому система имеет бесконечно много решений.

   Давайте проверим ваши знания 

   1. Решите каждую систему с помощью графика. Опишите решения.

   5x + y = -3 и 10x + 2y = -6

   2. Решение системы с графиком

   y = 3x + 5 и y = 2x + 4

   3. Solve System на график

99927777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777

3. . = x + 5 

   y = x + 10 

   Ответы:  

   1. Решите каждую систему с помощью графика. Опишите решения. 5x+y=-3 и 10x+2y=-6 

   Решение:

   Шаг 1:

   5x+y = -3

   Y = -5x-3

   Шаг 2:

   . −10x−62−10x−62

   или y = -5x – 3

   Шаг 3: Нарисуйте график для данных уравнений.

   Прямые одинаковые, поэтому система имеет бесконечно много решений.

   2. Решите систему, построив график y = 3x + 5 и y = 2x + 4  

   Решение: Шаг 1

   y = 3x + 5

   y=2x + 4

   Прямые пересекаются, значит, для этой системы уравнений есть одно решение.

   Решение x = -1 и y = 2

   3. Решение системы с графиком

   y = x + 3

   Y = X + 10

   Решение:

   9971

   Solution:

   . x + 3 

   Шаг 2   

   y = x + 10  

   Шаг 3:

   Нанесение точек на график

   На графике линии не пересекаются. Значит, данная система уравнений не имеет решения.

   Ключевое понятие  

   Решением линейного уравнения является точка пересечения линий, определяемых уравнениями.

   Ключевые понятия  

   • Решение системы с помощью графика 
   • График системы уравнений с единственным решением 
   • Нарисуйте график системы уравнений, не имеющей решений
   •  Нарисуйте график системы уравнений с бесконечным числом решений Опишите решения.

• x +y = 10
  • x — y = 4

• 5x +7y = 50
  • 7x +5y = 46
• 7x +5y = 46

7x +5y = 46

7x +5y = 46

7x +5y

7x +5y

7X +5y = 46

7x. Опишите решения.

9x + 3y + 12 = 0 и 18x + 6y + 24 = 0,

3. Решите систему с помощью графика. Опишите решения.

3x + 2y = 5 и 2x – 3y = 7

4. Решите систему с помощью графика.

   No related posts.