Закон распределения Пуассона | matematicus.ru
Artman Законы распределения случайной величины
Закон распределения СВ Пуассона вытекает из биномиального закона распределения СВ и относится к дискретному распределению.
В случая малых значений р→0 (то есть при р≤0,1) и большом значении n→∞ применяется закон распределения случайной величины Пуассона.
Вероятность того, что случайная величина X примет значение равное k, вычисляется по формуле:
Р(Х=k) = Pn(k) = λk⋅e-λ/k!
где λ=n⋅p = const
Это выражение описывает плотность вероятности.
Таблица ряда распределения случайной величины X по закону Пуассона:
График плотности распределения случайной величины, где красным цветом при λ=1
 2} = \lambda \cr} $
2} = \lambda \cr} $D(x) = λ
Пример
В магазин по продажи холодильников поступает примерно 100 звонков в день. Вероятность того, что закажут холодильник белого цвета 0,09; чёрного — 0,07 и бежевого — 0,03.
Требуется составить закон распределения заказов на покупку холодильников.
Решение
Здесь n=100 и p1=0,09, p2=0,07, p3=0,03.
Так как λ=np, тогда
λ1=9, λ2=7 и λ3=3
Составим таблицу распределения вероятностей при различных значениях k и λ.
| k | λ1=9 | λ2=5 | λ3=3 |
| 0 | 0,000123 | 0,006738 | 0,049787 |
| 1 | 0,001111 | 0,03369 | 0,149361 |
| 2 | 0,004998 | 0,084224 | 0,224042 |
| 3 | 0,014994 | 0,140374 | 0,224042 |
| 4 | 0,033737 | 0,175467 | 0,168031 |
| 5 | 0,060727 | 0,175467 | 0,100819 |
| 6 | 0,09109 | 0,146223 | 0,050409 |
| 7 | 0,117116 | 0,104445 | 0,021604 |
| 8 | 0,131756 | 0,065278 | 0,008102 |
| 9 | 0,131756 | 0,036266 | 0,002701 |
| 10 | 0,11858 | 0,018133 | 0,00081 |
На основании этой таблицы построим полигон распределения покупки холодильников.
6020
Функция ПУАССОН — Служба поддержки Майкрософт
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Возвращает распределение Пуассона. Обычное применение распределения Пуассона состоит в предсказании количества событий, происходящих за определенное время, например количества машин, появляющихся на площади за одну минуту.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новом варианте этой функции см. в статье Функция ПУАССОН.РАСП.
Синтаксис
Аргументы функции ПУАССОН описаны ниже.
-
X Обязательный. Количество событий.
-
Среднее Обязательный. Ожидаемое числовое значение.
-
Интегральная — обязательный аргумент. Логическое значение, определя которое определяет форму возвращаемого распределения вероятности. Если значение «совокупное» имеет значение ИСТИНА, то пуассон возвращает совокупное значение вероятности того, что число случайных событий включительно будет от нуля до x.
Если этот ложь, возвращается функция массовой вероятности Пуассона, которая вероятность того, что количество произошедших событий будет точно x.
Замечания
-
Если x не является целым числом, оно усекается.
-
Если x или «число» не является числом, то пуАССОН возвращает #VALUE! значение ошибки #ЗНАЧ!.
-
Если x < 0, то пуассон возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Если в < 0, то пуассон возвращает #NUM! значение ошибки #ЗНАЧ!.

-
Функция ПУАССОН вычисляется следующим образом.
Если интегральная = ЛОЖЬ:
Если интегральная = ИСТИНА:
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|
2 |
Число событий |
|
|
5 |
Ожидаемое среднее |
|
|
Формула |
Описание (результат) |
Результат |
|
=ПУАССОН(A2;A3;ИСТИНА) |
Интегральное распределение Пуассона для приведенных выше условий (0,124652) |
0,124652 |
|
=ПУАССОН(A2;A3;ЛОЖЬ) |
Функция плотности распределения Пуассона для приведенных выше условий (0,084224) |
0,084224 |
Формула распределения Пуассона и ее значение в финансах
Оглавление
Содержание
Что такое распределение Пуассона?
Как это работает
Формула
Распределение Пуассона в финансах
Часто задаваемые вопросы о распределении Пуассона
К
Адам Хейс
Полная биография
Адам Хейс, доктор философии, CFA, финансовый писатель с более чем 15-летним опытом работы на Уолл-стрит в качестве трейдера деривативов. Помимо своего обширного опыта торговли деривативами, Адам является экспертом в области экономики и поведенческих финансов. Адам получил степень магистра экономики в Новой школе социальных исследований и докторскую степень. из Университета Висконсин-Мэдисон по социологии. Он является обладателем сертификата CFA, а также лицензий FINRA Series 7, 55 и 63. В настоящее время он занимается исследованиями и преподает экономическую социологию и социальные исследования финансов в Еврейском университете в Иерусалиме.
Помимо своего обширного опыта торговли деривативами, Адам является экспертом в области экономики и поведенческих финансов. Адам получил степень магистра экономики в Новой школе социальных исследований и докторскую степень. из Университета Висконсин-Мэдисон по социологии. Он является обладателем сертификата CFA, а также лицензий FINRA Series 7, 55 и 63. В настоящее время он занимается исследованиями и преподает экономическую социологию и социальные исследования финансов в Еврейском университете в Иерусалиме.
Узнайте о нашем редакционная политика
Обновлено 19 мая 2022 г.
Рассмотрено
Сомер Андерсон
Рассмотрено Сомер Андерсон
Полная биография
Сомер Дж. Андерсон — дипломированный бухгалтер, доктор бухгалтерского учета и профессор бухгалтерского учета и финансов, проработавший в сфере бухгалтерского учета и финансов более 20 лет. Ее опыт охватывает широкий спектр областей бухгалтерского учета, корпоративных финансов, налогов, кредитования и личных финансов.
Узнайте о нашем Совет финансового контроля
Факт проверен
Сюзанна Квилхауг
Факт проверен Сюзанна Квилхауг
Полная биография
Сюзанна — контент-маркетолог, писатель и специалист по проверке фактов. Она имеет степень бакалавра финансов в Государственном университете Бриджуотер и помогает разрабатывать контент-стратегии для финансовых брендов.
Узнайте о нашем редакционная политика
Инвестопедия / Джоуль Гарсия
Что такое распределение Пуассона?
В статистике распределение Пуассона — это распределение вероятностей, которое используется, чтобы показать, сколько раз событие может произойти в течение определенного периода. Другими словами, это счетное распределение. Распределения Пуассона часто используются для понимания независимых событий, которые происходят с постоянной скоростью в течение заданного интервала времени.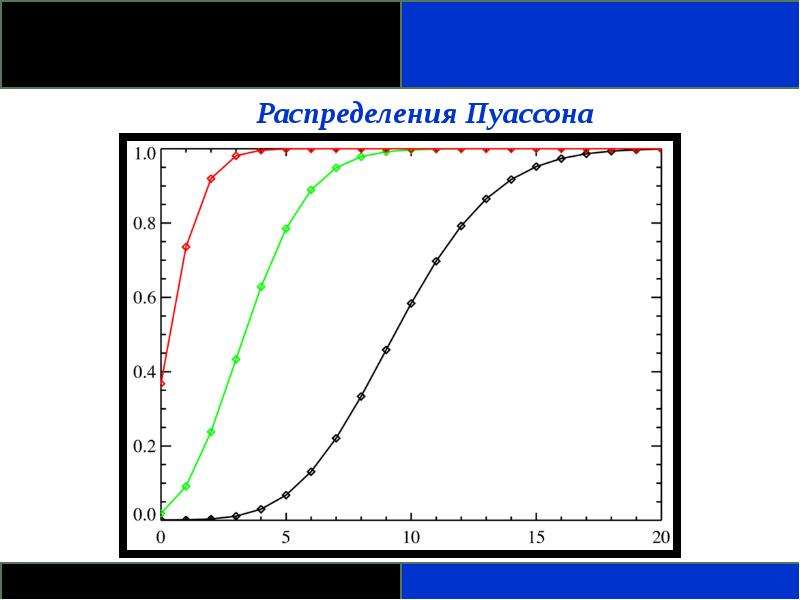 Он был назван в честь французского математика Симеона Дени Пуассона.
Он был назван в честь французского математика Симеона Дени Пуассона.
Распределение Пуассона является дискретной функцией, что означает, что переменная может принимать только определенные значения в (потенциально бесконечном) списке. Иными словами, переменная не может принимать все значения в любом непрерывном диапазоне. Для распределения Пуассона переменная может принимать только целые числа (0, 1, 2, 3 и т. д.), без дробей или десятичных знаков.
Ключевые выводы
- Распределение Пуассона, названное в честь французского математика Симеона Дени Пуассона, можно использовать для оценки того, сколько раз событие может произойти в течение «X» периодов времени.
- Распределения Пуассона используются, когда интересующая переменная является дискретной счетной переменной.
- Многие экономические и финансовые данные появляются в виде счетных переменных, например, сколько раз человек становится безработным в данном году, что позволяет анализировать их с помощью распределения Пуассона.

Понимание распределения Пуассона
Распределение Пуассона можно использовать для оценки вероятности того, что что-то произойдет «X» раз. Например, если среднее количество людей, которые покупают чизбургеры в сети быстрого питания в пятницу вечером в одном ресторане, составляет 200 человек, распределение Пуассона может ответить на такие вопросы, как «Какова вероятность того, что более 300 человек купить бургеры?» Таким образом, применение распределения Пуассона позволяет менеджерам вводить оптимальные системы планирования, которые не будут работать, скажем, при нормальном распределении.
Одним из самых известных исторических и практических применений распределения Пуассона была оценка ежегодного числа прусских кавалерийских солдат, убитых в результате ударов ногами. Современные примеры включают оценку количества автомобильных аварий в городе заданного размера; в физиологии это распределение часто используется для расчета вероятностных частот различных типов секреции нейротрансмиттеров.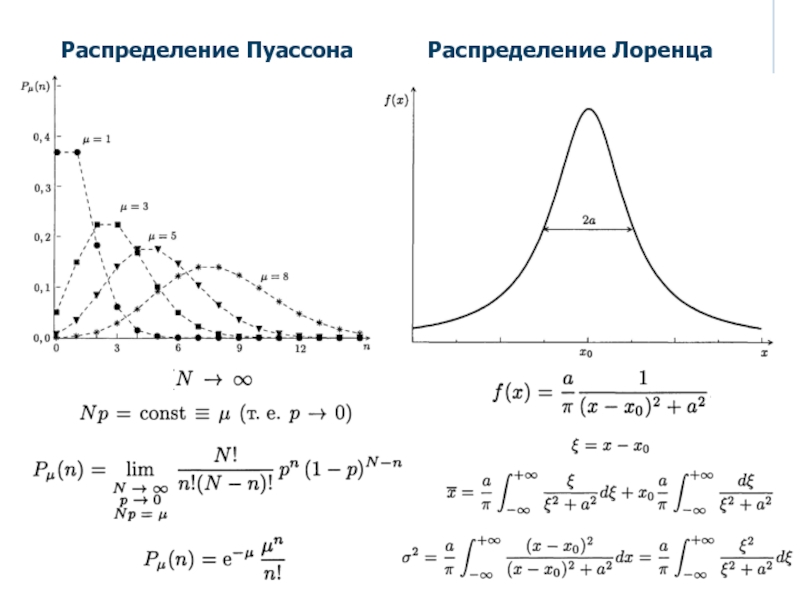 Или, если бы в видеомагазине каждую пятницу вечером в среднем было 400 покупателей, какова была бы вероятность того, что 600 покупателей пришли бы в любой конкретный вечер пятницы?
Или, если бы в видеомагазине каждую пятницу вечером в среднем было 400 покупателей, какова была бы вероятность того, что 600 покупателей пришли бы в любой конкретный вечер пятницы?
Формула распределения Пуассона
Формула распределения Пуассона. СК ТейлорГде:
- e число Эйлера ( e = 2,71828…)
- x количество вхождений
- х ! является факториалом x
- λ равно ожидаемому значению (EV) x , когда оно также равно его дисперсии
Учитывая данные, которые следуют распределению Пуассона, это выглядит графически как:
Пример распределения Пуассона. Инвестопедия В примере, изображенном на графике выше, предположим, что некоторый рабочий процесс имеет частоту ошибок 3%. Если мы дополнительно предположим 100 случайных испытаний, распределение Пуассона описывает вероятность получения определенного количества ошибок за некоторый период времени, например, за один день.
Если среднее значение очень велико, то распределение Пуассона является приблизительно нормальным распределением.
Распределение Пуассона в финансах
Распределение Пуассона также обычно используется для моделирования данных финансового подсчета, где сумма невелика и часто равна нулю. В качестве примера в финансах его можно использовать для моделирования количества сделок, которые типичный инвестор совершит в определенный день, что может быть равно 0 (часто), 1, 2 и т. д.
В качестве другого примера, эту модель можно использовать для прогнозирования количества «шоков» на рынке, которые произойдут в заданный период времени, скажем, за десятилетие.
Когда следует использовать распределение Пуассона?
Распределение Пуассона лучше всего применять для статистического анализа, когда рассматриваемая переменная является счетной переменной. Например, сколько раз X встречается на основе одной или нескольких независимых переменных. Например, чтобы оценить, сколько бракованных изделий сойдет с конвейера при различных исходных данных.
Какие предположения делает распределение Пуассона?
Чтобы распределение Пуассона было точным, все события независимы друг от друга, скорость событий во времени постоянна, и события не могут происходить одновременно. При этом среднее значение и дисперсия будут равны друг другу.
Является ли распределение Пуассона дискретным или непрерывным?
Поскольку оно измеряет дискретные значения, распределение Пуассона также является дискретным распределением. Это можно противопоставить нормальному распределению, которое является непрерывным.
распределений Пуассона | Определение, формула и примеры
Опубликован в 13 мая 2022 г. к Шон Терни. Отредактировано 5 декабря 2022 г.
A Распределение Пуассона — это дискретное распределение вероятностей. Он дает вероятность того, что событие произойдет определенное количество раз ( k ) в течение заданного интервала времени или пространства.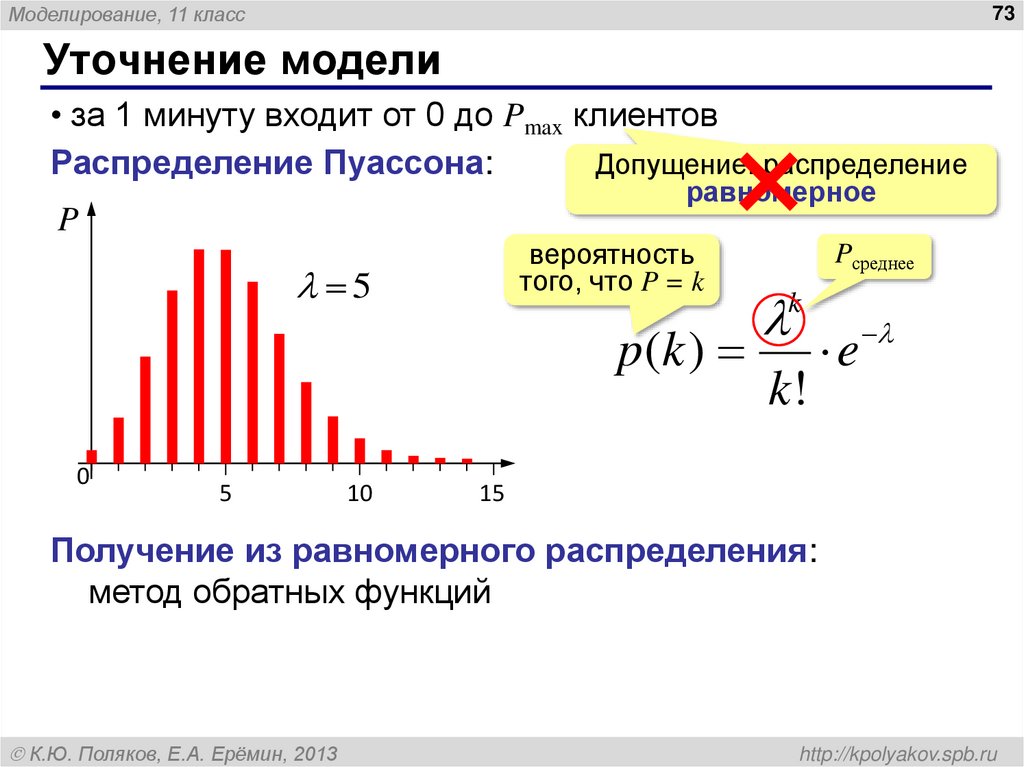
Распределение Пуассона имеет только один параметр, λ (лямбда), который представляет собой среднее число событий. На приведенном ниже графике показаны примеры распределения Пуассона с различными значениями λ.
Содержание
- Что такое распределение Пуассона?
- Примеры распределения Пуассона.
Что такое распределение Пуассона?
Распределение Пуассона — это дискретное распределение вероятностей, означающее, что оно дает вероятность дискретного (т. е. счетного) результата. Для распределений Пуассона дискретный результат — это количество раз, когда событие происходит, представленное k.
Вы можете использовать распределение Пуассона, чтобы предсказать или объяснить количество событий, происходящих в течение заданного интервала времени или пространства. «События» могут быть чем угодно: от случаев заболевания до покупок клиентов и ударов метеоритов. Интервал может быть любым конкретным количеством времени или пространства, например, 10 дней или 5 квадратных дюймов.
Вы можете использовать распределение Пуассона, если:
- Отдельные события происходят случайно и независимо. То есть вероятность одного события не влияет на вероятность другого события.
- Вы знаете среднее количество событий, происходящих в течение заданного интервала времени или пространства. Это число называется λ (лямбда) и считается постоянным.
Когда события следуют распределению Пуассона, λ — это единственное, что вам нужно знать, чтобы рассчитать вероятность того, что событие произойдет определенное количество раз.
Примеры распределения Пуассона
В целом, распределения Пуассона часто подходят для данных подсчета . Данные подсчета состоят из наблюдений, которые представляют собой неотрицательные целые числа (т. е. числа, которые используются для подсчета, например 0, 1, 2, 3, 4 и т. д.).
Смерть от удара лошади
Одним из первых применений распределения Пуассона был статистик Ладислав Борткевич. В конце 1800-х годов он расследовал случай смерти солдат прусской армии от несчастного случая, вызванного ударом лошади. Он проанализировал данные за 20 лет по 10 армейским корпусам, что эквивалентно 200 годам наблюдений за одним корпусом.
В конце 1800-х годов он расследовал случай смерти солдат прусской армии от несчастного случая, вызванного ударом лошади. Он проанализировал данные за 20 лет по 10 армейским корпусам, что эквивалентно 200 годам наблюдений за одним корпусом.
На следующей гистограмме показаны смоделированные данные, аналогичные наблюдаемым Борткевичем:
Он обнаружил, что каждый год в среднем 0,61 солдата на корпус умирает от ударов лошади. Однако в большинстве лет ни один солдат не погиб от конных ударов. На другом конце спектра в один трагический год четыре солдата того же корпуса погибли от ударов лошади.
Используя современную терминологию:
- Смерть от удара лошади — это «событие».
- Временной интервал равен одному году.
- Среднее количество событий за интервал времени, λ, равно 0,61.
- Количество смертей от ударов ногой лошади в указанном году составляет тыс.
 .
.
Армейский корпус, который наблюдал Борткевич, был образцом населения всех прусских армейских корпусов. Из-за случайного характера выборки выборки редко полностью соответствуют распределению вероятностей. Смертность от удара лошади в выборке примерно соответствует распределению Пуассона, поэтому мы можем разумно сделать вывод, что популяция подчиняется распределению Пуассона.
Другие примеры распределения Пуассона
Со времен Борткевича распределения Пуассона использовались для описания многих других вещей. Например, распределение Пуассона можно использовать для объяснения или предсказания:
- Текстовых сообщений в час
- Самцов гризли на гектар
- Неисправности машин в год
- посетителей сайта в месяц
- случаев гриппа в год
Что может сделать корректура для вашей статьи?
Редакторы Scribbr не только исправляют грамматические и орфографические ошибки, но и улучшают качество письма, следя за тем, чтобы в вашей статье не было неясных формулировок, избыточных слов и неудобных формулировок.
См. пример редактирования
Графики функции массы вероятности
Распределение Пуассона можно представить визуально в виде графика функции массы вероятности. Функция массы вероятности — это функция, описывающая дискретное распределение вероятностей.
Наиболее вероятное количество событий представлено пиком распределения — модой.
- Если λ не является целым числом, модой является ближайшее целое число, меньшее λ.
- Когда λ является целым числом, существует два режима: λ и λ−1.
Когда λ низкое, распределение намного длиннее справа от своего пика, чем слева (т. е. оно сильно смещено вправо).
По мере увеличения λ распределение становится все более и более похожим на нормальное распределение. Фактически, когда λ равно 10 или больше, нормальное распределение является хорошей аппроксимацией распределения Пуассона.
Среднее значение и дисперсия распределения Пуассона
Распределение Пуассона имеет только один параметр, называемый λ.
- Среднее значение распределения Пуассона равно λ.
- Дисперсия распределения Пуассона также равна λ.
В большинстве распределений среднее значение представлено µ (мю), а дисперсия представлена σ² (сигма в квадрате). Поскольку эти два параметра одинаковы в распределении Пуассона, мы используем символ λ для обозначения обоих.
Формула распределения Пуассона
Функция массы вероятности распределения Пуассона:
Где:
- — это случайная величина, следующая распределению Пуассона
- — количество раз, когда событие происходит
- ) — вероятность того, что событие произойдет k раз
- — постоянная Эйлера (примерно 2,718) 90 180 — среднее количество раз, когда событие происходит 90 010.
- ! является факториальной функцией
 В каждом прусском армейском корпусе в среднем 0,61 солдат умирает от ударов ногой в год. Вы хотите рассчитать вероятность того, что ровно два солдата погибли в VII армейском корпусе в 1898 г., предполагая, что число смертей от ударов лошадью в год подчиняется распределению Пуассона.
В каждом прусском армейском корпусе в среднем 0,61 солдат умирает от ударов ногой в год. Вы хотите рассчитать вероятность того, что ровно два солдата погибли в VII армейском корпусе в 1898 г., предполагая, что число смертей от ударов лошадью в год подчиняется распределению Пуассона.Расчет
Конкретный армейский корпус (VII армейский корпус) и год (1898) не имеют значения, поскольку вероятность постоянна.
= 2 смерти от удара лошади
= 0,61 смертей от удара лошади в год
= 2,718
Вероятность того, что в VII армейском корпусе в 1898 г. погибло ровно два солдата, равна 0,101.
Практические вопросы
Часто задаваемые вопросы о распределениях Пуассона
- Что означает «e» в формуле распределения Пуассона? org/Answer»>
- Что такое нормальное распределение?
При нормальном распределении данные распределяются симметрично без перекоса. Большинство значений группируются вокруг центральной области, при этом значения сужаются по мере удаления от центра.
Меры центральной тенденции (среднее, мода и медиана) в нормальном распределении точно такие же.
e в формуле распределения Пуассона означает число 2,718. Это число называется постоянной Эйлера. Вы можете просто заменить e на 2,718 при расчете вероятности Пуассона. Константа Эйлера — очень полезное число, особенно важное в исчислении.
Процитировать эту статью Scribbr
Если вы хотите процитировать этот источник, вы можете скопировать и вставить цитату или нажать кнопку «Цитировать эту статью Scribbr», чтобы автоматически добавить цитату в наш бесплатный генератор цитирования.




 .
.