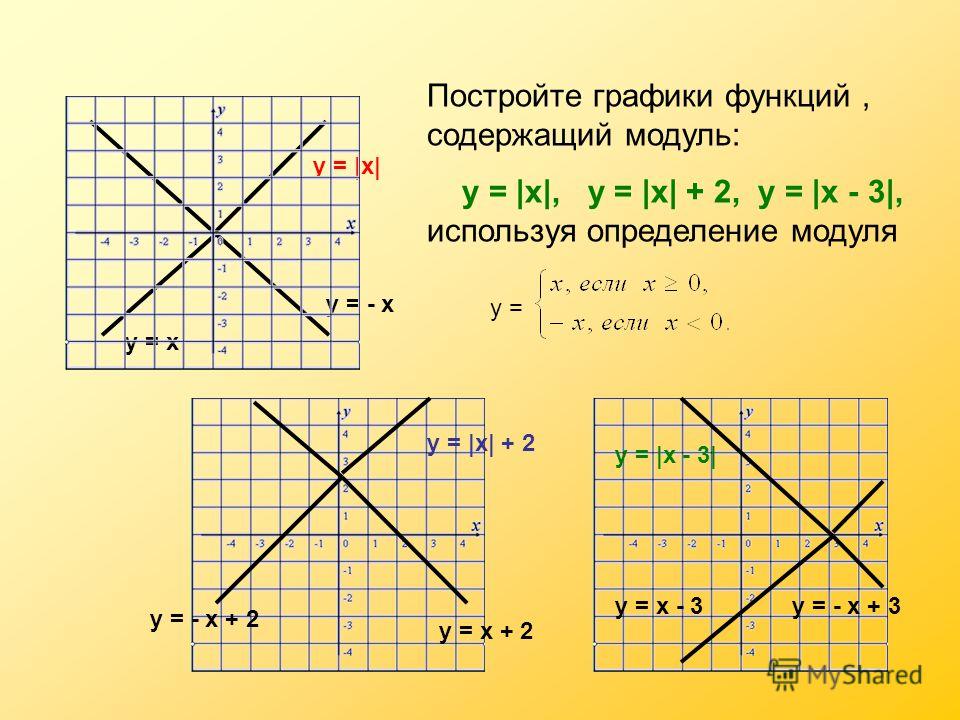
Задача 1. Построить графики функций y=|x| y=|x-1|.
Решение. Сравним его с графиком функции y=|x|.При положительных x имеем |x|=x. Значит, для положительных значений аргумента график y=|x| совпадает с графиком y=x, то есть эта часть графика является лучём, выходящим из начала координат под углом 45 градусов к оси абсцисс. При x< 0 имеем |x|= -x; значит, для отрицательных x график y=|x| совпадает с биссектрисой второго координатного угла.
Впрочем, вторую половину графика (для отрицательных X) легко получить из первой, если заметить, что функция y=|x| — чётная, так как |-a|=|a|. Значит, график функции y=|x| симметричен относительно оси Oy, и вторую половину графика можно приобрести, отразив относительно оси ординат часть, начерченную для положительных x. Получается график:
y=|x|
Для построения берём точки (-2; 2) (-1; 1) (0; 0) (1; 1) (2; 2).
Теперь график y=|x-1|.
Построим графики:
y=|x-1|
Для построения берём точки (-2; 3) (-1; 2) (0; 1) (1; 0) (2; 1).
Это была простенькая задачка. Теперь то, что многих приводит в ужас.
Задача 2. Постройте график функции y=3*|x-4| — x + |x+1|.
Решение. Найдем точки, в которых подмодульные выражения обращаются в нуль, т.е. так называемые «критические» точки функции. Такими точками будут х=-1 и х=4. В этих точках подмодульные выражения могут изменить знак.
Пусть x<-1. Тогда х+1<0, |x+1|=-x-1; x-4<0, |x-4|=-x+4; Следовательно y= 3(-х+4)-х+(-х-1)= -5х+11.
 2 — |x| — 3|
2 — |x| — 3|Итак, всем спасибо! Теперь мы получили ту базу знаний, необходимую для построения графиков со знаком модуля! А то его так все боятся.
Вот ссылка, которая поможет вам проверить ваши построения:
3-8Абсолютное значение — обзорное руководство по математическим навыкам
Что это значит?
Определения:
Абсолютное значение (или модуль) | х | действительного числа x является неотрицательным значением x независимо от его знака.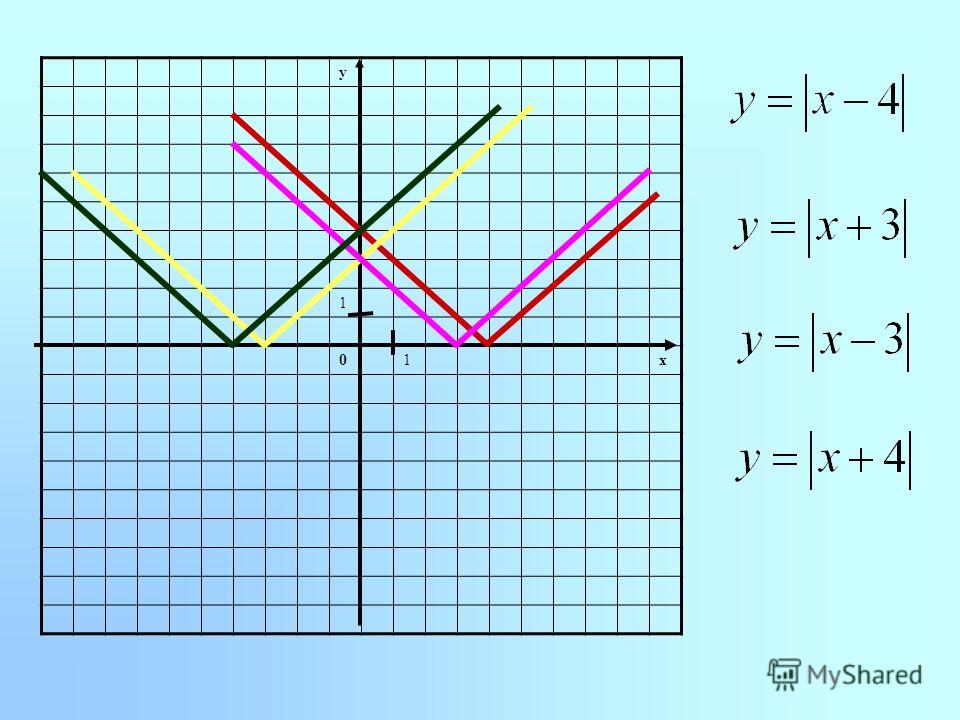
Например, абсолютное значение 5 равно 5, а абсолютное значение -5 также равно 5. Абсолютное значение числа можно рассматривать как его расстояние от нуля по линии действительных чисел. Кроме того, абсолютная величина разности двух действительных чисел есть расстояние между ними.
Абсолютное значение обладает следующими четырьмя фундаментальными свойствами:
Неотрицательность $$|a| ≥ 0$$ Положительная определенность $$|a| = 0 ⇔ a = 0$$ Мультипликативность $$|ab| = |a||b|$$ Субаддитивность $$|a + b| ≤ |а| + |b|$$
Другие важные свойства абсолютного значения включают:
Идемпотентность (абсолютное значение абсолютного значения является абсолютным значением) $$||a|| = |a|$$ Симметрия $$|-a| = |a|$$ Тождество неразличимых (эквивалентно положительной определенности) $$|a — b| = 0 ⇔ a = b$$ Неравенство треугольника (эквивалентное субаддитивности) $$|a — b| ≤ |а — с| + |c — b|$$ Сохранение деления (эквивалентно мультипликативности) $$|a / b| = |а| / |б| \space\space if \space\space b ≠ 0$$ (эквивалент субаддитивности) $$|a — b| ≥ ||а| — |b||$$
Два других полезных свойства, касающихся неравенств: $$|a| ≤ b ⇔ -b ≤ a ≤ b$$ $$|a| ≥ b ⇔ a ≤ -b \space или \space b ≤ a$$
Эти соотношения можно использовать для решения неравенств с абсолютными значениями. Например: $$|x — 3| ≤ 9 ⇔ -9 < x - 3 < 9$$ $$⇔ -6 < x < 12$$
Например: $$|x — 3| ≤ 9 ⇔ -9 < x - 3 < 9$$ $$⇔ -6 < x < 12$$
From:en.wikipedia.org/wiki/Absolute_value
Как это выглядит?
Абсолютное значение 5 равно 5, это расстояние от 0,5 единиц.
Абсолютное значение -5 равно 5, это расстояние от 0,5 единиц.
$$|x| = 2 $$
$$|x| > 2$$
$$Для \space |x| < 2, -2 < x < 2$$ $$For \space |x| = 4, -4 = x = 4$$
|7| = 7 означает, что абсолютное значение 7 равно 7.
|-7| = 7 означает, что абсолютное значение -7 равно 7.
|-2 — x| означает абсолютное значение -2 минус x.
-|х| означает отрицательное значение абсолютного значения x.
Тебе пригодится…
Абсолютное значение действительных чисел встречается в самых разных математических установках, например, абсолютное значение также определяется для комплексных чисел, кватернионов, упорядоченных колец, полей и векторных пространств.
