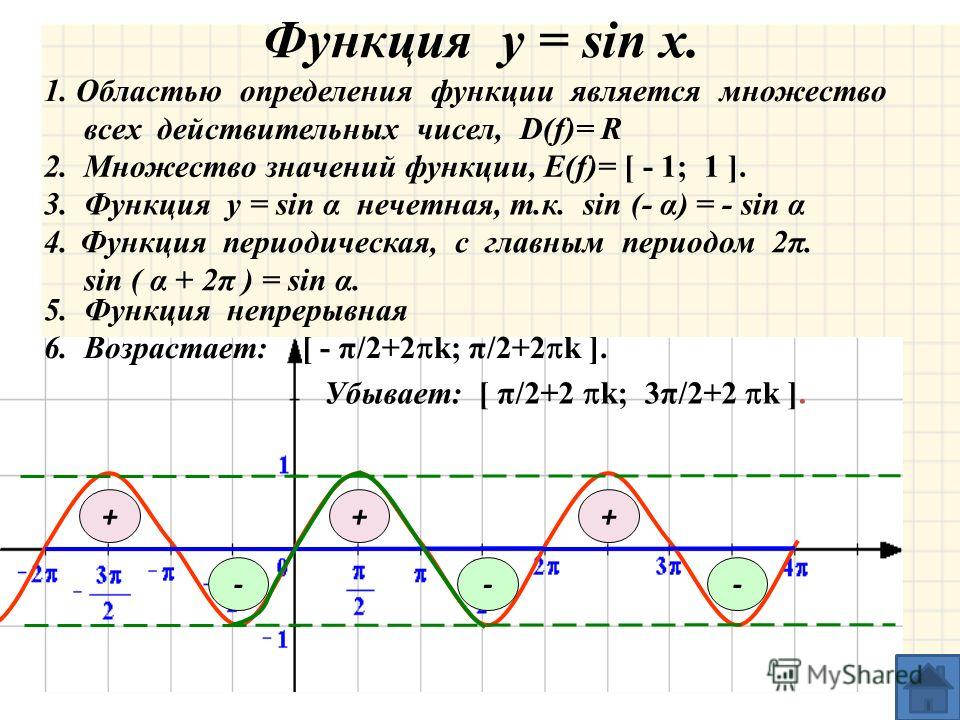
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | sin((4pi)/3) | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Проверочный тест по алгебре и началам анализа, 10 класс, I полугодие
Проверочный тест по алгебре и началам анализа, 10 класс, I полугодие
Вариант 1
1. Какие из данных функций в области определения являются четными?
А) у = х4 – cos2x
B) y = x
C) y = +
D) y = x6 – 2x3
E) y = — 2sinx
2. Найти область определения функции, являющейся ни четной, ни нечетной:
Найти область определения функции, являющейся ни четной, ни нечетной:
А) (-
В) [-1; 1]
С) R, кроме х = 5
D) (-5; 5)
Е) R, кроме х = 0
3. Укажите нечетную функцию:
А) у = + cos x
B) у = + sin x
C) у = + cos2x
D) у = + sin2 x
E) у = — sin2 x
4. Найти наименьший положительный период функции у = cos .
A)
B) 6
C) 5
D) 3
E) 2
5. Найти наименьший положительный период функции у = sin2xcos2x
A)
B)
C) 2
D) 4
E)
6. Найти область определения функции у = .
А) (5
В) (-
С) (-
D) (0; 5)
Е) (0
7. При каком из данных значений х выражение не имеет смысла?
А)
В)
С)
D)
E)
8. Найдите sinxcosx, если sinx + cosx = 1.
A) 1
B)
C) 0
D) — 1
E) — 2
9. Найдите наибольшее значение функции у = cos x + 3 sin2x + 3cos2x.
A) 3
B) 2
C) 5
D) 4
E) 1
10. Найти обратную функцию для функции у = .
A) у =
B) у = -2
C) у =
D) у = — 3
E)
11. Выберите из данных чисел наименьшее:
A) ctg 2
B) ctg 3
C) ctg 4
D) ctg 5
E) ctg (-1)
12. Какое из данных выражений не имеет смысла:
A) arctg
B) arcctg (1 –
C) arcsin
D) arccos
E) arcsin
13. Найдите значение выражения arctg(tg (4
А) 4
В) 10 — 4
С) 10
D) 10 — 2
Е) -10
14. Найдите значение выражения sin(arctg(-1))
A)
B) 1
C) — 1
D) —
E) не существует
15. Найдите значение выражения sin(arcos )
A)
B)
C)
D) —
E) –
16. Какие из данных уравнений имеют корни:
Какие из данных уравнений имеют корни:
1) cos x = 0,99; 2) sin = — 3) sin x = – 1; 4) cos x = 1 — 5) tg (x – 1) = 0; 6) tg = tg 1?
A) 1, 4, 5, 6
B) 1, 3, 4, 5, 6
C) все
D) 1, 4
E) 1, 5, 6
17. Найдите корни уравнения sin 2x = 1
A) x = — +
B) x = +
C) x = +
D) x = — +
E) верного ответа нет
18. Найдите наименьший положительный корень уравнения 2 sin 24x = 1
A)
B)
C)
D)
E) верного ответа нет
19. Найдите количество корней уравнения tg 2x = 1, принадлежащих промежутку [- ].
A) 1
B) 2
C) 3
D) 4
E) 5
20. Решить уравнение: cos x = —
A) + 2
B) — + 2
C) — +
D) + 2
E) +
21. Найдите корни уравнения 2sin(3x — ) =
A) +
B) (-1)n + +
C) +
D) (-1)n + +
E) (-1)n +
22. Вычислить arctg
Вычислить arctg
A) 1500
B) 1200
C) 1800
D) 600
E) 300
23. Решить уравнение cos3x cosx – sin3x sinx = — 1
A) + 2
B) +
C) +
D) (1 + 2n),
E) + 2
24. Какая из данных функций убывает на всей области определения
A) y = 2x
B) y = ctgx
C) y = x2
D) y = — x2
E) y = — ctgx
25. Упростить:
A) ctgx
B) 2cosx
C) cosx
D) — cosx
E) верного ответа нет
Проверочный тест по алгебре и началам анализа, 10 класс, I полугодие
Вариант 2
1. Какие из данных функций в области определения являются четными?
А) у = х2 + tg x4
B) y = x + tg x5
C) y = 3 – x2
D) y = x + cosx
E) y = sin2x+ x2
2. Найти область определения функции общего вида:
Найти область определения функции общего вида:
А) R
В) (- — 2]
С) [- 2 2]
D) (- 0) (0
Е) R, кроме х = 0
3. Укажите четную функцию:
1) y = xsinx; 2) y = x2cos2x; 3)y = x + sinx; 4) y = x + cosx
А) 1, 3, 4
B) 2, 3
C) 1, 2, 3
D) 1, 4
E) 1, 2
4. Найти наименьший положительный период функции у = 3sin
A) 2
B) 1
C) 0,5
D) 2
E)
5. Найти наименьший положительный период функции у = 2cos2x — 1
A)
B) 4
C)
D)
E)
6. Найти область определения функции у = .
А) (- 2
В) [0
С) [- 3 3]
D) [0; 2]
Е) (0
7. При каком из данных значений х выражение имеет смысла?
А)
В)
С)
D)
E) 3
8. Найдите tg2x + ctg2x, если tgx + ctgx = 2.
A) 3
B) 0
C) 2
D) 4
E) — 2
9. Найдите область изменения функции у = 3 – 5cosx
A) [- 2; 8]
B) [- 3; 5]
C) [- 5; 3]
D) [- 2; – 8)
E) [- 2; 2]
10. Найти обратную функцию для функции у = 5 – 4х
A) у = х
B) у = х— 1
C) у = 1 —
D) у = 4х —
E)
11.Какое из данных чисел наибольшее:
A) sin 2
B) sin 3
C) sin 4
D) sin 5
E) sin1
12. Какое из данных выражений не имеет смысла:
A) arctg
B) arcctg
C) arcsin(1 — )
D) arccos(5 – )
E) arctg(- 20
13. Найдите значение выражения arctg(tg 6,28)
А) 2
В) 6,28 — 2
С) 6,28
D) 6,28 +
Е) — 6,28
14. Найдите значение выражения sin(arccos)
A)
B)
C)
D)
E) —
15. Найдите значение выражения sin(arctg(-2))
A)
B) —
C) 0,2
D) не существует
E) – 0,2
16. Какие из данных уравнений имеют корни:
Какие из данных уравнений имеют корни:
1) cos x = ; 2) sin = 3) sin x = ; 4) cos x = 0,57 5) tg x = ; 6) сtg = 8?
A) 1, 5, 6
B) 2, 6
C) 2, 4, 5, 6
D) 3, 4
E) 3, 4, 5, 6
17. Решите уравнение ctg 3x = 1
A) x = +
B) x = — +
C) x = +
D) x = +
E) x = +
18. Найдите наименьший положительный корень уравнения cos 24x = 1
A)
B)
C)
D)
E) верного ответа нет
19. Найдите количество корней уравнения cosx = 1 + cos 2x, принадлежащих промежутку (0,5 ).
A) 4
B) 5
C) 6
D) 3
E) другой ответ
20. Решить уравнение: sin x =
A) (-1)n +
B) + 2
C) +
D) (-1)n +
E) (-1)n +
21. Найдите корни уравнения 2cos(2x + ) = 1
A) (-1)n+1 +
B) — +
C) —
D) —
E) (-1)n —
22. Вычислить arcsin(-
Вычислить arcsin(-
A) 1450
B) — 450
C) — 300
D) 300
E) 600
23. Решить уравнение sin3x cos3x = —
A) — +
B) +
C) +
D) +
E) +
24. Какая из данных функций возрастает на всей области определения:
A) у = —
B) у = х|x|
C) у =
D) у = — х|x|
E) y = — x
25. Упростите выражение
A) 2sinx
B) sinx
C) – 2sinx
D) cosx
E) верного ответа нет
Проверочный тест по алгебре и началам анализа, 10 класс, I полугодие
Вариант 3
1. Какая из данных функций в области определения является нечетной?
А) у = х5 — x2
B) у = х5 + x2
C) y = х4 + x5
D) у = х5 + x3
E) y =
2. Найти область определения нечетной функции:
Найти область определения нечетной функции:
А) (- 0]
В) [- 2]
С) [0
D) (0
Е) (- 0)
3. Укажите четную функцию:
А) y = x2sinx
B) y = xcosx
C) y = x2cosx
D) y = x2tgx
E) y = x2ctgx
4. Найти наименьший положительный период функции у = tg
A) 2
B) 3
C) 5
D)
E)
5. Найти наименьший положительный период функции у = 3 + sin2
A)
B) 2
C)
D)
E)
6. Найти область определения функции у = .
А) [- x 0
В) R, кроме х = 0
С) (
D) (— (
Е) (-
7. При каком из данных значений х выражение не имеет смысла?
А)
В)
С)
D) 0
E) 1
8. Найдите sinx cosx, если sinx — cosx = .
A) – 0,5
B) —
C) 0,5
D)
E) —
9. Найдите наибольшее значение функции у = 3sin2x
Найдите наибольшее значение функции у = 3sin2x
A) 3
B) 2
C) 5
D) 0
E) 1
10. Найти обратную функцию для функции у = 2х + 3
A) у = х
B) у =
C) у =
D) у = x
E) у =
11.Какое из данных чисел наибольшее:
A) cos 2
B) cos 3
C) cos(- 4)
D) cos 4
E) cos 5
12. Какое из данных выражений не имеет смысла:
A) arctg
B) arcctg ( –
C) arcsin
D) arccos
E) arcctg(3
13. Найдите значение выражения arctg(сtg)
А) 2
В) — 2
С)
D) +
Е) —
14. Найдите значение выражения tg(arcsin)
A)
B)
C) — 1
D)
E) 1
15. Найдите значение выражения cos(arctg)
A)
B) —
C) 2
D) — 2
E) не существует
16. Какие из данных уравнений не имеют корни:
1) cos 3x = 3; 2) sin = — 1 3) sin x2 = ; 4) cos x = 1 — 5) tg x = 0 ; 6) сtg 5х= tg 1?
A) 1, 5, 6
B) 2, 6
C) 2, 4, 5, 6
D) 1
E) 1, 5
17. Решите уравнение tg = — 1
Решите уравнение tg = — 1
A) x = — +
B) x = — +
C) x = — +
D) x = +
E) x = — +
18. Найдите наибольший отрицательный корень уравнения 2cos 23x = 1
A) —
B)
C) —
D) —
E) верного ответа нет
19. Из всех решений уравнения 2cos2 2x + 5sin2x – 4 = 0 укажите те значения х, которые принадлежат промежутку [ ]
A)
B)
C)
D)
E) корней нет
20. Решить уравнение: ctg x =
A) +
B) + 2
C) +
D) +
E) — +
21. Найдите корни уравнения sin(4x — ) =
A) (-1)n +
B) — +
C) (-1)n +
D)
E) (-1)n +
22. Вычислить arccos
A) 1500
B) 1200
C) 600
D) 450
E) 300
23. Решить уравнение cos3x + cos = 2
Решить уравнение cos3x + cos = 2
A) 4
B)
C) +
D) нет решений
E)
24. Какая из данных функций возрастает на всей области определения:
A) у = tgx
B) у = sinx
C) у =
D) у = — sinx
E) y = —
25. Упростите выражение
A) – 2sinx
B) — sinx
C) 2sinx
D) cosx
E) верного ответа нет
Проверочный тест по алгебре и началам анализа, 10 класс, I полугодие
Вариант 4
1. Какая из данных функций в области определения является нечетной?
А) у = cos2x + x2
B) у = sin2x + x2
C) y = cos2x + x3
D) у = cos2x + x
E) y = sin2x + x
2. Найти область определения четной функции:
А) [- 4 1]
В) [- 3]
С) (- 0] [3
D) (- 0)
Е) [0 )
3. Найдите четные функции:
1) у = 3х2 + х; 2) у = хsin2x; 3) у = ; 4) у =
А)1
B) 1, 2
C) 1, 2, 3
D) 2
E) 2, 3, 4
4. Найти наименьший положительный период функции у = sin(2x — )
Найти наименьший положительный период функции у = sin(2x — )
A)
B) 2
C)
D)
E)
5. Найти наименьший положительный период функции у = cos4x – sin4x
A)
B) 4
C)
D)
E)
6. Найти область определения функции у =
А) (- 1
В) [- 1; 1]
С) ( [1; +
D) ( [1; +
Е) ( (1; +
7. При каком из данных значений х выражение не имеет смысла?
А)
В)
С)
D)
E) -2
8. Найдите tg x + ctg x, если tg2x + ctg2x = 7
A) – 3; 3
B) 4
C) 3
D) — 4
E) 4,5
9. Найдите множество значений функции у = cos2xcosx + sin2xsinx — 5
A) [-4; 6)
B) [-6; 0]
C) (-6; 4)
D) [-6; -4]
E) (0; 6)
10. Найти обратную функцию для функции у = 1 + где х
A) у =х — 1
B) у = + х
C) у =
D) у = х + 1
E) у = х —
11. Какое из данных чисел наименьшее:
Какое из данных чисел наименьшее:
A) tg 2
B) tg 3
C) tg 4
D) tg 5
E) tg (- 1)
12. Какое из данных выражений не имеет смысла:
A) arctg 0
B) arcctg 1500
C) arcsin
D) arccos (5 —
E) arccos(
13. Найдите значение выражения arcsin(sin10)
А) 3 — 10
В) 10 — 3
С) 10
D) — 10
Е) 2 — 10
14. Найдите значение выражения cos(arcsin)
A)
B) 0
C) —
D) 1
E) — 1
15. Найдите значение выражения cos(arcsin)
A)
B)
C)
D) —
E)
16. Какие из данных уравнений не имеют решений:
1) cos x = ; 2) sin = 3) sin x = ; 4) cos x = 5) tg x = ; 6) сtg х= ?
A) 1, 4
B) 1, 5
C) 1, 6
D) 4, 6
E) 2, 4
17. Решите уравнение sin(x — = 0
A) +
B) +
C) — +
D)
E) 2
18. Найдите наименьший положительный корень уравнения sin 24x = 1
A)
B)
C)
D)
E) верного ответа нет
19. Найдите корни уравнения ctgx = , принадлежащие промежутку (0;
Найдите корни уравнения ctgx = , принадлежащие промежутку (0;
A)
B) —
C)
D) —
E)
20. Решить уравнение: sin x =
A) +
B) +
C) — +
D) (-1)n +
E) (-1)n +
21. Найдите корни уравнения 2cos(3x + ) = —
A) +
B) +
C)
D) —
E) —
22. Вычислить arcctg (-
A)
B)
C)
D)
E)
23. Решить уравнение cos 3x = cos 5x
A)
B)
C)
D) 2
E)
24. Какая из данных функций убывает на всей области определения:
A) у = 3cosx
B) у =
C) у =
D) у = — 3cosx
E) y =
25. Упростите выражение
A) 2tg3x
B) tg3x
C) – 2tg3x
D) – tg3x
E) 3tg2x
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Как построить график \\[y = \\sin 2x\\]?
Подсказка: Нам нужно построить график данной функции. Мы будем использовать домен и некоторые значения \[x\], лежащие между \[ — \pi \] и \[\pi \], чтобы найти некоторые значения \[y\]. Затем по значениям \[y\] найдем координаты точек, лежащих на искомом графике, и по полученным координатам построим график функции.
Мы будем использовать домен и некоторые значения \[x\], лежащие между \[ — \pi \] и \[\pi \], чтобы найти некоторые значения \[y\]. Затем по значениям \[y\] найдем координаты точек, лежащих на искомом графике, и по полученным координатам построим график функции.
Полное пошаговое решение:
Область определения всех синусоидальных функций — это множество всех действительных чисел.
Таким образом, область определения функции \[y = \sin 2x\] задается выражением \[\left\{ {x:x \in R} \right\}\]. Это означает, что функция \[y = \sin 2x\] существует для всех значений \[x\] и является непрерывной функцией.
Теперь мы найдем некоторые значения \[y\] для некоторых значений \[x\], лежащих между \[ — \pi \] и \[\pi \].
Подставляя \[x = — \pi \] в функцию \[y = \sin 2x\], получаем
\[\begin{array}{l}y = \sin \left( {2\left( { — \pi } \right)} \right)\\ \Rightarrow y = \sin \left( { — 2\pi } \right)\end{array}\]
Синус угла \[ — x\] можно записать как \[\sin \left( { — x} \right) = — \sin x\].
Упрощая выражение, получаем
\[\begin{array}{l} \Rightarrow y = — \sin \left( {2\pi } \right)\\ \Rightarrow y = 0\end{array}\]
Подставляя \[x = — \dfrac{{3\pi }}{4}\] в функцию \[y = \sin 2x\], получаем
\[\begin{array}{l} \Rightarrow y = \sin \left( {2\left( { — \dfrac{{3\pi }}{4}} \right)} \right)\\ \Rightarrow y = \sin \left( { — \dfrac{{ 3\pi }}{2}} \right)\end{array}\]
Поскольку функция синуса является нечетной функцией, мы можем записать вышеприведенное уравнение как
\[ \Rightarrow y = — \sin \left( {\ dfrac{{3\pi }}{2}} \right)\]
Подставляя значение угла, получаем
\[ \Rightarrow y = 1\]
Подставляя \[x = — \dfrac{\pi } {2}\] в функции \[y = \sin 2x\] получаем
\[\begin{array}{l} \Rightarrow y = \sin \left( {2\left( { — \dfrac{\pi} {2}} \right)} \right)\\ \Rightarrow y = \sin \left( { — \pi } \right)\end{array}\]
Поскольку синусоидальная функция является нечетной функцией, мы можем записать приведенное выше уравнение как
\[\begin{array}{l} \Rightarrow y = — \sin \left( \pi \right)\\ \Rightarrow y = 0\end{array}\]
Подстановка \[x = — \dfrac{\pi }{4}\] в функцию \[y = \sin 2x\], получаем
\[\begin{array}{l} \Rightarrow y = \sin \left( {2\left( { — \dfrac{\pi }{4}} \right)} \right)\\ \Rightarrow y = \sin \left( { — \dfrac{\pi }{2}} \right)\end{массив}\]
Подставляя значение угла, получаем
\[ \Rightarrow y = — 1\]
Подставляя \[x = 0\] в функцию \[y = \sin 2x\], получаем
\[\begin {array}{l} \Rightarrow y = \sin \left( {2\left( 0 \right)} \right)\\ \Rightarrow y = \sin \left( 0 \right)\end{array}\]
Подставляя значение угла, получаем
\[ \Rightarrow y = 0\]
Подставляя \[x = \dfrac{\pi }{4}\] в функцию \[y = \sin 2x\], мы получаем
\[\begin{array}{l} \Rightarrow y = \sin \left( {2\left( {\dfrac{\pi} {4}} \right)} \right)\\ \Rightarrow y = \sin\left( {\dfrac{\pi}{2}}\right)\end{массив}\]
Подставляя значение угла, получаем
\[ \Rightarrow y = 1\]
Подставляя \[x = \dfrac{\pi }{2}\] в функцию \[y = \sin 2x\], мы получаем
\[\begin{array}{l} \Rightarrow y = \sin \left( {2\left( {\dfrac{\pi} {2}} \right)} \right)\\ \Rightarrow y = \sin \left( \pi \right)\end{array}\]
Подставляя значение угла, получаем
\[ \Rightarrow y = 0\]
Подставляя \[x = \dfrac{{3\ pi }}{4}\] в функции \[y = \sin 2x\] получаем
\[\begin{array}{l} \Rightarrow y = \sin \left( {2\left( {\ dfrac{{3\pi}}{4}} \right)} \right)\\ \Rightarrow y = \sin \left( {\dfrac{{3\pi}}{2}} \right)\end{ массив}\]
Подставляя значение угла, получаем
\[ \Rightarrow y = — 1\]
Подставляя \[x = \pi \] в функцию \[y = \sin 2x\], получаем
\[\ begin{array}{l} \Стрелка вправо y = \sin \left( {2\left( \pi \right)} \right)\\ \Стрелка вправо y = \sin \left( {2\pi } \right)\ end{array}\]
Подставляя значение угла, получаем
\[ \Rightarrow y = 0\]
Располагая значения \[x\] и \[y\] в таблице и записывая координаты, получаем
| \[x\] | \[y\] | \[\left( {x,y} \right)\] |
| \[ — \pi \] | \[0\] | \[\left( { — \pi ,0} \right)\] |
| \[ — \dfrac{{3\pi }}{4}\] | \[1\] | \ [\left( { — \dfrac{{3\pi}}{4},1} \right)\] |
| \[ — \dfrac{\pi }{2}\] | \[0\ ] | \[\left( { — \dfrac{\pi }{2},0} \right)\] |
| \[ — \dfrac{\pi }{4}\] | \[ — 1\] | \[\left( { — \dfrac{\pi }{4}, — 1} \right)\] |
| \[0\] | \[0\] | \[\left( {0,0} \right)\] |
| \[\dfrac{\pi }{4}\] | \[1\] | \[\left( {\dfrac{\pi }{4 },1} \right)\] |
| \[\dfrac{\pi }{2}\] | \[0\] | \[\left( {\dfrac{\pi }{2} ,0} \right)\] |
| \[\dfrac{{3\pi}}{4}\] | \[ — 1\] | \[\left( {\dfrac{{3\ пи }}{4}, — 1} \справа)\] |
| \[\pi \] | \[0\] | \[\left( {\pi ,0} \right)\] |
Теперь воспользуемся координатами точек для построения нужного графика.