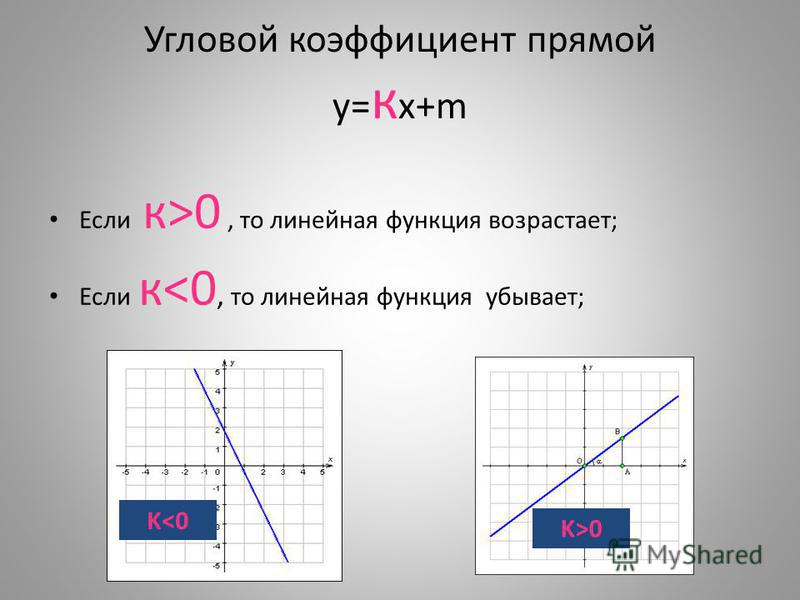
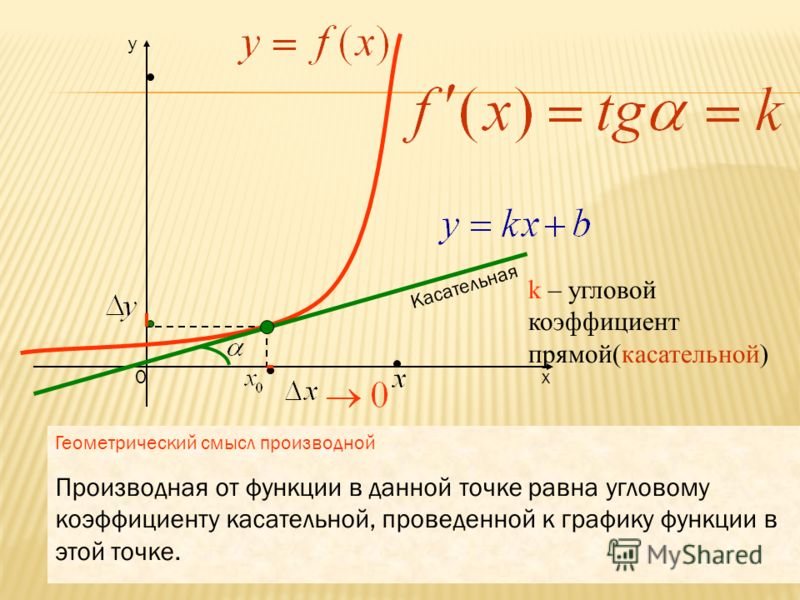
Угловой коэффициент прямой найти: Угловой коэффициент прямой

Угловой коэффициент прямой

  Угловой коэффициент прямой. В этой статье мы с вами рассмотрим задачи связанные с координатной плоскостью включённые в ЕГЭ по математике. Это задания на:

— определение углового коэффициента прямой, когда известны две точки через которые она проходит;
— определение абсциссы или ординаты точки пересечения двух прямых на плоскости.

Что такое абсцисса и ордината точки было описано в прошлой статье данной рубрики. В ней мы уже рассмотрели несколько задач связанных с координатной плоскостью. Что необходимо понимать для рассматриваемого типа задач? Немного теории.

Уравнение прямой на координатной плоскости имеет вид:

где k – это и есть угловой коэффициент прямой.

Следующий момент! Угловой коэффициент прямой равен тангенсу угла наклона прямой. Это угол между данной прямой и осью ох.

 

Он лежит в пределах от 0 до 180 градусов.

То есть, если мы приведём уравнение прямой к виду

y = kx + b, то далее всегда сможем определить коэффициент k (угловой коэффициент).

Так же, если мы исходя из условия сможем определить тангенс угла наклона прямой, то тем самым найдём её угловой коэффициент.

Следующий теоретический момент! Уравнение прямой походящей через две данные точки. Формула имеет вид:

Подробнее об этой формуле рассказано в этой статье!

Рассмотрим задачи (аналогичные задачам из открытого банка заданий):

Найдите угловой коэффициент прямой, проходящей через точки с координатами (–6;0) и (0;6).

В данной задаче самый рациональный путь решения это найти тангенс угла между осью ох и данной прямой. Известно, что он равен угловому коэффициенту. Рассмотрим прямоугольный треугольник образованный прямой и осями ох и оу:

Тангенсом угла в прямоугольном треугольнике является отношение противолежащего катета к прилежащему:

*Оба катета равны шести (это их длины).

Конечно, данную задачу можно решить используя формулу нахождения уравнения прямой проходящей через две данные точки. Но это будет более длительный путь решения.

Ответ: 1

Найдите угловой коэффициент прямой, проходящей через точки с координатами (5;0) и (0;5).

Формула уравнения прямой походящей через две данные точки имеет вид:

Наши точки  имеют координаты (5;0) и (0;5). Значит,

Приведём формулу к виду  y = kx + b   

Получили, что угловой коэффициент  k = – 1.

Ответ: –1

Прямая a проходит через точки с координатами (0;6) и (8;0). Прямая b проходит через точку с координатами (0;10) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b

с осью оx.

В данной задаче можно найти уравнение прямой a, определить угловой коэффициент для неё. У прямой b угловой коэффициент будет такой же, так как они параллельны. Далее можно найти уравнение прямой b. А затем, подставив в него значение y = 0, найти абсциссу. НО!

В данном случае, проще использовать свойство подобия треугольников.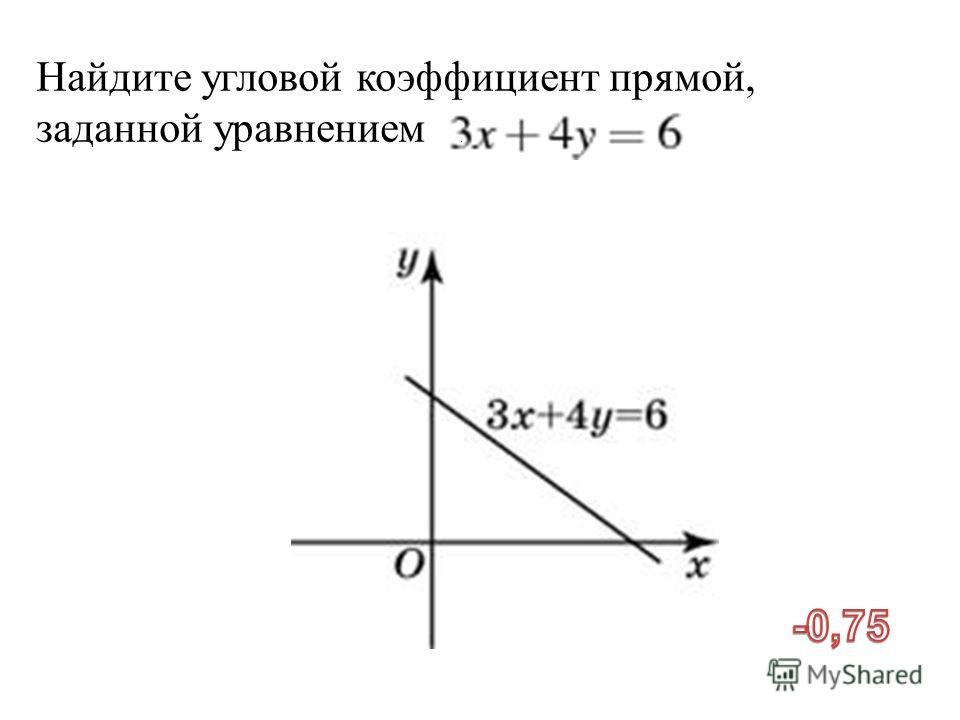

Прямоугольные треугольники, образованные данными (параллельными) прямыми о осями координат подобны, а это значит, что отношения их соответствующих сторон равны.

Искомая абсцисса равна 40/3.

Ответ: 40/3

Прямая a проходит через точки с координатами (0;8) и (–12;0). Прямая b проходит через точку с координатами (0; –12) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью оx.

Для данной задачи самый рациональный путь решения — это применение свойства подобия треугольников. Но мы решим её другим путём.

Нам известны точки, через которые проходит прямая а. Можем составить уравнение прямой. Формула уравнения прямой походящей через две данные точки имеет вид:

По условию точки  имеют координаты (0;8) и (–12;0). Значит,

Приведём к виду   y = kx + b:

Получили, что угловой  k = 2/3.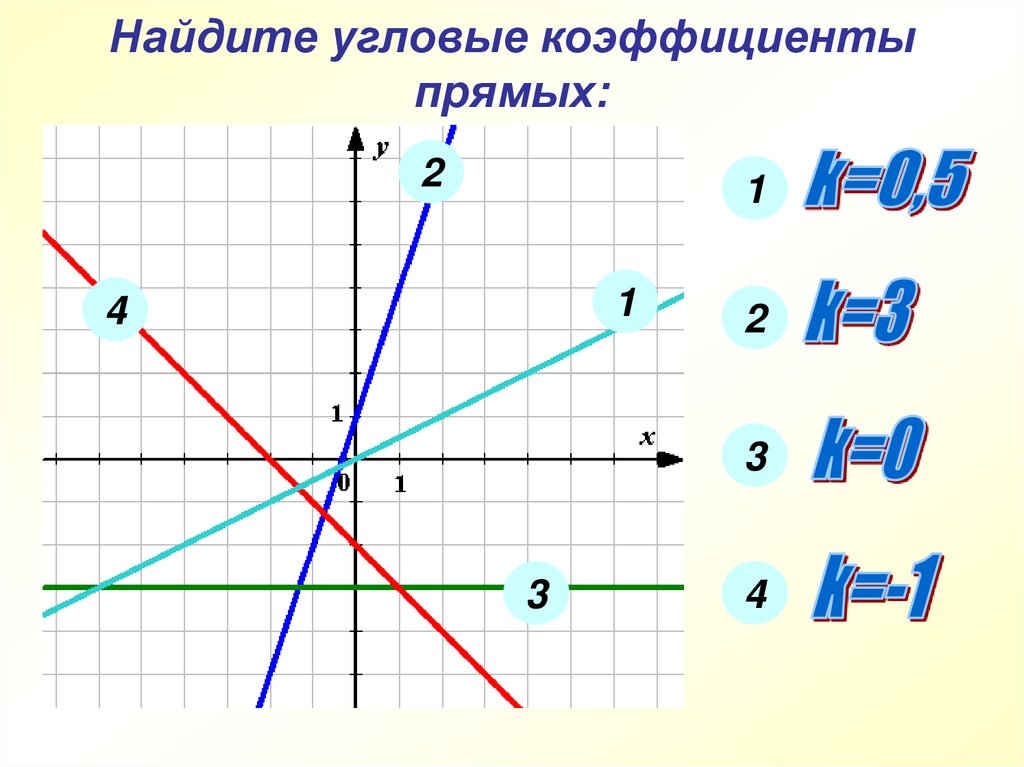

*Угловой коэффициент можно было найти через тангенс угла в прямоугольном треугольнике с катетами 8 и 12.

Известно, у параллельных прямых угловые коэффициенты равны. Значит уравнение прямой проходящей через точку (0;-12) имеет вид:

Найти величину b  мы можем подставив абсциссу и ординату в уравнение:

Таким образом, прямая имеет вид:

Теперь чтобы найти искомую абсциссу точки пересечения прямой с осью ох, необходимо подставить у = 0:

Ответ: 18

Найдите ординату точки пересечения оси оy и прямой, проходящей через точку В(10;12) и параллельной прямой, проходящей через начало координат и точку А(10;24).

Найдём уравнение прямой проходящей через точки с координатами (0;0) и (10;24).

Формула уравнения прямой походящей через две данные точки имеет вид:

Наши точки  имеют координаты (0;0) и (10;24). Значит,

Приведём к виду   y = kx + b   

Угловые коэффициенты параллельных прямых равны.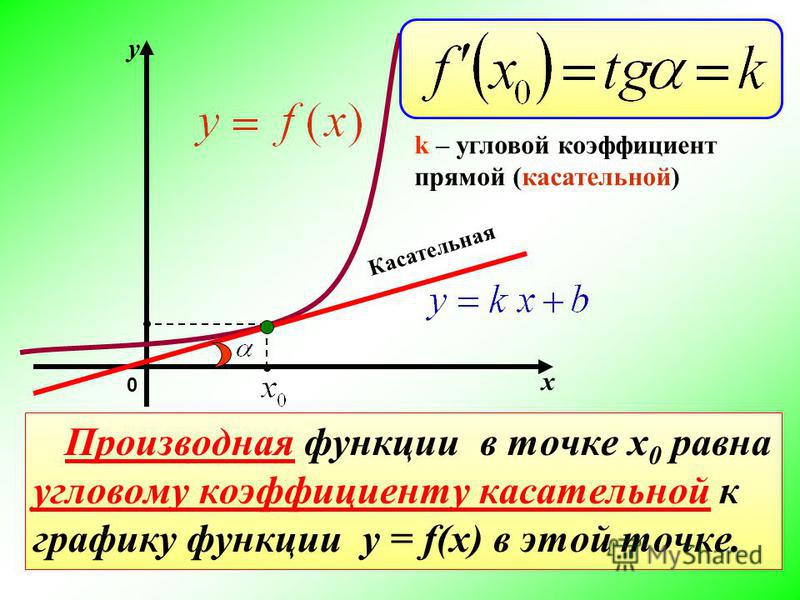 Значит, уравнение прямой, проходящей через точку В(10;12) имеет вид:

Значение b  найдём подставив в это уравнение координаты точки В(10;12):

Получили уравнение прямой:

Чтобы найти ординату точки пересечения этой прямой с осью оу  нужно подставить в найденное уравнение х = 0:

*Самый простой способ решения. При помощи параллельного  переноса сдвигаем данную прямую вниз вдоль оси оу до точки (10;12). Сдвиг происходит на 12 единиц, то есть точка А(10;24) «перешла» в точку В(10;12), а точка О(0;0) «перешла» в точку (0;–12). Значит, полученная прямая будет пересекать ось оу в точке (0;–12).

Искомая ордината равна  –12.

Ответ: –12

Найдите ординату точки пересечения прямой, заданной уравнением 

3х + 2у = 6, с осью Oy.

Координата точки пересечения заданной прямой с осью оу имеет вид (0;у). Подставим в уравнение абсциссу х = 0, и найдём ординату:

Ордината  точки пересечения прямой с осью оу равна 3.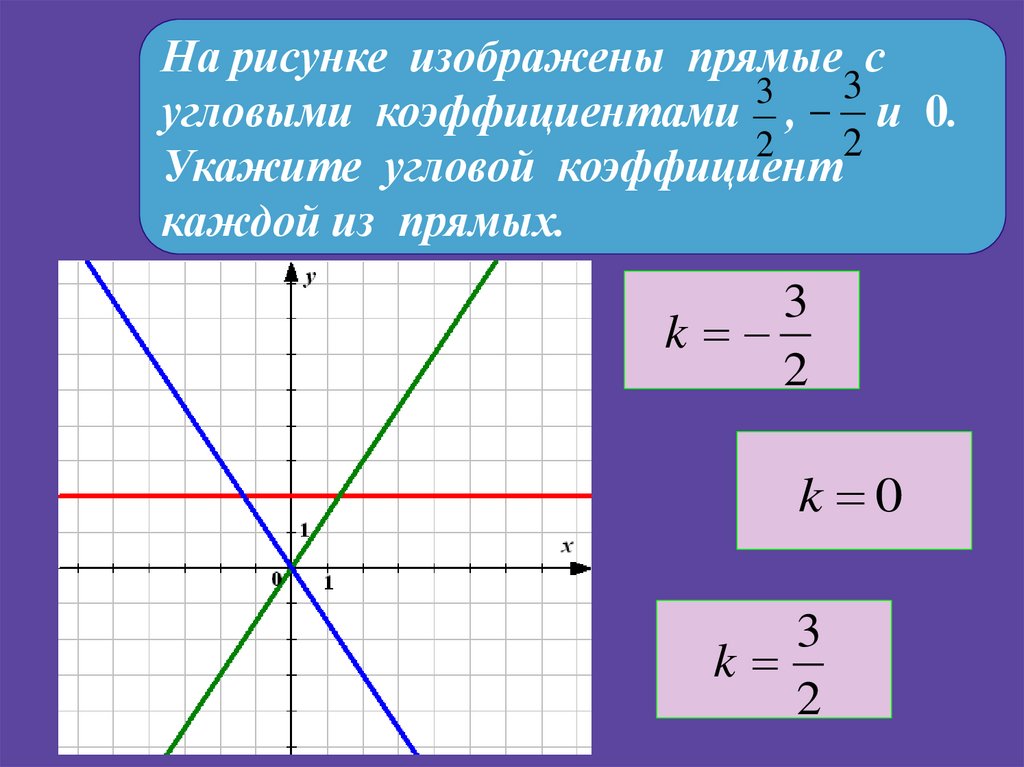

*Решается система:

Ответ: 3

Найдите ординату точки пересечения прямых, заданных уравнениями 

3х + 2у = 6   и  у = – х.

Когда заданны две прямые, и стоит вопрос о нахождении координат точки пересечения этих прямых, решается система из данных уравнений:

В первом уравнении подставляем    – х   вместо у:

Ордината равна минус шести.

Ответ: – 6

Найдите угловой коэффициент прямой, проходящей через точки с координатами (–2;0) и (0;2).

Посмотреть решение

Найдите угловой коэффициент прямой, проходящей через точки с координатами (2;0) и (0;2).

Посмотреть решение

Прямая a проходит через точки с координатами (0;4) и (6;0). Прямая b проходит через точку с координатами (0;8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.

Посмотреть решение

Прямая a проходит через точки с координатами (0;4) и (–6;0). Прямая b проходит через точку с координатами (0; –6) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.

Посмотреть решение

Найдите ординату точки пересечения оси оy и прямой, проходящей через точку B (6;4) и параллельной прямой, проходящей через начало координат и точку A (6;8).

Посмотреть решение

Найдите абсциссу точки пересечения прямой, заданной уравнением 2х + 2у = 6, с осью ох.

Посмотреть решение

Найдите абсциссу точки пересечения прямых, заданных уравнениями 3х + 2у = 6  и у = х.

Посмотреть решение

Конечно, некоторые задачи, которые мы рассмотрели можно было решить более рациональными способами. Но ставилась цель показать разные подходы к решению. Надеюсь, это удалось.

 

1. Необходимо чётко усвоить, что угловой коэффициент прямой равен тангенсу угла наклона прямой. Это поможет вам при решении многих задач данного типа.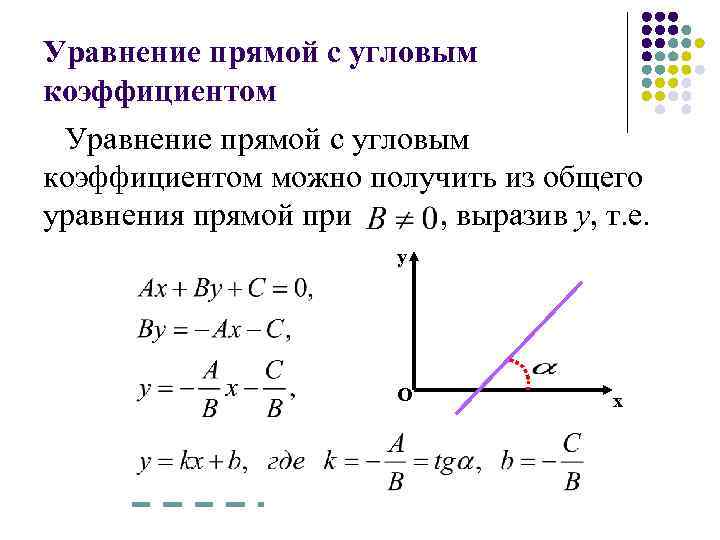

2. Формулу нахождения прямой проходящей через две данные точки нужно понимать обязательно. С её помощью всегда найдёте уравнение прямой, если даны координаты двух её точек.

3. Помните о том, что угловые коэффициенты параллельных прямых равны.

4. Как вы поняли, в некоторых задачах удобно использовать признак подобия треугольников. Задачи решаются практически устно.

5. Задачи в которых даны две прямые и требуется найти абсциссу или ординату точки их пересечения можно решить графическим способом. То есть, построить их на координатной плоскости (на листе в клетку) и определить точку пересечения визуально. *Но этот способ применим не всегда.

6. И последнее. Если дана прямая и координаты точек её пересечения с осями координат, то в таких задачах удобно находить угловой коэффициент через нахождение тангенса угла в образованном прямоугольном треугольнике. Как «увидеть» этот треугольник при различных расположениях прямых на плоскости схематично показано ниже:

>> Угол наклона прямой от 0 до 90 градусов <<

>> Угол наклона прямой от 90 до 180 градусов <<

В данных двух случаях, по свойству тангенса:

То есть, чтобы найти уголвой коэффициент прямой, необходимо вычислить тангенс бетта в полученном прямоугольном треугольнике и записать результат с отрицательным знаком.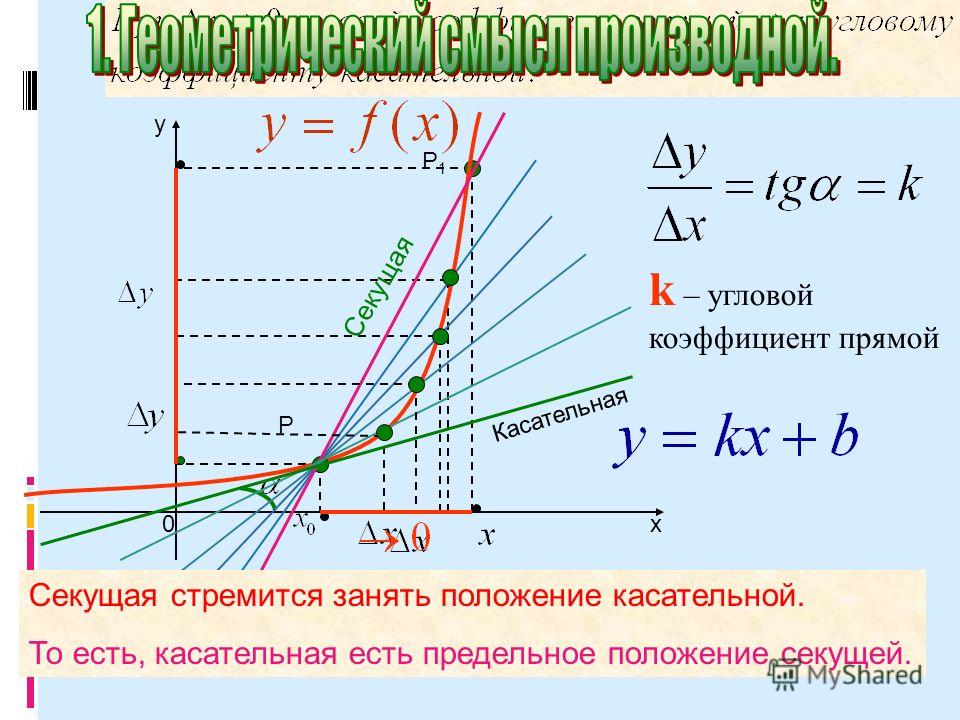 2

Как использовать формулу наклона и найти наклон линии, независимо от того, является ли наклон положительным, отрицательным или неопределенным.

Рабочий лист по наклону линии

Апплет наклона (html5)

Калькулятор формулы уклона (бесплатный онлайн-инструмент для расчета уклона по 2 точкам)

Наклон линии характеризует направление линии. Чтобы найти наклон, вы делите разницу координат y двух точек на прямой на разницу координат x тех же двух точек.

Разные слова, та же формула

Учителя используют разные слова для координат y и координат x.

1. Некоторые называют координаты у подъемом, а координатами х — бег.
2. Другие предпочитают использовать нотацию $$\Delta$$ и называть y-координаты $$\Delta y$$ , а x-координаты $$\Delta x$$ .

Все эти слова означают одно и то же , то есть значения y находятся вверху формулы (числитель), а значения x внизу формулы (знаменатель)!

Пример 1

Наклон линии , проходящей через точку (1, 2) и точку (4, 3), равен $$ \frac{1}{3}$$.

Помните: разница в значениях y идет в числителе формулы, а разница в значениях x идет в знаменателе формулы.

Может ли любая из точек быть $$( x_1 , y_1 ) $$ ?

Есть только один способ узнать!

Во-первых, мы будем использовать точку (1, 2) как $$x_1, y_1$$, и, как вы можете видеть: наклон: $ \boxed {\frac{1}{3} }$ .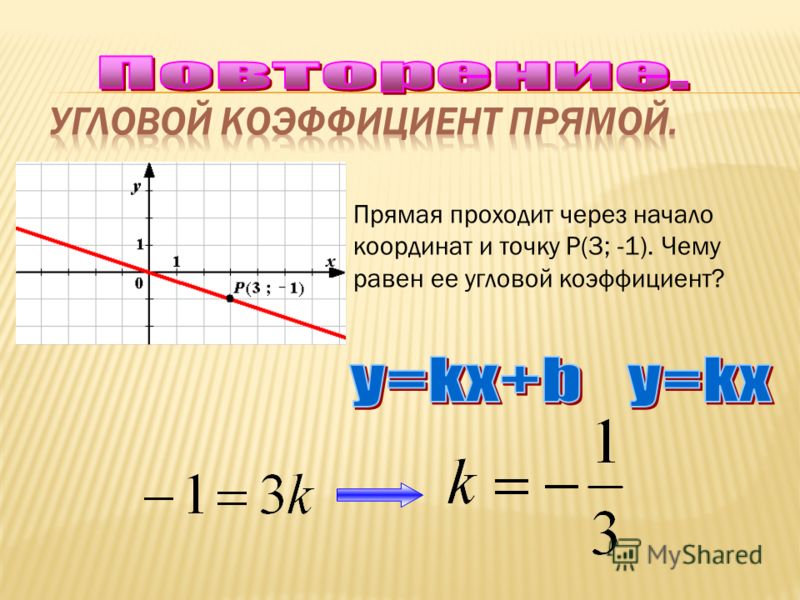

Теперь давайте используем точку (4, 3) как $$x_1, y_1$$, и, как вы можете видеть, наклон упрощается до того же значения: $ \boxed {\frac{1}{3} }$ .

Работа рядом

точка (4, 3) как $$ (x_1, y_1 )$$

Наклон $$ = \frac{y_{2}-y_{1}}{x_{2}-x_{1}} = \frac{3-2}{4-1} = \frac{1}{3} $$

точек (1, 2) как $$ (x_1, y_1 )$$

Наклон $$ = \frac{y_{2}-y_{1}}{x_{2}-x_{1}} = \frac{2-3}{1-4} = \frac{-1}{- 3} = \frac{1}{3} $$

Ответ: , а не не имеет значения, какую точку поставить первой. Вы можете начать с (4, 3) или с (1, 2), и в любом случае вы закончите точно таким же числом! $$ \фракция{1}{3} $$

Пример 2 наклона линии А

Наклон линии , проходящей через точки (3, 4) и (5, 1), равен $$- \frac{3}{2}$$, потому что каждый раз, когда линия опускается на 3 (изменение y или подъем) линия смещается вправо (разбег) на 2.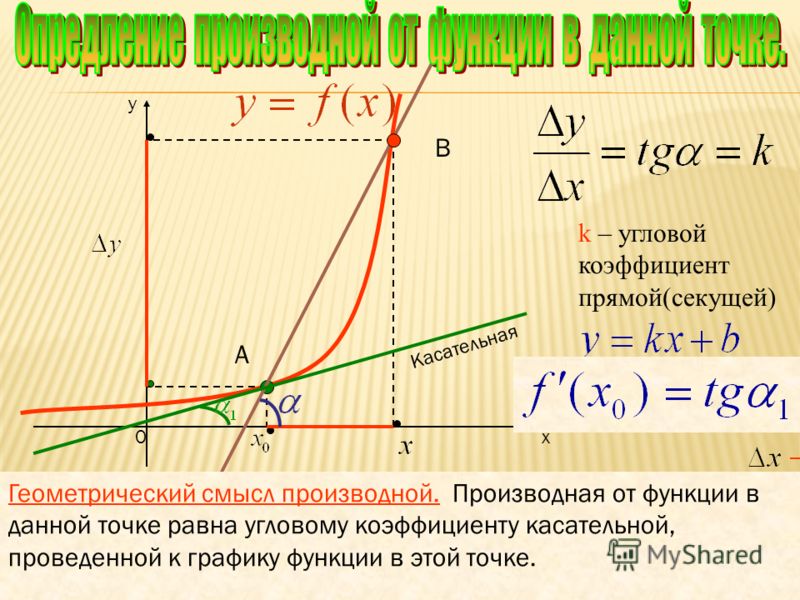

Эта страница:

• Формула
• Пример
• Видео
• Заказать?
• Любые две точки определяют наклон линии?
• Наклон вертикальной линии
• Наклон горизонтальной линии
• Практические задачи

Видеоруководство по наклону линии

Наклон вертикальных и горизонтальных линий

Наклон вертикальной линии не определен

Это связано с тем, что любая вертикальная линия имеет $$\Delta x$$ или «пробег» нуля. Всякий раз, когда ноль является знаменателем дроби в этом случае дроби, представляющей наклон линии, дробь не определена.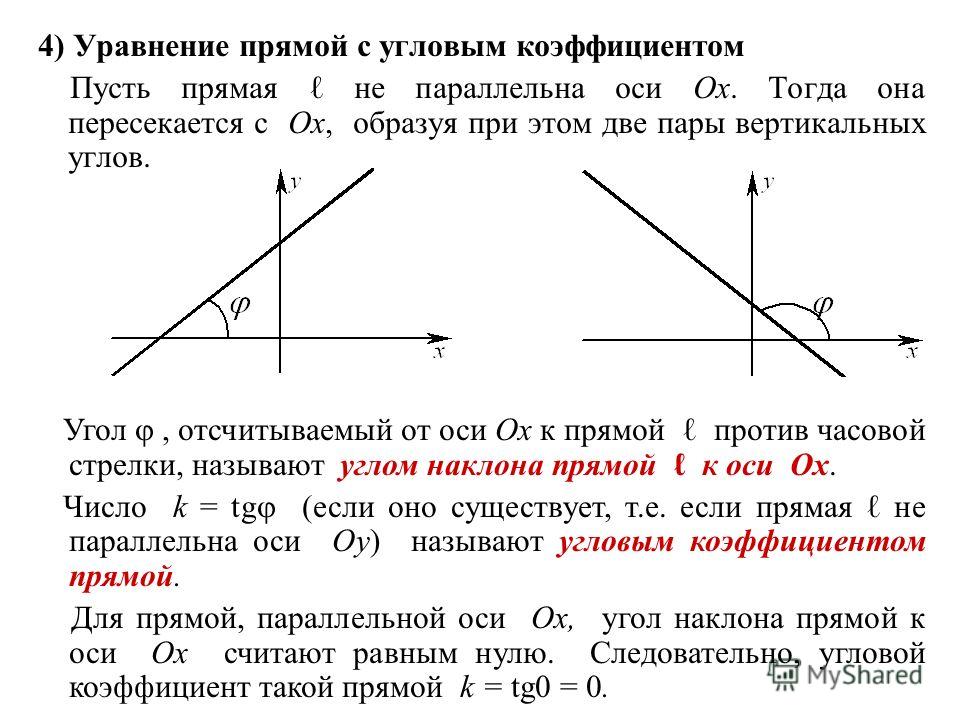 На рисунке ниже показана вертикальная линия (x = 1).

Наклон горизонтальной линии равен нулю

Это потому, что любая горизонтальная линия имеет $$\Delta y$$ или «подъем» нуля. Следовательно, независимо от того, каков пробег (при условии, что он не равен нулю!), дробь, представляющая уклон, имеет в числителе ноль. Следовательно, наклон должен оцениваться как нулевой. Ниже приведено изображение горизонтальной линии — вы можете видеть, что у нее нет «подъема».

Любые две точки на прямой имеют одинаковый наклон?

Ответ: Да, и это фундаментальный момент, который следует помнить при расчете уклона.

Каждая линия имеет постоянный наклон. Другими словами, наклон линии никогда не меняется.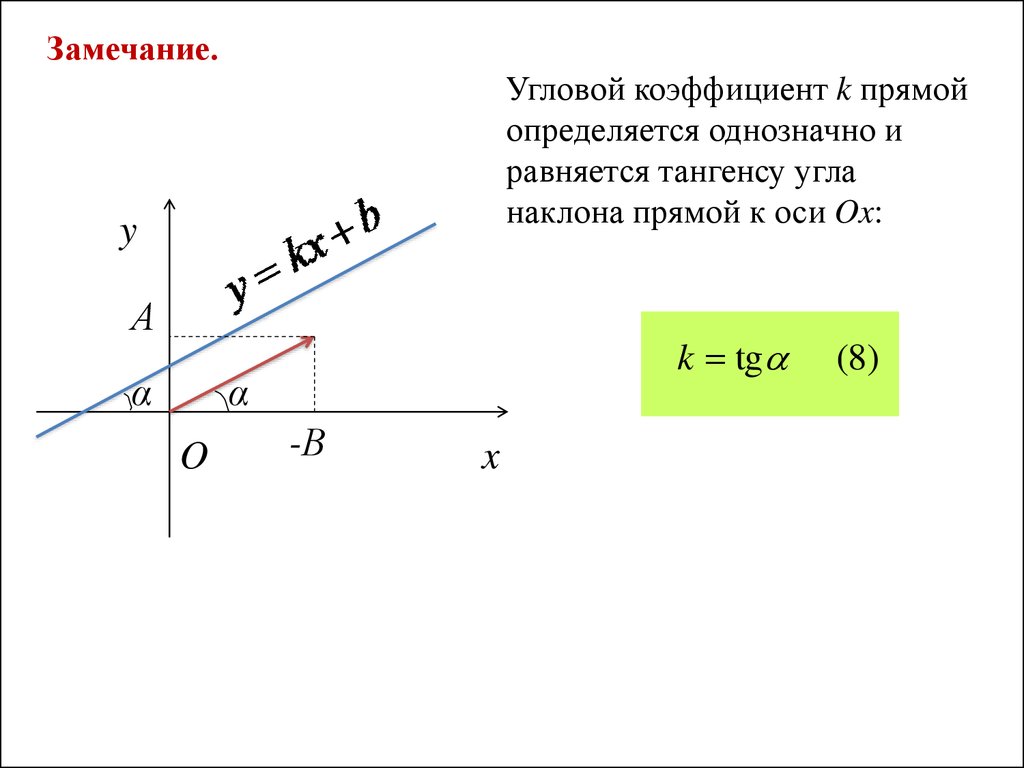 Эта фундаментальная идея означает, что вы можете выбрать 90 123 любых 90 124 2 точек на линии.

Подумайте об идее прямой линии. Если бы наклон линии изменился, то это была бы зигзагообразная линия, а не прямая линия, как вы можете видеть на рисунке выше.

Как вы можете видеть ниже, наклон одинаков независимо от того, какие 2 точки вы выбрали.

Наклон линии

Никогда не меняется

Эта страница:

• Формула
• Пример
• Видео
• Заказать?
• Любые две точки определяют наклон линии?
• Наклон вертикальной линии
• Наклон горизонтальной линии
• Практические задачи

Рабочий лист по наклону линии

Апплет наклона (html5)

Калькулятор формулы уклона (бесплатный онлайн-инструмент для расчета уклона по 2 точкам)

Практика Проблемы

Проблема 1

Каков наклон прямой, проходящей через точки (10,3) и (7, 9)?

$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $

---

Используя $$ \red{ (10,3)}$$ как $$x_1, y_1$$

$ \frac{9- \red 3}{7- \red{10}} \\ = \frac{6}{-3} \\ = \ в коробке {-2 } $

Используя $$ \red{ (7,9)} $$ как $$x_1, y_1$$

$ \frac{3- \red 9{10- \красное 7} \\ =\ гидроразрыв{-6}{3} \\ = \в коробке{-2} $

Проблема 2

Прямая проходит через (4, -2) и (4, 3). Каков его наклон?

$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $

---

---

Используя $$ \red{ ( 4,3 )}$$ как $$x_1, y_1$$

$ = \frac{-2 — \red 3}{4- \red 4} знак равно \frac{-5}{\color{red}{0}} \\ = \text{неопределенный} $

Используя $$ \red{ ( 4, -2 )}$$ как $$x_1, y_1$$

$ = \frac{3- \red{-2}}{4- \red 4} знак равно \frac{5}{\color{red}{0}} \\ = \текст{неопределенный} $

Всякий раз, когда длина линии равна нулю, наклон не определен. Это потому, что в знаменателе наклона стоит ноль! Любой наклон любой вертикальной линии не определен.

Проблема 3

Прямая проходит через (2, 10) и (8, 7).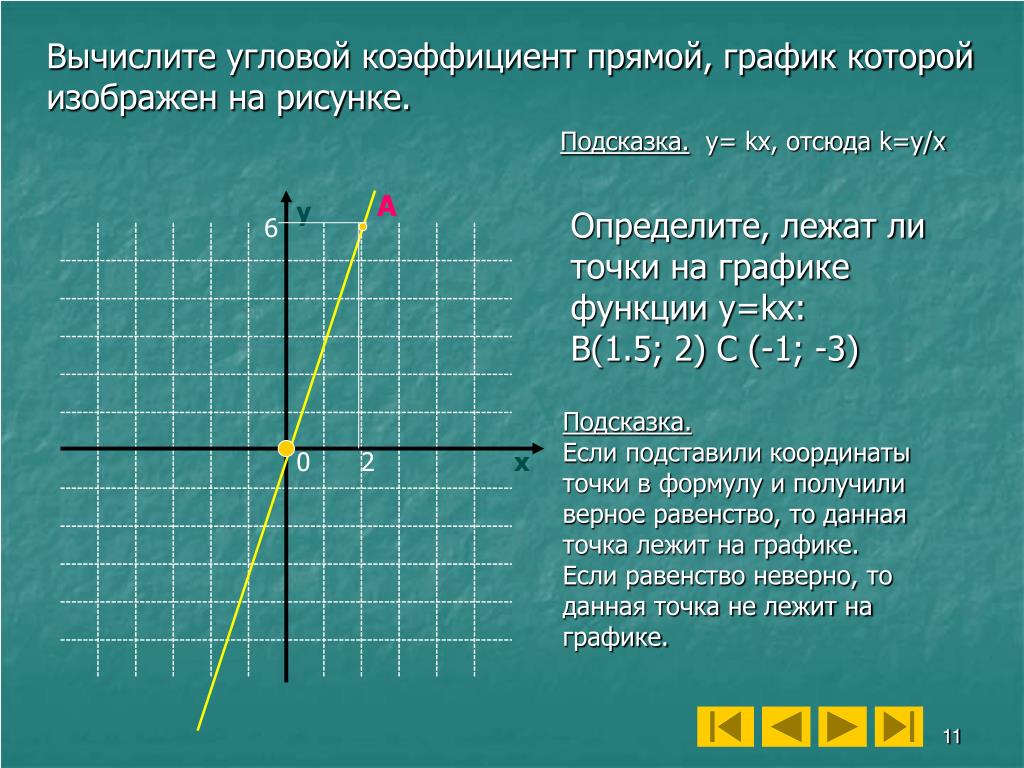 Каков его наклон?

$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $

---

Используя $$ \red{ ( 8, 7 )}$$ как $$x_1, y_1$$

$ \frac{10 — \red 7}{2 — \red 8} \\ = \ гидроразрыва {3}{-6} \\ = -\фракция{1}{2} $

Используя $$ \red{ ( 2,10 )}$$ как $$x_1, y_1$$

$ \frac{7 — \red {10}}{8- \red 2} \\ = \ гидроразрыв {-3} {6} \\ = -\фракция{1}{2} $

Проблема 4

Прямая проходит через (7, 3) и (8, 5). Каков его наклон?

$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $

---

Используя $$ \red{ (7,3 )}$$ как $$x_1, y_1$$

$$ \frac{ 5- \red 3}{8- \red 7} \\ = \ гидроразрыва {2} {1} \\ = 2 $$

Используя $$ \red{ ( 8,5 )}$$ как $$x_1, y_1$$

$$ \frac{ 3- \red 5}{7- \red 8} \\= \фракция{-2}{-1} \\ = 2 $$

Проблема 5

Прямая проходит через (12, 11) и (9, 5) .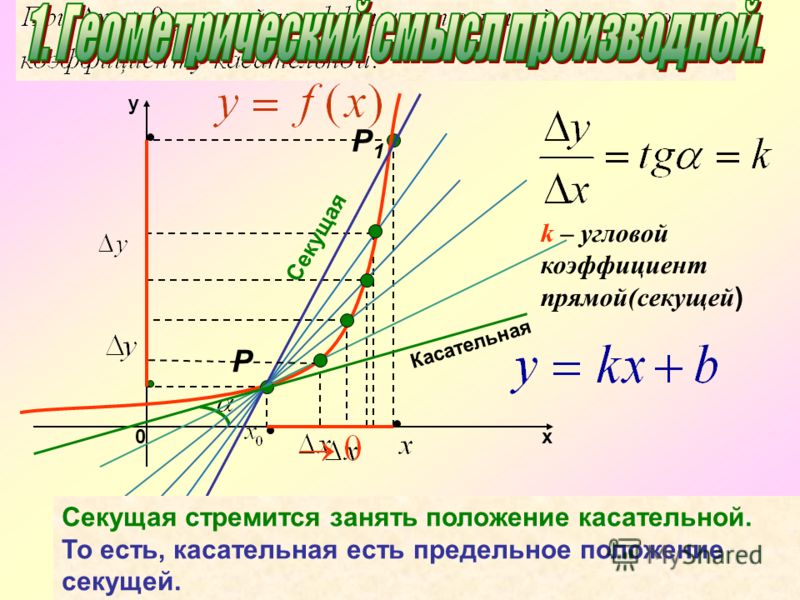 Каков его наклон?

$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $

---

Используя $$ \red{ ( 5, 9)}$$ как $$x_1, y_1$$

$$ \frac{ 11 — \red 5}{12- \red 9} \\ = \ гидроразрыва {6} {3} \\ =2 $$

Используя $$ \red{ (12, 11 )}$$ как $$x_1, y_1$$

$$ \frac{ 5- \red{ 11} }{9- \red { 12}} \\ = \фракция{-6}{-3} \\ = 2$$

Проблема 6

Каков наклон линии, проходящей через (4, 2) и (4, 5)?

$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $

---

Используя $$ \red{ ( 4,5 )}$$ как $$x_1, y_1$$

$$ \frac{ 2 — \red 5}{4- \red 4} \\ = \frac{-3}{\color{red}{0}} \\ = не определено $$

Используя $$ \red{ ( 4,2 )}$$ как $$x_1, y_1$$

$$ \frac{ 5 — \red 2}{4- \red 4} \\ = \frac{ 3}{\color{red}{0}} \\ = не определено $$

ПРЕДУПРЕЖДЕНИЕ! Уловите ошибку в следующей задаче: Дженнифер пыталась найти наклон, проходящий через точки $$(\color{blue}{1},\color{red}{3})$$ и $$ (\color {синий}{2}, \цвет{красный}{6})$$ .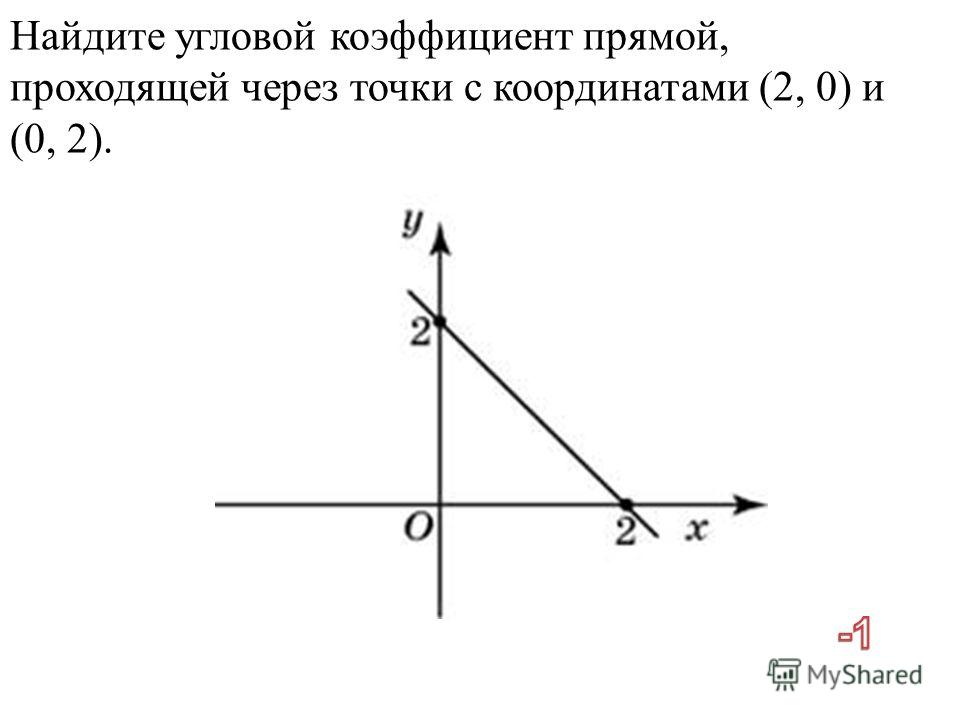 У нее были небольшие проблемы с применением формулы наклона, она пыталась вычислить наклон 3 раза и дала 3 разных ответа. Сможете ли вы определить правильный ответ?

Задача-вызов

Найдите наклон прямой через две точки.

Попытка №1

$ наклон = \ гидроразрыв {подъем} {бег} \\= \ frac{\ color {red} {y_ {2} -y_ {1}}} {\ color {blue} {x_ {2} -x_ {1}}} знак равно \ гидроразрыв {6-3} {1-2} \\= \фракция{3}{-1} =\в коробке{-3} $

---

Попытка #2

$$ наклон = \ гидроразрыв {подъем} {бег} \\= \ frac{\ color {red} {y_ {2} -y_ {1}}} {\ color {blue} {x_ {2} -x_ {1}}} знак равно \фракция{6-3}{2-1} \\= \фракция{3}{1} \\ = \в коробке{3} $$

---

Попытка №3

$$ уклон = \ гидроразрыв {подъем} {бег} \\= \ frac{\ color {red} {y_ {2} -y_ {1}}} {\ color {blue} {x_ {2} -x_ {1}}} \\ =\ гидроразрыва {2-1} {6-3} \\ =\в коробке{ \frac{1}{3}} $$

Правильный ответ — попытка №2.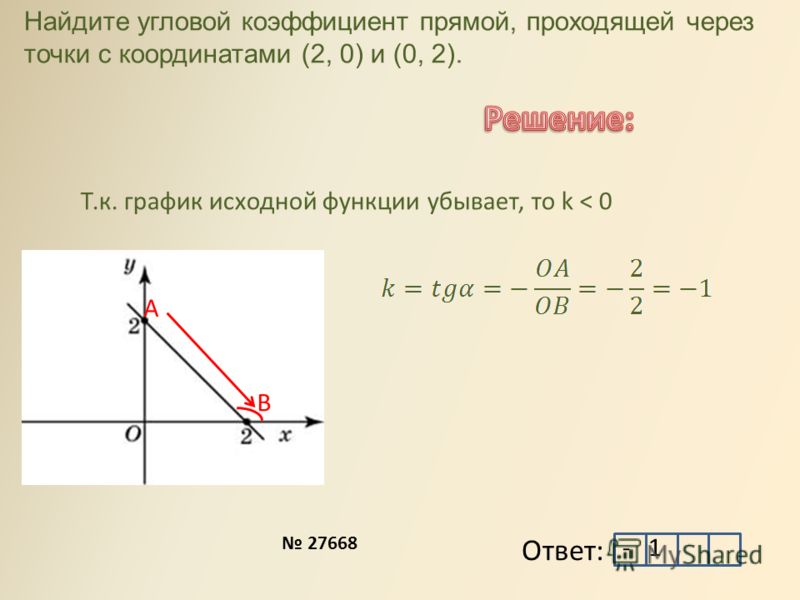

В попытке №1 она не всегда использовала очки. В первой попытке она сделала следующее:

$$ \frac{\color{red}{y{\boxed{_2}}-y_{1}}}{\color{blue}{x\boxed{_{1}}-x_{2}}} $$

Проблема с попыткой №3 заключалась в обратном подъеме и беге. Она поместила значения x в числитель (сверху), а значения y в знаменатель, что, конечно же, противоположно!

$$ \ отмена {\ frac {\ color {синий} {x_ {2} -x_ {1}}} {\ color {red} {y_ {2} -y_ {1}}}} $$

Тренировка склонов Генератор проблем

Вы можете сколько угодно практиковаться в решении подобных задач с помощью приведенного ниже генератора задач на уклон.

Он будет случайным образом генерировать числа и запрашивать наклон линии через эти две точки. Вы можете выбрать, насколько большими будут числа, регулируя уровень сложности.

Рабочий лист по наклону линии

Апплет наклона (html5)

Калькулятор формулы уклона (бесплатный онлайн-инструмент для расчета уклона по 2 точкам)

Как найти наклон прямой

Все ресурсы по алгебре 1

10 Диагностические тесты 557 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущие 1 2 … 9 10 11 12 13 14 15 16 17 18 Далее →

Алгебра 1 Помощь » Функции и линии » Уравнения прямых » Уравнения наклона и линии » Как найти наклон прямой

Найдите наклон прямой, проходящей через следующие точки:

Возможные ответы:

Правильный ответ:

Пояснение:

Найдите наклон линии, проходящей через следующие точки:

Наклон можно найти по следующей формуле:

Теперь просто подставьте полученные точки и убедитесь, что они совпадают!

Итак, наш уклон:

Сообщить об ошибке

У вас есть линия, соединяющая две точки.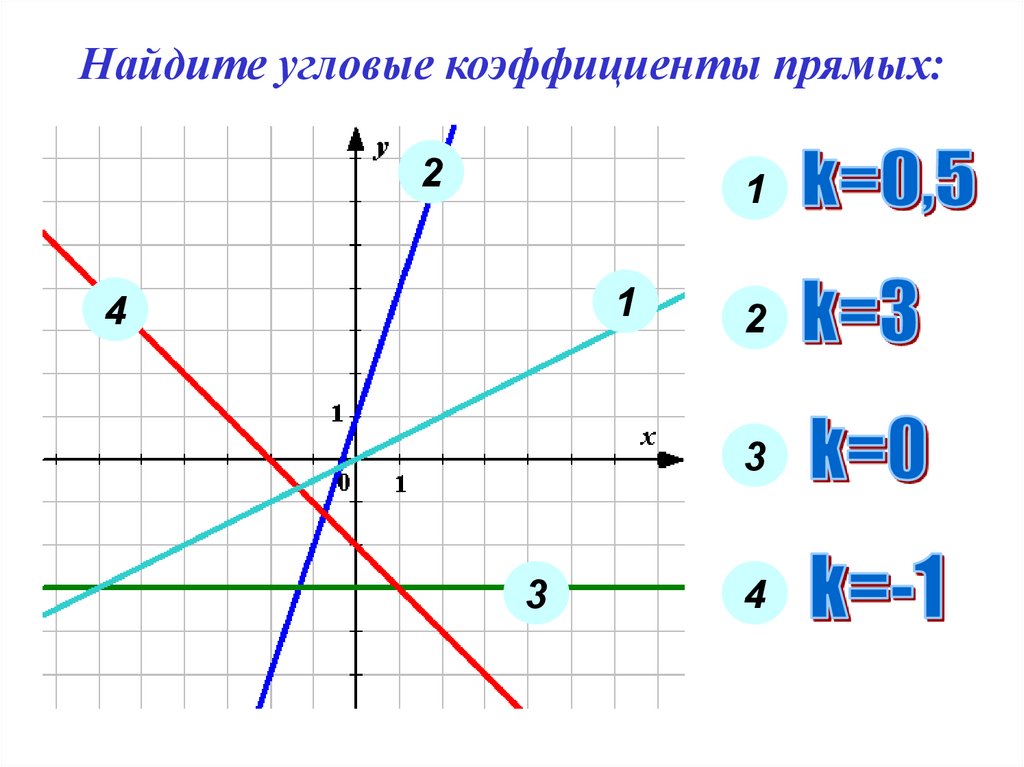 Каждая точка представлена ​​парой (x,y). Найдите наклон линии для точек, показанных на рисунке, где точки равны

(А)  

(В)  

Возможные ответы:

Правильный ответ:

Объяснение:

Наклон можно найти между двумя точками, найдя изменение значений  деленное на изменение значений  .

, который часто называют подъемом над пробегом,

На самом деле вы можете использовать любые две точки вдоль линии, чтобы найти наклон, если линия является линейной (прямой линией). Взятие конечных точек, поскольку они заданы, является удобным способом сделать это.

Таким образом, наклон этого сегмента линии составляет

Отчет о ошибке

Найдите наклон следующей линии:

Возможные ответы:

Правильный ответ:

5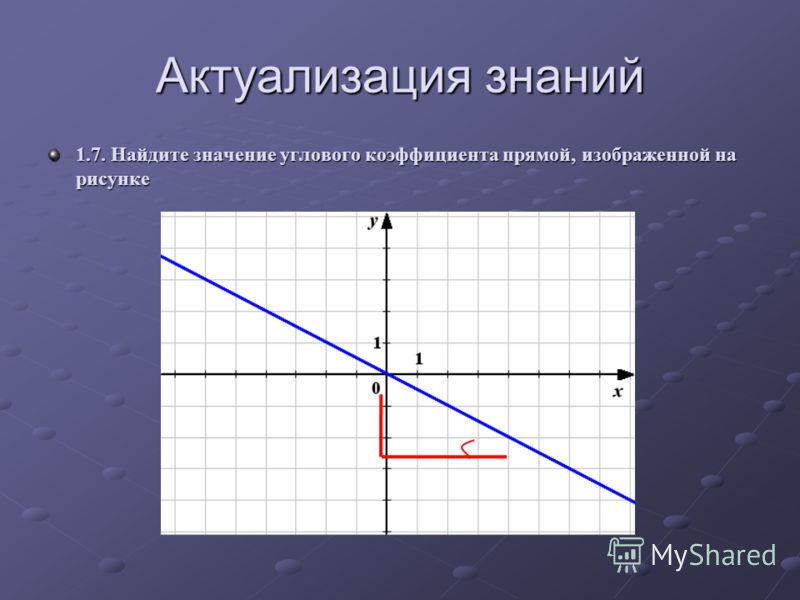

. Правильный ответ:

5

Объяснение:

Чтобы найти наклон линии, мы сначала запишем его в форме пересечения наклона

, где — наклон.

Итак, в уравнении

найдем и и получим сами. Для этого мы разделим каждое слагаемое на .

Глядя на это уравнение, мы видим, что это наклон.

Сообщить об ошибке

Каков наклон линии с точками  и .

Возможные ответы:

Правильный ответ:

Пояснение:

Напишите формулу для наклона.

Любой вариант даст один и тот же наклон. Используем первое уравнение.

Упростите, чтобы найти уклон.

Сообщить об ошибке

Вы знаете, что линия имеет следующие точки:

 и 

 

Вычислите наклон линии.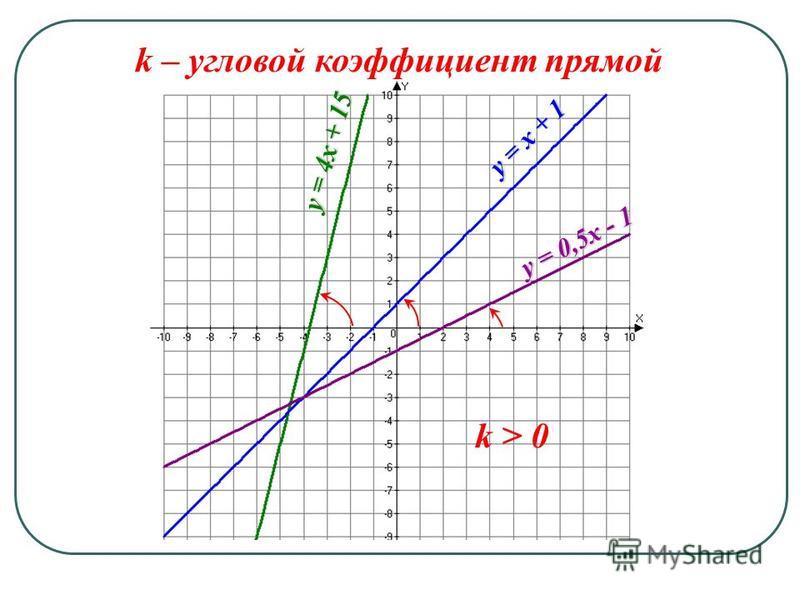

Возможные ответы:

Правильный ответ:

Объяснение:

Наклон линии можно определить, если известны хотя бы две точки, попадающие на линию, с помощью следующего уравнения:

Координаты всегда пишутся вторыми при просмотре пар координат, поэтому координаты идут первыми. Таким образом, мы можем вставить наши заданные точки в это уравнение:

Отчет о ошибке

Найдите наклон из линии, соединяющей следующие два балла:

Возможные ответы:

4

.

Правильный ответ:

Объяснение:

Найдите наклон линии, соединяющей следующие две точки:

 

Найдите наклон по следующей формуле:

, поэтому наш наклон равен просто 1

Сообщить об ошибке

4 .

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти наклон, нам нужно представить следующее уравнение в форме пересечения наклона.

Обозначает уклон.

Вычесть с обеих сторон.

Упростите левую часть и реорганизуйте правую.

Разделите на минус три с обеих сторон.

Упростите обе стороны.

Наклон .

Сообщить об ошибке

Найдите наклон следующей линии:

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти наклон этой линии, ее необходимо преобразовать из стандартной формы в форму пересечения наклона.

No related posts.