404 Cтраница не найдена
Мы используем файлы cookies для улучшения работы сайта МГТУ и большего удобства его использования. Более подробную информацию об использовании файлов cookies можно найти здесь. Продолжая пользоваться сайтом, вы подтверждаете, что были проинформированы об использовании файлов cookies сайтом ФГБОУ ВО «МГТУ» и согласны с нашими правилами обработки персональных данных.
Размер:
AAA
Изображения Вкл. Выкл.
Обычная версия сайта
К сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже
|
|
Педагогический (научно-педагогический) составФормулы приведения углов.
Примеры применения формул приведенияОни относятся к разделу «тригонометрия» в математике. Суть их заключается в приведении тригонометрических функций углов к более «простому» виду. О важности их знания написать можно много. Этих формул аж 32 штуки!
Не пугайтесь, учить их не надо, как и многие другие формулы в курсе математики. Лишней информацией голову забивать не нужно, необходимо запоминать «ключики» или законы, и вспомнить или вывести нужную формулу проблемой не будет. Кстати, когда я пишу в статьях «… нужно выучить!!!» – это значит, что действительно, это необходимо именно выучить.
Если вы с формулами приведения не знакомы, то простота их вывода вас приятно удивит – есть «закон», при помощи которого это легко сделать. И любую из 32 формул вы напишите за 5 секунд.
Перечислю лишь некоторые задачи, которые будут на ЕГЭ по математике, где без знания этих формул есть большая вероятность потерпеть фиаско в решении. Например:
– задачи на решение прямоугольного треугольника, где речь идёт о внешнем угле, да и задачах на внутренние углы некоторые из этих формул тоже необходимы.
– задачи на вычисление значений тригонометрических выражений; преобразования числовых тригонометрических выражений; преобразования буквенных тригонометрических выражений.
– задачи на касательную и геометрический смысл касательной, требуется формула приведения для тангенса, а также другие задачи.
– стереометрические задачи, по ходу решения не редко требуется определить синус или косинус угла, который лежит в пределах от 90 до 180 градусов.
И это лишь те моменты, которые касаются ЕГЭ. А в самом курсе алгебры есть множество задач, при решении которых, без знания формул приведения просто не обойтись.
Так что же к чему приводится и как оговоренные формулы упрощают для нас решение задач?
Например, вам нужно определить синус, косинус, тангенс или котангенс любого угла от 0 до 450 градусов:
угол альфа лежит пределах от 0 до 90 градусов
* * *
Итак, необходимо уяснить «закон», который здесь работает:
1. Определите знак функции в соответствующей четверти.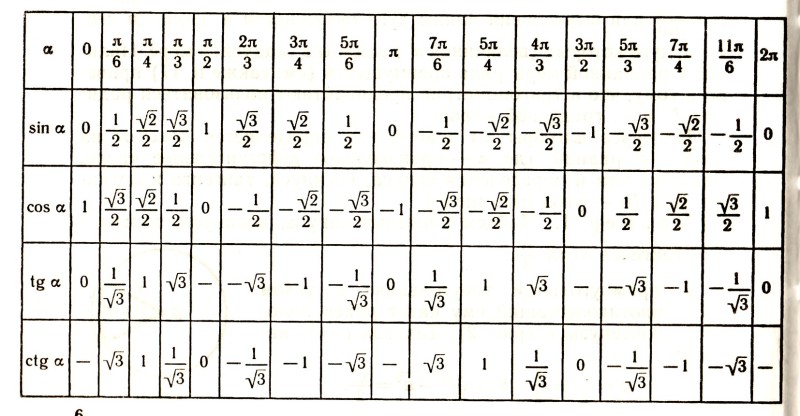
Напомню их:
2. Запомните следующее:
функция изменяется на кофункцию
функция на кофункцию не изменяется
Что означает понятие — функция изменяется на кофункцию?
Ответ: синус меняется на косинус или наоборот, тангенс на котангенс или наоборот.
Вот и всё!
Теперь по представленному закону запишем несколько формул приведения самостоятельно:
Данный угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Функцию на кофункцию не меняем, так как у нас 180 градусов, значит:
Угол лежит в первой четверти, синус в первой четверти положителен. Не меняем функцию на кофункцию, так как у нас 360 градусов, значит:
Вот вам ещё дополнительное подтверждение того, что синусы смежных углов равны:
Угол лежит во второй четверти, синус во второй четверти положителен. Не меняем функцию на кофункцию, так как у нас 180 градусов, значит:
Проработайте мысленно или письменно каждую формулу, и вы убедитесь, что ничего сложного нет.
\circ \pm \alpha`):
`sin(2\pi — \alpha)=-sin \ \alpha;` ` sin(2\pi + \alpha)=sin \ \alpha`
`cos(2\pi — \alpha)=cos \ \alpha;` ` cos(2\pi + \alpha)=cos \ \alpha`
`tg(2\pi — \alpha)=-tg \ \alpha;` ` tg(2\pi + \alpha)=tg \ \alpha`
`ctg(2\pi — \alpha)=-ctg \ \alpha;` ` ctg(2\pi + \alpha)=ctg \ \alpha`
Часто можно встретить формулы приведения в виде таблицы, где углы записаны в радианах:
Чтобы воспользоваться ею, нужно выбрать строку с нужной нам функцией, и столбец с нужным аргументом. Например, чтобы узнать с помощью таблицы, чему будет равно ` sin(\pi + \alpha)`, достаточно найти ответ на пересечении строки ` sin \beta` и столбца ` \pi + \alpha`. Получим ` sin(\pi + \alpha)=-sin \ \alpha`.
И вторая, аналогичная таблица, где углы записаны в градусах:
Мнемоническое правило формул приведения или как их запомнить
Как мы уже упоминали, заучивать все вышеприведенные соотношения не нужно. Если вы внимательно на них посмотрели, то наверняка заметили некоторые закономерности.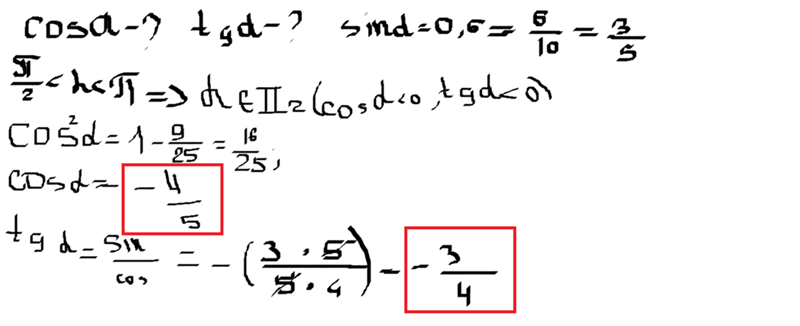
Они позволяют нам сформулировать мнемоническое правило (мнемоника — запоминать), с помощью которого легко можно получить любую с формул приведения.
Сразу отметим, что для применения этого правила нужно хорошо уметь определять (или запомнить) знаки тригонометрических функций в разных четвертях единичной окружности.
Само привило содержит 3 этапа:
- Аргумент функции должен быть представлен в виде `\frac {\pi}2 \pm \alpha`, `\pi \pm \alpha`, `\frac {3\pi}2 \pm \alpha`, `2\pi \pm \alpha`, причем `\alpha` — обязательно острый угол (от 0 до 90 градусов).
- Для аргументов `\frac {\pi}2 \pm \alpha`, `\frac {3\pi}2 \pm \alpha` тригонометрическая функция преобразуемого выражения меняется на кофункцию, то есть противоположную (синус на косинус, тангенс на котангенс и наоборот). Для аргументов `\pi \pm \alpha`, `2\pi \pm \alpha` функция не меняется.
- Определяется знак исходной функции. Полученная функция в правой части будет иметь такой же знак.
Чтобы посмотреть, как на практике можно применить это правило, преобразим несколько выражений:
1.
\circ`, их значения не изменятся, если на эти величины увеличить или уменьшить аргумент.
Исходя из этого, наше выражение можно записать следующим образом: `cos (\pi+(\frac{\pi}2-\alpha)`. Применив два раза мнемоническое правило, получим: `cos (\pi+(\frac{\pi}2-\alpha)= — cos (\frac{\pi}2-\alpha)= — sin \alpha`.
Ответ: `cos(\frac {7\pi}2 — \alpha)=- sin \alpha`.
Лошадиное правило
Второй пункт вышеописанного мнемонического правила еще называют лошадиным правилом формул приведения. Интересно, почему лошадиным?
Итак, мы имеем функции с аргументами `\frac {\pi}2 \pm \alpha`, `\pi \pm \alpha`, `\frac {3\pi}2 \pm \alpha`, `2\pi \pm \alpha`, точки `\frac {\pi}2`, `\pi`, `\frac {3\pi}2`, `2\pi` — ключевые, они располагаются на осях координат. `\pi` и `2\pi` на горизонтальной оси абсцисс, а `\frac {\pi}2` и `\frac {3\pi}2` на вертикальной оси ординат.
Задаем себе вопрос: «Меняется ли функция на кофункцию?». Чтобы ответить на этот вопрос, нужно подвигать головой вдоль оси, на которой расположена ключевая точка.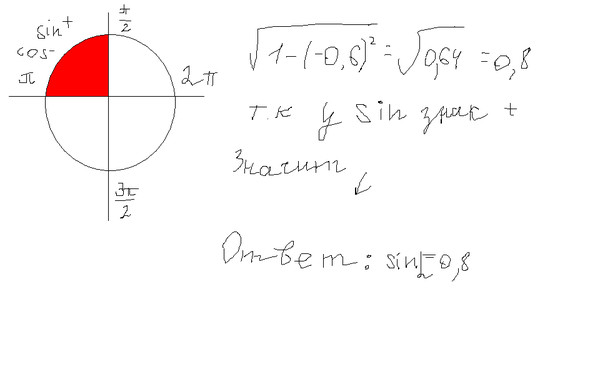
\circ=-\frac{\sqrt 3}2`.
Пример 2. Выразив косинус через синус по формулам приведения, сравнить числа: 1) `sin \frac {9\pi}8` и `cos \frac {9\pi}8`; 2) `sin \frac {\pi}8` и `cos \frac {3\pi}10`.
Решение: 1)`sin \frac {9\pi}8=sin (\pi+\frac {\pi}8)=-sin \frac {\pi}8`
`cos \frac {9\pi}8=cos (\pi+\frac {\pi}8)=-cos \frac {\pi}8=-sin \frac {3\pi}8`
`-sin \frac {\pi}8> -sin \frac {3\pi}8`
`sin \frac {9\pi}8>cos \frac {9\pi}8`.
2) `cos \frac {3\pi}10=cos (\frac {\pi}2-\frac {\pi}5)=sin \frac {\pi}5`
`sin \frac {\pi}8
`sin \frac {\pi}8
Докажем сначала две формулы для синуса и косинуса аргумента `\frac {\pi}2 + \alpha`: ` sin(\frac {\pi}2 + \alpha)=cos \ \alpha` и` cos(\frac {\pi}2 + \alpha)=-sin \ \alpha`. Остальные выводятся из них.
Возьмем единичную окружность и на ней точку А с координатами (1,0). Пусть после поворота на угол `\alpha` она перейдет в точку `А_1(х, у)`, а после поворота на угол `\frac {\pi}2 + \alpha` в точку `А_2(-у,х)`.
Опустив перпендикуляры с этих точек на прямую ОХ, увидим, что треугольники `OA_1H_1` и `OA_2H_2` равны, поскольку равны их гипотенузы и прилежащие углы. Тогда исходя из определений синуса и косинуса можно записать `sin \alpha=у`, `cos \alpha=х`, ` sin(\frac {\pi}2 + \alpha)=x`, ` cos(\frac {\pi}2 + \alpha)=-y`. Откуда можно записать, что ` sin(\frac {\pi}2 + \alpha)=cos \alpha` и ` cos(\frac {\pi}2 + \alpha)=-sin \alpha`, что доказывает формулы приведения для синуса и косинуса угла `\frac {\pi}2 + \alpha`.
Выходя из определения тангенса и котангенса, получим ` tg(\frac {\pi}2 + \alpha)=\frac {sin(\frac {\pi}2 + \alpha)}{cos(\frac {\pi}2 + \alpha)}=\frac {cos \alpha}{-sin \alpha}=-ctg \alpha` и ` сtg(\frac {\pi}2 + \alpha)=\frac {cos(\frac {\pi}2 + \alpha)}{sin(\frac {\pi}2 + \alpha)}=\frac {-sin \alpha}{cos \alpha}=-tg \alpha`, что доказывает формулы приведения для тангенса и котангенса угла `\frac {\pi}2 + \alpha`.
Чтобы доказать формулы с аргументом `\frac {\pi}2 — \alpha`, достаточно представить его, как `\frac {\pi}2 + (-\alpha)` и проделать тот же путь, что и выше.
Например, `cos(\frac {\pi}2 — \alpha)=cos(\frac {\pi}2 + (-\alpha))=-sin(-\alpha)=sin(\alpha)`.
Углы `\pi + \alpha` и `\pi — \alpha` можно представить, как `\frac {\pi}2 +(\frac {\pi}2+\alpha)` и `\frac {\pi}2 +(\frac {\pi}2-\alpha)` соответственно.
А `\frac {3\pi}2 + \alpha` и `\frac {3\pi}2 — \alpha` как `\pi +(\frac {\pi}2+\alpha)` и `\pi +(\frac {\pi}2-\alpha)`.
Тема урока
- Изменение синуса, косинуса и тангенса при возрастании угла.
Цели урока
- Познакомиться с новыми определениями и вспомнить некоторые уже изученные.
- Познакомится с закономерностью изменений значений синуса косинуса и тангенса при возрастании угла.
- Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
- Воспитательные — посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.
Задачи урока
- Проверить знания учащихся.
План урока
- Повторение ранее изученного материала.
- Задачи на повторение.
- Изменение синуса, косинуса и тангенса при возрастании угла.
- Практическое применение.
Повторение ранее изученного материала
Начнем с самого начала и вспомним то что будет полезно освежить в памяти. Что же такое синус, косинус и тангенс и к какому разделу геометрии относятся эти понятия.
Тригонометрия — это такое сложное греческое слово: тригонон — треугольник, метро — мерять. Стало быть по-гречески это означает: мерятся треугольниками.
Предмети > Математика > Математика 8 классКак запомнить формулы приведения тригонометрических функций? Это легко, если использовать ассоциацию.Данная ассоциация придумана не мной. Как уже говорилось, хорошая ассоциация должна «цеплять», то есть вызывать яркие эмоции. Не могу назвать эмоции, вызываемые этой ассоциацией, позитивными. Но она дает результат — позволяет запоминать формулы приведения, а значит, имеет право на существование.
В конце концов, если она вам не понравится, вы же ее можете не использовать, правильно?
Формулы приведения имеют вид: sin(πn/2±α), cos(πn/2±α), tg(πn/2±α), ctg(πn/2±α). Запоминаем, что +α дает движение против часовой стрелки, — α — движение по часовой стрелке.
Для работы с формулами приведения нужны два пункта:
1) ставим знак, который имеет начальная функция (в учебниках пишут: приводимая. Но, чтобы не запутаться, лучше назвать ее начальной), если считать α углом I четверти, то есть маленьким.
2) Горизонтальный диаметр — π±α, 2π±α, 3π±α… — в общем, когда нет дроби — название функции не меняет. Вертикальный π/2±α, 3π/2±α, 5π/2±α…- когда дробь есть — название функции меняет: синус — на косинус, косинус — на синус, тангенс — на котангенс и котангенс — на тангенс.
Теперь, собственно, ассоциация:
вертикальный диаметр (есть дробь) —
пьяный стоит. Что с ним случится рано
или поздно? Правильно, упадет.
Название функции изменится.
Если же диаметр горизонтальный — пьяный уже лежит.
Спит, наверное. С ним уже ничего не случится, он уже принял горизонтальное положение. Соответственно, название функции не меняется.
То есть sin(π/2±α), sin(3π/2±α), sin(5π/2±α) и т.д. дают ±cosα,
а sin(π±α), sin(2π±α), sin(3π±α), … — ±sinα.
Как , уже знаем.
Как это работает? Смотрим на примерах.
1) cos(π/2+α)=?
Становимся на π/2. Поскольку +α — значит, идем вперед, против часовой стрелки. Попадаем во II четверть, где косинус имеет знак «-«. Название функции меняется («пьяный стоит», значит — упадет). Итак,
cos(π/2+α)=-sin α.
Становимся на 2π. Так как -α — идем назад, то есть по часовой стрелке. Попадаем в IV четверть, где тангенс имеет знак «-«. Название функции не меняется (диаметр горизонтальный, «пьяный уже лежит»). Таким образом, tg(2π-α)=- tgα.
3) ctg²(3π/2-α)=?
Примеры, в которых функция возводится в четную степень, решаются еще проще. Четная степень «-» убирает, то есть надо только выяснить, меняется название функции или остается.
Диаметр вертикальный (есть дробь, «пьяный стоит», упадет), название функции меняется. Получаем: ctg²(3π/2-α)= tg²α.
Определение. Формулами приведения называют формулы, которые позволяют перейти от тригонометрических функций вида к функциям аргумента . С их помощью синус, косинус, тангенс и котангенс произвольного угла можно привести к синусу, косинусу, тангенсу и котангенсу угла из интервала от 0 до 90 градусов (от 0 до радиан). Таким образом, формулы приведения позволяют нам переходить к работе с углами в пределах 90 градусов, что, несомненно, очень удобно.
Формулы приведения:
Для использования формул приведения существует два правила.
1. Если угол можно представить в виде (π/2 ±a) или (3*π/2 ±a), то название функции меняется sin на cos, cos на sin, tg на ctg, ctg на tg. Если же угол можно представить в виде (π ±a) или (2*π ±a), то название функции остается без изменений.
Посмотрите на рисунок ниже, там схематично изображено, когда следует менять знак, а когда нет
2.
Знак приведенной функции остается прежним. Если исходная функция имела знак «плюс», то и приведенная функция имеет знак «плюс». Если исходная функция имела знак «минус», то и приведенная функция имеет знак «минус».
На рисунке ниже представлены знаки основных тригонометрических функций в зависимости от четверти.
Пример:
Вычислить
Воспользуемся формулами приведения:
Sin(150˚) находится во второй четверти, по рисунку видим что знак sin в этой четверти равен «+». Значит у приведенной функции тоже будет знак «+». Это мы применили второе правило.
Теперь 150˚ = 90˚ +60˚. 90˚ это π/2. То есть имеем дело со случаем π/2+60, следовательно по первому правилу меняем функцию с sin на cos. В итоге получаем Sin(150˚) = cos(60˚) = ½.
5.7 Решение тригонометрических уравнений | Тригонометрия
5.7 Решение тригонометрических уравнений (EMA3T)
В этом разделе мы сначала рассмотрим нахождение неизвестных длин в прямоугольных треугольниках, а затем рассмотрим
нахождение неизвестных углов в прямоугольных треугольниках.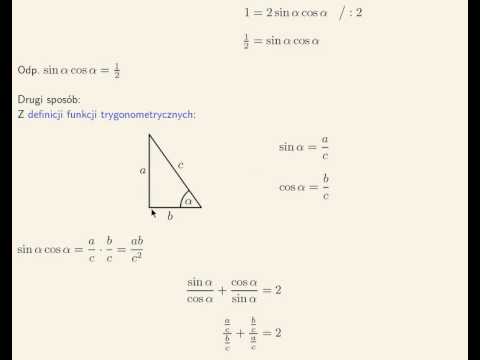
Наконец, мы рассмотрим, как решать более общие тригонометрические задачи.
уравнения.
Определение длин (EMA3V)
Из определений тригонометрических соотношений и того, что мы узнали об определении значений этих отношения для любого угла, теперь мы можем использовать это, чтобы помочь нам найти неизвестные длины в прямоугольных треугольниках. следующие рабочие примеры покажут вам, как это сделать.
Рабочий пример 4: Нахождение длин
Найдите длину \(x\) в следующем прямоугольном треугольнике, используя соответствующее тригонометрическое отношение (округлите ответ до двух знаков после запятой).
Определите противолежащие и прилежащие стороны и гипотенузу относительно данного угол
Помните, что сторона гипотенузы всегда напротив прямого угла, она никогда не меняется
позиция. Противоположная сторона лежит напротив интересующего нас угла, а прилежащая сторона – это
оставшаяся сторона.
\начать{выравнивать*} \ sin \ theta & = \ frac {\ text {напротив}} {\ text {гипотенуза}} \\ \sin 50° & = \frac{x}{100} \конец{выравнивание*}
Изменить уравнение для решения для \(x\)
\начать{выравнивать*} \sin 50° \times 100 & = \frac{x}{100} \times 100 \\ \sin 50° \times 100 & = x \\ х & = 100 \sin 50° \конец{выравнивание*}Используйте свой калькулятор, чтобы найти ответ
\начать{выравнивать*} х & = \текст{76,60444…} \\ х & \приблизительно \text{76,60} \конец{выравнивание*}Рабочий пример 5: Нахождение длин
Найдите длину \(x\) в следующем прямоугольном треугольнике, используя соответствующее тригонометрическое отношение (округлите ответ до двух знаков после запятой).
Определите противолежащие и прилежащие стороны и гипотенузу относительно данного угол
Помните, что сторона гипотенузы всегда напротив прямого угла, она никогда не меняется
позиция.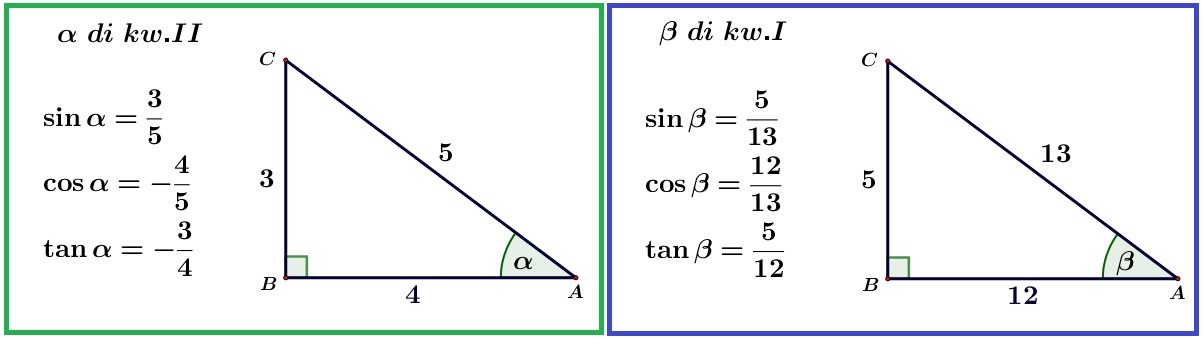
Противоположная сторона лежит напротив интересующего нас угла, а прилежащая сторона – это
оставшаяся сторона.
\начать{выравнивать*} \ cos \ theta & = \ frac {\ text {смежный}} {\ text {гипотенуза}} \\ \cos 25° & = \frac{7}{x} \конец{выравнивание*}
Изменить уравнение для решения для \(x\)
\начать{выравнивать*} \cos 25° \times x & = \frac{7}{x} \times x \quad \text{умножить обе стороны на } x\\ х \cos 25° & = 7 \\ \frac{x \cos 25°}{\cos 25°} & = \frac{7}{\cos 25°} \quad \text{разделите обе части на } \cos 25°\\ х & = \ гидроразрыва {7} {\ cos 25 °} \конец{выравнивание*}Используйте свой калькулятор, чтобы найти ответ
\начать{выравнивать*} х & = \frac{7}{\text{0,Рабочий пример 6: Нахождение длин
Найдите длины \(x\) и \(y\) в следующем прямоугольном треугольнике, используя соответствующие
тригонометрическое соотношение (округлите ответы до двух знаков после запятой).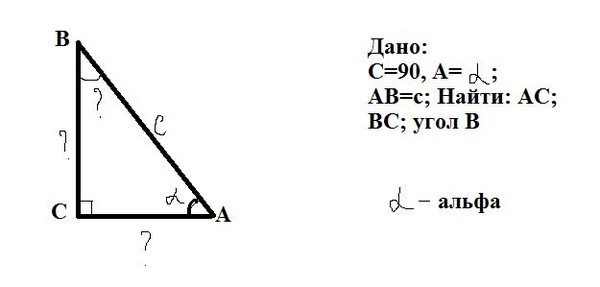
Определите противолежащие и прилежащие стороны и гипотенузу относительно данного угол
\начать{выравнивать*} \ tan \ theta & = \ frac {\ text {напротив}} {\ text {смежно}} \\ \tan 25° & = \frac{x}{7} \\ \\ \ cos \ theta & = \ frac {\ text {смежный}} {\ text {гипотенуза}} \\ \cos 25° & = \frac{7}{y} \end{выравнивание*}Переставьте уравнения для решения для \(x\) и \(y\)
\начать{выравнивать*} x & = 7 \times \tan 25° \\ \\ y & = \frac{7}{\cos 25°} \конец{выравнивание*}Используйте калькулятор, чтобы найти ответы
\начать{выравнивать*} х & = \текст{3,26415…} \\ х & \ приблизительно \ текст {3,26} \\ \\ у & = \текст{7,72364…} \\ у & \приблизительно \текст{7,72} \end{выравнивание*} В следующем видео показан пример нахождения неизвестных длин в треугольнике с помощью тригонометрических соотношений.
Видео: 2FQT
Учебник Упражнение 5.4
\begin{выравнивание*} \ sin \ theta & = \ frac {\ text {напротив}} {\ text {гипотенуза}} \\ \sin 37° & = \frac{a}{62} \\ 62(\text{0,6018…}) & = а \\ а & = \text{36,10890…} \\ & \ приблизительно \ текст {36,11} \end{выравнивание*}
\begin{выравнивание*} \ tan \ theta & = \ frac {\ text {напротив}} {\ text {смежно}} \\ \tan 23° & = \frac{b}{21} \\ 21(\текст{0,42447…}) & = б \\ б & = \текст{8,91397…} \\ & \ приблизительно \ текст {8,91} \end{выравнивание*}
\begin{выравнивание*}
\ cos \ theta & = \ frac {\ text {смежный}} {\ text {гипотенуза}} \\
\cos 55° & = \frac{c}{19} \\
19(\text{0,5735…}) & = с \\
с & = \текст{10,89795.
..} \\
& \ приблизительно \ текст {10,90}
\end{выравнивание*}
\begin{выравнивание*} \ cos \ theta & = \ frac {\ text {смежный}} {\ text {гипотенуза}} \\ \cos 49° & = \frac{d}{33} \\ 33(\text{0,65605…}) & = d \\ д & = \текст{21,64994…} \\ & \ приблизительно \ текст {21,65} \end{выравнивание*}
\begin{выравнивание*} \ sin \ theta & = \ frac {\ text {напротив}} {\ text {гипотенуза}} \\ \sin 17° & = \frac{12}{e} \\ e &= \frac{12}{\sin 17°} \\ е & = \text{41,0436}\ldots \\ & \ приблизительно \ текст {41,04} \end{выравнивание*}
\begin{выравнивание*}
\ cos \ theta & = \ frac {\ text {смежный}} {\ text {гипотенуза}} \\
\cos 22° & = \frac{31}{f} \\
f(\text{0,92718…}) & = 31 \\
f & = \text{33,434577.
\circ} & = \frac{\text{4,1}}{x} \\
х & = \текст{2,87}
\end{выравнивание*} 9\circ} & = \frac{x}{\text{4,23}} \\
х & = \текст{9,06}
\end{align*}
\(\sin \hat{B}\)
Обратите внимание, что треугольники \(ABC\) и \(ABD\) содержат угол \(B\), поэтому мы можем использовать эти треугольники к запишите соотношения:
\[\sin \hat{B} = \frac{AC}{AB} = \frac{AD}{BD}\]
\(\cos \hat{D}\)
Обратите внимание, что треугольники \(ACD\) и \(ABD\) содержат угол \(D\), поэтому мы можем использовать эти треугольники для запишите соотношение:
\[\cos \hat{D} = \frac{AD}{BD} = \frac{CD}{AD}\]
\(\tan \hat{B}\)
Обратите внимание, что треугольники \(ABC\) и \(ABD\) содержат угол \(B\), поэтому мы можем использовать эти треугольники для запишите соотношения:
\[\tan \hat{B} = \frac{AC}{BC} = \frac{AD}{AB}\]
В \(\треугольник MNP\), \(\шляпа{N} = 90°\), \(MP=20\) и \(\шляпа{P} = 40°\).
Вычислить \(НП\)
и \(MN\) (исправить до \(\text{2}\) знаков после запятой).
Нарисуйте треугольник:
Чтобы найти \(MN\), мы используем отношение синусов:
\начать{выравнивать*} \sin \шляпа{P} &= \frac{MN}{MP} \\ \sin 40° & = \frac{MN}{20} \\ 20(\text{0,642787…}) & = МН \\ MN & = \text{12,8557…} \\ & \ приблизительно \ текст {12,86} \конец{выравнивание*}
Чтобы найти \(NP\), мы можем использовать отношение косинусов:
\начать{выравнивать*} \cos\шляпа{P} &= \frac{NP}{MP} \\ \cos 40° & = \frac{NP}{20} \\ 20(\text{0,76604…}) & = НП \\ НП & = \text{15,32088…} \\ & \ приблизительно \ текст {15,32} \конец{выравнивание*}
Следовательно, \(MN = \text{12,86} \text{ и } NP = \text{15,32}\)
Вычислите \(x\) и \(y\) на следующей диаграмме.
Чтобы найти \(x\), мы используем \(\треугольник ABC\) и отношение тангенсов. Чтобы найти \(y\), мы используем \(\треугольник ABD\) и касательное отношение.
\начать{выравнивать*} \tan 38° & = \frac{\text{23,3}}{x} \\ х & = \ frac {\ text {23,3}} {\ tan 38 °} \\ & = \текст{29,82264…} \\ & примерно \текст{29,82} \\\\ \tan 47° & = \frac{y}{\text{29,82264…}} \\ y & = \text{29,82264…}\tan 47° \\ & = \текст{31,98086…} \\ & \приблизительно\текст{31,98} \конец{выравнивание*}
Следовательно, \(x = \text{29,82} \text{ и } y = \text{31,98}\).
Нахождение угла (EMA3W)
Если длины двух сторон треугольника известны, углы можно вычислить с помощью тригонометрических соотношений. В
В этом разделе мы находим углы внутри прямоугольных треугольников, используя отношения сторон.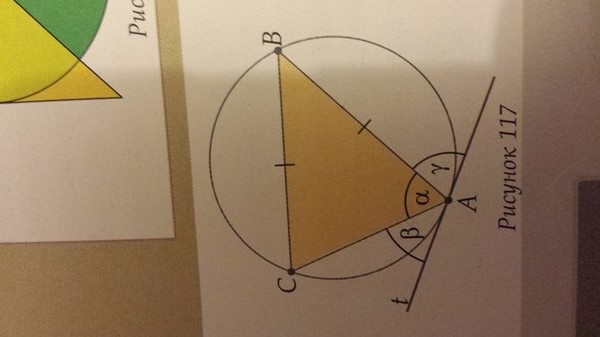
Рабочий пример 7: Нахождение углов
Найдите значение \(\theta\) в следующем прямоугольном треугольнике, используя соответствующий тригонометрический соотношение.
Определите противолежащие и смежные стороны относительно заданного угла и гипотенуза
В этом случае у вас есть противоположная сторона и смежная сторона для угла \(\theta\).
\начать{выравнивать*} \ tan \ theta & = \ frac {\ text {напротив}} {\ text {смежно}} \\ \загар \тета & = \фракция{50}{100} \конец{выравнивание*}
Используйте свой калькулятор, чтобы найти \(\theta\)
Чтобы найти \(\theta\), вам нужно будет использовать функцию арктангенса на вашем калькуляторе. Это работает назад, используя соотношение сторон, чтобы определить угол, который привел к этому соотношению.
Пресс
\(\boxed{\text{SHIFT}} \enspace
\boxed{\text{загар}} \enspace
\в коробке{50}
\ в коробке {\ div} \ enspace
\в коробке{100}
\в коробке{)} \enspace
\boxed{=} \enspace
\текст{26,56505.
..}
\приблизительно \текст{26,6}\)
Напишите окончательный ответ
\(\тета \приблизительно\текст{26,6}°\)Учебник Упражнение 5.5
\begin{выравнивание*} \tan \alpha & = \frac{4}{9} \\ & = \текст{0,4444…} \\ \alpha & = \text{23,9624…} \\ & \приблизительно \text{23,96}° \end{выравнивание*}
\begin{выравнивание*} \ грех \ альфа & = \ гидроразрыва {\ текст {7,5}} {13} \\ & = \текст{0,5769…} \\ \alpha & = \text{35,2344…} \\ & \приблизительно \text{35,23}° \end{выравнивание*}
\begin{выравнивание*} \sin \alpha & = \frac{\text{1,7}}{\text{2,2}} \\ \alpha & = \text{39,4005…} \\ & \приблизительно \text{39,40}° \end{выравнивание*}
\begin{выравнивание*}
\tan \alpha & = \frac{\text{4,5}}{\text{9,1}} \\
& = \текст{0,49450.
..} \\
\alpha & = \text{26,3126…} \\
& \приблизительно \text{26,31}°
\end{выравнивание*}
\begin{выравнивание*} \cos \alpha & = \frac{12}{15} \\ & = \текст{0,8} \\ \alpha & = \text{36,869897…} \\ & \приблизительно \text{36,87}° \end{выравнивание*}
\begin{выравнивание*} \sin \alpha & = \frac{1}{\sqrt{2}} \\ & = \текст{0,7071…} \\ \альфа & = 45° \end{выравнивание*}
\begin{выравнивание*} \sin{\alpha} & = \frac{\text{3,5}}{\text{7}} \\ & = \текст{0,5} \\ \альфа & = \текст{30}° \end{выравнивание*}
Теперь мы увидели, как решать тригонометрические уравнения в прямоугольных треугольниках. Мы можем использовать те же методы чтобы помочь нам решить тригонометрические уравнения, когда треугольник не показан.
Рабочий пример 8: Решение тригонометрических уравнений
Найдите значение \(\theta\), если \(\cos \theta = \text{0,2}\).
Используйте свой калькулятор, чтобы найти \(\theta\)
Чтобы найти \(\theta\), вам нужно будет использовать функцию арккосинуса на вашем калькуляторе. Это работает назад, используя соотношение сторон, чтобы определить угол, который привел к этому соотношению.
Нажмите \(\boxed{\text{SHIFT}} \enspace \boxed{\text{cos}} \enspace \boxed{0} \enspace \boxed{.} \enspace \boxed{2} \enspace \boxed{)} \enspace \boxed{=} \enspace \text{78,46304} \приблизительно \text{78,46}\)
Напишите окончательный ответ
\(\тета \приблизительно \текст{78,46}°\)Рабочий пример 9: Решение тригонометрических уравнений
Найдите значение \(\theta\), если \(3\sin \theta = \text{2,4}\).
Переставить уравнение
Нам нужно изменить уравнение так, чтобы \(\sin \theta\) стояло на одной стороне уравнения.
\начать{выравнивать*} 3\sin\theta&=\text{2,4}\\ \ грех \ тета & = \ гидроразрыва {\ текст {2,4}} {3} \конец{выравнивание*}
Используйте свой калькулятор, чтобы найти \(\theta\)
Чтобы найти \(\theta\), вам нужно будет использовать функцию обратного синуса на вашем калькуляторе.
Это работает
назад, используя соотношение сторон, чтобы определить угол, который привел к этому соотношению.
Нажмите \(\boxed{\text{SHIFT}} \enspace \boxed{\text{sin}} \enspace \boxed{(} \enspace \boxed{2} \enspace \boxed{.} \enspace \boxed{4} \enspace \boxed{\div} \enspace \boxed{3} \enspace \boxed{)} \enspace \boxed{=} \enspace \text{53,1301…} \приблизительно \text{53,13}\).
Напишите окончательный ответ
\(\тета \приблизительно \текст{53,13}°\)При решении тригонометрических уравнений может возникнуть ошибка при попытке вычислить \(\sin\) или \(\cos\) (помните, что функции синуса и косинуса имеют максимальное значение 1). Для этих случаев, когда уравнение не имеет решения.
Если учащиеся допустили математическую ошибку на своем калькуляторе, предложите им подумать о том, что могло произойти. Это
также важно убедиться, что они знают, что они должны записывать не решение, а математическую ошибку, когда это
бывает.
Рабочий пример 10: Решение тригонометрических уравнений
Найдите \(\alpha\): \(3 \sec \alpha = \text{1,4}\).
Преобразование \(\sec\) в \(\cos\)
На калькуляторе нет кнопки «\(\sec\)», поэтому нам нужно преобразовать \(\sec\) в \(\cos\ ) так мы можем найти \(\альфа\).
\начать{выравнивать*} 3 \сек \альфа & = \текст{1,4} \\ \frac{3}{\cos \alpha} & = \text{1,4} \конец{выравнивание*}
Изменить уравнение
Нам нужно изменить уравнение так, чтобы \(\cos \alpha\) стояло на одной стороне уравнения.
\начать{выравнивать*} \frac{3}{\cos \alpha} & = \text{1,4} \\ 3 & = \text{1,4} \cos \alpha \\ \frac{3}{\text{1,4}} & = \cos \alpha \конец{выравнивание*}
Используйте свой калькулятор, чтобы найти \(\alpha\)
Чтобы найти \(\alpha\), вам нужно будет использовать функцию арккосинуса на вашем калькуляторе.
Это работает
назад, используя соотношение сторон, чтобы определить угол, который привел к этому соотношению.
Нажмите \(\boxed{\text{SHIFT}} \enspace \boxed{\text{cos}} \enspace \boxed{3} \enspace \boxed{\div} \enspace \boxed{1} \enspace \boxed{.} \enspace \boxed{4} \enspace \boxed{)} \enspace \boxed{=}\) математическая ошибка
В этом случае мы получаем ошибку при попытке произвести расчет. Это потому, что \(\dfrac{3}{\text{1,4}}\) больше 1, а максимальное значение функции косинуса равно 1. Следовательно, решения нет. Это главное в этом случае написать не решение и не математическую ошибку.
Напишите окончательный ответ
Решения нет.
Учебник Упражнение 5.6
\(\тангенс \тета = \текст{1,7}\)
\begin{выравнивание*} \загар \тета & = \текст{1,7} \\ \тета & = \текст{59,5344…} \\ & \приблизительно \text{59,5}° \end{align*}
\(\sin \theta = \text{0,8}\)
\begin{align*}
\sin \тета & = \text{0,8} \\
\тета & = \текст{53,1301.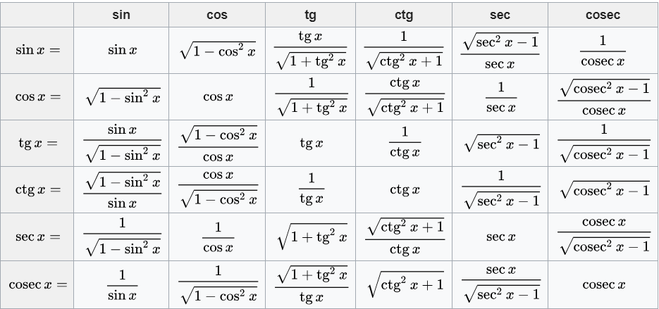
..} \\
& \приблизительно \text{53,1}°
\end{align*}
\(\cos \alpha = \text{0,32}\)
\begin{align*} \cos\alpha&=\text{0,32}\\ \alpha & = \text{71,3370…} \\ & \приблизительно \text{71,3}° \end{выравнивание*}
\(\tan \beta = \text{4,2}\)
\begin{align*} \тан\бета & = \текст{4,2} \\ \бета & = \текст{76,60750…} \\ & \приблизительно \text{76,6}° \end{align*}
\(\tan \theta = 5\frac{3}{4}\)
\begin{align*} \тангенс \тета & = 5\фракция{3}{4} \\ & = \текст{5,75} \\ \тета & = \текст{80,13419…} \\ & \приблизительно \text{80,1}° \end{выравнивание*}
\(\sin \theta = \frac{2}{3}\)
\begin{align*} \sin\theta & = \frac{2}{3} \\ & = \текст{0,666…} \\ \тета & = \текст{41,8103…} \\ & \приблизительно \text{41,8}° \end{align*}
\(\cos \beta = \text{1,2}\)
\begin{align*} \cos\бета & = \text{1,2} \\ & \text{ нет решения } \end{align*}
\(4\cos \theta = 3\)
\начать{выравнивать*}
4\cos\тета&=3\\
\cos\theta & = \frac{3}{4} \\
& = \текст{0,75} \\
\тета & = \текст{41,40962.
..} \\
& \приблизительно \text{41,4}°
\end{align*}
\(\cos 4\theta = \text{0,3}\)
\begin{align*} \cos 4 \тета & = \text{0,3} \\ 4 \тета & = \text{72,54239…} \\ \тета & = \text{18,135599…} \\ & \приблизительно \text{18,1}° \end{выравнивание*}
\(\sin\beta + 2 = \text{2,65}\)
\begin{align*} \sin\beta + 2 & = \text{2,65} \\ \sin\beta&=\text{0,65}\\ \бета & = \текст{40,54160…} \\ & \приблизительно \text{40,5}° \end{align*}
\(2\sin \theta + 5 = \text{0,8}\)
\begin{align*} 2 \sin \тета + 5 & = \text{0,8} \\ 2 \sin \theta & = -\text{4,2} \\ \sin \тета & = -\текст{2,1} \\ & \text{ нет решения } \end{выравнивание*}
\(3 \загар \бета = 1\)
\begin{align*}
3\загар \бета & = 1 \\
\загар \бета & = \фракция{1}{3} \\
& = \текст{0,3333.
..} \\
\бета & = \текст{18,434948…} \\
& \приблизительно \text{18,4}°
\end{align*}
\(\sin 3 \alpha = \text{1,2}\)
\begin{align*} \sin 3 \alpha & = \text{1,2} \\ & \text{ нет решения } \end{выравнивание*}
\(\tan \frac{\theta}{3} = \sin 48°\)
\begin{align*} \tan \frac{\theta}{3} & = \sin48° \\ & = \текст{0,7431…} \\ \frac{\theta}{3} & = \text{36,61769…} \\ \тета & = \текст{109,8530…} \\ & \приблизительно \text{109,9}° \end{align*}
\(\frac{1}{2}\cos 2\beta = \text{0,3}\)
\begin{align*} \frac{1}{2} \cos 2 \beta & = \text{0,3} \\ \cos 2 \бета & = \text{0,6} \\ 2 \бета & = \текст{53,1301…} \\ \бета & = \текст{26,56505…} \\ & \приблизительно \text{26,6}° \end{выравнивание*}
\(2 \sin 3\theta + 1 = \text{2,6}\)
\begin{align*}
2 \sin 3\тета + 1 & = \text{2,6} \\
2 \sin 3\тета & = \text{1,6} \\
\sin 3\тета & = \text{0,8} \\
3 \тета & = \текст{53,1301.
..} \\
\тета & = \text{17,71003…} \\
& \приблизительно \text{17,7}°
\end{align*}
\(\sin(x — y)\)
\begin{align*} \sin(x — y) & = \sin(16 — 36) \\ & = \sin (-20) \\ & = -\текст{0,3420201…} \\ & \ приблизительно — \ текст {0,342} \end{выравнивание*}
\(3\sin x\)
\begin{align*} 3 \sin x & = 3 \sin(16) \\ & = \текст{0,826912…} \\ & \ приблизительно \ текст {0,827} \end{align*}
\(\tan x — \tan y\)
\begin{align*} \tan x — \tan y & = \tan(16) — \tan(36) \\ & = -\текст{0,439797…} \\ & \ приблизительно — \ текст {0,440} \end{align*}
\(\cos x + \cos y\)
\begin{align*} \cos x + \cos y & = \cos(16) + \cos(36) \\ & = \текст{1,77027…} \\ & \ приблизительно \ текст {1770} \end{выравнивание*}
\(\frac{1}{3} \tan y\)
\begin{align*}
\frac{1}{3}\tan y & = \frac{1}{3}\tan(36) \\
& = \текст{0,24218.
..} \\
& \ приблизительно \ текст {0,242}
\end{align*}
\(\text{cosec }(x — y)\)
\begin{align*} \text{cosec}(x — y) & = \text{cosec}(16 — 36) \\ & = \text{cosec} (-20) \\ & = \frac{1}{\sin (-20)} \\ & = -\текст{2,92380…} \\ & \ приблизительно — \ текст {2,924} \end{align*}
\(2\cos x + \cos 3y\)
\begin{align*} 2\cos x + \cos 3y & = 2\cos(16) + \cos(3(36)) \\ & = 2\cos 16 + \cos 108 \\ & = \текст{1,61350…} \\ & \ приблизительно \ текст {1614} \end{align*}
\(\tan(2x — 5y)\)
\begin{align*} \тангенс (2x — 5y) & = \тангенс (2(16) — 5(36)) \\ & = \загар (-148) \\ & = \текст{0,624869…} \\ & \ приблизительно \ текст {0,625} \end{align*}
\(\sin x = \text{0,814}\)
\begin{align*}
\sin x & = \text{0,814} \\
х & = \текст{54,48860.
..} \\
& \приблизительно \text{54,49}°
\end{align*}
\(\sin x = \tan \text{45}°\)
\begin{align*} \sin x & = \tan \text{45}° \\ & = 1 \\ х & = \text{90}° \end{выравнивание*}
\(\tan 2x = \text{3,123}\)
\begin{align*} \tan 2x & = \text{3,123} \\ 2x & = \text{72,244677…} \\ х & = \текст{36,12233…} \\ & \приблизительно \text{36,12}° \end{align*}
\(\tan x = 3 \sin \text{41}°\)
\begin{align*} \tan x & = 3 \sin \text{41}° \\ & = \текст{1,96817…} \\ х & = \текст{63,06558…} \\ & \приблизительно \text{63,07}° \end{выравнивание*}
\(\sin(2x + 45) = \text{0,123}\)
\begin{align*}
\sin(2x + 45°) & = \text{0,123} \\
2x + 45 & = \text{7,06527…} \\
2x & = -\text{37,9347.
..} \\
х & = -\текст{18,9673…} \\
& \приблизительно -\text{18,97}°
\end{align*}
\(\sin(x — 10°) = \cos\text{57}°\)
\begin{align*} \sin(x — 10°) & = \cos\text{57}° \\ & = \текст{0,54463…} \\ х — 10 & = \text{33} \\ х & = \text{43}° \end{выравнивание*}
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найдите точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктический(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | грех((3pi)/4) | |
| 44 | Найти точное значение | желтовато-коричневый (пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найдите точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | соз(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найдите точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | желтовато-коричневый ((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 шт. |