Измерение углов. Транспортир. Виды углов / Геометрия / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Геометрия
- Измерение углов. Транспортир. Виды углов
Нам известно, что при измерении отрезков, мы сравниваем измеряемый отрезок с отрезком, который принят за единицу измерения (1 мм, 1 см, 1 м и т.д.). Аналогично происходит измерение углов: чтобы измерить угол его сравнивают с углом, который принят за единицу измерения — с градусом, записывают так 1°.
Градусная мера угла — это число, которое показывает, сколько раз градус и его части укладываются в данном угле.
Пример:
Градусная мера угла ABC  Говорят: «Угол ABC равен 120 градусам». Пишут: .
Говорят: «Угол ABC равен 120 градусам». Пишут: .
Транспортир — это измерительный инструмент, который используется для измерения и построения углов. Состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы: внутренней и внешней), который разделен на градусы от 0 до .
Для того чтобы измерить угол, необходимо совместить вершину угла с центром транспортира, при этом одна из сторон угла должна пройти через нулевое деление шкалы, тогда вторая сторона угла укажет градусную меру угла.
Пример: Измерим угол ABC, для этого совместим точку B с центром транспортира, и расположим транспортир так, чтобы сторона BC прошла через нулевое деление шкалы (обратите внимание отсчёт угла ведётся по той шкале, через нулевое деление которой пройдет одна из сторон угла: в нашем случае по внутренней шкале).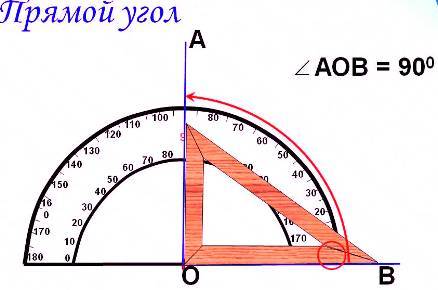
Вторая сторона при этом, как мы видим, проходит через деление шкалы 120, значит: .
Свойства:
- Равные углы имеют равные градусные меры.
- Меньший угол имеет меньшую градусную меру.
- Развернутый угол равен .
- Неразвернутый угол меньше .
- Если луч делит угол на два угла, градусная мера
АОС = АОВ + ВОС.
Виды углов:
- Острый угол — угол, градусная мера которого меньше 90°.
- Прямой угол — угол, градусная мера которого равна 90°.
- Тупой угол — угол, градусная мера которого больше 90°, но меньше 180°.

- Развернутый угол — угол, градусная мера которого равна 180°.
Биссектриса развернутого угла делит его на два угла, градусная мера каждого из которых равна 900.
АОС — развернутый, ОВ — биссектриса, АОВ = ВОС = 900.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Отрезок
Ломаная
Четырехугольники
Единицы измерения площадей. Свойства площадей
Прямоугольник, его периметр и площадь. Ось симметрии фигуры
Квадрат. Периметр и площадь квадрата.
Многоугольники. Правильные многоугольники. Равенство фигур.
Плоскость
Прямая
Луч
Шкалы и координаты
Прямоугольный параллелепипед. Пирамида.
Объем прямоугольного параллелепипеда
Куб. Площадь поверхности куба
Куб. Объем куба
Угол. Обозначение углов
Прямой и развернутый угол
Чертежный треугольник
Треугольник и его виды
Окружность, круг, шар
Цилиндр, конус
Отрезок-xx
Геометрия
Правило встречается в следующих упражнениях:
5 класс
Задание 1654, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1683, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1685, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 2, Мерзляк, Полонский, Якир, Учебник
Номер 11, Мерзляк, Полонский, Якир, Учебник
Номер 13, Мерзляк, Полонский, Якир, Учебник
Номер 308, Мерзляк, Полонский, Якир, Учебник
Номер 309, Мерзляк, Полонский, Якир, Учебник
Номер 311, Мерзляк, Полонский, Якир, Учебник
Номер 1, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 686, Мерзляк, Полонский, Якир, Учебник
Номер 687, Мерзляк, Полонский, Якир, Учебник
Номер 714, Мерзляк, Полонский, Якир, Учебник
Номер 1233, Мерзляк, Полонский, Якир, Учебник
Номер 1236, Мерзляк, Полонский, Якир, Учебник
Номер 1283, Мерзляк, Полонский, Якир, Учебник
Задание 287, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1352, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1534, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1545, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 759, Мерзляк, Полонский, Якир, Учебник
Урок математики в начальной школе.
 Тема: «Градус. Измерение углов транспортиром»
Тема: «Градус. Измерение углов транспортиром»Тип урока: формирование новых знаний.
Цели и задачи:
- проверить знания учащихся по теме “Угол”;
- познакомить с новой единицей измерения (градус) и прибором для измерения углов — транспортиром;
- составить алгоритм измерения угла;
- используя алгоритм измерения угла, научиться измерять разные виды углов;
- составить алгоритм для построения угла;
- используя алгоритм построения угла, научиться строить разные виды углов;
- классифицировать углы по видам;
Оборудование: презентация SMART Notebook к уроку по заданной теме, транспортир, угольники, карточки для самостоятельной работы
Проблемный вопрос: как измерить углы с помощью транспортира? (Какие нужно выполнять условия, чтобы точно измерить градусную меру угла транспортиром?)
Ход урока
I. Организационный момент.
Организационный момент.
II. Название темы урока, постановка цели.(слайд 1)
Введение
Французский писатель XIX столетия Анатоль Франц однажды заметил, что: “Учиться можно только весело. Чтобы переваривать эти знания, нужно поглощать эти знания с аппетитом”.
Давайте сегодня на уроке будем следовать этому совету. Будем активны, будем поглощать знания с большим желанием, потому что они пригодятся вам в дальнейшей жизни. (слайд 2)
III. Устная работа.
1. Математическая карусель. (слайд 2)
2. Назовите углы, изображенные на рисунке. Найдите среди этих углов прямые и развернутые. (слайд 3)
3. Какие углы образуют на циферблате часов минутная и часовая стрелки в:
а) 6 ч; б) 13 ч; в) 15 ч; г) 16 ч 30 мин; д) 8 ч 15 мин? (слайд 5)
IV. Объяснение нового материала.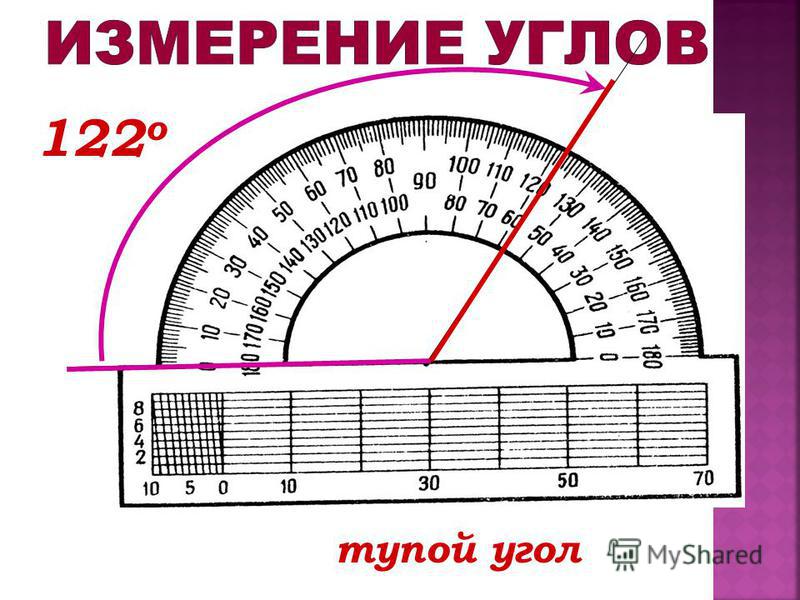
В соответствии с п. 5.2 учебника, рассмотреть вопросы;
Единица измерения углов.
Классификация углов по градусной мере.
Специальный измерительный прибор — транспортир. Сравнить шкалы транспортира со шкалой линейки, обращая внимание на сходства и различия: цена наименьшего деления на линейке — 1 мм, на транспортире — 1°, большее деление на линейке — 10 мм, на транспортире — 10°. ( слайды 6-8)
V. Доклад на тему “ История возникновения транспортира”.
(рассказ заранее подготовленного ученика) (слайд 9)
4. Измерение углов с помощью транспортира.
Дать алгоритм измерения углов с помощью транспортира (сдайды 11,12)
VI. Формирование умений и навыков. (слайды 13)
РТ, часть 2, № 49, 50, 51;
№49
- < AOC=400
- <AOM=1200
- < AOB =760
- <AOK =1650
№50 самостоятельно
- АОС=900,
- <AOB=450,
- <AOD=1300
№ 51
- <A= 600;
- <B=550 ;
- <C= 850 ;
- <D= 300 ;
- <E= 1100 ;
- <F=1500 .

2. У, № 478, 481 (а).
Физкультминутка “Истинно — ложно” (слайд 14)
Если утверждение верно, ученики должны встать, если ложно — присесть, руки на пояс: угол, равный 45°, — острый;
- угол, равный 170°, — острый;
- угол, равный 89°, — тупой;
- угол, равный 55°, — прямой;
- угол, равный 100°, — тупой;
- угол, равный 1°, — острый;
- угол, равный 137°, — острый;
- угол, равный 70°, — острый;
- угол, равный 890, — развернутый;
- угол, равный 155°, — прямой;
- угол, равный 100°, — тупой;
- угол, равный 1°,— прямой.
VII. Самостоятельная работа по карточкам (слайд 15,16)
Измерить выделенные углы.
Класс делится на 2 группы мальчиков и девочек. Мальчикам раздаются карточки с
“ракетами”, а девочкам с
“солнышком”.
VIII. Итоги урока. (слайд 17)
ВЫЧЕРКНИТЕ НЕВЕРНЫЕ ВЫСКАЗЫВАНИЯ
1) Углы измеряют с помощью линейки.
2) Углы измеряют с помощью транспортира.
3) Единицы измерения углов — килограммы.
4) Единицы измерения углов — градусы.
5) 1о равен 1/180 части развернутого угла.
6) Развернутый угол имеет градусную меру 180°.
7) Острый угол меньше развернутого.
8) Прямой угол имеет градусную меру 90°.
9) Тупой угол больше развернутого.
10) Острый угол меньше прямого.
11) Прямой угол больше тупого.
12) Тупой угол больше прямого, но меньше развернутого.
IХ. Домашнее задание. У, № 479, 481 (б), 482 (б), 289 (в). (слайд 18)
Линейки, рейсшины для черчения, транспортиры, угольники, трафареты и лекала
- Показать все
Похожие товары
Сортировать по цене ↓ ↑ популярности ↓ ↑
×
Линейка офицерская, гибкая, прозрачная. Необходима при создании графических изображений и построении карт. Содержит 65 специальных элемента и линейку 20 см с отливной
шкалой.
Необходима при создании графических изображений и построении карт. Содержит 65 специальных элемента и линейку 20 см с отливной
шкалой.
001221
Линейка 20см офицерская, арт.СТ-ТТ-02
26.55 р.
Купить
+ 1 шт
+ 5 шт
+ 10 шт
шт. × 26.55 р.
Итого: 26.55 р.
В корзину
Показать отфильтрованные товары ()
Дополнительные товары
цена от 26.55 р.
001221
Линейка 20см офицерская, арт.СТ-ТТ-02
26.55 р.
Купить
+ 1 шт
+ 5 шт
+ 10 шт
шт. × 26.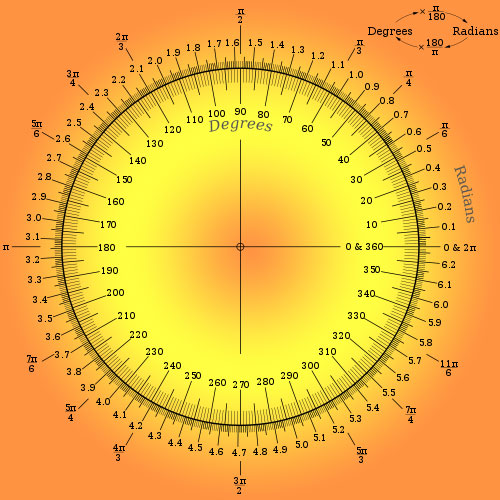 55 р.
55 р.
Итого: 26.55 р.
В корзину
Линейка выполнена из сертифицированного полистирола с гладкой глянцевой поверхностью. Предназначена для чертежных работ. На линейку нанесена ровная, четкая миллиметровая шкала. Линейка имеет безопасные закруглённые углы.
005431
Линейка 30см, пластмассовая, черная, Стамм арт.ст-лн-35, ст.20
43.66 р.
Купить
+ 1 шт
+ 5 шт
+ 10 шт
шт. × 43.66 р.
Итого: 43.66 р.
В корзину
Показать отфильтрованные товары ()
Дополнительные товары
цена от 43. 66 р.
66 р.
005431
Линейка 30см, пластмассовая, черная, Стамм арт.ст-лн-35, ст.20
43.66 р.
Купить
+ 1 шт
+ 5 шт
+ 10 шт
шт. × 43.66 р.
Итого: 43.66 р.
В корзину
×
Линейка яркого флуоресцентного цвета с гладкой глянцевой поверхностью. Предназначена для чертежных работ. Имеет безопасные закругленные углы. Изготовлена из сертифицированного полистирола.
013872
Линейка 20см, пластмассовая, флюоресц., Стамм, ЛФ20, ст.1
24.57 р.
Купить
+ 1 шт
+ 5 шт
+ 10 шт
шт. × 24.57 р.
× 24.57 р.
Итого: 24.57 р.
В корзину
Показать отфильтрованные товары ()
Дополнительные товары
цена от 24.57 р.
013872
Линейка 20см, пластмассовая, флюоресц., Стамм, ЛФ20, ст.1
24.57 р.
Купить
+ 1 шт
+ 5 шт
+ 10 шт
шт. × 24.57 р.
Итого: 24.57 р.
В корзину
30-сантиметровая линейка Attache выполнена из стали. Линейка применяется для чертежных и измерительных работ и имеет двойную градацию шкалы (сантиметр, дюйм). Ширина линейки
25 мм. Толщина стали — 0,8 мм.
Ширина линейки
25 мм. Толщина стали — 0,8 мм.
005873
Линейка 30см, металлическая, Attache, ст.10
87.02 р.
Купить
+ 1 шт
+ 5 шт
+ 10 шт
шт. × 87.02 р.
Итого: 87.02 р.
В корзину
Показать отфильтрованные товары ()
Дополнительные товары
цена от 87.02 р.
005873
Линейка 30см, металлическая, Attache, ст.10
87.02 р.
Купить
+ 1 шт
+ 5 шт
+ 10 шт
шт. × 87.02 р.
Итого: 87.02 р.
В корзину
×
Пластиковая линейка с закругленными безопасными углами. Длина — 30 см. цвет — прозрачный
000739
Линейка 30см, пластмассовая, прозрачная, арт.СТ-ЛН-31,32,33, ст.20
23.40 р.
Купить
+ 1 шт
+ 5 шт
+ 10 шт
шт. × 23.40 р.
Итого: 23.40 р.
В корзину
Показать отфильтрованные товары ()
Дополнительные товары
цена от 23.40 р.
000739
Линейка 30см, пластмассовая, прозрачная, арт.СТ-ЛН-31,32,33, ст.20
23.40 р.
Купить
+ 1 шт
+ 5 шт
+ 10 шт
шт. × 23.40 р.
× 23.40 р.
Итого: 23.40 р.
В корзину
×
Деревянный треугольник предназначен для чертежных работ.
023001
Угольник 11см, 45*45, деревянный, ст.1
45.28 р.
Купить
+ 1 шт
+ 5 шт
+ 10 шт
шт. × 45.28 р.
Итого: 45.28 р.
В корзину
Показать отфильтрованные товары ()
Дополнительные товары
цена от 45.28 р.
023001
Угольник 11см, 45*45, деревянный, ст. 1
1
45.28 р.
Купить
+ 1 шт
+ 5 шт
+ 10 шт
шт. × 45.28 р.
Итого: 45.28 р.
В корзину
×
Предназначены для чертежных работ.
026308
Угольник 23см, Можга, ст.1
45.12 р.
Купить
+ 1 шт
+ 5 шт
+ 10 шт
шт. × 45.12 р.
Итого: 45.12 р.
В корзину
Показать отфильтрованные товары ()
Дополнительные товары
цена от 45. 12 р.
12 р.
026308
Угольник 23см, Можга, ст.1
45.12 р.
Купить
+ 1 шт
+ 5 шт
+ 10 шт
шт. × 45.12 р.
Итого: 45.12 р.
В корзину
×
Безупречное качество пластика. Безопасные закругленные углы. Легкий корпус, ровная четкая миллиметровая шкала. Удобный держатель. Длина — 30 см. Цвет — прозрачный флуоресцентный
016853
Линейка 30см, пластмассовая, флюоресц, с держателем, Стамм, ст.20
74.51 р.
Купить
+ 1 шт
+ 5 шт
+ 10 шт
шт. × 74. 51 р.
51 р.
Итого: 74.51 р.
В корзину
Показать отфильтрованные товары ()
Дополнительные товары
цена от 74.51 р.
016853
Линейка 30см, пластмассовая, флюоресц, с держателем, Стамм, ст.20
74.51 р.
Купить
+ 1 шт
+ 5 шт
+ 10 шт
шт. × 74.51 р.
Итого: 74.51 р.
В корзину
×
Деревянная линейка для выполнения различных чертежных работ.
013229
Линейка 50см, деревянная, арт.ЛП, ст.50
65.93 р.
Купить
+ 1 шт
+ 5 шт
+ 10 шт
шт.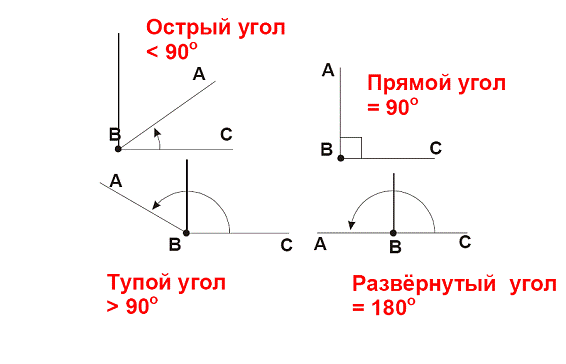 × 65.93 р.
× 65.93 р.
Итого: 65.93 р.
В корзину
Показать отфильтрованные товары ()
Дополнительные товары
цена от 65.93 р.
013229
Линейка 50см, деревянная, арт.ЛП, ст.50
65.93 р.
Купить
+ 1 шт
+ 5 шт
+ 10 шт
шт. × 65.93 р.
Итого: 65.93 р.
В корзину
30-сантиметровая линейка Attache Line выполнена из металла. Линейка — удобный инструмент для измерительных целей. Эргономичная вырубка вдоль линейки позволяет удобно использовать
ее. Двойная градация шкалы (сантиметр и дюйм)
Двойная градация шкалы (сантиметр и дюйм)
022757
Линейка 30см, металлическая, Attache Line, ст.20
140.07 р.
Купить
+ 1 шт
+ 5 шт
+ 10 шт
шт. × 140.07 р.
Итого: 140.07 р.
В корзину
Показать отфильтрованные товары ()
Дополнительные товары
цена от 140.07 р.
022757
Линейка 30см, металлическая, Attache Line, ст.20
140.07 р.
Купить
+ 1 шт
+ 5 шт
+ 10 шт
шт. × 140.07 р.
Итого: 140.07 р.
В корзину
Далее >
Углов
Углы используются в повседневной жизни. Инженеры и архитекторы используют углы для конструкций, дорог, зданий и спортивных сооружений. Спортсмены используют углы, чтобы повысить их производительность. Плотники используют углы, чтобы сделать стулья, столы и диваны. Художники используют свои знания ракурсов для набросков портретов и картины.
Если две прямые встречаются (или пересекаются) в одной точке, то образуется угол .
Точка пересечения линий называется 9.0004 вершина .
Ниже показан угол.
Линии AB и AC пересекаются в точке A , образуя
угол. Точка A является вершиной угла, и линии, которые
встречаются, образуя угол, называются плечами угла .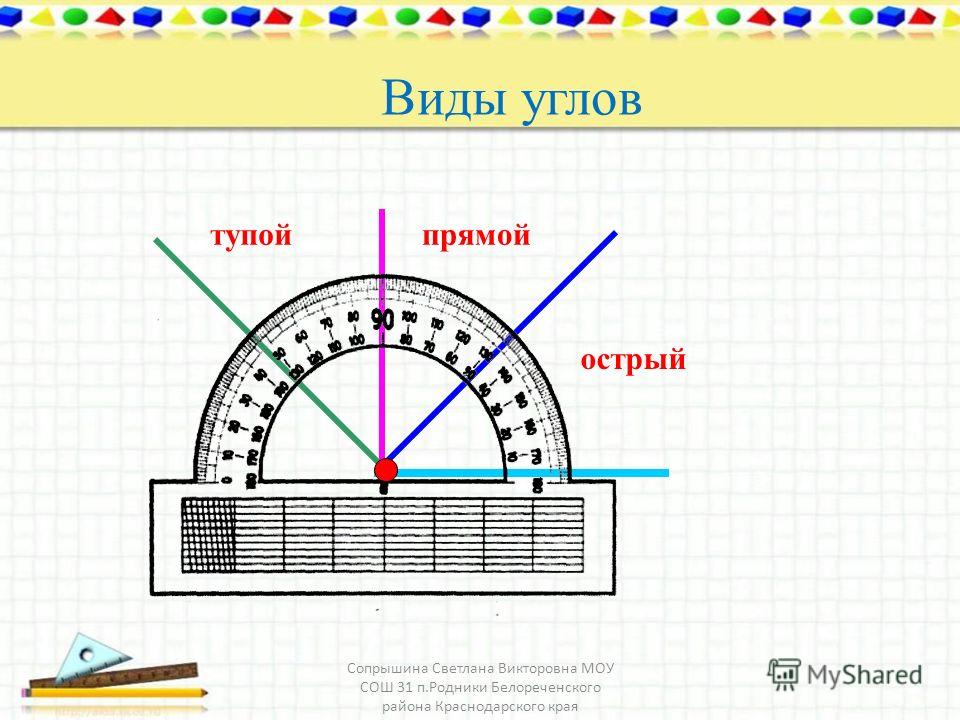
Именование углов
Размер угла
Величина поворота от одного плеча угла к другому называется размер угла .
Величина угла измеряется в градусах ; и используемый символ
представлять степень. В полном обороте (или круге) 360.
Примечание:
градуса определяется таким образом, что угол одного полного оборота (или окружность) составляет 360 градусов.
Измерение углов
Транспортир используется для измерения углов. В этом разделе мы будем
рассмотреть использование транспортира, который имеет форму полукруга и два
шкалы отмечены от 0 до 180.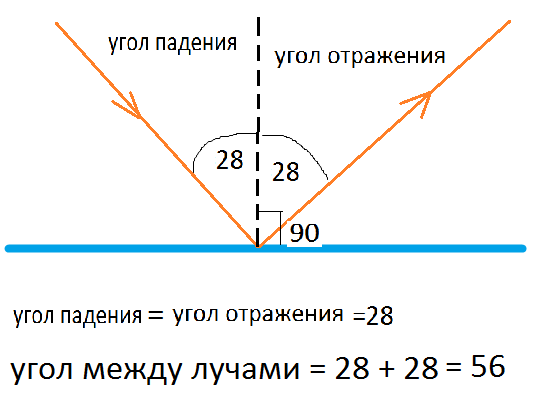
Две шкалы облегчают нам измерение
углы смотрят в разные стороны.
Чтобы измерить угол ABC , поместите транспортир на
угла так, чтобы центр транспортира находился прямо над углом
вершина, В; а базовая линия транспортира проходит по плечу, BA ,
угла.
Внутренней шкалой измеряем угол ABC , так как плечо AB проходит через ноль внутренней шкалы . Следующий внутренней шкалы вокруг транспортира, мы находим, что другое плечо, до н.э. , проходит через внутреннюю шкалу в точке 60. Итак, размер угла ABC равен 60 градусов. Запишем это так:
Чтобы измерить размер угла PQR , поместите транспортир на
угла так, чтобы центр транспортира находился прямо над углом
вершина, Q ; а базовая линия транспортира проходит по плечу PQ ,
угла.
Используем внешнюю шкалу для измерения угла PQR , так как плечо PQ проходит через ноль внешней шкалы . Следующий внешней шкалы вокруг транспортира, мы находим, что другой рычаг, QR , проходит через внешнюю шкалу под углом 120. Таким образом, размер угла PQR равен 120 градусов. Запишем это так:
Типы уголков
Углы классифицируются по размеру.
Острый угол больше 0 и меньше 90.
A прямой угол ровно равен 90.
Обратите внимание, что прямой угол отмечен на схеме маленьким квадратом.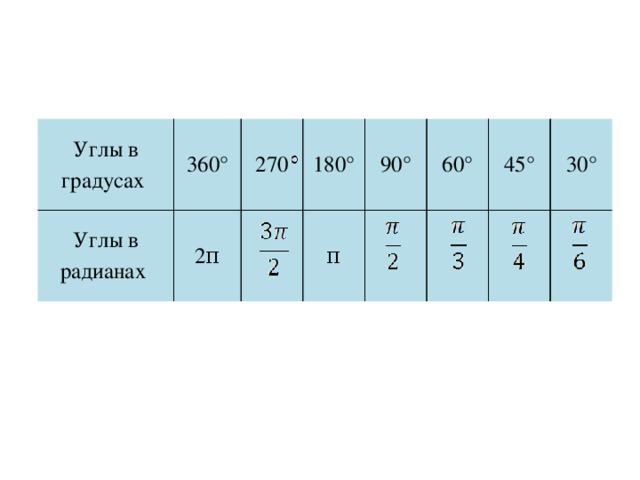
Тупой угол больше 90 и меньше 180.
Прямой угол ровно равен 180.
Угол рефлекса больше 180 и меньше 360.
Перигон (или оборот ) — это угол, который точно равен
360.
Измерение углов отражения
Напомним, что:
Транспортир можно использовать для измерения величины острого угла (между 0 и 90) и тупой угол (от 90 до 180).
Теперь мы будем использовать транспортир для измерения угла рефлекса PQR .
Чтобы измерить угол рефлекса PQR , вытяните рычаг PQ до A , чтобы сформировать угол PQA , который представляет собой прямой угол. Затем измерьте размер
угол AQR и добавить 180.
Затем измерьте размер
угол AQR и добавить 180.
Основные термины
точка, угол, вершина, плечи угла, величина угла, градусы, транспортир, внутренний шкала, внешняя шкала, острый угол, прямой угол, тупой угол, прямая угол, угол рефлекса, перигон, оборот
Углы и градусы, Скачать PDF бесплатно
Описание
Цели урока и обзор: Углы и градусы учит учащихся, как измерять угол в градусах. Урок иллюстрирует размер одного градуса и объясняет, почему в круге 360 градусов. Он также демонстрирует с иллюстрациями, как использовать транспортир для измерения угла. К концу урока учащиеся поймут, что угол, который проходит через n углов по одному градусу, называется угловой мерой n градусов. Данный урок предназначен для учащихся 4-х и 5-х классов.
Порядок занятий в классе
Каждый план урока содержит страницу порядка занятий, на которой изложено пошаговое руководство, которому необходимо следовать. Вам не обязательно точно следовать инструкции. Руководство поможет вам организовать урок и подробно расскажет, когда раздавать рабочие листы. В синем поле также указана информация, которая может оказаться полезной. В этой области вы найдете цели урока, государственные стандарты и количество занятий, которые должны пройти урок. Кроме того, в нем описываются необходимые материалы, а также то, что и как нужно подготовить заранее. Для этого урока вам понадобятся бумажные тарелки, маркеры и транспортиры. Чтобы заранее подготовиться к этому уроку, вы можете скопировать раздаточные материалы, собрать материалы и поместить центральную точку на каждой бумажной тарелке для выполнения задания.
Вам не обязательно точно следовать инструкции. Руководство поможет вам организовать урок и подробно расскажет, когда раздавать рабочие листы. В синем поле также указана информация, которая может оказаться полезной. В этой области вы найдете цели урока, государственные стандарты и количество занятий, которые должны пройти урок. Кроме того, в нем описываются необходимые материалы, а также то, что и как нужно подготовить заранее. Для этого урока вам понадобятся бумажные тарелки, маркеры и транспортиры. Чтобы заранее подготовиться к этому уроку, вы можете скопировать раздаточные материалы, собрать материалы и поместить центральную точку на каждой бумажной тарелке для выполнения задания.
Варианты для урока
В этот урок включен раздел «Варианты для урока», в котором перечислены несколько предложений по занятиям, которые можно добавить к уроку, или замены тем, которые уже есть в уроке. Одним из дополнительных дополнений к этому уроку является предложение учащимся нарисовать углы друг для друга, чтобы измерить их с помощью транспортира. Вы также можете предложить учащимся нарисовать картинку, используя разные ракурсы. Наконец, вы также можете предложить учащимся исследовать, почему в круге 360 градусов и какая история стоит за определением этого измерения.
Вы также можете предложить учащимся нарисовать картинку, используя разные ракурсы. Наконец, вы также можете предложить учащимся исследовать, почему в круге 360 градусов и какая история стоит за определением этого измерения.
Заметки учителя
На странице заметок учителя есть строки, которые вы можете использовать для добавления собственных заметок при подготовке к этому уроку.
УГЛЫ И ГРАДУСЫ ПЛАН УРОКА СОДЕРЖАНИЕ СТРАНИЦ
Углы и градусы
План урока «Углы и градусы» включает две страницы содержания. Урок начинается с некоторой базовой информации об углах и градусах. В нем говорится, что углы чаще всего измеряются в градусах, но также могут быть измерены в радианах. Однако основное внимание в этом уроке уделяется тому, как измерять углы в градусах. Математические градусы отличаются от градусов, которые мы используем для измерения температуры. Математические градусы измеряют дугу окружности, образованную двумя лучами с общей вершиной. Один полный оборот, или полный круг, составляет всего 360 градусов. Символ градуса (°) обозначает слово «градус». Один градус равен 1/360 части полного круга. Затем урок включает рисунок, показывающий, насколько велик один градус.
Символ градуса (°) обозначает слово «градус». Один градус равен 1/360 части полного круга. Затем урок включает рисунок, показывающий, насколько велик один градус.
Учащиеся узнают, почему в окружности 360 градусов. Древние календари, такие как персидский календарь, имели 360 дней в году. Они нанесли звезды на карту и заметили, что каждый день они вращаются вокруг Полярной звезды на один градус. Вот почему круги имеют 360 градусов! Использование 360 удобно, потому что оно легко делится на множество чисел, таких как 2, 3, 4 и 5 (и многие другие!). Это означает, что существует множество факторов, что, в свою очередь, означает, что базовые геометрические расчеты выполнять легко. Затем урок включает в себя несколько изображений, чтобы помочь учащимся запомнить названия различных градусов и углов.
Далее учащиеся узнают, что мы измеряем углы с помощью инструмента, называемого транспортиром, который может измерять от 0 до 180 градусов. Урок включает в себя несколько схем транспортиров, чтобы проиллюстрировать их различные особенности и то, как использовать их для измерения углов. Чтобы измерить угол с помощью транспортира, вы просто выстраиваете одну сторону угла в нижней части транспортира, а затем следите за другим углом до числа, чтобы найти измерение. Другой способ найти меру угла — использовать дробные части окружности.
Чтобы измерить угол с помощью транспортира, вы просто выстраиваете одну сторону угла в нижней части транспортира, а затем следите за другим углом до числа, чтобы найти измерение. Другой способ найти меру угла — использовать дробные части окружности.
Наконец, урок снова отмечает, что весь круг равен 360°. Чтобы найти угловые измерения равных частей круга, вы делите 360 на количество равных сегментов. Например, чтобы найти угол одной трети круга, вы делите 360 на общее количество частей (три), а затем умножаете на количество частей, для которых вы хотите найти угол (один). Градус измерения одной трети окружности равен 120°. Уравнение, которое вы используете, чтобы вычислить это, как указано в уроке, это (360 ÷ 3) = 120 x 1 = 120°. Урок также включает второй пример.
ПЛАН УРОКА «УГОЛЫ И ГРАДУСЫ» РАБОЧИЕ ЛИСТЫ
План урока «Углы и градусы» включает три рабочих листа: рабочий лист, практический рабочий лист и тест. Вы можете обратиться к руководству на странице процедур в классе, чтобы определить, когда раздавать каждый рабочий лист.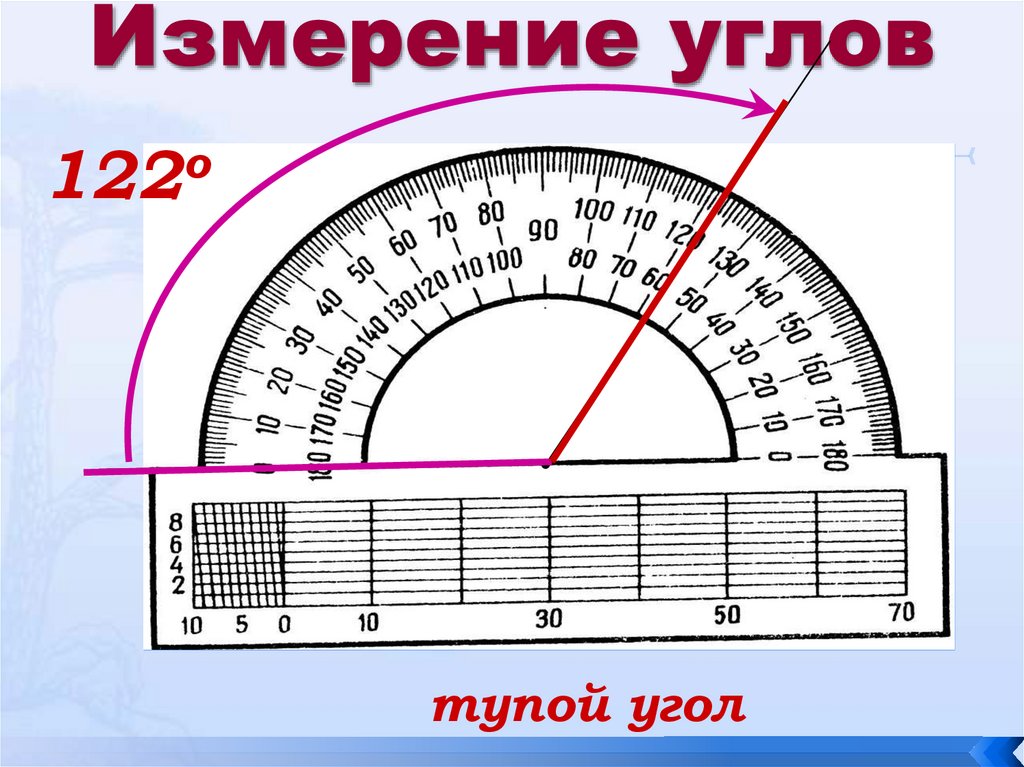
БУМАЖНАЯ ТАРЕЛКА ДЛЯ ЗАДАНИЙ
При выполнении заданий ученики будут следовать вашим устным инструкциям. Во-первых, вы должны спросить учащихся, знают ли они, как измерить окружность. Затем вы должны сообщить им, что полный круг измеряется 360 °, что окружности и углы измеряются в градусах, а угловые измерения измеряют распространение лучей в круге. Это хорошая идея, чтобы связать эту идею с часами. Затем вы дадите каждому ученику бумажную тарелку с отмеченной центральной точкой, попросите их сложить ее пополам и как можно точнее обвести эту линию маркером. Затем вы спросите учащихся, чему равна половина круга, если полный круг равен 360°. Учащиеся обозначают полукруг как 180°, а затем снова складывают его пополам. Они пометят эти четыре раздела 90° после того, как вы спросите их, какой будет половина 180°.
Для продвинутых групп вы можете продолжить упражнение с восемью секциями, попросив учащихся обозначить эти 45°. Вы можете продолжить этот шаблон и попросить учащихся подумать об определении закономерности увеличения количества частей путем умножения на два при делении измерения угла на два.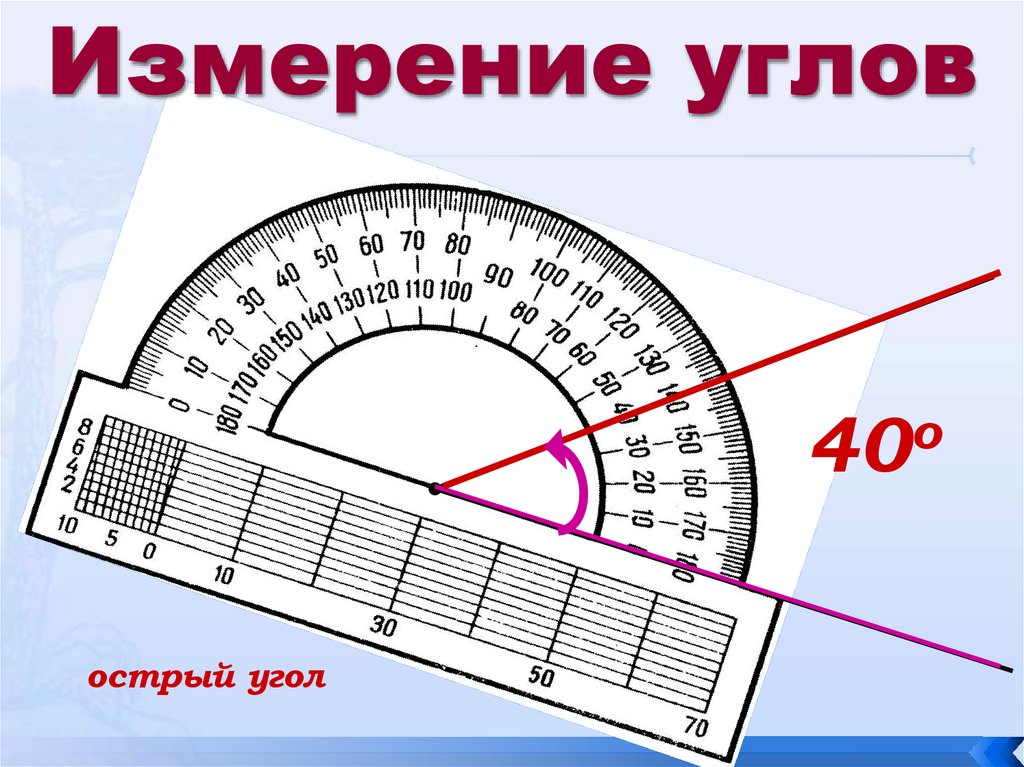
ПРОТРАКТОР ПРАКТИЧЕСКИЙ ЛИСТ
Практический лист состоит из двух разделов. В первом разделе учащиеся будут измерять заданные углы с помощью транспортира. Затем они попросят друга или члена семьи нарисовать восемь различных углов, а затем измерить эти углы с помощью транспортира.
ВИКТОРИНА ПО УГЛАМ И ГРАДУСАМ
Этот урок также включает викторину. Для викторины учащиеся сначала сопоставят угол с предполагаемым градусом. Далее они будут смотреть на диаграммы углов и оценивать степень каждого угла на глаз. Этот тест проверит понимание учащимися материала урока.
Ключи для ответов на рабочий лист
Этот план урока включает ключи для ответов на рабочий лист и тест. Для рабочего листа не предусмотрен ключ ответа. Если вы решите предоставить своим ученикам страницы урока в формате PDF, вам нужно будет сохранить новый файл, в котором эти страницы отсутствуют. В противном случае вы можете просто распечатать соответствующие страницы и сохранить их для справки при оценивании заданий.
Знакомство с углами | SkillsYouNeed
После того как вы усвоили идею точек, линий и плоскостей, следующее, что нужно рассмотреть, это то, что происходит, когда две линии или лучи встречаются в точке, образуя между ними угол .
Углы используются в геометрии для описания таких фигур, как многоугольники и многогранники, а также для объяснения поведения линий, поэтому полезно ознакомиться с некоторыми терминами, а также с тем, как мы измеряем и описываем углы.
Что такое угол?
Углы образуются между двумя лучами, исходящими из одной точки:
Углы обычно рисуются в виде дуги (части круга), как указано выше.
Свойства углов
Углы измеряются в градусах , что является мерой окружности или вращения.
Полный оборот, при котором вы возвращаетесь лицом в том же направлении, составляет 360°. Следовательно, полуокружность равна 180°, а четверть окружности или прямой угол равен 9°. 0°.
0°.
Два или более угла на прямой в сумме дают 180°. На приведенной выше диаграмме круг слева разделен на три сектора, углы зеленого и белого секторов равны 90°, что в сумме дает 180°.
На рисунке справа видно, что углы a и b также составляют в сумме 180°. Когда вы смотрите на диаграмму таким образом, это легко увидеть, но на практике это также удивительно легко забыть.
Обозначение разных углов
Угол меньше 90° считается острым , а угол больше 90°, но меньше 180° считается тупым .
Угол, равный 180°, называется прямым . Углы больше 180° называются рефлекторными углами.
На циферблате часов можно демонстрировать разные ракурсы. Часовая стрелка часов движется по кругу по мере прохождения времени в течение дня. Угол поворота выделен зеленым цветом.
Противоположные углы: пересекающиеся линии
При пересечении двух прямых противоположные углы равны. В этом случае не только а и а совпадают, но, конечно, а и b в сумме дают 180°:
Пересечения с параллельными прямыми: частный случай
Наша страница Введение в геометрию вводит понятие параллельных линий: линий, которые всегда идут бок о бок и никогда не пересекаются, как железнодорожные пути.
Углы вокруг любых прямых, пересекающих параллельные прямые, также обладают некоторыми интересными свойствами.
Если две параллельные прямые (А и В) пересекает третья прямая (С), то угол, под которым пересекаются пересекающиеся прямые, будет одинаковым для обеих параллельных прямых.
Два угла a и два угла b называются соответствующими.
Вы также сразу увидите, что a и b в сумме дают 180°, так как они лежат на прямой.
Угол с, который, как вы поняли из предыдущего раздела, идентичен углу а, считается альтернативным с.
Z и F Углы
c и a называются z-углами , потому что, если вы проследите линию от вершины c до низа a, она образует форму буквы z (обозначена красным на диаграмме выше). ).
a и a называются F-уголками , потому что линия образует F-образную форму от нижней части верхнего угла a вниз и вокруг нижней части нижнего угла a (на диаграмме выделена зеленым цветом)
Измерение углов
A транспортир обычно используется для измерения углов.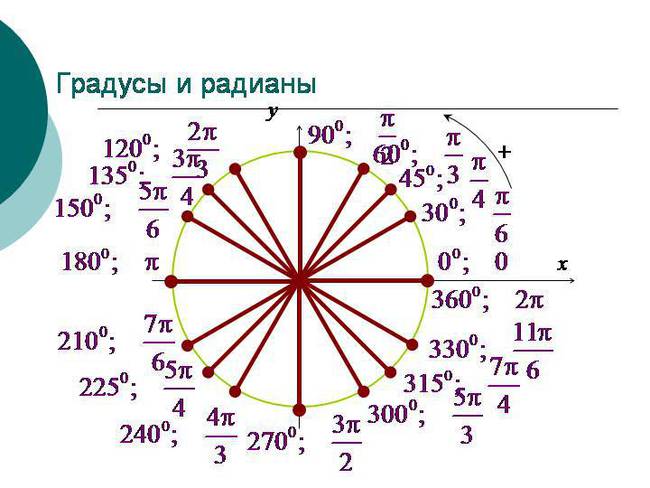 Транспортиры обычно имеют круглую или полукруглую форму и сделаны из прозрачного пластика, поэтому их можно накладывать на фигуры, нарисованные на листе бумаги, что позволяет измерить угол.
Транспортиры обычно имеют круглую или полукруглую форму и сделаны из прозрачного пластика, поэтому их можно накладывать на фигуры, нарисованные на листе бумаги, что позволяет измерить угол.
В этом примере показано, как использовать транспортир для измерения трех углов треугольника, но тот же метод применим и к другим фигурам или любым углам, которые вы хотите измерить.
- Совместите центральную отметку на основании транспортира с вершина, или точка, в которой пересекаются линии. Треугольник имеет три вершины, по одной на каждый измеряемый угол.
- Большинство транспортиров имеют двунаправленную шкалу, что означает, что вы можете выполнять измерения в любом направлении. Убедитесь, что вы используете правильный масштаб — вы сможете легко определить, больше или меньше ваш угол 90 °, и, следовательно, используйте правильный масштаб. Если вы не уверены, вернитесь к нашему разделу, посвященному именованию углов.
В этом примере записанные углы A=90° B=45° и C=45°.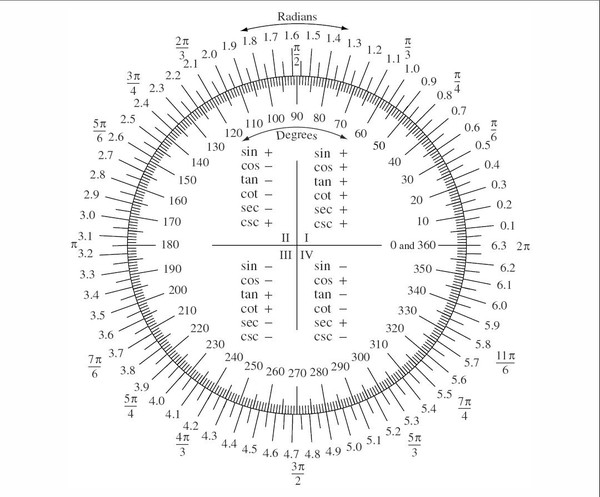
Многоугольники часто определяются своими внутренними углами, а сумма внутренних углов зависит от количества сторон. Например, сумма внутренних углов треугольника всегда равна 180°. Подробнее об этом читайте на нашей странице Polygons .
Градусы или радианы?
Когда нам нужно измерить или описать угол, мы обычно используем «градусы» в качестве единицы измерения. Однако очень редко можно встретить углы, упомянутые в 9.0269 радиан .
Радиан — это международная стандартная единица измерения углов (СИ), которая используется во многих областях науки и математики.
Выше мы сказали, что полный оборот углов через дугу окружности равен 360°. Оно также равно 2π радианам, где π (пи) — специальное число, равное (приблизительно) 3,142 (подробнее о π см. на нашей странице Special Numbers and Concepts ).
Один радиан равен 360/2π = 57,3°. Мы также используем пи, когда нам нужно вычислить площадь или окружность круга, или объем сферы (подробнее об этом читайте на нашей странице 9).