Углы в радианы: Онлайн калькулятор: Перевод градусов в радианы

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )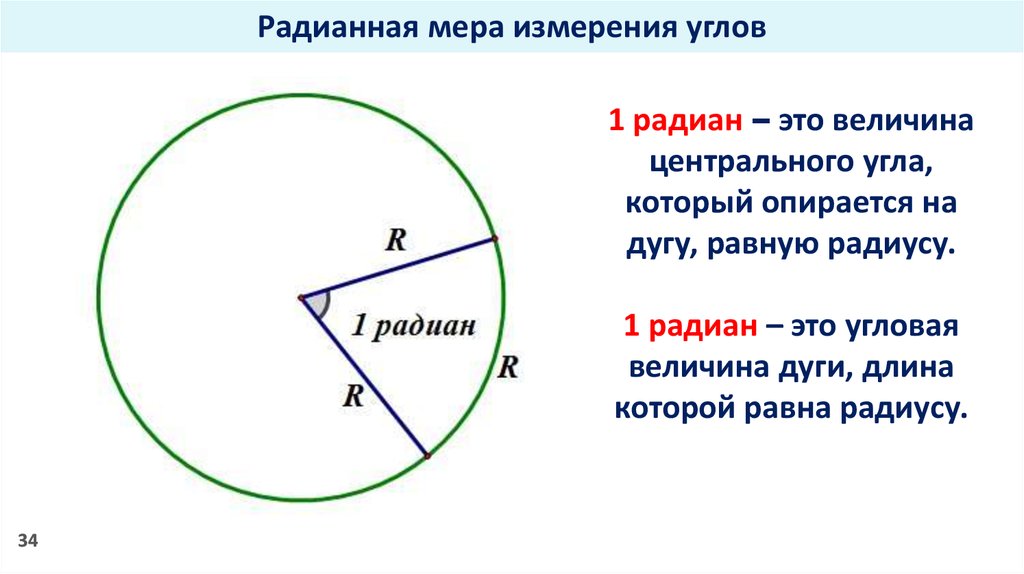
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значение
sin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значение tan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )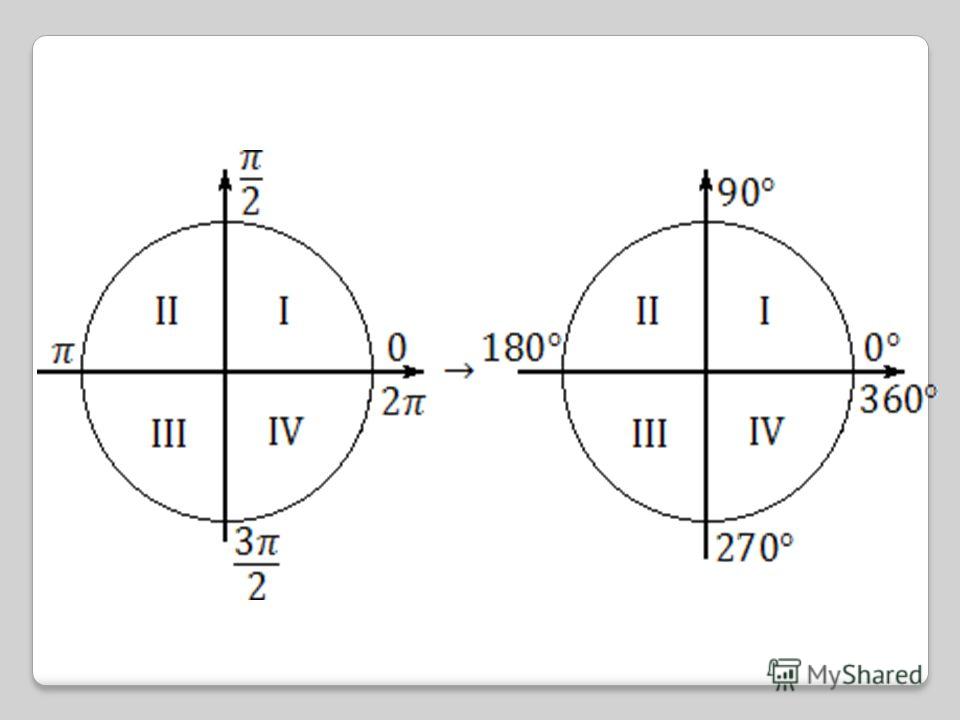
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Как конвертировать углы из градусов в радианы в Excel

В Excel есть встроенные тригонометрические функции, которые облегчают поиск косинуса, синуса и тангенса прямоугольного треугольника — треугольника, содержащего угол, равный 90 градусам.

Единственная проблема состоит в том, что эти функции требуют углов, выраженных в радианах, а не в градусах . В то время как радианы, единица углов, являются законным способом измерения углов, основанных на радиусе круга, они не являются чем-то, с чем большинство людей работают на регулярной основе.

Чтобы помочь среднему пользователю электронной таблицы обойти эту проблему, в Excel есть функция RADIANS , которая позволяет легко преобразовывать градусы в радианы.

Эти инструкции относятся к Excel 2019, 2016, 2013, 2010 и Excel для Office 365.

РАДИАНЫ Синтаксис и аргументы функций

Синтаксис функции относится к макету функции и включает в себя имя функции, скобки и аргументы.

Синтаксис для функции RADIANS :

= РАДИАНЫ (угол)

Аргумент Angle — это угол в градусах, который вы хотите преобразовать в радианы; он может быть введен в градусах или в виде  ссылки на ячейку для расположения этих данных в вашей рабочей таблице Excel.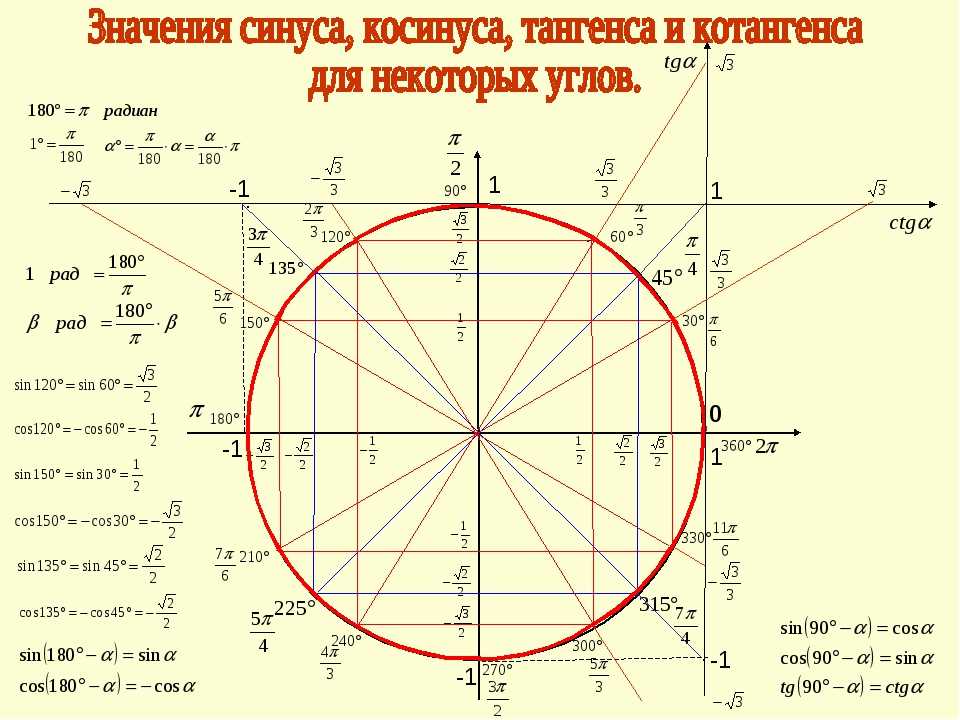

Пример функции Excel RADIANS

В этом примере функция RADIANS используется для преобразования угла в 45 градусов в радианы. Информация охватывает шаги, используемые для ввода  функции RADIANS в ячейку B2 примера рабочего листа.

= РАДИАНЫ (А2)
= РАДИАНЫ (45)

Варианты ввода функции включают в себя:

  • Ввод полной функции в ячейку B2 , как показано в ячейке C3
    выше
  • Выбор функции и ее аргументов с помощью диалогового окна « Функция»

Хотя можно ввести полную функцию вручную, многим людям легче использовать диалоговое окно «Функция», поскольку оно заботится о вводе синтаксиса функции, такого как скобки и разделители запятых, между аргументами.

Использование функционального блока (Formula Builder на Mac) для RADIANS

  1. Нажмите на ячейку  B2  на рабочем листе — вот куда пойдет функция.

  2. Нажмите на  вкладку » Формулы  » в   меню ленты .

  3. Выберите  Math & Trig  на ленте, чтобы открыть раскрывающийся список функций.

  4. Нажмите на  RADIANS  в списке, чтобы вызвать диалоговое окно Function .

  5. Нажмите на линию угла .

  6. Нажмите на ячейку A2 на рабочем листе, чтобы ввести ссылку на ячейку в качестве аргумента функции.

  7. Нажмите  Готово,  чтобы завершить функцию — ответ  0,785398163 ,  который выражен в радианах под 45 градусами, появляется в ячейке B2 .

  8. Если ваш рабочий лист показывает меньше чисел справа от десятичной точки, вы можете отформатировать ячейку, чтобы отобразить больше.

Вы можете вводить данные непосредственно в диалоговое окно, а не в ссылки на ячейки, но это усложняет обновление формул и функций.

Использование функции PI () для получения угла в радианах

Альтернативой, как показано в ячейке C4 примера изображения, является умножение угла на функцию PI () и затем деление результата на 180, чтобы получить угол в радианах.

Это выглядит так:

= А2 * ПИ () / 180

4.1: Радианы и градусы — Mathematics LibreTexts

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    3324
    • Майкл Коррал
    • Schoolcraft College

    До сих пор мы использовали градусы в качестве единицы измерения углов. Однако есть и другой способ измерения углов, часто более удобный.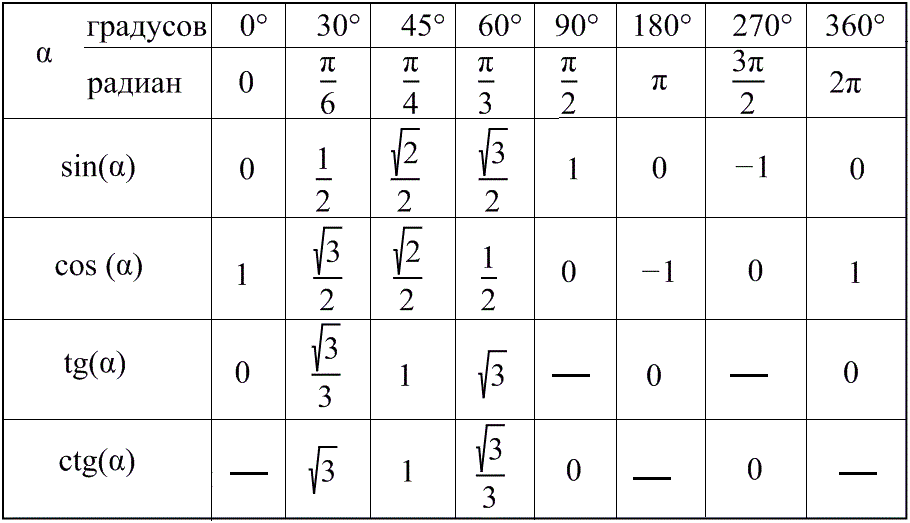 Идея проста: свяжите центральный угол окружности с дугой, которую он пересекает.

    Рассмотрим круг радиуса \(r>0 \), как на рис. 4.1.1. Из геометрии вы узнали, что длина окружности \(C\) круга равна \(C = 2\;\pi\;r \), где \(\pi = 3,14159265… \).

    Рисунок 4.1.1 Угол \(θ\) и дуга, на которую опирается \(\overparen{AB}\) на окружности \(C = 2πr\) 9\circ ~=~ 2\pi ~~\text{радианы}}
     \]

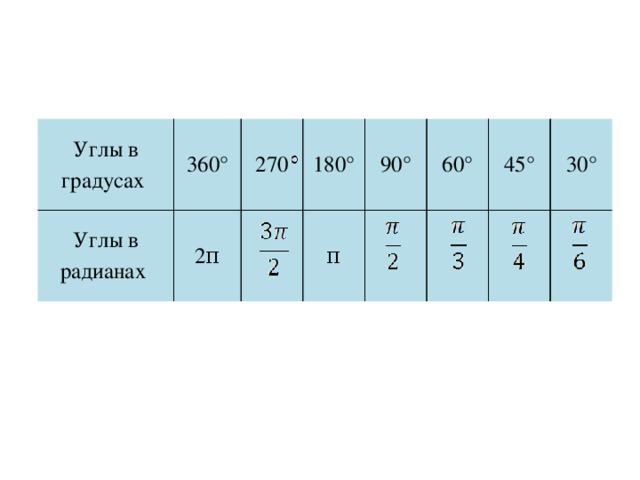
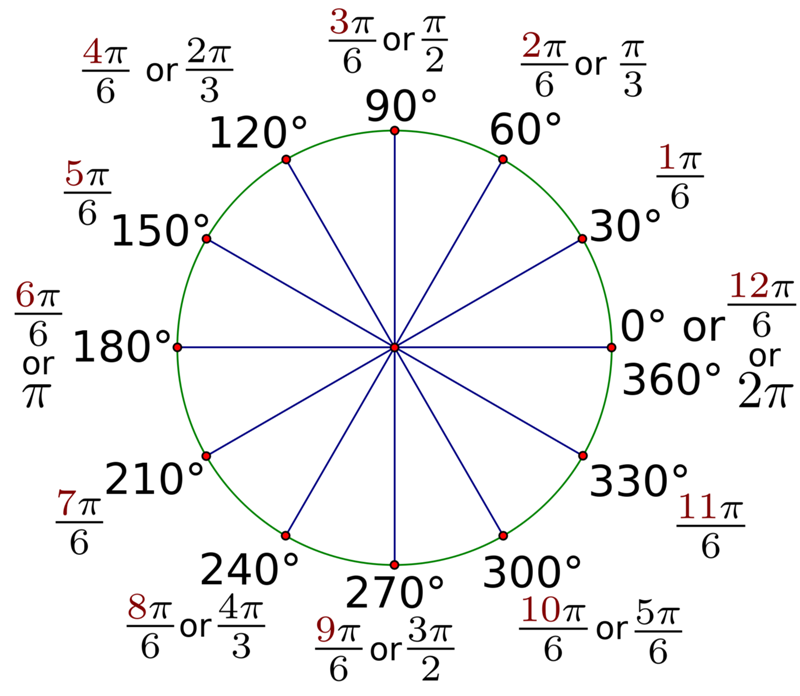
    Приведенное выше соотношение дает нам простой способ преобразования градусов в радианы:

    \[\begin{alignat}{3}
    \textbf{Градусы в радианы:}&\quad
    x~~\text{градусы}\quad&=\quad \left( \frac{\pi}{180} \ ;\cdot\; x \right)
    ~~\text{радианы}\label{eqn:deg2rad}\\
    \textbf{радианы в градусы:}&\quad
    x~~\text{радианы}\quad&= \quad \left( \frac{180}{\pi} \;\cdot\; x \right)
    ~~\text{градусы}\label{eqn:rad2deg} 9\circ = \frac{2\pi}{360} = \frac{\pi}{180} \) радиан, затем умножив обе части на \(x \). Уравнение \ref{eqn:rad2deg} получается аналогичным образом путем деления обеих частей уравнения \ref{4. 1} на \(2\pi \), а затем умножения обеих частей на \(x \).

    Утверждение \(\theta = 2\pi \) радианы обычно сокращается как \(\theta = 2\pi \) rad или просто \(\theta = 2\pi \), когда ясно, что мы используем радианы. Когда угол задается как некоторое число, кратное \(\pi \), вы можете предположить, что используемые единицы измерения — радианы. 9\циркуляр ~.
    \номер\]

    Рисунок 4.1.2

    Формально радиан определяется как центральный угол в окружности радиуса \(r \), которая пересекает дугу длины \(r \), как на рисунке 4.1.2. Это определение не зависит от выбора \(r\) (представьте себе изменение размера на рис. 4.1.2).

    Одна из причин, по которой используются радианы, заключается в том, что масштаб меньше, чем для градусов. Один оборот в радианах равен \(2\pi \приблизительно 6,283185307\), что намного меньше, чем \(360\), число градусов в одном обороте. Меньший масштаб приводит к тому, что графики тригонометрических функций (которые мы обсудим в главе 5) имеют одинаковые масштабы для горизонтальной и вертикальной осей. Другая причина заключается в том, что часто в физических приложениях используются переменные с точки зрения длины дуги, что делает радианы естественным выбором.

    По умолчанию большинство научных калькуляторов используют градусы для ввода углов. На многих калькуляторах есть кнопка с надписью \(\fbox{\(DRG\)}\) для переключения между режимом градусов (D), режимом радиана (R) и режимом градусов (G). На некоторых графических калькуляторах, таких как TI-83, есть кнопка \(\fbox{\(MODE\)}\) для переключения между градусами и радианами. Убедитесь, что ваш калькулятор находится в правильном режиме ввода углов от до , иначе ваши ответы, скорее всего, будут далекими. Например, 9Кнопки {-1}\)}\) в радианном режиме, конечно, дадут вам угол в виде десятичной дроби, а не выражения в терминах \(\pi \).

    Вы также должны знать, что математические функции во многих языках программирования используют радианы, поэтому вам придется писать свои собственные преобразования углов.

    Эта страница под названием 4.1: Радианы и градусы распространяется в соответствии с лицензией GNU Free Documentation License 1.3 и была создана, изменена и/или курирована Майклом Корралом с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

    1. Наверх
      • Была ли эта статья полезной?
      1. Тип изделия
        Раздел или Страница
        Автор
        Майкл Коррал
        Лицензия
        ГНУ ФДЛ
        Версия лицензии
        1,3
        Показать страницу TOC
        нет
      2. Теги
        1. источник@http://www. mecmath.net/trig/index.html

      Перевести ° в рад | градусы в радианы

      Количество: 1 градус (°) угла
      Равен: 0,017 радиан (рад) в углу

      Преобразование градусов в радиан в шкале угловых единиц.

      ПЕРЕКЛЮЧЕНИЕ :   из радианов в градусы наоборот.

      ПРЕОБРАЗОВАТЬ: между другими единицами измерения угла — полный список.

      Сколько радиан в 1 градусе? Ответ: 1° равен 0,017 рад

      0,017 рад превращается в 1 чего?

      Число радиан 0,017 рад преобразуется в 1 °, один градус. Это РАВНОЕ значение угла, равное 1 градусу, но в альтернативной единице измерения угла в радианах.

      °/rad angle conversion result
      From Symbol Equals Result Symbol
      1 ° = 0.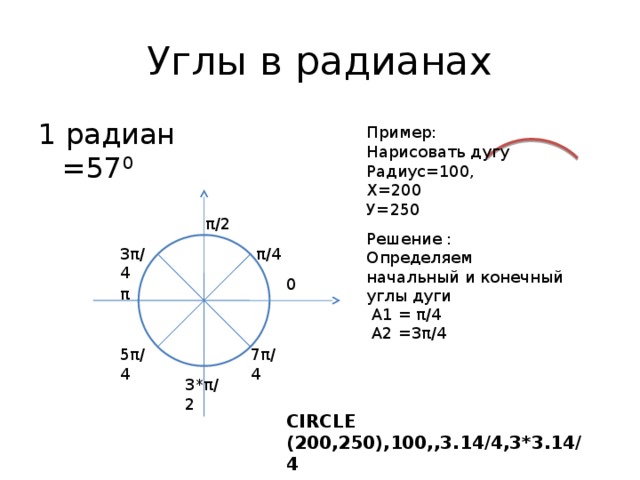 017 rad

      Таблица преобразования —

      градусов в радиан

      1 градус в радиан = 0,017 рад

      2 градуса в радиан = 0,035 рад

      3 градуса в радиан = 0,092 рад0032

      4 градуса с радианами = 0,070 рад

      5 градусов до радиан = 0,087 рад

      6 градусов до радиан = 0,10 рад

      7 градусов до радиан = 0,12 рад

      8 градусов до радианов = 0,14 радиции = 0,12

      8 градусов с радианами = 0,14 Радиана 9003 2 900 31 900 900 900 900 900 900. Радиан = 0,16 рад

      10 градусов до радиан = 0,17 рад

      11 градусов до радиан = 0,19 рад

      12 градусов до радиан = 0,21 рад

      13 градусов с радианами = 0,23 рад

      14 градусов до радиана = радиции = радиан = радиан = радиан = радиции = радиан = радиан = радиан = радиан = радиан = радиции = радиан = радиан = радиан = радиции = радиции = радиции = радиции = радицы = радиции = радиции = 0,23 Радиан

      14 градусов = радиции = радиции = радиции = радиции = 0,23 Радиан

      14 градусов = радиции = радиции = радиции = радиции = 0,23 Радиан

      14 градусов. 0032

      15 градусов в радианы = 0,26 рад

      Категория : главное меню • меню угла • градусы

      Преобразовать угол градусов (°) и в 9 радиан (3 рад) в обратном порядке. градусов.

      Углы

      Этот калькулятор основан на преобразовании двух угловых единиц. Угол состоит из двух лучей (как стороны угла, имеющие общую вершину или иначе называемые конечной точкой). Некоторые относятся к измерениям вращения — сферические углы измеряются длинами дуг, указывающими из центра, плюс радиус. Чтобы получить полный набор единиц измерения угла на одной странице, попробуйте конвертер Multiunit, в который встроены все варианты единиц измерения угла. Страница с отдельными угловыми единицами.

      Первая единица: градус (°) используется для измерения угла.
      Секунды: радиан (rad) — единица измерения угла.

      ВОПРОС :
      15 ° = ? рад

      ОТВЕТ :
      15 ° = 0,26 рад

      Аббревиатура или префикс для степени:
      °
      Сокращение для радиана:
      рад

      Другие приложения для этого углового калькулятора .

      No related posts.

      Добавить комментарий

      Ваш адрес email не будет опубликован. Обязательные поля помечены *