Нормальные конусности и углы
Нормальные конусности и углыГлавконструктор
3D сканирование и
конструкторские услуги
ru en
Источник: ГОСТ 8593-81
Конусность К есть отношение разности диаметров двух поперечных сечений конуса к расстоянию между ними.
Уклон «i» есть отношение разности размеров двух поперечных сечений к расстоянию между ними.
Таблица 1. Углы конусности
|
Конусность К |
Угол конуса 2а |
Угол уклона а |
Исходное значение (К или 2а) |
|
1:200 |
0°7’11» |
0°8’36» |
1:200 |
|
1:100 |
0°34’23» |
0°17’11» |
1:100 |
|
1:50 |
1°8’46» |
0°34’23» |
1:50 |
|
1:30 |
1°54’35» |
0°57’17» |
1:30 |
|
1:20 |
2°51’51» |
1°25’56» |
1:20 |
|
1:15 |
3°49’6″ |
1°54’33» |
1:15 |
|
1:12 |
4°46’19» |
2°23’9″ |
1:12 |
|
1:10 |
5°43’29» |
2°51’45» |
1:10 |
|
1:8 |
7°9’10» |
3°34’35» |
1:8 |
|
1:7 |
8°10’16» |
4°5’8″ |
1:7 |
|
1:5 |
11°25’16» |
5°42’38» |
1:5 |
|
1:3 |
18°55’29» |
9°27’44» |
1:3 |
|
1:1,866 |
30° |
15° |
30° |
|
1:1,207 |
45° |
22°30′ |
45° |
|
1:0,866 |
60° |
30° |
60° |
|
1:0,652 |
75° |
37°30′ |
75° |
|
1:0,500 |
90° |
45° |
90° |
|
1:0,289 |
120° |
60° |
120° |
К оглавлению
Уклон и Конусность — Определение, обозначение на чертеже, формула расчёта уклона и конусности ChertimVam.
 Ru
RuИногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.
Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ.
Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения.
Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов.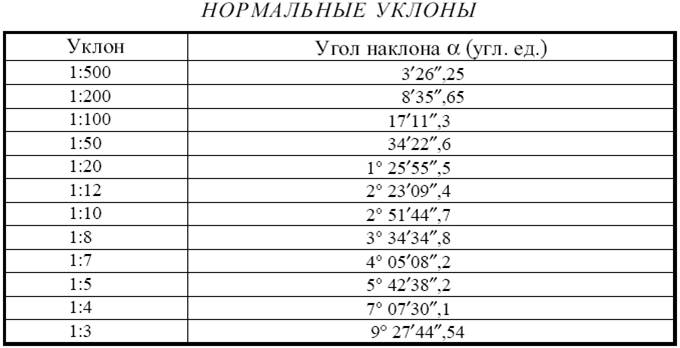 Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.
Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.
Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона. Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.
Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах.
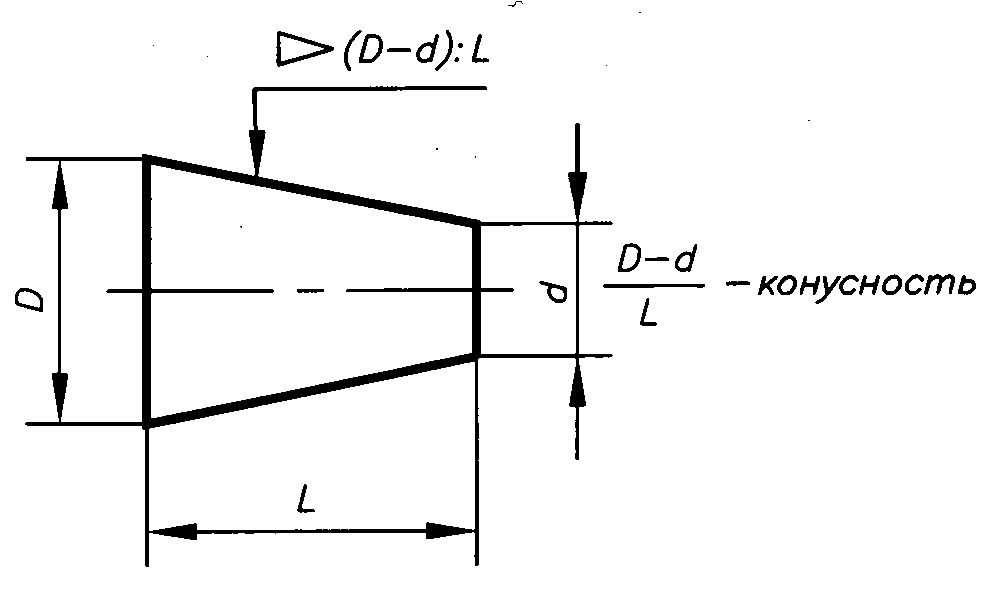
Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.
Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.
Обозначение конусности на чертежах. Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с . Также на чертеже допускается указывать и дополнительные размеры, как справочные.
Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.
Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах.
Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20.
Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.
Расчет уклона и общих уклонов в архитектуре
Архитекторы постоянно предоставляют информацию об уклоне на своих чертежах, используя градиенты, градусы или проценты в зависимости от приложения. Например, крыши отмечаются с помощью уклонов, а поперечные уклоны тротуаров обычно обозначаются в градусах. Полезно понять, как рассчитать каждый метод.
- Расчет градиента уклона
- Расчет уклона в процентах
- Расчет уклона в градусах
- Таблица общих уклонов в архитектуре
- Уклоны крыши
- Крыши с малым уклоном
- Крыши с крутым уклоном
- Откосы водопроводных труб
Существует три различных способа указания наклона поверхности относительно горизонтальной плоскости: градусы, градиент и проценты.
Расчет градиента уклона
Расчет градиента уклонаГрадиенты уклона записываются в виде Y:X, где Y — единица подъема, а X — протяженность. Оба числа должны использовать одни и те же единицы измерения. Например, если вы путешествуете на 3 дюйма по вертикали и на 3 фута (36 дюймов) по горизонтали, уклон составит 3:36 или 1:12. Это читается как «один из двенадцати наклонов».
Расчет процента уклона
Расчет процента уклонаПроцент уклона рассчитывается почти так же, как градиент. Переведите рост и пробег в одни и те же единицы, а затем разделите рост на пробег. Умножьте это число на 100, и вы получите процент наклона. Например, подъем 3 дюйма, разделенный на длину 36 дюймов = 0,083 x 100 = уклон 8,3%.
Вычисление уклона в градусах
Вычисление уклона в градусах Самый сложный способ вычисления уклона — в градусах, и он требует немного математики средней школы. Тангенс данного угла (в градусах) равен подъему, деленному на пробег.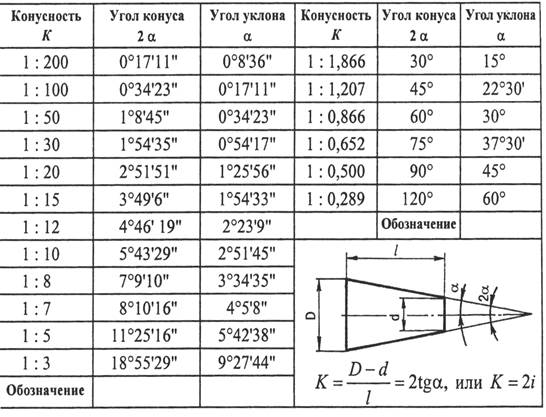 Следовательно, арктангенс подъема, деленный на разбег, даст угол.
Следовательно, арктангенс подъема, деленный на разбег, даст угол.
Таблица общих уклонов в архитектуре
В таблице ниже показаны некоторые распространенные уклоны. Полы с уклоном 1:20 не требуют поручней, но все, что круче 1:20, считается пандусом и требует наличия поручней. Пандусы с наклоном 1:12 — это максимальный уклон, разрешенный кодами ADA, и для них требуются поручни. Федеральные коды ADA указывают, что максимальный поперечный уклон доступного маршрута составляет 1:48, что составляет чуть более 2%. Однако мы видели некоторые юрисдикции, которые допускают максимальный поперечный уклон 1:50.
В следующей таблице представлены распространенные уклоны по уклону (градусы и проценты рассчитаны):
| Градиент | Градусы | Проценты |
|---|---|---|
| 4,76° | 8,33% | |
| 1 : 20 | 2,86° | 5% |
| 1 : 48 | 1,19° | 2,08% | 90 055
| 1 : 50 | 1,15° | 2% |
Далее у нас есть некоторые общие наклоны в градусах (градиент и процент вычисляются): 057
Наконец, вот список некоторых распространенных наклонов в процентах (градусы и градусы рассчитываются):0055
Уклоны крыши
Уклоны крыши идентифицируются с использованием описанного выше градиентного метода, где подъем варьируется, но уклон обычно равен 12. На некоторых очень крутых крышах вы можете увидеть инвертированный уклон, так что уклон меняется, но подъем сохраняется равным 12.
На некоторых очень крутых крышах вы можете увидеть инвертированный уклон, так что уклон меняется, но подъем сохраняется равным 12.
Крыши с малым уклоном
Крыши с малым уклоном имеют уклон 3:12 или меньше. Они должны иметь мембранную систему крыши для обеспечения водонепроницаемости.
| НАКЛОН КРЫШИ | ГРАДУСЫ | ПРОЦЕНТЫ |
|---|---|---|
| 1/4 : 12 | 9 0059 1,19°2,08% | |
| 1/2 : 12 | 2,39° | 4,17% |
| 1 : 12 | 4,76° | 8,3% |
| 2 : 12 | 9,46° | 16,67% |
| 3 : 12 | 14,04° | 25% |
Крыши с крутым уклоном
Все, что выше 3:12, считается крутой крышей и может быть покрыто с металлическими панелями, черепицей или черепицей — эти крыши не пропускают воду и не считаются водонепроницаемыми.
| НАКЛОН КРЫШИ | ГРАДУСЫ | ПРОЦЕНТЫ |
|---|---|---|
| 4 : 12 | 900 59 18,43°33,33% | |
| 5 : 12 | 22,62° | 41,67% |
| 6 : 12 900 60 | 26,57° | 50% |
| 7 : 12 | 30,26° | 58,33% |
| 8 : 12 | 33,69° | 66,67% |
| 9 : 12 | 36,87° | 90 059 75%|
| 10 : 12 | 39,81° | 83,33% |
| 11 : 12 | 42,51° | 91,67% |
| 12 : 12 | 45° | 100% |
 На самом деле крыша может быть почти вертикальной.
На самом деле крыша может быть почти вертикальной.Уклоны водопроводных труб
Как обсуждалось в нашей статье об уклонах труб, уклоны дренажных и канализационных труб, как правило, минимальны. Идея состоит в том, чтобы поддерживать поток воды и твердых частиц. Используются три общих уклона, на которые ссылаются в Международном сантехническом кодексе. 91 /4″ на фут
Статья обновлена: 29 ноября 2022 г.
Помогите сделать Archtoolbox лучше для всех. Если вы обнаружили ошибку или устаревшую информацию в этой статье (даже если это всего лишь незначительная опечатка), сообщите нам об этом.
Если вы обнаружили ошибку или устаревшую информацию в этой статье (даже если это всего лишь незначительная опечатка), сообщите нам об этом.
Полезные инструменты для архитекторов и проектировщиков зданий
Калькулятор центрального угла. Найдите длину дуги, радиус, центральный угол
Автор: Jasmine J Mah0003 Содержание:
- Что такое центральный угол?
- Откуда берется формула центрального угла?
- Калькулятор угла окружности в пересчете на пиццу
- Сколько кусочков пиццы с центральным углом в 1 радиан можно отрезать от круглой пиццы?
- Бонусное задание – Как далеко Земля перемещается в каждое время года?
- Часто задаваемые вопросы
Вы когда-нибудь задумывались, как найти центральный угол окружности? Калькулятор центрального угла здесь, чтобы помочь; единственные переменные, которые вам нужны, это длина дуги и радиус.
Читайте дальше, чтобы узнать определение центрального угла и как использовать формулу центрального угла.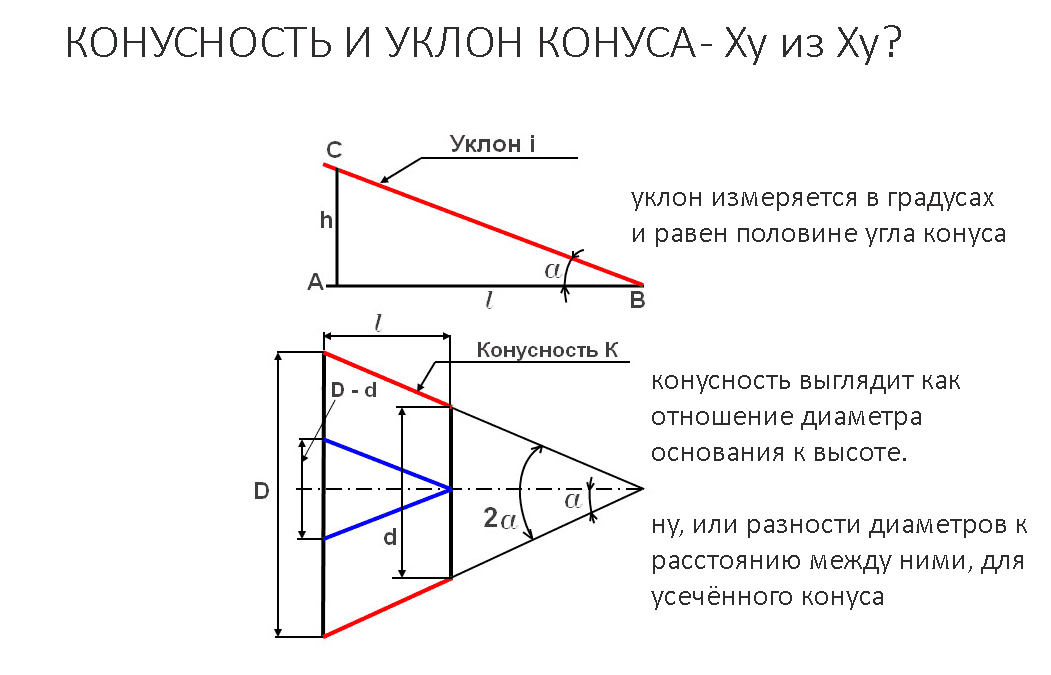
Что такое центральный угол?
Центральный угол — это угол с вершиной в центре круга, стороны которого выходят на окружность. Вы можете представить, что центральный угол находится на кончике куска пиццы в большой круглой пицце.
Центральный угол окружности можно найти по формуле:
θ = L / r
, где θ — центральный угол в радианах, L — длина дуги, а r — радиус.
Откуда берется формула центрального угла?
Простота формулы центрального угла проистекает из определения радиана. радиан — это единица углового размера, где 1 радиан определяется как центральный угол ( θ ), длина дуги которого равна радиусу ( L = r ).
Калькулятор угла окружности в терминах пиццы
Поскольку математика может сделать людей голодными, мы могли бы лучше понять центральный угол в терминах пиццы. Хотите верьте, хотите нет, но пицца отлично подходит для объяснения математики круга, как вы можете видеть на нашем калькуляторе размера пиццы Каким был бы центральный угол для куска пиццы, если длина корки (LLL) была равна радиусу ( ррр)?
Поскольку задача определяет L=rL = rL=r, и мы знаем, что 111 радиан определяется как центральный угол, когда L=rL = rL=r, мы можем видеть, что центральный угол равен 111 радианам.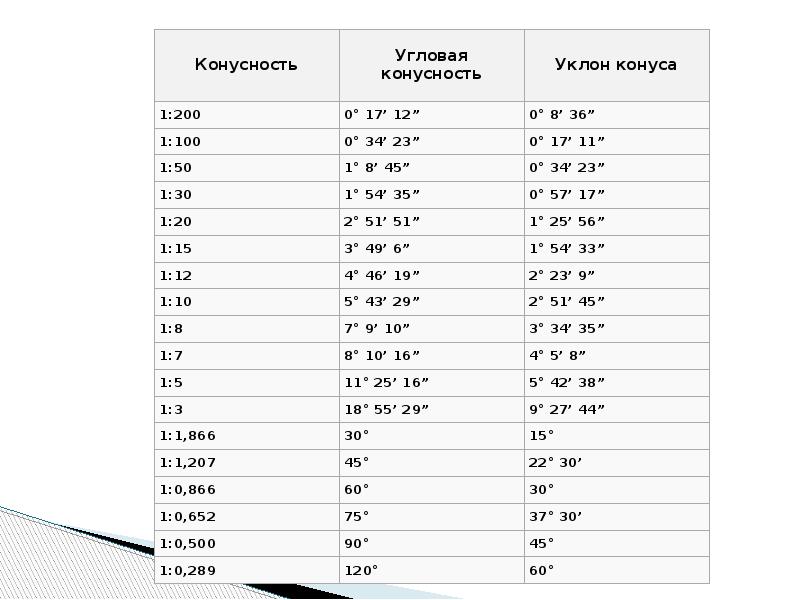 Мы также могли бы использовать формулу центрального угла следующим образом:
Мы также могли бы использовать формулу центрального угла следующим образом:
θ=Lr=LL=1 рад\begin{split} \theta&=\frac{L}{r}\\[1em] &=\frac{L}{L}\\[1em] &=1\ \mathrm{рад} \end{split}θ=rL=LL=1 рад
Сколько кусочков пиццы с центральным углом в 1 радиан вы могли бы отрезать от круглой пиццы?
Мы знаем, что в полной круглой пицце центральные углы всех ломтиков в сумме составляют 2π радиан = 360°. Поскольку каждый срез имеет центральный угол 111 радиан, нам потребуется 2π/1=2π2\pi / 1 = 2\pi2π/1=2π срезов или 6 286 286,28 срезов, чтобы заполнить полный круг.
Мы приходим к тому же ответу, если рассматривать эту задачу в терминах корочки для пиццы: мы вычисляем длину окружности 2πr2\pi r2πr. Так как длина корочки = радиус, то по периметру пиццы поместится 2πr/r=2π2\pi r / r = 2\pi2πr/r=2π корок.
Теперь, если вы все еще голодны, взгляните на калькулятор площади сектора, чтобы рассчитать площадь каждого кусочка пиццы!
Бонусное задание – Как далеко Земля перемещается в каждое время года?
Попробуйте использовать калькулятор центрального угла в обратном порядке, чтобы решить эту проблему. Земля примерно 1490,6 млн км от Солнца. Если Земля проходит около четверти своей орбиты каждый сезон, сколько километров Земля проходит каждый сезон (например, с весны до лета)?
Земля примерно 1490,6 млн км от Солнца. Если Земля проходит около четверти своей орбиты каждый сезон, сколько километров Земля проходит каждый сезон (например, с весны до лета)?
Давайте подойдем к этой проблеме шаг за шагом:
Упростите задачу, предположив, что орбита Земли круговая ( Орбита Земли на самом деле эллиптическая и постоянно меняется ). В этой модели Солнце находится в центре круга, а орбита Земли — это окружность.
Радиус — это расстояние от Земли и Солнца: 149,6149,6149,6 млн км.
Центральный угол равен четверти окружности: 360°/4=90°360\градус / 4 = 90\градус360°/4=90°.
Используйте калькулятор центрального угла, чтобы найти длину дуги .
Вы можете сами попробовать произвести окончательный расчет, изменив формулу следующим образом:
L=θ⋅rL = \theta \cdot rL=θ⋅r 96\ \mathrm{км} \end{split}L=1,57⋅149,6×106 км=234,9×106 км
Если предположить, что по идеально круговой орбите Земля проходит примерно 234,9 млн км каждый сезон!
Часто задаваемые вопросы
Как найти центральный угол окружности?
Чтобы найти центральный угол окружности, используйте формулу:
θ = L / r
где:
-
θ— центральный угол в радианах; -
L— Длина дуги; и -
r— Радиус окружности.

