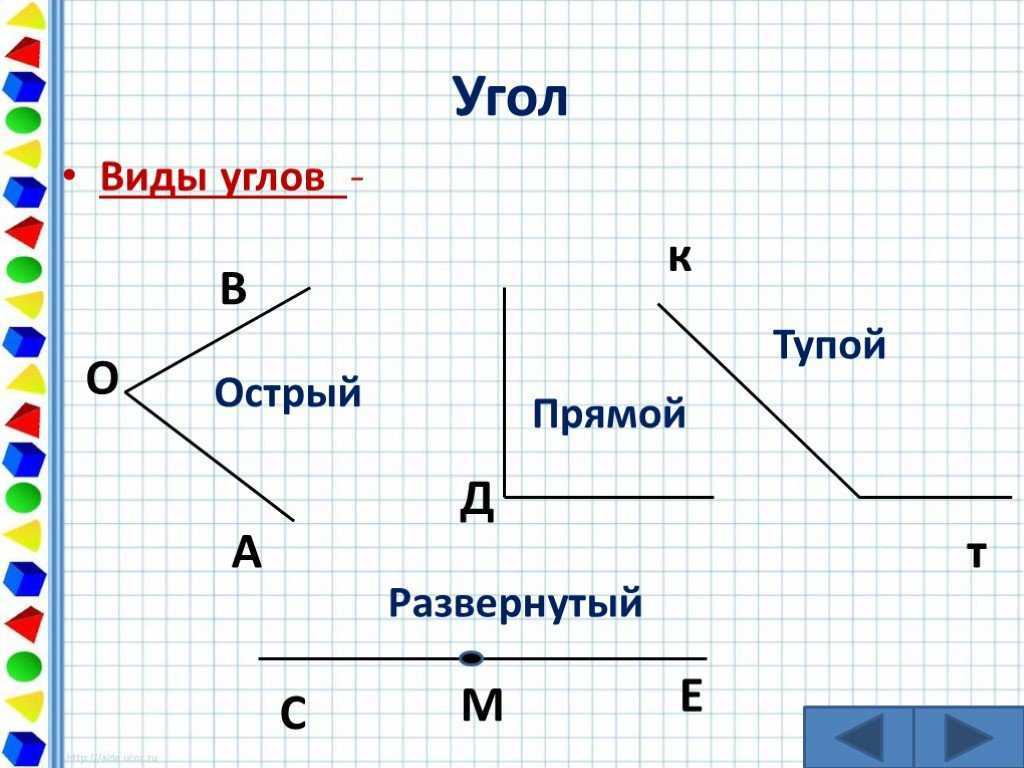
Что такое угол определение. Прямой, тупой, острый и развернутый угол
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Yandex.RTB R-A-339285-1 Определение 1
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения .
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Определение 2
Дана прямая a на плоскости. На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч , а точка O – начало луча .
Иначе говоря, луч или
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Определение 3
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Определение 4
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым .
На рисунке ниже изображен развернутый угол.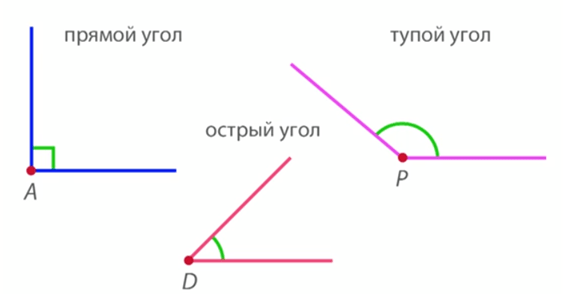
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O .
Угол в математике обозначается знаком « ∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h , то угол обозначается как ∠ k h или ∠ h k .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия O A и O B . В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠ A O B и ∠ B O A . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Определение 5
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение 6
Два угла называют смежными , если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.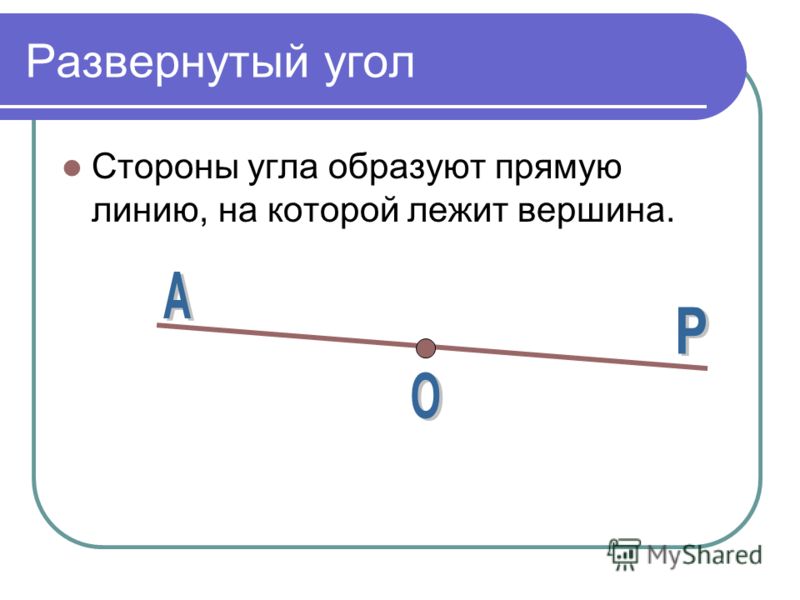
Определение 7
Два угла называют вертикальными , если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные .
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол.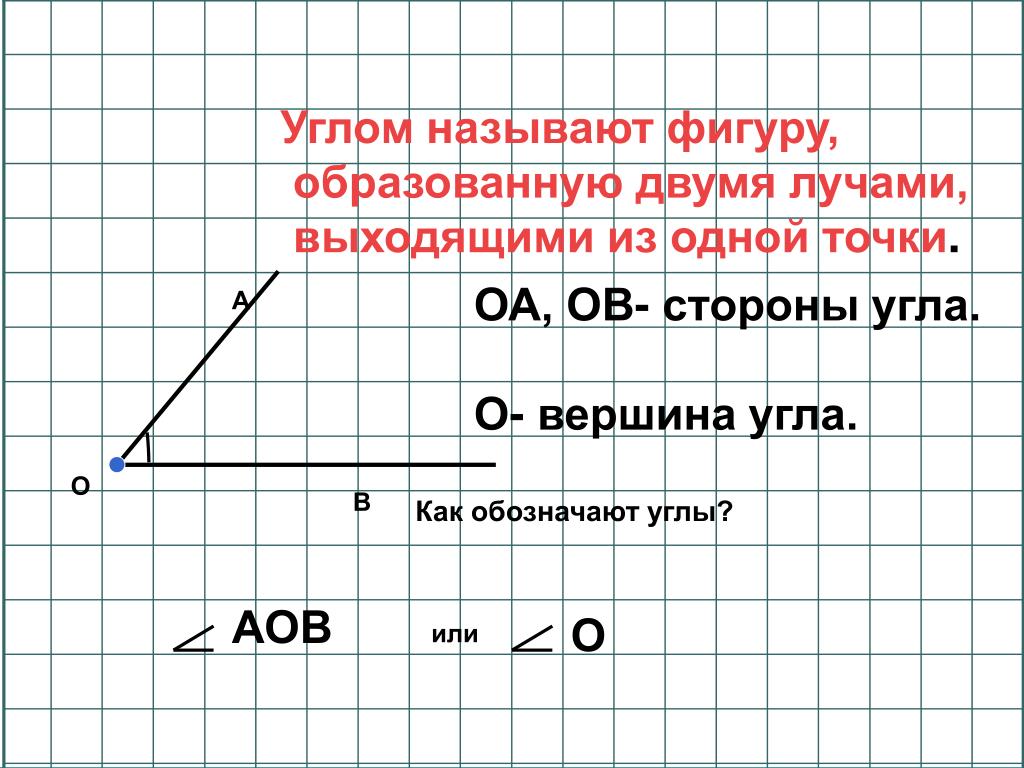 Ниже изображены неравные углы, не совмещенные при наложении.
Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус .
Определение 8
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи « ° », тогда один градус – 1 ° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла.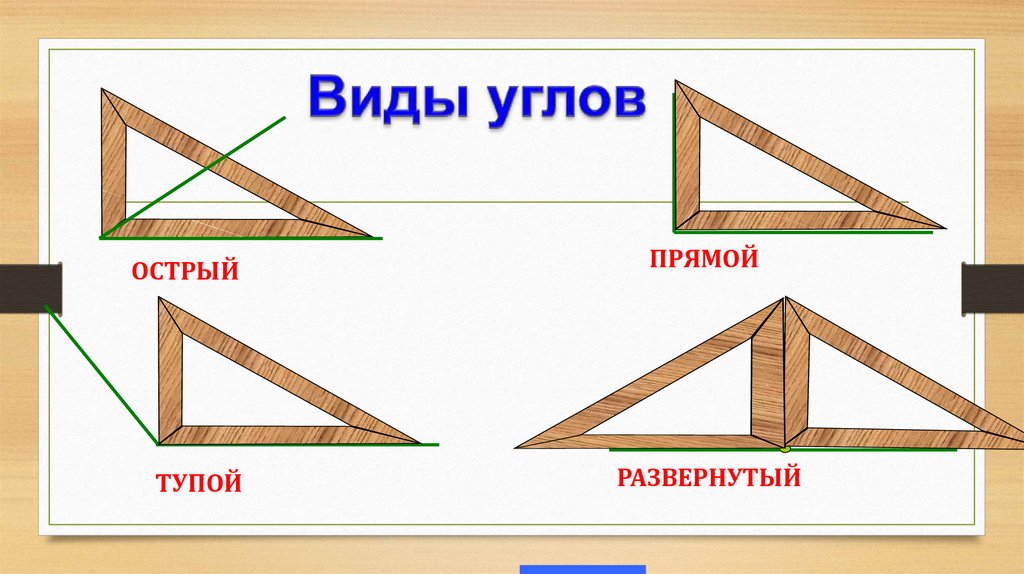 Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты.
Определение 9
Минутой называют одну шестидесятую часть градуса.
Определение 10
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают « » », а секунды « «» ». Имеет место обозначение:
1 ° = 60 » = 3600 «» , 1 » = (1 60) ° , 1 » = 60 «» , 1 «» = (1 60) » = (1 3600) ° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17 ° 3 » 59 «» .
Определение 11
Приведем пример обозначения градусной меры угла равного 17 ° 3 » 59 «» . Запись имеет еще один вид 17 + 3 60 + 59 3600 = 17 239 3600 .
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠ A O B и его градусной мере в 110 градусов применяют более удобную запись ∠ A O B = 110 ° , которая читается «Угол А О В равен 110 градусам».
В геометрии используется мера угла из интервала (0 , 180 ] , а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0 , 90) , а тупой – (90 , 180) . Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ.
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны . Если рассмотреть это на примере, мы получим, что угол А О В и С О D – вертикальные (на чертеже), тогда пары углов А О В и В О С, С О D и В О С считают смежными. В таком случает равенство ∠ A O B + ∠ B O C = 180 ° вместе с ∠ C O D + ∠ B O C = 180 ° считаются однозначно верными. Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом . Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Определение 12
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой, с двумя точками на окружности, соединенными и преобразованными в радиусы О А и О В. По определению данный треугольник A O B является равносторонним, значит длина дуги A B равна длинам радиусов О В и О А.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.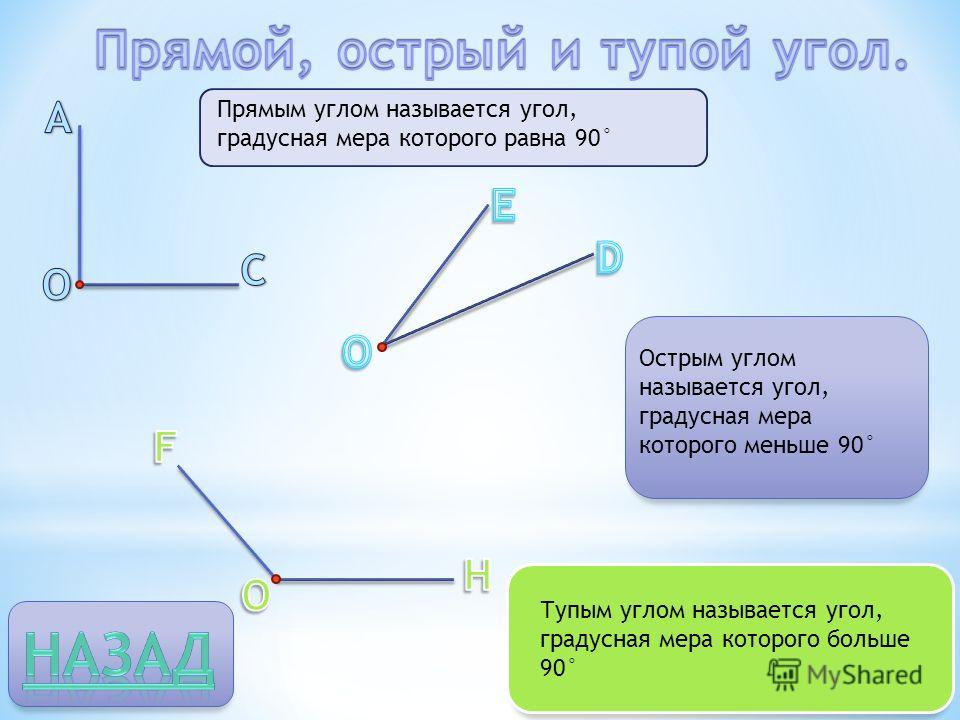
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
В этой статье будет рассматриваться одна из основных геометрических фигур — угол.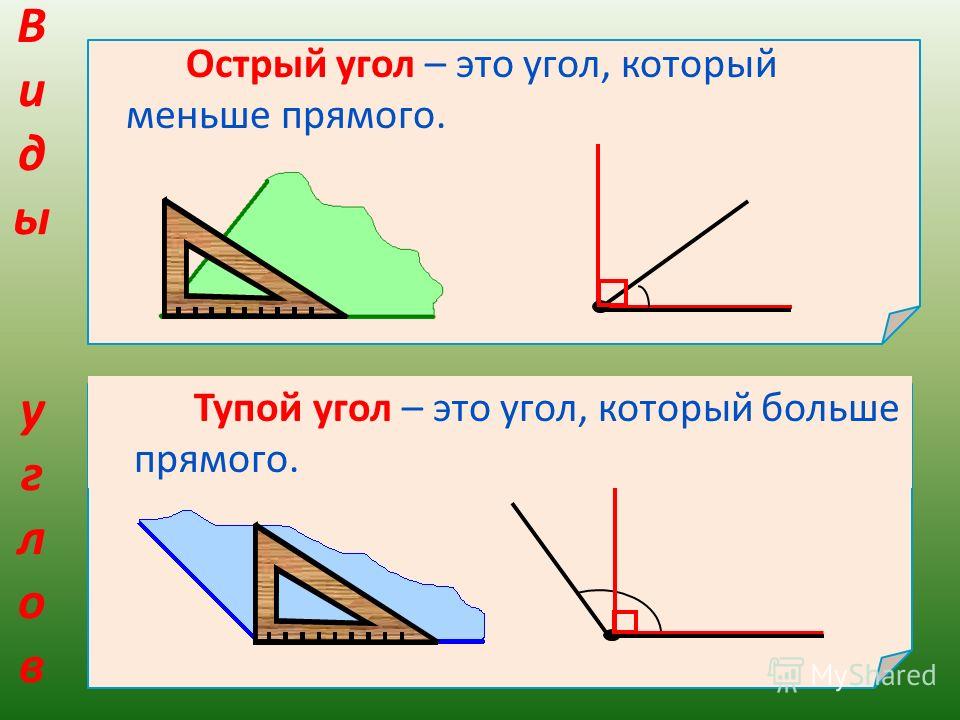 После общего введения в это понятие мы уделим основное внимание отдельному виду такой фигуры. Развернутый угол — важное понятие геометрии, которое и будет основной темой этой статьи.
После общего введения в это понятие мы уделим основное внимание отдельному виду такой фигуры. Развернутый угол — важное понятие геометрии, которое и будет основной темой этой статьи.
Введение в понятие геометрического угла
В геометрии существует ряд объектов, которые составляют основу всей науки. Угол как раз относиться к ним и определяется с помощью понятия луча, поэтому начнем именно с него.
Также перед тем, как приступать к определению самого угла, нужно вспомнить о нескольких не менее важных объектах в геометрии — это точка, прямая на плоскости и собственно сама плоскость. Прямой называют самую простую геометрическую фигуру, у которой нет ни начала, ни конца. Плоскостью — поверхность, которая имеет два измерения. Ну и луч (или же полупрямая) в геометрии — это часть прямой, у которой есть начало, но нет конца.
Используя данные понятия, можем составить утверждение, что углом является геометрическая фигура, которая полностью лежит в некоторой плоскости и состоит из двух несовпадающих лучей с общим началом.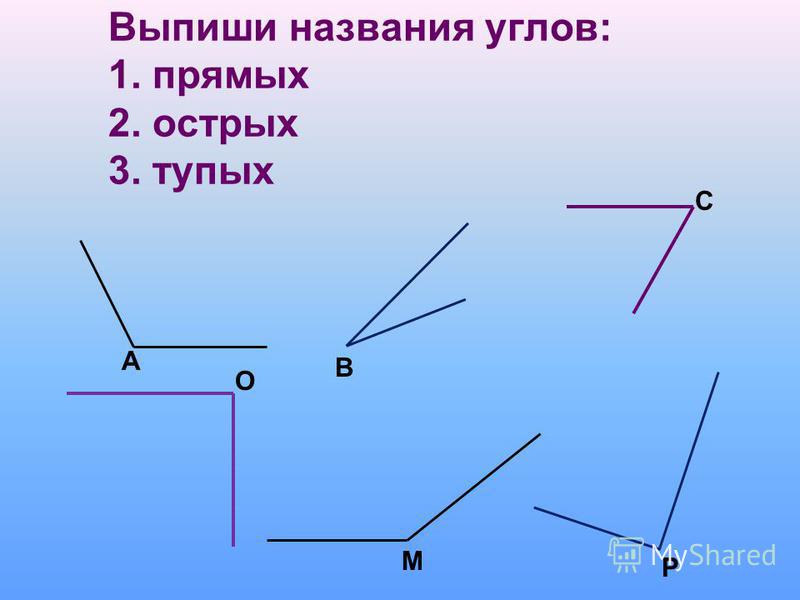 Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.
Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.
Виды углов и геометрии
Мы знаем о том, что углы могут быть совсем разными. А потому немного ниже будет приведена небольшая классификация, которая поможет лучше разобраться в видах углов и их главных особенностях. Итак, существует несколько видов углов в геометрии:
- Прямой угол. Он характеризируется величиной в 90 градусов, а значит, его стороны всегда перпендикулярны между собой.
- Острый угол. К таким углам относятся все их представители, имеющие размер меньше 90 градусов.
- Тупой угол. Здесь же могут быть все углы с величиной от 90 до 180 градусов.
- Развернутый угол. Имеет размер строго 180 градусов и внешне его стороны составляют одну прямую.
Понятие развернутого угла
Теперь давайте рассмотрим развернутый угол более подробно. Это тот случай, когда обе стороны лежат на одной прямой, что можно четко увидеть на рисунке немного ниже. Значит, мы можем с уверенностью сказать, что у развернутого угла одна из его сторон по сути есть продолжением другой.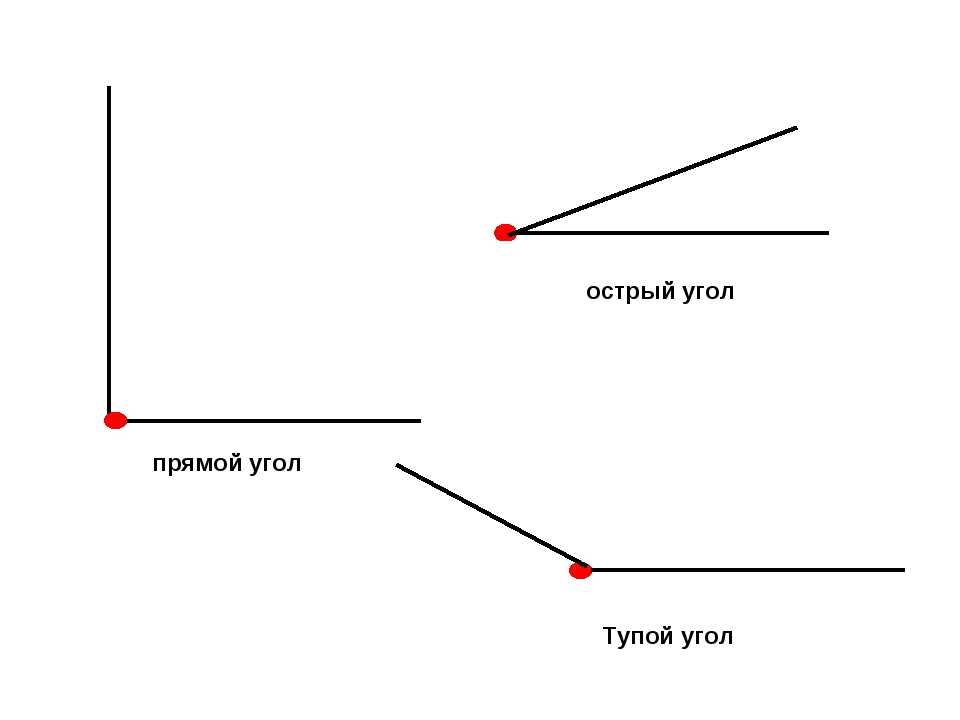
Стоит запомнить тот факт, что такой угол всегда можно разделить с помощью луча, который выходит из его вершины. В результате мы получим два угла, которые в геометрии называются смежными.
Также развернутый угол имеет несколько особенностей. Для того, чтобы рассказать о первой из них, нужно вспомнить понятие «биссектриса угла». Напомним, что это луч, который делит любой угол строго пополам. Что касается развернутого угла, то его биссектриса разделяет его таким образом, что образуется два прямых угла по 90 градусов. Это очень легко просчитать математически: 180˚ (градус развернутого угла) : 2 = 90˚.
Если же разделять развернутый угол совсем произвольным лучом, то в результате мы всегда получаем два угла, один из которых будет острым, а другой — тупым.
Свойства развернутых углов
Будет удобно рассматривать этот угол, собрав воедино все его главные свойства, что мы и сделали в данном списке:
- Стороны развернутого угла антипараллельны и составляют прямую.

- Величина развернутого угла всегда составляет 180˚.
- Два смежных угла вместе всегда составляют развернутый угол.
- Полный угол, который составляет 360˚, состоит из двух развернутых и равен их суме.
- Половина развернутого угла — это прямой угол.
Итак, зная все эти характеристики данного вида углов, мы можем использовать их для решения ряда геометрических задач.
Задачи с развернутыми углами
Для того, чтобы понять, усвоили ли вы понятие развернутого угла, попытайтесь ответить на несколько следующих вопросов.
- Чему равен развернутый угол, если его стороны составляют вертикальную прямую?
- Будут ли два угла смежными, если величина первого 72˚, а другого — 118˚?
- Если полный угол состоит из двух развернутых, то сколько в нем прямых углов?
- Развернутый угол разделили лучом на два таких угла, что их градусные меры относятся как 1:4. Вычислите полученные углы.
Решения и ответы:
- Как бы ни был расположен развернутый угол, он всегда по определению равен 180˚.

- Смежные углы имеют одну общую сторону. Поэтому, чтобы вычислить размер угла, который они составляю вместе, нужно просто прибавить значение их градусных мер. Значит, 72 +118 = 190. Но по определению развернутый угол составляет 180˚, а значит, два данных угла не могут быть смежными.
- Развернутый угол вмещает два прямых угла. А так как в полном имеется два развернутых, значит, прямых в нем будет 4.
- Если мы назовем искомые углы а и b, то пусть х — это коэффициент пропорциональности для них, а это значит, что а=х, и соответственно b=4х. Развернутый угол в градусах равен 180˚. И согласно своим свойствам, что градусная мера угла всегда равна сумме градусных мер тех углов, на которые он разбивается любым произвольным лучом, что проходит между его сторонами, можем сделать вывод, что х + 4х = 180˚, а значит, 5х = 180˚. Отсюда находим: х=а=36˚ и b = 4х = 144˚. Ответ: 36˚ и 144˚.
Если у вас получилось ответить на все эти вопросы без подсказок и не подглядывая в ответы, значит вы готовы переходить к следующему уроку по геометрии.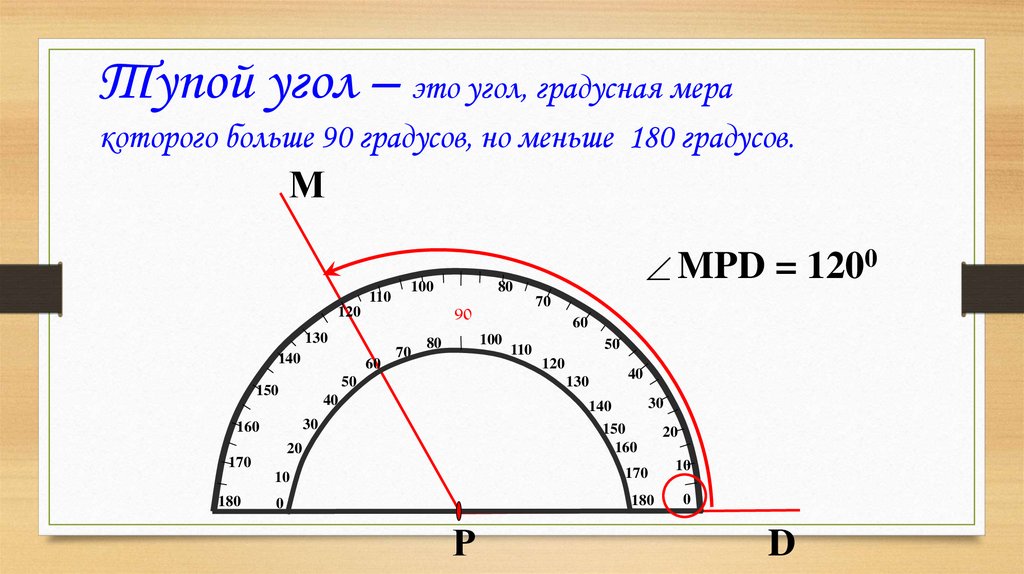
Что такое угол?
Углом называют фигуру, образованную двумя лучами, выходящими из одной точки (рис. 160).
Лучи, образующие угол , называют сторонами угла, а точку, из которой они выходят, — вершиной угла.
На рисунке 160 сторонами угла являются лучи ОА и ОБ, а его вершиной — точка О. Этот угол обозначают так: АОВ.
При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначить и одной буквой — названием его вершины.
Например, вместо «угол АОВ» пишут короче: «угол О».
Вместо слова «угол» пишут знак .
Например, AОВ, O.
На рисунке 161 точки С и D лежат внутри угла АОВ, точки X и У лежат вне этого угла, а точки М и Н — на сторонах угла.
Как и все геометрические фигуры, углы сравниваются с помощью наложения.
Если один угол можно наложить на другой так, что они совпадут, то эти углы равны.
Например, на рисунке 162 ABC = MNK.
Из вершины угла СОК (рис. 163) проведен луч ОР.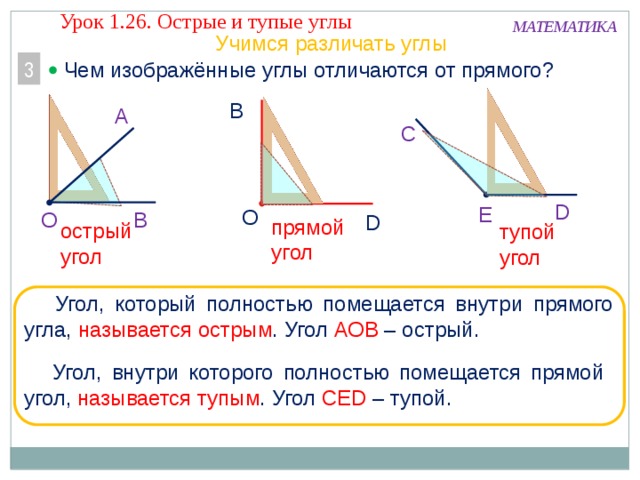 Он разбивает угол СОК на два угла — СОР и РОК. Каждый из этих углов меньше угла СОК.
Он разбивает угол СОК на два угла — СОР и РОК. Каждый из этих углов меньше угла СОК.
Пишут: COP
Прямой и развернутый угол
Два дополнительных друг другу луча образуют развернутый угол. Стороны этого угла вместе составляют прямую линию, на которой лежит вершина развернутого угла (рис. 164).
Часовая и минутная стрелки часов образуют в 6 ч развернутый угол (рис. 165).
Согнем два раза пополам лист бумаги, а потом развернем его (рис. 166).
Линии сгиба образуют 4 равных угла. Каждый из этих углов равен половине развернутого угла. Такие углы называют прямыми.
Прямым углом называют половину развернутого угла.
Чертежный треугольник
Для построения прямого угла пользуются чертежным треугольником (рис. 167). Чтобы построить прямой угол, одной из сторон которого является луч ОЛ, надо:
а) расположить чертежный треугольник так, чтобы вершина его прямого угла совпала с точкой О, а одна из сторон пошла по лучу ОА;
б) провести вдоль второй стороны треугольника луч ОВ.
В результате получим прямой угол АОВ.
Вопросы к теме
1.Что такое угол?
2.Какой угол называют развернутым?
3.Какие углы называют равными?
4.Какой угол называют прямым?
5.Как строят прямой угол с помощью чертежного треугольника?
Нам с вами уже известно, что любой угол делит плоскость на две части. Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.
Теперь давайте посмотрим на рисунок, на котором как раз и изображен развернутый угол О.
Если мы возьмем и проведем из вершины развернутого угла луч, то он разделит данный развернутый угол еще на два угла, которые будут иметь одну общую сторону, а другие два угла будут составлять прямую. То есть, с одного развернутого угла мы получили два смежных.
Если мы возьмем развернутый угол и проведем биссектрису, то эта биссектриса разделит развернутый угол на два прямых угла.
А, в том случае, если мы из вершины развернутого угла проведем произвольный луч, который не является биссектрисой, то такой луч разделит развернутый угол на два угла, один из которых будет острым, а другой тупым.
Свойства развернутого угла
Развернутый угол обладает такими свойствами:
Во-первых, стороны развёрнутого угла являются антипараллельными и образуют прямую;
во-вторых, развернутый угол равен 180°;
в-третьих, два смежных угла образуют развернутый угол;
в-четвертых, развернутый угол составляет половину полного угла;
в-пятых, полный угол будет равен сумме двух развёрнутых углов;
в-шестых, половина развернутого угла составляет прямой угол.
Измерение углов
Чтобы измерить любой угол, для этих целей чаще всего используют транспортир, у которого единица измерения равна одному градусу. При измерении углов следует помнить, что любой угол имеет свою определенную градусную меру и естественно эта мера больше нуля. А развернутый угол, как нам уже известно, равен 180 градусам.
То есть, если мы с вами возьмем любую плоскость круга и разделим ее радиусами на 360 равных частей, то 1/360 часть данного круга будет являться угловым градусом. Как вы уже знаете, что градус обозначается определенным значком, который имеет такой вид: « ° ».
Теперь мы также знаем, что один градус 1° = 1/360 части круга. Если угол равен плоскости круга и составляет 360 градусов, то такой угол является полным.
А теперь мы возьмем, и плоскость круга поделим с помощью двух радиусов, лежащих на одной прямой линии, на две равные части. То в этом случае, плоскость полукруга составит половину полного угла, то есть 360: 2 = 180°. Мы с вами получили угол, который равен полуплоскости круга и имеет 180°. Это и есть развернутый угол.
Практическое задание
1613. Назовите углы, изображенные на рисунке 168. Запишите их обозначения.
1614. Начертите четыре луча: ОА, ОВ, ОС и OD. Запишите названия шести углов, сторонами которых являются эти лучи. На сколько частей эти лучи делят плоскость ?
1615. Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ?
Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ?
1616. Начертите угол MOD и проведите внутри него луч ОТ. Назовите и обозначьте углы, на которые этот луч делит угол MOD.
1617. Минутная стрелка за 10 мин повернулась на угол АОВ, за следующие 10 мин — на угол ВОС, а еще за 15 мин — на угол COD. Сравните углы АОВ и ВОС, ВОС и COD, АОС и АОВ, АОС и COD (рис. 170).
1618. Изобразите с помощью чертежного треугольника 4 прямых угла в разных положениях.
1619. С помощью чертежного треугольника найдите на рисунке 171 прямые углы. Запишите их обозначения.
1620. Укажите прямые углы в классной комнате.
а) 0,09 200; б) 208 0,4; в) 130 0,1 + 80 0,1.
1629. Сколько процентов от 400 составляет число 200; 100; 4; 40; 80; 400; 600?
1630. Найдите пропущенное число:
а) 2 5 3 б) 2 3 5
13 6 12 1
2 3? 42?
1631. Начертите квадрат, сторона которого равна длине 10 клеток тетради.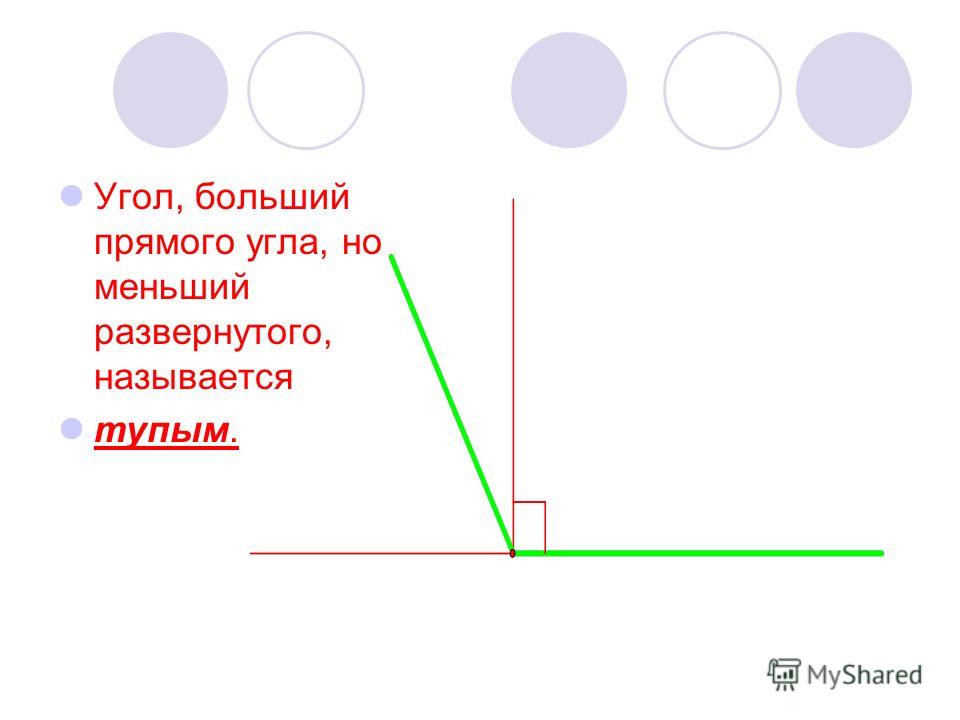 Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха?
Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха?
1632. За учебный год Петя израсходовал 40% купленных в начале года тетрадей, и у него осталось 30 тетрадей. Сколько тетрадей было куплено для Пети в начале учебного года?
1633. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди?
1634. Построенный в древности Александрийский маяк, который называли одним из семи чудес света, выше башен Московского Кремля в 1,7 раза, но ниже здания Московского университета на 119 м. Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.
1635. Найдите с помощью микрокалькулятора:
а) 4,5% от 168; в) 28,3% от 569,8;
б) 147,6% от 2500; г) 0,09% от 456 800.
1636. Решите задачу:
1) Площадь огорода 6,4 а.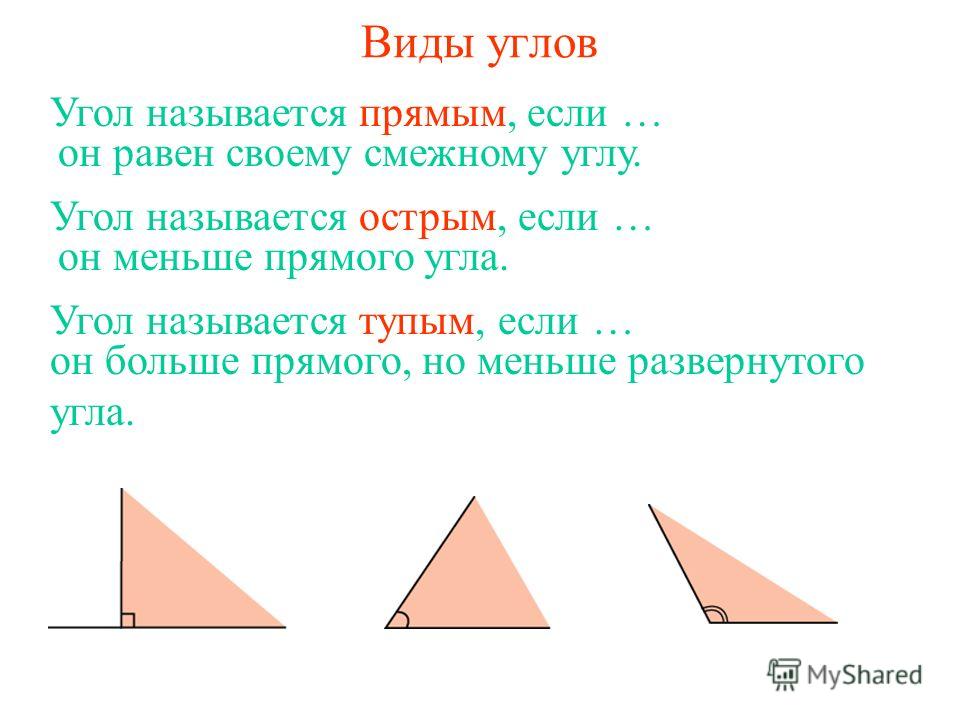 В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать?
В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать?
2) У Сережи было 4,8 ч свободного времени. 35% этого времени он потратил на чтение книги, а 40% на просмотр передач по телевизору. Сколько времени у него еще осталось?
1637. Выполните действия:
1) ((23,79: 7,8 — 6,8: 17) 3,04 — 2,04) 0,85;
2) (3,42: 0,57 9,5 — 6,6) : ((4,8 — 1,6) (3,1 + 0,05)).
1638. Начертите угол ВАС и отметьте по одной точке внутри угла, вне угла и на сторонах угла.
1639. Какие из отмеченных на рисунке 172 точек лежат внутри угла АМК.Какая точка лежит внутри угла АМВ> но вне угла АМК.Какие точки лежат на сторонах угла АМК?
1640. Найдите с помощью чертежного треугольника прямые углы на рисунке 173.
1641. Постройте квадрат со стороной 43 мм. Вычислите его периметр и площадь.
1642. Найдите значение выражения:
а) 14,791: а + 160,961: b, если а = 100, b = 10;
б) 361,62с + 1848: d, если с = 100, d =100.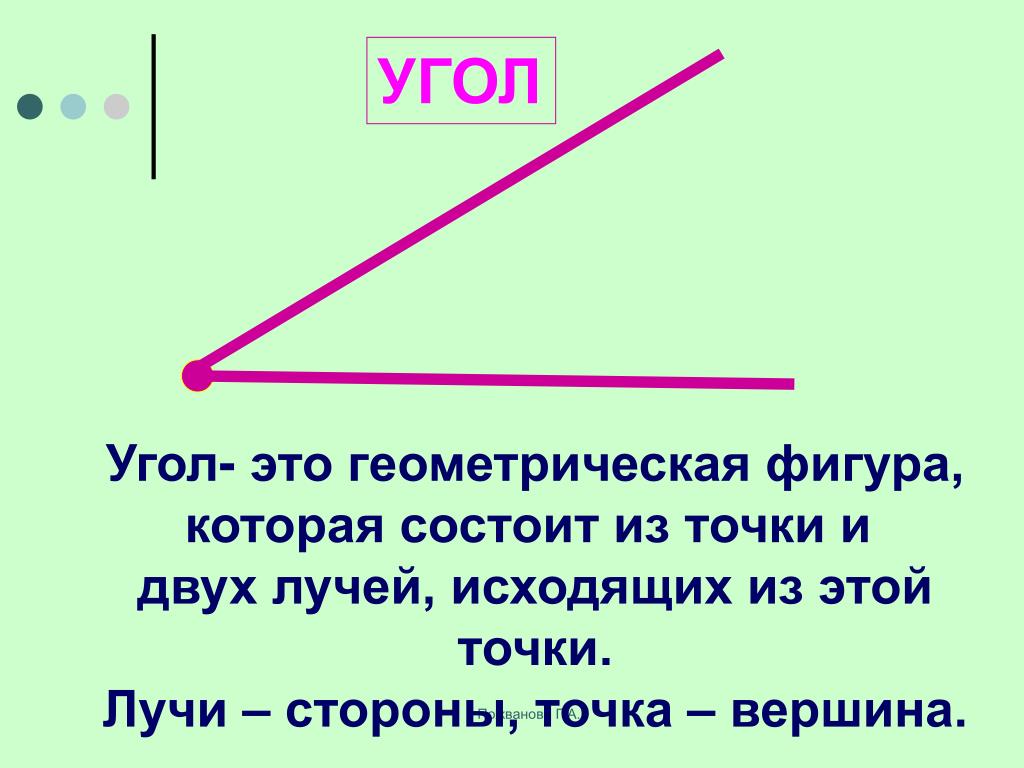
1643. Рабочий должен был изготовить 450 деталей. В первый день он изготовил 60% деталей, а остальные — во второй. Сколько деталей изготовил рабочий во второй день?
1644. В библиотеке было 8000 книг. Через год число их увеличилось на 2000 книг. На сколько процентов увеличилось число книг в библиотеке?
1645. Грузовики в первый день проехали 24% намеченного пути, во второй день — 46% пути, а в третий — остальные 450 км. Сколько километров проехали эти грузовики?
1646. Найдите, сколько составляют:
а) 1% от тонны; в) 5% от 7 т;
б) 1% от литра; г) 6% от 80 км.
1647. Масса детеныша моржа в 9 раз меньше массы взрослого моржа. Какова масса взрослого моржа, если вместе с детенышем их масса равна 0,9 т?
1648. Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат?
Н.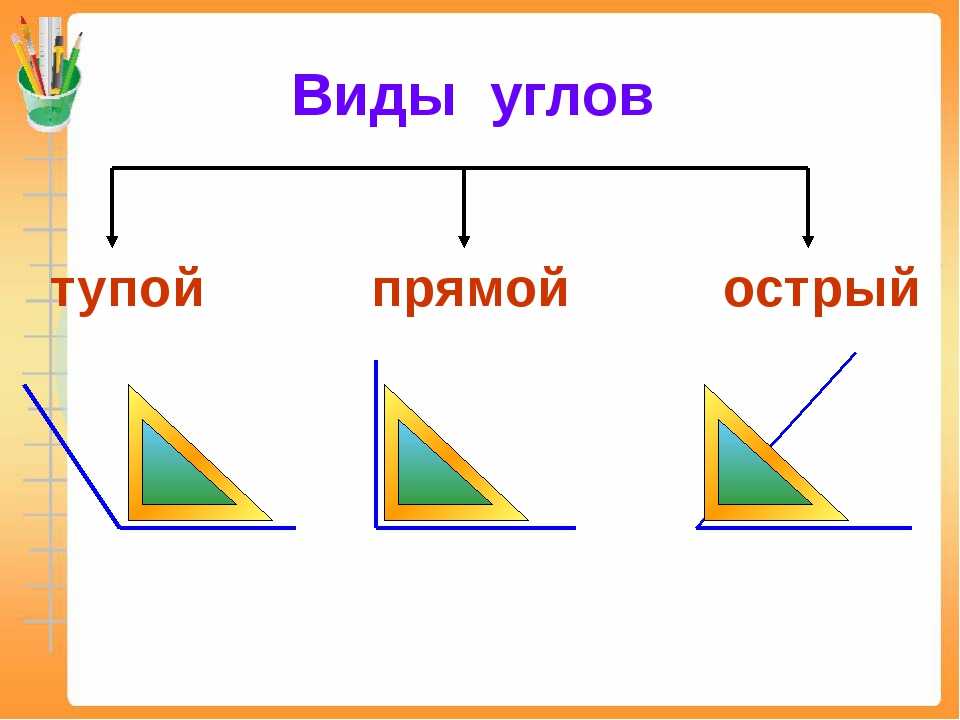 Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
Углом называется геометрическая фигура, которая состоит из двух различных лучей, исходящих из одной точки. В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О , и сторонами k и m .
На сторонах угла отмечены точки А и С. Этот угол можно обозначить как угол AOC. В середине обязательно должно стоять название точки, в которой находится вершина угла. Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок.
Развернутый и неразвернутый угол
Если у угла обе стороны лежат на одной прямой, то такой угол называется развернутым углом. То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О.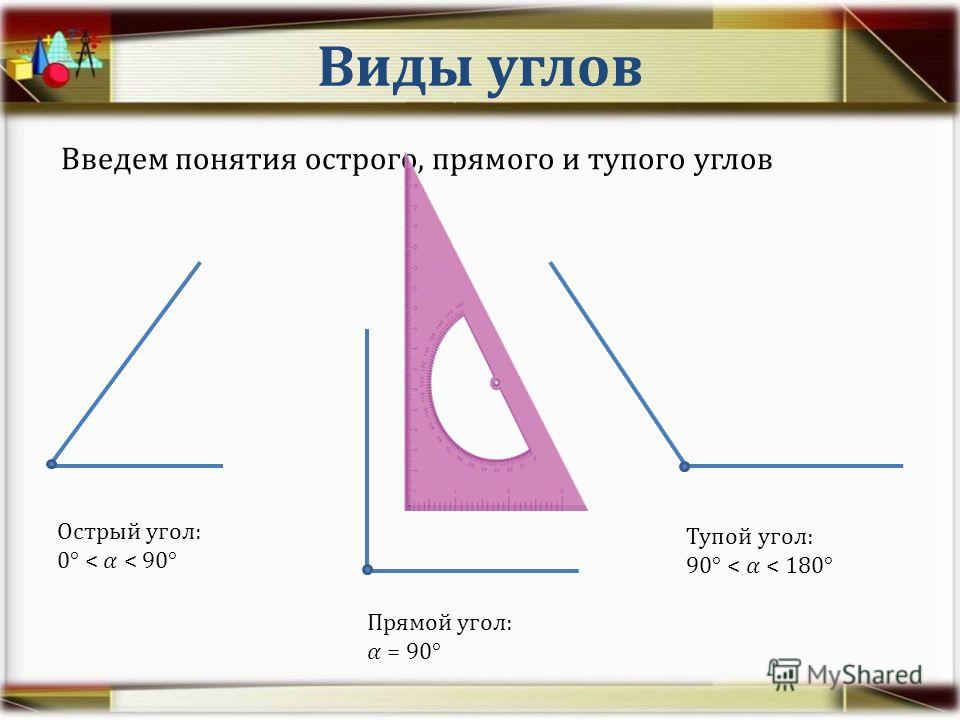
Следует отметить, что любой угол, разделяет плоскость на две части. Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла. На рисунке ниже представлен неразвернутый угол и отмечены внешняя и внутренняя области этого угла.
В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области).
На рисунке ниже, точка А лежит вне угла О, точка B лежит на одной из сторон угла, а точка С лежит внутри угла.
Измерение углов
Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус . Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля.
В зависимости от градусной меры углы делятся на несколько групп.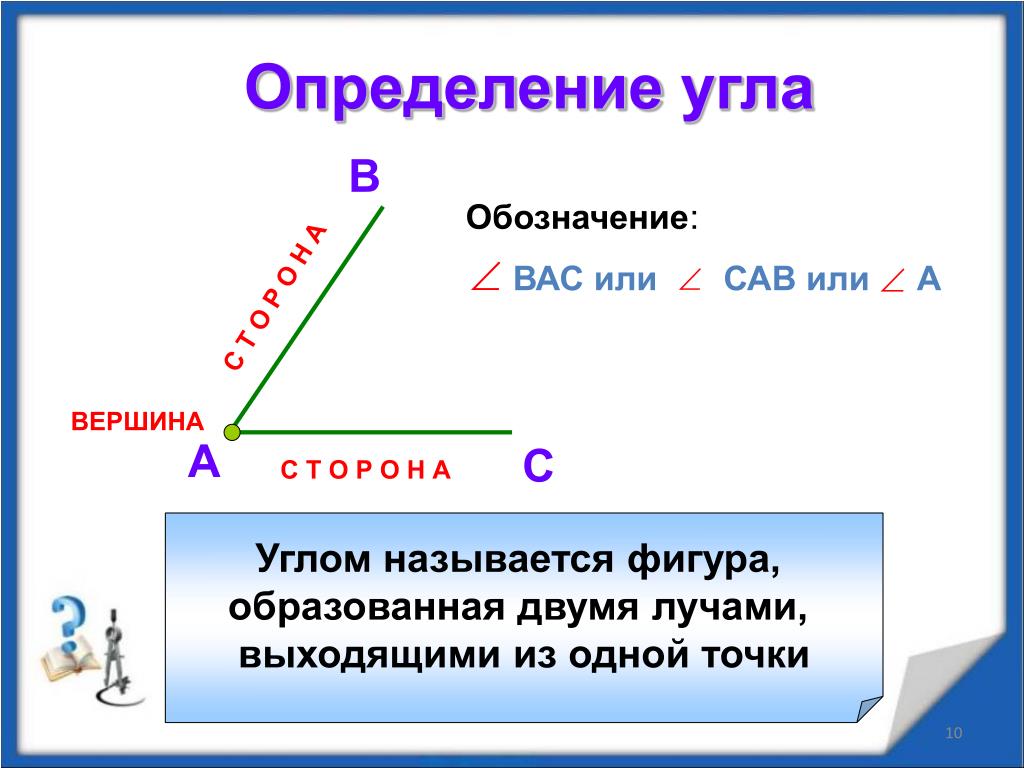
Угловая мера
Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L , в радианах — отношение длины дуги s к радиусу r ; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется.
1 оборот = 2π радианам = 360° = 400 градам .
В морской терминологии углы обозначаются румбами .
Типы углов
Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c)
Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым.
Wikimedia Foundation . 2010 .
Смотреть что такое «Развернутый угол» в других словарях:
Угол, равный двум прямым. *РАЗВЕРТКА поверхности фигура, получающаяся в плоскости при таком совмещении точек данной поверхности с этой плоскостью, при котором длины линий остаются неизменными. Развертка кривой см. Эвольвента … Большой Энциклопедический словарь
угол — ▲ разность направление (в пространстве) угол протяженность поворота от одного направления к другому; разность направлений; часть полного оборота (# наклона.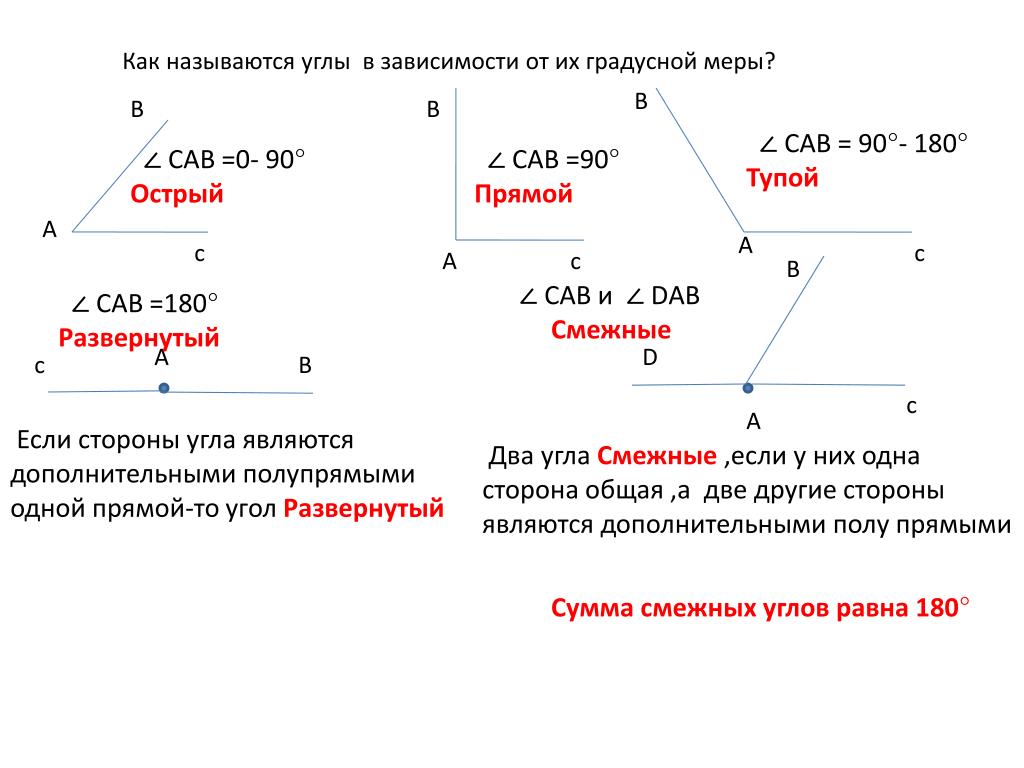 образовывать #). наклон. наклонный. отклонение. уклониться (дорога уклонилась вправо).… …
образовывать #). наклон. наклонный. отклонение. уклониться (дорога уклонилась вправо).… …
Угол — Углы: 1 общего вида; 2 смежные; 3 прилежащие; 4 вертикальные; 5 развернутый; 6 прямой, острый и тупой; 7 между кривыми; 8 между прямой и плоскостью; 9 между скрещивающимися прямыми (не лежащими в одной плоскостью) прямыми. УГОЛ, геометрическая… … Иллюстрированный энциклопедический словарь
Геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Лучи наз. сторонами У., а их общее начало вершиной У. Пусть [ ВА),[ ВС) стороны угла, В его вершина, плоскость, определяемая сторонами У. Фигура делит плоскость… … Математическая энциклопедия
Угол, равный двум прямым. * * * РАЗВЕРНУТЫЙ УГОЛ РАЗВЕРНУТЫЙ УГОЛ, угол, равный двум прямым … Энциклопедический словарь
Раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию.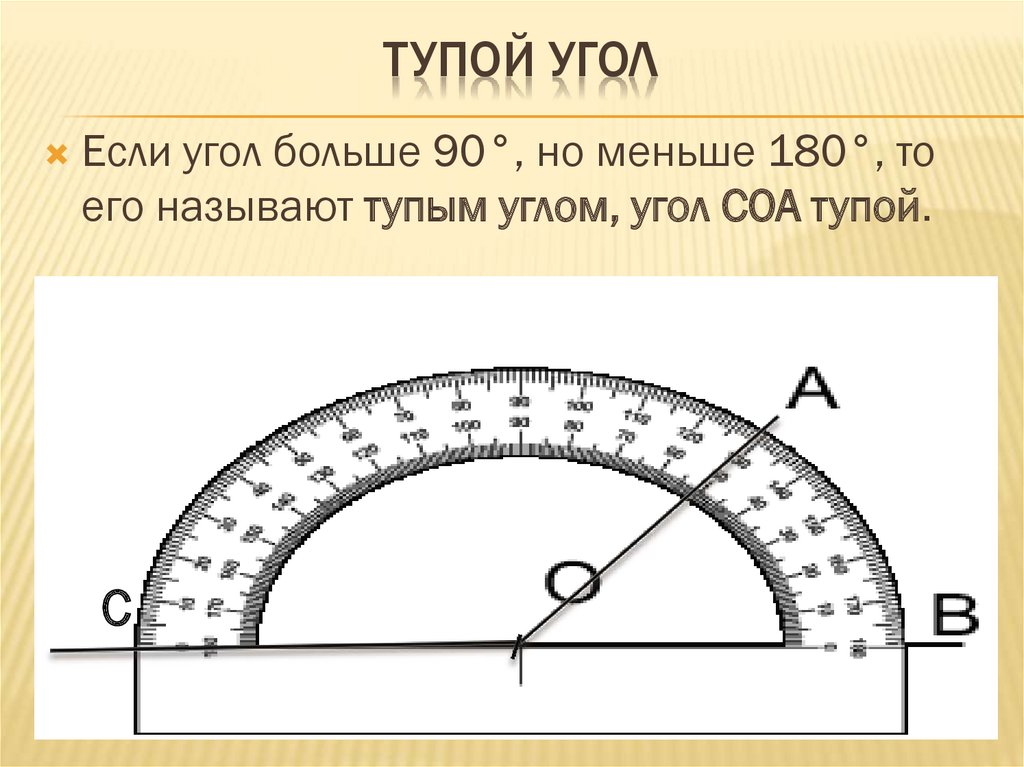 В… … Энциклопедия Кольера
В… … Энциклопедия Кольера
1) Замкнутая ломаная линия, именно: если различные точки, никакие последовательные три из к рых не лежат на одной прямой, то совокупность отрезков наз. многоугольником (см. рис. 1). М. могут быть пространственными или плоскими (ниже… … Математическая энциклопедия
поперек — ▲ под углом максимум, косой угол поперечный. поперек под прямым углом. . прямой угол угол максимального отклонения; угол, равный своему смежному; четверть оборота. перпендикуляр. перпендикулярный находящийся под прямым углом. перпендикулярно.… … Идеографический словарь русского языка
градус — а, м. 1) Единица измерения плоского угла, равная 1/90 прямого угла или соответственно 1/360 окружности. Угол в 90 градусов называется прямым углом. Развернутый угол составляет 180 градусов. 2) Единица измерения температурного интервала, имеющая… … Популярный словарь русского языка
Теорема Шварца Кристоффеля важная теорема в теории функций комплексного переменного, носит название немецких математиков Карла Шварца и Элвина Кристоффеля.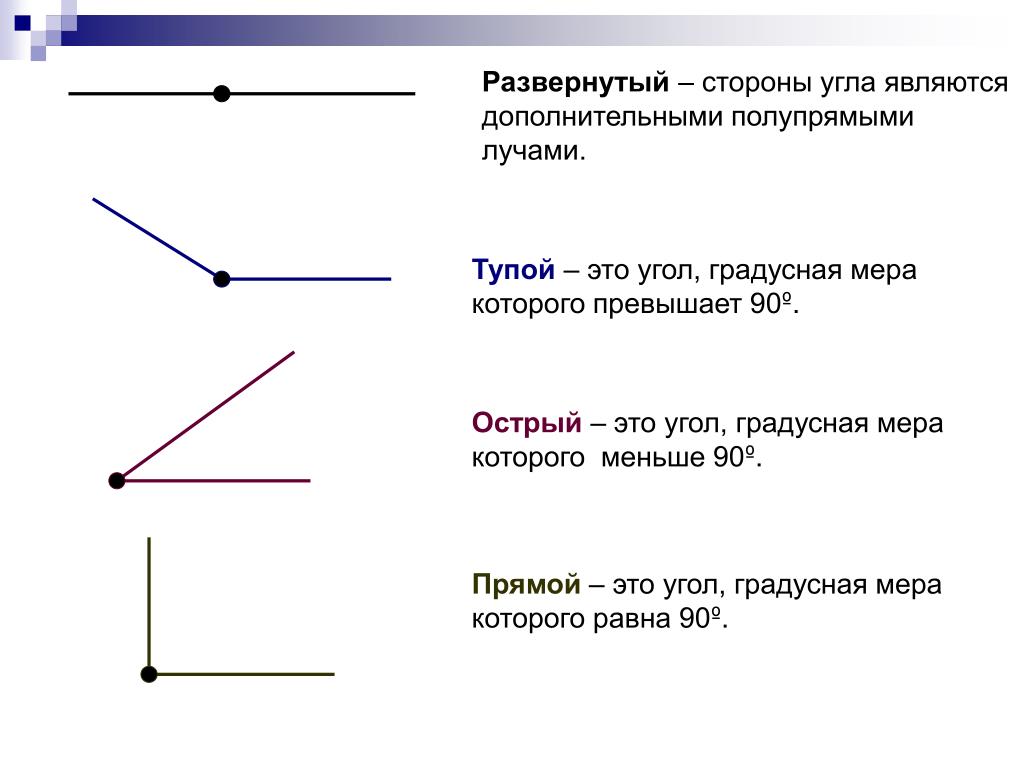 Очень важной с практической точки зрения является проблема о конформном… … Википедия
Очень важной с практической точки зрения является проблема о конформном… … Википедия
Как выглядят острые и тупые углы. Понятие и виды углов
Углом называется геометрическая фигура, которая состоит из двух различных лучей, исходящих из одной точки. В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О , и сторонами k и m .
На сторонах угла отмечены точки А и С. Этот угол можно обозначить как угол AOC. В середине обязательно должно стоять название точки, в которой находится вершина угла. Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок.
Развернутый и неразвернутый угол
Если у угла обе стороны лежат на одной прямой, то такой угол называется развернутым углом. То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О.
Следует отметить, что любой угол, разделяет плоскость на две части. Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла. На рисунке ниже представлен неразвернутый угол и отмечены внешняя и внутренняя области этого угла.
В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области).
На рисунке ниже, точка А лежит вне угла О, точка B лежит на одной из сторон угла, а точка С лежит внутри угла.
Измерение углов
Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус . Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля.
В зависимости от градусной меры углы делятся на несколько групп.
В этой статье будет рассматриваться одна из основных геометрических фигур — угол. После общего введения в это понятие мы уделим основное внимание отдельному виду такой фигуры. Развернутый угол — важное понятие геометрии, которое и будет основной темой этой статьи.
Введение в понятие геометрического угла
В геометрии существует ряд объектов, которые составляют основу всей науки. Угол как раз относиться к ним и определяется с помощью понятия луча, поэтому начнем именно с него.
Также перед тем, как приступать к определению самого угла, нужно вспомнить о нескольких не менее важных объектах в геометрии — это точка, прямая на плоскости и собственно сама плоскость. Прямой называют самую простую геометрическую фигуру, у которой нет ни начала, ни конца. Плоскостью — поверхность, которая имеет два измерения. Ну и луч (или же полупрямая) в геометрии — это часть прямой, у которой есть начало, но нет конца.
Используя данные понятия, можем составить утверждение, что углом является геометрическая фигура, которая полностью лежит в некоторой плоскости и состоит из двух несовпадающих лучей с общим началом.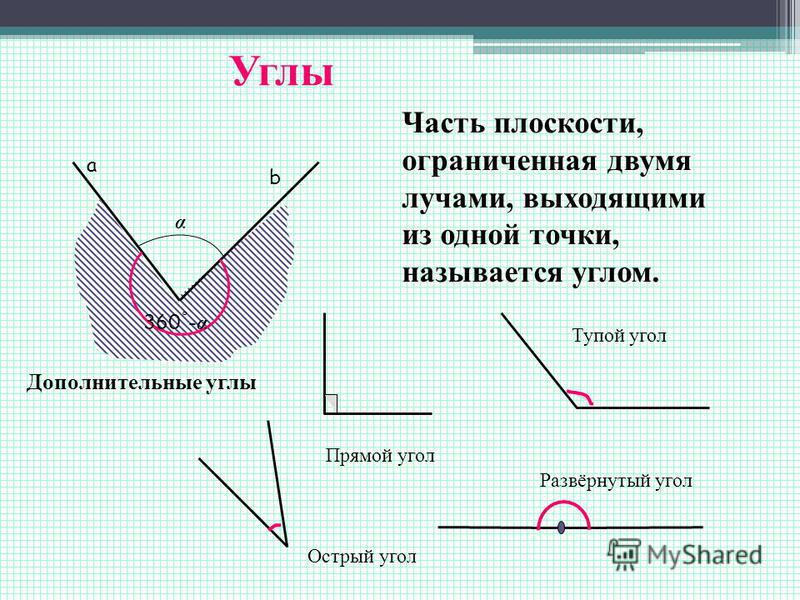 Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.
Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.
Виды углов и геометрии
Мы знаем о том, что углы могут быть совсем разными. А потому немного ниже будет приведена небольшая классификация, которая поможет лучше разобраться в видах углов и их главных особенностях. Итак, существует несколько видов углов в геометрии:
- Прямой угол. Он характеризируется величиной в 90 градусов, а значит, его стороны всегда перпендикулярны между собой.
- Острый угол. К таким углам относятся все их представители, имеющие размер меньше 90 градусов.
- Тупой угол. Здесь же могут быть все углы с величиной от 90 до 180 градусов.
- Развернутый угол. Имеет размер строго 180 градусов и внешне его стороны составляют одну прямую.
Понятие развернутого угла
Теперь давайте рассмотрим развернутый угол более подробно. Это тот случай, когда обе стороны лежат на одной прямой, что можно четко увидеть на рисунке немного ниже. Значит, мы можем с уверенностью сказать, что у развернутого угла одна из его сторон по сути есть продолжением другой.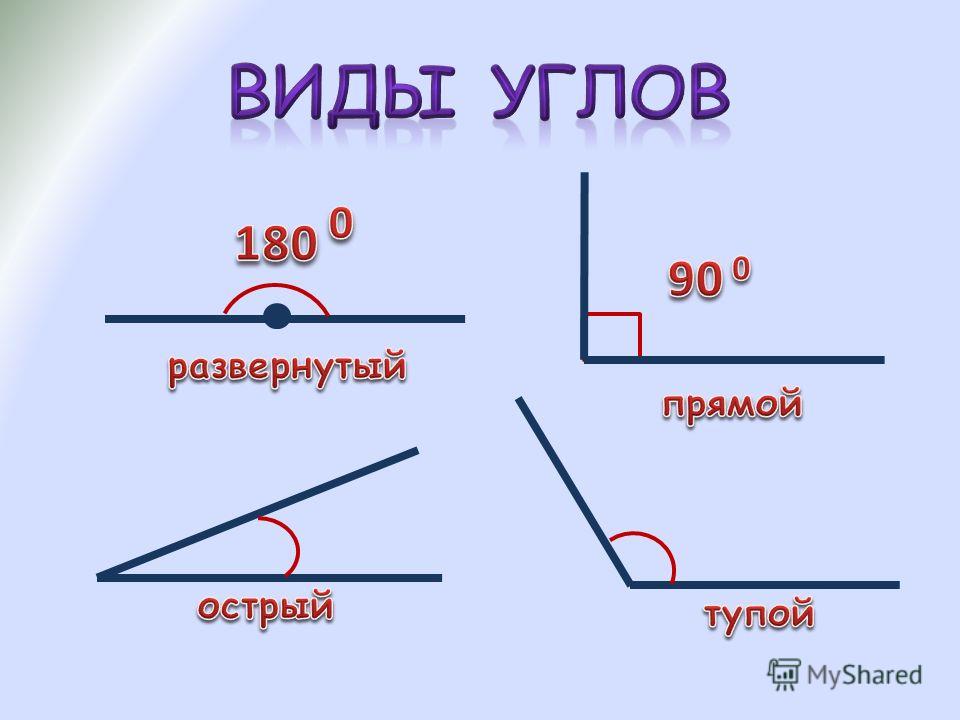
Стоит запомнить тот факт, что такой угол всегда можно разделить с помощью луча, который выходит из его вершины. В результате мы получим два угла, которые в геометрии называются смежными.
Также развернутый угол имеет несколько особенностей. Для того, чтобы рассказать о первой из них, нужно вспомнить понятие «биссектриса угла». Напомним, что это луч, который делит любой угол строго пополам. Что касается развернутого угла, то его биссектриса разделяет его таким образом, что образуется два прямых угла по 90 градусов. Это очень легко просчитать математически: 180˚ (градус развернутого угла) : 2 = 90˚.
Если же разделять развернутый угол совсем произвольным лучом, то в результате мы всегда получаем два угла, один из которых будет острым, а другой — тупым.
Свойства развернутых углов
Будет удобно рассматривать этот угол, собрав воедино все его главные свойства, что мы и сделали в данном списке:
- Стороны развернутого угла антипараллельны и составляют прямую.

- Величина развернутого угла всегда составляет 180˚.
- Два смежных угла вместе всегда составляют развернутый угол.
- Полный угол, который составляет 360˚, состоит из двух развернутых и равен их суме.
- Половина развернутого угла — это прямой угол.
Итак, зная все эти характеристики данного вида углов, мы можем использовать их для решения ряда геометрических задач.
Задачи с развернутыми углами
Для того, чтобы понять, усвоили ли вы понятие развернутого угла, попытайтесь ответить на несколько следующих вопросов.
- Чему равен развернутый угол, если его стороны составляют вертикальную прямую?
- Будут ли два угла смежными, если величина первого 72˚, а другого — 118˚?
- Если полный угол состоит из двух развернутых, то сколько в нем прямых углов?
- Развернутый угол разделили лучом на два таких угла, что их градусные меры относятся как 1:4. Вычислите полученные углы.
Решения и ответы:
- Как бы ни был расположен развернутый угол, он всегда по определению равен 180˚.

- Смежные углы имеют одну общую сторону. Поэтому, чтобы вычислить размер угла, который они составляю вместе, нужно просто прибавить значение их градусных мер. Значит, 72 +118 = 190. Но по определению развернутый угол составляет 180˚, а значит, два данных угла не могут быть смежными.
- Развернутый угол вмещает два прямых угла. А так как в полном имеется два развернутых, значит, прямых в нем будет 4.
- Если мы назовем искомые углы а и b, то пусть х — это коэффициент пропорциональности для них, а это значит, что а=х, и соответственно b=4х. Развернутый угол в градусах равен 180˚. И согласно своим свойствам, что градусная мера угла всегда равна сумме градусных мер тех углов, на которые он разбивается любым произвольным лучом, что проходит между его сторонами, можем сделать вывод, что х + 4х = 180˚, а значит, 5х = 180˚. Отсюда находим: х=а=36˚ и b = 4х = 144˚. Ответ: 36˚ и 144˚.
Если у вас получилось ответить на все эти вопросы без подсказок и не подглядывая в ответы, значит вы готовы переходить к следующему уроку по геометрии.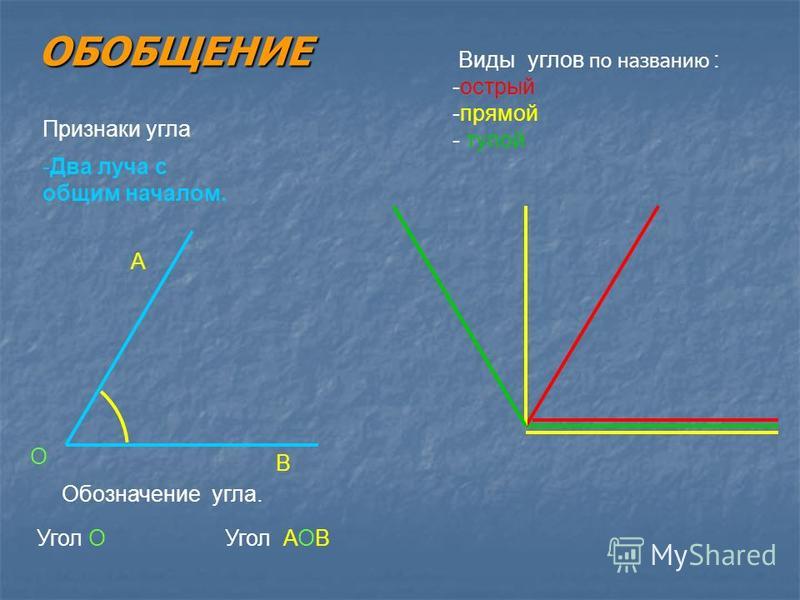
Что такое угол?
Углом называют фигуру, образованную двумя лучами, выходящими из одной точки (рис. 160).
Лучи, образующие угол , называют сторонами угла, а точку, из которой они выходят, — вершиной угла.
На рисунке 160 сторонами угла являются лучи ОА и ОБ, а его вершиной — точка О. Этот угол обозначают так: АОВ.
При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначить и одной буквой — названием его вершины.
Например, вместо «угол АОВ» пишут короче: «угол О».
Вместо слова «угол» пишут знак .
Например, AОВ, O.
На рисунке 161 точки С и D лежат внутри угла АОВ, точки X и У лежат вне этого угла, а точки М и Н — на сторонах угла.
Как и все геометрические фигуры, углы сравниваются с помощью наложения.
Если один угол можно наложить на другой так, что они совпадут, то эти углы равны.
Например, на рисунке 162 ABC = MNK.
Из вершины угла СОК (рис. 163) проведен луч ОР. Он разбивает угол СОК на два угла — СОР и РОК. Каждый из этих углов меньше угла СОК.
Он разбивает угол СОК на два угла — СОР и РОК. Каждый из этих углов меньше угла СОК.
Пишут: COP
Прямой и развернутый угол
Два дополнительных друг другу луча образуют развернутый угол. Стороны этого угла вместе составляют прямую линию, на которой лежит вершина развернутого угла (рис. 164).
Часовая и минутная стрелки часов образуют в 6 ч развернутый угол (рис. 165).
Согнем два раза пополам лист бумаги, а потом развернем его (рис. 166).
Линии сгиба образуют 4 равных угла. Каждый из этих углов равен половине развернутого угла. Такие углы называют прямыми.
Прямым углом называют половину развернутого угла.
Чертежный треугольник
Для построения прямого угла пользуются чертежным треугольником (рис. 167). Чтобы построить прямой угол, одной из сторон которого является луч ОЛ, надо:
а) расположить чертежный треугольник так, чтобы вершина его прямого угла совпала с точкой О, а одна из сторон пошла по лучу ОА;
б) провести вдоль второй стороны треугольника луч ОВ.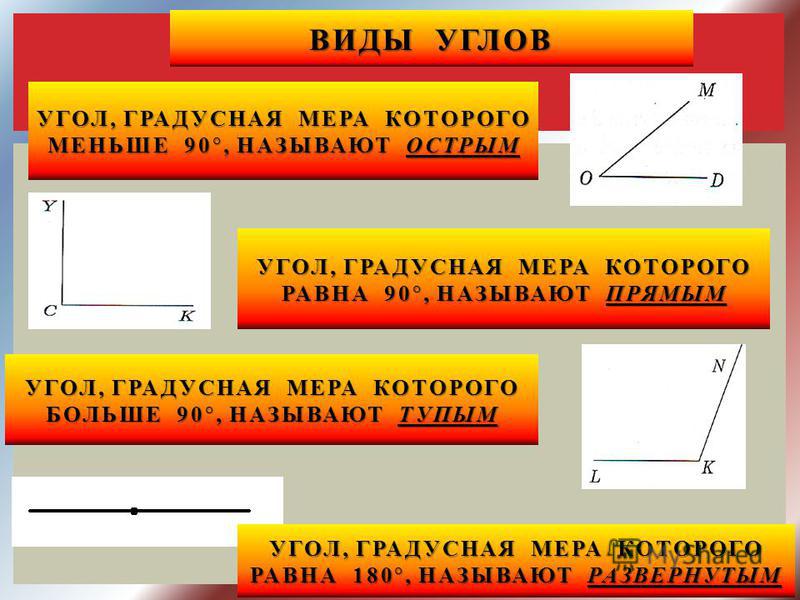
В результате получим прямой угол АОВ.
Вопросы к теме
1.Что такое угол?
2.Какой угол называют развернутым?
3.Какие углы называют равными?
4.Какой угол называют прямым?
5.Как строят прямой угол с помощью чертежного треугольника?
Нам с вами уже известно, что любой угол делит плоскость на две части. Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.
Теперь давайте посмотрим на рисунок, на котором как раз и изображен развернутый угол О.
Если мы возьмем и проведем из вершины развернутого угла луч, то он разделит данный развернутый угол еще на два угла, которые будут иметь одну общую сторону, а другие два угла будут составлять прямую. То есть, с одного развернутого угла мы получили два смежных.
Если мы возьмем развернутый угол и проведем биссектрису, то эта биссектриса разделит развернутый угол на два прямых угла.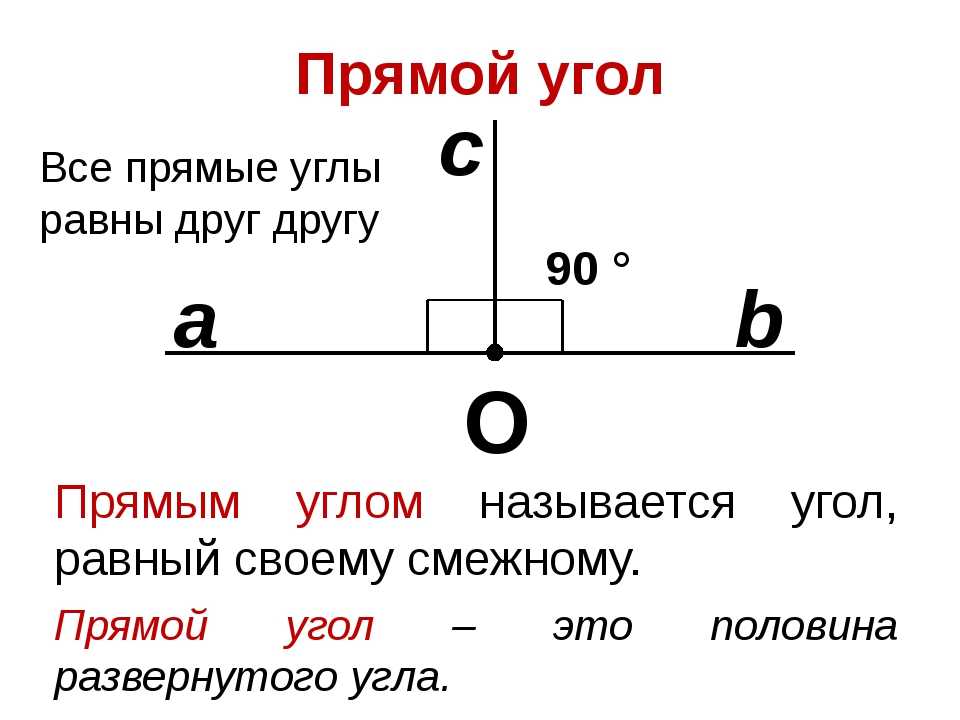
А, в том случае, если мы из вершины развернутого угла проведем произвольный луч, который не является биссектрисой, то такой луч разделит развернутый угол на два угла, один из которых будет острым, а другой тупым.
Свойства развернутого угла
Развернутый угол обладает такими свойствами:
Во-первых, стороны развёрнутого угла являются антипараллельными и образуют прямую;
во-вторых, развернутый угол равен 180°;
в-третьих, два смежных угла образуют развернутый угол;
в-четвертых, развернутый угол составляет половину полного угла;
в-пятых, полный угол будет равен сумме двух развёрнутых углов;
в-шестых, половина развернутого угла составляет прямой угол.
Измерение углов
Чтобы измерить любой угол, для этих целей чаще всего используют транспортир, у которого единица измерения равна одному градусу. При измерении углов следует помнить, что любой угол имеет свою определенную градусную меру и естественно эта мера больше нуля. А развернутый угол, как нам уже известно, равен 180 градусам.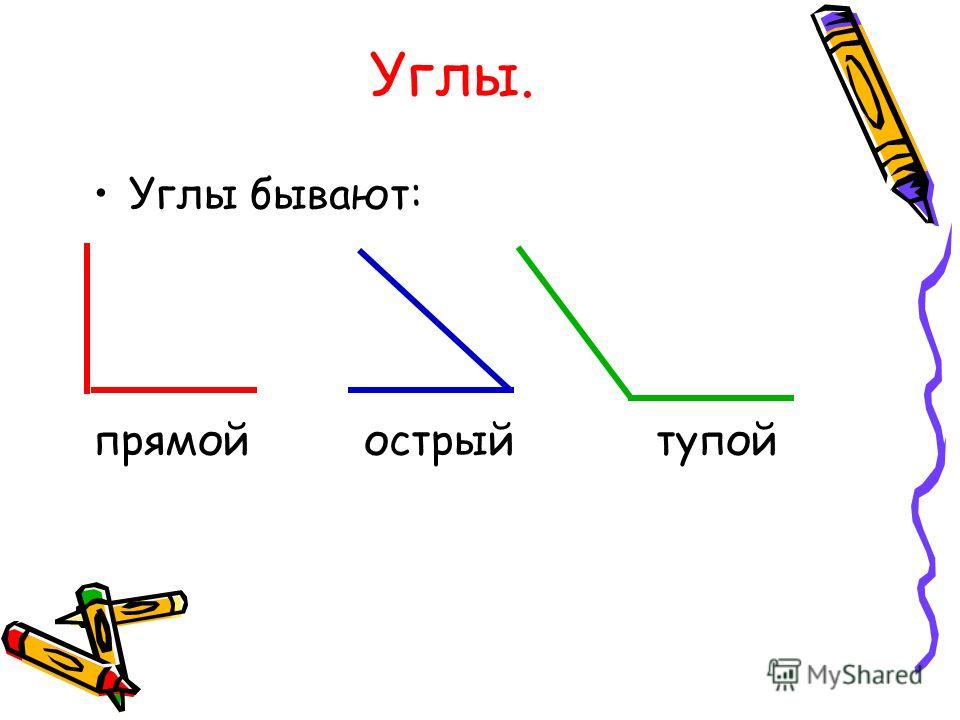
То есть, если мы с вами возьмем любую плоскость круга и разделим ее радиусами на 360 равных частей, то 1/360 часть данного круга будет являться угловым градусом. Как вы уже знаете, что градус обозначается определенным значком, который имеет такой вид: « ° ».
Теперь мы также знаем, что один градус 1° = 1/360 части круга. Если угол равен плоскости круга и составляет 360 градусов, то такой угол является полным.
А теперь мы возьмем, и плоскость круга поделим с помощью двух радиусов, лежащих на одной прямой линии, на две равные части. То в этом случае, плоскость полукруга составит половину полного угла, то есть 360: 2 = 180°. Мы с вами получили угол, который равен полуплоскости круга и имеет 180°. Это и есть развернутый угол.
Практическое задание
1613. Назовите углы, изображенные на рисунке 168. Запишите их обозначения.
1614. Начертите четыре луча: ОА, ОВ, ОС и OD. Запишите названия шести углов, сторонами которых являются эти лучи. На сколько частей эти лучи делят плоскость ?
1615.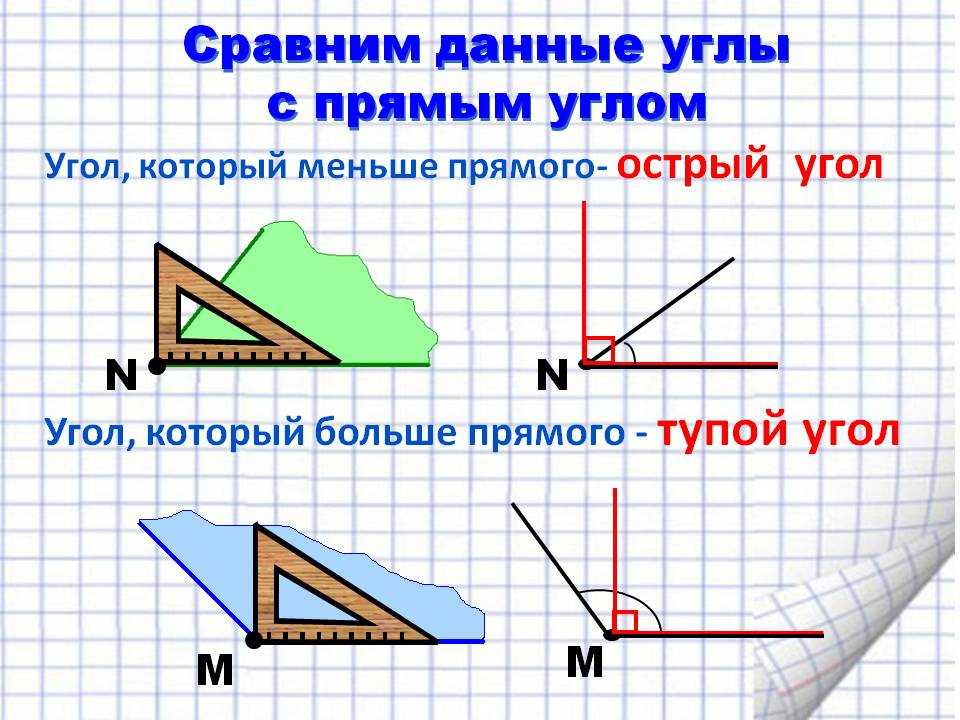 Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ?
Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ?
1616. Начертите угол MOD и проведите внутри него луч ОТ. Назовите и обозначьте углы, на которые этот луч делит угол MOD.
1617. Минутная стрелка за 10 мин повернулась на угол АОВ, за следующие 10 мин — на угол ВОС, а еще за 15 мин — на угол COD. Сравните углы АОВ и ВОС, ВОС и COD, АОС и АОВ, АОС и COD (рис. 170).
1618. Изобразите с помощью чертежного треугольника 4 прямых угла в разных положениях.
1619. С помощью чертежного треугольника найдите на рисунке 171 прямые углы. Запишите их обозначения.
1620. Укажите прямые углы в классной комнате.
а) 0,09 200; б) 208 0,4; в) 130 0,1 + 80 0,1.
1629. Сколько процентов от 400 составляет число 200; 100; 4; 40; 80; 400; 600?
1630. Найдите пропущенное число:
а) 2 5 3 б) 2 3 5
13 6 12 1
2 3? 42?
1631. Начертите квадрат, сторона которого равна длине 10 клеток тетради. Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха?
Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха?
1632. За учебный год Петя израсходовал 40% купленных в начале года тетрадей, и у него осталось 30 тетрадей. Сколько тетрадей было куплено для Пети в начале учебного года?
1633. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди?
1634. Построенный в древности Александрийский маяк, который называли одним из семи чудес света, выше башен Московского Кремля в 1,7 раза, но ниже здания Московского университета на 119 м. Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.
1635. Найдите с помощью микрокалькулятора:
а) 4,5% от 168; в) 28,3% от 569,8;
б) 147,6% от 2500; г) 0,09% от 456 800.
1636. Решите задачу:
1) Площадь огорода 6,4 а.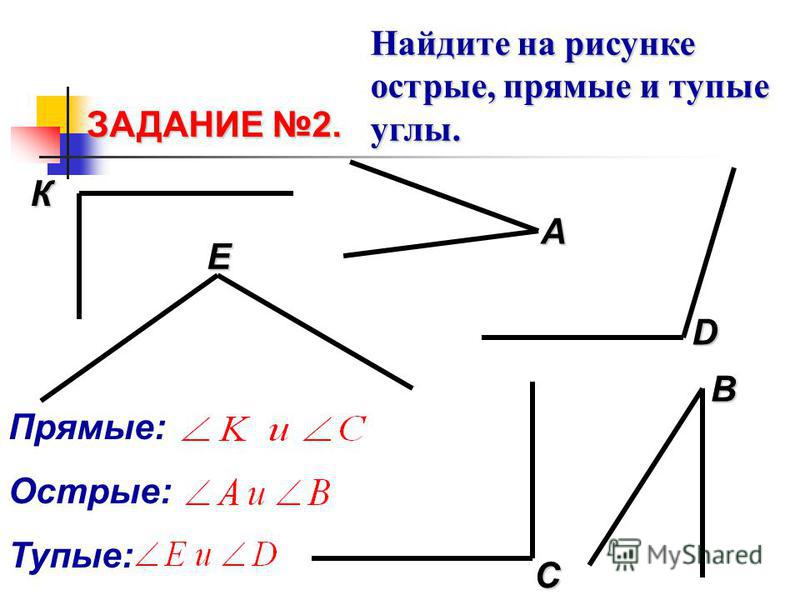 В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать?
В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать?
2) У Сережи было 4,8 ч свободного времени. 35% этого времени он потратил на чтение книги, а 40% на просмотр передач по телевизору. Сколько времени у него еще осталось?
1637. Выполните действия:
1) ((23,79: 7,8 — 6,8: 17) 3,04 — 2,04) 0,85;
2) (3,42: 0,57 9,5 — 6,6) : ((4,8 — 1,6) (3,1 + 0,05)).
1638. Начертите угол ВАС и отметьте по одной точке внутри угла, вне угла и на сторонах угла.
1639. Какие из отмеченных на рисунке 172 точек лежат внутри угла АМК.Какая точка лежит внутри угла АМВ> но вне угла АМК.Какие точки лежат на сторонах угла АМК?
1640. Найдите с помощью чертежного треугольника прямые углы на рисунке 173.
1641. Постройте квадрат со стороной 43 мм. Вычислите его периметр и площадь.
1642. Найдите значение выражения:
а) 14,791: а + 160,961: b, если а = 100, b = 10;
б) 361,62с + 1848: d, если с = 100, d =100.
1643. Рабочий должен был изготовить 450 деталей. В первый день он изготовил 60% деталей, а остальные — во второй. Сколько деталей изготовил рабочий во второй день?
1644. В библиотеке было 8000 книг. Через год число их увеличилось на 2000 книг. На сколько процентов увеличилось число книг в библиотеке?
1645. Грузовики в первый день проехали 24% намеченного пути, во второй день — 46% пути, а в третий — остальные 450 км. Сколько километров проехали эти грузовики?
1646. Найдите, сколько составляют:
а) 1% от тонны; в) 5% от 7 т;
б) 1% от литра; г) 6% от 80 км.
1647. Масса детеныша моржа в 9 раз меньше массы взрослого моржа. Какова масса взрослого моржа, если вместе с детенышем их масса равна 0,9 т?
1648. Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат?
Н. Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
С понятием угол учащиеся знакомятся еще в начальной школе. Но как геометрическую фигуру, имеющую определенные свойства, начинают изучать его с 7-го класса в геометрии. Кажется, довольно простая фигура , что о ней можно сказать. Но, приобретая новые знания, школьники всё больше понимают, что можно узнать о ней довольно интересные факты.
Вконтакте
Когда изучаются
Школьный курс геометрии разделён на два раздела: планиметрию и стереометрию. В каждом из них немалое внимание уделяется углам :
- В планиметрии дается их основное понятие, происходит знакомство с их видами по величине. Более подробно изучаются свойства каждого вида треугольников. Появляются новые определения для учащихся – это геометрические фигуры, образованные при пересечении двух прямых между собой и пересечении нескольких прямых секущей.
- В стереометрии изучаются пространственные углы – двугранные и трехгранные.

Внимание! В данной статье рассматриваются все виды и свойства углов именно в планиметрии.
Определение и измерение
Приступая к изучению, первоначально определяют, что такое угол в планиметрии.
Если на плоскости взять определённую точку и провести от нее два произвольных луча, то получим геометрическую фигуру – угол, состоящую из следующих элементов:
- вершина – та точка, из которой и проводились лучи, обозначается заглавной буквой латинского алфавита;
- стороны – полупрямые, проведенные из вершины.
Все элементы, образующие рассматриваемую нами фигуру, разбивают плоскость на две части :
- внутренняя — в планиметрии не превышает 180 градусов;
- внешняя.
Принцип измерения углов в планиметрии объясняют на интуитивной основе. Для начала знакомят учащихся с понятием развернутый угол.
Важно! Угол называется развернутым, если полупрямые, выходящие из его вершины, образуют прямую линию. Неразвернутый угол это все остальные случаи.
Неразвернутый угол это все остальные случаи.
Если его разделить на 180 равных частей, то принято считать меру одной части равной 10. В таком случае говорят, что измерение производится в градусах, а градусная мера такой фигуры составляет 180 градусов.
Основные виды
Виды углов подразделяются по таким критериям, как градусная мера, характер их образования и представленные ниже категории.
По величине
Учитывая величину, углы разделяют на:
- развернутый;
- прямой;
- тупой;
- острый.
Какой угол называется развернутым, было представлено выше. Определимся с понятием прямого.
Его можно получить при делении развернутого на две равные части. В этом случае легко ответить на вопрос: прямой угол, сколько градусов составляет?
180 градусов развернутого делим на 2 и получаем, что прямой угол равен 90 градусам . Это замечательная фигура, так как многие факты в геометрии связаны именно с ней.
Имеет она и свои особенности в обозначении.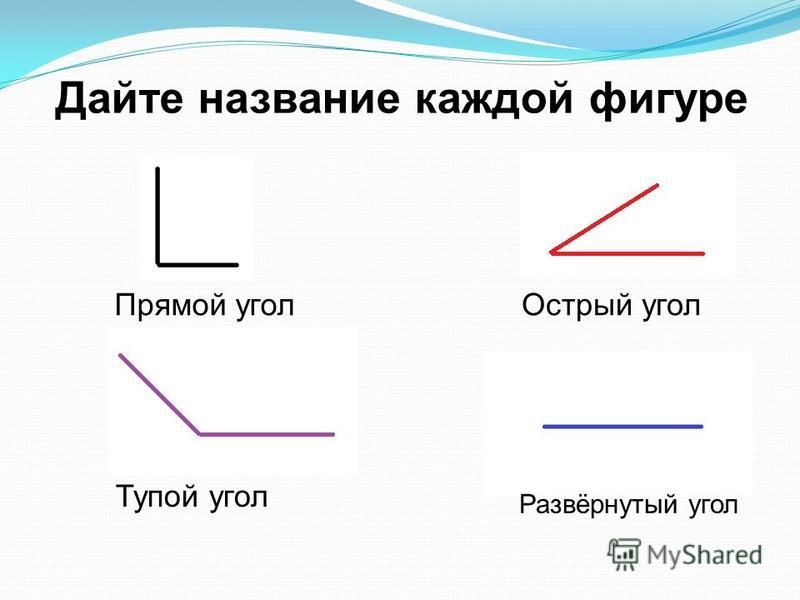 Чтобы на рисунке показать прямой угол, его обозначают не дугой, а квадратиком.
Чтобы на рисунке показать прямой угол, его обозначают не дугой, а квадратиком.
Углы, которые получаются при делении произвольным лучом прямого, называют острыми. По логике вещей следует, что острый угол меньше прямого, но его мера отлична от 0 градусов. То есть, он имеет величину от 0 до 90 градусов.
Тупой угол больше прямого, но меньше развернутого. Его градусная мера варьируется в интервале от 90 до 180 градусов.
Данный элемент можно разбить на разные виды рассматриваемых фигур, исключая развёрнутый.
Вне зависимости от того, как разбивается неразвернутый угол, всегда пользуются базовой аксиомой планиметрии — «основное свойство измерения».
При разделении угла одним лучом или несколькими, градусная мера данной фигуры равна сумме мер углов, на которые она разбита.
На уровне 7-го класса виды углов по их величине на этом заканчиваются. Но для повышения эрудиции можно добавить, что существуют и другие разновидности, которые обладают градусной мерой больше 180 градусов. Их называют выпуклыми.
Их называют выпуклыми.
Фигуры при пересечении прямых
Следующие типы углов, с которыми знакомятся учащиеся – элементы, образованные при пересечении двух прямых. Фигуры, которые размещаются друг напротив друга, называют вертикальными. Их отличительное свойство – они равны.
Элементы, которые прилегают к одной и той же прямой, называют смежными. Теорема, отображающая их свойство, говорит о том, что смежные углы в сумме дают 180 градусов .
Элементы в треугольнике
Если рассматривать фигуру как элемент в треугольнике, то углы подразделяют на внутренний и внешний. Треугольник ограничен тремя отрезками и состоит из трёх вершин. Углы, расположенные внутри треугольника при каждой вершине, называют внутренними .
Если взять любой внутренний элемент при любой вершине и продлить любую сторону, то угол, который образовался и является смежным с внутренним, называется внешним. Эта пара элементов имеет следующее свойство: их сумма равна 180 градусам.
Пересечение двух прямых секущей
Пересечение прямых
При пересечении двух прямых секущей также образуются углы , которые принято распределять по парам.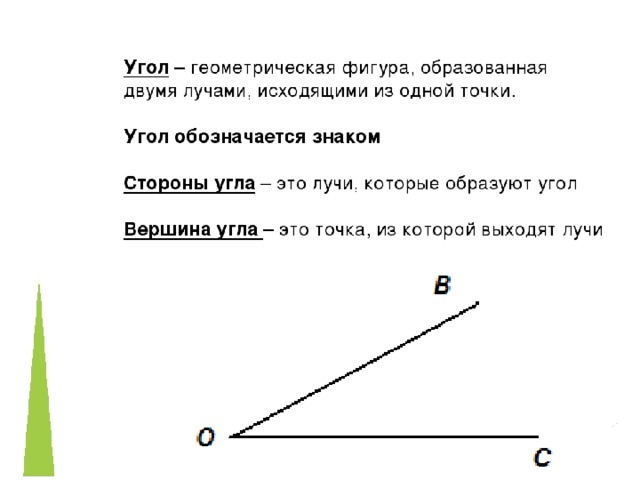 Каждая пара элементов имеет свое название. Выглядит это следующим образом:
Каждая пара элементов имеет свое название. Выглядит это следующим образом:
- внутренние накрест лежащие:∟4 и ∟6, ∟3 и ∟5;
- внутренние односторонние: ∟4 и ∟5, ∟3 и ∟6;
- соответствующие: ∟1 и ∟5, ∟2 и ∟6, ∟4 и ∟8, ∟3 и ∟7.
В том случае, когда секущая пересекает две
В этой статье мы всесторонне разберем одну из основных геометрических фигур – угол. Начнем со вспомогательных понятий и определений, которые нас приведут к определению угла. После этого приведем принятые способы обозначения углов. Далее подробно разберемся с процессом измерения углов. В заключении покажем как можно отметить углы на чертеже. Все теорию мы снабдили необходимыми чертежами и графическими иллюстрациями для лучшего запоминания материала.
Навигация по странице.
Определение угла.
Угол является одной из важнейших фигур в геометрии. Определение угла дается через определение луча. В свою очередь представление о луче невозможно получить без знания таких геометрических фигур как точка, прямая и плоскость. Поэтому, перед знакомством с определением угла, рекомендуем освежить в памяти теорию из разделов и .
Поэтому, перед знакомством с определением угла, рекомендуем освежить в памяти теорию из разделов и .
Итак, будем отталкиваться от понятий точки, прямой на плоскости и плоскости.
Дадим сначала определение луча.
Пусть нам дана некоторая прямая на плоскости. Обозначим ее буквой a . Пусть O – некоторая точка прямой a . Точка O разделяет прямую a на две части. Каждая из этих частей вместе с точкой О называется лучом , а точка О называется началом луча . Еще можно услышать, что луч называют полупрямой .
Для краткости и удобства ввели следующие обозначения для лучей: луч обозначают либо малой латинской буквой (например, луч p или луч k ), либо двумя большими латинскими буквами, первая из которых соответствует началу луча, а вторая обозначает некоторую точку этого луча (например, луч ОА или луч СD ). Покажем изображение и обозначение лучей на чертеже.
Теперь мы можем дать первое определение угла.
Определение.
Угол – это плоская геометрическая фигура (то есть целиком лежащая в некоторой плоскости), которую составляют два несовпадающих луча с общим началом. Каждый из лучей называют стороной угла , общее начало сторон угла называют вершиной угла .
Каждый из лучей называют стороной угла , общее начало сторон угла называют вершиной угла .
Возможен случай, когда стороны угла составляют прямую линию. Такой угол имеет свое название.
Определение.
Если обе стороны угла лежат на одной прямой, то такой угол называется развернутым .
Предлагаем Вашему вниманию графическую иллюстрацию развернутого угла.
Для обозначения угла используют значок угла «». Если стороны угла обозначены малыми латинскими буквами (например, одна сторона угла k
, а другая h
), то для обозначения этого угла после значка угла записывают подряд буквы, соответствующие сторонам, причем порядок записи значения не имеет (то есть, или ). Если стороны угла обозначены двумя большими латинскими буквами (к примеру, одна сторона угла OA
, а вторая сторона угла OB
), то угол обозначают следующим образом: после значка угла записывают три буквы, участвующие в обозначении сторон угла, причем буква, отвечающая вершине угла, располагается посередине (в нашем случае угол будет обозначен как или ). Если вершина угла не является вершиной еще какого-нибудь угла, то такой угол можно обозначать буквой, соответствующей вершине угла (например, ). Иногда можно видеть, что углы на чертежах отмечают цифрами (1
, 2
и т.д.), обозначают эти углы как и так далее. Для наглядности приведем рисунок, на котором изображены и обозначены углы.
Если вершина угла не является вершиной еще какого-нибудь угла, то такой угол можно обозначать буквой, соответствующей вершине угла (например, ). Иногда можно видеть, что углы на чертежах отмечают цифрами (1
, 2
и т.д.), обозначают эти углы как и так далее. Для наглядности приведем рисунок, на котором изображены и обозначены углы.
Любой угол разделяет плоскость на две части. При этом если угол не развернутый, то одну часть плоскости называют внутренней областью угла , а другую – внешней областью угла . Следующее изображение разъясняет, какая часть плоскости отвечает внутренней области угла, а какая — внешней.
Любую из двух частей, на которые развернутый угол разделяет плоскость, можно считать внутренней областью развернутого угла.
Определение внутренней области угла приводит нас ко второму определению угла.
Определение.
Угол – это геометрическая фигура, которую составляют два несовпадающих луча с общим началом и соответствующая внутренняя область угла.
Следует отметить, что второе определение угла строже первого, так как содержит больше условий. Однако не следует отметать первое определение угла, также не следует рассматривать первое и второе определения угла по отдельности. Поясним этот момент. Когда речь идет об угле как о геометрической фигуре, то под углом понимается фигура, составленная двумя лучами с общим началом. Если же возникает необходимость провести какие-либо действия с этим углом (например, измерение угла), то под углом уже следует понимать два луча с общим началом и внутренней областью (иначе возникла бы двоякая ситуация из-за наличия как внутренней так и внешней области угла).
Дадим еще определения смежных и вертикальных углов.
Определение.
Смежные углы – это два угла, у которых одна сторона общая, а две другие образуют развернутый угол.
Из определения следует, что смежные углы дополняют друг друга до развернутого угла.
Определение.
Вертикальные углы – это два угла, у которых стороны одного угла являются продолжениями сторон другого.
На рисунке изображены вертикальные углы.
Очевидно, что две пересекающиеся прямые образуют четыре пары смежных углов и две пары вертикальных углов.
Сравнение углов.
В этом пункте статьи мы разберемся с определениями равных и неравных углов, а также в случае неравных углов разъясним, какой угол считается большим, а какой меньшим.
Напомним, что две геометрические фигуры называются равными, если их можно совместить наложением.
Пусть нам даны два угла. Приведем рассуждения, которые помогут нам получить ответ на вопрос: «Равны эти два угла или нет»?
Очевидно, что мы всегда можем совместить вершины двух углов, а также одну сторону первого угла с любой из сторон второго угла. Совместим сторону первого угла с той стороной второго угла, чтобы оставшиеся стороны углов оказались по одну сторону от прямой, на которой лежат совмещенные стороны углов. Тогда, если две другие стороны углов совместятся, то углы называются равными .
Если же две другие стороны углов не совместятся, то углы называются неравными , причем меньшим считается тот угол, который составляет часть другого (большим является тот угол, который полностью содержит другой угол).
Очевидно, что два развернутых угла равны. Также очевидно, что развернутый угол больше любого неразвернутого угла.
Измерение углов.
Измерение углов основывается на сравнении измеряемого угла с углом, взятым в качестве единицы измерения. Процесс измерения углов выглядит так: начиная от одной из сторон измеряемого угла, его внутреннюю область последовательно заполняют единичными углами, плотно укладывая их один к другому. При этом запоминают количество уложенных углов, которое и дает меру измеряемого угла.
Фактически, в качестве единицы измерения углов может быть принят любой угол. Однако существует множество общепринятых единиц измерения углов, относящихся к различным областям науки и техники, они получили специальные названия.
Одной из единиц измерения углов является градус .
Определение.
Один градус – это угол, равный одной сто восьмидесятой части развернутого угла.
Градус обозначают символом «», следовательно, один градус обозначается как .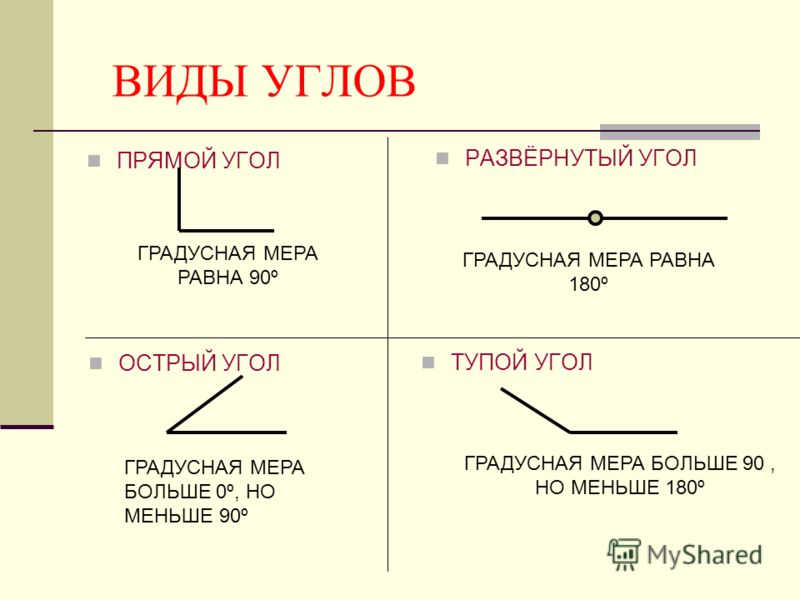
Таким образом, в развернутом угле мы можем уложить 180 углов в один градус. Это будет выглядеть как половинка круглого пирога, разрезанная на 180 равных кусочков. Очень важно: «кусочки пирога» плотно укладываются один к другому (то есть, стороны углов совмещаются), причем сторона первого угла совмещается с одной стороной развернутого угла, а сторона последнего единичного угла совпадет с другой стороной развернутого угла.
При измерении углов выясняют, сколько раз градус (или другая единица измерения углов) укладывается в измеряемом угле до полного покрытия внутренней области измеряемого угла. Как мы уже убедились, в развернутом угле градус укладывается ровно 180 раз. Ниже приведены примеры углов, в которых угол в один градус укладывается ровно 30 раз (такой угол составляет шестую часть развернутого угла) и ровно 90 раз (половина развернутого угла).
Для измерения углов, меньших одного градуса (или другой единицы измерения углов) и в случаях, когда угол не удается измерить целым числом градусов (взятых единиц измерения), приходится использовать части градуса (части взятых единиц измерения).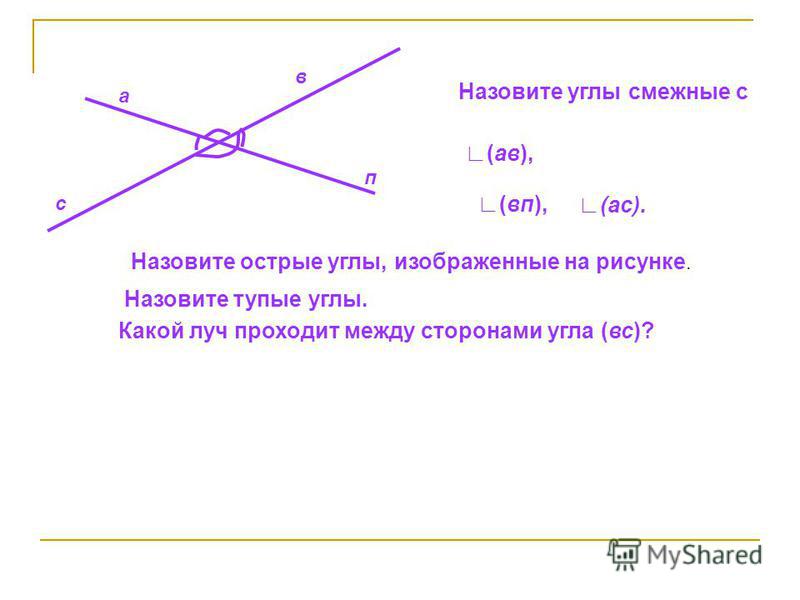 Определенные части градуса получили специальные названия. Наибольшее распространение получили, так называемые, минуты и секунды.
Определенные части градуса получили специальные названия. Наибольшее распространение получили, так называемые, минуты и секунды.
Определение.
Минута – это одна шестидесятая часть градуса.
Определение.
Секунда – это одна шестидесятая часть минуты.
Иными словами, в минуте содержится шестьдесят секунд, а в градусе – шестьдесят минут (3600 секунд). Для обозначения минут используют символ «», а для обозначения секунд – символ «» (не путайте со знаками производной и второй производной). Тогда при введенных определениях и обозначениях имеем , а угол, в котором укладываются 17 градусов 3 минуты и 59 секунд, можно обозначить как .
Определение.
Градусной мерой угла называется положительное число, которое показывает сколько раз градус и его части укладываются в данном угле.
Например, градусная мера развернутого угла равна ста восьмидесяти, а градусная мера угла равна .
Для измерения углов существуют специальные измерительные приборы, наиболее известным из них является транспортир.
Если известно и обозначение угла (к примеру, ) и его градусная мера (пусть 110 ), то используют краткую запись вида и говорят: «Угол АОВ равен ста десяти градусам».
Из определений угла и градусной меры угла следует, что в геометрии мера угла в градусах выражается действительным числом из интервала (0, 180] (в тригонометрии рассматривают углы с произвольной градусной мерой, их называют ). Угол в девяносто градусов имеет специальное название, его называют прямым углом . Угол меньший 90 градусов называется острым углом . Угол больший девяноста градусов называется тупым углом . Итак, мера острого угла в градусах выражается числом из интервала (0, 90) , мера тупого угла – числом из интервала (90, 180) , прямой угол равен девяноста градусам. Приведем иллюстрации острого угла, тупого угла и прямого угла.
Из принципа измерения углов следует, что градусные меры равных углов одинаковы, градусная мера большего угла больше градусной меры меньшего, а градусная мера угла, который составляют несколько углов, равна сумме градусных мер составляющих углов.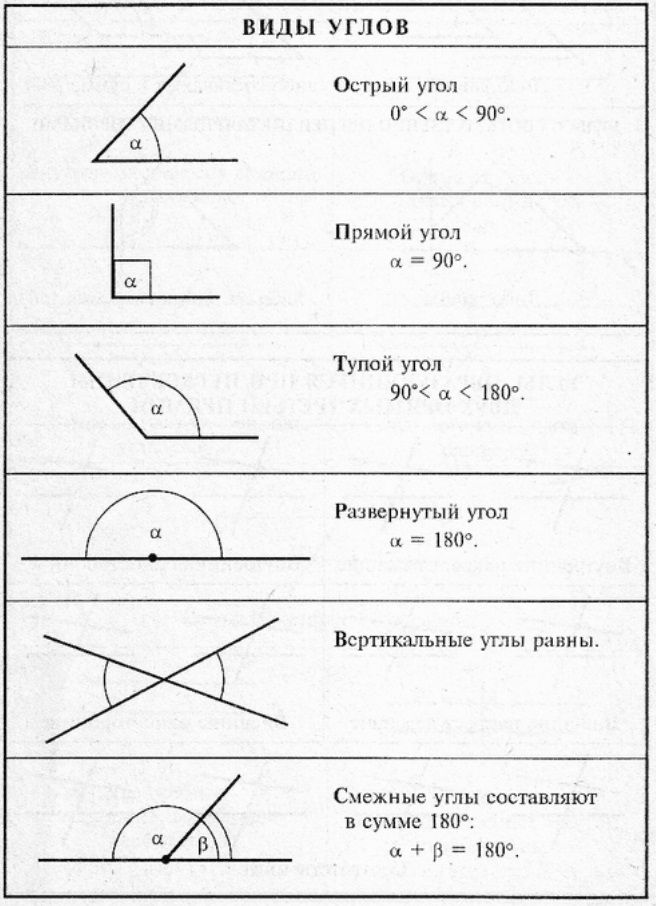 На рисунке ниже показан угол АОВ
, который составляют углы АОС
, СОD
и DОВ
, при этом .
На рисунке ниже показан угол АОВ
, который составляют углы АОС
, СОD
и DОВ
, при этом .
Таким образом, сумма смежных углов равна ста восьмидесяти градусам , так как они составляют развернутый угол.
Из этого утверждения следует, что . Действительно, если углы АОВ и СОD – вертикальные, то углы АОВ и ВОС — смежные и углы СОD и ВОС также смежные, поэтому, справедливы равенства и , откуда следует равенство .
Наряду с градусом удобна единица измерения углов, называемая радианом . Радианная мера широко используется в тригонометрии. Дадим определение радиана.
Определение.
Угол в один радиан – это центральный угол , которому соответствует длина дуги, равная длине радиуса соответствующей окружности.
Дадим графическую иллюстрацию угла в один радиан. На чертеже длина радиуса OA (как и радиуса OB ) равна длине дуги AB , поэтому, по определению угол AOB равен одному радиану.
Для обозначения радианов используют сокращение «рад».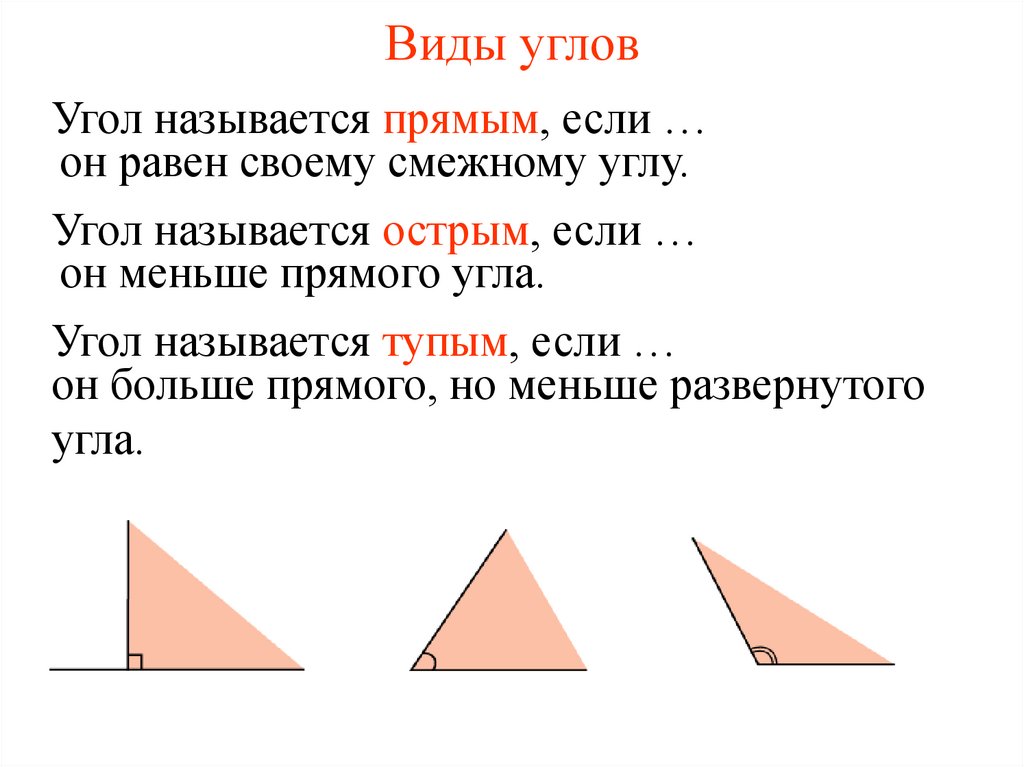 Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.
Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.
Стоит отдельно отметить, что величина угла, выраженная в радианах, не зависит от длины радиуса окружности. Это связано с тем, что фигуры, ограниченные данным углом и дугой окружности с центром в вершине данного угла, подобны между собой.
Измерение углов в радианах можно выполнять так же, как и измерение углов в градусах: выяснить, сколько раз угол в один радиан (и его части) укладываются в данном угле. А можно вычислить длину дуги соответствующего центрального угла, после чего разделить ее на длину радиуса.
Для нужд практики полезно знать, как соотносятся между собой градусная и радианная меры, так как довольно часть приходится осуществлять . В указанной статье установлена связь между градусной и радианной мерой угла, и приведены примеры перевода градусов в радианы и обратно.
Обозначение углов на чертеже.

На чертежах для удобства и наглядности углы можно отмечать дугами, которые принято проводить во внутренней области угла от одной стороны угла до другой. Равные углы отмечают одинаковым количеством дуг, неравные углы – различным количеством дуг. Прямые углы на чертеже обозначают символом вида «», который изображают во внутренней области прямого угла от одной стороны угла до другой.
Если на чертеже приходится отмечать много различных углов (обычно больше трех), то при обозначении углов кроме обычных дуг допустимо использование дуг какого-либо специального вида. К примеру, можно изобразить зубчатые дуги, или нечто подобное.
Следует отметить, что не стоит увлекаться с обозначением углов на чертежах и не загромождать рисунки. Рекомендуем обозначать только те углы, которые необходимы в процессе решения или доказательства.
Список литературы.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.

- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
- Погорелов А.В., Геометрия. Учебник для 7-11 классов общеобразовательных учреждений.
Произвольный тупой угол. Прямой, тупой, острый и развернутый угол. Смотреть что такое «Острый угол» в других словарях
В этой статье мы всесторонне разберем одну из основных геометрических фигур – угол. Начнем со вспомогательных понятий и определений, которые нас приведут к определению угла. После этого приведем принятые способы обозначения углов. Далее подробно разберемся с процессом измерения углов. В заключении покажем как можно отметить углы на чертеже. Все теорию мы снабдили необходимыми чертежами и графическими иллюстрациями для лучшего запоминания материала.
Навигация по странице.
Определение угла.
Угол является одной из важнейших фигур в геометрии. Определение угла дается через определение луча. В свою очередь представление о луче невозможно получить без знания таких геометрических фигур как точка, прямая и плоскость.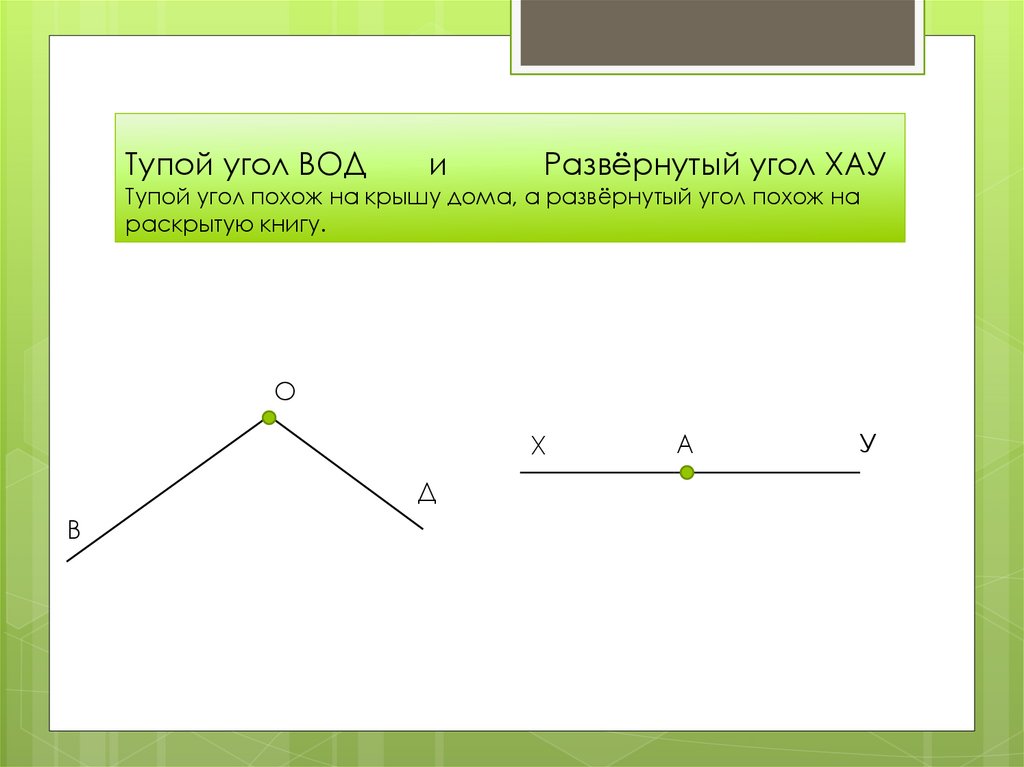 Поэтому, перед знакомством с определением угла, рекомендуем освежить в памяти теорию из разделов и .
Поэтому, перед знакомством с определением угла, рекомендуем освежить в памяти теорию из разделов и .
Итак, будем отталкиваться от понятий точки, прямой на плоскости и плоскости.
Дадим сначала определение луча.
Пусть нам дана некоторая прямая на плоскости. Обозначим ее буквой a . Пусть O – некоторая точка прямой a . Точка O разделяет прямую a на две части. Каждая из этих частей вместе с точкой О называется лучом , а точка О называется началом луча . Еще можно услышать, что луч называют полупрямой .
Для краткости и удобства ввели следующие обозначения для лучей: луч обозначают либо малой латинской буквой (например, луч p или луч k ), либо двумя большими латинскими буквами, первая из которых соответствует началу луча, а вторая обозначает некоторую точку этого луча (например, луч ОА или луч СD ). Покажем изображение и обозначение лучей на чертеже.
Теперь мы можем дать первое определение угла.
Определение.
Угол – это плоская геометрическая фигура (то есть целиком лежащая в некоторой плоскости), которую составляют два несовпадающих луча с общим началом. Каждый из лучей называют стороной угла , общее начало сторон угла называют вершиной угла .
Каждый из лучей называют стороной угла , общее начало сторон угла называют вершиной угла .
Возможен случай, когда стороны угла составляют прямую линию. Такой угол имеет свое название.
Определение.
Если обе стороны угла лежат на одной прямой, то такой угол называется развернутым .
Предлагаем Вашему вниманию графическую иллюстрацию развернутого угла.
Для обозначения угла используют значок угла «». Если стороны угла обозначены малыми латинскими буквами (например, одна сторона угла k
, а другая h
), то для обозначения этого угла после значка угла записывают подряд буквы, соответствующие сторонам, причем порядок записи значения не имеет (то есть, или ). Если стороны угла обозначены двумя большими латинскими буквами (к примеру, одна сторона угла OA
, а вторая сторона угла OB
), то угол обозначают следующим образом: после значка угла записывают три буквы, участвующие в обозначении сторон угла, причем буква, отвечающая вершине угла, располагается посередине (в нашем случае угол будет обозначен как или ).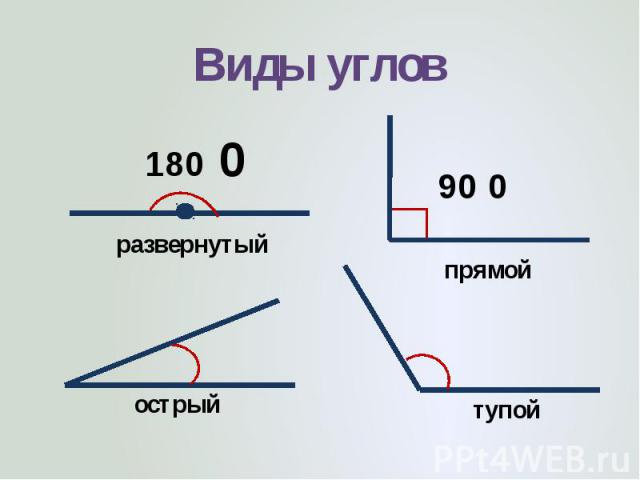 Если вершина угла не является вершиной еще какого-нибудь угла, то такой угол можно обозначать буквой, соответствующей вершине угла (например, ). Иногда можно видеть, что углы на чертежах отмечают цифрами (1
, 2
и т.д.), обозначают эти углы как и так далее. Для наглядности приведем рисунок, на котором изображены и обозначены углы.
Если вершина угла не является вершиной еще какого-нибудь угла, то такой угол можно обозначать буквой, соответствующей вершине угла (например, ). Иногда можно видеть, что углы на чертежах отмечают цифрами (1
, 2
и т.д.), обозначают эти углы как и так далее. Для наглядности приведем рисунок, на котором изображены и обозначены углы.
Любой угол разделяет плоскость на две части. При этом если угол не развернутый, то одну часть плоскости называют внутренней областью угла , а другую – внешней областью угла . Следующее изображение разъясняет, какая часть плоскости отвечает внутренней области угла, а какая — внешней.
Любую из двух частей, на которые развернутый угол разделяет плоскость, можно считать внутренней областью развернутого угла.
Определение внутренней области угла приводит нас ко второму определению угла.
Определение.
Угол – это геометрическая фигура, которую составляют два несовпадающих луча с общим началом и соответствующая внутренняя область угла.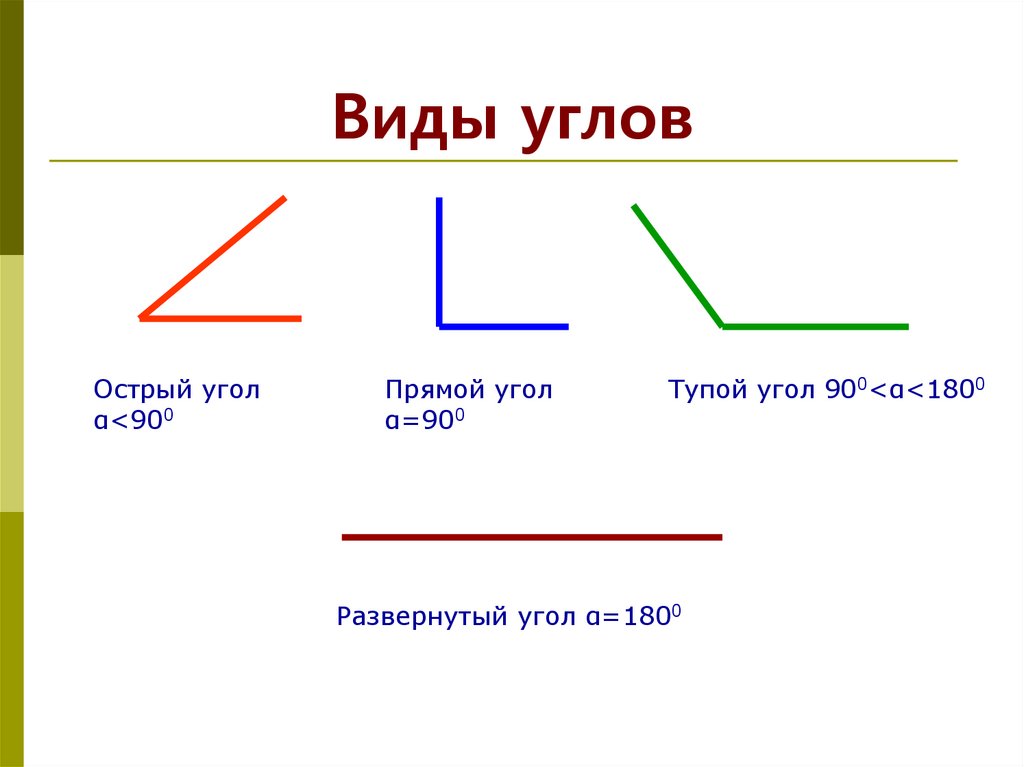
Следует отметить, что второе определение угла строже первого, так как содержит больше условий. Однако не следует отметать первое определение угла, также не следует рассматривать первое и второе определения угла по отдельности. Поясним этот момент. Когда речь идет об угле как о геометрической фигуре, то под углом понимается фигура, составленная двумя лучами с общим началом. Если же возникает необходимость провести какие-либо действия с этим углом (например, измерение угла), то под углом уже следует понимать два луча с общим началом и внутренней областью (иначе возникла бы двоякая ситуация из-за наличия как внутренней так и внешней области угла).
Дадим еще определения смежных и вертикальных углов.
Определение.
Смежные углы – это два угла, у которых одна сторона общая, а две другие образуют развернутый угол.
Из определения следует, что смежные углы дополняют друг друга до развернутого угла.
Определение.
Вертикальные углы – это два угла, у которых стороны одного угла являются продолжениями сторон другого.
На рисунке изображены вертикальные углы.
Очевидно, что две пересекающиеся прямые образуют четыре пары смежных углов и две пары вертикальных углов.
Сравнение углов.
В этом пункте статьи мы разберемся с определениями равных и неравных углов, а также в случае неравных углов разъясним, какой угол считается большим, а какой меньшим.
Напомним, что две геометрические фигуры называются равными, если их можно совместить наложением.
Пусть нам даны два угла. Приведем рассуждения, которые помогут нам получить ответ на вопрос: «Равны эти два угла или нет»?
Очевидно, что мы всегда можем совместить вершины двух углов, а также одну сторону первого угла с любой из сторон второго угла. Совместим сторону первого угла с той стороной второго угла, чтобы оставшиеся стороны углов оказались по одну сторону от прямой, на которой лежат совмещенные стороны углов. Тогда, если две другие стороны углов совместятся, то углы называются равными .
Если же две другие стороны углов не совместятся, то углы называются неравными , причем меньшим считается тот угол, который составляет часть другого (большим является тот угол, который полностью содержит другой угол).
Очевидно, что два развернутых угла равны. Также очевидно, что развернутый угол больше любого неразвернутого угла.
Измерение углов.
Измерение углов основывается на сравнении измеряемого угла с углом, взятым в качестве единицы измерения. Процесс измерения углов выглядит так: начиная от одной из сторон измеряемого угла, его внутреннюю область последовательно заполняют единичными углами, плотно укладывая их один к другому. При этом запоминают количество уложенных углов, которое и дает меру измеряемого угла.
Фактически, в качестве единицы измерения углов может быть принят любой угол. Однако существует множество общепринятых единиц измерения углов, относящихся к различным областям науки и техники, они получили специальные названия.
Одной из единиц измерения углов является градус .
Определение.
Один градус – это угол, равный одной сто восьмидесятой части развернутого угла.
Градус обозначают символом «», следовательно, один градус обозначается как .
Таким образом, в развернутом угле мы можем уложить 180 углов в один градус. Это будет выглядеть как половинка круглого пирога, разрезанная на 180 равных кусочков. Очень важно: «кусочки пирога» плотно укладываются один к другому (то есть, стороны углов совмещаются), причем сторона первого угла совмещается с одной стороной развернутого угла, а сторона последнего единичного угла совпадет с другой стороной развернутого угла.
При измерении углов выясняют, сколько раз градус (или другая единица измерения углов) укладывается в измеряемом угле до полного покрытия внутренней области измеряемого угла. Как мы уже убедились, в развернутом угле градус укладывается ровно 180 раз. Ниже приведены примеры углов, в которых угол в один градус укладывается ровно 30 раз (такой угол составляет шестую часть развернутого угла) и ровно 90 раз (половина развернутого угла).
Для измерения углов, меньших одного градуса (или другой единицы измерения углов) и в случаях, когда угол не удается измерить целым числом градусов (взятых единиц измерения), приходится использовать части градуса (части взятых единиц измерения). Определенные части градуса получили специальные названия. Наибольшее распространение получили, так называемые, минуты и секунды.
Определенные части градуса получили специальные названия. Наибольшее распространение получили, так называемые, минуты и секунды.
Определение.
Минута – это одна шестидесятая часть градуса.
Определение.
Секунда – это одна шестидесятая часть минуты.
Иными словами, в минуте содержится шестьдесят секунд, а в градусе – шестьдесят минут (3600 секунд). Для обозначения минут используют символ «», а для обозначения секунд – символ «» (не путайте со знаками производной и второй производной). Тогда при введенных определениях и обозначениях имеем , а угол, в котором укладываются 17 градусов 3 минуты и 59 секунд, можно обозначить как .
Определение.
Градусной мерой угла называется положительное число, которое показывает сколько раз градус и его части укладываются в данном угле.
Например, градусная мера развернутого угла равна ста восьмидесяти, а градусная мера угла равна .
Для измерения углов существуют специальные измерительные приборы, наиболее известным из них является транспортир.
Если известно и обозначение угла (к примеру, ) и его градусная мера (пусть 110 ), то используют краткую запись вида и говорят: «Угол АОВ равен ста десяти градусам».
Из определений угла и градусной меры угла следует, что в геометрии мера угла в градусах выражается действительным числом из интервала (0, 180] (в тригонометрии рассматривают углы с произвольной градусной мерой, их называют ). Угол в девяносто градусов имеет специальное название, его называют прямым углом . Угол меньший 90 градусов называется острым углом . Угол больший девяноста градусов называется тупым углом . Итак, мера острого угла в градусах выражается числом из интервала (0, 90) , мера тупого угла – числом из интервала (90, 180) , прямой угол равен девяноста градусам. Приведем иллюстрации острого угла, тупого угла и прямого угла.
Из принципа измерения углов следует, что градусные меры равных углов одинаковы, градусная мера большего угла больше градусной меры меньшего, а градусная мера угла, который составляют несколько углов, равна сумме градусных мер составляющих углов.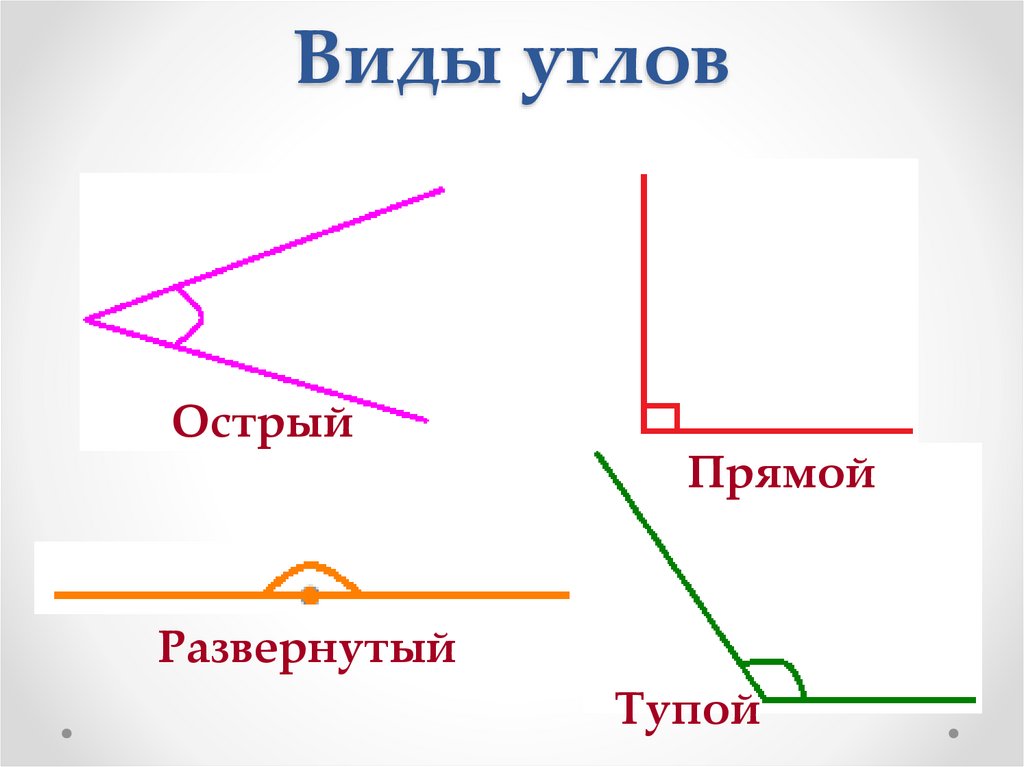 На рисунке ниже показан угол АОВ
, который составляют углы АОС
, СОD
и DОВ
, при этом .
На рисунке ниже показан угол АОВ
, который составляют углы АОС
, СОD
и DОВ
, при этом .
Таким образом, сумма смежных углов равна ста восьмидесяти градусам , так как они составляют развернутый угол.
Из этого утверждения следует, что . Действительно, если углы АОВ и СОD – вертикальные, то углы АОВ и ВОС — смежные и углы СОD и ВОС также смежные, поэтому, справедливы равенства и , откуда следует равенство .
Наряду с градусом удобна единица измерения углов, называемая радианом . Радианная мера широко используется в тригонометрии. Дадим определение радиана.
Определение.
Угол в один радиан – это центральный угол , которому соответствует длина дуги, равная длине радиуса соответствующей окружности.
Дадим графическую иллюстрацию угла в один радиан. На чертеже длина радиуса OA (как и радиуса OB ) равна длине дуги AB , поэтому, по определению угол AOB равен одному радиану.
Для обозначения радианов используют сокращение «рад». Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.
Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.
Стоит отдельно отметить, что величина угла, выраженная в радианах, не зависит от длины радиуса окружности. Это связано с тем, что фигуры, ограниченные данным углом и дугой окружности с центром в вершине данного угла, подобны между собой.
Измерение углов в радианах можно выполнять так же, как и измерение углов в градусах: выяснить, сколько раз угол в один радиан (и его части) укладываются в данном угле. А можно вычислить длину дуги соответствующего центрального угла, после чего разделить ее на длину радиуса.
Для нужд практики полезно знать, как соотносятся между собой градусная и радианная меры, так как довольно часть приходится осуществлять . В указанной статье установлена связь между градусной и радианной мерой угла, и приведены примеры перевода градусов в радианы и обратно.
Обозначение углов на чертеже.
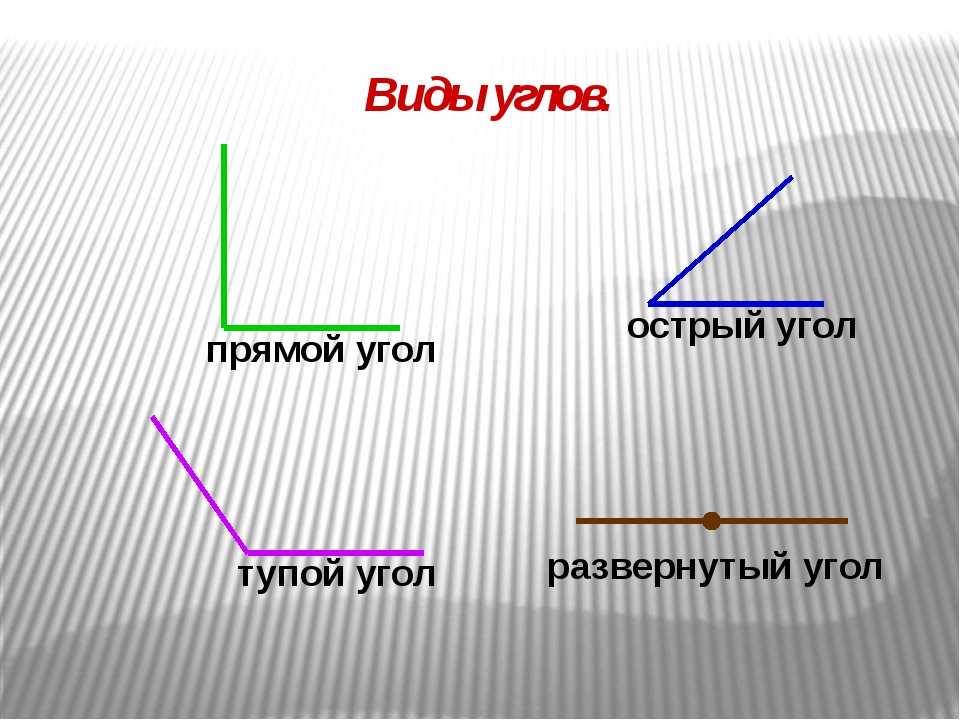
На чертежах для удобства и наглядности углы можно отмечать дугами, которые принято проводить во внутренней области угла от одной стороны угла до другой. Равные углы отмечают одинаковым количеством дуг, неравные углы – различным количеством дуг. Прямые углы на чертеже обозначают символом вида «», который изображают во внутренней области прямого угла от одной стороны угла до другой.
Если на чертеже приходится отмечать много различных углов (обычно больше трех), то при обозначении углов кроме обычных дуг допустимо использование дуг какого-либо специального вида. К примеру, можно изобразить зубчатые дуги, или нечто подобное.
Следует отметить, что не стоит увлекаться с обозначением углов на чертежах и не загромождать рисунки. Рекомендуем обозначать только те углы, которые необходимы в процессе решения или доказательства.
Список литературы.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.

- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
- Погорелов А.В., Геометрия. Учебник для 7-11 классов общеобразовательных учреждений.
Углом называется геометрическая фигура, которая состоит из двух различных лучей, исходящих из одной точки. В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О , и сторонами k и m .
На сторонах угла отмечены точки А и С. Этот угол можно обозначить как угол AOC. В середине обязательно должно стоять название точки, в которой находится вершина угла. Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок.
Развернутый и неразвернутый угол
Если у угла обе стороны лежат на одной прямой, то такой угол называется развернутым углом. То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О.
То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О.
Следует отметить, что любой угол, разделяет плоскость на две части. Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла. На рисунке ниже представлен неразвернутый угол и отмечены внешняя и внутренняя области этого угла.
В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области).
На рисунке ниже, точка А лежит вне угла О, точка B лежит на одной из сторон угла, а точка С лежит внутри угла.
Измерение углов
Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус . Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля.
Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля.
В зависимости от градусной меры углы делятся на несколько групп.
Острый угол это угол градусная мера которого до 90 градусов.
Прямой угол это угол градусная мера которого 90 градусов
Тупой угол это угол градусная мера которого больше 90 градусов. Острый угол — это угол меньше 90°. Тупой угол — это угол больше 90°, но меньше 180°. Прямой угол — это угол = 90°.
20. Какие углы называются смежными? Чему равна их сумма?
Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая) . Сумма смежных углов равна 180°. Или
Два угла называются смежными , если у них одна сторона общая, а другие стороны являются дополнительными лучами. сумма смежных углов равна 180°. Каждый из этих углов дополняет другой до развернутого угла.
21. Какие углы называются вертикальными? Каким свойством они обладают?
Вертикальные
углы — два угла, у которых стороны одного
являются продолжениями сторон другого. Вертикальные углы равны. (Вертикальными
называются углы, образованные пересекающимися прямыми
и не являющиеся прилегающими друг к
другу, то есть общей стороны у них нет,
но вертикальные углы имеют вершину в
одной точке. Вертикальные углы равны
между собой).
Вертикальные углы равны. (Вертикальными
называются углы, образованные пересекающимися прямыми
и не являющиеся прилегающими друг к
другу, то есть общей стороны у них нет,
но вертикальные углы имеют вершину в
одной точке. Вертикальные углы равны
между собой).
22. Какие прямые называются перпендикулярными? Две пересекающиеся прямые называются перпендикулярными (или взаимно перпендикулярными), если они образуют четыре прямых угла. Или Перпендикулярные прямые это прямые пересекающиеся под углом 90 градусов. Или Две прямые, образующие при пересечении прямые углы, называют перпендикулярными.
23. Объясните,
какой отрезок называется перпендикуляром,
проведенным из данной точки к данной
прямой. Что такое основание перпендикуляра?
называется отрезок прямой, перпендикулярной
к данной, который имеет одним из своих
концов их точку пересечения. Этот конец
отрезка называется основанием
перпендикуляра.Перпендикуляром
к данной прямой называется отрезок прямой, перпендикулярной
к данной, который имеет одним из своих
концов их точку пересечения.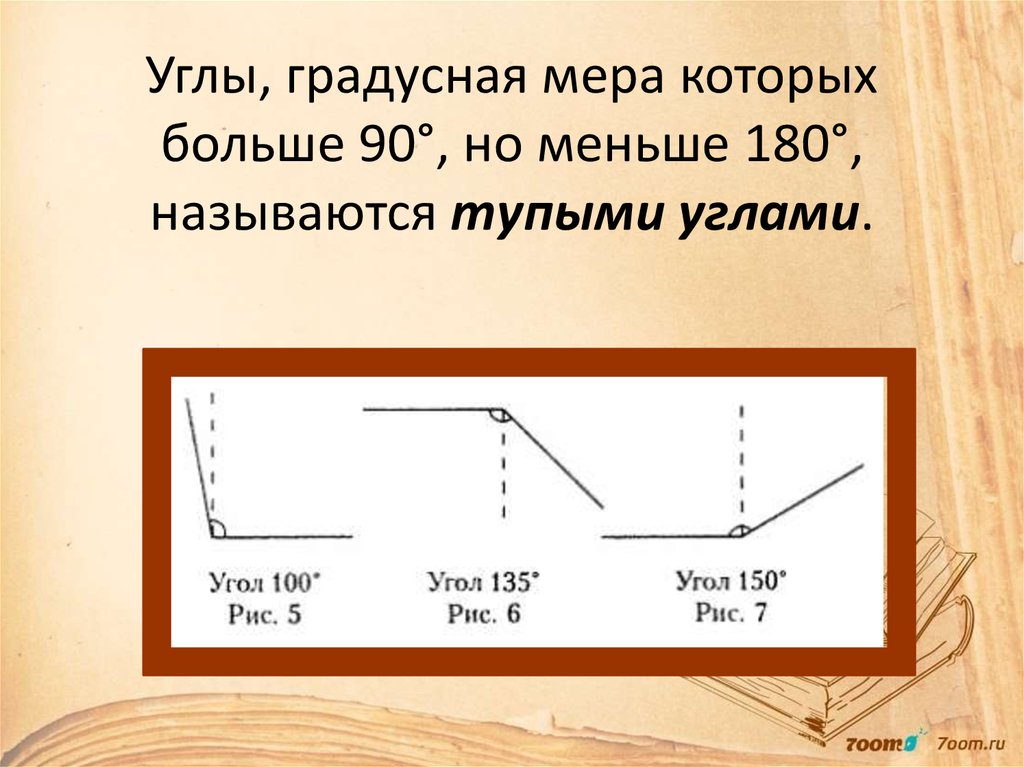 Конец
отрезка, лежащий на данной прямой,
называется основанием перпендикуляра.
Конец
отрезка, лежащий на данной прямой,
называется основанием перпендикуляра.
24. Что такое теорема и доказательство теоремы? В математике утверждение, справедливость которого устанавливается путем рассуждений, называется теоремой, а само рассуждение – доказательством теоремы.
Теоре́ма — утверждение, для которого в рассматриваемой теории существует доказательство (иначе говоря, вывод) . В отличие от теорем, аксиомами называются утверждения, которые, в рамках конкретной теории, принимаются истинными без всяких доказательств или обоснований. Доказательство — это утверждение, объясняющее теорему. Теорема — такая гипотеза, которую требуется доказать;Гипотеза всегда требует доказательства. Доказательство — доводы, подтверждающие действенность, правильность теоремы.
Давайте начнем с определения того, что такое угол. Во-первых, он является Во-вторых, он образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которую называют вершиной угла. Исходя из этих признаков, мы можем составить определение: угол — геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины).
Исходя из этих признаков, мы можем составить определение: угол — геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины).
Их классифицируют по градусной величине, по расположению относительно друг друга и относительно окружности. Начнем с видов углов по их величине.
Существует несколько их разновидностей. Рассмотрим подробнее каждый вид.
Основных типов углов всего четыре — прямой, тупой, острый и развернутый угол.
Прямой
Он выглядит так:
Его градусная мера всегда составляет 90 о, иначе говоря, прямой угол — это угол 90 градусов. Только они есть у таких четырехугольников, как квадрат и прямоугольник.
Тупой
Он имеет такой вид:
Градусная мера всегда больше 90 о, но меньше 180 о. Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках.
Острый
Он выглядит так:
Градусная мера острого угла всегда меньше 90 о.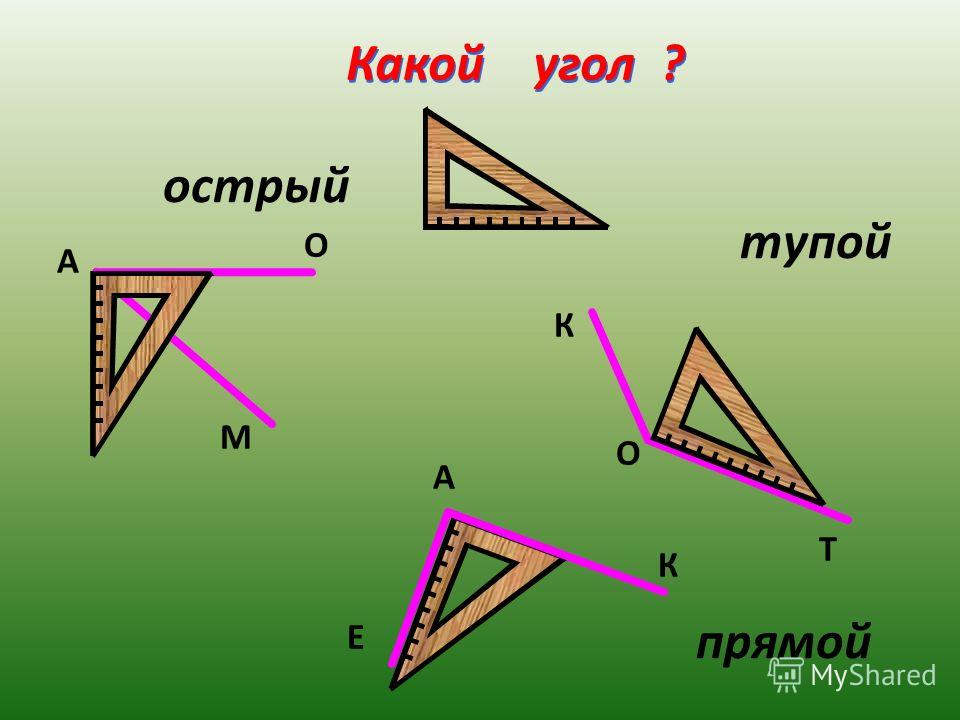 Он встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма.
Он встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма.
Развернутый
Развернутый угол имеет такой вид:
В многоугольниках он не встречается, но не менее важен, чем все остальные. Развернутый угол — это геометрическая фигура, градусная мера которой всегда равняется 180º. На нем можно построить проведя из его вершины один или несколько лучей в любых направлениях.
Есть еще несколько второстепенных видов углов. Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:
1. Нулевой
Он выглядит так:
Само название угла уже говорит о его величине. Его внутренняя область равняется 0 о, а стороны лежат друг на друге так, как показано на рисунке.
2. Косой
Косым может быть и прямой, и тупой, и острый, и развернутый угол. Главное его условие — он не должен равняться 0 о, 90 о, 180 о, 270 о.
3. Выпуклый
Выпуклыми являются нулевой, прямой, тупой, острый и развернутый углы.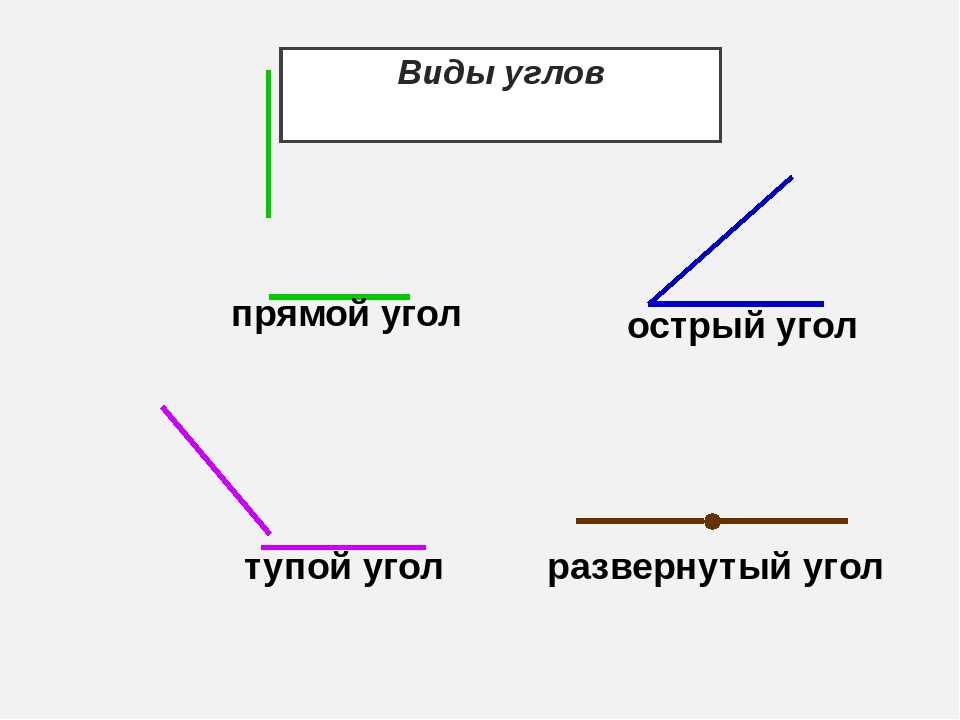 Как вы уже поняли, градусная мера выпуклого угла — от 0 о до 180 о.
Как вы уже поняли, градусная мера выпуклого угла — от 0 о до 180 о.
4. Невыпуклый
Невыпуклыми являются углы с градусной мерой от 181 о до 359 о включительно.
5. Полный
Полным является угол с градусной мерой 360 о.
Это все типы углов по их величине. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.
1. Дополнительные
Это два острых угла, образовывающие один прямой, т.е. их сумма 90 о.
2. Смежные
Смежные углы образуются, если через развернутый, точнее, через его вершину, провести луч в любом направлении. Их сумма равна 180 о.
3. Вертикальные
Вертикальные углы образуются при пересечении двух прямых. Их градусные меры равны.
Теперь перейдем к видам углов, расположенным относительно окружности. Их всего два: центральный и вписанный.
1. Центральный
Центральным является угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, стянутой сторонами.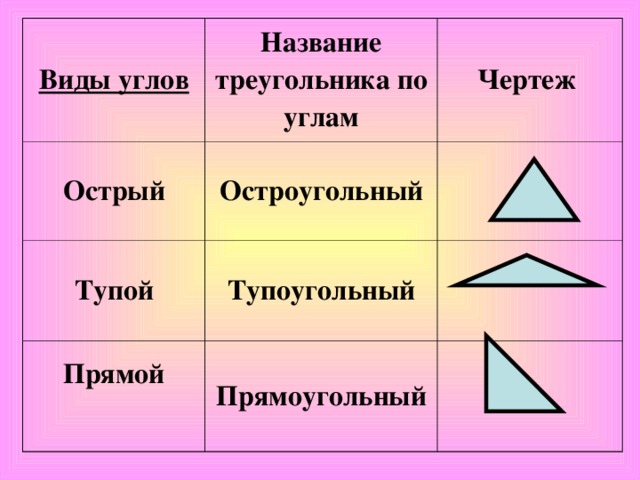
2. Вписанный
Вписанным называется угол, вершина которого лежит на окружности, и стороны которого ее пересекают. Его градусная мера равна половине дуги, на которую он опирается.
Это все, что касается углов. Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.
Тупой угол — определение, градус, треугольник, примеры
Тупой угол в геометрии определяется как угол, который больше 90° и меньше 180° . Часто в течение дня в течение 24 часов мы можем видеть часы, обрамляющие множество градусов тупого угла между минутной стрелкой и часовой стрелкой. Давайте узнаем больше о тупом угле и его свойствах.
| 1. | Что такое тупой угол? |
| 2. | Тупой угол Градус |
| 3. | Тупой угол в реальной жизни |
4.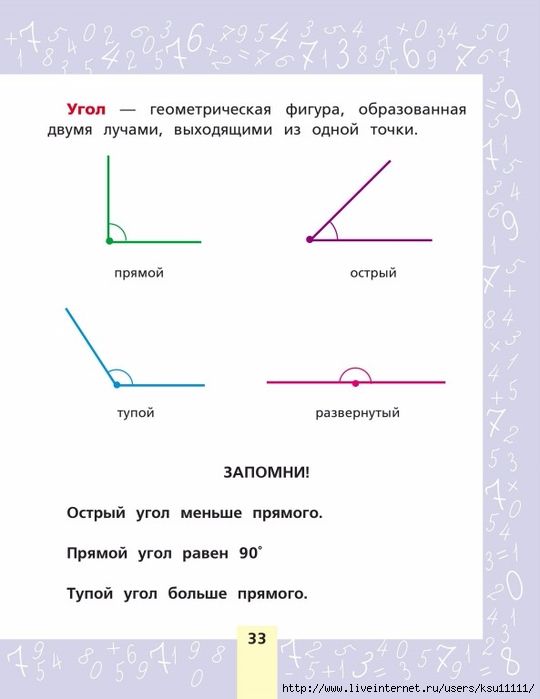 | Тупоугольный треугольник |
| 5. | Острые и тупые углы |
| 6. | Часто задаваемые вопросы о тупом угле |
Что такое тупой угол?
Определение тупой угол в геометрии говорится, что «угол, градусная мера которого больше 90° и меньше 180°, называется тупым углом». Другими словами, тупой угол — это угол между прямым углом и прямым углом. Посмотрите на некоторые примеры тупых углов, приведенные ниже.
Тупой угол Градус
В предыдущем разделе мы читали, что угол, который меньше 180 градусов и больше 90 градусов, называется тупым углом. Примеры градусов тупого угла: 165°, 135°, 110°, 179°.°, 91° и т. д. Следовательно, градус тупого угла лежит в пределах от 90° до 180°.
Тупые углы в реальной жизни
Мы знаем, что углы больше 90° и меньше 180° называются тупыми. Вот несколько реальных примеров тупых углов.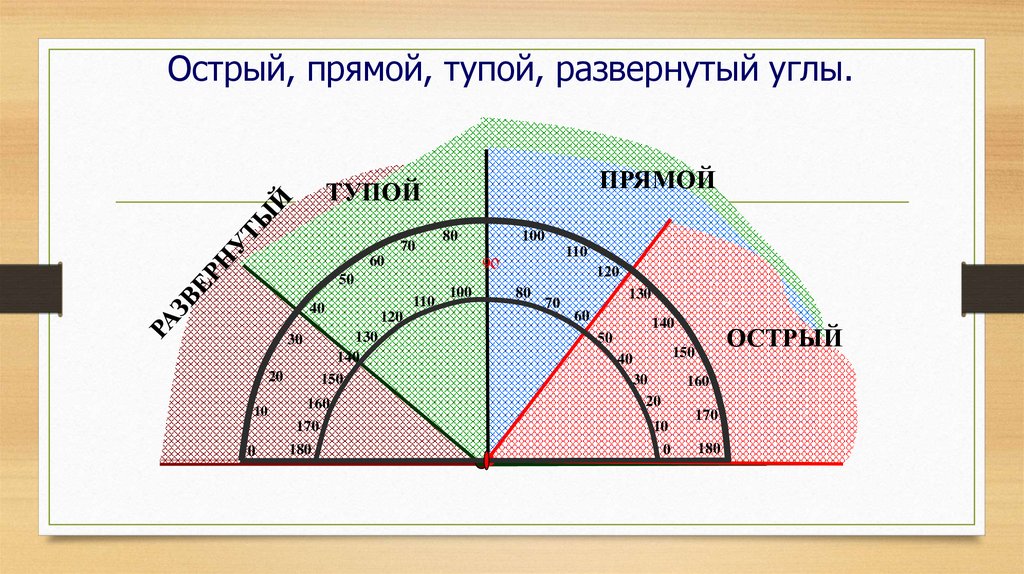 Можете ли вы заметить тупые углы на всех этих изображениях? Можете ли вы вспомнить больше объектов в реальной жизни, которые имеют тупые углы?
Можете ли вы заметить тупые углы на всех этих изображениях? Можете ли вы вспомнить больше объектов в реальной жизни, которые имеют тупые углы?
Некоторые другие примеры тупых углов в реальной жизни приведены ниже:
- Угол между часовой и минутной стрелками часов в положении «4 часа».
- Угол между основанием открытого ноутбука и его экраном.
- Углы, образованные лопастями потолочного вентилятора.
Тупоугольный треугольник
Если один из углов треугольника больше 90°, такой треугольник называется тупоугольным. Тупоугольный треугольник может быть равнобедренным или разносторонним. Равносторонний треугольник не может быть тупоугольным. Сторона, лежащая против тупого угла в треугольнике, является наибольшей стороной этого треугольника. Точно так же треугольник никогда не может быть прямым углом и тупым углом одновременно в соответствии со свойством суммы углов треугольника. Таким образом, можно сделать вывод, что если один из углов треугольника тупой, то два других угла треугольника должны быть острыми.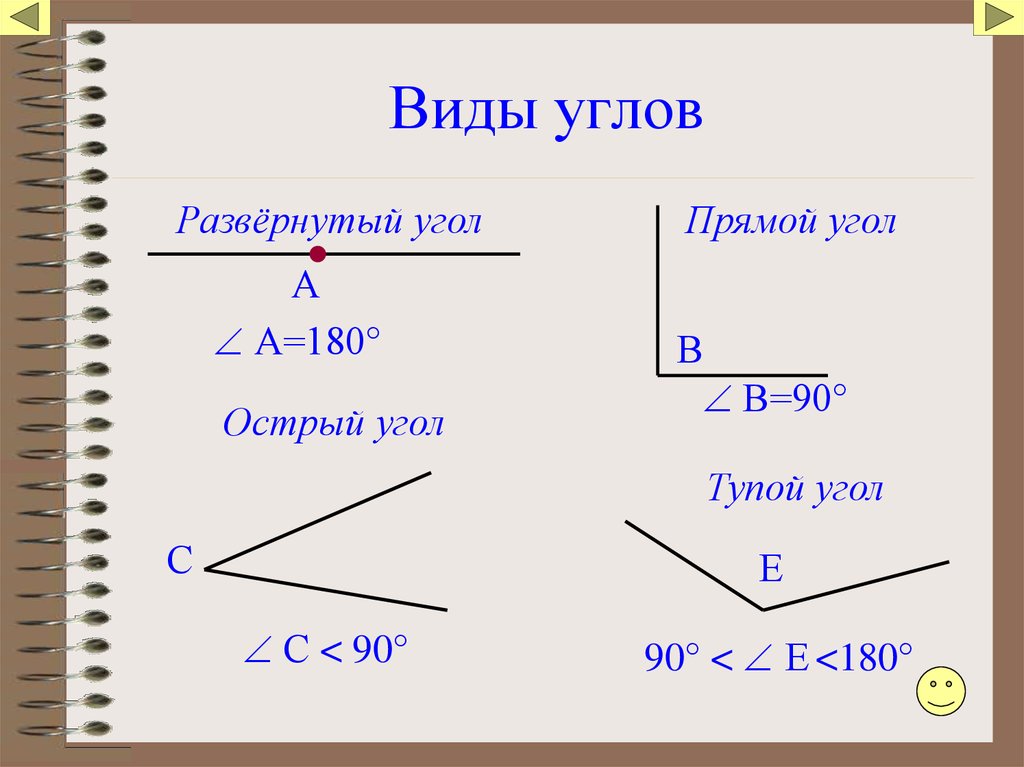
В приведенных выше треугольниках один угол больше 90°. Поэтому их называют тупоугольными треугольниками или просто тупоугольными треугольниками . В тупоугольном треугольнике сумма квадратов двух сторон меньше квадрата большей стороны. В ΔABC стороны измеряются a,b,c так, что c является наибольшей стороной, мы имеем: a 2 + b 2 < c 2 . Наоборот, если в треугольнике, если a 2 + b 2 < c 2 , то треугольник тупоугольный.
Острые и тупые углы
Существуют различные типы углов в зависимости от измерения. Углы меньше 90° называются острыми углами, а углы больше 90°, но меньше 180° называются тупыми. Посмотрите на изображение острых и тупых углов, приведенное ниже, а затем их разницу.
Теперь давайте разберемся с острым и тупым углом в таблице ниже:
| Острый угол | Тупой угол |
|---|---|
Он измеряет менее 90 градусов. | Он имеет размеры больше 90 и меньше 180 градусов. |
| Треугольник с тремя острыми углами называется остроугольным треугольником. | Треугольник с 1 тупым и 2 острыми углами называется тупоугольным треугольником. |
| Примеры острых углов: 56°, 12°, 79°°, 43° и т. д. | Примеры тупых углов: 124°, 179°, 150°, 95° и т. д. |
Важные примечания
- Все углы величиной больше 90° и меньше 180° называются тупыми углами.
- В тупоугольном треугольнике сумма квадратов двух сторон меньше квадрата наибольшей стороны.
Нестандартное мышление!
- Может ли треугольник иметь более одного тупого угла?
- У какого многоугольника все внутренние углы тупые?
- Может ли быть параллелограмм без тупого угла? Если да, то какой формы это может быть?
Темы, относящиеся к тупым углам
Ознакомьтесь с еще несколькими интересными статьями, посвященными тупому углу и его свойствам.
- Тупоугольный разносторонний треугольник
- Равнобедренный тупоугольный треугольник
- Калькулятор треугольника
- Острые прямые и тупые углы Рабочие листы
Примеры тупого угла
Пример 1: Найдите тупые углы на следующих рисунках.
Решение:
Вариант (б) — 117° и вариант (в) — 121° больше 90° и меньше 180°. Следовательно, это тупые углы. Следовательно, 117° и 121° — тупые углы.
Пример 2: В какие моменты времени на показанных ниже часах образуется тупой угол?
Решение:
Мы можем заметить, что во всех случаях между часовой и минутной стрелками часов образуется тупой угол.
- В 5:00 часовая стрелка находится на 5, а минутная на 12. Таким образом, наблюдая, мы можем заключить, что образовавшийся угол больше 90º, но меньше 180°, что является тупым углом.
 Используя транспортир, мы можем убедиться, что он образует угол между (9от 0° до 180°).
Используя транспортир, мы можем убедиться, что он образует угол между (9от 0° до 180°). - В 8:00 часовая стрелка находится на 8, а минутная на 12. Таким образом, наблюдая, мы можем заключить, что образовавшийся угол больше 90°, но меньше 180°. Таким образом, это тупой угол.
- В 10:15 часовая стрелка находится на 10, а минутная на 3. Таким образом, наблюдая, мы можем заключить, что образовавшийся угол является тупым.
- В 2:40 часовая стрелка находится чуть выше 3, а минутная стрелка на 8. Таким образом, наблюдая, мы можем заключить, что образовавшийся угол больше 90°, но менее 180°. Используя транспортир, мы можем убедиться, что он образует тупой угол.
Следовательно, тупой угол образуется в 5:00, 8:00, 10:15 и 2:40.
- В 5:00 часовая стрелка находится на 5, а минутная на 12. Таким образом, наблюдая, мы можем заключить, что образовавшийся угол больше 90º, но меньше 180°, что является тупым углом.
Пример 3: Могут ли стороны тупоугольного треугольника иметь стороны, равные 4 единицам, 5 единицам и 8 единицам?
Решение:
В тупоугольном треугольнике сумма квадрата двух сторон должна быть меньше квадрата наибольшей стороны, т.
 е. 2 + b 2 < c 2 где c — наибольшая сторона. Пусть a = 4 единицы, b = 5 единиц, c = 8 единиц (наибольшая сторона) ⇒ a 2 = 16, b 2 = 25, c 2 = 64 ⇒ a 2 + b 2 = 16 + 25 = 41. Поскольку 41 < 64. Отсюда следует, что a 2 + b 2 меньше c 2 . Следовательно, данные меры образуют тупоугольный треугольник. Следовательно, стороны, равные 4 единицам, 5 единицам и 8 единицам, образуют тупоугольный треугольник.
е. 2 + b 2 < c 2 где c — наибольшая сторона. Пусть a = 4 единицы, b = 5 единиц, c = 8 единиц (наибольшая сторона) ⇒ a 2 = 16, b 2 = 25, c 2 = 64 ⇒ a 2 + b 2 = 16 + 25 = 41. Поскольку 41 < 64. Отсюда следует, что a 2 + b 2 меньше c 2 . Следовательно, данные меры образуют тупоугольный треугольник. Следовательно, стороны, равные 4 единицам, 5 единицам и 8 единицам, образуют тупоугольный треугольник.
перейти к слайдуперейти к слайдуперейти к слайду
Хотите создать прочную основу в математике?
Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.
Записаться на бесплатный пробный урок
Практические вопросы по тупому углу
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о тупом угле
Что такое тупой угол в геометрии?
В геометрии мы читаем о различных типах углов.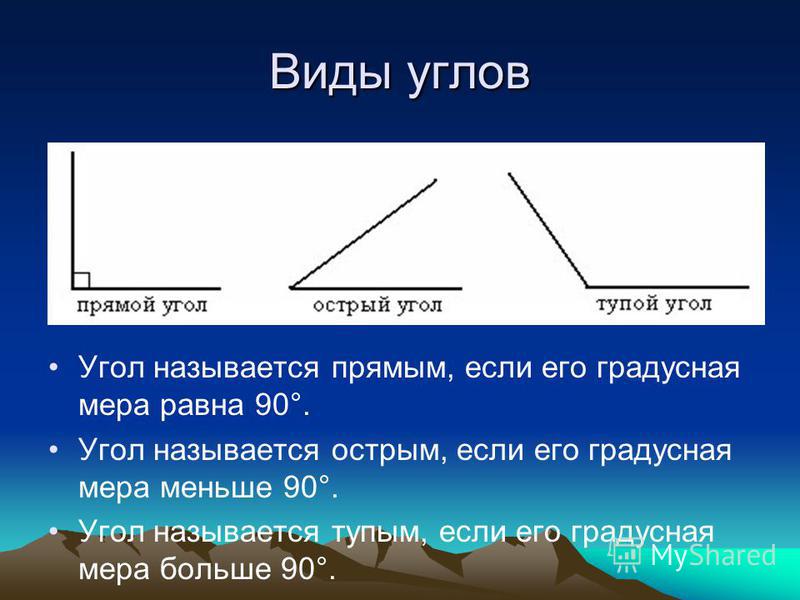 Каждый тип угла имеет свои характеристики, с помощью которых мы можем его идентифицировать. Точно так же тупой угол — это угол, который всегда меньше 180 градусов и больше 90 градусов.
Каждый тип угла имеет свои характеристики, с помощью которых мы можем его идентифицировать. Точно так же тупой угол — это угол, который всегда меньше 180 градусов и больше 90 градусов.
Как выглядит тупой угол?
Углы с величиной больше 90° и меньше 180° в геометрии называются тупыми углами. Тупой угол находится между 90° и 180° и выглядит как откинутое кресло, угол под лестницей или угол, образованный между минутной и часовой стрелками часов в 10:15.
Как нарисовать тупой угол?
Определение тупого угла в геометрии гласит, что угол больше 90°, но меньше 180° называется тупым углом. Мы можем использовать транспортир и отметить любой угол между 90° и 180°, чтобы получился тупой угол.
Каковы некоторые примеры тупых углов?
145°, 150°, 178°, 149°, 91° являются примерами градусов тупого угла, поскольку они больше 90° и меньше 180°.
Каковы свойства тупых углов?
Ниже приведены свойства тупого угла:
- Углы, составляющие от 90 до 180 градусов.

- Углы лежат между прямым и прямым углом.
Могут ли два тупых угла быть дополнительными?
Два тупых угла, каждый из которых больше 90°, не могут образовывать дополнительную пару углов, так как сумма будет больше 180°, что не удовлетворяет условию дополнительных углов.
Что такое тупоугольный треугольник?
Треугольник с одним тупым углом и двумя другими острыми углами является тупоугольным. Сумма всех трех внутренних углов будет 180 градусов.
Что такое острый и тупой углы?
Острый угол — это угол, размер которого меньше 90 градусов, а углы больше 90°, но меньше 180° — тупые.
Сколько градусов составляет тупой угол?
Градус тупого угла всегда лежит в пределах от 90° до 180°.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочий лист тупого угла
Тупой угол: определение, степень, примеры
Геометрия имеет дело с формами и их измерениями. Когда два отрезка или луча встречаются под наклоном, они образуют угол, называемый углом.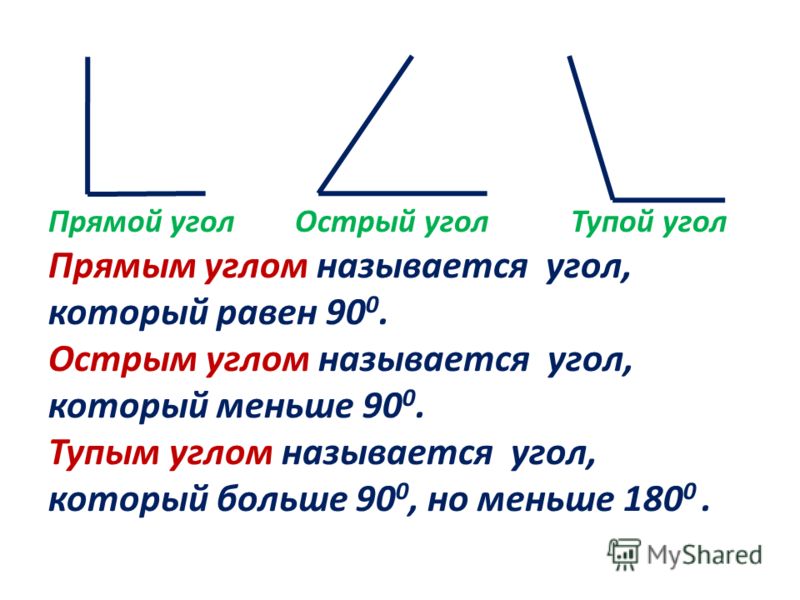 Углы подразделяются на различные типы
Углы подразделяются на различные типы
- Острый угол. Угол меньше 90 градусов называется острым углом.
- Прямой угол. Угол в 90 градусов называется прямым углом.
- Тупой угол — угол больше 90 градусов, но меньше 180 градусов называется тупым углом.
- Прямой угол — угол 180 градусов — это прямой угол.
- Угол рефлекса. Угол, который больше 180 градусов, но меньше 360 градусов, называется углом рефлекса.
- Полный угол — угол 360 градусов — это полный угол.
В статье ниже вы узнаете важные понятия, связанные с тупым углом. Вот что мы рассмотрим:
- Что такое тупой угол?
- Тупой угол Градус
- Тупоугольный треугольник
- Решенные вопросы о тупых углах
Определение тупого угла : В геометрии угол, который больше 90 градусов, но меньше 180 градусов, называется тупым углом. Мы можем легко распознать тупой угол, потому что он выходит за пределы прямого угла.
Обычный пример для понимания того, как выглядит тупой угол, — это наблюдение за минутной и часовой стрелкой петуха. Часто в течение 24-часового дня часы образуют множество градусов тупого угла между часовой стрелкой и минутной стрелкой. Например, когда сейчас 12:25, две стрелки часов образуют тупой угол.
Тупой угол Градус
Теперь мы знаем, что угол, который меньше 180 градусов, но больше 90 градусов, является тупым углом. Некоторые примеры градусов тупого угла: 110°, 135°, 150°, 179°, 91° и более. Следовательно, все углы, лежащие в диапазоне от 90° до 180°, являются тупыми углами.
| Некоторые тупые углы в реальной жизни, с которыми вы сталкиваетесь каждый день Оглянитесь вокруг, и вы найдете несколько объектов, изображающих тупые углы вокруг себя. Открытая книга, когда вы ее читаете, ножницы и широко открытая дверь — тупые углы. |
Как построить тупой угол?
Два луча встречаются в одной точке, образуя угол.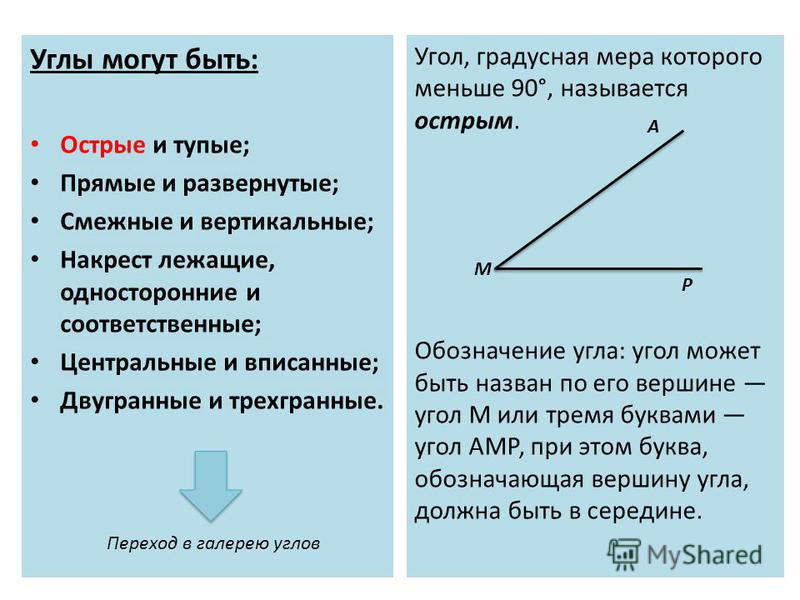 Два луча образуют плечи угла. Вершина — это точка/угол, где встречаются руки. Здесь мы узнаем, как нарисовать тупой угол с помощью транспортира и циркуля.
Два луча образуют плечи угла. Вершина — это точка/угол, где встречаются руки. Здесь мы узнаем, как нарисовать тупой угол с помощью транспортира и циркуля.
Построение тупого угла с помощью транспортира
Следующие шаги помогут вам построить тупой угол с помощью транспортира.
Шаг 1: Сначала проведите прямую линию с помощью линейки.
Шаг 2: Теперь поместите центр транспортира на один конец линии.
Шаг 3: Считайте от нуля и отметьте точку под нужным углом. На рисунке показано 129 градусов.
Шаг 4: Теперь снимите транспортир. Присоедините конец линии к отмеченной точке с помощью линейки.
Шаг 5: Отметьте угол и снова проверьте его с помощью транспортира, чтобы убедиться, что вы правильно присоединили линию.
Построение тупого угла с помощью компаса Следующие шаги помогут вам построить тупой угол в 120 градусов с помощью циркуля и линейки, т. е. без использования транспортира.
е. без использования транспортира.
Этапы построения угла 120 градусов
Шаг 1: Нарисуйте луч OA.
Шаг 2 : Теперь возьмем О в качестве центра и нарисуем дугу, пересекающую ОА. Вы можете взять любой радиус по вашему выбору и использовать тот же радиус на протяжении всего строительства. Отметьте точку как B, где дуга пересекает OA.
Шаг 3: Затем возьмите B в качестве центра и того же радиуса, что и раньше, и нарисуйте дугу, которая пересекает первую дугу в точке C.
Шаг 4: Теперь возьмите C в качестве центра и того же радиуса и нарисуйте дугу, пересекающую начальную дугу. Отметьте точку как D.
Шаг 5: Соедините OD, чтобы получить угол AOD 120 градусов.
Этапы построения угла 105 градусов
Следующие шаги помогут вам построить угол 105 градусов с помощью циркуля и линейки.
Шаг 1: Нарисуйте луч OA.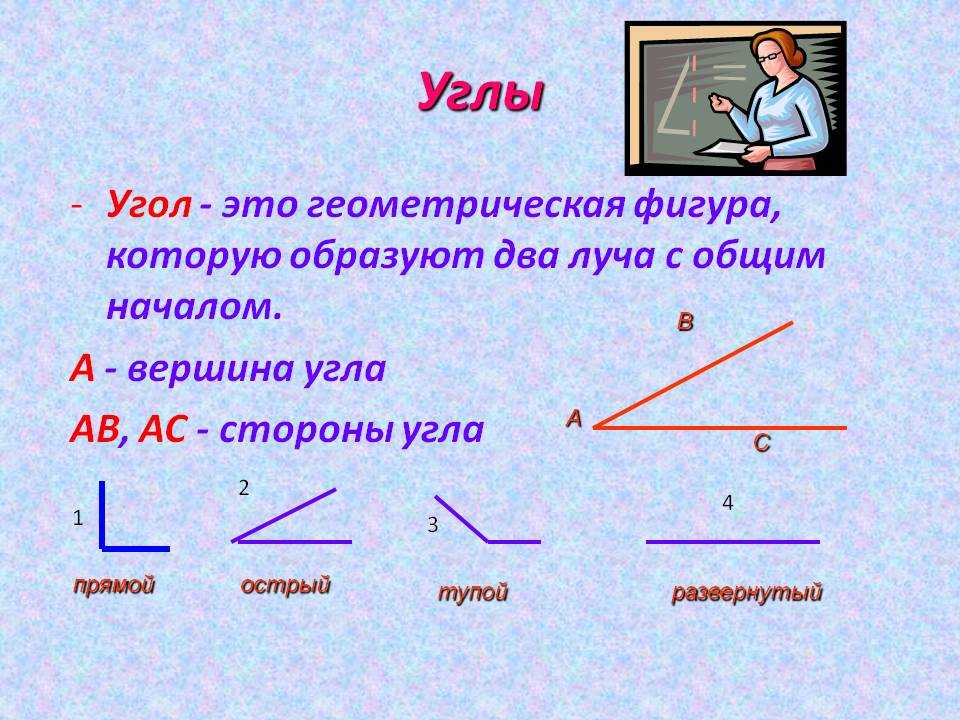
Шаг 2 : Теперь возьмем О в качестве центра и нарисуем дугу, пересекающую ОА. Вы можете взять любой радиус по вашему выбору и использовать тот же радиус на протяжении всего строительства. Отметьте точку как B, где дуга пересекает OA.
Шаг 3: Затем возьмите B в качестве центра и того же радиуса, что и раньше, и нарисуйте дугу, которая пересекает первую дугу в точке C.
Шаг 4: Теперь возьмите C в качестве центра и того же радиуса и нарисуйте дугу, пересекающую начальную дугу. Отметьте точку как D
Шаг 5 : Теперь нарисуйте лучи OE и OF, проходящие через точки C и D соответственно. Теперь угол AOE равен 60 градусам, а угол EOF равен 60 градусам.
Шаг 6: Теперь, взяв C и D за центры, проведите дугу между двумя лучами OE и OF так, чтобы эти две дуги пересекались друг с другом. Отметьте точку пересечения как P. Теперь угол AOP будет равен 90 градусов, а угол POD равен 30 градусам.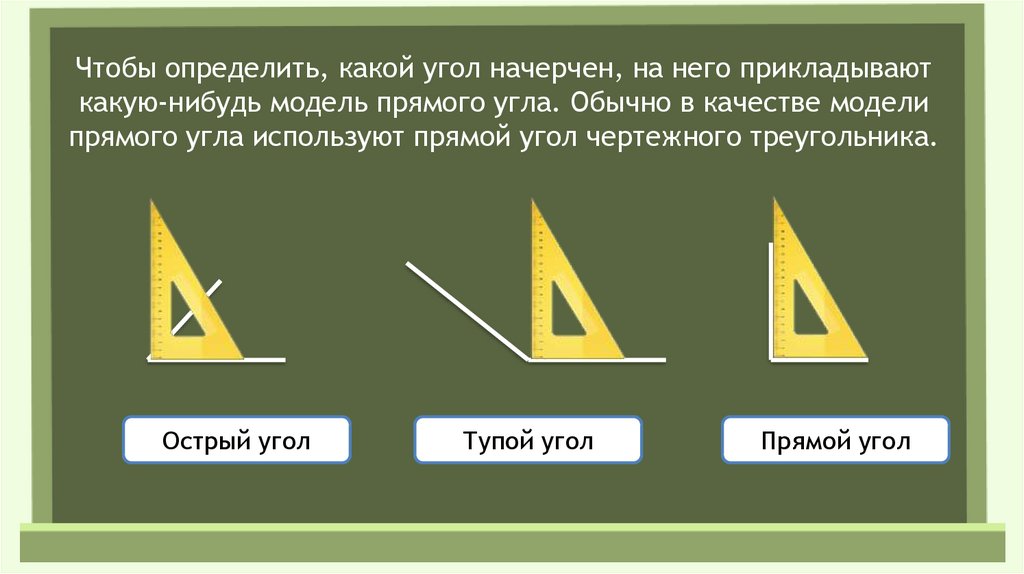
Шаг 7 : Теперь разделите пополам угол POD для этой отметки точки Q, где OP пересекает начальную дугу.
Шаг 8 : Взяв Q и D за центры, начертите пересекающиеся дуги. Отметьте точку пересечения как R.
Шаг 9 : Соедините ИЛИ, чтобы получить угол 105 градусов. Проверьте угол с помощью транспортира.
Тупоугольный треугольник
Мы знаем, что треугольники состоят из трех углов. Если один из углов тупой, такой треугольник называется тупоугольным.
Примечание: Треугольник может иметь только один тупой угол, потому что сумма всех углов треугольника должна быть 180 градусов.
Таким образом, когда любой из углов треугольника больше 90°, это тупоугольный треугольник. Кроме того, тупоугольный треугольник может быть равнобедренным или разносторонним. Таким образом, равносторонний треугольник никогда не может быть тупоугольным, потому что его углы равны 60 градусам. Кроме того, тупоугольный треугольник не может быть прямоугольным треугольником по свойству суммы углов (сумма углов треугольника = 180 градусов).
Вот некоторые важные свойства треугольника с тупым углом:
- Один угол больше 90 градусов.
- Два других угла всегда меньше 90 градусов.
- Сторона, противоположная тупому углу, является наибольшей стороной этого треугольника.
- Когда один угол треугольника тупой, два других угла всегда острые.
Мы можем легко определить, является ли треугольник тупым, если мы знаем два угла треугольника. Используя свойство суммы углов, мы найдем третий угол и решим, является ли треугольник тупоугольным или нет.
Но как определить, является ли треугольник тупым, если мы знаем только стороны треугольника, а не углы. Здесь мы воспользуемся неравенством в линиях тождества Пифагора, чтобы найти тупоугольный треугольник.
Треугольник тупоугольный, если сумма квадратов меньших сторон меньше квадрата наибольшей стороны.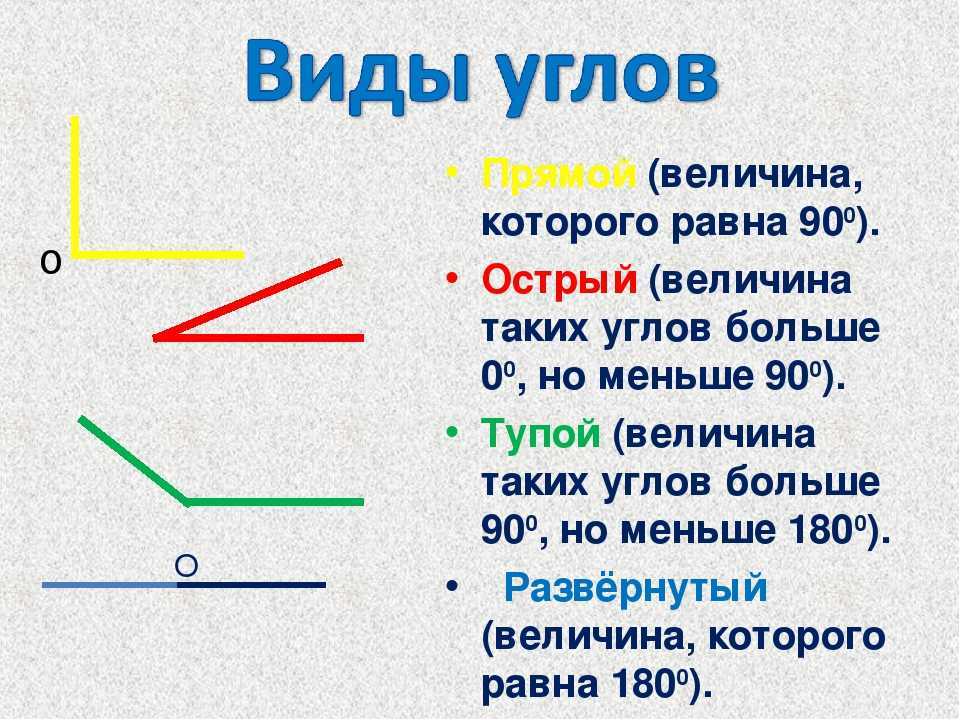
Если a, b и c — три длины сторон треугольника ABC. Если c — самая длинная сторона, то треугольник будет тупоугольным, только если a 2 + b 2 < c 2 .
Примеры вопросов о тупых углах
Вот несколько примеров тупых углов с решениями, которые помогут объяснить концепцию тупых углов.
Пример 1: Какой из следующих углов равен 130°.
Ответ: Угол B тупой, потому что он больше 90 градусов, но меньше 180 градусов.
Пример 2. Назовите тупой угол на следующем рисунке?
Ответ: Тупыми углами являются угол BOD, угол AOC и угол AOD, так как они больше 90 градусов, но меньше 180 градусов.
«Тупой» и «заумный» означают одно и то же?
На уроке геометрии мы изучаем тупые углы: это широкие, больше 90 градусов, в отличие от острых углов, которые меньше 90 градусов. Острый угол дает острое острие, а тупой человек не так уж сообразителен интеллектуально.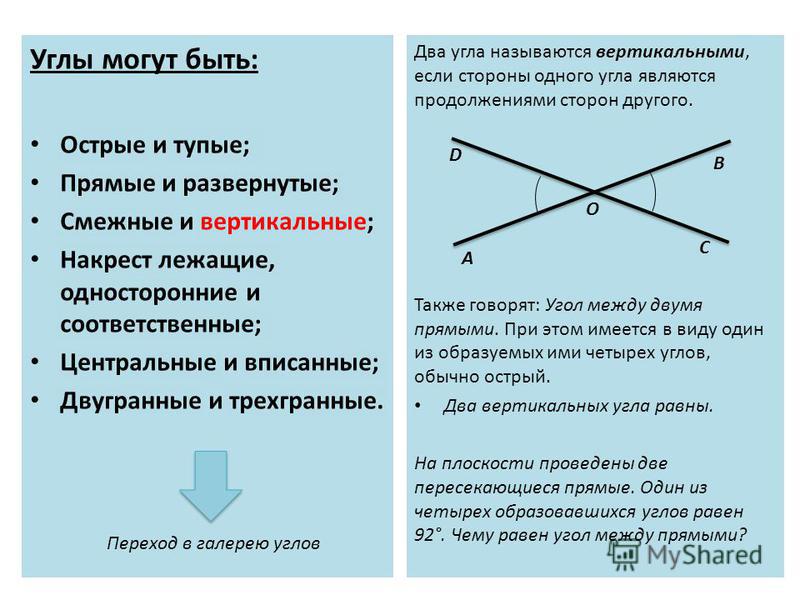 Соответственно, тупой имеет корни от латинского obtusus , что означает «тупой» или «тупой».
Соответственно, тупой имеет корни от латинского obtusus , что означает «тупой» или «тупой».
Граница между «тупым» и «заумным» стала более размытой, чем когда-то.
Быть тупым — это не просто быть тусклым. В частности, это предполагает отказ видеть что-то очевидное для других или преднамеренное невежество или нечувствительность к реальным фактам ситуации.
«Похоже, он из тех, кто не желает делать самые скромные вещи, чтобы закрыть эту историю, а на самом деле делает наоборот», — сказал Стивен Филдинг, профессор политической истории Ноттингемского университета в Англии.
Мистер Корбин, добавил он, «либо невероятно тупой , либо ему просто все равно», и он создал кризис, который мог бы предотвратить, просто «прислушиваясь к советам людей, которые ему не нравятся».
— Стивен Кастл, The New York Times , 3 апреля 2018 г.Как и в телевизионных ситкомах, здесь родители больше запутались, чем дети.
Митчелл одновременно чрезмерно опекает и тупой , неспособный видеть в Кайле кого-либо, кроме ребенка.
— Дэниел Иган, 9 лет0555 Киножурнал , 3 апр. 2018
Слово, которое звучит как тупое , является заумным , определяемым как «трудное для понимания». Они оба происходят из латыни, хотя и не связаны между собой. Abstruse происходит от причастия прошедшего времени от abstrudere , глагола, означающего «скрывать». Тупой происходит от причастия прошедшего времени от obtundere , что означает «бить» или «притуплять».
Abstruse используется для описания вещей, которые не так легко доступны для непрофессионала или обычного человека. В частности, он предполагает использование языка или другого материала, подходящего для продвинутых уровней предмета, о котором остальные из нас могут иметь лишь элементарное представление.
Книгу Шиндлера нелегко читать; его проза техническая, а его предмет заумный .
Но читать тоже одно удовольствие.
— Майкл Шон Уинтерс, Новая Республика , 30 августа 1999 г.В книге «Монополия: самая известная игра в мире и как она появилась » (Da Capo, 2006) Филип Э. Орбанес описывает, как «Монополия» развилась из гораздо более заумного чисто образовательного инструмента под названием «Игра домовладельца», созданного в 1903 некой Элизабет Дж. Мэги, чтобы рассказать о реформированном налоговом кодексе.
— Джозеф Гилденхорн, The Wilson Quarterly , зима 2007 г.
Обычно тупой используется вместо заумный — настолько распространенный, что тупой имеет в словаре другое значение: «трудно понять: неясно или точно в мысли или выражении».
Она также с любовью представила работы художников-авангардистов, делая их работы доступными и привлекательными – а не тупой и отталкивающий – как бы ни был строг.
— Джон Р. Киллаки, The Burlington Free Press , 30 марта 2018 г.Работа с настройками конфиденциальности Facebook — точная настройка того, к каким данным могут получить доступ друзья, рекламодатели и приложения — это утомительная работа. Меню запутанные, формулировка тупая .
— Брайан Барретт, Wired , 27 марта 2018 г.
Подмена понятна: конечно, заумная тема может оставить чувство тупости. Подумайте о том, как неуместно вы чувствуете себя на вечеринке, когда кто-то говорит о малоизвестном авторе или фильме, о котором, кажется, слышали все, кроме вас. (Наше решение: больше читать и смотреть больше фильмов.)
Но использование тупого для чего-то, во что трудно проникнуть, не избежало критики некоторых комментаторов. Когда тупой появилось в опубликованном письме генерала военно-морского флота в 1983 году, Уильям Сэфайр упомянул об этом в своей колонке New York Times , потому что генерал использовал это прилагательное для описания «политических целей», которые, как объяснил Сэфайр, «требует модификатора, приписывающего хитрость, а не тупость».
— Генерал может быть единственным, кто придал этому слову такое значение, — продолжал Сэфайр. «Большинству остального англоязычного мира тупой означает «тупой и бесчувственный», а не «расплывчатый и неясный». Сэфайр, тем не менее, с некоторым извинением заметил, что на генерала могло повлиять сочетание заумный с непонятный , слово, которое разделяет пересекается с заумным , потому что это может означать, среди прочего, «непонятно или ясно выражено», как в « малоизвестный рок-текст».
Другая сложность заключается в том, что тупой также может использоваться для описания чего-то вроде бестактного замечания, грубого и плохо продуманного:
Заменивший Шинсеки Роберт Макдональд сразу же продемонстрировал полное отсутствие уважения к ветеранам своими тупыми замечаниями, сравнивая уход за ветеранами с поездкой в Диснейленд.
— Кори Франклин, The Chicago Tribune , 2 апреля 2018 г.

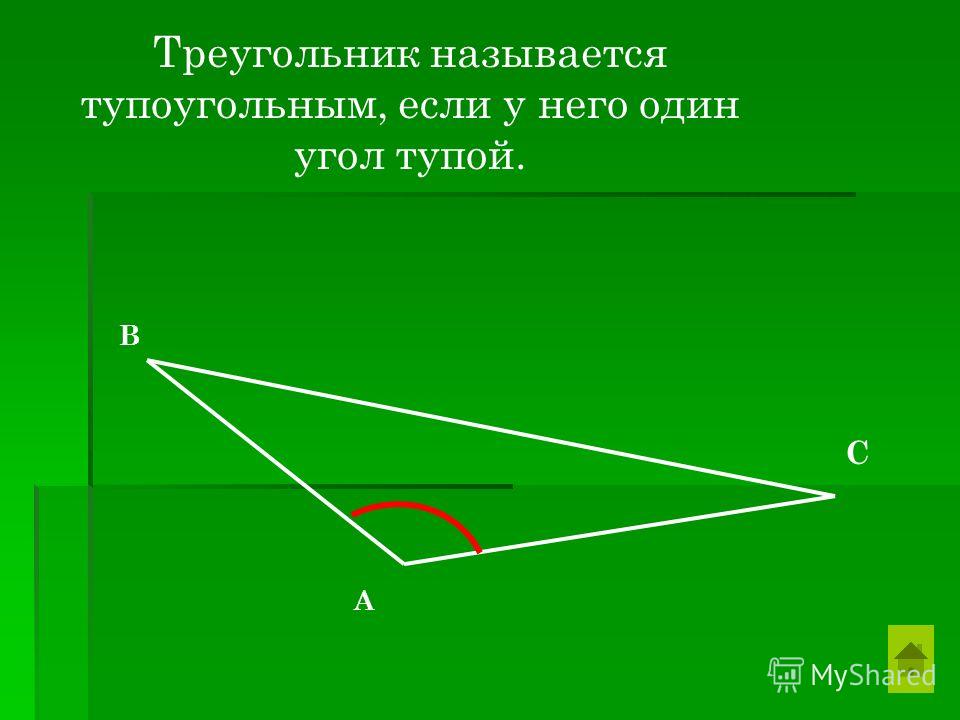




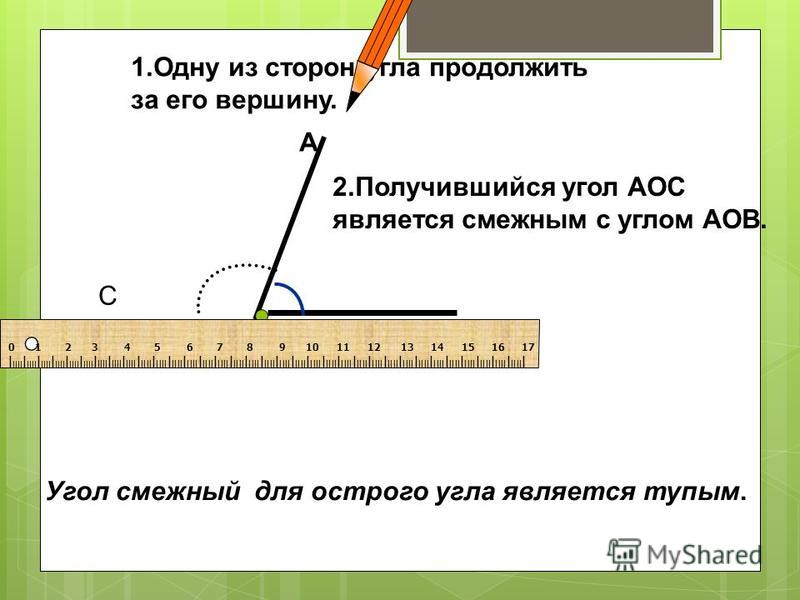
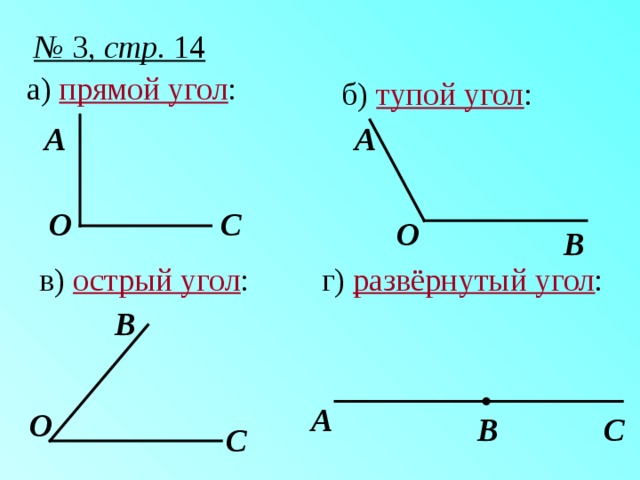
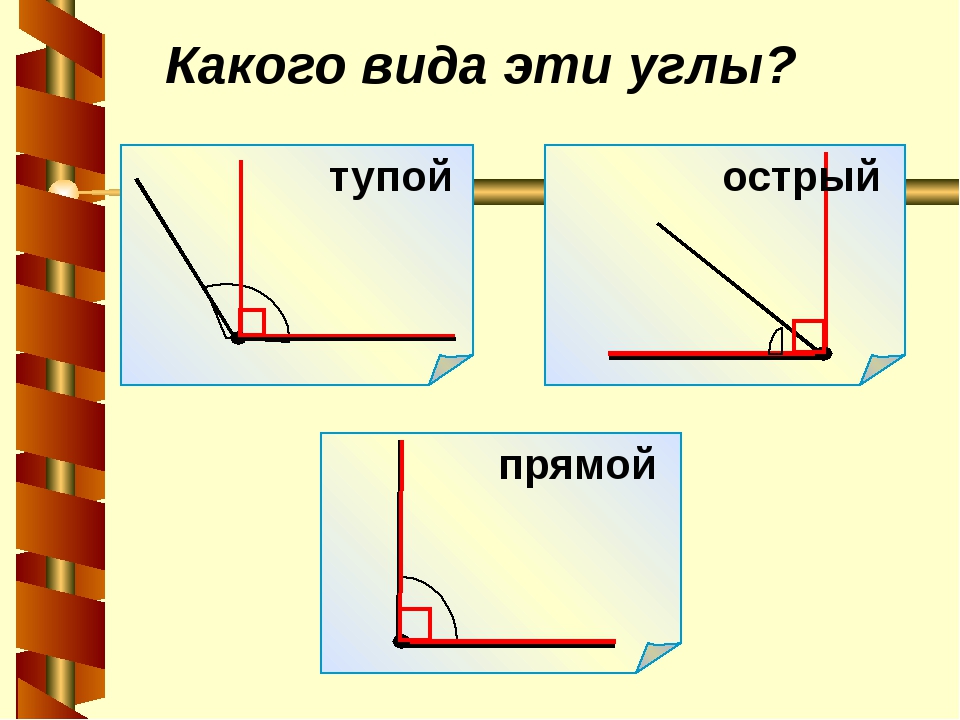 Используя транспортир, мы можем убедиться, что он образует угол между (9от 0° до 180°).
Используя транспортир, мы можем убедиться, что он образует угол между (9от 0° до 180°). е. 2 + b 2 < c 2 где c — наибольшая сторона. Пусть a = 4 единицы, b = 5 единиц, c = 8 единиц (наибольшая сторона) ⇒ a 2 = 16, b 2 = 25, c 2 = 64 ⇒ a 2 + b 2 = 16 + 25 = 41. Поскольку 41 < 64. Отсюда следует, что a 2 + b 2 меньше c 2 . Следовательно, данные меры образуют тупоугольный треугольник. Следовательно, стороны, равные 4 единицам, 5 единицам и 8 единицам, образуют тупоугольный треугольник.
е. 2 + b 2 < c 2 где c — наибольшая сторона. Пусть a = 4 единицы, b = 5 единиц, c = 8 единиц (наибольшая сторона) ⇒ a 2 = 16, b 2 = 25, c 2 = 64 ⇒ a 2 + b 2 = 16 + 25 = 41. Поскольку 41 < 64. Отсюда следует, что a 2 + b 2 меньше c 2 . Следовательно, данные меры образуют тупоугольный треугольник. Следовательно, стороны, равные 4 единицам, 5 единицам и 8 единицам, образуют тупоугольный треугольник.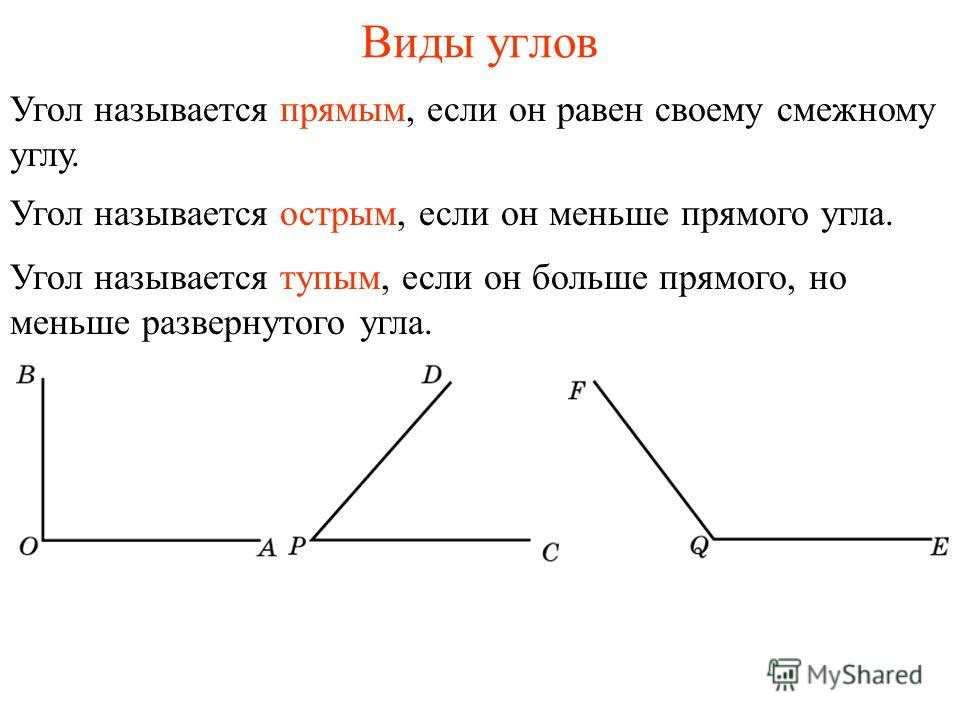
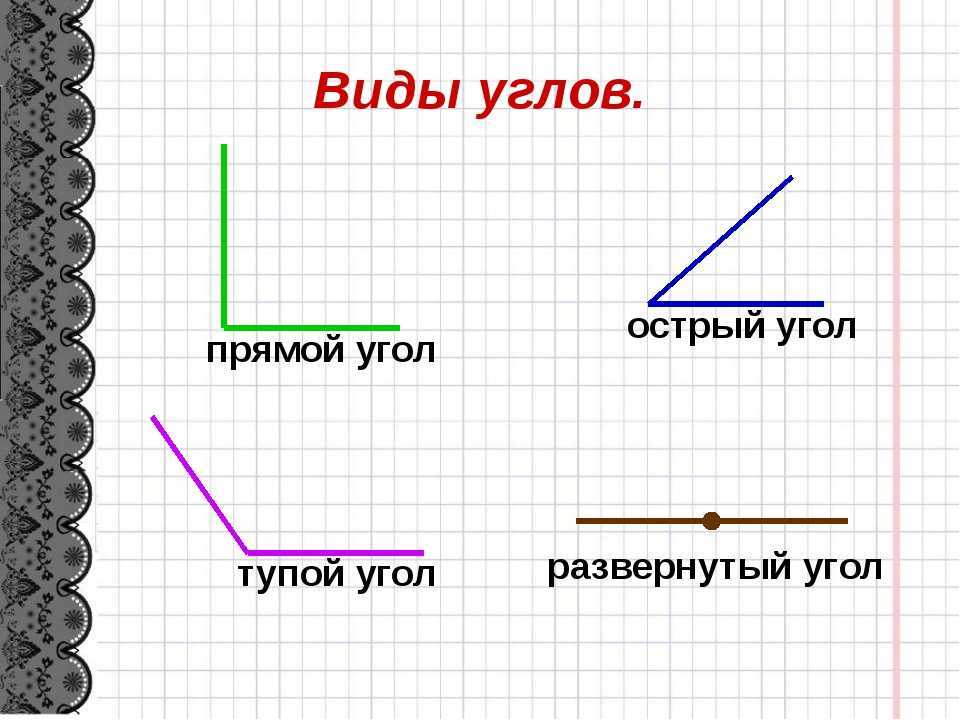 Митчелл одновременно чрезмерно опекает и тупой , неспособный видеть в Кайле кого-либо, кроме ребенка.
Митчелл одновременно чрезмерно опекает и тупой , неспособный видеть в Кайле кого-либо, кроме ребенка.  Но читать тоже одно удовольствие.
Но читать тоже одно удовольствие.