Угол сектора круга: Радиус и угол сектора круга

Угол кругового сектора при заданной длине дуги Калькулятор

✖Длина дуги кругового сектора — это длина криволинейного граничного края кругового сектора.ⓘ Длина дуги кругового сектора [lArc]		створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр	+10% -10%
✖Радиус кругового сектора — это радиус круга, из которого образован круговой сектор. ⓘ Радиус кругового сектора [r]		створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр	+10% -10%

✖Угол кругового сектора — это угол между радиальными ребрами кругового сектора или центральный угол, в котором круг разрезается, образуя круговой сектор. ⓘ Угол кругового сектора при заданной длине дуги [∠Sector]

КругЦиклстепеньГонГрадианМилМиллирадианМинутаМинуты дугиТочкаквадрантЧетверть кругаРадианРеволюцияПрямой уголВторойПолукругсекстанЗнакОчередь

⎘ копия

👎

Формула

сбросить

👍

Угол кругового сектора при заданной длине дуги Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1.

Преобразование входов в базовый блок

Длина дуги кругового сектора: 4 метр —> 4 метр Конверсия не требуется
Радиус кругового сектора: 5 метр —> 5 метр Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

0.8 Радиан —>45.8366236104745 степень (Проверьте преобразование здесь)

< 2 Угол кругового сектора Калькуляторы

Угол кругового сектора при заданной длине дуги формула

Угол кругового сектора = Длина дуги кругового сектора/Радиус кругового сектора
∠_Sector = l_Arc/r

Что такое круговой сектор?

Круговой сектор — это, по сути, часть площади круга, прорезанная через два радиуса. Геометрически круговой сектор — это область, окруженная дугой окружности и соответствующими радиусами под определенным центральным углом.

Что такое Круг?

Окружность — это базовая двухмерная геометрическая фигура, которая определяется как совокупность всех точек на плоскости, находящихся на фиксированном расстоянии от фиксированной точки. Фиксированная точка называется центром круга, а фиксированное расстояние называется радиусом круга. Когда два радиуса становятся коллинеарными, эта общая длина называется диаметром круга. То есть диаметр — это длина отрезка внутри круга, проходящего через центр, и он будет в два раза больше радиуса.

Share

Copied!

Вычисли площадь сектора, если радиус круга равен 5 см и центральный … — Учеба и наука

Вычисли площадь сектора, если радиус круга равен 5 см и центральный угол сектора равен 180°. 2

06.02.21

Лучший ответ по мнению автора Ответ понравился автору вопроса

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Eleonora Gabrielyan Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Решено

решите уравнение, пожалуйста: (4cos^2(3x)-4sin(3x)-1)*(корень из:(-ctg(x))=0

Здравствуйте! Прошу помощи! Алеша сказал: «У Змея Горыныча больше трех голов».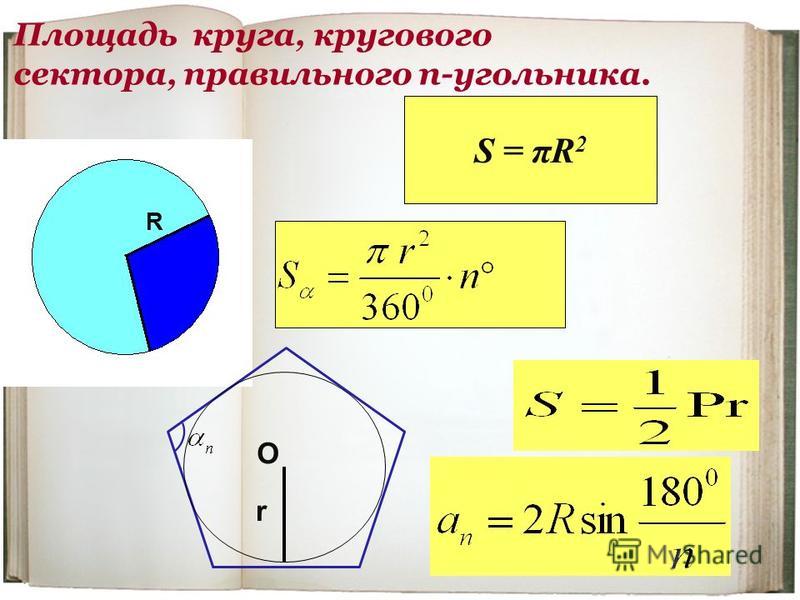 Добрыня сказал: » У Змея больше 4-х голов». Илья сказал:»У Змея больше

Осевое сечение цилиндра –квадрат, диагональ которого равна 4 см. Найти площадь полной поверхности цилиндра.

Шар с центром в точке O касается плоскости в точке A. Точка B лежит в плоскости касания. Найди объём шара, если AB=1,2см , а BO=1,3см.

Решено

Период синуса, косинуса, тангенса и котангенса + область определений

Как рассчитать угол сектора

Обновлено 3 ноября 2020 г.

Автор: Mariecor Agravante

В реальном мире круги повсюду, поэтому их радиусы, диаметры и длина окружности важны в реальных приложениях. Но есть и другие части кругов — например, секторы и углы, — которые также важны в повседневных приложениях. Примеры включают размеры секторов круглых продуктов, таких как пирожные и пироги, угол поворота колеса обозрения, размер шины для конкретного автомобиля и особенно размер кольца для помолвки или свадьбы. По этим и другим причинам в геометрии также есть уравнения и расчеты задач, связанные с центральными углами, дугами и секторами окружности.

​ Что такое центральный угол? ​

Центральный угол определяется как угол, образованный двумя лучами или радиусами, исходящими из центра круга, при этом центр круга является вершиной центрального угла. Центральные углы особенно важны, когда речь идет о равномерном распределении пиццы или любой другой круглой еды среди определенного количества людей. Скажем, есть пять человек на вечеринке, где они должны разделить большую пиццу и большой торт. Под каким углом должны быть разделены пицца и торт, чтобы всем достался одинаковый кусок? Поскольку в круге 360 градусов, вычисление становится равным 360 градусам, деленным на 5, чтобы получить 72 градуса, так что каждый кусочек, будь то пицца или торт, будет иметь центральный угол, или тета (θ), равный 72 градусам. градусов.

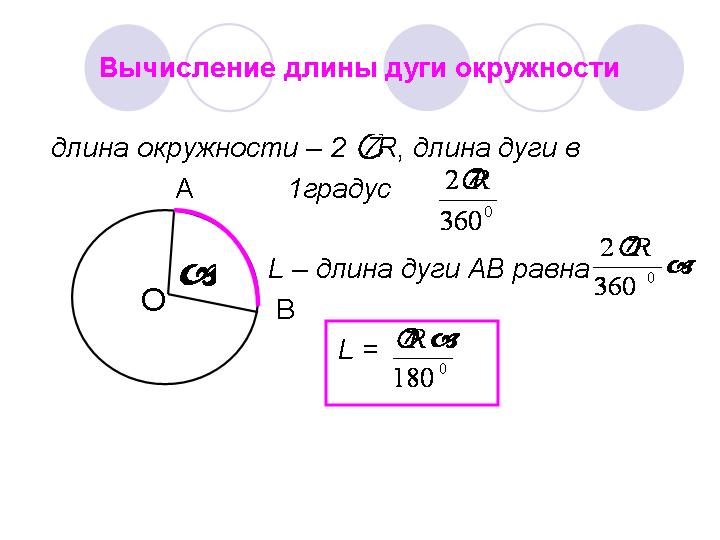
​ Определение центрального угла по длине дуги ​

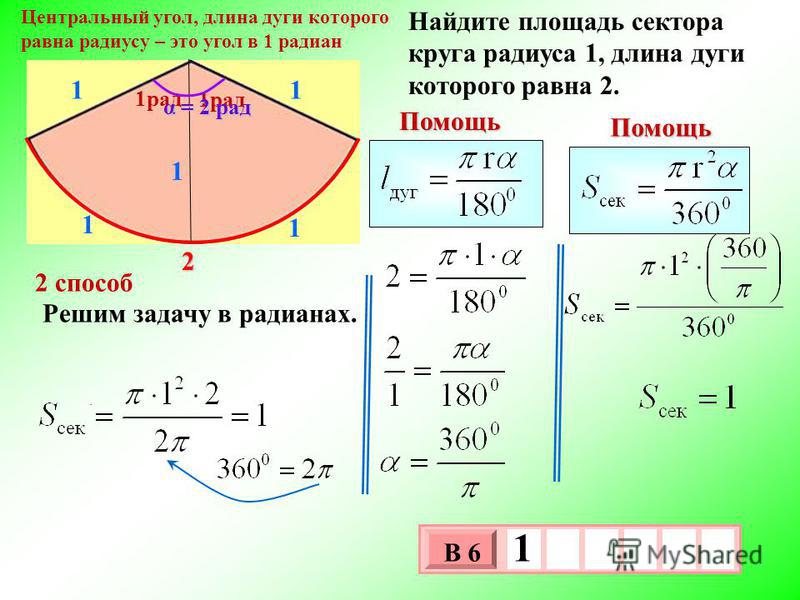
Дуга окружности относится к «части» окружности окружности. Следовательно, длина дуги — это длина этой «части». Если вы представляете себе кусок пиццы, площадь сектора можно представить как весь кусок пиццы, но длина дуги — это длина внешнего края корочки для этого конкретного кусочка. По длине дуги можно рассчитать центральный угол. Действительно, одна формула, которая может помочь в определении центрального угла, гласит, что длина дуги (s) равна радиусу, умноженному на центральный угол, или

s = r × θ

где угол тета должен измеряться в радианах. Таким образом, чтобы определить центральный угол тета, нужно только разделить длину дуги на радиус, или

\frac{s}{r} = θ

Для иллюстрации, если длина дуги равна 5,9, а радиус равен 3,5329. , то центральный угол становится равным 1,67 радиан. Другой пример: если длина дуги равна 2, а радиус равен 2, центральный угол становится равным 1 радиану. Если вы хотите перевести радианы в градусы, помните, что 1 радиан равен 180 градусам, деленным на π, или 57,29.58 градусов. И наоборот, если в уравнении требуется преобразовать градусы обратно в радианы, то сначала умножьте на π, а затем разделите на 180 градусов.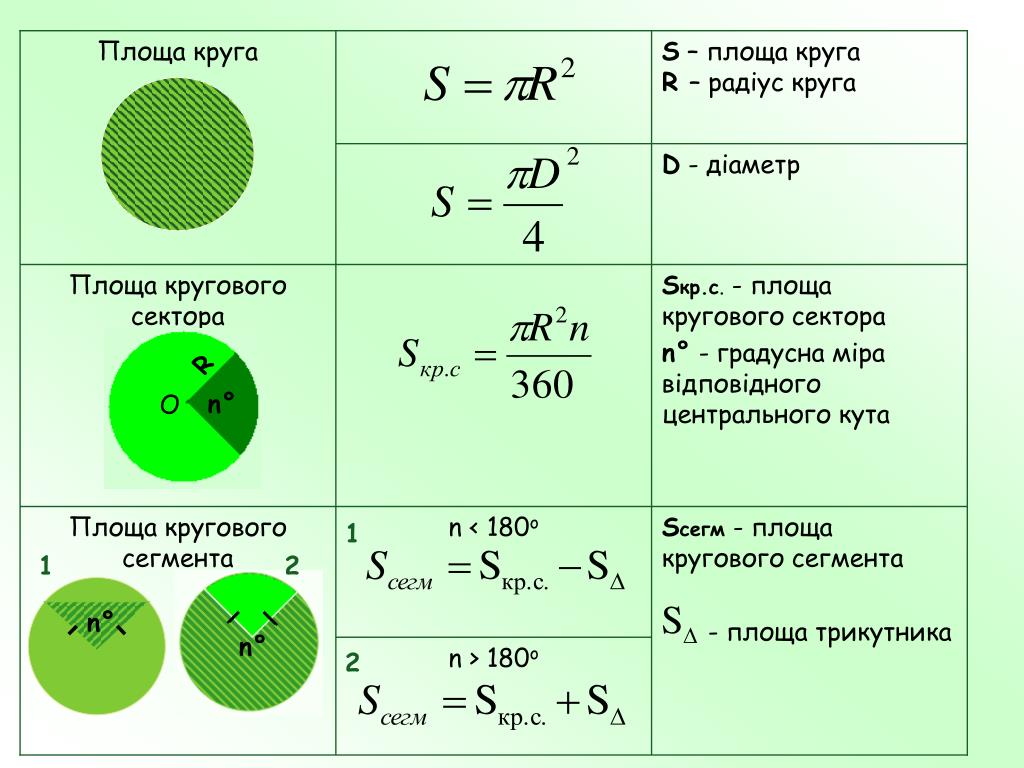

​ Определение центрального угла по площади сектора ​

Другая полезная формула для определения центрального угла обеспечивается площадью сектора, которую снова можно визуализировать как кусок пиццы. Эту конкретную формулу можно рассматривать двумя способами. Первый имеет центральный угол, измеренный в градусах, так что площадь сектора равна π, умноженному на квадрат радиуса, а затем умножается на величину центрального угла в градусах, деленную на 360 градусов. Другими словами: 92

Так как радиус (​ r ​) равен 10, все уравнение может быть записано как:

\frac{52.3}{100π} × 360

так что тета может быть записана как:

\frac {52.3}{314} × 360

Таким образом, окончательный ответ становится центральным углом 60 градусов.

Объяснение урока: Площади круглых секторов

В этом объяснении мы научимся находить площадь круглого сектора и решать задачи, связывающие эту площадь с длиной дуги и периметром сектора.

Прежде чем определить, как найти площадь кругового сектора, давайте начнем с напоминания терминологии частей сектора круга. Во-первых, напомним, что дуга окружности — это часть окружности между двумя радиусами. Однако, учитывая два радиуса, есть две возможные дуги между двумя радиусами. Мы можем увидеть пример этого на следующей диаграмме.

Мы видим, что обе дуги являются сечением окружности между двумя заданными радиусами. Чтобы обойти эту проблему, мы обозначаем большую дугу как «большую», а меньшую — как «второстепенную».

Это равносильно утверждению, что если центральный угол меньше 180∘ или 𝜋 радиан, то мы знаем, что он малый, а если он больше этих значений, то он большой. Затем мы можем определить дуги окружности следующим образом.

Резюме: Дуга окружности

Дуга окружности — это часть окружности окружности между двумя радиусами.

Учитывая два радиуса, мы обозначаем большую из дуг как большую дугу , а меньшую из дуг как малая дуга .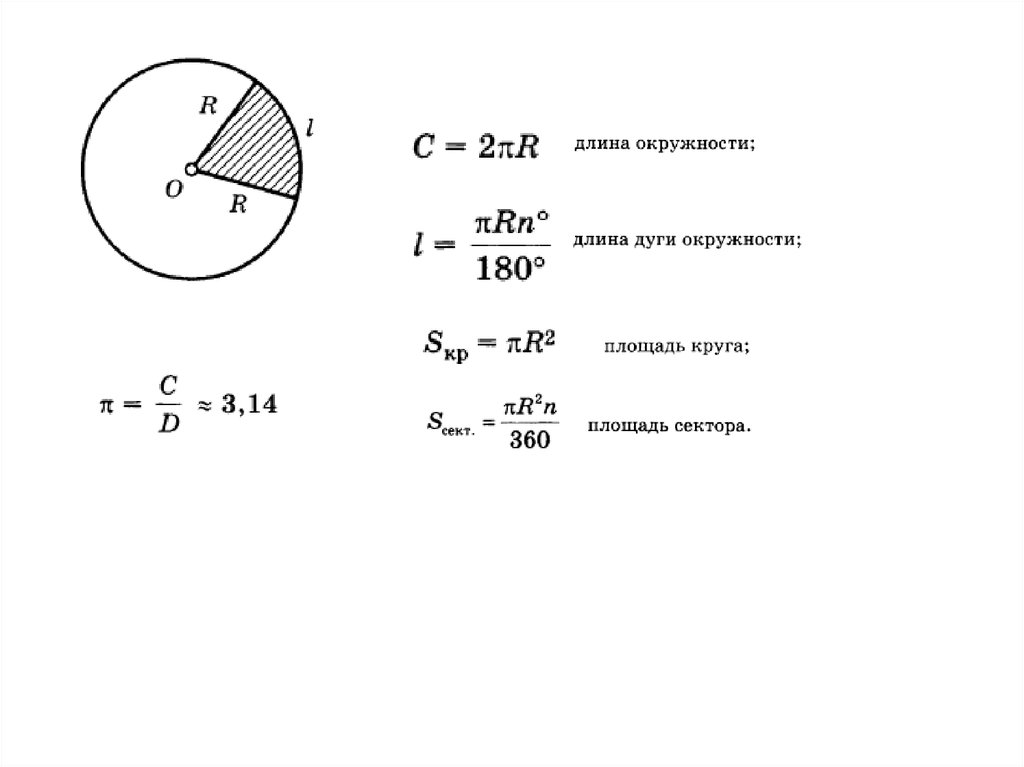 Большая дуга та, у которой больший центральный угол.

Наконец, если две дуги имеют одинаковую длину, то мы называем их дугами полуокружности . Это происходит, когда центральный угол составляет 180 ∘ или 𝜋 рад, или, что то же самое, когда радиусы образуют диаметр.

Определение: Сектор круга

Сектор круга — это часть круга, заключенная в два радиуса и дугу между ними. Мы называем сектора в зависимости от типа дуги между радиусами.

Если центральный угол меньше 180∘ или 𝜋 рад, мы называем это малым сектором . Если центральный угол больше этого, мы называем это основным сектором . А если угол равен 180∘, то наш сектор представляет собой полуокружность .

Как вычислить площадь кругового сектора

Теперь мы готовы найти площадь сектора. Начнем с примера, где центральный угол равен 90∘.

Это четверть круга, поэтому мы можем рассчитать площадь этого сектора, умножив площадь всего круга 𝜋𝑟 на 14. В более общем случае, для сектора с центральным углом 𝜃, измеренным в градусах, это 𝜃360 часть круга и его площадь можно рассчитать по формуле 𝜃360𝜋𝑟.

Мы можем сделать то же самое в радианах. Если центральный угол сектора, измеренный в радианах, равен 𝜃, то сектор представляет собой 𝜃2𝜋 часть круга. Значит, площадь этого сектора 𝜃2𝜋𝜋𝑟=12𝑟𝜃.

Это дает нам следующие формулы для нахождения площадей круговых секторов.

Формулы: Площадь кругового сектора

Площадь сектора с радиусом 𝑟 и центральным углом 𝜃, измеренная в градусах, определяется выражением 𝐴=𝜃360𝜋𝑟.

Площадь сектора с радиусом 𝑟 и центральным углом 𝜃, измеренная в радианах, определяется выражением 𝐴=12𝑟𝜃.

Рассмотрим пример применения формулы площади круглого сектора.

Пример 1: Расчет площади сектора по величине его угла в радианах

Дуга имеет меру 𝜋3 радиана и радиус 5. Задайте площадь сектора в терминах 𝜋 в простейшем виде форма.

Ответ

Напомним, что для круга радиуса 𝑟, если мера центрального угла сектора равна 𝜃 радианам, то площадь сектора определяется выражением 𝐴=12𝑟𝜃. 

Если бы мы зарисовали полученную информацию, то получили бы следующее:

Имеем 𝑟=5 и 𝜃=𝜋3, что дает нам 𝐴=12𝜋35=25𝜋6.

Следовательно, площадь этого сектора составляет 25𝜋6 единиц площади.

Мы также можем использовать формулу площади сектора для определения площади более сложных форм, как мы увидим в следующем примере.

Пример 2. Нахождение площади кругового сектора по радиусу и величине угла сектора

Найдите площадь закрашенной части диаграммы, давая ответ с точностью до одного десятичного знака.

Ответ

Заштрихованная область на диаграмме — это разница площадей между двумя секторами двух кругов, имеющих общий центр, как показано на диаграмме ниже.

Радиус внутреннего круга 7 см, радиус внешнего круга 15 см. Мы можем найти заштрихованную площадь, найдя площадь сектора большего круга, а затем вычтя площадь сектора внутреннего круга. Начнем с сектора внешнего круга.

Напомним, площадь сектора круга радиуса 𝑟 с центральным углом 𝜃, измеренная в градусах, равна 𝐴=𝜃360𝜋𝑟. 

Радиус равен 15 см, а центральный угол равен 60∘. Подстановка их в формулу дает externalsectorareacm=60360𝜋(15)=75𝜋2.

Затем мы можем найти площадь сектора внутреннего круга.

Радиус равен 7 см, а центральный угол равен 60∘, что дает innersectorareacm=60360𝜋(7)=49𝜋6.

Наконец, заштрихованная область представляет собой разницу этих значений: шейддариасм=75𝜋2−49𝜋6=88𝜋3≈92,153….

Следовательно, площадь заштрихованной области на диаграмме равна 92,2 см ² с точностью до десятых.

В нашем следующем примере мы будем использовать радиус круга и периметр сектора для определения площади сектора. Прежде чем сделать это, напомним, что для окружности радиуса 𝑟 и дуги с центральным углом 𝜃 длина дуги 𝑙 может быть найдена следующим образом:

• Если 𝜃 измеряется в радианах, длина дуги равна 𝑙= 𝑟, а площадь сектора 𝐴=12𝑟𝜃; так 𝐴=12𝑟𝜃=12𝑟(𝑟𝜃)=12𝑟𝑙.
• Если 𝜃 измеряется в градусах, длина дуги 𝑙=2𝜋𝑟𝜃360, а площадь сектора 𝐴=𝜃360𝜋𝑟; так 𝐴=𝜃360𝜋𝑟=12𝑟2𝜋𝑟𝜃360=12𝑟𝑙. 

В обоих случаях площадь сектора равна половине произведения радиуса на длину дуги.

Формула: площадь кругового сектора с использованием длины дуги

Если сектор круга радиуса 𝑟 имеет длину дуги 𝑙, то площадь 𝐴 сектора определяется выражением 𝐴=12𝑟𝑙.

Давайте посмотрим, как применить этот результат в нашем следующем примере.

Пример 3: Нахождение площади сектора по радиусу круга и периметру сектора

Радиус круга равен 10 см, а периметр сектора равен 25 см. Найдите площадь сектора.

Ответ

Поскольку нам не дан центральный угол сектора, а вместо этого задан периметр сектора, мы начнем с того, что вспомним следующую формулу для площади сектора. Если сектор круга радиуса 𝑟 имеет длину дуги 𝑙, то площадь 𝐴 сектора определяется выражением 𝐴=12𝑟𝑙.

Нам сказали, что 𝑟=10 см, и мы можем найти значение 𝑙, используя периметр. Мы начинаем с зарисовки данной информации.

Периметр сектора равен сумме длин его сторон, поэтому имеем 25=10+10+𝑙𝑙=5.

Следовательно, подставив 𝑙=5 и 𝑟=10 в формулу площади, получим 𝐴=12×5×10=25 см

Следовательно, площадь этого сектора равна 25 см ² .

В следующем примере мы увидим, как мы можем применить геометрические свойства вместе с формулой площади сектора круга, чтобы найти площадь, указанную на диаграмме.

Пример 4. Круговые сектора и площади кругов

Три конгруэнтных круга радиусом 43 см касаются друг друга. Найдите площадь части между кружками, дающую ответ с точностью до ближайшего квадратного сантиметра.

Ответ

Чтобы найти площадь между кругами, мы начнем с соединения центров кругов отрезками. Область, которую нам нужно найти, — это заштрихованная область на следующей диаграмме. Все три окружности имеют радиус 43 см, поэтому мы можем отметить длины следующих радиусов.

Теперь мы видим, что это равносторонний треугольник со стороной 86 см. Так как это равнобедренный треугольник, то внутренние углы равны 60∘. Вместо того, чтобы находить заштрихованную область, мы можем найти площадь треугольника, а затем вычесть площади секторов.

Площадь треугольника равна половине произведения длины основания на высоту. Чтобы найти высоту треугольника, мы строим следующий прямоугольный треугольник:

Высота равностороннего треугольника делит его на два конгруэнтных прямоугольных треугольника. Гипотенуза одного из этих прямоугольных треугольников имеет длину 86 см, а основание равно половине стороны равностороннего треугольника, поэтому длина 862 = 43 см. Затем мы можем использовать теорему Пифагора, чтобы найти ℎ: 86=43+ℎℎ=86−43ℎ=√5547.

Тогда, используя площадь треугольника, половину длины основания, умноженную на перпендикулярную высоту, мы имеем площадь треугольника см=12×86×√5547=1849√3.

Напомним, что площадь сектора с радиусом 𝑟 и центральным углом 𝜃, измеренная в градусах, равна 𝐴=𝜃360𝜋𝑟.

Подстановка 𝜃=60∘ и 𝑟=43см в формулу площади сектора дает 𝐴=60360𝜋(43)=1849𝜋6.

Затем мы можем найти площадь между кругами, вычитая площади трех секторов из площади треугольника. Это дает нам площадьсм=1849√3−31849𝜋6=1849√3−1849𝜋2≈298,159….

Следовательно, площадь области между кружками на диаграмме с точностью до ближайшего квадратного сантиметра равна 298 см ² .

В нашем последнем примере мы увидим, как применить формулу площади сектора к реальной задаче.

Пример 5: Решение задач, связанных с секторами

Ландшафтный садовник решает, что он хочет спроектировать газон, разделенный на ряд секторов с круглыми внутренними двориками, уложенными в траву, как показано на данном рисунке. Круглая лужайка будет разделена на шесть равных секторов, каждый радиусом восемь метров. Прямые 𝑂𝐴 и 𝑂𝐵 касаются окружности, а дуга 𝐴𝐵 касается окружности в одной точке.

1. Рассчитать площадь сектора 𝑂𝐴𝐵. Дайте ответ в терминах 𝜋.
2. Садовнику необходимо рассчитать радиус круглого патио. Используя тригонометрические соотношения, рассчитайте радиус внутреннего дворика. Дайте ответ в виде дроби.
3. Рассчитать общую площадь травы в одном секторе. Дайте свой ответ в терминах 𝜋 в самой простой форме.

Ответ

Часть 1

Напомним, что площадь сектора радиуса 𝑟 и центрального угла 𝜃, измеренная в градусах, определяется следующим образом: площадь множителя = 𝜃360𝜋𝑟.

Подстановка 𝑟=8 и 𝜃=60∘ в эту формулу дает нам площадь сектора=60360𝜋(8)=32𝜋3.

Поскольку длины измеряются в метрах, площадь этого сектора равна 32𝜋3 квадратных метра.

Часть 2

Чтобы найти радиус этой окружности, мы начинаем с добавления следующих линий и точек к диаграмме:

Поскольку 𝑂𝐴 является касательной к окружности, она пересекает окружность под прямым углом, что означает что 𝑂𝑃𝐶 — прямоугольный треугольник. Мы знаем, что длины 𝑃𝐶 и 𝐶𝐷 равны 𝑟, так как они являются радиусами внутренней окружности. Мы также знаем, что 𝑂𝐷 имеет длину 8, потому что это радиус внешнего круга. Мы выбираем 𝑂𝐷 таким образом, чтобы он делил пополам угол при 𝑂.

Чтобы использовать тригонометрию для треугольника 𝑂𝑃𝐶, нам нужно найти длину 𝑂𝐶: 𝑂𝐷=𝑂𝐶+𝐶𝐷.