Угол треугольника через стороны: Калькулятор расчета углов треугольника зная длину сторон

Содержание

Углы и стороны в треугольниках

85. Построим равнобедренный ∆ABC (чер. 92), у которого AB = BC. Тогда мы знаем, что его углы при основании равны, т. е. ∠A = ∠C. Пронумеруем эти углы, – тогда ∠1 = ∠2. Станем теперь строить новые треугольники ABC’, ABC» и т. д. так, чтобы сторона AB и ∠B оставались неизменными, но сторона BC увеличивалась. Тогда угол A должен увеличиваться (что очевидно), а угол C станет уменьшаться: мы видим, что ∠3 < ∠2, ∠4 < ∠3 и т. д., потому что ∠2 есть внешний угол для ∆ACC’ и, следов., ∠2 > ∠3 или ∠3 < ∠2, также ∠3 есть внешний угол ∆AC’C» и, след., ∠3 > ∠4 или ∠4 < ∠3 и т. д. (уменьшение угла C видно еще из того, что сумма углов треугольника всегда равна 2d: угол B не изменяется, угол A увеличивается, – след., ∠C должен уменьшаться).

Из этих построений мы вправе сделать заключения:

1) Если в треугольнике две стороны равны, то против них лежат равные углы.

2) Если в треугольнике две стороны не равны, то против большей из них лежит и больший угол.

86. Теперь, наоборот, построим: 1) треугольник с двумя равными углами и 2) треугольник с двумя неравными углами и сравним стороны, противолежащие этим углам. Для решения вопросов, здесь возникающих, воспользуемся способом рассуждения, часто употребляемым в математике.

1) Пусть ∆ABC (чер. 93) постоен так, что ∠A = ∠C. Сравнить стороны BC и BA.

Пока, не зная ничего про стороны AB и BC, мы можем сделать об них 3 предположения: 1) AB = BC, 2) AB > BC и 3) AB < BC – иных предположений быть не может. Рассматривая эти предположения, мы можем заметить, что два из них не годятся, так как противоречат предыдущему. В самом деле, 2-е предположение, что AB > BC должно, на основании предыдущего п., повлечь за собою следствие, что ∠C > ∠A, а у нас построено: ∠C = ∠A. Следовательно, это предположение должно быть вычеркнуто. Также из 3-го предположения, что AB < BC следует, что ∠A > ∠C, что также противоречит нашему построению. Следовательно, и это предположение должно быть вычеркнуто.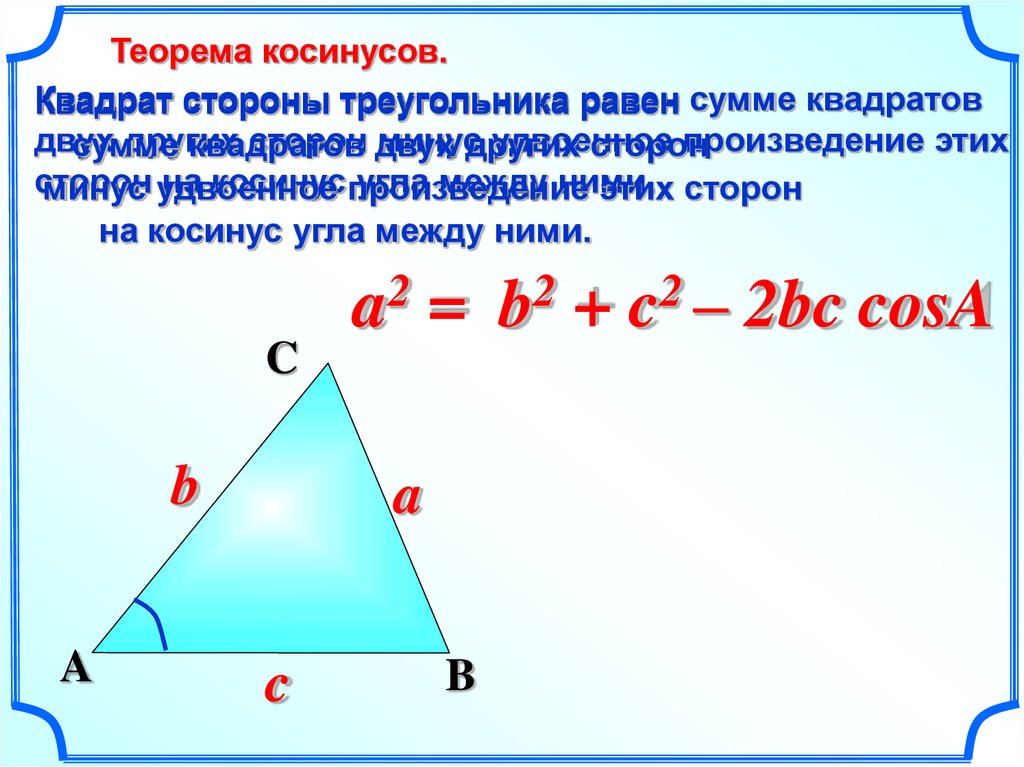 Остается поэтому лишь одно предположение, что AB = BC, которое и должно быть верно, так как иных сделать нельзя. Поэтому имеем:

Если в треугольнике два угла равны, то против них лежат равные стороны.

2) Пусть ∆ABC (чер. 93) постоен так, что ∠A > ∠C. Сравнить стороны BA и BC.
Опять мы можем сделать 3 предположения: 1) AB = BC, 2) AB > BC и 3) AB < BC. Теперь видим, что первое предположение не годится, так как на основании п. 85 из него вытекало бы, что ∠C = ∠A, что противоречит нашему построению; также найдем, что 2-е предположение, что AB > BC не годится, так как из него вытекало бы, что ∠C > ∠A, что противоречит построению. Остается лишь 3-е предположение, что AB < BC, которое и должно быть верно. Поэтому имеем:

Если два угла в треугольнике неравны, то против большего из них лежит большая сторона.

Теперь легко решаются вопросы: 1) какая из сторон прямоугольного треугольника самая большая? 2) Какая из сторон тупоугольного треугольника самая большая?

87. В двух предыдущих пп. мы имели дело с двумя положениями: 1) против большей стороны лежит больший угол и 2) против большего угла лежит большая сторона. Мы нашли, что эти мысли справедливы для одного треугольника. Возникает вопрос, справедливы ли они для двух треугольников? Несомненно справедливы для двух равных треугольников, так как равные треугольники можно наложением слить в один треугольник. Но, вообще говоря, к двум различным (не равным) треугольникам эти положения не могут быть применимы: мы можем построить два таких треугольника ∆ABC и ∆A’B’C’ (чер. 94), чтобы ∠B был > ∠B’, но AC была бы < A’C’. Чертеж пояснений не требует. Но есть один случай, когда указанные мысли применимы и к двум различным треугольникам).

Этот случай легко уясняется наглядно. Возьмем две палочки AB и BC (чер. 95 bis) и сложим их концами (в точке B). Если вращать палочку BC около точки B по стрелке, то ∠B станет увеличиваться: сторона BC будет менять свое положение (пусть одно из них есть BC’), но все время BC останется равным самому себе; не изменяется также и отрезок AB. Обратим внимание, что точками A и C определяется еще отрезок AC, на чертеже не изображенный. При вышеуказанном вращении точка C меняет свое место и нам ясно, что этот отрезок AC, не изображенный на чертеже, должен увеличиваться (напр. AC’ > AC), т. е., если 2 стороны треугольника не изменяются, а угол между ними увеличивается, то третья сторона так же увеличивается. В тексте этот случай выяснен без помощи такого наглядного представления.

Построим два таких треугольника, чтобы у них было по две равных стороны, но чтобы углы между ними не были равны. Пусть в ∆ABC и в ∆A’B’C’ (чер. 95) имеем AB = A’B’, BC = B’C’, но ∠B > ∠B’. Сравним стороны AC и A’C’, лежащие против неравных углов. Для этого наложим ∆A’B’C’ на ∆ABC так, чтобы сторона A’B’ совпала с равною ей стороною AB. Тогда сторона B’C’ должна пойти внутри ∠B, потому что ∠B’ < ∠B, но где кончится эта сторона, т. е., где расположится точка C’, неизвестно. Может быть, она расположится как раз на стороне AC, может быть, расположится вне ∆ABC, а может быть внутри этого треугольника.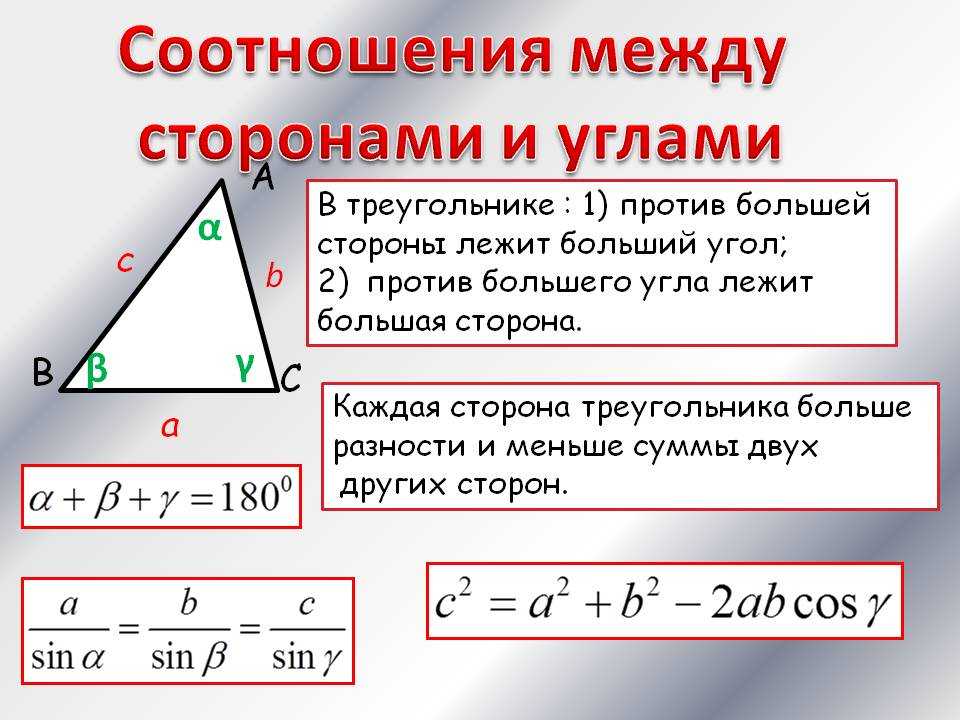 Разберем эти три случая отдельно.

1) Пусть ∆A’B’C’ расположится так, что займет положение ∆ABD (чер. 96), так что точка C’ попадет в D, на сторону AC; тогда, очевидно, AD < AC или A’C’ < AC (AD есть та же сторона A’C’, только перенесенная в другое место).

2) Пусть ∆A’B’C’ при наложении займет положение ∆ABD (чер. 97), т. е. точка C’ расположится в точке D, вне ∆ABC. Тогда, соединив точки C и D, получим ∆BCD, у которого BC = BD, так как, по построению, B’C’ = BC, а BD есть та же сторона B’C’, лишь перенесенная в другое место. Поэтому ∆BCD – равнобедренный, и ∠BCD = ∠BDC. Рассмотрим теперь ∆ACD; про два его угла, а именно про ∠C (или ∠ACD) и про ∠D (или ∠ADC) легко сообразить, пользуясь отмеченными равными углами равнобедренного треугольника, какой из них больше другого. В самом деле, мы видим, что ∠ACD < отмеченного угла BCD при основании равнобедренного треугольника, а ∠ADC > отмеченного угла BDC при основании равнобедренного треугольника. Но ∠BCD = ∠BDC, следовательно, ∠ADC > ∠ACD.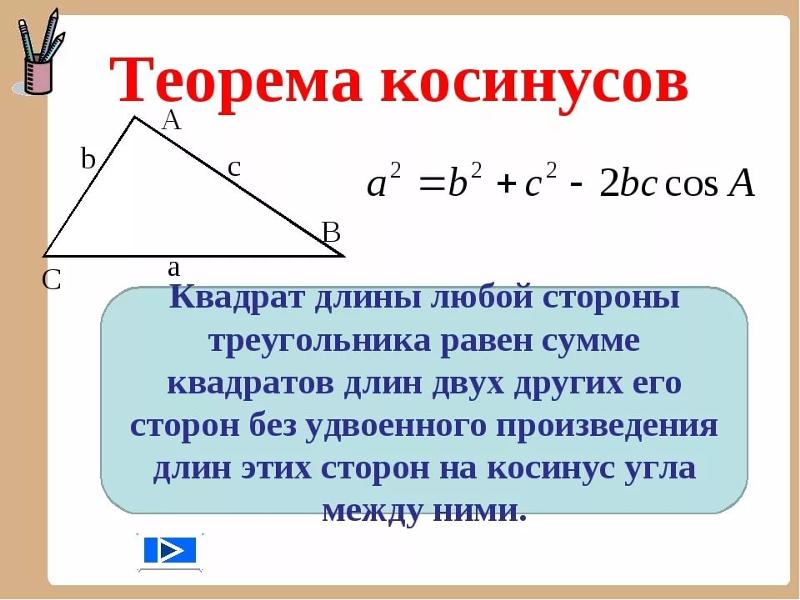 Поэтому на основании п. 86 (применяя его к ∆ACD) имеем AC > AD, но AD есть сторона A’C’, перенесенная в другое место, – следовательно, AC > A’C’.

3) Пусть ∆A’B’C’ при наложении займет положение ∆ABD (чер. 98), т. е. точка C’ расположится внутри ∆ABC. Тогда, соединив точки C и D, получим равнобедренный ∆CBD (BD = BC, ибо BD есть сторона B’C’, перенесенная в другое положение, а B’C’ = BC по построению) и, следовательно, ∠BCD = ∠BDC. Если продолжить стороны BD и BC по направлениям DM и CN, то получим два внешних угла этого равнобедренного треугольника ∠MDC и ∠NCD, но ∠MDC = ∠NCD, следовательно, ∠ADC > ∠ACD, а поэтому, на основании п. 86, имеем AC > AD, или AC > A’C’ (AD есть сторона A’C’, перенаправленная в другое положение).

Итак, во всех трех случаях оказалось, что

AC > A’C’,

т. е., если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, но углы между ними не равны, то против большого угла лежит большая сторона.

88. Разберем обратный вопрос. Пусть построены ∆ABC и ∆A’B’C’ (чер. 95) так, что AB = A’B’, BC = B’C’, но AC > A’C’, т. е. два треугольника имеют по две равных стороны, но третьи стороны их не равны. Сравнить ∠B и ∠B’.
Воспользуемся тем же способом рассуждения, как в п. 86.

Пока мы можем об углах B и B’ сделать три предположения: 1) ∠B = ∠B’, 2) ∠B > ∠B’ и 3) ∠B < ∠B’.

Первое предположение не годится, так как тогда наши треугольники, имея по построению по две равных стороны и равные углы между ними, были бы равны, и, следовательно, AC’ = A’C’, а это противоречит построению. Третье предположение, что ∠B < ∠B’ также не годится, так как тогда к этим треугольникам был бы применим результат, найденный в предыдущем п., на основании которого имели бы AC < A’C’, что также противоречит построению. Остается второе предположение, что ∠B > ∠B’, которое и должно быть верно. Итак:

Если две стороны одного треугольника равны соответственно двум сторонам другого, но третьи стороны этих треугольников не равны, то против большей стороны лежит и больший угол.

📐 Калькулятор сторон и углов треугольника

Интернет-магазин детских книг » Калькуляторы онлайн для решения математических задач »

Треугольник ΔABC,
a = BC, b = AC, c = AB — стороны треугольника,

A = CAB, B = ABC, C = BCA − углы, противолежащие сторонам a, b, c соответственно.

Как пользоваться онлайн-калькулятором. В форме укажите три значения: одну сторону и 2 дополнительных параметра (например, угол и сторону, два угла или две стороны). Заполните поле «Текст». Нажмите «Решить».

Калькулятор треугольника нужен, если требуется найти решение треугольников – длины сторон и величину углов треугольника.

Решить треугольник − найти все углы и стороны треугольника. Данный калькулятор предназначен для нахождения элементов треугольника.

Как решить треугольник

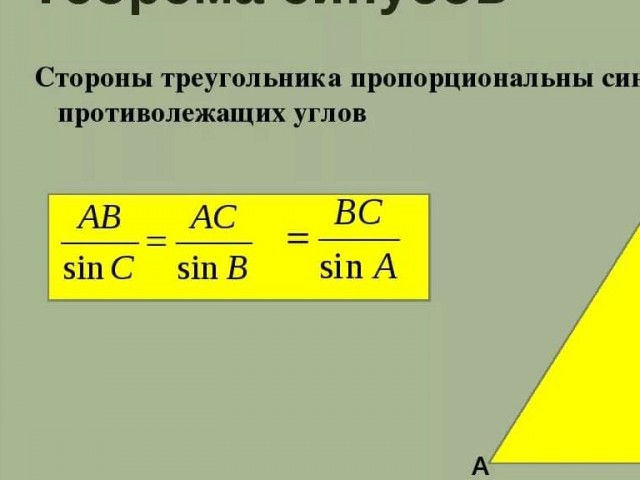
Здесь размещен онлайн-калькулятор, с помощью которого можно решить треугольник по трем, двум сторонам и углам, по теореме синусов и косинусов, то есть показывается, как находить углы в треугольнике.

Решение треугольников можно находить с помощью таблицы Брадиса. Здесь ответ вычисляется автоматически компьютерной программой онлайн, быстро и удобно.

Если нужны формулы и решения задач на теоремы косинусов и синусов с ответами, то можно найти подробное и точное решение, если использовать бесплатный калькулятор треугольника.

В решении подробно показывается, как найти третью сторону по двум сторонам и углу между ними или как определить неизвестные стороны треугольника, если известна одна сторона.

Примеры решений практических задач

1) решить треугольник по двум сторонам и противолежащему углу, т.е. углу между ними. Даны стороны а = 12 см, b = 8 см, угол=60°. Для того, чтобы решить задачу, требуется указать в онлайн-форме на данной странице условия задачи. В поле для стороны «a» указывается 12, в поле для стороны «b» ставится 8, в поле для углов «A» указывается 60. Нажать «Решить».

В ходе решения задачи получаем ответ:
сторона c = 13,8 см;
угол B = 35,2644° = 35°15’52» = 35°16′ = 0,1959π = 0,6155 rad;
угол C = 84,7356° = 84°44’8» = 84°44′ = 0,4708π = 1,4789 rad;
Периметр = 33,8 см;
Полупериметр = 16,9 см;
Площадь = 47,7984 см²;
Высота h_a = 7,9664 см;
Высота h_b = 11,9496 см;
Высота h_c = 6,9273 см;
Медиана m_a = 9,5513 см;
Медиана m_b = 12,2958 см;
Медиана m_c = 7,5107 см;
Радиус окружности R, описанной около треугольника = 6,9291 см;
Радиус окружности r, вписанной в треугольник = 2,8283 см.
Таким образом, был найден угол треугольника по двум сторонам и углу.

2) как найти угол треугольника, зная его стороны или решите треугольник по трем сторонам. Даны три стороны a = 2 см, b = 3 см, c = 4 см. В поле онлайн-формы «a» ставим 2, в поле «b» указываем 3, в поле «c» ставим 4. Далее следует нажать «Решить».

Используя теорему косинусов, получаем
угол A = 28,955° = 28°57’18» = 28°57′ = 0,1609π = 0,5054 rad;
угол B = 46,5675° = 46°34’3» = 46°34′ = 0,2587π = 0,8128 rad;
угол C = 104,4775° = 104°28’39» = 104°29′ = 0,5804π = 1,8235 rad;
Периметр = 9 см;
Полупериметр = 4,5 см;
Площадь = 2,9046 см²;
Высота h_a = 2,9046 см;
Высота h_b = 1,9364 см;
Высота h_c = 1,4523 см;
Медиана m_a = 3,3912 см;
Медиана m_b = 2,7839 см;
Медиана m_c = 1,5811 см;
Радиус окружности R, описанной около треугольника = 2,0657 см;
Радиус окружности r, вписанной в треугольник = 0,6455 см.

Таким образом, были найдены все углы треугольника.

3) решить треугольник по двум углам и стороне. В треугольнике ABC сторона a = 5 см, два угла B = 30°, C = 45°.
Ответ:
сторона b = 2,59 см;
сторона c = 3,66 см;
угол A = 105° = 0,5833π = 1,8326 rad;
Периметр = 11,25 см;
Полупериметр = 5,625 см;
Площадь = 4,5785 см²;
Высота h_a = 1,8314 см;
Высота h_b = 3,5355 см;
Высота h_c = 2,5019 см;
Медиана m_a = 1,9488 см;
Медиана m_b = 4,1857 см;
Медиана m_c = 3,537 см;
Радиус окружности R, описанной около треугольника = 2,588 см;
Радиус окружности r, вписанной в треугольник = 0,814 см.

Треугольники

Треугольник – многоугольник, который состоит из трех точек, соединенных тремя отрезками. Три точки в этом многоугольнике – вершины треугольника, а отрезки – стороны или ребра треугольника. На рисунке показан треугольник ΔABC, где A, B, C – его вершины, а AB, BC, AC – его стороны. Вершины треугольника дают треугольнику его обозначение. Угол при вершине A образуется сторонами AB и AC, обозначается как угол CAB.

Треугольники бывают разными. Название треугольников зависит от длины его сторон и величины его углов.

Стороны треугольника

Равносторонний или правильный треугольник состоит из трех равных сторон и трех равных углов. Все три угла в равностороннем треугольнике равны 60 градусам.

Если в треугольнике две стороны имеют одинаковую длину, то это равнобедренный треугольник.
В равнобедренном треугольнике две равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника.

Теоремы равнобедренных треугольников:
1) углы при основании равны,
2) если в треугольнике два угла равны, то это равнобедренный треугольник,
3) медиана, которая проведена к основанию, является биссектрисой и высотой.

Равные стороны в треугольниках обозначают одним, двумя или тремя штрихами или черточками, равные углы – одной, двумя или тремя дуговыми линиями.

Углы треугольника

Треугольники бывают остроугольными, тупоугольными и прямоугольными.

Треугольник является прямоугольным, если один из трех углов треугольника равен 90 градусам. Сторона, которая расположена напротив угла в 90 градусов, называется гипотенузой. Гипотенуза – самая большая сторона в прямоугольном треугольнике. Две другие стороны называются катетами.

Тупоугольный треугольник – треугольник, в котором один из углов больше 90 градусов.

Остроугольный треугольник – треугольник, в котором все три угла меньше 90 градусов.

Свойства треугольников

В треугольнике только один угол может быть больше 90 градусов.

В треугольнике сумма углов равна 180 градусам.

Внешний угол треугольника – смежный угол при этой вершине.
Варианты, как найти внешний угол при вершине:
а) суммировать два внутренних угла, не смежных с ним,
б) вычислить разность между 180 и внутренним углом этой вершины.

Если сложить любые две стороны треугольника, то сумма длин этих сторон всегда больше длины третьей стороны.

Радиус вписанной окружности

Окружность, вписанная в треугольник, – это круг, расположенный внутри треугольника.

Радиус этого круга (r) – отрезок, проведенный из центра вписанной окружности перпендикулярно к одной из сторон треугольника.

Центр вписанной окружности – точка пересечения двух биссектрис и равноудален от каждой стороны треугольника.

Для вычисления радиуса вписанной окружности используются площадь и периметр треугольника

Радиус описанной окружности

Окружность, описанная около треугольника, проходит через 3 вершины треугольника.

Для вычисления радиуса описанной окружности (R) используются площадь и длины всех сторон треугольника.

Тригонометрия — Терминология

Чтобы лучше понять некоторые проблемы, связанные с самолетами и движение необходимо использовать некоторые математические идеи из

тригонометрия , изучение треугольников. Большинство людей знакомятся с тригонометрией в средней школе.

В тригонометрии много сложных частей, но на этой странице нас интересуют главным образом определения и терминология. Начнем с общего треугольника. Треугольник – это замкнутая фигура, имеющая три стороны и три внутренних угла. Сумма трех углов любой треугольник равен 180 градусам. Если мы обозначим углы треугольника c , d и e , тогда:

с + d + е = 180 градусов

Существует два способа измерения углов внутри треугольника. Один из способов — измерить угол в градусов , где 360 градусов равняется полному кругу. другой способ — измерить угол в радианах , где 2 пи радиана равны полный круг. Следовательно;

360 (градусов) = 2 * пи (радиан)

1 градус = 0,01745 радиан

1 радиан = 57,2957 градуса

Прямоугольный треугольник является частным случаем общего треугольника с один из его углов равен 90 градусов. Угол 90 градусов называется прямым углом , и именно отсюда прямоугольный треугольник получил свое название. Прямоугольный треугольник обладает некоторыми особыми свойствами, которые очень полезны для решения задач. Сумма трех углов прямоугольного треугольника равна 180 градусам и единице углов равно 90 градусов. Тогда сумма двух других углов также равна 90 градусов. Для прямоугольного треугольника:

c + d = 90 градусов = пи/2 радиана

Важным фактором здесь является то, что если мы знаем (или измеряем) один угол прямоугольного треугольника, мы автоматически знаем значение другого угла. Если мы знаем значение d , то

в = 90 — г

Чтобы описать треугольник в целом, нам нужно знать значение двух углов; за право треугольника нам нужно знать (или измерить) только один угол.

Еще одна важная информация касается размер сторон прямоугольного треугольника. Назовем сторону прямоугольного треугольника, противоположную прямому углу гипотенуза . Это самая длинная сторона из трех сторон прямоугольного треугольника. Слово «гипотенуза» происходит от двух греческих слов что означает «растягиваться», так как это самая длинная сторона. Обозначим гипотенузу символом ч и мы пометим две другие стороны а и б .

Независимо от величины гипотенузы, соотношение от размера стороны a по гипотенузе h зависит Только от величины угла между катетом и гипотенузой. Значение коэффициента равно функция угла и получил название косинус угла. На фигуре,

cos(c) = а/ч

Из соотношения углов прямоугольного треугольника можно определить другая функция угла, называемая синус угла, соединяющего сторону

b и гипотенуза:

грех (с) = б / ч

Ключевым моментом здесь является то, что если мы измеряем один угол, мы знаем значение всех три угла прямоугольного треугольника. А если дополнительно измерить одну сторону, мы можем использовать эти тригонометрические функции для определения длины со всех трех сторон. Мы можем определить 5 единиц информации (2 угла и 3 стороны), сделав всего два измерения.

Между сторонами прямоугольного треугольника существует дополнительное отношение. Если мы нарисуем квадрат на гипотенузе и квадрат на каждой из двух сторон, площадь квадрата на гипотенузе равна сумме квадраты по бокам. Это называется Теорема Пифагора и известно с древних времен: 92

Теорему Пифагора можно использовать с тригонометрическими функциями определить величину всех сторон прямоугольного треугольника.

Виды деятельности:

Экскурсии с гидом

Навигация ..

Домашняя страница руководства для начинающих

math — Вычислить угол треугольника Python

спросил 9 лет, 3 месяца назад

Изменено 3 года, 4 месяца назад

Просмотрено 50 тысяч раз

Я пытаюсь найти угол треугольника в следующем, я знаю, что он должен быть 90 градусов, однако я не знаю, как его рассчитать в следующем:

Вот что я пробовал:

 angle = math. cos(7/9.899)
angleToDegrees = math.степени(угол)
возвращает: 43.ХХ

Что я делаю не так?

питон
математика
геометрия
угол

Это немного сложнее. Вам нужно использовать закон косинусов

 >>> A = 7
>>> В = 7
>>> С = 9,899
>>> из математики импортировать acos, градусы
>>> градусы(acos((A * A + B * B - C * C)/(2.0 * A * B)))
89.99594878743945

Точность до 4 значащих цифр. Если вы укажете более точное значение C, вы получите более точный результат.

 >>> С=9,899494936611665
>>> градусы(acos((A * A + B * B - C * C)/(2.0 * A * B)))
90,0

Вы также можете использовать это.

 print(str(int(round(math.степени(math.atan2(x,y)))))+'°')

Это принимает два входа как две высоты треугольника, и вы можете получить выходной угол в правильном формате градусов.