Угол в радианах: Измерение углов. Градусы и радианы

Измерение углов: градусы и радианы

Анна Малкова

Почему полный круг составляет 360 градусов? Что такое радиан и как перевести градусы в радианы? И при чем здесь число ? Статья для тех, кто сдает ЕГЭ или просто интересуется математикой.

Для измерения углов принято использовать две основные единицы: градусы и радианы.

Начнем с привычных градусов.

Полный круг составляет 360 градусов – это мы все знаем.

Да, но почему 360?

В метре 100 сантиметров. В рубле 100 копеек, в килограмме 1000 граммов. Мы привыкли к десятичной системе, и возникла она оттого, что на каждой руке у нас по 5 пальцев, а на двух руках — по 10.

А вот в часе 60 минут, в круге 360 градусов. И в сутках 24 часа. Древние шумеры умудрились придумать двенадцатеричную систему счисления! И при этом они тоже считали по пальцам. Нет, у них не было по 6 пальцев на каждой руке. Просто считали не пальцы, а фаланги четырех пальцев (кроме большого).

Кстати, круг легко делится именно на 6 частей (умеете?). А число 12 (дюжина) делится на 2, 3, 4, 6 и, собственно, 12.

И это не все. Древние шумерские астрономы обнаружили, что в день равноденствия Солнце встает почти точно на Востоке и заходит почти точно на Западе, причем от восхода до заката проходит по небу путь, в 360 раз больший, чем видимый с Земли диаметр Солнца. Небесную полуокружность разделили на 180 градусов.

Точнее, угловой диаметр Солнца равен примерно 32 угловых минуты, то есть чуть больше 0,5 градуса. Он еще и немного меняется в течение года из-за того, что орбита Земли не круговая, а эллиптическая.

Так что утверждение о том, что в День равноденствия Солнце проходит по небу путь, равный 360 своим «шагам» (то есть 360 видимым диаметрам солнца) – верно с некоторой точностью.
Конечно, древние астрономы наблюдали не только за движением Солнца. Они заметили, что яркая планета Юпитер совершает полный оборот вокруг Солнца за 12 лет. Точнее, не 12, а 11,86 лет, но уж очень им хотелось округлить до своего любимого числа.

Да что там Юпитер! Посмотрим на Луну. Юпитер на небе еще и не каждый найдет (а вы сможете?) – зато Луну, особенно полную, трудно не заметить! Месяц – промежуток от полнолуния до полнолуния – равен примерно 29,5 суток. Почти 30, верно?

Наша Земля совершает полный оборот вокруг Солнца за 365 дней (точнее, за 365,242 суток), и это – солнечный год.

И тогда лунный год – это 12 месяцев, в каждом месяце 30 дней (округлили), вот и получается 360 дней в году, почти столько же, сколько в солнечном, в котором 365 дней.

«Может быть, боги хотели сделать в году ровно 360 дней, но им кто-нибудь помешал, вот и получилось 365». Возможно, так и рассуждали древние астрономы, деля круг на 360 частей, 360 градусов. Тем более, что 360 – число, имеющее целых 24 делителя.

Число 360 делится на 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180 и 360. Очень удобно делить 360 градусов на части!

Обозначается: 360°. Этот кружок вверху – специальный символ для обозначения градуса.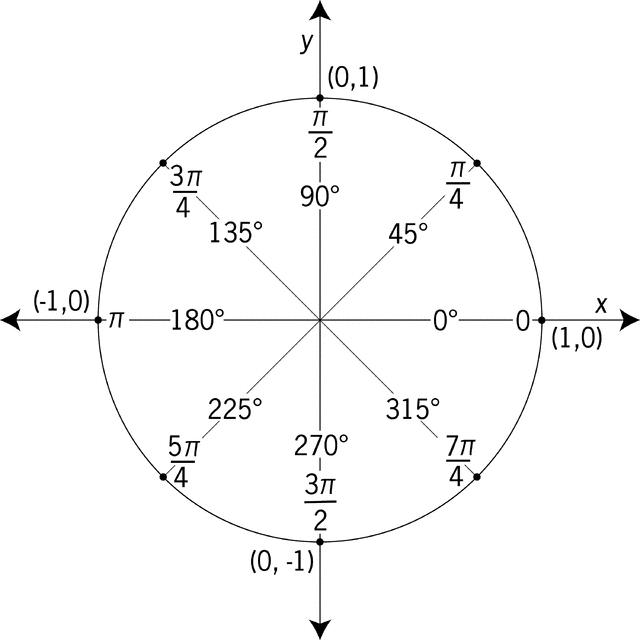

Есть и другая мера измерения углов – радианная.

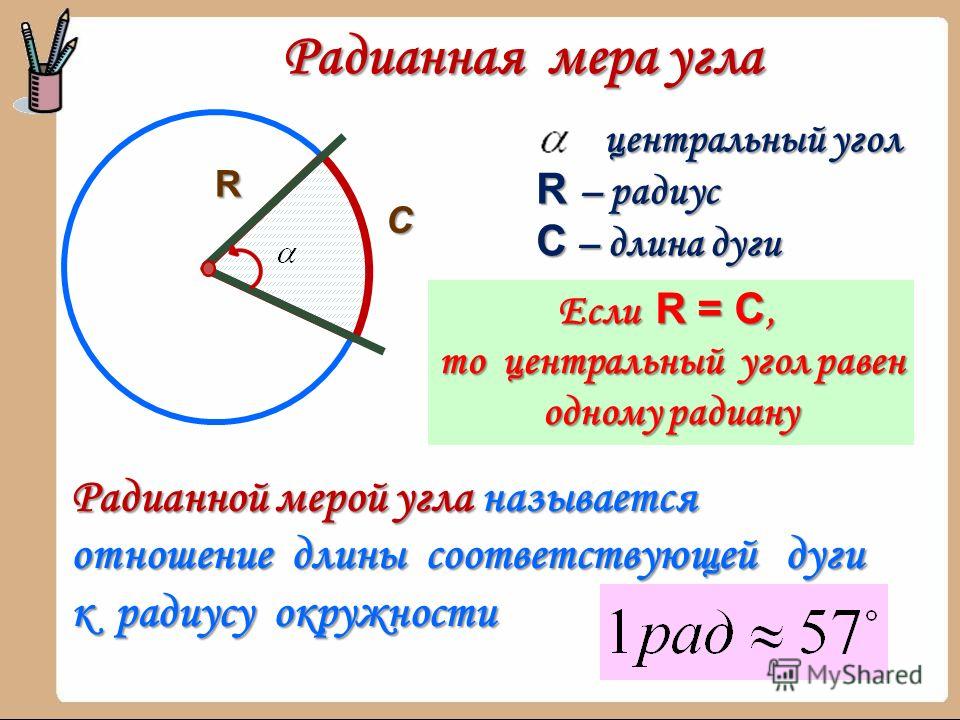
1 радиан – центральный угол, опирающийся на дугу, равную радиусу окружности.

Как перевести градусы в радианы и наоборот?

Полный круг – это 360 градусов. Отношение длины окружности к ее диаметру равно числу , приближенно Значит, длина окружности равна где – радиус.

Составим пропорцию. Длина окружности так относится к длине дуги на нашем рисунке, как – к величине угла, опирающегося на эту дугу, то есть к углу в 1 радиан.

1 радиан –

Слева в нашей пропорции углы, справа – длина полной окружности и длина отмеченной на рисунке дуги.

Из этой пропорции получаем, что радиан. Значит, полный круг – это радиан. Тогда полкруга – это радиан, четверть круга (то есть ) – это радиан.

Любой угол, выраженный в градусах, можно перевести в радианы. И наоборот, 1 радиан приблизительно равен 57 градусам.

Радианы и градусы онлайн

С помощю этого онлайн калькулятора можно перевести радианы в градусы и наоборот.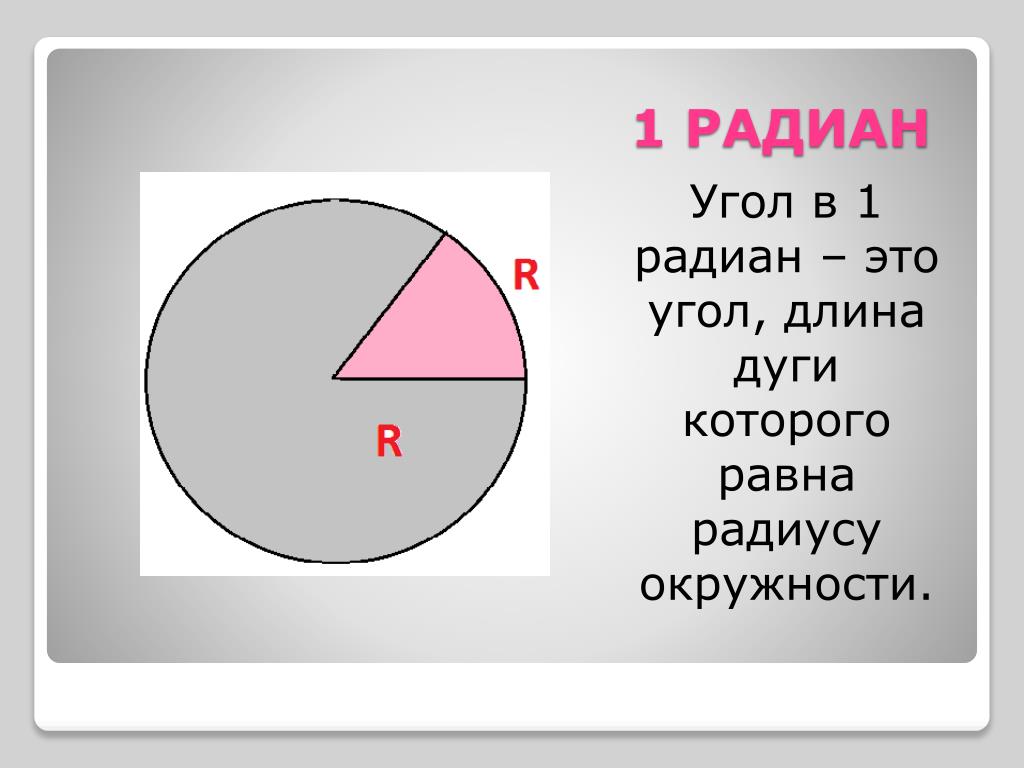 Теоретическую часть и численные примеры смотрите ниже.

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Определение 1. 1 радиан − это величина центрального угла окружности радиуса R, которая опирается на дугу длины R.

Другое определение:

Определение 2. 1 радиан − это угловая величина дуги, длина которой равна радиусу.

Из геометрии известно, что угловая величина не зависит от радиуса окружности. Поэтому мы будем рассматривать окружности радиусом R=1. При R=1 формула, определяющая длину окружности имеет вид

l=2πR=2π·1=2π ≈ 6.28.

Поскольку длина окружности (при R=1) равна 2π, то совершив один полный оборот мы получим угол в 2π радиан. Но этот угол равен 360°. Тогда имеем

360°=2π радиан.

(1)

Из уравнения (1) следует:

Mы получили формулы, определяющие всязь между градусом и радианом. Запись «радиан» обычно опускают, но подразумевают. Например можно записать:

В тригонометрии угловая величина может быть любым, даже отрицательным.

Пусть задана прямоугольная система координат xOy. Рассмотрим окружность радиусом 1 с центром в начале координат и пусть заданы векторы (Рис.2.).

Поворот вектора против часовой стрелки назовем положительным направлением, а по часовой стрелке − отрицательным. На рисунке Рис.2 вектор получится поворотом вектора в положительном направлении на 90° Это эквивалентно радианам. Вектор получен поворотом вектора в положительном направлении на 135°, что эквивалентно радианам.

Можно продолжить поворот и получить углы больше 180°. На Рис.2 вектор получен поворотом вектора в положительном направлении на 315° или на радиан. Еще раз напомним что − это длина дуги, которая рисует конец вектора продвигаясь до точки D.

Вектор в положительном направлении может совершить поворот, больше 360°.На рисунке Рис.3 вектор получен поворотом вектора в положительном направлении на 405°, что эквивалентно радианам. Т.е. можно сказать, что вектор получен поворотом вектора в положительном направлении на 45° и поворотом еще на один полный оборот в положительном направлении (на 360°). В радианном представлении имеем: . Т.е. вектор получен поворотом вектора в положительном направлении на радиан и еще поворотом на один полный оборот в положительном направлении (на радиан) .

Рассмотрим, теперь поворот вектора в отрицательном направлении, т.е. в направлении по часовой стрелке (Рис.4).

Вектор получен поворотом вектора по отрицательному направлению на −45° или на радиан. Вектор получен поворотом вектора по отрицательному направлению на −135° или на радиан и т.д.

Наконец можем отметить, что для любого действительного числа α существует единственный угол, радианная мера которого равна α радиан и этот угол отложен от начального вектора в положительном направлении, при α≥0 и в отрицательном направлении, при α≤0. При α=0, этот угол равен нулю.

Таким образом, для любого угла его меру α (радиан) можно записать в виде

где k-некоторое целое число, а (радиан) удовлетворяет следующему неравенству.

Пример 1. Радианная мера угла равна 51. Найти градусную меру этого угла.

Решение:

Ответ:

Этот угол получается поворотом единичного вектора, лежащего на оси Ox на 42.085° в положительном направлении и поворотом еще на 8 полных оборотов в положительном направлении.

Пример 2. Радианная мера угла равна -21. Найти градусную меру этого угла.

Решение:

Ответ:

Этот угол получается поворотом единичного вектора, лежащего на оси Ox на 123.211° в отрицательном направлении и поворотом еще на 3 полных оборотов в отрицательном направлении.

Пример 3. Градусная мера угла равна 457°. Найти радианную меру этого угла.

Решение:

Ответ:

Этот угол получается поворотом единичного вектора, лежащего на оси Ox на 1.

653 радиан в положительном направлении и поворотом еще на 1 полный оборот () в положительном направлении.

радиан — формула, определение | Радианы и градусы

Радиан — это единица измерения углов. У нас есть две единицы измерения углов: градус и радиан. До этого этапа вы могли использовать градусы для измерения размеров углов. Однако по разным причинам угловые меры в высшей математике часто описываются с использованием системы единиц, отличной от системы градусов. Эта система известна как радианная система. Знаете ли вы, что радиан был дополнительной единицей СИ для измерения углов до 19 века?95? Позже он был изменен на производную единицу.

Приходите, давайте подробно узнаем о формуле радианов, формуле длины дуги и о том, как преобразовать угол из радианов в градусы и из градусов в радианы.

1.	Что такое радиан?
2.	Радиан Формула
3.	Преобразование радианов в градусы
4.	Различия между радианами и градусами
5.	Часто задаваемые вопросы о Radian

Что такое радиан?

радиан — это единица СИ, используемая для измерения углов, а один радиан — это угол, образуемый в центре окружности дугой, длина которой равна радиусу окружности. Один радиан, показанный чуть ниже, приблизительно равен 57,296 градусам. Мы используем радианы вместо градусов, когда хотим вычислить угол через радиус. Поскольку «°» используется для обозначения степени, рад или ^c используется для представления радианов. Например, 1,5 радиана записывается как 1,5 рад или 1,5 ^c

.

Радиан Определение

Радиан — единица измерения угла. Вот несколько фактов о «радиане»

• Радиан обозначается «рад» или с использованием символа «с» в показателе степени.
• Если угол написан без единиц измерения, то это значит, что он в радианах.
• Некоторые примеры углов в радианах: 2 рад, π/2, π/3, 6 ^с и т. д.

Радиан Использование

• Углы обычно измеряются в радианах в исчислении и в большинстве других разделов математики.
• Радиан также широко используется в физике. Они предпочтительнее градусов, когда угловые измерения выполняются в физике.

Формула радиана

Мы уже узнали, что 1 радиан равен углу, образуемому дугой окружности, длина которой равна радиусу окружности. Таким образом, угол, образуемый дугой в радианах окружности, определяется как отношение длины дуги к радиусу окружности.

Если считать дугу полной окружностью окружности, то длина дуги = 2πr. Кроме того, мы знаем, что угол, образуемый в центре круга его окружностью, равен 360°. Тогда по приведенной выше формуле

Стягиваемый угол = (длина дуги)/(радиус)

360° = (2πr)/r

360° = 2π

Таким образом, формула радианов 2π = 360°.

Преобразование радианов в градусы

Угол может быть преобразован из «радианов в градусы» и из «градусов в радианы» в зависимости от необходимости. Мы используем формулу радиана (из предыдущего раздела), 2π = 360 ° для выполнения этих преобразований. Мы можем увидеть, как сделать преобразование между радианами и градусами на рисунке ниже.

Преобразование радианов в градусы

Формула радианов может быть записана как

2π радиан = 360°

Отсюда 1 радиан = 360°/2π (или)

1 радиан = 180°/π.

Таким образом, чтобы преобразовать радианы в градусы, мы умножаем угол на 180°/π.

Примеры преобразования радианов в градусы:

• π/2 = π/2 × 180°/π = 90°
• π/4 = π/4 × 180°/π = 45°
• 7π/6 = 7π/6 × 180°/π = 210°
• 2 рад = 2 × 180°/π ≈ 114,59°

Если мы посмотрим на первые три примера, где угол выражается в виде числа π, то число π сокращается при преобразовании его в градусы.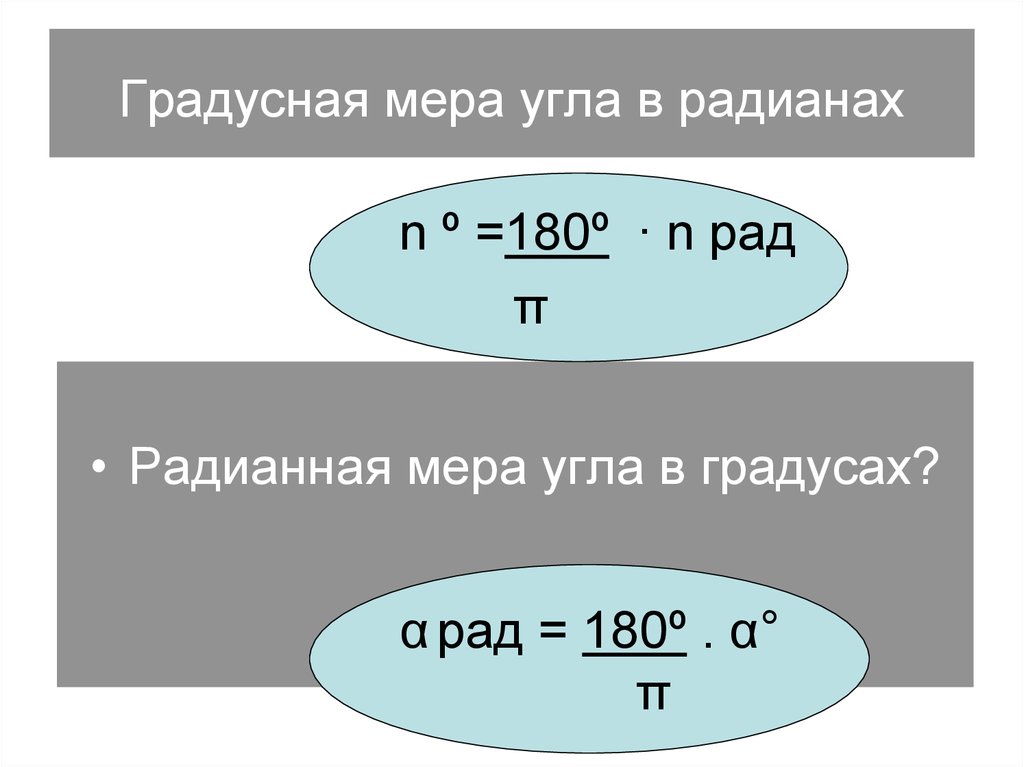 Итак, чтобы преобразовать угол в радианах, выраженный в π, в градусы, просто замените π на 180°. Это трюк для преобразования радианов в градусы. Здесь вы можете увидеть первые три примера использования трюка.

• π/2 = 180°/2 = 90°
• π/4 = 180°/4 = 45°
• 7π/6 = 7(180°)/6 = 210°

Преобразование градусов в радианы

Из формулы радианов

2π радиан = 360°

Отсюда 1° = (2π радиан)/360°

1° = (π/180) радиан

Таким образом, чтобы преобразовать градусы в радианы, мы умножаем угол на π/180 радиан.

Примеры преобразования градусов в радианы:

• 90° = 90 × π/180 = π/2
• 180° = 180 × π/180 = π
• 210° = 210 × π/180 = 7π/6

Таблица радианов и градусов

Вот таблица с некоторыми стандартными углами в градусах и соответствующими углами в радианах. Эта таблица помогает узнать эквивалентные углы в радианах (или градусах).

Степень	Радиан
30°	№/6
45°	№/4
60°	№/3
90°	№/2
180°	№
270°	3π/2
360°	2π

Различия между радианами и градусами

Радианы и градусы являются измерениями только углов. Вот несколько различий между радианами и градусами.

Радиан	Степень
Угол, образуемый дугой длины ‘r’ окружности с радиусом ‘r’, известен как 1 радиан.	1/360 th Часть полного угла называется градусом.
1 радиан обозначается как 1 c или иногда просто 1.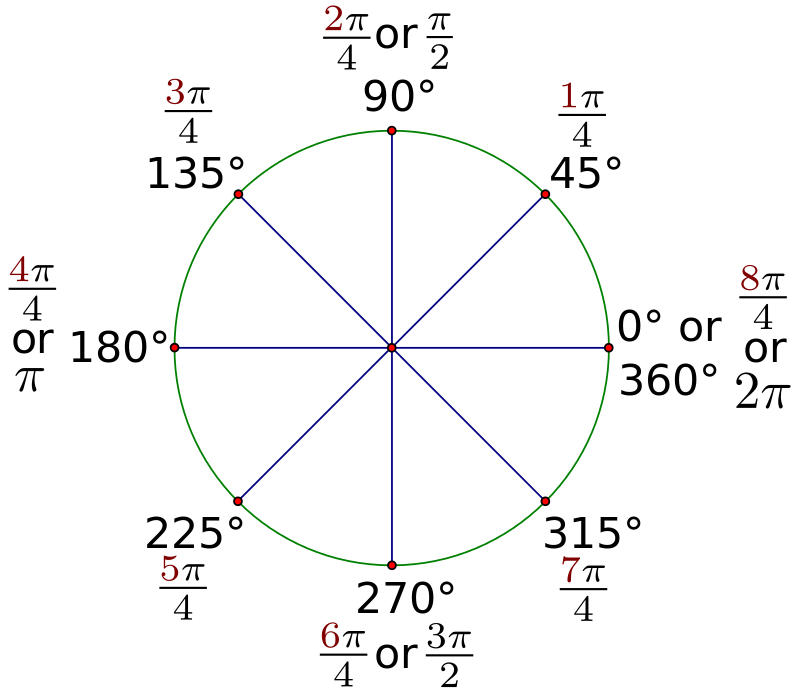	1 градус обозначается 1°.
Чтобы преобразовать угол из градусов в радианы, умножьте его на π/180.	Чтобы преобразовать угол из радианов в градусы, умножьте его на 180/π.

Важные примечания по радианам:

• Мы можем преобразовать угол из градусов в радианы, умножив его на π/180.
• Мы можем преобразовать угол из радианов в градусы, умножив его на 180/π.
• Длина дуги = радиус × угол, стягиваемый в центре.
  При применении этой формулы угол (если он указан в градусах) следует сначала преобразовать в радианы.

☛ Связанные темы:

• Тригонометрические отношения в радианах
• Калькулятор градусов в радианы
• Калькулятор радианов в градусы

Часто задаваемые вопросы о Radian

Что такое радиан?

Радиан — это единица измерения углов в системе СИ, основанная на длине дуги и радиусе. 1 радиан равен углу, образуемому дугой в центре окружности, длина которой равна радиусу окружности.

Что такое формула преобразования радианов в градусы?

Чтобы преобразовать радианы в градусы, мы умножаем угол на 180/π. Например, 3π/2 = 3π/2 × 180/π = 270°. Таким образом, градусный эквивалент угла 3π/2 равен 270°.

Что такое формула преобразования градусов в радианы?

Чтобы преобразовать градусы в радианы, мы умножаем угол на π/180. Например, 270° = 270 × π/180 = 3π/2. Таким образом, эквивалентный угол 270° в радианах равен 3π/2.

Сколько радианов в полном круге?

В полном круге угол равен 360°, а по формуле радиана 360° = 2π. Таким образом, в полном круге 2π радиан.

Что такое формула длины дуги в радианах?

Длина дуги окружности равна произведению ее радиуса на угол, образуемый дугой, в радианах. то есть длина дуги = радиус × угол в радианах. Если угол задан в градусах, мы сначала должны преобразовать этот угол в радианы, а затем применить формулу длины дуги.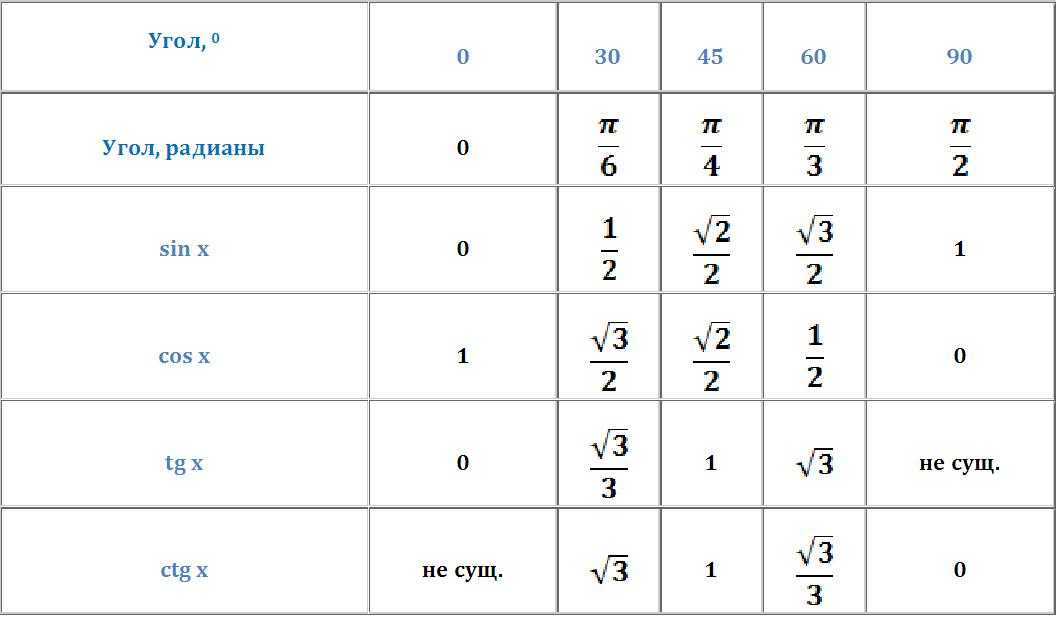

Что такое формула радиана для длины дуги?

Чтобы найти угол, образуемый дугой в радианах, мы просто делим ее длину на радиус окружности. т. е. θ (в радианах) = (длина дуги) / радиус.

Чему равен 1 радиан?

Мы знаем, что 2π радиан = 360°. Разделив это уравнение на 2 с обеих сторон, π радиан = 180°. Разделив это уравнение на π с обеих сторон, 1 радиан = 180°/π. Таким образом, 1 радиан = 57,296°. Это может быть использовано для преобразования любого угла в радианы. Например, 2 радиана в градусах = 2 × 57,296 = 114,592°.

Какова мера 0 радиан в градусах?

Чтобы преобразовать 0 радиан в градусы, мы умножаем это на 180/π. Таким образом, 0 радиан = 0 × 180/π = 0°. т. е. 0 радиан — это не что иное, как 0 градусов.

Что такое 360 градусов в радианах?

Чтобы преобразовать 360 градусов в радианы, мы умножаем угол на π/180. 360° = 360 × π/180 = 2π. Таким образом, эквивалентный угол 360° в радианах равен 2π.

Углы — градусы и радианы

• Дом
• О
• Страницы математики и статистики
• R Программирование
• Предметы Python

 

Привет. Эта страница будет о мерах углов от градусов до радианов.

 

Содержание

 

 

Краткое введение в радианы

. В математике более высокого уровня степени не очень часто используются, когда дело доходит до вычислений. Вместо градусов для представления углов используются радианы. Один радиан равен 57,29.{\circ}\) .

(В Канаде километры используются для измерения расстояния. В других странах, например, в Соединенных Штатах, вместо километров используются мили. Термин «радиан» подобен километрам, а градус — милям.)

Радиан — это мера угла исходя из радиуса окружности. В 4-квадрантной системе 0\(\pi\) начинается, когда \(y= 0\) и для \(x \geq 0\). Положительный угол (в градусах или радианах) находится в направлении против часовой стрелки, а отрицательный угол — в направлении по часовой стрелке.

В (научном) калькуляторе углы указываются в градусах, когда калькулятор находится в режиме градусов, указанном DEG в верхней части экрана калькулятора.

No related posts.