Что значит вогнутый угол в Blender? | Render.ru
Дмитрий Порфирьев
Пользователь сайта
#1
#1
Почему вогнутый угол это плохо ? И как определить что это вогнутый угол?
ProcXel.A
Знаток
#2
Кто говорит, что вогнутные углы — это плохо?))
Дмитрий Порфирьев
Пользователь сайта
#3
#3
Я смотрю курс.
Учитель всегда старается избегать их
ProcXel.A
Знаток
#4
#4
Можно скриншот «плохого вогнутого угла» в Блендере?
Дмитрий Порфирьев
Пользователь сайта
#5
#5
Дмитрий Порфирьев
Пользователь сайта
#6
#6
Я указал вогнутый угол красными кружками
Дмитрий Порфирьев
Пользователь сайта
#7
#7
И чтобы его убрать, учитель, прокинул новое ребро
ProcXel.
AЗнаток
#8
#8
А-а-а, вон оно что. Это скорее не вогнутый угол, а вогнутый полигон. 3Д модели состоят из полигонов. Каждый полигон состоит из треугольников. Эти треугольники рассчитываются программой автоматически. И если модель из полигонов перенести из одной программы в другую, то другая программа может рассчитывать эти треугольники как-то подругому, из-за чего у вогнутого полигона треугольники могут повылазить за границы полигона. Чтобы этого не произошло, и добавляют ребра явно, чтобы все полигоны в модели были выпуклыми.
Screenshot 2022-04-11 184555.
png105,6 КБ Просмотров: 74
pngДмитрий Порфирьев
Пользователь сайта
#9
#9
Спасибо большое! Теперь я понял
Дмитрий Порфирьев
Пользователь сайта
#10
#10
Еще почему 180 градусов это плохо?
Дмитрий Порфирьев
Пользователь сайта
#11
#11
Учитель сделал так что его избежать
ProcXel.
AЗнаток
#12
#12
Дмитрий Порфирьев сказал(а):
Еще почему 180 градусов это плохо?
Нажмите, чтобы раскрыть…
По той же самой причине. Другая программа может пересчитать треугольники в полигоне таким образом, что один треугольник получится из трех вершин, лежащих на одной прямой. Чтобы таких треугольников не получилось, полигон разделяют ребром на два полигона без углов в 180гр.
Дмитрий Порфирьев
Пользователь сайта
#13
#13
Спасибо большое
Кирпич фасонный вогнутый «Терракотовый» Голицыно 1NF
В связи с нестабильностью ценовой политики производителей, точные цены на стройматериалы уточняйте по телефону.
Цена 3596₽ — купить
Голицынский кирпич Кирпич Кирпич облицовочный (фасадный)
Описание
Фасонный кирпич в наиболее распространенном формате 1НФ терракотового цвета. Стоит также отметить что этот фасонный кирпич имеет гладкую поверхность и вогнутый угол. Дом построенный с применением фасонного кирпича «Терракотовый» вне всяких сомнений будет примечателен на фоне прочих строений. Кирпич произведен на «Голицынском керамическом заводе» который находится в городе Голицыно Московской области.
Если вы собрались покупать фасонный кирпич, то делать это нужно у лидеров рынка кирпича – прежде всего в компании «Строй-С». Обязательно приезжайте к нам в офис на Мачуги 40. Тут наши специалисты помогут советом ну а вы сможете выбрать кирпич в нашем шоуруме. Весь кирпич мы бережно доставляем по Краснодарскому краю с выгрузкой на объекте заказчика. Есть вопросы или сомнения? Звоните нам и уточняйте стоимость кирпича с доставкой.
Характеристики
| Название | Описание | Скачать |
|---|---|---|
| Сертификат соответствия 1,4 НФ | Кирпич керамический лицевой размером 1,4 НФ (250x120x88 мм) с гладкой и рельефной лицевой поверхностью, класса средней плотности 1,4, M175,200, F 100 Выпускается по ГОСТ 530-2012. Серийный выпуск. ОАО «Голицынский керамический завод» по 14.02.2021 | Скачать |
| Сертификат соответствия 1 НФ | Кирпич керамический лицевой размером 1,0 НФ (250x120x65 мм) с гладкой и рельефной лицевой поверхностью, класса средней плотности 1,4, M175,200, F 100 Выпускается по ГОСТ 530-2012. Серийный выпуск. ОАО «Голицынский керамический завод» по 14.02.2021 | Скачать |
| Сертификат соответствия 0,96 НФ | Кирпич керамический лицевой размером 250x85x88 мм, с гладкой и рельефной лицевой поверхностью, класса средней плотности 1,4, M175,200, F 100 Выпускается по ГОСТ 530-2012. | Скачать |
| Сертификат соответствия 0,7 НФ | Кирпич керамический лицевой размером 250x85x65 мм, с гладкой и рельефной лицевой поверхностью, класса средней плотности 1,4, M150,175,200, F 100 Выпускается по ГОСТ 530-2012. Серийный выпуск. ОАО «Голицынский керамический завод» по 14.02.2021 | Скачать |
| Сертификат соответствия 0,5 НФ | Кирпич керамический лицевой размером 250x60x65 мм, с гладкой и рельефной лицевой поверхностью, класса средней плотности 1,4, M150,175,200, F 100 Выпускается по ГОСТ 530-2012. Серийный выпуск. ОАО «Голицынский керамический завод» по 14.02.2021 | Скачать |
Вогнутые многоугольники — определение, свойства, примеры
Вогнутые многоугольники — это такие многоугольники, в которых хотя бы один внутренний угол является углом отражения и направлен внутрь. У них минимум 4 стороны, и несколько диагоналей вогнутого многоугольника могут частично или полностью выходить за его пределы. Все вогнутые многоугольники неправильные, потому что внутренние углы не равны. Давайте узнаем больше о вогнутых многоугольниках в этой статье.
| 1. | Что такое вогнутый многоугольник? |
| 2. | Вогнутый и выпуклый многоугольник |
| 3. | Вогнутые многоугольники в реальной жизни |
4. | Часто задаваемые вопросы о вогнутом многоугольнике |
Что такое вогнутый многоугольник?
Многоугольник, который не является выпуклым, является вогнутым многоугольником. Если какой-либо внутренний угол в многоугольнике больше 180°, то это вогнутый многоугольник. Вогнутый многоугольник выглядит как многоугольник, в котором по крайней мере две стороны кажутся вдавленными внутрь. Например, звезда — это вогнутый многоугольник.
Определение вогнутого многоугольника
Вогнутый многоугольник определяется как многоугольник, в котором один или несколько внутренних углов больше 180°. Если какая-либо из диагоналей многоугольника частично или полностью выходит за пределы многоугольника, то такой многоугольник называется вогнутым. Обратите внимание на следующий рисунок, на котором показаны вогнутые многоугольники.
Свойства вогнутого многоугольника
Вогнутый многоугольник имеет некоторые отличительные свойства, которые помогают отличить его от других многоугольников.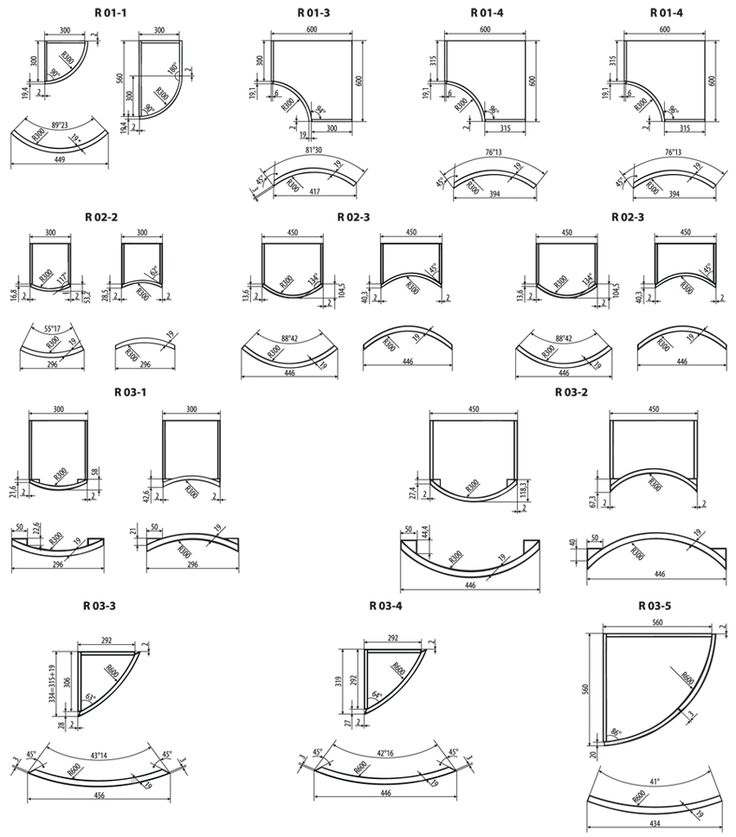
- Вогнутый многоугольник имеет по крайней мере один угол, который является углом отражения, то есть он больше 180° и меньше 360°.
- Некоторые диагонали вогнутого многоугольника могут частично или полностью лежать за его пределами.
- В вогнутом многоугольнике есть по крайней мере одна вершина, которая кажется вдавленной внутрь, чтобы придать многоугольнику отчетливую форму «пещеры».
- Если отрезок пересекает вогнутый многоугольник, он касается более двух сторон.
- Правильные многоугольники никогда не могут быть вогнутыми.
- Все вогнутые многоугольники неправильные, потому что внутренние углы имеют разную величину.
Вогнутый и выпуклый многоугольник
Выпуклый и вогнутый многоугольник можно легко отличить по их свойствам. Обратите внимание на следующий рисунок и таблицу, чтобы увидеть разницу между выпуклыми и вогнутыми многоугольниками.
| Выпуклые многоугольники | Вогнутые многоугольники |
|---|---|
| Выпуклый многоугольник не имеет внутреннего угла больше 180° | Вогнутый многоугольник имеет по крайней мере один угол отражения (более 180°). |
| Выпуклый многоугольник может иметь 3 стороны. | Вогнутый многоугольник имеет по крайней мере 4 стороны. |
| Когда линия проводится внутри выпуклой фигуры с любой стороны, она касается только двух сторон. | Когда линия проведена внутри вогнутой формы с одной стороны, она касается более чем двух сторон. |
| Диагонали выпуклого многоугольника не лежат вне его. | Некоторые диагонали вогнутого многоугольника могут частично или полностью лежать за его пределами. |
Углы вогнутого многоугольника
Вогнутый многоугольник имеет внутренние и внешние углы, как и другие многоугольники. Единственное свойство вогнутых многоугольников, о котором здесь следует помнить, заключается в том, что один или несколько внутренних углов образуют угол отражения, который делает его похожим на вогнутый многоугольник. Другими словами, этот рефлекторный угол делает вершину направленной внутрь, что придает ей своеобразную форму.
Давайте узнаем больше о сумме внешних и внутренних углов вогнутого многоугольника.
Сумма внешних углов вогнутого многоугольника
Сумма внешних углов вогнутого многоугольника равна 360°. Это означает, что, как и у всех других многоугольников, сумма внешних углов всегда составляет 360° для всех вогнутых многоугольников.
Сумма внутренних углов вогнутого многоугольника
Чтобы найти сумму внутренних углов вогнутого многоугольника, мы используем ту же формулу, которая применяется для других выпуклых многоугольников. Сумма внутренних углов = (n — 2) × 180°, где n представляет количество сторон многоугольника.
Вогнутые многоугольники в реальной жизни
Вогнутые многоугольники имеют заметную форму, в которой хотя бы одна из вершин направлена внутрь. Мы можем заметить вогнутые многоугольники в нашей повседневной жизни. Например, звездочка, наконечник стрелки, знак плюс и многое другое.
☛ Похожие темы
- Типы многоугольников
- Неправильные многоугольники
- Полигон Формула
- Площадь полигонов
Примеры на вогнутом многоугольнике
Пример 1:
Напишите верно или неверно для следующих утверждений.
а.) Все внутренние углы вогнутого многоугольника меньше 180°.
b.) Вогнутые формы — это фигуры, у которых хотя бы одна вершина направлена внутрь.
Решение:
а.) Неверно, хотя бы один внутренний угол вогнутого многоугольника больше 180°.
b.) Верно, вогнутые формы — это те фигуры, у которых хотя бы одна вершина указывает внутрь. Это придает отчетливую форму вогнутому многоугольнику.
Пример 2:
Какие из следующих фигур представляют вогнутый многоугольник?
а.) Звезда
б.) Стрелка
в.) Ромб
Решение:
а.) Звезда — Вогнутый многоугольник
б.) Стрелка — Вогнутый x2 многоугольник
ромб полигон
Пример 3: Заполните пропуски правильным словом.
а.) В _____ многоугольнике некоторые диагонали могут частично или полностью выходить за его пределы.
b.) Многоугольник ______ может иметь 3 стороны.
Решение:
а.) В вогнутом многоугольнике некоторые диагонали могут частично или полностью лежать вне его.
b.) Выпуклый многоугольник может иметь 3 стороны.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по вогнутому многоугольнику
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о вогнутом многоугольнике
Что такое вогнутый многоугольник в геометрии?
Вогнутый многоугольник определяется как многоугольник, в котором один или несколько внутренних углов больше 180°. Если какая-либо из диагоналей многоугольника частично или полностью выходит за пределы многоугольника, то такой многоугольник называется вогнутым.
В вогнутом многоугольнике есть по крайней мере одна вершина, которая, кажется, вдавлена внутрь, чтобы придать многоугольнику отчетливую «пещерную» форму.
Чему равна сумма внешних углов вогнутого многоугольника?
Сумма внешних углов вогнутого многоугольника равна 360°. Это означает, что, как и у всех других многоугольников, сумма внешних углов всегда составляет 360° для всех вогнутых многоугольников.
Какова сумма внутренних углов вогнутого многоугольника?
Чтобы найти сумму внутренних углов вогнутого многоугольника, мы используем ту же формулу, которая применяется для других выпуклых многоугольников. Сумма внутренних углов = (n — 2) × 180°, где n представляет количество сторон многоугольника.
Что является примером вогнутого многоугольника?
Мы сталкиваемся с множеством реальных примеров вогнутых многоугольников, таких как звезда, наконечник стрелы и многие другие, которые имеют особую форму и удовлетворяют всем характеристикам вогнутого многоугольника.
Как найти периметр вогнутого многоугольника?
Периметр вогнутого многоугольника можно вычислить так же, как находится периметр других выпуклых многоугольников. Все стороны многоугольника складываются, чтобы найти периметр.
Как найти площадь вогнутого многоугольника?
Поскольку вогнутые многоугольники имеют неправильную форму, специальной формулы для нахождения площади нет. Вогнутый многоугольник можно разделить на треугольники или другие меньшие многоугольники в соответствии с формой. Затем площадь этих фигур можно рассчитать по соответствующим формулам, и эти площади можно сложить вместе, чтобы получить площадь вогнутого многоугольника.
В чем разница между вогнутым и выпуклым многоугольником?
Различие между вогнутыми и выпуклыми многоугольниками можно перечислить следующим образом.
- Выпуклый многоугольник не имеет внутреннего угла больше 180°, тогда как вогнутый многоугольник имеет по крайней мере один угол отражения больше 180°.
- Диагонали выпуклого многоугольника не лежат вне его. Некоторые из диагоналей вогнутого многоугольника могут частично или полностью лежать за его пределами.
- Выпуклый многоугольник может иметь 3 стороны, тогда как вогнутый многоугольник имеет по крайней мере 4 стороны.
Является ли звезда вогнутым многоугольником?
Да, звезда является вогнутым многоугольником, потому что она удовлетворяет всем свойствам вогнутого многоугольника. У него более 4 сторон, углы больше 180°, а диагонали звезды лежат вне формы.
Является ли стрелка вогнутым многоугольником?
Да, стрелка является вогнутым многоугольником, потому что она удовлетворяет всем условиям вогнутого многоугольника. У него внутренние углы больше 180°, а одна диагональ в стрелке лежит вне формы.
Является ли треугольник выпуклым или вогнутым многоугольником?
Треугольник является выпуклым многоугольником, потому что это трехсторонняя фигура. Вогнутый многоугольник имеет по крайней мере 4 стороны.
Является ли квадрат вогнутым многоугольником?
Нет, квадрат не является вогнутым многоугольником, это выпуклый многоугольник, потому что все диагонали квадрата лежат внутри него и нет внутреннего угла больше 180°.
Всегда ли вогнутый многоугольник правильный?
Нет, все вогнутые многоугольники неправильные, потому что один из их углов является углом отражения. Другими словами, внутренние углы вогнутого многоугольника не равны, следовательно, все вогнутые многоугольники неправильные.
Скачать БЕСПЛАТНЫЕ учебные материалы
Вогнутые многоугольники
Вогнутые многоугольники
Вогнутый многоугольник — это многоугольник, один или несколько внутренних углов которого больше 180 0 . Создается впечатление, что вершина «вдавлена» внутрь многоугольника. Стоит отметить, что треугольник (3-угольник) не может быть вогнутым. Противоположностью выпуклого многоугольника является вогнутый многоугольник. Вогнутый многоугольник — это тот, по крайней мере две стороны которого кажутся вдавленными внутрь.
Например, вогнутый многоугольник — это звезда.
Выпуклый многоугольник — это невогнутый многоугольник. Вогнутый многоугольник имеет неровную форму. Внутри многоугольника сумма углов может быть любой. Он также может быть больше 360°. В результате угол отражения должен существовать внутри вогнутого многоугольника. Многоугольник может быть построен как во внутреннем, так и во внешнем направлении.
Поскольку сумма углов трехстороннего многоугольника, т. е. треугольника, уже равна 180 градусам, это не приведет ни к какому вогнутому многоугольнику. Также нам нужен один угол больше 180° для вогнутого многоугольника. В результате треугольник не является вогнутым многоугольником.
Определение вогнутого многоугольника
Вогнутый многоугольник — это невыпуклый многоугольник. Если хотя бы один из внутренних углов простого многоугольника больше, то он вогнутый».
Типы вогнутых многоугольников
Правильный вогнутый многоугольник: Все стороны правильного вогнутого многоугольника равны, и все внутренние углы равны.
Согласно определению, один из углов вогнутого многоугольника должен быть больше или равен 180 градусам.
Кроме того, сумма углов внутри многоугольника равна (n – 2) x 180°, где n – количество сторон.
Из этого можно сделать вывод, что этот критерий не может быть выполнен ни при каких обстоятельствах. Вогнутый многоугольник со всеми равными сторонами и всеми равными углами невозможен. В результате не существует такого понятия, как правильный вогнутый многоугольник.
Неправильный вогнутый многоугольник: Неправильные многоугольники легко найти. Количество сторон и углов неправильного многоугольника может быть разным. Должно присутствовать только условие вогнутости, т. е. один угол должен быть рефлекторным. В неправильном вогнутом многоугольнике сумма внутренних углов имеет разные единицы измерения. Наконец, все вогнутые многоугольники являются неправильными многоугольниками.
Диаграмма вогнутого многоугольника
Вогнутый многоугольник — это многоугольник, у которого хотя бы один угол больше 180°.
В шестиугольной форме шесть внутренних углов, а именно ∠ABC, ∠BCD, ∠CDE, ∠DEF, ∠EFA и ∠FAB. ∠CDE больше 180° среди шести внутренних углов.
Свойства вогнутого многоугольника
Вогнутый многоугольник имеет следующие свойства:
- Он имеет по крайней мере один внутренний угол между 1800 и 3600 градусами. Можно сказать, что вогнутый многоугольник имеет по крайней мере один угол отражения.
- Он имеет по крайней мере одну вершину, обращенную внутрь, что придает ему вогнутую форму.
- Хотя бы одна пара сторон, соединяющих вершину, выходит за ее пределы.
- Может быть более одной диагонали, лежащей за пределами края многоугольника.
- Отрезок линии, проведенный через вогнутый многоугольник, пересекает границу многоугольника более двух раз.
Углы вогнутых многоугольников
Как и другие многоугольники, вогнутый многоугольник имеет внутренние и внешние углы. Важно помнить о вогнутых многоугольниках: один или несколько внутренних углов образуют угол отражения, придавая ему вид вогнутого многоугольника.
Другими словами, рефлекторный угол заставляет вершину указывать внутрь, придавая ей характерную форму. Давайте узнаем больше о сумме внешних и внутренних углов вогнутого многоугольника.
Сумма внешних углов вогнутого многоугольника
Сумма внешних углов вогнутого многоугольника составляет 360°. Это означает, что, как и у всех других многоугольников, сумма внешних углов всех вогнутых многоугольников всегда равна 360°.
Сумма внутренних углов вогнутого многоугольника
Та же самая формула, которая используется для получения суммы внутренних углов других выпуклых многоугольников, используется для нахождения суммы внутренних углов вогнутого многоугольника. Сумма внутренних углов равна (n – 2) 180°, где n – количество сторон многоугольника.
Заключение
В этой статье мы узнаем, что многоугольник, у которого хотя бы один внутренний угол больше 180 градусов, называется вогнутым многоугольником. У него должно быть как минимум четыре стороны. Форма вогнутого многоугольника часто бывает неровной.