Укажите множество решений системы неравенств: УКАЖИТЕ МНОЖЕСТВО РЕШЕНИЙ СИСТЕМЫ НЕРАВЕНСТВ х>8 , 9-х>0 .

Содержание

13.4. Системы неравенств (Задачи ОГЭ)

Задачи ОГЭ

№3125

Сложность:

32 %

Укажите решение системы неравенств

$\begin{cases} -9+3x< 0,\\ 2-3x< -10.\end{cases}$

1) $(-\infty; 3)$
2) нет решений
3) $(4;+\infty)$

4) $(3;4)$

Подпишись на ютуб канал

№1925

Сложность:

32 %

Решите систему неравенств
$\begin{cases} x+2{,}6\leqslant 0\\x+5\geqslant 1\end{cases}$
На каком рисунке изображено множество её решений?

Подпишись на ютуб канал

№2546

Сложность:

32 %

Решите систему неравенств \(\begin{cases} 5(x+3) > 7(x+1),\\ -5-1{,}25x<0.

\end{cases}\)

В каком из приведённых случаев изображено множество её решений?

Подпишись на ютуб канал

№2322

Сложность:

33 %

Укажите множество решений системы неравенств

$\begin{cases} -12 + 3x > 0\\ 9 — 4x> -3\end{cases}$

1) Система не имеет решений

Подпишись на ютуб канал

№2133

Сложность:

34 %

На каком рисунке изображено множество решений системы неравеств?

$\begin{cases} x<3\\ 4-x< 0 \end{cases}$

Подпишись на ютуб канал

№2558

Сложность:

37 %

На какой из координатных прямых изображено множество решений системы неравенств

$\begin{cases} 2x-3> 0,\\ 16-5x<1. \end{cases}$

Подпишись на ютуб канал

№2342

Сложность:

38 %

Укажите множество решений системы неравенств

$\begin{cases} -35 + 5x < 0\\ 6 — 3x > -18\end{cases}$

Подпишись на ютуб канал

№1693

Сложность:

38 %

Выберите верное множество решений системы неравенств:

$\begin{cases} -12x+12\geqslant 4x+4\\-4x+11\leqslant 3x+9\end{cases}$

1) $\left(-\infty;\dfrac27\right]\cup\left[\dfrac12;+\infty\right)$

2) $\left[ \dfrac27; \dfrac12\right]$

3)$\left[ \dfrac12; \dfrac72\right]$

4)$\left[ -\dfrac12; \dfrac27\right]$

Подпишись на ютуб канал

№3146

Сложность:

40 %

Укажите решение системы неравенств

$\begin{cases} -35+5x< 0,\\ 6-3x>-18.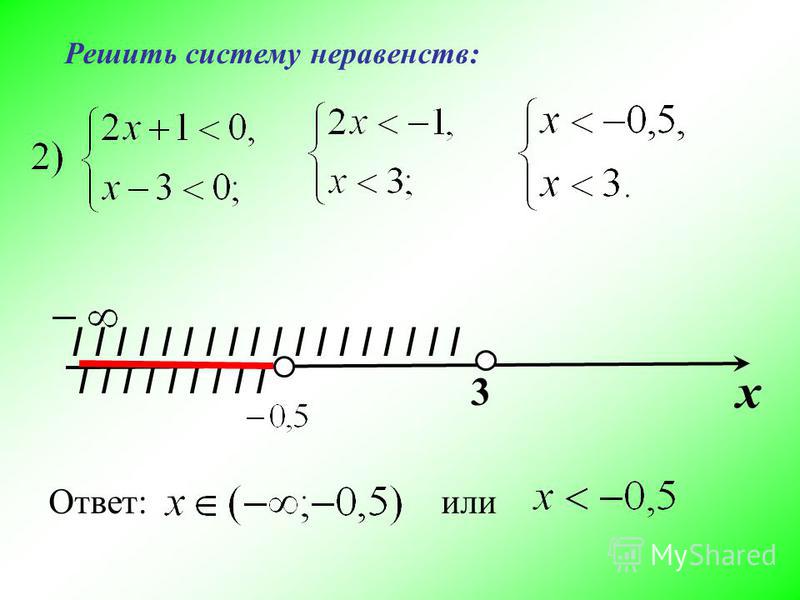 \end{cases}$

1) $(-\infty; 8)$
2) $(-\infty; 7)$
3) $(7;8)$
4) $(7; +\infty)$

Подпишись на ютуб канал

№2403

Сложность:

41 %

Укажите решение системы неравенств

$\begin{cases} x+2{,}8 \leqslant 0\\ x+0{,}3\leqslant -1{,}4\end{cases}$

1) $(-\infty; -2{,}8]$
2) $(-\infty; -2{,}8] \cup [-1{,}7;+\infty)$
3) $[-2{,}8;-1{,}7]$
4) $[-1{,}7;+\infty)$

Подпишись на ютуб канал

Загрузка…

Укажите множество решений системы неравенств. Вариант 26. Часть 1. Задание 8. ОГЭ 36 вариантов ответов по Математике 9 класс Ященко. – Рамблер/класс

Укажите множество решений системы неравенств. Вариант 26. Часть 1. Задание 8. ОГЭ 36 вариантов ответов по Математике 9 класс Ященко.

– Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Укажите множество решений системы неравенств

ответы

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения

похожие темы

Олимпиады

Экзамены

Оценки

3 класс

похожие вопросы 5

Привет! Какое тут соответствие? Вариант 21. Часть 1. Задание 5. ОГЭ 36 вариантов ответов по Математике 9 класс Ященко.

Установите соответствие между функциями и их графиками.
А) у = 2х2-14х + 23 Б) у = 2х2+ 14х-23 В) У = (Подробнее…)

ГДЗМатематикаОГЭ9 классЯщенко И.В.

Какой угол описывает минутная стрелка? Вариант 21. Часть 1. Задание 17. ОГЭ 36 вариантов ответов по Математике 9 класс Ященко.

Какой угол (в градусах) описывает минутная стрелка за 29 минут?
(Подробнее…)

ГДЗМатематикаОГЭ9 классЯщенко И.В.

Хело! Помогите рассчитать по формуле. Вариант 22. Часть 1. Задание 20. ОГЭ 36 вариантов ответов по Математике 9 класс Ященко.

В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) длительностью более 5 минут рассчитывается по формуле С = 150 + 11(t — 5), (Подробнее…)

ГДЗМатематикаОГЭ9 классЯщенко И.В.

ГДЗ по Физике Громов 10 класс, вопросы Гл. 1§9№4. Что нужно знать для того…

Как ответить на вопрос Гл.1§9№4.
Что нужно знать для того, чтобы вычислить координату тела в любой момент времени при его (Подробнее…)

ГДЗФизикаГромов С.В.10 класс

ГДЗ. Математика. Базовый уровень ЕГЭ — 2017. Вар.№37. Зад.№11.Под руководством Ященко. Помогите определить по диаграмме.

Здравствуйте! На диаграмме показана среднемесячная температура воздуха в Нижнем Новгороде за каждый месяц 1994 года. По горизонтали (Подробнее…)

ГДЗЭкзаменыМатематикаЯщенко И.В.

Объяснение урока: Решение систем линейных неравенств

В этом объяснении мы научимся решать системы линейных неравенств с помощью графически и определите области, представляющие решение.

Система неравенств (представленная символами ,≤,> и ≥) представляет собой набор два или более линейных неравенства с несколькими переменными и они используются, когда проблема требует ряда решений, и существует более одного ограничения на эти решения. решения.

На графике, представляющем систему неравенств, затенение выше означает, что больше в то время как затенение ниже означает, что меньше . Кроме того, мы должны также взять границу с учетом региона, где сплошная линия означает , равное , а пунктирная линия означает, что не равно .

Неравенства вида 𝑥>𝑎 или 𝑥𝑎 будут представлены в виде вертикали пунктирная линия на 𝑥=𝑎 (параллельно оси 𝑦), поскольку сама линия не включена в области, представляющей неравенство, а заштрихованная область будет либо на справа для 𝑥>

𝑎 или слева для 𝑥𝑎. То же самое относится к 𝑥≥𝑎 или 𝑥≤𝑎, за исключением того, что теперь регион также будет включать строку 𝑥=𝑎, что было бы представлено сплошной линией, но направление затенение будет таким же.

Аналогично, неравенства вида 𝑦>𝑏 или 𝑦𝑏 будет представлен в виде горизонтальной пунктирной линии на 𝑦=𝑏 (параллельно оси 𝑥), так как сама линия не входит в область, представляющую неравенство, а заштрихованная область будет либо выше, для 𝑦>𝑏, либо ниже, для 𝑦𝑏, строка 𝑦=𝑏. То же самое применимо для 𝑦≥𝑏 или 𝑦≤𝑏, за исключением того, что теперь область также будет включать строку 𝑦=𝑏, которая будет представлена сплошная линия, но направление штриховки будет таким же.

Например, рассмотрим неравенства 𝑥≥3 и 𝑦5 представлено на графике:

Неравенство 𝑥≥3 — сплошная линия при 𝑥=3, так как имеем ≥; следовательно, сама линия включена в область и заштрихованная область находится справа от линии, представляющей все значения 𝑥 больше 3. Если бы у нас было 𝑥>3, у нас было бы то же самое, за исключением того, что линия в 𝑥=3 была бы пунктирной поскольку он сам не будет включен в регион. Для 𝑥≤3 или 𝑥3, штриховка будет слева, представляя все числа меньше 3, а линия будет сплошной или пунктирной соответственно, в зависимости от входит ли линия 𝑥=3 в регион.

Неравенство 𝑦5 представлено пунктирной линией на 𝑦=5, так как имеем ; следовательно, сама линия не включена в регионе, а заштрихованная область находится ниже линии, представляющей все значения 𝑦 меньше 5.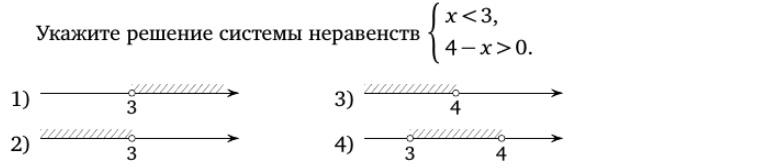 Если бы у нас было 𝑦≤5, мы бы то же самое, за исключением того, что линия в 𝑦=5 будет сплошной, как если бы себя включить в регион. За 𝑦≥5 или 𝑦>

5, штриховка будет выше, представляя все числа больше 5, а линия будет сплошной или пунктирной соответственно, в зависимости от того, линия 𝑦=5 включена в регион.

Пересечение областей каждого из неравенств в системе находится там, где множество решений лежат, так как эта область удовлетворяет каждому неравенству в системе. Мы включаем только значения на краях пересечений области, если на обоих есть сплошная линия, так как все неравенства должны быть удовлетворены, и строгое неравенство, представленное пунктирной строка, исключает ее из набора решений. В приведенном выше примере две линии пересекаются в точке (3,5), но это исключается из набора решений, так как не удовлетворяют строгому неравенству 𝑦5.

Первый квадрант может быть представлен неотрицательными значениями 𝑥 и 𝑦 и, следовательно, область, где 𝑥≥0 и 𝑦≥0. Давайте рассмотрим пример, чтобы увидеть, как это визуально интерпретируется по графику.

Пример 1. Определение системы неравенств, представленной данным графом

Укажите систему неравенств, решение которой представлено следующим графом.

Ответ

Заштрихованная область представляет все неотрицательные значения 𝑥 и 𝑦, которые можно перевести в неравенства 𝑥≥0, 𝑦≥0.

Чтобы это увидеть, рассмотрим каждое неравенство отдельно и посмотрим, где они перекрывать. 𝑥≥0, то есть все неотрицательные значения 𝑥 включая ось 𝑦, заштрихована в первом и четвертом квадрантах.

Аналогично, 𝑦≥0, т.е. все неотрицательные значения 𝑦, включая ось 𝑥, заштрихована в первой и второй квадрант.

Область, в которой оба неравенства перекрываются, находится в первом квадранте, представленном где заштрихованные области каждого неравенства перекрываются.

Перекрывающаяся область точно соответствует решению, представленному на приведенном графике.

У нас может быть несколько неравенств этой формы, ограничивающих значения сверху и/или ниже. Например, если бы у нас была система неравенств 2𝑥≤6,−2≤𝑦7, где второе неравенство — это все значения 𝑦 между −2 и 7, который также может быть записан отдельно как 𝑦≥−2 и 𝑦7. Эту систему неравенств можно представить следующим образом:

Теперь есть сплошная линия в точке 𝑦=−2, но пунктирная линия в точке 𝑦=7, что показывает, что 𝑦=−2 включено в регионе, а 𝑦=7 нет, как показано синим цветом на графике выше. Снова набор решений для системы неравенств находится там, где пересекаются заштрихованные области неравенств.

Четыре точки пересечения (2,7), (2,−2), (6,7) и (6,−2) на краю областей. Однако только точка (6,−2) входит в множество решений, так как остальные точки не удовлетворяют строгим неравенствам.

У нас также могут быть неравенства с уравнением линии. Например, неравенство вида 𝑦≥𝑚𝑥+𝑐 представлена сплошной линией, где заштрихованная область будет выше прямой линии 𝑦=𝑚𝑥+𝑐, тогда как неравенство 𝑦>𝑚𝑥+𝑐 имеет ту же заштрихованную область, но граница представлена пунктирной линией. Сходным образом, то же самое применимо к 𝑦≤𝑚𝑥+𝑐 или 𝑦𝑚𝑥+𝑐, за исключением того, что заштриховано область будет ниже прямой линии. Например, регион для 2𝑥+3𝑦>30, что эквивалентно 𝑦>−23𝑥+10 в приведенной выше форме будет следующим:

Между тем, регион для 2𝑥+3𝑦≤30 или 𝑦≤−23𝑥+10 будет заштриховано ниже сплошной линией. Если есть множественные неравенства (т. е. система неравенств), то возможные решения будут лежат внутри пересечения заштрихованных областей для всех неравенств.

Рассмотрим пример, в котором мы формулируем систему неравенств, представленную заданный граф.

Пример 2. Определение системы неравенств, представленных заданным графом

Укажите систему неравенств, решение которой представлено на следующем графике.

Ответ

Напомним, что на графике, представляющем систему неравенств, штриховка выше или вправо означает, что больше, чем , а затенение ниже или влево означает меньше, чем конкретная линия, определяемая 𝑥=𝑎, 𝑦=𝑏, или общая строка 𝑦=𝑚𝑥+𝑏. Кроме того, мы должны также взять границу региона, где сплошная линия означает равно , а пунктирная линия означает, что не равно .

Если имеется система неравенств, то возможные решения будут лежать внутри пересечения заштрихованных областей для всех неравенств в система. Мы включаем только ребра пересечений всех неравенства в наборе решений, если у нас есть сплошная линия для обеих линий, так как должны выполняться все неравенства и строгое неравенство, представленный пунктирной линией, с одной или обеих сторон исключил бы его из набор решений.

Заштрихованная область находится в первом квадранте для всех неотрицательных значений 𝑥 и 𝑦, что можно перевести как неравенства 𝑥≥0, 𝑦≥0.

Вертикальные линии, параллельные оси 𝑦, равны 𝑥=3 и 𝑥=6. Поскольку граница слева от красной области, при 𝑥=3, изображается сплошной линией и границей на справа от красной области при 𝑥=6 представлено пунктирной линией, имеем неравенства 𝑥≥3 и 𝑥6, что эквивалентно 3≤𝑥6.

Аналогично, горизонтальные линии, параллельные оси 𝑥, равны 𝑦=2 и 𝑦=6. Поскольку линии по обе стороны синей области сплошные, мы имеем неравенства 𝑦≥2 и 𝑦≤6, что эквивалентно 2≤𝑦≤6.

Уравнение прямой, проходящей через точки (8,0) и (0,8) равно определяется как 𝑦=8−𝑥, что является сплошной линией на графике. Поскольку заштрихованная область, желтым, находится ниже этой линии, имеем неравенство 𝑦≤8−𝑥, который можно переставить как 𝑥+𝑦≤8.

Таким образом, представленная графом система неравенств имеет вид 𝑥≥0,𝑦≥0,3≤𝑥6,2≤𝑦≤6,𝑥+𝑦≤8.

Теперь рассмотрим другую систему неравенств, включающую уравнение линия. Рассмотрим систему неравенств 𝑥>3,𝑦≤6,𝑥+𝑦≤10.

Неравенство 𝑥>3 показано пунктирной линией на 𝑥=3 и заштрихованная область (красным цветом) справа, и неравенство 𝑦≤6 показано сплошной линией при 𝑦=6 и заштрихованной областью (синим цветом) ниже. Наконец, неравенство 𝑥+𝑦≤10 показано сплошной линией с уравнением 𝑦=10−𝑥 и заштрихованной областью внизу (зеленым цветом).

Заштрихованные области, где все они пересекаются, — это места, где все неравенства в система удовлетворена; все решения можно найти в этом регионе.

Рассмотрим пример, в котором мы определяем неравенство этого типа из заданный график и заштрихованная область, представляющая набор решений.

Пример 3: Определение неравенства, представленного заданным графиком

Заполните пропуск: Заштрихованная область представляет набор решений неравенств 𝑦≥3, 𝑥≥0 и .

2𝑦+𝑥+8PT через (0,4) и (8,0) определяется как 2𝑦=8−𝑥. Поскольку заштрихованная область лежит ниже этой линии, это представляет область 𝑦≤4−12𝑥, что эквивалентно неравенству 2𝑦+𝑥−8≤0.
Это вариант B.
Теперь давайте рассмотрим несколько примеров, чтобы попрактиковаться и углубить наше понимание решать системы линейных неравенств, изображая их в виде графиков и выделяя области представляющий решение.
Первые несколько примеров связаны с определением системы неравенств из области, представленной на графике. В следующем примере используется область, ограниченная двумя прямые линии.
Пример 4. Определение системы неравенств, представленной заданным графом
Укажите систему неравенств, решение которой представлено следующим графом.
Ответ
Напомним, что на графике, представляющем систему неравенств, заштрихованное выше означает больше , а заштрихованное ниже означает меньше общая линия определяется как 𝑦=𝑚𝑥+𝑏. Кроме того, мы также должны принять граница области, где сплошная линия означает равное , а пунктирная линия означает, что не равно .
Если имеется система неравенств, то возможные решения будут лежать внутри пересечения заштрихованных областей для всех неравенств в система. Мы включаем только ребра пересечений всех неравенств в наборе решений, если у нас есть сплошная линия на обеих линиях, так как все неравенства должно выполняться и строгое неравенство, изображенное пунктирной линией, с одной или обеих сторон исключит его из набора решений.
Уравнение прямой, проходящей через точки (0,3) и (−1,0) равно 𝑦=3𝑥+3, что является сплошной линией на графике. Поскольку заштриховано область, выделенная желтым цветом, находится выше этой линии, мы имеем неравенство 𝑦≥3𝑥+3.
Аналогично уравнение прямой, проходящей через точки (0,−8) и (−4,4) есть 𝑦=−3𝑥−8, что является пунктирной линией на графике. С заштрихованная красным цветом область выше этой линии, имеем неравенство 𝑦>−3𝑥−8.
Таким образом, система неравенств, представленная на графике, имеет вид 𝑦≥3𝑥+3,𝑦>−3𝑥−8.
В следующем примере мы определим систему неравенств, описывающую область в графе, ограниченная тремя прямыми линиями.
Пример 5. Запись системы неравенств, описывающей область на графике
Найдите систему неравенств, которая образует треугольник, показанный на графике.
Ответ
Напомним, что в графе, представляющем систему неравенств, затенение выше означает больше , а заштрихованное ниже означает меньше общая линия определяется 𝑦=𝑚𝑥+𝑏. Кроме того, мы также должны принять границы области, где сплошная линия означает , равное , а пунктирная линия означает, что не равно .
Если имеется система неравенств, то возможные решения будут лежать внутри пересечения заштрихованных областей для всех неравенств в система. Мы включаем только ребра пересечений всех неравенств в решение установлено, если у нас есть сплошная линия на обеих линиях, так как все неравенства должно выполняться и строгое неравенство, изображенное штриховой линией, на одна или обе стороны исключили бы его из набора решений.
Уравнение прямой, проходящей через начало координат и пересекающей другие строки в (−2,2) и (2,−2) есть 𝑦=−𝑥, сплошная линия на график. Поскольку заштрихованная область находится выше этой линии, имеем неравенство 𝑦≥−𝑥.
Аналогично, уравнение прямой с положительным градиентом, пересекающей другие строки в (1,8) и (−2,2) равно 𝑦=2𝑥+6, что является пунктирной линией на график. Поскольку заштрихованная область находится ниже этой линии, имеем неравенство 𝑦2𝑥+6.
Наконец, уравнение линии с отрицательным градиентом, пересекающей другие строки в (1,8) и (2,−2) равно 𝑦=−10𝑥+18, что является сплошной линией на графике. Поскольку заштрихованная область находится ниже этого прямой имеем неравенство 𝑦≤−10𝑥+18.
Таким образом, система неравенств, представленная графом, имеет вид 𝑦2𝑥+6,𝑦≥−𝑥,𝑦≤−10𝑥+18.
Теперь давайте рассмотрим несколько примеров, в которых мы идентифицируем определенные регионы, показанные на график по заданной системе неравенств, а не определять их по график. В следующем примере мы определим область, которая представляет решение одного неравенства.
Пример 6. Идентификация областей, представляющих решения для Система неравенств
Какие из областей на графике содержат решения неравенства 𝑦≥2𝑥−4?
Ответ
Напомним, что в графе, представляющем систему неравенств, затенение выше означает больше , а заштрихованное ниже означает меньше общая линия определяется 𝑦=𝑚𝑥+𝑏. Кроме того, мы должны также взять границу с учетом региона, где сплошная линия означает равно , а пунктир строка означает, что не равно .
Если имеется система неравенств, то возможные решения будут лежать внутри пересечения заштрихованных областей для всех неравенств в система. Мы включаем только ребра пересечений всех неравенств в решение установлено, если у нас есть сплошная линия на обеих линиях, так как все неравенства должно выполняться и строгое неравенство, изображенное пунктирной линией, с одной или обеих сторон исключит его из набора решений.
На графике есть три отчетливые линии на границах областей показано. Две линии пунктирные, а одна сплошная. Есть две линии с положительным градиентом, один из которых проходит через начало координат, а третий с отрицательным градиентом.
Неравенство 𝑦≥2𝑥−4 может быть представлено сплошным телом прямой, так как граница области 𝑦=2𝑥−4 входит в область и заштрихованная область будет областью над линией из-за неравенства ≥. Это сплошная линия, проходящая через точки (0,−4) и (2,0) с положительным градиентом, как показано на графике.
Таким образом, области на графе, содержащие решения неравенства 𝑦≥2𝑥−4 — это A, B, C и D.
Теперь давайте рассмотрим пример, в котором мы идентифицируем области, представляющие решения к системе неравенств, на этот раз определяемой двумя прямыми линиями.
Пример 7. Идентификация областей, представляющих решения для Система неравенств
Какие области на графике содержат решения, удовлетворяющие обоим неравенствам 𝑦𝑥,𝑦≥2𝑥−4?
Ответ
Напомним, что на графике, представляющем систему неравенств, заштрихованное выше означает больше , а заштрихованное ниже означает меньше общая линия определяется как 𝑦=𝑚𝑥+𝑏. Кроме того, мы также должны принять граница области с учетом, где сплошная линия означает равное , а пунктирная линия означает, что не равно .
Если имеется система неравенств, то возможные решения будут лежать внутри пересечения заштрихованных областей для всех неравенств в система. Мы включаем только ребра пересечений всех неравенств в решение установлено, если у нас есть сплошная линия на обеих линиях, так как все неравенства должно выполняться и строгое неравенство, изображенное пунктирной линией, с одной или обеих сторон исключит его из набора решений.
Неравенство 𝑦𝑥 можно изобразить штриховой линией, так как граница области, 𝑦=𝑥, не входит в область и заштрихована площадь будет областью ниже линии из-за неравенства . Это пунктирная линия, проходящая через начало координат с положительным градиентом.
Аналогично можно представить неравенство 𝑦≥2𝑥−4 сплошной линией, так как граница области 𝑦=2𝑥−4 входит в область, а заштрихованная область будет областью выше линии из-за неравенство ≥. Это сплошная линия, проходящая через точки (0,−4) и (2,0), как показано на графике.
Таким образом, области графа, содержащие решения системы неравенства 𝑦𝑥 и 𝑦≥2𝑥−4 C и D.
Наконец, давайте рассмотрим пример, в котором мы идентифицируем область, которая представляет решения системы неравенств, представленной тремя неравенствами.
Пример 8. Идентификация областей, представляющих решения для Система неравенств
Какая область на графике содержит решения системы неравенств 𝑦>2,𝑦≥−𝑥,𝑥1?
Ответ
Напомним, что на графике, представляющем систему неравенств, штриховка выше или вправо означает, что больше, чем , а затенение ниже или влево означает меньше, чем конкретная линия, определяемая 𝑥=𝑎, 𝑦=𝑏 или общая линия 𝑦=𝑚𝑥+𝑏. Кроме того, мы должны также принять во внимание границу области, где сплошная линия означает равное , а пунктирная линия означает не равное .
Если имеется система неравенств, то возможные решения будут лежат внутри пересечения заштрихованных областей для всех неравенств в системе. Мы включаем только ребра пересечений всех неравенства в наборе решений, если у нас есть сплошная линия на обеих линиях, как должны выполняться все неравенства и строгое неравенство, представленный пунктирной линией, с одной или обеих сторон исключил бы его из набор решений.
Неравенство 𝑦>2 можно изобразить штриховой линией, так как граница области, 𝑦=2, не входит в область и заштрихована площадь будет областью над линией из-за неравенства >. Это пунктирная линия параллельна оси 𝑥, как показано на графике.
Аналогично, неравенство 𝑦≥−𝑥 можно изобразить сплошной линией, поскольку граница области 𝑦=−𝑥 включена в область и заштрихованная область будут областью выше линии из-за неравенство ≥. Это сплошная линия, которая проходит через начало координат с отрицательным градиентом.
Наконец, неравенство 𝑥1 можно изобразить штриховой линией, поскольку граница области 𝑥=1 не входит в область и заштрихованная область будет областью ниже линии из-за неравенства . Это пунктирная линия, параллельная 𝑦-ось, как показано на графике.
Область, удовлетворяющая всем неравенствам, будет пересечением все заштрихованные области отдельных неравенств.
Таким образом, области на графе, содержащие решения системы неравенства 𝑦>2,𝑦≥−𝑥,𝑥1 есть D.
Ключевые точки
- Затенение вправо означает, что больше , а закрашивание влево означает меньше конкретная линия, параллельная оси 𝑦, определяемая формулой 𝑥=𝑎.
- Затенение вверху означает больше , а затенение внизу означает меньше a конкретная линия, параллельная оси 𝑥, определяемой 𝑦=𝑏.
- Затенение вверху означает, что больше , а затенение внизу означает меньше общая линия определяется как 𝑦=𝑚𝑥+𝑏.
- Сама линия не попадает в заштрихованную область, если у нас есть строгий неравенство.
- Если есть система неравенств, то возможные решения будут лежат внутри пересечения заштрихованных областей для всех неравенств в системе.
- Кроме того, следует учитывать и границу области, где сплошная линия означает равно , а пунктирная линия означает, что не равно .
- Пересечение границ входит только в набор решений если обе прямые сплошные (т. е. не содержат строгих неравенств).
неравенств — Определение числа решений системы линейных неравенств.
$\begingroup$
Я хочу определить количество решений системы линейных неравенств, и мне было интересно, есть ли для этого простой способ. Я знаю, что линейное программирование часто используется для проверки того, существует ли нулевое или ненулевое количество решений, т. е. допустима ли система/границы, но можно ли отличить конечное количество уникальных решений от бесконечно много решений? Например, система $$ \begin{массив}{lcl} х & \leq & у \\ х & \geq & у \\ х + у & \leq & 1 \\ х + у & \geq & 1 \конец{массив} $$
имеет 1 единственное решение, а именно $x=y=\frac{1}{2}$, а система
$$ \begin{массив}{lcl} х & \geq & у \\ х + у & \leq & 1 \\ х + у & \geq & 1 \конец{массив} $$
имеет бесконечно много решений. Есть ли способ узнать, сколько решений имеет система линейных неравенств, если они есть?
- неравенство
- системы уравнений
$\endgroup$
6
$\begingroup$
Как отметил @Milten в комментариях, количество решений системы линейных неравенств (над $\mathbb{R}$) может быть только $0,1$ или бесконечным. Это происходит из-за выпуклости: если $v,w$ — два решения, то $\alpha v + (1-\alpha)w$ — решение для любого $0 \leq \alpha \leq 1$, а для $v \ neq w$ это дает бесконечное число решений. Это означает, что вам нужно найти только два различных решения, чтобы решить, существует ли их бесконечное количество.
Как вы сказали, линейное программирование может быть использовано для определения того, существует ли какое-либо решение, но, немного поработав, оно также может сказать вам, существует ли несколько решений или только одно. Эвристически вы можете использовать линейное программирование, чтобы максимизировать случайную целевую функцию $c\cdot x$ в допустимой области; можно было бы ожидать, что если допустимая область имеет более одной точки, то с высокой вероятностью вы получите несколько решений. Конечно, это всего лишь эвристика, но для практических целей этого должно быть достаточно. (См. также этот ответ.)
Если вам нужен честный полиномиальный алгоритм для определения уникальности решения, вы можете ознакомиться с этой статьей, в которой авторы сводят задачу определения уникальности к поиску решения другой линейной программы. В статье также содержится обзор предыдущих результатов по этой проблеме. К сожалению, все (легальные) ссылки на статью, которые я смог найти, защищены платным доступом. Если хотите, могу более подробно описать их решение.
Наконец, я просто хотел бы отметить, что в общем случае вы «не можете избежать» линейного программирования в том смысле, что решить, существует ли хотя бы одно решение для линейной программы, почти так же сложно, как найти оптимальное решение. Это верно в том смысле, что если вы можете решить, существует ли решение, то вы можете использовать алгоритм, подобный бинарному поиску, чтобы найти оптимальное решение за разумное время.
$\endgroup$
2
$\begingroup$
Приемы решения систем линейных неравенств отличаются от таковых для линейных уравнений тем, что знаки неравенств не позволяют производить замену, как в уравнениях. Многие из концепций, которые мы узнали при изучении систем линейных уравнений, переводятся в решение системы линейных неравенств, но этот процесс может быть несколько сложным. Возможно, самый понятный способ одновременного решения набора линейных неравенств — это использование графиков. Решением системы являются все точки, удовлетворяющие обоим неравенствам, или область, в которой штриховка перекрывается.
Система линейных неравенств с двумя переменными состоит из не менее двух линейных неравенств с теми же переменными. Он включает в себя несколько выражений, решение которых может привести к целому ряду решений. Решением линейного неравенства является упорядоченная пара, являющаяся решением всех неравенств в системе. Для системы линейных неравенств существует только одно множество решений, которое может содержать любое количество решений или не содержать решений.
Чтобы найти количество наборов решений, мы используем графическое представление неравенств и оттенков в значениях, которые удовлетворяют каждому отдельному неравенству. Визуально представляя потенциальные значения каждого из них, мы быстро заметим, есть ли перекрытия. Везде, где штриховка перекрывается, говорят, что это набор решений для системы. Если они не пересекаются, то система не имеет решения. Например, рассмотрим две параллельные прямые. Если решением одной являются значения над линией, а решением другой — значения под другой линией, пересечения нет, а значит, и решения системы нет.
Следующие ссылки (и ссылки в них) могут дать представление о некотором алгоритме решения линейного неравенства.
Алгоритм поиска целочисленных решений линейных неравенств
Решение системы линейных неравенств — какова размерность множества решений?
$\endgroup$
2
$\begingroup$
Во-первых, представим систему неравенств в унифицированном виде. Например, \begin{случаи} -х+у\ге 0\\ х-у\ге 0\\ -x-y+1\ge0\\ х+у-1\ge0\\ х+3y-2\ge0,\tag1 \end{случаи} $$L_k(x,y,1)\ge 0, \quad k=1,2,\dots,5. $$
Легко видеть, что
- $L_1+L_2=0,\;$ т.е. сумма неотрицательных значений равна нулю. Тогда должно быть $L_1=L_2=0.\;$ Следовательно, вместо пары неравенств имеем уравнение.
- Аналогично $L_3+L_4=0,\;\Стрелка вправо\;L_3=L_4=0.$
- $L_2+2L_3+L_5 = 0,\;$т.е. положительная линейная комбинация неотрицательных значений равна нулю. Тогда следует переопределить $L_2=L_3=L_5=0,$ и действительно мы имеем два независимых равенства вместо трех неравенств.
- $L_5 =L_1+2L_4,\;$ т. е. неравенство $(1.5)$ следует из пары $(1.1),(1.4)$ и может быть исключено.
В итоге имеем систему $\;L_1=L_3=0,\;$ ранга $2$ и единственное решение.
В общем случае можно дополнительно применить алгоритм Жордана. Наконец, это приводит к системе неравенств для «независимых» неизвестных и набору линейных функций для остальных.
Поскольку система $(1)$ представлена в гомогенной форме, то решения могут существовать только в том случае, если ее матрица имеет ранг $2$ или меньше и любые три выражения $\;L_k\;$ линейно зависимы.
No related posts.