Укажите решение неравенства 3 x 4x 7: conf__edu_age }) }) edu_group = edu_age_conf.groups[conf__edu_age] edu_ad = edu_age_conf.ads[edu_group] } $(document).ready(() => { if (typeof KrApi != ‘undefined’) { edu_group = edu_age_conf.pods[KrApi.settings.base_pod] if (typeof edu_group != ‘undefined’) { edu_ad = edu_age_conf.ads[edu_group] } } })

Содержание

Как решать неравенства из ОГЭ (ГИА)

Несмотря на то, что решение неравенств очень напоминает решение уравнений, все-таки неравенства вызывают у школьников больше затруднений.

Ученики часто спрашивают как решать неравенства те или иные, просят оценить решение неравенства, полученное у доски в школе или помочь в решении домашнего задания с неравенством. В основном они связаны не с решением неравенства как такового, а с проблемой записи решения и с проблемой знака неравенства, которое в определенные моменты заменяется на противоположный.

Решение неравенств – это материал, который помогает выявить у экзаменуемого сразу несколько умений и навыков: умение решать уравнения, работать со знаком неравенства, оценить полученное решение с точки зрения постановки неравенства. Поэтому неравенства включены в ОГЭ (ГИА).

Содержание

Как решать простейшие неравенства из ОГЭ (ГИА)

Итак, первое неравенство:

3х-4<6x-6

Решаем неравенство как уравнение – перенесем все неизвестные в левую часть, а все числа – в правую. Неизвестные – это все выражения с х: 3х и 6х.

3х уже находится слева, а вот 6х – справа, и 6х мы перенесем в левую часть нашего неравенства. Не забываем, что когда мы переносим любые выражения и числа из одной части неравенства, как и равенства, в другую, то мы обязательно меняем знак. То есть слева у нас запишется:

3х-6х.

Что будет справа? Справа останется число -6 (со знаком минус), и еще мы перенесем 4 из левой части в правую. Перед четверкой в левой части неравенства стоит знак минус, значит, при переносе мы получим четверку со знаком +. Смотрите, что получилось:

3х-6х<-6+4

Упростим левую и правую части, получим:

-3х<-2

Если бы у нас вместо неравенства было уравнение: -3х=-2, то x мы бы нашли разделив -2 на -3. Точно также поступают и в неравенстве, но, помнят одно простое правило,

если мы делим или умножаем на отрицательное число (число со знаком минус), то знак неравенства меняется на противоположный.

То есть мы запишем решение нашего неравенства вот так:

Мы поменяли знак, так как делили на отрицательное число – -3. При этом знак бы не менялся, если бы мы делили отрицательное число на положительное. Знак неравенства меняется только тогда – когда отрицательным является число на которое делят или умножают.

Итак, ответ у нас будет таким:

Как решать нестрогое неравенство

Нестрогим неравенством называется неравенство, у которого вместо строгого знака “больше” или “меньше”, стоит знак “больше или равно” или “меньше или равно”. Например, давайте решим нестрогое неравенство. Возьмем простое неравенство, чтобы вы поняли суть вопроса.

Решаем аналогично – только сначала упростим правую часть нашего неравенства. Переносим неизвестные в левую часть неравенства, а известные (числа) в правую часть неравенства:

Упрощаем правую часть:

Посчитаем, получим:

Ответ: .

Обратите внимание на запись ответа. Так как у нас неравенство нестрогое, то число 2 будет входить в решение этого неравенства, поэтому мы его включаем в ответ, отмечая квадратной скобкой.

Вот так:

Решение неравенств из сборника ОГЭ по математике ФИПИ

Неравенство 1

Укажите решение неравенства

Решение:

Перенесем неизвестные в левую часть неравенства, а известные – в правую часть неравенства:

Посчитаем:

, отсюда

искомый интервал: . Таким образом, из списка предложенных интервалов нам подходит интервал под номером 2.

Ответ 2.

Неравенство 2

Укажите множество решений неравенства:

Решение:

Как обычно, переносим неизвестные влево от знака неравенства, а известные величины – вправо:

Обратите внимание – здесь мы делим отрицательное число. Но делим то мы его на положительное число 6. Поэтому знак неравенства остается прежним!

или

Нам подходит вариант решения 4.

Ответ: 4.

Неравенство 3

Укажите решение неравенства

Решение:

Подходит вариант решения 2.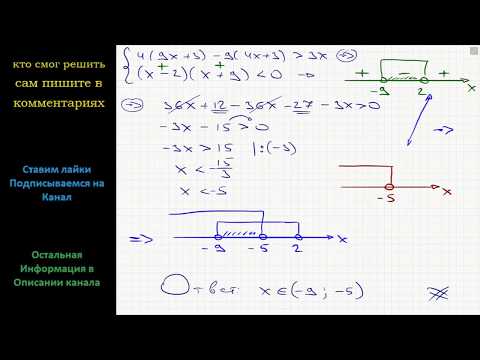

Ответ: 2

Неравенство 4

Укажите множество решений неравенства

Решение:

Итак, решение неравенство иллюстрируется графиком 3.

Ответ: 3.

Теперь вы знаете, как решать неравенства, которые даны в части “Алгебра” ОГЭ (ГИА).

Решение линейных неравенств — презентация онлайн

Похожие презентации:

Решение линейных неравенств

Неравенства. Линейные неравенства. Квадратные неравенства

Решение линейных неравенств

Линейные неравенства. 8 класс

Линейные неравенства

Линейные неравенства. Квадратные неравенства

Решение линейных неравенств. 8 класс

Решение линейных неравенств

Решение неравенств с одной переменной

(Электронное пособие)
(с) Кочагин Вадим Витальевич, 2005 год
Данная работа является началом пути в
создании электронной версии учебника по
математике.
Материал данной презентации может
использоваться как на уроках объяснения
нового материала, так и на уроках
обобщающего повторения.
Выберите необходимый раздел
Простейшими среди неравенств с одной
переменной являются линейные неравенства, т.е.

неравенства вида ax<b (>b, b, b).
При решении линейных неравенств слагаемые с
неизвестным переносят в одну часть уравнения, а
известные слагаемые в другую часть. Затем
выражают неизвестную переменную, т.е. делят на
коэффициент при этой переменной ( если он не
равен нулю).
Если коэффициент равен нулю, то …(см. далее
справочный материал).
Особые случаи (коэффициент при х равен 0):
0x<0
0x 0
0x< a
(a>0)
0x< a
(a<0)
0x a
(a>0)
0x a
(a<0)
Ответ.
Решений нет
Ответ.
Ответ.
Ответ.
(- ;+ )
(- ;+ )
Ответ.
Решений нет.
(- ;+ )
Ответ.
Решений нет.
0x>0
0x 0
0x> a
(a>0)
0x> a
(a<0)
0x a
(a>0)
0x a
(a<0)
Ответ.

Решений нет
Ответ.

Ответ.
Решений нет.
Ответ.
Ответ.
Решений нет.
Ответ.
(- ;+ )
(- ;+ )
(- ;+ )
Если делим обе части неравенства на
отрицательное число, то знак неравенства
меняется на противоположный .
Например: -2х>4.
Делим на (-2). Получим: х<-2.
Если делим обе части неравенства на
положительное число, то знак неравенства
не меняется.
Например: 3х< 12.
Делим на 3. Получим: х<4.
Выберете номер задания
Задание 1. Решите неравенство 5х-3>3x-7.
Задание 2. Решите неравенство
12 11x
3 2x
2
Задание 3. Решите систему неравенств
( x 5) 2 ( x 1) 2
23x 5 22 x 13
В ответе укажите наибольшее целое решение.
Задание 1. Решите неравенство 5х-3>3x-7.
Перенесем неизвестные слагаемые в левую часть неравенства,
а известные в правую.
5х-3х>-7+3
Приведем подобные слагаемые в левой части
и упростим правую часть.
2х>-4
Выразим переменную х,
т.

е. разделим обе части неравенства на 2.
х>-2
Ответ запишем в виде промежутка.
Ответ: (-2;+ )
Задание
2. Решите неравенство
12 11x
3 2.x
2
Умножим обе части неравенства на 2.
12-11x>6-4x
Перенесем неизвестные слагаемые в левую часть, а
известные в правую
-11x+4х>6-12
Приведем подобные слагаемые
-7х>-6
Выразим переменную х. Знак неравенства изменится на противоположный.
x
Ответ.
6
7
6
;
7
Если делим обе части неравенства на
отрицательное число, то знак неравенства меняется
на противоположный .
Например: -2х>4. Делим на (-2). Получим: х<-2.
Если делим обе части неравенства на
положительное число, то знак неравенства не
меняется.
Например: 3х< 12. Делим на 3. Получим: х<4.
Вернуться к решению Задания 2
Задание 2. Решите неравенство
12 11x
3 2 x

2
Умножим обе части неравенства на 2.
12-11x>6-4x
Перенесем неизвестные слагаемые в левую часть, а
известные в правую
-11x+4х>6-12
Приведем подобные слагаемые
-7х>-6
Выразим переменную х.

Знак неравенства изменится на противоположный.
x
Ответ.
6
7
6
;
7
•Задание 3. Решите систему неравенств
( x 5) 2 ( x 1) 2
23x 5 22 x 13
В ответе укажите наибольшее целое решение.
Чтобы решить систему неравенств, необходимо сначала решить каждое
неравенство в отдельности.
Решением первого неравенства является промежуток
-2
Решение второго неравенства промежуток
( ; 2)
13;
-13
Решением системы неравенств является пересечение промежутков
-13
-2
Наибольшим целым решением является (-3)
Ответ: -3.
13; 2
Сейчас Вам предстоит решить
различные линейные неравенства .
Если Вы укажете номер правильного
ответа, то Вам откроется часть
красивой фотографии.
Итак, Вы играете в математическое
лото.
Задание 1.
Решением неравенства 6x – 5 < 4x +19
является промежуток
Задание 2.
3 2x
Решением неравенства 5 x
3
является промежуток
1) ( ; 12)
1) ( ; 12)
2) ( ;12)
2) ( ;12)
3) (12; )
3) (12; )
4) ( 12; )
4) ( 12; )
Задание 3.

Задание 4.
Укажите число целых решений системы
неравенств 2006 x 3 2005 x 2
2
2
x 4 x 2
1) 6
2) 7
3) 5
4) 4
1) ( ; 12)
1) ( ; 12)
Решите неравенство
0х> 2005
1) ;
2) ;0
3) 0;
4) Решений нет

15. Ваш выбор неверен. Подумайте еще.

Вернуться к решению Задания 1
Задание 2.
Решением неравенства
5 x
3 2x
3
является промежуток
1) ( ; 12)
2) ( ;12)
3) (12; )
4) ( 12; )
Задание 3.
Укажите число целых решений системы
неравенств 2006 x 3 2005 x 2
2
2
x 4 x 2
1) 6
2) 7
3) 5
4) 4
1) ( ; 12)
1) ( ; 12)
Задание 4.
Решите неравенство 0х> 2005
1) ;
2) ;0
3) 0;
4) Решений нет

17. Ваш выбор неверен. Подумайте еще.

Вернуться к решению Задания 2
1) ( ; 12)
Задание 3.
Укажите число целых решений системы
неравенств 2006 x 3 2005 x 2
2
2
x 4 x 2
1) 6
2) 7
3) 5
4) 4
1) ( ; 12)
Задание 4.

Решите неравенство 0х> 2005
1) ;
2) ;0
3) 0;
4) Решений нет

19. Ваш выбор неверен. Подумайте еще.

Вернуться к решению Задания 3
1) ( ; 12)
Задание 4.
Решите неравенство 0х> 2005
1) ( ; 12)
1) ;
2) ;0
3) 0;
4) Решений нет

21. Ваш выбор неверен. Подумайте еще.

Вернуться к решению Задания 4
1) ( ; 12)
1) ( ; 12)

English Русский Правила

Решите следующее неравенство: 4x-7

Курс
- NCERT
  - Класс 12
  - Класс 11
  - Класс 10
  - Класс 0 90 90 90 9003 80008
  - Класс 6
- IIT JEE

экзамен
- JEE MAINS
- JEE ADVANCED
- X BOARDS
- XII BOARDS
- NEET Year 3 Neet Year 9000 )
- Физика Предыдущий год
- Химия Предыдущий год
- Биология Предыдущий год
- Нет Все образцы работ
- Образцы работ Биология
- Образцы работ Физика
- Образцы работ Химия

000208

Скачать PDF-файлы
- Класс 12
- Класс 11
- Класс 10
- Класс 9
- Класс 8
- Класс 7
- Класс 6

Экзаменационный уголок

Онлайн-класс

Викторина

Задать вопрос в Whatsapp

Поиск Doubtnut

0 Английский словарь 02
Toppers Talk

Блог

О нас

Карьера

Скачать

Получить приложение

Вопрос

Обновлено: 24/08/2021

0131 20 видео

Ab Padhai каро бина объявления ке

Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке! Похожие видео 131

00 :58

निम्नलिखित असमिकाओं को हल करें
(i) x+10>4x+5 (ii) 4x+9 4x+3<0 >х+3 (iv)х+12<4х- 2

104444309