Укажите решение неравенства 5х 3 5х 8 меньше 7: Укажите решение неравенства 5х-3(5х-8) < -7

Урок 34. Решение неравенств с одной переменной

Класс

• 1 класс

• 2 класс

  • Математика
  • Английский язык

• 3 класс

  • Английский язык
  • Русский язык
  • Математика

• 4 класс

  • Математика
  • Русский язык
  • Английский язык

• 5 класс

  • Биология
  • Английский язык
  • Русский язык
  • Математика

• 6 класс

  • Математика
  • Биология
  • Английский язык
  • Русский язык

• 7 класс

  • Химия
  • Английский язык
  • Русский язык
  • Физика
  • Математика
  • Биология

• 8 класс

  • Английский язык
  • Биология
  • Химия
  • Математика
  • Физика
  • Русский язык

• 9 класс

  • Химия
  • Биология
  • Английский язык
  • Физика
  • Русский язык
  • Математика

• 10 класс

  • Биология
  • Математика
  • Физика
  • Химия
  • Английский язык

• 11 класс

  • Химия
  • Английский язык
  • Биология

8 КЛАСС

Урок 34.

Решение неравенств с одной переменной

Упрости, используя свойства неравенств

Упрости, используя свойства неравенств

Используй свойства неравенств

Используй свойства неравенств

Используй свойства неравенств

Используй свойства неравенств

Используй свойства неравенств

Используй свойства неравенств

Используй свойство неравенств

Составь и реши неравенство

Составь и реши неравенство

Используй свойства неравенств

Используй свойства неравенств

Используй свойства неравенств

Используй свойства неравенств

Используй свойства неравенств

Используй свойство неравенств

Используй свойства неравенств

Составь и реши неравенство

Используй свойства неравенств

Используй свойства неравенств

Используй свойства неравенств

Используй свойства неравенств

Составь и реши неравенство

Используй свойства неравенств

Составь неравенство и реши его

Вспомни ОДЗ корня и составь неравенство

Составь систему неравенств

Реши неравенство и ответь на вопрос

Составь неравенство и реши его

Уравнение не имеет корней при отрицательном дискриминанте.  Составь неравенство

Уравнение имеет два корня при положительном дискриминанте . Составь уравнение

Составь и реши неравенство

Составь и реши неравенство

Составь и реши неравенство

Составь и реши неравенство

Составь и реши неравенство

Подставь значение х в дробь

Реши через дискриминант

Построй графики функций, найди координаты точки пересечения

Составь уравнение, найди неизвестное

Вопросники:

Вопрос:

Вопрос:

Вопрос:

Вопрос:

Вопрос:

Тайны квадратных уравнений, электив. — математика, уроки

Приложение:

Занятие №1 Входной тест:

1. Определение квадратного уравнения.

Количество его корней.

Решить уравнения: 2х² + 3х – 5 = 0 7х² – 5х + 4 = 0

1. Определение неполного квадратного уравнения.

Решить уравнения: 12х² + 3х = 0 2х² – 14 = 0

1. Определение приведенного квадратного уравнения.

Выделить такие из предложенных уравнений: 7х² – 5х + 4 = 0

х² – 5х + 4 = 0 -х² + 5х + 9 = 0 7х² – х = 0 х² – 3х = 0 х² — 4 = 0

1. Теорема Виета.

Найти корни уравнений, используя эту теорему: х² – 7х + 6 = 0

Определить знаки корней квадратного уравнения: 3х² – 7х + 12 = 0 2х²

+ 3х — 7 = 0

5. Решить уравнение: (х² – 3х + 3)( х² – 3х _ 4) + 10 = 0

2 2

6. При каких значениях с уравнение сх² + 2х + 3 = 0 имеет 2 корня?

Занятие №2 1. Анализ теста: (из данного анализа следуют цели курса)

2. Простейшие применения квадратных уравнений.

1. Всегда ли имеет корни квадратное уравнение?

2. Можно ли указать корни квадратного уравнения 2х² + 3х – 5 = 0, не решая его?

3. Все ли справились с заданием №5 теста? Как можно проще решить его?

4. Все ли справились с заданием №6 теста? Какая причина неверного решения?

5. Выявление совместно с учащимися целей элективного курса.

6. Решение задач:

1. Решить уравнение: а) 6(10 – х)(3х + 4) = 0

б) х² + 4х – 12 = 0

х + 6

в) х _ 7 = 8

х – 2 х+2 х²-4

г) 2х⁴ + 3х³ – 8х² – 12х = 0

2. Найти область определения функции: у = х² — 3

х² + 5х — 6

3. Решить задачу: Катер может проплыть 8км против течения реки и еще 30км по течению

за то же время, за которое плот может проплыть по этой реке 4км. Скорость катера в

стоячей воде равна 18км/ч. Найти скорость течения реки.

Занятия №3, 4 Первые тайны квадратных уравнений.

1. Свойства коэффициентов квадратного уравнения при определении его корней:

а) если а + в + с = 0, то х₁ = 1, х₂ = с/а

б) если а + с = в, то х₁ = -1, х₂ = -с/а

2.

Свойства корней и коэффициентов квадратного уравнения при решении графических задач.

3. Свойства корней и коэффициентов квадратного уравнения при разложении квадратного

трехчлена на множители.

4. Решение задач:

1. Решить уравнение: а) х² + 3х – 4 = 0 б) 7х² — 2х + 5 = 0 в) 3х² + 8х + 5 = 0

2. Сократить дробь: а) х² – 5,5х б) х² + 7х +6

2х² + 9х — 11 7х² +15х + 8

в) х⁴ – 11х² + 10

х² — 1

3. Решить уравнение: а) х + х + 2 = 8

х + 2 х – 2 х² — 4

б) 2х _ 15 – 32х² = 3х

2х — 3 4х² – 9 2х + 3

в) х + 2 + 3 = 3 + 1

х + 1 х – 2 х

2 – х — 2

4. Решить систему уравнений: ху = -8

(х – у)(у – 2) = -12

5. Найти область определения функции: у = х

7х² — 5х – 2

6. Построить график функции и указать ее область значений:

а) у = 7х² – 9х + 2 б) у = -1/2х² + 3х – 1/2

7. Построить график функции, указав сначала ее область определения:

у = х² – 6х + 5

5 — х

Найти наибольшее или наименьшее значение функции и указать промежутки ее

возрастания и убывания:

8. Решить уравнение: х³ – 3х + 2 = 0

Занятия №5,6 Тайны квадратного уравнения при решении неравенств

второй степени.

1. Метод решения неравенств второй степени и его алгоритм.

2. Тайна старшего коэффициента при решении неравенств методом интервалов.

3. Решение задач:

1. Решить неравенство: а) 2х² – 7х + 5 0 б) (3х + 7)(1 – х)

в) х² ≤ 6х — 2 г) 3х² – 11х + 8

2 9 х + 1

г) х² – 4х + 3 ≥ 0

х² + 5х + 4

2. Найти область определения функции: а) у = √ х + 1/3х²

б) у = 1

√ 1/4х² + 2х + 4

в) у = √ 6 – 5х – х²

х + 6

г) у = √ 3 – 5х – 2х²

10х

3. Найти решения неравенства 0,8х² ≤ х + 0,3 из промежутка [1⅓; 2]

4. При каких положительных значениях х верно неравенство х² – 2х ≤ 2 ?

5. Решить систему неравенств: а) 6х² – 5х + 1 0

4х – 1 ≥ 0

б) 1/2х

2 ≤ 1

х² ≥ 4

6. Решить задачу: Один из катетов прямоугольного треугольника на 5см больше

другого, а его площадь больше 75см². Какую длину может иметь больший катет?

7. Одна из сторон прямоугольника на 4см больше другой, а его площадь меньше 165см².

Какую длину может иметь большая сторона прямоугольника?

8. Без построения графика найти значения аргумента при которых значения функции

у = 3х² — 7х + 4 положительны.

9. При каких значениях аргумента значения функции у = 9х – 2х² не меньше 7?

Занятия №7,8 Тайны решения уравнений высших степеней.

1. Известный нам способ разложения на множители.

2. Способ замены переменной.

3. Решение задач:

1. Решить уравнения: а) 2х⁴ + 3х³ – 8х² – 12х = 0 б) х

3 – 3х + 2 = 0

в) 2х⁴ — 5х² – 12 = 0 г) (х² – 2)(х² + 2) – 3х² – 6 = 0

2. Найти координаты точек пересечения графика функции у = х⁴ – 10х² + 9 с осью абсцисс.

3. Решить систему уравнений: х² + у² = 20

ху = 8

4. Решить неравенство: а) х⁴ – 9х² + 10 ≤ 0 б) х⁴ – 3х² – 4 0

в) 4х⁴ – 13х² + 9 ≥ 0

х + 1

5. Решить уравнение: а) (х² – 3х)² – 2(х² – 3х) = 8

б) (х² + 4х)(х² + 4х — 17) + 60 = 0

в) (2 — х² + 2х)(4 — х² + 2х) = 3

3 3

6. Сократить дробь: а) х — √х – 2 б)

х — 6√х + 8

√х – 2 4 — √х

7. Найти область определения функции: а) у = √ х⁴ – 5х² + 4

б) у = √ х⁴ – 10х² + 9

х² — 16

8. Предложить способ решения уравнения и начать его решение

(как пропедевтика курса алгебры 10-11): а) cos²x + 7cosx + 6 = 0

б) 3lg²x – 8lgx + 5 = 0

в) 7^2х – 7^х + 1 = 0

Занятие №9 Тайна существования корней квадратного уравнения.

1. Всегда ли имеет корни квадратное уравнение?

2. Немного о новом множестве чисел (как пропедевтика курса высшей математик).

3. Решение задач:

1. Являются ли корнями уравнения х² + 8х + 25 = 0 числа -4 + 3i и -4 – 3i ? Как это

узнать? Cделать это двумя способами (по определению корней и по теореме Виета).

2.

Найти корни уравнения х² + 2х + 5 = 0. К какому множеству чисел они относятся?

3. Решить уравнение: х² – 6х + 25 = 0

Занятия №10,11 Тайны квадратных уравнений, содержащих модуль.

1. Определение модуля.

2. Правила раскрытия модуля: а) если | f(x)| = a, то f(x) = a или f(x) = -a

б) если | f(x)| = g(x), то f(x) = g(x) или f(x) = — g(x) при g(x) 0.

в) если | f(x)| g(x), то f(x) g(x) и f(x) -g(x).

г) если |f(x)| g(x), то f(x) g(x) или f(x) g(x).

д) если |f(x)| |g(x)|, то f²(x) g²(x).

3. Решение задач:

1. Решить уравнение: а) |х² – 2х – 7| = 4; х² – |х| – 2 = 0 ;

|2х + 1|х — 3х – 4 = 0; х² + 5х – 6 = 2.

|х – 2|

б) |х² – х – 8| = — х; |3х – 4| = 4х² + 3х – 2;

х²

+ 4|х – 3| — 7х + 11 = 0;

|х² – 4х + 3| + |х² – 4х – 5| = 8

|х² – 9| + |х – 2| = 5

2.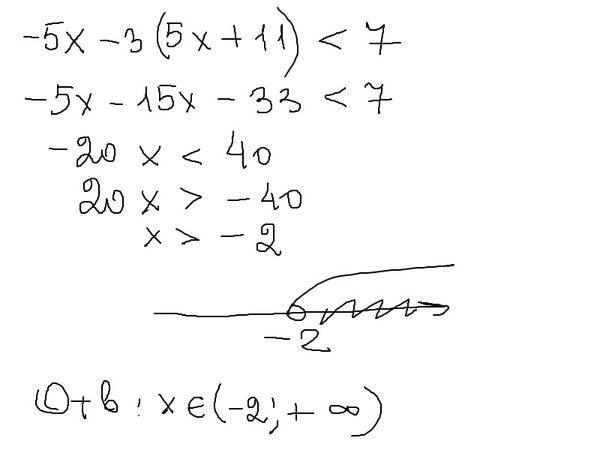 Решить неравенство: в) |3х + 2| ≤ х² + 7х + 6; х² — 5х + 9 | х – 6|

г) |х² – 4| -2х – 1; х² – х – 2

д) |2х² + х – 1| |х + 1|;

|24х² – 39х — 8| ≤ |18х² – 25х + 32|.

3. Решить неравенство, не подчиняющееся данным правилам:

х² – 4|х| 2 + |5х – 4| — 1 ≤ | 3х – 2|

Занятия №12 – 14 Задачи с параметром.

1. Определение квадратного уравнения.

2. Количество действтительных корней уравнения.

3. Немного о параметре.

4. Решение задач:

1.а) При каких значениях с уравнение х² + 2х + с = 0 не имеет корней?

б) При каких значениях к уравнение 16х² + кх + 1 = 0 имеет корни?

в) При каких значениях а уравнение ах² + х + 2 = 0 имеет два корня?

г) При каких значениях к уравнение кх² — 5х + 1/4к = 0 имеет два корня ?

2. а) При каких значениях а уравнение (а – 2)х² + (4 – 2а) х + 3 = 0 имеет

единственное решение?

б) При каких значениях а уравнение ах² — 4х + а + 3 =0 имеет более одного корня?

в) При каких значениях а уравнение а(а + 3)х² + (2а + 6)х – 3а — 9 =0 имеет

более одного корня?

г) При каких значениях а уравнение х² – ах + 1 = 0 имеет единственное

х + 3

решение?

3. Решить уравнение: а) х² – 4х + 3 = 0 б) х – а = 0

х – а х² – 4х + 3

в) ах² + 3ах – (а + 2) = 0 .

4. При каких значениях а уравнение (а² – 6а + 8)х² + (а² – 4)х + (10 – 3а – а²) = 0

имеет более двух корней?

5. При каких значениях а один из корней квадратного уравнения

(а² – 5а + 3)х² + (3а – 1)х + 2 = 0 в 2 раза больше другого?

6. При каких значениях а оба корня уравнения (а – 1)х² – ах + 1 = 0 положительны?

7. При каких значениях а уравнения х² + ах + 8 = 0 и х² + х + а = 0 имеют

общий корень?

8. При каких значениях к оба корня уравнения х² – (к + 1)х + к + 4 = 0

отрицательны?

9. Найти все значения с, при которых корни уравнения х² + х + с = 0

действительны, различны, и оба больше с.

10. При каких значениях к оба корня уравнения —кх² + (2к + 1)х – к + 1 = 0

удовлетворяют условию -2

11. Найти все значения параметра а которых графики функций у = (а + 5)х² – 7

и у = (3а + 15)х — 4 не имеют общих точек.

12. При каких значениях к неравенство кх² + (1 + к)х + 5 0 выполняется при

всех х из множества действительных чисел?

13. Найти все значения параметра а, при которых всякое решение неравенства

1 ≤ х ≤ 2 является решением неравенства х² – ах + 1 ≤ 0.

Занятие №15 Итоговый тест.

1. При каких значениях аргумента значение функции у = 3х² – 11х + 8 неотрицательны?

х – 2

2. Найти нули функции: у = 7(х² – 3х + 3) + 2(х² – 3х +3) – 9

3. Решить уравнение: |х² – 2х| = 3 – 2х

4. При каком целом значении b уравнения 2х² + (3b – 1)х – 3 = 0 и 6х² – (2b – 3)х – 1 = 0

имеют общий корень?

Занятие №16 Анализ итогового теста. Разбор заданий. Ребята

самостоятельно подводят итоги элективного курса.

8

2+4х-5<0 \\ -5 < х < 1\\ $

Общий регион $3-2\sqrt2

Но книга дает ответ $-5