Уравнение функции: Функциональные уравнения

Функциональные уравнения

Общепризнано, что решение задач является важнейшим средством формирования у школьников системы основных математических знаний, умений и навыков, ведущей формой учебной деятельности учащихся в процессе учения математики, является одним из основных средств их математического развития.

Ориентируя школьников на поиски красивых, изящных решений математических задач, учитель тем самым способствует эстетическому воспитанию учащихся и повышению их математической культуры. И всё же главная цель задач — развить творческое и математическое мышление учащихся, заинтересовать их математикой, привести к “открытию” математических фактов.

Достичь этой цели с помощью одних стандартных задач невозможно. Необходимы задачи, направленные на воспитание у учащихся устойчивого интереса к изучению математики, творческого отношения к учебной деятельности математического характера.

Необходимы специальные упражнения для обучения школьников способам самостоятельной деятельности, для овладения ими методами научного познания реальной действительности и приемами умственной деятельности, которыми пользуются ученые-математики, решая ту или иную задачу.

В данной статье речь идет о функциональных уравнениях, о методах их решения. Функциональным уравнением называется соотношение, выражающее определённое свойство, которым обладает некоторый класс функций (некоторая функция).

Простейшими примерами функциональных уравнений могут служить : f(x) =f(- x) – уравнение чётности, f(x+Т) = f(x) – уравнение периодичности и др.

Функция f(x) называется решением данного функционального уравнения, если она удовлетворяет ему при всех значениях аргумента в области её определения.

Например, функции f(x) = ax²,f(x)=sin2x, где aR, являются частными решениями приведённых соответственно выше уравнений, в чём убедимся подстановкой ах

2= а (-х)².

Решить функциональное уравнение – значит установить, имеет ли оно решения, и найти их, если они имеются.

Приведем примеры решения функциональных уравнений методом подстановки. Этот метод заключается в том, что, применяя вместо х (или у) различные подстановки и комбинируя полученные уравнения с исходным, получаем (обычно путём исключения) алгебраическое уравнение относительно искомой функции.

Пример 1.

1) Пусть

2) Подставим в исходное уравнение, получим

3)Заменим z на получим или после преобразований в правой части уравнения:

4)Итак, получили два уравнения:

5)Умножим обе части 1-го уравнения на (-2) и сложим со 2-ым уравнением, получим:

 Пример 2. ²

1)Заменим в уравнении на , получим ² .

2) Умножим обе части исходного уравнения ² на (-2) и сложим с уравнением ² ,

получим:

.

Пример 3.

1. Пусть тогда уравнение принимает вид:.
2. Заменим в уравнении на , получим .
3. Умножим уравнение на (-2) и сложим с уравнением , получим Таким образом,

Пример 4.

1) Заменим в уравнение на , .

2)Умножим уравнение на и вычтем из уравнения ,получим —

, где

Пример 5. ,

1)Заменим в уравнении на получим .

2)Выразим из исходного уравнения , получим

или .

3)Подставим в уравнение , получим .

Выполним преобразования

Пример 6. .

1. Заменим на , получим
2. Умножим обе части уравнения на и вычтем из уравнения

получим

Пример 7.

1)Пусть , тогда уравнение принимает вид:

2)Пусть тогда исходноеуравнение принимает вид:

3)Умножим обе части уравнения из п.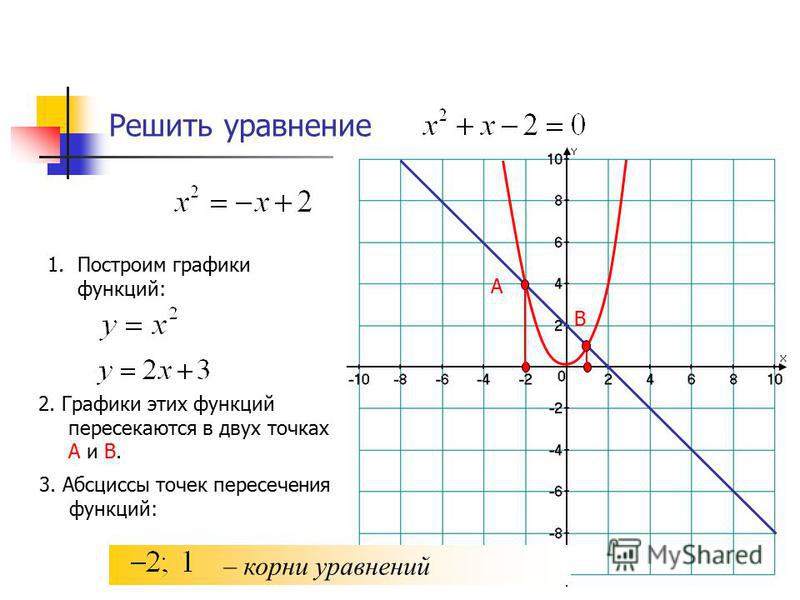 1 на 2, а обе части уравнения из п.2 на (-3) и почленно сложим получившиеся уравнения:

Пример 8.

1) Заменим на , получим или .

2)Умножим обе части уравнения из п.1 на (-2) и сложим с исходным уравнением:

получаем :

Литература

1. Кострикина Н.П. “Задачи повышенной трудности в курсе алгебры 7-9 классов” — М: “Просвещение”, 1991г.
2. Смышляев В.К.. Практикум по решению задач школьной математики. – М: “Просвещение”, 1978г.

 

Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа

Справочник по математике

Элементы математического анализа

Производная функции

Секущая графика функции. Уравнение секущей графика функции

Касательная к графику функции

Производная функции

Уравнение касательной к графику функции

Геометрический смысл производной

Секущая графика функции.

Уравнение секущей графика функции

      Рассмотрим график некоторой функции   y = f (x),   точки   A= (x₀;  f (x₀))   и   B = (x₁;  f (x₁))   на графике, прямую, проходящую через точки   A   и   B,   и произвольную точку   C = (x; y)   на этой прямой (рис. 1).

Рис.1

      Определение 1. Прямую, проходящую через две произвольные точки графика функции, называют секущей графика функции.

      В соответствии с определением 1 прямая, проходящая через точки   A   и   B   графика функции   y = f (x),   является секущей этого графика.

      Выведем уравнение секущей графика функции.

      Для этого рассмотрим векторы и , координаты которых имеют вид:

      Поскольку векторы и лежат на одной прямой, то справедливо равенство

(1)

где   k   – некоторое число.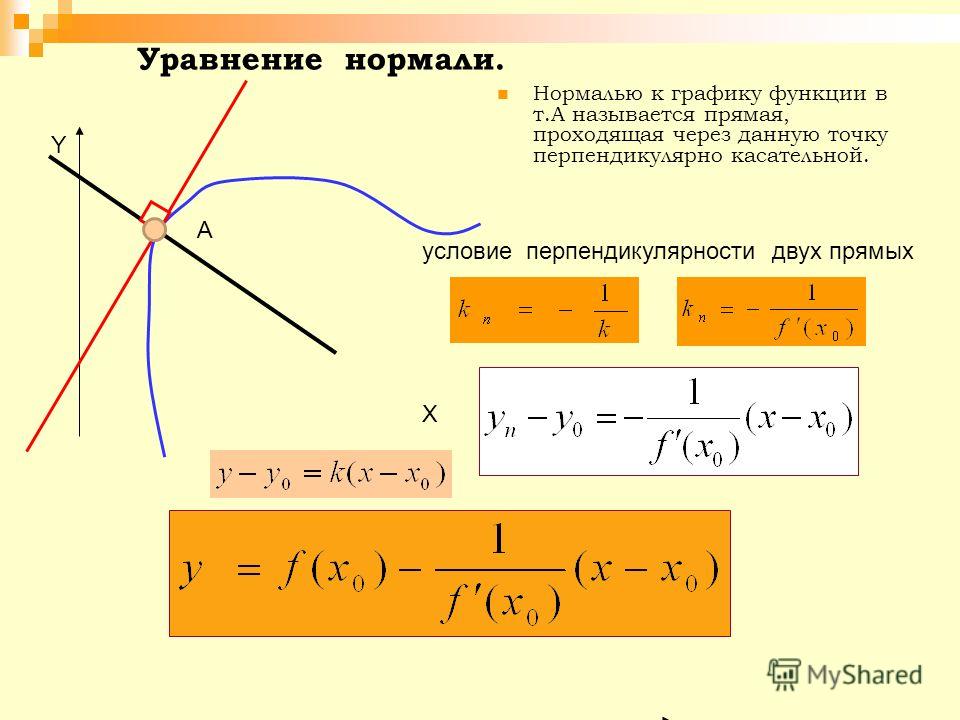

      Переписывая равенство (1) в координатах, получим систему (2):

(2)

      Исключая из системы (2) переменную   k ,  получим систему (3):

(3)

второе уравнение которой можно записать в следующем виде

(4)

      Уравнение (4) и является уравнением секущей графика функции   y = f (x),   проходящей через точки   A = (x₀;  f (x₀))   и   B = (x₁;  f (x₁))   этого графика.

Касательная к графику функции

      Проведем секущую графика функции   y = f (x),   проходящую через точки   A   и   B   этого графика, и рассмотрим случай, когда точка   A   неподвижна, а точка   B   неограниченно приближается к точке   A   по графику функции   y = f (x)   (рис. 2).

Рис.2

      Неограниченное приближение точки   B   к точке   A   принято обозначать

B → A

и произносить   «B   стремится к   A».

      Заметим, что, если   B → A   для точек   A = (x₀;  f (x₀))   и   B = (x₁;  f (x₁))  графика функции  y = f (x),   то это означает, что   x₁ → x₀ .

      Определение 2. Если при   x₁ → x₀   существует предельное положение секущей графика фукнкции   y = f (x),   то это предельное положение секущей называют касательной к графику функции   y = f (x)   в точке   A = (x₀;  f (x₀))  (рис. 3) .

Рис.3

Производная функции

      Определение 3. Если при   x₁ → x₀   отношение

(5)

входящее в формулу (4), стремится к некоторому числу, то это число называют производной функции   y = f (x) в точке   x₀ ,   обозначают   f ′(x₀)   или и записывают так:

(6)

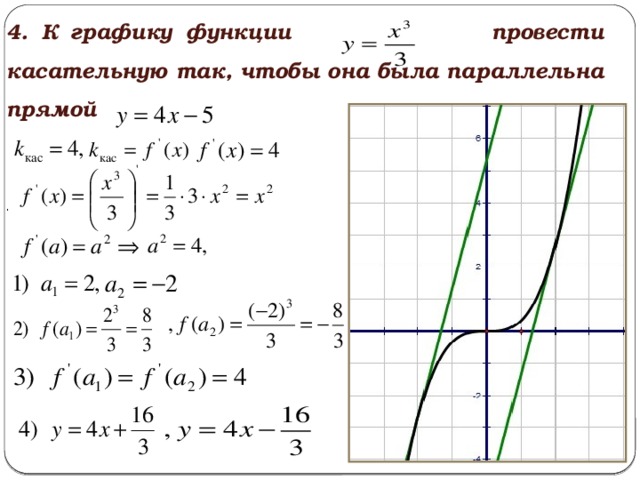
Уравнение касательной к графику функции

      Из формул (4) и (6) вытекает следующее

      Утверждение. Если у функции   y = f (x)   существует производная в точке   x₀ ,   то к графику функции   y = f (x)   в точке с координатами  (x₀;  f (x₀))   можно провести касательную, а уравнение этой касательной имеет вид:

y = f′(x0) (x – x0) + f (x0)

(7)

Геометрический смысл производной

      Рассмотрим сначала возрастающую функцию   y = f (x)   и проведем секущую графика этой функции, проходящую через точки   A = (x₀;  f (x₀))   и   B = (x₁;  f (x₁)) (рис.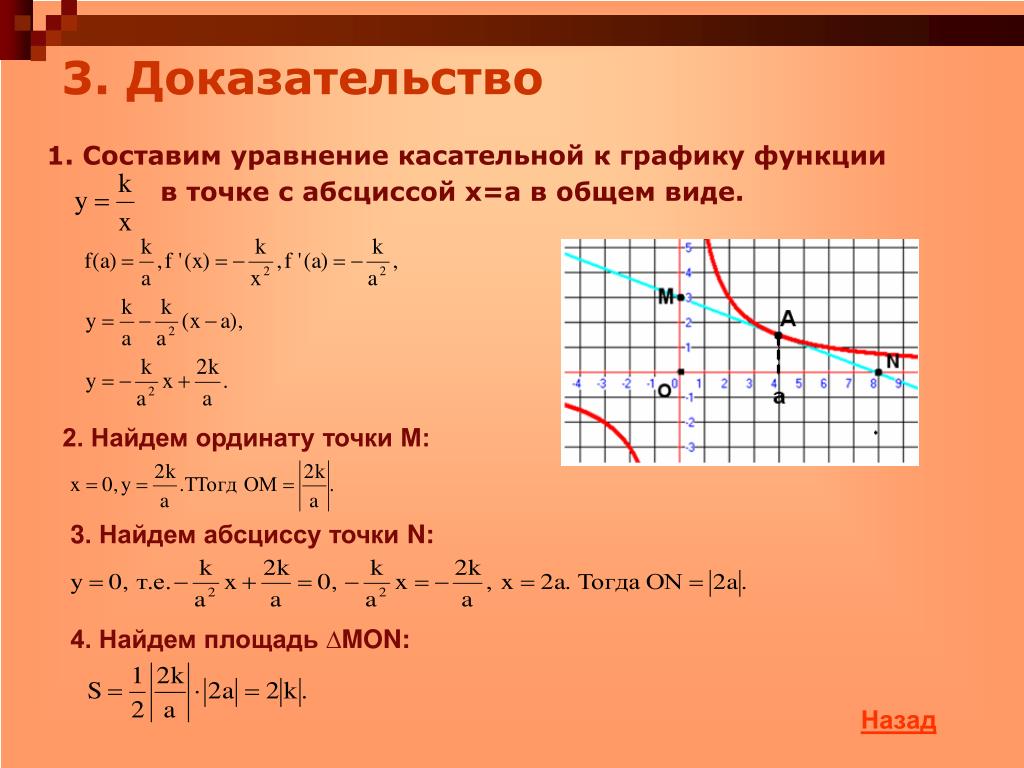 4).

Рис.4

      Обозначим буквой   φ   угол, образованный секущей и положительным направлением оси   Ox,   отсчитываемый против часовой стрелки. Тогда угол   BAD   в треугольнике   ABD   на рисунке 4 равен   φ ,   и по определению тангенса угла получаем равенство

(8)

причем по определению углового коэффициента прямой   tg φ   является угловым коэффициентом секущей графика функции   y = f (x),   проходящей через точки   A = (x₀;  f (x₀))   и   B = (x₁;  f (x₁))   этого графика.

      Случай, когда функция   y = f (x)   убывает, изображен на рисунке 5

Рис.5

      В этом случае угол   φ  является тупым, причем

то есть формула (8) справедлива и для случая, когда функция   y = f (x)   убывает.

      Отсюда в соответствии с определением производной функции вытекает соотношение:

где буквой   α   обозначен угол, образованный касательной к графику функции   y = f (x)   в точке   A = (x₀;  f (x₀))   с положительным направлением оси   Ox   (рис. 6).

Рис.6

      Таким образом, если у функции   y = f (x)   в точке   x₀   существует производная, то эта производная равна тангенсу угла наклона касательной к графику функции   y = f (x)   в точке   (x₀;  f (x₀)) :

f′(x₀) = tg α ,

где угол наклона   α   образован касательной и положительным направлением оси   Ox   и отсчитывается в положительном направлении (то есть против часовой стрелки).

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.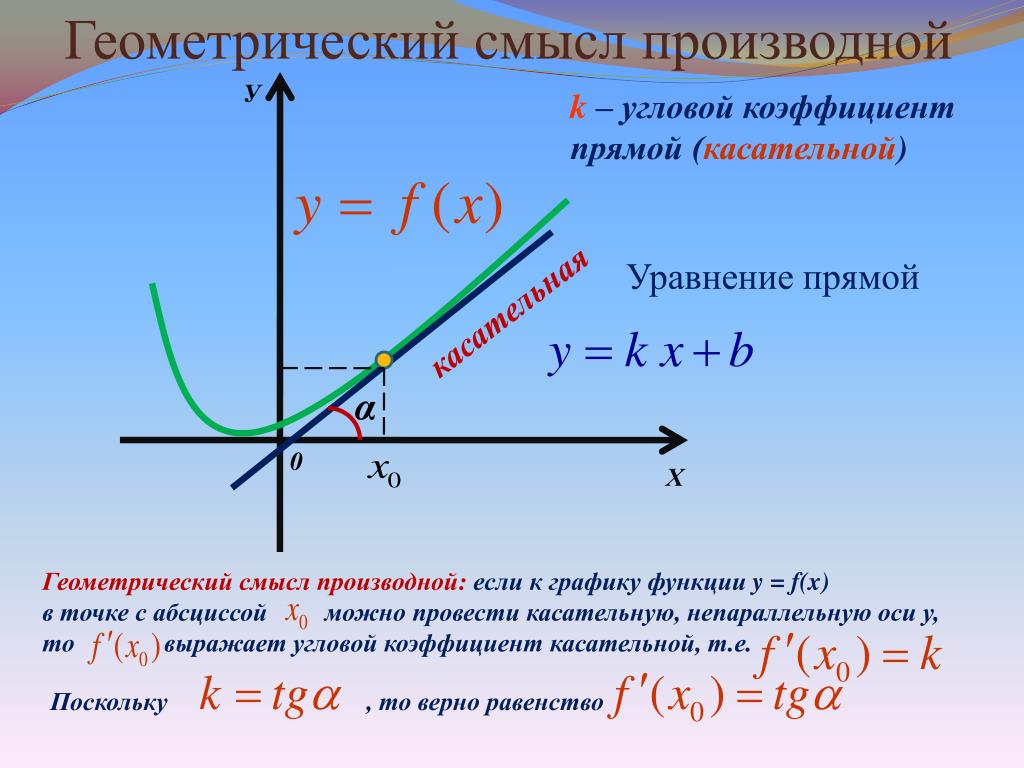

Разница между функциями и уравнениями (3 ключевые идеи) – JDM Educational

Функции и уравнения часто используются в математике. Однако остается вопрос, как соотносятся эти два понятия – и являются ли они одним и тем же.

Итак, в чем разница между функциями и уравнениями? Функция имеет как минимум 2 переменные: выходную переменную и одну или несколько входных переменных. Уравнение утверждает, что два выражения равны, и оно может включать любое количество переменных (ни одной, одной или более). Функция часто может быть записана как уравнение, но не каждое уравнение является функцией.

Конечно, уравнение может быть очень простым (например, 1 + 2 = 3), и оно не обязательно должно содержать какие-либо переменные. Некоторые уравнения выражают отношение, которое не является функцией.

В этой статье мы поговорим о разнице между функциями и уравнениями. Мы также рассмотрим несколько примеров, которые помогут прояснить идеи.

Начнем.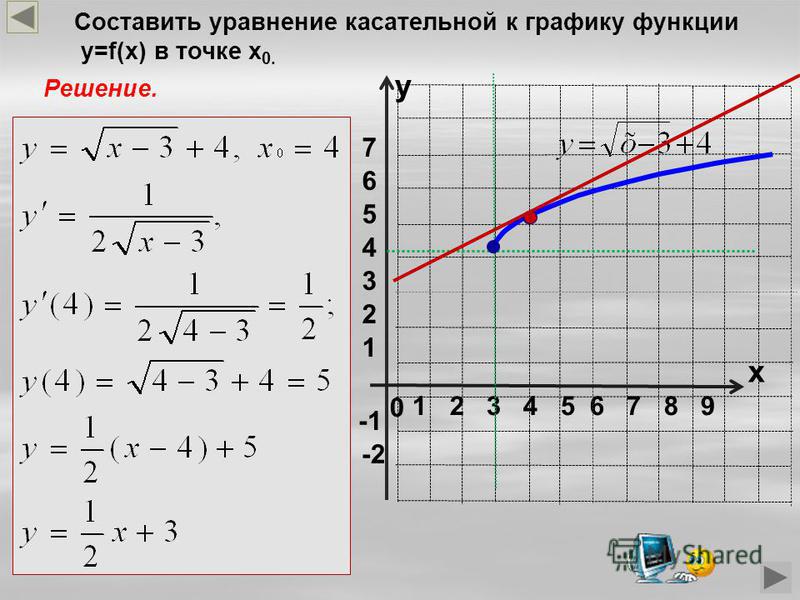

В чем разница между функциями и уравнениями?

Основное отличие состоит в том, что функция всегда имеет две или более переменных, а уравнение может иметь 0, 1 или более переменных.

Функция	Уравнение
2 или более переменных: — минимум 1 вход — минимум 1 выход например. y = 2x + 3 x вход y выход	Не обязательно иметь переменных, но может иметь 1, 2 или более. напр. 2 = 6/3 (без переменных) 4x = 12 (1 переменная) xy = 5 (2 переменные)
Можно записать в виде уравнения, например y = f(x), или y = 2x + 3, или f(x) = 2x + 3	Может или не может быть функцией; например x 2 + y 2 = 1 есть уравнение окружности, но это уравнение не представляет функцию.

В этой таблице приведены некоторые из
важных различий между функциями и уравнениями.

Многие функции можно записать в виде уравнения, но не каждое уравнение представляет собой функцию. В частности, уравнение с менее чем двумя переменными не может представлять функцию.

Что такое уравнение?

Уравнение — это математическое утверждение, что два выражения равны. Он всегда содержит символ равенства (знак равенства) или «=».

Выражение представляет собой комбинацию символов (чисел, переменных, показателей степени, круглых скобок и т. д.). Мы можем вычислить выражение   с определенными значениями для каждой из появляющихся переменных.

Уравнение с переменными может иметь ноль, одно или несколько решений.

Примеры уравнений

Уравнения могут варьироваться от простых до абсурдно сложных. Вот несколько примеров уравнений:

• 1 + 2 = 3  [уравнение без переменных]
• x + 4 = 7  [уравнение с одной переменной]
• 2x + 3y = 18  [a линейное уравнение с двумя переменными — это представляет собой линейную функцию!]
• log ₁₀ (x) + log ₁₀ (y ² ) = 5 [логарифмическое уравнение с двумя переменными]
• 2x ³ + 5y ⁴ – 9z ² = 4x + 8y + z – 20 [уравнение с тремя переменными]
• x + 3 = уравнение с одной переменной [уравнение с одной переменной решения нет, так как 3 не равно 4]

Для последнего примера мы можем легко увидеть, что решения нет, вычитая x из обеих частей. Это дает нам 3 = 4, что всегда является ложным утверждением, независимо от значения переменной x.

Помните, что некоторые уравнения представляют функции (или отношения), но не все.

Что такое функция?

Функция представляет собой особый тип отношения, в котором каждый вход имеет только один выход. Отношение представляет собой набор упорядоченных пар (или троек, или четверок, или n-кортежей для большего количества входных переменных).

Примеры функций

Некоторые функции легко записать в виде уравнений, например: ]

h(x) = x ² + 5x + 2 [квадратичная функция]

i(x) = sin(x) [тригонометрическая функция]

j(x) = log ₁₀ (x) [логарифмическая функция]

k(r, s) = 2r + 3s – 5rs + 9 [функция двух переменных]

Некоторые функции немного сложнее записать в виде уравнения . Например, кусочная функция состоит из двух или более частей, которые мы должны записать отдельно:

В определении кусочной функции есть как минимум две части.

График диаграммы рассеяния, где каждый вход имеет только один выход, также является функцией. Однако было бы ужасно много времени, чтобы написать кусочную функцию для большого количества точек данных.

Гораздо быстрее и проще представить данные в виде графика или, возможно, в виде таблицы входных и выходных значений – см. ниже.

Диаграмма рассеяния функции. Так гораздо проще представить функцию, чем с помощью уравнения (или набора уравнений) или кусочной функции.

Как определить, является ли уравнение функцией

Если мы можем построить график отношения из уравнения, то мы можем использовать тест вертикальной линии, чтобы определить, является ли график функцией или нет.

Тест вертикальной линии утверждает, что:

• Если любая вертикальная линия пересекает график отношения более одного раза, то отношение не является функцией.
• В противном случае отношение является функцией (каждая вертикальная линия пересекает график отношения не более одного раза, то есть один раз или ноль раз).

Эта концепция станет ясной с некоторыми примерами каждого случая.

Примеры отношений, не являющихся функциями

Вот несколько примеров отношений, не являющихся функциями (поскольку они не проходят проверку вертикальной линией).

Пример 1: x

⁴ = y ⁴

Отношение x ⁴ = y ⁴ не является функцией. Это легко увидеть даже без графика.

Например, упорядоченные пары (1, 1) и (1, -1) являются решениями уравнения x ² = y ² Потому что:

• 1 ⁴ = 1 ⁴ [1 = 1]
• 1 ⁴ = (-1) ⁴ [1 = 1, 1 = 1, 1 = 1, 1 = 1, 1 = 1, 1 = 1, 1 = 1, 1 = 1, 1 = 1, 1 = 1, 1, (1) поскольку отрицательное число, возведенное в любую четную степень, является положительным]

Мы знаем, что (1, 1) и (1, -1) имеют один и тот же вход (значение x), но разные выходы (значения v).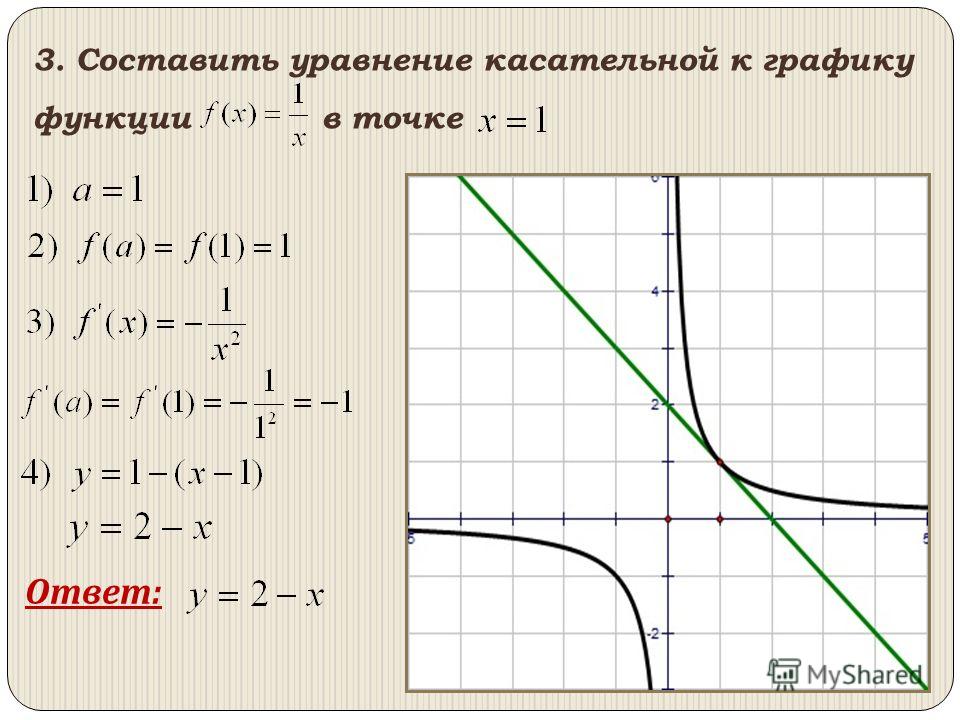 Таким образом, это две разные точки на одной вертикальной линии.

Таким образом, это отношение не проходит тест на вертикальную линию и не является функцией.

Пример 2: единичный круг

Единичный круг представлен уравнением x ² + y ² = 1. Однако это соотношение не является функцией.

Мы можем видеть это без графика. Например, упорядоченные пары (0, 1) и (0, -1) являются решениями уравнения x ² + y ² = 1, потому что:

• 0 ² + 1 ² = 0 + 1 = 1
• 0 ² + (-1) ² = 0 + 1 = 1  [поскольку отрицательное число, возведенное в любую четную степень, является положительным]

Мы знаем, что (0, 1) и (0, -1) имеют одинаковый вход (значение x), но разные выходы ( v значения). Таким образом, это две разные точки на одной вертикальной линии.

Таким образом, это отношение не проходит тест на вертикальную линию и не является функцией.

Вы можете легко убедиться в этом с помощью графика единичного круга, изображенного ниже.

Единичный круг. Вертикальная линия x = 0, проходящая через начало координат, дважды пересекает окружность единиц, что означает, что она не проходит тест на вертикальную линию (окружность не является функцией).

Примеры отношений, являющихся функциями

Вот несколько примеров отношений, являющихся функциями (поскольку они проходят тест вертикальной линии).

Пример 1: Линия y = 2x

Линия y = 2x имеет только один выход (y) для каждого входа (x). В этом легко убедиться, если мы посмотрим на график линии y = 2x, изображенный ниже.

Строка y = 2x, которая является функцией.

Любая вертикальная линия x = a, которую мы начертим, будет пересекать линию только в одной точке: (a, 2a). Таким образом, отношение проходит тест на вертикальную линию и, следовательно, является функцией (точнее, линейной функцией).

Пример 2: Парабола y = x

² + 1

Парабола y = x ² + 1 имеет только один выход (y) для каждого входа (x).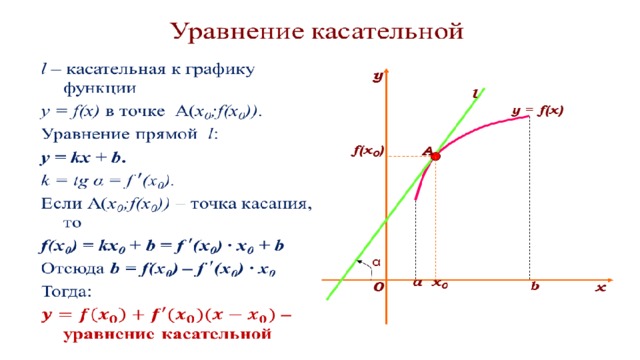 В этом легко убедиться, если мы посмотрим на график параболы y = x ² + 1, изображенный ниже.

График параболы parabola y = x ² + 1.

Любая проведенная нами вертикальная линия x = a будет пересекать параболу только в одной точке: (a, a ² + 1). Таким образом, отношение проходит тест на вертикальную линию и является функцией (точнее, квадратичной функцией).

Как определить, является ли функция один к одному

Если мы можем построить график функции из уравнения, то мы можем использовать тест горизонтальной линии, чтобы определить, является ли функция один к одному (инъективная) или нет.

Тест горизонтальной линии утверждает, что:

• Если любая горизонтальная линия пересекает график функции более одного раза, то функция не является однозначной.
• В противном случае функция является однозначной (каждая горизонтальная линия пересекает график функции не более одного раза, то есть один раз или ноль раз).

Эта концепция станет ясной с некоторыми примерами каждого случая.

Примеры функций, которые не являются взаимно однозначными

Вот несколько примеров функций, которые не являются взаимно однозначными (поскольку они не проходят тест горизонтальной линии).

Пример 1: Парабола y = x

² + 1

Парабола y = x ² + 1 не является один к одному, так как есть два входа (значения x), которые приводят к одному и тому же результату (y ценность). В этом легко убедиться, если мы посмотрим на график параболы y = x ² + 1, на фото ниже.

График параболы parabola y = x ² + 1, которая не один к одному.

Горизонтальная линия y = 1 пересечет параболу в двух точках: (1, 2) и (-1, 2). Таким образом, функция не проходит тест на горизонтальную линию, и поэтому она не один к одному.

Пример 2: Горизонтальная линия y = 5

Горизонтальная линия y = 5 не является один к одному, поскольку есть два входа (значения x), которые приводят к одному и тому же выходу (значение y).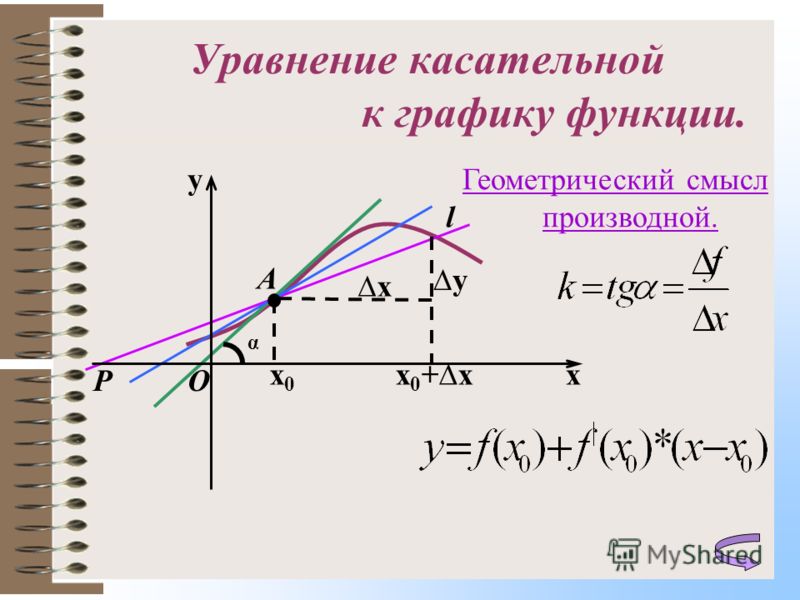 В этом легко убедиться, если мы посмотрим на график параболы y = 5, изображенный ниже.

Горизонтальная линия y=5, что не один к одному.

Горизонтальная прямая y = 5 пересекает прямую y = 5 в бесконечном числе точек. Таким образом, функция не проходит тест на горизонтальную линию, и поэтому она не один к одному.

Примеры функций один к одному

Вот несколько примеров функций один к одному (поскольку они проходят тест горизонтальной линии).

Пример 1: Линия y = 2x

Линия y = x проходит тест горизонтальной линии. В этом легко убедиться, если мы посмотрим на график линии y = 2x, изображенный ниже.

Строка y = 2x, которая является функцией один к одному.

Любая горизонтальная линия y = b, которую мы начертим, будет пересекать линию только в одной точке: (b, b). Таким образом, функция проходит тест горизонтальной линии, а значит она один в один.

Пример 2. Кубическая функция y = x

³

Кубическая функция y = x ³ проходит тест горизонтальной линии. В этом легко убедиться, если мы посмотрим на график линии y = x ³ , изображенный ниже.

Функция y = x ³ , которая является однозначной функцией.

Любая горизонтальная линия y = b, которую мы нарисуем, будет пересекать линию только в одной точке: (b ^1/3 , b). Поскольку b — действительное число, оно имеет только один действительный кубический корень (два других — комплексные).

Таким образом, функция проходит тест горизонтальной линии, а значит она один в один.

Заключение

Теперь вы знаете основные отличия функции от уравнения. У вас также есть несколько примеров, которые помогут вам запомнить, как выглядит каждый из них.

Вы можете узнать о разнице между функциями и отношениями в моей статье здесь.

Надеюсь, эта статья оказалась вам полезной. Если это так, пожалуйста, поделитесь ею с теми, кто может использовать эту информацию.

Не забудьте подписаться на мой канал YouTube и получать обновления о новых математических видео!

Подпишитесь на мой канал на YouTube!

~Джонатон

Разница между уравнениями и функциями

Ключевое отличие: В математике уравнение используется для обозначения равенства между двумя выражениями. С другой стороны, функция гораздо сложнее, чем уравнение. Функция используется для обозначения отношения между набором входов и набором соответствующих выходов.

Уравнение и функция являются двумя основными основами алгебры, предметом изучения математики. Оба могут быть довольно сложными по своей природе, однако в своей основной форме их можно спутать друг с другом. Основное различие между уравнением и функцией заключается в том, что уравнение обычно имеет дело с одним входом, тогда как функция может иметь множество входов.

В математике уравнение используется для обозначения равенства между двумя выражениями. По сути, уравнение записывается как выражение, равное другому выражению. Например: x + 2 = 5. Это означает, что любое значение x, если вы прибавите к нему 2, будет равно 5. Следовательно, мы можем решить уравнение для x, которое равно 3, как 3 + 2 = 5.

Уравнения могут быть более сложными и могут включать более одной переменной, например x, y, z и т. д. в одном уравнении. Например: 3x + 2y — z = 4. Однако каждому алфавиту будет соответствовать одно число. В этом случае x = 1, y = 2 и z = 3.

Следовательно,

3x + 2y – z = 4 становится

3(1) + 2(2) – 3 = 4, что равно

3 + 4 – 3 = 4 существенно

4 = 4

С другой стороны, функция гораздо сложнее уравнения. Функция используется для обозначения отношения между набором входов и набором соответствующих выходов. По сути, вход должен давать один выход. Функция — это связь между двумя переменными. Например: f(x) = x + 2. В соответствии с этой функцией, какими бы ни были входные данные, она даст вам один выход, который будет входом плюс 2. Давайте решим эту функцию:

Ввод	Функция	Выход
х	f(x) = x + 2	ф(х)
1	1 + 2	3
2	2 + 2	4
3	3 + 2	5
4	4 + 2	6
5	5 + 2	7

И так далее…

Функции имеют различные применения в математике, физике, информатике и т.