Вычисление площади фигуры в полярных координатах
В этом разделе мы продолжим разбирать тему вычисления площадей плоских фигур. Рекомендуем тем, кто изучает темы не по порядку, сначала обратиться к статье «Геометрический смысл определенного интеграла» и разобрать способы вычисления площади криволинейной трапеции. Нам понадобится вычислять площади фигур, которые ограничены ограничены линиями y=f(x), x=g(y) в прямоугольной системе координат. А также раздел «Свойства площади фигур», где была разобрана квадрируемость плоских фигур.
Краткий обзор статьи
- Начнем с определения понятия криволинейного сектора, получим формулу для вычисления его площади. Для этого мы используем понятие определенного интеграла Дарбу.
- Подробно разберем решения задач с использованием таких кривых как кардиоида, архимедова спираль и лемниската Бернулли.
- В отдельную подтему мы выделили нахождение площади фигуры, которая представлена как разность двух криволинейных секторов.
Полярная система координат и криволинейный сектор
Определение 1Точка, расположенная в полярной системе координат, имеет полярный угол φ0 и полярный радиус r0≥0. Полярный угол φ0 отсчитывается от полярной оси по часовой стрелке, а r0 — это расстояние от заданной точки до начала координат.
На рисунке мы отметили начало координат (полюс) жирной черной точкой, полярная ось имеет вид луча черного цвета, а красная точка определяется углом φ0=3π4 и расстоянием до полюса r0=4.
Мы можем рассматривать полярную систему координат одновременно с прямоугольной декартовой. Для этого необходимо совместить начала координат обеих систем, а ось абсцисс и полярной осью.
Задать связь полярных и декартовых координат можно соотношениями r=x2+y2φ=arctgyx, x≠0 и обратно x=r·cosφy=r·sinφ.
Координаты красной точки на чертеже 23; 2. Положение этой точки задается углом φ0=arctg223=π6 и расстоянием r0=232+22=4.
В полярной системе координат равенство φ=α задает луч, который выходит из точки начала координат и составляет угол α с полярной осью.
При этом, угол α может быть задан как в радианах, так и в градусах. Полярную ось мы можем задать уравнением вида φ=0. Равенство r=C>0 задает окружность с центром в начале координат, где — это радиус.
Функция r=p(φ), φ∈α; β определяет некоторую линию в полярных координатах.
Следует учитывать тот факт, что с позиции геометрии функция r=p(φ), φ∈α; β во всех случаях будет неотрицательной. Связано это с тем, что она задает расстояние от начала координат до точки для заданного значения угла φ=φ0∈α; β. Однако мы будем встречать и отрицательные значенияr=p(φ) функции, что зависит от отношения к данному вопросу конкретных исследователей и преподавателей.
На рисунке мы изобразили несколько примеров линий в полярной системе координат.
Дадим определение криволинейному сектору.
Определение 2Криволинейный сектор представляет собой фигуру, которая ограничена лучами φ=α, φ=β и некоторой линией r=p(φ)≥0, непрерывной на участке α; β.
На рисунке мы привели несколько примеров криволинейных секторов.
На последнем рисунке мы рассмотрели случай, когда фигура располагается между лучами φ=-π6, φ=π6, которые не являются ее границами.
Площадь криволинейного сектора — вывод формулы
Для вычисления площади криволинейного сектора мы можем вывести формулу. Для этого мы можем использовать формулу площади кругового сектора радиуса R с внутренним углом γ из школьного курса геометрии: Sкругового сектора=γ·R22. Задаем внутренний угол γ в радианах.
Разобьем криволинейный сектор на n частей такими лучами
φ=φ1, φ=φ2,…, φ=φn-1, что α=φ0<φ1<φ2<…<φn-1<β и λ=maxi=1, 2,…, nφi-φi-1→0 при n→+∞.
Учитывая свойства площади фигуры, мы можем представить площадь исходного криволинейного сектора S(G) как сумму площадей секторов S(Gi) на каждом из участков разбиения:
S(G)=∑i=1nS(Gi)
Обозначим наибольшее и наименьшее значения функции r=p(φ) на i-ом отрезке φi-1; φi, i=1, 2,…, n как Rmini и Rmaxi . На каждом из отрезков построим по два круговых сектора Pi и Qi с максимальным и минимальным радиусами Rmini и Rmaxi соответственно.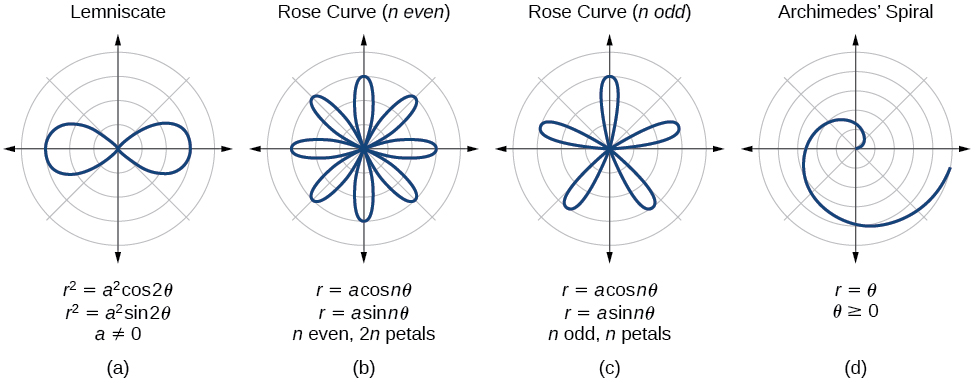
Фигуры, которые являются объединением круговых секторов Qi, i=1, 2,…, n; Pi, i=1, 2,…, n , обозначим как P и Q соответственно.
Их площади будут равны S(P)=∑i=1nS(Pi)=∑i=1n12(Rmini)2·φi-φi-1 и S(Q)=∑i=1nS(Qi)=∑i=1n12(Rmaxi)2·φi-φi-1, причем S(P)≤S(G)≤S(Q).
Так как функция r=pφ непрерывна на отрезке α; β, то функция 12p2φ будет непрерывна на этом отрезке. Если рассматривать S(P) и S(Q) для этой функции как нижнюю и верхнюю суммы Дарбу, то мы можем прийти к равенству:
limλ→0S(P)=limλ→0S(Q)=S(G)⇒S(G)=limλ→0∑ i=1n12(Rmini)2·φi-φi-1==limλ→0∑ i=1n12(Rmaxi)·φi-φi-1=12∫βαp2φdφ
Определение 3Формула для определения площади криволинейного сектора имеет вид:
S(G)=12∫βαp2φdφ
Примеры вычисления площади криволинейного сектора
Рассмотрим алгоритмы вычисления площади криволинейного сектора с полярной системе координат на конкретных примерах.
Пример 1Необходимо вычислить площадь плоской фигуры в полярных координатах, которая ограничена линией r=2sin2φи лучами φ=π6, φ=π3.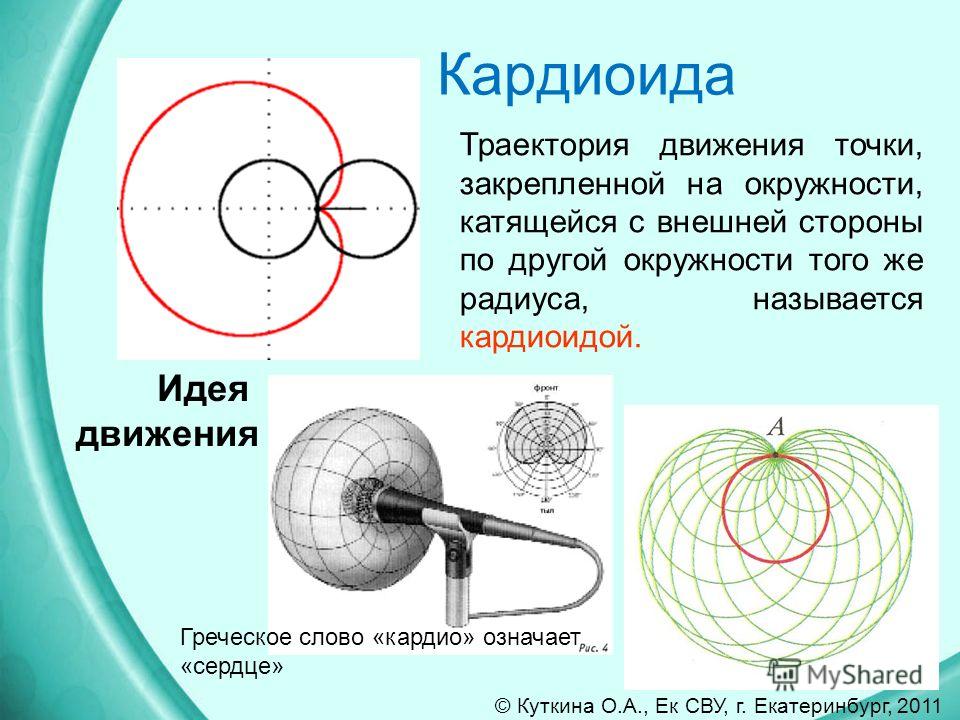
Решение
Для начала, изобразим описанную в условии задачи фигуру в полярной системе координат. Функция r=2sin(2φ)положительна и непрерывна на отрезке φ∈π6, π3.
Полученная фигура является криволинейным сектором, что позволяет нам применить формулу для нахождения площади этого сектора.
S(G)=12∫π6π3(2sin(2φ)2dφ=∫π6π32(sin(2φ)2dφ=∫π6π32·1-cos4φ2dφ=∫π6π3(1-cos(4φ))dφ=φ-14sin(4φ)π6π3==π3-14sin4π3-π6-14sin4π6=π6+34
Ответ: S(G)=π6+34
Задача упрощается в тех случаях, когда лучи φ=φ1, φ=φ2, ограничивающие фигуру, заданы. Тогда нам не нужно задумываться о пределах интегрирования при проведении вычисления площади.
Чаще встречаются задачи, где фигуру ограничивает лишь кривая r=p(φ). В этих случаях применить формулу S(G)=12∫αβp2(φ)dφ сразу не получится. Для начала придется решить неравенство p(φ)≥0 для нахождения пределов интегрирования. Так мы можем поступить в тех случаях, когда функция r=pφ неотрицательная.
В противном случае нам придется ориентироваться только на область определения и период функции.
Необходимо вычислить площадь фигуры, которая ограничена кривой в полярных координатах r=-3·cos3φ.
Решение
Функция определена для всех действительных значений аргумента. Решим неравенство -3·cos3φ≥0:
-3·cos3φ≥0⇔cos3φ≤0⇔cos φ≤0⇔⇔π2+2πk≤φ≤3π2+2πk, k∈Z
Построим функцию в полярных координатах на отрезке φ∈π2; 3π2 (при k=0). Для других значений k в силу периодичности косинуса мы будем получать ту же самую кривую.
Применим формулу для вычисления площади фигуры в полярных координатах. В качестве нижнего и верхнего предела можно брать π2+2πk и 3π2+2πk соответственно для любого целого значения k.
S(G)=12∫π23π2(-3·cos3φ)dφ=92∫π23π2cos6φdφ
Для того, чтобы получить ответ, нам необходимо вычислить полученный определенный интеграл. Для этого мы можем использовать формулу Ньютона-Лейбница. Первообразную для формулы Ньютона-Лейбница мы можем с помощью рекуррентной формулы вида Kn(x)=sin x·cosn-1(x)n+n-1nKn-2(x), где Kn(x)=∫cosn(x)dx.
∫cos6φdφ=sin φ·cos5φ6+56∫cos4φdφ==sin φ·cos5φ6+56sin φ·cos3φ4+34cos2φdφ==sin φ·cos5φ6+5sin φ·cos3φ24+1524sin φ·cos φ2+12∫cos0φdφ==∫π23π2cos6φdφ=sin φ·cos5φ6+5sin φ·cos3φ24+15sin φ·cos φ48+15φ48π23π2==1548·3π2-1548·π2=5π16
Таким образом, искомая площадь фигуры, ограниченной линией в полярной системе координат, равна S(G)=92∫π23π2cos6φdφ=92·5π16=45π32.
Ответ: S(G)=45π32
В тех случаях, когда в полярной системе координат задается множество кривых, которые по форме напоминают листья клевера или цветка, площадь фигур, ограниченных этими кривыми, часто одинаковы. В этих случаях можно вычислить площадь одного «лепестка» и умножить ее на количество криволинейных фигур.
Пример 3Необходимо вычислить площадь плоской фигуры в полярной системе координат, которая ограничена линией r=3·cos(3φ).
Решение
Найдем область определения, исходя из того, что эта функция неотрицательна для любого φ из области определения.
cos(3φ)≥0⇔-π2+2πk≤3φ≤π2+2πk, k∈Z-π6+2π3k≤φ≤π6+2π3k, k∈Z
Таким образом, период функции r=3·cos3φ равен 2π3.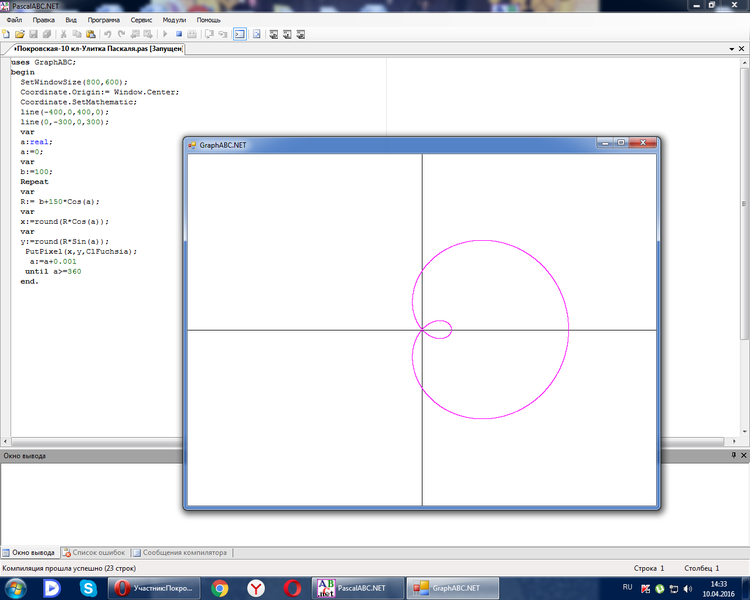
Построим фигуру на графике.
Вычислим площадь одного участка, расположенного на интервале φ∈π2; 5π6(при k=1):
12∫π25π69cos(3φ)dφ=12·3sin(3φ)π25π6=32sin3·5π6-sin3·π2=32(1-(-1)=3
Ответ: Площадь всей фигуры будет равна площади найденного участка, умноженной на 3.
Аналогичным образом можно найти площади фигур, имеющих сходное строение. Примером может служить лемниската Бернулли.
Площадь фигуры, которую ограничивает лемниската Бернулли
Определение 4Лемниската Бернулли задается уравнением r=α·cos2φ где a – положительное число, влияющее на размер линии (но не на конфигурацию, схожую с символом бесконечности). Лемниската Бернулли строится при -π4+π·k≤φ≤π4+π·k, k∈Z.
Лемниската служит границей фигуры, которую можно представить как два равных по площади участка.
Для вычисления площади используем нужную формулу:
S(G)=2·12∫-π4π4a2cos(2φ)2φ=a22(sin(2φ))-π4π4==a22sin2·π4-sin2·-π4=a2
Получается, что площадь фигуры, которую ограничивает лемниската Бернулли, равна квадрату коэффициента a.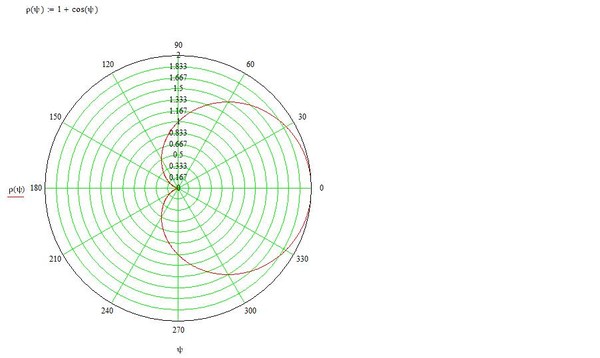
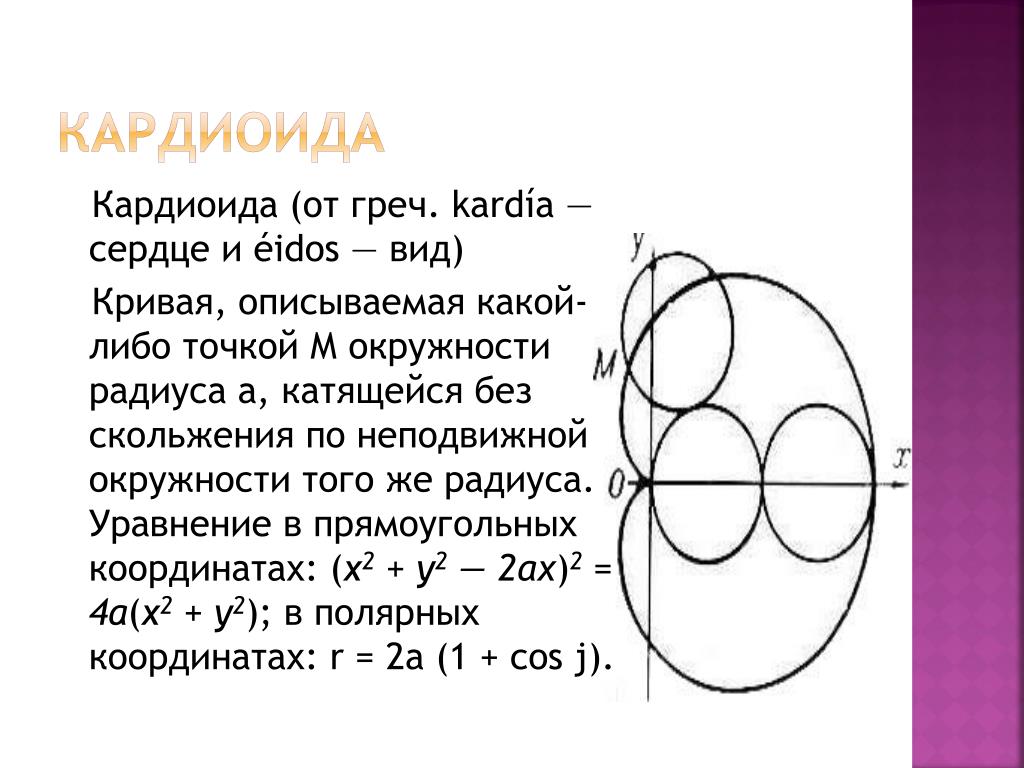
Площадь фигуры, границей которой является кардиоида
В полярной системе координат кардиоида задается уравнением вида r=2a(1+cosφ). В этом уравнении a – некоторое положительное число. Задающая кардиоиду функция является периодической с периодом 2π. Она определена для всех действительных значений угла. Это значит, что для вычисления площади нижним пределом интегрирования мы будем считать любое число, а верхним, то, которое на 2π больше нижнего.
Вычислим площадь фигуры, ограниченной кардиоидой r=2a(1+cosφ), для φ∈0; 2π:
S(G)=12∫02π(2a(1+cosφ))2dφ=2a2∫02π(1+2cosφ+cos2φ)dφ==2a2∫02π1+2cosφ+1+cos2φ2dφ==2a2∫02π32+2cosφ+cos(2φ)2dφ==2a232φ+2sin φ+14sin2φ02π=6π·a2
Площадь фигуры, которую ограничивает улитка Паскаля
В полярной системе координат улитка Паскаля может быть задана уравнением r=b+2a·cosφ. В этом уравнении a – это некоторое положительное число, b – любое действительное число. Кардиоиду можно рассматривать как частный случай улитки Паскаля. Получить кардиоиду можно при b=2a.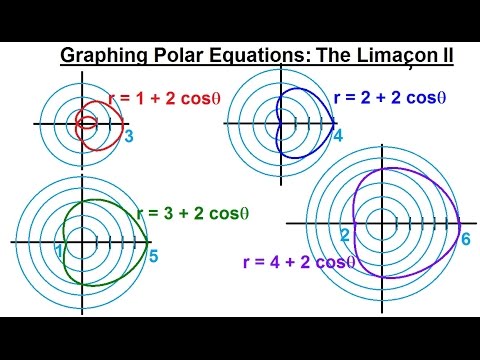
Улитка Паскаля в зависимости от значений параметров a и b может принимать различный вид. В данном разделе мы рассмотрим случаи, когда функцию r неотрицательная.
При b<-2a функция r=b+2a·cosφ будет отрицательной для любого значения угла φ.
При b=-2a улитка Паскаля имеет вид точки, которая совпадает с полюсом.
При -2a< b< 0 функция r=b+2a·cosφ неотрицательна для φ∈-arccos-b2a+2πk; arccos-b2a+2πk, k∈Z.
При 0<b<2a функция r=b+2a·cosφ неотрицательна для φ∈-arccos-b2a+2πk; arccos-b2a+2πk, k∈Z. Она ограничивает фигуру, которая по конфигурации напоминает кардиоиду.
При b>2a функция r=b+2a·cosφ является неотрицательной для любого значения угла. Графическая иллюстрация этого случая приведена ниже
Для того, чтобы правильно определить пределы интегрирования, необходимо учитывать соотношение параметров a и b.
Пример 4Необходимы вычислить площадь фигуры, которая ограничена линиями, заданными уравнениями r=-3+6cosφ и r=5+4cosφ в полярной системе координат.
Решение
Формула r=-3+6cosφ соответствует фигуре, известной как улитка Паскаля..
Функция r=-3+6cosφ определена для всех значений угла φ. Нам необходимо выяснить, при каких φ функция будет неотрицательной:
-3+6cosφ≥0⇔cosφ≥12⇔-π3+2πk≤φ≤π3+2πk, k∈Z
Проведем вычисление площади фигуры, которая ограничена данной улиткой Паскаля:
S(G)=12∫-π3π3(-3+6cosφ)2dφ=92∫-π3π3(1-4cosφ+4cos2φ)dφ==92∫-π3π31-4cosφ+4·1+cos2φ2dφ==92∫-π3π3(3-4cosφ+2cos(2φ))dφ=92·3φ-4sinφ+sin(2φ-π3π3==92·3·π3-4sinπ3+sin2π3-3·-π3-4sin-π3+sin-2π3==92·2π-33
Улитка Паскаля, определяемая формулой r=5+4cosφ, соответствует пятому пункту. Функция r=5+4cosφ определена и положительна для всех действительных значений φ. Поэтому, площадь фигуры в этом случае равна:
S(G)=12∫02π(5+4cosφ)2dφ=12∫02π(25+40cosφ+16cos2φ)dφ==12∫02π25+40cosφ+16·1+cos(2φ)2dφ==12∫02π(33+40cosφ+8cos(2φ))dφ=12·33φ+40sinφ+4sin(2φ02π==12·33·2π+40sin(2π+4sin(4π)-33·0+40sin 0+4sin 0=33π
Ответ: S(G)=33π
Площадь фигур, границей которых является спираль Архимеда или логарифмическая спираль
Сразу обратимся к примеру.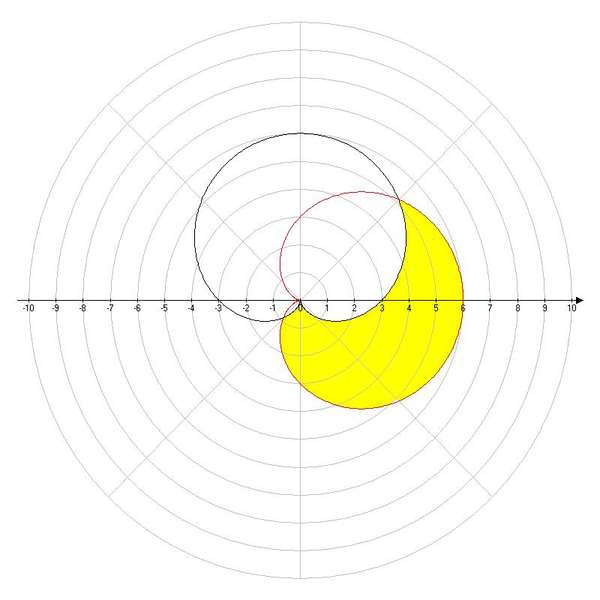
Необходимо вычислить площадь фигур в полярной системе координат, первая из которых ограничена первым витком спирали Архимеда r=αφ, α>0, а вторая первым витком логарифмической спирали r=αφ, α>1.
Решение
Если в задаче сказано, что фигура ограничена первым витком спирали Архимеда, то угол φ изменяется от нуля до двух пи.
Исходя из этого, найдем площадь фигуры по формуле:
S(G)=12∫02π(αφ)2dϕ=α22∫02πφ2dφ=α22·φ3302π=4α3π33
Аналогично вычисляется площадь фигуры, ограниченной первым витком логарифмической спирали:
S(G)=12∫02π(αϕ)2dϕ=12∫02πa2φdφ=14ln a·a2φ02π==14ln a·a4π-1
Нахождение площади фигуры, которую можно представить как разность двух криволинейных секторов
Пусть фигура в полярной системе координат ограничена лучами φ=α, φ=β и непрерывными и неотрицательными на интервале φ∈α; β функциями r=p1(φ) и r=p2(φ), причем p1(φ)≤p2(φ) для любого угла φ=φ0∈α; β.
Находим площадь фигуры по формуле S(G)=12∫αβp22(φ)-p12(φ)dφ.
Действительно, в силу свойства аддитивности площади, фигуру G можно представить как разность двух криволинейных секторов G2 и G1.
Тогда площадь фигуры G равна разности площадей этих криволинейных секторов:
S(G)=S(G2)-S(G1)=12∫αβp22(φ)dφ-12∫αβp12(φ)dφ==12∫αβp22(φ)-p12(φ)dφ
Последний переход возможен в силу третьего свойства определенного интеграла.
Пример 6Необходимо вычислить площадь фигуры, которая ограничена линиями φ=0, φ=π3, r=32, r=12φв полярной системе координат.
Решение
Построим заданную фигуру на графике.
Очевидно, что r=32 больше r=12φ для любого φ∈0; π3. Применяем полученную формулу для вычисления площади фигуры:
S(G)=12∫0π3322-12φ2dφ=12∫0π394-2-2φdφ==12·94φ+12·2-2φln 20π3=12·94φ+1ln 2·122φ+10π3==12·94·π3+1ln 2·122·π3+1-94·0+1ln 2·122·0+1==12·3π4+2-2π3-12·ln 2
Ответ: S(G)=12·3π4+2-2π3-12·ln 2
А теперь рассмотрим пример, когда фигура ограничена линиями, заданными в прямоугольной системе координат.
Площадь такой фигуры намного проще вычислять, используя полярные координаты.
Необходимо вычислить площадь фигуры, которая ограничена прямыми линиями y=13x, x=3x, окружностями (x-2)2+(y-3)2=13, (x-4)2+(y-3)2=25.
Решение
В прямоугольной системе координат вычислить площадь полученной фигуры можно, но дело это долгое и хлопотное. Намного проще перейти к полярной системе координат, воспользовавшись формулами перехода.
x=r·cosφy=r·sinφ⇒y=13x⇔r·sinφ=r·cosφ3⇔tgφ=13⇔φ=π6+πky=3x⇔r·sinφ=3·r·cosφ⇔tgφ=3⇔φ=π3+πk(x-2)2+(y-3)2=13⇔x2+y2=4x+6y⇔r=4cosφ+6sinφ(x-4)2+(y-3)2=25⇔x2+y2=8x+6y⇔r=8cosφ+6sinφ
Функция r=8cosφ+6sinφ больше r=4cosφ+6sinφ для любого φ∈π6; π3. Вычисляем площадь фигуры в полярных координатах:
S(G)=12∫π6π38cosφ+6sinφ2-4cosφ+6sinφ2dφ==12∫π6π3(48cos2φ+48cosφ·sinφ)dφ==24∫π6π3cos2φdφ+24∫π6π3cosφ·sinφdφ==12∫π6π3(1+cos2φ)dφ+24∫π6π3sinφd(sinφ)==12·φ+12sin(2φ)π6π3+12·sin2φπ6π3==12·π3+12sin2π3-π6+12sin2π6+12·sin2π3-sin2π6==12·π6+12·322-122=2π+6
Ответ: S(G)=2π+6
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Лимакон | bartleby
Что такое Лимакон?
Маршрут точки, прикрепленной к окружности, когда эта окружность катится по периметру другой окружности такого же радиуса, определяется как лимакон.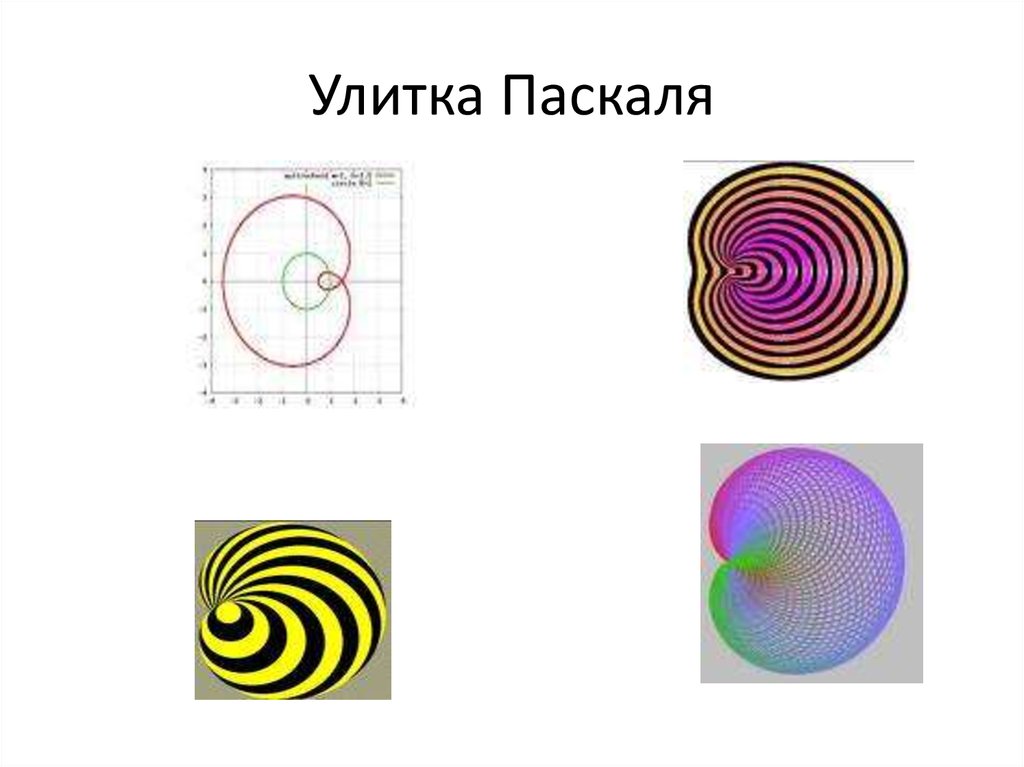
Он широко известен как лимасон Паскаля. Он также известен как колесо рулетки, которое получается, когда оно вращается вокруг круга с половиной своего радиуса, в результате чего меньший круг оказывается внутри большего круга.
Полярная кривая обычно используется для описания limacon. Когда кругу разрешено вращаться вокруг другого круга, фиксированная точка круга образует путь. Это имя, данное этому маршруту. Радиусы обеих окружностей не обязательно должны быть одинаковыми.
История Лимакона
Лимакон Паскаля был открыт Этьеном Паскалем (отцом ученого мистера Блеза Паскаля). Кривая была названа французом Жилем-де Робервалем в 1650 году, когда он впервые использовал ее в качестве примера для своих методов рисования касательных, которые теперь читаются как дифференцирование.
Название «лимакон» происходит от латинского слова «limax», что означает «улитка».
Немецкому ученому Альбрехту Дюреру также следует отдать должное за открытие этого, поскольку у него есть метод рисования лимакона, но в то время он не называл его лимаконом.
Уравнения Лимакона
Кривые Лимакона напоминают окружности. Они бывают разных форм и размеров, в зависимости от значений в их уравнениях.
Лимакон в полярных координатах записывается в виде r=b+acosθ.
Когда b = 2a, то этот лимакон становится кардиоидой, но если b = a, он становится трисектрисой. Обратите внимание, что это не трисектриса Маклорена. Ниже приведена схема лимакона для различных значений a и b.
Уравнение полярности можно изменить на новые координаты, умножив r на обе части уравнения (теперь включая исходную точку) и используя r2=x2+y2 и rcosθ=x, чтобы получить:
r=b+acosθr2=br+arcosθx2+y2=bx2+y2+axx2+y2-ax=bx2+y2x2+y2-ax2=b2x2+y2.
Теперь, используя параметрическую структуру полярной замены на декартову, получаем: Используя замену z=x+iy=b+acosθcosθ+isinθ, параметризация в комплексных координатах получается как:
z=a2+beiθ+a2e2iθ
стать:
z=beit+a2e2it
Это можно сделать, изменив местоположение источника.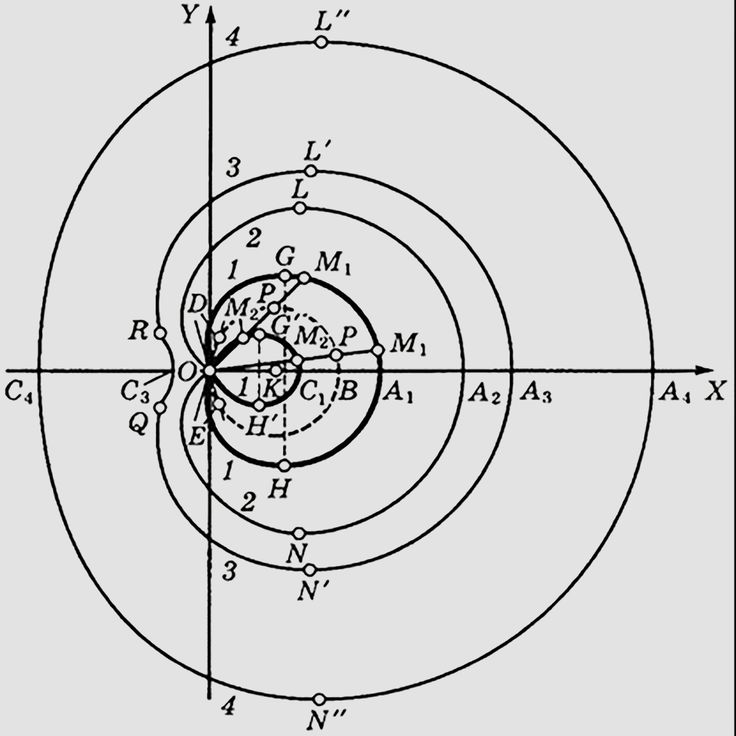
Это привело бы к преобразованию уравнения в уравнение центрированной трохоиды.
Обратите внимание, что это изменение в независимой переменной означает, что параметризация полярных координат по умолчанию θ=argz больше не используется.
Особые случаи
- Если a=b, полярное уравнение принимает следующий вид:0005
Таким образом, кривая становится членом семейства синусоидальных кривых, и этот особый тип называется кардиоидным.
2. Если a=2b, то полярное уравнение принимает вид:
r=2bcosθ3
Таким образом, кривая становится членом семейства кривых-роз, и этот особый тип называется трисектрисой или limacon trisectrix.
В этом случае уравнение центроида трохоиды принимает вид0049 Петлевой
- Полярный
- Кардиоидный
- Ямочный
- Limacon имеет широкий спектр применений в машиностроении и машиностроении.
- Они используются для создания различных машин, включая зубчатые, винтовые и лопастные машины.
- Их модели часто используются при разработке систем управления.
- Эта тема важна для профессиональных экзаменов как для бакалавров, так и для выпускников, особенно для бакалавров наук.
и магистр наук. - Bean
- Cardioid
- Evolute
В случае лимакона необходимо рассмотреть несколько случаев. Эти сценарии основаны на соединении a и b. Всего существует пять экземпляров, каждый из которых демонстрирует свою форму.
К ним относятся следующие:
Случай I: Если b больше, чем a, полученный лимакон представляет собой простую замкнутую кривую.
Случай II: Если значение b находится между a и 2a, узор лимакон будет ямочным.
Случай III: Если значение a равно значению b, сгенерированный лимакон является кардиоидным.
Случай IV: Если значение b меньше значения a, limacon будет включать внутренний цикл.
Случай V: Если b равно половине a, лимакон будет иметь трехсекционную структуру.
Отношение между другими петлями и этой
Предположим, что существуют точка P и окружность C, центр которой не находится в P. Набор окружностей, проходящих через P так, что их центры лежат на C это лимакон.
Ортогональная проекция круга теперь называется лимакон. Проекция относительно начала координат окружности радиуса b с центром в точке (a, 0) имеет уравнение r=b+acosθ.
Противоположным кругу r=b+acosθ является r=1b+acosθ. Полученная инверсия представляет собой конику с фокусом в начале координат и эксцентриситетом ab.
Таким образом, любой лимакон может быть определен как инверсия коники, так что фокусы являются центром инверсии. В этом случае обратная парабола станет кардиоидой. Инверсия гиперболы станет лимаконом с внутренней петлей. Инверсия эллипса станет лимаконом без петли.
Раковина этого круга по отношению к месту на этом круге является лимаконом.
Одним из особых лимаконов является декартов овал.
Общие ошибки
В этом случае люди, скорее всего, запутаются между различными типами кривых, которые присутствуют в этом, и формулой, которую нужно понять.
Контекст и области применения
Мы предоставим вам пошаговые решения миллионов задач из учебников, круглосуточную помощь экспертов в данной области, когда вы запутались, и многое другое.
Ознакомьтесь с примером решения вопросов и ответов по геометрии здесь!
*Время ответа зависит от темы и сложности вопроса. Среднее время отклика составляет 34 минуты для платных подписчиков и может быть больше для рекламных предложений.
Лимасон-де-Паскаль
Лимасон-де-Паскаль| следующая кривая | предыдущая кривая | 2D кривые | Трехмерные кривые | поверхностей | фракталов | многогранники |
ЛИМАСОН (ИЛИ УЛИТКА) ПАСКАЛЯ
Кривая, изученная Дюрером в 1525 году (под именем Арахна),
Этьен Паскаль в 1630 году и Роберваль (который назвал кривую) в 1650 году.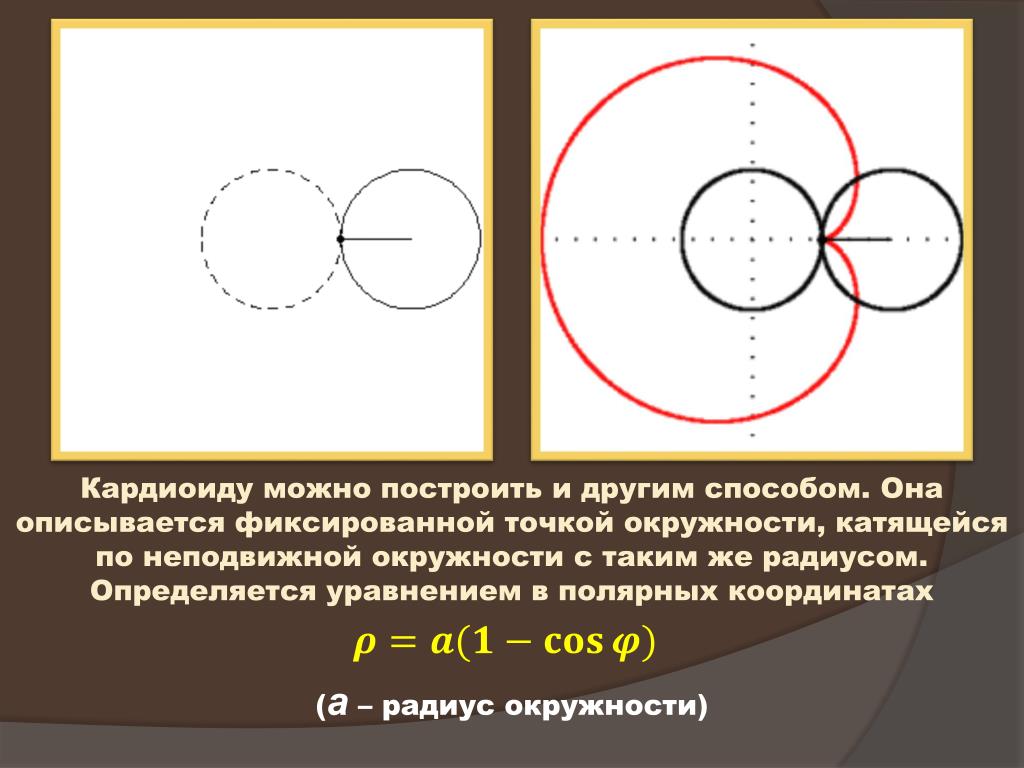
Этьен Паскаль (1588–1651): судья и любитель математик, отец Блеза. |
| Полярное уравнение:
( а , и > 0).
Комплексная параметризация: (). Декартово уравнение: . Рационал бициркулярная квартика (особая точка O ). Зона для e 1: . |
| Лимасоны Паскаля — это раковины
окружности относительно одной из ее точек O (здесь окружность
диаметром [ OA ] с A ( шт. , 0)).
Следовательно, механическая конструкция предполагала противоположное, благодаря палке длиной 2 a , скользящей через точку окружности диаметром ea и середина которого ограничена описанием круг. |
Кривые принимают различную форму в зависимости от случаев:
| e < 1: эллиптический лимасон (обратный
эллипса относительно его фокуса), или с изолированной точкой ,
или акнодаль ;
.  e
<
1/2: выпуклая кривая, которая «стремится» к окружности C ( O , a )
когда e переходит в 0.
.e = 1/2: лимасон Паскаля с меплатой. . 1/2 < e < 1: кривая бобовидной формы; e = 1: клык лимасон чаще называется кардиоидной. e > 1: гиперболический лимасон (обратный гиперболы относительно ее фокуса) или с петлей , или крунодали ; это замкнутая кривая с петлей; для e = 2 получаем трисектрису лимасон, который также является розой. |
Вышеприведенная комплексная параметризация показывает, что лимасоны
Паскаля являются эпитрохоидами
создается точкой, связанной с кругом, катящимся без скольжения
окружность того же радиуса (здесь неподвижной окружностью является окружность с
диаметр [ OA ] и точка трассировки расположена на расстоянии a
от центра движущегося круга).
— педали кругов (здесь педаль круга с центром A и радиусом a по отношению к O ).
|
|
|
|
|
|
— циссоиды
двух окружностей, одна из которых проходит через центр другой,
относительно этого центра (здесь циссоида относительно O окружности
с центром (- ea /2, 0), проходящим через O и окружность с центром
О
и радиус a — это определение фактически эквивалентно раковистому
определение).
Лимасоны Паскаля суть рациональные декартовы кривые и являются частными случаями полных декартовы овалы; когда и 1 (т.е. когда это не кардиоида), биполярное уравнение относительно О и О’ (, 0) это: .
Точнее:
— гиперболический лимасон — это воссоединение
из двух декартовых овалов:
(большая петля) и
(маленькая петля).
— эллиптический лимасон является декартовым
овал:
(плюс изолированная точка O ).
Мы также находим limaçons Паскаля в Белидор система разводных мостов.
Эволюты лимасонов — это каустики
отражением кругов (источник света на конечном расстоянии).
|
|
Арахны… |
Кривые с уравнением
(циссоиды окружности, проходящей
к O и роза) обеспечивают
элегантная подача лимасона;
здесь k = 55/37 (идея Тьерри ЛЕГЕ). |
