в столбец и в уме
Умножение двузначных чисел – навык, крайне необходимый для нашей повседневной жизни. Люди постоянно сталкиваются с потребностью перемножить что-либо в уме: ценник в магазине, массу продуктов или размер скидки. Но как умножать двузначные числа быстро и без проблем? Давайте разберемся.
Как умножить двузначное число на однозначное?
Начнем с простой задачи – как умножать двузначные числа на однозначные.
Для начала, двузначное число – это такое число, которое состоит из определенного количества десятков и единиц.
Для того чтобы умножить двузначное число на однозначное в столбец, нужно написать нужное двузначное число, а под ним соответствующее однозначное. Далее следует поочередно умножить на заданное число сначала единицы, а потом – десятки. Если при умножении единиц получилось число больше 10, то количество десятков нужно просто перенести в следующий разряд, прибавив их.
Умножение двузначных чисел на десятки
Умножение двузначных чисел на десятки – задача ненамного сложнее, чем умножение на однозначные числа. Основной порядок действий остается тем же:
Основной порядок действий остается тем же:
- Выписать числа друг под другом в столбец, при этом нуль должен находиться как бы «сбоку», чтобы не мешать при арифметических действиях.
- Умножить двузначное число на количество десятков, не забыть про перенос некоторых цифр в следующие разряды.
- Единственное, что отличает этот пример от предыдущего – в конце получившегося ответа нужно добавить нуль, так что десятки, которые были опущены в начале, становятся учтенными.
Как перемножить два двузначных числа?
После того как вы полностью разобрались с умножением двузначных и однозначных чисел, можно начинать думать, как умножать столбиком двузначные числа друг на друга. На самом деле это действие тоже не должно потребовать от вас больших усилий, так как принцип все еще остается тем же.
- Выписываем данные числа в столбец – единицы под единицами, десятки под десятками.
- Начинаем умножение с единицы точно так же, как в примерах с однозначными числами.

- После того как вы получили первое число, умножив единицы на данную цифру, нужно таким же образом умножить десятки на эту же цифру. Внимание: ответ нужно записывать строго под десятками. Пустое место под единицами – это неучтенный нуль. Вы можете записывать его, если вам так удобнее.
- Перемножив и десятки, и единицы и получив два числа, записанных одно под одним, их нужно сложить в столбец. Получившееся значение и является ответом.
Как правильно умножать двузначные числа? Для этого недостаточно просто прочитать или выучить приведенную инструкцию. Помните, для того чтобы освоить принцип, как умножать двузначные числа, в первую очередь нужно постоянно практиковаться – решать как можно больше примеров, как можно реже пользоваться калькулятором.
Как умножать в уме
Научившись блестяще умножать на бумаге, можно задаться вопросом, как быстро умножить двузначные числа в уме.
Конечно, это не самая простая задача. Она требует некоторой концентрации, хорошей памяти, а также способности удерживать в голове некоторое количество информации. Однако и этому можно научиться, приложив достаточно усилий, тем более если подобрать правильный алгоритм. Очевидно, что легче всего умножать на круглые числа, поэтому самым простым способом является разложение чисел на множители.
Однако и этому можно научиться, приложив достаточно усилий, тем более если подобрать правильный алгоритм. Очевидно, что легче всего умножать на круглые числа, поэтому самым простым способом является разложение чисел на множители.
- Для начала следует разбить одно из данных двузначных чисел на десятки. Например, 48 = 4 × 10 + 8.
- Далее нужно последовательно перемножить сначала единицы, а потом десятки со вторым числом. Это достаточно сложные для выполнения в уме операции, так как нужно одновременно умножать числа друг на друга и держать в уме уже получившийся результат. Вероятнее всего, вам будет трудно справиться с этой задачей с первого раза, но, если быть достаточно усердным, этот навык можно развить, ведь понять, как правильно умножать двузначные числа в уме, можно только на практике.
Некоторые хитрости при умножении двузначных чисел
Но существует ли более легкий способ в уме умножать двузначные числа, и как это сделать?
Есть несколько хитростей. Они помогут вам легко и быстро умножать двузначные числа.
Они помогут вам легко и быстро умножать двузначные числа.
- При умножении на одиннадцать нужно просто поставить сумму десятков и единиц в середину данного двузначного числа. К примеру, нам понадобилось умножить 34 на 11.
3 + 4 = 7
Ставим 7 в середину, 374. Это и есть ответ.
Если при сложении получается число больше 10, то следует просто добавить единицу к первому числу. Например, 79 × 11.
7 + 9 = 16
(7 + 1)69 = 869
- Иногда легче разложить число на множители и последовательно умножить их. Например, 16 = 2 × 2 × 2 × 2, поэтому можно просто 4 раза умножить исходное число на 2.
14 = 2 × 7, поэтому при выполнении математических операций можно умножить сначала на 7, а потом на 2.
- Для того чтобы умножить число на числа, кратные 100, например, 50 или 25, можно умножить это число на 100, а потом разделить на 2 или 4 соответственно.
- Еще нужно помнить, что иногда при умножении легче не складывать, а отнимать числа друг от друга.

Например, чтобы умножить число на 29, можно сначала умножить его на 30, а потом отнять от полученного числа данное число один раз. Это правило справедливо для любых десятков.
умножение двузначных чисел до 100
Самым эффективным способом умножения в уме больших чисел считается методика опорного числа. После того, как вы освоите его – возможности вашего интеллекта станут безграничны
В предыдущей статье, когда была продемонстрирована системы умножения чисел до 20, мы фактически использовали 10 – своеобразное опорное число.
Основные закономерности применения опорного числа
Наибольшая польза применения опорного числа достигается при попытке находящихся близко друг к другу чисел, а также при необходимости возвести некоторое число в квадрат. Сущность применения такой методик подсчета подробно описывалась в ЭТОЙ статье, теперь же постараемся пересказать только самое существенное.
При умножении X на Y опорным для них будет такое число, с которым наиболее близко соседствуют и тот и другой множители. Если привести пример, то в процессе умножения двух двузначных чисел в качестве своеобразной опоры имеет смысл использовать кратные 10 числа (100, 50, 40, 20 и 10 особенно).
На применение способа опорного числа во много влияет тот факт — являются ли оба множителя (или один из них) меньше (или наоборот больше) числа, на которое опираемся. В связи с этим возможные следующие варианты умножения.
1. Если опорное число больше обоих множителей
Например, нужно умножить 98 и 97. Так как оба числа находятся буквально «впритык» к 100, то, как опорное, лучше его и взять
Чтобы умножить 48 на 47, используя опорное число 50, нужно:
- От 97 отнять ровно столько, сколько не достает 98, чтобы достичь 100. Речь идет о числе 2. После нехитрой операции получаем 95 (можно, кстати, пойти альтернативным методом и от 48 отнять 3-ку – разницы особой не будет)
- Полученное число – 95 умножаем на опорное число 100 и получаем = 9500
- Ну и завершающий штрих: добавляем к такому результату 3 помноженное на 2 (это разница обоих чисел при вычете их из опорного числа)
- В результате получаем – 9506! (можете проверить по калькулятору!)
Схематично в уме удобно представлять приведенную ниже табличку.
|
100 «опорное число» |
97 |
* |
98 |
(97-2)*100 = 95*100 =9500 (или (98-3)*100 = 95*100 |
|
3 |
|
2 |
прибавляем 6 |
|
|
Итого: |
9500 + 6 =9506 |
Вот как мы наполняли представленную выше таблицу. Слева от произведения написали опорное число. Так как в нашем случае все числа меньше, чем опорное, то разница между опорным числом и ними заносится строго под этими числами. Справа же от 97*98 вписываем расчет, произведенный с опорным числом. В правой ячейке от «остатков» 3 и 2 заносим их произведение.
Слева от произведения написали опорное число. Так как в нашем случае все числа меньше, чем опорное, то разница между опорным числом и ними заносится строго под этими числами. Справа же от 97*98 вписываем расчет, произведенный с опорным числом. В правой ячейке от «остатков» 3 и 2 заносим их произведение.
Упрощенная схема умножения без таблицы записывается таким образом: 98*97=95*100 + 6= 9506
А вот другие примеры:
Умножаем 98*95
|
50 «опорное число» |
48 |
* |
45 |
(45-2)*50 =2150 |
|
2 |
* |
5 |
прибавляем 10 |
|
|
Итого: |
2160 |
Решение одной строкой:48*45 = 50*43 + 10 = 2160
Умножаем 39*38
|
40 «опорное число» |
39 |
* |
38 |
(38-1)*40 =1480 |
| 1 |
* |
2 |
прибавляем 2 |
|
|
Итого: |
1482 |
Решение одной строкой:39*38 = 40*37+2 = 1482
Умножаем 97*73
|
100 «опорное число» |
97 |
|
73 |
(73-3)*100 =7000 |
|
3 |
* |
27 |
прибавляем 81 |
|
|
Итого: |
7081 |
Решение одной строкой:97*73 = 100*70 + 81 = 7081
2.
 Если опорное число меньше обоих множителей
Если опорное число меньше обоих множителей
Например, нужно нам перемножить 55 и 54. И то и другое число располагаются неподалеку от 50, а значит в качестве опорного числа удобнее и быть не может. Если раньше мы рассматривали примеры, когда числа были меньше опорного, то в данном случае все наоборот. Однако пугаться не стоит, так как модель их умножения сохранится. Только теперь придется не отнимать остатки, а наоборот – добавлять их.
- К 55 нужно добавить такое число, на которое 54 больше 50-ти. Добавляем 4 и получаем 59 (можем пойти по обратному пути и к 54 прибавить 5 – разницы особой не будет)
- Потом 59 перемножаем на 50 и получаем 2950
- Ну и остается последний штрих: умножаем 5 и 4, чтобы добавить к 2950
В вот результат: 2970
|
|
5 |
|
4 |
прибавляем 20 |
|
50 «опорное число» |
55 |
* |
54 |
(55+4)*50 =2950 или (54+5)*50 = 59*50 |
|
Итого: |
2970 |
А вот другие примеры:
Умножаем 22*26
|
|
2 |
* |
6 |
прибавляем 12 |
|
20 «опорное число» |
22 |
* |
26 |
(22+6)*20 =560 |
|
Итого: |
572 |
Решение одной строкой: 22*26 = 20*28 + 12 = 572
Умножаем 52*65
|
|
2 |
* |
15 |
прибавляем 30 |
|
50 «опорное число» |
52 |
* |
65 |
(65+2)*50 =3350 |
|
Итого: |
3380 |
Решение одной строкой: 52*65 = 67*50 + 15 = 3380
3.
 Если одно из чисел больше опорного, а другое меньше
Если одно из чисел больше опорного, а другое меньше
Вот и подошли мы к последнему из возможных вариантов применения опорного числа при умножении. Такие задачи, когда одно число меньше опорного, а другое больше – только кажутся сложными. На самом деле в них действуют все те же элементарные принципы.
- Постараемся умножить 46 на 53. Выглядеть это будет так:
- Из 53 вычитаем 4 (ровно столько, сколько не хватает 46, чтобы добраться до расположенного НАД ним опорного числа) или к 46 прибавляем 3 (именно столько нужно вычесть из 53, чтобы добраться до расположенного ПОД ним опорного числа). В любом из этих случаев получаем цифру 49
- Потом 49 умножаем на 50 м получаем 2450
- Ну и напоследок вычитаем продукт умножения 4 и 3 (НЕ прибавляем, как было ранее!)
В результате имеем 2438
|
|
3 |
|||
|
50 «опорное число» |
46 |
* |
53 |
(46+3)*50 =2450 |
|
4 |
|
|
вычитаем 12 |
|
|
Итого: |
2438 |
Решение одной строкой: 46*53 = 49*50-12 = 2438
А вот другой пример:
Умножаем 92*104
|
|
4 |
|||
|
100 «опорное число» |
92 |
* |
104 |
(92+4)*100 =9600 |
|
8 |
|
|
вычитаем 28 |
|
|
Итого: |
9628 |
Решение одной строкой: 92*104 = 96*100-28 = 9628
4.
 Когда одно число близко к опорному, а другое далеко от него
Когда одно число близко к опорному, а другое далеко от него
Уже рассмотренные примеры показали, что особенно удобно пользоваться опорным числом даже тогда, когда только один из множителей близок к нему. Тем не менее было бы неплохо подбирать такие опорные числа, чтобы разница с ним составляла не более 3-x. А еще было бы лучше, если б она равнялась числу, с котором удобно решать задачи на умножение (имеются ввиду числа по типу 25, 10 или 5). Однако не всегда желаемое является действительным. Постараемся порешать примеры более сложноые.
Умножаем 49*74
|
|
24 |
|||
|
50 «опорное число» |
49 |
* |
74 |
(74-1)*50 =3650 |
|
1 |
|
|
вычитаем 24 |
|
|
Итого: |
3626 |
Решение одной строкой: 49*74 = (74-1)*50 – 24*1 = 3626
Умножаем 22*68
|
|
2 |
48 |
96 |
|
|
20 «опорное число» |
22 |
* |
68 |
(2+68)*20 =1400 |
|
Итого: |
1496 |
Решение одной строкой: 22*68 = (2+68)*20 + 96 = 1496 — чуть сложнее
Умножаем 97*42
|
100 «опорное число» |
97 |
* |
42 |
(42-3)*100 =3900 |
|
3 |
* |
58 |
прибавляем 174 |
|
|
Итого: |
4074 |
Решение одной строкой: 97*42 = 100*(42-3) + 174 = 4074
Со временем, если потренироваться, вы научитесь неплохо умножать, используя такие опорные числа, как 80, 70, 60, 40 или 30. Когда это произойдет (а без небольшой практики в этом вопросе не обойтись), вы приобретете полезнейший навык совершать умножение чисел до 100 и больше.
Когда это произойдет (а без небольшой практики в этом вопросе не обойтись), вы приобретете полезнейший навык совершать умножение чисел до 100 и больше.
5. Применение сразу двух опорных чисел
Умножать можно, используя два опорных числа одновременно. Порою это можно сделать для удобства, особенно такой финт актуален при задаче выразить опорное число одного множителя через опорное число другого. Так при умножении 88 и 23 имеет смысл использовать опорное число 80 для 88 и 20 для 23. Почему нужно использовать сразу два опорных числа? Да дело в том, что 20 это в действительность 80 деленное на 4.
Способ сразу двух опорных чисел характерен тем, что первым делом нам следует разделить 88 на 4. Получив таким образом 22, умножаем это число на 23 (второе участвовавшее в умножении число), то, что получится, умножаем 4. Иными словами, первым делом мы разделили произведение на 4-ку, и затем умножили результат на туже 4-ку. Вот решение одной строкой: 22*23=250*2+6=506. И последний штрих 506 умножаем на 4 и получаем 2024. Вот и вся наука!
И последний штрих 506 умножаем на 4 и получаем 2024. Вот и вся наука!
Для лучшего понимания описанной выше схемы пройдемся по привычной для нас схеме из нескольких пунктов. Итак, когда нужно умножить 88 на 23, мы поступаем следующим образом:
- Заносим в таблицу «20» — очень красивое опорное число, добавив рядышком множитель 4 (именно посредством мы выразим опорное число 80 через 20).
- А потом по заведенному распорядку. Пишем в соответствующую ячейку таблицы «3» — это то, насколько 23 превышает опорное число 20. Тоже самое проделываем с числом 88 по отношению к 80 (в данном случае разница ровно 8).
- Над 3-ой вставляем произведение 3-х и 4-х (на множитель опорного умножаем число три).
- Затем к 88 добавляем полученное произведение 3-х и 4-х, совершаем умножение полученного результата на опорное число 20. Имеем 100*20, а это у нас — 2000
- Под конец к 2000 подставляем полученный при умножении 3-ки и 8-ки результат.
 Итого: 2024
Итого: 2024
|
|
3*4=12 |
|||
|
|
8 |
* |
3 |
добавляем 24 |
|
20*4 «опорное число» |
88 |
* |
23 |
(88+12)*20 =2000 |
|
Итого: |
2024 |
Решение одной строкой:88*23=(88+3*4)*20+24=2024
Напоследок умножим 88 на 23 с помощью других опорных чисел. Для числа 88 пусть это будет 100, а для 23-х — 25. В таком случае 100 — основное опорное числом, при этом 25 мы представляем в таблице вот таким образом: 100:4 = 25
Для числа 88 пусть это будет 100, а для 23-х — 25. В таком случае 100 — основное опорное числом, при этом 25 мы представляем в таблице вот таким образом: 100:4 = 25
|
100:4 «опорное число» |
88 |
* |
23 |
(23-3)*100 =2000
|
|
|
12 |
2 |
добавляем 24 |
|
|
|
12:4=3 |
|||
|
Итого: |
2024 |
Решение одной строкой: 88*23=(23 — 12:4)*100+24=2024
Рассмотрев два представленных выше примера, резюмируем: опорные числа разные, но результат один и тот же.
Конечно, применение сразу 2-х опорных чисел – задача более сложная, чем одного, так как для осуществления нужно осуществлять дополнительные операции. С одной стороны, от вас требуется понять, какие два опорных числа подойдут вам больше всего. С другой — следует организовать определенные измышления, чтобы обнаружить для умножения на опорное необходимое число. Так что к работе сразу с двумя опорными числами лучше прибегайте в том случае, когда неплохо освоили работу с одним из них.
Хитрости умножения в уме любых чисел до 100
Теперь, когда мы разобрали с вами теорию опорных чисел, важно бегло отметить другие математические полезные приемы, которые могут помочь вас существенным образом облегчить задачу умножения в уме. О них подробнее можно прочесть, перейдя по ссылкам ниже
Похожие статьи
Please enable JavaScript to view the comments powered by Disqus.
252 | 144 | 276 | |
Й | Д | Ю | М |
34 | 42 | 36 | 57 |
Й | Д | Ю | М |
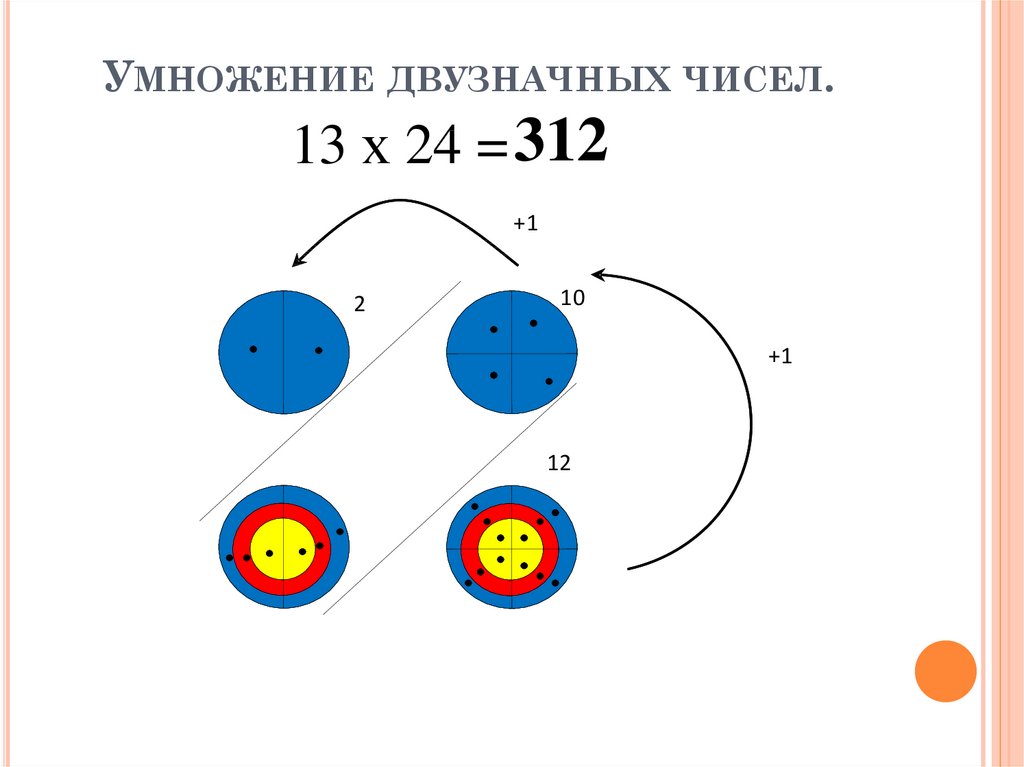
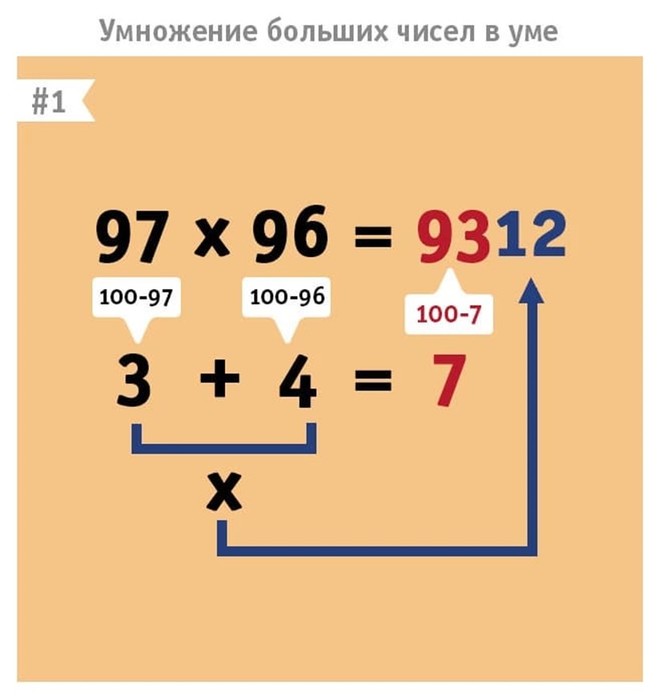
Умножение. Правило умножения двузначных чисел на двузначные Перемножение двузначных чисел
Например: 98 х 97 = 9506
Здесь я пользуюсь таким алгоритмом: если хочешь перемножить два
двузначных числа, близких к 100, то поступай так:
1) найди недостатки сомножителей до сотни;
2) вычти из одного сомножителя недостаток второго до сотни;
3) к результату припиши двумя цифрами произведение недостатков
сомножителей до сотни.
2.9 Умножение трёхзначного числа на 999
Любопытная особенность числа 999 проявляется при умножении на него всякого другого трёхзначного числа. Тогда получается шестизначное произведение: первые три цифры есть умножаемое число, только уменьшенное на единицу, а остальные три цифры (кроме последней) – «дополнения » первых до 9. Например:
385 * 999 = 384615
573 * 999 = 572427 943 * 999 = 942057
2.10 Умножение на шесть (по Трахтенбергу)
Нужно прибавить к каждой цифре половину «соседа ».
Пример: 0622084 * 6
0622084 * 6 4 является правой цифрой этого числа и, так 4 как «соседа » у неё нет, прибавлять нечего.
06222084 * 6 Вторая цифра 8, е «сосед » — 4. Мы берём 8 04 прибавляем половину 4 (2) и получаем 10, ноль пишем, 1 в перенос.
06222084 * 6 Следующая цифра ноль. Мы прибавляем к ней
504 половину «соседа » 8 (4), то есть 0 + 4 = 4 плюс
перенос (1).
Остальные цифры аналогичны.
Ответ: 06222084 * 6
Правило умножения на 6: является «сосед » чётным или не чётным – никакой роли не играет. Мы смотрим только на саму цифру: если она чётная, прибавляем к ней её целую часть половины «соседа », если нечётная, то кроме половины «соседа » прибавляем еще 5.
Пример: 0443052 * 6
0443052 * 6 2 – чётная и не имеет «соседа », напишем её снизу
0443052 * 6 5 – нечётная: 5+5 и плюс половина «соседа » 2 (1)
12 будет 11. Запишем 1 и в перенос 1
0443052 * 6 половина от 5 будет 2, и прибавим перенос 1, то будет 3
0443052 * 6 3 – нечетная, 3 + 5 = 8
0443052 * 6 4 + половина от 3 (1) будет 5
0443052 * 6 4 + половина от 4 (2) будет 6
0443052 * 6 ноль + половина от 4 (2) будет 2
2658312 Ответ: 2658312.
Выводы
Знание приемов быстрого счета позволяет упрощать вычисления, экономить время, развивает логическое мышление и гибкость ума.
В школьных учебниках практически нет приемов быстрого счета, поэтому результат данной работы – памятка для быстрого счета будет очень полезной для учащихся 5-6 классов.
Как мы видим, быстрый счёт это уже не тайна за семью печатями, а научно разработанная система. Раз есть система, значит, её можно изучать, ей можно следовать, ею можно овладевать.
Все рассмотренные мною методы устного умножения говорят о многолетнем интересе ученых, и простых людей к игре с цифрами.
Используя некоторые из этих методов на уроках или дома, можно развить скорость вычислений, привить интерес к математике, добиться успехов в изучении всех школьных предметов.
Заключение
Описывая старинные способы вычислений и современные приёмы быстрого счёта, я попытался показать, что как в прошлом, так и в будущем, без математики, науки созданной разумом человека, не обойтись.
Изучение старинных способов вычислений показало, что эти арифметические действия были трудными и сложными из-за многообразия способов и их громоздкости выполнения.
Современные способы вычислений просты и доступны всем.
При знакомстве с научной литературой обнаружил более быстрые и надежные способы вычислений.
Результаты своей работы я оформил в памятку (Приложение 2), которую предложу всем своим одноклассникам. Возможно, что с первого раза не у всех получится быстро, с ходу выполнять вычисления с применением этих приемов, даже если сначала не получится использовать прием, показанный в памятке, ничего страшного, просто нужна постоянная вычислительная тренировка. Она и поможет приобрести полезные навыки.
Список использованной литературы
1. Ванцян А.Г. Математика: Учебник для 5 класса. — Самара: Издательский дом «Фёдоров », 1999г.
2. Зайкин М.Н. Математический тренинг. — Москва, 1996.
3. Зимовец К.А., Пащенко В.А. Интересные приемы устных вычислений. //Начальная школа. – 1990, №6.
//Начальная школа. – 1990, №6.
4. Иванова Т. Устный счёт. // Начальная школа. – 1999, №7.
5. Кордемский Б.А., Ахадов А.А. Удивительный мир чисел: Книга учащихся,- М. Просвещение, 1986г.
6. Минских Е.М. «От игры к знаниям », М., «Просвещение », 1982г.
7. Перельман Я.И. Живая математика. — Екатеринбург, Тезис, 1994.
8. Свечников А.А. Числа, фигуры, задачи. М., Просвещение, 1977г.
Интернет-источники
1. school.edu.ru
Существуют три общих способа: прямое умножение, метод опорного числа и метод Трахтенберга.
Освойте их все, так как каждый может быть более предпочтительным в той или иной ситуации.
Отрабатывать полученные навыки можно с помощью тренировочной таблицы.
Прямое умножение
Этот метод удобен, когда один из множителей находится в диапазоне 12-18 или заканчивается на 1, а другой значительно от него отличается.
Один из множителей мысленно разбивают на десятки и единицы. Затем умножают другой множитель на десятки, потом на единицы и складывают.
Например, 62×13 = 62×10 + 62×3 = 620 + 186 = 806.
Иногда удобно разбивать на десятки и единицы больший множитель: 42×17 = 17×40 + 17×2 = 714.
Метод опорного числа
Для освоения метода требуется небольшая практика, однако он очень удобен, когда два множителя — близкие числа. В частности, это основной способ для возведения двузначных чисел в квадрат.
Опорное число — это круглое число, близкое к обоим множителям. Оно может быть меньше обоих множителей, больше обоих множителей или находится между ними.
В качестве опорного числа следует выбирать числа, на которые легко умножать. Например, 50 или 100, если они близки к двум множителям.
В зависимости от того, как соотносятся опорное число и множители, техника умножения немного различается.
а. Опорное число меньше двух множителей. Например, нужно умножить 32 на 36.
- Опорное число — 30. Множители больше опорного числа на 2 и 6.
- Добавьте к первому множителю 6 и умножьте на опорное число: 38 × 30 = 1140.

- Добавьте произведение 2 и 6: 1140 + 2×6 = 1152.
б. Опорное число больше двух множителей. Например, нужно умножить 43 на 48.
- Опорное число — 50. Множители меньше опорного числа на 7 и 2.
- Вычтите из первого множителя 2 и умножьте на опорное число: 41 × 50 = 2050.
- Добавьте произведение 7 и 2: 2050 + 7×2 = 2064.
в. Опорное число — между множителями. Например, нужно умножить 37 на 42.
- Опорное число — 40. Первый множитель меньше на 3, второй — больше на 2.
- Добавьте к меньшему множителю 2 и умножьте на опорное число: 39 × 40 = 1560.
- Вычтите произведение 3 и 2: 1440 − 3×2 = 1554.
Метод Трахтенберга
Метод Трахтенберга — самый общий. Им удобно пользоваться всегда, когда не работают специальные приемы. Он также распространяется на умножение многозначных чисел.
Поскольку метод Трахтенберга не совсем привычен, при его освоении лучше иметь множители перед глазами. В дальнейшем практикуйтесь без записи исходных чисел.
Разберем метод на примере умножения 87 на 32.
- Представьте числа последовательно: 8732. Перемножьте два внутренних числа (7 и 3), два внешних числа (8 и 2) и сложите. Получается 37.
- Перемножьте десятки: 80×30 = 2400. Добавьте 37×10. Получается 2770.
- Добавьте произведение единиц (7 и 2). Итого 2784.
Страница 1 из 4
Точные произведения двузначных чисел 11 — 50 (Таблица Брадиса 1)
Таблица брадиса произведения двузначных чисел состоит из 89 табличек произведений каждого из натуральных чисел от 11 до 99, указанных полужирными цифрами справа, на все целые числа от 0 до 99. Чтобы получить, например, произведение 57-49, надо взять табличку с номером 57 и найти пересечение строки с заголовком (слева) 40 и Столбца с заголовком (сверху) 9. То же самое произведение 2793 можно получить по таблич-ке 49 в пересечении строки 50 и столбца 7.
Применяя распределительное свойство, можно с помощью таблицы брадиса упростить произведение любого многозначного числа на двузначное, а также умножение любого многозначного на многозначное. Трехзначные произведения, как например 35-17 = 595, во избежание ошибок лучше записывать как четырехзначные, добавляя слева нуль: 35-17 = 0595. Если сомножитель содержит нечетное число цифр, полезно добавлять справа нуль, отбра-сывая его в окончательном результате.
Трехзначные произведения, как например 35-17 = 595, во избежание ошибок лучше записывать как четырехзначные, добавляя слева нуль: 35-17 = 0595. Если сомножитель содержит нечетное число цифр, полезно добавлять справа нуль, отбра-сывая его в окончательном результате.
Таблица брадиса 1 упрощает и деление любого многозначного числа на двузначное: в то время как обычное письменное деление дает цифры частного по одной, примене-ние таблицы дает их сразу по две. Используется табличка с номером, равным дели-телю, сносить надо сразу по две цифры делимого. Если при делении с остатком сно-сится только одна (крайняя справа) цифра делимого, то в частном получается только одна (последняя) цифра. Но если частное надо найти в виде десятичной дроби, то последняя цифра делимого сносится вместе с нулем десятых.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 0 | 0 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 11 |
| 10 | 110 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | |
| 20 | 220 | 231 | 242 | 253 | 264 | 275 | 286 | 297 | 308 | 319 | |
| 30 | 330 | 341 | 352 | 363 | 374 | 385 | 396 | 407 | 418 | 429 | |
| 40 | 440 | 451 | 462 | 473 | 484 | 495 | 506 | 517 | 528 | 539 | |
| 50 | 550 | 561 | 572 | 583 | 594 | 605 | 616 | 627 | 638 | 649 | |
| 60 | 660 | 671 | 682 | 693 | 704 | 715 | 726 | 737 | 748 | 759 | |
| 70 | 770 | 781 | 792 | 803 | 814 | 825 | 836 | 847 | 858 | 869 | |
| 80 | 880 | 891 | 902 | 913 | 924 | 935 | 946 | 957 | 968 | 979 | |
| 90 | 990 | 1001 | 1012 | 1023 | 1034 | 1045 | 1056 | 1067 | 1078 | 1089 | |
| 0 | 0 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 12 |
| 10 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | |
| 20 | 240 | 252 | 264 | 276 | 288 | 300 | 312 | 324 | 336 | 348 | |
| 30 | 360 | 372 | 384 | 396 | 408 | 420 | 432 | 444 | 456 | 468 | |
| 40 | 480 | 492 | 504 | 516 | 528 | 540 | 552 | 564 | 576 | 588 | |
| 50 | 600 | 612 | 624 | 636 | 648 | 660 | 672 | 684 | 696 | 708 | |
| 60 | 720 | 732 | 744 | 756 | 768 | 780 | 792 | 804 | 816 | 828 | |
| 70 | 840 | 852 | 864 | 876 | 888 | 900 | 912 | 924 | 936 | 948 | |
| 80 | 960 | 972 | 984 | 996 | 1008 | 1020 | 1032 | 1044 | 1056 | 1068 | |
| 90 | 1080 | 1092 | 1104 | 1116 | 1128 | 1140 | 1152 | 1164 | 1176 | 1188 | |
| 0 | 0 | 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 | 13 |
| 10 | 130 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | |
| 20 | 260 | 273 | 286 | 299 | 312 | 325 | 338 | 351 | 364 | 377 | |
| 30 | 390 | 403 | 416 | 429 | 442 | 455 | 468 | 481 | 494 | 507 | |
| 40 | 520 | 533 | 546 | 559 | 572 | 585 | 598 | 611 | 624 | 637 | |
| 50 | 650 | 663 | 676 | 689 | 702 | 715 | 728 | 741 | 754 | 767 | |
| 60 | 780 | 793 | 806 | 819 | 832 | 845 | 858 | 871 | 884 | 897 | |
| 70 | 910 | 923 | 936 | 949 | 962 | 975 | 988 | 1001 | 1014 | 1027 | |
| 80 | 1040 | 1053 | 1066 | 1079 | 1092 | 1105 | 1118 | 1131 | 1144 | 1157 | |
| 90 | 1170 | 1183 | 1196 | 1209 | 1222 | 1235 | 1248 | 1261 | 1274 | 1287 | |
| 0 | 0 | 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 | 14 |
| 10 | 140 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | |
| 20 | 280 | 294 | 308 | 322 | 336 | 350 | 364 | 378 | 392 | 406 | |
| 30 | 420 | 434 | 448 | 462 | 476 | 490 | 504 | 518 | 532 | 546 | |
| 40 | 560 | 574 | 588 | 602 | 616 | 630 | 644 | 658 | 672 | 686 | |
| 50 | 700 | 714 | 728 | 742 | 756 | 770 | 784 | 798 | 812 | 826 | |
| 60 | 840 | 854 | 868 | 882 | 896 | 910 | 924 | 938 | 952 | 966 | |
| 70 | 980 | 994 | 1008 | 1022 | 1036 | 1050 | 1064 | 1078 | 1092 | 1106 | |
| 80 | 1120 | 1134 | 1148 | 1162 | 1176 | 1190 | 1204 | 1218 | 1232 | 1246 | |
| 90 | 1260 | 1274 | 1288 | 1302 | 1316 | 1330 | 1344 | 1358 | 1372 | 1386 | |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 0 | 0 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 15 |
| 10 | 150 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | |
| 20 | 300 | 315 | 330 | 345 | 360 | 375 | 390 | 405 | 420 | 435 | |
| 30 | 450 | 465 | 480 | 495 | 510 | 525 | 540 | 555 | 570 | 585 | |
| 40 | 600 | 615 | 630 | 645 | 660 | 675 | 690 | 705 | 720 | 735 | |
| 50 | 750 | 765 | 780 | 795 | 810 | 825 | 840 | 855 | 870 | 885 | |
| 60 | 900 | 915 | 930 | 945 | 960 | 975 | 990 | 1005 | 1020 | 1035 | |
| 70 | 1050 | 1065 | 1080 | 1095 | 1110 | 1125 | 1140 | 1155 | 1170 | 1185 | |
| 80 | 1200 | 1215 | 1230 | 1245 | 1260 | 1275 | 1290 | 1305 | 1320 | 1335 | |
| 90 | 1350 | 1365 | 1380 | 1395 | 1410 | 1425 | 1440 | 1455 | 1470 | 1485 | |
| 0 | 0 | 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 | 16 |
| 10 | 160 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | |
| 20 | 320 | 336 | 352 | 368 | 384 | 400 | 416 | 432 | 448 | 464 | |
| 30 | 480 | 496 | 512 | 528 | 544 | 560 | 576 | 592 | 608 | 624 | |
| 40 | 640 | 656 | 672 | 688 | 704 | 720 | 736 | 752 | 768 | 784 | |
| 50 | 800 | 816 | 832 | 848 | 864 | 880 | 896 | 912 | 928 | 944 | |
| 60 | 960 | 976 | 992 | 1008 | 1024 | 1040 | 1056 | 1072 | 1088 | 1104 | |
| 70 | 1120 | 1136 | 1152 | 1168 | 1184 | 1200 | 1216 | 1232 | 1248 | 1264 | |
| 80 | 1280 | 1296 | 1312 | 1328 | 1344 | 1360 | 1376 | 1392 | 1408 | 1424 | |
| 90 | 1440 | 1456 | 1472 | 1488 | 1504 | 1520 | 1536 | 1552 | 1568 | 1584 | |
| 0 | 0 | 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 17 |
| 10 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | |
| 20 | 340 | 357 | 374 | 391 | 408 | 425 | 442 | 459 | 476 | 493 | |
| 30 | 510 | 527 | 544 | 561 | 578 | 595 | 612 | 629 | 646 | 663 | |
| 40 | 680 | 697 | 714 | 731 | 748 | 765 | 782 | 799 | 816 | 833 | |
| 50 | 850 | 867 | 884 | 901 | 918 | 935 | 952 | 969 | 986 | 1003 | |
| 60 | 1020 | 1037 | 1054 | 1071 | 1088 | 1105 | 1122 | 1139 | 1156 | 1173 | |
| 70 | 1190 | 1207 | 1224 | 1241 | 1258 | 1275 | 1292 | 1309 | 1326 | 1343 | |
| 80 | 1360 | 1377 | 1394 | 1411 | 1428 | 1445 | 1462 | 1479 | 1496 | 1513 | |
| 90 | 1530 | 1547 | 1564 | 1581 | 1598 | 1615 | 1632 | 1649 | 1666 | 1683 | |
| 0 | 0 | 18 | 36 | 54 | 72 | 90 | 108 | 126 | 144 | 162 | 18 |
| 10 | 180 | 198 | 216 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | |
| 20 | 360 | 378 | 396 | 414 | 432 | 450 | 468 | 486 | 504 | 522 | |
| 30 | 540 | 558 | 576 | 594 | 612 | 630 | 648 | 666 | 684 | 702 | |
| 40 | 720 | 738 | 756 | 774 | 792 | 810 | 828 | 846 | 864 | 882 | |
| 50 | 900 | 918 | 936 | 954 | 972 | 990 | 1008 | 1026 | 1044 | 1062 | |
| 60 | 1080 | 1098 | 1116 | 1134 | 1152 | 1170 | 1188 | 1206 | 1224 | 1242 | |
| 70 | 1260 | 1278 | 1296 | 1314 | 1332 | 1350 | 1368 | 1386 | 1404 | 1422 | |
| 80 | 1440 | 1458 | 1476 | 1494 | 1512 | 1530 | 1548 | 1566 | 1584 | 1602 | |
| 90 | 1620 | 1638 | 1656 | 1674 | 1692 | 1710 | 1728 | 1746 | 1764 | 1782 | |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
С лучшей бесплатной игрой учится очень быстро. Проверьте это сами!
Проверьте это сами!
Учить таблицу умножения — игра
Попробуйте нашу обучающую электронную игру. Используя её, вы уже завтра сможете решать математические задачи в классе у доски без ответов, не прибегая к табличке, чтобы умножить числа. Стоит только начать играть, и уже минут через 40 будет отличный результат. А для закрепления результата тренируйтесь несколько раз, не забывая о перерывах. В идеале – каждый день (сохраните страницу, чтобы не потерять). Игровая форма тренажера подходит как для мальчиков, так и для девочек.
Смотрите ниже шпаргалки в полной форме.
Умножение прямо на сайте (онлайн)
*
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 | 120 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 | 126 | 135 | 144 | 153 | 162 | 171 | 180 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 | 130 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 | 140 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 |
| 17 | 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 18 | 36 | 54 | 72 | 90 | 108 | 126 | 144 | 162 | 180 | 198 | 216 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 19 | 38 | 57 | 76 | 95 | 114 | 133 | 152 | 171 | 190 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
Как умножать числа столбиком (видео по математике)
Чтобы потренироваться и быстро выучить, можно также попробовать умножать числа столбиком.
Умножение двузначных чисел | Онлайн-тренажёр
Упражнение считается выполенным после 7 правильных ответов
Норма выполнения упражнения — 3 минуты
Для успешного выполнения упражнения ознакомьтесь с теорией и проработайте предыдущие уроки
Умножение двузначных чисел | Теория
В общем случае умножение в уме двузначных чисел удобно выполнять в следующем порядке:
- за базовое (первое или находящееся слева) число примите число с наибольшей второй цифрой;
- умножьте базовое (первое) двузначное число на десятки другого (второго) двузначного числа;
- умножьте базовое (первое) двузначное число на единицы другого (второго) двузначного числа;
- сложите два результата.
Задача: 42 x 36
1) 36 x 42 (число 36 принято за базовое (первое) число, так как 6>1)
2) 36 x 40 = (30+6) x 4 x 10
30 x 4 = 120; 6 x 4 = 24; 120 + 24 = 144; 144 x 10 = 1440*
3) 36 x 2 = (30+6) x 2
30 x 2 = 60; 6 x 2 = 12; 60 + 12 = 72
4) 1440 + 72 = 1752
Задача: 47 x 52
1) 47 x 52 (число 47 принято за базовое (первое) число, так как 7>2)
2) 47 x 50 = 2350
4) 2350 + 94 = 2444
Если одно из чисел заканчивается на 9, то задачу удобнее решать в следующем порядке:
- за второе (находящееся справа) число примите число, заканчивающееся на 9;
- округлите второе число в большую сторону до десятков, прибавив к нему 1;
- умножьте первое число на округлённое второе число;
- вычтите из результата пункта 3 первое число.

Задача: 39 x 56
1) 56 x 39 (число 39 принято за второе (находящееся справа) число, так как оно заканчивается на 9)
2) 56 x 39(40-1)
3) 56 x 40 = (50+6) x 4 x 10
50 x 4 = 200; 6 x 4 = 24; 200 + 24 = 224; 224 x 10 = 2240
4) 2240 — 56 = 2184
Если одно из двузначных чисел равно 11, то решить такую задачу будет намного проще, если вы воспользуетесь методикой, изложенной в Уроке 1.
Во многих случаях решение задачи умножения двузначных чисел в уме намного упрощается, если воспользоваться методом факторизации.
Факторизация — это преобразование числа в произведение более простых чисел. Например, число 24 можно преобразовать в произведение 8 и 3 (24 = 8 x 3) или 6 и 4 (24 = 6 x 4). Число 24 также можно представить в виде произведения 12 и 2 (24 = 12 x 2), но при выполнении арифметических операций в уме удобнее иметь дело с однозначными числами.
Отдельные двузначные числа также можно представить в виде произведения трёх однозначных чисел. Например, 84 = 7 x 6 x 2 = 7 x 4 x 3.
Например, 84 = 7 x 6 x 2 = 7 x 4 x 3.
Решим задачу умножения с помощью факторизации.
Задача: 34 x 42
Факторизация числа 24 даёт 8 и 3 или 6 и 4. Для решения задачи представим число 24 в виде произведения 6 и 4, но, если вам удобнее, вы можете выбрать произведение 8 и 3.
Умножаем первое число на 6, после чего умножаем результат на 4:
34 x 6 = 204
204 x 4 = 816
Чтобы знать, какие из двузначных чисел поддаются факторизации, необходимо тщательно изучить таблицу умножения. Можно выписать все двузначные числа, поддающиеся факторизации, с указанием возможных способов их факторизации.
Если оба из перемножаемых двузначных чисел поддаются факторизации, то в большинстве случае удобнее факторизовать меньшее число.
Задача: 36 x 72
Число 36 можно представить в виде произведения 6 и 6, а число 72 — в виде произведения 9 и 8.
Так как 36
72 x 6 = 432
432 x 6 = 2592
Пример с факторизацией на три числа.
Задача: 57 x 75
В случае, если одно из перемножаемых двузначных чисел состоит из одинаковых цифр (22, 33, 44 и т. д.), то его удобнее факторизовать на 11 и 2, 3, 4 и т.д.), так как умножение на 11 не представляет труда, как было показано в уроке 11.
д.), то его удобнее факторизовать на 11 и 2, 3, 4 и т.д.), так как умножение на 11 не представляет труда, как было показано в уроке 11.
Задача: 81 x 44
Если числа близки по значению с круглым числом, то при их перемножении в уме удобно пользоваться следующими формулами: (C+a)(C+b) = (C+a+b)C+ab; (C-a)(C-b) = (C-a-b)C+ab; (C+a)(C-b) = (C+a-b)C-ab**, где “C” – близкое к двум перемножаемым числам круглое число, а “а” и “b” – это разницы между перемножаемыми числами и круглым числом.
Задача: 67 x 64
(60 + 7) x (60 + 4) = (60 + 7 + 4) x 60 + 7 x 4 = 71 x 60 + 28 = 4260 + 28 = 4288
Задача: 39 х 38
(40 — 1) x (40 — 2) = (40 — 1 — 2) x 40 + 1 x 2 = 37 x 40 + 2 = 1480 + 2 = 1482
Задача: 41 x 38
(40 + 1) x (40 – 2) = (40 + 1 – 2) x 40 + 1 x 2 = 39 x 40 — 2 = 1558
Умножение двузначных чисел, первые цифры (десятки) которых равны, а вторые цифры (единицы) дают в сумме 10, удобнее производить в следующем порядке:
- умножьте первую цифру двузначных чисел на эту же цифру, увеличенную на единицу;
- перемножить вторые цифры двузначных чисел;
- поместите один за другим результаты пункта 1 и пункта 2.

Задача: 76 x 74
Не расстраивайтесь и не сдавайтесь, если на первых порах у вас возникнут трудности с умножением двузначных чисел. Для уверенного выполнения такой операции в уме необходима практика, а также творческий подход.
* Для запоминания в уме промежуточных результатов вычислений можете применять мнемотехники, основанные на ассоциации цифр с образами.
** Доказательства формул путём преобразования: (C+a)(C+b) = (C+a)C+(C+a)b = C 2 +Ca+Cb+ab = (C+a+b)C+ab; (C-a)(C-b) = (C-a)C-(C-a)b = C 2 -Ca-Cb+ab = (C-a-b)C+ab; (C+a)(C-b) = (C+a)C-(C+a)b = C 2 +Ca-Cb-ab = (C+a-b)C-ab.
*** Доказательство метода: согласно формуле, применяемой в предудущем методе (C+a)(C+b) = (C+a+b)C+ab; так как a+b=10, то (C+a)(C+b) = (C+10)C+ab; поскольку произведение двузначных круглых чисел С и С+10 даёт число с двумя нулями на конце, а произведение a и b даёт двузначное число, то для нахождения суммы этих двух выражений достаточно поставить произведение a и b вместо двух последних нулей первого выражения.
УМНОЖЕНИЕ СТОЛБИКОМ ДВУЗНАЧНЫХ ЧИСЕЛ — Математика и Английский
Занимательная математика умножение двузначных чисел
Программа — тренажер по математике для закрепления навыков Умножения столбиком двузначных чисел.
Предлагается 20 примеров для решения. Два случайных двузначных числа нужно умножить столбиком.
Для перехода к началу решения примеров нажимаем кнопку «START»
В левой верхней части страницы тренажера по математике указывается число примеров, которые осталось решить.
В правой части страницы пример, который нужно решить. В левой части этот же пример записан столбиком.
Клавишами управления курсором передвигаемся вверх/вниз/вправо/влево по клеточками. Нажимаем на клавиатуре кнопки 0-9 и вводим промежуточные ответы и итоговый ответ.
В случае, если пример решен верно, начисляется 5 очков. Если дать правильный ответ три раза подряд — начисляется бонус.
За неправильный ответ вычитается 3 очка.
Ошибки, допущенные в ходе вычисления, исправляются красным цветом. Сразу будет видно на каком этапе вычислений допущена ошибка.
В итоговой страничке тренажера по математике представлены результаты: количество очков, ошибок, бонусов.
Если при Умножении столбиком были допущены ошибки, ниже будут перечислены примеры, в которых они были.
В левой части этот же пример записан столбиком.
Cool-kid. ru
23.08.2017 10:59:09
2017-08-23 10:59:09
Источники:
Https://cool-kid. ru/matematika/umnozhenie-dvuznachnykh-chisel-stolbikom
Ровочная ение двузначных чисел | Методическая разработка (3 класс) на тему: | Образовательная социальная сеть » /> » /> .keyword { color: red; }
Занимательная математика умножение двузначных чисел
В пакете 25 шоколадных конфет, а карамелек в 3 раза больше. На сколько меньше шоколадных конфет в пакете, чем карамелек?
Найди значение выражения:
81 : 9 ∙ 100 – (140 + 20) : 8 =
Проверь, верно ли равенство:
607 – 438 + 584 = 753
В саду собрали 20 корзин белой смородины, а красной в 4 раза больше. На сколько больше собрали красной смородины, чем белой?
На сколько больше собрали красной смородины, чем белой?
Найди значение выражения:
20 ∙ 10 : 5 + (290 – 50) : 6 =
Проверь, верно ли равенство:
459 + 107 – 264 = 301
17 ∙ 13 = 23 ∙ 24 = 18 ∙ 24 =
78 ∙ 12 = 63 ∙ 14 = 26 ∙ 40 =
5.Длина ломаной линии, состоящей из трёх звеньев, равна 17 см. Построй ломаную линию. Запиши длину каждого её звена.
15 ∙ 29 = 59 ∙ 11 = 35 ∙ 23 =
52 ∙ 17 = 16 ∙ 48 = 38 ∙ 30 =
5.Длина ломаной линии, состоящей из трёх звеньев, равна 16 см. Построй ломаную линию. Запиши длину каждого её звена.
По теме: методические разработки, презентации и конспекты
Состав двузначных чисел(Математика 2 класс)
Формировать умение представлять двузначные числа в виде суммы разрядных слагаемых, развивать вычислительный навык; логическое мышление; навыков решения задач; закрепить.
План — конспект урока Разработка урока математики (2 класс УМК ПНШ) «Сравнение двузначных чисел. Самостоятельная работа №3 по теме «Двузначные и однозначные числа и действия над ними».

План — конспект урока математики (2 класс УМК ПНШ) по теме «Сравнение двузначных чисел. Самостоятельная работа №3 по теме «Двузначные и однозначные числа и действия над ними». Этот материал поможет на.
Конспект по математике 3 класс. Самостоятельная работа. Умножение на двузначное число столбиком.
Предмет: математикаКласс: 3-2Тема урока: Самостоятельная работа. Умножение на двузначное число столбикомЦели урока: составить алгоритм умножения на двузначное число столбиком; совершенствовать вычисли.
2 класс «Чтение и запись двузначных чисел. Сравнение чисел в пределах 100»
Данный материал поможет учителю отработать материал по теме: «Чтение и запись двузначных чисел. Сравнение чисел в пределах 100».
Конспект урока математики 2 класс Тема урока: Состав двузначных чисел 11, 12 из двух однозначных чисел с переходом через десяток.
Цель урока: Создание условий для закрепления знаний обучающихся по данной теме. Задачи урока:Образовательные:-развивать навыки устного счёта;-закрепить знания нумерации в пределах.
Контрольная работа «умножение и деление круглых чисел » 3 класс
Контрольная работа «Умножение и деление круглых чисел» 3 класс.
Письменный прием умножения двузначных чисел на двузначное число
Предметная область: математика, УМК « Школа России» Тип урока: урок «открытия» новых знаний.
Цель урока Создание условий для закрепления знаний обучающихся по данной теме.
Nsportal. ru
07.08.2020 18:25:02
2020-08-07 18:25:02
Источники:
Https://nsportal. ru/nachalnaya-shkola/materialy-dlya-roditelei/2012/04/12/matematikatrenirovochnaya-rabotaumnozhenie
Умножение двузначных чисел | Ментальная арифметика онлайн бесплатно » /> » /> .keyword { color: red; }
Занимательная математика умножение двузначных чисел
В общем случае умножение в уме двузначных чисел удобно выполнять в следующем порядке:
за базовое (первое или находящееся слева) число примите число с наибольшей второй цифрой; умножьте базовое (первое) двузначное число на десятки другого (второго) двузначного числа; умножьте базовое (первое) двузначное число на единицы другого (второго) двузначного числа; сложите два результата.
1) 36 x 42 (число 36 принято за базовое (первое) число, так как 6>1)
2) 36 x 40 = (30+6) x 4 x 10
30 x 4 = 120; 6 x 4 = 24; 120 + 24 = 144[120+20=140;140+4=144]; 144 x 10 = 1440*
3) 36 x 2 = (30+6) x 2
30 x 2 = 60; 6 x 2 = 12; 60 + 12 = 72[60+10=70;70+2=72]
4) 1440 + 72 = 1752 [1440+70=1510;1510+2=1512]
1) 47 x 52 (число 47 принято за базовое (первое) число, так как 7>2)
2) 47 x 50 = 2350
4) 2350 + 94 = 2444
Если одно из чисел заканчивается на 9, то задачу удобнее решать в следующем порядке:
за второе (находящееся справа) число примите число, заканчивающееся на 9; округлите второе число в большую сторону до десятков, прибавив к нему 1; умножьте первое число на округлённое второе число; вычтите из результата пункта 3 первое число.
1) 56 x 39 (число 39 принято за второе (находящееся справа) число, так как оно заканчивается на 9)
3) 56 x 40 = (50+6) x 4 x 10
50 x 4 = 200; 6 x 4 = 24; 200 + 24 = 224; 224 x 10 = 2240
4) 2240 — 56 = 2184[2240-50=2190;2190-6=2184]
Если одно из двузначных чисел равно 11, то решить такую задачу будет намного проще, если вы воспользуетесь методикой, изложенной в Уроке 1.
Во многих случаях решение задачи умножения двузначных чисел в уме намного упрощается, если воспользоваться методом факторизации.
Факторизация — это преобразование числа в произведение более простых чисел. Например, число 24 можно преобразовать в произведение 8 и 3 (24 = 8 x 3) или 6 и 4 (24 = 6 x 4). Число 24 также можно представить в виде произведения 12 и 2 (24 = 12 x 2), но при выполнении арифметических операций в уме удобнее иметь дело с однозначными числами.
Отдельные двузначные числа также можно представить в виде произведения трёх однозначных чисел. Например, 84 = 7 x 6 x 2 = 7 x 4 x 3.
Решим задачу умножения с помощью факторизации.
Факторизация числа 24 даёт 8 и 3 или 6 и 4. Для решения задачи представим число 24 в виде произведения 6 и 4, но, если вам удобнее, вы можете выбрать произведение 8 и 3.
Умножаем первое число на 6, после чего умножаем результат на 4:
34 x 6 = 204[30×6=180;4×6=24;180+24=204]
204 x 4 = 816[200×4=800;4×4=16;800+16=816]
Чтобы знать, какие из двузначных чисел поддаются факторизации, необходимо тщательно изучить таблицу умножения. Можно выписать все двузначные числа, поддающиеся факторизации, с указанием возможных способов их факторизации.
Можно выписать все двузначные числа, поддающиеся факторизации, с указанием возможных способов их факторизации.
Если оба из перемножаемых двузначных чисел поддаются факторизации, то в большинстве случае удобнее факторизовать меньшее число.
Число 36 можно представить в виде произведения 6 и 6, а число 72 — в виде произведения 9 и 8.
Так как 36 2 +Ca+Cb+ab = (C+a+b)C+ab; (C-a)(C-b) = (C-a)C-(C-a)b = C 2 — Ca-Cb+ab = (C-a-b)C+ab; (C+a)(C-b) = (C+a)C-(C+a)b = C 2 +Ca-Cb-ab = (C+a-b)C-ab.
*** Доказательство метода: согласно формуле, применяемой в предудущем методе (C+a)(C+b) = (C+a+b)C+ab; так как a+b=10, то (C+a)(C+b) = (C+10)C+ab; поскольку произведение двузначных круглых чисел С и С+10 даёт число с двумя нулями на конце, а произведение a и b даёт двузначное число, то для нахождения суммы этих двух выражений достаточно поставить произведение a и b вместо двух последних нулей первого выражения.
Умножение двузначных чисел Ментальная арифметика онлайн.
Drdo. ru
ru
12.08.2019 1:50:55
2019-08-12 01:50:55
Источники:
Https://drdo. ru/mentalnaya-arifmetika/umnozhenie-dvuznachnyh-chisel/
Как научиться быстро считать в уме любые числа: техники устного счета
Устный счет – занятие, которым в наше время себя утруждает все меньшее количество людей. Гораздо проще достать калькулятор на телефоне и вычислить любой пример.
Но так ли это на самом деле? В этой статье мы представим математические лайфхаки, которые помогут научиться быстро складывать, вычитать, умножать и делить числа в уме. Причем оперируя не единицами и десятками, а минимум двухзначными и трехзначными числами.
После освоения методов из этой статьи идея лезть в телефон за калькулятором уже не покажется такой хорошей. Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).
Итак, добро пожаловать в увлекательный мир вычислений! Мы собрали советы от наших авторов о том, как улучшить устный счет и стать математическим героем и гением. Кстати, если вам интересна математика, вы можете почитать статью «Пределы для чайников» в нашем блоге.
Кстати, если вам интересна математика, вы можете почитать статью «Пределы для чайников» в нашем блоге.
Предупреждаем! Если вы обычный человек, а не вундеркинд, то для развития навыка счета в уме понадобятся тренировки и практика, концентрация внимания и терпение. Сначала все может получаться медленно, но потом дело пойдет на лад, и вы сможете быстро считать в уме любые числа.
Гаусс и устный счет
Карл Фридрих Гаусс
Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.
По его собственным словам, он научился считать раньше, чем говорить. Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.
В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.
До самой смерти большую часть вычислений Гаусс производил в уме.
Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.
Сложение чисел в уме
Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.
Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.
Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14
Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14
Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.
Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6. Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:
356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084
Вычитание чисел в уме
Вычитание чисел тоже будет даваться легко. Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.
Например, сколько будет 528-321? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1.
Теперь считаем: 528-300-20-1=228-20-1=208-1=207
Попробуйте визуализировать процессы сложения и вычитания. В школе всех учили считать в столбик, то есть сверху вниз. Один из способов перестроить мышление и ускорить счет – считать не сверху вниз, а слева направо, разбивая числа на разрядные части.
Умножение чисел в уме
Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.
8*4=8+8+8+8=32
Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.
К тому же учить там, по сути, нечего.
Таблица умножения
Умножение многозначных чисел на однозначные
Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.
528=500+20+8
528*6=500*6+20*6+8*6=3000+120+48=3168
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Умножение двузначных чисел
Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.
Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2
28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896
Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.
Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.
- 79*50=(70+9)*50=3500+450=3950
- 79*7=(70+9)*7=490+63=553
- 3950+553=4503
Умножение на 11
Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.
Чтобы умножить двузначное число на 11, две цифры числа складываем друг с другом, и получившуюся сумму вписываем между цифрами исходного числа. Получившееся в итоге трехзначное число — результат умножения исходного числа на 11.
Проверим и умножим 54 на 11.
- 5+4=9
- 54*11=594
Возьмите любое двузначное число, умножьте его на 11 и убедитесь сами — эта хитрость работает!
Возведение в квадрат
С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.
Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.
Проверим! Возведем в квадрат число 75.
- 7*8=56
- 5*5=25
- 75*75=5625
Раньше все считали без калькуляторов
Деление чисел в уме
Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.
Деление на однозначное число
При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.
Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600. Представим пример в виде:
6144:8=(5600+544):8=700+544:8
Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:
Имеем:
544:8=(480+64):8=60+64:8
Осталось разделить 64 на 8 и получить результат, сложив все результаты деления
64:8=8
6144:8=700+60+8=768
Деление на двузначное число
При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.
При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.
Например, умножим 1325 на 656. По правилу, последняя цифра в получившемся числе будет 0, так как 5*6=30. Действительно, 1325*656=869200.
Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.
Сколько будет 4424:56?
Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.
56*80=4480
Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления может быть либо число 74, либо 79. Проверяем:
79*56=4424
Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.
Картина Н.П. Богданова-Бельского «Устный счёт. В народной школе С. А. Рачинского»
Полезные советы
В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:
- Не забывайте тренироваться каждый день;
- не бросайте тренировки, если результат не приходит так быстро, как хотелось бы;
- скачайте мобильное приложение для устного счета: так вам не придется самостоятельно придумывать себе примеры;
- почитайте книги по методикам быстрого устного счета. Существуют разные техники устного счета, и вы сможете овладеть той, которая лучше всего подходит именно вам.
Польза устного счета неоспорима. Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!
Как умножать двузначные числа: стратегии и идеи для игр
Когда я заканчивал учебный год с моим третьеклассником, мы потратили некоторое время, работая над умножением и пытаясь закрепить факты умножения. Но наряду со знанием того, что означает умножение, и важностью знания фактов, я также хотел, чтобы он увидел, как мы можем распространить это знание на , умножая двузначные числа, и дальше . Хотя вид таких больших задач на умножение может пугать, это не обязательно. Узнать простые, но мощные стратегии для того, как с легкостью умножать двузначные числа . Затем вы можете применить эти идеи к еще большим числам и умножению десятичных дробей.
Но наряду со знанием того, что означает умножение, и важностью знания фактов, я также хотел, чтобы он увидел, как мы можем распространить это знание на , умножая двузначные числа, и дальше . Хотя вид таких больших задач на умножение может пугать, это не обязательно. Узнать простые, но мощные стратегии для того, как с легкостью умножать двузначные числа . Затем вы можете применить эти идеи к еще большим числам и умножению десятичных дробей.
* Обратите внимание : Этот пост содержит партнерские ссылки, которые поддерживают работу этого сайта. Подробное описание читайте здесь.*
Как умножать двузначные числа: используйте модель площадиМой любимый метод умножения двузначных цифр — это нарисовать модель площади
0004 . Это полезно, потому что дает наглядное представление о том, что представляет собой проблема.
Кроме того, впоследствии его можно будет применить к более сложным задачам, включая многочлены умножения в алгебре.
Один из способов представить умножение как площадь прямоугольника. Это означает, что в любой заданной задаче на умножение вы можете думать о каждом множителе как о длине и ширине прямоугольника.
Допустим, мы хотим умножить 24 x 35. Вы можете начать с рисования прямоугольника шириной 24 и длиной 35.
В этот момент вы можете подумать: «Хорошо, отлично. Теперь это коробка, но как, черт возьми, это поможет мне ее решить??»
Ну, тогда вы можете разбить коробку на части , которые легче решить, как будто вы раскрашиваете область по одной небольшой секции .
Например, я могу разделить ширину на 20 и 4, затем я могу разделить 35 на 30 и 5, например:
Теперь у меня есть меньшие прямоугольные секции, которые мне легче умножать. Например, начиная с самого большого прямоугольника, мы имеем 30 х 20 = 600:9.0007
Затем я могу продолжить с остальными ячейками:
30 х 4 = 120,
И 5 х 20 = 100,
И, наконец, 5 х 4 = 20.
Теперь, когда я нашел площадь каждого маленького участка, я могу сложить их вместе , чтобы найти общую площадь (или окончательное решение исходной задачи умножения двузначного числа: 24 x 35): 600 + 120 + 100 + 20 = 840
Преимущества использования модели площадиЭто наглядное изображение также полезно, поскольку оно показывает, что умножение больших чисел дает более крупные ответы, что видно на рисунке (большие участки всего прямоугольника).
Другая замечательная особенность этого метода заключается в том, что дети могут разбить исходный прямоугольник на миллионами различных способов . Они могут делать то, что имеет для них наибольший смысл, или использовать любые задачи на умножение, которые им будет легче всего решить в уме.
Нет «правильного» или «неправильного» пути. Это дает детям свободу разобраться в проблеме самостоятельно и исследовать ее по-своему.
И если вы видите, что они склонны всегда выбирать одну и ту же стратегию (например, разделение десятков и единиц), попросите их решить ее другим способом. Это заставит их подумайте о других способах декомпозиции чисел , которые могли бы работать лучше или сделать решение проблемы проще и эффективнее.
Это заставит их подумайте о других способах декомпозиции чисел , которые могли бы работать лучше или сделать решение проблемы проще и эффективнее.
Кроме того, это дает им дополнительную практику умножения. 😉
Чтобы узнать больше о настройке и решении с использованием моделей площадей, см. эту статью и скачайте бесплатный шаблон.
Как умножать двузначные числа: использовать разрядное значение для нахождения частичных произведенийЕще одна полезная стратегия, которую могут использовать дети, не обученные формальному алгоритму, — использовать 9.0003 поместите значение, чтобы разбить задачу на части и решить ее по частям .
Это похоже на использование модели области, но не включает визуал.
Это может быть особенно полезно, когда одно из чисел включает младшие, легко умножаемые цифры, такие как 2 или 3.
Например, предположим, что вы хотите умножить 78 x 12.
Вместо этого вы можете представить это как (78 х 10) + (78 х 2).
Умножить на десять несложно, и это даст вам 780.
Умножение на 2 равно удвоению, поэтому 78 x 2 = 156
Затем вы можете просто сложить частичные произведения вместе , чтобы получить 780 + 156 = 936
Вот еще один пример: 48 x 14
В этом примере мы можем думать об этом как (48 x 10) + (48 x 4)
Первая часть проста, давая нам 48 x 10 = 480
Умножение 48 x 4 не так просто сделать в уме, но затем его можно разбить на 48 x 2, а затем снова x 2.
Другими словами, 48 х 2 = 96 и тогда 96 х 2 = 192
Тогда снова мы можем сложите частичные произведения вместе , чтобы получить 480 + 192 = 672
Как умножать двузначные числа: используя формальный алгоритмпосредством задач умственного вычисления вы можете ввести формальный алгоритм .
Я предлагаю поделиться этим последним, потому что, если дети уже хорошо понимают, как работать с двузначными числами и умножать их, алгоритм не так страшен.
Если на самом деле, это, скорее всего, будет иметь смысл для большинства детей. Потому что теперь это не похоже на случайные правила, которым нужно следовать и помнить, а на удобный способ денди отслеживать то, что они раньше делали в своей голове.
Итак, если вы не знакомы, вот пошаговый пример умножения двузначных цифр с использованием традиционного алгоритма . Допустим, теперь мы хотим умножить 34 x 62.
Шаг первый: выровняйте все цифрыСначала выровняйте все числа в соответствии с их разрядностью.
Шаг второй: Умножьте на цифру единицЗатем начните с , умножая каждую цифру верхнего числа на цифру единиц (в данном случае 2). В этом примере у нас есть 4 x 2 = 8 (запишите это в единицах), а затем 3 (что на самом деле означает 30) x 2 = 6 (что на самом деле означает 60). Затем вы записываете 6 в разряде десятков.
Шаг третий: добавьте нулевой заполнитель Затем поместите ноль под столбцом единиц , когда вы начнете умножать 34 на 6 (что на самом деле означает 60).
Причина этого нуля в том, что вы не просто умножаете 34 на 6. Вы умножаете 34 x 60 . Другими словами, кратно десяти , поэтому мы знаем, что должны иметь этот ноль там .
Шаг четвертый: Умножение на десяткиЗатем вы можете умножить каждую цифру на 6 .
Это дает 6 х 4 (что на самом деле 60 х 4) = 24 (что на самом деле 240).
Поскольку это на самом деле представляет 240, 4 идет в столбце десятков в нашем решении, а затем мы «переносим» 2, то есть помещаем его в столбец десятков вверху.
Я обычно записываю это как «+2» , а не просто как 2, потому что часто дети забывают, должны ли они сложить это или умножить.
Затем мы умножаем 3 x 6 = 18 и к добавляем 2 , чтобы получить 20 (что на самом деле представляет собой 2000, потому что мы на самом деле умножили 30 x 60 и добавили к нему еще 200).
Следовательно, мы получаем 2040 во второй строке нашего ответа.
Затем, как и в случае с частичными произведениями, мы складываем вместе две строки решений , чтобы получить 68 + 2040 = 2,108
Когда я учу своих детей В этой процедуре я обычно записываю каждый шаг как частичный продукт по мере решения проблемы. Это позволяет им увидеть, откуда берутся все числа, почему мы добавляем ноль и почему мы складываем строки ответов вместе для окончательного ответа.
Затем я позволяю им практиковаться, используя любой метод или стратегию, которые наиболее эффективны и удобны для них!
Умножение двузначных чисел: идеи для игрЕсли вы хотите, чтобы ваши дети попрактиковались в умножении двузначных чисел, вот несколько игр, которые могут вам понравиться.
- Распечатанные настольные игры для тренировки двузначного умножения
- Многоразрядное умножение страниц вырезания и вставки
- Настольные игры с многозначным умножением
И обязательно ознакомьтесь с этой стратегией, которая поможет детям понять и увидеть закономерности при умножении больших чисел: Как умножать большие числа с помощью таблиц
Надеюсь, вы нашли это полезным и, возможно, даже узнали новых способа умножения двузначных чисел. числа !
числа !
Математические идеи никогда не заканчиваются
Если вам понравился этот пост, вам понравится быть частью сообщества Math Geek Mama! Каждую неделю я отправляю электронное письмо с забавными и увлекательными математическими идеями, бесплатными ресурсами и специальными предложениями. Присоединяйтесь к более чем 163 000 читателей, поскольку мы помогаем каждому ребенку добиться успеха и преуспеть в математике! ПЛЮС, получи мою БЕСПЛАТНУЮ электронную книгу, 5 математических игр, в которые можно играть СЕГОДНЯ , в подарок вам !
Завершите игру «Умножение двух двузначных чисел» — Math Games
Завершите игру «Умножение двух двузначных чисел» — Math Games — SplashLearnГлавная > Игры > Математические игры > Завершите игру «Умножение двух двузначных чисел»
.Помогите своему ребенку научиться летать, научившись выполнять умножение двух двузначных чисел.

Играть в игру
Присвоить классу
ПРЕДМЕТЫ И ТЕМЫ
Узнайте больше о Завершите игру «Умножение двух двузначных чисел»
Проблемы с умножением можно легко преодолеть, если учащиеся будут практиковать это понятие весело и увлекательно! Игра требует, чтобы учащиеся выполнили ряд сложных задач, и в процессе учащиеся изучают концепцию умножения. Этот набор задач имеет дело с двумя двузначными числами; студенты получат возможность работать с различными наборами по пути.
Исследуйте удивительные игры на Умножение двузначных чисел на двузначные
Просмотреть все 12 игр
Умножение
Умножение двузначных чисел с использованием модели площади
Используйте свои навыки умножения, чтобы умножить двузначные числа с использованием модели площади.
ПОДРОБНЕЕ
Умножение
Игра «Умножение двузначных чисел»
Добавьте больше стрелок в математический колчан вашего ребенка, умножая двузначные числа.

ПОСМОТРЕТЬ ПОДРОБНОСТИ
Умножение
Игра «Найди произведение путем умножения двузначных чисел»
Используй свои математические способности, чтобы найти произведение путем умножения двузначных чисел.
ПОДРОБНЕЕ
Умножение
Игра «Умножение двузначных чисел и составление произведения»
Дети должны умножить двузначные числа и составить произведение.
ПОДРОБНЕЕ
Умножение
Введите ответ и завершите игру на умножение
Дети должны ввести ответ, чтобы завершить умножение.
ПОДРОБНЕЕ
Умножение
Выберите произведение двузначных чисел
Окунитесь в безумие математической мультивселенной, исследуя, как выбрать произведение двузначных чисел.
ПОДРОБНЕЕ
Умножение
Сопоставьте продукт с его игрой выражения умножения
Проявите себя в мире математики, сопоставив произведение с его выражением умножения.

ПОДРОБНЕЕ
Умножение
Игра «Выбери недостающую цифру в произведении»
Насладись чудом математической мультивселенной, исследуя, как выбрать недостающую цифру в произведении.
ПОДРОБНЕЕ
Умножение
Завершите игру «Умножение двух двузначных чисел»
Помогите своему ребенку взлететь, научившись выполнять умножение двух двузначных чисел.
ПОСМОТРЕТЬ ПОДРОБНОСТИ
Умножение
Умножение двух двузначных чисел с использованием разрядной игры
Проявите себя в мире математики, научившись умножать два двузначных числа с помощью разрядных значений.
ПОДРОБНЕЕ
Умножение
Игра «Определи недостающую цифру в произведении»
Раскрой мудрость математики, научившись определять недостающую цифру в произведении.

ПОДРОБНЕЕ
Умножение
Игра «Произведение двузначных чисел»
Используйте свои навыки умножения, чтобы найти произведение двузначных чисел.
ПОДРОБНЕЕ
Откройте для себя забавные игры на многозначное умножение
Посмотреть все 39 игр
Умножение
Игра «Счет строк и столбцов»
Сделайте первый шаг к построению своего математического замка, потренировавшись считать строки и столбцы.
ПОСМОТРЕТЬ ПОДРОБНОСТИ
Умножение
Игра «Создание массивов»
Наслаждайтесь чудом математики, научившись создавать массивы.
ПОДРОБНЕЕ
Умножение
Понимание строк в массиве Игра
Войдите в безумие математической мультивселенной, поняв строки в массиве.
ПОДРОБНЕЕ
Умножение
Понимание столбцов в игре с массивами
Добавьте больше стрелок в математический колчан вашего ребенка, поняв столбцы в массиве.

ПОДРОБНЕЕ
Умножение
Игра «Представление массивов с помощью повторного сложения»
Наслаждайтесь чудом математики, исследуя, как представлять массивы с помощью многократного сложения.
ПОДРОБНЕЕ
Умножение
Нахождение суммы с помощью игры с многократным сложением
Практикуйте суперсилу умножения, находя сумму с помощью многократного сложения.
ПОСМОТРЕТЬ ПОДРОБНОСТИ
Умножение
Игра «Создай модель для заданного предложения сложения»
Дети должны создать модель для заданных предложений сложения, чтобы попрактиковаться в умножении.
ПОДРОБНЕЕ
Умножение
Игра «Найти равные группы и размер группы»
Практикуйте суперсилу умножения, научившись находить равные группы и размер группы.

ПОДРОБНЕЕ
Умножение
Игра «Определение количества и размера групп»
Примените свои знания об умножении, чтобы определить количество и размер групп.
ПОДРОБНЕЕ
Умножение
Игра «Создание равных групп»
Упростите изучение умножения, создав равные группы.
ПОДРОБНЕЕ
Умножение
Пропустить счет, чтобы найти ответ Игра
Используйте свои математические способности, чтобы пропустить счет, чтобы найти ответ.
ПОДРОБНЕЕ
Умножение
Представление равных групп с помощью игры с повторяющимся сложением
Дети должны представлять равные группы с помощью повторяющегося сложения, чтобы попрактиковаться в умножении.
ПОДРОБНЕЕ
Умножение
Использование многократного сложения для нахождения суммы Игра
Наслаждайтесь чудом математической мультивселенной, изучая, как использовать многократное сложение для нахождения суммы.

ПОСМОТРЕТЬ ПОДРОБНОСТИ
Умножение
Моделирование сложения предложений с использованием игры равных групп
Добавьте больше стрелок в математический колчан вашего ребенка, моделируя сложение предложений с использованием равных групп.
ПОДРОБНЕЕ
Умножение
Количество групп и размер групп Игра
Проявите себя в мире математики, научившись находить количество групп и размер групп.
ПОДРОБНЕЕ
Найдите увлекательные игры на умножение
Просмотреть все 199 игр
Умножение
Игра «Создай несколько групп»
Наслаждайтесь чудом математической мультивселенной, изучая, как создавать несколько групп.
ПОДРОБНЕЕ
Умножение
Игра «Сделай равные группы»
Сними нагрузку, упростив умножение, создав равные группы.

ПОДРОБНЕЕ
Умножение
Использование повторного сложения для подсчета в группах Игра
Дети должны использовать многократное сложение для подсчета в группах.
ПОДРОБНЕЕ
Умножение
Моделирование повторяющегося сложения с использованием игры равных групп
Наслаждайтесь чудом математики, изучая, как моделировать повторяющееся сложение с использованием равных групп.
ПОДРОБНЕЕ
Умножение
Определите количество строк и столбцов Игра
Наслаждайтесь чудом математики, исследуя, как определить количество строк и столбцов.
ПОДРОБНЕЕ
Умножение
Игра «Создание массива»
Наслаждайтесь чудом математической мультивселенной, изучая, как создать массив.
ПОДРОБНЕЕ
Умножение
Моделирование повторяющегося сложения с использованием массивов Игра
Насладитесь чудом математической мультивселенной, исследуя, как моделировать повторяющееся сложение с использованием массивов.

ПОСМОТРЕТЬ ПОДРОБНОСТИ
Умножение
Использование многократного сложения для подсчета в игре с массивами
Посмотрите, как использовать многократное сложение для подсчета в этой игре на умножение.
ПОДРОБНЕЕ
Умножение
Игра «Определи выражение умножения»
Проявите себя в мире математики, научившись определять выражение умножения.
ПОДРОБНЕЕ
Умножение
Выберите игру с выражением умножения
Пусть ваш ребенок увидит мир сквозь математические оттенки, выбрав выражение умножения!
ПОДРОБНЕЕ
Умножение
Моделирование умножения с использованием игры равных групп
Используйте свои математические способности для моделирования умножения с использованием равных групп.
ПОДРОБНЕЕ
Умножение
Выберите выражение умножения для игры с массивами
Дети должны выбрать выражение для умножения для игры.

ПОДРОБНЕЕ
Умножение
Представление массивов с помощью предложений умножения Игра
Используйте свои навыки умножения для представления массивов с помощью предложений умножения.
ПОДРОБНЕЕ
Умножение
Определение выражения умножения для массивов Игра
Помогите своему ребенку освоить умножение, определив выражение умножения для массивов.
ПОДРОБНЕЕ
Умножение
Игра «Умножение моделей с использованием массивов»
Пусть ваш ребенок увидит мир сквозь математические оттенки, моделируя умножение с использованием массивов!
ПОДРОБНЕЕ
Связанные рабочие листы
Просмотреть все 371 рабочие листы
Умножение
Рабочий лист «Описание равных групп»
Превратите математику в увлекательное занятие, потренировавшись описывать равные группы.

ПОДРОБНЕЕ
Умножение
Рабочий лист «Представление равных групп»
В этом рабочем листе учащиеся попрактикуются в представлении равных групп.
ПОДРОБНЕЕ
Умножение
Решите с использованием повторяющегося сложения Рабочий лист
Помогите своему ребенку повторить умножение, решая с помощью повторяющегося сложения.
ПОСМОТРЕТЬ ПОДРОБНОСТИ
Умножение
Найдите рабочий лист выражения умножения
Погрузитесь в этот увлекательный печатный рабочий лист, потренировавшись, чтобы найти выражение умножения.
ПОДРОБНЕЕ
Умножение
Представление равных групп с помощью таблицы умножения
Учащиеся должны представлять равные группы с помощью умножения, чтобы улучшить свои математические навыки.
ПОДРОБНЕЕ
Умножение
Умножение с использованием равных групп Рабочий лист
Распечатайте этот рабочий лист, чтобы попрактиковаться в умножении с использованием равных групп, как математическую легенду!
ПОДРОБНЕЕ
Умножение
Умножение с использованием равных групп Рабочий лист
Помогите ребенку попрактиковаться в умножении с использованием равных групп.

ПОДРОБНЕЕ
Умножение
Строки и столбцы Рабочий лист
Распечатайте этот рабочий лист, чтобы практиковать строки и столбцы, как математическую легенду!
ПОДРОБНЕЕ
Умножение
Массивы и их атрибуты Рабочий лист
Распечатайте этот рабочий лист, чтобы попрактиковаться с массивами и их атрибутами, как с математической легендой!
ПОДРОБНЕЕ
Умножение
Рабочий лист по выражениям сложения и умножения
В этом рабочем листе учащиеся смогут попрактиковаться в выражениях сложения и умножения.
ПОСМОТРЕТЬ ПОДРОБНОСТИ
Умножение
Рабочий лист «Представление массивов с помощью выражений»
Превратите математику в увлекательное занятие, решая задачи на представление массивов с помощью выражений.

ПОДРОБНЕЕ
Умножение
Умножение с использованием массивов Рабочий лист
Изучите умножение со скоростью молнии, умножая с помощью массивов.
ПОДРОБНЕЕ
Умножение
Рабочий лист «Используйте массивы для умножения»
Дети должны использовать массивы для умножения, чтобы укрепить свои математические навыки.
ПОДРОБНЕЕ
Умножение
Рабочий лист «Работа с равными группами»
Сосредоточьтесь на основных математических навыках с помощью этого забавного рабочего листа, решив работать с равными группами.
ПОДРОБНЕЕ
Умножение
Рабочий лист «Представление равных групп»
Закрепите свои математические навыки, потренировавшись представлять равные группы.
ПОСМОТРЕТЬ ПОДРОБНОСТИ
Универсальное решение для всех потребностей обучения в классе.

Дайте вашему ребенку страсть и уверенность, чтобы безбоязненно учиться чему-либо самостоятельно
Родители, зарегистрируйтесь бесплатно
Учителя, используйте бесплатно
4413+
4417+
ПОХОЖИЕ ТЕМЫУмножение двузначных чисел | Как умножать, методы, примеры
ВведениеУмножение — одна из четырех основных математических операций, а остальные три — сложение, вычитание и деление. Прежде чем мы перейдем к изучению того, как умножать двузначные числа, давайте вспомним, что мы подразумеваем под умножением.
Как определить умножение? Умножение определяется как процесс нахождения произведения двух или более чисел. Полученный таким образом результат называется продуктом . Предположим, вы купили 6 ручек в один день и 6 ручек на следующий день. Всего ручек, которые вы купили, теперь 2 умножить на 6 или 6 + 6 = 12.
Это также можно записать как 2 x 6 = 12
Не тот символ, который используется для умножения. Символ (x) обычно используется для обозначения умножения. Другими распространенными символами, которые используются для умножения, являются звездочка (*) и точка (.)
Символ умноженияОбратите внимание на символ, используемый в приведенном выше примере для умножения. Символ (x) обычно используется для обозначения умножения. Другими распространенными символами, которые используются для умножения, являются звездочка (*) и точка (.)
Теперь давайте рассмотрим некоторые важные термины, которые используются при умножении двух чисел.
Важные термины при умноженииНекоторые важные термины, используемые при умножении –
Множимое . Число, которое нужно умножить, называется множимым.
Множитель — Число, на которое мы умножаем, называется множителем.
Произведение – Результат, полученный после умножения множителя на множимое, называется произведением.
Связь между множителем, множимым и произведением может быть выражена как –
Множитель × Множитель = Произведение
Давайте разберемся с этим на примере.
Предположим, у нас есть два числа 9 и 5. Мы хотим умножить 9 на 5.
Итак, мы выражаем это как 9 x 5, что дает нам 45.
Следовательно, 9 x 5 = 45
Здесь 9 равно множимое, 5 — множитель, 45 — произведение.
Теперь, когда мы поняли, что мы подразумеваем под умножением и терминами, связанными с ним, давайте перейдем к изучению умножения однозначных чисел.
Теперь давайте разберемся, как выполнять умножение, когда у нас есть многозначные числа.
Как умножать двузначные числа?Прежде чем мы приступим к пониманию умножения двузначных чисел, важно вспомнить, что подразумевается под двузначными числами?
Напомним, что каждая цифра числа имеет разрядное значение. Например, число 5 — это однозначное число, где 5 стоит на месте единицы. Точно так же в числе 27 цифра 2 стоит на месте десятков, а цифра 7 — на месте единиц. Итак, как мы определяем двузначные числа? Двузначные числа — это числа, состоящие из 2 цифр, т. е. числа, состоящие из цифр только на разрядах единиц и десятков. Например, числа 55 и 67 двузначные.
Например, число 5 — это однозначное число, где 5 стоит на месте единицы. Точно так же в числе 27 цифра 2 стоит на месте десятков, а цифра 7 — на месте единиц. Итак, как мы определяем двузначные числа? Двузначные числа — это числа, состоящие из 2 цифр, т. е. числа, состоящие из цифр только на разрядах единиц и десятков. Например, числа 55 и 67 двузначные.
Теперь давайте перейдем к изучению умножения двузначных чисел. Когда дело доходит до умножения двузначных чисел, есть два метода умножения чисел. Этими методами являются метод расширенной записи и метод столбца. Давайте разберемся в обоих методах.
Метод расширенной записиВ методе расширенной записи мы расширяем множимое по разрядным значениям, а затем умножаем каждое число на множитель. Затем мы суммируем все полученные результаты, чтобы получить окончательный ответ. Давайте разберемся на примере.
Например, умножить 35 на 40
Решение
Мы решим это шаг за шагом.
Шаг 1 – Запишите число (множимое) в развернутом виде. Получаем,
Получаем,
35 = 30 + 5
Шаг 2 – Умножаем каждое число на заданное число (множитель) один за другим. Получаем,
30 х 40 + 5 х 40 = 1200 + 200
Шаг 3 — Складываем полученные результаты. Получаем,
1200 + 200 = 1400
Отсюда 35 х 40 = 1400
Хотя этот метод и прост, он может не подходить для больших чисел. Но он используется для понимания основных понятий умножения.
Метод столбцаВ этом методе мы разбиваем числа на столбцы и умножаем числа на множимое одно за другим. Есть два сценария использования этого метода.
Давайте разберемся с ними один за другим
Умножение без перегруппировкиЭтот метод вступает в силу, когда у нас есть меньшие числа, которые не требуют переноса каких-либо чисел на разряд следующего разряда. Давайте разберемся на примере.
Например, умножьте 21 на 32
Решение
Чтобы получить результат, выполните следующие действия.
Шаг 1. Сначала мы записываем множимое и множитель в столбцах. Здесь у нас есть 21 как множимое и 32 как множитель.
Шаг 2. Теперь умножаем число, стоящее на месте множимого, т. е. 1, на число, стоящее на месте множителя, которое в данном случае равно 2. Получаем
. Шаг 3. Теперь умножаем число в десятом месте множимого на 2. Получаем
Шаг 4. Теперь нам нужно поставить 0 на место единиц в следующей строке в качестве заполнителя. Мы получим
. Шаг 5. Поскольку мы завершили умножение множимого на первую цифру множителя, мы выполняем те же действия, что и выше для умножения множимого на следующее число множителя, а затем пишем результатом будет строка напротив 0, которую мы поместили в качестве заполнителя на предыдущем шаге. Получим –
Шаг 6 Теперь, когда мы перемножили все цифры множителя с множимым, сложим полученные цифры по вертикали. мы получим
Полученный таким образом результат является нашим ответом. Следовательно, 21 x 32 = 672
Умножение с перегруппировкой В приведенном выше случае мы имеем небольшие умножения, которые ни на одном шаге не требуют двузначных результатов. Но в случае больших чисел потребуется перенести число на число со следующим значением разряда. Это называется умножением с перегруппировкой. Давайте разберемся на примере.
Но в случае больших чисел потребуется перенести число на число со следующим значением разряда. Это называется умножением с перегруппировкой. Давайте разберемся на примере.
Например, умножить 25 на 34
Решение
Мы будем использовать следующие шаги, чтобы получить наш результат.
Шаг 1. Сначала мы записываем множимое и множитель в столбцах.
Шаг 2. Умножьте цифру единицы множимого на 4. У нас есть 4 x 5 = 20. Запишите 0 в столбце единиц и перенесите 2 в столбец десятков.
Шаг 3. Умножаем десятый разряд множимого на 4. Получаем 2 x 4 = 8. Прибавляем к нему перенесенные 2, получаем 8 + 2 = 10. Теперь запишем 0 в столбце десятков и перенесем 1 в сто столбик.
Шаг 4 Теперь нам нужно поставить 0 вместо единиц в следующей строке в качестве заполнителя. Мы получим
. Шаг 5. Поскольку мы завершили умножение множимого на первую цифру множителя, мы выполняем те же действия, что и выше для умножения множимого на следующее число множителя, а затем пишем результатом будет строка напротив 0, которую мы поместили в качестве заполнителя на предыдущем шаге. Получим –
Получим –
Шаг 6 Теперь, когда мы перемножили все цифры множителя с множимым, сложим полученные цифры по вертикали. мы получим
Полученный таким образом результат является нашим ответом. Следовательно, 25 x 34 = 850
Вышеуказанные шаги могут быть обобщены для определения умножения, которое обычно известно как длинное умножение. Определим эти шаги.
Длинное умножениеДлинное умножение похоже на метод столбца, за исключением того факта, что здесь мы умножаем большие числа. Этот метод используется, когда множимое больше 9, т. е. множимое больше однозначного числа. Этот метод включает в себя следующие этапы –
- Сначала запишем множимое и множитель столбцами.
- Сначала умножьте число, стоящее на месте единицы множителя, на все числа множимого и запишите их горизонтально.
- Убедитесь, что вы записываете числа справа налево и каждое число находится под соответствующим разрядом множимого.

- Теперь перейдите к следующей строке.
- Поставьте 0 на месте единицы в этой строке.
- Теперь найдите цифру в разряде десятков множителя. Умножьте число, стоящее в десятом разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили 0,9.0221
- Снова перейти на следующую строку.
- Поставьте 0 на месте единиц и десятков в этой строке.
- Теперь найдите цифру в разряде сотен множителя. Умножьте число, стоящее в сотенном разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили два нуля.
- Продолжайте в том же духе, добавляя дополнительный ноль в каждую строку, пока не дойдете до конца множителя
- Сложите числа по вертикали в соответствии с их разрядностью.
- Полученное таким образом число и есть ваш результат.
Разберем это на примере
Например, Умножьте 32 на 13
Решение
- Сначала мы запишем множимое и множитель в столбцах.

- Затем умножьте число, стоящее на месте единицы множителя, на все числа множимого и запишите их горизонтально.
- Поместите 0 на место единицы следующей строки
- Теперь найдите цифру в разряде десятков множителя. Умножьте число, стоящее в десятом разряде множителя, на все числа множимого и запишите их горизонтально в строке, где вы отметили 0.
- В множимом больше нет числа. Теперь сложите числа по вертикали в соответствии с их разрядностью.
Окончательный ответ: 416. Следовательно, 32 x 13 = 416
Давайте посмотрим на другой пример, где мы 3 цифры в множимом.
Например, Умножить 53 на 25
Решение
1. Сначала запишем множимое и множитель в столбцы
- Затем умножим число, стоящее на месте единицы, на все числа множителя множимое и запишем их горизонтально.

- Поставьте 0 на месте единицы следующей строки
- Теперь найдите цифру в разряде десятков множителя. Умножьте десятичное число множителя на все числа множимого и запишите их горизонтально в строке, где вы отметили 0.
- Теперь, когда мы умножили все цифры множителя на множимое, мы добавит полученные цифры по вертикали. Получим
Отсюда 53 х 25 = 1325
Решенные примерыПример 1 В кинозале 58 рядов, в каждом ряду 25 мест. Сколько человек может разместиться в зале?
Решение Нам дано, что в кинозале 58 рядов и в каждом ряду 25 мест. Нам нужно найти количество человек, которое может разместиться в зале. Подытожим предоставленную нам информацию.
Количество рядов в кинозале = 58
Количество мест в каждом ряду = 25
Количество человек, которые могут разместиться в зале = ?
Количество человек, которые могут разместиться в зале, можно найти, умножив количество рядов на количество мест в каждом ряду. Это означает, что –
Это означает, что –
Количество человек, которые могут разместиться в зале = (Количество рядов в кинозале) x (Количество мест в каждом ряду) ……………………… ( 1 )
Подставляя данное значения в приведенном выше уравнении, мы будем иметь,
Количество человек, которые могут быть размещены в зале = 58 x 25
Теперь
Отсюда количество человек, которое может разместиться в зале = 1450
Пример 2 Ресторан приобрел 81 коробку пакетов с кетчупом. В каждой коробке было 49 пакетов кетчупа. Сколько всего пакетов с кетчупом купил ресторан?
Решение Нам сообщили, что ресторан приобрел 81 коробку пакетов с кетчупом. В каждой коробке было 49 пакетов кетчупа. Нам нужно узнать, сколько всего пакетов кетчупа купил ресторан. Подытожим предоставленную нам информацию.
Количество коробок кетчупа, купленных рестораном = 81
Количество пачек кетчупа в каждой коробке = 49
Общее количество пачек кетчупа, купленных рестораном = ?
Чтобы найти значение количества упаковок кетчупа, купленных рестораном, нам нужно будет умножить количество упаковок кетчупа, купленных рестораном, на количество упаковок кетчупа в каждой коробке. Это означает, что
Это означает, что
Общее количество упаковок кетчупа, купленных рестораном = (Количество упаковок кетчупа, купленных рестораном) x (Количество упаковок кетчупа в каждой коробке) ……………………………. ( 1 )
Подставив данные значения в приведенное выше уравнение, мы получим,
Общее количество пакетов кетчупа, купленных рестораном = 81 x 49
Теперь,
Следовательно, общее количество пакетов кетчупа, купленных рестораном ресторан = 3969.
Пример 3 Уильям купил 60 упаковок бумажных салфеток. В каждой упаковке было 56 салфеток. Сколько салфеток купил Уильям?
Решение Нам сообщили, что Уильям купил 60 упаковок бумажных салфеток. В каждой упаковке было 56 салфеток. Нам нужно найти количество салфеток, купленных Уильямом. Подытожим предоставленную нам информацию.
Количество упаковок бумажных салфеток, купленных Уильямом = 60
Количество салфеток в каждой упаковке = 56
Общее количество салфеток, купленных Уильямом = ?
Чтобы найти общее количество салфеток, купленных Вильямом, нам нужно будет умножить количество упаковок бумажных салфеток, купленных Вильямом, на количество салфеток в каждой упаковке. Это означает, что
Это означает, что
Общее количество салфеток, купленных Вильямом = (Количество упаковок бумажных салфеток, купленных Вильямом) x (Количество салфеток в каждой упаковке) ………. ( 1 )
Подставив данные значения в приведенное выше уравнение, мы получим,
Общее количество тканей, купленных Уильямом = 60 x 56
Теперь,
Следовательно, общее количество тканей, купленных Уильямом = 3360
Основные факты и резюме- Умножение определяется как процесс нахождения произведения двух или более чисел.
- Число, которое нужно умножить, называется множимым.
- Число, на которое мы умножаем, называется множителем.
- Результат, полученный после умножения множителя на множимое, называется произведением.
- Двузначные числа — это числа, состоящие из двух цифр, одной цифры на месте десятков и одной цифры на месте единиц.
- В методе расширенной записи мы расширяем множимое по разрядным значениям, а затем умножаем каждое число на множитель.
 Затем мы суммируем все полученные результаты, чтобы получить окончательный ответ.
Затем мы суммируем все полученные результаты, чтобы получить окончательный ответ. - В методе столбцов мы разбиваем числа на столбцы и умножаем числа на множимое одно за другим.
Рабочие листы по умножению двузначных чисел (на тему путешествий и туров)
Рабочие листы по вычитанию двузначных чисел (на тему больницы)
Свойства умножения (на тему недвижимости) Рабочие листы
Просмотреть все рабочие листы
много времени, исследуя и собирая информацию на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Умножение двузначных чисел на однозначные числа
Извините, вы использовали все доступные подсказки для этого урока.
Достигнут предел практики
Вы достигли ежедневного лимита практики в 12 вопросов.
Когда вы зарегистрируете бесплатную учетную запись и войдете в нее, вы сможете играть во все, что захотите.
(Для регистрации необходимо быть старше 18 лет.)
Интерактивная математическая игра — Умножение двузначных чисел на однозначные числа
Учащиеся третьего класса будут практиковать базовые навыки умножения в этом интерактивном математическом задании от iKnowIt.com. Учащиеся укрепят свои навыки умножения, практикуя умножение двузначных чисел на однозначные числа. Вот несколько учебных целей этого математического занятия в третьем классе:
- Решите задачи на вертикальное умножение, содержащие одно двузначное и однозначное числа.
- Решите задачи на горизонтальное умножение, содержащие одно двузначное и однозначное числа.
- Решите задачи на умножение слов, содержащие одно двузначное число и одно однозначное число.
- Умножайте единицы, умножайте десятки и перегруппировывайте при необходимости.
Вопросы в этом интерактивном математическом задании представлены в формате заполнения пробелов. Если учащимся нужна дополнительная помощь в решении задачи на умножение, они могут нажать кнопку «Подсказка». Они увидят иллюстрированную или письменную подсказку, которая подтолкнет их к первому шагу «Умножьте единицы», не выдавая ответа. Когда учащиеся дают неправильный ответ, страница с подробным объяснением покажет им шаг за шагом, как умножать, чтобы получить правильный результат. Таким образом, дети будут продвигаться по математической деятельности, учась на предыдущих ошибках.
Они увидят иллюстрированную или письменную подсказку, которая подтолкнет их к первому шагу «Умножьте единицы», не выдавая ответа. Когда учащиеся дают неправильный ответ, страница с подробным объяснением покажет им шаг за шагом, как умножать, чтобы получить правильный результат. Таким образом, дети будут продвигаться по математической деятельности, учась на предыдущих ошибках.
Все математические задания на iKnowIt.com, в том числе эта игра на умножение для третьего класса, оснащены встроенными функциями, помогающими учащимся максимизировать свои математические навыки. Вот некоторые из них:
- Отслеживание успеваемости — учащиеся могут проверить отслеживание успеваемости, чтобы узнать, на сколько вопросов они ответили из общего числа вопросов на уроке математики.
- Счетчик очков. Дети могут посмотреть на счетчик очков, чтобы узнать, сколько баллов они заработали за правильные ответы на вопросы.
- Функция чтения вслух. Учащиеся могут щелкнуть значок динамика в верхнем левом углу экрана практики, чтобы вопрос был прочитан им вслух четким голосом.
 Это отличный ресурс для учащихся ESL/ELL и детей, которые учатся на слух.
Это отличный ресурс для учащихся ESL/ELL и детей, которые учатся на слух.
Каждая из встроенных функций, которую учащиеся находят в своих интерактивных математических занятиях, предназначена для того, чтобы улучшить их математический опыт и помочь им достичь большего.
Подарите своим ученикам практику цифровой математики, которая им понравится
Цифровая математическая практика, предлагаемая iKnowIt.com, — это отличная возможность помочь малышам укрепить математические навыки с помощью математической практики, которая им действительно нравится. Вот лишь несколько причин, по которым учащимся нравятся наши интерактивные математические игры:
- Веселый, удобный для детей формат — учащимся нравятся яркие цвета и смелый дизайн наших уроков математики для начальной школы.
- Очаровательные анимационные друзья. Причудливые анимационные персонажи готовы подбадривать учеников в их математических занятиях умным трюком или милым танцем каждый раз, когда они правильно отвечают на вопрос.

- Награды по математике. Учащиеся имеют возможность зарабатывать виртуальные математические награды, которые добавляются в их ящик с трофеями за каждый новый освоенный математический навык.
- Положительные отзывы. Большое количество положительных отзывов побуждают детей «Продолжать!» даже когда они ошибаются.
Студенты не единственные, кто любит математическую онлайн-программу «Я знаю это». Учителям тоже нравится ощущать разницу, которую интерактивная математическая практика может сделать в их классах. Вот несколько вещей, которые больше всего нравятся учителям начальных классов, школьным администраторам и воспитателям в нашей дополнительной математической программе.
- Уроки математики, соответствующие стандарту Common Core. Математические задания в нашей коллекции соответствуют стандарту Common Core Standard и продуманно написаны такими же аккредитованными учителями математики начальных классов, как и вы.
- Широкий выбор тем по математике.
 Учителя ценят множество тем по математике, которые мы освещаем среди сотен интерактивных уроков по математике на нашем веб-сайте.
Учителя ценят множество тем по математике, которые мы освещаем среди сотен интерактивных уроков по математике на нашем веб-сайте. - Быстро и легко находите и назначайте практические занятия по математике. Все уроки математики на iKnowIt.com упорядочены на веб-сайте по классам и темам, что позволяет легко находить и назначать практические задания всего за несколько кликов.
Мы надеемся, что вам и вашим учащимся третьего класса понравится практиковаться в умножении двузначных и однозначных чисел в этой интерактивной математической игре! Обязательно ознакомьтесь с сотнями других уроков математики для третьего класса, которые также доступны на нашем веб-сайте.
Попробуйте базовые упражнения на умножение в своем классе бесплатно
Хотите узнать, подходит ли я знаю это вам и вашим ученикам? Подпишитесь на нашу бесплатную 30-дневную пробную версию и попробуйте любое математическое задание на нашем веб-сайте бесплатно в течение полных 30 дней — кредитная карта не требуется! Мы уверены, что вам и вашему классу понравится разница, которую может дать интерактивная математическая практика, и мы надеемся, что вы, не колеблясь, присоединитесь к нашему сообществу в качестве члена после окончания бесплатного пробного периода. Ваша подписка I Know It дает вашему классу неограниченный доступ к интерактивным математическим играм в течение всего календарного года. У нас есть варианты членства для семей, отдельных учителей, школ и школьных округов. Посетите нашу страницу с информацией о членстве, чтобы узнать подробности: https://www.iknowit.com/order.html.
Ваша подписка I Know It дает вашему классу неограниченный доступ к интерактивным математическим играм в течение всего календарного года. У нас есть варианты членства для семей, отдельных учителей, школ и школьных округов. Посетите нашу страницу с информацией о членстве, чтобы узнать подробности: https://www.iknowit.com/order.html.
Ваше членство в программе «Я знаю это» дает вам доступ к удобным административным функциям веб-сайта, которые помогут вам максимизировать математическую практику вашего класса:
- Создание списка класса для всех ваших учеников всем учащимся
- Выдача конкретных заданий по математике разным учащимся
- Изменение основных настроек урока, например, ограничение количества подсказок на уроке
- Печать, загрузка и сохранение отчетов об успеваемости учащихся
Ваши ученики войдут в удобную для детей версию iKnowIt.com, где они смогут быстро и легко найти математические задания, которые вы им назначили для практики. Если вы хотите предоставить им возможность через свою учетную запись администратора, ваши учащиеся также могут изучать другие математические задания в своем классе и за его пределами для дополнительного повторения или дополнительной задачи. Уровни оценок в студенческом режиме I Know It помечены буквами (например, «Уровень C» для третьего класса), что упрощает назначение математических заданий в зависимости от потребностей и уровня навыков каждого учащегося.
Если вы хотите предоставить им возможность через свою учетную запись администратора, ваши учащиеся также могут изучать другие математические задания в своем классе и за его пределами для дополнительного повторения или дополнительной задачи. Уровни оценок в студенческом режиме I Know It помечены буквами (например, «Уровень C» для третьего класса), что упрощает назначение математических заданий в зависимости от потребностей и уровня навыков каждого учащегося.
Уровень
Этот онлайн-урок математики относится к уровню C. Он может быть идеальным для третьего класса.
Common Core Standard
4.NBT.5
Числа и операции с основанием 10
Учащиеся будут использовать свое понимание разрядного значения и свойств операций для выполнения многозначной арифметики. Учащиеся будут умножать целое число до четырех цифр на однозначное целое число и умножать два двузначных числа, используя стратегии, основанные на разрядности и свойствах операций.
Вас также может заинтересовать.
 ..
.. Умножение на число, кратное десяти (уровень C)
На этом уроке математики для третьего класса учащиеся будут практиковаться в умножении на число, кратное десяти. Вопросы представлены в формате заполнения пробелов.
Ассоциативное свойство (умножение) (уровень C)
На этом уроке математики, предназначенном для учащихся третьего класса, учащиеся будут практиковать ассоциативное свойство умножения. Вопросы представлены в формате заполнения пробелов и в формате перетаскивания.
Двузначное умножение стало проще! — Caffeine Queen Teacher
Умножение двузначных чисел — сложная задача, требующая много практики и повторения (и повторения и повторения). В прошлом я преподавал множество методов, включая ящик, частичные произведения, решетку и традиционный алгоритм.
Некоторые учащиеся быстро и легко адаптируются к целому ряду методов, в то время как другие с трудом усваивают даже один метод.
Многие учащиеся (и большинство родителей) с облегчением концентрируются на стандартном алгоритме. Стандартный алгоритм — это традиционный метод, которым пользуется большинство людей.
Стандартный алгоритм — это традиционный метод, которым пользуется большинство людей.
К 5-му классу в большинстве штатов требуется, чтобы учащиеся свободно владели стандартным алгоритмом. На протяжении многих лет я провел много поисков и не смог найти графический органайзер, который приносил бы пользу моим ученикам, испытывающим затруднения.
Некоторым моим ученикам было трудно выучить шаги и выполнить их в правильном порядке. Я понял, что мои борцы, как правило, были визуальными и практическими учениками, поэтому я разработал графический органайзер, чтобы помочь студентам с алгоритмом.
Щелкните, чтобы получить БЕСПЛАТНЫЙ набор навыков стратегии умножения!Визуальный органайзер для умножения на 2 цифры
Этот органайзер представляет собой метод, который учителя могут использовать для обучения традиционному алгоритму. Органайзер удобен для учащихся и использует формы и цвета , чтобы помочь учащимся выполнять шаги по порядку.
Во время обучения я постоянно говорю: «Кружки идут к кругам» или «Квадраты идут к квадратам». Это побуждает учащихся искать следующий шаг в этой конкретной форме. Эти утверждения помогают учащимся помнить, куда класть их продукты, когда они решают задачи на умножение. Например, учащиеся выполняют каждый шаг для красных кругов, прежде чем перейти к синим квадратам.
Как видно на картинках, органайзеры используют не только формы, но и цвета. Цвета и формы могут быть добавлены или удалены в зависимости от уровня адаптации, в котором нуждаются ваши ученики.
Цвета и формы помогают новичкам. По мере того, как учащиеся становятся более опытными, цвета могут быть удалены или даже добавлены учащимися, если это необходимо. Маркеры также можно использовать, чтобы подчеркнуть и сфокусировать внимание на конкретных шагах, которые необходимо укрепить учащимся.
Якорная диаграмма визуальной стратегии
FYI — приведенная выше якорная диаграмма — это года выпуска — 2014 года, но вы поняли идею. Первоначально в этих наборах использовались треугольники, а не пятиугольники. Мне показалось, что треугольники не дают ученикам достаточно места для письма, поэтому форму заменили на пятиугольники.
Первоначально в этих наборах использовались треугольники, а не пятиугольники. Мне показалось, что треугольники не дают ученикам достаточно места для письма, поэтому форму заменили на пятиугольники.
2-значное умножение с использованием органайзера фигур
Я ОБОЖАЮ эти Карманные диаграммы C-Line , которые можно приобрести в магазинах для учителей, Wal-Mart или Amazon. Вы просто вставляете страницу в карманную таблицу и ВУАЛЯ! Ламинировать не надо.
Это пластиковый футляр, который можно использовать для маркеров с сухим стиранием. Студенты часто пользуются ими.Ученикам нравится использовать карманные рукава, потому что маркеры с сухим стиранием позволяют легко писать и стирать, не беспокоясь об ошибках.
Органайзеры и рабочие листы для умножения двузначных чисел
Мне было трудно найти рабочие листы без перегруппировки. Я хотел, чтобы мои ученики сосредоточились на стандартном алгоритме умножения без дополнительного шага перегруппировки.
Когда учащиеся освоятся с умножением без перегруппировки, они готовы к изучению этого дополнительного шага. Перегруппировка должна пройти гладко после того, как вы потратите время на решение проблем без перегруппировки и изучения процесса двузначного умножения.
Выделение или раскрашивание начальной точки помогает учащимся запомнить, с чего начать.Эти наборы органайзеров для умножения Shape Math содержат множество практических страниц, поэтому используйте столько страниц, сколько нужно вашим ученикам. Кроме того, наборы облегчают дифференциацию в зависимости от уникальных потребностей учащихся.
Моим ученикам, как правило, требовалась дополнительная практика и МНОГО повторений, поэтому в первоначальный набор включено множество различных рабочих листов для умножения с перегруппировкой.
Кроме того, в набор входят три графических органайзера разного размера. Первый и самый большой органайзер занимает целую страницу. На других страницах есть четыре органайзера; другая страница содержит девять пустых органайзеров. Эти страницы идеально подходят для вас (или ваших учеников) для решения задач. Мои ученики любят составлять рабочие листы друг для друга и быть «учителем».
Эти страницы идеально подходят для вас (или ваших учеников) для решения задач. Мои ученики любят составлять рабочие листы друг для друга и быть «учителем».
Страница ниже свернута, что является простым приспособлением для студентов, которые перегружены просмотром целой страницы задач.
Страница свернута для учащихся, которые перегружены объемом работы, которую от них ожидают.размеры , цвета и рабочие листы упрощают дифференциацию и построение лесов. Эти наборы для умножения и деления Shape Math — мои любимые, они протестированы учащимися и одобрены учителями!
После того, как учащиеся научатся решать задачи на умножение с перегруппировкой и без нее, учащиеся готовы решать задачи без графического органайзера. Два рабочих листа на миллиметровой бумаге включены, чтобы помочь им перейти к независимости.
Если вы также учите деление, вам понравится этот комплект, который сэкономит ваше время!
Советы по обучению учащихся двухэтапному умножению
В коротком (5-минутном) видео ниже объясняется, как я обучаю учащихся двузначному умножению с помощью шаблона Shape Multiplication.
Хотите узнать больше?
Если вы хотите узнать больше об этой новой стратегии умножения (а также о стратегиях деления!), вот несколько статей, которые вы можете прочитать:
Рабочие листы дифференцированного умножения:
Все ресурсы по умножению – Ознакомьтесь все ресурсы умножения, которые я предлагаю в моем магазине учителей, платных учителям.
Двузначное умножение — дифференцированная стратегия обучения многозначному умножению с использованием органайзеров и рабочих листов, чтобы помочь учащимся визуализировать процесс умножения.
2-значное и 3-значное умножение – Этот метод многозначного (3-х 2-значного) умножения использует цвета и формы для визуальной, конкретной стратегии.
Статьи об умножении:
3 идеи для обучения многозначному умножению . Вот 3 идеи FAST для обучения многозначному умножению. Эти вмешательства просты и быстры для занятых учителей.
Рабочие листы по умножению 2-значных чисел: дифференцированные . Ниже представлен визуальный метод обучения умножению 2-значных чисел с использованием дифференцированных визуальных подсказок, которые помогут учащимся добиться успеха в обучении.
Двузначное умножение стало проще! – Вот как использовать организаторы двузначного умножения и рабочие листы.
Статьи о длинном делении:
БЕСПЛАТНЫЕ дифференцированные рабочие листы для длинного деления – БЕСПЛАТНО возьмите эти дифференцированные рабочие листы для длинного деления и значительно повысьте успеваемость учащихся и ваши успехи в обучении!
Как преподавать многозначное умножение и деление в длинное число – Эта статья в блоге познакомит вас с имеющимися у меня ресурсами по дифференцированному умножению и делению в длинное число.



 Итого: 2024
Итого: 2024 Пролетарска
Пролетарска


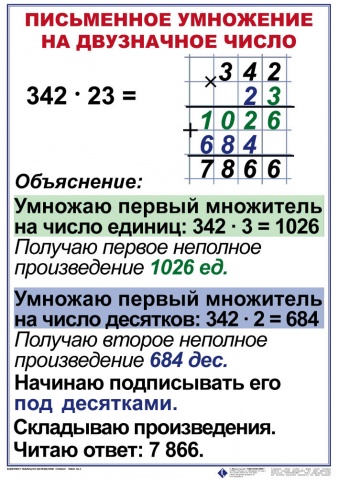 Он равен ширине большого пальца или длине трех сухих зерен ячменя, взятых из средней части колоса. 1 дюйм =2,54 см.
Он равен ширине большого пальца или длине трех сухих зерен ячменя, взятых из средней части колоса. 1 дюйм =2,54 см.