Гражданцева Светлана Васильевна | |||
Место работы | МБОУ «Раздорская СОШ им. Губернатора А.П.Гужвина» | ||
Должность | Учитель начальных классов | ||
Тип урока | урок закрепления материала (технология деятельностного подхода) | ||
Цель | закрепить табличные случаи умножения; отработать вычислительные навыки; умение решать задачи. | ||
Задачи | 1) Закрепить знание табличного умножения и деления на 2 и на 3. 2) Продолжить обучение решению задач с использованием действий умножения и деления. 3) Работать над формированием универсальных учебных действий (УУД), повышением познавательной активности обучающихся. 4) Воспитывать у учащихся чувство взаимовыручки. | ||
Формируемые УУД | Предметные: знать название компонентов и результата действия умножения, понимать связь между умножением и сложением (умножение – есть сумма одинаковых слагаемых), правильно употреблять в речи математические понятия; понимать суть арифметических действий – умножения и деления; знать как связаны между собой арифметические действия умножения и деления; табличные случаи умножения и деления на 2 и на 3; различные устные и письменные приемы сложения и вычитания двузначных чисел; отличительные особенности задачи; уметь читать произведения и частные, используя названия компонентов умножения и деления; умножать на 10 и 1; умножать десять на однозначное число; решать задачи и выражения изученных видов, в том числе те, которые решаются умножением и делением. Личностные: проявлять положительное отношение к учебному предмету «Математика», осознавать её значение; интерес к учебному материалу, способность к самооценке на основе критерия успешности учебной деятельности. Регулятивные: определять тему урока, ставить цель, сохранять её в течение всего урока, выполнять под руководством учителя учебные действия в практической и мыслительной форме, фиксировать в диалоге с учителем в конце урока удовлетворённость/неудовлетворённость своей работой на уроке. Прогнозировать результат решения практической учебной задачи, оценивать по критериям. Находить и исправлять ошибки, выяснять их причины, намечать путь исправления. Познавательные: ориентироваться в информационном материале учебника, осуществлять поиск необходимой информации (по необходимости совместно с учителем), развитие умений использовать при вычислениях черновик, создавать алгоритм деятельности; логически рассуждать; контролировать и оценивать процесс и результаты деятельности, находить рациональные пути решения, отличать новое от уже известного; добывать новые знания. Коммуникативные: планировать учебное сотрудничество с одноклассниками: договариваться о распределении работы между собой и соседом, уметь находить и исправлять ошибки в работе соседа, осуществлять взаимоконтроль и взаимную помощь, использовать простые речевые средства, включаться в диалог с учителем, уважать другую точку зрения. | ||
Ресурсы: — основные — дополнительные | Учебник «Математика» 2 класс авторы В.Н.Рудницкая и Т.В.Юдачева Наглядный (презентация) и раздаточный материал, карточки | Деятельность учителя | Деятельность ученика | Планируемые результаты Формируемые УУД |
1.Организационный момент Задача: Включение детей в деятельность на личностно-значимом уровне. | — Здравствуйте, дорогие ребята, гости. Какое у вас настроение? (смайлики) Слайд 1. -Начинаем урок математики. Давайте настроимся на работу. Предлагаю сказать, под каким девизом мы будем работать? (на экране) Слайды 2 и 3 | Учащиеся настраиваются на работу. Девиз: С хорошим настроением принимайся за работу! | Коммуникативные УУД — планирование учебного сотрудничества с учителем и сверстниками. Познавательные УУД построение монологического высказывания. Личностные УУД Формирование внутренней позиции школьника на уровне положительного отношения к урокам математики; смыслообразование |
2. Устный счёт Задача: Актуализация опорных знаний | Слайд 4. Найдите закономерность и продолжите числовой ряд 2,4,6,8,10,12,14,16,18,20 (увеличение на 2) — На какие группы можно поделить числа? (однозначные, двузначные, круглые) -Назовите однозначные числа (2,4,6,8) — назовите двузначные и круглые числа (10,12,14,16,18,20) — найдите половину числа (5,6,7,8,9,10) — От каких чисел можно найти треть числа? (6→2, 9→3). Слайд 5 — молодцы! Теперь откроем тетрадь и запишем число. — Составим примеры на умножение и деление с числами 2 и 3 (2х3=6, 6:2=3, 6:3=2) | Дают ответы с помощью сигнальных карточек Самоконтроль. Работа с листами самооценки. Работа в тетради. составляют из данных чисел примеры и записывают их, понимают роль каждой цифры в записи примеров; взаимосвязь между действиями умножения и деления. | Познавательные УУД Умение формулировать выводы на основе сравнения, обобщения; проводить классификацию изучаемых объектов. Регулятивные УУД: контролируют свою деятельность Личностные УУД: принимают и осваивают роль обучающегося. Понимают важность приобретаемых знаний и умений |
3. Постановка учебной задачи Задача: Формулирование темы и цели урока. | — догадались ли вы какова тема нашего урока? (Умножение и деление чисел на 2 и на 3) Слайд 6 — Давайте вместе подумаем, что нам нужно повторить и чему учиться на уроке. Слайд 7 — Таковы задачи нашего урока и мы должны их выполнить. | Высказывают предположения Формулируют цель и задачи урока Под руководством учителя определяют учебные задачи | Регулятивные УУД: Целеполагание, планирование. Умение проявлять инициативу в учебно-познавательной деятельности. Познавательные УУД. Самостоятельно выделять и формулировать познавательные задачи. |
4. Повторение таблицы умножения и деления на 2, на 3. Задача: Повторение изученного материала. | 1. Игра «Лучший знаток таблицы умножения и деления » — Работать будем в группах. Синоним слова помогать – спасать, выручать. Повторение правил работы в группах. Слайд 8 — Кто из членов вашей команды лучший знаток таблицы? Аплодисменты. Вывод: — Какие правила (законы умножения) повторили? -Мы выполнили одну из поставленных задач. 2. Игра «Не скажу». -Встаньте, пожалуйста, поиграем в игру «Не скажу». Ведущий называет пример и подаёт мяч кому-то из детей. Стараемся ответить и передать мяч водящему очень быстро, он горячий. 3. Игра-тест «Помоги львенку найти друзей» Слайды 9-21 -Выручите Львенка, помогите ему собрать друзей. А вместе с тем повторим таблицу деления на 3. — Молодцы! У Львенка много друзей. Вывод:- Что мы повторили и закрепили (таблицу деления на 3) Мы справились ещё с одной задачей урока. | Учащиеся разбиваются на три группы. Повторяют правила работы в группах. Проверка 2 -3 человек с группы (сигнальные карточки) Ответы учащихся Переместительный закон, умножение на 0 и на 1, деление числа само на себя, на 0 делить нельзя. Учащиеся передают мяч друг другу, называя табличные случаи умножения или деления. Следующий учащийся не называет ответ, а составляет свой пример начиная с ответа предыдущего. Например: 3х2→6х3→18:2→9х3 и т.д. Работа на интерактивной доске. Один учащийся, у доски решив пример, выбирает друга. Остальные дают ответы с помощью сигнальных карточек. | Познавательные УУД. Умение кодировать информацию в знаково — символической форме. Проявлять инициативу в учебно- познавательной деятельности. Регулятивные УУД Контроль и оценка процесса и результатов деятельности. Уметь вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок . Коммуникативные УУД Уметь оформлять свои мысли в устной и письменной форме; Принимать активное участие в работе группами. слушать и понимать речь других. Личностные УУД Контролировать свои действия в коллективной работе. Принимать учебную задачу и следовать инструкции учителя. Ориентация на понимание оценок учителя и одноклассников. |
5. Проверка знания таблицы умножения и деления на 2, на 3. Задача: Проверить умения в нахождении значений произведений и частного, самоконтроль усвоения знаний. | — А сейчас мы проверим свои знания. Математический диктант — 2 умножить на 7 — по 3 взять 5 раз — Запишите произведение чисел 5 и 2 — 3 разделить на 3 — первый множитель – 3, второй множитель – 9, запишите произведение — 12 разделить на 2 — чему равно произведение чисел 2 и 0? -Поменялись тетрадями по кругу, взаимопроверка, проверяем работу соседа. -Правильные ответы на доске: 14,15, 10, 1, 27, 6, 0. -Поменялись тетрадями опять по кругу, но в обратном направлении. Вывод: -Что мы проверили? (знание таблицы умножения и деления на 2, на 3). -Результатами я осталась довольна, спасибо, вы старались.
| Один ученик работает у доски. Остальные самостоятельно работают в тетрадях. Самоконтроль с интерактивной доской. Слайд 22 Оценивание и занесение результатов оценивания в лист самоконтроля (высокий, средний, низкий) Ответы учащихся. | Познавательные УУД — знание компонентов действия умножения и деления; -знание таблицы умножения и деления на 2, на 3. Регулятивные УУД прогнозируют результаты собственной деятельности, контролируют и оценивают себя. Коммуникативные УУД Уметь оформлять свои мысли в устной и письменной форме; слушать и понимать речь других. Личностные УУД Контролировать свои действия в коллективной работе. Принимать учебную задачу и следовать инструкции учителя. Ориентация на понимание оценок учителя и одноклассников. Понимание чувств одноклассников. |
6. Физминутка | Слайд 23 – 42. Видеоролик. Я предлагаю отдохнуть. | Встают с мест. Выполняют танцевальные движения. | |
7. Решение задач с использованием действий умножения и деления. Задача: Проверить умение решать задачи на умножение и деление. | Работа в группах. — Посовещайтесь в группе, каким действием решается задача? Выберите карточку с верным решением. 1)Задача №1. Слайд 43 2)Задача №2. Слайд 45 — Что такое неделя? Почему неделю так назвали? (7 дней. 3)Задача №3. Слайд 47. -Что узнаем 1 действием? (сколько съели) — Что узнаем 2 действием? (сколько яблок было) 4)Работа по учебнику. Задание №18 стр.102 — Из предложенных задач выбери и реши только задачу на деление. 5) Задание №21 с 111. 6) Немое кино. Вы ничего не услышите, а все, что увидите, считайте. — Расскажите, что вы увидели? (Мама купила 14 конфет. Дома она дала трём детям по 2 конфеты.) — Можно ли это назвать задачей? Почему? Чего не хватает? (вопроса) -Поставьте к задаче вопрос. (Сколько конфет осталось у мамы?) (Анализ задачи: Чтобы узнать сколько конфет осталось у мамы, нужно знать сколько конфет мама купила и сколько она отдала детям. -Обсудите план решения в группах. -Что узнаем 1 действием? ( Сколько конфет мама отдала.) -Что узнаем 1 действием? ( Сколько конфет осталось у мамы.) — Один из вас за доской будет решать задачу, а остальные решат её самостоятельно. 1) 2*3=6(к.) – отдала. 2) 14-6=8(к.)- осталось. -Самопроверка. Сверьте своё решение с решением ученика на доске. -А теперь проверим, сколько конфет лежит в пакете. Вывод? (Задача решена верно) -Чему мы учились? (Решать задачи) Вывод: Мы выполнили еще одну задачу, которую поставили в начале урока. Значит все задачи выполнены. Молодцы! | Выбирают карточку с правильным решением, обосновывают свой выбор. Самоконтроль с доской. Слайд 44 Самоконтроль с доской. Самостоятельно в паре решают задачу №3 с последующей самопроверкой с доской. Слайд 48 Оценивание в листе самоконтроля Самостоятельная работа в тетради Коллективное составление задачи по слайдам. Анализ задачи. Совместная запись условия вместе с учителем. Самостоятельная запись решения. | Познавательные УУД Формирование интереса к познанию математических фактов. Умение осуществлять поиск нужной информации, строить небольшие математические сообщения в устной форме. создают алгоритмы деятельности; устанавливают причинно- следственные связи, строят логическую цепочку рассуждений. Интерес к различным видам учебной деятельности, включая элементы предметно- исследовательской деятельности. Применять усвоенный способ действий к решению новой задачи. Коммуникативные УУД Умение стремиться к координации различных мнений в сотрудничестве; умение договариваться, приходить к общему решению. |
8. Подведение итога урока | Слайд 54. Организация деятельности учащихся по анализу и оцениванию своей деятельности. -Молодцы, ребята. Я очень довольна вашей работой на уроке. Подведём итог нашей работы. Нам поможет карточка – помощница. (Дети читают начало в карточке и сами заканчивают мысль) —На уроке я повторил… таблицу умножения и деления на 2, на 3. —Я учился… решать задачи. —На уроке мне было… (интересно, скучно, легко, трудно…) —Я понял, что… надо знать таблицу, уметь решать задачи —Я радовался… (успехам товарищей, своим успехам, полученным знаниям) —Я всегда буду… выручать своих товарищей. | Отвечают на вопросы, делают выводы, обобщения. | Познавательные УУД логически рассуждают, строят цепочку умозаключений. Регулятивные УУД осознают важность полученных знаний; понимают причины успеха и неуспеха. Личностные УУД Самооценка на основе заданных критериев успешности учебной деятельности |
9. Домашнее задание Инструктаж | А теперь послушайте домашнее задание на завтра. -Всем спасибо. Урок закончен | Записывают домашнее задание. | |
10. Рефлексия. Задача: Осознание обучающимися своей учебной деятельности, самооценка результатов деятельности своей и всего класса. | -Поднимите тот смайлик, который выражает ваше настроение после урока. -Спасибо за урок. | Регулятивные УУД Уметь оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки. Личностные УУД Формирование самооценки на основе заданных критериев успешности учебной деятельности . Понимание причин успеха в учёбе. |
«Умножение и деление на 2, 3, 4»
Цели:
- закрепить знание табличных случаев умножения и деления на 2, 3, 4;
- закрепить умение решать задачи на увеличение и уменьшение числа в несколько раз;
- развивать технику счета;
- пробуждать интерес к предмету через дидактическую игру, логические задания.
Оборудование:
- рисунки:
- внучки,
- внука,
- бабушки,
- дедушки,
- яблони с яблоками,
- печки,
- избушки,
- Бабы-Яги;
- кассета с записью крика гусей, слов яблоньки, печки, Бабы-Яги;
- магнитофон;
- учебник математики для 3 кл.
 , ч.1.
, ч.1.
ХОД УРОКА
I. Организационный момент
Учитель. Проверим готовность к уроку. Сегодня нам нужны учебник, тетрадь, ручка, карандаш, карточки со знаками <, >, = .
Дети глазами проверяют, всё ли у них готово к уроку.
II. Сообщение темы и целей урока
Учитель. Сегодня на уроке мы закрепим
ваше умение решать примеры на табличное
умножение и деление на 2, 3, 4 и продолжим решать
задачи на увеличение и уменьшение числа в
несколько раз. Но урок у нас будет необычным. Я
расскажу вам сказку “Гуси-лебеди”.
Жили-были дед да баба.
Учитель прикрепляет на доску рисунок деда и бабы.
– Были у них внучка да внучок маленький Ванюша.
Учитель прикрепляет на доску рисунки внучки и внучка Ванюши.
– “Внучка, – говорили баба с дедом, – мы поедем
на базар. Не ходи со двора, береги Ванюшу. А мы
тебе подарки привезем!”
Не ходи со двора, береги Ванюшу. А мы
тебе подарки привезем!”
Учитель убирает с доски рисунки деда и бабы.
– Уехали баба с дедом, а внучка позабыла, что ей наказывали, посадила Ванюшу на травку, а сама убежала с девчонками играть.
Учитель убирает с доски рисунки внучки.
– А Ване скучно стало. Стал он от скуки считать. Давайте и мы посчитаем.
III. Устный счет
Учитель приглашает учащихся к доске для индивидуальной работы.
На доске:
| 8. 2 2. 3 6. 2 2. 9 |
Гусей – 9 |
9 · х = 27 |
Три ученика решают у доски.
Учитель: Пока ребята выполняют задание, мы с вами решим веселые задачки.
К 2 зайчатам в час обеда
Прискакали 3 соседа.
В огороде зайцы сели
И по 3 морковки съели.
Кто считать, ребята, ловок?
Сколько съедено морковок?Дарит бабушка-лисица
Трем внучатам рукавицы:
“Это вам на зиму, внуки,
Рукавичек по 2 штуки.
Берегите, не теряйте.
Сколько всех, пересчитайте.”
– Молодцы! Давайте сравним, что длиннее, что короче, что больше, что меньше. Я показываю выражение, а вы знак >, <, =.
Учитель показывает выражение на карточках.
39 мм * 3 см 9 мм
48 см * 4 дм 9 см
56 дм * 5 м 4 дм
– Молодцы! Со всеми заданиями справились. А теперь проверим, как наши ребята, которые работали индивидуально, справились с заданием.
Учитель вместе с ребятами проверяет работу учащихся и оценивает. Звучит запись крика гусей.
Учитель: Но вдруг налетели злые
гуси-лебеди, подхватили мальчика и унесли. А кто
им приказал это сделать, мы узнаем, решив примеры.
А кто
им приказал это сделать, мы узнаем, решив примеры.
Открывается разрезанный на 8 частей портрет Бабы-Яги обратной стороной.
| 16 : 2 12 : 6 10 : 5 21 : 3 |
14 : 2 24 : 8 36 : 4 |
Учитель: Выходим к доске, читаем пример, называем ответ и переворачиваем карточку.
Появляется рисунок Бабы-Яги.
– Вот кто похитил нашего Ванюшу! Поможем сестрице спасти братца?
Дети: Поможем!
Учитель: Но сначала откроем тетради. Запишем число, классная работа. Чтобы начать путь, нужно найти лишнее число.
На доске:
3 6 9 12 15 18 20 24
Дети: Лишнее число 20, потому что каждое
число увеличивается на 3. Вместо числа 20 должно
быть 21.
Вместо числа 20 должно
быть 21.
Учитель: Пропишем число 20.
| 2 | 0 |
|
2 |
0 |
|
2 |
0 |
|
2 |
0 |
|
IV. Физминутка
Физминутка
Учитель: Вы много трудились, пришла пора отдохнуть. Легли на парту, закрыли глаза и слушаем.
Учитель включает продолжение записи крика гусей и говорит:
– Теплый, летний ветер гладит вам щеки, волосы, яркое солнышко улыбается и посылает свои жаркие лучи. Кричат гуси, указывают путь к Иванушке.
V. Закрепление пройденного
Учитель: На пути у нас яблонька.
Учитель прикрепляет на доску яблоньку.
– Яблонька, яблонька, покажи нам дорогу к Бабе-Яге.
Учитель включает запись слов яблоньки.
Яблонька. Покажу, если съедите мои яблочки. Яблочки у меня не простые – волшебные. Чтобы яблочко съесть, надо решить пример, расставив порядок действий.
На доске рисунок яблоньки с яблоками, а на яблоках с обратной стороны записаны примеры.
Учитель: Срываем “яблочки”,
записываем пример и решаем на доске.
Вызываются слабые учащиеся к доске. Они “срывают яблочки” с примерами, записывают на доске и с объяснением решают.
– Остальные ребята самостоятельно решают примеры № 6 (3 столбик) с. 56.
8 · 4 – 18 : 6
32 : 4 + 3 · 4
24 : 3 – 2 · 4
После решения примеров из учебников осуществляется коллективная проверка.
Учитель: Идем дальше. На нашем пути печка. Печка, печка, покажи нам дорогу к Бабе-Яге.
Учитель прикрепляет рисунок печки.
Учитель включает запись слов печки.
Печка: Покажу, если съедите мой пирожок. Пирожок не простой, а трудная задача.
Учитель: Так. Посмотрим. Послушайте задачу.
Учитель из-за заслонки достает рисунок пирожка, на котором записана задача:
Учитель вызывает к доске “сильного”
учащегося, чтобы составить краткую запись. Решение же он записывает за доской. Остальные
самостоятельно решают. После открывается доска,
и дети проверяют, правильно ли они решили задачу.
Решение же он записывает за доской. Остальные
самостоятельно решают. После открывается доска,
и дети проверяют, правильно ли они решили задачу.
Учитель: А вот и избушка Бабы-Яги.
Учитель прикрепляет рисунок избушки Бабы-Яги.
– Ребята, давайте скажем: “Баба-Яга! Отдай нам Ванюшу!”
Дети хором повторяют слова учителя. Учитель включает запись слов Бабы-Яги.
Баба-Яга: Отдам. Но сначала самостоятельно решите задачу из учебника на с. 58, № 18.
| Два механика открыли автомастерскую. В день они ремонтировали по 3 машины. Сколько машин отремонтировано за 4 дня? |
Со “слабыми” учениками учитель разбирает
задачу. Кто решил вперед и правильно, идет
записывать за доску. После ребята проверяют
решение задачи. На доске появляется рисунок
Иванушки.
На доске появляется рисунок
Иванушки.
VI. Итог урока
Учитель:
Учитель показывает вазу с конфетами. На перемене раздает детям. За ответы учащимся выставляются отметки.
Учитель: Урок окончен.
Приложение
Деление. Математика 2 класс Богданович. ГДЗ, решебник.
Категория: —>> Математика 2 класс Богданович
Задание: —>> 643 — 657
наверх
|
|
Задание 643.

Было 6 груш. Их разложили на 3 тарелки поровну. Сколько груш на каждой тарелке?
Решение:
- 6 : 3 = 2 (гр.)
- Ответ: 2 груши
Две точки (:) — знак деления.
Примеры на деление читают так: шесть разделить на три, будет два
Задание 644.
Прочитай примеры.
| 10 : 2 = 5 | 6 : 2 = 3 | 100 : 10 = 10 |
| 20 : 4 = 5 | 15 : 3 = 5 | 80 : 20 = 4 |
Задание 645.
Составь по рисунку и запиши пример на деление.
Решение:
12 : 4 = 3
Задание 646.
Измерь длину полоски и её частей, а затем составь задачу на деление.
Решение:
- Длинна полоски — 12 см.
- Длина каждой из частей 6 см.
- 12 : 2 = 6
Задание 647.
Реши задачу по рисунку.
Сколько литров сока осталось?
Решение:
- 1) 2 * 6 = 12
- 2) 12 — 9 = 3
- Выражение: 2 * 6 — 9 = 3
- Ответ: 3 литра.

Задание 648.
Измерь длину полоски и её частей, а затем составь пример на деление.
Решение:
- Длинна полоски – 8 см.
- Длина каждой из частей 2 см.
- 8 : 2 = 4
Задание 649.
Реши примеры.
Решение:
| 100 — 33 = 67 | 25 — (14 — 8) = 19 | 100 — 52 = 48 |
| 100 — 45 = 55 | 40 — (13 + 8) = 19 | 100 — 65 = 35 |
Задание 650.
Прочитай примеры на умножение и деление.
| 2 * 5 = 10 | 10 : 2 = 5 |
| 2 * 6 = 12 | 12 : 2 = 6 |
Задание 651.
Рассмотри рисунки и объясни, какие примеры составлены по каждому из них.
Из каждого примера на умножение можно составить два примера на деление.
Решение:
- 2 * 5 = 10 – верхний.

- 10 : 2 = 5 – нижний левый.
- 10 : 5 = 2 – нижний правый.
Задание 652.
Из примера на умнолсение составили два примера на деление. Прочитай их.
| 2 * 9 = 18 | 18 : 2 = 9 | 18 : 9 = 2 |
Задание 653.
Решение:
| 2 * 2 = 4 | 2 * 3 = 6 | 2 * 4 = 8 | 2 * 5 = 10 |
| 2 * 6 = 12 | 2 * 7 = 14 | 2 * 8 = 16 | 2 * 9 = 18 |
Задание 654.
Реши примеры.
Решение:
| 14 — 7 + 4 = 11 | 23 + 8 = 21 | 13 — 6 = 7 | 2 * 8 — 6 = 10 |
| 14 — (7 + 4) = 3 | 23 + 48 = 71 | 53 — 6 = 47 | 2 * 8 + 6 = 22 |
Задание 655.
На трёх одинаковых участках посеяли просо, овёс и кукурузу. Осенью собрали 18 кг проса, 23 кг овса, а кукурузы на 9 кг больше, чем проса и овса вместе. Сколько килограммов кукурузы собрали?
Решение:
- 1) 18 + 23 = 41
- 2) 41 + 9 = 50
- Выражение: (18 + 23) + 9 = 50
- Ответ: 50 кг.
Задание 656.
Из каждого примера на умножение составь два примера на деление.
| 2 * 4 = 8 | 2 * 3 = 6 | 2 * 7 = 14 |
Решение:
| 8 : 4 = 2 | 6 : 3 = 2 | 14 : 7 = 2 |
| 8 : 2 = 4 | 6 : 2 = 3 | 14 : 2 = 7 |
Задание 657.
В каждой из четырёх маленьких палаток по 2 туриста, а в большой палатке — 10. Сколько всего туристов в палатках?
Решение:
- 1) 2 * 4 = 8
- 2) 8 + 10 = 18
- Выражение: 2 * 4 + 10 = 18
- Ответ: 18 туристов.

Задание: —>> 643 — 657
Обучение соотношению умножения и деления с использованием массивов
Расположение объектов, изображений или чисел в столбцах и строках называется массивом . В этой статье вы узнаете, как использовать массивы, чтобы показать взаимосвязь между умножением и делением.
Ключевой стандарт: Используйте умножение и деление в пределах 100 для решения текстовых задач в ситуациях, связанных с массивами. (3.OA.A.3)
Учащиеся 3-х классов и старше узнают, что о делении можно думать двумя способами: разделением и измерением. Хотя на этом уровне учащиеся могут не использовать эти названия, вы можете передать значение обоих видов деления, чтобы они могли лучше понять процесс деления. Когда вы делите, чтобы найти количество объектов в каждой группе, это деление называется справедливым разделением или разделением. Например:
Фермер наполняет корзины яблоками. У фермера 24 яблока и 4 корзины. Если она разделит их поровну, сколько яблок она положит в каждую корзину?
У фермера 24 яблока и 4 корзины. Если она разделит их поровну, сколько яблок она положит в каждую корзину?
Когда вы делите, чтобы найти количество групп, деление называется измерением или повторным вычитанием. Вы можете продолжать вычитать 4 из 24, пока не достигнете 0. Каждые 4, которые вы вычитаете, представляют собой группу или корзину.
У фермера 24 яблока. Она хочет продать их по цене 4 яблока за 1 доллар. Сколько корзин по 4 штуки она может заполнить?
Array Division
Манипуляции и наглядные пособия важны при обучении умножению и делению. Студенты использовали массивы, чтобы проиллюстрировать процесс умножения. Массивы также могут иллюстрировать деление.
Поскольку деление является обратным или «противоположным» умножению, вы можете использовать массивы, чтобы помочь учащимся понять, как связаны умножение и деление. Если при умножении мы находим произведение двух множителей , то при делении находим недостающий множитель, если известны другой множитель и произведение.
В приведенной ниже модели умножения вы умножаете, чтобы найти общее количество счетчиков. В модели разделения массива вы делите, чтобы найти количество счетчиков в каждой группе. Используются те же три числа. Модель показывает, что деление «отменяет» умножение, а умножение «отменяет» деление. Поэтому при умножении или делении учащиеся могут использовать факт из обратной операции. Например, если учащиеся знают, что 4 × 5 = 20 , они также знают соответствующий факт деления 20 ÷ 4 = 5 9.0004 или 20 ÷ 5 = 4 . Студенты также могут проверить свою работу, используя обратную операцию.
Связь умножения и деления
Обратите внимание, что числа в предложениях умножения и деления имеют специальные имена. При умножении умножаемые числа называются множителями; результат умножения называется произведением. При делении делимое число — это делимое , число, на которое оно делится, — это делитель , а результат деления — частное . Обсудите взаимосвязь этих чисел, объясняя, как связаны умножение и деление.
Обсудите взаимосвязь этих чисел, объясняя, как связаны умножение и деление.
Есть и другие модели, которые учащиеся могут использовать для изучения связи между умножением и делением. Познакомьте учащихся с различными моделями и позвольте учащимся выбрать наиболее полезную модель. Вот пример использования счетчиков для умножения и деления.
Вот пример использования числовой строки.
Еще одна стратегия, которая может оказаться полезной для ваших учеников, — это использование связанного факта умножения для деления. Вот пример.
18 ÷ 6 = ?
Подумайте: 6 × ? = 18 Какое число в шесть раз больше 18?
6 × 3 = 18 , поэтому 18 ÷ 6 = 3 .
Деление на 0 и 1
Когда учащиеся понимают концепцию деления, они могут приступить к изучению правил деления на 0 и 1. Предложите учащимся самостоятельно открыть правила, предложив им использовать счетчики для моделирования деления. Ниже приведены несколько примеров.
Ниже приведены несколько примеров.
Когда любое число (кроме 0) делится само на себя, в частном получается 1.
Когда любое число делится на 1, это число получается в частном.
Когда 0 делится на любое число (кроме 0), частное равно 0.
Учащимся может быть любопытно, что произойдет, если они разделят на 0. Объясните, что это непростая концепция, и даже профессиональные математики пытаются ее объяснить ! Одна из стратегий, чтобы показать, почему это невозможно, состоит в том, чтобы предложить учащимся разделить любое число на группы нулей. Неважно, сколько групп вы создадите, это не сработает.
Деление в реальном мире
Предложите учащимся подумать о взаимосвязи между умножением и делением при решении реальных задач. Например, они могут использовать связанный факт умножения, чтобы найти стоимость единицы товара — например, стоимость одной бейсболки по цене 3 за 18 долларов.
$18 ÷ 3 = ? Подумай: 3 × ? = 18
3 × 6 долларов = 18 долларов, поэтому 18 долларов ÷ 3 = 6 долларов.
Стоимость одной бейсболки составляет 6 долларов.
***
Ищете дополнительную поддержку по вопросу «Как связаны умножение и деление?» Изучите Math 180 , наш революционный подход к математическому вмешательству для 5–12 классов.
Математика 3-5 классы Мероприятия и уроки 1-2 классы Вмешательство
Связанные материалыД-р Эми Эндо
Директор по исследованиям в области образования, дополнительный язык и интервенция, язык и грамотностьНоэль Моррис
Старший директор по взаимодействию с общественностью, HMH; Ведущий HMH Learning Moments: Подкаст учителей в АмерикеКристин Кондон
Shaped Главный редактор
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражения с дробями:
Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически конвертируются в дроби — т. е. 1,45 .
е. 1,45 .
Math Symbols
| Symbol | Symbol name | Symbol Meaning | Example | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| + | plus sign | addition | 1/2 + 1/3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| — | знак минус | вычитание | 1 1/2 — 2/3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| * | asterisk | multiplication | 2/3 * 3/4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| × | times sign | multiplication | 2 /3 × 5/6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| : | division sign | division | 1/2 : 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| / | division slash | division | 1/3 / 5 91/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
больше задач по математике »
Умножение и деление целых чисел Умножение и деление целых чисел — две основные операции, выполняемые над целыми числами. Умножение целых чисел — это то же самое, что и повторяющееся сложение, которое означает добавление целого числа определенное количество раз. Например, 4 × 3 означает прибавление 4 три раза, т. е. 4 + 4 + 4 = 12. Деление целых чисел означает равное группирование или деление целого числа на определенное количество групп.
Что такое умножение и деление целых чисел?Четыре основные арифметические операции, связанные с целыми числами:
Умножение и деление целых чисел являются наиболее важными часто используемыми арифметическими операциями. Умножение целых чиселУмножение целых чисел — это процесс многократного сложения положительных и отрицательных чисел, или мы можем просто сказать целые числа. Когда мы подходим к случаю умножения целых чисел, необходимо учитывать следующие случаи:
При умножении целых чисел с двумя положительными знаками: Положительное x Положительное = Положительное = 2 × 5 = 10. При умножении целых чисел с двумя отрицательными знаками Отрицательное x Отрицательное = Положительное = –2 × –3 = 6. При умножении целых чисел с одним знаком минус и одним знаком плюс Отрицательное x Положительное = Отрицательное = –2 × 5 = –10. Следующая таблица поможет вам запомнить правила умножения целых чисел:
Пример: Анна съедает 4 печенья в день. Умножение целых чисел Правила и шагиУмножение целых чисел очень похоже на обычное умножение. Однако, поскольку целые числа имеют дело как с отрицательными, так и с положительными числами, у нас есть определенные правила или условия, которые следует помнить при умножении целых чисел, как мы видели в предыдущем разделе. Давайте посмотрим на шаги для умножения целых чисел.
Давайте рассмотрим пример, чтобы лучше понять шаги. Умножить — 7 × 8. Шаг 1: Определить абсолютное значение — 7 и 8. |-7| = 7 и |8| = 8. Шаг 2: Найдите произведение абсолютных значений чисел 7 и 8. 7 × 8 = 56 Шаг 3: Определите знак произведения в соответствии с правилами умножения целых чисел. Следовательно, — 7 × 8 = — 56. Деление целых чиселДеление целых чисел включает группировку элементов. Он включает в себя как положительные числа, так и отрицательные числа. Точно так же, как и умножение, деление целых чисел связано с теми же случаями.
При делении целых чисел с двумя положительными знаками: Положительный ÷ Положительный = Положительный → 16 ÷ 8 = 2. При делении целых чисел с двумя отрицательными знаками: Отрицательный ÷ Отрицательный = Положительный → –16 ÷ –8 = 2 При делении целых чисел с одним знаком минус и одним знаком плюс Отрицательный ÷ Положительный = Отрицательный → –16 ÷ 8 = –2. Следующая таблица поможет вам запомнить правила деления целых чисел:
Чтобы подвести итог и упростить задачу, при умножении или делении целых чисел нужно помнить две вещи:
Примеры умножения и деления целых чиселНесколько примеров умножения и деления целых чисел приведены в таблице ниже:
Свойства умножения и деления целых чисел Свойства умножения и деления целых чисел помогают нам определить отношения между двумя или более целыми числами, когда они связаны операцией умножения или деления между ними. Свойства, связанные с умножением и делением целых чисел, перечислены ниже:
Давайте подробно разберем каждое свойство, связанное с делением и умножением целых чисел. Свойство замыкания умножения целых чиселСвойство замыкания указывает, что множество замкнуто для любой конкретной математической операции. Целые числа замкнуты относительно сложения, вычитания и умножения. Однако они не закрываются при делении.
Свойство перестановочности умножения целых чисел Согласно свойству перестановочности перестановка операндов местами в операции не влияет на результат.
Ассоциативное свойство умножения целых чиселСогласно ассоциативному свойству изменение группировки целых чисел не меняет результат операции. Ассоциативность применяется к сложению и умножению двух целых чисел, но не к делению целых чисел.
Распределительное свойство умножения целых чисел Распределительное свойство утверждает, что для любого выражения формы a (b + c), что означает a × (b + c), операнд a может быть распределен между операндами b и c как (a × b + a × c), т.
Свойство тождества умножения целых чиселВ случае умножения целых чисел 1 является мультипликативным тождеством. В случае деления целых чисел нет элемента идентичности.
Умножение и деление целых чисел Советы и рекомендации:
Статьи по теме:Ознакомьтесь с этими интересными статьями, посвященными концепции умножения и деления целых чисел.
Часто задаваемые вопросы об умножении и делении целых чиселЧто такое умножение целых чисел?Умножение целых чисел — это повторяющееся сложение чисел, означающее, что число добавляется само к себе определенное количество раз. Например, 4 × 2 означает, что 4 добавляется два раза. Отсюда следует, что 4 + 4 = 4 × 2 = 8, Каковы свойства умножения целых чисел с примерами?Свойства умножения целых чисел приведены ниже:
Каковы правила умножения и деления целых чисел?Основные правила деления и умножения целых чисел приведены ниже:
Каковы свойства деления целых чисел?Свойства деления целых чисел приведены ниже:
Что такое правило деления целых чисел?Ниже приведены правила деления целых чисел:
Как умножать целые числа?При умножении целых чисел следуйте этому трюку, чтобы легко получить ответ:
Как умножать несколько целых чисел?Если целых чисел больше двух, выполните следующие простые действия, чтобы их умножить:
|

 Развивать вычислительные навыки учащихся.
Развивать вычислительные навыки учащихся.

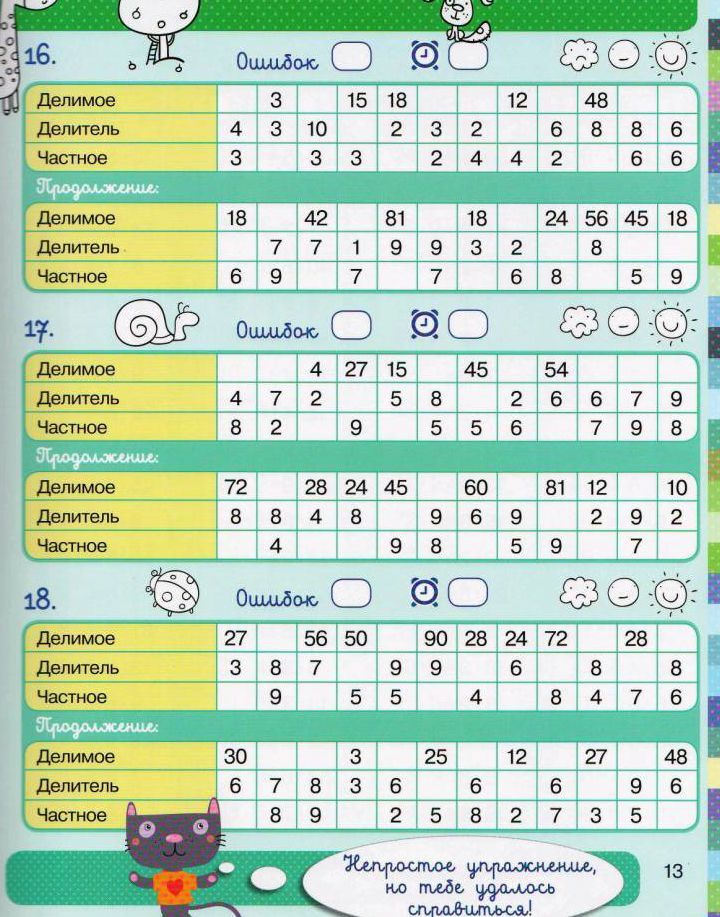


 Я очень хотела бы, чтобы вы всегда выручали друг друга не только на уроке, но и в жизни.
Я очень хотела бы, чтобы вы всегда выручали друг друга не только на уроке, но и в жизни. Работа по карточкам.
Работа по карточкам.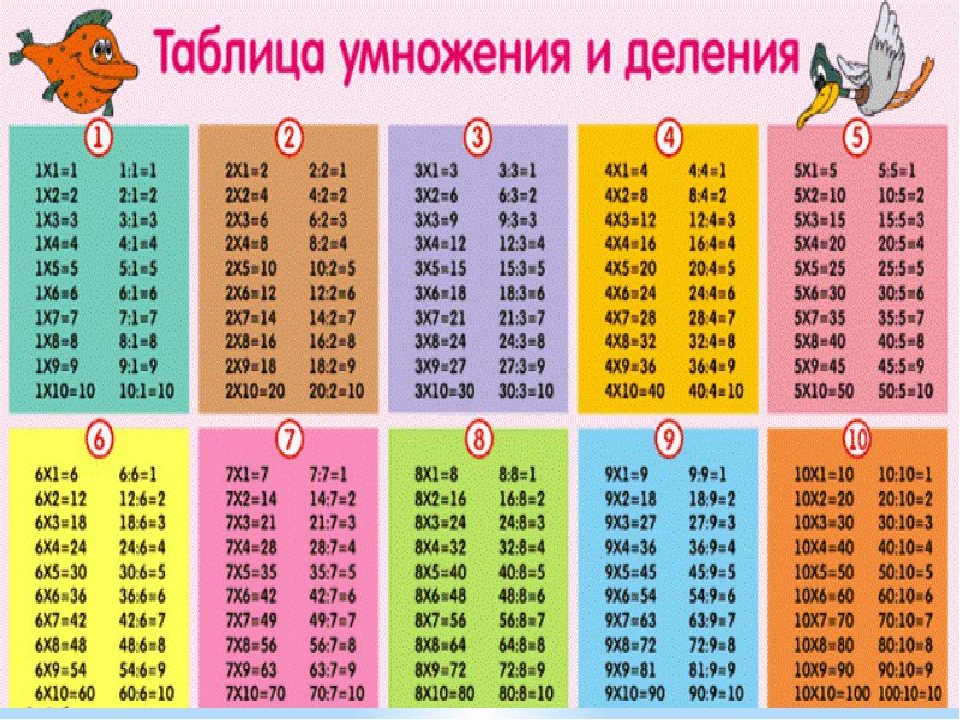

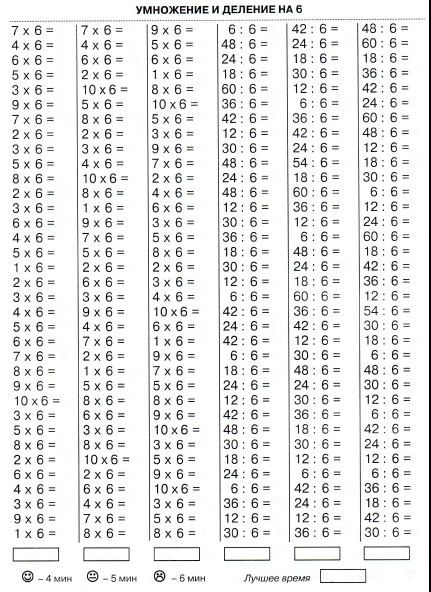
 Особым почетом в древности была окружена семерка. Отголоски почитания числа 7 дошли до наших дней. Вспомните пословицы «Семеро одного не ждут», «Семь бед – один ответ. Наша неделя состоит из 7 дней. Древние заметили, что 7 нельзя поделить на равные части. Вот и назвали 7 не-деля. Неделя – образовано от словосочетания «не делать», то есть отдыхать. Неделя – означало «день отдыха»
Особым почетом в древности была окружена семерка. Отголоски почитания числа 7 дошли до наших дней. Вспомните пословицы «Семеро одного не ждут», «Семь бед – один ответ. Наша неделя состоит из 7 дней. Древние заметили, что 7 нельзя поделить на равные части. Вот и назвали 7 не-деля. Неделя – образовано от словосочетания «не делать», то есть отдыхать. Неделя – означало «день отдыха» Сколько конфет купили известно, а сколько отдали мы не знаем, но знаем, что трём детям по 2 конфеты, а значит можем узнать.
Сколько конфет купили известно, а сколько отдали мы не знаем, но знаем, что трём детям по 2 конфеты, а значит можем узнать. Слайд 46
Слайд 46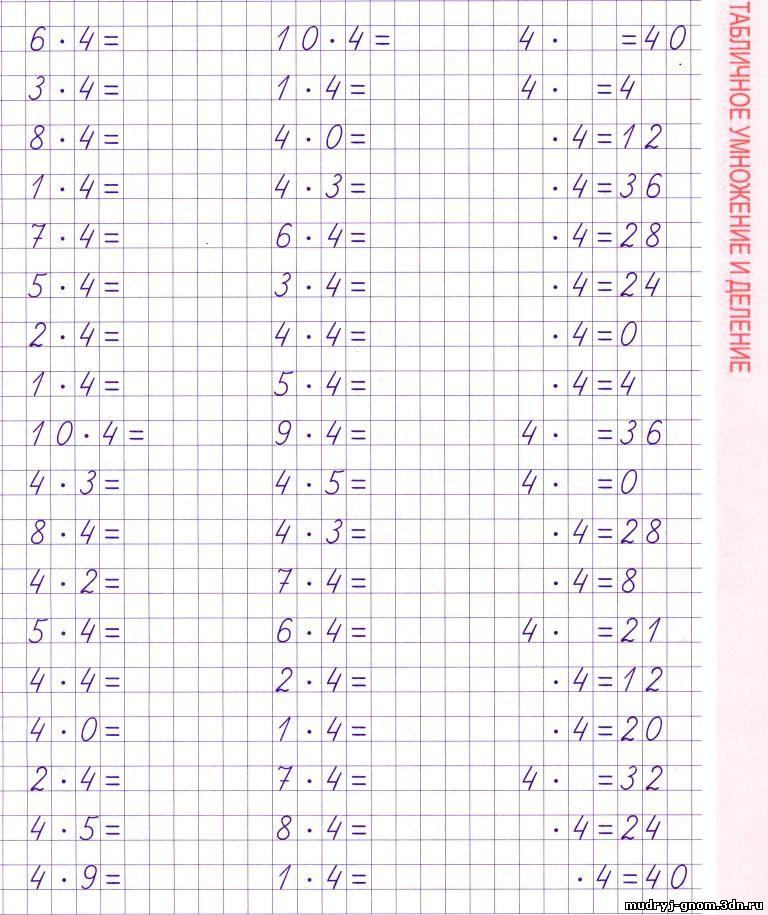


 , ч.1.
, ч.1.


 Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  Использовала 1/3 яйца. Какая часть яиц использовалась?
Использовала 1/3 яйца. Какая часть яиц использовалась? Какая часть карандашей не имеет ластика на конце?
Какая часть карандашей не имеет ластика на конце? Например, -6 ÷ 2 означает деление -6 на 2 равные части, что дает -3. Давайте узнаем больше об умножении и делении целых чисел в этой статье.
Например, -6 ÷ 2 означает деление -6 на 2 равные части, что дает -3. Давайте узнаем больше об умножении и делении целых чисел в этой статье. Давайте подробно изучим умножение и деление целых чисел.
Давайте подробно изучим умножение и деление целых чисел.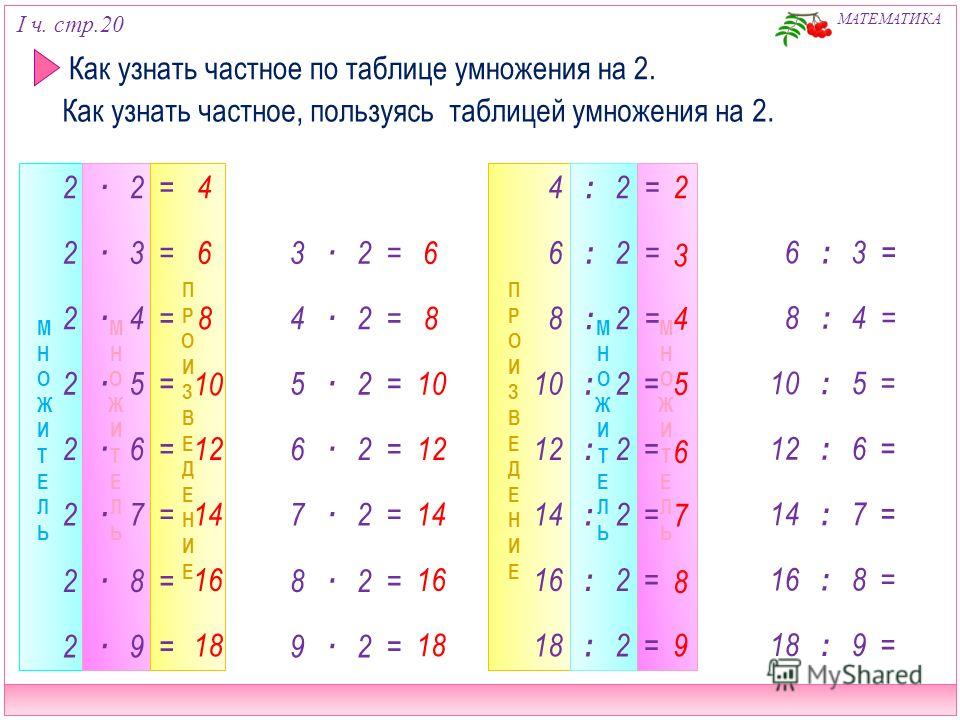 Сколько печенья она съест за 5 дней? ⇒ 5 × 4 = 20 печенек.
Сколько печенья она съест за 5 дней? ⇒ 5 × 4 = 20 печенек. Согласно правилу умножения целых чисел, если отрицательное число умножить на положительное число, то произведение будет отрицательным числом.
Согласно правилу умножения целых чисел, если отрицательное число умножить на положительное число, то произведение будет отрицательным числом.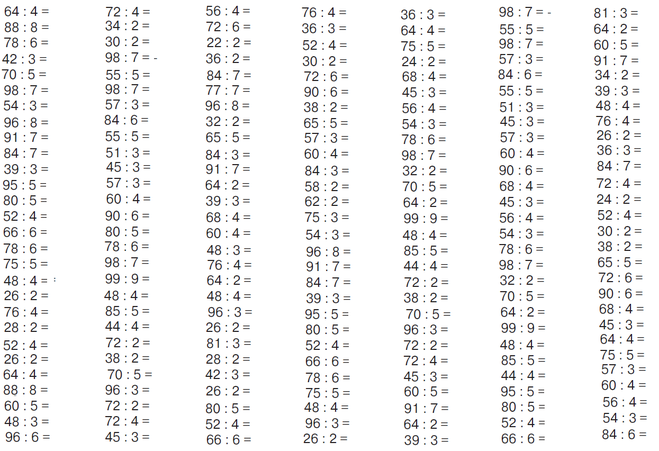
 Есть несколько свойств, связанных с умножением и делением целых чисел.
Есть несколько свойств, связанных с умножением и делением целых чисел. Сложение и умножение целых чисел следуют коммутативному свойству, в то время как деление целых чисел не обладает этим свойством.
Сложение и умножение целых чисел следуют коммутативному свойству, в то время как деление целых чисел не обладает этим свойством. е. a × (b + c) = a × b + a × c. Умножение целых чисел является распределительным над сложением и вычитанием. Распределительное свойство не выполняется для деления целых чисел.
е. a × (b + c) = a × b + a × c. Умножение целых чисел является распределительным над сложением и вычитанием. Распределительное свойство не выполняется для деления целых чисел.