Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Квадратный оконный проем образован двумя прямоугольными рамами.Внутри каждой из них написали число равное периметру рамы. Напишите чему равна сторона квадрата всего оконного проема и объясните как вы
Решено
1.Диагонали ромба KMNP пересекаются в точке О. Найдите углы треугольника КОМ, если угол MNP=80 градусов.
2.На стороне ВС параллелограмма ABCD взята точка М так, что АВ=ВМ.
Найдите углы треугольника КОМ, если угол MNP=80 градусов.
2.На стороне ВС параллелограмма ABCD взята точка М так, что АВ=ВМ.
Известно, что сегодня не выходной, завтра не воскресенье, после завтра не суббота, позавчера была не среда. Сегодняшний день не идет ни вслед за понедельником, ни перед четвергом. Какой сегодня день?
тело находится в равновесии под действием трех сил. Одна сила (6H) действует на восток, другая (3H) под углом 60°- на северо-восток. Определите модуль и направление третьей силы.
Диагонали прямоугольника АВСД пересекаются в точке О, угол АВО равен 36 градуса.Нйдите угол АОД
Пользуйтесь нашим приложением
Чему равен модуль sin x
Обновлено: 06.10.2022
Математика — это очень просто, даже проще, чем мы можем себе представить. Сложной математику делают сами математики.
понедельник, 16 января 2012 г.
Модуль синуса
Меня попросили показать способ упростить тригонометрическое выражение, содержащее сумму синуса и модуля синуса угла, зная, что угол альфа оканчивается в 4 четверти. Выглядит это выражение так:
Выглядит это выражение так:
Сразу скажу честно, что я понятия не имею, как такие выражения упрощаются. Но про модуль синуса рассказать могу и что получится в итоге, то же. Все вы хорошо знаете, что синус, как и все тригонометрические функции, может принимать положительные и отрицательные значения. Так вот, синус в китайских палочках, что в математике читается как «модуль синуса угла А», не может иметь отрицательных значений, только положительные. Когда математики брезгуют притрагиваться к отрицательным числам, они применяют эти китайские палочки (или модуль числа), как презерватив при сексе, чтоб не заразиться минусом. Этим они спасают свою жизнь, поскольку все числа в модуле из отрицательных превращаются в положительные.
Ну а теперь немного о знаковой жизни синуса угла А. Синус — это у нас вверх и вниз по оси игрек от единицы до минус единицы. Когда угол А принимает значения от 0 до 180 градусов, все синусы этих углов положительны. В данном случае китайские палочки модуля являются излишней мерой предосторожности и их можно отбросить. В этом диапазоне значений угла А наше выражение примет вид:
В этом диапазоне значений угла А наше выражение примет вид:
Если значение угла А увеличивать дальше, от 180 до 360 градусов, значения синусов этих углов будут отрицательными, то есть со знаком «минус». В этом случае модуль начинает играть свою роковую роль в судьбе нашего математического выражения. Значение синуса с модулем остается положительным, а значение синуса без модуля становится отрицательным, как и положено всем порядочным синусам. Что мы получим, если от числа отнимем точно такое же число? Правильно, ноль. Наше выражение вымирает, как динозавры. Кстати, если все люди всегда будут использовать презервативы во время секса, человечество тут же полностью вымрет. Эффект модуля. Посмотрим, что происходит с нашим выражением в этом случае:
Применение формул приведения тригонометрических функций даст точно такой же результат. При этом модуль заставляет нас отбрасывать в мусор все знаки минус, получаемые в результате преобразований.
При углах 0, 180, 360 и так далее градусов наше выражение будет равняться нулю, поскольку нулю равны значения синуса этих углов.
Как всё это правильно записать в полном соответствии с правилами математической бюрократии, я не знаю. Но смысл происходящего, я надеюсь, вам понятен и вы без труда оформите это выражение в самом лучшем виде.
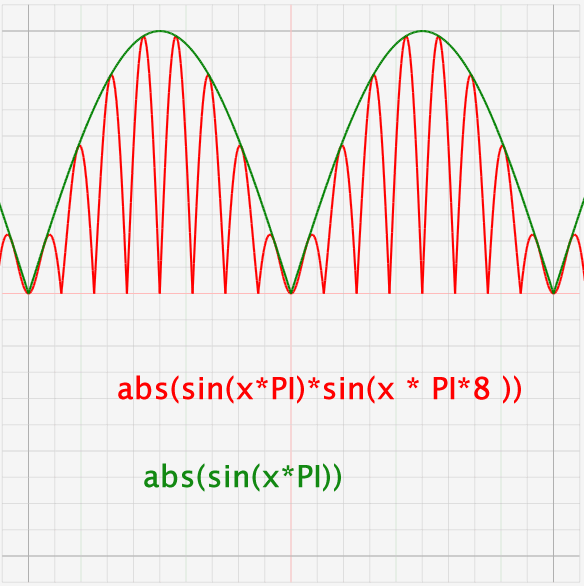
y= модуль sinx разделить на sinx как решать, какой график обьясните пожалуйста.
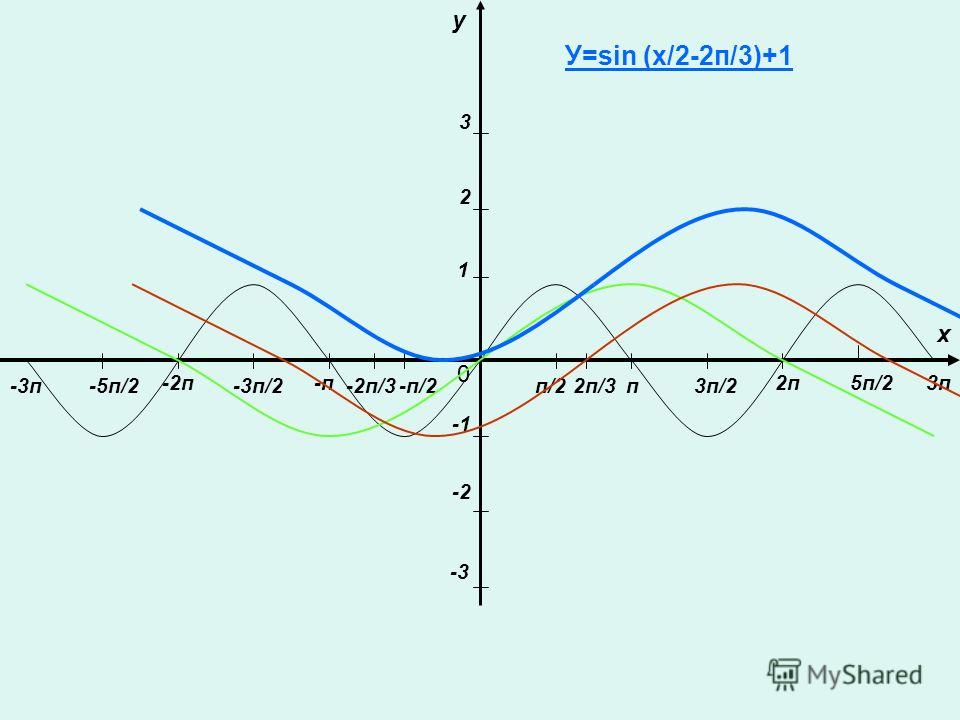
Для начала, чему равен модуль sin x? Он равен +sin x, когда синус положительный, т. е. при x от 2*pi*n до pi+2*pi*n, где n — целое число. И -sin x, когда синус отрицательный, т. е. при х от pi+2*pi*n до 2*pi+2*pi*n. Когда sin x = 0, его модуль тоже равен нулю. Отсюда вывод:
y=1 при x от 2*pi*n до pi+2*pi*n
y=-1 при х от pi+2*pi*n до 2*pi+2*pi*n
А в точках, где синус равен нулю, я думаю, что игрек не определен, т. к. на ноль делить нельзя.
Тригонометрическое уравнение с модулем
Так как уравнение содержит модуль, нам нужно этот модуль раскрыть по определению модуля.
Рассмотри два случая:
а) — в этом случае модуль раскрываем с тем же знаком.
б) — в этом случае модуль раскрываем с противоположным знаком.
а)
Раскрываем модуль с тем же знаком и получаем уравнение
Представим сумму косинусов в виде произведения, а правую часть уравнения разложим по формуле синуса двойного угла.
Отсюда =0″ />
или -sin=0″ />
=0″ />
при /2+n,
Введем замену переменной:
Решим квадратное уравнение относительно :
или =1/2″ />
Итак, если , корни уравнения
и /2+n,
Рассмотрим второй случай:
б)
В этом случае, так как подмодульное выражение отрицательно, раскрываем модуль с противоположным знаком:
. Получим:
n» />
И.В. Фельдман, репетитор по математике.
Решение простейших тригонометрических уравнений
Решение тригонометрических уравнений любого уровня сложности в конечном итоге сводится к решению простейших тригонометрических уравнений. И в этом наилучшим помощником снова оказывается тригонометрический круг.
И в этом наилучшим помощником снова оказывается тригонометрический круг.
Вспомним определения косинуса и синуса.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол .
Положительным направлением движения по тригонометрическому кругу считается движение против часовой стрелки. Повороту на 0 градусов ( или 0 радиан) соответствует точка с координатами (1;0)
Используем эти определения для решения простейших тригонометрических уравнений.
1. Решим уравнение
Этому уравнению удовлетворяют все такие значения угла поворота , которые соответствуют точкам окружности, ордината которых равна .
Отметим на оси ординат точку с ординатой :
Проведем горизонтальную линию параллельно оси абсцисс до пересечения с окружностью.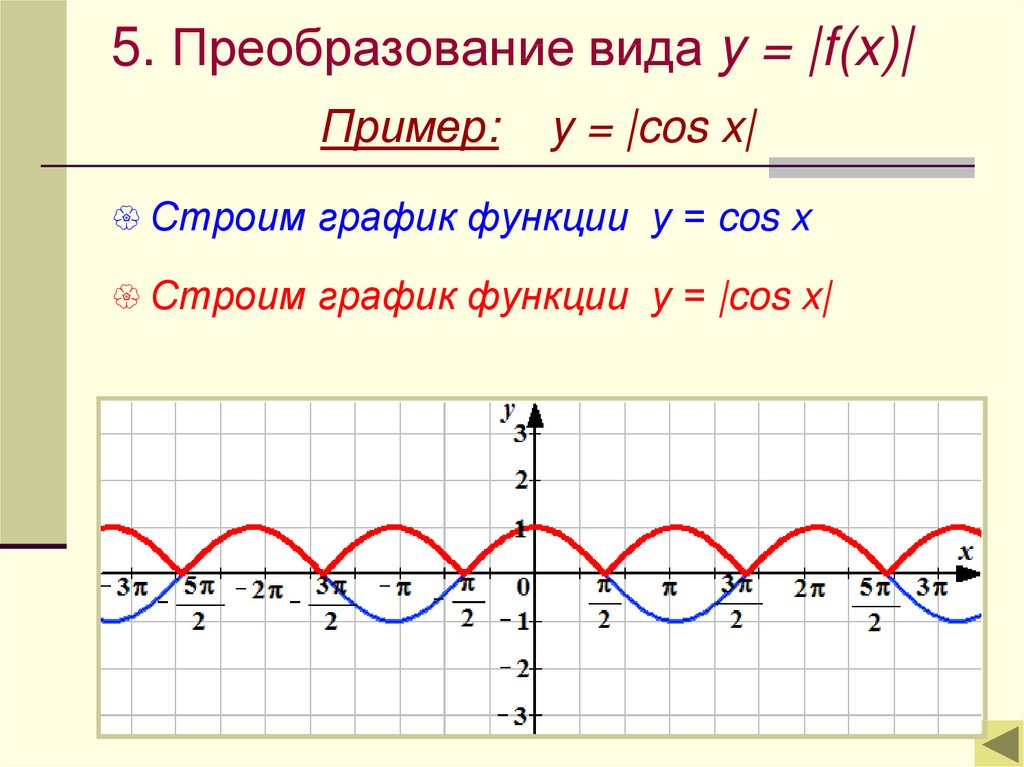 Мы получим две точки, лежащие на окружности и имеющие ординату . Эти точки соответствуют углам поворота на и радиан:
Мы получим две точки, лежащие на окружности и имеющие ординату . Эти точки соответствуют углам поворота на и радиан:
Если мы, выйдя из точки, соответствующей углу поворота на радиан, обойдем полный круг, то мы придем в точку, соответствующую углу поворота на радиан и имеющую ту же ординату. То есть этот угол поворота также удовлетворяет нашему уравнению. Мы можем делать сколько угодно «холостых» оборотов, возвращаясь в ту же точку, и все эти значения углов будут удовлетворять нашему уравнению. Число «холостых» оборотов обозначим буквой (или ). Так как мы можем совершать эти обороты как в положительном, так и в отрицательном направлении, (или ) могут принимать любые целые значения.
То есть первая серия решений исходного уравнения имеет вид:
, , — множество целых чисел (1)
Аналогично, вторая серия решений имеет вид:
, где , . (2)
Как вы догадались, в основе этой серии решений лежит точка окружности, соответствующая углу поворота на .
Эти две серии решений можно объединить в одну запись:
Если мы в этой записи возьмем ( то есть четное ), то мы получим первую серию решений.
Если мы в этой записи возьмем ( то есть нечетное ), то мы получим вторую серию решений.
2. Теперь давайте решим уравнение
Так как — это абсцисса точки единичной окружности, полученной поворотом на угол , отметим на оси точку с абсциссой :
Проведем вертикальную линию параллельно оси до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие абсциссу . Эти точки соответствуют углам поворота на и радиан. Вспомним, что при движении по часовой стрелки мы получаем отрицательный угол поворота:
Запишем две серии решений:
,
,
(Мы попадаем в нужную точку, пройдя из основной полный круг, то есть .
Объедим эти две серии в одну запись:
3. Решим уравнение
Линия тангенсов проходит через точку с координатами (1,0) единичной окружности параллельно оси OY
Отметим на ней точку, с ординатой равной 1 (мы ищем, тангенс каких углов равен 1):
Соединим эту точку с началом координат прямой линией и отметим точки пересечения прямой с единичной окружностью.
Так как точки, соответствующие углам поворота, которые удовлетворяют нашему уравнению, лежат на расстоянии радиан друг от друга, то мы можем записать решение таким образом:
,
4. Решим уравнение
Линия котангенсов проходит через точку с координатами единичной окружности параллельно оси .
Отметим на линии котангенсов точку с абсциссой -1:
Соединим эту точку с началом координат прямой и продолжим ее до пересечения с окружностью. Эта прямая пересечет окружность в точках, соответствующих углам поворота на и радиан:
Поскольку эти точки отстоят друг от друга на расстояние, равное , то общее решение этого уравнения мы можем записать так:
В приведенных примерах, иллюстрирующих решение простейших тригонометрических уравнений были использованы табличные значения тригонометрических функций.
Однако, если в правой части уравнения стоит не табличное значение, то мы в общее решение уравнения подставляем значение обратной тригонометрической функции:
1
Отметим на окружности точки, ордината которых равна 0:
2.
Отметим на окружности единственную точку, ордината которой равна 1:
3.
Отметим на окружности единственную точку, ордината которой равна -1:
Так как принято указывать значения, наиболее близкие у нулю, решение запишем так:
4.
Отметим на окружности точки, абсцисса которых равна 0:
5.
Отметим на окружности единственную точку, абсцисса которой равна 1:
6.
Отметим на окружности единственную точку, абсцисса которой равна -1:
И чуть более сложные примеры:
1.
Синус равен единице, если аргумент равен
Аргумент у нашего синуса равен , поэтому получим:
. Разделим обе части равенства на 3:
Ответ:
2.
Косинус равен нулю, если аргумент косинуса равен
Аргумент у нашего косинуса равен , поэтому получим:
Выразим , для этого сначала перенесем вправо с противоположным знаком:
Упростим правую часть:
Разделим обе части на -2:
Заметим, что перед слагаемым знак не меняется, поскольку k может принимать любые целые значения.
Ответ:
И в заключение посмотрите видеоурок «Отбор корней в тригонометрическом уравнении с помощью тригонометрической окружности»
На этом разговор о решении простейших тригонометрических уравнений мы закончим. Следующий раз мы с вами поговорим о том, как решать простейшие тригонометрические неравенства.
Читайте также:
- Fallout 1 как спать
- Как начать играть самп радмир
- Как зовут карася из эдисона в реальной жизни
- Как сделать приют для животных в симс 4
- Игры как command conquer generals
Python. Модуль math. Тригонометрические функции
Содержание
- 1. Особенности применения тригонометрических функций. Преобразование радиан в градусы и наоборот
- 2. Средства языка Python для конвертирования из градусов в радианы и наоборот. Функции math.degrees(x) и math.radians(x)
- 3. Ограничения на использование тригонометрических функций
- 4.
 Функция math.acos(x). Арккосинус угла
Функция math.acos(x). Арккосинус угла - 5. Функция math.asin(x). Арксинус
- 6. Функция math.atan(x). Арктангенс
- 7. Функция math.atan2(x, y). Арктангенс от x/y
- 8. Функция math.cos(x). Косинус угла
- 9. Функция math.sin(x)
- 10. Функция math.hypot(x, y). Евклидовая норма (Euclidean norm)
- 11. Функция math.tan(x). Тангенс угла x
- Связанные темы
Поиск на других ресурсах:
1. Особенности применения тригонометрических функций. Преобразование радиан в градусы и наоборот
Чтобы использовать тригонометрические функции в программе, нужно подключить модуль math
import math
Все тригонометрические функции оперируют радианами. Зависимость между радианами и градусами определяется по формуле:
1 радиан = 180°/π = 57.2958°
Если известен угол в градусах, то для корректной работы тригонометрических функций, этот угол нужно преобразовать в радианы.
Например. Задан угол, имеющий n градусов. Найти арккосинус этого угла. В этом случае формула вычисления результата будет следующей:
... n_rad = n*3.1415/180 # получить угол в радианах ac = math.acos(n_rad) # вычислить арккосинус ...
Чтобы получить более точное значение результата, в программе можно использовать константу math.pi, которая определяет число π. В этом случае текст программы будет иметь следующий вид
n_rad = n*math.pi/180 # получить угол в радианах ac = math.acos(n_rad) # вычислить арккосинус
⇑
2. Средства языка Python для конвертирования из градусов в радианы и наоборот. Функции math.degrees(x) и math.radians(x)
В языке Python существуют функции преобразования из градусов в радианы и, наоборот, из радиан в градусы.
Функция math.degrees(x) конвертирует значение параметра x из радиан в градусы.
Функция math.radians(x) конвертирует значение параметра x из градусов в радианы.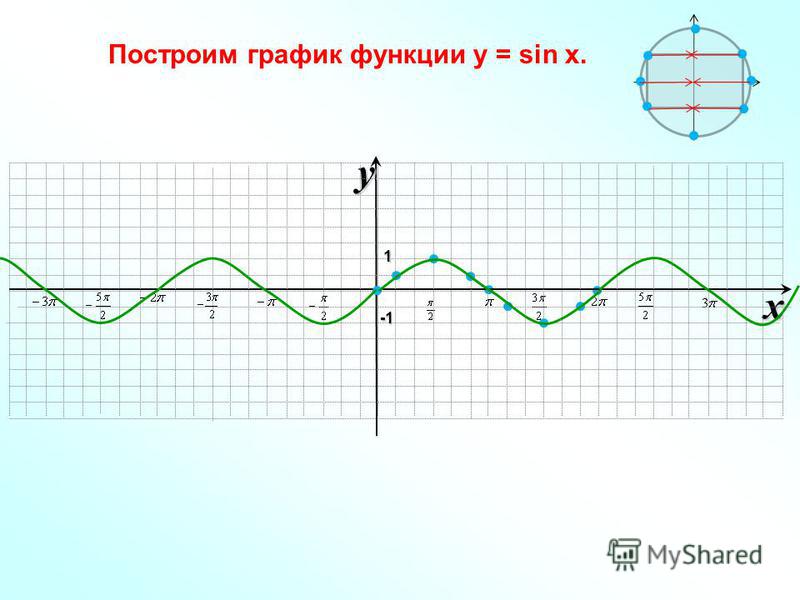
Пример.
# Функция math.degrees(x) import math x = 1 # x - угол в радианах y = math.degrees(x) # y = 57.29577951308232 - угол в градусах x = math.pi # x = 3.1415... y = math.degrees(x) # y = 180.0 # Функция math.radians(x) x = 180.0/math.pi y = math.radians(x) # y = 1.0 x = 45 # x - угол в градусах y = math.radians(x) # y = 0.7853981633974483
⇑
3. Ограничения на использование тригонометрических функций
При использовании тригонометрических функций следует учитывать соответствующие ограничения, которые следуют из самой сущности этих функций. Например, не существует арксинуса из числа, которое больше 1.
Если при вызове функции задать неправильный аргумент, то интерпретатор выдаст соответствующее сообщение об ошибке
ValueError: math domain error
⇑
4. Функция math.acos(x). Арккосинус угла
Функция acos(x) возвращает арккосинус угла x. Аргумент x задается в радианах и может быть как целым числом, так и вещественным числом.
Аргумент x задается в радианах и может быть как целым числом, так и вещественным числом.
Пример.
# Функция math.acos(x)
import math
n = float(input('n = ')) # ввести n
n_rad = n*math.pi/180 # получить угол в радианах
ac = math.acos(n_rad) # вычислить арккосинус
print('n_rad = ', n_rad)
print('ac = ', ac)Результат работы программы
n = 35 n_rad = 0.6108652381980153 ac = 0.913643357298706
⇑
5. Функция math.asin(x). Арксинус
Функция math.asin(x) вычисляет арксинус угла от аргумента x. Значение аргумента x задается в радианах.
Пример.
# Функция math.asin(x) import math n = 10 # n - угол в градусах # конвертировать из градусов в радианы n_rad = n*math.pi/180 # n_rad = 0.17453292519943295 # вычислить арксинус asn = math.asin(n_rad) # asn = 0.17543139267904395
⇑
6. Функция math.
 atan(x). Арктангенс
atan(x). АрктангенсФункция math.atan(x) возвращает арктангенс аргумента x, значение которого задается в радианах. При использовании функции важно помнить допустимые значения x, которые можно задавать при вычислении арктангенса.
Пример.
# Функция math.atan(x) import math n = 60 # n - угол в градусах # конвертировать из градусов в радианы n_rad = n*math.pi/180 # n_rad = 1.0471975511965976 # вычислить арктангенс atn = math.atan(n_rad) # atn = 0.808448792630022
⇑
7. Функция math.atan2(x, y). Арктангенс от x/y
Функция math.atan2(x, y) вычисляет арктангенс угла от деления x на y. Функция возвращает результат от —π до π. Аргументы x, y определяют координаты точки, через которую проходит отрезок от начала координат. В отличие от функции atan(x), данная функция правильно вычисляет квадрант, влияющий на знак результата.
Пример.
# Функция math.atan2(x,y) import math x = -2 y = -1 res = math.atan2(x, y) # res = -2.0344439357957027
⇑
8. Функция math.cos(x). Косинус угла
Функция math.cos(x) вычисляет косинус угла для аргумента x. Значение аргумента x задается в радианах.
Пример.
# Функция math.cos(x) import math x = 0 y = math.cos(x) # y = 1.0 x = math.pi y = math.cos(x) # y = -1.0 x = 2 # 2 радианы y = math.cos(x) # y = -0.4161468365471424
⇑
9. Функция math.sin(x)
Функция math.sin(x) возвращает синус угла от аргумента x, заданного в радианах.
Пример.
# Функция math.sin(x) import math x = math.pi y = math.sin(x) # y = 1.2246467991473532e-16 x = 0 y = math.sin(x) # y = 0.0 x = 2 # 2 радиана y = math.sin(x)
⇑
10. Функция math.hypot(x, y). Евклидовая норма (Euclidean norm)
Функция возвращает Евклидовую норму, которая равна длине вектора от начала координат до точки x, y и определяется по формуле
Пример.
# Функция math.hypot(x, y) import math x = 1.0 y = 1.0 z = math.hypot(x, y) # z = 1.4142135623730951 x = 3.0 y = 4.0 z = math.hypot(x, y) # z = 5.0
⇑
11. Функция math.tan(x). Тангенс угла x
Функция math.tan(x) возвращает тангенс от аргумента x. Аргумент x задается в радианах.
Пример.
# Функция math.tan(x, y) import math x = 1.0 y = math.tan(x) # y = 1.5574077246549023 x = 0.0 y = math.tan(x) # y = 0.0
⇑
Связанные темы
- Теоретико-числовые функции и функции представления
- Степенные и логарифмические функции
- Гиперболические функции
- Специальные функции и константы
⇑
stdlib.real.html
Этот файл содержит основы теории действительных чисел и несколько дополнительные теории классических вещественных функций.
Вещественные числа и основные унарные и бинарные операторы
модуль Вещественный
постоянный ноль: реальный = 0,0
постоянный один: реальный = 1,0
val (=) (x y : real) : bool обеспечивает { результат <-> x = y }
функция val (-_) действительная : действительная
функция val (+) реальное реальное : реальное
функция val (*) реальное реальное : реальное
предикат val (<) реальное реальное : bool
пусть предикат (>) (x y : вещественный) = y < x
пусть предикат (<=) (x y : реальный) = x < y || х = у
пусть предикат (>=) (x y : реальный) = y <= x
клонировать экспорт алгебры. OrderedField с типом t = реальный,
постоянный ноль = ноль, постоянный один = один,
функция (-_) = (-_), функция (+) = (+),
функция (*) = (*), предикат (<=) = (<=)
пусть (-) (x y : реальный)
гарантирует { результат = x - y }
= х + -у
val (/) (x y:real) : real
требуется {y <> 0.0}
гарантирует {результат = x/y}
конец
OrderedField с типом t = реальный,
постоянный ноль = ноль, постоянный один = один,
функция (-_) = (-_), функция (+) = (+),
функция (*) = (*), предикат (<=) = (<=)
пусть (-) (x y : реальный)
гарантирует { результат = x - y }
= х + -у
val (/) (x y:real) : real
требуется {y <> 0.0}
гарантирует {результат = x/y}
конец
Альтернативные инфиксные операторы
Эту теорию следует использовать вместо Real, когда нужно использовать оба целочисленные и действительные бинарные операторы.
модуль RealInfix использовать реальный пусть функция (+.) (x:real) (y:real) : real = x + y пусть функция (-.) (x:real) (y:real) : real = x - y пусть функция ( *.) (x:real) (y:real) : real = x * y функция (/.) (x:real) (y:real) : real = x/y пусть функция (-._) (x:real) : real = - x функция inv (x:real) : real = Real.inv x пусть (=.) (x: вещественное) (y: вещественное) = x = y пусть предикат (<=.) (x:real) (y:real) = x <= y пусть предикат (>=.) (x:real) (y:real) = x >= y пусть предикат ( <.) (x:real) (y:real) = x < y пусть предикат (>.) (x:real) (y:real) = x> y val (/.) (x y:real) : real требуется {y <> 0.0} гарантирует {результат = х/. у } конец
Абсолютное значение
Модуль Абс.
использовать реальный
function abs(x : real) : real = если x >= 0.0, то x иначе -x
лемма Abs_le: forall x y:real. абс х <= у <-> -у <= х <= у
лемма Abs_pos: forall x:real. абс х >= 0,0
лемма Abs_sum: forall x y:real. абс(х+у) <= абс х + абс у
лемма Abs_prod: forall x y:real. абс (х * у) = абс х * абс у
лемма triangular_inequality:
forall x y z: реальный. абс (x-z) <= абс (x-y) + абс (y-z)
конец
Минимум и максимум
модуль Мин.Макс. использовать реальный клонировать отношения экспорта.MinMax с типом t = реальный, предикат le = (<=), цель . конец
Вставка целых чисел в вещественные числа
модуль FromInt использовать int.Int как Int использовать реальный функция from_int int: реальный аксиома Ноль: from_int 0 = 0.0 аксиома первая: from_int 1 = 1.0 аксиома Добавить: forall x y:int. from_int (Int.(+) x y) = from_int x + from_int y аксиома Под: forall x y:int. from_int (Int.(-) x y) = from_int x - from_int y аксиома Мул: forall x y:int. from_int (Int.(*) x y) = from_int x * from_int y аксиома Отрицательное: для всех x:int. from_int (Int.(-_) (x)) = - from_int x лемма Инъективный: forall x y: инт. from_int x = from_int y -> x = y аксиома монотонная: forall x y:int. Int.(<=) x y -> from_int x <= from_int y конец
Различные функции усечения
модуль Truncate использовать реальный использовать FromInt
truncate: округление до нуля
function truncate real : int
аксиома Truncate_int :
для всех я: инт. обрезать (from_int я) = я
аксиома Truncate_down_pos:
для всех x: реальный. х >= 0,0 ->
from_int (усечение x) <= x < from_int (Int.(+) (усечение x) 1)
аксиома Truncate_up_neg:
для всех x: реальный. х <= 0,0 ->
from_int (Int. (-) (урезать x) 1) < x <= from_int (урезать x)
аксиома Real_of_truncate:
для всех x: реальный. x - 1.0 <= from_int (усечение x) <= x + 1.0
аксиома Truncate_monotonic:
forall x y: реальный. x <= y -> Int.(<=) (урезать x) (урезать y)
аксиома Truncate_monotonic_int1:
forall x:real, i:int. x <= from_int i -> Int.(<=) (усекать x) i
аксиома Truncate_monotonic_int2:
forall x:real, i:int. from_int i <= x -> Int.(<=) i (обрезать x)
(-) (урезать x) 1) < x <= from_int (урезать x)
аксиома Real_of_truncate:
для всех x: реальный. x - 1.0 <= from_int (усечение x) <= x + 1.0
аксиома Truncate_monotonic:
forall x y: реальный. x <= y -> Int.(<=) (урезать x) (урезать y)
аксиома Truncate_monotonic_int1:
forall x:real, i:int. x <= from_int i -> Int.(<=) (усекать x) i
аксиома Truncate_monotonic_int2:
forall x:real, i:int. from_int i <= x -> Int.(<=) i (обрезать x)
округление вверх и вниз
этаж функции real : int
функция ceil real : int
аксиома Floor_int :
для всех я: инт. этаж (from_int i) = i
аксиома Ceil_int :
для всех я: инт. ceil (from_int я) = я
аксиома Floor_down:
для всех x: реальный. from_int (этаж x) <= x < from_int (Int.(+) (этаж x) 1)
аксиома
для всех x: реальный. from_int (Int.(-) (ceil x) 1) < x <= from_int (ceil x)
аксиома Floor_monotonic:
forall x y: реальный. x <= y -> Int.(<=) (этаж x) (этаж y)
аксиома Ceil_monotonic:
forall x y: реальный. x <= y -> Int.(<=) (ceil x) (ceil y)
конец
x <= y -> Int.(<=) (ceil x) (ceil y)
конец
квадратный и квадратный корень
модуль квадратный
использовать реальный
функция sqr (x : вещественный) : вещественный = x * x
функция val sqrt real : real
аксиома Sqrt_positive:
для всех x: реальный. х >= 0,0 -> sqrt х >= 0,0
аксиома Sqrt_square:
для всех x: реальный. x >= 0,0 -> sqr (sqrt x) = x
аксиома Square_sqrt:
для всех x: реальный. х >= 0,0 -> sqrt (х * х) = х
аксиома Sqrt_mul:
forall x y: реальный. х >= 0,0 /\ у >= 0,0 ->
sqrt (x * y) = sqrt x * sqrt y
аксиома Sqrt_le :
forall x y: реальный. 0.0 <= x <= y -> sqrt x <= sqrt y
конец
Экспонента и логарифм
модуль ExpLog
использовать реальный
val функция выражение реальное: реальное
аксиома Exp_zero : exp(0.0) = 1.0
аксиома Exp_sum : forall x y:real. ехр (х+у) = ехр х * ехр у
постоянная e : real = exp 1.0
журнал функции val реальный : реальный
аксиома Log_one : log 1.0 = 0.0
аксиома Log_mul :
forall x y: реальный. х > 0,0 /\ у > 0,0 -> журнал (х * у) = журнал х + журнал у
аксиома Log_exp: forall x:real. журнал (эксп х) = х
аксиома Exp_log: forall x:real. х > 0,0 -> ехр (лог х) = х
функция log2 (x: действительная) : действительная = log x / log 2.0
функция log10 (x : реальное): действительное = log x / log 10,0
конец
х > 0,0 /\ у > 0,0 -> журнал (х * у) = журнал х + журнал у
аксиома Log_exp: forall x:real. журнал (эксп х) = х
аксиома Exp_log: forall x:real. х > 0,0 -> ехр (лог х) = х
функция log2 (x: действительная) : действительная = log x / log 2.0
функция log10 (x : реальное): действительное = log x / log 10,0
конец
Степень действительного числа в целое число
модуль PowerInt
использовать int.Int
использовать RealInfix
клонировать экспорт int.Exponentiation с
тип t = реальный, постоянный один = реальный.один, функция (*) = реальный.(*),
цель Assoc, цель Unit_def_l, цель Unit_def_r, аксиома Power_0, аксиома Power_s
лемма Pow_ge_one:
forall x:real, n:int. 0 <= п/\ 1,0 <=. х -> 1,0 <=. мощность х п
конец
Степень действительного числа в действительном показателе
Модуль PowerReal
использовать реальный
использовать ExpLog
функция pow real real : real
аксиома Pow_def:
forall x y: реальный. x > 0.0 -> pow x y = exp (y * log x)
лемма Pow_pos:
для всех х у. х > 0,0 -> мощность х у > 0,0
лемма Pow_plus :
для всех x y z. z > 0,0 -> pow z (x + y) = pow z x * pow z y
лемма Pow_mult :
для всех x y z. x > 0.0 -> pow (pow x y) z = pow x (y * z)
лемма Pow_x_zero:
для всех x: реальный. х > 0,0 -> мощность х 0,0 = 1,0
лемма Pow_x_one:
для всех x: реальный. х > 0,0 -> мощность х 1,0 = х
лемма Pow_one_y:
вообще у: настоящий. мощность 1,0 у = 1,0
использовать квадрат
лемма Pow_x_two:
для всех x: реальный. х > 0,0 -> мощность х 2,0 = кв х
лемма Pow_half:
для всех x: реальный. х> 0,0 -> мощность х 0,5 = квадратный х
использовать FromInt
использовать внутреннюю мощность
лемма pow_from_int: forall x y: int. Int.(<) 0 x -> Int.(<=) 0 y ->
pow (from_int x) (from_int y) = from_int (степень x y)
конец
х > 0,0 -> мощность х у > 0,0
лемма Pow_plus :
для всех x y z. z > 0,0 -> pow z (x + y) = pow z x * pow z y
лемма Pow_mult :
для всех x y z. x > 0.0 -> pow (pow x y) z = pow x (y * z)
лемма Pow_x_zero:
для всех x: реальный. х > 0,0 -> мощность х 0,0 = 1,0
лемма Pow_x_one:
для всех x: реальный. х > 0,0 -> мощность х 1,0 = х
лемма Pow_one_y:
вообще у: настоящий. мощность 1,0 у = 1,0
использовать квадрат
лемма Pow_x_two:
для всех x: реальный. х > 0,0 -> мощность х 2,0 = кв х
лемма Pow_half:
для всех x: реальный. х> 0,0 -> мощность х 0,5 = квадратный х
использовать FromInt
использовать внутреннюю мощность
лемма pow_from_int: forall x y: int. Int.(<) 0 x -> Int.(<=) 0 y ->
pow (from_int x) (from_int y) = from_int (степень x y)
конец
Тригонометрические функции
См. страницу в Википедии.
модуль Тригонометрия
использовать реальный
использовать квадрат
использовать Абс
функция cos real : real
функция sin real : real
аксиома Pyphagorean_identity:
для всех x: реальный. sqr (cos x) + sqr (sin x) = 1,0
лемма Cos_le_one: для всех x:real. абс (cos x) <= 1,0
лемма Sin_le_one: для всех x:real. абс (sin x) <= 1,0
аксиома Cos_0: cos 0,0 = 1,0
аксиома Sin_0: sin 0.0 = 0.0
val константа пи : действительная
аксиома Pi_double_precision_bounds:
0x1.921fb54442d18p+1 < пи < 0x1.921fb54442d19p+1
(*
аксиома Pi_интервал:
3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196
< пи <
3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038197
*)
аксиома Cos_pi: cos pi = -1,0
аксиома Sin_pi: sin pi = 0,0
аксиома Cos_pi2: cos (0,5 * пи) = 0,0
аксиома Sin_pi2: sin (0,5 * pi) = 1,0
аксиома Cos_plus_pi: forall x:real. соз (х + пи) = - соз х
аксиома Sin_plus_pi: forall x:real.
sqr (cos x) + sqr (sin x) = 1,0
лемма Cos_le_one: для всех x:real. абс (cos x) <= 1,0
лемма Sin_le_one: для всех x:real. абс (sin x) <= 1,0
аксиома Cos_0: cos 0,0 = 1,0
аксиома Sin_0: sin 0.0 = 0.0
val константа пи : действительная
аксиома Pi_double_precision_bounds:
0x1.921fb54442d18p+1 < пи < 0x1.921fb54442d19p+1
(*
аксиома Pi_интервал:
3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196
< пи <
3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038197
*)
аксиома Cos_pi: cos pi = -1,0
аксиома Sin_pi: sin pi = 0,0
аксиома Cos_pi2: cos (0,5 * пи) = 0,0
аксиома Sin_pi2: sin (0,5 * pi) = 1,0
аксиома Cos_plus_pi: forall x:real. соз (х + пи) = - соз х
аксиома Sin_plus_pi: forall x:real. грех (х + пи) = - грех х
аксиома Cos_plus_pi2: для всех x:real. потому что (х + 0,5 * пи) = - грех х
аксиома Sin_plus_pi2: forall x:real. грех (х + 0,5 * пи) = потому что х
аксиома Cos_neg:
для всех x: реальный. потому что (-х) = потому что х
аксиома Sin_neg:
для всех x: реальный. грех (-х) = - грех х
аксиома Cos_sum:
forall x y: реальный. cos (x + y) = cos x * cos y - sin x * sin y
аксиома Sin_sum:
forall x y: реальный. грех (x+y) = грех x * cos y + cos x * sin y
функция tan (x : вещественный) : вещественный = sin x / cos x
функция atan real : real
аксиома Tan_atan:
для всех x: реальный. загар (атан х) = х
конец
грех (х + пи) = - грех х
аксиома Cos_plus_pi2: для всех x:real. потому что (х + 0,5 * пи) = - грех х
аксиома Sin_plus_pi2: forall x:real. грех (х + 0,5 * пи) = потому что х
аксиома Cos_neg:
для всех x: реальный. потому что (-х) = потому что х
аксиома Sin_neg:
для всех x: реальный. грех (-х) = - грех х
аксиома Cos_sum:
forall x y: реальный. cos (x + y) = cos x * cos y - sin x * sin y
аксиома Sin_sum:
forall x y: реальный. грех (x+y) = грех x * cos y + cos x * sin y
функция tan (x : вещественный) : вещественный = sin x / cos x
функция atan real : real
аксиома Tan_atan:
для всех x: реальный. загар (атан х) = х
конец
Гиперболические функции
См. страницу в Википедии.
модуль Гиперболический
использовать реальный
использовать квадрат
использовать ExpLog
функция sinh (x : действительное) : действительное = 0,5 * (exp x - exp (-x))
функция ch (x : действительное) : действительное = 0,5 * (exp x + exp (-x))
функция tanh (x : вещественный) : вещественный = sinh x / ch x
функция asinh (x: вещественное число): вещественное значение = log (x + sqrt (sqr x + 1,0))
функция acosh (x : реальное) : реальное
аксиома Acosh_def:
для всех x: реальный. x >= 1,0 -> acosh x = log (x + sqrt (sqr x - 1,0))
функция atanh (x : реальный) : реальный
аксиома Atanh_def:
для всех x: реальный. -1,0 < x < 1,0 -> atanh x = 0,5 * log ((1,0+x)/(1,0-x))
конец
x >= 1,0 -> acosh x = log (x + sqrt (sqr x - 1,0))
функция atanh (x : реальный) : реальный
аксиома Atanh_def:
для всех x: реальный. -1,0 < x < 1,0 -> atanh x = 0,5 * log ((1,0+x)/(1,0-x))
конец
Полярные координаты
См. страницу в Википедии.
модуль Полярный
использовать реальный
использовать квадрат
использовать тригонометрию
гипотетическая функция (x y : действительная) : действительная = sqrt (sqr x + sqr y)
функция atan2 реальное реальное: реальное
аксиома X_from_polar:
forall x y: реальный. x = гипот x y * cos (atan2 y x)
аксиома Y_from_polar:
forall x y: реальный. y = гипот x y * sin (atan2 y x)
конец
Вычисления по формулам
Вычисления по формулам $$ \newcommand{\tp}{\thinspace .} $$« Предыдущий | Далее » |
Эта глава взята из книги HP Langtangen A Primer on Scientific Programming with Python, 5-е издание, Springer, 2016.
Математические формулы часто включают такие функции, как sin, cos,
tan, sinh, cosh, exp, log и т. д. На карманном калькуляторе у вас есть
специальные кнопки для таких функций. Точно так же в программе вы также
иметь готовый функционал для оценки этих типов
математические функции. В принципе можно написать свою программу
для вычисления, например, функции \(\sin(x)\), но как это сделать в
Эффективный способ - нетривиальная тема. Над этим работали специалисты
проблему на десятилетия и реализовали свои лучшие рецепты в кусках
программное обеспечение, которое мы должны повторно использовать. В этом разделе рассказывается, как добраться
sin, cos и подобные функции в контексте Python.
92 - 2gy_c}}\right)/g\tp
\тег{4}
\end{уравнение}
$$
Есть два решения, потому что мяч достигает высоты \( y_c \) на
на пути вверх \( (t=t_1 \)) и на пути вниз (\( t=t_2 > t_1 \)).
д. На карманном калькуляторе у вас есть
специальные кнопки для таких функций. Точно так же в программе вы также
иметь готовый функционал для оценки этих типов
математические функции. В принципе можно написать свою программу
для вычисления, например, функции \(\sin(x)\), но как это сделать в
Эффективный способ - нетривиальная тема. Над этим работали специалисты
проблему на десятилетия и реализовали свои лучшие рецепты в кусках
программное обеспечение, которое мы должны повторно использовать. В этом разделе рассказывается, как добраться
sin, cos и подобные функции в контексте Python.
92 - 2gy_c}}\right)/g\tp
\тег{4}
\end{уравнение}
$$
Есть два решения, потому что мяч достигает высоты \( y_c \) на
на пути вверх \( (t=t_1 \)) и на пути вниз (\( t=t_2 > t_1 \)).
Программа
Чтобы оценить выражения для \( t_1 \) и \( t_2 \) из
(4) в компьютерной программе нам нужен доступ к
функция квадратного корня. В Python функция извлечения квадратного корня и множество
другие математические функции, такие как sin, cos, sinh, exp и log,
доступны в модуле под названием математика . Сначала мы должны импортировать
модуль, прежде чем мы сможем его использовать, то есть мы должны написать
Сначала мы должны импортировать
модуль, прежде чем мы сможем его использовать, то есть мы должны написать import math .
После этого, чтобы извлечь квадратный корень из переменной из , мы можем написать мат.кв.(а) . Это демонстрируется в программе для вычисления \( t_1 \)
и \(t_2\):
v0 = 5 г = 9,81 ук = 0,2 импортировать математику t1 = (v0 - math.sqrt(v0**2 - 2*g*yc))/g t2 = (v0 + math.sqrt(v0**2 - 2*g*yc))/g print 'При t=%g s и %g s высота равна %g m.' % (t1, t2, гк)Вывод этой программы становится
При t=0,0417064 с и 0,977662 с высота 0,2 м.Вы можете найти программу как файл ball_yc.py в папке
src/formulas .Два способа импорта модуля
Стандартный способ импорта модуля, скажем, math , состоит в том, чтобы написать
импорт математикиа затем получить доступ к отдельным функциям в модуле с именем модуля как префикс как в
х = мат.кв.(у)Люди, работающие с математическими функциями, часто находят число
. math.sqrt(y)
math.sqrt(y) менее приятно, чем просто sqrt(y) . К счастью, есть
альтернативный синтаксис импорта, который позволяет нам пропустить имя модуля
префикс. Этот альтернативный синтаксис имеет форму из импорта модуля.
функция . Конкретным примером являетсяиз математического импорта sqrtТеперь мы можем работать с
sqrt напрямую, без математики . префикс .
Можно импортировать более одной функции:из математического импорта sqrt, exp, log, sinИногда просто пишут
из математического импорта *для импорта всех функций в модуль
math . Сюда входят грехов , cos , tan , asin , acos , atan , sinh , cosh , tanh 9010 log (основание \(e\)), log10 (основание 10), sqrt , а также известные
числа e и pi . Импорт всех функций из модуля с помощью
звездочка (
Импорт всех функций из модуля с помощью
звездочка ( * ) синтаксис, удобен, но это может сильно вылиться
дополнительных имен в программе, которые не используются. это вообще
рекомендуется не импортировать больше функций, чем реально
используется в программе. Тем не менее, удобство компактного из математического импорта * синтаксис иногда побеждает общий
рекомендация среди практиков - и в этом документе. С оператором from math import sqrt мы можем написать
формулы для корней в более приятной форме:
t1 = (v0 - sqrt(v0**2 - 2*g*yc))/g
t2 = (v0 + sqrt(v0**2 - 2*g*yc))/g
Импорт с новыми именами
Импортированным модулям и функциям можно давать новые имена в окне импорта.
заявление, например,
импортировать математику как m
# m теперь является именем математического модуля
v = m.sin(m.pi)
из журнала импорта математики как ln
v = пер(5)
из математики импортируйте sin как s, cos как c, log как ln
v = s(x)*c(x) + ln(x)
В Python все является объектом, а переменные относятся к объектам, поэтому
новые переменные могут относиться к модулям и функциям, а также к числам и
струны. Приведенные выше примеры с новыми именами также можно
кодируется путем явного введения новых переменных:
9{-x}\справа)\tp
\тег{5}
\end{уравнение}
$$
Мы можем оценить \( \sinh(x) \) тремя способами: i) вызвав
Приведенные выше примеры с новыми именами также можно
кодируется путем явного введения новых переменных:
9{-x}\справа)\tp
\тег{5}
\end{уравнение}
$$
Мы можем оценить \( \sinh(x) \) тремя способами: i) вызвав math.sinh ,
ii) путем вычисления правой части (5),
используя math.exp , или iii) путем вычисления правой части
(5) с помощью степенных выражений math.e**x и math.e**(-x) . Программа, выполняющая эти три
альтернативные расчеты находятся в файле 3sinh.py. Ядро программы выглядит так
это: из математического импорта sinh, exp, e, pi
х = 2*пи
г1 = грех(х)
г2 = 0,5*(ехр(х) - ехр(-х))
г3 = 0,5*(е**х - е**(-х))
напечатать r1, r2, r3
Вывод из программы
показывает, что все три вычисления дают одинаковые результаты: 267,744894041 267,744894041 267,744894041
Первый взгляд на ошибки округления
В предыдущем примере функция вычисляется в трех разных
математически эквивалентными способами, а вывод из напечатать показывает, что три полученных числа равны. Тем не менее, это не вся история. Попробуем распечатать
Тем не менее, это не вся история. Попробуем распечатать р1 , р2 , r3 с 16 десятичными знаками:
напечатать '%.16f %.16f %.16f' % (r1,r2,r3)
Это утверждение приводит к выводу 267,7448940410164369 267,7448940410164369 267,7448940410163232
Теперь r1 и r2 равны, а r3 разные!
Почему это так? Наша программа вычисляет с действительными числами, а действительные числа нуждаются в
вообще бесконечное число десятичных знаков должно быть представлено точно.
компьютер усекает последовательность десятичных знаков, потому что память
конечный. На самом деле вполне стандартно хранить только 17 цифр в реальном
номер на комп. Как именно это усечение делается, не
объясняется в этом документе, но вы можете прочитать больше в Википедии. На данный момент
цель состоит в том, чтобы сообщить читателю, что реальные числа на компьютере часто
есть небольшая ошибка. Можно представить только несколько действительных чисел
точно, остальные действительные числа являются лишь приближениями.
По этой причине в большинстве арифметических операций используются неточные вещественные числа.
числа, что приводит к неточным расчетам. Подумайте о следующем
два вычисления: \(1/49\cdot 49\) и \(1/51\cdot 51\). Оба выражения
идентичны 1, но когда мы выполняем вычисления в Python,
напечатать '%.16f %.16f' % (1/49.0*49, 1/51.0*51)
результат становится 0,9999999999999999 1,0000000000000000
Причина, по которой мы не получаем точно 1.0 в качестве ответа в первом случае
потому что 1/49неправильно отображается в компьютере. Также
1/51 имеет неточное представление, но ошибка не распространяется
к окончательному ответу. Подводя итог, ошибки в числах с плавающей запятой могут распространяться через
математические расчеты и приводят к ответам, которые только
приближения к точным лежащим в основе математическим значениям. Ошибки
в ответах обычно называют ошибок округления . Как только
вы используете Python в интерактивном режиме, как описано в следующем разделе, вы
довольно часто будут сталкиваться с ошибками округления.
В Python есть специальный модуль decimal , а в пакете SymPy есть модуль
альтернативный модуль mpmath , который позволяет отображать действительные числа.
представлены с регулируемой точностью, так что ошибки округления могут быть
сделать как можно меньше (пример появляется документ
Функции и разветвления
[5]). Однако мы вряд ли будем использовать такие
модули, потому что приближения, подразумеваемые многими математическими методами
применяемые в этом документе, обычно приводят к (гораздо) большим ошибкам
чем вызванные округлением.
93
6 Решить для ? cos(x)=1/2 7 Найдите x sin(x)=-1/2 8 Преобразование градусов в радианы 225 9 Решить для ? cos(x)=(квадратный корень из 2)/2 10 Найдите x cos(x)=(квадратный корень из 3)/2 11 Найдите x sin(x)=(квадратный корень из 3)/2 14 Преобразование градусов в радианы 120 градусов 15 Преобразование градусов в радианы 180 16 Найдите точное значение желтовато-коричневый(195) 92-4 38 Найдите точное значение грех(255) 39 Оценить лог база 27 из 36 40 Преобразование из радианов в градусы 2 шт.

 10.17
10.17

 Функция math.acos(x). Арккосинус угла
Функция math.acos(x). Арккосинус угла atan2(x,y)
import math
x = -2
y = -1
res = math.atan2(x, y) # res = -2.0344439357957027
atan2(x,y)
import math
x = -2
y = -1
res = math.atan2(x, y) # res = -2.0344439357957027 OrderedField с типом t = реальный,
постоянный ноль = ноль, постоянный один = один,
функция (-_) = (-_), функция (+) = (+),
функция (*) = (*), предикат (<=) = (<=)
пусть (-) (x y : реальный)
гарантирует { результат = x - y }
= х + -у
val (/) (x y:real) : real
требуется {y <> 0.0}
гарантирует {результат = x/y}
конец
OrderedField с типом t = реальный,
постоянный ноль = ноль, постоянный один = один,
функция (-_) = (-_), функция (+) = (+),
функция (*) = (*), предикат (<=) = (<=)
пусть (-) (x y : реальный)
гарантирует { результат = x - y }
= х + -у
val (/) (x y:real) : real
требуется {y <> 0.0}
гарантирует {результат = x/y}
конец
 ) (x:real) (y:real) = x >= y
пусть предикат ( <.) (x:real) (y:real) = x < y
пусть предикат (>.) (x:real) (y:real) = x> y
val (/.) (x y:real) : real
требуется {y <> 0.0}
гарантирует {результат = х/. у }
конец
) (x:real) (y:real) = x >= y
пусть предикат ( <.) (x:real) (y:real) = x < y
пусть предикат (>.) (x:real) (y:real) = x> y
val (/.) (x y:real) : real
требуется {y <> 0.0}
гарантирует {результат = х/. у }
конец
 0
аксиома первая: from_int 1 = 1.0
аксиома Добавить:
forall x y:int. from_int (Int.(+) x y) = from_int x + from_int y
аксиома Под:
forall x y:int. from_int (Int.(-) x y) = from_int x - from_int y
аксиома Мул:
forall x y:int. from_int (Int.(*) x y) = from_int x * from_int y
аксиома Отрицательное:
для всех x:int. from_int (Int.(-_) (x)) = - from_int x
лемма Инъективный:
forall x y: инт. from_int x = from_int y -> x = y
аксиома монотонная:
forall x y:int. Int.(<=) x y -> from_int x <= from_int y
конец
0
аксиома первая: from_int 1 = 1.0
аксиома Добавить:
forall x y:int. from_int (Int.(+) x y) = from_int x + from_int y
аксиома Под:
forall x y:int. from_int (Int.(-) x y) = from_int x - from_int y
аксиома Мул:
forall x y:int. from_int (Int.(*) x y) = from_int x * from_int y
аксиома Отрицательное:
для всех x:int. from_int (Int.(-_) (x)) = - from_int x
лемма Инъективный:
forall x y: инт. from_int x = from_int y -> x = y
аксиома монотонная:
forall x y:int. Int.(<=) x y -> from_int x <= from_int y
конец
 (-) (урезать x) 1) < x <= from_int (урезать x)
аксиома Real_of_truncate:
для всех x: реальный. x - 1.0 <= from_int (усечение x) <= x + 1.0
аксиома Truncate_monotonic:
forall x y: реальный. x <= y -> Int.(<=) (урезать x) (урезать y)
аксиома Truncate_monotonic_int1:
forall x:real, i:int. x <= from_int i -> Int.(<=) (усекать x) i
аксиома Truncate_monotonic_int2:
forall x:real, i:int. from_int i <= x -> Int.(<=) i (обрезать x)
(-) (урезать x) 1) < x <= from_int (урезать x)
аксиома Real_of_truncate:
для всех x: реальный. x - 1.0 <= from_int (усечение x) <= x + 1.0
аксиома Truncate_monotonic:
forall x y: реальный. x <= y -> Int.(<=) (урезать x) (урезать y)
аксиома Truncate_monotonic_int1:
forall x:real, i:int. x <= from_int i -> Int.(<=) (усекать x) i
аксиома Truncate_monotonic_int2:
forall x:real, i:int. from_int i <= x -> Int.(<=) i (обрезать x)
 x <= y -> Int.(<=) (ceil x) (ceil y)
конец
x <= y -> Int.(<=) (ceil x) (ceil y)
конец
 х > 0,0 /\ у > 0,0 -> журнал (х * у) = журнал х + журнал у
аксиома Log_exp: forall x:real. журнал (эксп х) = х
аксиома Exp_log: forall x:real. х > 0,0 -> ехр (лог х) = х
функция log2 (x: действительная) : действительная = log x / log 2.0
функция log10 (x : реальное): действительное = log x / log 10,0
конец
х > 0,0 /\ у > 0,0 -> журнал (х * у) = журнал х + журнал у
аксиома Log_exp: forall x:real. журнал (эксп х) = х
аксиома Exp_log: forall x:real. х > 0,0 -> ехр (лог х) = х
функция log2 (x: действительная) : действительная = log x / log 2.0
функция log10 (x : реальное): действительное = log x / log 10,0
конец
 х > 0,0 -> мощность х у > 0,0
лемма Pow_plus :
для всех x y z. z > 0,0 -> pow z (x + y) = pow z x * pow z y
лемма Pow_mult :
для всех x y z. x > 0.0 -> pow (pow x y) z = pow x (y * z)
лемма Pow_x_zero:
для всех x: реальный. х > 0,0 -> мощность х 0,0 = 1,0
лемма Pow_x_one:
для всех x: реальный. х > 0,0 -> мощность х 1,0 = х
лемма Pow_one_y:
вообще у: настоящий. мощность 1,0 у = 1,0
использовать квадрат
лемма Pow_x_two:
для всех x: реальный. х > 0,0 -> мощность х 2,0 = кв х
лемма Pow_half:
для всех x: реальный. х> 0,0 -> мощность х 0,5 = квадратный х
использовать FromInt
использовать внутреннюю мощность
лемма pow_from_int: forall x y: int. Int.(<) 0 x -> Int.(<=) 0 y ->
pow (from_int x) (from_int y) = from_int (степень x y)
конец
х > 0,0 -> мощность х у > 0,0
лемма Pow_plus :
для всех x y z. z > 0,0 -> pow z (x + y) = pow z x * pow z y
лемма Pow_mult :
для всех x y z. x > 0.0 -> pow (pow x y) z = pow x (y * z)
лемма Pow_x_zero:
для всех x: реальный. х > 0,0 -> мощность х 0,0 = 1,0
лемма Pow_x_one:
для всех x: реальный. х > 0,0 -> мощность х 1,0 = х
лемма Pow_one_y:
вообще у: настоящий. мощность 1,0 у = 1,0
использовать квадрат
лемма Pow_x_two:
для всех x: реальный. х > 0,0 -> мощность х 2,0 = кв х
лемма Pow_half:
для всех x: реальный. х> 0,0 -> мощность х 0,5 = квадратный х
использовать FromInt
использовать внутреннюю мощность
лемма pow_from_int: forall x y: int. Int.(<) 0 x -> Int.(<=) 0 y ->
pow (from_int x) (from_int y) = from_int (степень x y)
конец
 sqr (cos x) + sqr (sin x) = 1,0
лемма Cos_le_one: для всех x:real. абс (cos x) <= 1,0
лемма Sin_le_one: для всех x:real. абс (sin x) <= 1,0
аксиома Cos_0: cos 0,0 = 1,0
аксиома Sin_0: sin 0.0 = 0.0
val константа пи : действительная
аксиома Pi_double_precision_bounds:
0x1.921fb54442d18p+1 < пи < 0x1.921fb54442d19p+1
(*
аксиома Pi_интервал:
3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196
< пи <
3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038197
*)
аксиома Cos_pi: cos pi = -1,0
аксиома Sin_pi: sin pi = 0,0
аксиома Cos_pi2: cos (0,5 * пи) = 0,0
аксиома Sin_pi2: sin (0,5 * pi) = 1,0
аксиома Cos_plus_pi: forall x:real. соз (х + пи) = - соз х
аксиома Sin_plus_pi: forall x:real.
sqr (cos x) + sqr (sin x) = 1,0
лемма Cos_le_one: для всех x:real. абс (cos x) <= 1,0
лемма Sin_le_one: для всех x:real. абс (sin x) <= 1,0
аксиома Cos_0: cos 0,0 = 1,0
аксиома Sin_0: sin 0.0 = 0.0
val константа пи : действительная
аксиома Pi_double_precision_bounds:
0x1.921fb54442d18p+1 < пи < 0x1.921fb54442d19p+1
(*
аксиома Pi_интервал:
3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196
< пи <
3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038197
*)
аксиома Cos_pi: cos pi = -1,0
аксиома Sin_pi: sin pi = 0,0
аксиома Cos_pi2: cos (0,5 * пи) = 0,0
аксиома Sin_pi2: sin (0,5 * pi) = 1,0
аксиома Cos_plus_pi: forall x:real. соз (х + пи) = - соз х
аксиома Sin_plus_pi: forall x:real. грех (х + пи) = - грех х
аксиома Cos_plus_pi2: для всех x:real. потому что (х + 0,5 * пи) = - грех х
аксиома Sin_plus_pi2: forall x:real. грех (х + 0,5 * пи) = потому что х
аксиома Cos_neg:
для всех x: реальный. потому что (-х) = потому что х
аксиома Sin_neg:
для всех x: реальный. грех (-х) = - грех х
аксиома Cos_sum:
forall x y: реальный. cos (x + y) = cos x * cos y - sin x * sin y
аксиома Sin_sum:
forall x y: реальный. грех (x+y) = грех x * cos y + cos x * sin y
функция tan (x : вещественный) : вещественный = sin x / cos x
функция atan real : real
аксиома Tan_atan:
для всех x: реальный. загар (атан х) = х
конец
грех (х + пи) = - грех х
аксиома Cos_plus_pi2: для всех x:real. потому что (х + 0,5 * пи) = - грех х
аксиома Sin_plus_pi2: forall x:real. грех (х + 0,5 * пи) = потому что х
аксиома Cos_neg:
для всех x: реальный. потому что (-х) = потому что х
аксиома Sin_neg:
для всех x: реальный. грех (-х) = - грех х
аксиома Cos_sum:
forall x y: реальный. cos (x + y) = cos x * cos y - sin x * sin y
аксиома Sin_sum:
forall x y: реальный. грех (x+y) = грех x * cos y + cos x * sin y
функция tan (x : вещественный) : вещественный = sin x / cos x
функция atan real : real
аксиома Tan_atan:
для всех x: реальный. загар (атан х) = х
конец
 x >= 1,0 -> acosh x = log (x + sqrt (sqr x - 1,0))
функция atanh (x : реальный) : реальный
аксиома Atanh_def:
для всех x: реальный. -1,0 < x < 1,0 -> atanh x = 0,5 * log ((1,0+x)/(1,0-x))
конец
x >= 1,0 -> acosh x = log (x + sqrt (sqr x - 1,0))
функция atanh (x : реальный) : реальный
аксиома Atanh_def:
для всех x: реальный. -1,0 < x < 1,0 -> atanh x = 0,5 * log ((1,0+x)/(1,0-x))
конец
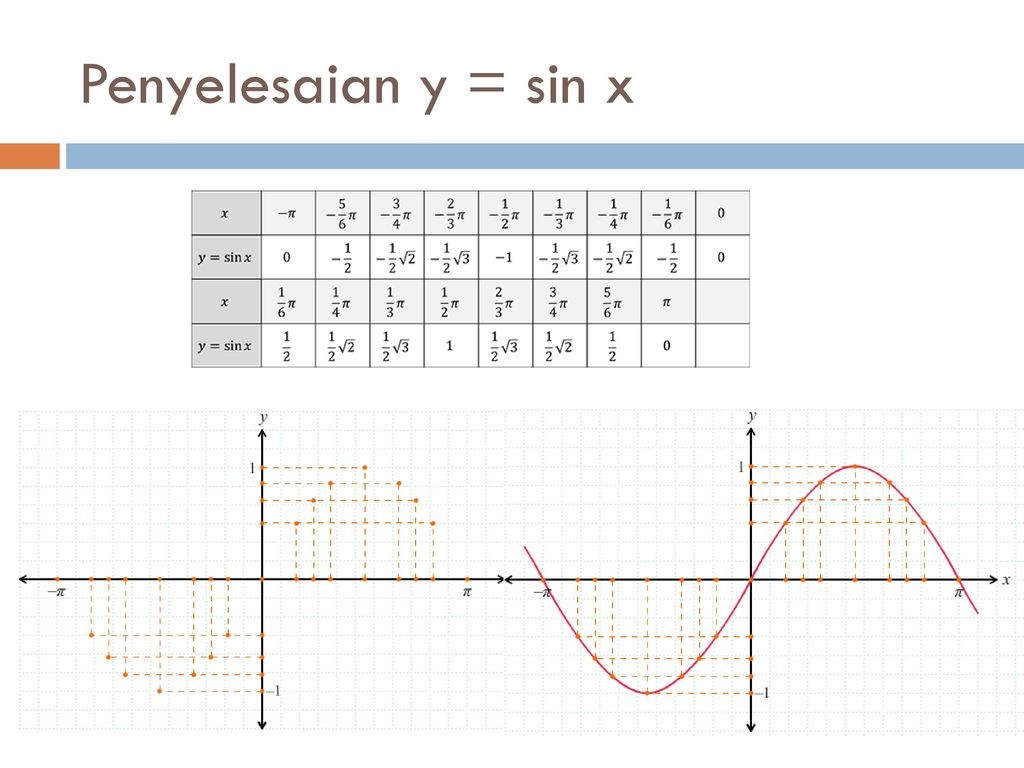 math.sqrt(y)
math.sqrt(y)  Импорт всех функций из модуля с помощью
звездочка (
Импорт всех функций из модуля с помощью
звездочка (  Приведенные выше примеры с новыми именами также можно
кодируется путем явного введения новых переменных:
9{-x}\справа)\tp
\тег{5}
\end{уравнение}
$$
Мы можем оценить \( \sinh(x) \) тремя способами: i) вызвав
Приведенные выше примеры с новыми именами также можно
кодируется путем явного введения новых переменных:
9{-x}\справа)\tp
\тег{5}
\end{уравнение}
$$
Мы можем оценить \( \sinh(x) \) тремя способами: i) вызвав 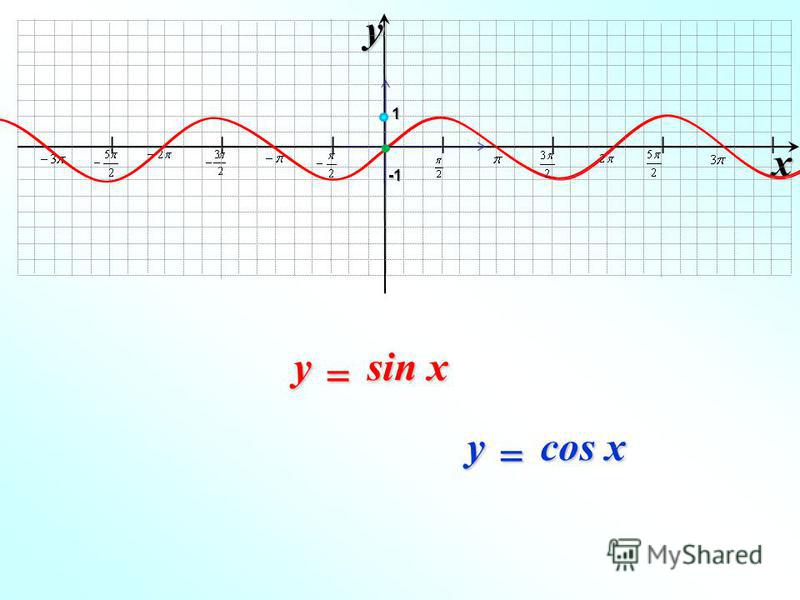 Тем не менее, это не вся история. Попробуем распечатать
Тем не менее, это не вся история. Попробуем распечатать