Умножение координат векторов: Умножение вектора на число — урок. Геометрия, 9 класс.

Сложение и вычитание векторов. Умножение вектора на число в координатах 9 класс онлайн-подготовка на Ростелеком Лицей |

Напоминание предыдущего материала

 

Ранее для выполнения действий с векторами мы применяли правило треугольника, правило параллелограмма, сжимали или растягивали вектор. Теперь мы научимся выполнять действия над векторами в координатах.

 

Пример

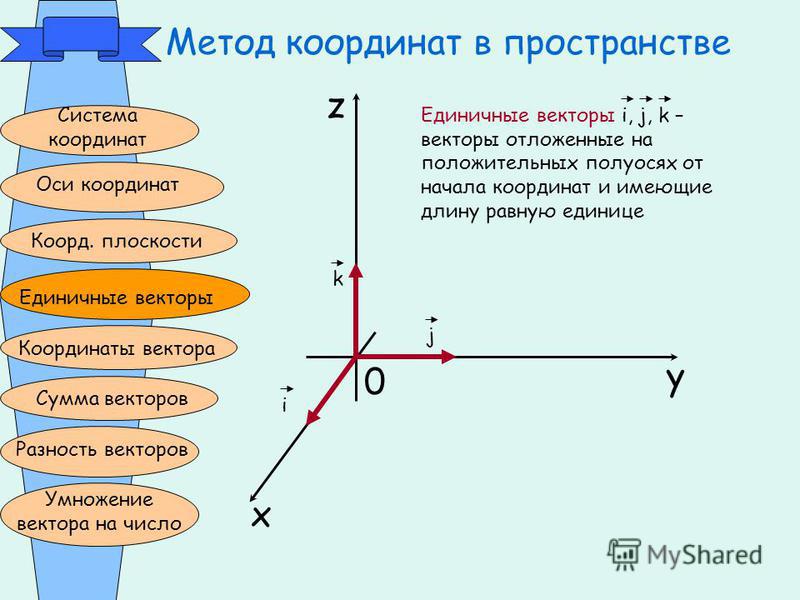
Даны векторы , ,  (см. рис. 1).

Рис. 1. Задача о сложении векторов

Найти:

Решение

Из произвольной точки  строим вектор . Далее из конца вектора  строим вектор , он сонаправлен вектору , а длина в два раза больше. Теперь из конца вектора  строим вектор , он противоположно направлен вектору , а длина в 4 раза больше. Теперь соединяем точку  и конец вектора  – получен ответ, вектор  (см. рис. 2).

Рис. 2. Решение задачи

Пусть заданы два неколлинеарных вектора. Будучи отложены из одной точки, они задают косоугольную систему координат (см. рис. 3).

Рис. 3. Косоугольная система координат

Любой третий вектор однозначно выражается через векторы , :

Пара чисел  однозначно задает вектор – это и есть его координаты: .

 

Сложение векторов в координатах

 

 

Теорема

 

Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.

Дано:; .

Доказать:.

Доказательство

В системе координат относительно векторов ,  имеем:

;

Тогда сумма:

Что и требовалось доказать: .

 

Умножение вектора на число в координатах

 

 

Теорема

 

Каждая координата произведения вектора на число равна произведению соответствующей координаты на это число.

Дано:.

Доказать:.

Доказательство

В системе координат относительно векторов ,  имеем:

Умножим обе части равенства на число :

Что и требовалось доказать: .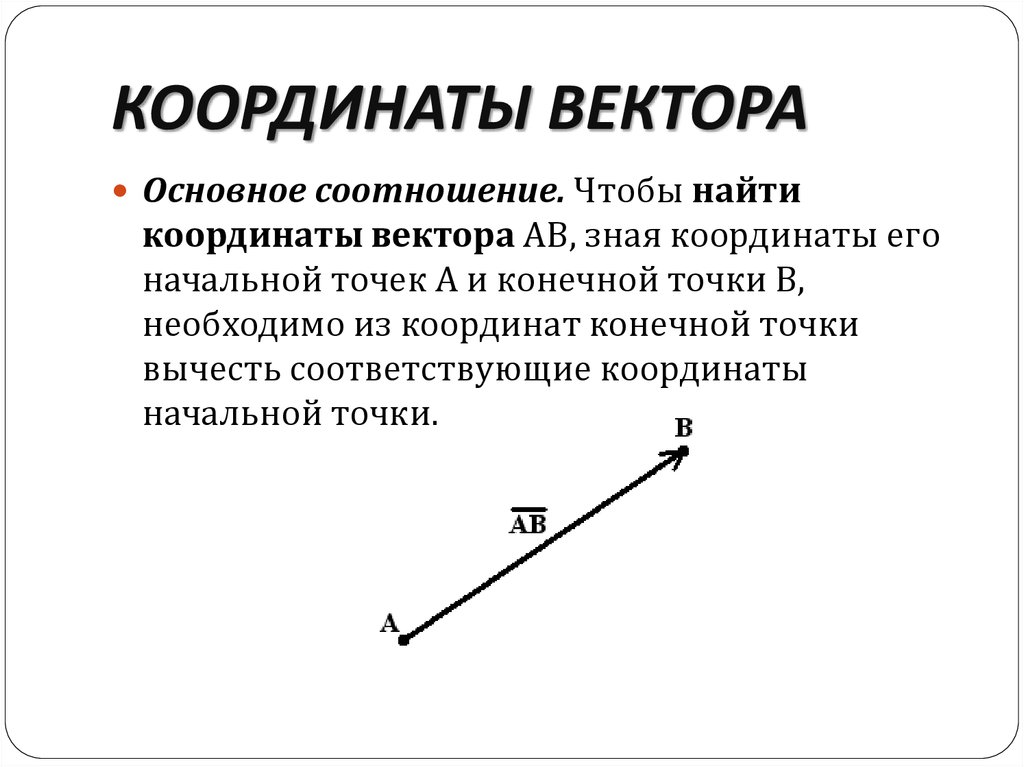

 

Вычитание векторов в координатах

 

 

Рассмотрим разность векторов.

 

Дано: ; .

Координаты вектора  определяем как координаты вектора, умноженного на число:

Тогда разность векторов:

 

Решение примеров

 

 

Пример

 

Доказать, что если два вектора коллинеарны, то их координаты пропорциональны.

Решение

Дано: ; , .

Доказать: ; .

По определению коллинеарных векторов векторы  и  лежат на одной прямой или на параллельных прямых. В таком случае вектор  можно получить из вектора  умножением на некоторое число:

 по условию;  по правилу умножения вектора на число.

Равные векторы имеют равные координаты, отсюда:

;

Что и требовалось доказать.

Пример

; ; ;

Найти попарно коллинеарные векторы.

Решение

Очевидно, что нужно искать пропорциональные координаты. Рассмотрим первый и третий векторы:

Получено верное равенство, следовательно, векторы коллинеарны: .

Рассмотрим второй и четвертый векторы:

Также получено истинное выражение, а значит, векторы коллинеарны: .

Ответ:; .

 

Вывод

 

 

Итак, мы научились складывать и вычитать векторы, умножать вектор на число в координатах.

 

 

Список литературы

1. Атанасян Л.С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.

2. Фарков А.В. Тесты по геометрии: 9 класс. К учебнику Л.С. Атанасяна и др. – М.: Экзамен, 2010.

3. Погорелов А.В. Геометрия, уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-сайт mathprofi.ru (Источник)

2. Интернет-сайт cleverstudents.ru (Источник)

3. Интернет-сайт edu.dvgups.ru (Источник)

 

Домашнее задание

1. Вектор  с началом в точке  имеет координаты . Найдите сумму координат точки .

2. Заданы векторы  и . Найти координаты вектора .

3. Даны векторы  и . Найти векторы ; .

4.Даны векторы ,  и . Найти   и  

 

Умножение вектора на число

Умножение вектора на число

Навигация по странице:

• Геометрическая интерпретация умножения вектора на число.
• Алгебраическая интерпретация умножения вектора на число.
• Формулы умножения вектора на число
  • для плоских задач
  • для пространственных задач
  • для n -мерного вектора
• Свойства вектора умноженного на число
• Примеры задач на умножение вектора и числа
  • плоская задача
  • пространственных задача

Онлайн калькулятор. Умножение вектора на число.

Геометрическая интерпретация.

Произведение ненулевого вектора на число — это вектор, коллинеарный данному (сонаправленный данному, если число положительное, имеющий противоположное направление, если число отрицательное), а его модуль равен модулю данного вектора, умноженному на модуль числа.

Алгебраическая интерпретация. Произведение ненулевого вектора на число — это вектор, координаты которого равны соответствующим координатам данного вектора, умноженным на число.

Формулы умножения вектора на число

Формула умножения вектора на число для плоских задач

В случае плоской задачи произведение вектора a = {a_x ; a_y} и числа k можно найти воспользовавшись следующей формулой:

k · a = {k · a_x ; k · a_y}

Формула умножения вектора на число для пространственных задач

В случае пространственной задачи произведение вектора a = {a_x ; a_y ; a_z} и числа k можно найти воспользовавшись следующей формулой:

k · a = {k · a_x ; k · a_y ; k · a_z}

Формула умножения n -мерного вектора

В случае n-мерного пространства произведение вектора a = {a₁ ; a₂; . .. ; a_n} и числа k можно найти воспользовавшись следующей формулой:

k · a = {k · a₁; k · a₂; … ; k · a_n}

Свойства вектора умноженного на число

Если вектор b равен произведению ненулевого числа k и ненулевого вектора a, то есть b = k · a, тогда:

• b || a — вектора b и a параллельны

• a↑↑b, если k > 0 — вектора b и a сонаправленные, если число k > 0

• a↑↓b, если k < 0 — вектора b и a противоположно направленные, если число k < 0

• |b| = |k| · |a| — модуль вектора b равен модулю вектора a умноженному на модуль числа k

Примеры задач на умножение вектора и числа

Пример умножения вектора на число для плоских задачи

Пример 1. Найти произведение вектора a = {1; 2} на 3.

Решение: 3 · a = {3 · 1; 3 · 2} = {3; 6}.

Пример умножения вектора на число для пространственных задачи

Пример 2. Найти произведение вектора a = {1; 2; -5} на -2.

Решение: (-2) · a = {(-2) · 1; (-2) · 2; (-2) · (-5)} = {-2; -4; 10}.

Вектора Вектор: определение и основные понятия Определение координат вектора заданного координатами его начальной и конечной точки Модуль вектора. Длина вектора Направляющие косинусы вектора Равенство векторов Ортогональность векторов Коллинеарность векторов Компланарность векторов Угол между векторами Проекция вектора Сложение и вычитание векторов Умножение вектора на число Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Линейно зависимые и линейно независимые вектора Разложение вектора по базису

Онлайн калькуляторы с векторами

Онлайн упражнения с векторами на плоскости

Онлайн упражнения с векторами в пространстве

Сложение и скалярное умножение векторов — Концепция

Сложение и скалярное умножение векторов являются основными операциями, которые можно выполнять, используя их геометрическое или алгебраическое представление. Глядя на геометрическое представление, мы можем понимать скалярное

умножение векторов как масштабирование. Сложение векторов можно также выполнить двумя способами, используя геометрическое представление.

компонентов вектора горизонтальная составляющая вертикальная составляющая форма компонента сложение векторов нулевой вектор скалярное умножение

Теперь, когда у нас есть понятие компонентов векторов, мы можем переопределить способ сложения векторов, а также ввести другую операцию, называемую скалярным умножением.
Добавляя векторы алгебраически, предположим, что у нас есть два вектора, данные нам в компонентной форме, поэтому u — это u1, запятая u2, а вектор v — это v1, запятая v2.

Какова будет их сумма? Ну, сумма равна u1+v1, вы добавляете первые компоненты, а затем u2+v2 вы добавляете вторые компоненты, поэтому вы добавляете компоненты двух векторов.
Теперь я также хочу представить идею нулевого вектора. Нулевой вектор — это вектор с компонентами 0, 0 имеет длину 0. Этот вектор обладает тем свойством, что вы можете добавить его к любому другому вектору и получить этот вектор обратно, так что u плюс нулевой вектор равен u, а нулевой вектор плюс u равен u.
Векторы во многом действуют как действительные числа с точки зрения их алгебры, но они не идентичны действительным числам с точки зрения их алгебры, но они немного отличаются. Одно из отличий заключается в том, что умножение векторов немного сложнее, поэтому первый вид умножения, о котором я хочу поговорить, — скалярное умножение. Теперь вы помните, что скаляр — это величина, которая имеет только величину, а не направление, поэтому мы собираемся умножать векторы на скаляры, и давайте посмотрим так: если k — действительное число, а u — некоторый вектор u1, u2, то скаляр несколько k раз u будет определено как ku1, ku2, поэтому вы просто умножаете скаляр на каждый из компонентов, таких как распределение.
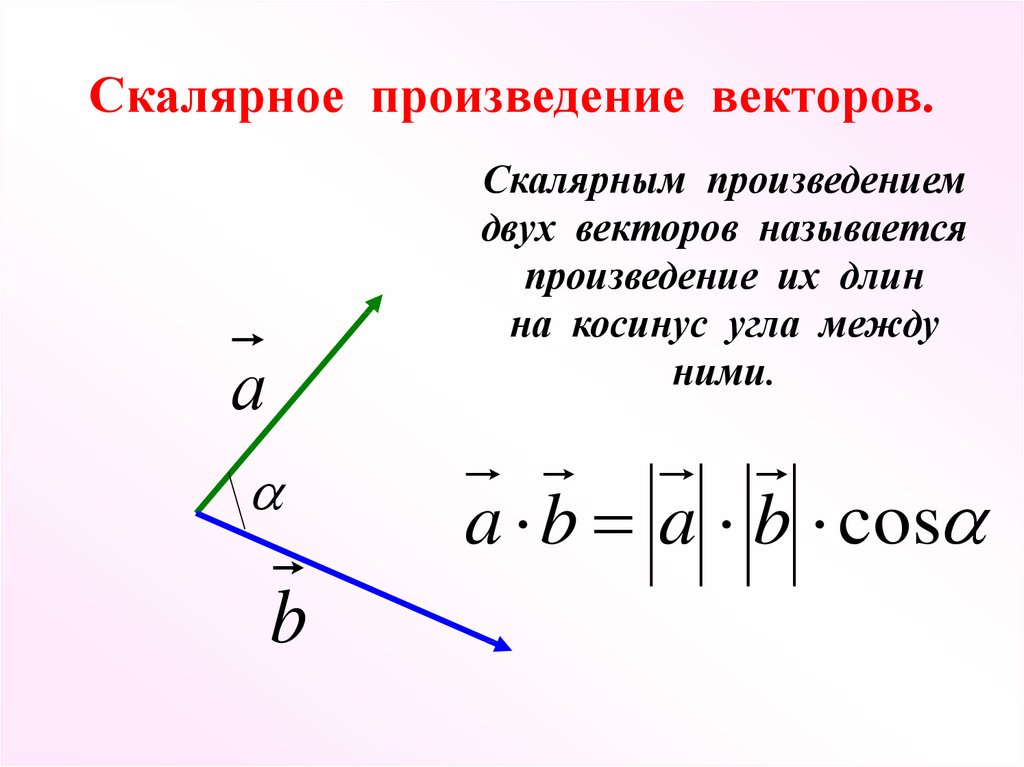
Давайте посмотрим, что делает скалярное умножение на примере, допустим, что u равно -3, 1, и я на самом деле изобразил этот вектор здесь, так что -3, 1 выглядит вот так. Каким бы ты был в 3 раза? Ну, согласно этому определению, я умножаю 3 внутри и получаю -9, 3 умножить на 1 3, так что это 3 умножить на u. -2 умножить на u, я умножаю -2 на -3 и получаю 6, -2 на 1 -2, 6, -2 и 0 скаляр 0 на s вектор u будет равен 0 на -3 0 и 0 на 1 , 0, и это, конечно, вектор 0, поэтому скалярный ноль, умноженный на любой вектор, дает вам нулевой вектор. Просто имейте в виду, что эти два нуля различны, это действительное число 0, а это вектор 0.
Теперь просто хочу, чтобы вы знали, как выглядят эти некоторые из этих векторов. Позвольте мне построить -2 раза u. Его компоненты равны 6, -2, поэтому я иду на 6 вправо и на 2 вниз, чтобы он закончился здесь, поэтому обратите внимание, что этот вектор в конечном итоге будет вдвое длиннее u, так что это -2 раза u, это вдвое больше длинный, но в противоположном направлении, потому что коэффициент k в этом случае отрицательный, и это всегда будет происходить всякий раз, когда вы умножаете вектор на отрицательное число, вы меняете его направление, поэтому скалярное умножение может удлинить или укоротить вектор, и это может изменить свое направление, но если мы умножаем на положительную константу, мы всегда получаем вектор в одном и том же направлении.

оборотов

оборотов

Next:

Векторная производная Up: Векторы и вращения Previous: Перекрестные произведения и аксиальные Содержимое

Для наших пассивных вращений мы перейдем от одного ортонормированного правого базиса к другому ортонормированному,

правосторонняя основа. Обратите внимание, что единичные векторы являются векторами в исходной (не заштрихованной) системе координат.

Если мы вращаем оси координат, мы можем вычислить вектор в новых (штрихованных) координатах исходного вектора путем умножения на Матрица вращения .

Это обычный способ написания матричного умножения.

Немного подумав, мы можем вычислить элементы матрицы поворота . Давайте вычислим вектор , вектор положения в повернутых координатах. Чтобы получить компонент , просто возьмите вектор и добавьте точки к новому единичному вектору , записанный в исходных координатах.

Обратите внимание, что в приведенном выше уравнении — вектор, не зависящий от координат. Компоненты вектора в заштрихованной системе отсчета зависят от заштрихованных осей координат.

Таким образом, матрица вращения просто дается

куда записывается в исходных координатах.

Таким образом, каждый элемент матрицы поворота представляет собой просто косинус угла между новой осью координат и старой осью координат.

Физически легко увидеть, что произведение двух вращений есть просто какое-то другое вращение.

Это означает, что вращения образуют группа . Мы также можем физически увидеть, что вращения (как и матрицы) не коммутируют.

В качестве примера сделаем поворот на небольшой угол в самолет, покидая ось без изменений. Угол между и ось . Угол между и ось тоже . Угол между и ось . Угол между и ось .

Угол между и ось 0. Все остальные углы с оси .

Итак, мы можем написать матрицу вращения.

В трех измерениях вращение в можно сказать, что самолет вращение вокруг ось . Это не так в четырех измерениях.

Можно запишите скалярное произведение между двумя векторами только с точки зрения длин векторов.

Следовательно, сохранение длины векторов подразумевает инвариантность скалярных произведений. Инвариантность скалярных произведений означает, что и длины векторов, и угол между векторами не меняются при вращении.

Воспользуемся тем, что Скалярные произведения являются инвариантными для получения свойства матриц вращения.

, обратная матрице вращения, является ее транспонированием . Мы называем эти матрицы Ортогональные матрицы . Вращения в трех измерениях представляют собой Специальная ортогональная группа SO(3) . Эти матрицы имеют определитель 1. Если мы включим инверсии четности с поворотами, мы получим большее Ортогональная группа O(3) .