Онлайн вычисление ранга матрицы: Онлайн калькулятор. Ранг матрицы

Отыскание ранга матрицы способом окаймляющих миноров — КиберПедия

Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров… Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие… Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования… Интересное: Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все… Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей… Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция

⇐ ПредыдущаяСтр 3 из 10Следующая ⇒ Окаймляющим минором называется минор большего порядка по отношению к данному, если этот минорм большего порядка содержит в себе данный минор. Например, дана матрица . Возьмём минор , окаймляющими будут такие миноры: . Алгоритм нахождения ранга матрицы следующий. 1. Находим не равные нулю миноры второго порядка. Если все миноры второго порядка равны нулю, то ранг матрицы будет равен единице (r =1). 2. Если существует хотя бы один минор второго порядка, не равный нулю, то составляем окаймляющие миноры третьего порядка. Если все окаймляющие миноры третьего порядка равны нулю, то ранг матрицы равен двум ( r =2). 3. Если хотя бы один из окаймляющих миноров третьего порядка не равен нулю, то составляем окаймляющие его миноры. Если все окаймляющие миноры четвёртого порядка равны нулю, то ранг матрицы равен трём (r =2). 4. Продолжаем так, пока позволяет размер матрицы. Пример 1. Найти ранг матрицы . Решение. Минор второго порядка . Окаймляем его. Окаймляющих миноров будет четыре: , , , . Таким образом, все окаймляющие миноры третьего порядка равны нулю, следовательно, ранг данной матрицы равен двум (r =2). Проверить решение можно на калькуляторе онлайн Вычисление ранга матрицы. Пример 2. Найти ранг матрицы . Решение. Ранг данной матрицы равен 1, так как все миноры второго порядка этой матрицы равны нулю (в этом, как и в случаях окаймляющих миноров в двух следующих примерах, дорогим студентам предлагается убедиться самостоятельно, возможно, используя правила вычисления определителей), а среди миноров первого порядка, то есть среди элементов матрицы, есть не равные нулю. Проверить решение можно на калькуляторе онлайн Вычисление ранга матрицы. Пример 3. Найти ранг матрицы . Решение. Минор второго порядка этой матрицы , в все миноры третьего порядка этой матрицы равны нулю. Следовательно, ранг данной матрицы равен двум. Проверить решение можно на калькуляторе онлайн Вычисление ранга матрицы. Пример 4. Найти ранг матрицы . Решение. Ранг данной матрицы равен 3, так как единственный минор третьего порядка этой матрицы равен 3. Проверить решение можно на калькуляторе онлайн Вычисление ранга матрицы. Нет времени вникать в решение? Можно заказать работу! К началу страницы Пройти тест по теме Матрицы Отыскание ранга матрицы способом элементарных преобразований (методом Гаусса) Уже на примере 1 видно, что задача определения ранга матрицы способом окаймляющих миноров требует вычисления большого числа определителей. Существует, однако, способ, позволяющий свести объём вычислений к минимуму. Этот способ основан на использовании элементарных преобразований матриц и ещё называется также методом Гаусса. Под элементарными преобразованиями матрицы понимаются следующие операции: 1) умножение какой-либо строки или какого либо столбца матрицы на число, отличное от нуля; 2) прибавление к элементам какой-либо строки или какого-либо столбца матрицы соответствующих элементов другой строки или столбца, умноженных на одно и то же число; 3) перемена местами двух строк или столбцов матрицы; 4) удаление «нулевых» строк, то есть таких, все элементы которых равны нулю; 5) удаление всех пропорциональных строк, кроме одной. Теорема. При элементарном преобразовании ранг матрицы не меняется. Другими словами, если мы элементарными преобразованиями от матрицы A перешли к матрице B, то . Используя эту теорему, отправляясь от любой матрицы A всегда можно прийти к такой матрице B, вычисление ранга которой не представляет затруднений. Для этого следует добиться, чтобы матрица B была трапециевидной. Тогда ранг полученной матрицы будет равен числу строк в ней кроме строк, полностью состоящих из нулей. Пример 5. Найти ранг матрицы . Решение. Подвергнем эту матрицу следующим преобразованиям. Ко второй строке прибавим третью, умноженную на — 2, а затем к третьей строке прибывам первую, умноженную на 2, и, наконец, из четвёртой вычтем первую. После этих трёх последовательно выполненных преобразований получим матрицу . Вычитая из четвёртой строки третью, а затем переставив местами вторую и третью строки, получаем матрицу . Получили трапециевидную матрицу. Ранг полученной матрицы равен трём (r=3), так как после вычёркивания последней строки, полностью состоящей из нулей, в ней останется три строки. Желающие могут проверить это решение способом окаймляющих миноров (минор третьего порядка, находящийся в левом верхнем углу, не равен нулю, а все миноры четвёртого порядка равны нулю).   ⇐ Предыдущая12345678910Следующая ⇒ Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций. .. 

Нахождение ранга матрицы — Стоматология в Химках

Матрица математика что это

Из статьи вы узнаете, что такое ранг матрицы, научитесь его находить методом определений, окаймляющих миноров и методом элементарных преобразований (методом Гаусса).

Ранги матриц

Минором k-ого порядка матрицы называется определитель матрицы, вырезанной из заданной матрицы удалением одной или более её строк и столбцов.

Объясним это понятие на примерах. Допустим нам дана матрица

Чтобы найти минор M23 вычёркиваем из неё вторую строку и третий столбец. В результате получаем

Это и есть искомый, нужный нам минор. Посмотрим матрицы низших порядков.

Если нам дана матрица первого порядка, то её минором будет сама эта матрица. Если нам дана матрица второго порядка, допустим

Для матрицы порядка pxn число миноров k-го порядка равно C k p*C k n, где C k p=p!/k!(p-k)!, C k n=n!/k!(n-k)! являются числом сочетаний из p по k и из n по k.

Ранг матрицы — это максимальный порядок её миноров, для которых определитель не равен нулю. Обозначается ранг матрицы A, как rang A.

Из выше приведённого определения можно сделать два важных заключения:

Ранг любой ненулевой матрицы отличен от нуля; Ранг нулевой матрицы равняется нулю.

Эквивалентными матрицами называют матрицы, которые имеют один и тот же ранг.

Методы нахождения ранга матрицы

Каким именно способом нахождения ранга матрицы пользоваться в конкретной ситуации зависит от вашего умения, предпочтений и самой предложенной матрицы.

Нет времени решать самому?

Наши эксперты помогут!

Нахождение ранга матрицы по определению

Нам нужно узнать, какой ранг матрицы А порядка p×n. Для нахождения ранга матрицы по определению последовательность действий и рассуждений следующая:

Проверяем миноры первого порядка. Если все они (именно все) в нашей матрице равны нулю, то rang A = 0; Проверяем миноры второго порядка. Если они оказались равными нулю, то. rang A = 1; Проверяем миноры третьего порядка. Если они нулевые, то rang A = 2.

Продолжаем исследования, каждый раз увеличивая порядок на один. Возможны следующие две ситуации:

Если среди миноров k-го порядка будет иметься хоть один, отличающийся от нуля, а все без исключения миноры (k+1)-го порядка окажутся нулевыми, то ранг будет равным k. Если из миноров k-го порядка хоть один ненулевой, а миноры (k+1)-го порядка получить уже нельзя, то ранг матрицы тоже будет k.

Пример 1. Требуется определить ранг матрицы A

\[\begin5 & 0 & -3 & 0 & 2 \\7 & 0 & -4 & 0 & 3 \\2 & 0 & -1 & 0 & 1\end\]

Решение:

Т. к. размер матрицы 3 на 5, и минимальным из этих чисел является 3, то rang A≤ 3. Связано это с тем, что миноры 4-го порядка из данной матрицы уже не создашь, предел достигнут.

В нашем примере из миноров первого порядка есть те, что не равны нулю. Известно, что для перехода к вычислению миноров второго порядка достаточно, чтобы хоть один из них (не важно какой) был неравным нулю.

Из миноров 2-го порядка \[\begin5 & 0 \\7 & 0\end\] равен нулю, поэтому смотрим следующий минор. Ясно, что \[\begin7 & 0 \\2 & 0\end\] тоже будет равняться нулю. Постараемся найти более удачные варианты. Возможно \[\begin5 & 2 \\7 & 3\end\] нулю не будет равен. Вычислим его. 5*3 – 7*2 = 1.

Наши предположения оправдались. Так как нашёлся хоть один минор второго порядка, который не равен нулю, нужно приступить к исследованию миноров третьего порядка. Выберем тот из них, в котором нет нулей, например:

Вычисляем его. -20 — 18 — 14 + 16 + 21 + 16 = 0. Как видим, он нулевой. Исследовав другие миноры третьего порядка тоже узнаем, что они тоже нулевые. Нет ни одного отличного от нуля. Следовательно, rang A = 2. Задачу можно считать решённой.

Ответ: rang A = 2.

Пример 2. Определить ранг матрицы B

\[\begin-1 & 3 & 2 & -3 \\4 & -2 & 5 & 1 \\-5 & 0 & -4 & 0 \\9 & 7 & 8 & -7\end\]

Это квадратная матрица четвёртого порядка. Ранг её не должен превышать четырёх. Видно, что среди миноров первого ранга есть ненулевые.

Сразу переходим к исследованию миноров второго ранга. Посмотрим, например, \[\begin4 & -2 \\5 & 0 \end\]. Он равен 0 – 10 = -10. Приступаем к исследованию миноров третьего ранга. Возьмём:

Его значение 105 – 105 =0. Придётся исследовать другой подобный минор. Берём

\[\begin-2 & 5 & 1 \\0 & -4 & 0 \\7 & 8 & -7\end\]

Он равен -28, т. е. отличен от нулевого, поэтому переходим к минорам ещё на один порядок выше. Здесь у нас только один выбор – сама матрица.

\[\begin-1 & 3 & 2 & -3 \\4 & -2 & 5 & 1 \\5 & 0 & -4 & 0 \\9 & 7 & 8 & -7\end\]

Её минор равен 86, т. е. опять же отличен от нуля. Это значит, что ранг нашей матрицы равен 4. Решение найдено.

Ответ: rang B = 4.

Нахождение ранга матрицы методом окаймляющих миноров

Во многих случаях он позволяет сократить количество проделываемых вычислений довольно значительно.

Если все миноры, которые окаймляют минор k-го порядка, относящийся к матрице А, имеющей порядок p на n, равны нулю, то все миноры порядка (k+1) матрицы А будут тоже нулевыми.

Алгоритм нахождения ранга матрицы при пользовании этим методом следующий:

Смотрим на миноры первого порядка. Если они все нулевые, значит и ранг нашей матрицы будет равным нулю. Если хотя бы один из них отличен от нуля, переходим к следующему шагу; Смотрим, какие миноры окаймляют минор M1. Если они все равны нулю, то ранг матрицы будет равен 1. При наличии хотя бы одного отличного от нуля ранг матрицы будет равен 2 или числу, превосходящему 2; Исследуем миноры, окаймляющие минор M2.. Они будут третьего порядка. Если все они нулевые, то ранг нашей матрицы будет равным 2. Если найдётся хотя бы один отличный от нуля, то ранг матрицы будет больше или равен 3.

Как и в предыдущем методе, продолжаем исследования, увеличивая каждый раз порядок на 1 до тех пор, пока все миноры не окажутся нулевыми, или не получится составить окаймляющий минор.

Пример 3. Дана матрица С

\[\begin-1 & 2 & 1 & 3 \\-3 & 0 & 5 & 4 \\-5 & 4 & 7 & 10\end\]

Решение: Сразу приступим к исследованию миноров второго порядка. Возьмём \[\begin-1 & 2 \\-3 & 0\end\].

Он будет равным 6, т. е. отличным от нуля.

Составляем окаймляющий минор. Для этого прибавляем к нашему минору следующую строку и следующий столбец. Получаем:

\[\begin-1 & 2 & 1 \\-3 & 0 & 5 \\-5 & 4 & 7\end\]

Он равен нулю. Исследование окаймляющих миноров придётся продолжить. Берём следующий за добавленным столбец и получаем

\[\begin-1 & 2 & 3 \\-3 & 0 & 4 \\-5 & 4 & 10\end\]

Он тоже оказывается равным нулю. Других окаймляющих миноров нет, а значит ранг нашей матрицы будет равен 2. Решение найдено.

Ответ: rang С = 2.

Пример 4. Дана матрица D

\[\begin1 & 2 & 0 & 4 & 5 \\3 & 6 & -2 & -1 & 3 \\-2 & -4 & 2 & 5 & 7 \\-1 & -2 & 2 & 9 & 11\end\]

Как и в предыдущем случае, лучше его начать с вычисления минора второго порядка. Посмотрим \[\begin1 & 2 \\3 & 6\end\]. Он равен нулю. Берём другой минор \[\begin2 & 0 \\6 & -2\end\]. Он оказался равен -4.

Берём один из окаймляющих его миноров, например, \[\begin1 & 2 & 0 \\3 & 6 & -2 \\-2 & -4 & 2\end\].

Он равен нулю. Берём ещё один \[\begin2 & 0 & 4 \\3 & 6 & -2 \\-2 & -4 & 2\end\].

Он также равен нулю.

Посмотрим \[\begin2 & 0 & 5 \\6 & -2 & -3 \\-4 & 2 & 7\end\]. Он равен 4.

Переходим к четвёртому порядку.

\[\begin1 & 2 & 0 & 5 \\3 & 6 & -2 & -3 \\-2 & -4 & 2 & 7 \\-1 & -3 & 2 & 1\end\]

Он равен нулю. Придётся взять другой.

\[\begin2 & 0 & 4 & 5 \\6 & -2 & -1 & -3 \\-4 & 2 & 5 & 7 \\-2 & 2 & 9 & 11\end\]

Он оказывается также равным нулю. Т. к. последний ненулевой минор у нас был третьего порядка, то и ранг матрицы будет равным 3. Решение найдено.

Ответ: rang E = 3.

Нахождение ранга матрицы методом элементарных преобразований или методом Гаусса

Под элементарными преобразованиями понимают перестановку строк, умножение строки на отличное от нуля число, прибавление к одной из строк, умноженных на некоторое число элементов другой строки.

Все указанные преобразования не меняют ранга матрицы. Пользуясь ими можно привести матрицу к виду, когда все из её элементов кроме a11, a22, a33 … arr будут равны нулю, а значит ранг матрицы станет равняться r.

При нахождении ранга матрицы методом Гаусса нужно предвидеть, какие преобразования приведут к упрощению матрицы, а какие нет. К сожалению, сделать это далеко не всегда бывает просто.

Дана матрица F

\[\begin25 & 31 & 17 & 43 \\75 & 94 & 53 & 132 \\75 & 94 & 54 & 134 \\25 & 32 & 20 & 48\end\]

Из третьей строки этой матрицы вычитаем вторую, Из второй строки вычитаем первую

\[\begin25 & 31 & 17 & 43 \\75 & 94 & 53 & 132 \\0 & 0 & 1 & 2 \\0 & 1 & 2 & 5\end\]

Далее из второй строки вычитаем первую, умноженную на три

\[\begin25 & 31 & 17 & 43 \\0 & 1 & 2 & 3 \\0 & 0 & 1 & 2 \\0 & 1 & 3 & 5\end\]

Из четвёртой строки отнимаем третью и вторую

\[\begin25 & 31 & 17 & 43 \\0 & 1 & 2 & 3 \\0 & 0 & 1 & 2 \\0 & 0 & 0 & 0\end\]

Из четвёртого столбца вычитаем третий, предварительно помноженный на два

\[\begin25 & 31 & 17 & 0 \\0 & 1 & 2 & -1 \\0 & 0 & 1 & 0 \\0 & 0 & 0 & 0\end\]

Делим первый столбец на 25 и вычитаем из второго столбца первый, до этого помножив его на 31

\[\begin1 & 0 & 17 & 9 \\0 & 1 & 2 & -1 \\0 & 0 & 1 & 0 \\0 & 0 & 0 & 0\end\]

От третьего столбца отнимаем первый до этого помножив его на 17, а второй на 2; от четвёртого столбца отнимаем первый, умноженный на 9 и прибавляем второй, помноженный на 2

\[\begin1 & 0 & 0 & 0 \\0 & 1 & 0 & 0 \\0 & 0 & 1 & 0 \\0 & 0 & 0 & 0\end\]

Так как ранг полученной матрицы равен 3, то у исходной матрицы он тоже будет равняться 3.

Решение найдено.

Ответ: rang F = 3.

Как видите, находить ранг даже больших матриц с неравным количеством строк и столбцов достаточно просто. Чтобы проделывать указанную математическую операцию без серьёзных для себя затруднений, требуется лишь понимание сущности изложенных методов и некоторая практика. После этого проблем у вас возникать не должно.

Из статьи вы узнаете, что такое ранг матрицы, научитесь его находить методом определений, окаймляющих миноров и методом элементарных преобразований (методом Гаусса).

Минором k-ого порядка матрицы называется определитель матрицы, вырезанной из заданной матрицы удалением одной или более её строк и столбцов.

Объясним это понятие на примерах. Допустим нам дана матрица

Чтобы найти минор M23 вычёркиваем из неё вторую строку и третий столбец. В результате получаем

Это и есть искомый, нужный нам минор. Посмотрим матрицы низших порядков.

Если нам дана матрица первого порядка, то её минором будет сама эта матрица. Если нам дана матрица второго порядка, допустим

Для матрицы порядка pxn число миноров k-го порядка равно C k p*C k n, где C k p=p!/k!(p-k)!, C k n=n!/k!(n-k)! являются числом сочетаний из p по k и из n по k.

Ранг матрицы — это максимальный порядок её миноров, для которых определитель не равен нулю. Обозначается ранг матрицы A, как rang A.

Из выше приведённого определения можно сделать два важных заключения:

Ранг любой ненулевой матрицы отличен от нуля; Ранг нулевой матрицы равняется нулю.

Эквивалентными матрицами называют матрицы, которые имеют один и тот же ранг.

Наши эксперты помогут.

Www. napishem. ru

06.04.2018 16:34:30

2017-08-13 18:00:15

Источники:

Https://www. napishem. ru/spravochnik/matematika/nahozhdenie-ranga-matritsy. html

Примеры решения матриц: виды матриц, формулы » /> » /> .keyword { color: red; }

Матрица математика что это

Матрица — это математическая таблица с числовыми значениями. Обозначаются матрицы латинскими знаками.

Есть два вида матриц:

Комплексные матрицы. Одно из чисел равно комплексному. Действительные матрицы. Матрица в которой содержаться действительные числа.

С матрицей выполняют самые простейшие действия: умножение, деление, сложение, вычитание и трансформацию. Данные действия можно совершать тогда, когда матрицы схожи меж собой, чтобы в самом конце вышло выражение схожей размерности. Сложение и вычитание производятся подобно друг другу.

Эти числа, являются элементами матрицы.

Матрицу можно записать в следующем виде:

Квадратная матрица — это число строк, которое равно числу столбцов (m=n), при этом число N – это порядок матрицы.

Пример квадратной матрицы 3-го порядка:

Главная диагональ квадратной матрицы – это диагональ, которая состоит из a21,a22, a23, идущая из левого верхнего угла этой матрицы в правый нижний угол. Побочной диагональю квадратной матрицы называется диагональ, составленная из элементов идущая из правого верхнего угла этой матрицы в левый нижний угол.

В квадратной матрице, у которой все элементы, стоящие выше или ниже главной диагонали, равны нулю, называют треугольной, пример:

Квадратная матрица, у которой все элементы, стоящие на верхней и нижней грани, равны нулю, является диагональной:

Для того чтобы получить квадратную диагональную матрицу с единичными элементами, нужно использовать букву E. Например, квадратная диагональная матрица 3-го порядка имеет такой вид:

Трансформированием квадратной матрицы называется такое преобразование, при котором ее строки становятся столбцом с теми же номерами, а столбец — строкой.

Матрицу, транспонированную по отношению к матрице A, обозначают А T.

Например, А T для матрицы А 1 имеет вид:

Матрица называется Нулевой, если все ее элементы равны нулю.

Матрицы А и В называются Равными, если они имеют одинаковую размерность, и все их соответствующие элементы совпадают.

Определитель матриц второго и третьего порядка

Определителем второго порядка квадратной матрицы называется число, равное:

Суммой А + В двух матриц А=(аij ) и В= (bij) одинакового размера m*n, называется матрица C=(cij), элементы которой cij=aij + bij, для всех i=1,2,…,m и j=1,2…,n.

Задача

\[ \left(\begin 1 & 4 & 3 \\ 8 & -3 & 2 \end\right)+\left(\begin 3 & 1 & 1 \\ 4 & -1 & 0 \end\right)=\left(\begin 4 & 5 & 4 \\ 12 & -4 & 2 \end\right) \]

Согласно правилу сложения матриц A+O=A, где A — произвольная матрица, а O — нулевая матрица того же размера, что и A.

Вычитание матриц

Разность двух матриц одинакового размера определяется с помощью операции умножения матрицы B на число —1 и последующего сложения матриц A и (—1) B т. е.

Некоторые свойства, присущие операциям над числами, справедливы и для операций над матрицами. В частности, из определений операций умножения матрицы на число и сложения матриц следует, что

Вышеуказанная формула показывает свойство коммуникативности при сложении матриц.

Доказательство. Так как операция сложения определена только для матриц одинакового размера, причем сумма матриц является матрицей того же размера, что и слагаемые матрицы, то очевидно, что размер матрицы

Равен размеру матрицы

Докажем, что и все элементы матрицы F равны соответствующим элементам матрицы G. Из определения суммы двух матриц следует, что:

\[\text I=1,2, \ldots, m \text J=1,2, \ldots, n \].

Согласно определению равенства матриц, это означает, что:

Умножение матриц

Умножение матрицы на матрицу определено, лишь когда число столбцов первой матрицы в произведении равно числу строк второй.

Произведением двух Матриц А и В называется Матрица С, элемент которой, находящийся на пересечении i-й строки и j-го столбца, равен сумме Произведений элементов i-й строки Матрицы А на соответствующие (по порядку) элементы j-го столбца Матрицы В. Произведение матрицы А на Матрицу В обозначается АВ.

Обратим внимание на размеры матрицы C, число строк матрицы-произведения совпадает с числом строк первой, а число столбцов — с числом столбцов второй из перемножаемых матриц (см. Рис. 1).

Пример. Вычислить произведение матриц AB, если

\[ A=\left(\begin 1 & 2 & 3 \\ 5 & 4 & -5 \end\right), \quad B=\left(\begin 1 & 2 & 4 \\ 3 & -3 & 1 \\ 1 & 0 & 2 \end\right) \]

Определим размер матрицы — произведения:

Далее, вычислим элементы матрицы — произведения:

\[ C=\left(\begin 1+6+3 & 2-6+0 & 4+2+6 \\ 5+12-5 & 10-12+0 & 20+4-10 \end\right) =\left(\begin 10 & -4 & 12 \\ 12 & -2 & 14 \end\right) \]

Нет времени решать самому?

Наши эксперты помогут!

Обратная матрица

Прежде чем переходить к понятию обратного выражения матрицы, следует рассмотреть алгоритм её транспонирования. Во время операции строки и столбцы переставляются местами.

На рисунке представлен метод решения обратной матрицы:

Для вычисления матрицы приведем ее к верхнетреугольному виду, используя преобразования над строками матрицы и свойства определителя матрицы.

По аналогии обратная матрица сходна с обратными числами. Например, противоположной цифре 5 будет дробь 1/5 = 5 (-1) степени. Произведение этих чисел равно 1, выглядит оно так: 5*5 (-1) = 1. Умножение обычной матричной таблицы на обратную даст в итоге единичную: А* А (-1) = Е. Это аналог числовой единицы.

Но для начала нужно понять алгоритм вычисления обратной матрицы. Для этого находят её определитель. Разработано два метода решения: с помощью элементарных преобразований или алгебраических дополнений.

Более простой способ решения — путём алгебраических дополнений. Рассмотрим матричную таблицу А, обратная ей А (-1) степени находится по формуле:

Матрица обратного вида возможна только для квадратного размера таблиц 2*2, 3*3 и т. д. Обозначается она надстроенным индексом (-1). Задачу легче рассмотреть на более простом примере, когда размер таблицы равен 2*2.

На первом этапе выполняют действия:

Обратного выражения матрицы не может быть, если определитель равен нулю. В рассматриваемом случае он равен -2, поэтому всё в порядке.

2 этап: рассчитывают матрицу миноров, которая имеет те же знАЧения, что и первоначальная. Под минором k-того порядка понимается определитель квадратной матрицы порядка k*k, составленный из её элементов, которые располагаются в выбранных k — столбцах и k-строках. При этом расположение элементов таблицы не меняется. Чтобы найти минор верхнего левого числа, вычёркивают строчку и столбец, в которых прописан этот элемент. Оставшееся число и будет являться минором. На выходе должна получиться таблица:

Наши эксперты помогут.

Www. napishem. ru

07.09.2019 16:49:40

2019-09-07 16:49:40

Источники:

Https://www. napishem. ru/spravochnik/matematika/primery-resheniya-matric-s-otvetami. html

Что такое определитель матрицы » /> » /> .keyword { color: red; }

Матрица математика что это

Нередко при решении задач в высшей математике требуется провести вычисление определителя матрицы. Для того, чтобы делать это правильно, нужно знать ключевые определения, свойства и различные вычислительные методы. В аналитической геометрии, математическом анализе, линейной алгебре и остальных разделах высшей математики специалисты применяют определитель матрицы.

Что такое матрица?

На первом шаге стоит чётко понимать, что Матрица — типичная таблица, внутри которой расположены цифры. Размерность — основополагающая характеристика матрицы, которая говорит о том, сколько столбцов и строк прописано в матричной структуре. При этом определитель можно посчитать для квадратной матрицы. Принято говорить, что та или иная матрица А имеет размер [m x n], когда в ней расположено M строчек и N столбиков.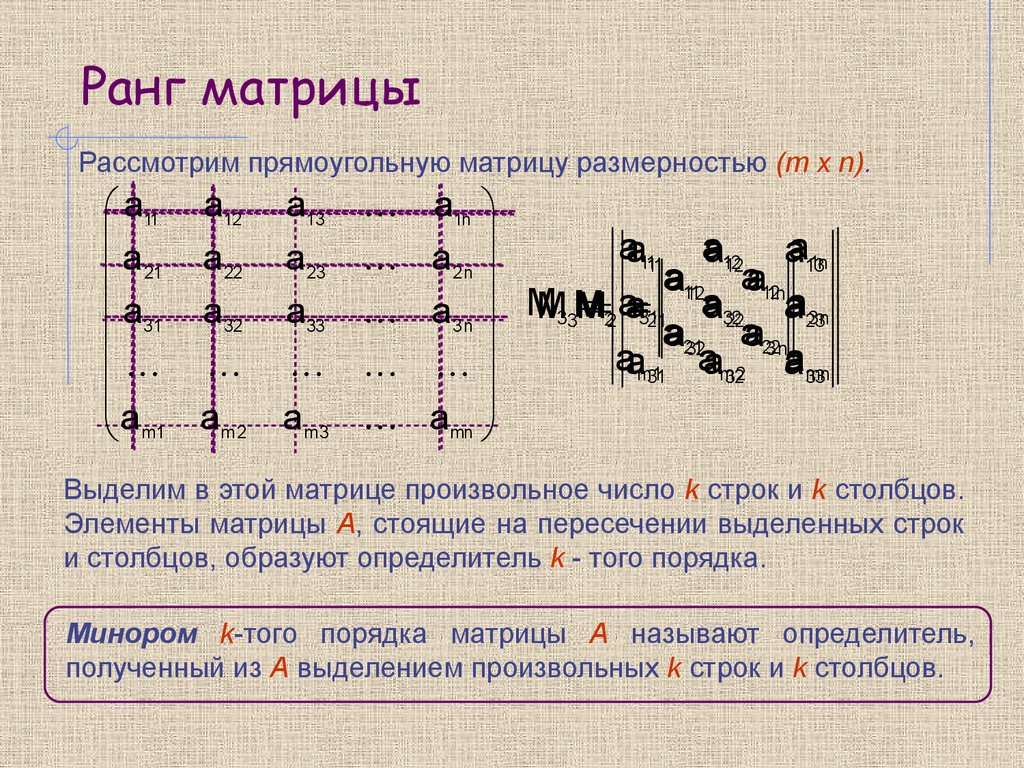 Визуально это выглядит следующим образом: \[A=[m \times n]\].

В некоторых случаях запись такая: \[A=\left(a_\right), \quad 1 \leq i \leq m ; \quad 1 \leq j \leq n\].

7 свойств определителя

Когда 2 строчки/столбца меняются местами, меняется знак у определителя на противоположный; В случае умножения одной строки/столбца на число k, весь определитель также умножится на данное число; Определитель будет неизменным в случае, если взять одну строку и сложить/отнять её любое количество раз из другой; В целом определитель равен 0, когда 2 строчки определителя равны, или пропорциональны, или одна из строчек заполнена нулями; Столбцы также имеют все эти свойства; Определитель будет неизменным, если матрица транспонируется; Определитель произведения матриц численно равен произведению определителей.

Как можно найти определитель матрицы второго порядка?

В основном студенты и ученики получают от преподавателей задание вычислить определитель матрицы второго, третьего, иногда четвёртого порядка. * a_ * a_: a_ * a_\] и \[-a_ * a_\]

В итоге получаем:

Проанализировав ранее сказанное, получаем типовой алгоритм для нахождения определителя матрицы 2-го порядка 2х2:

Если рассмотреть данную формулу на наглядном примере, то это будет вот так:

Вычислить определитель матрицы \[2 \times 2\]:

Итак, у нас получается \[a_=2, a_=3, a_=-6, a_=1\].

Для решения необходимо воспользоваться ранее рассмотренной формулой:

Подставляем числа с примера и находим:

Определитель матрицы второго порядка = 21.

Чтобы упростить понимание процесса, как в данном случае находится определитель матрицы, можно представить такой расчёт: от произведения элементов основной диагонали отнимается произведение элементов другой диагонали.

Нередко при решении задач в высшей математике требуется провести вычисление определителя матрицы. Для того, чтобы делать это правильно, нужно знать ключевые определения, свойства и различные вычислительные методы. В аналитической геометрии, математическом анализе, линейной алгебре и остальных разделах высшей математики специалисты применяют определитель матрицы.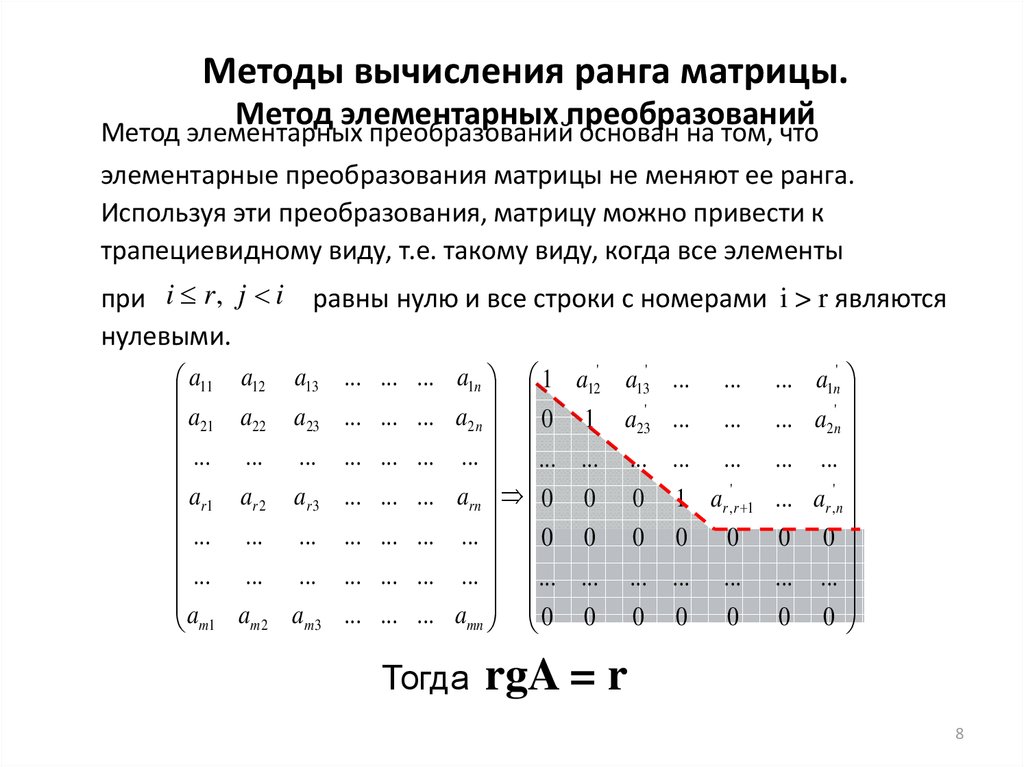

На первом шаге стоит чётко понимать, что Матрица — типичная таблица, внутри которой расположены цифры. Размерность — основополагающая характеристика матрицы, которая говорит о том, сколько столбцов и строк прописано в матричной структуре. При этом определитель можно посчитать для квадратной матрицы. Принято говорить, что та или иная матрица А имеет размер [m x n], когда в ней расположено M строчек и N столбиков. Визуально это выглядит следующим образом: \[A=[m \times n]\].

В некоторых случаях запись такая: \[A=\left(a_\right), \quad 1 \leq i \leq m ; \quad 1 \leq j \leq n\].

Вычислить определитель матрицы 2 times 2.

Www. napishem. ru

11.04.2017 14:44:05

2017-04-11 14:44:05

Источники:

Https://www. napishem. ru/spravochnik/matematika/opredelitel-matritsy-algoritm-i-primery-vychisleniya-opredelitelya-matritsy. html

Калькулятор ранга матрицы с шагами, формулой и решением

Введение в калькулятор ранга матрицы

Калькулятор ранга матрицы — это бесплатный онлайн-инструмент, полезный для вычисления ранга матрицы порядка 2, 3 или 4. Он вычисляет количество ненулевых строки или столбцы, оставшиеся после приведения матрицы к ступенчатой ​​форме.

В матричной алгебре ранг матрицы используется, чтобы узнать, является ли система управляемой или наблюдаемой. Обычно мы используем ранг матрицы, чтобы найти количество ненулевых строк или столбцов. Найти ранг матрицы вручную непросто. Поэтому мы представляем онлайн-инструмент, который может легко вычислить ранг матрицы.

Формула, используемая калькулятором ранга матрицы.

Ранг матрицы — это количество ненулевых строк или столбцов. Он используется для проверки того, является ли матрица вырожденной или невырожденной. Калькулятор рангов использует ступенчатую форму, применяя к матрице операции со строками и столбцами.

Ранг матрицы можно узнать, выполнив следующие шаги:

1. Чтобы сделать матрицу ступенчатой, преобразуйте числа под диагональными элементами в нуль.
2. Чтобы сделать нули, мы можем использовать операции со столбцами или строками.
3. После преобразования в нули количество оставшихся ненулевых строк является рангом матрицы.

Также можно проверить, является ли данная матрица вырожденной или невырожденной, если:

• Если порядок матрицы равен рангу, то матрица будет невырожденной.
• Если порядок матрицы больше ранга, матрица будет вырожденной.

Как рассчитать ранг матрицы с помощью калькулятора?

Вы можете вычислить ранг матрицы, выполнив следующие действия:

1. На первом этапе вам необходимо ввести количество строк и столбцов матрицы в соответствующие поля.
2. Теперь введите значение всех элементов матрицы. Или вы можете использовать случайную кнопку, чтобы выбрать случайную матрицу.
3. Нажмите кнопку расчета.

Вы получите результат через несколько секунд после нажатия на кнопку расчета этого калькулятора ранга матрицы.

Зачем использовать калькулятор для определения ранга матрицы?

Понятие ранга важно в матричной алгебре, поскольку оно проверяет, является ли матрица сингулярной или неособой. Он также используется для нахождения системы линейных уравнений, которая является управляемой или наблюдаемой. Но когда вы делаете расчеты вручную, иногда вы не знаете, какую операцию следует применить. Вы можете застрять на нем. Мы предоставляем вам бесплатный инструмент, который может помочь вам найти ранг матрицы без выполнения каких-либо ручных вычислений, потому что этот инструмент предлагает вам пошаговое решение, в котором объясняется каждая строка операции со столбцом.

Преимущества расчета ранга матрицы с комплексными числами

Поскольку матрицы используются для решения системы линейных уравнений и нахождения их решений, ранг матрицы также важен. Он сообщает, имеет ли система один или несколько ответов. Калькулятор ранга может помочь вам во многих отношениях, таких как:

1. Калькулятор ранга матрицы может сэкономить ваше время от ручных вычислений.
2. Дает пошаговое решение для вычисления ранга матрицы 4×4. Чтобы вы могли понять каждый выполняемый шаг.
3. Используя этот инструмент, вы никогда не застрянете в операциях со столбцами или строками при вычислении ранга матрицы 3×3.
4. Это бесплатный онлайн-инструмент, который предоставляет множество функций для улучшения ваших навыков обучения вычислению ранга матрицы 2×2.
5. Он надежен, потому что в его расчетах нет шансов на ошибку.
6. Калькулятор рангов матриц может легко обрабатывать матрицы до порядка 4 на 4.

Хамза Харун

Последнее обновление 05 апреля 2022 г.

Я автор и создатель контента. Мне нравится писать контент на разные темы. Помимо писательства, я SEO-ASO-SMM специалист и любитель футбола.

Диапазон M.6, нулевое пространство и проекции

 

Диапазон матрицы

Диапазон м × n 9{n} c_i a_i , c_i \in \mathbb{R} \} \]

Размерность (количество линейных независимых столбцов) диапазона A называется рангом A . Таким образом, если 6 × 3-мерная матрица B имеет 2-мерный диапазон, то \(rank(A) = 2\).

Например

\[C =\begin{pmatrix}
  1 и 4 и 1\\
 -8 и -2 и 3\\
  8 и 2  и -2
\end{pmatrix} =  \begin{pmatrix}
х_1 и х_2 и х_3
\end{pmatrix}= \begin{pmatrix}
  у_1  \\
  у_2\\
  у_3
\end{pmatrix}\]

C имеет ранг 3, потому что \(x_1\), \(x_2\) и \(x_3\) линейно независимы.

 

Пустое пространство

p> нулевое пространство из m \(\times\) 9Матрица 0087 n представляет собой набор всех n -мерных векторов, которые равны n -мерному нулевому вектору (вектору, где каждый элемент равен 0) при умножении на A . Это часто обозначается как

\[N(A) = \{ v | Ср = 0 \}\]

Размерность нулевого пространства A называется ничтожностью A . Таким образом, если 6 \(\times\) трехмерная матрица B имеет одномерный диапазон, то \(недействительность (A) = 1\). 9{m \times n} \Rightarrow rank(A) + nullity(A) = n\]

Например, если B является матрицей размера 4 \(\times\) 3 и \(rank(B) = 2\), то из теоремы ранг-недействительность можно вывести, что

\[ранг (B) + недействительность (B) = 2 + недействительность (B) = 3 \правая недействительность (B) = 1\]

 

Проекция

Проекция вектора x на векторное пространство J , обозначается как Proj ( X , J ) , — это вектор \(v \in J\), который минимизирует \(\vert x — v \vert\). Часто векторное пространство J представляет собой диапазон матрицы A , а используемая норма является евклидовой нормой.

No related posts.