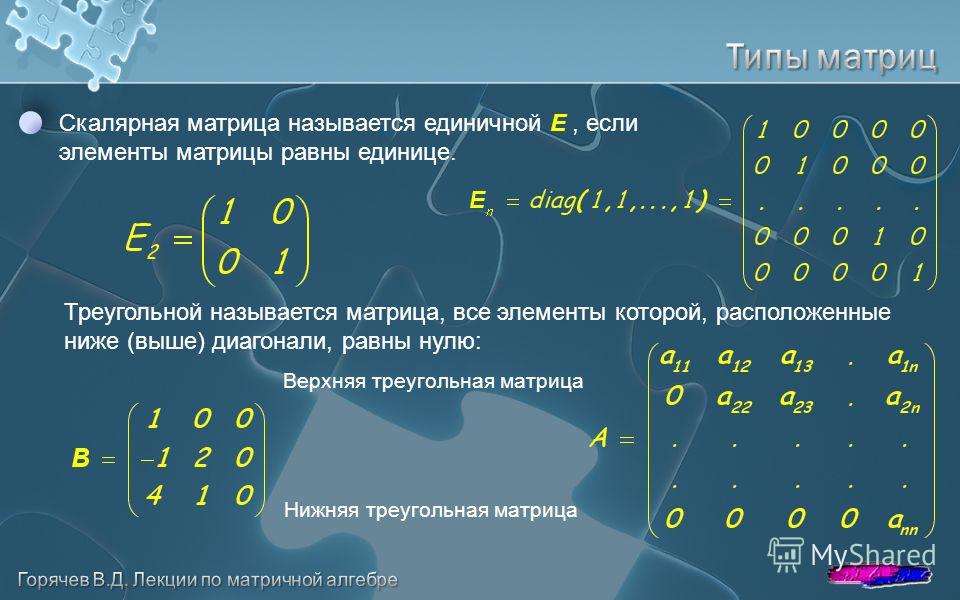
Умножение матрицы на вектор онлайн: Онлайн калькулятор. Умножение матриц

Умножение матрицы на вектор с примерами решения

Содержание:

1. Примеры с решением

Каждый вектор можно рассматривать как одностолбцовую или однострочную матрицу. Одностолбцовую матрицу будем называть вектор-столбцом, а однострочную матрицу — вектор-строкой.

Если — матрица размера , вектор-столбец имеет размерность , а вектор-строка — размерность , то определены произведения и , причем — вектор-столбец размерности , а — вектор-строка размерности . Таким образом, при умножении матрицы на вектор, надо рассматривать вектор как вектор-столбец. При умножении вектора на матрицу его нужно рассматривать как вектор-строку.

Примеры с решением

Пример 1.

Даны матрица и векторы и :

.

Вычислить координаты векторов и . Имеем

Свойства умножения матрицы на вектор ( — число; — матрица; — векторы):

• 1. .
• 2. .
• 3. .
• 4. .
• 5. .

Элемент новой матрицы, стоящий на пересечении — й строки и — ro столбца, равен сумме произведений элементов — й строки первой матрицы на соответствующие элементы — ro столбца второй матрицы.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

Операция определена при условии, что число столбцов первой матрицы равно числу строк второй.

Произведением матрицы на матрицу называется матрица такая, что . Элементы матрицы вычисляются по формуле . (1)

Матрица умножается на вектор в соответствии с правилом «строк на столбец». При умножении матрицы на вектор столбцов количество столбцов в матрице должно соответствовать количеству строк в векторе столбцов.

Пример 2.

Замечание 1. Используя знак сокращенного суммирования, формулу (1) можно записать в виде .

Замечание 2. Введем обозначение матрицы в виде , означающее, что матрица содержит строк и столбцов. Тогда произведение матриц можно записать следующим образом: .

Возможно вам будут полезны данные страницы:

Единичная матрица: вид, примеры, онлайн

Матрица смежности графа

Собственные значения матрицы

Найти определитель матрицы

Замечание 3. Порядок матриц-сомножителей существен. Поэтому говорят об умножении матрицы на матрицу справа или слева. Если произведение матриц существует, то произведение матриц может не существовать. Если существуют произведения матриц и , они могут быть матрицами разных размеров. Если матрицы и квадратные, то их произведения и существуют и имеют одинаковый порядок, но в общем случае .

Замечание 4. Умножение единичной матрицы на квадратную матрицу не изменяет последней: .

Замечание 5. Произведение двух ненулевых матриц может дать нулевую матрицу , например:

.

Блочные матрицы и операции над ними. решение слау с помощью блочных матриц

Задание 1. Перемножить матрицы и , разбив их на блоки:

, .

Решение. Разобьём матрицы и на блоки следующим образом:

, , где , , а , .

Выполним умножение матриц и , представленных в блочном виде, по правилам умножения обычных матриц («строка на столбец»):

.

Пусть в результате умножения получена матрица . Тогда

,,, ,

Значит, .

Ответ: .

Задание 2. Квадратные матрицы и 4-го порядка разбить на 4 блока – квадратные матрицы 2-го порядка – и выполнить заданные действия:

, . Найти и .

Решение. Пусть в результате разбиения на блоки матрицы и примут вид:

, ,

Где и − квадратные матрицы второго порядка, причём

, , , , , , , .

Найдём . По правилам действий над матрицами имеем:

,

Но , ,

, , тогда

.

Пользуясь правилом умножения матриц, найдём :

Обозначим результат умножения матрицей , тогда

,

,

,

.

Таким образом, .

Ответ: ; .

Задание 3. Решая СЛАУ с помощью блочных матриц, найти .

Решение. Представим заданную систему в матричном виде . Так как достаточно найти , то разобьём матрицу системы на блоки следующим образом: , т. е. , , , . Тогда столбец правых частей , т. е. , , а столбец неизвестных , т. е. , .

В этих обозначениях система примет вид: Переходя от этого матричного уравнения к поэлементному равенству, получим:

Умножая левую и правую части второго уравнения системы слева на , получим , откуда . Подставим в первое уравнение системы выражение для :

или

.

Зная , из последнего равенства найдём .

Так как , то

,

Тогда и , т. е. , значит, .

Ответ: .

Задание 4. В пространстве задан произвольный базис , . Построить ОНБ. Координаты базисных векторов заданы в ОНБ .

Решение. Построение ОНБ начнём с построения ортогонального базиса .

Пусть , , где − некоторая константа. Для нахождения умножим равенство, определяющее , скалярно на : . Так как , то , т. е. .

Тогда . Таким образом, и образуют ортогональный базис пространства .

ОНБ получим нормировкой ортогонального базиса:

, .

Ответ: , .

Задание 5. В пространстве задан произвольный базис , , . Построить ОНБ. Координаты базисных векторов заданы в ОНБ .

Решение. Построение ОНБ начнём с построения ортогонального базиса {,,}.

Пусть , , . Умножая равенство, определяющее , скалярно на , найдём константу :

,

Тогда

Аналогично, умножая равенство, определяющее , скалярно на , найдём , а умножая на , найдём :

, ,

Тогда .

ОНБ получим, нормируя построенный ортогональный базис:

, , .

Ответ:, , .

Задание 6. В пространстве заданы два базиса: , , и , , . Найти матрицу перехода от базиса к базису . Координаты базисных векторов заданы в ОНБ .

Решение. Рассмотрим матрицы и , в столбцах которых находятся координаты заданных базисных векторов:

, .

Если – матрица перехода от базиса к базису , то , откуда . Так как , то

.

Окончательно,

.

Ответ: .

Задание 7. В базисе пространства задан вектор , – матрица перехода от базиса к базису . Найти разложение в базисе .

Решение. Если , , то , а , где – матрица перехода от базиса к базису .

По условию , , . Так как , то , т. е. , , а .

Ответ: .

Задание 8. В пространстве заданы два базиса: , и , . Известно, что . Найти разложение в базисе . Координаты базисных векторов заданы в ОНБ .

Решение. Если , , то , а , где – матрица перехода от базиса к базису .

По условию , . Матрицу найдём из равенства , т. е. , при этом , . Так как , то

.

Следовательно, , т. е. , .

Окончательно, .

Ответ: .

< Предыдущая		Следующая >

Умножение матриц на вектор — Math Insight

Умножение матриц на вектор — Math Insight

Умножение матриц на вектор

Math 2241, Spring 2022
Имя:
ID #:

Срок сдачи: 2 февраля 2022 г. , 23:59.
Номер стола/группы:
Члены группы:

Всего баллов: 1

1. Векторное представление.
   1. Запишите вектор $\vc{x}=\left ( 1, \quad 2\right )$ в виде матрицы-столбца. $\vc{x} =$

      Запишите вектор $\vc{z} = \left[\begin{matrix}- \frac{3}{2}\\2\end{matrix}\right]$ в виде упорядоченная пара. $\vc{z} =$
      

   2. Ответ от апплета
      векторов:

      Нанесите каждый из следующих векторов на оси справа. Нарисуйте стрелку, начинающуюся в начале координат, которая простирается по горизонтали на величину, равную первой координате, и по вертикали на величину, равную второй координате.

      $\left ( 1, \quad 2\right )$, $\left[\begin{matrix}- \frac{3}{2}\\2\end{matrix}\right]$, $\left ( 1, \quad — \frac{1}{2}\right )$, $\left[\begin{matrix}-1\\1\end{matrix}\right]$, $\left ( 0, \quad 1\right )$, $\left ( \frac{3}{2}, \quad 0\right )$, $\left[\begin{matrix}-2\\- \frac{3}{2}\ end{matrix}\right]$, $\left ( -2, \quad 0\right )$

      На графике справа увеличьте $n_v$, чтобы открыть векторы. Затем перетащите точки на векторах так, чтобы каждый вектор выше был представлен стрелкой. (Цвет или порядок векторов не имеет значения.)

   3. Определите координаты четырех векторов, начерченных на графике справа. Введите их в любом порядке. (Все координаты являются целыми числами.)
      
      
      
      
      

4. Умножение матрицы на вектор в двух измерениях.
   1. Пусть $A$ — матрица $A=\left[\begin{matrix}1 & 2\\3 & 4\end{matrix}\right]$. Пусть $\vc{x}$ — вектор $\vc{x} = \left[\begin{matrix}5\\6\end{matrix}\right]$.
      Матрично-векторный продукт $A\vc{x} = $
      .
   2. Вычислить $B\vc{y}$, где $B=\left[\begin{matrix}-3 & 7\\-2 & 1\end{matrix}\right]$ и $\vc{y} = \left ( 4, \quad 1\right )$.
      $B\vc{у} =$
      
   3. Если $A=\left[\begin{matrix}a & b\\c & d\end{matrix}\right]$ и $\vc{x} = \left[\begin{matrix}x\\y\ end{matrix}\right]$, затем $A\vc{x} = $
      
   4. Если $I=\left[\begin{matrix}1 & 0\\0 & 1\end{matrix}\right]$ и $\vc{x} = \left[\begin{matrix}x\\y\ end{matrix}\right]$, затем $I\vc{x} = $

      Как умножение на матрицу $I$ преобразовало вектор $\vc{x}$? Это вдвое уменьшило длину вектора. Это удвоило длину вектора. Вектор не изменился. Он повернул вектор против часовой стрелки на 90 градусов. Он перевернул вектор. Он повернул вектор по часовой стрелке на 90 градусов.
      

   5. Обратная связь от апплета
      векторов:

      Пусть вектор $\vc{v}$ является произведением матрицы $B=\left[\begin{matrix}2 & 0\\0 & 2\end{matrix}\right]$ и вектора $\vc {u}=\left ( 2, \quad -1\right )$.
      Затем $\vc{v} =B\vc{u}=$

      . На графике справа измените $n_v$ на 1 и начертите вектор $\vc{u}$, используя появившийся синий вектор. Затем измените $n_v$ на 2 и начертите вектор $\vc{v}$ с появившимся зеленым вектором.

      Как умножение на матрицу $B$ преобразовало вектор $\vc{u}$? Он повернул вектор против часовой стрелки на 90 градусов. Это удвоило длину вектора. Вектор не изменился. Он повернул вектор по часовой стрелке на 90 градусов. Он перевернул вектор. Это вдвое уменьшило длину вектора.
      

   6. Обратная связь от апплета
      векторов:

      Если $A=\left[\begin{matrix}-2 & 4\\1 & -3\end{matrix}\right]$ и $\vc{y}=\left[\begin{matrix}4\\ 1\end{matrix}\right]$, затем
      $\vc{z} = A\vc{y}=$
      .

      На графике справа измените $n_v$ на 1 и начертите вектор $\vc{y}$, используя появившийся синий вектор. Затем измените $n_v$ на 2 и начертите вектор $\vc{z}$ с появившимся зеленым вектором.

Навигация по резьбе

Математика 2241, Весна 2022

Калькулятор тензорного произведения (произведение Кронекера)

Автор Анна Щепанек, доктор философии

Отзыв от Rijk de Wet

Последнее обновление: 7 октября 2022 г.

Содержание:

• Что такое тензорное произведение матриц?
• Как рассчитать произведение Кронекера?
• Тензорное произведение матриц 2×2
• Какова формула произведения матриц Кронекера?
• Как использовать этот калькулятор тензорного произведения?
• Свойства произведения Кронекера
• Часто задаваемые вопросы

Если вы только что наткнулись на эту причудливую матричную операцию под названием матрично-тензорное произведение или Произведение Кронекера матриц , больше не ищите помощи — калькулятор тензорного произведения Omni здесь, чтобы научить вас всему, что вам нужно знать о:

• Что такое произведение Кронекера;
• Каковы основные свойства продукта Кронекера ;
• Как вычислить тензорное произведение матриц 2×2 вручную ; и
• Как выглядит наиболее общая формула продукта Кронекера .

В качестве бонуса мы объясним взаимосвязь между абстрактное тензорное произведение против произведения Кронекера двух матриц!

⚠️ Произведение Кронекера не то же самое как обычное умножение матриц! Если вас интересует последнее, посетите калькулятор умножения матриц Omni. Чтобы узнать больше о матричных произведениях, попробуйте наш самый общий матричный калькулятор.

Что такое тензорное произведение матриц?

Произведение матричного тензора, также известное как произведение Кронекера или прямое произведение матрицы, представляет собой операцию, которая занимает две матрицы произвольного размера и выводит другую матрицу, которая чаще всего намного больше , чем любая из входных матриц.

Допустим, входные матрицы:

• AAA со строками rAr_ArA​ и столбцами cAc_AcA​ и
• BBB со строками rBr_BrB и столбцами cBc_BcB.

Результирующая матрица имеет rA⋅rBr_A \cdot r_BrA​⋅rB​ строк и cA⋅cBc_A \cdot c_BcA​⋅cB​ столбцов.

🔎 В частности, мы можем взять матрицы с одной строкой или одним столбцом, т. е. векторы (будь то столбец или строка по форме). В этом случае мы называем эту операцию произведение векторного тензора .

Как рассчитать произведение Кронекера?

Когда у нас есть приблизительное представление о том, что такое тензорное произведение матриц, давайте более подробно обсудим, как его вычислить. Произведение Кронекера определяется как следующая блочная матрица :

A⊗B=[a11B⋯a1cAB⋮⋱⋮arA1B⋯arAcAB]\footnotesize А \otimes B = \! \begin{bматрица} a_{11} {B} & \cdots & a_{1c_A} {B} \\ \vdots &\ddots &\vdots \\a_{r_A1}{B} &\cdots &a_{r_Ac_A}{B} \end{bmatrix}A⊗B=⎣

⎡​a11​B⋮arA​1​B​⋯⋱⋯​a1cA​B⋮arA​cA​​B​⎦

⎤​

Следовательно, вычисление произведения Кронекера двух матриц сводится к выполнению число умножение числа на матрицу много раз. Как вы наверняка помните, идея состоит в том, чтобы умножить каждый член матрицы на это число, сохраняя при этом форму матрицы:

aijB=[aijb11⋯aijb1cB⋮⋱⋮aijbrB1⋯aijbrBcB]\footnotesize a_{ij} B =\! \begin{bматрица} a_{ij} b_{11} & \cdots & a_{ij} b_{1c_B} \\ \vdots &\ddots &\vdots \\a_{ij}b_{r_B1} &\cdots &a_{ij} b_{r_Bc_B} \end{bmatrix}aij​B=⎣

⎡​aij​b11​⋮aij​brB​1​​⋯⋱⋯​aij​b1cB​​⋮aij​brB​cB​​⎦

⎤​

Тензорное произведение матриц 2×2

Давайте обсудим что такое произведение Кронекера в случае матриц 2×2, чтобы убедиться, что мы действительно все прекрасно понимаем. Предположим, что

A=[a11a12a21a22], B=[b11b12b21b22]\footnotesize A = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}\!,\ B = \begin{bmatrix} b_{11} & b_{ 12} \\ b_{21} & b_{22} \end{bmatrix}A=[a11​a21​​a12​a22​​], B=[b11​b21​​b12​b22​]

Как мы видели выше, имеем:

A⊗B=[a11Ba12Ba21Ba22B]\footnotesize А \otimes B = \begin{bmatrix} а_{11} {В} и а_{12} {В} \\a_{21}{B} &a_{22}{B} \end{bmatrix}A⊗B=[a11​Ba21​B​a12​Ba22​B​]

Записав явно члены BBB, получим:

A⊗B=[a11[b11b12b21b22]a12[b11b12b21b22] a21[b11b12b21b22]a22[b11b12b21b22]]\размер сноски А \otimes B = \\ \begin{bmatrix} a_{11} \begin{bmatrix} б_{11} и б_{12} \\b_{21} &b_{22} \end{bmatrix} и a_{12}\begin{bmatrix} б_{11} и б_{12} \\b_{21} &b_{22} \end{bmatrix} \\a_{21}\begin{bmatrix} б_{11} и б_{12} \\b_{21} &b_{22} \end{bmatrix} &a_{22}\begin{bmatrix} б_{11} и б_{12} \\b_{21} &b_{22} \end{bmatrix} \end{bmatrix} А⊗В=⎣

⎡​a11​[b11​b21​​b12​b22​]a21​[b11​b21​​b12​b22​​]​a12​[b11​b21​​b12​b22​]a22​[ b11​b21​​b12​b22​​]​⎦

⎤​

Performing the number-by-matrix multiplication, we arrive at the final result:

A⊗B=[a11b11a11b12a12b11a12b12a11b21a11b22a12b21a12b22a21b11a21b12a22b11a22b12a21b21a21b22a22b21a22b22]\footnotesize А \otimes B = \\ \begin{bматрица} а_{11} б_{11} и а_{11}б_{12} и а_{12} б_{11} и а_{12} б_{12} \\ а_{11}б_{21} и а_{11}б_{22} и а_{12}б_{21} и а_{12}б_{22} \\ a_{21} b_{11} & a_{21}b_{12} & a_{22} b_{11} & a_{22} b_{12} \\ а_{21}б_{21} и а_{21}б_{22} и а_{22} б_{21} и а_{22} б_{22} \end{bmatrix} А⊗В=⎣

⎡​a11​b11​a11​b21​a21​b11​a21​b21​a11​b12​a11​b22​a21​b12​a21​b22​​a12​b11​a12​b21​a22​b11 a22​b21​​a12​b12​a12​b22​a22​b12​a22​b22​​⎦

⎤​

Следовательно, тензорное произведение матриц 2×2 является матрицей 4×4. Это совсем не сложно, не так ли? Но вы, конечно, можете себе представить, насколько грязно было бы явно записывать тензорное произведение гораздо больших матриц! К счастью, есть краткая формула для матричного тензорного произведения — давайте ее обсудим!

Какова формула произведения матрицы Кронекера?

Мы можем вычислить элемент (A⊗B)ij(A\otimes B)_{ij}(A⊗B)ij​ произведения Кронекера как:

a⌈i/rB⌉,⌈j/cB⌉ ⋅b((i−1)%rB+1),((j−1)%cB+1)\footnotesize a_{\lceil i/r_B\rceil,\lceil j/c_B\rceil} \cdot b_{\ влево((i-1)\% r_B+1\вправо),\влево((j-1)\% c_B+1\вправо)}a⌈i/rB​⌉,⌈j/cB​⌉​⋅b ((i−1)%rB​+1),((j−1)%cB​+1)​

где ⌈x⌉\lceil x \rceil⌈x⌉ — функция потолка (т. е. наименьшая целое число, большее xxx), а %\%% обозначает операцию по модулю. Напомним также, что rBr_BrB и cBc_BcB обозначают количество строк и столбцов BBB соответственно.

Мы обсудили два метода вычисления произведения тензорных матриц. Есть и третий метод, и он наш любимый — просто используйте калькулятор тензорного произведения Omni!

Как использовать этот калькулятор тензорного произведения?

Чтобы вычислить произведение Кронекера двух матриц с помощью нашего инструмента, просто выберите размеры ваших матриц и введите коэффициенты в соответствующие поля.

🙋 Ой, вы перепутали порядок матриц? Не беспокойтесь — наш калькулятор тензорного произведения позволяет вам выбрать, хотите ли вы умножать A⊗BA \otimes BA⊗B или B⊗AB \otimes AB⊗A. Наслаждаться!

Свойства произведения Кронекера

Ассоциативность

Произведение тензорных матриц ассоциативно, т.е. для любых A,B,CA, B, CA,B,C имеем

(A⊗B)⊗C=A⊗( B⊗C)\footnotesize ({A} \otimes {B} )\otimes {C} = {A} \otimes ({B} \otimes {C})(A⊗B)⊗C=A⊗(B⊗ C)

Билинейность

Тензорное матричное произведение также билинейно, т.е. линейно по каждому аргументу в отдельности:

(A+B)⊗C=A⊗C+B⊗C,(xA)⊗B=x( A⊗B)\размер сноски (A + B)\otimes C =A \otimes C +B \otimes C, \\[0.5em] (x{A}) \otimes {B} = x({A} \otimes {B} )(A+B)⊗C=A⊗C+B⊗C,(xA)⊗B=x(A⊗B ) 9{*}.(А⊗В)∗=А∗⊗В∗.

Сингулярные значения и ранг

💡 Не беспокойтесь, если вы еще не знакомы с концепцией сингулярных значений — можете пропустить этот раздел или перейти к калькулятору сингулярных значений.

Если σ1,…,σpA\sigma_1, \ldots, \sigma_{p_A}σ1​,…,σpA​​ являются ненулевыми сингулярными значениями AAA и s1,…,spBs_1, \ldots, s_{p_B }s1​,…,spB​​ являются ненулевыми сингулярными значениями BBB, тогда ненулевых сингулярных значений A⊗BA \otimes BA⊗B являются σisj\sigma_{i}s_jσi​sj​ с i=1,…,pAi=1, \ldots, p_{A}i=1,…,pA​ и j=1,…,pBj=1, \ldots, p_{B}j=1,…,pB .

Напомним, что количество ненулевых сингулярных значений матрицы равно рангу этой матрицы. В результате получаем формулу ранга:

ранг⁡(A⊗B)=ранг⁡(A)⋅ранг⁡(B)\footnotesize \operatorname{rank}(A \otimes B) = \operatorname{rank}(A) \cdot \operatorname{rank}(B)rank(A⊗B)=rank(A)⋅rank(B)

Инверсия тензорное произведение

В оставшейся части этого раздела мы предполагаем, что AAA и BBB являются квадратными матрицами размера mmm и nnn соответственно. 9{-1}.(А⊗В)−1=А−1⊗В−1.

Собственные значения, трассировка, определитель

💡 Нахождение собственных значений — еще одна сложная тема.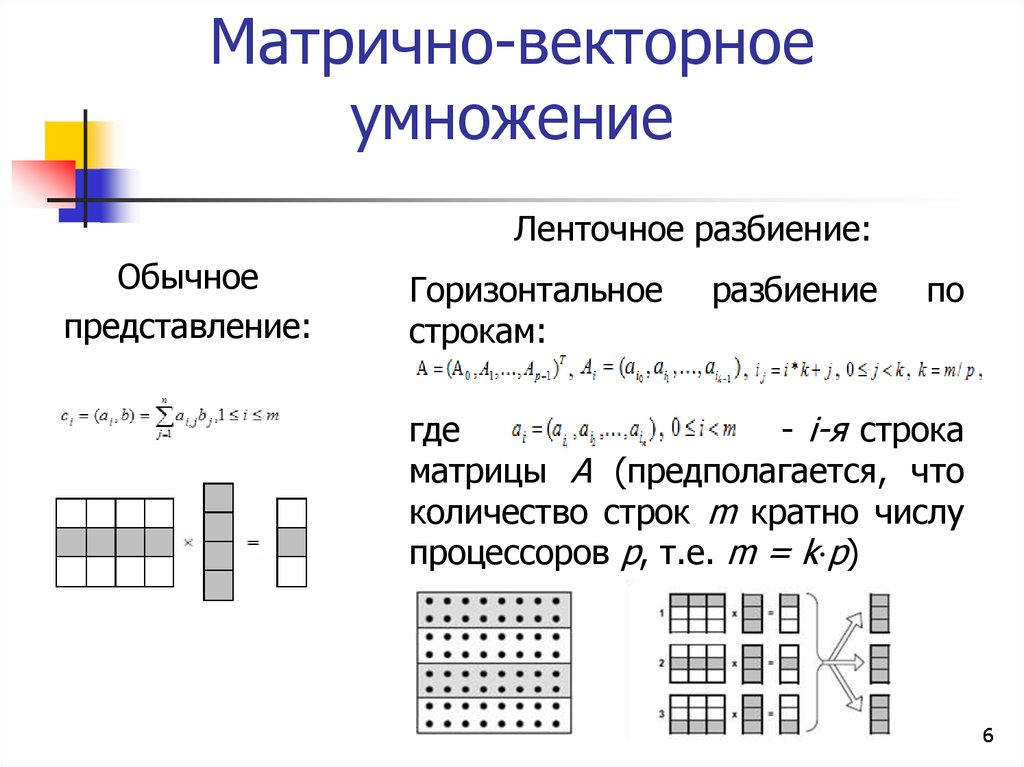 Если вам нужно освежить знания, посетите наш калькулятор собственных значений и собственных векторов.

Если α1,…,αm\alpha_1, \ldots, \alpha_mα1​,…,αm​ и β1,…,βn\beta_1, \ldots, \beta_nβ1​,…,βn​ являются собственными значениями AAA и BBB ( перечисленные с кратностями) соответственно, то собственные значения матрицы A⊗BA \otimes BA⊗B имеют вид
αiβj\alpha_{i}\beta_{j}αi​βj​ с i=1,…,mi=1,\ ldots ,mi=1,…,m и j=1,…,nj=1,\ldots ,nj=1,…,n. 9mdet(A⊗B)=det(A)ndet(B)m

след⁡(A⊗B)=след⁡(A)след⁡(B)\footnotesize \operatorname{trace}(A \otimes B) = \operatorname{trace}(A) \operatorname{trace}(B)trace(A⊗B)=trace(A)trace(B)

Часто задаваемые вопросы

Ассоциативный продукт Кронекера?

Да , произведение кронекеровых матриц ассоциативно: (A ⊗ B) ⊗ C = A ⊗ (B ⊗ C) для всех матриц A, B, C.

Является ли произведение Кронекера коммутативным?

Нет , произведение матриц Кронекера не коммутативно: A ⊗ B ≠ B ⊗ A для некоторых матриц A, B.

Является ли произведение тензора таким же, как произведение Кронекера?

Тензорное произведение является более общим понятием, но если мы имеем дело с конечномерными линейными пространствами, то матрица тензорного произведения двух линейных операторов (относительно базиса, являющегося тензорным произведением исходных базисов) дается в точности произведением Кронекера матриц этих операторов по начальным основаниям.

Как найти размер матричного тензорного произведения?

Чтобы определить размер тензорного произведения двух матриц:

1. Вычислить произведение количества строк входных матриц.
2. Вычислить произведение количества столбцов входных матриц.
3. В выходной матрице будет столько строк, сколько вы получили на шаге 1, и столько столбцов, сколько вы получили на шаге 2.
4. В частности, если у вас есть матриц одинакового размера , выходная матрица имеет размеры, равные исходные размеры в квадрате .

   No related posts.