«Сложение и вычитание, деление и умножение обыкновенных дробей» (стр. 1 из 2)
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ КАЗАХСТАН
КОСТАНАЙСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ
Реферат
На тему: «Сложение и вычитание, деление и умножение обыкновенных дробей».
Костанай
2011 год
СОДЕРЖАНИЕ
1. Из истории обыкновенных дробей ………………………………………..3
2. Действия с обыкновенными дробями …………..…………………………..5
2.1. Сложение и вычитание обыкновенных дробей …………………………..5
2.2. Умножение и деление обыкновенных дробей ………………………….7
3. Примеры на сложение, вычитание, умножение и деление дробей ……. 10
4. Список литературы ……………………………………………………………11
1. Из истории возникновения обыкновенных дробей.
Дроби появились в глубокой древности. При разделе добычи, при измерениях величин, да и в других похожих случаях люди встретились с необходимостью ввести дроби.
Древние египтяне уже знали, как поделить 2 предмета на троих, для этого числа –2/3- у них был специальный значок. Между прочим, это была единственная дробь в обиходе египетских писцов, у которой в числителе не стояла единица – все остальные дроби непременно имели в числителе единицу (так называемые основные дроби): 1/2; 1/3; 1/28; … . Если египтянину нужно было использовать другие дроби, он представлял их в виде суммы основных дробей. Например, вместо 8/15 писали 1/3+1/5. Иногда это бывало удобно. В папирусе Ахмеса есть задача :
Между прочим, это была единственная дробь в обиходе египетских писцов, у которой в числителе не стояла единица – все остальные дроби непременно имели в числителе единицу (так называемые основные дроби): 1/2; 1/3; 1/28; … . Если египтянину нужно было использовать другие дроби, он представлял их в виде суммы основных дробей. Например, вместо 8/15 писали 1/3+1/5. Иногда это бывало удобно. В папирусе Ахмеса есть задача :
«Разделить 7 хлебов между 8 людьми». Если резать каждый хлеб на 8 частей, придётся провести 49 разрезов.
А по-египетски эта задача решалась так: Дробь 7/8 записывали в виде долей: 1/2+1/4+1/8. Значит каждому человеку надо дать полхлеба, четверть хлеба и восьмушку хлеба; поэтому четыре хлеба разрезали пополам, два хлеба- на 4 части и один хлеб на 8 долей, после чего каждому дали его часть.
Но складывать такие дроби было неудобно. Ведь в оба слагаемых могут входить одинаковые доли, и тогда при сложении появится дробь вида 2/n. А таких дробей египтяне не допускали. Поэтому, папирус Ахмеса начинается с таблицы, в которой все дроби такого вида от 2/5 до 2/99 записаны в виде суммы долей. С помощью этой таблицы выполняли и деление чисел. Вот, например, как 5 делили на 21: 5/21
Поэтому, папирус Ахмеса начинается с таблицы, в которой все дроби такого вида от 2/5 до 2/99 записаны в виде суммы долей. С помощью этой таблицы выполняли и деление чисел. Вот, например, как 5 делили на 21: 5/21
Умели египтяне также умножать и делить дроби. Но для умножения приходилось умножать доли на доли, а потом, быть может, снова использовать таблицу. Ещё сложнее обстояло с делением.
В древнем Вавилоне предпочитали наоборот, — постоянный знаменатель, равный 60-ти. Шестидесятеричными дробями, унаследованными от Вавилона, пользовались греческие и арабские математики и астрономы. Но было неудобно работать над натуральными числами, записанными по десятичной системе, и дробями, записанными по шестидесятеричной. А работать с обыкновенными дробями было уже совсем трудно. Поэтому голландский математик Симон Стевин предложил перейти к десятичным дробям.
Интересная система дробей была в Древнем Риме. Она основывалась на делении на 12 долей единицы веса, которая называлась асс. Двенадцатую долю асса называли унцией. А путь, время и другие величины сравнивали с наглядной вещью- весом. Например, римлянин мог сказать, что он прошел семь унций пути или прочел пять унций книги. При этом, конечно, речь шла не о взвешивании пути или книги. Имелось в виду, что пройдено 7/12 пути или прочтено 5/12 книги. А для дробей, получающихся сокращением дробей со знаменателем 12 или раздроблением двенадцатых долей на более мелкие, были особые названия.
Двенадцатую долю асса называли унцией. А путь, время и другие величины сравнивали с наглядной вещью- весом. Например, римлянин мог сказать, что он прошел семь унций пути или прочел пять унций книги. При этом, конечно, речь шла не о взвешивании пути или книги. Имелось в виду, что пройдено 7/12 пути или прочтено 5/12 книги. А для дробей, получающихся сокращением дробей со знаменателем 12 или раздроблением двенадцатых долей на более мелкие, были особые названия.
Даже сейчас иногда говорят:”Он скрупулёзно изучил этот вопрос.” Это значит, что вопрос изучендо конца, что не одной самой малой неясности не осталось. А происходит странное слово “скрупулёзно” от римского названия 1/288 асса — “скрупулус”. В ходу были и такие названия: ”семис”- половина асса, “секстанс”- шестая его доля, “семиунция”- половина унции, т.е. 1/24 асса и т.д. Всего применялось 18 различных названий дробей. Чтобы работать с дробями, надо было помнить для этих дробей таблицу сложения и таблицу умножения. Поэтому римские купцы твёрдо знали, что при сложении триенса (1/3 асса) и секстанса получается семис, а при умножении беса (2/3 асса) на сескунцию( 2/3 унции, т. е.1/8 асса) получается унция. Для облегчения работы составлялись специальные таблицы, некоторые из которых дошли до нас.
е.1/8 асса) получается унция. Для облегчения работы составлялись специальные таблицы, некоторые из которых дошли до нас.
Современную систему записи дробей с числителем и знаменателем создали в Индии. Только там писали знаменатель сверху, а числитель — снизу, и не писали дробной черты. А записывать дроби в точности, как сейчас, стали арабы.
Обыкновенная дробь – это число вида
, где m и n – натуральные числа, например
. Число m называется числителем дроби,n – знаменателем. Среди обыкновенных дробей различают правильные и неправильные дроби. Дробь
называется правильной, если ее числитель меньше знаменателя, и неправильной, если ее числитель больше знаменателя или равен ему.
2. Действия с обыкновенными дробями.
2.1. Сложение и вычитание обыкновенных дробей.
Сложение обыкновенных дробей выполняется так:
а) если знаменатели дробей одинаковы, то к числителю первой дроби прибавляют числитель второй дроби и оставляют тот же знаменатель, т. е.
е.
;
б) если знаменатели дробей различны, то дроби сначала приводят к общему знаменателю, предпочтительнее к наименьшему, а затем к числителю первой дроби прибавляют числитель второй дроби, т.е.
.
Вычитание обыкновенных дробей выполняют следующим образом:
а) если знаменатели дробей одинаковы, то от числителя первой дроби вычитают числитель второй дроби и оставляют тот же знаменатель, т.е.
.
б) если знаменатели различны, то сначала дроби приводят к общему знаменателю, а затем от числителя первой дроби вычитают числитель второй дроби, т.е.
.
Сложение и вычитание дробей. Если знаменатели дробей одинаковы, то для того, чтобы сложить дроби, надо сложить их числители, а для того, чтобы вычесть дроби, надо вычесть их числители (в том же порядке). Полученная сумма или разность будет числителем результата; знаменатель останется тем же.
Например:
1.
2.
3.
4.
5.
6.
Если знаменатели дробей различны, необходимо сначала привести дроби к общему знаменателю. При сложении смешанных чисел их целые и дробные части складываются отдельно. При вычитании смешанных чисел мы рекомендуем сначала преобразовать их к виду неправильных дробей, затем вычесть из одной другую, а после этого вновь привести результат, если требуется, к виду смешанного числа.
Например:
1.
2.
3.
4.
5.
6.
7.
8.
2.2. Умножение и деление обыкновенных дробей.
Умножение обыкновенных дробей выполняется следующим образом:
,
т.е. перемножаются отдельно числители, отдельно знаменатели, первое произведение делают числителем, второе – знаменателем.
При умножении дроби на натуральное число, числитель дроби умножают на это число, а знаменатель оставляют без изменения.
Если множители являются смешанными числами, то сначала их нужно записать в виде неправильных дробей, затем воспользоваться правилом умножения дробей.
Деление обыкновенных дробей выполняют следующим образом:
,
т.е. делимое
умножают на дробь
, обратную делителю
.
Умножение обыкновенной дроби на целое число.
Чтобы умножить дробь на целое число, достаточно числитель дроби умножить на это число, оставив прежний знаменатель.
Правила деления обыкновенных дробей с разными знаменателями. Дроби. Умножение и деление дробей
Дробь – это одна или более долей целого, за которое обычно принимается единица (1). Как и с натуральными числами, с дробями можно выполнять все основные арифметические действия (сложение, вычитание, деление, умножения), для этого нужно знать особенности работы с дробями и различать их виды. Существует несколько видов дробей: десятичные и обыкновенные, или простые. Своя специфика есть у каждого вида дробей, но, обстоятельно разобравшись один раз, как с ними обращаться, вы сможете решать любые примеры с дробями, поскольку будете знать основные принципы выполнения арифметических вычислений с дробями. Рассмотрим на примерах как разделить дробь на целое число, используя разные виды дробей.
Рассмотрим на примерах как разделить дробь на целое число, используя разные виды дробей.
Как разделить простую дробь на натуральное число?
Обыкновенными или простыми называют дроби, записывающиеся в виде такого отношения чисел, при котором вверху дроби указывается делимое (числитель), а внизу – делитель (знаменатель) дроби. Как разделить такую дробь на целое число? Рассмотрим на примере! Допустим, нам нужно разделить 8/12 на 2.
Для этого мы должны выполнить ряд действий:
Таким образом, если перед нами стоит задача разделить дробь на целое число, схема решения будет выглядеть примерно так:
Подобным образом можно разделить любую обыкновенную (простую) дробь на целое число.
Как разделить десятичную дробь на целое число?
Десятичная дробь — это такая дробь, которая получается вследствие деления единицы на десять, тысячу и так далее частей. Арифметические действия с десятичными дробями выполняются довольно просто.
Арифметические действия с десятичными дробями выполняются довольно просто.
Рассмотрим на примере как разделить дробь на целое число. Допустим, нам нужно поделить десятичную дробь 0,925 на натуральное число 5.
Подводя итоги, остановимся на двух основных моментах, которые важны при выполнении операции деления десятичных дробей на целое число:
- для разделения десятичной дроби на натуральное число применяют деление в столбик;
- запятая ставится в частном тогда, когда закончено деление целой части делимого.
Применяя эти простые правила, всегда можно без особого труда разделить любую десятичную или простую дроби на целое число. Содержание урока
Сложение дробей с одинаковыми знаменателямиСложение дробей бывает двух видов:
- Сложение дробей с одинаковыми знаменателями
- Сложение дробей с разными знаменателями
Сначала изучим сложение дробей с одинаковыми знаменателями.
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы:
Пример 2. Сложить дроби и .
В ответе получилась неправильная дробь . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два равно единице:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:
Пример 3 . Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части.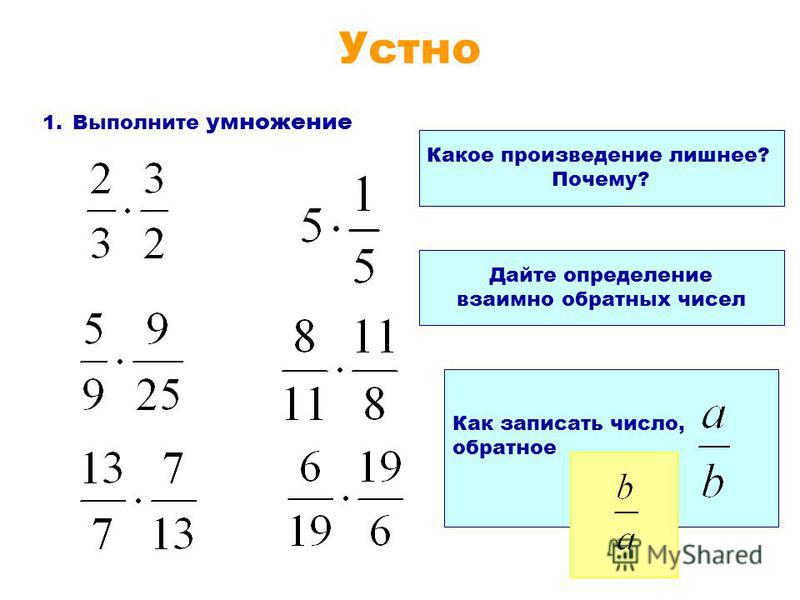 Если к пиццы прибавить ещё пиццы, то получится пиццы:
Если к пиццы прибавить ещё пиццы, то получится пиццы:
Пример 4. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1 целая и ещё пиццы.
Как видите в сложении дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателя, нужно сложить их числители, а знаменатель оставить без изменения;
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби и сложить можно, поскольку у них одинаковые знаменатели.
А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.
Пример 1 . Сложим дроби и
В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6
Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Таким образом, пример завершается. К прибавить получается .
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы:
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести). Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы).
В результате получили (одну целую пиццу и еще одну шестую пиццы).
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби? «.
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби, у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
Пример 2. Найти значение выражения .
Найти значение выражения .
Воспользуемся инструкцией, которая приведена выше.
Шаг 1. Найти НОК знаменателей дробей
Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4
Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:
Шаг 3.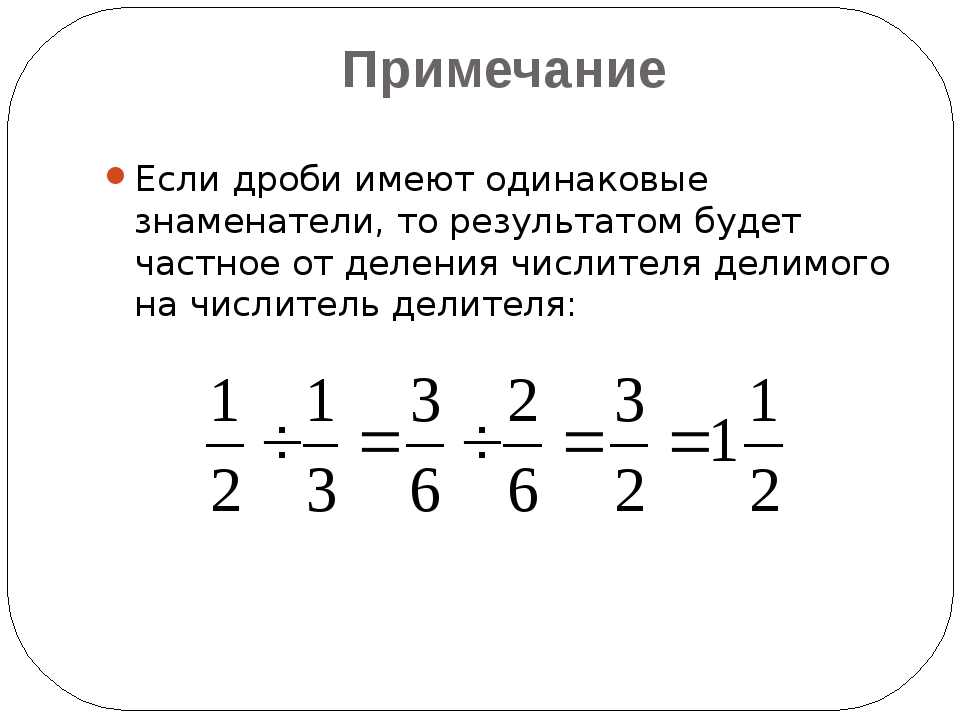 Умножить числители и знаменатели дробей на свои дополнительные множители
Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:
Выделяем:
Получили ответ
Вычитание дробей с одинаковыми знаменателямиВычитание дробей бывает двух видов:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
Сначала изучим вычитание дробей с одинаковыми знаменателями. Тут всё просто. Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним.
Например, найдём значение выражения . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 2. Найти значение выражения .
Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от пиццы отрезать пиццы, то получится пиццы:
Если от пиццы отрезать пиццы, то получится пиццы:
Пример 3. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:
Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям и
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Получили ответ
Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Пример 2. Найти значение выражения
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
Не забываем про знак равенства (=) на новой строке:
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь , нужно разделить её числитель и знаменатель на (НОД) чисел 20 и 30.
Итак, находим НОД чисел 20 и 30:
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10
Получили ответ
Умножение дроби на число
Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить прежним.
Пример 1 . Умножить дробь на число 1 .
Умножим числитель дроби на число 1
Запись можно понимать, как взять половину 1 раз. К примеру, если пиццы взять 1 раз, то получится пиццы
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:
Пример 2 . Найти значение выражения
Умножим числитель дроби на 4
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Выражение можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы
А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
Умножение дробейЧтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения .
Найти значение выражения .
Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:
Выражение можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:
Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:
И взять от этих трех кусочков два:
У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:
Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения равно
Пример 2 . Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Пример 3. Найти значение выражения
Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдём НОД чисел 105 и 450:
Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15
Представление целого числа в виде дробиЛюбое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Обратные числаСейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».
Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.
Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:
Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.
Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:
Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую:
Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:
Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.
Обратное число можно найти также для любого другого целого числа.
Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.
Деление дроби на число
Допустим, у нас имеется половина пиццы:
Разделим её поровну на двоих. Сколько пиццы достанется каждому?
Сколько пиццы достанется каждому?
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы.
Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.
Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.
Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.
Итак, требуется разделить дробь на число 2 . Здесь делимым является дробь , а делителем число 2.
Чтобы разделить дробь на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь . Значит нужно умножить на
Для решения различных заданий из курса математики, физики приходится производить деление дробей. Это сделать очень легко, если знать определенные правила выполнения этого математического действия.
Прежде чем перейти к формулированию правило том, как делить дроби, давайте вспомним некоторые математические термины:
- Верхняя часть дроби называется числителем, а нижняя – знаменателем.

- При делении числа называются так: делимое: делитель = частное
Как делить дроби: простые дроби
Для выполнения деления двух простых дробей следует умножить делимое на дробь, обратную делителю. Эту дробь по-другому называют еще перевернутой, потому что она получается в результате замены местами числителя и знаменателя. Например:
3/77: 1/11 = 3 /77 * 11 /1 = 3/7
Как делить дроби: смешанные дроби
Если нам предстоит разделить смешанные дроби, то здесь тоже все достаточно просто и понятно. Сначала переводим смешанную дробь в обычную неправильную дробь. Для этого умножаем знаменатель такой дроби на целое число и числитель прибавляем к полученному произведению. В итоге мы получили новый числитель смешанной дроби, а знаменатель ее останется без изменения. Дальше деление дробей будет осуществляться точно так же, как и деление простых дробей. Например:
10 2/3: 4/15 = 32/3: 4/15 = 32/3 * 15 /4 = 40/1 = 40
Как делить дробь на число
Для того чтобы разделить простую дробь на число, последнее следует написать в виде дроби (неправильной). Это сделать очень легко: на месте числителя пишется это число, а знаменатель такой дроби равен единице. Дальше деление выполняется обычным способом. Рассмотрим это на примере:
Это сделать очень легко: на месте числителя пишется это число, а знаменатель такой дроби равен единице. Дальше деление выполняется обычным способом. Рассмотрим это на примере:
5/11: 7 = 5/11: 7/1 = 5/11 * 1/7 = 5/77
Как делить десятичные дроби
Нередко взрослый человек испытывает затруднения при необходимости без помощи калькулятора разделить целое число или десятичную дробь на десятичную дробь.
Итак, чтобы выполнить деление десятичных дробей, нужно в делителе просто зачеркнуть запятую и перестать обращать на нее внимание. В делимом запятую нужно передвинуть вправо ровно на столько знаков, сколько было в дробной части делителя, при необходимости дописывая нули. И дальше производят обычное деление на целое число. Чтобы это стало более понятно, приведем следующий пример.
Умножение и деление дробей.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже. ..»)
..»)
Эта операция гораздо приятнее сложения-вычитания ! Потому что проще. Напоминаю: чтобы умножить дробь на дробь, нужно перемножить числители (это будет числитель результата) и знаменатели (это будет знаменатель). То есть:
Например:
Всё предельно просто . И, пожалуйста, не ищите общий знаменатель! Не надо его здесь…
Чтобы разделить дробь на дробь, нужно перевернуть вторую (это важно!) дробь и их перемножить, т.е.:
Например:
Если попалось умножение или деление с целыми числами и дробями — ничего страшного. Как и при сложении, делаем из целого числа дробь с единицей в знаменателе — и вперёд! Например:
В старших классах часто приходится иметь дело с трехэтажными (а то и четырехэтажными!) дробями. Например:
Как эту дробь привести к приличному виду? Да очень просто! Использовать деление через две точки:
Но не забывайте о порядке деления! В отличие от умножения, здесь это очень важно! Конечно, 4:2, или 2:4 мы не спутаем. А вот в трёхэтажной дроби легко ошибиться. Обратите внимание, например:
А вот в трёхэтажной дроби легко ошибиться. Обратите внимание, например:
В первом случае (выражение слева):
Во втором (выражение справа):
Чувствуете разницу? 4 и 1/9!
А чем задается порядок деления? Или скобками, или (как здесь) длиной горизонтальных черточек. Развивайте глазомер. А если нет ни скобок, ни черточек, типа:
то делим-умножаем по порядочку, слева направо !
И еще очень простой и важный приём. В действиях со степенями он вам ох как пригодится! Поделим единицу на любую дробь, например, на 13/15:
Дробь перевернулась! И так бывает всегда. При делении 1 на любую дробь, в результате получаем ту же дробь, только перевернутую.
Вот и все действия с дробями. Вещь достаточно простая, но ошибок даёт более, чем достаточно. Примите к сведению практические советы, и их (ошибок) будет меньше!
Практические советы:
1. Самое главное при работе с дробными выражениями — аккуратность и внимательность! Это не общие слова, не благие пожелания! Это суровая необходимость! Все вычисления на ЕГЭ делайте как полноценное задание, сосредоточенно и чётко. Лучше написать две лишние строчки в черновике, чем накосячить при расчёте в уме.
Лучше написать две лишние строчки в черновике, чем накосячить при расчёте в уме.
2. В примерах с разными видами дробей — переходим к обыкновенным дробям.
3. Все дроби сокращаем до упора.
4. Многоэтажные дробные выражения сводим к обыкновенным, используя деление через две точки (следим за порядком деления!).
5. Единицу на дробь делим в уме, просто переворачивая дробь.
Вот вам задания, которые нужно обязательно прорешать. Ответы даны после всех заданий. Используйте материалы этой темы и практические советы. Прикиньте, сколько примеров вы смогли решить правильно. С первого раза! Без калькулятора! И сделайте верные выводы…
Помните – правильный ответ, полученный со второго (тем более – третьего) раза – не считается! Такова суровая жизнь.
Итак, решаем в режиме экзамена ! Это уже подготовка к ЕГЭ, между прочим. Решаем пример, проверяем, решаем следующий. Решили все — проверили снова с первого по последний. И только потом смотрим ответы.
И только потом смотрим ответы.
Вычислить:
Порешали?
Ищем ответы, которые совпадают с вашими. Я специально их в беспорядке записал, подальше от соблазна, так сказать… Вот они, ответы, через точку с запятой записаны.
0; 17/22; 3/4; 2/5; 1; 25.
А теперь делаем выводы. Если всё получилось — рад за вас! Элементарные вычисления с дробями — не ваша проблема! Можно заняться более серьёзными вещами. Если нет…
Значит, у вас одна из двух проблем. Или обе сразу.) Нехватка знаний и (или) невнимательность. Но… Это решаемые проблемы.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей »). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.
Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.
Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.
Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе — знаменателем.
Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.
Обозначение:
Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.
В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь — ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.
Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.
По определению имеем:
Умножение дробей с целой частью и отрицательных дробей
Если в дробях присутствует целая часть, их надо перевести в неправильные — и только затем умножать по схемам, изложенным выше.
Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:
- Плюс на минус дает минус;
- Минус на минус дает плюс.
До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:
- Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить — тот, которому не нашлось пары;
- Если минусов не осталось, операция выполнена — можно приступать к умножению.
 Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.
Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.
Задача. Найдите значение выражения:
Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:
Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).
Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.
Сокращение дробей «на лету»
Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения . Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:
Взгляните на примеры:
Задача. Найдите значение выражения:
По определению имеем:
Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.
Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.
Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:
Так делать нельзя!
Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.
Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:
Правильное решение:
Как видите, правильный ответ оказался не таким красивым.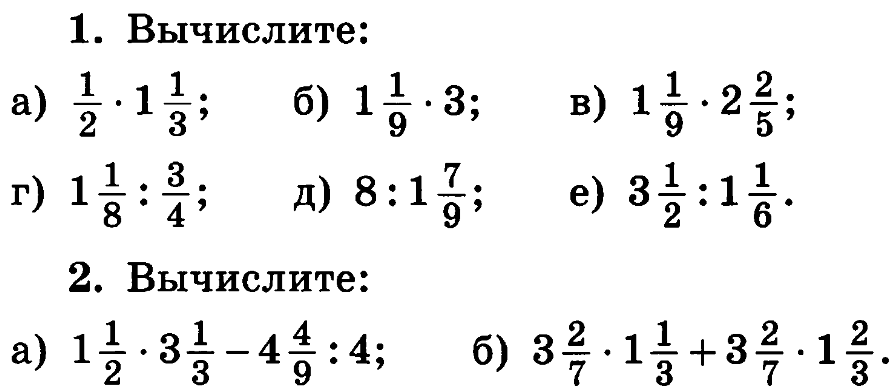 В общем, будьте внимательны.
В общем, будьте внимательны.
Как делить обыкновенные. Дроби. Деление дробей. Формула умножения дробей
Содержание урока Сложение дробей с одинаковыми знаменателямиСложение дробей бывает двух видов:
- Сложение дробей с одинаковыми знаменателями;
- Сложение дробей с разными знаменателями.
Сначала изýчим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения.
Например, слóжим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы:
Пример 2. Сложить дроби и .
В ответе получилась неправильная дробь . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два будет один:
Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два будет один:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:
Пример 3 . Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:
Пример 4. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1 целая и ещё пиццы.
Как видите в сложении дробей с одинаковыми знаменателями нет ничего сложного. Достаточно понимать следующие правила:
Достаточно понимать следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения;
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби и сложить можно, поскольку у них одинаковые знаменатели.
А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.
Пример 1 . Сложим дроби и
В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Таким образом, пример завершается. К прибавить получается .
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы:
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка.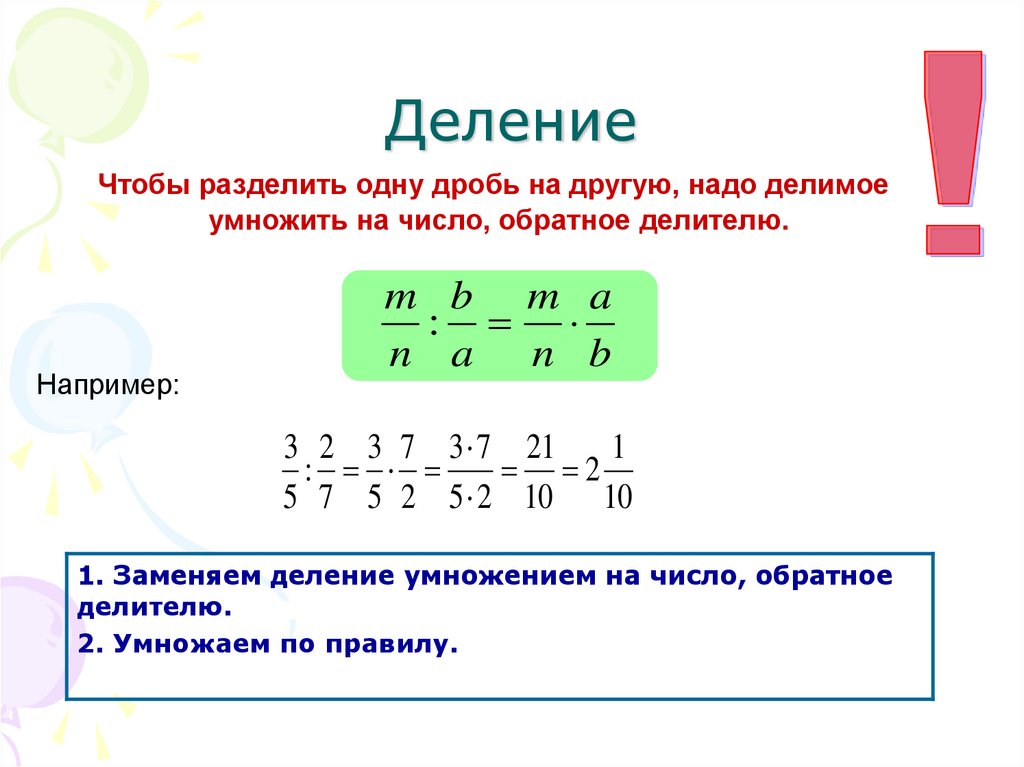 Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести). Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы).
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби? «.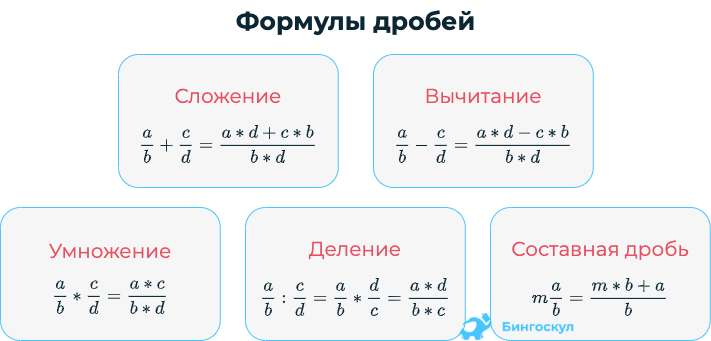
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби, у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
Пример 2. Найти значение выражения .
Воспользуемся инструкцией, которая приведена выше.
Шаг 1. Найти НОК знаменателей дробей
Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4
Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
Получили первый дополнительный множитель 6. Записываем его над первой дробью:
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:
Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку.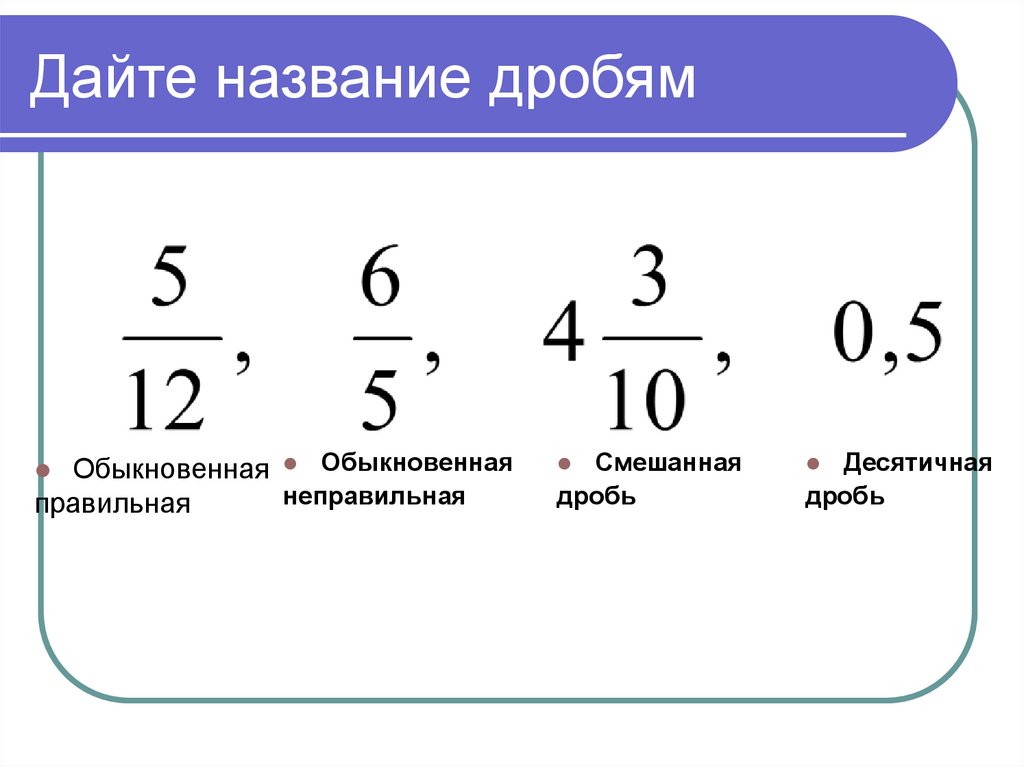 Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:
Получили ответ
Вычитание дробей с одинаковыми знаменателямиВычитание дробей бывает двух видов:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
Сначала изучим вычитание дробей с одинаковыми знаменателями.
Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения.
Например, найдём значение выражения . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 2. Найти значение выражения .
Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 3. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:
Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.

Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
Найти значение выражения:
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям и
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Получили ответ
Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Пример 2. Найти значение выражения
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь , нужно разделить её числитель и знаменатель на (НОД) чисел 20 и 30.
Итак, находим НОД чисел 20 и 30:
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10
Получили ответ
Умножение дроби на число
Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить без изменений.
Пример 1 . Умножить дробь на число 1 .
Умножим числитель дроби на число 1
Запись можно понимать, как взять половину 1 раз. К примеру, если пиццы взять 1 раз, то получится пиццы
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:
Пример 2 . Найти значение выражения
Умножим числитель дроби на 4
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Выражение можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы
А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
Число, которое умножается на дробь, и знаменатель дроби разрешается , если они имеют общий делитель, бóльший единицы.
Например, выражение можно вычислить двумя способами.
Первый способ . Умножить число 4 на числитель дроби, а знаменатель дроби оставить без изменений:
Второй способ . Умножаемую четвёрку и четвёрку, находящуюся в знаменателе дроби , можно сократить. Сократить эти четвёрки можно на 4 , поскольку наибольший общий делитель для двух четвёрок есть сама четвёрка:
Получился тот же результат 3. После сокращения четвёрок, на их месте образуются новые числа: две единицы. Но перемножение единицы с тройкой, и далее деление на единицу ничего не меняет. Поэтому решение можно записать покороче:
Сокращение может быть выполнено даже тогда, когда мы решили воспользоваться первым способом, но на этапе перемножения числа 4 и числителя 3 решили воспользоваться сокращением:
А вот к примеру выражение можно вычислить только первым способом — умножить 7 на знаменатель дроби , а знаменатель оставить без изменений:
Связано это с тем, что число 7
и знаменатель дроби не имеют общего делителя, бóльшего единицы, и соответственно не сокращаются.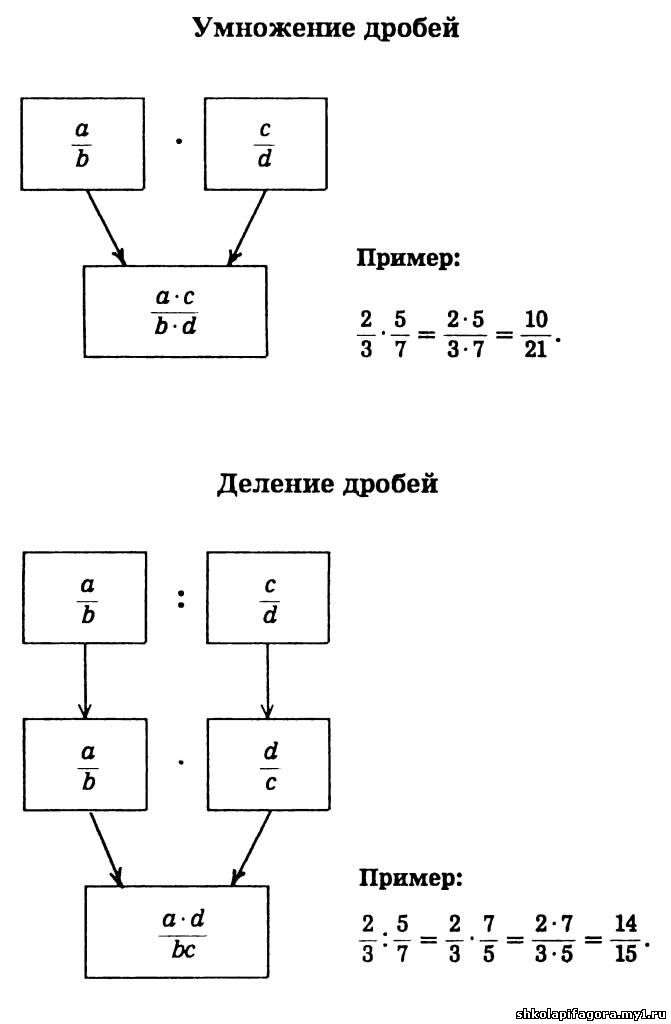
Некоторые ученики по ошибке сокращают умножаемое число и числитель дроби. Делать этого нельзя. Например, следующая запись не является правильной:
Сокращение дроби подразумевает, что и числитель и знаменатель будет разделён на одно и тоже число. В ситуации с выражением деление выполнено только в числителе, поскольку записать это всё равно, что записать . Видим, что деление выполнено только в числителе, а в знаменателе никакого деления не происходит.
Умножение дробейЧтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения .
Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:
Выражение можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:
Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:
И взять от этих трех кусочков два:
У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:
Вспомните, как выглядит пицца, разделенная на три части:
Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения равно
Пример 2 . Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Пример 3. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдём НОД чисел 105 и 450:
Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15
Представление целого числа в виде дробиЛюбое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Сейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».
Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.
Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:
Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.
Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:
Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую:
Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:
Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.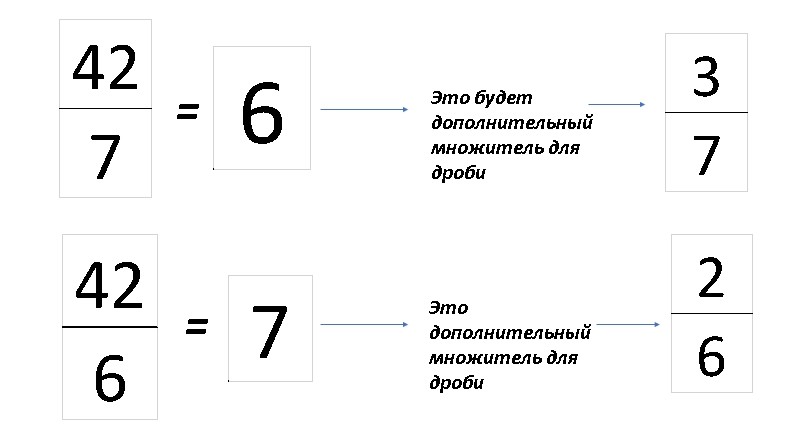
Обратное число можно найти также для любого другого целого числа.
Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.
Деление дроби на число
Допустим, у нас имеется половина пиццы:
Разделим её поровну на двоих. Сколько пиццы достанется каждому?
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы.
Умножение и деление дробей.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Эта операция гораздо приятнее сложения-вычитания ! Потому что проще. Напоминаю: чтобы умножить дробь на дробь, нужно перемножить числители (это будет числитель результата) и знаменатели (это будет знаменатель). То есть:
Например:
Всё предельно просто . И, пожалуйста, не ищите общий знаменатель! Не надо его здесь…
Чтобы разделить дробь на дробь, нужно перевернуть вторую (это важно!) дробь и их перемножить, т. е.:
е.:
Например:
Если попалось умножение или деление с целыми числами и дробями — ничего страшного. Как и при сложении, делаем из целого числа дробь с единицей в знаменателе — и вперёд! Например:
В старших классах часто приходится иметь дело с трехэтажными (а то и четырехэтажными!) дробями. Например:
Как эту дробь привести к приличному виду? Да очень просто! Использовать деление через две точки:
Но не забывайте о порядке деления! В отличие от умножения, здесь это очень важно! Конечно, 4:2, или 2:4 мы не спутаем. А вот в трёхэтажной дроби легко ошибиться. Обратите внимание, например:
В первом случае (выражение слева):
Во втором (выражение справа):
Чувствуете разницу? 4 и 1/9!
А чем задается порядок деления? Или скобками, или (как здесь) длиной горизонтальных черточек. Развивайте глазомер. А если нет ни скобок, ни черточек, типа:
то делим-умножаем по порядочку, слева направо !
И еще очень простой и важный приём. В действиях со степенями он вам ох как пригодится! Поделим единицу на любую дробь, например, на 13/15:
В действиях со степенями он вам ох как пригодится! Поделим единицу на любую дробь, например, на 13/15:
Дробь перевернулась! И так бывает всегда. При делении 1 на любую дробь, в результате получаем ту же дробь, только перевернутую.
Вот и все действия с дробями. Вещь достаточно простая, но ошибок даёт более, чем достаточно. Примите к сведению практические советы, и их (ошибок) будет меньше!
Практические советы:
1. Самое главное при работе с дробными выражениями — аккуратность и внимательность! Это не общие слова, не благие пожелания! Это суровая необходимость! Все вычисления на ЕГЭ делайте как полноценное задание, сосредоточенно и чётко. Лучше написать две лишние строчки в черновике, чем накосячить при расчёте в уме.
2. В примерах с разными видами дробей — переходим к обыкновенным дробям.
3. Все дроби сокращаем до упора.
4. Многоэтажные дробные выражения сводим к обыкновенным, используя деление через две точки (следим за порядком деления!).
5. Единицу на дробь делим в уме, просто переворачивая дробь.
Вот вам задания, которые нужно обязательно прорешать. Ответы даны после всех заданий. Используйте материалы этой темы и практические советы. Прикиньте, сколько примеров вы смогли решить правильно. С первого раза! Без калькулятора! И сделайте верные выводы…
Помните – правильный ответ, полученный со второго (тем более – третьего) раза – не считается! Такова суровая жизнь.
Итак, решаем в режиме экзамена ! Это уже подготовка к ЕГЭ, между прочим. Решаем пример, проверяем, решаем следующий. Решили все — проверили снова с первого по последний. И только потом смотрим ответы.
Вычислить:
Порешали?
Ищем ответы, которые совпадают с вашими. Я специально их в беспорядке записал, подальше от соблазна, так сказать… Вот они, ответы, через точку с запятой записаны.
0; 17/22; 3/4; 2/5; 1; 25.
А теперь делаем выводы. Если всё получилось — рад за вас! Элементарные вычисления с дробями — не ваша проблема! Можно заняться более серьёзными вещами. Если нет…
Если всё получилось — рад за вас! Элементарные вычисления с дробями — не ваша проблема! Можно заняться более серьёзными вещами. Если нет…
Значит, у вас одна из двух проблем. Или обе сразу.) Нехватка знаний и (или) невнимательность. Но… Это решаемые проблемы.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Обыкновенные дробные числа впервые встречают школьников в 5 классе и сопровождают их на протяжении всей жизни, так как в быту зачастую требуется рассматривать или использовать какой-то объект не целиком, а отдельными кусками. Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.
Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.
Вконтакте
Дробные выражения продолжительное время считали самым сложным разделом математики. В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.
Современному виду простых дробных остатков, части которых разделены именно горизонтальной чертой, впервые поспособствовал Фибоначчи — Леонардо Пизанский. Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.
Умножение дробей с разными знаменателями
Изначально стоит определить разновидности дробей :
- правильные;
- неправильные;
- смешанные.
Далее нужно вспомнить, как происходит умножение дробных чисел с одинаковыми знаменателями. Само правило этого процесса несложно сформулировать самостоятельно: результатом умножения простых дробей с одинаковыми знаменателями является дробное выражение, числитель которой есть произведение числителей, а знаменатель — произведение знаменателей данных дробей. То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.
То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.
При умножении простых дробей с разными знаменателями для двух и более множителей правило не меняется:
a/ b * c/ d = a*c / b*d.
Единственное отличие в том, что образованное число под дробной чертой будет произведением разных чисел и, естественно, квадратом одного числового выражения его назвать невозможно.
Стоит рассмотреть умножение дробей с разными знаменателями на примерах:
- 8/ 9 * 6/ 7 = 8*6 / 9*7 = 48/ 63 = 16/2 1 ;
- 4/ 6 * 3/ 7 = 2/ 3 * 3/7 2*3 / 3*7 = 6/ 21 .
В примерах применяются способы сокращения дробных выражений. Можно сокращать только числа числителя с числами знаменателя, рядом стоящие множители над дробной чертой или под ней сокращать нельзя.
Наряду с простыми дробными числами, существует понятие смешанных дробей. Смешанное число состоит из целого числа и дробной части, то есть является суммой этих чисел:
1 4/ 11 =1 + 4/ 11.
Как происходит перемножение
Предлагается несколько примеров для рассмотрения.
2 1/ 2 * 7 3/ 5 = 2 + 1/ 2 * 7 + 3/ 5 = 2*7 + 2* 3/ 5 + 1/ 2 * 7 + 1/ 2 * 3/ 5 = 14 + 6/5 + 7/ 2 + 3/ 10 = 14 + 12/ 10 + 35/ 10 + 3/ 10 = 14 + 50/ 10 = 14 + 5=19.
В примере используется умножение числа на обыкновенную дробную часть , записать правило для этого действия можно формулой:
a * b/ c = a*b / c.
По сути, такое произведение есть сумма одинаковых дробных остатков, а количество слагаемых указывает это натуральное число. Частный случай:
4 * 12/ 15 = 12/ 15 + 12/ 15 + 12/ 15 + 12/ 15 = 48/ 15 = 3 1/ 5.
Существует еще один вариант решения умножения числа на дробный остаток. Стоит просто разделить знаменатель на это число:
d * e/ f = e/ f: d.
Этим приемом полезно пользоваться, когда знаменатель делится на натуральное число без остатка или, как говорится, нацело.
Перевести смешанные числа в неправильные дроби и получить произведение ранее описанным способом:
1 2/ 3 * 4 1/ 5 = 5/ 3 * 21/ 5 = 5*21 / 3*5 =7.
В этом примере участвует способ представления смешанной дроби в неправильную, его также можно представить в виде общей формулы:
a b c = a * b + c / c, где знаменатель новой дроби образуется при умножении целой части со знаменателем и при сложении его с числителем исходного дробного остатка, а знаменатель остается прежним.
Этот процесс работает и в обратную сторону. Для выделения целой части и дробного остатка нужно поделить числитель неправильной дроби на ее знаменатель «уголком».
Умножение неправильных дробей производят общепринятым способом. Когда запись идет под единой дробной чертой, по мере необходимости нужно сделать сокращение дробей, чтобы уменьшить таким методом числа и проще посчитать результат.
В интернете существует множество помощников, чтобы решать даже сложные математические задачи в различных вариациях программ. Достаточное количество таких сервисов предлагают свою помощь при счете умножения дробей с разными числами в знаменателях — так называемые онлайн-калькуляторы для расчета дробей. Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.
Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.
Тема арифметических действий с дробными числами актуальна на всем протяжении обучения школьников среднего и старшего звена. В старших классах рассматривают уже не простейшие виды, а целые дробные выражения , но знания правил по преобразованию и расчетам, полученные ранее, применяются в первозданном виде. Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.
В заключение имеет смысл привести слова Льва Николаевича Толстого, который писал: «Человек есть дробь. Увеличить своего числителя — свои достоинства, — не во власти человека, но всякий может уменьшить своего знаменателя — своё мнение о самом себе, и этим уменьшением приблизиться к своему совершенству».
С дробями можно выполнять все действия, в том числе и деление. Данная статья показывает деление обыкновенных дробей. Будут даны определения, рассмотрены примеры. Подробно остановимся на делении дробей на натуральные числа и наоборот. Будет рассмотрено деление обыкновенной дроби на смешанное число.
Деление обыкновенных дробей
Деления является обратным умножению. При делении неизвестный множитель находится при известном произведении и другого множителя, где и сохраняется его данный смысл с обыкновенными дробями.
Если необходимо произвести деление обыкновенной дроби a b на c d , тогда для определения такого числа нужно произвести умножение на делитель c d , это даст в итоге делимое a b . Получим число и запишем его a b · d c , где d c является обратным c d числу. Равенства можно записать при помощи свойств умножения, а именно: a b · d c · c d = a b · d c · c d = a b · 1 = a b , где выражение a b · d c является частным от деления a b на c d .
Отсюда получим и сформулируем правило деления обыкновенных дробей:
Определение 1
Чтобы разделить обыкновенную дробь a b на c d , необходимо делимое умножить на число, обратное делителю.
Запишем правило в виде выражения: a b: c d = a b · d c
Правила деления сводятся к умножению. Чтобы придерживаться его, нужно хорошо разбираться в выполнении умножения обыкновенных дробей.
Перейдем к рассмотрению деления обыкновенных дробей.
Пример 1
Выполнить деление 9 7 на 5 3 . Результат записать в виде дроби.
Решение
Число 5 3 – это обратная дробь 3 5 . Необходимо использовать правило деления обыкновенных дробей. Это выражение запишем так: 9 7: 5 3 = 9 7 · 3 5 = 9 · 3 7 · 5 = 27 35 .
Ответ: 9 7: 5 3 = 27 35 .
При сокращении дробей следует выделять целую часть, если числитель больше знаменателя.
Пример 2
Разделить 8 15: 24 65 . Ответ записать в виде дроби.
Решение
Для решения нужно перейти от деления к умножению. Запишем это в такой форме: 8 15: 24 65 = 2 · 2 · 2 · 5 · 13 3 · 5 · 2 · 2 · 2 · 3 = 13 3 · 3 = 13 9
Необходимо произвести сокращение, а это выполняется следующим образом: 8 · 65 15 · 24 = 2 · 2 · 2 · 5 · 13 3 · 5 · 2 · 2 · 2 · 3 = 13 3 · 3 = 13 9
Выделяем целую часть и получаем 13 9 = 1 4 9 .
Ответ: 8 15: 24 65 = 1 4 9 .
Деление необыкновенной дроби на натуральное число
Используем правило деления дроби на натуральное число:чтобы разделить a b на натуральное число n , необходимо умножить только знаменатель на n . Отсюда получим выражение: a b: n = a b · n .
Правило деления является следствием правила умножения. Поэтому представление натурального числа в виде дроби даст равенство такого типа: a b: n = a b: n 1 = a b · 1 n = a b · n .
Рассмотрим данное деление дроби на число.
Пример 3
Произвести деление дроби 16 45 на число 12 .
Решение
Применим правило деления дроби на число. Получим выражение вида 16 45: 12 = 16 45 · 12 .
Произведем сокращение дроби. Получим 16 45 · 12 = 2 · 2 · 2 · 2 (3 · 3 · 5) · (2 · 2 · 3) = 2 · 2 3 · 3 · 3 · 5 = 4 135 .
Ответ: 16 45: 12 = 4 135 .
Деление натурального числа на обыкновенную дробь
Правило деления аналогично правилу деления натурального числа на обыкновенную дробь: чтобы разделить натуральное число n на обыкновенную a b , необходимо произвести умножение числа n на обратное дроби a b .
Исходя из правила, имеем n: a b = n · b a , а благодаря правилу умножения натурального числа на обыкновенную дробь, получим наше выражение в виде n: a b = n · b a . Необходимо рассмотреть данное деление на примере.
Пример 4
Делить 25 на 15 28 .
Решение
Нам необходимо переходить от деления к умножению. Запишем в виде выражения 25: 15 28 = 25 · 28 15 = 25 · 28 15 . Сократим дробь и получим результат в виде дроби 46 2 3 .
Ответ: 25: 15 28 = 46 2 3 .
Деление обыкновенной дроби на смешанное число
При делении обыкновенной дроби на смешанное числолегко можно свети к делению обыкновенных дробей. Нужно совершить перевод смешанного числа в неправильную дробь.
Пример 5
Разделить дробь 35 16 на 3 1 8 .
Решение
Так как 3 1 8 — смешанное число, представим его в виде неправильной дроби. Тогда получим 3 1 8 = 3 · 8 + 1 8 = 25 8 . Теперь произведем деление дробей. Получим 35 16: 3 1 8 = 35 16: 25 8 = 35 16 · 8 25 = 35 · 8 16 · 25 = 5 · 7 · 2 · 2 · 2 2 · 2 · 2 · 2 · (5 · 5) = 7 10
Ответ: 35 16: 3 1 8 = 7 10 .
Деление смешанного числа производится таким же образом, как и обыкновенных.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Дробь – это одна или более долей целого, за которое обычно принимается единица (1). Как и с натуральными числами, с дробями можно выполнять все основные арифметические действия (сложение, вычитание, деление, умножения), для этого нужно знать особенности работы с дробями и различать их виды. Существует несколько видов дробей: десятичные и обыкновенные, или простые. Своя специфика есть у каждого вида дробей, но, обстоятельно разобравшись один раз, как с ними обращаться, вы сможете решать любые примеры с дробями, поскольку будете знать основные принципы выполнения арифметических вычислений с дробями. Рассмотрим на примерах как разделить дробь на целое число, используя разные виды дробей.
Как разделить простую дробь на натуральное число?Обыкновенными или простыми называют дроби, записывающиеся в виде такого отношения чисел, при котором вверху дроби указывается делимое (числитель), а внизу – делитель (знаменатель) дроби.
 Как разделить такую дробь на целое число? Рассмотрим на примере! Допустим, нам нужно разделить 8/12 на 2.
Как разделить такую дробь на целое число? Рассмотрим на примере! Допустим, нам нужно разделить 8/12 на 2.Для этого мы должны выполнить ряд действий:
Таким образом, если перед нами стоит задача разделить дробь на целое число, схема решения будет выглядеть примерно так:
Подобным образом можно разделить любую обыкновенную (простую) дробь на целое число.
Как разделить десятичную дробь на целое число?
Десятичная дробь — это такая дробь, которая получается вследствие деления единицы на десять, тысячу и так далее частей. Арифметические действия с десятичными дробями выполняются довольно просто.
Рассмотрим на примере как разделить дробь на целое число. Допустим, нам нужно поделить десятичную дробь 0,925 на натуральное число 5.
Подводя итоги, остановимся на двух основных моментах, которые важны при выполнении операции деления десятичных дробей на целое число:
- для разделения десятичной дроби на натуральное число применяют деление в столбик;
- запятая ставится в частном тогда, когда закончено деление целой части делимого.

Как складывать, вычитать, умножать и делить дроби: с видео и примерами
Большинство учителей научат вас, как складывать и вычитать дроби, прежде чем они научат вас, как их умножать. Однако проще всего выучить его в обратном порядке. Посмотрим, как это работает.
Вы также можете попробовать наш Калькулятор дробей
Как умножать дробиВопрос:- Умножить 3 0 ⁄ 92 и 5 ⁄ 4
Ответ:
В чем подвох: Ничего. Просто добавьте верхнее число и нижнее число, и все готово.
Вопрос: Умножение 2 ⁄ 6 и 8 ⁄ 2 и 4 ⁄ 5
Ответ: Упростит эти цифры, которые могут быть упрощены (или вы можете сделать это. после умножения. Это зависит от вас, когда вы хотите упростить. Поскольку это умножение, поэтому не имеет значения, когда вы это делаете.)
после умножения. Это зависит от вас, когда вы хотите упростить. Поскольку это умножение, поэтому не имеет значения, когда вы это делаете.)
2 ⁄ 6 После упрощения = 1 ⁄ 3
8 ⁄ 2 После упрощения = 4 ⁄ 1
. 3 X 4 ⁄ 1 X 4 ⁄ 5 = 16 ⁄ 15Мы снова перемножили верхние числа и числа снизу.
Как делить дроби
Опять же, это просто. Если вы знаете, как умножать, вы уже знаете, как делить. Посмотрим, как.
Вопрос: Решите это: 3/8 ÷ 4/7
Решение:
Для понимания: Все, что вам нужно сделать, это повернуть значение второй дроби. Например, 4/7 будет 7/4, затем умножьте дроби, и вы получите ответ.
Например, 4/7 будет 7/4, затем умножьте дроби, и вы получите ответ.
так, 3/8 x 7/4
=> 21/32
просто их везде где надо.
Другой вопрос: Решите это 10/4 ÷ 8/5
Решение:
10/4 ÷ 8/5
=> 10/4 x 5/8
=> 50/32
=> 25 /16
Сложение и вычитание дробейКак складывать дроби, если нижние числа совпадают? Или как складывать дроби с одинаковыми знаменателями или одинаковыми знаменателями?
Один и тот же вопрос ответил 2 способами. Те же самые нижние числа известны как идентичные или похожие знаменатели.
ВОПРОС: Добавить 1 ⁄ 2 и 3 ⁄ 2
Ответ: 2
. Поясните: Таким образом, ответ — 4 or 29006 2 2 2
. вы можете еще больше упростить, и это будет 2 ⁄ 1 , и мы напишем это как 2, потому что 1 внизу не имеет смысла.
Вопрос: Добавить 3 ⁄ 2 и 7 ⁄ 2 и 4 ⁄ 2
Ответ:
Подсказка: Можно упростить 4 ⁄ 2 , но мы не будем этого делать до сложения. Если мы это сделаем, мы потеряем общее нижнее значение из нашей третьей дроби, равное 2. Поэтому мы собираемся упростить позже, после завершения процесса сложения.
SO, 3 ⁄ 2 + 7 ⁄ 2 + 4 ⁄ 2
=> 14 ⁄ 2
=> 14 ~ 2 020 (Мы просто добавили верхние числа и взяли 2 в качестве общего числа для нижних, потому что все они имеют одно и то же число внизу) => Упростите 14 ⁄ 2 , и вы получите 7 ⁄ 1 то будет записано как 7 Итак, 7 это ответ на вопрос. Вычитание дроби работает так же, как мы говорили о добавлении вычитания. Question: Subtract 1 ⁄ 3 from 4 ⁄ 3 (Or get the value of 4 ⁄ 3 – 1 ⁄ 3 ) Answer: Уточнение: Как мы сказали, когда нижнее значение одинаково для обоих чисел, мы принимаем его за общее. Таким образом, мы взяли 3 как общее для нижнего значения. Мы вычли 4 – 1, чтобы получить максимальное значение. Итак, мы получили 3 ⁄ 3 . Затем мы упростили 3 ⁄ 3 и получили 1 как окончательное значение, которое является ответом. Будь то 2 значения, 3 или 4, мы будем применять один и тот же метод, когда нижнее значение одинаково. Вопрос: Получите значение для 2 ⁄ 3 — 1 ⁄ 3 — 6 ⁄ 3 . Возьмем 3 в качестве нижнего значения и вычтем 2 – 1 – 6. Получаем => -5 ⁄ 3 7 вычесть неидентичную или неидентичную дробь (когда нижние значения не совпадают для обоих чисел) Давайте решим несколько примеров, чтобы увидеть это в действии. Ответ: Поскольку нижнее значение для обоих не одно и то же, нам нужно преобразовать их в подобные дроби. Но как мы это делаем? Это очень легко. Возьмите нижнее значение первой дроби, а затем умножьте его на верхнее и нижнее значение второй дроби. So our question was to get the value of 2 ⁄ 7 + 1 ⁄ 3 so we are going to multiply 3 ⁄ 3 with 2 ⁄ 7 and 7 ⁄ 7 with 1 ⁄ 3 => 3 ⁄ 3 x 2 ⁄ 7 + 1 ⁄ 3 х 7 ⁄ 7 => 6 ⁄ 21 + 7 ⁄ 21 Сейчас у нас нравятся фракции. Мы готовы добавить их, поскольку мы добавили похожие дроби в разделе похожих дробей выше. Возьмем 21 в качестве общего значения для нижнего, потому что обе дроби имеют 21 в нижней части и добавят верхние значения. Вычитание дроби при одинаковом нижнем значении (например, знаменатели или идентичный знаменатель)

 вычитание, иначе изменится нижнее значение третьей дроби.
вычитание, иначе изменится нижнее значение третьей дроби. А также возьмите нижнее значение второй дроби и умножьте его на верхнее и нижнее значение первой дроби.
А также возьмите нижнее значение второй дроби и умножьте его на верхнее и нижнее значение первой дроби. 0006 13 ⁄ 21
0006 13 ⁄ 21
. .
2 ⁄ 7 – 1 ⁄ 3
=> 3 ⁄ 3 x 2 ⁄ 7 – 1 ⁄ 3 x 7 ⁄ 7
=> 6 ⁄ 21 — 7 ⁄ 21
=> -1 ~ 21
9000 2 . или вычесть?Как складывать и вычитать дроби, которые имеют более 2 значений
Как добавить их: 3 ⁄ 2 + 7 ⁄ 4 + 4 ⁄ 3Этот метод также можно использовать для сложения и вычитания дробей, которые имеют только 2 значения, но вышеупомянутый метод был самым простым, поэтому мы не не обсуждайте это там.
Первый, нам нужно получить LCD (по меньшей мере, DENININTATR)
. Как получить наименьший общий знаменатель (LCD)?
Как получить наименьший общий знаменатель (LCD)?
Умножьте нижние числа на 2, 3, 4 и так далее… пока не найдете наименьший общий знаменатель для всех 3.
| 2 | 4 | 3 | |
| 2 х | 4 | 8 | 6 |
| 3 х | 6 | 12 | 9 |
| 4 х | 8 | 16 | 12 |
| 5 х | 10 | 20 | 15 |
| 6 х | 12 | 24 | 18 |
Наш наименьший общий знаменатель равен 12, потому что 12 — единственное число, доступное во всех трех столбцах, которые мы выделили зеленым цветом.
Наш вопрос был 3 ⁄ 2 + 7 ⁄ 4 + 4 ⁄ 3 , где
- Первое дно составляет 2, что мы умножены на 6, чтобы получить наименьшее общее.
 посмотрите на таблицу выше), поэтому мы собираемся умножить 3 ⁄ 2 на 6 ⁄ 6 . Получается: 3 ⁄ 2 x 6 ⁄ 6
посмотрите на таблицу выше), поэтому мы собираемся умножить 3 ⁄ 2 на 6 ⁄ 6 . Получается: 3 ⁄ 2 x 6 ⁄ 6 - Второе нижнее значение — 4, которое мы умножили на 3, чтобы получить ЖК-дисплей (см. таблицу выше), поэтому мы собираемся умножить 7 ⁄ 4 на 3 ⁄ 3 . Значит будет: 7 ⁄ 4 х 3 ⁄ 3
- Третье нижнее значение равно 3, которое мы умножили на 4, чтобы получить ЖК-дисплей (см. таблицу выше), поэтому мы собираемся умножить 4 ⁄ 3 с 4 ⁄ 4 . Значит будет: 4 ⁄ 3 х 4 ⁄ 4
S0, 3 ⁄ 2 + 7 ⁄ 4 + 4 ⁄ 3
=> 3 ⁄ 2 x 6 ⁄ 6 + 7 ⁄ 4 x 3 ⁄ 3 + 4 ⁄ 3 x 4 ⁄ 4
Помните, что в математике мы всегда сначала умножаем перед сложением или вычитанием.
Это математическое правило.
После упрощения. Таким образом, мы возьмем 12 как обычные для нижних и добавим верхние числа.
Итак, 18 ⁄ 12 + 21 ⁄ 12 + 16 ⁄ 12
= 55 ⁄ 12
Таким образом, ответ 55 ⁄ 12
Другой Вопрос: Подтереж 5. Другой Вопрос: подтережнит 5 . 2 – 7 ⁄ 9| 6 | 2 | 9 | |
| 2 х | 12 | 4 | 18 |
| 3 х | 18 | 6 | 27 |
| 4 х | 24 | 8 | 36 |
| 5 х | 30 | 10 | 45 |
| 6 х | 36 | 12 | 54 |
| 7 х | 42 | 14 | 63 |
| 8 х | 48 | 16 | 72 |
| 9 х | 54 | 18 | 81 |
Таким образом, наименьший общий знаменатель для нижних значений (6, 2 и 9) равен 18.
Теперь мы собираемся умножить каждую дробь так же, как мы делали это в предыдущем вопросе, глядя на таблицу.
- 5 ⁄ 6 будет умножено на 3 ⁄ 3
- 1 ⁄ 2 будет умножено на 9 ⁄9
- 7 ⁄ 9 будет умножено на 2 ⁄ 2
S0, 5 ⁄ 6 – 1 ⁄ 2 – 7 ⁄ 9
=> 5 ⁄ 6 x 3 ⁄ 3 – 1 ⁄ 2 x 9 ⁄ — 7 ⁄ 9 x 2 ⁄ 2
=> 15 ~ 18 – 9 ⁄ 18 – 14 ⁄ 18
Теперь у нас одинаковые дроби. Таким образом, мы возьмем 18 в качестве общего значения для нижних и вычтем верхние числа.
=> -8 ⁄ 18
=> -4 ⁄ 9
youtube.com/embed/pZEmFSP3Z0I?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Как насчет сложения или вычитания больших чисел, которые содержат дроби?
Вопрос: — Получите значение для 35 ⁄ 105 + 70 ⁄ 80 + 42 ⁄ 90Совет:- Когда нижние значения дробей не совпадают. Вы всегда должны сначала упростить их, прежде чем вычислять. Это сэкономит ваше время.
Let’s Simplify: 35 ⁄ 105 + 70 ⁄ 80 + 42 ⁄ 90
and you will get: 1 ⁄ 5 + 7 ⁄ 8 + 7 ⁄ 15
Теперь нам нужно найти наименьший общий знаменатель для чисел 5, 8 и 15
| 5 | 8 | 15 | |
| 2 х | 10 | 16 | 30 |
| 3 х | 15 | 24 | 45 |
| 4 х | 20 | 32 | 60 |
| 5 х | 25 | 40 | 75 |
| 6 х | 30 | 48 | 90 |
| 7 х | 35 | 56 | 105 |
| 8 х | 40 | 64 | 120 |
| 9 х | 45 | 72 | 135 |
| 10 х | 50 | 80 | 150 |
| 11 х | 55 | 88 | 165 |
| 12 х | 60 | 96 | 180 |
| 13 х | 65 | 104 | 195 |
| 14 х | 70 | 112 | 210 |
| 15 х | 75 | 120 | 225 |
| 16 х | 80 | 128 | 240 |
| 17 х | 85 | 136 | 255 |
| 18 х | 90 | 144 | 270 |
| 19 х | 95 | 152 | 285 |
| 20 х | 100 | 160 | 300 |
| 21 х | 105 | 168 | 315 |
| 22 х | 110 | 176 | 330 |
| 23 х | 115 | 184 | 345 |
| 24 х | 120 | 192 | 360 |
Таким образом, мы получили 120 в качестве наименее распространенного знаменателя (ЖК -дисплей) для 5, 8 и 15
- 1 ⁄ 5 будут умножены с 24 ⁄ 24 20202024024024024024024024024012
- 7 ⁄ 8 будет умножено на 15 ⁄ 15
- 7 ⁄ 15 будет умножено на 8 ⁄ 8
So, it will be written like this: 1 ⁄ 5 x 24 ⁄ 24 + 7 ⁄ 8 x 15 ⁄ 15 + 7 ⁄ 15 х 8 ⁄ 8
=> 24 ⁄ 120 + 105 ⁄ 120 + 5 6 900019 120
Теперь у нас есть похожие дроби. Мы возьмем 120 в качестве общего значения для нижней части и добавим верхние значения.
Мы возьмем 120 в качестве общего значения для нижней части и добавим верхние значения.
=> 185 ⁄ 120
=> После упрощения, вы получите: 37 ⁄ 24
, так что наш ответ 37 ⁄ 24
9 37 ⁄ 24. Не стесняйтесь комментировать.
Операции над дробями | Математика для гуманитарных наук Corequisite
Результаты обучения
- Сложение или вычитание дробей.
- Упростите дроби.
- Умножение дробей.
- Разделить дроби.
Студенты-математики и работающие взрослые часто обнаруживают, что их знания о том, как складывать, вычитать, умножать и делить дроби, заржавели от неиспользования. Мы склонны полагаться на калькуляторы, которые делают за нас большую часть работы с дробями. Тем не менее, студенческая алгебра создает некоторые важные методы работы с выражениями и уравнениями, основанные на операциях над дробями. Поэтому важно заново освоить эти навыки. Этот раздел напомнит вам, как выполнять действия над дробями. По мере прохождения оставшейся части курса вы можете возвращаться к этому разделу по мере необходимости для быстрого напоминания об операциях с дробями.
Поэтому важно заново освоить эти навыки. Этот раздел напомнит вам, как выполнять действия над дробями. По мере прохождения оставшейся части курса вы можете возвращаться к этому разделу по мере необходимости для быстрого напоминания об операциях с дробями.
Прежде чем мы начнем, давайте определимся с терминологией.
- произведение: результат умножения
- фактор: что-то умножается — для [латекс]3 \cdot 2 = 6[/латекс] , и [латекс]3[/латекс] и [латекс]2[/латекс] являются множителями [латекс]6[ /латекс]
- числитель: верхняя часть дроби – числитель дроби [латекс]\крупный\фрак{2}{3}[/латекс] равен [латекс]2[/латекс]
- знаменатель: нижняя часть дроби — знаменатель дроби [латекс]\большой\фракция{2}{3}[/латекс] равен [латекс]3[/латекс]
Примечание об инструкциях
Определенные слова используются в учебниках по математике и учителями, чтобы предоставить учащимся инструкции о том, что делать с данной задачей. Например, вы можете увидеть такие инструкции, как найти или упростить. Важно понимать, что означают эти слова, чтобы успешно решать задачи этого курса. Вот краткий список некоторых инструкций по решению проблем вместе с их описаниями, поскольку они будут использоваться в этом модуле.
Например, вы можете увидеть такие инструкции, как найти или упростить. Важно понимать, что означают эти слова, чтобы успешно решать задачи этого курса. Вот краткий список некоторых инструкций по решению проблем вместе с их описаниями, поскольку они будут использоваться в этом модуле.
| Инструкция | Интерпретация |
|---|---|
| Найти | Выполнить указанные математические операции, которые могут включать в себя сложение, вычитание, умножение, деление (позже использование слова найти будет расширено до решения уравнений, как в найти значение переменной). |
| Упростить | 1) Выполнять указанные математические действия, включая сложение, вычитание, умножение, деление 2) Запишите математическую формулировку в наименьших выражениях, чтобы не было других математических операций, которые можно было бы выполнить — часто встречается в задачах, связанных с дробями и порядком операций |
| Оценка | 1) Выполнять указанные математические действия, включая сложение, вычитание, умножение, деление 2) Подставить заданное значение переменной в выражение и затем выполнить указанные математические операции |
| Уменьшить | Запишите математическое выражение в наименьшем или минимальном выражении, чтобы не было других математических операций, которые можно было бы выполнить — часто встречается в задачах, связанных с дробями или делением |
Сложение дробей
Когда вам нужно складывать или вычитать дроби, сначала нужно убедиться, что дроби имеют одинаковый знаменатель.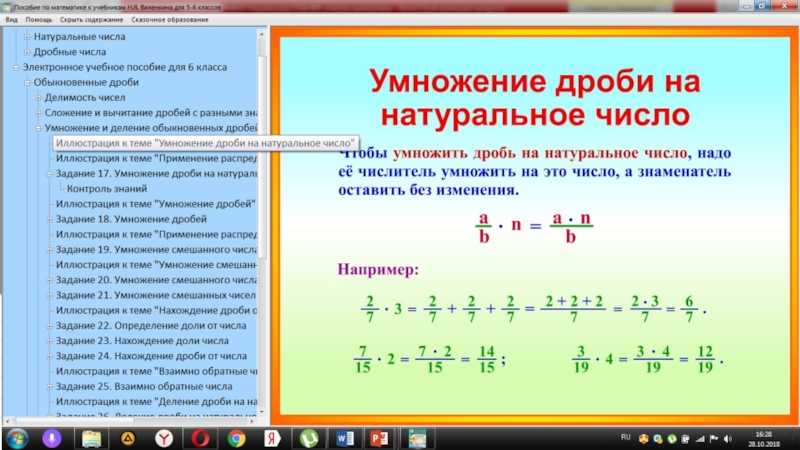 Знаменатель говорит вам, на сколько частей разбито целое, а числитель говорит вам, сколько из этих частей вы используете.
Знаменатель говорит вам, на сколько частей разбито целое, а числитель говорит вам, сколько из этих частей вы используете.
Концепция «части целого» может быть смоделирована с помощью пиццы и кусочков пиццы. Например, представьте, что пицца разрезана на [латекс]4[/латекс] куска, и кто-то берет [латекс]1[/латекс] кусок. Теперь [latex]\Large\frac{1}{4}[/latex] из пиццы исчезает, а [latex]\Large\frac{3}{4}[/latex] остается. Обратите внимание, что обе эти дроби имеют знаменатель [латекс]4[/латекс], который относится к количеству ломтиков, на которые была разрезана вся пицца. Что, если у вас есть еще одна пицца, разрезанная на [латекс]8[/латекс] равных частей, и [латекс]3[/латекс] из этих частей исчезли, оставив [латекс]\большой\фрак{5}{8} [/латекс]?
Как описать общее количество оставшейся пиццы одним числом, а не двумя разными дробями? Вам нужен общий знаменатель, технически называемый наименьшим общим кратным . Помните, что если число кратно другому, вы можете разделить их и не получить остатка.
Один из способов найти наименьшее общее кратное двух или более чисел – сначала умножить каждое из них на [латекс]1, 2, 3, 4[/латекс] и т. д. Например, найти наименьшее общее кратное [латекс] 2[/латекс] и [латекс]5[/латекс].
| Сначала перечислите все кратные [латекс]2[/латекс]: | Затем перечислите все числа, кратные 5: |
| [латекс]2\cdot 1 = 2[/латекс] | [латекс]5\cdot 1 = 5[/латекс] |
| [латекс]2\cdot 2 = 4[/латекс] | [латекс]5\cdot 2 = 10[/латекс] |
| [латекс]2\cdot 3 = 6[/латекс] | [латекс]5\cdot 3 = 15[/латекс] |
| [латекс]2\cdot 4 = 8[/латекс] | [латекс]5\cdot 4 = 20[/латекс] |
| [латекс]2\cdot 5 = 10[/латекс] | [латекс]5\cdot 5 = 25[/латекс] |
Наименьшее кратное, которое у них есть, будет общим знаменателем, используемым для преобразования каждой дроби в эквивалентные дроби. См. пример ниже для демонстрации нашей задачи о пицце.
См. пример ниже для демонстрации нашей задачи о пицце.
Пример
В одной пицце, разрезанной на четыре ломтика, один отсутствует. Другая пицца того же размера была разрезана на восемь частей, три из которых были удалены. Опишите общее количество пиццы, оставшейся в двух пиццах, используя общие термины.
Показать решение
Чтобы сложить дроби с разными знаменателями, сначала перепишите их с одинаковыми знаменателями. Затем добавьте или вычтите числители над общим знаменателем.
Сложение дробей с разными знаменателями
- Найдите общий знаменатель.
- Перепишите каждую дробь в виде эквивалентной дроби, используя общий знаменатель.
- Теперь, когда дроби имеют общий знаменатель, можно сложить числители.
- Упростите, убрав все общие множители в числителе и знаменателе.
Упростить дробь
В математике принято представлять дроби в наименьшем выражении. Мы называем эту практику упрощением или сокращением дроби, и ее можно осуществить путем сокращения (разделения) общих множителей в числителе и знаменателе дроби. Мы можем сделать это, потому что дробь представляет собой деление, и для любого числа [latex]a[/latex], [latex]\dfrac{a}{a}=1[/latex].
Мы можем сделать это, потому что дробь представляет собой деление, и для любого числа [latex]a[/latex], [latex]\dfrac{a}{a}=1[/latex].
Например, чтобы упростить [латекс]\dfrac{6}{9}[/latex] вы можете переписать [latex]6[/latex] и [latex]9[/latex] , используя наименьшие возможные множители следующим образом:
[latex]\dfrac{6}{9}=\dfrac{ 2\cdot3}{3\cdot3}[/latex]
Поскольку [latex]3[/latex] есть и в числителе, и в знаменателе, а дроби можно считать делением, мы можем разделить [latex]3[ /latex] вверху и [latex]3[/latex] внизу, чтобы сократить до [latex]1[/latex].
[латекс]\dfrac{6}{9}=\dfrac{2\cdot\cancel{3}}{3\cdot\cancel{3}}=\dfrac{2\cdot1}{3}=\dfrac {2}{3}[/латекс]
В следующем примере показано, как сложить две дроби с разными знаменателями, а затем упростить ответ.
Пример
Добавить [латекс]\Большой\фракция{2}{3}+\Большой\фракция{1}{5}[/латекс]. Упростите ответ.
Показать решение
Вы можете найти общий знаменатель, найдя общие кратные знаменателей. Наименьшее общее кратное является самым простым в использовании.
Наименьшее общее кратное является самым простым в использовании.
Пример
Добавить [latex]\Large\frac{3}{7}+\Large\frac{2}{21}[/latex]. Упростите ответ.
Показать решение
В следующем видео вы увидите пример сложения двух дробей с разными знаменателями.
Вы также можете сложить более двух дробей, если сначала найдете для них общий знаменатель. Пример суммы трех дробей показан ниже. В этом примере вы будете использовать метод простой факторизации, чтобы найти LCM.
Подумай об этом
Добавить [латекс]\Большой\фракция{3}{4}+\Большой\фракция{1}{6}+\Большой\фракция{5}{8}[/латекс]. Упростите ответ и запишите в виде смешанного числа.
Чем этот пример отличается от предыдущих? Используйте поле ниже, чтобы записать несколько мыслей о том, как бы вы сложили вместе три дроби с разными знаменателями.
Показать решение
Вычитание дробей
Вычитание дробей выполняется так же, как и сложение. Сначала определите, одинаковы ли знаменатели. Если нет, перепишите каждую дробь как эквивалентную дробь с одинаковым знаменателем. Ниже приведены примеры вычитания дробей, знаменатели которых не совпадают.
В приведенном ниже примере показано, как с помощью кратных найти наименьшее общее кратное, которое будет являться наименьшим общим знаменателем.
Пример
Вычесть [латекс]\крупный\фрак{5}{6}-\крупный\фрак{1}{4}[/латекс]. Упростите ответ.
Показать решение
В следующем видео вы увидите пример вычитания дробей с разными знаменателями.
Умножение дробей
Точно так же, как сложение, вычитание, умножение и деление при работе с целыми числами, вы также используете эти операции при работе с дробями.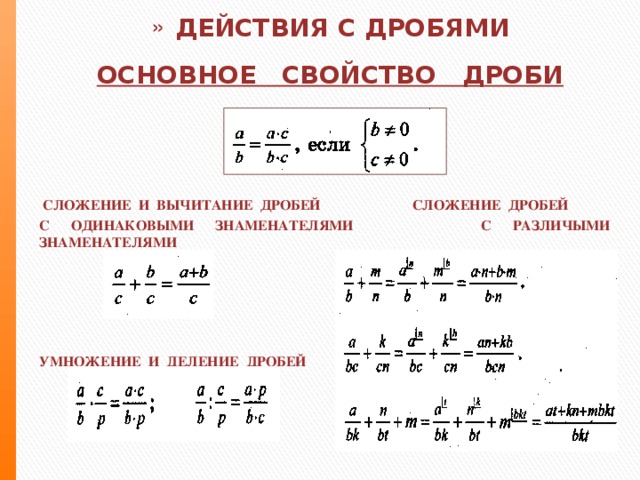 Есть много случаев, когда необходимо умножить дроби. Модель может помочь вам понять умножение дробей.
Есть много случаев, когда необходимо умножить дроби. Модель может помочь вам понять умножение дробей.
Когда вы умножаете дробь на дробь, вы получаете «долю дроби». Предположим, у вас есть [latex]\Large\frac{3}{4}[/latex] конфеты, и вы хотите найти [latex]\Large\frac{1}{2}[/latex] из [latex ]\Large\frac{3}{4}[/latex]:
Разделив каждую четверть пополам, вы можете разделить шоколадный батончик на восьмые части.
Затем выберите половину из них, чтобы получить [latex]\Large\frac{3}{8}[/latex].
В обоих вышеперечисленных случаях, чтобы найти ответ, вы можете перемножить числители вместе и знаменатели вместе.
Умножение двух дробей
[latex]\Large\frac{a}{b}\cdot\Large\frac{c}{d}=\Large\frac{a\cdot c}{b\cdot d}= \Large\frac{\text{произведение числителей}}{\text{произведение знаменателей}}[/latex]
Умножение более двух дробей
[латекс]\Large\frac{a}{b} \cdot\Large\frac{c}{d}\cdot\Large\frac{e}{f}=\Large\frac{a\cdot c\cdot e}{b\cdot d\cdot f}[/latex ]
Пример
Умножить [latex]\Large\frac{2}{3}\cdot\Large\frac{4}{5}[/latex]
Показать решение
Повторим: если у дроби есть общие делители в числителе и знаменателе, мы можем привести дробь к упрощенной форме, удалив общие делители.
Например,
- Учитывая [латекс]\большой\фрак{8}{15}[/латекс], коэффициенты [латекс]8[/латекс] равны: [латекс]1, 2, 4, 8 [/latex] и коэффициенты [latex]15[/latex]: [latex]1, 3, 5, 15[/latex]. [latex]\Large\frac{8}{15}[/latex] упрощен, потому что нет общих множителей для [latex]8[/latex] и [latex]15[/latex].
- Учитывая [латекс]\большой\фрак{10}{15}[/латекс], множители [латекс]10[/латекс] следующие: [латекс]1, 2, 5, 10[/латекс] и множители из [латекс]15[/латекс]: [латекс]1, 3, 5, 15[/латекс]. [latex]\Large\frac{10}{15}[/latex] не упрощается, поскольку [latex]5[/latex] является общим делителем [latex]10[/latex] и [latex]15[/latex]. ].
Вы можете сначала упростить, прежде чем умножать две дроби, чтобы облегчить себе работу. Это позволяет вам работать с меньшими числами при умножении.
В следующем видео вы увидите пример того, как умножить две дроби, а затем упростить ответ.
Подумай об этом
Умножить [латекс]\Большой\фракция{2}{3}\cdot\Большая\фракция{1}{4}\cdot\Большая\фракция{3}{5}[/латекс ]. Упростите ответ.
Упростите ответ.
Чем этот пример отличается от предыдущих? Используйте поле ниже, чтобы записать несколько мыслей о том, как бы вы умножили три дроби.
Показать решение
Разделить дроби
Бывают случаи, когда вам нужно использовать деление для решения проблемы. Например, если для покраски одного слоя краски на стенах комнаты требуется [латекс]3[/латекс] литра краски, и у вас есть ведро, содержащее [латекс]6[/латекс] кварт краски, сколько слоев краски краской можно красить стены? Вы делите [латекс]6[/латекс] на [латекс]3[/латекс] для ответа [латекс]2[/латекс] слоев. Также будут случаи, когда вам нужно разделить на дробь. Предположим, что для покраски шкафа в один слой требуется всего [латекс]\большой\фрак{1}{2}[/латекс] литр краски. Сколько слоев можно нанести 6 литрами краски? Чтобы найти ответ, вам нужно разделить [латекс]2[/латекс] на дробь [латекс]\большой\фракция{1}{2}[/латекс].
Прежде чем мы начнем делить дроби, давайте рассмотрим некоторые важные термины.
- обратное: две дроби являются обратными, если их произведение равно [латекс]1[/латекс] (не волнуйтесь, мы покажем вам примеры того, что это значит.)
- частное: результат деления
Для деления дробей необходимо использовать обратное число или дробь. Если вы умножаете два числа вместе и получаете в результате [латекс]1[/латекс], тогда эти два числа являются обратными. Вот несколько примеров взаимного обмена:
| Исходный номер | Взаимное | Продукт |
|---|---|---|
| [латекс]\большой\фрак{3}{4}[/латекс] | [латекс]\большой\фрак{4}{3}[/латекс] | [латекс]\Large\frac{3}{4}\cdot\Large\frac{4}{3}=\Large\frac{3\cdot 4}{4\cdot 3}=\Large\frac{12 {12}=1[/латекс] |
| [латекс]\большой\фрак{1}{2}[/латекс] | [латекс]\большой\фрак{2}{1}[/латекс] | [латекс]\Large\frac{1}{2}\cdot\Large\frac{2}{1}=\Large\frac{1\cdot2}{2\cdot1}=\Large\frac{2}{ 2}=1[/латекс] |
| [латекс] 3=\Large\frac{3}{1}[/латекс] | [латекс]\большой\фрак{1}{3}[/латекс] | [латекс]\Large\frac{3}{1}\cdot\Large\frac{1}{3}=\Large\frac{3\cdot 1}{1\cdot 3}=\Large\frac{3 {3}=1[/латекс] |
| [латекс]2\Большой\фракция{1}{3}=\Большой\фракция{7}{3}[/латекс] | [латекс]\большой\фрак{3}{7}[/латекс] | [латекс]\Large\frac{7}{3}\cdot\Large\frac{3}{7}=\Large\frac{7\cdot3}{3\cdot7}=\Large\frac{21}{ 21}=\нормальный размер 1[/латекс] |
Иногда мы называем обратное «отражением» другого числа: переверните [латекс]\Большой\фрак{2}{5}[/латекс], чтобы получить обратное [латекс]\Большой\фрак{5}{ 2}[/латекс].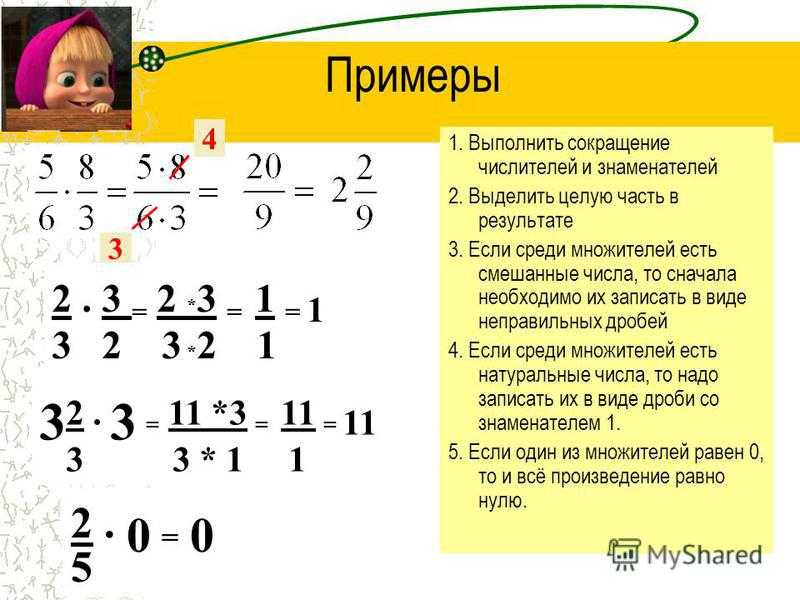
Деление на ноль
Вы знаете, что значит делить на [латекс]2[/латекс] или делить на [латекс]10[/латекс], но что значит делить количество на [латекс]0[ /латекс]? Это вообще возможно? Можете ли вы разделить [латекс]0[/латекс] на число? Рассмотрим дробь
[латекс]\большой\фрак{0}{8}[/латекс]
Мы можем прочитать это как «ноль разделить на восемь». Поскольку умножение обратно делению, мы могли бы переписать это как задачу на умножение.
[латекс]\текст{?}\cdot{8}=0[/латекс].
Мы можем сделать вывод, что неизвестное должно быть [латекс]0[/латекс], так как это единственное число, которое даст результат [латекс]0[/латекс] при умножении на [латекс]8[/латекс]. ].
Теперь рассмотрим обратную величину [латекс]\большой\фрак{0}{8}[/латекс], которая будет [латекс]\большой\фрак{8}{0}[/латекс]. Если мы перепишем это как задачу на умножение, у нас будет
[латекс]\текст{?}\cdot{0}=8[/латекс].
Это не имеет никакого смысла. Не существует чисел, которые можно умножить на ноль, чтобы получить результат 8. Обратная величина [латекс]\большой\фрак{8}{0}[/латекс] не определена, и фактически любое деление на ноль не определено. .
Обратная величина [латекс]\большой\фрак{8}{0}[/латекс] не определена, и фактически любое деление на ноль не определено. .
Внимание! Деление на ноль не определено, как и обратная величина любой дроби с нулем в числителе. Для любого действительного числа a [латекс]\большой\фрак{а}{0}[/латекс] не определен. Кроме того, обратная величина [latex]\Large\frac{0}{a}[/latex] всегда будет неопределенной.
Деление дроби на целое число
При делении на целое число вы умножаете его на обратное. В примере покраски, где вам нужно [латекс]3[/латекс] кварты краски для слоя и у вас есть [латекс]6[/латекс] кварты краски, вы можете найти общее количество слоев, которые можно покрасить, разделив [ латекс]6[/латекс] от [латекс]3[/латекс], [латекс]6\div3=2[/латекс]. Вы также можете умножить [латекс]6[/латекс] на обратную величину [латекс]3[/латекс], которая равна [латекс]\большой\фрак{1}{3}[/латекс], поэтому задача умножения становится
[latex]\Large\frac{6}{1}\cdot\Large\frac{1}{3}=\Large\frac{6}{3}=\normalsize2[/latex]
Деление равно умножению по обратному
Для всех делений вы можете превратить операцию в умножение с помощью обратного. Деление равносильно умножению на обратное.
Деление равносильно умножению на обратное.
Та же идея будет работать, когда делитель (вещь, которую делят) является дробью. Если у вас есть [latex]\Large\frac{3}{4}[/latex] шоколадного батончика и вам нужно разделить его между [latex]5[/latex] людьми, каждый человек получает [latex]\Large\frac {1}{5}[/latex] доступных конфет:
[латекс]\Large\frac{1}{5}\normalsize\text{ of }\Large\frac{3}{4}=\Large\frac{1}{5}\cdot\Large\frac{ 3}{4}=\Large\frac{3}{20}[/latex]
Каждый человек получает [latex]\Large\frac{3}{20}[/latex] целого батончика.
Если у вас есть рецепт, который нужно разделить пополам, вы можете разделить каждый ингредиент на [латекс]2[/латекс] или умножить каждый ингредиент на [латекс]\большой\фрак{1}{2} [/latex], чтобы найти новую сумму.
Например, деление на [латекс]6[/латекс] равносильно умножению на обратную величину [латекс]6[/латекс], которая равна [латекс]\большой\фрак{1}{6}[/ латекс]. Посмотрите на схему двух пицц ниже. Как можно справедливо разделить то, что осталось (область, заштрихованная красным), между [латекс]6[/латекс] людьми?
Каждый человек получает один кусок, поэтому каждый человек получает [latex]\Large\frac{1}{4}[/latex] пиццы.
Деление дроби на целое — это то же самое, что и умножение на обратную, поэтому вы всегда можете использовать умножение дробей для решения задач на деление.
Пример
Найти [latex]\Large\frac{2}{3}\div \normalsize 4[/latex]
Показать решение
Пример
Разделить. [latex] 9\div\Large\frac{1}{2}[/latex]
Показать решение
Разделить дробь на дробь
Иногда вам нужно решить задачу, требующую деления на дробь. Предположим, у вас есть пицца, которая уже нарезана на [латекс]4[/латекс] ломтика. Сколько существует фрагментов [latex]\Large\frac{1}{2}[/latex]?
Есть [латекс]8[/латекс] срезов. Вы можете видеть, что деление [латекс]4[/латекс] на [латекс]\большой\фрак{1}{2}[/латекс] дает тот же результат, что и умножение [латекс]4[/латекс] на [латекс]2. [/латекс].
Что произойдет, если вам потребуется разделить каждый срез на три части?
У вас будет [латекс]12[/латекс] срезов, что равносильно умножению [латекс]4[/латекс] на [латекс]3[/латекс].
Деление дробями
- Найдите обратную величину числа, следующего за символом деления.
- Умножьте первое число (то, что перед знаком деления) на величину, обратную второму числу (после знака деления).
Самый простой способ запомнить, как делить дроби, — это фраза «сохранить, изменить, перевернуть». Это значит до СОХРАНИТЬ первое число, ЗАМЕНИТЬ знак деления на умножение, а затем ПЕРЕВЕРНУТЬ (использовать обратное) второго числа.
Пример
Разделить [latex]\Large\frac{2}{3}\div\Large\frac{1}{6}[/latex]
Показать решение
Пример
Разделить [latex]\Large\frac{3}{5}\div\Large\frac{2}{3}[/latex]
Показать решение
При решении задачи на деление путем умножения на обратное число не забудьте записать все целые числа и смешанные числа в виде неправильных дробей. Окончательный ответ следует упростить и записать в виде смешанного числа.
В следующем видео вы увидите пример того, как разделить целое число на дробь, а также пример того, как разделить одну дробь на другую дробь.
Дроби и как их складывать, вычитать, умножать и делить
1.2 — Дроби и как их складывать, вычитать, умножать и делить1.2 — Дроби и как их складывать, вычитать, умножать и делить
Обозначение дроби
Дроби (или обыкновенных дроби ) используются для описания части целого объекта. Существует несколько обозначений дробей: a называется числителем , а b называется знаменателем . Обозначение означает, что мы разбиваем объект на b равных частей и у нас есть и таких штук. Часть или часть объекта, который у нас есть это а / б . Например, если мы разобьем пирог на
4 равных куска и берем 1 кусок то у нас получается 1/4 часть пирога:
Например, если мы разобьем пирог на
4 равных куска и берем 1 кусок то у нас получается 1/4 часть пирога: Эквивалентные дроби
Обратите внимание, что мы получаем одинаковое количество пирога как в предыдущем примере, если разделить пирог на 8 равных частей и получить 2 из них: Такие дроби, как 1/4 и 2/8, имеющие одинаковое значение, называются эквивалентные дроби . Этот пример предлагает следующий метод для проверка на равенство двух дробей.| Две дроби равны , если умножить числитель и знаменатель одной дроби на то же целое число дает другая дробь. |
Например, 4/5 и 24/30 эквивалентны, потому что мы можем начать с 4/5. и умножьте числитель и знаменатель на 6, чтобы получить 24/30: Движение в обратном направлении (от 24/30 до 4/5) предполагает следующий метод.
 для сокращения дроби до младших членов или его простейшая эквивалентная дробь :
для сокращения дроби до младших членов или его простейшая эквивалентная дробь : | Чтобы привести дробь к наименьшему члену или к ее простейшему эквиваленту дроби , полностью разложить как числитель, так и знаменатель (т. е. на простые числа). Затем сократите каждый множитель, который встречается как в числителе, так и в числителе. и знаменатель. Остается простейшая эквивалентная дробь . |
Например вот как уменьшить дробь 24/42 это самое простое эквивалентная дробь, а именно 4/7:
| Упражнения тренера по алгебре |
Неправильные дроби, смешанные дроби и длинное деление
Дробь, у которой числитель меньше знаменателя, называется правильной дробью и дробь, у которой числитель больше знаменателя, называется неправильной дробью . Пример неправильной дроби 7/4. Используя пример пирога, это означает, что вы сломали много пирогов, каждый из которых разделен на 4 равные части, и у вас есть 7 таких частей: Неправильные дроби иногда записывают в виде смешанной дроби , которая представляет собой сумму
целое число и правильная дробь, но без знака +. Например, 7/4 в обозначении смешанной дроби.
выглядит так: Обозначение смешанной дроби не используется в этой книге Algebra Help e или в программе Algebra Coach, потому что
его слишком легко спутать с произведением целого числа на дробь. Вместо того, чтобы писать мы будем держать знак + и писать.
Пример неправильной дроби 7/4. Используя пример пирога, это означает, что вы сломали много пирогов, каждый из которых разделен на 4 равные части, и у вас есть 7 таких частей: Неправильные дроби иногда записывают в виде смешанной дроби , которая представляет собой сумму
целое число и правильная дробь, но без знака +. Например, 7/4 в обозначении смешанной дроби.
выглядит так: Обозначение смешанной дроби не используется в этой книге Algebra Help e или в программе Algebra Coach, потому что
его слишком легко спутать с произведением целого числа на дробь. Вместо того, чтобы писать мы будем держать знак + и писать. Длинное деление — это метод преобразования неправильной дроби в смешанную. Проиллюстрируем метод на дроби . Выполните следующие шаги:
- Установите формат длинного деления, а именно .
- Так как 5 в 9 идет 1 раз, напишите «1» над 9, напишите 1 × 5 или «5» ниже 9 и вычтите 5 из 9, чтобы получить разницу в 4, например:
- Затем опустите 2 следующим образом: Вот что мы на самом деле сделали: «1» и «5» находятся в
десятки место, поэтому они
на самом деле представляют числа 10 и 50, как показано здесь: Поэтому мы фактически показали, что
.

- Теперь повторите весь процесс с остатком 42. Поскольку 5 в 42 идет 8 раз, напишите «8» над 2, напишите 8 × 5 или «40» ниже 42, и вычтите 40 из 42, чтобы получить остаток 2, например:
- Это показывает, что . Поскольку остаток 2 меньше делителя 5, это наш окончательный вариант. результат смешанной фракции.
Некоторые специальные дроби
Есть несколько специальных дробей, которые важно распознать:- . Любое число n можно превратить в дробь, написав ее над знаменателем 1.
- . Все, что делится само на себя, равно 1. Мы называем это UFOO (a u seful f orm o f o ne). Подробнее об НЛО позже.
- Если числитель дроби кратен знаменателю то дробь равна целому числу. Примером является .
- не определено для любого числителя n .
Деление на ноль в математике запрещено.

- . Нулевой числитель не проблема. Эта дробь равна 0, .
Сложение или вычитание дробей
На этом рисунке показано, что 2/8 пирога плюс 3/8 пирога равняются 5/8 пирога: Дроби, имеющие одинаковые знаменатели, называются , как и дроби . Если подумать об этом примере, то следующая процедура добавления или вычитание подобных дробей очевидно:| Чтобы сложить или вычесть две одинаковые дроби (дроби, имеющие общий знаменатель) , просто сложите или вычтите числители и приведите результат к общему знаменателю, как это: |
А что, если дроби не имеют общего знаменателя? Ответ заключается в том, что они должны быть затем преобразованы к эквивалентным дробям, которые делают имеют общий знаменатель. Процедура проиллюстрирована на этом примере:
Шаги:- Найдите наименьшее общее кратное двух
знаменатели 24 и 30.
 Применительно к дробям это число называется наименьшим общим
знаменатель (ЖК-дисплей). В этом примере ЖК-дисплей равен 120.
Применительно к дробям это число называется наименьшим общим
знаменатель (ЖК-дисплей). В этом примере ЖК-дисплей равен 120. - Преобразуйте каждую дробь в эквивалентную дробь, имеющую ЖК 120 в знаменателе. Для этого в данном примере умножьте числитель и знаменатель первой дроби на 5, а числитель и знаменатель второй дроби на 4 (показаны красным).
- Сложите числители и поместите над общим знаменателем.
Вот еще несколько примеров:
| Упражнения тренера по алгебре |
Умножение дробей
| Умножение дробей дает новую дробь. Умножьте числители, чтобы получить новый числитель и умножить знаменатели, чтобы получить новый знаменатель, как это: Затем упростите, сократив новую дробь до наименьших членов.  Чтобы умножить дробь на целое число, просто умножьте числитель дроби на целое число, чтобы получить новый числитель, например: Затем упростите, сократив новую дробь до наименьших членов. |
Вот пример того, почему работает первая процедура. Предположим, что есть половина пирога (т. дробь 1/2), как показано слева. Теперь предположим, что вы взяли 2/3 из этой половины пирога. (Слово «из» переводится как математическая операция «умножить».) Это означает, что вы разрезаете половину пирога на 3 равные части и берете 2 из них. В результате получается 2/6 части пирога.
Вот пример того, почему вторая процедура работает. Предположим, вы съели 1/4 часть пирога. и что твой друг съел в 3 раза больше пирога, чем ты. Это означает, что ваш друг съел 3/4 пирога.
Вот еще несколько примеров умножения:
| Упражнения тренера по алгебре |
Обратные и делящие дроби
Обратные числа играют важную роль при делении дробей. Два числа или дроби называются обратными друг другу.
если их произведение равно 1. Например:
Два числа или дроби называются обратными друг другу.
если их произведение равно 1. Например:4/5 и 5/4 обратны, потому что8 и 1/8 обратны, потому что
| Деление дробей: Процедура заключается в замене деления на дробь на умножение обратным значением этой дроби , например: |
Обратите внимание, что вы берете обратная дробь на дне!
| Вот почему эта процедура работает: Суть в том, что вместо того, чтобы видеть дробь, деленную на дробь, ищите одну дробь, числитель и знаменатель которой являются дробями. На первом шаге мы умножили эту дробь на UFOO числитель и знаменатель которого являются дробями. НЛО был выбран так, чтобы дроби в знаменателе сокращались и давали 1. После другого упрощение, оставившее только окончательное умножение дробей.  |


 Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.
Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.

 посмотрите на таблицу выше), поэтому мы собираемся умножить 3 ⁄ 2 на 6 ⁄ 6 . Получается: 3 ⁄ 2 x 6 ⁄ 6
посмотрите на таблицу выше), поэтому мы собираемся умножить 3 ⁄ 2 на 6 ⁄ 6 . Получается: 3 ⁄ 2 x 6 ⁄ 6  Это математическое правило.
Это математическое правило.

 Применительно к дробям это число называется наименьшим общим
знаменатель (ЖК-дисплей). В этом примере ЖК-дисплей равен 120.
Применительно к дробям это число называется наименьшим общим
знаменатель (ЖК-дисплей). В этом примере ЖК-дисплей равен 120.