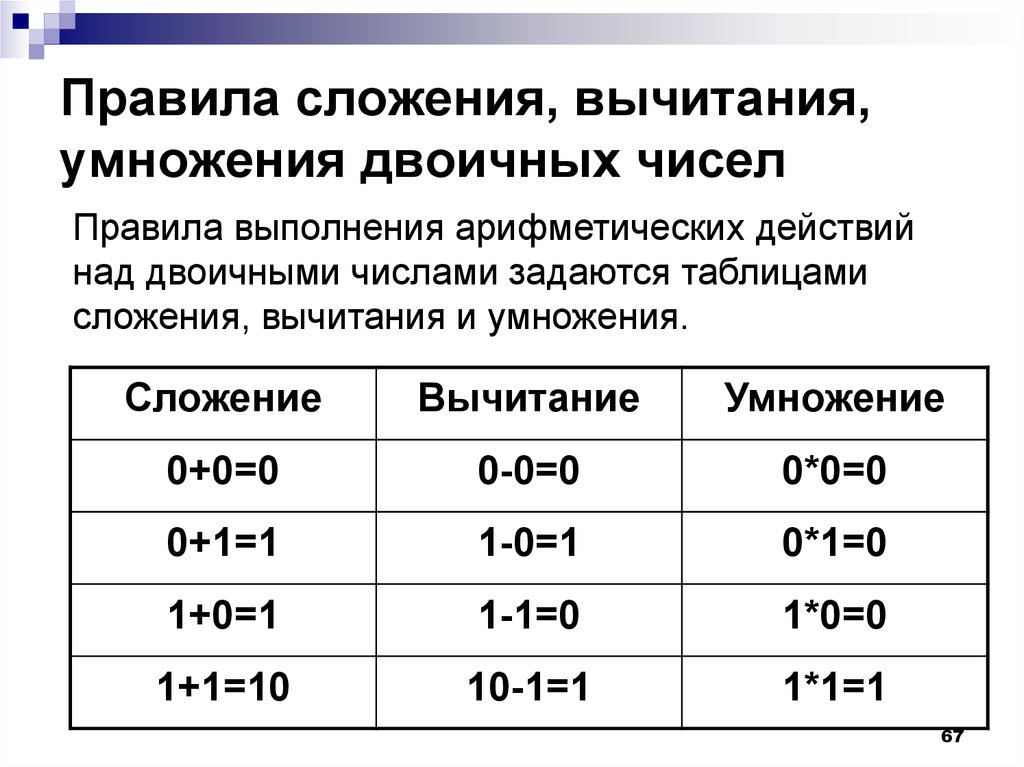
c++ — Быстрее ли работают сложение/вычитание и битовые операции по сравнению с делением/умножением в SIMD?
Вопрос задан
Изменён 1 год 4 месяца назад
Просмотрен 342 раза
Как известно, обычные инструкции сложения/вычитания и битовых сдвигов в процессорах x86 работают быстрее, чем инструкции умножения/деления. По-этому, для повышения производительности, операции *,/ как правило по возможности стараются заменить на +,-,>>,<<.
Мой вопрос: верно ли это утверждение для команд SIMD-расширений, как например SSE2? Или все инструкции SSE2 или другого расширения выполняются за равное количество тактов, а значит с заменой, скажем, операции деления на битовые сдвиги со сложениями можно не париться?
- c++
- x86
- simd
Важно понимать, что:
Современный компилятор достаточно умен и сообразителен, чтобы делать такие замены самостоятельно.

Прагматичный подход к оптимизации идет от лога профайлера, а не от того, что вы что-то где-то слышали от кого-то или даже читали, даже в учебнике, даже в именитом. Times, they are changing. Рекомендашки по ускорению устаревают раз в три года, а через пять лет покрываются плесенью. В олдскульных книжках, например, можно прочесть, что по массивам лучше ходить задом неперед из-за инструкции
loop, которая отматывает регистрCXдо нуля. Ага, советы из 80х, транслируемые преподами ВТУЗОВ студентам 2020хВремя выполнения инструкции в современном конвейерном SIMD процессоре, который еще перегоняет у себя CISC в RISC внутри, зависит от большого сочетания факторов, которые теоретически трудно предсказать.
Главными является ширина кэш-линий, число свободных каналов памяти, мгновенная тактовая частота, зависящая от режима энергопитания и температуры в данный момент времени (см. Turbo Boost и аналоги). Побочным может выступить такой фактор как внезапное попадание данных в другой NUMA-регион. Последним процессором, для которого можно было это четко узнать из мануала (была прямо табличка — опкод | число тактов) был не то
i386, не тоi486
Вывод. В каждом конкретном случае требуется проводить профилирование, на основании которого сравнивать полученную производительность с той, которую дает процессор на стандартных тестах LAPACK и похожих. Портить код, заменяя умножения на сдвиги смысла скорее всего нет вообще, потому что это сделает за вас компилятор. Если вы ему не доверяете, посмотрите машинный листинг, сделав его самостоятельно, или воспользовавшись онлайн-инструментом.
3
Как известно, обычные инструкции сложения/вычитания и битовых сдвигов в процессорах x86 работают быстрее, чем инструкции умножения/деления.
Это скорее бабушка на двое сказала. Во-первых, «обычные инструкции» — это на самом деле целое семейство инструкций. Которые еще и по-разному реализованы в разных процессорах. Во-вторых, в целом у них сходная производительность (если мерять в тактах), в каких-то вариантах может быть быстрее допустим умножение, а в других сдвиг. Например (для Sandy Bridge) IMUL m 2 CPI, SHL m,cl 4 CPI. При этом SHL r,i 0.5 CPI, а IMUL r,i 1 CPI. Для MMX psllw mm, mm и pmullw mm, mm — 1 CPI. Для SSE vpsllw ymm, ymm, xmm 1 CPI, а вот vpmulhw ymm, ymm, ymm на Skylake 0.5 CPI, а на более ранних те же 1 CPI. Вот деление да, оно гарантировано медленнее, там десятки CPI. В-третьих, собственно скорость вычисления в тактах — это далеко не единственная и не самая важная характеристика производительности инструкций. Если заглянуть в каталог таких характеристик, то там глаза разбегаются. В-четвертых, сложное устройство конвейера в современных процессорах также вносит свою лепту в определение производительности тот или иной инструкции, ведь реальная производительность варьируется в зависимости от состояния конвейера.
Что касается парится или нет — парится надо, но делать это надо системно, а не пытаться сэкономить байты разбрасывая хитрые вставки в коде.
Зарегистрируйтесь или войдите
Регистрация через Google
Регистрация через Facebook
Регистрация через почту
Отправить без регистрации
Почта
Необходима, но никому не показывается
Отправить без регистрации
Почта
Необходима, но никому не показывается
Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки
4.
 3. Сложение, умножение и вычитание понятий (точнее
3. Сложение, умножение и вычитание понятий (точнееО, как это заметно, что некоторые ферзи когда были пешками! / Николай Михальченко
Кроме ограничения, обобщения и деления, существуют и другие операции с объемами понятий, в результате которых образуются новые понятия. Речь идет об операциях, которые по аналогии с математическими называют сложением, умножением и вычитанием. Эти операции, как правило, называют операциями с множествами.
Сложение понятий — операция с объемами понятий, которая заключается в объединении двух или нескольких множеств, составляющих объемы соответствующих понятий, в одно множество.
Полученный результат является множеством, что составляет объем нового понятия, имя которого содержит имена исходных понятий, связанных союзом «или».
Результат сложения зависит от того, каковы исходные понятия — они совместимы или несовместимы, а если совместимы, то к какому виду совместимых понятий относятся — тождественных, перекрестных или до тех, что находятся в отношении подчинения.
Результат сложения несовместимых понятий равна сумме слагаемых. Скажем, взяв выходными понятие «злаковая растение» (обозначим объем этого понятия буквой а) и «бобовое растение» (объем которого — Ь) и добавив объемы этих понятий, получим новое понятие «злаковое или бобовое растение», объем которого будет равен а + Ь
Добавление совместимых понятий связано с определенными трудностями, которые легче преодолеть, приняв во внимание то, что слагаемые могут быть и недодатними числами. Так, добавив объемы понятий «студент» (а) и «спортсмен» (Ь), получим понятие «студент или спортсмен», объем которого будет меньше а + Ь, но больше или по крайней мере равным объему одного слагаемого, поскольку названные понятия являются перекрестными (схема 9).
Схема 9
Результатом сложения понятий, находящихся в отношении подчинения, понятие, объем которого равен объему соответствующего родового понятия. Так, понятие «житель села Городище или человек, который
совершила преступление X» равен объему понятия «житель села Городище», если известно, что преступник является жителем указанного села: а + Ь = а (схема 10).
Схема 10
Результатом добавления тождественных понятий является понятие с объемом, который равен объему одного из этих понятий (любого из них, поскольку они имеют одинаковый объем). Так, объем понятия «квадрат или прямоугольный ромб» равен объему понятия «квадрат» (или объема понятия «прямоугольный ромб»): а + Ь = а(а + Ь = Ь) (схема 11).
Схема 11
Умножение понятий — операция с понятиями, которая заключается в образовании нового понятия, объемом которого есть элементы, общие для всех исходных понятий.
Результатом умножения несовместимых понятий является понятие с мнимым объемом, т.е. нулевое. Так, умножив понятие «существительное» и «глагол», получим новое понятие, имя которого будет «существительное и глагол», а объем — пустое множество, поскольку нет таких слов, которые одновременно были бы и глаголами, и существительными.
Перемножив совместимые понятия, получим новое понятие, в объеме которого мыслятся реально существующие (или существовавшие) предметы.
В результате умножения двух перекрестных понятий получают новое понятие, объем которого будет уже от объема одного из исходных понятий. Так, перемножив понятия «водитель» и «футболист», получим новое понятие «водитель и футболист» или «водитель-футболист».
Объем нового понятия, получают при умножении понятий, находящихся в отношении подчинения, совпадает с объемом подчиненного понятия. Так, перемножив понятия «юрист» и «прокурор», получим понятие «юрист и прокурор», объем которого равен объему «прокурор», поскольку только прокуроры является одновременно и прокурорами и юристами.
Новое понятие, которое образуется при умножении тождественных понятий, совпадает по объему с любым исходным понятием. Так, перемножив понятия «представление» и «воссоздания в памяти облика предметов», получим понятие «представление и воссоздания в памяти облика предметов», объем которого равен как первому, так и второму исходным понятием (в одиночку). Ведь каждое представление и только представление, является воспроизведением в памяти внешности предметов.
Так, имея понятие «число натурального ряда», объемом которого охвачено всю соответствующую предметную сферу, и, мысленно выделив из него часть объема с помощью понятия «простое число», мы получим остаток (разницу) — «простое число». Именно поэтому операцию и называют вычитанием.
Иногда вычитанием называют и такую логическую операцию, в процессе которой «не-а» конкретизируется. Так, с исходным понятием «пора года» операцию вычитания можно осуществить двумя способами. Первый: «весна» — «невесна». Второй: «весна» — «лето», «осень», «зима».
Книга: ЛОГИКА ДЛЯ ЮРИСТОВ: ЛЕКЦИИ. / Правовой колледж ЛНУ им. Франко
СОДЕРЖАНИЕ
1. | ЛОГИКА ДЛЯ ЮРИСТОВ: ЛЕКЦИИ. / Правовой колледж ЛНУ им. Франко |
| 2. | 2. Логика как наука: ее предмет, метод, а также практическое значение ее знаний. |
| 3. | 3. Исторические этапы развития логического знания: логика Древней Индии, логика Древней Греции |
| 4. | 4. Особенности общей или традиционной (арістотелівської) логики. |
| 5. | 5. Особенности символической или математической логики. |
| 6. | 6. Теоретическая и практическая логика. |
| 7. | Тема 2: МЫШЛЕНИЕ И РЕЧЬ 1. Мышления (рассуждения): определение и особенности. |
| 8. | 2. Деятельность и мышление |
| 9. | 3. Структура мышления |
| 10. | 4. Правильные и неправильные рассуждения. Понятие о логической ошибке |
| 11. | 5. Логическая форма рассуждения |
| 12. | 6. Виды и типы мышления. |
| 13. | 7. Особенности мышления юриста |
| 14. | 8. Значение логики для юристов |
| 15. | Тема 3: Семиотика как наука о знаках. Язык как знаковая система. 1. Семиотика как наука о знаках Язык как знаковая система. 1. Семиотика как наука о знаках |
| 16. | 2. Понятие о знаке. Виды позамовних знаков |
| 17. | 3. Язык как знаковая система. Языковые знаки. |
| 18. | 4. Структура знакового процесса. Структура значения знака. Типичные логические ошибки |
| 19. | 5. Измерения и уровни знакового процесса |
| 20. | 6. Язык права |
| 21. | Раздел III. МЕТОДОЛОГИЧЕСКАЯ ФУНКЦИЯ ФОРМАЛЬНОЙ ЛОГИКИ 1. Метод и методология. |
| 22. | 2. Логические методы исследования (познания) Логические методы исследования (познания) |
| 23. | 3. Метод формализации |
| 24. | ОСНОВНЫЕ ФОРМЫ И ЗАКОНЫ АБСТРАКТНО-ЛОГИЧЕСКОГО МЫШЛЕНИЯ 1. Общая характеристика понятия как формы мышления. Структура понятия |
| 25. | 2. Виды понятий. Логическая характеристика понятий |
| 26. | 3. Типы отношений между понятиями |
| 27. | 4. Операции с понятиями 4.1. Ограничение и обобщение понятий |
| 28. | 4.2. Операция деления понятий |
| 29. | 4. 3. Сложение, умножение и вычитание понятий (точнее — их объемов) 3. Сложение, умножение и вычитание понятий (точнее — их объемов) |
| 30. | 4.4 Операция определения понятия |
| 31. | ОСНОВНЫЕ ФОРМЫ И ЗАКОНЫ АБСТРАКТНО-ЛОГИЧЕСКОГО МЫШЛЕНИЯ II. Высказывания. 1. Общая характеристика высказывания |
| 32. | 2. Истинность и ложность высказывания. |
| 33. | 3. Простые высказывания, их структура и виды |
| 34. | 4. Отношения между простыми высказываниями. |
| 35. | 5. Язык логики высказываний. |
| 36. | 6. Сложные высказывания. Логические союзы и их табличное определение Сложные высказывания. Логические союзы и их табличное определение |
| 37. | 7. Высказывания об отношении (реляционные выражения) |
| 38. | 8. Логический анализ вопросов и ответов вопрос Определения. Структура вопроса |
| 39. | Раздел 6. Дедуктивные умозаключения § 1. Понятие о дедуктивное умозаключение. Виды дедуктивных умозаключений |
| 40. | § 2. Прямые дедуктивные рассуждения Чисто условные умозаключения. |
| 41. | § 3. Непрямые дедуктивные рассуждения |
| 42. | Раздел 7. Недедуктивные (правдоподобные) умозаключения § 1. Общая характеристика правдоподобных рассуждений. Виды правдоподобных рассуждений Общая характеристика правдоподобных рассуждений. Виды правдоподобных рассуждений |
| 43. | § 2. Индуктивные умозаключения Понятие об индуктивном умозаключении |
| 44. | § 3. Умозаключения по аналогии |
| 45. | Раздел 8. Основы теории аргументации 1. Понятие об аргументации. Структура аргументации |
| 46. | § 2. Аргументация и спор |
| 47. | § 3. Виды аргументации Доказательная и недоказательная аргументация |
| 48. | § 4. Понятие о критике. Опровержение как частный случай критики |
49. | § 5. Виды критики |
| 50. | § 6. Правила, ошибки, уловки в аргументации/критике |
На предыдущую
Сложение, вычитание, умножение, деление дробей
Предоставил:
Диего Чт, 27 января 2022 г., 06:10 UTC
В этом PDF-файле мы будем выполнять различные арифметические операции над дробями. Дробь представляет собой часть целого или, в более общем смысле, любое количество равных частей. Дробь описывает, сколько имеется частей определенного размера, например, половина, восемь пятых, три четверти.
1.
Добавление дробей
Взято с сайта MathisFun.com
Чтобы сложить дроби, нужно выполнить 3 простых шага:
Шаг 1: Убедитесь, что нижние числа (знаменатели) совпадают
Шаг 2: Сложите верхние числа (числители). Поместите ответ над знаменателем.
Поместите ответ над знаменателем.
Шаг 3: Упростите дробь (при необходимости).
Пример 1:
1 1
+
4 4
Шаг 1. Нижние числа (знаменатели) уже совпадают. Сразу переходите к шагу 2.
Шаг 2. Сложите верхние числа и поставьте ответ над тем же знаменателем:
1 1 1+1 2
+ = =
4 4 4 4
Шаг 3. Упростим дробь:
2 1
=
4 2
На картинке это выглядит так:
1 1 2 1
/4 + /4 = /4 = /2
(Если вы не уверены в последнем шаге, см. Эквивалентные дроби.)
2.
Пример 2:
1 1
+
3 6
Шаг 1: Нижние числа разные. Видите, как кусочки разного размера?
1 1
/3 + /6 = ?
Нам нужно сделать их одинаковыми, прежде чем мы сможем продолжить, потому что мы не можем добавлять их таким образом.
Число «6» в два раза больше числа «3», поэтому, чтобы сделать нижние числа одинаковыми, мы можем
умножить верхнюю и нижнюю части первой дроби на 2, например:
× 2
1 2
=
3 6
× 2
Важно: вы умножаете верхнее и нижнее число на одинаковую величину, чтобы сохранить значение дроби
тем же самым
Теперь дроби имеют одинаковое нижнее число («6»), и наш вопрос выглядит так:
3. 2 1
2 1
/6 + /6
Нижние числа теперь одинаковы, поэтому мы можем перейти к шагу 2.
Шаг 2: Сложите верхние числа и поместите их над тем же знаменателем:
2 1 2+1 3
+ = =
6 6 6 6
В виде рисунка это выглядит так:
2 1 3
/6 + /6 = /6
Шаг 3: Упростите дробь:
3 1
=
6 2
В виде рисунка весь ответ выглядит так:
4.
2 1 3 1
/6 + /6 = /6 = /2
Стихотворение, которое поможет вам запомнить
♫ «Если вашей целью является сложение или вычитание,
Нижние числа должны быть одинаковыми!
♫ «Изменение нижнего значения, используйте умножение или деление,
Но то же самое нужно применить и к верхнему,
♫ «И не забудьте упростить,
Прежде чем прощаться»
Пример 3:
1 1
+
3 5
Опять же, нижние числа разные ( ломтики разного размера)!
1 1
/3 + /5 = ?
Но давайте попробуем разделить их на меньшие размеры, каждый из которых будет одинаковым:
5. 5 3
5 3
/15 + /15
Первая дробь: умножив верх и низ на 5, мы получили 5/15 :
× 5
1 5
=
3 15
× 5
Вторая дробь: умножив сверху и снизу по 3, мы получили 3/15 :
× 3
1 3
=
5 15
× 3
Нижние числа теперь одинаковы, поэтому мы можем продолжить и добавить верхние числа:
5 3 8
/15 + /15 = /15
6.
Сложение дробей с разными знаменателями
Но что, если знаменатели (нижние числа) не совпадают? Как в этом примере:
3 1
/8 + /4 = ?
+ =
Вы должны каким-то образом сделать знаменатели одинаковыми.
В данном случае это легко, потому что мы знаем, что 1/4 равно 2/8:
3 2 5
/8 + /8 = /8
+ =
В этом примере было легко вычислить знаменатели то же самое, но это может быть сложнее … поэтому вам
может потребоваться использовать любой из этих методов (нахождение наименьшего общего знаменателя или нахождение
Общий знаменатель), чтобы сделать их одинаковыми (они оба работают, используйте то, что вам больше нравится).
Вычитание дробей
Существует 3 простых шага для вычитания дробей
Шаг 1. Убедитесь, что нижние числа (знаменатели) совпадают
Шаг 2. Вычтите верхние числа (числители). Поместите ответ над тем же знаменателем
.
Шаг 3. Упростите дробь.
7.
Пример 1:
3 1
–
4 4
Шаг 1. Нижние числа уже совпадают. Сразу переходите к шагу 2.
Шаг 2. Вычтите верхние числа и поставьте ответ над тем же знаменателем:
3 1 3–1 2
– = =
4 4 4 4
Шаг 3. Упростите дробь:
2 1
=
4 2
Пример 2:
1 1
–
2 6
Шаг 1. Нижние числа разные. Видите, как кусочки разного размера? Нам нужно
сделайте их одинаковыми, прежде чем мы сможем продолжить, потому что мы не можем вычесть их следующим образом:
1 1
/2 — /6 = ?
8.
Чтобы нижние числа были одинаковыми, умножьте верхнюю и нижнюю части первой дроби (1/2) на 3
следующим образом:
× 3
1 3
=
2 6
× 3
А теперь наш вопрос выглядит так :
3 1
/6 — /6
Нижние числа (знаменатели) совпадают, поэтому мы можем перейти к шагу 2.
Шаг 2. Вычесть верхние числа и поставить ответ над тем же знаменателем:
3 1 3–1 2
– = =
6 6 6 6
На картинке это выглядит так:
3 1 2
/6 — /6 = /6
9.
Шаг 3. Упростите дробь:
2 1
=
6
Сложение и вычитание смешанных дробей
Краткое определение: смешанная дробь представляет собой целое число
и дробь вместе,
, например 1 3/4.
1 3/4
(одна и три четверти)
Чтобы их было легко складывать и вычитать, просто сначала преобразуйте их в неправильные дроби:
Краткое определение: неправильная дробь имеет
верхнее число, большее или равное
нижний номер,
, например, 7/4 или 4/3
7
/4 (это «тяжелое сверху»)
(семь четвертей или семь четвертей)
Добавление смешанных дробей
Я считаю, что это лучший способ сложения смешанных дробей :
преобразовать их в неправильные дроби
затем сложить их (используя сложение дробей)
затем преобразовать обратно в смешанные дроби:
Пример: Сколько будет 2 3/4 + 3 1/2 ?
10. Преобразовать в неправильные дроби:
Преобразовать в неправильные дроби:
2 3/4 = 11/4
3 1/2 = 7/2
Общий знаменатель 4:
11
/4 остается как 11/4
7
/2 становится 14/4
(путем умножения верхнего и нижнего на 2)
Теперь добавим:
11
/4 + 14/4 = 25/4
Преобразование обратно в смешанные дроби:
25
/4 = 6 1/4
Когда у вас будет больше опыта, вы сможете сделать это быстрее, например:
Пример: Что такое 3 5/8 + 1 3/4
Преобразуйте их в неправильные дроби:
3 5/8 = 29/8
1 3/4 = 7/4
Сделайте тот же знаменатель: 7/4 станет 14/8 (путем умножения верхнего и нижнего на 2 )
И прибавьте:
/8 + 14/8 = 43/8 = 5 3/8
Вычитание смешанных дробей
Просто следуйте тому же методу, но вместо прибавления вычтите:
Пример: Сколько будет 15 3/4 — 8 5/ 6 ?
11.
Преобразование в неправильные дроби:
15 3/4 = 63/4
8 5/6 = 53/6
Общий знаменатель числа 12:
63
/4 становится 189/12
53
/6 становится 106/12
Теперь вычитаем :
189
/12 — 106/12 = 83/12
Преобразование обратно в смешанные дроби:
83
/12 = 6 11/12
12. Умножение дробей
Умножение дробей
Умножьте верхние части, умножьте нижние.
Есть 3 простых шага, чтобы умножить дроби
1. Умножьте верхние числа (числители).
2. Умножьте нижние числа (знаменатели).
3. При необходимости упростите дробь.
Пример 1
1 2
×
2 5
Шаг 1. Умножьте верхние числа:
1 2 1×2 2
× = =
2 5
Шаг 2. Умножьте нижние числа:
1 2 1×2 2
× = =
2 5 2×5 10
Шаг 3. Упростите дробь:
2 1
=
10 5
Пример 2
1 9
×
3 16
13.
Шаг 1. Умножьте верхние числа:
1 9 1×9 9
× = =
3 16
Шаг 2. Умножьте нижние числа:
1 9 1×9 9
× = =
3 16 3 × 16 48
Шаг 3. Упростите дробь:
9 3
=
48 16
Стихотворение, которое поможет вам запомнить
♫ «Умножение дробей: не проблема» ,
Верх умножить на верх над низом умножить на низ.» ♫
Умножение смешанных дробей
(«Смешанные дроби» также называются «смешанными числами»)
Чтобы умножить смешанные дроби:
1. преобразовать в неправильные дроби
преобразовать в неправильные дроби
2. Умножить дроби
3. преобразовать результат обратно в смешанные дроби
Пример: Что такое 13/8 × 3 ?
Подумайте о пицце.
1 3/8 — это 1 пицца и 3 восьмых другой пиццы.
14.
Сначала преобразуем смешанную дробь (1 3/8) в неправильную дробь (11/8):
Разрежьте всю пиццу на восьмые части и сколько у вас всего
восьмых?
1 партия из 8 плюс 3 восьмых = 8+3 = 11 восьмых.
Теперь умножьте это на 3:
1 3/8 × 3 = 11/8 × 3/1 = 33/8
У вас 33 восьмых.
И, наконец, преобразовать в смешанную дробь (только потому, что исходная дробь была в таком виде):
15.
33 восьмых — это 4 целых пиццы (4 × 8 = 32) и 1 восьмая
осталась.
А вот как это выглядит в одной строке:
1 3/8 × 3 = 11/8 × 3/1 = 33/8 = 4 1/8
Другой пример: что такое 11/2 x 21/5?
Выполните действия, описанные выше:
1. Преобразуйте в неправильные дроби
Преобразуйте в неправильные дроби
2. Умножьте дроби
3. преобразовать результат обратно в смешанные дроби
Шаг за шагом это:
16.
Преобразование обеих дробей в неправильные дроби
1 1/2 × 2 1/5 = 3/2 × 11/5
Умножьте дроби (умножьте верхние числа на нижние числа):
3
/2 × 11/5 = (3 × 11)/(2 × 5) = 33/10
Преобразование в смешанное число
33
/10 = 3 3/10
Если вы сообразительны, вы можете сделать все это в одной строке, например:
1 1/2 × 2 1/5 = 3/2 × 11/5 = 33/10 = 3 3/10
Еще один пример: что такое 31/4 x 31/3?
Преобразовать оба числа в неправильные дроби
3 1/4 × 3 1/3 = 13/4 × 10/3
13
/4 × 10/3 = 130/12
Преобразовать в смешанное число (и упростить):
130
/12 = 10 10/12 = 10 5/6
Еще раз, здесь в одной строке:
3 1/4 × 3 1/3 = 13/4 × 10/3 = 130/12 = 10 10/ 12 = 10 5/6
У этого есть отрицания: сколько будет -15/9 × -21/7 ?
Преобразование смешанных дробей в неправильные:
1 5/9 = 9/9 + 5/9 = 14/9
2 1/7 = 14/7 + 1/7 = 15/7
17. Затем умножьте неправильные дроби (Примечание: отрицательное умножение на отрицательное дает нам положительное значение):
Затем умножьте неправильные дроби (Примечание: отрицательное умножение на отрицательное дает нам положительное значение):
-14
/9 × -15/7 = -14×-15 / 9×7 = 210/63
Затем я решил упростить следующее, сначала на 7 (потому что я заметил, что 21 и 63 оба кратны
7 ), затем снова на 3 (но я мог бы сделать это за один шаг, разделив на 21):
210
/63 = 30/9 = 10/3
Наконец, преобразовать в смешанную дробь (потому что это был стиль вопрос):
10
/3 = (9+1)/3 = 9/3 + 1/3 = 3 1/3
18.
Разделение дробей
Переверните вторую дробь вверх ногами и просто умножьте.
Есть 3 простых шага для деления дробей:
Шаг 1. Переверните вторую дробь (ту, на которую вы хотите разделить) вверх ногами
(теперь это обратная дробь).
Шаг 2. Умножьте первую дробь на обратную
Шаг 3. Упростите дробь (при необходимости)
Пример 1
1 1
÷
2 6
Шаг 1. Переверните вторую дробь (она станет обратной) :
Переверните вторую дробь (она станет обратной) :
1 6
становится
6 1
Шаг 2. Умножьте первую дробь на обратную:
1 6 1×6 6
× = =
2 1 2×1 2
Шаг 3. Упростите дробь:
6
= 3
2
Имеет ли это смысл?
1 1
Действительно ли ÷ равно 3 ?
2 6
Вы можете изменить вопрос типа «Сколько будет 20 разделить на 5?» в «Сколько пятерок вписывается в 20?»
Точно так же наш дробный вопрос может стать:
19.
1 1 1 1
÷ Сколько в ?
2 6 6 2
Теперь посмотрите на пиццу ниже… сколько «1/6 кусочков» помещается в «1/2 кусочка»?
Сколько в ? Ответ: 3
1 1
Итак, теперь вы видите, что ÷ =3 действительно имеет смысл!
2 6
Пример 2
1 1
÷
8 4
Шаг 1. Переверните вторую дробь вверх ногами (обратное число):
1 4
станет
4 1
Шаг 2. Умножьте первую дробь на это обратное число:
1 4 1×4 4
× = =
8 1 8×1 8
Шаг 3. Упростите дробь:
Упростите дробь:
4 1
=
8 2
И это все, что вам нужно сделать.
20.
Стихотворение, которое поможет вам запомнить
♫ «Делить дроби так же просто, как пирог,
Переверните вторую дробь, а затем умножьте». ♫
Но, может быть, вы хотите знать, почему мы делаем это именно так…
Зачем переворачивать дробь вверх дном?
Ну… что делает дробь?
Дробь говорит:
умножить на большее число
разделить на нижнее число
Пример: 3/4 означает разрезать на 4 части, а затем взять 3 из них.
Итак, вы:
делите на 4
умножаете на 3
Но когда вы ДЕЛИТЕ на дробь, вас просят сделать обратное умножению…
Итак, вы:
делите на большее число
умножаете на нижнее число
Таким образом, деление на 5/2 равносильно умножению на 2/5
21.
Деление на 5, затем умножение на 2
равно
Умножение на 2, затем деление на 5
Таким образом, вместо деления на дробь проще перевернуть эту дробь, а затем выполнить
Событийные потенциалы сложения, вычитания и умножения однозначных чисел
Сравнительный анализ Исследование
. 2006;44(12):2500-7.
2006;44(12):2500-7.
doi: 10.1016/j.neuropsychologia.2006.04.003. Epub 2006 7 июля.
Синьлинь Чжоу 1 , Чуаньшэн Чен, Ци Дун, Хунчуань Чжан, Жэньлай Чжоу, Хуэй Чжао, Чуньхуэй Чен, Сибин Цяо, Тин Цзян, И Го
Филиалы
принадлежность
- 1 Государственная ключевая лаборатория когнитивной неврологии и обучения, Институт когнитивной неврологии и обучения, Пекинский педагогический университет, Пекин, 100875, Китай.
- PMID: 16828126
- DOI: 10.1016/ж.нейропсихология.2006.04.003
Бесплатная статья
Сравнительное исследование
Xinlin Zhou et al. Нейропсихология.
2006.
Нейропсихология.
2006.
Бесплатная статья
. 2006;44(12):2500-7.
doi: 10.1016/j.neuropsychologia.2006.04.003. Epub 2006 7 июля.
Авторы
Синьлинь Чжоу 1 , Чуаньшэн Чен, Ци Дун, Хунчуань Чжан, Жэньлай Чжоу, Хуэй Чжао, Чуньхуэй Чен, Сибин Цяо, Тин Цзян, И Го
принадлежность
- 1 Государственная ключевая лаборатория когнитивной неврологии и обучения, Институт когнитивной неврологии и обучения, Пекинский педагогический университет, Пекин, 100875, Китай.
- PMID: 16828126
- DOI:
10.
 1016/ж.нейропсихология.2006.04.003
1016/ж.нейропсихология.2006.04.003
Абстрактный
В этом исследовании сравнивались связанные с событиями потенциалы, возникающие при выполнении задач на сложение, вычитание и умножение однозначных чисел. С парадигмой отложенной проверки 18 китайских студентов сначала попросили решить арифметические задачи, которые были представлены визуально, в течение 200 мс, а через 1,5 с оценить, было ли представленное решение правильным или нет. Результаты показали, что по сравнению со сложением и вычитанием умножение вызывало большее N300 на левых лобных электродах с пиком около 320 мс (в интервале между 275 и 334 мс после начала арифметической задачи). Чтобы контролировать смешанные эффекты сложности задачи и размера решения, были дополнительно проведены сравнения между «большими» задачами на сложение (с суммами от 11 до 17) и «малыми» задачами на умножение (с произведениями от 6 до 24). Были получены аналогичные результаты (т. е. значительная разница между сложением и умножением в компоненте N300 между 296 и 444 мс). Анализ источников показал, что один диполь в левой передней области мозга мог внести свой вклад в топографию разностных сигналов («умножение-сложение», «умножение-вычитание» и «маленькое» умножение-«большое» сложение»). Эти результаты интерпретируются с точки зрения большей зависимости от фонологической обработки для поиска фактов умножения, чем для поиска фактов сложения и вычитания.
е. значительная разница между сложением и умножением в компоненте N300 между 296 и 444 мс). Анализ источников показал, что один диполь в левой передней области мозга мог внести свой вклад в топографию разностных сигналов («умножение-сложение», «умножение-вычитание» и «маленькое» умножение-«большое» сложение»). Эти результаты интерпретируются с точки зрения большей зависимости от фонологической обработки для поиска фактов умножения, чем для поиска фактов сложения и вычитания.
Похожие статьи
Потенциалы, связанные с событиями, для простой арифметики в арабских цифрах и китайских числовых словах: исследование мысленного представления арифметических фактов с помощью обозначений и эффектов операций.
Чжоу С., Чен С., Цяо С., Чен С., Чен Л., Лу Н., Дун Ц. Чжоу С и др. Мозг Res. 2009 11 декабря; 1302: 212-24. doi: 10.1016/j.brainres.2009.
 09.024. Epub 2009, 16 сентября.
Мозг Res. 2009.
PMID: 19765567
09.024. Epub 2009, 16 сентября.
Мозг Res. 2009.
PMID: 19765567Влияние числового расстояния и вероятности стимула на компоненты ERP, вызванные числовыми несоответствиями в умственном сложении.
Шуц Д., Чепе В. Шукс Д. и соавт. Мозг Res Cogn Brain Res. 2005 февраля; 22 (2): 289-300. doi: 10.1016/j.cogbrainres.2004.04.010. Мозг Res Cogn Brain Res. 2005. PMID: 15653300
Диссоциированная организация мозга для сложения и умножения однозначных чисел.
Чжоу С, Чен С, Цзан Ю, Донг Ц, Чен С, Цяо С, Гун Ц. Чжоу С и др. Нейроизображение. 2007 1 апреля; 35 (2): 871-80. doi: 10.1016/j.neuroimage.2006.12.017. Epub 2006 23 декабря. Нейроизображение. 2007. PMID: 17292628
Факты, правила и стратегии умножения однозначных чисел: данные потенциалов мозга, связанных с событиями.

Йост К., Бейнхофф У., Хеннигхаузен Э., Рёслер Ф. Йост К. и др. Мозг Res Cogn Brain Res. 2004 г., июль; 20 (2): 183–93. doi: 10.1016/j.cogbrainres.2004.02.005. Мозг Res Cogn Brain Res. 2004. PMID: 15183390
Четность влияет на сложность простого сложения и вычитания, но не на проблемы умножения у детей.
ТМ Хайнс. Хайнс ТМ. Psychol Rep. 2013 Aug; 113 (1): 1048-65. дои: 10.2466/10.11.pr0.113x16z4. Psychol Rep. 2013. PMID: 24340800 Рассмотрение.
Посмотреть все похожие статьи
Цитируется
Влияние ожирения на арифметическую обработку у подростков с высокими и низкими математическими навыками: исследование потенциальных возможностей, связанных с событиями.

Alatorre-Cruz GC, Downs H, Hagood D, Sorensen ST, Williams DK, Larson-Prior LJ. Alatorre-Cruz GC, et al. Передний шум нейронов. 2022 10 марта; 16:760234. дои: 10.3389/fnhum.2022.760234. Электронная коллекция 2022. Передний шум нейронов. 2022. PMID: 35360282 Бесплатная статья ЧВК.
Различные языковые модальности, но схожие когнитивные процессы в арифметическом поиске фактов.
Бертелетти И., Кимбли С.Е., Салливан С.Дж., Квандт Л.С., Миякоши М. Бертелети I и др. наук о мозге. 2022 22 января; 12 (2): 145. doi: 10.3390/brainsci12020145. наук о мозге. 2022. PMID: 35203909 Бесплатная статья ЧВК.
Осцилляторные электроэнцефалографические паттерны решения арифметических задач у четвероклассников.




 1016/ж.нейропсихология.2006.04.003
1016/ж.нейропсихология.2006.04.003 09.024. Epub 2009, 16 сентября.
Мозг Res. 2009.
PMID: 19765567
09.024. Epub 2009, 16 сентября.
Мозг Res. 2009.
PMID: 19765567