Как умножать корни — Wiki How To Русский
‘).insertAfter(«#intro»),$(‘
‘).insertBefore(«.youmightalsolike»),$(‘
‘).insertBefore(«#quiz_container»),$(‘
‘).insertBefore(«#newsletter_block_main»),fa(! 0),b=document.getElementsByClassName(«scrolltomarker»),a=0;a
В этой статье:
Умножение корней без множителей
Умножение корней с множителями
Умножение корней с разными показателями
Дополнительные статьи
Источники
Знак корня (√) означает квадратный корень из некоторого числа. Знак корня встречается не только в алгебре, но и в повседневной жизни, например, в деревообрабатывающем производстве, которое включает расчет относительных размеров. Два любых корня с одинаковыми показателями (степени корня) можно умножать. Если у корней разные показатели, необходимо привести корни к одному показателю. Если вы хотите узнать, как умножать корни с или без множителей, прочитайте эту статью.
Если у корней разные показатели, необходимо привести корни к одному показателю. Если вы хотите узнать, как умножать корни с или без множителей, прочитайте эту статью.
Шаги
1
Убедитесь, что корни имеют одинаковый показатель (степень). Степень записывается слева над знаком корня. Если степени нет, то корень считается квадратным (то есть его степень равна 2) и его можно умножить на другие квадратные корни (об умножении корней с разными показателями читайте далее). Вот несколько примеров умножения корней с одинаковыми показателями:
- Пример 1: √(18) x √(2) = ?
- Пример 2: √(10) x √(5) = ?
- Пример 3: 3√(3) x 3√(9) = ?
2
Перемножьте числа под корнем. Вот как это делается:
- Пример 1: √(18) x √(2) = √(36)
- Пример 2: √(10) x √(5) = √(50)
- Пример 3 : 3√(3) x 3√(9) = 3√(27)
3
Упростите подкоренное выражение.
 При умножении корней полученное подкоренное выражение можно упростить (не всегда) до произведения некоторого числа (или выражения) на полный квадрат или куб. Вот как это делается:
При умножении корней полученное подкоренное выражение можно упростить (не всегда) до произведения некоторого числа (или выражения) на полный квадрат или куб. Вот как это делается:- Пример 1: √(36) = 6. 36 является квадратом числа 6, потому что 6*6=36.
- Пример 2: √(50) = √(25*2) = √([5*5]*2) = 5√(2). Число 50 можно разложить на произведение чисел 25 и 2. Корень из 25 равен 5, поэтому выносим 5 за знак корня и таким образом упрощаем подкоренное выражение.
- Если внести число 5 обратно под знак корня, оно возводится в квадрат, и вы получите число 25 под знаком корня.
- Пример 3: 3√(27) = 3. Кубический корень из числа 27 равен 3, потому что 3*3*3 = 27.
Реклама
1
Умножьте множители. Множитель — число, стоящее перед знаком корня. Если его нет, то множитель равен 1. Перемножьте множители. Вот как это делается:
- Пример 1: 3√(2) x √(10) = 3√(?)
- 3 x 1 = 3
- Пример 2: 4√(3) x 3√(6) = 12√(?)
- 4 x 3 = 12
- Пример 1: 3√(2) x √(10) = 3√(?)
2
Умножьте числа под знаком корня.
 После того как вы перемножили множители, перемножьте числа под знаком корня. Вот как это делается:
После того как вы перемножили множители, перемножьте числа под знаком корня. Вот как это делается:- Пример 1: 3√(2) x √(10) = 3√(2 x 10) = 3√(20)
- Пример 2: 4√(3) x 3√(6) = 12√(3 x 6) = 12√(18)
3
Упростите подкоренное выражение.
Далее упростите полученные значения под знаком корня, вынеся соответствующие числа за знак корня. После этого просто перемножьте эти вынесенные числа и множители, стоящие перед знаком корня. Вот как это делается:- 3√(20) = 3√(4 x 5) = 3√([2 x 2] x 5) = (3 x 2)√(5) = 6√(5)
- 12√(18) = 12√(9 x 2) = 12√(3 x 3 x 2) = (12 x 3)√(2) = 36√(2)
Реклама
1
Найдите НОК (наименьшее общее кратное) показателей. НОК показателей — наименьшее число, которое делится на оба показателя. Найдите НОК показателей для следующего выражения:3√(5) x 2√(2) = ?
- Показатели равны 3 и 2.
 Число 6 является НОК этих двух чисел, потому что это наименьшее число, которое делится без остатка как на 3, так и на 2: 6/3=2 и 6/2=3. Чтобы умножить корни, их показатель должен быть равен 6.
Число 6 является НОК этих двух чисел, потому что это наименьшее число, которое делится без остатка как на 3, так и на 2: 6/3=2 и 6/2=3. Чтобы умножить корни, их показатель должен быть равен 6.
- Показатели равны 3 и 2.
2
Запишите каждый корень с НОК в качестве нового показателя. Вот как записать выражение с новым показателем:
- 6√(5) x 6√(2) = ?
3
Найдите числа, на которые необходимо умножить каждый исходный показатель, чтобы получить НОК. В выражении 3√(5) вам нужно умножить показатель 3 на 2, чтобы получить 6. В выражении 2√(2) вам нужно умножить показатель 2 на 3, чтобы получить 6.
4
Возведите число, стоящее под знаком корня, в степень равную числу, найденному в предыдущем шаге. Для первого выражения возведите 5 в степень 2. Для второго выражения возведите 2 в степень 3. Вот как это будет выглядеть:
- 2 —> 6√(5) = 6√(5)2
- 3 —> 6√(2) = 6√(2)3
5
Проделайте операцию возведения в степень и запишите результат под знаком корня.
 Вот как это делается:
Вот как это делается:- 6√(5)2 = 6√(5 x 5) = 6√25
- 6√(2)3 = 6√(2 x 2 x 2) = 6√8
6
Перемножьте числа под знаком корня: 6√(8 x 25)
7
Запишите ответ. 6√(8 x 25) = 6√(200). В некоторых случаях можно упростить подкоренное выражение, например, найдя множитель числа 200, из которого можно взять корень 6 степени. Но в данном случае выражение не упрощается.
Реклама
Советы
- Если «множитель» отделяется от корня знаком плюс или минус, то это уже вообще не множитель — это отдельный член выражения, и операции с ним проводятся отдельно от корня.
- Знак корня является еще одним способом записи дробных показателей. Например, квадратный корень из любого числа есть это число в степени 1/2; кубический корень из любого числа есть это число в степени 1/3 и так далее.

- Множитель — число, стоящее непосредственно перед знаком корня. Так, например, в выражении 2(квадратный корень)5, число 5 является подкоренным выражением, а число 2 — множителем. Когда множитель и корень записаны рядом, то это означает их умножение: 2*(квадратный корень)5.
Реклама
Источники
Об этой статье
На других языках
Как умножать корни — Wiki How Русский
Знак корня (√) означает квадратный корень из некоторого числа. Знак корня встречается не только в алгебре, но и в повседневной жизни, например, в деревообрабатывающем производстве, которое включает расчет относительных размеров. Два любых корня с одинаковыми показателями (степени корня) можно умножать. Если у корней разные показатели, необходимо привести корни к одному показателю. Если вы хотите узнать, как умножать корни с или без множителей, прочитайте эту статью.
Эту страницу просматривали 442 724 раза.
Реклама
Корень и его свойства — intmag24.ru
Тема в математике «Корень и его свойства» нередко вызывает затруднения у школьников, особенно при решении примеров. В данной статье описаны основные свойства корней, а также правила сложения, вычитания, умножения и деления. Наглядные примеры помогаю понять, как решать задания с корнями.
Определение «Корень» Корень второй степени (квадратный корень) из числа a — это число, которое становится равным a, если число a возвести во вторую степень (в квадрат).
Например, √64 = 8 (√64 равно числу 8).
Формула: √a2 = a
Число, стоящее под знаком корня, называется подкоренным числом. Если под знаком корня стоит целое выражение, то его называют подкоренным выражением.
Если под знаком корня стоит целое выражение, то его называют подкоренным выражением.
Свойство квадратного корня: для действительных чисел не существует квадратный корень из отрицательного числа, так как возведение числа в квадрат будет всегда неотрицательным числом.
Извлечь корень — значит найти значение корня (то есть найти число, при возведении которого в степень, получается подкоренное значение).
Например, извлечь корень из 64 – значит найти √64.
Найти корень из числа можно одним из следующих способов:
- Использование таблицы квадратов, таблицы кубов и т.д. В данном случае нужно просто найти нужное число в таблице и посмотреть, какому значению оно соответствует.
- Разложение подкоренного выражения (числа) на простые множители.
Порядок нахождения корня в этом случае будет следующим: Разложение подкоренного значения на простые множители,
Разложение подкоренного значения на простые множители,
2. Объединение одинаковых множителей и их представление в виде степени с необходимым показателем.
Например, √144 = √2х2х2х2х3х3 = √(2х2)х(2х2)х(3х3) = √22х22х32 = √122 = 12
3. В случае, если невозможно найти корень из числа, то можно упростить подкоренное выражение (число). В этом случае применяется следующее правило: корень из произведения чисел равен произведению корней этих чисел.
Например, √72 = √2х2х2х3х3 = √(2х2)х2х(3х3) = √22х2х32 = √62х2 = 6√2 - Когда невозможно получить два одинаковых числа под знаком корня, это значит, что упростить такой корень нельзя.
Например, √130=√13х5х2 – упростить нельзя.
- Извлечение корня из дроби. В этом случае применяются следующие правила:
1. дробное число должно быть записано в виде обыкновенной дроби;
дробное число должно быть записано в виде обыкновенной дроби;
2. корень из дроби равен частному от деления корня числителя на корень знаменателя.
Например, √3,24 = √324/100 = √81/25 = √81 / √25 = 9/5 = 1,8. - Извлечение нечетной степени из отрицательных чисел. Чтобы извлечь корень нечетной степени из отрицательного числа необходимо извлечь его из положительного числа и поставить перед ним знак минус.
Например, чтобы найти корень третьей степени из (-125), нужно найти корень третьей степени из 125 (будет 5) и подставить знак минуса (будет -5).
Для того, чтобы упростить выражение с корнями, которое содержит корни разных степеней, необходимо привести все корни к одной степени.
Для этого воспользуемся следующим свойством дроби: a = n√an.
Например, есть квадратный корень (второй степени √2 ) и кубический корень (третьей степени 3√3).
Во-первых, необходимо найти наименьшее общее кратное (НОК) для степеней. В нашем примере НОК=6 (2х3).
Во-вторых, применим свойство a = n√an: √2 = 2√2 = 6√23 = 6√8; 3√3 = 6√32 = 6√9
Получилось два корня одинаковой степени, с которыми можно совершать различные математические действия.
Основное правила сложения и вычитания квадратных корней: сложение и вычитание квадратного корня возможны только при условии одинакового подкоренного выражения.
Примеры:
2√3 + 3√3 = 5√3
2√3 + 2√4 – не выполняется.
При этом, нужно рассмотреть возможность упростить выражения.
Пример: 2√3 + 3√12 = 2√3 + 3√2х2х3 = 2√3 + 3√ 22х3 = 2√3 + 6√3 = 8√3.
Алгоритм действия:
1. Упростить подкоренное выражение путем разложения на простые множители.
2. Затем нужно извлечь корень из квадратного числа и записать полученное значение перед знаком корня.
3. После процесса упрощения необходимо подчеркнуть корни с одинаковыми подкоренными выражениями — только их можно складывать и вычитать.
4. У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня. Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!
Произведение корней из чисел равно корню из произведения этих чисел.
√a*b=√a*√b
Важно: между собой можно умножать только одинаковые степени корней, то есть можно умножить один квадратный корень на другой, но нельзя умножить квадратный корень на корень кубической степени.
Примеры:
√2 х √3 = √6
√6 х √3 = √18 = √3х3х2 = 3√2
При умножении корней с множителями нужно отдельно перемножить множители и подкорневые выражения (числа). Подкорневые числа можно перемножать между собой только в том случае, если они имеют одинаковые степени (см. умножение корней без множителей). В случае отсутствия множителя, он равен единице.
Подкорневые числа можно перемножать между собой только в том случае, если они имеют одинаковые степени (см. умножение корней без множителей). В случае отсутствия множителя, он равен единице.
Примеры:
3√2 х √5 = (3х1) √(2*5) = 3√10
4√2 х 3√3 = (3х4) √(2х3) = 12√6
Основной правило деления — подкоренные выражения делятся на подкоренные выражения, а множители на множители.
√a:b=√a:√b
В процессе деления квадратных корней дроби упрощаются.
Частное корней из чисел равно корню из частного этих чисел.
Важно: между собой можно делить только одинаковые степени корней, то есть можно делить один квадратный корень на другой, но нельзя делить квадратный корень на корень кубической степени.
Пример. √21:√3=√21:3=√7
При делении корней с множителями нужно отдельно разделить множители и подкорневые выражения (числа). Подкорневые числа можно делить между собой только в том случае, если они имеют одинаковые степени. В случае отсутствия множителя, он равен единице.
Подкорневые числа можно делить между собой только в том случае, если они имеют одинаковые степени. В случае отсутствия множителя, он равен единице.
Пример. 12√32 : 6√16 = (12:6) √(32:16) = 2√2.
Чтобы попрактиковаться решать примеры на вычисление квадратный корней, можно скачать программу «Корни квадратные«
Как найти целые числа между корнями
Корень и его свойства
Тема в математике «Корень и его свойства» нередко вызывает затруднения у школьников, особенно при решении примеров. В данной статье описаны основные свойства корней, а также правила сложения, вычитания, умножения и деления. Наглядные примеры помогаю понять, как решать задания с корнями.
Определение «Корень»Корень второй степени (квадратный корень) из числа a — это число, которое становится равным a, если число a возвести во вторую степень (в квадрат).
Например, √ 64 = 8 (√ 64 равно числу 8).
Формула: √ a 2 = a
Число, стоящее под знаком корня, называется подкоренным числом. Если под знаком корня стоит целое выражение, то его называют подкоренным выражением.
Свойство квадратного корня: для действительных чисел не существует квадратный корень из отрицательного числа, так как возведение числа в квадрат будет всегда неотрицательным числом.
Извлечь корень — значит найти значение корня (то есть найти число, при возведении которого в степень, получается подкоренное значение).
Например, извлечь корень из 64 – значит найти √ 64 .
Найти корень из числа можно одним из следующих способов:
- Использование таблицы квадратов, таблицы кубов и т.
 д. В данном случае нужно просто найти нужное число в таблице и посмотреть, какому значению оно соответствует.
д. В данном случае нужно просто найти нужное число в таблице и посмотреть, какому значению оно соответствует.
Для того, чтобы упростить выражение с корнями, которое содержит корни разных степеней, необходимо привести все корни к одной степени.
Для этого воспользуемся следующим свойством дроби: a = n √ a n .
Например, есть квадратный корень (второй степени √ 2 ) и кубический корень (третьей степени 3 √ 3 ).
Во-первых, необходимо найти наименьшее общее кратное (НОК) для степеней. В нашем примере НОК=6 (2х3).
Во-вторых, применим свойство a = n √ a n : √ 2 = 2 √ 2 = 6 √ 2 3 = 6 √ 8 ; 3 √ 3 = 6 √ 3 2 = 6 √ 9
Получилось два корня одинаковой степени, с которыми можно совершать различные математические действия.
Основное правила сложения и вычитания квадратных корней: сложение и вычитание квадратного корня возможны только при условии одинакового подкоренного выражения.
Примеры:
2√ 3 + 3√ 3 = 5√ 3
2√ 3 + 2√ 4 – не выполняется.
При этом, нужно рассмотреть возможность упростить выражения.
Пример: 2√ 3 + 3√ 12 = 2√ 3 + 3√ 2х2х3 = 2√ 3 + 3√ 2 2 х3 = 2√ 3 + 6√ 3 = 8√ 3 .
Алгоритм действия:
1. Упростить подкоренное выражение путем разложения на простые множители.
2. Затем нужно извлечь корень из квадратного числа и записать полученное значение перед знаком корня.
3. После процесса упрощения необходимо подчеркнуть корни с одинаковыми подкоренными выражениями — только их можно складывать и вычитать.
4. У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня. Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!
Произведение корней из чисел равно корню из произведения этих чисел.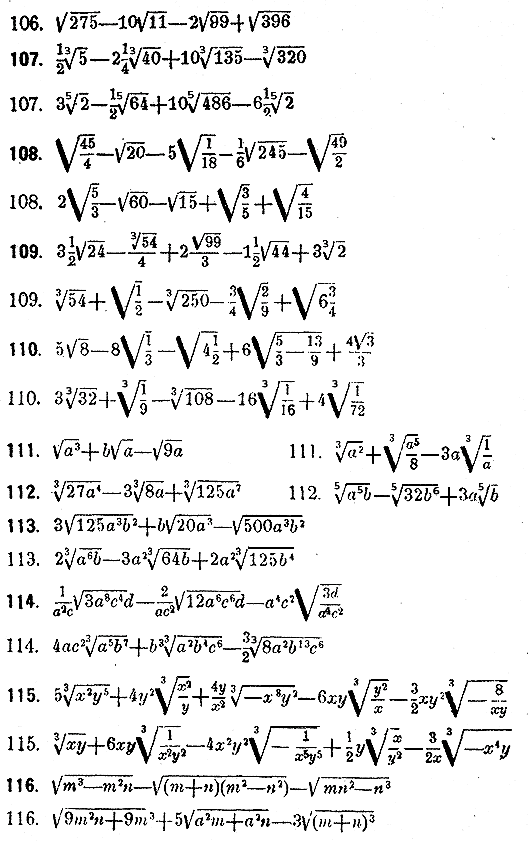
√ a*b =√ a *√ b
Важно: между собой можно умножать только одинаковые степени корней, то есть можно умножить один квадратный корень на другой, но нельзя умножить квадратный корень на корень кубической степени.
Примеры:
√ 2 х √ 3 = √ 6
√ 6 х √ 3 = √ 18 = √ 3х3х2 = 3√ 2
При умножении корней с множителями нужно отдельно перемножить множители и подкорневые выражения (числа). Подкорневые числа можно перемножать между собой только в том случае, если они имеют одинаковые степени (см. умножение корней без множителей). В случае отсутствия множителя, он равен единице.
Примеры:
3√ 2 х √ 5 = (3х1) √ (2*5) = 3√ 10
4√ 2 х 3√ 3 = (3х4) √ (2х3) = 12√ 6
Основной правило деления — подкоренные выражения делятся на подкоренные выражения, а множители на множители.
√ a:b =√ a :√ b
В процессе деления квадратных корней дроби упрощаются.
Частное корней из чисел равно корню из частного этих чисел.
Важно: между собой можно делить только одинаковые степени корней, то есть можно делить один квадратный корень на другой, но нельзя делить квадратный корень на корень кубической степени.
Пример. √ 21 :√ 3 =√ 21:3 =√ 7
При делении корней с множителями нужно отдельно разделить множители и подкорневые выражения (числа). Подкорневые числа можно делить между собой только в том случае, если они имеют одинаковые степени. В случае отсутствия множителя, он равен единице.
Пример. 12√ 32 : 6√ 16 = (12:6) √ (32:16) = 2√ 2 .
Чтобы попрактиковаться решать примеры на вычисление квадратный корней, можно скачать программу «Корни квадратные«
Решение №903 Сколько целых чисел расположено между числами √13 и √130?
Сколько целых чисел расположено между числами √13 и √130?
Решение:
Видим, что в данном промежутке расположены числа от 4 до 11, это:
4, 5, 6, 7, 8, 9, 10, 11
Получаем 8 целых чисел.
Ответ: 8.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 3.6 / 5. Количество оценок: 40
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, чтобы я тебе ответил.
Вычисление квадратного корня из числа: как вычислить вручную
При решении различных задач из курса математики и физики ученики и студенты часто сталкиваются с необходимостью извлечения корней второй, третьей или n-ой степени. Конечно, в век информационных технологий не составит труда решить такую задачу при помощи калькулятора. Однако возникают ситуации, когда воспользоваться электронным помощником невозможно.
К примеру, на многие экзамены запрещено приносить электронику. Кроме того, калькулятора может не оказаться под рукой. В таких случаях полезно знать хотя бы некоторые методы вычисления радикалов вручную.
В таких случаях полезно знать хотя бы некоторые методы вычисления радикалов вручную.
Извлечение квадратного корня при помощи таблицы квадратов
Один из простейших способов вычисления корней заключается в использовании специальной таблицы. Что же она собой представляет и как ей правильно воспользоваться?
При помощи таблицы можно найти квадрат любого числа от 10 до 99. При этом в строках таблицы находятся значения десятков, в столбах — значения единиц. Ячейка на пересечении строки и столбца содержит в себе квадрат двузначного числа. Для того чтобы вычислить квадрат 63, нужно найти строку со значением 6 и столбец со значением 3. На пересечении обнаружим ячейку с числом 3969.
Поскольку извлечение корня — это операция, обратная возведению в квадрат, для выполнения этого действия необходимо поступить наоборот: вначале найти ячейку с числом, радикал которого нужно посчитать, затем по значениям столбика и строки определить ответ. В качестве примера рассмотрим вычисление квадратного корня 169.
Находим ячейку с этим числом в таблице, по горизонтали определяем десятки — 1, по вертикали находим единицы — 3. Ответ: √169 = 13.
Аналогично можно вычислять корни кубической и n-ой степени, используя соответствующие таблицы.
Преимуществом способа является его простота и отсутствие дополнительных вычислений. Недостатки же очевидны: метод можно использовать только для ограниченного диапазона чисел (число, для которого находится корень, должно быть в промежутке от 100 до 9801). Кроме того, он не подойдёт, если заданного числа нет в таблице.
Разложение на простые множители
Если таблица квадратов отсутствует под рукой или с её помощью оказалось невозможно найти корень, можно попробовать разложить число, находящееся под корнем, на простые множители. Простые множители — это такие, которые могут нацело (без остатка) делиться только на себя или на единицу. Примерами могут быть 2, 3, 5, 7, 11, 13 и т. д.
Рассмотрим вычисление корня на примере √576. Разложим его на простые множители. Получим следующий результат: √576 = √(2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 3 ∙ 3) = √(2 ∙ 2 ∙ 2)² ∙ √3². При помощи основного свойства корней √a² = a избавимся от корней и квадратов, после чего подсчитаем ответ: 2 ∙ 2 ∙ 2 ∙ 3 = 24.
Разложим его на простые множители. Получим следующий результат: √576 = √(2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 3 ∙ 3) = √(2 ∙ 2 ∙ 2)² ∙ √3². При помощи основного свойства корней √a² = a избавимся от корней и квадратов, после чего подсчитаем ответ: 2 ∙ 2 ∙ 2 ∙ 3 = 24.
Что же делать, если у какого-либо из множителей нет своей пары? Для примера рассмотрим вычисление √54. После разложения на множители получаем результат в следующем виде: √54 = √(2 ∙ 3 ∙ 3 ∙ 3) = √3² ∙ √(2 ∙ 3) = 3√6. Неизвлекаемую часть можно оставить под корнем. Для большинства задач по геометрии и алгебре такой ответ будет засчитан в качестве окончательного. Но если есть необходимость вычислить приближённые значения, можно использовать методы, которые будут рассмотрены далее.
Метод Герона
Как поступить, когда необходимо хотя бы приблизительно знать, чему равен извлечённый корень (если невозможно получить целое значение)? Быстрый и довольно точный результат даёт применение метода Герона. Его суть заключается в использовании приближённой формулы:
где R — число, корень которого нужно вычислить, a — ближайшее число, значение корня которого известно.
Рассмотрим, как работает метод на практике, и оценим, насколько он точен. Рассчитаем, чему равен √111. Ближайшее к 111 число, корень которого известен — 121. Таким образом, R = 111, a = 121. Подставим значения в формулу:
√111 = √121 + (111 — 121) / 2 ∙ √121 = 11 — 10 / 22 ≈ 10,55.
Теперь проверим точность метода:
Погрешность метода составила приблизительно 0,3. Если точность метода нужно повысить, можно повторить описанные ранее действия:
√111 = √111,3025 + (111 — 111,3025) / 2 ∙ √111,3025 = 10,55 — 0,3025 / 21,1 ≈ 10,536.
Проверим точность расчёта:
После повторного применения формулы погрешность стала совсем незначительной.
Вычисление корня делением в столбик
Этот способ нахождения значения квадратного корня является чуть более сложным, чем предыдущие. Однако он является наиболее точным среди остальных методов вычисления без калькулятора.
Допустим, что необходимо найти квадратный корень с точностью до 4 знаков после запятой. Разберём алгоритм вычислений на примере произвольного числа 1308,1912.
Разберём алгоритм вычислений на примере произвольного числа 1308,1912.
- Разделим лист бумаги на 2 части вертикальной чертой, а затем проведём от неё ещё одну черту справа, немного ниже верхнего края. Запишем число в левой части, разделив его на группы по 2 цифры, двигаясь в правую и левую сторону от запятой. Самая первая цифра слева может быть без пары. Если же знака не хватает в правой части числа, то следует дописать 0. В нашем случае получится 13 08,19 12.
- Подберём самое большое число, квадрат которого будет меньше или равен первой группе цифр. В нашем случае это 3. Запишем его справа сверху; 3 — первая цифра результата. Справа снизу укажем 3×3 = 9; это понадобится для последующих расчётов. Из 13 в столбик вычтем 9, получим остаток 4.
- Припишем следующую пару чисел к остатку 4; получим 408.
- Число, находящееся сверху справа, умножим на 2 и запишем справа снизу, добавив к нему _ x _ =. Получим 6_ x _ =.
- Вместо прочерков нужно подставить одно и то же число, меньшее или равное 408.
 Получим 66×6 = 396. Напишем 6 справа сверху, т. к. это вторая цифра результата. Отнимем 396 от 408, получим 12.
Получим 66×6 = 396. Напишем 6 справа сверху, т. к. это вторая цифра результата. Отнимем 396 от 408, получим 12. - Повторим шаги 3—6. Поскольку снесённые вниз цифры находятся в дробной части числа, необходимо поставить десятичную запятую справа сверху после 6. Запишем удвоенный результат с прочерками: 72_ x _ =. Подходящей цифрой будет 1: 721×1 = 721. Запишем её в ответ. Выполним вычитание 1219 — 721 = 498.
- Выполним приведённую в предыдущем пункте последовательность действий ещё три раза, чтобы получить необходимое количество знаков после запятой. Если не хватает знаков для дальнейших вычислений, у текущего слева числа нужно дописать два нуля.
В результате мы получим ответ: √1308,1912 ≈ 36,1689. Если проверить действие при помощи калькулятора, можно убедиться, что все знаки были определены верно.
Поразрядное вычисление значения квадратного корня
Метод обладает высокой точностью. Кроме того, он достаточно понятен и для него не требуется запоминать формулы или сложный алгоритм действий, поскольку суть способа заключается в подборе верного результата.
Извлечём корень из числа 781. Рассмотрим подробно последовательность действий.
- Выясним, какой разряд значения квадратного корня будет являться старшим. Для этого возведём в квадрат 0, 10, 100, 1000 и т. д. и выясним, между какими из них находится подкоренное число. Мы получим, что 10² < 781 < 100², т. е. старшим разрядом будут десятки.
- Подберём значение десятков. Для этого будем по очереди возводить в степень 10, 20, …, 90, пока не получим число, превышающее 781. Для нашего случая получим 10² = 100, 20² = 400, 30² = 900. Значение результата n будет находиться в пределах 20 < n <30.
- Аналогично предыдущему шагу подбирается значение разряда единиц. Поочерёдно возведём в квадрат 21,22, …, 29: 21² = 441, 22² = 484, 23² = 529, 24² = 576, 25² = 625, 26² = 676, 27² = 729, 28² = 784. Получаем, что 27 < n < 28.
- Каждый последующий разряд (десятые, сотые и т. д. ) вычисляется так же, как было показано выше. Расчёты проводятся до тех пор, пока не будет достигнута необходимая точность.

Видео
Из видео вы узнаете, как извлекать квадратные корни без использования калькулятора.
Правило умножения корней с разными показателями. Формулы корней. Свойства корней. Как умножать корни? Примеры
Приветствую, котаны! В прошлый раз мы подробно разобрали, что такое корни (если не помните, рекомендую почитать). Главный вывод того урока: существует лишь одно универсальное определение корней, которое вам и нужно знать. Остальное — брехня и пустая трата времени.
Сегодня мы идём дальше. Будем учиться умножать корни, изучим некоторые проблемы, связанные с умножением (если эти проблемы не решить, то на экзамене они могут стать фатальными) и как следует потренируемся. Поэтому запасайтесь попкорном, устраивайтесь поудобнее — и мы начинаем.:)
Вы ведь тоже ещё не вкурили?
Урок получился довольно большим, поэтому я разделил его на две части:
- Сначала мы разберём правила умножения. Кэп как бы намекает: это когда есть два корня, между ними стоит знак «умножить» — и мы хотим что-то с этим сделать.

- Затем разберём обратную ситуацию: есть один большой корень, а нам приспичило представить его в виде произведения двух корней попроще. С какого перепугу это бывает нужно — вопрос отдельный. Мы разберём лишь алгоритм.
Тем, кому не терпится сразу перейти ко второй части — милости прошу. С остальными начнём по порядку.
Основное правило умножения
Начнём с самого простого — классических квадратных корней. Тех самых, которые обозначаются $\sqrt{a}$ и $\sqrt{b}$. Для них всё вообще очевидно:
Правило умножения. Чтобы умножить один квадратный корень на другой, нужно просто перемножить их подкоренные выражения, а результат записать под общим радикалом:
\[\sqrt{a}\cdot \sqrt{b}=\sqrt{a\cdot b}\]
Никаких дополнительных ограничений на числа, стоящие справа или слева, не накладывается: если корни-множители существуют, то и произведение тоже существует.
Примеры. Рассмотрим сразу четыре примера с числами:
\[\begin{align} & \sqrt{25}\cdot \sqrt{4}=\sqrt{25\cdot 4}=\sqrt{100}=10; \\ & \sqrt{32}\cdot \sqrt{2}=\sqrt{32\cdot 2}=\sqrt{64}=8; \\ & \sqrt{54}\cdot \sqrt{6}=\sqrt{54\cdot 6}=\sqrt{324}=18; \\ & \sqrt{\frac{3}{17}}\cdot \sqrt{\frac{17}{27}}=\sqrt{\frac{3}{17}\cdot \frac{17}{27}}=\sqrt{\frac{1}{9}}=\frac{1}{3}.
\\ \end{align}\]
Как видите, основной смысл этого правила — упрощение иррациональных выражений. И если в первом примере мы бы и сами извлекли корни из 25 и 4 без всяких новых правил, то дальше начинается жесть: $\sqrt{32}$ и $\sqrt{2}$ сами по себе не считаются, но их произведение оказывается точным квадратом, поэтому корень из него равен рациональному числу .
Отдельно хотел бы отметить последнюю строчку. Там оба подкоренных выражения представляют собой дроби. Благодаря произведению многие множители сокращаются, а всё выражение превращается в адекватное число.
Конечно, не всегда всё будет так красиво. Иногда под корнями будет стоять полная лажа — непонятно, что с ней делать и как преобразовывать после умножения. Чуть позже, когда начнёте изучать иррациональные уравнения и неравенства, там вообще будут всякие переменные и функции. И очень часто составители задач как раз и рассчитывают на то, что вы обнаружите какие-то сокращающиеся слагаемые или множители, после чего задача многократно упростится.
Кроме того, совсем необязательно перемножать именно два корня. Можно умножить сразу три, четыре — да хоть десять! Правило от этого не поменяется. Взгляните:
\[\begin{align} & \sqrt{2}\cdot \sqrt{3}\cdot \sqrt{6}=\sqrt{2\cdot 3\cdot 6}=\sqrt{36}=6; \\ & \sqrt{5}\cdot \sqrt{2}\cdot \sqrt{0,001}=\sqrt{5\cdot 2\cdot 0,001}= \\ & =\sqrt{10\cdot \frac{1}{1000}}=\sqrt{\frac{1}{100}}=\frac{1}{10}. \\ \end{align}\]
И опять небольшое замечание по второму примеру. Как видите, в третьем множителе под корнем стоит десятичная дробь — в процессе вычислений мы заменяем её обычной, после чего всё легко сокращается. Так вот: очень рекомендую избавляться от десятичных дробей в любых иррациональных выражениях (т.е. содержащих хотя бы один значок радикала). В будущем это сэкономит вам кучу времени и нервов.
Но это было лирическое отступление. Теперь рассмотрим более общий случай — когда в показателе корня стоит произвольное число $n$, а не только «классическая» двойка. {2n}}}=\left| a \right|. \\ \end{align}\]
{2n}}}=\left| a \right|. \\ \end{align}\]
Подобные «махинации» могут здорово сэкономить вам время на экзамене или контрольной работе, поэтому запомните:
Не спешите перемножать числа в подкоренном выражении. Сначала проверьте: вдруг там «зашифрована» точная степень какого-либо выражения?
При всей очевидности этого замечания должен признать, что большинство неподготовленных учеников в упор не видят точные степени. Вместо этого они перемножают всё напролом, а затем удивляются: почему это получились такие зверские числа?:)
Впрочем, всё это детский лепет по сравнению с тем, что мы изучим сейчас.
Умножение корней с разными показателями
Ну хорошо, теперь мы умеем перемножать корни с одинаковыми показателями. А что, если показатели разные? Скажем, как умножить обычный $\sqrt{2}$ на какую-нибудь хрень типа $\sqrt{23}$? Можно ли вообще это делать?
Да конечно можно. Всё делается вот по этой формуле:
Правило умножения корней.
{2}}}=\sqrt{5}. \\ \end{align}\]
Но тогда получается какая-то хрень:
\[\sqrt{-5}=\sqrt{5}\]
Этого не может быть, потому что $\sqrt{-5} \lt 0$, а $\sqrt{5} \gt 0$. Значит, для чётных степеней и отрицательных чисел наша формула уже не работает. После чего у нас есть два варианта:
- Убиться об стену констатировать, что математика — это дурацкая наука, где «есть какие-то правила, но это неточно»;
- Ввести дополнительные ограничения, при которых формула станет рабочей на 100%.
В первом варианте нам придётся постоянно вылавливать «неработающие» случаи — это трудно, долго и вообще фу. Поэтому математики предпочли второй вариант.:)
Но не переживайте! На практике это ограничение никак не влияет на вычисления, потому что все описанные проблемы касаются лишь корней нечётной степени, а из них можно выносить минусы.
Поэтому сформулируем ещё одно правило, которое распространяется вообще на все действия с корнями:
Прежде чем перемножать корни, сделайте так, чтобы подкоренные выражения были неотрицательны.
{2}}}=\sqrt{75}. \end{align}\]
Ну что ж, с умножением корней разобрались. Теперь рассмотрим обратную операцию: что делать, когда под корнем стоит произведение?
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Известно, что знак корня является квадратным корнем из некоторого числа.
Однако знак корня означает не только алгебраическое действие, но и применяется в деревообрабатывающем производстве — в расчете относительных размеров.
Yandex.RTB R-A-339285-1
Если вы хотите узнать, как умножить корни «с» или «без» множителей, то эта статья для вас. В ней мы рассмотрим методы умножения корней:
- без множителей;
- с множителями;
- с разными показателями.
Метод умножения корней без множителей
Алгоритм действий:
Убедиться, что у корня одинаковые показатели (степени). Вспомним, что степень записывается слева над знаком корня. Если нет обозначения степени, это значит, что корень квадратный, т.е. со степенью 2, и его можно умножать на другие корни со степенью 2.
Пример
Пример 1: 18 × 2 = ?
Пример 2: 10 × 5 = ?
Пример
Пример 1: 18 × 2 = 36
Пример 2: 10 × 5 = 50
Пример 3: 3 3 × 9 3 = 27 3
Упростить подкоренные выражения. Когда мы умножаем корни друг на друга, мы можем упростить полученное подкоренное выражение до произведения числа (или выражения) на полный квадрат или куб:
Пример
Пример 1: 36 = 6 .
36 — квадратный корень из шести (6 × 6 = 36) .
Пример 2: 50 = (25 × 2) = (5 × 5) × 2 = 5 2 . Число 50 раскладываем на произведение 25 и 2 . Корень из 25 — 5 , поэтому выносим 5 из-под знака корня и упрощаем выражение.
Пример 3: 27 3 = 3 . Кубический корень из 27 равен 3: 3 × 3 × 3 = 27 .
Метод умножения показателей с множителями
Алгоритм действий:
Умножить множители. Множитель — число, которое стоит перед знаком корня. В случае отсутствия множителя, он, по умолчанию, считается единицей. Далее необходимо перемножить множители:
Пример
Пример 1: 3 2 × 10 = 3 ? 3 × 1 = 3
Пример 2: 4 3 × 3 6 = 12 ? 4 × 3 = 12
Умножить числа под знаком корня. Как только вы перемножили множители, смело умножайте числа, стоящие под знаком корня:
Пример
Пример 1: 3 2 × 10 = 3 (2 × 10) = 3 20
Пример 2: 4 3 × 3 6 = 12 (3 × 6) = 12 18
Упростить подкоренное выражение. Далее следует упростить значения, которые стоят под знаком корня, — требуется вынести соответствующие числа за знак корня.
После этого, необходимо перемножить числа и множители, которые стоят перед знаком корня:
Пример
Пример 1: 3 20 = 3 (4 × 5) = 3 (2 × 2) × 5 = (3 × 2) 5 = 6 5
Пример 2: 12 18 = 12 (9 × 2) = 12 (3 × 3) × 2 = (12 × 3) 2 = 36 2
Метод умножения корней с разными показателями
Алгоритм действий:
Найти наименьшее общее кратное (НОК) показателей. Наименьшее общее кратное — наименьшее число, делящееся на оба показателя.
Пример
Необходимо найти НОК показателей для следующего выражения:
Показатели равны 3 и 2 . Для этих двух чисел наименьшим общим кратным является число 6 (оно делится без остатка и на 3 , и на 2). Для умножения корней необходим показатель 6 .
Записать каждое выражение с новым показателем:
Найти числа, на которые нужно умножить показатели, чтобы получить НОК.
В выражении 5 3 необходимо умножить 3 на 2 , чтобы получить 6 . А в выражении 2 2 — наоборот, необходимо умножить на 3 , чтобы получить 6 .
Возвести число, которое стоит под знаком корня, в степень равную числу, которое было найдено в предыдущем шаге. Для первого выражения 5 нужно возвести в степень 2 , а втором — 2 в степень 3:
2 → 5 6 = 5 2 6 3 → 2 6 = 2 3 6
Возвести в степень выражения и записать результат под знаком корня:
5 2 6 = (5 × 5) 6 = 25 6 2 3 6 = (2 × 2 × 2) 6 = 8 6
Перемножить числа под корнем:
(8 × 25) 6
Записать результат:
(8 × 25) 6 = 200 6
По возможности необходимо упростить выражение, но в данном случае оно не упрощается.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Формулы степеней используют в процессе сокращения и упрощения сложных выражений, в решении уравнений и неравенств.
Число c является n -ной степенью числа a когда:
Операции со степенями.
1. Умножая степени с одинаковым основанием их показатели складываются:
a m ·a n = a m + n .

2. В делении степеней с одинаковым основанием их показатели вычитаются:
3. Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:
(abc…) n = a n · b n · c n …
4. Степень дроби равняется отношению степеней делимого и делителя:
(a/b) n = a n /b n .
5. Возводя степень в степень, показатели степеней перемножают:
(a m) n = a m n .
Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.
Например . (2·3·5/15)² = 2²·3²·5²/15² = 900/225 = 4 .
Операции с корнями.
1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:
2. Корень из отношения равен отношению делимого и делителя корней:
3. При возведении корня в степень довольно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в n раз и в тоже время возвести в n -ую степень подкоренное число, то значение корня не поменяется:
5.
Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:
Степень с отрицательным показателем. Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:
Формулу a m :a n =a m — n можно использовать не только при m > n , но и при m n .
Например . a 4:a 7 = a 4 — 7 = a -3 .
Чтобы формула a m :a n =a m — n стала справедливой при m=n , нужно присутствие нулевой степени.
Степень с нулевым показателем. Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.
Например . 2 0 = 1,(-5) 0 = 1,(-3/5) 0 = 1.
Степень с дробным показателем. Чтобы возвести действительное число а в степень m/n , необходимо извлечь корень n -ой степени из m -ой степени этого числа а .
Формулы квадратных корней деление вычитания умножения сложения. Что такое квадратные корни и как они складываются
Интернет
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
В математике любое действие имеет свою пару-противоположность – в сущности, это представляет собою одно из проявлений гегелевского закона диалектики: «единство и борьба противоположностей».
Одно из действий в такой «паре» направлено на увеличение числа, а другое, обратное ему – на уменьшение. Например, действие, противоположное сложению – это вычитание, умножению соответствует деление. Имеется и своя диалектическая пара-противоположность и у возведения в степень. Речь идет об извлечении корня.
Извлечь из числа корень такой-то степени – это значит вычислить, какое число необходимо возвести в соответствующую степень, чтобы в итоге получилось данное число. Две степени имеют свои отдельные названия: вторая степень называется «квадратом», а третья – «кубом». Соответствено, корни данных степеней приятно именовать квадратным корнем и кубическим. Действия с кубическими корнями – тема для отдельного разговора, а сейчас поговорим о сложении квадратных корней.
Начнем с того, что в ряде случаев квадратные корни проще сначала извлечь, а потом уже складывать результаты. Предположим, нам необходимо найти значение такого выражения:
Ведь совсем не сложно вычислить, что корень квадратный из 16 равен 4, а из 121 – 11.
Следовательно,
√16+√121=4+11=15
Впрочем, это самый простой случай – здесь речь идет о полных квадратах, т.е. о таких числах, которые получаются при возведении в квадрат целых чисел. Но так бывает не всегда. Например, число 24 – это не полный квадрат (не найти такого целого числа, которое при возведении его во вторую степень дало бы в результате 24). То же самое относится к такому числу, как 54… Что делать, если нам необходимо сложить корни квадратные из этих чисел?
В таком случае мы получим в ответе не число, а другое выражение. Максимум, что мы можем тут сделать – это максимально упростить исходное выражение. Для этого придется вынести множители из-под корня квадратного. Посмотрим, как это делается, на примере упомянутым чисел:
Для начала разложим на множители 24 – таким образом, чтобы из одного из них легко можно было извлечь корень квадратный (т.е., чтобы он был полным квадратом). Такое числи есть – это 4:
Теперь проделаем то же самое с 54. В его составе таким числом будет 9:
Т.
2 = x, ?x = a. Как и над всякими числами, над квадратными корнями дозволено исполнять арифметические операции сложения и вычитания.
Инструкция
1. Во-первых, при сложении квадратных корней испробуйте извлечь эти корни. Это будет допустимо, если числа под знаком корня являются полными квадратами. Скажем, пускай задано выражение?4 + ?9. Первое число 4 – это квадрат числа 2. Второе число 9 – это квадрат числа 3. Таким образом получается, что: ?4 + ?9 = 2 + 3 = 5.
2. Если под знаком корня нет полных квадратов, то испробуйте перенести из под знака корня множитель числа. Скажем, пускай дано выражение?24 + ?54. Разложите числа на множители: 24 = 2 * 2 * 2 * 3, 54 = 2 * 3 * 3 * 3. В числе 24 имеется множитель 4, тот, что дозволено перенести из под знака квадратного корня. В числе 54 — множитель 9. Таким образом, получается что: ?24 + ?54 = ?(4 * 6) + ?(9 * 6) = 2 * ?6 + 3 * ?6 = 5 * ?6. В данном примере в итоге выноса множителя из под знака корня получилось упростить заданное выражение.
3. Пускай сумма 2-х квадратных корней является знаменателем дроби, скажем, A / (?a + ?b). И пускай перед вами стоит задача «избавиться от иррациональности в знаменателе». Тогда дозволено воспользоваться дальнейшим методом. Умножьте числитель и знаменатель дроби на выражение?a — ?b. Таким образом в знаменателе получится формула сокращенного умножения: (?a + ?b) * (?a — ?b) = a – b. По аналогии, если в знаменателе дана разность корней: ?a — ?b, то числитель и знаменатель дроби нужно умножить на выражение?a + ?b. Для примера, пускай дана дробь 4 / (?3 + ?5) = 4 * (?3 — ?5) / ((?3 + ?5) * (?3 — ?5)) = 4 * (?3 — ?5) / (-2) = 2 * (?5 — ?3).
4. Разглядите больше непростой пример избавления от иррациональности в знаменателе. Пускай дана дробь 12 / (?2 + ?3 + ?5). Нужно умножить числитель и знаменатель дроби на выражение?2 + ?3 — ?5:12 / (?2 + ?3 + ?5) = 12 * (?2 + ?3 — ?5) / ((?2 + ?3 + ?5) * (?2 + ?3 — ?5)) = 12 * (?2 + ?3 — ?5) / (2 * ?6) = ?6 * (?2 + ?3 — ?5) = 2 * ?3 + 3 * ?2 — ?30.
5. И наконец, если вам нужно только примерное значение, то дозволено посчитать значения квадратных корней на калькуляторе. Вычислите значения отдельно для всего числа и запишите с нужной точностью (скажем, два знака позже запятой). А после этого совершите требуемые арифметические операции, как с обыкновенными числами. Скажем, пускай нужно узнать примерное значение выражения?7 + ?5 ? 2,65 + 2,24 = 4,89.
Видео по теме
Обратите внимание!
Квадратные корни ни в коем случае невозможно складывать как примитивные числа, т.е. ?3 + ?2 ? ?5!!!Полезный совет
Если вы раскладываете число на множители, дабы перенести квадрат из под знака корня, то совершите обратную проверку — перемножьте все получившиеся множители и получите изначальное число.Содержимое:
В математике корни могут быть квадратными, кубическими или иметь любой другой показатель (степень), который пишется слева над знаком корня. Выражение, стоящее под знаком корня, называется подкоренным выражением.
Сложение корней похоже на сложение членов алгебраического выражения, то есть требует определения подобных корней.
Часть 1 Определение корней
- 1 Обозначение корней. Выражение под знаком корня (√) означает, что из этого выражения необходимо извлечь корень определенной степени.
- Корень обозначают знаком √.
- Показатель (степень) корня пишется слева над знаком корня. Например, кубический корень из 27 записывается так: 3 √(27)
- Если показатель (степень) корня отсутствует, то показатель считается равным 2, то есть это квадратный корень (или корень второй степени).
- Число, записанное перед знаком корня, называется множителем (то есть это число умножается на корень), например 5√(2)
- Если множителя перед корнем нет, то он равен 1 (напомним, что любое число, умноженное на 1, равняется самому себе).
- Если вы впервые работаете с корнями, сделайте соответствующие пометки над множителем и показателем корня, чтобы не запутаться и лучше понять их назначение.
- 2 Запомните, какие корни можно складывать, а какие нельзя. Также, как нельзя складывать разные члены выражения, например, 2а + 2b ≠ 4ab, вы не можете складывать разные корни.
- Нельзя складывать корни с разными подкоренными выражениями, например, √(2) + √(3) ≠ √(5). Но вы можете сложить числа, стоящие под одним корнем, например, √(2 + 3) = √(5) (квадратный корень из 2 примерно равен 1,414, квадратный корень из 3 примерно равен 1,732, а квадратный корень из 5 примерно равен 2,236).
- Нельзя складывать корни с одинаковыми подкоренными выражениями, но разными показателями, например, √(64) + 3 √(64) (эта сумма не равна 5 √(64), так как квадратный корень из 64 равен 8, кубический корень из 64 равен 4, 8 + 4 = 12, что гораздо больше, чем корень пятой степени из 64, который примерно равен 2,297).
Часть 2 Упрощение и сложение корней
- 1 Определите и сгруппируйте подобные корни. Подобные корни – корни, у которых одинаковые показатели и одинаковые подкоренные выражения.
Например, рассмотрим выражение:
2√(3) + 3 √(81) + 2√(50) + √(32) + 6√(3)
- Во-первых, перепишите выражение так, чтобы корни с одинаковым показателем располагались последовательно.
2√(3) + 2√(50) + √(32) + 6√(3) + 3 √(81)- Затем перепишите выражение так, чтобы корни с одинаковым показателем и с одинаковым подкоренным выражением располагались последовательно.
2√(50) + √(32) + 2√(3) + 6√(3) + 3 √(81)- 2 Упростите корни. Для этого разложите (где возможно) подкоренные выражения на два множителя, один из которых вынесите из-под корня. В этом случае вынесенное число и множитель корня перемножаются.
- В приведенном выше примере разложите число 50 на 2*25, а число 32 – на 2*16. Из 25 и 16 можно извлечь квадратные корни (соответственно 5 и 4) и вынести 5 и 4 из-под корня, соответственно умножив их на множители 2 и 1. Таким образом, вы получите упрощенное выражение: 10√(2) + 4√(2) + 2√(3) + 6√(3) + 3 √(81)
- Число 81 можно разложить на множители 3*27, а из числа 27 можно извлечь кубический корень, равный 3.
Это число 3 можно вынести из-под корня. Таким образом, вы получите еще более упрощенное выражение: 10√(2) + 4√(2) + 2√(3)+ 6√(3) + 3 3 √(3)
- 3 Сложите множители подобных корней. В нашем примере есть подобные квадратные корни из 2 (их можно сложить) и подобные квадратные корни из 3 (их тоже можно сложить). У кубического корня из 3 подобных корней нет.
- 10√(2) + 4√(2) = 14√(2).
- 2√(3)+ 6√(3) = 8√(3).
- Окончательное упрощенное выражение: 14√(2) + 8√(3) + 3 3 √(3)
- Не существует общепринятых правил порядка записи корней в выражении. Потому вы можете записывать корни в порядке возрастания их показателей и в порядке возрастания подкоренных выражений.
Свойства квадратных корней
До сих пор мы осуществляли над числами пять арифметических операций: сложение, вычитание, умножение , деление и возведение в степень, причем при вычислениях активно использовали различные свойства этих операций, например а + b = b + а, аn-bn = (аb)n и т.
д.
В этой главе введена новая операция — извлечение квадратного корня из неотрицательного числа. Чтобы успешно ее использовать, нужно познакомиться со свойствами этой операции, что мы и сделаем в настоящем параграфе.
Доказательство. Введем следующие обозначения:https://pandia.ru/text/78/290/images/image005_28.jpg» alt=»Равенство»Задание»> Имеются только свойства, касающиеся умножения и деления квадратных корней. Будьте внимательны и осторожны, не принимайте желаемое за действительное.
Завершая параграф, отметим еще одно достаточно простое и в то же время важное свойство:
если a > 0 и n — натуральное число , тоПреобразование выражений, содержащих операцию извлечения квадратного корня
До сих пор мы с вами выполняли преобразования толькорациональных выражений , используя для этого правила действий над многочленами и алгебраическими дробями, формулы сокращенного умножения и т. д. В этой главе мы ввели новую операцию — операцию извлечения квадратного корня; мы установили, что
где, напомним, a, b — неотрицательные числа.
Используя эти формулы , можно выполнять различные преобразования выражений, содержащих операцию извлечения квадратного корня. Рассмотрим несколько примеров, причем во всех примерах будем предполагать, что переменные принимают только неотрицательные значения.
Пример 3. Внести множитель под знак квадратного корня:
Пример 6 . Упростить выражение Решение. Выполним последовательные преобразования:
Умножение квадратов и квадратных корней
Чтобы умножить радикалы, мы умножаем подкоренные. Математика тоже может быть простой. Кто знал?Пример задачи
Это имеет смысл, потому что квадратный корень из 20 — это число, которое дает нам 20 при умножении на себя. Не убежден? Мы выглядим невероятно заслуживающими доверия, поэтому понятия не имею, почему. Мы проведем вас шаг за шагом и покажем, почему это имеет смысл.
Умножение само на себя дает:
Следовательно, это квадратный корень из 20.
Вуаля!
В общем, если x и y неотрицательные числа (а это значит, что мы можем извлечь из них квадратный корень), то:
Достаточно справедливо. К сожалению, это не работает с хромосомами. Извините за дождь на вашем «Эврика!» момент.
Примеры задач
Упрощенный подкоренной термин имеет только один подкоренной знак. Например, выражение проще, чем .
Плюс, разве не приятнее смотреть? Не хочу показаться поверхностным, но внешность — это все, когда дело доходит до математики. Ну, почти все. Точность тоже важна. К тому же приятная личность.
Мы также можем «не умножить» что-то, разбив подкоренное число на множители. «Эй, разве это не разделение?» Тсс. Может быть. Если x и y неотрицательны, тогда:
Это дает нам способ упростить подкоренные выражения, разложив подкоренное число на множители. Мы не будем делать это ради развлечения, но мы за все, что помогает нам добраться до сути конкретной проблемы.
Пример задачи
Чему равен квадратный корень из 20 в самой упрощенной форме?
Поскольку мы можем разложить 20 как 4 × 5, мы можем переписать квадратный корень из 20 следующим образом:
Поскольку квадратный корень из 4 равен 2, мы можем переписать его как:
Теперь мы иметь подкоренное число 5 вместо подкоренного числа 20. Поскольку ни один из множителей 5 не является полным квадратом, мы закончили. Это был относительно безболезненный корневой канал.
Пример задачи
Упростить .
Мы можем разложить 90 как 9 × 10. Следовательно:
Обратите внимание, что мы могли бы также разложить 90 как 6 × 15, 5 × 18, 3 × 30 или 2 × 45. Мы выбрали факторизацию 9 × 10. потому что 9 — совершенный квадрат, поэтому радикал исчезает, когда мы упрощаем . Мы хотим, чтобы радикал ушел, потому что он груб с официантами и продолжает рассказывать о том времени, когда видел Кэррот Топ в Вегасе.
Факторы, представляющие собой совершенные квадраты, идеально подходят для разложения на множители подкоренного числа для упрощения, как мы можем видеть в предыдущем примере.
Это факторы, которые упростят термины без радикала.
Иногда для упрощения нам нужно перемножить радикалы вместе, а иногда мы хотим разбить их на части. Это зависит от того, в каком деструктивном настроении мы находимся. Хорошо, это на самом деле зависит от того, что будет наиболее полезным в решении проблемы. Выплесните свою агрессию на боксерскую грушу.
Пример задачи
Упрощение .
Перемножьте радикалы вместе, а затем упростите:
Если вы считаете кого-то очень привлекательным (а также обладает фантастическим характером), скажите своим друзьям, что он или она «идеален». Они, вероятно, не поймут, о чем вы говорите, но это нормально. Это делает вас интересным.
До сих пор все термины, которые мы умножали и не умножали, включали только числа. Вы знали , что должен был быть слишком хорош, чтобы продолжаться. Упрощение, умножение и разбиение радикалов также можно выполнять, когда у нас есть переменные в подкоренном члене.
Давайте немного полюбим x и посмотрим, как это делается.
Пример задачи
Если x ≥ 0, то . Мы можем умножить x само на себя, чтобы получить x 2 , поэтому x является квадратным корнем из x 2 .
Пример задачи
Если x < 0, то . Для этого вам нужно надеть кепку мышления. Нет, не тот думающий колпак; ту, которую твоя тетя Джуди связала для тебя прошлой зимой, с пайетками в форме арбузов. Это сделает ее счастливой.
Мы знаем, что оно будет положительным, поэтому главный квадратный корень из x 2 будет положительным. Так как это положительное значение, а x отрицательное, это не может быть правдой, что .
Однако, — x является положительным (подумайте о числовой прямой: если x меньше нуля, то поставив перед ним знак минус, он отразится через ноль и сделает его положительным), а квадрат — x это x 2 , так что это правда что .
Вы следили за всем этим? Не стесняйтесь прочесть ее еще раз, чтобы она закрепилась в вашем мозгу. Не забудьте повесить табличку «Мокрый цемент», чтобы прохожие случайно не произвели на вас впечатление.
Чтобы избежать осложнений, подобных предыдущему примеру, в некоторых книгах просто предполагается, что переменная, стоящая под радикалом, должна быть неотрицательной. Мы также сделаем это предположение, но спросите своего учителя, безопасно ли делать это предположение в вашей домашней работе. У него или у нее может быть другой способ делать вещи. «Но Шмуп сказал…» редко выдерживает критику в классе.
Пример задачи
Упрощение .
Хотя непосвященным это может показаться не сразу, это идеальный квадрат. У нас есть 4 копии x в качестве нашего подкореня, или ( x )( x )( x )( x ). Чтобы найти x 4 , мы умножаем x 2 само на себя.
Пример задачи
Упрощение .
Возможно, вы хотели бы, чтобы мы все еще были на числах, и думали, что эта переменная штука для птиц, но это не так уж плохо. Мы справимся с этим так же, как с числами; нам просто нужно помнить, что показатель степени говорит нам, сколько копий у нас есть для каждой переменной.
Мы можем разбить это на:
И мы можем разбить первый радикал дальше как:
Мы не можем упростить , но мы можем упростить два других радикала:
4 Примечание 90 что и в конце — это , а не в подкоренном члене. Он просто болтается там на конце, что-то вроде группы радикалов. Поскольку кто-то может легко предположить, что является частью подкоренного числа и , мы обычно ставим радикал в конце подкоренного члена. Измените порядок и напишите наш окончательный ответ так:
Не так уж и плохо. Вы жалеете, что так сильно упирались в переменные? Возможно, вам стоило дать им больше шансов, прежде чем вырезать их из каждой вашей совместной фотографии.
Точно так же, как мы делали с подкоренными, у которых были только числа, мы по-прежнему пытаемся разложить на множители полные квадраты, когда подкоренные имеют переменные… даже когда и числа, и переменные висят. Ох, брататься с врагом.
Как сделать простую факторизацию | Хацуди
Из квадратного корня мы изучаем умножение и деление. Вообще, в математике мы сначала изучаем сложение и вычитание. Однако в случае квадратных корней умножение и деление выполняются проще. Все, что вам нужно сделать, это умножить числа в корневом символе.
Однако существуют правила умножения квадратных корней. И мало кто понимает, почему можно умножать числа в подкоренном знаке друг на друга. Вы должны узнать об умножении и делении квадратного корня, включая причины.
Кроме того, существует метод вычисления, уникальный для квадратных корней. Это первичная факторизация. Первичная факторизация упрощает вычисления и дает нам правильный ответ. При умножении и делении квадратного корня мы должны одновременно изучать простую факторизацию.
При умножении квадратного корня мы должны изучить новую концепцию. Мы объясним, как умножать и делить квадратные корни.
Содержание
- 1 Умножение и деление квадратных корней
- 1.1 Умножение или деление целых чисел и квадратных корней по отдельности
- 1.2 Почему мы можем умножать и делить между квадратными корнями
- 2 Использование простых чисел и факторизация простых чисел
- 2.1 Как проводить факторизацию простых чисел? Шаги для умножения
- 2.2 Ответ на факторизацию простых чисел один и тот же в любом порядке
- 2.3 Извлечение квадратного числа из подкоренного символа
- 2.4 Не делите кроме простых чисел
- 3 Научитесь умножать и делить Квадратные корни
- 3.1 Разложение квадратного корня на простые множители
- 4 Упражнения: умножение и деление квадратного корня
- 5 Умножение квадратного корня и вычисление простых чисел
Умножение и деление квадратного корня5 9022
корнями, как было сказано ранее, мы изучаем умножение и деление раньше, чем сложение и вычитание.
Почему мы сначала изучаем умножение квадратных корней? Причина в том, что умножение между квадратными корнями легко выполнить. Числа в корневом символе можно умножать.
В случае умножения знака корня формула выглядит следующим образом.
Так, например, расчет выглядит следующим образом.
- $\sqrt{2}×\sqrt{3}=\sqrt{6}$
- $\sqrt{7}×\sqrt{11}=\sqrt{77}$
Также деление то же, что умножение. Это потому, что деление может быть преобразовано в умножение дробей. Поскольку квадратные корни можно умножать друг на друга, числа в подкоренном символе можно делить таким же образом.
Следовательно, мы вычисляем деление следующим образом.
- $\sqrt{21}÷\sqrt{3}=\sqrt{7}$
- $\sqrt{15}÷\sqrt{5}=\sqrt{3}$
При умножении и делении между квадратными корнями мы можем выполнять обычное умножение и деление. Разница лишь в том, есть ли корневые знаки или нет.
Раздельное умножение или деление целых чисел и квадратных корней
Важно разделять целые числа и квадратные корни для умножения и деления.
Целые числа и квадратные корни — это совершенно разные числа.
В квадратном корне это описывается как $3\sqrt{2}$ и так далее. Это умножение 3 на $\sqrt{2}$, что имеет то же значение, что и $3×\sqrt{2}$. Однако, поскольку основное правило состоит в том, чтобы опустить $×$, то оно записывается как $3\sqrt{2}$.
Поскольку числа (целые числа) перед подкоренным знаком рассматриваются отдельно, целые числа и квадратный корень должны умножаться отдельно. Вкратце дело обстоит следующим образом.
Целые числа умножаются на целые числа. С другой стороны, квадратные корни умножаются на квадратные корни. Целые числа никогда не умножаются на квадратные корни. При умножении и делении целые числа и квадратные корни должны быть полностью разделены. 92}=\sqrt{4}$. Точно так же $3=\sqrt{9}$. Кроме того, $4=\sqrt{16}$.
Мы не можем умножать и делить целое число на квадратный корень. Итак, если мы изменим целое число на квадратный корень, мы сможем умножать и делить квадратные корни друг на друга.
Например, как решить следующую задачу?
- $\displaystyle\frac{\sqrt{12}}{2}$
$\sqrt{12}$ и 2 нельзя умножать или делить. Итак, давайте используем знак корня для представления 2. Поскольку $2=\sqrt{4}$, мы можем вычислить следующим образом.
- $\displaystyle\frac{\sqrt{12}}{2}=\displaystyle\frac{\sqrt{12}}{\sqrt{4}}=\sqrt{3}$
Вы не можете умножать целое число на квадратный корень. Однако целые числа можно преобразовать в квадратные корни. То есть, если быть более точным, преобразуя целое число в квадратный корень, вы можете умножать и делить целое число на квадратный корень.
Почему мы можем умножать и делить квадратные корни
Почему можно умножать и делить корневые знаки друг на друга? Мало кто понимает эту причину.
Чтобы понять эту причину, мы используем линейное уравнение. Линейные уравнения обладают тем свойством, что не имеет значения, умножаются ли обе части на одно и то же число. Например, предположим, что у нас есть следующие балансы.
Если два одинаковы, они равны независимо от того, сколько раз умножаются обе стороны.
Чтобы понять, почему умножение квадратного корня справедливо, давайте рассмотрим свойства линейных уравнений.
-Докажите, почему умножение квадратного корня допустимо
Далее, давайте докажем, почему можно умножать и делить квадратные корни при вычислении квадратных корней. Итак, давайте рассмотрим ситуацию, когда мы перемножаем $\sqrt{a}$ и $\sqrt{b}$.
Сначала возводим в квадрат $\sqrt{a}×\sqrt{b}$. Не думайте: «Почему мы уравниваем это?» Во всяком случае, в квадрате. Что происходит, когда вы возводите его в квадрат? Поскольку это умножение, смысл остается тем же, есть скобки или нет. При умножении скобки можно убрать по желанию.
Например, следующие вычисления дают одинаковый ответ. 92=а×б$.
Теперь давайте преобразуем это уравнение. Сначала мы возвели в квадрат $\sqrt{a}×\sqrt{b}$. Затем вернитесь в исходное состояние.
В частности, давайте добавим корневой символ с обеих сторон.
Степень — это тип умножения. Кроме того, целые числа можно преобразовать в квадратные корни, задействовав их. Другими словами, преобразование целого числа в квадратный корень является разновидностью умножения. В уравнении мы можем умножить обе части уравнения на одно и то же число. Давайте воспользуемся этим свойством и добавим знак радикала к обеим сторонам. Таким образом, мы получаем следующее.
Итак, мы доказали, что $\sqrt{a}×\sqrt{b}=\sqrt{a×b}$. Мы можем доказать, что мы можем умножать и делить квадратные корни, используя наши предыдущие знания математики.
Использование простых чисел и факторинг простых чисел
Обратите внимание, что числа в радикальном символе должны быть как можно меньше. Как мы можем это сделать? Мы можем получить квадратный корень, возведя в квадрат целое число. Точно так же, если в корневом знаке есть квадрат, мы можем преобразовать его в целое число, а затем убрать его из корневого символа.
92×3}=2\sqrt{3}$
Как мы можем эффективно найти степени в корневом символе? Метод — простая факторизация. Факторизация простых чисел — это процесс деления с использованием простых чисел.
Числа состоят из простых чисел. Простое число — это число, которое делится только на 1 и на свое число. К простым числам относятся, например, следующие.
- Простые числа: 2, 3, 5, 7, 11, 13, 17, 19
Например, есть только два делителя 7: 1 и 7. Точно так же есть только два делителя 11: 1 и 11. Деление на любое другое число не дает целого числа. С другой стороны, число 4 имеет делители на 1, 2 и 4; не только 1 и 4, но и 2 тоже делитель. Следовательно, 4 не является простым числом.
Мы можем преобразовать целое (натуральное число) в уравнение умножения, разделив его на простые числа. Поймите, что обратным вычислению умножения является простая факторизация.
Когда дело доходит до простой факторизации, этот термин трудно понять. Однако концепция простой факторизации проста, если понимать ее как способ разложения чисел на выражения умножения.
Простые числа не могут делиться дальше. Итак, используя простые числа, мы можем преобразовать их в умножение.
Как провести простую факторизацию? Шаги к умножению
Как сделать простую факторизацию? В качестве примера попробуем разложить 300 на простые числа.
Это можно сделать, разделив числа по порядку, начиная с наименьшего простого числа. Наименьшее простое число — 2. Итак, давайте разделим 300 на 2. Если мы разделим 300 на 2, мы можем разделить его на 2 и 150. 300 долларов = 2×150 долларов.
Этот метод позволил нам провести факторизацию одного простого числа. Однако 150 не является простым числом. Далее его можно разделить на простое число. Итак, давайте снова разделим его на простое число. Разделив на 2, получим следующее.
Чтобы получить 300, разделите его дважды на 2, чтобы получить 75. Другими словами, 300 долларов = 2×2×75 долларов. Однако 75 не является простым числом. Итак, давайте проведем еще простую факторизацию.
75 не делится на 2. Итак, делим на 3.
Получится $300=2×2×3×25$. Действуя таким же образом с простой факторизацией, поскольку 25 не является простым числом, мы можем разделить его на 5. Таким образом, мы получаем следующее.
Разделив на простые числа, мы наконец нашли следующие факты.
- 300$=2×2×3×5×5$
Поскольку 5 — простое число, его нельзя разделить дальше. При простой факторизации останавливайте деление, когда в конце появляется простое число. После этого мы собираем все простые числа, которые мы разделили, и последнее появившееся простое число. Поскольку умножение всех простых чисел в круге на рисунке выше дает 300, разложение простых чисел завершено.
-Символ факторизации простых чисел
Когда мы действительно занимаемся факторизацией простых чисел, мы должны вычислять ее эффективно и быстро. Поэтому мы почти никогда не используем стрелки для факторизации простых чисел, как показано выше.
Вместо этого мы используем следующий символ.
Чтобы использовать его, напишите целое (натуральное число) внутри символа. Кроме того, напишите простое число слева от символа. Похоже на это.
Использование такое же, как на предыдущем рисунке со стрелкой. Разложим целое число, разделив его на простые числа. Например, простая факторизация числа 300 выглядит так.
Если в конце стоит простое число, разложение на простые множители завершено. Затем, собрав все простые числа, мы можем составить уравнение умножения. Смысл тот же, что и у стрелки. Разница в том, что, используя этот символ, мы можем более эффективно выполнять простую факторизацию.
Ответ на простую факторизацию одинаков в любом порядке
Кстати, простую факторизацию можно вычислять в любом порядке, потому что окончательный ответ будет одинаковым. Например, простая факторизация 300 даст тот же ответ, даже если порядок деления другой, как показано ниже.
Ранее мы объясняли, что при разложении на простые множители мы делим числа, начиная с наименьшего простого числа.
Это связано с тем, что чем меньше простое число, например 2 или 3, тем легче его делить и тем меньше ошибок делается. Однако в некоторых случаях может быть лучше разделить на большее простое число, чтобы избежать просчета.
Если целое число, которое мы хотим разделить, является четным числом, мы всегда можем разделить его на 2. С другой стороны, если это нечетное число, иногда неясно, можем ли мы разделить его на меньшее простое число.
Например, на какое простое число можно разделить 105? 105 можно разделить на 3. Однако трудно заметить, что оно делится на 3. С другой стороны, легко заметить, что 105 делится на 5. предотвратить просчеты в математике. Используя простую факторизацию, мы можем преобразовать целое число в уравнение умножения. В этом случае не беспокойтесь о порядке деления на простые числа.
Извлечение квадратного числа из подкоренного символа
Зачем нам нужно изучать разложение на простые множители? Это потому, что мы часто используем простую факторизацию при вычислении квадратного корня.
При вычислении квадратного корня существует правило, согласно которому число в символе корня должно быть как можно меньше. Для этого нам нужно провести простую факторизацию. В частности, мы должны убрать квадраты чисел в корневом символе.
Как упоминалось ранее, если в подкоренном символе есть квадраты, мы можем поставить число вне знака корня. 92$
Так как же вычислить $\sqrt{300}$? Рассмотрим $\sqrt{300}$ следующим образом и поместим число вне знака корня.
Причина изучения простой факторизации заключается в том, что она используется при вычислении квадратного корня. Когда мы убираем числа внутри корневого символа, мы все делаем простую факторизацию.
Так зачем же нам убирать числа из радикального символа? Причина проста: цифры легче понять. Например, на число $\sqrt{300}$ сложно ответить мгновенно. С другой стороны, в случае $10\sqrt{3}$ все просто.
$\sqrt{3}≈1,73$. Поскольку это значение в 10 раз больше, мы знаем, что $10\sqrt{3}$ составляет около 17,3.
Математика — это наука о понимании того, что означают числа. Мы должны сделать числа простыми для понимания, поэтому мы должны убрать числа из корневого символа.
Не делить ничего, кроме простых чисел
Обратите внимание, что при разложении простых чисел мы не должны использовать для деления непростые числа. Если мы смешаем непростые числа, мы не сможем убрать числа в подкоренном знаке. Например, если мы разложим число 300 на простые множители, что произойдет, если мы разделим его на 4? 92}$
В результате мы получаем ответ $5\sqrt{12}$. Этот ответ неверен, потому что мы можем сделать число в корневом символе еще меньше.
Не простое число, например 4, можно разделить на другое число. В результате мы не можем перейти к уравнению умножения, используя наименьшее число. Таким образом, числа в корневом знаке становятся больше и вызывают ошибку вычисления. При простой факторизации обязательно делите на простые числа.
Узнайте, как умножать и делить квадратные корни
Много раз нам нужно умножить или разделить два квадратных корня.
В таких случаях простая факторизация упрощает размещение чисел вне квадратного корня.
Например, как мы можем рассчитать следующее?
- $\sqrt{15}×\sqrt{21}$
Разложение 15 на простые множители равно $3×5$. Кроме того, если разложить 21 на простые множители, получится $3×7$. Следовательно, мы можем рассчитать следующим образом.
$\sqrt{15}×\sqrt{21}$
$=\sqrt{3×5}×\sqrt{3×7}$
$=\textcolor{red}{\sqrt{3} }×\sqrt{5}×\textcolor{red}{\sqrt{3}}×\sqrt{7}$
$=3×\sqrt{5×7}$
$=3\sqrt{35}$
При умножении простая факторизация показывает, что $\sqrt{15}$ и $\sqrt{21}$ содержат $\sqrt{3}$ в корневом знаке соответственно; мы можем сделать 3 2 , так что мы можем получить 3 из радикального символа. С помощью простой факторизации мы можем понять, какие числа можно вынести из знака корня.
Заметьте, что если мы не можем создавать способности, мы не можем получить числа из подкоренного знака. В предыдущем расчете внутренняя часть корневого знака вычислялась как $\sqrt{5×7}=\sqrt{35}$.
Это потому, что хотя квадрат и существует для 3, мы не можем создать квадрат для 5 и 7.
Сначала выполните разложение квадратного корня на простые множители
Кстати, при умножении и делении квадратного корня первое, что мы должны сделать, это уменьшить числа в подкоренном символе. Как при умножении, так и при делении, чем меньше число, тем меньше ошибок в вычислениях. По этой причине при вычислении квадратного корня лучше сначала провести разложение на простые множители.
Например, как уменьшить количество просчетов в следующей задаче?
- $\sqrt{28}×\sqrt{18}$
Есть два способа вычислить это следующим образом.
Проверяя два метода вычисления, становится очевидным, что вычисление упрощается, если сначала вы выполняете простую факторизацию. Умножение 28 на 18 сложно. Кроме того, сделать простую факторизацию 504 сложно.
Поэтому всегда следует сначала выполнять простую факторизацию, будь то умножение или деление.
Так вы сделаете меньше просчетов.
Упражнения: умножение и деление квадратного корня
Q1: Выполните следующие вычисления.
- $2\sqrt{3}×4\sqrt{21}$
- $\sqrt{15}×\sqrt{30}$
- $\sqrt{75}÷2\sqrt{3}$
- $(3+\sqrt{5})(3-\sqrt{5})$
A1: Ответы.
(a)
$2\sqrt{3}×4\sqrt{21}$
$=2\sqrt{\textcolor{red}{3}}×4\sqrt{\textcolor{red} {3}×7}$
$=2×4×3×\sqrt{7}$
$=24\sqrt{7}$
(b)
$\sqrt{15}×\sqrt{30}$
$=\sqrt{\textcolor{red}{3}×\textcolor {синий}{5}}×\sqrt{2×\textcolor{красный}{3}×\textcolor{синий}{5}}$
$=3×5×\sqrt{2}$
$= 15\sqrt{2}$
(c)
Если есть деление, обязательно преобразуйте его в умножение дробей.
$\sqrt{75}÷2\sqrt{3}$
$=\sqrt{3×5×5}×\displaystyle\frac{1}{2\sqrt{3}}$
$= 5\textcolor{red}{\sqrt{3}}×\displaystyle\frac{1}{2\textcolor{red}{\sqrt{3}}}$ 92$
$=9-5$
$=4$
Умножение квадратного корня и вычисление простых чисел
Вычисление квадратного корня часто включает умножение и деление.
Вы можете умножать и делить квадратные корни друг на друга. Метод аналогичен обычному умножению. Однако важно понимать правило вычисления целых чисел и квадратных корней отдельно.
Обратите внимание, что при вычислении квадратного корня мы всегда должны использовать простую факторизацию. Нам нужно преобразовать целое число в уравнение умножения. Выполняя простую факторизацию, мы можем получить числа в корневом символе.
Кроме того, сначала выполнив разложение на простые множители, мы можем упростить вычисление квадратного корня. Будет меньше ошибок в вычислениях, если мы сначала проведем разложение на простые множители. Разберемся, как уменьшить просчет, в том числе и как это сделать.
Когда вы умножаете и делите квадратные корни, мы объяснили не только как, но и почему вычисление выполняется именно таким образом. Изучив их, вы сможете выполнять математические вычисления, включая квадратные корни.
Рейтинг
Потребности, желания и требования: три основных понятия в маркетинге (с примерами)
ЯМР-соединение бензольных колец: орто-мета-пик и химические сдвиги
ВЗМО и НСМО: энергия связывания Antibonding Orbital
Тонкослойная хроматография (ТСХ): принципы, значения Rf и проявляющий растворитель
Ориентация и реакционная способность ароматических соединений: орто, мета, пара
9.
4: Умножение выражений квадратного корня
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 49396
- Денни Бурзински и Уэйд Эллис-младший
- Колледж Южной Невады через OpenStax CNX
Свойство произведения квадратных корней
В нашей работе с упрощением выражений квадратного корня мы отметили, что
\(\sqrt{xy} = \sqrt{x} \sqrt{y}\)
Поскольку это уравнение , мы можем записать это как:
\(\sqrt{x} \sqrt{y} = \sqrt{xy}\)
Чтобы умножить два выражения квадратного корня, мы используем свойство произведения квадратных корней.
Свойство продукта \(\sqrt{x} \sqrt{y} = \sqrt{xy}\)
\(\sqrt{x} \sqrt{y} = \sqrt{xy}\)
Произведение квадратных корней является квадратным корнем произведения
На практике обычно проще упростить квадратный корень выражения перед фактическим выполнением умножения.
Чтобы увидеть это, рассмотрим следующее произведение:
\(\sqrt{8} \sqrt{48}\)
Мы можем умножить эти квадратные корни в либо двумя способами:
Упростить, затем умножить
\( \sqrt{4 \cdot 2} \sqrt{16 \cdot 3} = (2 \sqrt{2})(4 \sqrt{3}) = 2 \cdot 4 \sqrt{2 \cdot 3} = 8 \sqrt {6}\)
Умножить, затем упростить
\(\sqrt{8} \sqrt{48} = \sqrt{8 \cdot 48} = \sqrt{384} = \sqrt{64 \cdot 6} = 8 \sqrt{6} \)
Обратите внимание, что во втором методе расширенный член (третье выражение, \(\sqrt{384}\)) может быть трудно разложить на множители полного квадрата и некоторого другого числа.
Правило умножения выражений квадратного корня
В предыдущем примере показано следующее правило умножения двух выражений квадратного корня.
Правило умножения квадратного корня
- При необходимости упростите каждое выражение квадратного корня.
- Выполнить умножение.
- При необходимости упростите.
Набор образцов A
Найдите каждый из следующих продуктов.
Пример \(\PageIndex{1}\)
\(\sqrt{3} \sqrt{6} = \sqrt{3 \cdot 6} = \sqrt{18} = \sqrt{9 \cdot 2} = 3\sqrt{2}\)
Пример \(\PageIndex{2}\)
\(\sqrt{8} \sqrt{2} = 2 \sqrt{2} \sqrt{2} = 2 \ sqrt{2 \cdot 2} = 2 \sqrt{4} = 2 \cdot 2 = 4\) 92 + x — 2}
\end{массив}\)Пример \(\PageIndex{6}\)
\(\begin{array}{flushleft}
\sqrt{3}(7+\sqrt{ 6})=7 \sqrt{3}+\sqrt{3} \sqrt{6} &=7 \sqrt{3}+\sqrt{18} \\
&=7 \sqrt{3}+\sqrt{ 9 \cdot 2} \\
&=7 \sqrt{3}+3 \sqrt{2}
\end{массив}\)Пример \(\PageIndex{7}\)
\(\begin{ array}{flushleft}
\sqrt{6}(\sqrt{2} — \sqrt{10}) &= \sqrt{6} \sqrt{2} — \sqrt{6}\sqrt{10}\\
&= \sqrt{12} — \sqrt{60}\\
&= \sqrt{4 \cdot 3} — \sqrt{4 \cdot 15}\\ 9{3} b(b-3) \sqrt{b(b-3)}
\end{array}\)Практический набор A
Найдите каждый из следующих продуктов.
Практическая задача \(\PageIndex{1}\)
\(\sqrt{5} \sqrt{6}\)
- Ответ
\(\sqrt{30}\)
Практическая задача \(\PageIndex{2}\)
\(\sqrt{32} \sqrt{2}\)
- Ответ
\(8\)
Практическая задача \(\PageIndex{3}\) 95\кв.
м{5м}\)
Упражнения
Упражнение \(\PageIndex{1}\)
\(\sqrt{2} \sqrt{10}\)
- Ответ
\(2 \sqrt{5}\)
Упражнение \(\PageIndex{2}\)
\(\sqrt{3} \sqrt{15}\)
Упражнение \(\PageIndex{3}\)
\(\sqrt{7} \ sqrt{8}\)
- Ответ
\(2 \кв{14}\)
Упражнение \(\PageIndex{4}\)
\(\sqrt{20} \sqrt{3}\)
Упражнение \(\PageIndex{5}\)
\(\sqrt{32} \sqrt {27}\)
- Ответить
\(12 \кв{6}\)
Упражнение \(\PageIndex{6}\)
\(\sqrt{45} \sqrt{50}\)
Упражнение \(\PageIndex{7}\)
\(\sqrt{5} \ sqrt{5}\)
- Ответ
\(5\)
Упражнение \(\PageIndex{8}\)
\(\sqrt{7} \sqrt{7}\)
Упражнение \(\PageIndex{9}\)
\(\sqrt{8} \ sqrt{8}\)
- Ответ
\(8\)
Упражнение \(\PageIndex{10}\)
\(\sqrt{15} \sqrt{15}\)
Упражнение \(\PageIndex{11}\)
\(\sqrt{48} \ sqrt{27}\)
- Ответ
\(36\)
Упражнение \(\PageIndex{12}\)
\(\sqrt{80} \sqrt{20}\)
Упражнение \(\PageIndex{13}\)
\(\sqrt{5} \ sqrt{m}\)
- Ответ
\(\ кв.
м.{5м}\)
Упражнение \(\PageIndex{14}\)
\(\sqrt{7} \sqrt{a}\)
Упражнение \(\PageIndex{15}\)
\(\sqrt{6} \ sqrt{m}\)
- Ответ
\(\квт{6м}\)
Упражнение \(\PageIndex{16}\)
\(\sqrt{10} \sqrt{h}\)
Упражнение \(\PageIndex{17}\)
\(\sqrt{20} \ sqrt{a}\)
- Ответ
\(2 \sqrt{5a}\)
Упражнение \(\PageIndex{18}\)
\(\sqrt{48} \sqrt{x}\)
Упражнение \(\PageIndex{19}\)
\(\sqrt{75} \ sqrt{y}\)
- Ответ
\(5 \sqrt{3y}\)
Упражнение \(\PageIndex{20}\)
\(\sqrt{200} \sqrt{m}\)
Упражнение \(\PageIndex{21}\)
\(\sqrt{a} \ sqrt{a}\)
- Ответ
\(а\)
Упражнение \(\PageIndex{22}\)
\(\sqrt{x} \sqrt{x}\)
Упражнение \(\PageIndex{23}\)
\(\sqrt{y} \ sqrt{y}\)
- Ответ
\(у\)
Упражнение \(\PageIndex{24}\)
\(\sqrt{h} \sqrt{h}\)
Упражнение \(\PageIndex{25}\)
\(\sqrt{3} \ sqrt{3}\)
- Ответ
\(3\)
Упражнение \(\PageIndex{26}\)
\(\sqrt{6} \sqrt{6}\)
Упражнение \(\PageIndex{27}\)
\(\sqrt{k} \ sqrt{k}\)
- Ответ
- 5}\)
\(к\)
Упражнение \(\PageIndex{40}\)
\(\sqrt{x+2} \sqrt{x-3}\)
- Ответ
\(\ sqrt{(х+2)(х-3)}\)
Упражнение \(\PageIndex{41}\)
\(\sqrt{a-6} \sqrt{a+1}\)
Упражнение \(\PageIndex{42}\)
\(\sqrt {y+3} \sqrt{y — 2}\)
- Ответ
\(\ sqrt{(у+3)(у-2)}\)
Упражнение \(\PageIndex{43}\) 97} \sqrt{48a — 96}\)
Упражнение \(\PageIndex{60}\)
\(\sqrt{2} (\sqrt{8} + \sqrt{6})\)
- Ответить
\(2(2 + \sqrt{3})\)
Упражнение \(\PageIndex{61}\)
\(\sqrt{5}(\sqrt{3} + \sqrt{7})\)
Упражнение \(\PageIndex{62}\)
\(\sqrt{3} (\sqrt{x} + \sqrt{2})\)
- Ответ
\(\sqrt{3x} + \sqrt{6}\)
94 \sqrt{3xy}\)Эта страница под названием 9.
4: Умножение выражений квадратного корня распространяется под лицензией CC BY, автором, ремиксом и/или куратором являются Денни Бурзински и Уэйд Эллис-младший (OpenStax CNX).
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Денни Бурзински и Уэйд Эллис-младший
- Лицензия
- СС BY
- Программа OER или Publisher
- OpenStax CNX
- Теги
На этой странице нет тегов.
9.4 Умножение квадратных корней — Элементарная алгебра 2e
Цели обучения
К концу этого раздела вы сможете:
- Умножение квадратных корней
- Использовать полиномиальное умножение для умножения квадратных корней
Приготовься 9,9
Прежде чем приступить к работе, пройдите этот тест на готовность.
Упрощение: (3u)(8v)(3u)(8v).
Если вы пропустили эту проблему, просмотрите пример 6.26.Приготовься 9.10
Упростить: 6(12−7n)6(12−7n).
Если вы пропустили эту проблему, просмотрите пример 6.28.Приготовься 9.11
Упрощение: (2+а)(4−а)(2+а)(4−а).
Если вы пропустили эту проблему, просмотрите пример 6.39.Умножение квадратных корней
Мы использовали свойство произведения квадратных корней, чтобы упростить квадратные корни, удалив совершенные квадратные множители.
Свойство продукта квадратных корней говорит
аб=а·баб=а·б
Мы можем использовать свойство произведения квадратных корней «в обратном порядке», чтобы умножить квадратные корни.
а·б=аба·б=аб
Помните, мы предполагаем, что все переменные больше или равны нулю.
Мы перепишем свойство произведения квадратных корней, чтобы мы видели оба пути одновременно.
Свойство продукта квадратных корней
Если a , b неотрицательные действительные числа, то
ab=a·banda·b=abab=a·banda·b=ab
Итак, мы можем умножить 3·53·5 следующим образом:
3·53·5153·53·515
Иногда произведение дает нам идеальный квадрат:
2·82·81642·82·8164
Даже если произведение не является идеальным квадратом, мы должны искать множители идеального квадрата и по возможности упрощать радикал.
Умножение радикалов с коэффициентами очень похоже на умножение переменных с коэффициентами.
Чтобы умножить 4x·3y4x·3y, мы перемножаем коэффициенты, а затем переменные. Результат 12xy12xy. Имейте это в виду, выполняя эти примеры.
Пример 9,44
Упрощение: ⓐ 2·62·6 ⓑ (43)(212)(43)(212).
Решение
ⓐ
2·62·6 Умножение с использованием свойства продукта. 1212 Упростите радикальное. 4·34·3 Упрощение. 2323 ⓑ
(43)(212)(43)(212) Умножение с использованием свойства продукта. 836836 Упростите радикальное. 8·68·6 Упрощение. 4848 Обратите внимание, что в (b) мы перемножили коэффициенты и радикалы.
Также мы не стали упрощать 1212. Мы подождали, чтобы получить продукт, а затем упростили.
Попытайся 9,87
Упрощение: ⓐ 3·63·6 ⓑ (26)(312)(26)(312).
Попытайся 9,88
Упрощение: ⓐ 5·105·10 ⓑ (63)(56)(63)(56).
Пример 9,45
Упрощение: (62)(310)(62)(310).
Решение
(62)(310)(62)(310) Умножение с использованием свойства продукта. 18201820 Упростите радикальное. 184·5184·5 Упрощение. 18·2·518·2·5 365365 Попытайся 9,89
Упрощение: (32)(230)(32)(230).
Попытайся 9,90
Упрощение: (33)(36)(33)(36).
Когда нам нужно умножить квадратные корни, мы сначала находим произведение, а затем удаляем все совершенные квадратные множители.
Пример 9,46
Упрощение: ⓐ (8×3)(3x)(8×3)(3x) ⓑ (20y2)(5y3)(20y2)(5y3).
Решение
ⓐ
(8×3)(3x)(8×3)(3x) Умножение с использованием свойства продукта. 24x424x4 Упростите радикальное. 4×4·64×4·6 Упрощение. 2x262x26 ⓑ
(20у2)(5у3)(20у2)(5у3) Умножение с использованием свойства продукта. 100y5100y5 Упростите радикальное. 10г2г10г2г Попытайся 9,91
Упрощение: ⓐ (6×3)(3x)(6×3)(3x) ⓑ (2y3)(50y2)(2y3)(50y2).
Попытайся 9,92
Упрощение: ⓐ (6×5)(2x)(6×5)(2x) ⓑ (12y2)(3y5)(12y2)(3y5).
Пример 9,47
Упрощение: (106p3)(318p)(106p3)(318p).
Решение
Попытайся 9,93
Упрощение: (62×2)(845×4)(62×2)(845×4).
Попытайся 9,94
Упрощение: (26y4)(1230y)(26y4)(1230y).
Пример 9,48
Упрощение: ⓐ (2)2(2)2 ⓑ (−11)2(−11)2.
Решение
ⓐ
(2)2(2)2 Переписать как продукт. (2)(2)(2)(2) Умножить. 44 Упрощение. 22 ⓑ
(−11)2(−11)2 Переписать как продукт. (-11)(-11)(-11)(-11) Умножить. 121121 Упрощение. 1111 Попытайся 9,95
Упрощение: ⓐ (12)2(12)2 ⓑ (−15)2(−15)2.
Попытайся 9,96
Упрощение: ⓐ (16)2(16)2 ⓑ (−20)2(−20)2.
Результаты предыдущего примера приводят нас к этому свойству.
Возведение квадратного корня
Если a — неотрицательное действительное число, то
(a)2=a(a)2=a
Поняв, что возведение в квадрат и извлечение квадратного корня являются «противоположными» операциями, мы можем упростить (2)2(2)2 и сразу получить 2.
Когда мы умножаем два одинаковых квадратных корня в части (а) следующего примера, это то же самое, что возведение в квадрат.
Пример 9,49
Упрощение: ⓐ (23)(83)(23)(83) ⓑ (36)2(36)2.
Решение
ⓐ
(23)(83)(23)(83) Умножить. Помните, (3)2=3. (3)2=3. 16·316·3 Упрощение. 4848 ⓑ
(36)2(36)2 Умножить. 9·69·6 Упрощение. 5454 Попытайся 9,97
Упрощение: ⓐ (611)(511)(611)(511) ⓑ (58)2(58)2.
Попытайся 9,98
Упрощение: ⓐ (37)(107)(37)(107) ⓑ (−46)2(−46)2.
Использование полиномиального умножения для умножения квадратных корней
В следующих нескольких примерах мы будем использовать Распределяющее свойство для умножения выражений с квадратными корнями.
Сначала мы будем распределять, а затем упрощать квадратные корни, когда это возможно.
Пример 9.50
Упрощение: ⓐ 3(5−2)3(5−2) ⓑ 2(4−10)2(4−10).
Решение
ⓐ
3(5−2)3(5−2) Распределить. 15−3215−32 ⓑ
2(4−10)2(4−10) Распределить. 42−2042−20 42-2542-25 Попытайся 9,99
Упростить: ⓐ 2(3−5)2(3−5) ⓑ 3(2−18)3(2−18).
Попытайся 9.100
Упрощение: ⓐ 6(2+6)6(2+6) ⓑ 7(1+14)7(1+14).
Пример 9,51
Упрощение: ⓐ 5(7+25)5(7+25) ⓑ 6(2+18)6(2+18).
Решение
ⓐ
5(7+25)5(7+25) Умножить. 75+2·575+2·5 Упрощение. 75+1075+10 10+7510+75 ⓑ
6(2+18)6(2+18) Умножить. 12+10812+108 Упрощение. 4·3+36·34·3+36·3 23+6323+63 Комбинируйте как радикалы. 8383 Попытайся 9.101
Упрощение: ⓐ 6(1+36)6(1+36) ⓑ 12(3+24)12(3+24).
Попытайся 9.102
Упрощение: ⓐ 8(2−58)8(2−58) ⓑ 14(2+42)14(2+42).
Когда мы работали с многочленами, мы умножали двучлены на двучлены. Помните, что это дало нам четыре продукта, прежде чем мы объединили какие-либо похожие термины. Чтобы наверняка получить все четыре продукта, мы строили свою работу — обычно по методу ФОЛЬГИ.
Пример 9,52
Упрощение: (2+3)(4−3)(2+3)(4−3).
Решение
(2+3)(4−3)(2+3)(4−3) Умножить. 8−23+43−38−23+43−3 Объедините похожие термины. 5+235+23 Попытайся 9.103
Упрощение: (1+6)(3−6)(1+6)(3−6).
Попытайся 9.104
Упрощение: (4−10)(2+10)(4−10)(2+10).
Пример 9,53
Упрощение: (3−27)(4−27)(3−27)(4−27).
Решение
(3−27)(4−27)(3−27)(4−27) Умножить. 12-67-87+4·712-67-87+4·7 Упрощение. 12−67−87+2812−67−87+28 Объедините похожие термины. 40−14740−147 Попытайся 9.105
Упрощение: (6−37)(3+47)(6−37)(3+47).
Попытайся 9.106
Упрощение: (2−311)(4−11)(2−311)(4−11).
Пример 9,54
Упрощение: (32−5)(2+45)(32−5)(2+45).
Решение
(32−5)(2+45)(32−5)(2+45) Умножить. 3·2+1210-10-4·53·2+1210-10-4·5 Упрощение. 6+1210-10-206+1210-10-20 Объедините похожие термины. −14+1110−14+1110 Попытайся 9.107
Упрощение: (53−7)(3+27)(53−7)(3+27).
Попытайся 9.108
Упрощение: (6−38)(26+8)(6−38)(26+8)
Пример 9,55
Упрощение: (4−2x)(1+3x)(4−2x)(1+3x).
Решение
(4−2x)(1+3x)(4−2x)(1+3x) Умножить. 4+12x-2x-6×4+12x-2x-6x Объедините похожие термины. 4+10x−6×4+10x−6x Попытайся 9.109
Упрощение: (6−5м)(2+3м)(6−5м)(2+3м).
Попытайся 9.110
Упрощение: (10+3n)(1−5n)(10+3n)(1−5n).
Обратите внимание, что некоторые специальные продукты облегчили нашу работу, когда мы раньше умножали биномы. Это верно и при умножении квадратных корней. Формулы специальных продуктов, которые мы использовали, показаны ниже.
Специальные формулы продукта
Биномиальные квадраты Произведение сопряженных чисел(a+b)2=a2+2ab+b2(a−b)(a+b)=a2−b2(a−b)2=a2−2ab+b2Биномиальные квадраты Произведение сопряженных чисел(a+ b)2=a2+2ab+b2(a−b)(a+b)=a2−b2(a−b)2=a2−2ab+b2
В следующих нескольких примерах мы будем использовать специальные формулы продукта. Начнем с формулы биномиальных квадратов.
Пример 9,56
Упрощение: ⓐ (2+3)2(2+3)2 ⓑ (4−25)2(4−25)2.
Решение
Не забудьте включить член 2ab2ab при возведении в квадрат бинома.
- ⓐ
Умножение с использованием биномиального квадратного шаблона. Упрощение. Объедините похожие термины. - ⓑ
Умножение с использованием биномиального квадратного шаблона. Упрощение. Объедините похожие термины. Попытайся 9.111
Упрощение: ⓐ (10+2)2(10+2)2 ⓑ (1+36)2(1+36)2.
Попытайся 9.112
Упрощение: ⓐ (6−5)2(6−5)2 ⓑ (9−210)2(9−210)2.
Пример 9,57
Упрощение: (1+3x)2(1+3x)2.
Решение
Умножение с использованием биномиального квадратного шаблона. Упрощение. Попытайся 9.113
Упрощение: (2+5м)2(2+5м)2.
Попытайся 9.114
Упростить: (3−4n)2(3−4n)2.
В следующих двух примерах мы найдем произведение сопряженных чисел.
Пример 9,58
Упрощение: (4−2)(4+2)(4−2)(4+2).
Решение
Попытайся 9.
115
Упрощение: (2−3)(2+3)(2−3)(2+3).
Попытайся 9.116
Упрощение: (1+5)(1−5)(1+5)(1−5).
Пример 9,59
Упрощение: (5−23)(5+23)(5−23)(5+23).
Решение
Умножение с использованием биномиального квадратного шаблона. Упрощение. Попытайся 9.117
Упрощение: (3−25)(3+25)(3−25)(3+25).
Попытайся 9.118
Упрощение: (4+57)(4−57)(4+57)(4−57).
Раздел 9.4 Упражнения
Практика ведет к совершенству
Умножение квадратных корней
В следующих упражнениях упрощайте.
233.
ⓐ 2·82·8 ⓑ (33)(218)(33)(218)
234.
ⓐ 6·66·6 ⓑ (32)(232)(32)(232)
235.
ⓐ 7·147·14 ⓑ (48)(58)(48)(58)
236.
ⓐ 6·126·12 ⓑ (25)(210)(25)(210)
237.
(52)(36)(52)(36)
238.
(23)(46)(23)(46)
239.
(−23)(318)(−23)(318)
240.
(−45)(510)(−45)(510)
241.
(56)(−12)(56)(−12)
242.
(62)(−10)(62)(−10)
243.
(−27)(−214)(−27)(−214)
244.
(−211)(−422)(−211)(−422)
245.
ⓐ (15л)(5л3)(15л)(5л3) ⓑ (2н2)(18н3)(2н2)(18н3)
246.
ⓐ (14×3)(7×3)(14×3)(7×3) ⓑ (3q2)(48q3)(3q2)(48q3)
247.
ⓐ (16y2)(8y4)(16y2)(8y4) ⓑ (11s6)(11s)(11s6)(11s)
248.
ⓐ (8×3)(3x)(8×3)(3x) ⓑ (7r)(7r8)(7r)(7r8)
249.
(25б3)(415б)(25б3)(415б)
250.
(38с5)(26с3)(38с5)(26с3)
251.
(52d7)(350d3)(52d7)(350d3)
252.
46т233т246т233т2
253.
34y439y534y439y5
254.
(−27z3)(314z8)(−27z3)(314z8)
255.
(42k5)(−332k6)(42k5)(−332k6)
256.
ⓐ (7)2(7)2 ⓑ (−15)2(−15)2
257.
ⓐ (11)2(11)2 ⓑ (−21)2(−21)2
258.
ⓐ (19)2(19)2 ⓑ (−5)2(−5)2
259.
ⓐ (23)2(23)2
ⓑ (−3)2(−3)2260.
ⓐ (411)(−311)(411)(−311) ⓑ (53)2(53)2
261.
ⓐ (213)(−913)(213)(−913) ⓑ (65)2(65)2
262.
ⓐ (−312)(−26)(−312)(−26) ⓑ (−410)2(−410)2
263.
ⓐ (−75)(−310)(−75)(−310) ⓑ (−214)2(−214)2
Использование полиномиального умножения для умножения квадратных корней
В следующих упражнениях упрощайте.
264.
ⓐ 3(4−3)3(4−3) ⓑ 2(4−6)2(4−6)
265.
ⓐ 4(6−11)4(6−11) ⓑ 2(5−12)2(5−12)
266.
ⓐ 5(3−7)5(3−7) ⓑ 3(4−15)3(4−15)
267.
ⓐ 7(−2−11)7(−2−11) ⓑ 7(6−14)7(6−14)
268.
ⓐ 7(5+27)7(5+27) ⓑ 5(10+18)5(10+18)
269.
ⓐ 11(8+411)11(8+411) ⓑ 3(12+27)3(12+27)
270.
ⓐ 11(−3+411)11(−3+411) ⓑ 3(15−18)3(15−18)
271.
ⓐ 2(−5+92)2(−5+92) ⓑ 7(3−21)7(3−21)
272.
(8+3)(2−3)(8+3)(2−3)
273.
(7+3)(9−3)(7+3)(9−3)
274.
(8−2)(3+2)(8−2)(3+2)
275.
(9−2)(6+2)(9−2)(6+2)
276.
(3−7)(5−7)(3−7)(5−7)
277.
(5−7)(4−7)(5−7)(4−7)
278.
(1+310)(5−210)(1+310)(5−210)
279.
(7−25)(4+95)(7−25)(4+95)
280.
(3+10)(3+210)(3+10)(3+210)
281.
(11+5)(11+65)(11+5)(11+65)
282.
(27−511)(47+911)(27−511)(47+911)
283.
(46+713)(86−313)(46+713)(86−313)
284.
(5−и)(3+и)(5−и)(3+и)
285.
(9-ш)(2+ш)(9-ш)(2+ш)
286.
(7+2м)(4+9м)(7+2м)(4+9м)
287.
(6+5н)(11+3н)(6+5н)(11+3н)
288.
ⓐ (3+5)2(3+5)2
ⓑ (2−53)2(2−53)2289.
ⓐ (4+11)2(4+11)2 ⓑ (3−25)2(3−25)2
290.
ⓐ (9−6)2(9−6)2 ⓑ (10+37)2(10+37)2
291.
ⓐ (5−10)2(5−10)2 ⓑ (8+32)2(8+32)2
292.
(3−5)(3+5)(3−5)(3+5)
293.
(10−3)(10+3)(10−3)(10+3)
294.
(4+2)(4−2)(4+2)(4−2)
295.
(7+10)(7−10)(7+10)(7−10)
296.
(4+93)(4−93)(4+93)(4−93)
297.
(1+82)(1−82)(1+82)(1−82)
298.
(12−55)(12+55)(12−55)(12+55)
299.
(9−43)(9+43)(9−43)(9+43)
Смешанная практика
В следующих упражнениях упрощайте.
300.
3·213·21
301.
(46)(−18)(46)(−18)
302.
(−5+7)(6+21)(−5+7)(6+21)
303.
(−57)(621)(−57)(621)
304.
(−42)(218)(−42)(218)
305.
(35у3)(7у3)(35у3)(7у3)
306.
(412×5)(26×3)(412×5)(26×3)
307.
(29)2(29)2
308.
(−417)(−317)(−417)(−317)
309.
(−4+17)(−3+17)(−4+17)(−3+17)
Математика на каждый день
310.
Ландшафтный дизайнер хочет разместить квадратный отражающий бассейн рядом с треугольной площадкой, как показано ниже. Треугольная колода представляет собой прямоугольный треугольник с катетами длиной 9 футов и 11 футов, а бассейн будет примыкать к гипотенузе.
- ⓐ Используйте теорему Пифагора, чтобы найти длину стороны бассейна. Округлите ответ до ближайшей десятой доли фута.
- ⓑ Найдите точную площадь бассейна.
311.
Художник хочет сделать небольшой памятник в форме квадратного основания, увенчанного прямоугольным треугольником, как показано ниже. Квадратное основание будет примыкать к одной стороне треугольника. Другой катет треугольника будет равен 2 футам, а гипотенуза будет равна 5 футам.
- ⓐ Используйте теорему Пифагора, чтобы найти длину стороны квадратного основания. Округлите ответ до ближайшей десятой доли фута.
- ⓑ Найдите точную площадь лица квадратного основания.
312.
Квадратный сад будет сделан с каменным бордюром по одному краю. Если доступно только 3+103+10 футов камня, упростите (3+10)2(3+10)2, чтобы определить площадь самого большого такого сада. Округлите ответ до ближайшей десятой доли фута.
313.
Сад будет состоять из двух квадратных секций, одной секции со стороной 5+65+6 ярдов и одной секции с длиной стороны 2+32+3 ярда.
Упростите 5+62+2+325+62+2+32, чтобы определить общую площадь сада. Округлите ответ до десятых.
314.
Предположим, в предыдущем упражнении к саду будет добавлена третья секция. Третья секция должна иметь ширину 432432 ярда. Напишите выражение, которое дает общую площадь сада.
Письменные упражнения
315.
- ⓐ Объясните, почему (−n)2(−n)2 всегда положительно при n≥0n≥0.
- ⓑ Объясните, почему −n2−n2 всегда отрицательно при n≥0n≥0.
316.
Используйте биномиальный квадрат для упрощения (3+2)2(3+2)2. Объясни все свои действия. 93-8
9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92 5.
1 Квадраты и квадратные корни | Умножение и деление
5.1 Умножение и деление целых чисел
В прошлом году вы научились складывать и вычитать целых чисел . Множество целых чисел состоит из положительных и отрицательные целые числа, включая ноль. Вы использовали числовую прямую для представления целых чисел.
- Числа справа от нуля на числовой прямой называются положительными числами . Мы представляем их со знаком плюс или без него. Например, положительное число пять можно записать как или просто .
- Числа слева от нуля называются отрицательными числами . Мы всегда представляем их с минусом знак впереди. Например, отрицательное число три записывается как .
- Номер не является ни положительным, ни отрицательным.
целое число Целые числа — это положительные и отрицательные целые числа, включая ноль.
положительное число Положительные числа — это числа, которые больше нуля; они лежат справа от ноль на числовой прямой.
отрицательное число Отрицательные числа — это числа, которые меньше нуля; они лежат слева от ноль на числовой прямой.
Положительные и отрицательные числа иногда называют направленными числами . Это связано с тем, что знак число (положительное или отрицательное) говорит нам, в каком направлении от нуля они появляются на числовой прямой.
направленное число направленное число — это положительные и отрицательные числа. Знак направленного число говорит нам, в каком направлении от нуля оно лежит на числовой прямой.
В этом разделе вы узнаете, как умножать и делить направленные числа.
Умножение направленных чисел
Из младших классов вы знаете, что мы можем умножать числа в любом порядке.
Например, а также .
В математике коммутативные законы сложения и умножения утверждают, что порядок, в котором мы сложение или умножение чисел не влияет на ответ. Это означает, что мы можем поменять местами числа и все равно получить то же самое. отвечать.
Из прошлого года вы знаете, что умножение можно рассматривать как форму сложения. Следовательно:
или
Это означает, что вы получите положительный ответ при умножении двух положительных чисел:
Мы можем использовать тот же метод, чтобы узнать, что происходит, когда мы умножаем положительное число на отрицательное число или отрицательное число положительным числом.
или
Запомнить означает, что мы начинаем с на числовой прямой и отсчитайте три единицы влево. Это приводит нас к .
Это показывает, что при умножении двух чисел с противоположными знаками вы получаете отрицательный ответ:
Немного сложнее объяснить, что происходит, когда мы умножаем два отрицательных числа.
Один из способов мышления утверждает, что для того, чтобы все законы математики работали, мы условно принимаем, что . Другой способ — посмотреть на числовые закономерности. В этой таблице показано умножение на :
\begin{массив}{|с|с|с|с|с|} \hline -2 & \times & & = & \newline -2 & \times & & = & \newline -2 & \times & & = & \newline -2 & \times & & = & \newline -2 & \times & & = & \newline -2 & \times & & = & \newline -2 & \times & & = & \newline -2 & \times & & = & \newline \hline \конец{массив}
Давайте вставим числовой шаблон в средний столбец:
\begin{массив}{|с|с|г|с|с|} \hline -2 & \times & +4 & = & \newline -2 & \times & +3 & = & \newline -2 & \times & +2 & = & \newline -2 & \times & +1 & = & \newline -2 & \times & 0 & = & \newline -2 & \times & -1 & = & \newline -2 & \times & -2 & = & \newline -2 & \times & -3 & = & \newline -2 & \times & -4 & = & \newline \hline \конец{массив}
Мы знаем, что отрицательное число, умноженное на положительное число, дает отрицательное число в качестве ответа.
Использовать это знаний для заполнения первых четырех строк таблицы:
\begin{массив}{|r|c|r|c|r|} \hline -2 & \times & +4 & = & -8 \newline -2 & \times & +3 & = & -6 \newline -2 & \times & +2 & = & -4 \newline -2 & \times & +1 & = & -2 \newline -2 & \times & 0 & = & \newline -2 & \times & -1 & = & \newline -2 & \times & -2 & = & \newline -2 & \times & -3 & = & \newline -2 & \times & -4 & = & \newline \hline \конец{массив}
Теперь, не глядя на то, что происходит в рядах, просто завершите узор из чисел в последнем столбец сверху вниз:
\begin{массив}{|r|c|r|c|r|} \hline -2 & \times & +4 & = & -8 \newline -2 & \times & +3 & = & -6 \newline -2 & \times & +2 & = & -4 \newline -2 & \times & +1 & = & -2 \newline -2 & \times & 0 & = & 0 \новая строка -2 & \times & -1 & = & +2 \новая строка -2 & \times & -2 & = & +4 \новая строка -2 & \times & -3 & = & +6 \новая строка -2 & \times & -4 & = & +8 \newline \hline \конец{массив}
Последние четыре строки таблицы показывают, что:
Всякий раз, когда вы умножаете направленные числа, помните:
Следовательно, умножая:
- дает те же знаки
- противоположных знаков дает .
Существуют различные способы записи умножения. Все следующие обозначения означают одно и то же:
Обратите внимание, что а также НЕ означает то же самое. Когда ты решал алгебраические выражения в прошлом году, ты узнал, что:
- скобки, написанные рядом, означают умножение:
- знаки плюс и минус между двумя числами отдельные термины:
Рабочий пример 5.1: Умножение направленных чисел
Выполнить расчет:
Шаг 1: Найдите знаки плюс и минус, разделяющие термины.
Шаг 2: Выполните умножение перед сложением или вычитанием. Используйте правила умножения для знаков, когда вы умножить.
Запомните правильный порядок действий: Б ракетки, О ф, D ivision, M умножение, A дополнение, S вычитание
Шаг 3: Делайте сложение и вычитание последними.
Помните, что вычитание отрицательного числа равносильно добавлению его положительного числа.
Упражнение 5.1. Умножение направленных чисел
Вычислите каждое из следующих чисел.
Помните, что при умножении любого числа на 1 число остается прежним. Но вам все еще нужно использовать правила умножения для определения знака ответа.
Деление направленных чисел
Из предыдущих классов вы знаете, что мы можем делить такие вещи, как деньги и сладости, между определенным количеством людей.
Например, если вы разделите упаковку из 48 конфет на 3 детей, каждый ребенок получит по 16 конфет. Мы можем написать это в качестве: или же .
При делении двух положительных чисел получается положительное число:
Мы можем использовать банковские балансы, чтобы объяснить деление положительных и отрицательных чисел. Предположим, у трех друзей есть магазин. В определенный месяц магазин не преуспевает. Он приносит убыток, и его банковский баланс отображается как \(- ₦15,000\). Это означает, что предприятие должно деньги банку. Если долг общий одинаково среди трех друзей, каждая из их банковских выписок будет показывать \(- ₦5,000\). Мы можем записать это как: .
Если вы разделите отрицательное число на положительное число, вы получите отрицательное число:
Аналогичным образом, предположим, что в следующем месяце магазин преуспевает, а его банковский баланс составляет \(+ ₦6000\). Трое друзей хотят снять эти деньги тремя равными частями, поэтому что каждый из них получает \(₦2000\).
Каждое снятие средств будет отображаться как минус в банке магазина. утверждение. Мы можем сказать, что есть 3 «отрицательных» транзакции, каждая из которых снимает одну и ту же сумму с банковского счета. Так мы можем записать это как: .
Вы получите отрицательное число, если разделите положительное число на отрицательное число:
Предположим, банк взимает плату с магазина \(₦750\) банковские сборы. Кто-то в банке делает ошибку и случайно вводит транзакцию несколько раз, а не только один раз. Бухгалтер магазина видит сумму \(- ₦3,000\) в выписке по счету и хочет узнать, во сколько раз увеличатся банковские сборы. были проведены. Она сделает следующий расчет: .
Положительное число получается при делении отрицательного числа на отрицательное число:
Всякий раз, когда вы делите направленные числа, помните:
Следовательно, деление:
- дают те же знаки
- дают противоположные знаки .
Обратите внимание, что, поскольку деление двух противоположных знаков всегда дает отрицательный ответ, не имеет значения, где мы ставим знак минус, когда пишем дробь:
Когда вы даете окончательный ответ, вы должны поставить знак минус перед целой дробью, как показано в последнем шаг выше.
Рабочий пример 5.2: Деление направленных чисел
Рассчитать:
Шаг 1: Найдите знаки плюс и минус, разделяющие термины.
Шаг 2: Сначала упростите числитель. Выполняйте умножение перед сложением или вычитанием. Применять правила для знаки при умножении.
Шаг 3: Теперь упростим знаменатель. Выполняйте умножение перед сложением или вычитанием. Применять правила для знаки при умножении.
Шаг 4: Упростите дробь.
Применяйте правила знаков при делении.
Упражнение 5.2. Деление ориентированных чисел
Вычислите каждое из следующих чисел. Дайте свои ответы в виде смешанных чисел, где это необходимо.
Помните, что число 1 также является разделяющей личностью. Это означает, что при делении любого числа на 1 число остается прежним. Но нужно применять правила для знаков.
Помните, что ноль, разделенный на любое число, равен нулю.
\начать{выравнивать} &\frac{-3-5(-1)-2}{-1\times-5} \\ =&\;\frac{-3+5-2}{5} \\ =&\;\frac{-5+5}{5} \\ =&\фракция{0}{5} \\ =&\;0 \end{выравнивание}5.2 Квадраты и квадратные корни
Квадраты
В главе 1 вы узнали, что квадрат — это ответ, который мы получаем, когда мы умножаем число само на себя. Вы должны пересмотреть раздел о квадратах в Главе 1, прежде чем продолжить.
квадрат Квадрат — это ответ, полученный при умножении любого числа на себя.
Из того, что вы узнали об умножении направленных чисел, вы должны быть в состоянии видеть, что квадрат всегда положительный.
Отрицательное число не может быть квадратом, потому что нет числа, которое можно умножить само на себя, чтобы получить отрицательное число в качестве ответа. Это потому что:
- положительное число, умноженное само на себя, дает положительный ответ, например
- отрицательное число, умноженное само на себя, также дает положительный ответ, например .
Вы также узнали, что полный квадрат всегда можно представить как произведение простых множителей, каждый из которых имеет сила двух. Например, мы знаем, что 144 — это идеальный квадрат, потому что мы можем записать его так: . Мы знаем, что 72 не является полным квадратом, потому что мы не можем запишите это как произведение простых множителей, все из которых имеют степень два. Множители 72 .
Рабочий пример 5.3: Определение квадратных чисел
Определить, является ли является квадратом. Это не так, найдите наименьшее число, которым оно должно быть умножить так, чтобы ответ был квадратом.
Шаг 1: Определите, является число положительным или отрицательным. Если он отрицательный, то это не квадрат. Это должно умножить хотя бы на .
отрицательно, значит, это не квадрат.
Необходимо умножить не менее чем на :Шаг 2: Выразите число из шага 1 как произведение его простых множителей.
\начать{массив}{г | р} 2 и 162 \новая строка \hline 3 и 81 \новая строка \hline 3 и 27 \новая строка \hline 3 и 9 \новая строка \hline 3 и 3 \новая строка \hline & 1 \конец{массив}Шаг 3: Сгруппируйте одинаковые простые множители по два и запишите их в индексной форме.
Шаг 4: Оцените мощности сгруппированных простых множителей. Если есть степени, НЕ равные 2, число вы получили в Шаге 1, все еще не квадрат.
В простых делителях числа 162 степень двойки НЕ равна 2.
Следовательно, 162 НЕ является квадратом.
Шаг 5: Решите, на какое простое число (числа) мы должны умножить, чтобы все степени были равны 2.
В этом случае мы должны умножить еще на 2:
Новые сгруппированные простые множители:
Новый номер:Шаг 6: Объедините ответы из шагов 1 и 5.
Для чтобы получить квадрат, его нужно умножить на а затем :
Если умножается на , ответ квадрат: 324.Упражнение 5.3. Определение квадратных чисел
Определите, являются ли следующие числа или дроби квадратами. Если нет, найдите наименьшее число по что каждое число или дробь должны быть умножены, чтобы получить квадрат.
196
\начать{массив}{г | р} 2 и 196 \новая строка \hline 2 и 98 \новая строка \hline 7 и 49 \новая строка \hline 7 и 7 \новая строка \hline & 1 \конец{массив}196 — это квадрат.
Числитель отрицательный, значит, это не квадрат.
Дробь должна быть умножена не менее чем на .является квадратом.
надо умножить на и упрощено, чтобы дать квадрат .
Число отрицательное, значит, это не квадрат.
\начать{массив}{г | р} 2 и 700 \новая строка \hline 2 и 350 \новая строка \hline 5 и 175 \новая строка \hline 5 и 35 \новая строка \hline 7 и 7 \новая строка \hline & 1 \конец{массив}
Необходимо умножить не менее чем на :700 не квадрат. Его нужно умножить еще на 7:
надо умножить на чтобы дать квадрату 4900.
Квадратные корни
В главе 1 вы узнали, что квадратный корень — это величина, обратная квадрату.
квадратный корень числа является множителем числа, которое при умножении само на себя дает число. Вы должны пересмотреть раздел на площади корни в главе 1, прежде чем продолжить.
квадратный корень Множитель числа, который при умножении на себя дает количество.
Не путайте квадраты и квадратные корни:
- 49 — это квадрат 7, и мы пишем
- 7 — это квадратный корень из 49, и мы пишем .
Вы только что видели, что отрицательное число не может быть квадратом. Это означает, что мы не можем найти квадратный корень из отрицательное число. Не существует множителя отрицательного числа, которое можно умножить само на себя, чтобы получить это отрицательное число. номер в качестве ответа. Например, не существует. Это потому что:
Как видите, это означает, что квадрат имеет два квадратных корня: положительное число и такое же отрицательное число.
Мы напиши так:
Знак означает «плюс-минус».
Рабочий пример 5.4: Вычисление квадратных корней
Найдите квадратный корень из .
Шаг 1: Запишите дробь как неправильную дробь в виде .
Шаг 2: Запишите числитель и знаменатель как произведения их простых множителей.
Шаг 3: Найдите квадратные корни из числителя и знаменателя по отдельности. Написать распишитесь перед ответом. 92=900 & \sqrt{900}=\pm30\новая строка \hline \конец{массив}
Упражнение 5.4. Вычисление квадратных корней
Вычислите квадратные корни следующих чисел и дробей. Вы можете использовать таблицу квадратного и квадратного корня выше.
Из таблицы:
Из таблицы:
Из таблицы:
Из таблицы:
Обозначение квадрата и квадратного корня
Обратите внимание на следующие обозначения при работе с квадратами и квадратным корнем:
- Степень двойки применяется только к тому, что находится непосредственно перед ней.
2 \\ =&\;-(+4)+(+16)\\ =&\;-4+16\ знак равно 12 \end{выравнивание} 92-2\раз-3\\ =&\;-9-(-6)\\ =&\;-9+6\ знак равно -3 \end{выравнивание}
или
\начать{выравнивать} &\ гидроразрыва {\ sqrt {81}} {(-3) (-3) (3)} \\ =&\;\frac{-9}{(+9)(3)} \\ =&\;\frac{-9}{+27} \\ знак равно -\фракция{1}{3} \end{выравнивание}или
\начать{выравнивать} &\frac{\sqrt 4 \times 2 — 2 \times -2}{-2} \\ =&\;\frac{-2\times2-(-4)}{-2} \\ =&\;\frac{-4+4}{-2} \\ знак равно \фракция{0}{-2} \\ =&\;0 \end{выравнивание}5.
3 Использование таблиц, диаграмм и графиков
Таблица квадратного корня
Помимо таблицы квадратного корня и таблицы квадратного корня, которую вы использовали в предыдущем разделе, вы можете использовать следующую таблицу для определить квадратные корни чисел, которые составляют , а не полных квадратов. Рабочий пример 5.5 покажет вам, как сделай это.
Где применимо, в этой таблице квадратные корни округляются до двух знаков после запятой.
Рабочий пример 5.5: Использование таблицы квадратного корня
Найти из таблицы квадратного корня.
Шаг 1: Найдите первую цифру в вертикальном столбце, где перечислены числа от 1 до 9.
Первая цифра — 7, поэтому вы будете искать по ряду цифру 7.
Шаг 2: Найдите вторую цифру в горизонтальном ряду, где перечислены числа от 0 до 9.
Вторая цифра 6, так что вы посмотрите вниз по столбцу с номером 6.
Шаг 3. Ответ: где строка из шага 1 встречается со столбцом из шага 2.
Шаг 4: Проверьте, имеет ли смысл ваш ответ.
Два полных квадрата по обе стороны от 76 равны 64 и 81. Это означает должно лежать между а также .
Ответ 8,72 лежит между 8 и 9.
Квадратные корни однозначных цифр от 1 до 9 показаны в крайнем левом столбце таблицы.
Диаграммы расстояний
Диаграмму расстояний можно использовать для отображения расстояний между разными городами. Мы читаем таблицу расстояний в подобном путь к таблице квадратного корня. В этой таблице показаны кратчайшие расстояния по дорогам в километрах по данным Google . Карты , 2019.
Рабочий пример 5.6: Использование карты расстояний
Найдите расстояние от Акуре до Порт-Харкорта.
Шаг 1: Найдите названия двух городов.
Обратите внимание на число, написанное рядом с каждым городом.
Акуре — номер 2, а Порт-Харкорт — номер 9.
Шаг 2: Двигайтесь вниз по столбцу города с наименьшим номером, пока не дойдете до строки с тем же номером, что и второй город.
Идите вниз по столбцу с пометкой Akure 2 , пока не дойдете до строки номер 9.
Шаг 3: Ответ находится там, где пересекаются столбец и строка из шага 2. Запишите это правильно единицы.
Расстояние 452 км.
Таблица затрат
Следующая таблица может быть использована для расчета стоимости любого количества изделий.
Рабочий пример 5.7: Использование графика затрат
Используйте таблицу себестоимости, чтобы определить стоимость 76 чашек фасоли в \(₦80.50\) за чашку.
Шаг 1: Разбейте количество предметов на десятки и единицы.
Это говорит вам, какие строки в расписании использовать.
Используйте ряды 6 и 7.
Шаг 2: Разбейте цену на сотни, десятки, единицы и десятые доли. Это говорит вам, какие столбцы в график использования.
\[₦80,50= ₦80+ ₦0,5=( ₦\цвет{красный}8 \цвет{черный} \умножить на 10)+( ₦\цвет{красный}5 \цвет{черный} \div 10)\]Используйте столбцы 5 и 8.
Шаг 3: Запишите в таблицу строки и столбцы, которые вы определили на шагах 1 и 2.
\начать{массив}{|с|с|с|} \hline \вниз\, \вправо и 5 и 8 \\ \hline 6 & & \\ \hline 7 & & \\ \hline \конец{массив}Шаг 4: Вставьте число, кратное 10, которое вы определили в шагах 1 и 2.
\начать{массив}{|с|с|с|} \hline \downarrow \, \rightarrow & 5\, (\div 10) & 8\, (\times 10) \\ \hline 6\, (\times1) & & \\ \hline 7\, (\ умножить на 10) & & \\ \hline \конец{массив}Шаг 5: См.
\начать{массив}{|с|с|с|} \hline \downarrow \, \rightarrow & 5\, (\div 10) & 8\, (\times 10) \\ \hline 6\, (\раз1) и 30 и 48 \\ \hline 7\, (\ умножить на 10), 35 и 56 \\ \hline \конец{массив}таблицу затрат. Запишите числа на пересечениях строк и столбцов.
Шаг 6: Определите общую стоимость, сложив числа на пересечениях строк и столбцов. Подать заявление умножения или деления, которые вы вставили на шаге 4.
\начать{выравнивать} &(30\times1\div10)+(48\times1\times10)+(35\times10\div10)+(56\times10\times10) \\ =&\;3+480+35+5600\ знак равно ₦6,118 \end{выравнивание}Таблица стоимости не включает юниты, поэтому ее можно использовать и для кобосов.
Упражнение 5.6. Использование таблиц, диаграмм и графиков
Используйте таблицы, графики и графики, представленные в этой главе, чтобы ответить на следующие вопросы.
- Рассчитать:
- длина стороны квадрата площадью 83 см
Из таблицы квадратного корня:
- площадь квадрата со стороной 22 см
Из таблицы квадратных и квадратных корней:
- Мустафа хочет выложить плиткой пол в квадратной комнате.
У него 95 тайлов. Он хочет выяснить, существуют ли достаточно плитки или он должен купить больше.
- Подсчитайте максимальное количество плиток, которые он может положить вдоль одной стороны пола.
Из таблицы квадратного корня:
Разбивать плитки не имеет смысла, поэтому максимум, что он может положить вдоль одной стороны — 9 плиток.
- Если он выложит пол в соответствии с предыдущим ответом, сколько из 95 плиток останется?
Он будет использовать плитка.
Будет плитка осталась.
- Длина одной стороны пола 150 см. Плитки квадратные, каждая шириной 15 см. Рассчитать сколько еще плиток Мустафа должен купить.
На одну длину пола ему нужно плитка.
Комната квадратная, значит, на весь этаж ему нужно плитка.
Он должен купить еще один плитка.Сравните расстояние от Бенин-Сити до Кано с расстоянием от Порт-Харкорта до Абуджи.
Из карты расстояний:
Расстояние от Бенин-Сити до Кано: 848 км
Расстояние от Порт-Харкорта до Абуджи: 658 кмРасстояние от Бенин-Сити до Кано равно длиннее, чем расстояние от Порт-Харкорта до Абуджа.
Используйте таблицу себестоимости, чтобы рассчитать цену 42 буханок хлеба по 50 ₦ каждая.
Предметы:
\начать{выравнивать} \text{Стоимость}&=(20\times10\times10)+(10\times10) \\ &=2 000+100 \\ &= ₦2,100 \end{выравнивание}
Стоимость: ₦50
Номера на перекрестках: 4 ряд и 5 столбец ; строка 2 и столбец 5Владелец магазина позволяет своим покупателям покупать в кредит.
У брата и сестры одинаковый аккаунт и магазин. В конце определенного месяца они должны владельцу магазина 1 250,00 фунтов стерлингов. Затем они решают разделить дебет поровну. После этого сестра покупает 12 литров растительного масла по 580,00 ₦ за литр. Просят владельца магазина прислать у каждого свой аккаунт. Каким будет баланс на каждом счете?
\(\frac{- ₦1,250}{2}=- ₦625\) на человека
литров растительного масла:
\начать{выравнивать} \text{Стоимость}&=(5\times10\times100)+(8\times10\times10)+(10\times100)+(16\times10) \\ &=5 000+800+1 000+160 \\ &= 6 960 ₦ \end{выравнивание}
Стоимость: \(₦500+ ₦80\)
Номера на перекрестках:Баланс сестры: \(-625+(-6,960)=- ₦7,585\)
Баланс брата: \(- ₦625\)5.4 Резюме
- Направленные числа — это положительные и отрицательные числа.

 При умножении корней полученное подкоренное выражение можно упростить (не всегда) до произведения некоторого числа (или выражения) на полный квадрат или куб. Вот как это делается:
При умножении корней полученное подкоренное выражение можно упростить (не всегда) до произведения некоторого числа (или выражения) на полный квадрат или куб. Вот как это делается: После того как вы перемножили множители, перемножьте числа под знаком корня. Вот как это делается:
После того как вы перемножили множители, перемножьте числа под знаком корня. Вот как это делается: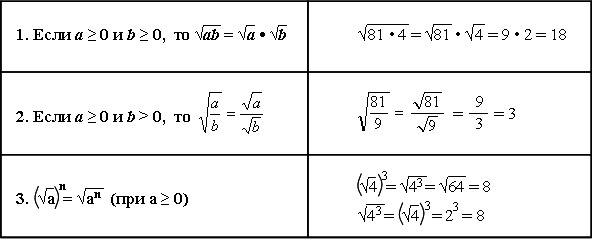 Число 6 является НОК этих двух чисел, потому что это наименьшее число, которое делится без остатка как на 3, так и на 2: 6/3=2 и 6/2=3. Чтобы умножить корни, их показатель должен быть равен 6.
Число 6 является НОК этих двух чисел, потому что это наименьшее число, которое делится без остатка как на 3, так и на 2: 6/3=2 и 6/2=3. Чтобы умножить корни, их показатель должен быть равен 6. Вот как это делается:
Вот как это делается:
 Разложение подкоренного значения на простые множители,
Разложение подкоренного значения на простые множители,  дробное число должно быть записано в виде обыкновенной дроби;
дробное число должно быть записано в виде обыкновенной дроби; д. В данном случае нужно просто найти нужное число в таблице и посмотреть, какому значению оно соответствует.
д. В данном случае нужно просто найти нужное число в таблице и посмотреть, какому значению оно соответствует. Получим 66×6 = 396. Напишем 6 справа сверху, т. к. это вторая цифра результата. Отнимем 396 от 408, получим 12.
Получим 66×6 = 396. Напишем 6 справа сверху, т. к. это вторая цифра результата. Отнимем 396 от 408, получим 12.
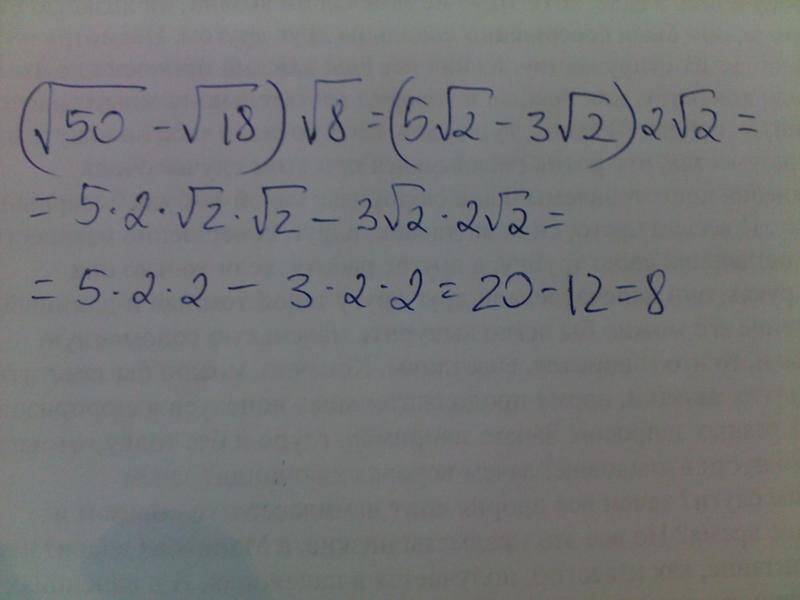
 \\ \end{align}\]
\\ \end{align}\] {2}}}=\sqrt{5}. \\ \end{align}\]
{2}}}=\sqrt{5}. \\ \end{align}\]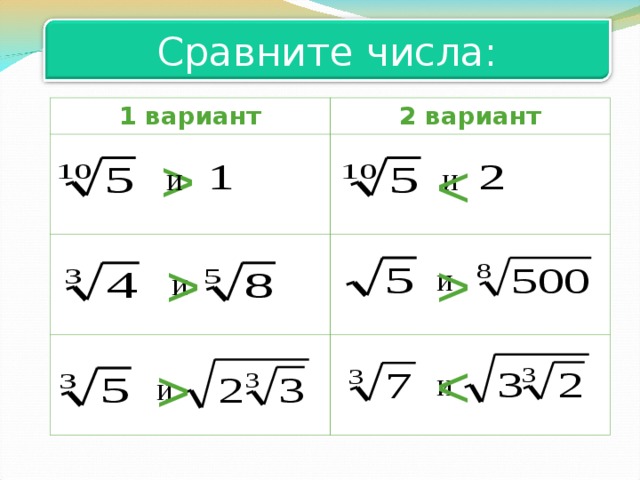 {2}}}=\sqrt{75}. \end{align}\]
{2}}}=\sqrt{75}. \end{align}\] д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. Однако знак корня означает не только алгебраическое действие, но и применяется в деревообрабатывающем производстве — в расчете относительных размеров.
Однако знак корня означает не только алгебраическое действие, но и применяется в деревообрабатывающем производстве — в расчете относительных размеров. 36 — квадратный корень из шести (6 × 6 = 36) .
36 — квадратный корень из шести (6 × 6 = 36) . После этого, необходимо перемножить числа и множители, которые стоят перед знаком корня:
После этого, необходимо перемножить числа и множители, которые стоят перед знаком корня:

 Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:
Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:
 д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. Одно из действий в такой «паре» направлено на увеличение числа, а другое, обратное ему – на уменьшение. Например, действие, противоположное сложению – это вычитание, умножению соответствует деление. Имеется и своя диалектическая пара-противоположность и у возведения в степень. Речь идет об извлечении корня.
Одно из действий в такой «паре» направлено на увеличение числа, а другое, обратное ему – на уменьшение. Например, действие, противоположное сложению – это вычитание, умножению соответствует деление. Имеется и своя диалектическая пара-противоположность и у возведения в степень. Речь идет об извлечении корня. Следовательно,
Следовательно, 2 = x, ?x = a. Как и над всякими числами, над квадратными корнями дозволено исполнять арифметические операции сложения и вычитания.
2 = x, ?x = a. Как и над всякими числами, над квадратными корнями дозволено исполнять арифметические операции сложения и вычитания.

 Сложение корней похоже на сложение членов алгебраического выражения, то есть требует определения подобных корней.
Сложение корней похоже на сложение членов алгебраического выражения, то есть требует определения подобных корней.
 Например, рассмотрим выражение:
Например, рассмотрим выражение: Это число 3 можно вынести из-под корня. Таким образом, вы получите еще более упрощенное выражение: 10√(2) + 4√(2) + 2√(3)+ 6√(3) + 3 3 √(3)
Это число 3 можно вынести из-под корня. Таким образом, вы получите еще более упрощенное выражение: 10√(2) + 4√(2) + 2√(3)+ 6√(3) + 3 3 √(3) д.
д.
 Вуаля!
Вуаля!
 Это факторы, которые упростят термины без радикала.
Это факторы, которые упростят термины без радикала.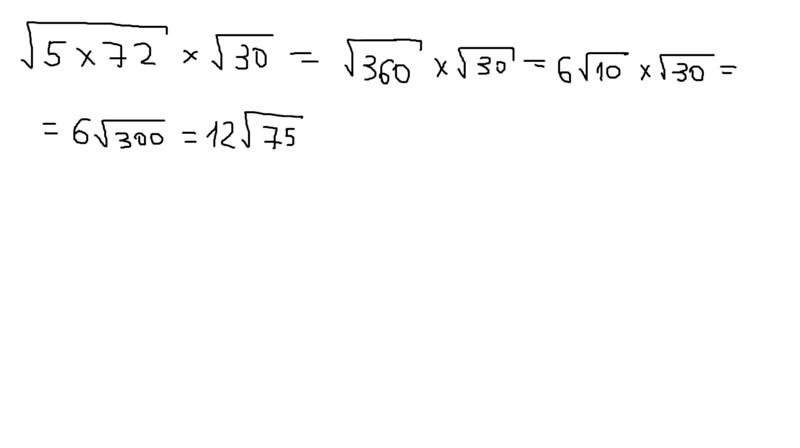 Давайте немного полюбим x и посмотрим, как это делается.
Давайте немного полюбим x и посмотрим, как это делается.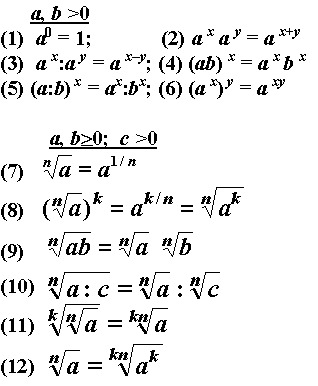



 Почему мы сначала изучаем умножение квадратных корней? Причина в том, что умножение между квадратными корнями легко выполнить. Числа в корневом символе можно умножать.
Почему мы сначала изучаем умножение квадратных корней? Причина в том, что умножение между квадратными корнями легко выполнить. Числа в корневом символе можно умножать. Целые числа и квадратные корни — это совершенно разные числа.
Целые числа и квадратные корни — это совершенно разные числа. Например, как решить следующую задачу?
Например, как решить следующую задачу?