Лучший ответ по мнению автора
| ||||||||||||||||
Другие ответы
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Вычисли и заполни таблицу. 2 — 2x — 3. Найдите: а)наименьшее значение функции; б) значения x, при которых значение функции равно 5; в) значение…
2 — 2x — 3. Найдите: а)наименьшее значение функции; б) значения x, при которых значение функции равно 5; в) значение…
Пользуйтесь нашим приложением
График y x 2 4x 1. График функции
Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
1. Построение графика функции y = |f(x)|
Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.
Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.
1) Построить аккуратно и внимательно график функции y = f(x).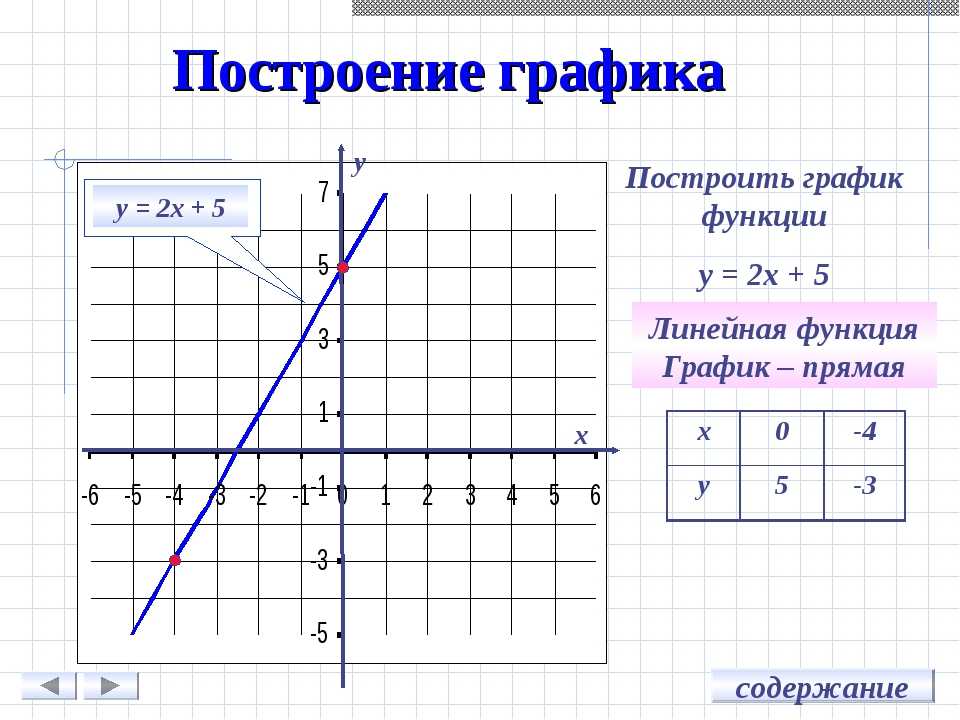
2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.
3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.
Пример 1. Изобразить график функции y = |x 2 – 4x + 3|
1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).
y = 0 2 – 4 · 0 + 3 = 3.
Следовательно, парабола пересекает ось 0y в точке (0, 3).
Координаты вершины параболы:
x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.
Следовательно, точка (2, -1) является вершиной данной параболы.
Рисуем параболу, используя полученные данные (рис. 1)
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.
3) Получаем график исходной функции (рис.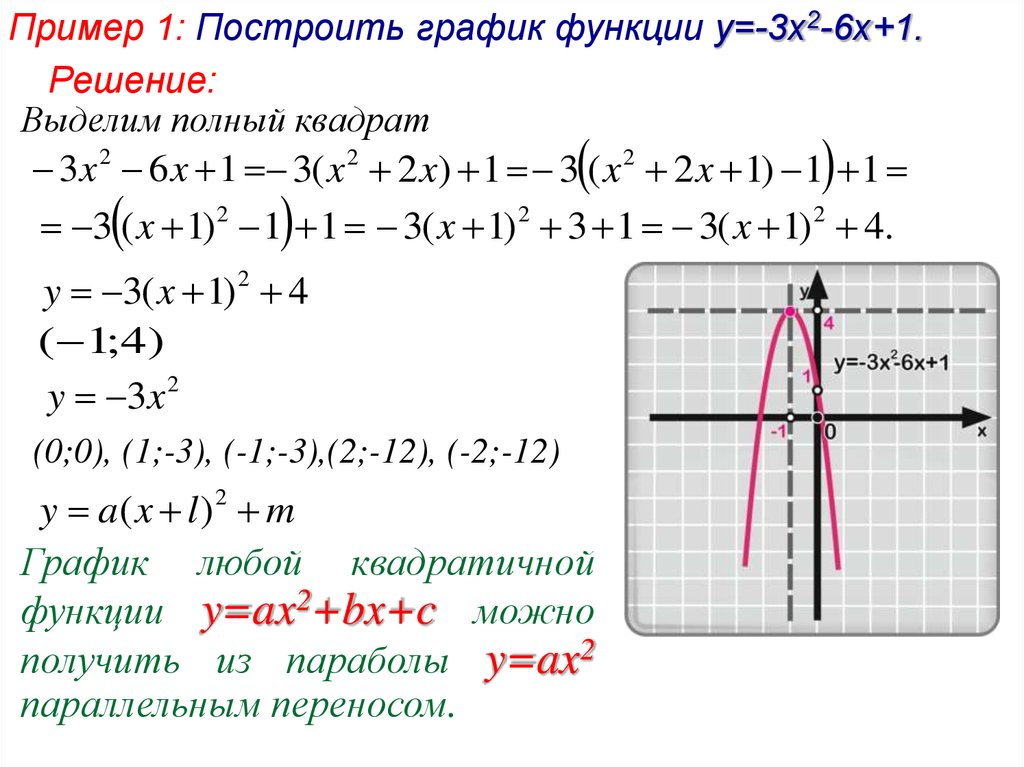 2 , изображен пунктиром).
2 , изображен пунктиром).
2. Построение графика функции y = f(|x|)
Заметим, что функции вида y = f(|x|) являются четными:
y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.
Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.
1) Построить график функции y = f(x).
2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3
Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.
1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).
также рис. 1 ).
2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отображаем правую часть графика симметрично оси 0y.
(рис. 3) .
Пример 3. Изобразить график функции y = log 2 |x|
Применяем схему, данную выше.
1) Строим график функции y = log 2 x (рис. 4) .
3. Построение графика функции y = |f(|x|)|
Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Чтобы построить график функции y = |f(|x|)|, необходимо:
1) Построить аккуратно график функции y = f(|x|).
2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.
3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.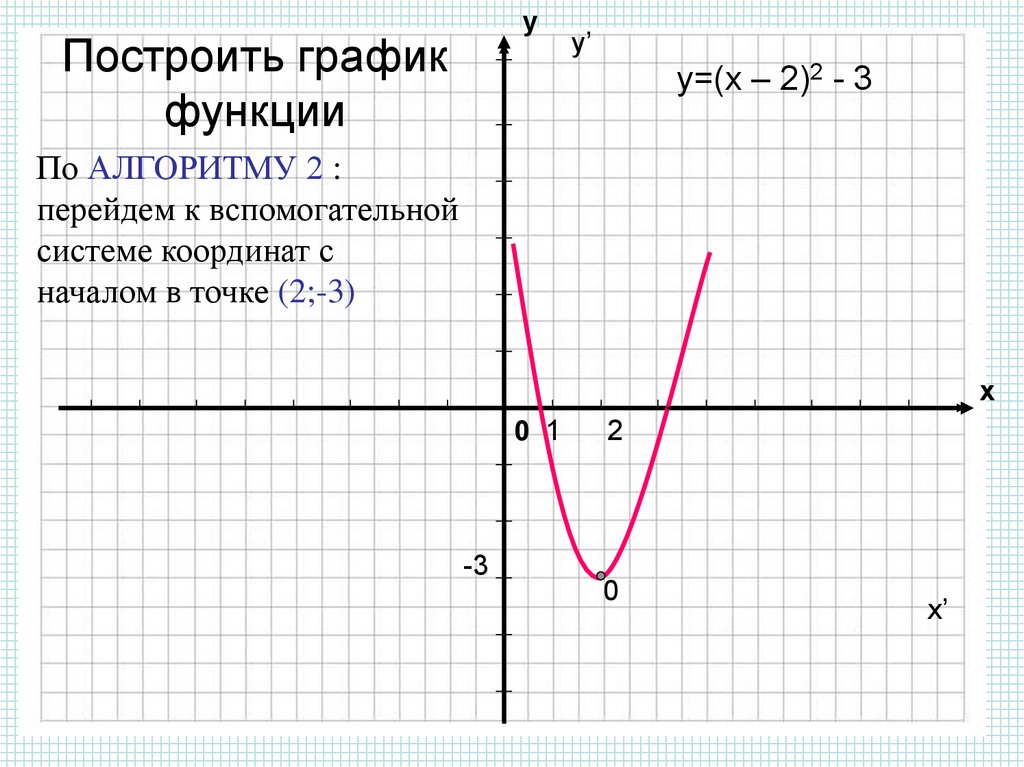
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.
1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1
можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.
Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.
a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.
c) Отображаем полученную часть графика симметрично оси 0y.
d) Полученный график изображен на рисунке пунктиром (рис. 7) .
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.
3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.
4) Полученный график изображен на рисунке пунктиром (рис. 8) .
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|
Построить график функции y = |(2|x| – 4) / (|x| + 3)|
1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.
a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .
Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.
2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.
3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.
4) Окончательный график изображен на рисунке (рис. 11) .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Степенной называется функция вида y=x n (читается как y равно х в степени n), где n – некоторое заданное число.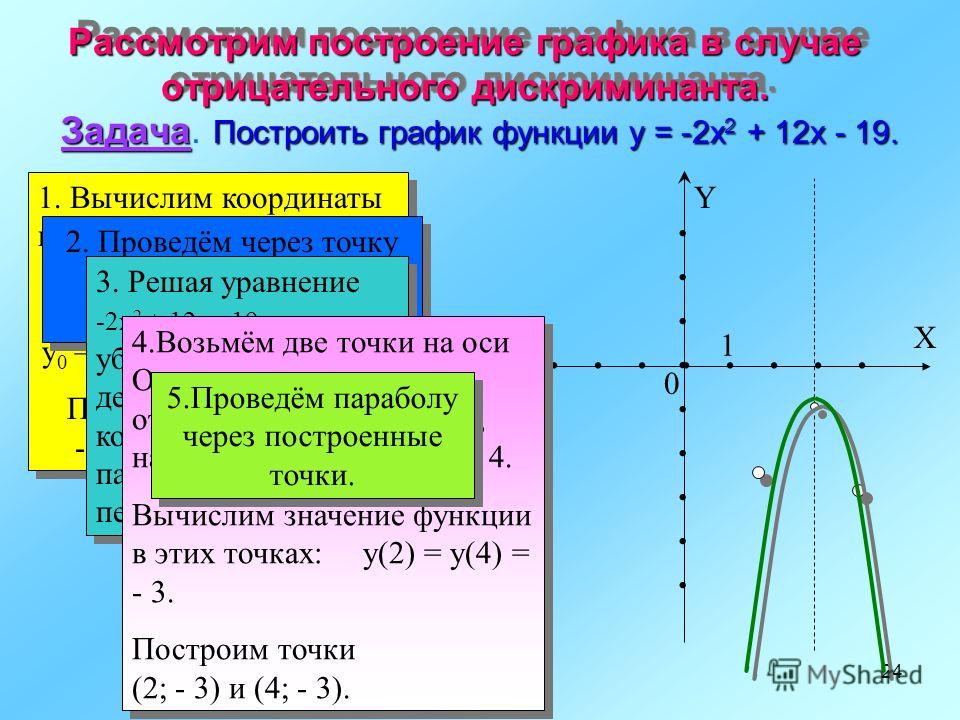 Частными случаями степенных функций является функции вида y=x, y=x 2 , y=x 3 , y=1/x и многие другие. Расскажем подробнее о каждой из них.
Частными случаями степенных функций является функции вида y=x, y=x 2 , y=x 3 , y=1/x и многие другие. Расскажем подробнее о каждой из них.
Линейная функция y=x 1 (y=x)
График прямая линия, проходящая через точку (0;0) под углом 45 градусов к положительному направлению оси Ох.
График представлен ниже.
Основные свойства линейной функции:
- Функция возрастающая и определена на всей числовой оси.
- Не имеет максимального и минимального значений.
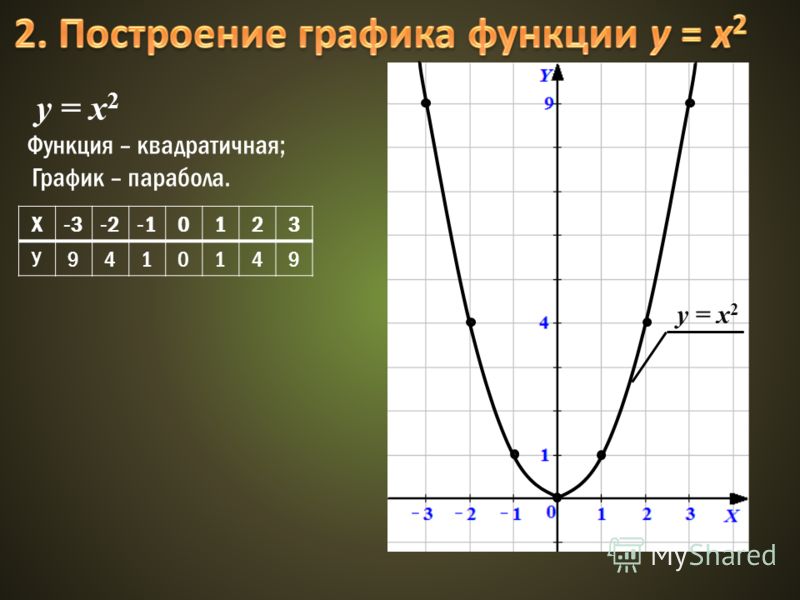
Квадратичная функция y=x 2
Графиком квадратичной функции является парабола.
Основные свойства квадратичной функции:
- 1. При х =0, у=0, и у>0 при х0
- 2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
- 3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке }
График функции y x 2 2x 1. Функции и графики
СТЕПЕНЬ С РАЦИОНАЛЬНЫМ ПОКАЗАТЕЛЕМ,
СТЕПЕННАЯ ФУНКЦИЯ IV
§
74. Функции у = х n при п = -1 и п = -2
Функции у = х n при п = -1 и п = -2
1. Функция у = х -1 . Областью определения функции у = х -1 , или у = 1 / x , является множество всех действительных чисел, кроме нуля. Эта функция нечетна, так как 1 / — x =- 1 / x . Поэтому для построения ее графика достаточно составить таблицу значений только для положительных значений аргумента х :
Используя эту таблицу и свойство нечетности функции у = х -1 , построим ее график (рис. 97). Этот график, как видно из рисунка, состоит из двух кривых, одна из которых целиком находится в первом, а другая — в третьем координатном углу. Они симметричны друг другу относительно начала координат. Вместе эти кривые называются гиперболой , а каждая из кривых в отдельности — ветвью гиперболы .
Заметим, что при всех положительных значениях x : функция у = х -1 монотонно убывает.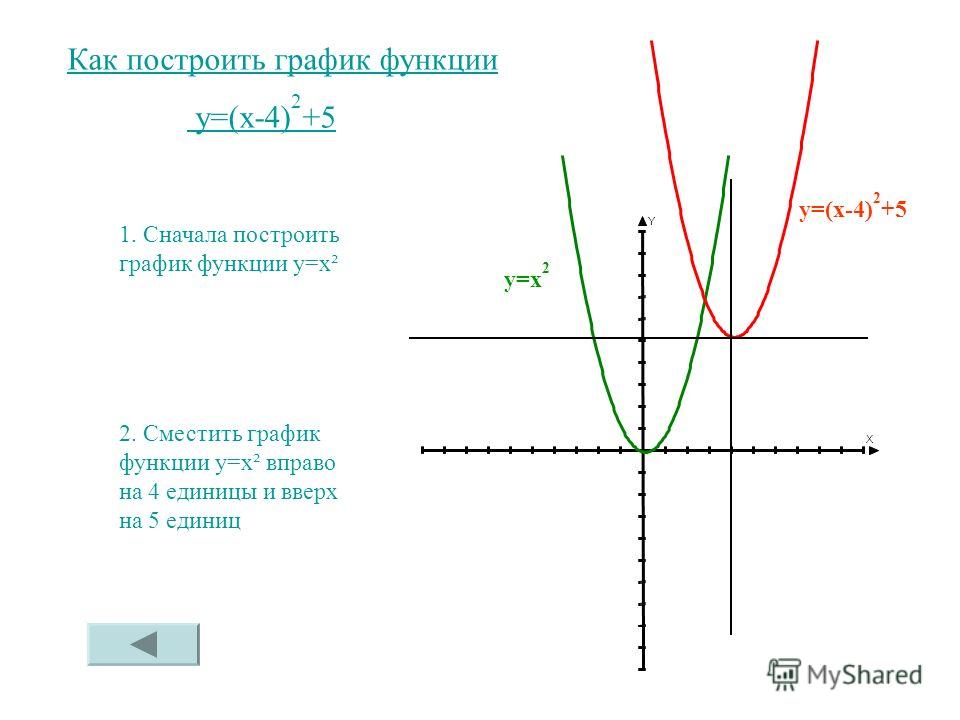 То же верно и для всех отрицательных значений х . Однако былo бы ошибочно утверждать, что эта функция является монотонно убывающей всюду. Например, значению аргумента x 1 = — 1 соответствует значение функции y 1 = -1, а значению аргумента x 2 = +1 — значение функции y 2 = + 1. Имеем: x 1 > x 2 и y 2 > y 1 . Для монотонно убывающей функции из x 1 > x 2 должно вытекать y 2 y 1. Но здесь это условие не выполняется. Следовательно, говорить, что функция у = х -1 всюду монотонно убывает, нельзя. Однако можно сказать, что эта функция убывает на любом отрезке, на котором она определена (то есть на любом отрезке оси х , не содержащем нуля).
То же верно и для всех отрицательных значений х . Однако былo бы ошибочно утверждать, что эта функция является монотонно убывающей всюду. Например, значению аргумента x 1 = — 1 соответствует значение функции y 1 = -1, а значению аргумента x 2 = +1 — значение функции y 2 = + 1. Имеем: x 1 > x 2 и y 2 > y 1 . Для монотонно убывающей функции из x 1 > x 2 должно вытекать y 2 y 1. Но здесь это условие не выполняется. Следовательно, говорить, что функция у = х -1 всюду монотонно убывает, нельзя. Однако можно сказать, что эта функция убывает на любом отрезке, на котором она определена (то есть на любом отрезке оси х , не содержащем нуля).
Функция у = х -1 принимает любые числовые значения, кроме нуля. Значит, областью ее изменения, так же как и областью определения, является множество всех действительных чисел, кроме нуля.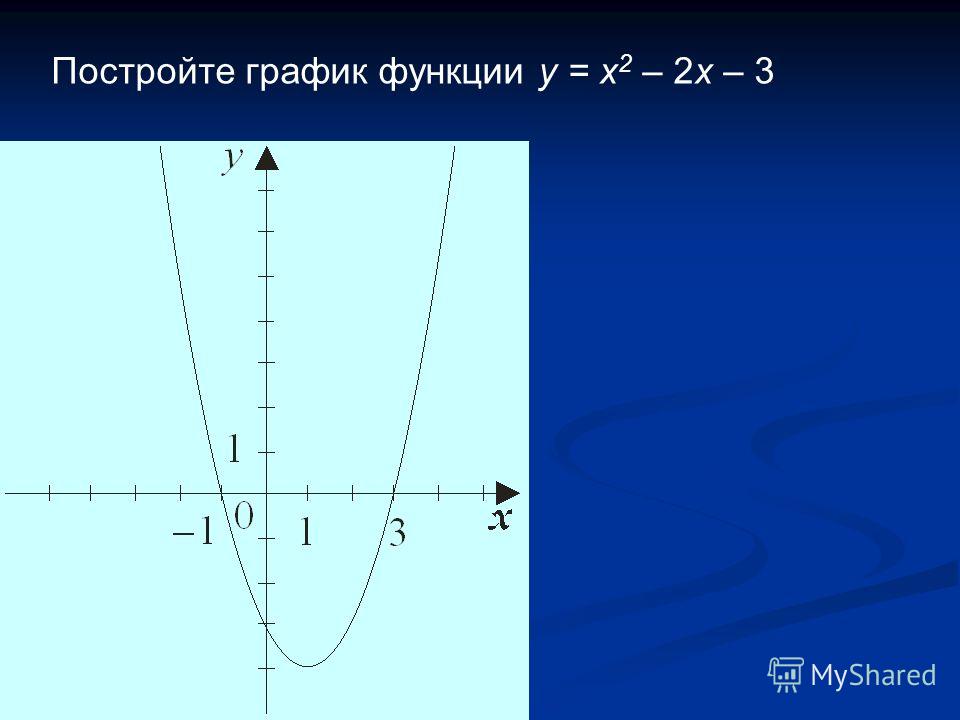
Следует обратить внимание на поведение функции у = х -1 вблизи точки х = 0. Если значения аргумента х неограниченно приближаются к нулю, оставаясь положительными, то соответствующие значения функции у неограниченно растут. Если же значения аргумента х неограниченно приближаются к нулю, оставаясь отрицательными, то соответствующие значения функции у неограниченно убывают.
2. Функция у = х -2 . Областью определения функции у = х -2 , или , является множество всех действительных чисел, кроме нуля. Так как
то функция у = х -2 четна. Поэтому для построения графика этой функции достаточно составить таблицу ее значений только для положительных значений х :
Значения этой функции при отрицательных х равны ее значениям при соответствующих положительных х .
Например.(- 1 / 4) -2 = (1 / 4) -2 =16.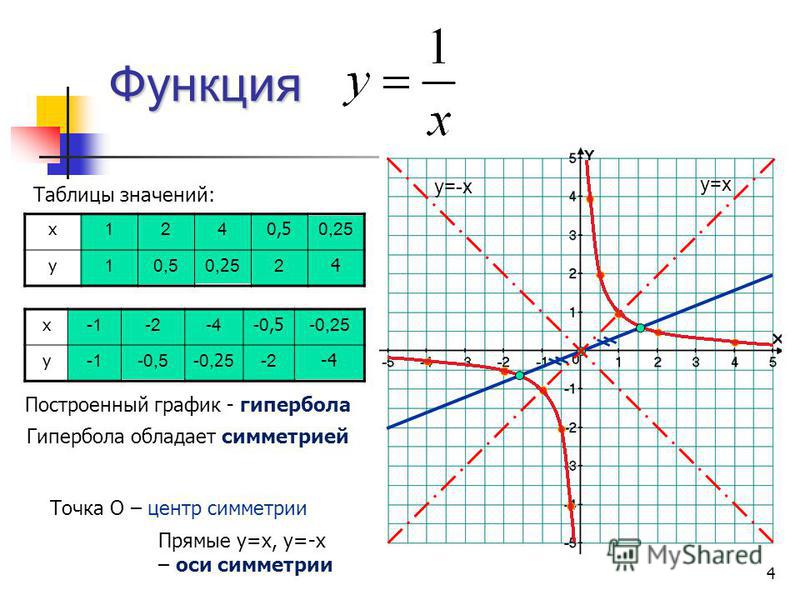 Используя составленную таблицу и свойство четности функции у = х -2 , построим ее график (рис. 98).
Используя составленную таблицу и свойство четности функции у = х -2 , построим ее график (рис. 98).
Он состоит из двух ветвей, одна из которых целиком расположена в первом, а другая- во втором координатном углу. Эти кривые симметричны друг другу относительно оси ординат. Необходимо подчеркнуть, что ни одну из них в отдельности нельзя считать графиком функции у = х -2 . Только взятые вместе, они образуют этот график.
Функция у = х -2 , или , принимает только положительные значения. Поэтому график ее расположен целиком свыше оси х .
Когда значения аргумента х неограниченно растут (или неограниченно убывают), соответствующие значения функции у неограниченно приближаются к нулю, оставаясь все время положительными. При неограниченном приближении значений аргумента х к нулю (как слева, так и справа) соответствующие значения функции у неограниченно растут. Областью изменения функции у = х -2 является совокупность всех положительных чисел.
Упражнение
538. Построить графики функций:
a) y = (x — l) -1 ; в) у = |x -1 |; д) у = x -2 -2;
б) у = (х + 2) -1 ; г) y = | x | -1 ; е)
Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .
Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.
Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .
На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .
Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости).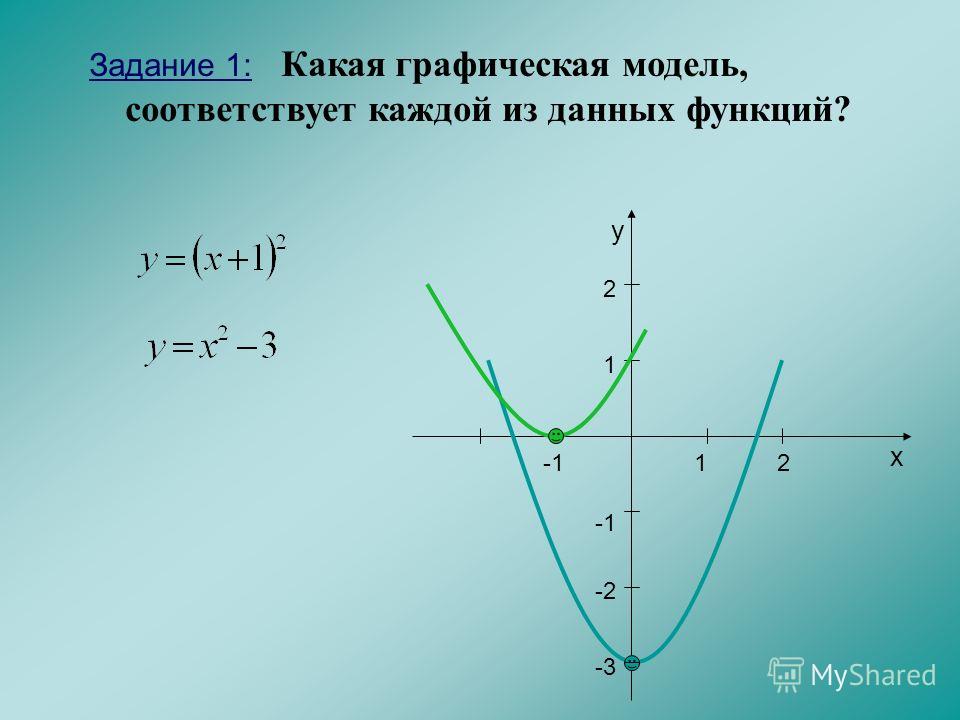 В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.
График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 — 2х принимает положительные значения при х и при х > 2 , отрицательные — при 0 у = х 2 — 2х принимает при х = 1 .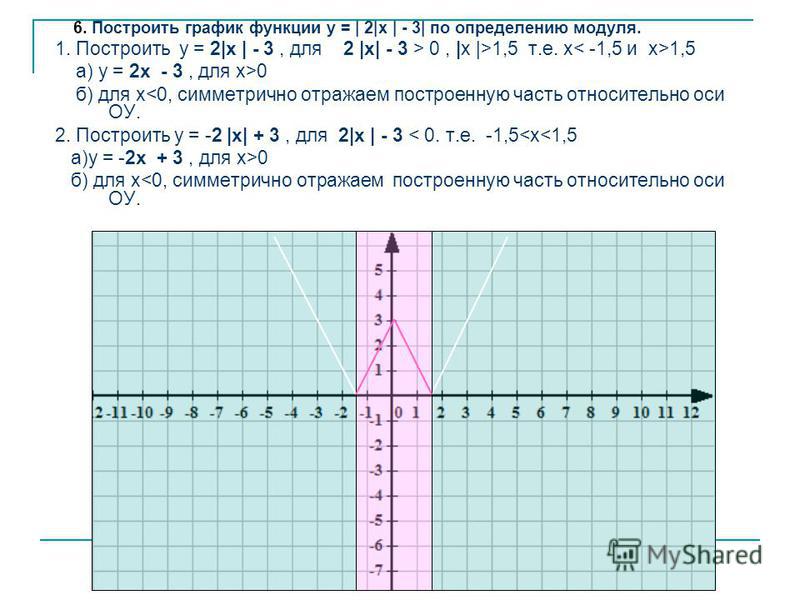
Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.
Таблица выглядит следующим образом:
Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).
Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.
Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:
Соответствующие пять точек показаны на рис. 48.
На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.
Для обоснования своего утверждения рассмотрим функцию
.
Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.
Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.
График функции у = |f(x)|.
Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать
Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т. е. часть графика функции
е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).
Пример 2. Построить график функции у = |х|.
Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).
Пример 3 . Построить график функции y = |x 2 — 2x|.
Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x
График функции y = f(x) + g(x)
Рассмотрим задачу построения графика функции y = f(x) + g(x).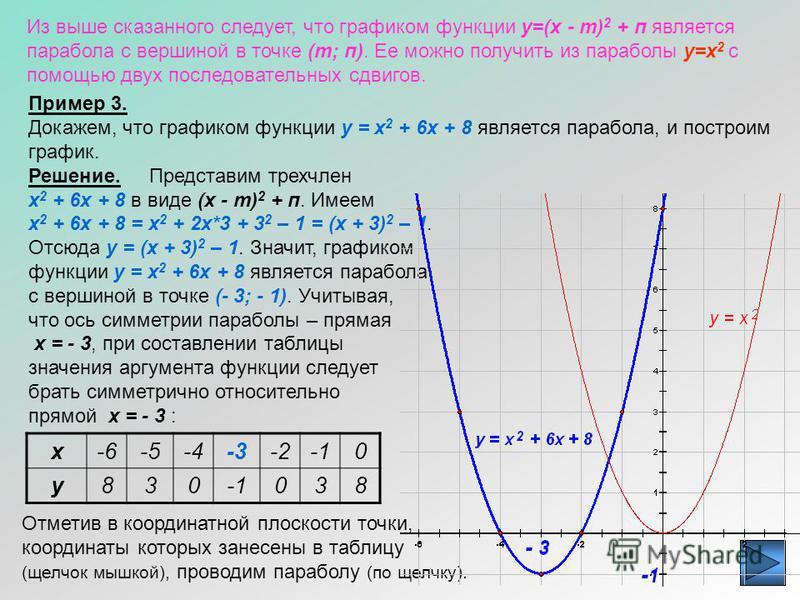 если заданы графики функций y = f(x) и y = g(x) .
если заданы графики функций y = f(x) и y = g(x) .
Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).
Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т.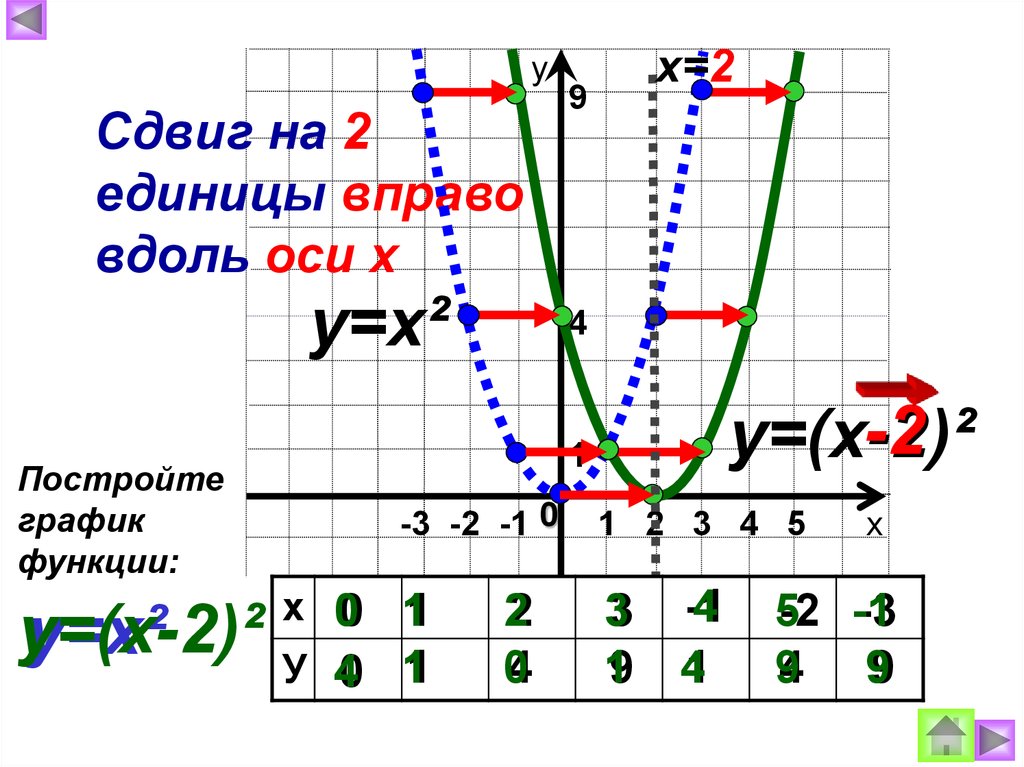 е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)
Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .
При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.
Областью определения функций является множество действительных чисел, кроме нуля. X Y y = x -1 Свойства функции у = х-1 и особенности ее графика. 1. Если х > 0, то у >0; если х
0, то у >0; если х «>
0, то у >0; если х «>
0, то у >0; если х » title=»Областью определения функций является множество действительных чисел, кроме нуля.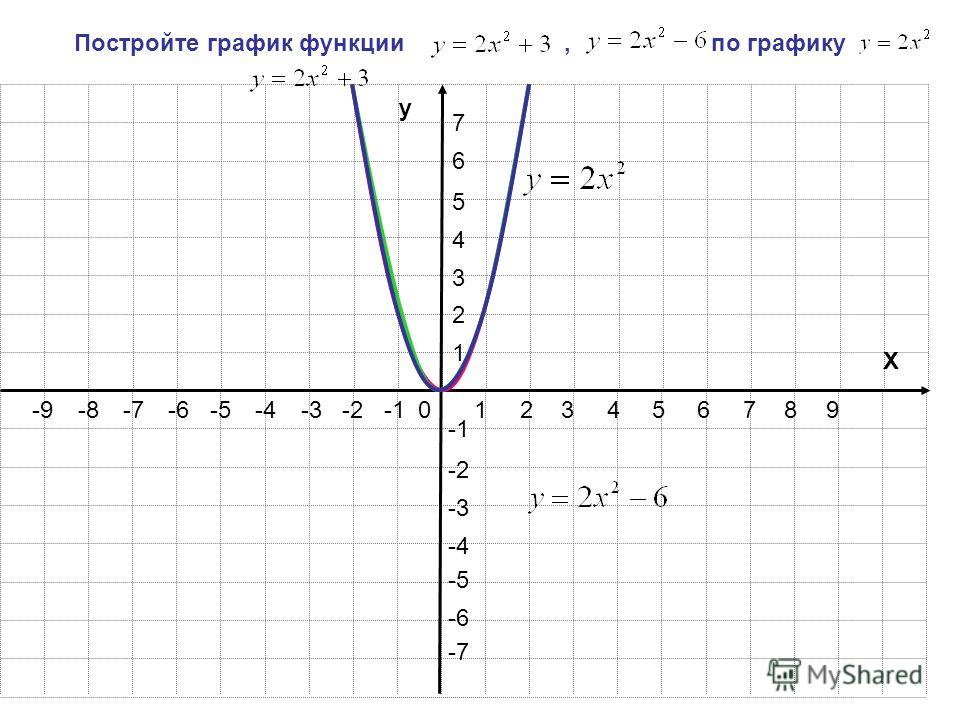 X Y y = x -1 Свойства функции у = х-1 и особенности ее графика. 1. Если х > 0, то у >0; если х «>
title=»Областью определения функций является множество действительных чисел, кроме нуля. X Y y = x -1 Свойства функции у = х-1 и особенности ее графика. 1. Если х > 0, то у >0; если х «>
X Y y = x -1 Свойства функции у = х-1 и особенности ее графика. 1. Если х > 0, то у >0; если х «>
title=»Областью определения функций является множество действительных чисел, кроме нуля. X Y y = x -1 Свойства функции у = х-1 и особенности ее графика. 1. Если х > 0, то у >0; если х «>
0 неограниченно возрастают(x +),то соответствующие значения функции убывают, т.е. стремятся к нулю (y 0). Если значения аргумента при x>0 убывают, т.е. стремятся к нулю (x 0),то соответствующие значения функции неогра» title=»3.Если значения аргумента при x>0 неограниченно возрастают(x +),то соответствующие значения функции убывают, т.е. стремятся к нулю (y 0). Если значения аргумента при x>0 убывают, т.е. стремятся к нулю (x 0),то соответствующие значения функции неогра»>
4
3.Если значения аргумента при x>0 неограниченно возрастают(x +),то соответствующие значения функции убывают, т.е. стремятся к нулю (y 0). Если значения аргумента при x>0 убывают, т.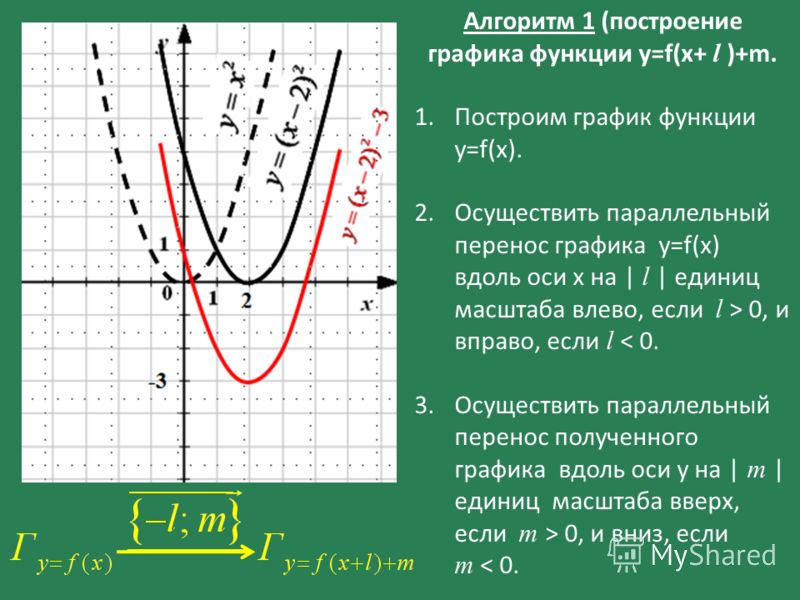 е. стремятся к нулю (x 0),то соответствующие значения функции неограниченно возрастают (y +) X Y y = x -1
0 неограниченно возрастают(x +),то соответствующие значения функции убывают, т.е. стремятся к нулю (y 0). Если значения аргумента при x>0 убывают, т.е. стремятся к нулю (x 0),то соответствующие значения функции неогра»>
0 неограниченно возрастают(x +),то соответствующие значения функции убывают, т.е. стремятся к нулю (y 0). Если значения аргумента при x>0 убывают, т.е. стремятся к нулю (x 0),то соответствующие значения функции неограниченно возрастают (y +) X Y y = x -1″>
0 неограниченно возрастают(x +),то соответствующие значения функции убывают, т.е. стремятся к нулю (y 0). Если значения аргумента при x>0 убывают, т.е. стремятся к нулю (x 0),то соответствующие значения функции неогра» title=»3.Если значения аргумента при x>0 неограниченно возрастают(x +),то соответствующие значения функции убывают, т.е. стремятся к нулю (y 0). Если значения аргумента при x>0 убывают, т.
е. стремятся к нулю (x 0),то соответствующие значения функции неограниченно возрастают (y +) X Y y = x -1
0 неограниченно возрастают(x +),то соответствующие значения функции убывают, т.е. стремятся к нулю (y 0). Если значения аргумента при x>0 убывают, т.е. стремятся к нулю (x 0),то соответствующие значения функции неогра»>
0 неограниченно возрастают(x +),то соответствующие значения функции убывают, т.е. стремятся к нулю (y 0). Если значения аргумента при x>0 убывают, т.е. стремятся к нулю (x 0),то соответствующие значения функции неограниченно возрастают (y +) X Y y = x -1″>
0 неограниченно возрастают(x +),то соответствующие значения функции убывают, т.е. стремятся к нулю (y 0). Если значения аргумента при x>0 убывают, т.е. стремятся к нулю (x 0),то соответствующие значения функции неогра» title=»3.Если значения аргумента при x>0 неограниченно возрастают(x +),то соответствующие значения функции убывают, т.е. стремятся к нулю (y 0). Если значения аргумента при x>0 убывают, т. е. стремятся к нулю (x 0),то соответствующие значения функции неогра»>
title=»3.Если значения аргумента при x>0 неограниченно возрастают(x +),то соответствующие значения функции убывают, т.е. стремятся к нулю (y 0). Если значения аргумента при x>0 убывают, т.е. стремятся к нулю (x 0),то соответствующие значения функции неогра»>
е. стремятся к нулю (x 0),то соответствующие значения функции неогра»>
title=»3.Если значения аргумента при x>0 неограниченно возрастают(x +),то соответствующие значения функции убывают, т.е. стремятся к нулю (y 0). Если значения аргумента при x>0 убывают, т.е. стремятся к нулю (x 0),то соответствующие значения функции неогра»>
Степенной называется функция вида y=x n (читается как y равно х в степени n), где n – некоторое заданное число. Частными случаями степенных функций является функции вида y=x, y=x 2 , y=x 3 , y=1/x и многие другие. Расскажем подробнее о каждой из них.
Линейная функция y=x 1 (y=x)
График прямая линия, проходящая через точку (0;0) под углом 45 градусов к положительному направлению оси Ох.
График представлен ниже.
Основные свойства линейной функции:
- Функция возрастающая и определена на всей числовой оси.
- Не имеет максимального и минимального значений.
Квадратичная функция y=x 2
Графиком квадратичной функции является парабола.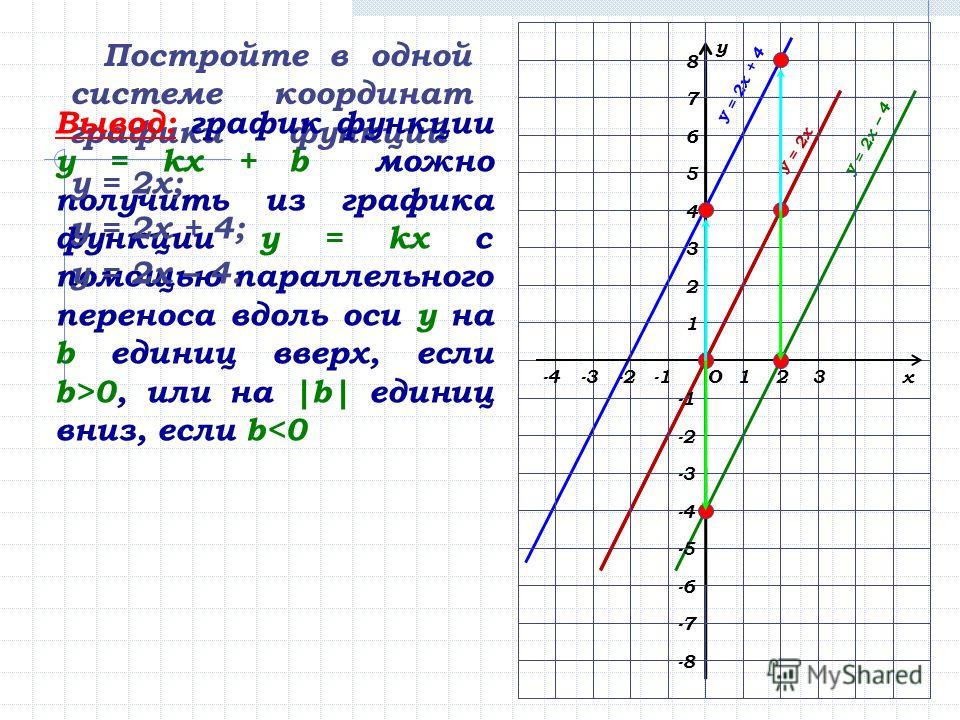
Основные свойства квадратичной функции:
- 1. При х =0, у=0, и у>0 при х0
- 2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
- 3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке }
График y x 2 3. Построение графиков онлайн. Этап актуализации знаний
Разделы: Математика
Тема: “Построение графика квадратной
функции, содержащей модуль”.
(На примере графика функции у = х 2 — 6x + 3.)
Цель.
- Исследовать расположение графика функции на координатной плоскости в зависимости от модуля.
- Развить навыки построения графика функции, содержащей модуль.
Ход урока.
1. Этап актуализации знаний.
а) Проверка домашнего задания.
Пример 1. Построить график
функции у = х 2 — 6х + 3. Найти нули функции.
Решение.
2. Координаты вершины параболы: х= — b/2а = — (-6)/2=3, у(3) = 9 – 18 + 3 = — 6, А(3; -6).
4. Нули функции: у(х) = 0, х 2 — 6х + 3 = 0, D = 36 — 4·3 = 36 – 12 = 24, D>0,
x 1,2 = (6 ± )/2 = 3 ± ; В(3 — ;0), С(3 + ;0).
График на рис.1.
Алгоритм построения графика квадратной функции.
1. Определить направление “ветвей” параболы.
2. Вычислить координаты вершины параболы.
3. Записать уравнение оси симметрии.
4. Вычислить несколько точек.
б) Рассмотрим построение графиков линейных функций, содержащих модуль:
1. у = |х|. График функции на рисунке 2.
2.у = |х| + 1. График функции на рисунке 3.
3. у = |х + 1|. График функции рисунке 4.
Вывод.
1. График функции у = |х| + 1 получается из графика функции у = |х| параллельным переносом на вектор {0;1}.
2. График функции у = |х + 1| получается из графика
функции у = |х| параллельным переносом на вектор
{-1;0}.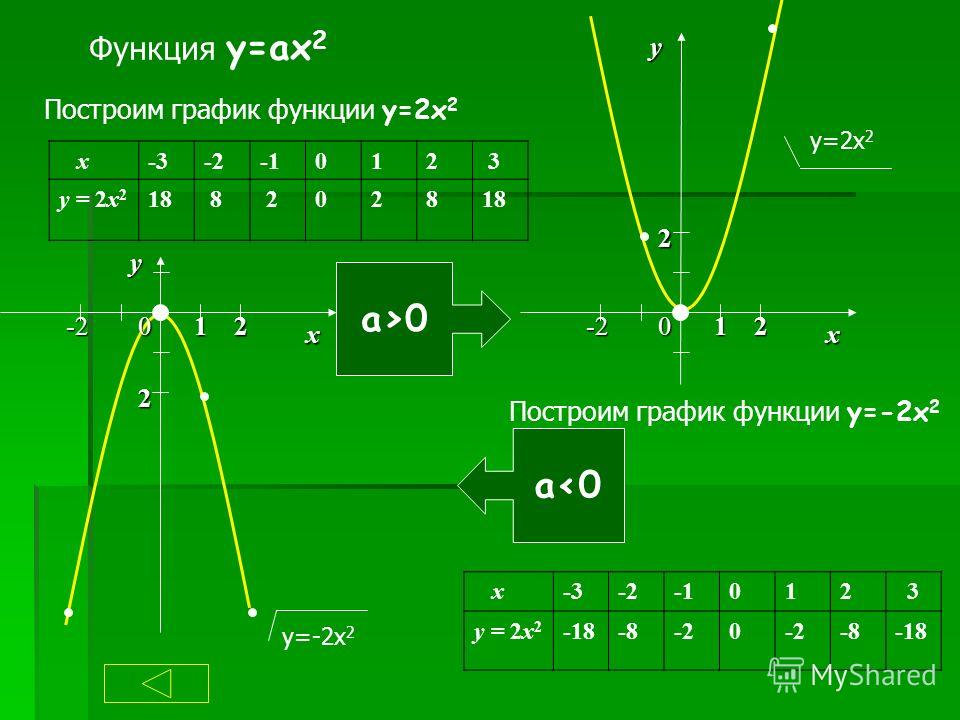
2.Опирационно-исполнительная часть.
Этап исследовательской работы. Работа в группах.
Группа 1. Построить графики функций:
а) у = х 2 — 6|x| + 3,
б) у = |х 2 — 6х + 3|.
Решение.
1.Построить график функции у = х 2 -6х+3.
2. Отобразить его симметрично относительно оси Оу.
График на рисунке 5.
б) 1. Построить график функции у = х 2 — 6х + 3.
2. Отобразить его симметрично относительно оси Ох.
График функции на рисунке 6.
Вывод.
1. График функции у = f(|x|) получается из графика функции у = f(x), отображением относительно оси Оу.
2. График функции у = |f(x)| получается из графика функции у = f(x), отображением относительно оси Ох.
Группа 2.Построить графики функций:
а) у = |x 2 — 6|x| + 3|;
б) y = |x 2 — 6x + 3| — 3.
Решение.
1. График функции у = х 2 + 6x + 3 отображаем
относительно оси Оу, получается график функции у
= х 2 — 6|x| + 3.
2. Полученный график отображаем симметрично относительно оси Ох.
График функции на рисунке 7.
Вывод.
График функции y = |f (|x|)| получается из графика функции у = f(х), последовательным отображением относительно осей координат.
1. График функции у = х 2 — 6х + 3 отображаем относительно оси Ох.
2. Полученный график переносим на вектор {0;-3}.
График функции на рисунке 8.
Вывод. График функции у = |f(x)| + a получается из графика функции у = |f(x)| параллельным переносом на вектор {0,a}.
Группа 3.Построить график функции:
а) у = |x|(х — 6) + 3; б) у = х|x — 6| + 3.
Решение.
а) у = |x| (x — 6) + 3, имеем совокупность систем:
Строим график функции у = -х 2 + 6x + 3 при х
График функции на рисунке 9.
б) у = х |х — 6| + 3, имеем совокупность систем:
Строим график функции у = — х 2 + 6х + 3 при х 6.
2.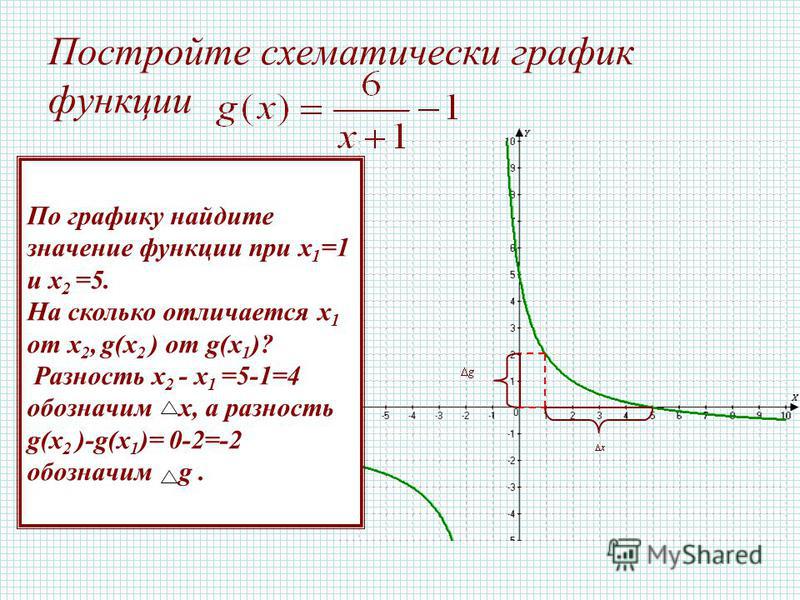 Координаты вершины параболы: х = — b/2a = 3, у(3) =1 2,
А(3;12).
Координаты вершины параболы: х = — b/2a = 3, у(3) =1 2,
А(3;12).
3. Уравнение оси симметрии: х = 3.
4. Несколько точек: у(2) = 11, у(1) = 3; у(-1) = — 4.
Строим график функции у = х 2 — 6х + 3 при х = 7 у(7) = 10.
График на рис.10.
Вывод. При решении данной группы уравнений необходимо рассматривать нули модулей, содержащихся в каждом из уравнений. Затем строить график функции на каждом из полученных промежутков.
(При построении графиков данных функций каждая группа исследовала влияние модуля на вид графика функции и сделала соответствующие заключения.)
Получили сводную таблицу для графиков функций, содержащих модуль.
Таблица построения графиков функций, содержащих модуль.
Группа 4.
Построить график функции:
а) у = х 2 — 5x + |x — 3|;
б) у = |x 2 — 5x| + x — 3.
Решение.
а) у = х 2 — 5х + |х — 3|, переходим к совокупности систем:
Строим график функции у = х 2 -6х + 3 при х 3,
затем график функции у = х 2 — 4х — 3 при х > 3 по
точкам у(4) = -3, у(5) = 2, у(6) = 9.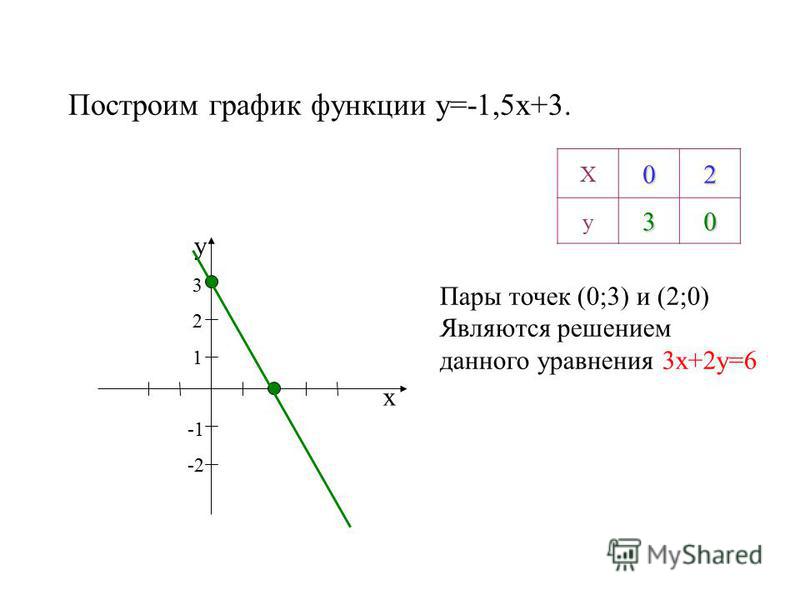
График функции на рисунке 11.
б) у = |х 2 — 5х| + х — 3, переходим к совокупности систем:
Строим каждый график на соответствующем интервале.
График функции на рисунке 12.
Вывод.
Выяснили влияние модуля в каждом слагаемом на вид графика.
Самостоятельная работа.
Построить график функции:
а) у = |х 2 — 5х + |x — 3||,
б) у= ||x 2 — 5x| + х — 3|.
Решение.
Предыдущие графики отображаем относительно оси Ох.
Группа.5
Построить график функции: у =| х — 2| (|x| — 3) — 3.
Решение.
Рассмотрим нули двух модулей: x = 0, х – 2 = 0. Получим интервалы постоянного знака.
Имеем совокупность систем уравнений:
Строим график на каждом из интервалов.
График на рисунке 15.
Вывод. Два модуля в предложенных
уравнениях существенно усложнили построение
общего графика, состоящего из трех отдельных
графиков. 2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
Квадратичная функция
Рис 1. Общий вид параболы
Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).
Основные свойства квадратичной функции
1. При х =0, у=0, и у>0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.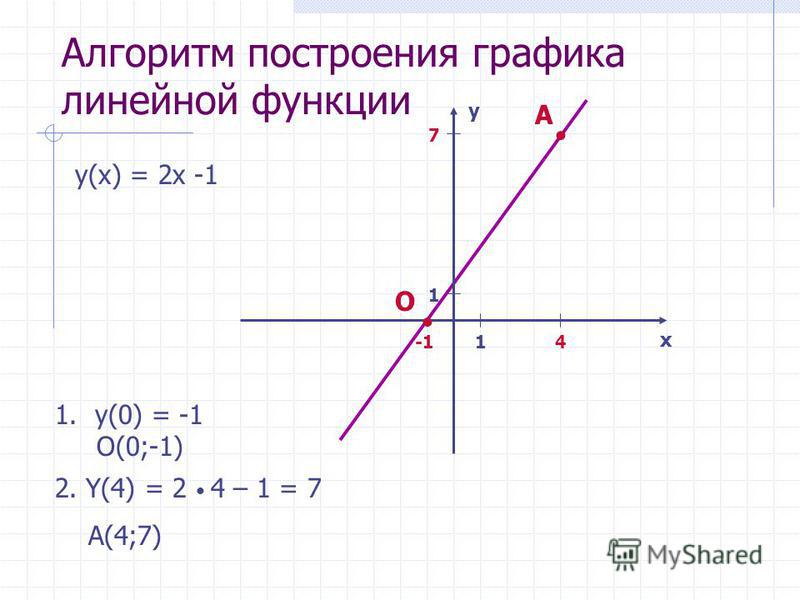
3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке }
Графические функции абсолютного значения | Purplemath
Curvy Lines
Purplemath
Получение абсолютного значения отрицательного числа делает его положительным. По этой причине графики функций абсолютного значения, как правило, не совсем похожи на графики линейных функций, которые вы уже изучали. Однако из-за того, как ведут себя абсолютные значения, важно включать отрицательные входные данные в вашу T-диаграмму при графическом отображении функций абсолютных значений. Если вы не выберете x -значения, которые помещают отрицательные значения в абсолютное значение, вы, как правило, вводите себя в заблуждение относительно того, как выглядит график.
Например, предположим, что ваш класс проходит следующий тест:
Содержание продолжается ниже
MathHelp.com
График
г = | x + 2 |
Один из других студентов делает то, что обычно делают: он выбирает только положительные значения x для своей T-диаграммы:
Затем он наносит свои точки:
Эти точки хороши, насколько они идут, но их недостаточно; они не дают точного представления о том, как должен выглядеть график.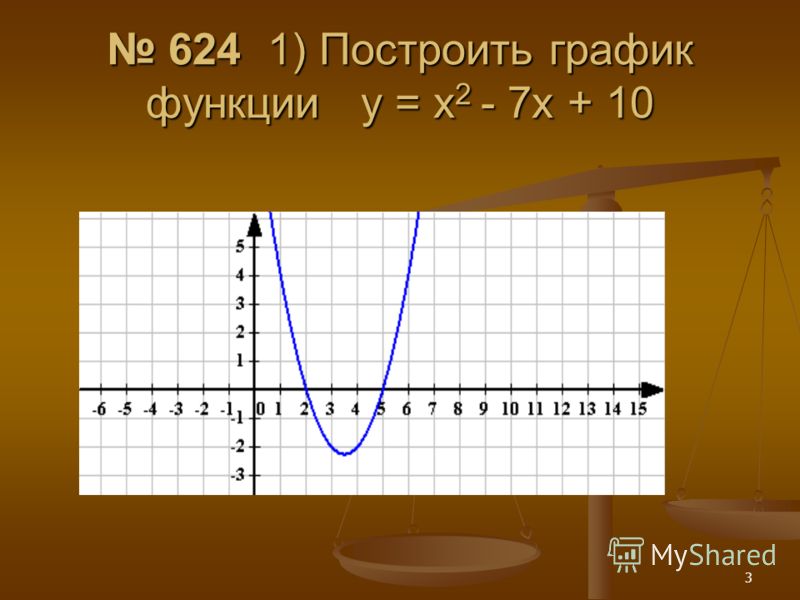 В частности, они не включают никаких «минусовых» входных данных, так что легко забыть, что эти столбцы абсолютных значений означает что-то. В результате учащийся забывает учитывать эти столбцы и рисует ошибочный график:
В частности, они не включают никаких «минусовых» входных данных, так что легко забыть, что эти столбцы абсолютных значений означает что-то. В результате учащийся забывает учитывать эти столбцы и рисует ошибочный график:
НЕПРАВИЛЬНЫЙ ОТВЕТ!
Аааааа… он только что завалил тест.
Но ты осторожнее. Вы помните, что графики абсолютных значений включают абсолютные значения, и что абсолютные значения влияют на «минусовые» входные данные. Таким образом, вы выбираете x значений, которые помещают «минус» в абсолютное значение, и вы выбираете еще несколько точек. Ваша Т-диаграмма выглядит примерно так:
Затем вы наносите точки:
…и, наконец, соединяете точки:
У вас есть правильный график:
Правильный ответ!
Ааааа… ты только что прошел тест. Хорошая работа!
Хотя графики абсолютных значений обычно выглядят так, как показано выше, с «локтем» посередине, это не всегда так.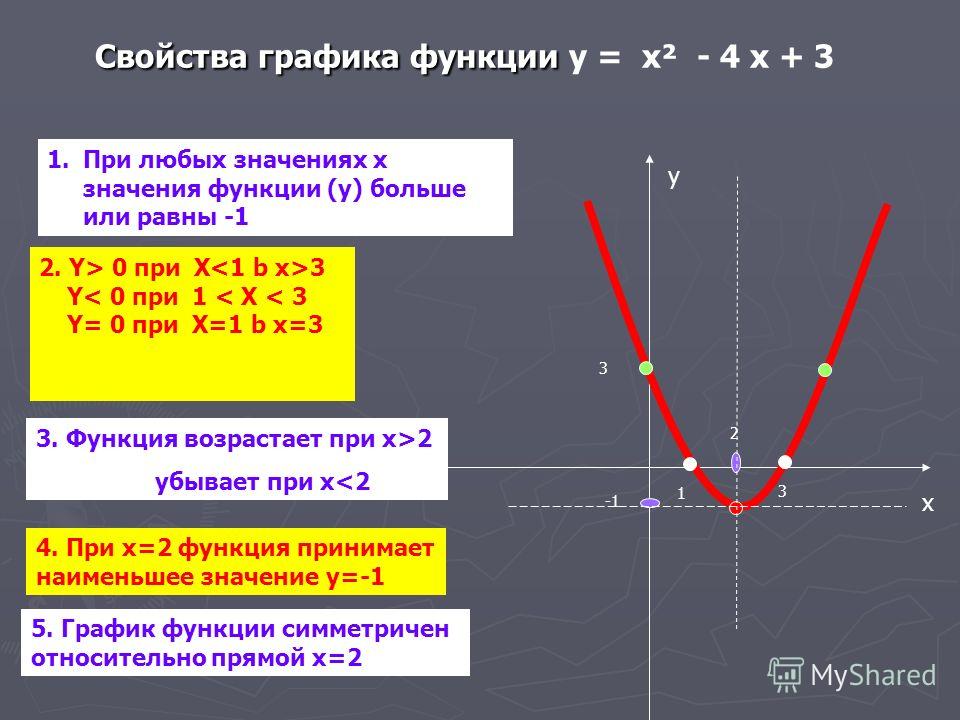 Однако, если вы видите график с таким изгибом, вы должны ожидать, что уравнение графика, вероятно, включает абсолютное значение. Во всех случаях вы должны позаботиться о том, чтобы выбрать хороший диапазон из x -значения, потому что три x -значения рядом друг с другом почти наверняка не дадут вам достаточно информации, чтобы нарисовать правильное изображение.
Однако, если вы видите график с таким изгибом, вы должны ожидать, что уравнение графика, вероятно, включает абсолютное значение. Во всех случаях вы должны позаботиться о том, чтобы выбрать хороший диапазон из x -значения, потому что три x -значения рядом друг с другом почти наверняка не дадут вам достаточно информации, чтобы нарисовать правильное изображение.
Примечание. Полосы абсолютных значений позволяют оценивать введенные значения как всегда неотрицательные (т. е. положительные или нулевые). В результате буква «V» на приведенном выше графике возникла там, где знак внутри был равен нулю. Когда x было меньше -2, выражение x + 2 было меньше нуля, а столбцы абсолютных значений отображали эти «минусовые» значения ниже x -ось над ним. Когда x равняется -2, тогда аргумент (то есть выражение внутри столбцов) равняется нулю. Для всех x -значений справа от -2 аргумент был положительным, поэтому столбцы абсолютных значений ничего не изменили.
Другими словами, графически столбцы абсолютных значений взяли этот график:
…и перевернули «минусовую» часть (выделенную зеленым на графике) из-под оси x вверх. Заметив, где аргумент столбцов абсолютного значения будет равен нулю, можно убедиться, что вы правильно строите график.
График
y = | x | + 2
Эта функция практически аналогична предыдущей.
Однако аргумент предыдущего выражения абсолютного значения был x + 2. В этом случае только x находится внутри столбцов абсолютного значения. Этот аргумент будет равен нулю, если x = 0, поэтому я должен ожидать появления изгиба в этой области. Кроме того, поскольку «плюс два» находится за пределами столбцов абсолютного значения, я ожидаю, что мой график будет выглядеть как обычный график абсолютного значения (представляющий собой букву «V» с изгибом в начале координат), но сдвинутый вверх на две единицы.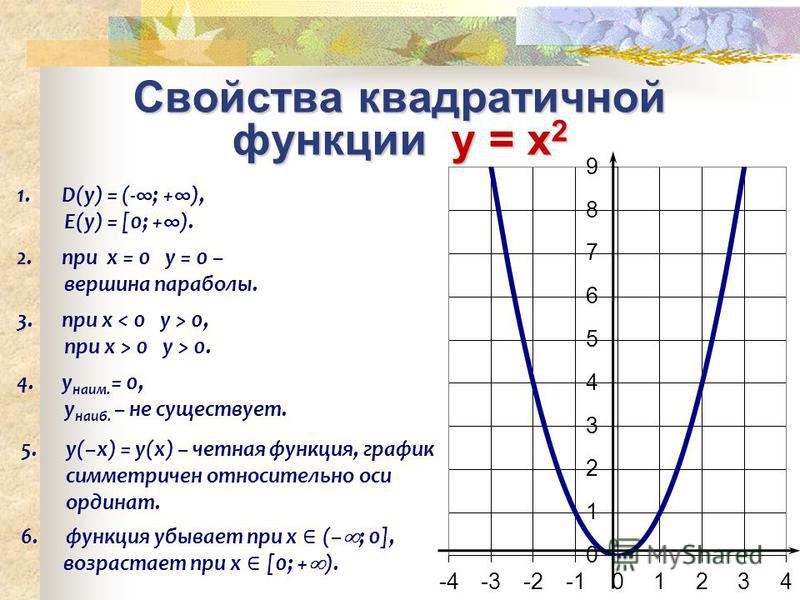 .
.
Сначала я заполню свою Т-диаграмму, обязательно выбирая отрицательные значения x по мере продвижения:
Затем я нарисую точки и заполню график:
Потому что абсолютный гистограммы всегда отображают неотрицательные значения, может возникнуть соблазн предположить, что графики абсолютных значений не могут опускаться ниже оси x . Но они могут:
Эта функция является своего рода противоположностью первой функции (выше), потому что в выражении абсолютного значения в правой части уравнения есть «минус». Из-за этого «минуса» все положительные значения, представленные столбцами абсолютных значений, будут заменены отрицательными значениями. Другими словами, я должен ожидать, что колено этого графика будет находиться в точке (−2, 0), как и на первом графике выше, но остальная часть графика будет перевернута вверх дном и окажется ниже 9.0007 x — ось. — ось. Графики могут пересекаться:
Моя T-диаграмма:
…и мой график:
URL: https://www.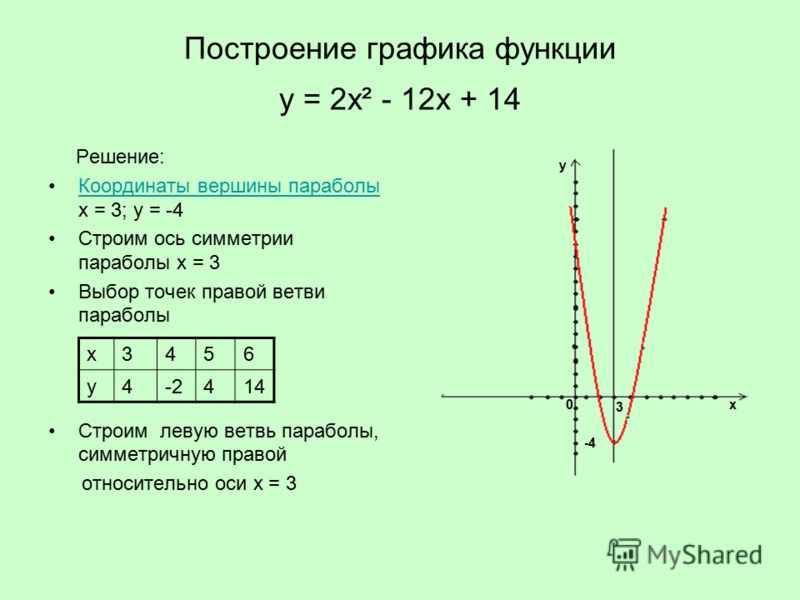 purplemath.com/modules/graphabs.htm
purplemath.com/modules/graphabs.htm
Page 2 gnuplot Отображение данных с помощью gnuplot
Это руководство предназначено в качестве дополнения к информации содержится на веб-сайте физического факультета: Графики и подгонка данных и данных построения с калейдографом. Он показывает, как выполнять те же функции описано в этих руководствах с использованием gnuplot, управляемого из командной строки программа для построения графиков, обычно доступная на машинах Unix (хотя и доступная и для других платформ). Возможно, вам будет полезно ознакомиться с другие учебники, а также; этот предназначен, чтобы следовать за ними довольно близко.
Приведенные инструкции и примеры соответствуют работающей версии 3.7 под Linux, но результаты везде должны быть одинаковыми. Если ты однако, используя более старую версию, вы можете найти несколько более расширенные функции отсутствуют.
gnuplot кажется почти полной противоположностью Kaleidagraph:
Учебник Kaleidagraph называет Kaleidagraph «простым в использовании, хотя и несколько
ограниченная графическая программа». gnuplot не так уж и прост в использовании,
хотя и чрезвычайно мощная программа для построения графиков из командной строки.
gnuplot не так уж и прост в использовании,
хотя и чрезвычайно мощная программа для построения графиков из командной строки.
Запустить gnuplot очень просто: из командной строки в любой системе введите гнуплот. Это можно сделать даже через телнет или ssh. подключение и просматривать графики в текстовом режиме! Для лучших результатов, однако вам следует запускать gnuplot из X Window, чтобы вы могли видеть лучшие предварительные просмотры ваших участков.
Все наборы данных, которые вы используете в gnuplot, должны быть введены в текстовый файл. первый. В каждой строке должна быть одна точка данных. Каждая точка данных будет состоят из нескольких чисел: независимая переменная, зависимая переменная и, возможно, планки погрешностей. Каждое из этих полей должно быть разделены табуляцией.
На самом деле в каждой строке может быть указано любое количество полей; Это
полезно, если у вас есть несколько измерений для каждой точки данных, для
пример. Для получения информации о том, как получить доступ к этому дополнительному
информацию на ваших графиках см. (fixme: добавить раздел) ниже.
(fixme: добавить раздел) ниже.
Вы можете включить в файл любую дополнительную информацию, такую как описание данных, заголовки для каждого из столбцов данных и т. д. on, если каждая такая строка начинается с символа комментария, #.
9. Так после запустив gnuplot, в приглашении gnuplot> вы должны тип:график exp(-x**2/2)
Обычно вам нужно немного больше контроля над сюжетом, по крайней мере указание диапазонов для осей x и y. Вы можете указать их в [минимум:максимум] перед функцией. Сначала укажите диапазон x, затем диапазон y. Вы можете оставить y диапазон, или оба. Мы можем изменить нашу предыдущую команду сюжета на:
.график [-4:4] exp(-x**2/2)
Здесь диапазон y будет определен автоматически.
Дополнительные функции построения графиков
Если вы хотите построить более одной функции, просто перечислите все функции, разделенные запятыми. Например:
график [-4:4] exp(-x**2/2), x**2/16
Вы также можете переименовать независимую переменную, если хотите. Это
сделано в сочетании с указанием диапазона графика:
Это
сделано в сочетании с указанием диапазона графика:
график [t=-4:4] exp(-t**2/2), t**2/16
Определение функций
Иногда бывает удобно определить функцию, чтобы она не нужно каждый раз перепечатывать. Это легко сделать. Давайте создадим функцию f(x), чтобы представить нашу кривую нормального распределения, а затем использовать ее в сюжет:
f(x) = ехр(-x**2/2) график [t=-4:4] f(t), t**2 / 16
Названия сюжетов, метки и легенды
Возможно, вы заметили, что при создании сюжетов легенда был автоматически создан в правом верхнем углу графика. По по умолчанию имя каждой кривой — это просто введенная вами формула. может дать им другие имена, используя название атрибут. Просто следуйте формуле для функции с заголовком «Заголовок». Мы можем изменить наши предыдущие команда на:
сюжет [t=-4:4] f(t) заголовок "Гаустическая кривая", t**2 / 16 заголовок "Парабола"
Обратите внимание, что запятые никогда не используются, кроме как для разделения
функции.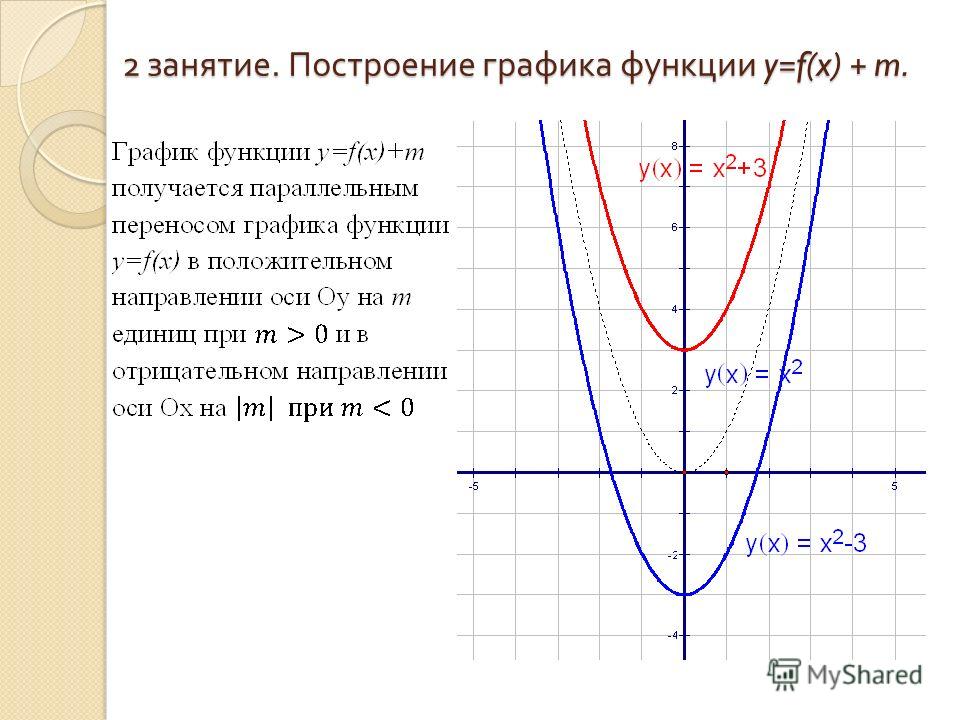 Если вы хотите, чтобы кривая не отображалась в легенде, установите
его название на «».
Если вы хотите, чтобы кривая не отображалась в легенде, установите
его название на «».
Мы также можем добавить заголовок к нашему графику и несколько меток на осях. Используется команда set. Вот пример:
установить заголовок «Некоторые образцы участков» установить xlabel "Независимая переменная (без единиц измерения)" установить ylabel "Зависимая переменная (без единиц измерения)"
Эти изменения не действуют, пока вы не перерисуете график. Этот можно сделать, снова введя команду plot, но если сам график не меняется, достаточно набрать:
переделывать
, чтобы перерисовать последние заданные функции.
Другие приятные мелочи
Часто полезно добавить на график сетку, чтобы было легче видеть где функции и данные попадают на график. Для этого введите
установить сетку
После того, как вы научились строить графики функций, пришло время научиться
данные графика. Синтаксис почти такой же, за исключением того, что вместо
при указании функции необходимо указать имя файла, содержащего
данные для построения, заключенные в двойные кавычки.
Во-первых, так как мы играли с графиками выше, мы очистим метки на осях и другие настройки:
перезагрузить
Вы также можете выйти из gnuplot и перезапустить его для того же эффекта. В настоящее время, мы построим наши образцы данных. Избавимся от записи в легенде для наши точки данных, используя заголовок «», а также настроить топоров на участке:
установить заголовок «Данные Кавендиша» установить xlabel "Время (с)" установить ylabel "Угол (мрад)" установить сетку сюжет "cavendish.data" заголовок ""
При построении данных обычно нет необходимости указывать диапазоны для независимые и зависимые переменные, так как они могут быть вычислены со входа. При необходимости, конечно, всегда можно их подарить.
Включая планки погрешностей
Поскольку наши входные данные содержат погрешности для измеренного (зависимое) количество, мы можем создать y планок погрешностей. Еще раз, gnuplot делает это легко:
сюжет "cavendish.data" заголовок "" с yerrorbars
Можно построить x баров ошибок, используя xerrorbars, или и то, и другое x и y errorbars с помощью xyerrorbars. Когда обе ошибки x и y используются бары, должно быть четыре столбца, и должно быть x баров ошибок. быть указан первым в файле данных. Возможны другие варианты; видеть интерактивную справку для получения дополнительной информации.
Учтите, что gnuplot может быть очень придирчив к тому, какой порядок вы отдаете. модификаторы к графикам. Если бы вместо этого вы набрали
график "cavendish.data" с заголовком yerrorbars ""
Вы получите довольно странное сообщение об ошибке: неопределенная переменная: заглавие. Если вы видите подобные сообщения об ошибках, проверьте порядок в ваши сюжетные команды. Если вы не уверены, введите help plot привести вас в порядок.
Ни одна программа для построения графиков не была бы полной без возможности
данные в кривую. Для эксперимента Кавендиша нам нужно
данные к синусоидальной кривой с экспоненциальным затуханием. gnuplot поддерживает
эти нелинейные кривые подходят и могут даже принимать экспериментальные
во внимание неопределенность точек данных.
gnuplot поддерживает
эти нелинейные кривые подходят и могут даже принимать экспериментальные
во внимание неопределенность точек данных.
Во-первых, необходимо определить форму функции, которую мы попробуем подходит для. Определите это так же, как и любую другую функцию в gnuplot, но оставить переменные для подгонки параметров. Мы будем использовать
theta(t) = theta0 + a * exp(-t / tau) * sin(2 * pi * t / T + phi)
Различные параметры установки:
- а: амплитуда колебаний
- тау: период колебаний
- фи: начальная фаза
- T: время экспоненциального затухания
- тета0: сдвиг от положения равновесия
Для такой нелинейной кривой, как эта, часто необходимо предоставить начальное предположение для каждого из подходящих параметров, или попытка установки может быть неудачной. Для простых уравнений, таких как многочлены, в этом не будет необходимости (но никогда не помешает).
а = 40 тау = 15 фи = -0,5 Т = 15 тета0 = 10
Наконец, мы выполним настоящую аппроксимацию кривой. Синтаксис для этого:
Синтаксис для этого:
подогнать тета(х) "cavendish.data" с использованием 1:2:3 через а, тау, фи, Т, тета0
Вот как интерпретируется команда: fit сообщает gnuplot мы делаем кривую подгонку. Следующая часть, тета(х), должна быть функция, которую мы используем, чтобы соответствовать данным. Здесь мы должны использовать x как независимая переменная. Следующая часть, «cavendish.data», должна быть файл данных, содержащий данные, которые мы хотим подогнать. Использование 1:2:3 указывает gnuplot взять столбцы 1, 2 и 3 из файла данных и использовать их как x, y и неопределенности соответственно. Если эта часть останется out, то экспериментальные погрешности не будут использоваться для кривой поместиться. См. ниже более подробное обсуждение чрезвычайно мощного квалификатора using. Наконец, мы должны сообщить gnuplot какие переменные он может настроить, чтобы лучше соответствовать. Для этого случая мы говорим через а, тау, фи, Т, тета0.
gnuplot будет производить вывод по мере выполнения подгонки, и если Подгонка прошла успешно, вы должны увидеть что-то вроде этого:
степеней свободы (ndf): 34
Среднеквадратичное значение невязок (стандартное соответствие) = sqrt (WSSR/ndf): 1,07102
дисперсия остатков (приведенный хи-квадрат) = WSSR/ndf: 1,14708
Окончательный набор параметров Асимптотическая стандартная ошибка
======================= ===========================
а = 44,5389 +/- 2,127 (4,776%)
тау = 57,5667 +/- 8,132 (14,13%)
фи = -0,377254 +/- 0,04235 (11,22%)
Т = 13,1026 +/- 0,06465 (0,4934%)
тета0 = 2,45704 +/- 0,6081 (24,75%)
корреляционная матрица подгоночных параметров:
тау фи Т тета0
1. 000
тау -0,844 1,000
фи -0,100 0,088 1,000
Т -0,072 0,072 0,806 1,000
тета0 -0,166 0,127 -0,182 -0,166 1,000
000
тау -0,844 1,000
фи -0,100 0,088 1,000
Т -0,072 0,072 0,806 1,000
тета0 -0,166 0,127 -0,182 -0,166 1,000
Важные величины, на которые следует обратить внимание, — приведенный хи-квадрат (дисперсия остатки), который в данном случае равен 1,15, и значения для каждого из параметры подгонки. Каждый параметр подгонки также имеет неопределенность перечислено. Корреляционную матрицу в конце обычно можно игнорировать.
gnuplot также сохранил параметры подгонки в переменных, поэтому построить график с соответствующей кривой наилучшего соответствия так же просто, как:
график "cavendish.data" заголовок "" с yerrorbars, тета (x) заголовок "Best-Fit Curve"
Использование Использование
Квалификатор using, использованный в приведенной выше команде настройки, является чрезвычайно мощный инструмент в gnuplot. С ним вы можете тренироваться почти безграничный контроль над вашими данными по мере их построения.
gnuplot обычно ожидает определенное количество столбцов данных при использовании
файл данных (будь то для построения графика или подгонки). Обычно только два
используются столбцы: независимая переменная и зависимая переменная.
С планками погрешностей можно использовать еще один или два столбца. Обычно эти
столбцы извлекаются из файла данных напрямую. Иногда это
необходимо осуществлять немного больше контроля. Вот где
использование приходит.
Обычно только два
используются столбцы: независимая переменная и зависимая переменная.
С планками погрешностей можно использовать еще один или два столбца. Обычно эти
столбцы извлекаются из файла данных напрямую. Иногда это
необходимо осуществлять немного больше контроля. Вот где
использование приходит.
Допустим, вам нужно поменять местами два столбца данных, так как зависимый сначала идет переменная, затем независимая переменная в данных файл. Вы можете создать этот график с помощью команды:
построить «обратные.данные» с использованием 2: 1
Команда using ожидает несколько значений, по одному для каждого требуемый столбец данных, где каждое значение отделяется двоеточием. Если это просто число, gnuplot возьмет этот фрагмент данных из указанный столбец в файле данных. В этом случае мы говорим gnuplot взять независимая переменная из столбца 2 и зависимая переменная из столбец 1.
Предыдущий пример был немного надуманным. Но есть очень распространенный
случай, когда используется использование: когда есть несколько наборов данных в
вход. Предположим, у вас есть файл данных с тремя столбцами:
независимая переменная и две зависимые переменные. Вы хотите построить
обе зависимые переменные как отдельный набор точек. Вы можете использовать:
Предположим, у вас есть файл данных с тремя столбцами:
независимая переменная и две зависимые переменные. Вы хотите построить
обе зависимые переменные как отдельный набор точек. Вы можете использовать:
график «double.data» с использованием заголовка 1: 2 «Серия 1», «double.data» с использованием заголовка 1: 3 «Серия 2»
В приведенном выше примере подгонки, указав использование 1:2:3, мы заставляли команду fit принимать три столбца в качестве входных данных вместо обычные два (чтобы включить информацию об ошибке), но мы не выполняли любое изменение порядка на них.
Это все еще только царапает поверхность того, что можно использовать делать. Вместо указания номера столбца вы также можете указать полный выражение, которое должно быть заключено в круглые скобки. В рамках этого выражение, значения из столбцов могут быть доступны как $1, 2 доллара, 3 доллара и т. д. Например, если мы хотим построить график натуральный логарифм нашей зависимой переменной, мы могли бы использовать:
построить «log.data», используя 1: (log ($ 2))
Обратите внимание, что как часть квалификатора using ($2) точно эквивалентно 2,
Другой пример см. в следующем разделе: построение графика остатков.
Построение остатков
Чтобы понять этот раздел, вам необходимо понять раздел «Использование using» выше.
Во-первых, мы создадим график разницы между каждой точкой данных и подобранная кривая:
построить "cavendish.data" с использованием 1:(тета($1) - $2):3 заголовок "Остатки" с yerrorbars
Возможно, уместно небольшое объяснение оператора using.
Мы создаем график с y планками погрешностей, поэтому нам нужны три столбца данных.
Следовательно, квалификатор using состоит из трех частей, разделенных
двоеточия. Первая, 1, говорит первая часть, независимая
переменная, это просто первый столбец из входного файла. Секунда
часть представляет собой выражение: мы вычислим разницу между нашей функцией
(тета), оценивается по значению независимой переменной
($1 — первый столбец файла данных) и измеренное значение
($2 — второй столбец файла данных или зависимая переменная) для
эта точка. Третий столбец, 3, просто говорит использовать
существующая неопределенность, хранящаяся в столбце 3 файла данных без
модификация.
Третий столбец, 3, просто говорит использовать
существующая неопределенность, хранящаяся в столбце 3 файла данных без
модификация.
Было бы еще лучше, если бы мы могли положить остатки на тот же график в виде подогнанной кривой. Чтобы это выглядело хорошо, мы будем использовать другой масштаб для остатков, чтобы их можно было отделить от остальная часть графика. gnuplot позволяет использовать два разных масштаба для по каждой оси: существуют независимые шкалы x и x2 для осей x, y и y2 шкалы для оси Y и т. д.
Существует другой синтаксис для определения диапазонов для каждой из осей, что необходимо для использования более чем одной шкалы одновременно. Первый, давайте сдвинем график наших данных и кривой немного вверх, чтобы сделать номер.
установить yrange [-80:60] график "cavendish.data" заголовок "" с yerrorbars, тета (x) заголовок ""
Это похоже на указание диапазона как часть команды построения графика, но
настройки будут сохраняться до тех пор, пока они не будут переопределены, и мы можем
укажите y-диапазон без x-диапазона.
Теперь мы создадим вторую шкалу для оси Y справа. сторона. Это можно сделать с помощью:
установить диапазон y2 [-20:120] установить границу y2tics
Команда set y2tics border указывает gnuplot отображать это масштаб на границе участка. Без него новая шкала была бы установлен, но он не будет отображаться в правой части графика.
Теперь пришло время добавить наши остатки. Добавляем их в команду plot, и укажите, что они должны использовать новую шкалу Y. Они будут использовать та же шкала x, что и раньше:
график "cavendish.data" заголовок "" с yerrorbars, theta(x) title "", "cavendish.data" с использованием 1:(theta($1) - $2):3 оси x1y2 заголовок "" с yerrorbars
Здесь оси x1y2 означают использование обычной оси x и новой ось y, которую мы только что определили.
Наконец, для дополнительного штриха, давайте нарисуем ось X для остатки:
установить x2zeroaxis lt -1 установить y2label "Остатки" переделывать
Здесь lt -1 означает «тип строки -1», где -1 — стиль
обычно используется для границ участка.
Если вы следовали всему руководству, теперь вам следует иметь окно графика, которое выглядит примерно так:
gnuplot не зависит от устройств: при создании графиков он может не заботится о том, производит ли он предварительный просмотр на дисплее X Window, Версия ASCII-art для терминала или любая другая форма вывода. Сюжет все команды будут работать одинаково. Получив свой сюжет так, как вы как это, однако, вы хотите, чтобы сохранить его или распечатать его. Для этого вы захотите изменить формат вывода, что можно сделать с помощью команда установки срока.
При работе в X тип терминала по умолчанию — x11. Если, после сохранения вывода в другом месте вы хотите снова просмотреть вывод в X, вы хотите ввести
установить срок x11
Если вы работаете через telnet или где графика недоступна, вы можете ввести
установить термин немой
, чтобы выбрать немой терминал. Хотя это и некрасиво, вы часто можете получить
представление о том, как выглядит ваш сюжет с этим. Данные Кавендиша выглядят так
это на немом терминале:
Данные Кавендиша выглядят так
это на немом терминале:
Кавендиш Данные
Угол (мрад) Остатки
60 ++------+--------+-------+--------+-------+------ --+-------+-------++120
+ * *+ + + + + + + +
| А#А# * : : : : : : |
40 ++...#..#А.А......#*#...................... ....*.........++100
| A : #* : : A AA## : : *#A#** A : |
20 ++.#......##.............А#*..*.А#..............*А. ..АА.*..........++80
| * : # : * * А : #А : #* : |
|#A : A : #: # * : A# : #* : |
0 +#...........#.........А...........#А........#... ........А#........++60
*# : A : *# : : # : A# : *# |
-20 A+............**....A#A..............*#...A#...... .........А#**#А..++40
| : A#: *# : : A#A#A* : : AA * |
| : #A#A : : * : : : |
-40++.............*.*............................ ...................++20
| : : : $ : $ : : $ $ $$ |
-60 B+$-$--$-B--B-$$-B-B--BB-$-B-BB-B---$B-$-$$-$-$-BB-$-B ---$-B-BB-B--++0
$ B BB B: $ $ $ BB $ $ B $ B $ B B B BB B B $ $ B B $ B : $ |
+ $ + В + $ + + $ + + В + +
-80 ++------+--$-----+-------+--------+-------+----- ---+----$--+-------++-20
0 5 10 15 20 25 30 35 40
Время (с)
Линейные диаграммы в Python
питон > Основные диаграммы > Линейные графики
Предложить редактирование этой страницы Как сделать линейные диаграммы в Python с помощью Plotly. Примеры создания и оформления линейных диаграмм в Python с помощью Plotly.
Примеры создания и оформления линейных диаграмм в Python с помощью Plotly.
Впервые в Plotly?
Plotly — бесплатная графическая библиотека с открытым исходным кодом для Python. Мы рекомендуем вам прочитать наше руководство по началу работы, чтобы получить последние инструкции по установке или обновлению, а затем перейти к нашим учебным пособиям по основам Plotly или погрузиться прямо в некоторые учебные пособия по базовым диаграммам.
Линейные графики с plotly.express¶
Plotly Express — это простой в использовании высокоуровневый интерфейс к Plotly, который работает с различными типами данных и создает простые в стилизации фигуры. С px.line , каждая точка данных представлена как вершина (расположение которой указано столбцами x и y ) полилинии метки в 2D-пространстве.
Дополнительные примеры линейных графиков см. в записной книжке с линиями и рассеянием.
В [1]:
импортировать plotly.express как px df = px.data.gapminder().query("country=='Канада'") fig = px.line(df, x="year", y="lifeExp", title='Ожидаемая продолжительность жизни в Канаде') рис.шоу()
Линейные графики с кодировкой цвета столбца¶
В [2]:
импортируйте plotly.express как px.
df = px.data.gapminder().query("континент=='Океания'")
fig = px.line(df, x="year", y="lifeExp", color='country')
рис.шоу()
Линейные диаграммы в Dash¶
Dash — лучший способ создавать аналитические приложения на Python с использованием рисунков Plotly. Чтобы запустить приложение ниже, запустите pip install dash , нажмите «Загрузить», чтобы получить код, и запустите python app.py .
Начните работу с официальной документации Dash и узнайте, как легко создавать и развертывать подобные приложения с помощью Dash Enterprise.
Выход[3]:
Порядок данных в линейных диаграммах¶
Графики линейных графиков реализованы в виде связанных диаграмм рассеяния (см.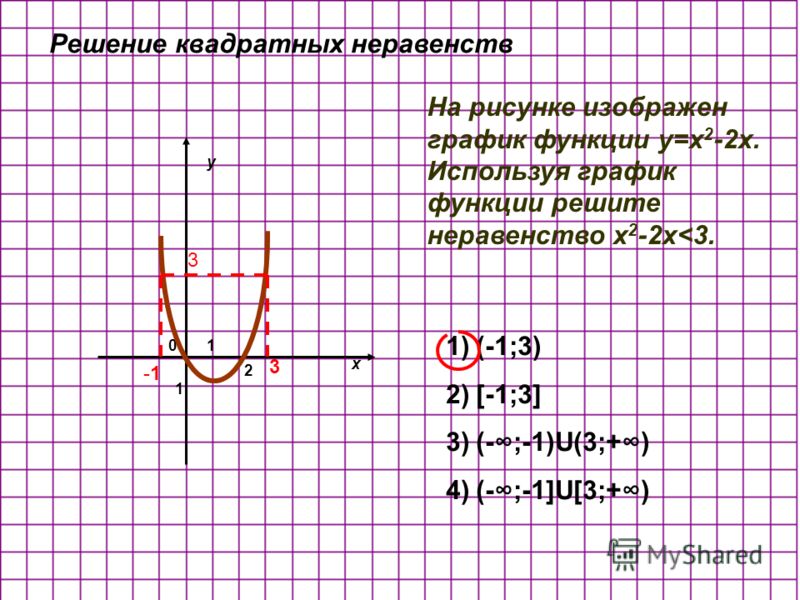 ниже), что означает, что точки отображаются и соединяются линиями в том порядке, в котором они предоставлены, без автоматического изменения порядка .
ниже), что означает, что точки отображаются и соединяются линиями в том порядке, в котором они предоставлены, без автоматического изменения порядка .
Это позволяет создавать диаграммы, подобные приведенной ниже, но также означает, что может потребоваться явная сортировка данных перед их передачей в Plotly, чтобы линии не перемещались «назад» по диаграмме.
В [4]:
импортировать plotly.express как px
импортировать панд как pd
df = pd.DataFrame(dict(
х = [1, 3, 2, 4],
у = [1, 2, 3, 4]
))
fig = px.line(df, x="x", y="y", title="Несортированный ввод")
рис.шоу()
df = df.sort_values(by="x")
fig = px.line(df, x="x", y="y", title="Sorted Input")
рис.шоу()
Связанные диаграммы рассеяния¶
На связанной диаграмме рассеяния две непрерывные переменные нанесены друг против друга с линией, соединяющей их в некотором значимом порядке, обычно это временная переменная. На графике ниже мы показываем «траекторию» пары стран в пространстве, определяемом ВВП на душу населения и ожидаемой продолжительностью жизни. Продолжительность жизни в Ботсване
Продолжительность жизни в Ботсване
В [5]:
импортировать plotly.express как px
df = px.data.gapminder().query("страна в ['Канада', 'Ботсвана']")
fig = px.line(df, x="lifeExp", y="gdpPercap", color="country", text="year")
fig.update_traces(textposition="внизу справа")
рис.шоу()
Линейные диаграммы с маркерами¶
Аргумент markers можно установить равным True , чтобы маркеры отображались на линиях.
В [6]:
импортируйте plotly.express как px.
df = px.data.gapminder().query("континент == 'Океания'")
fig = px.line(df, x='year', y='lifeExp', color='country', markers=True)
рис.шоу()
Аргумент символа можно использовать для сопоставления поля данных с символом маркера. Доступен широкий выбор символов.
В [7]:
импортируйте plotly.express как px.
df = px.data.gapminder().query("континент == 'Океания'")
fig = px.line(df, x='year', y='lifeExp', color='country', symbol="country")
рис. шоу()
шоу()
Линейные графики на осях дат¶
Линейные графики могут быть построены с использованием декартовых осей любого типа, включая линейные, логарифмические, категориальные оси или оси дат. Линейные графики на осях дат часто называют диаграммами временных рядов.
Plotly автоматически устанавливает тип оси в формат даты, когда соответствующие данные являются либо строками даты в формате ISO, либо столбцом даты pandas или массивом datetime NumPy.
В [8]:
импортируйте plotly.express как px. df = px.data.stocks() рис = px.line(df, x='date', y="GOOG") рис.шоу()
Спарклайны с Plotly Express¶
Спарклайны — это точечные графики внутри подграфиков, с удаленными линиями сетки, осевыми линиями и делениями.
В [9]:
импортировать plotly.express как px df = px.data.stocks(indexed=True) рис. = px.line(df, facet_row="company", facet_row_spacing=0,01, высота=200, ширина=200) # скрыть и заблокировать оси fig.update_xaxes(visible=False, fixedrange=True) fig.update_yaxes(visible=False, fixedrange=True) # удалить метки фасета/подграфика fig.update_layout(аннотации=[], перезапись=Истина) # убираем остальную часть сюжета fig.update_layout( showlegend=ложь, plot_bgcolor="белый", маржа = dict (t = 10, l = 10, b = 10, r = 10) ) # отключаем модбар для такого маленького сюжета fig.show (config = dict (displayModeBar = False))
Линейный график с go.Scatter¶
Если Plotly Express не обеспечивает хорошей отправной точки, можно использовать более общий класс go.Scatter из plotly.graph_objects . Тогда как plotly.express имеет две функции scatter и line , go.Scatter можно использовать как для построения точек (мейкеров) так и линий, в зависимости от значения режима . Различные варианты go.Scatter задокументированы на его справочной странице.
Простой линейный график¶
В [10]:
импортировать plotly.graph_objects как есть импортировать numpy как np х = np.arange (10) рис = идти.Рисунок (данные = идти.Scatter (х = х, у = х ** 2)) рис.шоу()
Режимы линейного графика¶
В [11]:
импортировать plotly.graph_objects как есть
# Создать случайные данные с помощью numpy
импортировать numpy как np
np.random.seed (1)
N = 100
random_x = np.linspace(0, 1, N)
random_y0 = np.random.randn(N) + 5
random_y1 = np.random.randn(N)
random_y2 = np.random.randn(N) - 5
# Создаем трассы
рис = идти.Рисунок()
fig.add_trace(go.Scatter(x=random_x, y=random_y0,
режим = 'линии',
имя = 'линии'))
fig.add_trace(go.Scatter(x=random_x, y=random_y1,
режим='линии+маркеры',
name='линии+маркеры'))
fig.add_trace(go.Scatter(x=random_x, y=random_y2,
режим='маркеры', имя='маркеры'))
рис.шоу()
Стилизация линейных графиков¶
В этом примере стилизуется цвет и пунктир трасс, добавляются имена трасс,
изменяет ширину линии и добавляет заголовки графиков и осей.
В [12]:
импортировать plotly.graph_objects как есть
# Добавить данные
месяц = ['январь', 'февраль', 'март', 'апрель', 'май', 'июнь', 'июль',
«Август», «Сентябрь», «Октябрь», «Ноябрь», «Декабрь»]
high_2000 = [32,5, 37,6, 49,9, 53,0, 69,1, 75,4, 76,5, 76,6, 70,7, 60,6, 45,1, 29,3]
low_2000 = [13,8, 22,3, 32,5, 37,2, 49.9, 56.1, 57.7, 58.3, 51.2, 42.8, 31.6, 15.9]
high_2007 = [36,5, 26,6, 43,6, 52,3, 71,5, 81,4, 80,5, 82,2, 76,0, 67,3, 46,1, 35,0]
low_2007 = [23,6, 14,0, 27,0, 36,8, 47,6, 57,7, 58,9, 61,2, 53,3, 48,5, 31,0, 23,6]
high_2014 = [28,8, 28,5, 37,0, 56,8, 69,7, 79,7, 78,5, 77,8, 74,1, 62,6, 45,3, 39,9]
low_2014 = [12,7, 14,3, 18,6, 35,5, 49,9, 58,0, 60,0, 58,6, 51,7, 45,2, 32,2, 29,1]
рис = идти.Рисунок()
# Создавать и стилизовать трассировки
fig.add_trace(go.Scatter(x=месяц, y=high_2014, name='High 2014',
строка = dict (цвет = 'огнеупорный кирпич', ширина = 4)))
fig.add_trace(go.Scatter(x=месяц, y=low_2014, name = 'Минимум 2014',
строка = dict (цвет = 'королевский синий', ширина = 4)))
fig. add_trace(go.Scatter(x=месяц, y=high_2007, name='High 2007',
строка = dict (цвет = 'огнеупорный кирпич', ширина = 4,
dash='dash') # варианты тире включают 'dash', 'dot' и 'dashdot'
))
fig.add_trace(go.Scatter(x=месяц, y=low_2007, name='Минимум 2007',
строка = dict (цвет = 'королевский синий', ширина = 4, тире = 'тире')))
fig.add_trace(go.Scatter(x=месяц, y=high_2000, name='Максимум 2000',
строка = dict (цвет = 'огнеупорный кирпич', ширина = 4, тире = 'точка')))
fig.add_trace(go.Scatter(x=месяц, y=low_2000, name='Минимум 2000',
строка = dict (цвет = 'королевский синий', ширина = 4, тире = 'точка')))
# Редактировать макет
fig.update_layout(title='Средние высокие и низкие температуры в Нью-Йорке',
xaxis_title = 'Месяц',
yaxis_title='Температура (градусы F)')
рис.шоу()
add_trace(go.Scatter(x=месяц, y=high_2007, name='High 2007',
строка = dict (цвет = 'огнеупорный кирпич', ширина = 4,
dash='dash') # варианты тире включают 'dash', 'dot' и 'dashdot'
))
fig.add_trace(go.Scatter(x=месяц, y=low_2007, name='Минимум 2007',
строка = dict (цвет = 'королевский синий', ширина = 4, тире = 'тире')))
fig.add_trace(go.Scatter(x=месяц, y=high_2000, name='Максимум 2000',
строка = dict (цвет = 'огнеупорный кирпич', ширина = 4, тире = 'точка')))
fig.add_trace(go.Scatter(x=месяц, y=low_2000, name='Минимум 2000',
строка = dict (цвет = 'королевский синий', ширина = 4, тире = 'точка')))
# Редактировать макет
fig.update_layout(title='Средние высокие и низкие температуры в Нью-Йорке',
xaxis_title = 'Месяц',
yaxis_title='Температура (градусы F)')
рис.шоу()
Connect Data Gaps¶
connectgaps определяет, отображаются ли отсутствующие значения в предоставленных данных как пробелы на графике или нет. В этом уроке мы показали, как воспользоваться этой функцией и проиллюстрировать несколько областей в mapbox.
В этом уроке мы показали, как воспользоваться этой функцией и проиллюстрировать несколько областей в mapbox.
В [13]:
импортировать plotly.graph_objects по ходу
х = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]
рис = идти.Рисунок()
fig.add_trace(go.Scatter(
х=х,
у=[10, 20, Нет, 15, 10, 5, 15, Нет, 20, 10, 10, 15, 25, 20, 10],
name = 'Нет пробелов', # Запись имени/легенды стиля с тегами html
connectgaps=True # переопределить значение по умолчанию для соединения пробелов
))
fig.add_trace(go.Scatter(
х=х,
у=[5, 15, Нет, 10, 5, 0, 10, Нет, 15, 5, 5, 10, 20, 15, 5],
имя = 'Пробелы',
))
рис.шоу()
Интерполяция с помощью линейных графиков¶
В [14]:
импортировать plotly.graph_objects по ходу
импортировать numpy как np
х = np.массив ([1, 2, 3, 4, 5])
у = np.массив ([1, 3, 2, 3, 1])
рис = идти.Рисунок()
fig.add_trace(go.Scatter(x=x, y=y, name="linear",
line_shape='линейный'))
fig.add_trace(go. Scatter(x=x, y=y + 5, name="spline",
text=["настроить гладкость линии
Scatter(x=x, y=y + 5, name="spline",
text=["настроить гладкость линии
с помощью 'сглаживания' в линейном объекте"],
hoverinfo='текст+имя',
line_shape='сплайн'))
fig.add_trace(go.Scatter(x=x, y=y + 10, name="vhv",
line_shape='вхв'))
fig.add_trace(go.Scatter(x=x, y=y + 15, name="hvh",
line_shape='hvh'))
fig.add_trace(go.Scatter(x=x, y=y + 20, name="vh",
line_shape='вх'))
fig.add_trace(go.Scatter(x=x, y=y + 25, name="hv",
line_shape='hv'))
fig.update_traces(hoverinfo='текст+имя', режим='линии+маркеры')
fig.update_layout (легенда = dict (y = 0,5, traceorder = 'обратный', font_size = 16))
рис.шоу()
Строки меток с аннотациями¶
В [15]:
import plotly.graph_objects as go импортировать numpy как np title = 'Основной источник новостей' labels = ['Телевидение', 'Газета', 'Интернет', 'Радио'] цвета = ['rgb(67,67,67)', 'rgb(115,115,115)', 'rgb(49,130,189)', 'rgb(189,189,189)'] mode_size = [8, 8, 12, 8] размер_линии = [2, 2, 4, 2] x_data = np.vstack((np.arange(2001, 2014)),)*4) y_data = np.массив([ [74, 82, 80, 74, 73, 72, 74, 70, 70, 66, 66, 69], [45, 42, 50, 46, 36, 36, 34, 35, 32, 31, 31, 28], [13, 14, 20, 24, 20, 24, 24, 40, 35, 41, 43, 50], [18, 21, 18, 21, 16, 14, 13, 18, 17, 16, 19, 23], ]) рис = идти.Рисунок() для я в диапазоне (0, 4): fig.add_trace(go.Scatter(x=x_data[i], y=y_data[i], mode='lines', имя=метки[я], линия = dict (цвет = цвета [я], ширина = размер_линии [я]), connectgaps=Верно, )) # конечные точки fig.add_trace(go.Scatter( х=[x_data[i][0], x_data[i][-1]], y=[y_data[i][0], y_data[i][-1]], режим = 'маркеры', маркер = dict (цвет = цвета [i], размер = mode_size [i]) )) fig.update_layout( ось = дикт ( шоулайн = Верно, шоугрид=ложь, showticklabels=Верно, цвет линии='rgb(204, 204, 204)', ширина линии=2, тики='снаружи', тикфонт = дикт ( семья = 'Ариал', размер=12, цвет = 'rgb (82, 82, 82)', ), ), ось = дикт ( шоугрид=ложь, нулевая линия = ложь, шоулайн=ложь, showticklabels = Ложь, ), авторазмер=ложь, маржа = дикт( авторазвертывание=ложь, л=100, г=20, т=110, ), showlegend=ложь, plot_bgcolor = 'белый' ) аннотации = [] # Добавление меток для y_trace, label, color in zip (y_data, labels, colors): # маркировка левой_стороны графика annotations.
append(dict(xref='бумага', x=0,05, y=y_trace[0], xanchor='правый', yanchor='средний', текст = метка + '{}%'.format (y_trace [0]), шрифт = dict (семья = 'Arial', размер=16), showarrow=ложь)) # маркировка правой_стороны графика annotations.append(dict(xref='бумага', x=0,95, у=у_след[11], xanchor='левый', yanchor='средний', текст = '{}%'. формат (y_trace [11]), шрифт = dict (семья = 'Arial', размер=16), showarrow=ложь)) # Заголовок annotations.append(dict(xref='бумага', yref='бумага', x=0.0, y=1.05, xanchor='левый', yanchor='нижний', text='Основной источник новостей', шрифт = dict (семья = 'Arial', размер=30, цвет = 'rgb (37,37,37)'), showarrow=ложь)) # Источник annotations.
append(dict(xref='бумага', yref='бумага', x=0,5, y=-0,1, xanchor='центр', yanchor='сверху', text='Источник: PewResearch Center & ' + «Рассказывание историй с данными», шрифт = dict (семья = 'Arial', размер=12, цвет='rgb(150,150,150)'), showarrow=ложь)) fig.update_layout(аннотации=аннотации) рис.шоу()
Закрашенные строки¶
В [16]:
импортировать plotly.graph_objects как есть импортировать numpy как np х = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] х_об = х[::-1] # Линия 1 у1 = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] y1_upper = [2, 3, 4, 5, 6, 7, 8, 9, 10, 11] y1_lower = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] y1_нижний = y1_нижний[::-1] # Строка 2 у2 = [5, 2,5, 5, 7,5, 5, 2,5, 7,5, 4,5, 5,5, 5] y2_upper = [5,5, 3, 5,5, 8, 6, 3, 8, 5, 6, 5,5] y2_lower = [4,5, 2, 4,4, 7, 4, 2, 7, 4, 5, 4,75] y2_нижний = y2_нижний[::-1] # Строка 3 у3 = [10, 8, 6, 4, 2, 0, 2, 4, 2, 0] y3_upper = [11, 9, 7, 5, 3, 1, 3, 5, 3, 1] y3_lower = [9, 7, 5, 3, 1, -.5, 1, 3, 1, -1] y3_нижний = y3_нижний[::-1] рис = идти.Рисунок() fig.add_trace(go.Scatter( х=х+х_об, y=y1_верхний+y1_нижний, заполнить = 'себя', fillcolor='rgba(0,100,80,0,2)', line_color='rgba(255,255,255,0)', showlegend=ложь, имя = 'Ярмарка', )) fig.add_trace(go.Scatter( х=х+х_об, y=y2_верхний+y2_нижний, заполнить = 'себя', fillcolor='rgba(0,176,246,0,2)', line_color='rgba(255,255,255,0)', имя = 'Премиум', showlegend=ложь, )) fig.add_trace(go.Scatter( х=х+х_об, y=y3_верхний+y3_нижний, заполнить = 'себя', fillcolor='rgba(231,107,243,0,2)', line_color='rgba(255,255,255,0)', showlegend=ложь, имя = 'Идеально', )) fig.add_trace(go.Scatter( х=х, у=у1, line_color='rgb(0,100,80)', имя = 'Ярмарка', )) fig.add_trace(go.Scatter( х=х, у=у2, line_color='rgb(0,176,246)', имя = 'Премиум', )) fig.add_trace(go.Scatter( х=х, у=у3, line_color = 'rgb (231 107 243)', имя = 'Идеально', )) fig.

 data" заголовок "" с yerrorbars
data" заголовок "" с yerrorbars
 000
тау -0,844 1,000
фи -0,100 0,088 1,000
Т -0,072 0,072 0,806 1,000
тета0 -0,166 0,127 -0,182 -0,166 1,000
000
тау -0,844 1,000
фи -0,100 0,088 1,000
Т -0,072 0,072 0,806 1,000
тета0 -0,166 0,127 -0,182 -0,166 1,000
 data», используя 1: (log ($ 2))
data», используя 1: (log ($ 2))
 express как px
df = px.data.gapminder().query("country=='Канада'")
fig = px.line(df, x="year", y="lifeExp", title='Ожидаемая продолжительность жизни в Канаде')
рис.шоу()
express как px
df = px.data.gapminder().query("country=='Канада'")
fig = px.line(df, x="year", y="lifeExp", title='Ожидаемая продолжительность жизни в Канаде')
рис.шоу()
 шоу()
шоу()
 update_yaxes(visible=False, fixedrange=True)
# удалить метки фасета/подграфика
fig.update_layout(аннотации=[], перезапись=Истина)
# убираем остальную часть сюжета
fig.update_layout(
showlegend=ложь,
plot_bgcolor="белый",
маржа = dict (t = 10, l = 10, b = 10, r = 10)
)
# отключаем модбар для такого маленького сюжета
fig.show (config = dict (displayModeBar = False))
update_yaxes(visible=False, fixedrange=True)
# удалить метки фасета/подграфика
fig.update_layout(аннотации=[], перезапись=Истина)
# убираем остальную часть сюжета
fig.update_layout(
showlegend=ложь,
plot_bgcolor="белый",
маржа = dict (t = 10, l = 10, b = 10, r = 10)
)
# отключаем модбар для такого маленького сюжета
fig.show (config = dict (displayModeBar = False))
 graph_objects как есть
импортировать numpy как np
х = np.arange (10)
рис = идти.Рисунок (данные = идти.Scatter (х = х, у = х ** 2))
рис.шоу()
graph_objects как есть
импортировать numpy как np
х = np.arange (10)
рис = идти.Рисунок (данные = идти.Scatter (х = х, у = х ** 2))
рис.шоу()
 add_trace(go.Scatter(x=месяц, y=high_2007, name='High 2007',
строка = dict (цвет = 'огнеупорный кирпич', ширина = 4,
dash='dash') # варианты тире включают 'dash', 'dot' и 'dashdot'
))
fig.add_trace(go.Scatter(x=месяц, y=low_2007, name='Минимум 2007',
строка = dict (цвет = 'королевский синий', ширина = 4, тире = 'тире')))
fig.add_trace(go.Scatter(x=месяц, y=high_2000, name='Максимум 2000',
строка = dict (цвет = 'огнеупорный кирпич', ширина = 4, тире = 'точка')))
fig.add_trace(go.Scatter(x=месяц, y=low_2000, name='Минимум 2000',
строка = dict (цвет = 'королевский синий', ширина = 4, тире = 'точка')))
# Редактировать макет
fig.update_layout(title='Средние высокие и низкие температуры в Нью-Йорке',
xaxis_title = 'Месяц',
yaxis_title='Температура (градусы F)')
рис.шоу()
add_trace(go.Scatter(x=месяц, y=high_2007, name='High 2007',
строка = dict (цвет = 'огнеупорный кирпич', ширина = 4,
dash='dash') # варианты тире включают 'dash', 'dot' и 'dashdot'
))
fig.add_trace(go.Scatter(x=месяц, y=low_2007, name='Минимум 2007',
строка = dict (цвет = 'королевский синий', ширина = 4, тире = 'тире')))
fig.add_trace(go.Scatter(x=месяц, y=high_2000, name='Максимум 2000',
строка = dict (цвет = 'огнеупорный кирпич', ширина = 4, тире = 'точка')))
fig.add_trace(go.Scatter(x=месяц, y=low_2000, name='Минимум 2000',
строка = dict (цвет = 'королевский синий', ширина = 4, тире = 'точка')))
# Редактировать макет
fig.update_layout(title='Средние высокие и низкие температуры в Нью-Йорке',
xaxis_title = 'Месяц',
yaxis_title='Температура (градусы F)')
рис.шоу()
 Scatter(x=x, y=y + 5, name="spline",
text=["настроить гладкость линии
Scatter(x=x, y=y + 5, name="spline",
text=["настроить гладкость линии vstack((np.arange(2001, 2014)),)*4)
y_data = np.массив([
[74, 82, 80, 74, 73, 72, 74, 70, 70, 66, 66, 69],
[45, 42, 50, 46, 36, 36, 34, 35, 32, 31, 31, 28],
[13, 14, 20, 24, 20, 24, 24, 40, 35, 41, 43, 50],
[18, 21, 18, 21, 16, 14, 13, 18, 17, 16, 19, 23],
])
рис = идти.Рисунок()
для я в диапазоне (0, 4):
fig.add_trace(go.Scatter(x=x_data[i], y=y_data[i], mode='lines',
имя=метки[я],
линия = dict (цвет = цвета [я], ширина = размер_линии [я]),
connectgaps=Верно,
))
# конечные точки
fig.add_trace(go.Scatter(
х=[x_data[i][0], x_data[i][-1]],
y=[y_data[i][0], y_data[i][-1]],
режим = 'маркеры',
маркер = dict (цвет = цвета [i], размер = mode_size [i])
))
fig.update_layout(
ось = дикт (
шоулайн = Верно,
шоугрид=ложь,
showticklabels=Верно,
цвет линии='rgb(204, 204, 204)',
ширина линии=2,
тики='снаружи',
тикфонт = дикт (
семья = 'Ариал',
размер=12,
цвет = 'rgb (82, 82, 82)',
),
),
ось = дикт (
шоугрид=ложь,
нулевая линия = ложь,
шоулайн=ложь,
showticklabels = Ложь,
),
авторазмер=ложь,
маржа = дикт(
авторазвертывание=ложь,
л=100,
г=20,
т=110,
),
showlegend=ложь,
plot_bgcolor = 'белый'
)
аннотации = []
# Добавление меток
для y_trace, label, color in zip (y_data, labels, colors):
# маркировка левой_стороны графика
annotations.
vstack((np.arange(2001, 2014)),)*4)
y_data = np.массив([
[74, 82, 80, 74, 73, 72, 74, 70, 70, 66, 66, 69],
[45, 42, 50, 46, 36, 36, 34, 35, 32, 31, 31, 28],
[13, 14, 20, 24, 20, 24, 24, 40, 35, 41, 43, 50],
[18, 21, 18, 21, 16, 14, 13, 18, 17, 16, 19, 23],
])
рис = идти.Рисунок()
для я в диапазоне (0, 4):
fig.add_trace(go.Scatter(x=x_data[i], y=y_data[i], mode='lines',
имя=метки[я],
линия = dict (цвет = цвета [я], ширина = размер_линии [я]),
connectgaps=Верно,
))
# конечные точки
fig.add_trace(go.Scatter(
х=[x_data[i][0], x_data[i][-1]],
y=[y_data[i][0], y_data[i][-1]],
режим = 'маркеры',
маркер = dict (цвет = цвета [i], размер = mode_size [i])
))
fig.update_layout(
ось = дикт (
шоулайн = Верно,
шоугрид=ложь,
showticklabels=Верно,
цвет линии='rgb(204, 204, 204)',
ширина линии=2,
тики='снаружи',
тикфонт = дикт (
семья = 'Ариал',
размер=12,
цвет = 'rgb (82, 82, 82)',
),
),
ось = дикт (
шоугрид=ложь,
нулевая линия = ложь,
шоулайн=ложь,
showticklabels = Ложь,
),
авторазмер=ложь,
маржа = дикт(
авторазвертывание=ложь,
л=100,
г=20,
т=110,
),
showlegend=ложь,
plot_bgcolor = 'белый'
)
аннотации = []
# Добавление меток
для y_trace, label, color in zip (y_data, labels, colors):
# маркировка левой_стороны графика
annotations.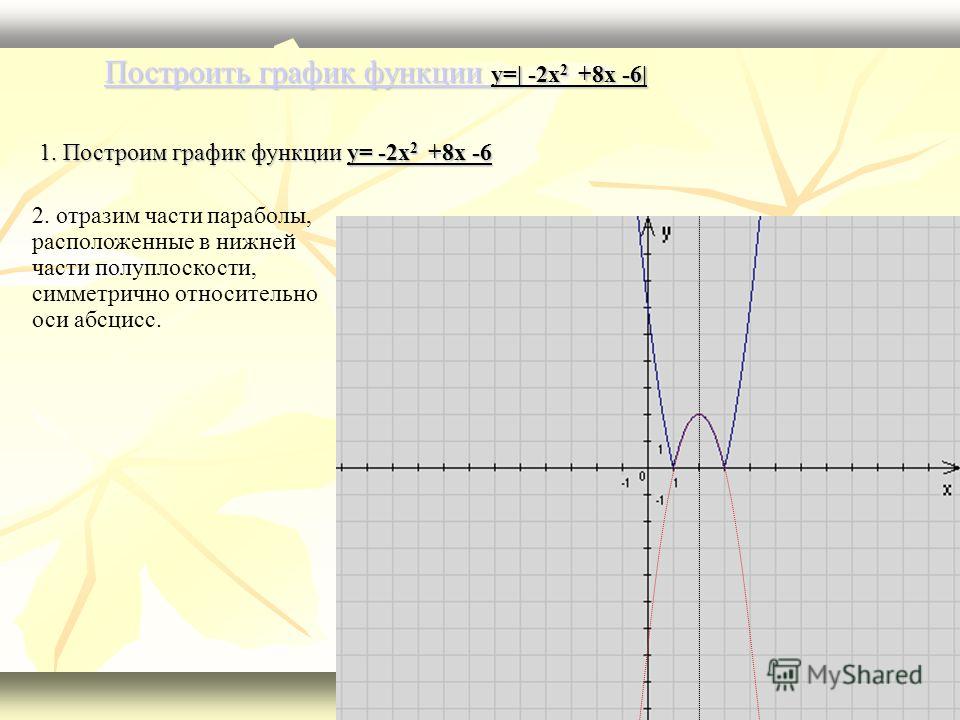 append(dict(xref='бумага', x=0,05, y=y_trace[0],
xanchor='правый', yanchor='средний',
текст = метка + '{}%'.format (y_trace [0]),
шрифт = dict (семья = 'Arial',
размер=16),
showarrow=ложь))
# маркировка правой_стороны графика
annotations.append(dict(xref='бумага', x=0,95, у=у_след[11],
xanchor='левый', yanchor='средний',
текст = '{}%'. формат (y_trace [11]),
шрифт = dict (семья = 'Arial',
размер=16),
showarrow=ложь))
# Заголовок
annotations.append(dict(xref='бумага', yref='бумага', x=0.0, y=1.05,
xanchor='левый', yanchor='нижний',
text='Основной источник новостей',
шрифт = dict (семья = 'Arial',
размер=30,
цвет = 'rgb (37,37,37)'),
showarrow=ложь))
# Источник
annotations.
append(dict(xref='бумага', x=0,05, y=y_trace[0],
xanchor='правый', yanchor='средний',
текст = метка + '{}%'.format (y_trace [0]),
шрифт = dict (семья = 'Arial',
размер=16),
showarrow=ложь))
# маркировка правой_стороны графика
annotations.append(dict(xref='бумага', x=0,95, у=у_след[11],
xanchor='левый', yanchor='средний',
текст = '{}%'. формат (y_trace [11]),
шрифт = dict (семья = 'Arial',
размер=16),
showarrow=ложь))
# Заголовок
annotations.append(dict(xref='бумага', yref='бумага', x=0.0, y=1.05,
xanchor='левый', yanchor='нижний',
text='Основной источник новостей',
шрифт = dict (семья = 'Arial',
размер=30,
цвет = 'rgb (37,37,37)'),
showarrow=ложь))
# Источник
annotations.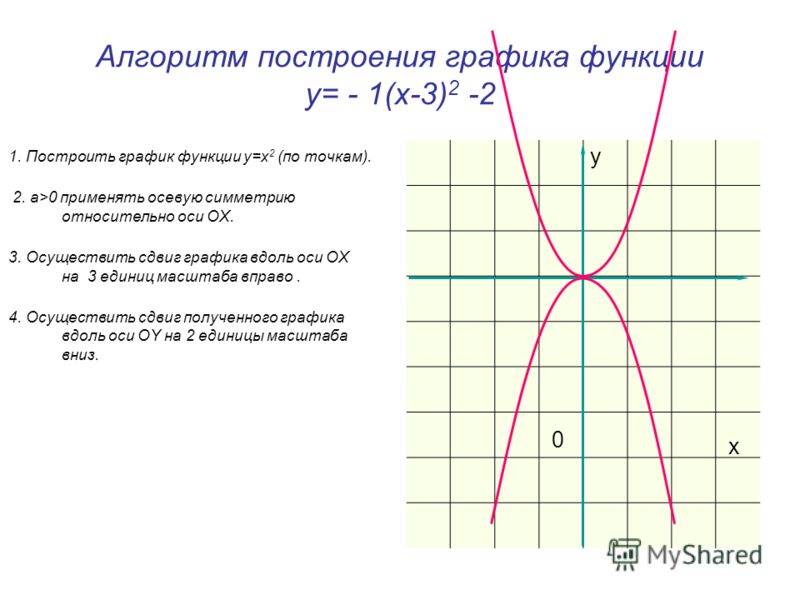 append(dict(xref='бумага', yref='бумага', x=0,5, y=-0,1,
xanchor='центр', yanchor='сверху',
text='Источник: PewResearch Center & ' +
«Рассказывание историй с данными»,
шрифт = dict (семья = 'Arial',
размер=12,
цвет='rgb(150,150,150)'),
showarrow=ложь))
fig.update_layout(аннотации=аннотации)
рис.шоу()
append(dict(xref='бумага', yref='бумага', x=0,5, y=-0,1,
xanchor='центр', yanchor='сверху',
text='Источник: PewResearch Center & ' +
«Рассказывание историй с данными»,
шрифт = dict (семья = 'Arial',
размер=12,
цвет='rgb(150,150,150)'),
showarrow=ложь))
fig.update_layout(аннотации=аннотации)
рис.шоу()
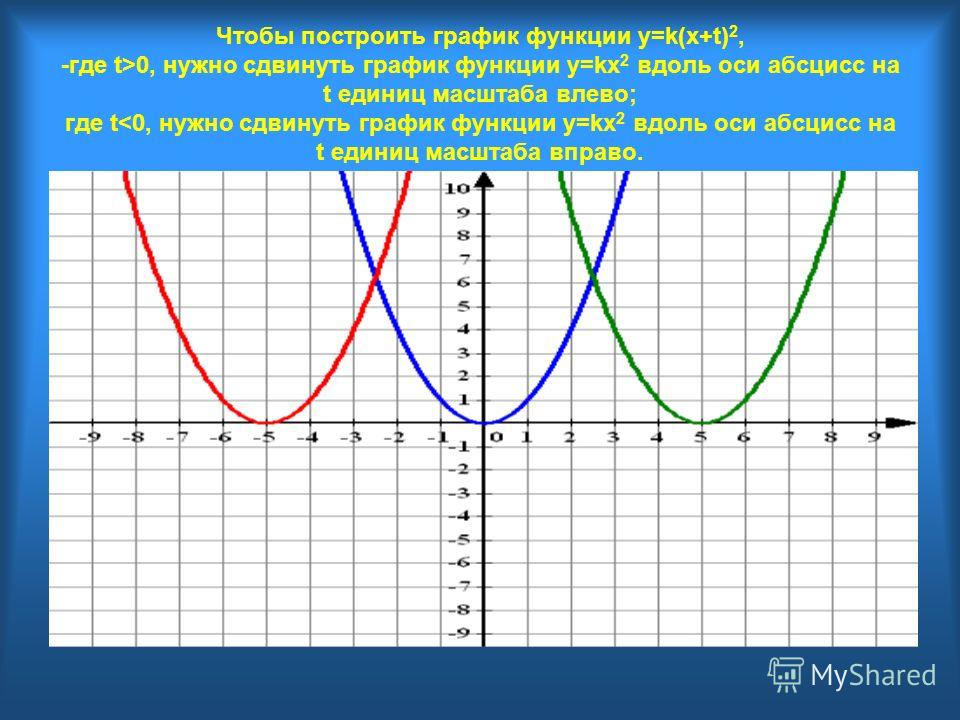 5, 1, 3, 1, -1]
y3_нижний = y3_нижний[::-1]
рис = идти.Рисунок()
fig.add_trace(go.Scatter(
х=х+х_об,
y=y1_верхний+y1_нижний,
заполнить = 'себя',
fillcolor='rgba(0,100,80,0,2)',
line_color='rgba(255,255,255,0)',
showlegend=ложь,
имя = 'Ярмарка',
))
fig.add_trace(go.Scatter(
х=х+х_об,
y=y2_верхний+y2_нижний,
заполнить = 'себя',
fillcolor='rgba(0,176,246,0,2)',
line_color='rgba(255,255,255,0)',
имя = 'Премиум',
showlegend=ложь,
))
fig.add_trace(go.Scatter(
х=х+х_об,
y=y3_верхний+y3_нижний,
заполнить = 'себя',
fillcolor='rgba(231,107,243,0,2)',
line_color='rgba(255,255,255,0)',
showlegend=ложь,
имя = 'Идеально',
))
fig.add_trace(go.Scatter(
х=х, у=у1,
line_color='rgb(0,100,80)',
имя = 'Ярмарка',
))
fig.add_trace(go.Scatter(
х=х, у=у2,
line_color='rgb(0,176,246)',
имя = 'Премиум',
))
fig.add_trace(go.Scatter(
х=х, у=у3,
line_color = 'rgb (231 107 243)',
имя = 'Идеально',
))
fig.
5, 1, 3, 1, -1]
y3_нижний = y3_нижний[::-1]
рис = идти.Рисунок()
fig.add_trace(go.Scatter(
х=х+х_об,
y=y1_верхний+y1_нижний,
заполнить = 'себя',
fillcolor='rgba(0,100,80,0,2)',
line_color='rgba(255,255,255,0)',
showlegend=ложь,
имя = 'Ярмарка',
))
fig.add_trace(go.Scatter(
х=х+х_об,
y=y2_верхний+y2_нижний,
заполнить = 'себя',
fillcolor='rgba(0,176,246,0,2)',
line_color='rgba(255,255,255,0)',
имя = 'Премиум',
showlegend=ложь,
))
fig.add_trace(go.Scatter(
х=х+х_об,
y=y3_верхний+y3_нижний,
заполнить = 'себя',
fillcolor='rgba(231,107,243,0,2)',
line_color='rgba(255,255,255,0)',
showlegend=ложь,
имя = 'Идеально',
))
fig.add_trace(go.Scatter(
х=х, у=у1,
line_color='rgb(0,100,80)',
имя = 'Ярмарка',
))
fig.add_trace(go.Scatter(
х=х, у=у2,
line_color='rgb(0,176,246)',
имя = 'Премиум',
))
fig.add_trace(go.Scatter(
х=х, у=у3,
line_color = 'rgb (231 107 243)',
имя = 'Идеально',
))
fig.