Упрощение корней: Выражения с квадратными корнями — урок. Алгебра, 8 класс.

Урок по теме «Преобразование выражений с арифметическим квадратным корнем»

Цели урока:

• научить обучающихся применять вынесение множителя за знак корня к преобразованию выражений; закрепить навыки применения свойства корней: преобразования корня из произведения, корня из дроби, умножение корней, деление корней для преобразований выражений.
• развивающая: развивать концентрацию внимания, мышление: умение анализировать, обобщать, объяснять;
• воспитательная — воспитание коммуникативных навыков (умение слушать).

Ход урока

1. Организационный момент

Учитель сообщает тему урока и просит учащихся определить две составляющие в названии темы. Учащиеся отмечают

• арифметический квадратный корень,
• преобразование выражений

Это те понятия, с которыми учащимся недавно приходилось работать.

2. Актуализация опорных знаний

Учащимся предлагаются упражнения на развитие высших психических функций.

Цель упражнений — подготовить мыслительную деятельность обучающихся к активной работе на уроке, повторить ранее изученные вопросы, необходимые при изучении новой темы.

Упражнение на развитие логического мышления:

a) Известно, что , а обратно

б) Проверьте, верны ли данные равенства, и объясните почему, определив какое из преобразований было выполнено в каждом примере:

Преобразования, оформленные в виде опор:

Корень из произведения…

Корень из дроби…

Умножение корней

Деление корней

Вынесение множителя за знак корня

Внесение множителя под знак корня

Учащиеся выбирают из предложенных преобразований то, с опорой на которое можно объяснить правильность или неправильность решения.

Подготовка к изучению нового

Учащимся предлагается математический диктант с проверкой (проверку можно осуществить с обратной стороны доски, пригласив для работы двух учащихся или проектируя ответы на экран, используя мультимедийную установку). Цель диктанта — корректировать знания учащихся, необходимые для изучения новой темы.

Перед диктантом учитель напоминает:

• при решении нужно использовать разложение на множители и свойство квадратного корня , где и .
• когда число, стоящее под корнем большое, то при разложении его на множители можно пользоваться таблицей чисел, из которых извлекается квадратный корень:

4

9

16

25

36

49

64

81

100

Один из множителей должен быть числом из таблицы.

Математический диктант

Вынесите множитель за знак корня:

Изучениее новой темы.

Учащимся предлагается ответить на вопрос: какое преобразование позволяет упростить выражение:

(Учащиеся отвечают: приведение подобных слагаемых).

Учитель. Найдите в следующих выражениях подобные слагаемые:

(учащиеся определяют подобными те слагаемые, у которых равны подкоренные выражения).

Учитель. Как упростить выражение, если подкоренные выражения разные?

Какое из преобразований можно применить для упрощения выражения?

(Учащиеся отвечают: вынесение множителя за знак корня)

Решение:

Учитель. Как изменится решение выражения, если в каждое подкоренное выражение добавить переменную ?

(Учащиеся отвечают: под знаком корня появится ).

Закрепление нового материала.

Со всеми учащимися класса рассматриваются решения упражнений из учебника на доске и в тетрадях № 421, №422 в, используя таблицу чисел, из которых извлекается квадратный корень.

Самостоятельная работа по карточкам.

Каждому ученику дается индивидуальное задание из первого столбика карточки, в ходе которого он постепенно самостоятельно отрабатывает математический прием под контролем учителя.

Или можно организовать работу в группах (каждая группа получает по одному примеру, решают вместе, а потом представляют свое решение классу, идет обсуждение).

Упростите выражение (обучающиеся получают задание первого столбика, остальные задания карточки будут использоваться на следующих уроках):

1. 2. 3. 4.

5. 6. 7. 8. 9.

10. 11. 12. 13. 14. 15.

Подведение итога.

Повторение шагов алгоритма преобразования выражения с арифметическим квадратным корнем - приведения подобных слагаемых

Задание: закончите фразу (начало и окончание фраз оформлены на отдельных карточках, учащимся надо продолжить предложение, подобрав соответствующую карточку)

Учитель. Итак, чтобы увидеть подобные слагаемые, надо:

Отвечают учащиеся.

Разложить на множители… (подкоренное выражение)

Применить преобразование корней…()

Вынести множитель… ( за знак корня )

Привести подобные …(слагаемые)

Домашнее задание

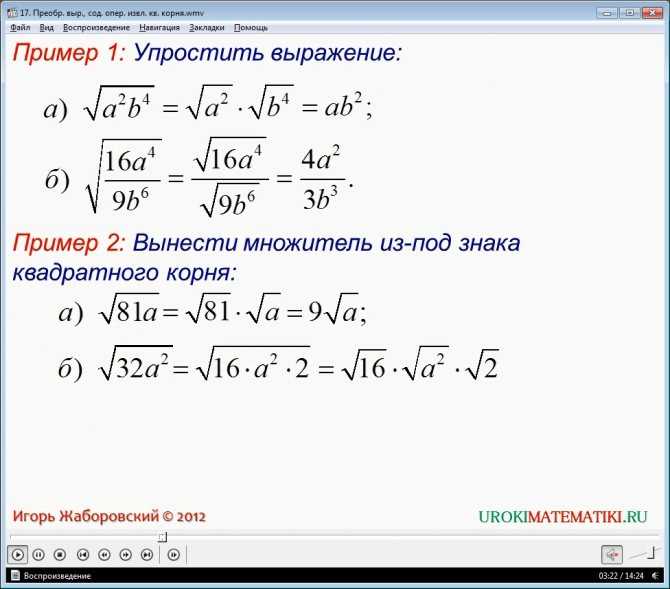
• Стр. 95п.19 пример1.
• № 422(а,б, г, д, е)
• № 440,
• повторить формулы сокращенного умножения стр. 252. п.6 а),б),д).

Выставление оценок

Как упростить квадратный корень

Все математические ресурсы SAT

16 диагностических тестов 660 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 4 5 6 Следующая →

SAT Math Help » Арифметика » Базовое возведение в квадрат / квадратные корни » Упрощение квадратных корней » Как упростить квадратный корень

Упростить

9 ÷ √3

Возможные ответы:

2

3√3

ни один из этих

3

невозможно

Правильный ответ:

3 10004

5 300 Объяснение:

, чтобы упростить квадратный корень внизу, умножить верхнюю часть и снизу на корень

Отчет о ошибке

Упрощение:

√112

Возможные ответы:

20

9004 40017 √10

10√12

4√7

12

Правильный ответ:

4√7

Объяснение:

√112 = {√2 * √56} = {√2 * √2 * √28} = {2√28} = {2√4 * √7} = 4√7 

Сообщить об ошибке

Упрощение:

√192

Возможные ответы:

4√3

4√2

8√2

8√3

Ни один из этих

Правильный ответ:

8 8 8 8 Ни один из них

. 3

Объяснение:

√192 = √2 x √96

√96 = √2 x √48

√48 = √4 x√12

√12 = √4 x √3

√192 = √ (2x2x4x4. ) X √3

        = √4X√4X√4  X √3

        = 8√3

Сообщить об ошибке

Как проще всего выразить ?

Возможные ответы:

Правильный ответ:

Объяснение:

Сначала мы перечислим множители 3888:

Отчет о ошибке

Упрощайте:

Возможные ответы:

Правильный ответ:

. Объяснение:

4√27 + 16√75 +3√12 =

4*(√3)*(√9)  + 16*(√3)*(√25)  +3*(√3)*( √4) =

4*(√3)*(3) + 16*(√3)*(5) + 3*(√3)*(2) =

12√3  + 80√3 +6 √3= 98√3

Сообщить об ошибке

Упростите следующее: (√(6) + √(3)) / √(3)

Возможные ответы:

3 адрес (2)

1

Ни один из других ответов

√ (3)

√ (2) + 1

Правильный ответ:

√ (2

. ) + 1

Объяснение:

Начните с умножения верхнего и нижнего пределов на √(3):

(√(18) + √(9)) / 3

Обратите внимание на следующее:

√(9) = 3

√(18 ) = √(9 * 2) = √(9) * √(2) = 3 * √(2)

Таким образом, числитель: 3 * √(2) + 3. (√(2) + 1)

Перепишите всю дробь:

(3 * (√(2) + 1)) / 3

Упростите делением, отменив 3, общие для числителя и знаменателя: √(2) + 1

Сообщить об ошибке

Что представляет собой

√0.0000490

Возможные ответы:

0,07

7

0,007

0,00007

49

Правильный ответ:

0,0016

Правильный Ответ:

0,0016

. Правильный ответ:

,0,00166

. Правильный ответ:

9,0016

. Правильный ответ. Объяснение:

самый простой способ упростить: перевести в экспоненциальное представление

√0,0000490= √4,9 X 10 ^-5

Найти квадратный корень из четной степени несложно, а 49 – это полный квадрат, поэтому мы можем записать неправильную научную запись:

√4,9 X 10 ^-5 = √49 X 10 ^-6

√49 = 7; √10 ^-6 = 10 ^-3 это эквивалентно возведению 10 ^-6 в степень 1/2, и в этом случае все, что нужно сделать, это умножить два показателя степени: 7 X 10 ^-3 = 0,007

Сообщить об ошибке

Упрощение:

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы извлечь квадратный корень, разделите 576 на 2.

No related posts.