примеры решения интегралов
Интеграл функции является основным понятием интегрального исчисления. Интеграл широко используется при решении целого ряда задач по математике, физике и в других науках. Именно поэтому мы собрали на сайте более 100 примеров решения интегралов и постоянно добавляем новые! Список тем находится в правом меню.
Перед изучением примеров вычисления интегралов советуем вам прочитать теоретический материал по теме: определения, свойства и таблицу интегралов, методы их вычисления и другой материал по интегралам.
Таблица интегралов
Основные ссылки — таблица интегралов и примеры решений (10 шт).
Пример
Задание. Вычислить неопределенный интеграл
Решение. Для решения данного интеграла не нужно использовать свойства неопределенных интегралов, достаточно формулы интеграла степенной функции:
В нашем случае , тогда искомый интеграл равен:
Ответ.
Больше примеров решений →
Метод непосредственного интегрирования
Основные ссылки — метод непосредственного интегрирования и примеры решений (10 шт).
Пример
Задание. Вычислить неопределенный интеграл
Решение. Преобразуем подынтегральное выражение. Для этого вынесем из знаменателя за знак интеграла
далее, используя таблицу интегралов (Формула №11), получим
Ответ.
Больше примеров решений →
Внесение под знак дифференциала
Основные ссылки — внесение под знак дифференциала и примеры решений (10 шт).
Пример
Задание. Вычислить неопределенный интеграл
Решение. Распишем подынтегральную сумму, используя тригонометрические функции (определение котангенса)
Внесем под знак дифференциала:
Полученный интеграл можно вычислить, используя табличный интеграл
В результате получим
Ответ.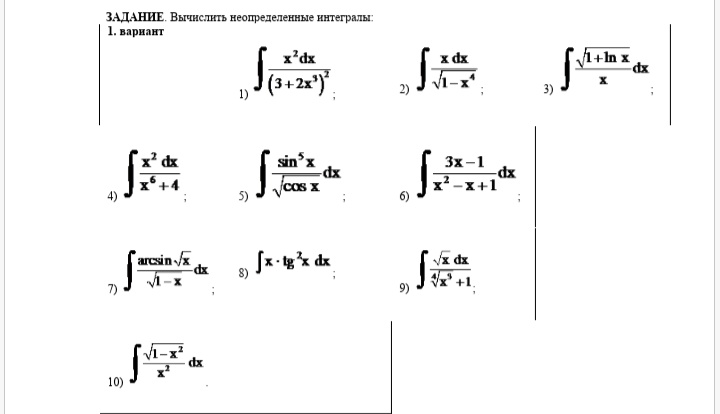
Больше примеров решений →
Интегрирование заменой переменной
Основные ссылки — интегрирование заменой переменной и примеры решений (10 шт).
Пример
Задание. Найти неопределенный интеграл
Решение. Введем замену и полученный интеграл находим как интеграл от степенной функции:
Сделаем обратную замену
Ответ.
Больше примеров решений →
Интегрирование по частям
Основные ссылки — интегрирование по частям и примеры решений (10 шт).
Пример
Задание. Найти неопределенный интеграл
Решение. Воспользуемся методом интегрирования по частям. Для этого положим
Подставим это в формулу для интегрирования по частям, затем воспользуемся формулой интеграла косинуса из таблицы интегралов
Ответ.
Больше примеров решений →
Метод неопределенных коэффициентов
Основные ссылки — метод неопределенных коэффициентов и примеры решений (10 шт).
Пример
Задание. Разложить рациональную дробь на простые дроби.
Решение. Так как корнями знаменателя являются значения , , то его можно разложить на множители следующим образом:
А тогда
Искомое разложение имеет вид:
Приводим к общему знаменателю в правой части равенства и приравниваем числители:
Приравнивая коэффициенты, при соответствующих степенях, получаем:
Отсюда, искомое разложение:
Ответ.
Больше примеров решений →
Интегрирование тригонометрических функций
Основные ссылки — универсальная тригонометрическая подстановка и примеры решений (10 шт).
Пример
Задание. {2}-x-1)dx\approx 100$
{2}-x-1)dx\approx 100$
Задача 11
Какова приблизительная площадь розовой области, используя аппроксимацию верхней и нижней сумм.
Используйте $\Delta x=1$
$10
$5
$12
$0
Задача 12
Какова приблизительная площадь розовой области, используя аппроксимацию верхней и нижней сумм.
Используйте $\Delta x=1$
$0
$3
$3
$3
Задача 13
Используйте верхнюю и нижнюю суммы, чтобы приблизительно рассчитать площадь области под кривой $y=\sqrt{x}$.
$0\leq \text{площадь} \leq 1$
$1\leq \text{площадь} \leq 1,5$
$0,518\leq \text{площадь} \leq 0,768$
$0,518\leq \text{площадь} \leq 4$
Задача 14
Используйте верхнюю и нижнюю суммы, чтобы приблизительно рассчитать площадь области под кривой $y=\frac{1}{x}$
$0,646\leq \text{площадь} \leq 0,746$
$0\leq \text{площадь} \leq 2$
$1\leq \text{площадь} \leq 2$
$0,646\leq \text{площадь} \leq 3$
Задача 15
Чему равен интеграл $\int \left( 2x+1\right) \left( x^{2}+x\right) dx$
$\int \left( 2x+1\right) \left( x^{2}+x\right) dx=2x+1+C$
$\int \left(2x+1\right) \left(x^2+x\right) dx=\frac{\left(x^2+x\right)^2}{2}+C$
$\int \left( 2x+1\right) \left( x^{2}+x\right) dx=x^{2}+x+C$
$\int \left(2x+1\right) \left(x^2+x\right) dx=\frac{\left(2x+1\right)^2}{2}+C$
Задача 16
Решите интеграл, используя замену переменной. {3}x+C$
{3}x+C$
Прислать задачу
Правильный:
Неверный:
Неразрешенные задачи:
Исчисление I — Интегралы (задачи о назначениях)
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т.е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Уведомление о проблемах с назначением
Пожалуйста, не пишите мне по электронной почте, чтобы получить решения и/или ответы на эти проблемы. Я не буду их раздавать ни при каких обстоятельствах и не буду отвечать на любые просьбы об этом. Цель этих задач состоит в том, чтобы инструкторы использовали их для заданий, а наличие легкодоступных решений / ответов побеждает эту цель.
Я не буду их раздавать ни при каких обстоятельствах и не буду отвечать на любые просьбы об этом. Цель этих задач состоит в том, чтобы инструкторы использовали их для заданий, а наличие легкодоступных решений / ответов побеждает эту цель.
Вот набор задач на присваивание для главы «Интегралы» в «Исчислении I». Обратите внимание, что эти проблемы не имеют доступных решений. Они предназначены в основном для инструкторов, которые могут захотеть назначить набор задач для сдачи. Наличие доступных решений (или даже только окончательных ответов) лишило бы цели задачи.
Если вы ищете практические задачи (с доступными решениями), пожалуйста, ознакомьтесь с практическими задачами. Там вы найдете набор задач, которые должны дать вам немного практики.
Вот список всех разделов, для которых были написаны задачи на задания, а также краткое описание материала, затронутого в примечаниях к этому конкретному разделу.
Неопределенные интегралы. В этом разделе мы начнем главу с определения и свойств неопределенных интегралов. В этом разделе мы не будем вычислять много неопределенных интегралов. Этот раздел посвящен простому определению того, что такое неопределенный интеграл, и описанию многих свойств неопределенного интеграла. Собственно вычисление неопределенных интегралов начнется в следующем разделе.
В этом разделе мы не будем вычислять много неопределенных интегралов. Этот раздел посвящен простому определению того, что такое неопределенный интеграл, и описанию многих свойств неопределенного интеграла. Собственно вычисление неопределенных интегралов начнется в следующем разделе.
Вычисление неопределенных интегралов. В этом разделе мы будем вычислять некоторые неопределенные интегралы. Интегралы в этом разделе будут, как правило, такими, которые не требуют большого количества манипуляций с функцией, которую мы интегрируем, чтобы фактически вычислить интеграл. Как мы увидим в следующем разделе, многие интегралы требуют некоторых манипуляций с функцией, прежде чем мы сможем вычислить интеграл. Мы также кратко рассмотрим применение неопределенных интегралов.
Правило подстановки для неопределенных интегралов. В этом разделе мы начнем использовать один из наиболее распространенных и полезных методов интегрирования — правило подстановки. С помощью правила подстановки мы сможем интегрировать более широкий спектр функций. Все интегралы в этом разделе потребуют некоторых манипуляций с функцией перед интегрированием, в отличие от большинства интегралов из предыдущего раздела, где все, что нам действительно нужно, это основные формулы интегрирования.
Все интегралы в этом разделе потребуют некоторых манипуляций с функцией перед интегрированием, в отличие от большинства интегралов из предыдущего раздела, где все, что нам действительно нужно, это основные формулы интегрирования.
Подробнее Правило подстановки. В этом разделе мы продолжим рассмотрение правила подстановки. Проблемы в этом разделе, как правило, немного сложнее, чем в предыдущем разделе.
Областная задача. В этом разделе мы начнем с мотивации определенных интегралов и дадим одну из интерпретаций определенных интегралов. Мы будем аппроксимировать площадь, лежащую между функцией и осью \(x\). Как мы увидим в следующем разделе, эта проблема приведет нас к определению определенного интеграла и будет одной из основных интерпретаций определенного интеграла, которые мы будем рассматривать в этом материале.
Определение определенного интеграла. В этом разделе мы дадим формальное определение определенного интеграла, дадим многие его свойства и обсудим пару интерпретаций определенного интеграла. Мы также рассмотрим первую часть основной теоремы исчисления, которая показывает очень тесную связь между производными и интегралами 9.0003
Мы также рассмотрим первую часть основной теоремы исчисления, которая показывает очень тесную связь между производными и интегралами 9.0003
Вычисление определенных интегралов. В этом разделе мы рассмотрим вторую часть основной теоремы исчисления. Это покажет нам, как мы вычисляем определенные интегралы без использования (часто очень неприятного) определения. Все примеры в этом разделе можно выполнить с базовыми знаниями о неопределенных интегралах и не потребуют использования правила подстановки. В примеры этого раздела включены вычисления определенных интегралов кусочных и абсолютных функций.
Правило подстановки для определенных интегралов. В этом разделе мы вернемся к правилу подстановки применительно к определенным интегралам. Единственными реальными требованиями для выполнения примеров в этом разделе являются умение использовать правило подстановки для неопределенных интегралов и понимание того, как вообще вычислять определенные интегралы.
Исчисление II. Методы интеграции (задачи назначения)
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Уведомление о проблемах назначения
Пожалуйста, не пишите мне по электронной почте, чтобы получить решения и/или ответы на эти проблемы. Я не буду их раздавать ни при каких обстоятельствах и не буду отвечать на любые просьбы об этом. Цель этих задач состоит в том, чтобы инструкторы использовали их для заданий, а наличие легкодоступных решений / ответов побеждает эту цель.
Вот набор задач на присваивание для главы «Техники интеграции» заметок «Исчисление II». Обратите внимание, что эти проблемы не имеют доступных решений. Они предназначены в основном для инструкторов, которые могут захотеть назначить набор задач для сдачи. Наличие доступных решений (или даже только окончательных ответов) лишило бы цели задачи.
Наличие доступных решений (или даже только окончательных ответов) лишило бы цели задачи.
Если вы ищете практические задачи (с доступными решениями), пожалуйста, ознакомьтесь с практическими задачами. Там вы найдете набор задач, которые должны дать вам немного практики.
Вот список всех разделов, для которых были написаны задачи на задания, а также краткое описание материала, охваченного в примечаниях к этому конкретному разделу.
Интеграция по частям — в этом разделе мы рассмотрим интеграцию по частям. Из всех техник, которые мы рассмотрим на этом занятии, именно с этой учащиеся, скорее всего, столкнутся в будущем на других занятиях. Мы также даем вывод формулы интегрирования по частям.
Интегралы с триггерными функциями. В этом разделе мы рассмотрим интегралы с триггерными функциями. В частности, мы концентрируемся на интегрировании произведений синусов и косинусов, а также произведений секущих и тангенсов. Мы также кратко рассмотрим, как модифицировать произведение этих триггерных функций для некоторых частных триггерных функций.
Подстановки триггеров — в этом разделе мы рассмотрим интегралы (как неопределенные, так и определенные), которые требуют использования подстановок, включающих триггерные функции, и то, как их можно использовать для упрощения некоторых интегралов.
Частичные дроби. В этом разделе мы будем использовать дроби для преобразования подынтегральных выражений в форму, которая позволит нам вычислять интегралы, включающие некоторые рациональные функции.
Интегралы с корнями. В этом разделе мы рассмотрим замену, которую иногда можно использовать с интегралами с корнями.
Интегралы, включающие квадратичные уравнения. В этом разделе мы рассмотрим некоторые интегралы, включающие квадратичные выражения, для которых предыдущие методы не будут работать сразу. В некоторых случаях необходимо произвести манипуляции с квадратичным выражением, прежде чем мы сможем вычислить интеграл. В этом разделе мы увидим несколько случаев, когда это необходимо.
Стратегия интеграции. В этом разделе мы даем общий набор рекомендаций по определению того, как вычислять интеграл. Приведенные здесь рекомендации включают в себя сочетание методов исчисления I и исчисления II, чтобы быть как можно более общими. Также обратите внимание, что на самом деле не существует единого набора рекомендаций, который будет работать всегда, поэтому вам всегда нужно быть гибким в следовании этому набору рекомендаций.
В этом разделе мы даем общий набор рекомендаций по определению того, как вычислять интеграл. Приведенные здесь рекомендации включают в себя сочетание методов исчисления I и исчисления II, чтобы быть как можно более общими. Также обратите внимание, что на самом деле не существует единого набора рекомендаций, который будет работать всегда, поэтому вам всегда нужно быть гибким в следовании этому набору рекомендаций.
Несобственные интегралы. В этом разделе мы рассмотрим интегралы с бесконечными интервалами интегрирования и интегралы с разрывными подынтегральными выражениями. В совокупности они называются несобственными интегралами, и, как мы увидим, они могут иметь или не иметь конечное (то есть не бесконечное) значение. Фактически, определение того, имеют ли они конечные значения, будет одной из основных тем этого раздела.
Сравнительный тест для неправильных интегралов. Не всегда возможно вычислить неправильные интегралы, и все же нам необходимо определить, сходятся они или расходятся (т.
