Минимизация логических функции.
Минимизацией называют процедуру упрощения выражения логической функции, с тем, чтобы она содержала минимальное количество членов при минимальном числе переменных. Чем проще логические выражения, описывающие функции, тем проще и дешевле реализующая их схема.
В некоторых простых случаях минимизацию можно осуществить непосредственно используя основные законы булевой алгебры. В качестве примера упростим выражение (1.1), используя закон склеивания:
(1.3)
Полученное выражение равносильно исходному, но значительно проще его.
Следует отметить, что такие элементарные приемы минимизации удается использовать не часто — при малом количестве членов функции и небольшом числе переменных. В других случаях применяются графические методы минимизации, облегчающие поиск склеивающихся членов. К ним относится метод минимизации с помощью карт Карно.
Карта Карно – это таблица, построенная так, что в ее соседние клетки попадают смежные наборы переменных функции — наборы, отличающиеся значением одной переменной: в один набор эта переменная входит в прямой форме, а в другой — в инверсной.
Карта Карно имеет столько клеток, сколько комбинаций (наборов) можно составить из прямых и инверсных значений n переменных по n членов в каждой –2n. Так, при n =2 карта содержит четыре клетки (рис. 1.5, а), при n=3 — восемь клеток (рис. 1.5, б), при n =4 — шестнадцать клеток (рис. 1.5, в) и при n=5 – тридцать две клетки (рис. 1.5, г).
Каждые строка и столбец имеют строго определенную комбинацию значений переменных. Каждая клетка карты соответствует определенной комбинации значений переменных и могут быть обозначены номерами строк таблицы истинности – j.
Наборы переменных, на которых у= 1, т. е. минтермы функции, отмечаются в соответствующих клетках карты единицами. Наборы переменных, на которых у= 0, т. е. макстермы функции, отмечаются в соответствующих клетках карты нулями или их оставляют пустыми. Две стоящие в соседних клетках единицы — свидетельство того, что в составе СДНФ имеются наборы, отличающиеся значением одной переменной. Такие наборы склеиваются (объединяются в контуры). Аналогично, два стоящих в соседних клетках нуля также могут объединяться в контуры.
Такие наборы склеиваются (объединяются в контуры). Аналогично, два стоящих в соседних клетках нуля также могут объединяться в контуры.
Минимизация функции заключается в объединении клеток карты с единицами (или нулями) контурами. Объединение каждой пары минтермов (макстермов) контуром уменьшает число входящих в них переменных на единицу.
Общие правила склеивания членов, занесенных в карту Карно, следующие:
1) охватывать контуром можно только соседние клетки;
2) контур должен быть только прямоугольным или квадратным и возможно большей площади;
3) количество клеток в контуре должно быть равно 2i, т. е. 2, 4, 8, 16 клеток;
4) контуры могут частично накладываться друг на друга;
5) крайние клетки строки, а также крайние клетки столбца карты считаются смежными; их можно таковыми представить, если мысленно свернуть карту в горизонтальный или вертикальный цилиндр;
6) количество охватывающих контуров должно быть минимальным.
Функция, минимизированная по единицам с помощью карты Карно, состоит из суммы простых конъюнкций. Каждая из них получается в результате склеивания членов, которым соответствует охваченные контуром единицы. В такую конъюнкцию войдут только те переменные, значения которых в пределах контура не меняются.
Порядок минимизации логической функции следующий:
1) построить карту Карно требуемого размера;
2) внести в карту единицы, соответствующие отдельным минтермам СДНФ функции;
3) охватить клетки карты возможно меньшим числом контуров. Чем больше клеток охвачено контуром, тем проще будет искомое выражение.
4) составить выражение для каждого контура;
5) записать минимизированное выражение функции.
Существует жёсткая однозначная связь между таблицей истинности, аналитическим выражением для функции и картой Карно.
Пусть логическая функция задана таблицей истинности (табл.5) или в СДНФ (1.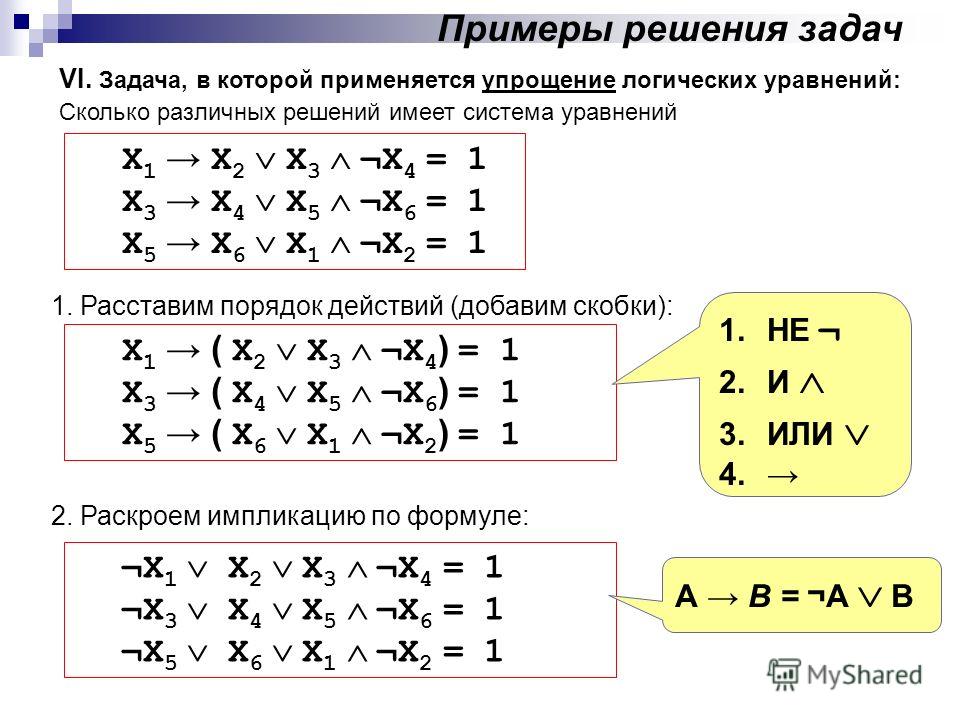 1):
1):
.
Непосредственно из таблицы истинности в клетки карты Карно (рис. 1.6) заносятся соответствующие значения функции у. Или в карту Карно можно занести только единичные значения для всех минтермов СДНФ функции.
В результате объединения клеток карты с единичными значениями получены три контура (черного цвета) по две клетки в каждом. Составив выражения для каждого контура, получим общую аналитическую запись функции:
(1.4)
Такая форма функции называется минимальной дизъюнктивной нормальной формой (МДНФ).
При объединении клеток карты с нулевыми значениями также получены три контура (голубого цвета) по две клетки в каждом. Составив выражения для каждого такого контура, получим общую аналитическую запись функции:
(1.5)
Полученная форма функции называется минимальной конъюнктивной нормальной формой (МКНФ).
Минимизация с помощью карт Карно не приводит к однозначной форме и для получения наиболее простой формы необходимо рассматривать всевозможные варианты склеивания.
При числе аргументов, большем пяти, используют обычно другие методы минимизации — применение карт Карно становится трудоемким.
Встречается необходимость минимизировать функцию, значения которой при некоторых комбинациях переменных не определены. Такой случай может иметь место, если значение функции при этих комбинациях безразлично или если определенные комбинации переменных невозможны по условиям задачи. На таких избыточных (запрещенных, факультативных) комбинациях можно придать функции любое значение — 0 или 1.
Пусть, например, функция представлена в виде карты Карно, изображенной на рис. 1.7. Здесь в клетках J=0 и J=1 функция у не определена и отмечена звездочкой (*). При объединении контурами единичных значений функции целесообразно клетке J=1 придать значение «1», а J=0 – значение «0». Тогда можно объединить в один контур 4 клетки. В результате аналитическая запись функции в форме МДНФ будет иметь следующий вид:
Рациональное доопределение функции может оказаться весьма эффективным для ее минимизации и, следовательно, для упрощения устройства, реализованного в соответствии с ней.
Базисные логические элементы
Известно, что совокупность элементарных логических функций ИЛИ, И, НЕ представляет функционально полную систему (базис), т. е. с помощью этих функций может быть записана логическая функция любой сложности.
Такие операции реализуются (выполняются) логическими элементами (ЛЭ) в соответствии с аксиомами алгебры логики.
Логические элементы могут быть представлены идеализированными моделями, т. е. условными графическими обозначениями (УГО), выполненные в соответствии с ГОСТ УГО ЛЭ изображаются прямоугольниками, в которых ставится символ выполняемой операции, а на линиях входных и выходных переменных могут изображаться окружности (индикаторы инверсии), если эти переменные имеют в выражении инверсные значения (рис.1.8).
Логические элементы физически могут быть реализованы в виде электрических ключевых схем или электронных схем с применением диодов и транзисторов.
Логические элементы И—НЕ, ИЛИ—НЕ
Значительный интерес представляют следующие функции двух переменных:
функция И—НЕ ;
функция ИЛИ—НЕ. .
.
| Таблица 5 | ||
| Х1 | X2 | УИЛИ-НЕ |
Таблицы истинности этих функций приведены в табл. 4 и табл. 5 соответственно.
| Таблица 4 | ||
| Х1 | X2 | УИ-НЕ |
Функционально элемент И—НЕ представляет собой совокупность конъюнктора и инвертора (рис.
 1.12, а), а элемент ИЛИ—НЕ — совокупность дизъюнктора и инвертора (рис. 1.12, в).Условное изображение элемента И—НЕ показано на рис. 1.12, б,а элемента ИЛИ—НЕ — на рис. 1.12, г.
1.12, а), а элемент ИЛИ—НЕ — совокупность дизъюнктора и инвертора (рис. 1.12, в).Условное изображение элемента И—НЕ показано на рис. 1.12, б,а элемента ИЛИ—НЕ — на рис. 1.12, г.
Можно показать, что набором однотипных элементов И—НЕ (ИЛИ—НЕ) можно реализовать функции И, ИЛИ, НЕ. Этим доказано, что каждый такой набор является базисом, так как базисом является совокупность элементов И, ИЛИ, НЕ.
Функцию И—НЕ называют функцией Шеффера (штрихом Шеффера), обозначая ее в виде у=x1|x2, а функцию ИЛИ — НЕ — функцией Пирса (стрелкой Пирса), обозначая ее в виде у=х1↑x2. Базис И—НЕ называют базисом Шеффера, а базис ИЛИ—НЕ — базисом Пирса.
Логическое устройство, реализованное в базисе И—НЕ (ИЛИ—НЕ), имеет преимущества по сравнению с устройством, реализованным в базисе И, ИЛИ, НЕ. Оно состоит в уменьшении номенклатуры элементов до одного типа, что упрощает компоновку устройства и его ремонт; другое связано с наличием в каждом элементе инвертора (усилителя), который компенсирует затухание потенциалов при передаче их через конъюнктор или дизъюнктор элемента. Благодаря этому не накапливается затухание сигнала при прохождении его через ряд последовательно включенных элементов, что могло бы вызвать снижение уровня U
Благодаря этому не накапливается затухание сигнала при прохождении его через ряд последовательно включенных элементов, что могло бы вызвать снижение уровня U
Построение логических схем по аналитическим выражениям функций
Логической схемой (ЛС) называется схема, составленная из ЛЭ путем соединения выходов одних ЛЭ со входами других.
Построение логических схем по аналитическим выражениям функций другими словами называется реализацией логических функций.
Существует ряд базисов, из числа которых были рассмотрены И, ИЛИ, НЕ; И—НЕ и ИЛИ—НЕ. В каждом базисе могут быть реализованы любые логические функции.
В каждом базисе могут быть реализованы любые логические функции.
Схема, которая получается на основании логического выражения, носит название комбинационной схемой.
При переходе от логического выражения к логической схеме элементы, выполняющие в выражении те или иные операции, располагаются в схеме, начиная от входов.
Рассмотрим принцип построения логических схем на примере выражения (1.1) для мажоритарной функции в СДНФ, полученной ранее:
.
На логической схеме сначала изображаются 3 инвертора, для отрицания входных переменных, затем 3 элемента И на три входа каждый и наконец 1 элемент ИЛИ на четыре входа. После размещения элементов изо
бражаются электрические связи (проводники), соединяющие входные переменных и выходные сигналы одних элементов со входами других согласно логическому выражению.
Построение ЛС основано на следующих правилах:
1. Выход ЛЭ можно подсоединять ко входам нескольких ЛЭ;
Выход ЛЭ можно подсоединять ко входам нескольких ЛЭ;
2. На входы ЛЭ можно подавать сигналы, представляющие собой константы 0 и 1.
3. Выходы ЛЭ нельзя соединять вместе;
4. Выходы ЛЭ нельзя подключать к собственным входам.
Логическая схема для рассматриваемой функции в СДНФ реализована в базисе И, ИЛИ, НЕ и изображена на рис. 1.13.
Аналогично строится логическая схема для этой же функции после её минимизации по аналитической записи в МДНФ (1.4):
Такая логическая схема в булевом базисе приведена на рис.1.14. Сравнив две построенные схемы можно видеть что последняя схема содержит в два раза меньшее количество ЛЭ, которые имеют меньшее число входов.
Можно построить логическую схему в булевом базисе для этой же функции после её минимизации по аналитической записи в МКНФ (1.5),
,
которая представлена на рис. 1.15.
Часто необходимо построить схему из однотипных ЛЭ. Для этого требуется реализовать схему в базисе И–НЕ или в базисе ИЛИ–НЕ. Переход к другому базису осуществляется путем выполнения тождественных преобразований исходных выражений в формах СДНФ, МДНФ или СКНФ, МКНФ.
Для этого требуется реализовать схему в базисе И–НЕ или в базисе ИЛИ–НЕ. Переход к другому базису осуществляется путем выполнения тождественных преобразований исходных выражений в формах СДНФ, МДНФ или СКНФ, МКНФ.
Для построения схемы в базисе И–НЕ можно преобразовать аналитическую запись функции в МДНФ (1.4) путем её двойного инвертирования и применения закона Де Моргана:
.
Логическая схема в базисе И–НЕ приведена на рис.1.16.
Для построения схемы в базисе ИЛИ–НЕ можно преобразовать аналитическую запись функции в МКНФ (1.5) также путем её двойного инвертирования и применения закона Де Моргана:
Логическая схема в базисе ИЛИ–НЕ приведена на рис.1.17.
Далее рассматривается несколько простых логических функций, реализуемых элементами рассмотренных базисов.
Элемент «Сравнение». На выходе такого элемента должна быть логическая 1, если на входах одновременно присутствуют одинаковые логические переменные (единицы или нули).
Легко установить, что при равнозначности переменных х1 и х0 конъюнкции их прямых или инверсных значений равны единице, т. е. функция рассматриваемого элемента выразится в базисе как
Используя теорему де Моргана, представим эту функцию в базисе И—НЕ:
На рис. 1.17, а, б приведены логические схемы элемента «Сравнение» на ЛЭ базисов И, ИЛИ, НЕ и И—НЕ соответственно. Условное графическое изображение элемента дано на рис. 1.18, в.
Элемент «Исключающее ИЛИ». На выходе такого элемента должна быть логическая 1, если на входах присутствуют неравнозначные логические переменные:
у=1, если х1=1, x0=0или ;х1=0, x0= 1.
Исходя из самого определения, легко записать логическую функцию: конъюнкции неравнозначных переменных должны быть равны единице, т. е.
е.
.
Применяя теорему де Моргана, запишем эту функцию в базисе И—НЕ:
,
где правая часть выражения дополнительно дважды инвертирована.
Функциональные схемы рассматриваемого элемента в соответствии с выражениями приведены на рис. 1.18, а, б. Условное обозначение элемента «Неравнозначность» дано на рис. 1.18,в.
Элемент «исключающее ИЛИ» иначе называют сумматором по модулю два: сумма двоичных цифр дает в результате 1; если одна из них 1, а другая — 0; эта сумма равна 0, если обе цифры одинаковы – 0 или 1.
Дата добавления: 2017-06-13; просмотров: 18304; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
НОУ ИНТУИТ | Лекция | Минимизация логических функций
< Лекция 2 || Лекция 3: 12345678910111213 || Лекция 4 >
Аннотация: Цель лекции: познакомить студента с основными методами минимизации логических функций: методом Квайна – Мак-Класки, методом минимизирующих карт. Ключевые слова: импликанта, простая импликанта, сокращенная нормальная форма, тупиковая нормальная форма.
Ключевые слова: импликанта, простая импликанта, сокращенная нормальная форма, тупиковая нормальная форма.
Минимизация логических функций
Преобразование логических функций с целью упрощения их аналитического представления называются минимизацией.
Понятие «упрощение» требует определенных договоренностей, что под этим будет пониматься. Упрощение можно рассматривать с точки зрения числа переменных в получаемоq эквивалентной функции, уменьшения количества отрицаний в результирующем выражении, более простой схемотехнической реализации при переводе получающейся ФАЛ на уровень интегральных микросхем и так далее.
Мы будем считать, что дизъюнктивная или конъюнктивная нормальная форма являются минимальными, если они содержат наименьшее суммарное число переменных среди всех ДНФ или КНФ, эквивалентных ей. При этом количество отрицаний над переменными учитывать не будем.
Методы минимизации можно разделить на несколько типов:
- Метод непосредственных преобразований логических функций.
- Метод неопределенных коэффициентов.
Аналитические методы (метод Квайна11Квайн, Уиллард Ван Орман — американский философ, логик и математик, метод Квайна – Мак-Класки).
- Метод минимизирующих карт (карты Карно, диаграммы Вейча).
Рассмотрим их более подробно. Рассмотрение будем проводить на основе дизъюнктивных нормальных форм. Для КНФ теоретические рассуждения будут аналогичными.
В то же время, иллюстрировать соответствующие положения будем как на примерах дизъюнктивны, так и конъюнктивных форм.
intuit.ru/2010/edi»>Если некоторая логическая функция равна нулю на тех же наборах, на которых равняется нулю другая функция f, то говорят, что функция входит в функцию f. Другими словами, функция входит в функцию f тогда, когда она накрывает нулями все нули функции f, а единицы функции f могут быть накрыты как нулями, так и единицами функции .Очевидно, что ФАЛ «Константа ноль» входит во все функции, а в ФАЛ «Константу единица» входят все функции.
Функцию , входящую в данную функцию f, называют ее импликантой.
Простыми (первичными) импликантами (имплицентами для КНФ) логической функции f называют такие элементарные произведения или элементарные суммы (для имплицент), которые сами входят в данную функцию, но никакая собственная частьэтих произведений (сумм) не входит в функцию f.
ru/2010/edi»>Собственной частью называют произведение, полученное путем исключения из данного произведения одного или нескольких сомножителей.Примеры этих определений показаны в Табл. 3.1.
| x | y | z | f(x,y,z) | ||||
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Импликанта ф-ии f(x,y,z) | Простая импликанта | Неимпликанта | Неимпликанта |
Дальше >>
< Лекция 2 || Лекция 3: 12345678910111213 || Лекция 4 >
Упрощение логических выражений
Государственное бюджетное общеобразовательное учреждение Республики Крым «Керченская школа-интернат с усиленной физической подготовкой»
РАЗРАБОТКА УРОКА
« УПРОЩЕНИЕ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ»
РАЗДЕЛ «ЛОГИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ» ДЛЯ КУРСА ИНФОРМАТИКИ В СТАРШЕЙ ШКОЛЕ (10 КЛ. )
)
Учитель Романец К.С.
Керчь, 2017 год
Введение. Основная образовательная задача урока по теме «Упрощение логических выражений» – научить школьника умению упрощать логические выражения, правильно определять порядок выполнения операций в логическом выражении, устанавливать смысловые связи между различными частями сложных логических выражений, умение выбирать лучший вариант решения.
Цель урока: научить учащихся упрощать логические выражения с помощью законов алгебры логики.
Задачи:
Образовательные:
умение четко разделять изучаемый объект на составные части;
умение правильно определять порядок выполнения операций в логическом выражении;
умение устанавливать смысловые связи между различными частями сложных логических выражений;
умение выбирать лучший вариант решения.

Развивающие:
Воспитательные:
Планируемый результат: приобретение навыков работы с логическими выражениями.
Тип урока: традиционный.
Формы работы: работа в классе, самостоятельная работа.
План проведения занятия
Вводная часть (объявление темы урока, цели и задач урока).
Изложение материала по упрощению логических выражений с помощью законов алгебры логики с демонстрацией примера с помощью визуальных средств (интерактивная доска).
Выдача индивидуальных заданий.
Контроль работы учащихся по упрощению логических выражений, консультация по возникающим вопросам.
Подведение итогов работы учащихся.
Домашнее задание по теме «Упрощение логических выражений».

1. Вводная часть урока
В начале урока учитель объявляет тему урока, цели и задачи. Затем учитель предлагает вспомнить, что такое логика и где ученики уже встречались с элементами логики, задавая соответствующие вопросы.
Вопросы учителя и примерные ответы учеников:
1. Вопрос учителя: Что такое логика?
Ответ ученика:
Логика — это наука о формах и способах мышления.
2. Вопрос учителя: Что такое алгебра логики?
Ответ ученика:
Алгебра логики — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.
3. Вопрос учителя: Что такое логическое высказывание?
Ответ ученика:
Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно (1) оно или ложно (0).
4. Вопрос учителя: Что такое логическая формула?
Ответ ученика:
Логическая формула — это логические переменные (высказывания, обозначенные буквами), соединенные знаками логических операций.
5. Вопрос учителя: Какие логические операции вы знаете?
Ответ ученика:
Логические операции: отрицание (инверсия), конъюнкция, дизъюнкция, импликация, эквиваленция.
6. Вопрос учителя: Какие законы алгебры логики вы знаете?
Ответ ученика:
Основные законы алгебры логики:
Закон | Для ИЛИ | Для И |
Переместительный | ||
Сочетательный | ||
Распределительный | В отличие от алгебры переменных и функций, где за скобки можно выносить только общие множители, в алгебре логики за скобки можно выносить как общие множители, так и общие слагаемые. | |
Правила де Моргана | ||
Идемпотенции | ||
Поглощения | ||
Склеивания | ||
Операция переменной с ее инверсией | ||
Операция с константами | ||
Двойного отрицания | ||
Импликация | ||
Эквиваленция | ||
Исключающее ИЛИ | ||
2. Изложение материала по упрощению логических выражений с помощью законов алгебры логики с демонстрацией примера с помощью визуальных средств (интерактивная доска)
Изложение материала по упрощению логических выражений с помощью законов алгебры логики с демонстрацией примера с помощью визуальных средств (интерактивная доска)
Упрощение логических выражений
Приоритет выполнения логических операций: отрицание, конъюнкция, дизъюнкция, импликация. Если же порядок выполнения операций надо изменить, то применяют скобки. Операции эквиваленция и исключающее ИЛИ имеют самый низкий приоритет.
Формула называется тождественно истинной, или тавтологией, если она принимает значение истина при любых значениях входящих в нее переменных. Примером простейшей тавтологии является формула .
Формула называется тождественно ложной, или противоречием, если она принимает значение ложь при любых значениях входящих в нее переменных. Примером простейшего противоречия является формула.
Если две формулы одновременно, т. е. при одинаковых наборах входящих в них переменных, принимают одинаковые значения, то они называются равносильными.
е. при одинаковых наборах входящих в них переменных, принимают одинаковые значения, то они называются равносильными.
Равносильные преобразования логических формул служат для упрощения формул или приведения их к определённому виду путем использования основных законов алгебры логики.
Под упрощением формулы, не содержащей операций импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных.
Обозначим:
X – логическое высказывание,
– инверсия,
& – конъюнкция,
– дизъюнкция,
– импликация,
– эквиваленция.
Упростить логическое выражение:
1).
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций:
Воспользуемся распределительным законом и вынесем за скобки общий множитель, затем операцией переменной с ее инверсией.
Воспользуемся распределительным законом и вынесем за скобки общий множитель, затем операцией переменной с ее инверсией, затем операцией с константами.
Таким образом,
2)
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций. В выражении присутствуют два выражения в скобках, соединенных дизъюнкцией. Сначала преобразуем выражения в скобках.
В первой скобке воспользуемся распределительным законом, во второй скобке – раскроем инверсию по правилу де Моргана и избавимся от инверсии по закону двойного отрицания.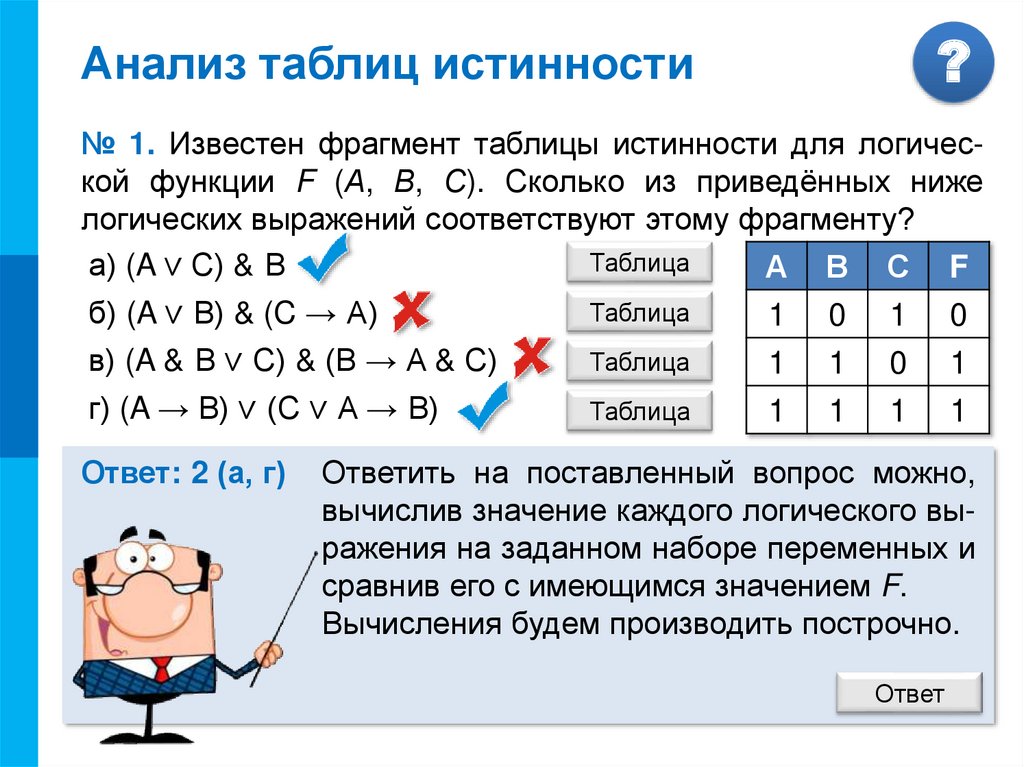
Воспользуемся операцией переменной с ее инверсией.
Таким образом,
3)
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций. В выражении присутствуют два выражения в скобках, соединенных конъюнкцией. Сначала преобразуем выражения в скобках.
Раскроем инверсию по правилу де Моргана, избавимся от инверсии по закону двойного отрицания.
Воспользуемся переместительным законом и поменяем порядок логических сомножителей.
Воспользуемся законом склеивания
Воспользуемся распределительным законом, затем операцией переменной с ее инверсией, затем операцией с константами.
Таким образом,
4).
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций.
В выражении присутствует импликация. Сначала преобразуем импликацию .
Воспользуемся правилом де Моргана, затем законом двойного отрицания, затем раскроем скобки.
Воспользуемся законом идемпотенции и перегруппируем логические слагаемые.
Воспользуемся распределительным законом и вынесем за скобки общий логический множитель.
Воспользуемся операцией с константами.
Таким образом,
5).
Рассмотрим 3 способа упрощения этого логического выражения.
1 способ.
Перепишем выражение с помощью более привычных операций умножения и сложения.
Воспользуемся распределительным законом и раскроем скобки, затем операцией переменной с ее инверсией и законом идемпотенции.
Воспользуемся распределительным законом и раскроем скобки, затем операцией переменной с ее инверсией.
Воспользуемся законом идемпотенции.
Таким образом,
2 способ.
Перепишем выражение с помощью более привычных операций умножения и сложения.
Воспользуемся законом склеивания
Воспользуемся операцией переменной с ее инверсией.
Таким образом,
3 способ.
Перепишем выражение с помощью более привычных операций умножения и сложения.
Повторим второй сомножитель , что разрешено законом идемпотенции.
Сгруппируем два первых и два последних сомножителя.
Воспользуемся законом склеивания
Таким образом,
Вывод: используя разные законы алгебры логики, получили один и тот же результат.
6).
Рассмотрим 2 способа упрощения этого логического выражения.
1 способ.
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций.
Воспользуемся распределительным законом и вынесем общий логический множитель за скобки.
Как видно, логическое выражение не очень-то и упростилось. Попробуем 2 способ.
2 способ.
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций.
Введем вспомогательный логический сомножитель
Сгруппируем 1 и 4, 2 и 3 логические слагаемые. Вынесем общие логические множители за скобки.
Воспользуемся операцией с константами и операцией переменной с ее инверсией.
Таким образом,
Получили два логических выражения:
Теперь построим таблицы истинности и посмотрим, правильно ли упрощено логическое выражение
X | Y | Z | ||||
0 | 0 | 0 | 0 | 0 | 0 | 0 |
0 | 0 | 1 | 0 | 0 | 0 | 0 |
0 | 1 | 0 | 0 | 0 | 0 | 0 |
0 | 1 | 1 | 0 | 1 | 0 | 1 |
1 | 0 | 0 | 1 | 0 | 0 | 1 |
1 | 0 | 1 | 1 | 0 | 1 | 1 |
1 | 1 | 0 | 0 | 0 | 0 | 0 |
1 | 1 | 1 | 0 | 0 | 1 | 1 |
X | Y | Z | ||||
0 | 0 | 0 | 1 | 0 | 0 | 0 |
0 | 0 | 1 | 1 | 0 | 0 | 0 |
0 | 1 | 0 | 0 | 0 | 0 | 0 |
0 | 1 | 1 | 1 | 0 | 1 | 1 |
1 | 0 | 0 | 1 | 1 | 0 | 1 |
1 | 0 | 1 | 1 | 1 | 0 | 1 |
1 | 1 | 0 | 0 | 0 | 0 | 0 |
1 | 1 | 1 | 1 | 1 | 0 | 1 |
X | Y | Z | |||
0 | 0 | 0 | 0 | 0 | 0 |
0 | 0 | 1 | 0 | 0 | 0 |
0 | 1 | 0 | 0 | 0 | 0 |
0 | 1 | 1 | 0 | 1 | 1 |
1 | 0 | 0 | 1 | 0 | 1 |
1 | 0 | 1 | 1 | 0 | 1 |
1 | 1 | 0 | 0 | 0 | 0 |
1 | 1 | 1 | 0 | 1 | 1 |
X | Y | Z | |||
0 | 0 | 0 | 0 | 0 | 0 |
0 | 0 | 1 | 0 | 0 | 0 |
0 | 1 | 0 | 0 | 0 | 0 |
0 | 1 | 1 | 1 | 1 | 1 |
1 | 0 | 0 | 1 | 1 | 1 |
1 | 0 | 1 | 1 | 1 | 1 |
1 | 1 | 0 | 0 | 0 | 0 |
1 | 1 | 1 | 1 | 1 | 1 |
Как видно из сравнения таблиц истинности формулы являются равносильными.
Вывод: используя разные законы алгебры логики, получили один и тот же результат, записанный разными способами.
3. Выдача индивидуальных заданий
После изложения материала по упрощению логических выражений с демонстрацией примера с помощью интерактивной доски учащимся выдаются следующие материалы для выполнения задания:
В процессе выполнения задания преподаватель осуществляет контроль поэтапной работы учащихся по упрощению логических выражений и консультацию по возникающим вопросам.
Задание: Упрощение логических выражений
Вариант №1
Какие из высказываний А, В, С должны быть истинны и какие ложны, чтобы было ложно высказывание:
Вариант №2
Какие из высказываний А, В, С должны быть истинны и какие ложны, чтобы было ложно высказывание:
Домашнее задание по теме «Упрощение логических выражений».
Ответы
№ | 1 вариант | 2 вариант | Домашнее задание |
1 | |||
2 | 0 | ||
3 | 1 | 0 | |
4 | А | А | 1 |
5 | A=true, B=true, C=false | B=true, C=false, A – любое |
Хронометраж урока (2 ак. часа):
часа):
Действие | Продолжительность |
Вводная часть (объявление темы урока, цели и задач урока, повторение ранее пройденного материала). | 15 минут |
Изложение материала | 25 минут |
Выдача задания | 3 минуты |
Контроль поэтапной работы учащихся по упрощению логических выражений, консультация по возникающим вопросам. | 25 минут |
Подведение итогов работы учащихся. Домашнее задание. | 12 минут |
Используемая литература
А.Г.Гейн. Материалы курса «Математические основы информатики»: лекции 5-8. – М.:Педагогический университет «Первое сентября», 2008.
 – 116с.
– 116с.Информатика и ИКТ. Профильный уровень: учебник для 10 класса / Н.Д. Угринович. – 3-е изд., испр. – М. : БИНОМ. Лаборатория знаний, 2008. – 387 с.
Информатика : Учеб. Пособие для 10 – 11 кл. общеобразоват. учреждений / Л.З.Шауцукова. – 2-е изд., дораб. – М.:Просвещение, 2012. – 416с.
Конспекты уроков информатики в 9-11 классах: практикум по программированию / авт.-сост. А.А.Чернов. – Волгоград: Учитель, 2012. – 235с.
Фалина И.Н., Богомолова Т.С., Большакова Е.А., Гущин И.С., Шухардина В.А. Алгоритмизация и программирование.–М.:КУДИЦ-ПРЕСС, 2010. – 276с.
Под редакцией Вовк Е.Т. Информатика: пособие для подготовки к ЕГЭ. – М.: КУДИЦ-ПРЕСС, 2013. – 304 с.
Лихтарников Л.М. Первое знакомство с математической логикой / Оформление А.Олексенко, С.Шапиро. – СПб.:Лань, 1997. – 112с.
Информатика.
 Упрощение логических выражений
Упрощение логических выраженийОпределение 1
Упрощение логических выражений — это замена их на равнозначные на базе законов алгебры логики с целью получения высказываний более простой формы.
Введение
Чтобы написать любую логическую функцию, можно использовать логическое выражение, а затем можно сформировать логическую схему. Обычно каждую логическое выражение стараются упростить с целью формирования самой простой и дешевой логической схемы. По сути, логическая схема, выражение и логическая функция, считаются тремя разными языками, которые повествуют об одном и том же.
Логические выражения могут быть упрощены с помощью разных законов алгебры логики. Отдельные преобразования напоминают преобразования формул, которые выполняются в стандартной алгебре. К примеру, использование сочетательного и переместительного законов, вынесение за скобки равенства общего множителя и тому подобное. Для других преобразований применяют свойства, которых нет в операциях классической алгебры.
Упрощением формулы, которая не содержит операций импликации и эквивалентности, является равнозначное преобразование, ведущее к формуле, либо содержащей, по сравнению с исходной формулой, меньшее количество операций конъюнкции и дизъюнкции и не содержащей отрицаний неэлементарных формул, либо содержащей меньшее количество вхождений переменных.
Метод, позволяющий определить истинность логического выражения за счёт формирования его таблицы истинности, превращается в неудобный при возрастании количества логических переменных, так как за счет значительного роста количества строк таблицы могут стать достаточно громоздкими. В таком случае осуществляется преобразование логических выражений в равнозначные. Для этого применяются свойства логических операций, которые по-другому именуются законами алгебры логики.
Упрощение логических выражений
Все законы алгебры логики выводятся для главных логических операций следующим образом:
- НЕ является инверсией, то есть, отрицанием.

- ИЛИ является дизъюнкцией, то есть, логическим сложением.
- И является конъюнкцией, то есть, логическим умножением.
Правило двойного отрицания заключается в том, что операция НЕ является обратимой, то есть, если ее применить два раза, логический итог в результате останется неизменным.
Смысл правила исключенного третьего заключается в том, что каждое логическое выражение при всех условиях может быть или истинным, или ложным. Если A=1, тогда A=0, а также наоборот. Конъюнкция данных величин всегда равняется 0, дизъюнкция равна 1.
Закон повторения и операции с константами может быть просто проверен путём применения таблицы истинности операций ИЛИ и И.
Сочетательный и переместительный законы обладают таким же видом, как в математике. Здесь существует аналогия с понятной всем стандартной алгеброй.
Для дизъюнкции распределительный закон заключается просто в раскрытии скобок. Для конъюнкции выражение неизвестно, в математике подобное равенство является неверным. Приведём доказательство, начиная с правой части. В начале следует раскрыть скобки:
Приведём доказательство, начиная с правой части. В начале следует раскрыть скобки:
(A + B) ⋅ (A + C) = A ⋅ A + A ⋅ C + B ⋅ A + B ⋅ C
Применим закон повторения, который гласит, что A ⋅ A = A. Далее:
A ⋅ A + C ⋅ A = A + C ⋅ A = A ⋅ (1 + C) = A ⋅ 1 = A
A + A ⋅ B =A⋅ (1 + B) = A ⋅ 1 = A, следовательно, (A + B) ⋅ (A + C) = A + B ⋅ C.
Таким образом, равенство доказано.
Правила, применяемые для раскрытия инверсии сложных выражений, были названы в честь знаменитого логика и математика де Моргана. Их смысл заключается в том, что общее отрицание не только может быть распространено на отдельные выражения, а еще и то, что дизъюнкция может быть заменена конъюнкцией (а также наоборот). Для доказательства этих правил была использована таблица истинности.
Главная часть аксиом и законов алгебры логики записаны парами. Если внимательно изучить пары, то возможно сформулировать принцип двойственности, который формулируется следующим образом. Если выполнить в тождестве замены конъюнкции, а также дизъюнкции, а также элементов 1 и 0 (при их наличии), то получится тождество. Данное свойство называется принципом двойственности.
Данное свойство называется принципом двойственности.
Введём следующие обозначения:
- X является логическим высказыванием.
- x̅ является инверсией.
- & является конъюнкцией.
- V является дизъюнкцией.
- → является импликацией.
- ↔ является логической эквивалентностью.
Рассмотрим конкретный пример. Необходимо упростить следующее логическое выражение:
X & Y V X & Y ̅& ZV Y ̅& X& Z ̅ V X & Z ̅
Запишем данное выражение при помощи наиболее привычных действий умножения и сложения:
XY + XY ̅ Z +Y ̅X Z ̅ + X Z ̅ =
Далее следует воспользоваться распределительным законом и вынести за скобки общий множитель, затем операцией переменной с ее инверсией:
XY + X Y ̅ (Z + Z ̅) + X Z ̅ = XY + X Y ̅ + X * Z ̅ =
Затем следует снова воспользоваться распределительным законом и вынести за скобки общий множитель, а далее операцией переменной с ее инверсией, затем операцией с константами:
X (Y + Y ̅ + Z ̅) = X (1+ Z ̅) = X* 1 = X
Подводя итог, можем сделать следующий вывод, что:
X & Y V X & Y ̅& ZV Y ̅& X& Z ̅ V X & Z ̅= X
Рассмотрим ещё один пример. Требуется определить, кто из рабочих, условно обозначаемых, как A, B, C, D работает на заводе, а кто не работает, если имеются следующие начальные условия:
Требуется определить, кто из рабочих, условно обозначаемых, как A, B, C, D работает на заводе, а кто не работает, если имеются следующие начальные условия:
- Когда работает A или работает B, то в этом случае не работает C.
- Когда не работает B, тогда работает D, а также работает C.
Решение задачи данной задачи может быть выполнено следующим образом. Введём обозначения следующих простых высказываний:
- A рабочий A работает на заводе.
- B рабочий B работает на заводе.
- C рабочий C работает на заводе.
- D рабочий D работает на заводе.
Если сформулировать данные из условия с помощью этих простых высказываний, то можно получить следующую конъюнкцию:
((A + B) → C) ⋅ (B → C ⋅ D) ⋅ C.
Если упростить данную формулу, то можно получить, что A равняется 0, B равняется 1, C равняется 1, D равняется 1. Следовательно, это означает, что рабочий A на заводе не работает, а работники B, C, D работают.
В данном примере использовано правило де Моргана, далее применён распределительный закон, после этого использован закон исключенного третьего, а затем использовался переместительный закон. За ним осуществлён закон повторения, потом снова использован переместительный закон и в конце использовался закон поглощения.
За ним осуществлён закон повторения, потом снова использован переместительный закон и в конце использовался закон поглощения.
Основы логики По основам л
Основы логики По основам лОсновы логики На главную
(Из рубрики: Начинающим о компьютерных технологиях. Автор — NK) nk-inform.narod.ru
По основам логики написаны большие книги. Данная страничка содержит сжато-концентрированное описание базовых начал логики необходимое для осмысленного рассмотрения основ компьютерных технологий, основ программирования и основ компьютерной микросхематики. В случае затруднений в понимании материала необходимо обратиться к источникам с более объемным и подробным рассмотрением данной темы.
Предлагаются к рассмотрению следующие темы:
1. Введение. Основные понятия.
2. Логические функции.
3. Построение логических выражений.
4. Основные законы логики.
5. Преобразование и упрощение логических выражений.
6. Решение логических задач.
7. Основы компьютерной микросхематики.
Введение. Основные понятия. В начало
Логика – наука о формах и способах рассуждений.
Зачем необходимо знать ее основы?
Зная законы физики, вы прекрасно представляете, что с метровой высоты прыгать можно, а с десятиметровой опасно. Зная логические законы, вы сможете, совершенно однозначно, определять: произойдет то или иное событие при наличии определенных условий или нет, а не действовать наугад.
Когда мы бросаем камень, он летит, подчиняясь законам физики, когда мы солим
пищу, соль растворяется, подчиняясь законам химии, когда мы рассуждаем или
просто общаемся, не замечая этого, мы подчиняем свои рассуждения законам логики.
Когда мы говорим, это правда, а это ложь, или, если получится, это и это, то
будет то, или это никогда не произойдет без этого – мы выстраиваем суждения по
законам логики.
Формальная логика отделяет содержание процесса мышления от его общих принципов.
Это означает, например, если вы обещаете прибыть на встречу, то для логики важно
прибудете или нет, а на каком виде транспорта и в какой одежде для нее не имеет
значения.
Или, когда вы говорите: я выпью кофе, если он будет крепким, сладким и горячим,
для логики не имеет значения, кто, как, когда и каким способом будет готовить
условия для логичного завершения действия.
Логика изучает структуру процесса мышления. Мышление это сложный процесс, но и его можно разложить на некоторое количество форм (то, при помощи чего мы выражаем свои мысли), которые объединяются по общим признакам.
Итак, мышление может быть выражено следующими формами.
1. Понятие
2. Суждение (высказывание).
3. Умозаключение
4. Доказательство.
Понятие – форма мышления, отражающая существенные формы предмета или явления. (Яркий
свет, круглый камень, холодная погода).
Высказывание это форма мышления, выраженная при помощи понятий, когда что-то
утверждается или отрицается.
— Половины бака бензина недостаточно, чтобы доехать до места.
— Монета упала изображением номинала (решкой) вверх.
— Спортсмен преодолел планку на высоте 2.20.
— Из-за обрыва провода не воспроизводится звук в наушниках MP3 плейера.
— Я еду с требуемой скоростью при виде знака по ее ограничению.
Высказывание существует в двух формах – ИСТИНА и ЛОЖЬ
Суждение истинно, если оно правильно отражает свойства или отношения реальных
вещей.
Суждение ложно, если оно искажает объективные отношения.
Фундаментальное понятие логики – она не рассматривает обоснование истинности.
В естественном языке высказывание – повествовательное предложение. Высказывания
используют формальные языки – математика, физика, химия. Электронные устройства,
в том числе и компьютерные тоже могут обмениваться высказываниями (сообщениями),
которые, тоже могут подчиняться законам логики.
Высказывание считается простым, если никакая из его частей не является высказыванием.
Логические функции. В начало
Основная задача — логики рассмотрение сложных логических выражений.
Простые высказывания соединяются в сложные при помощи логических связок (функций).
Логическая функция это формальное правило преобразования или объединения высказываний, пришедшее в логику из обычной жизни.
Основные логические функции:
Инверсия – НЕ
Функция преобразующая исходное высказывание в обратное.
— Приятель будет звонить мне в 17.00. (А он не позвонил)
— Кран сможет поднять груз на эту высоту. (А он не смог)
— Прошел дождь — полив не требуется
Дизъюнкция – ИЛИ логическое сложение.
— Ты должен помыть посуду или убраться в комноте, тогда пойдешь гулять. (Необходимо
выполнить или то, или то, в этом случае результатом будет истина и вы пойдете
гулять)
Конъюнкция – И логическое умножение.
— Вы должны владеть иностранным языком и иметь высшее образование, только тогда
вас возьмут на работу. (Наличие одного из условий не обеспечивает вашего приема
на работу. Только в случае если и первое и второе выполняется тогда результатом
станет истина — прием на работу)
Импликация – следование.
(Импликация не имеет простой жизненной интерпретации). Для себя я ее определяю
по следующему правилу. Трагедия в том, что хотел, но не получилось.
В результате: Хотел и получилось — это истина. Не хотел, а получилось, тоже
истина. Не хотел и не получилось истина потому, что мне нет до этого никакого
дела.
Эквиваленция – равенство. Здесь все просто — результат — истина если исходные высказывания эквивалентны: оба истины или ложны.
Договоримся обозначать простые высказывания заглавными буквами английского
алфавита.
И сведем обозначения логических связок в таблицу
Таблица обозначений логических связок — функций
| Логическая связка (функция) | Обозначение | Название |
| A и B | A & B, A and B, A Λ B | Конъюнкция |
| A или B | A V B, A or B | Дизъюнкция |
| Не А , A неверно |
_ ¬ A, A | Инверсия |
| Из A
следует B, Если A то B, A влечет B, B следствие A | A -> B, If A then B | Импликация Следование |
| A равно B | A <—> B | Эквиваленция |
Результирующее
высказывание, полученное из простых путем их объединения при помощи
логической функции может быть, как истинным так и
ложным. Для каждой из функций объединение
происходит по определенным правилам. Необходимо рассматривать все случаи исходных высказываний. Правила
объединения исходных высказываний принято сводить в
таблицы. Такие таблицы называются таблицами
истинности.
Для каждой из функций объединение
происходит по определенным правилам. Необходимо рассматривать все случаи исходных высказываний. Правила
объединения исходных высказываний принято сводить в
таблицы. Такие таблицы называются таблицами
истинности.
Принято ложь определять как 0, а истину, как 1.
Таблицы истинности для логических функций.
Конъюнкция. И &
| A | B | C |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Дизъюнкция. ИЛИ V
ИЛИ V
| A | B | C |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
Инверсия. НЕ
| A | B |
| 0 | 1 |
| 1 | 0 |
Импликация. ->
| A | B | C |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
Эквиваленция. <—>
<—>
| A | B | C |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Построение (запись) логических выражений. В начало
Каждое сложное (составное) высказывание можно выразить в виде формулы – логического выражения.
В выражение входят:
— логические переменные,
которые обозначают высказывания
— знаки логических операций, которые обозначают логические функции.
Для
составления выражений на языке алгебры логики нужно
выделить простые высказывания и логические связки
между ними.
Рассмотрим пример логического выражения.
(X * Y = 5 или X * Y = 4 ) И (X * Y ≠ 5 или X * Y ≠ 4)
Подставим в выражение значения x=2, y=2
(2 * 2 = 5 или 2 * 2 = 4) И (2 * 2 ≠ 5 или 2 * 2 ≠ 4)
Выделяем простые высказывания и связки
( A или B ) И (¬A или ¬B )
Запишем выражение логической функции
F = ( A V B ) & (¬A V ¬B )
Подставим в функцию формальные значения высказываний.
F = ( 0 V 1) & (1 V 0) = 1 & 1 = 1 — для данных условий результирующим значением функции является истина
Для выяснения поведений функций в любых ситуациях строят для них таблицы истинности.
Количество проверяемых комбинаций равно 2n
— где n – количество логических переменных.
Рассмотрим следующую функцию: F = ( A V B ) & (¬A V ¬B )
| А | B | A V B | ¬A | ¬B | ¬A V ¬B | F |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Хотя логика работает с формальными логическими
выражениями, всегда подразумевается, что эти выражения запись жизненной
ситуации, математической задачи, режимов работы электронных или компьютерных
устройств и так далее.
Рассмотрим несколько примеров построения логических выражений.
Пример 1.
Постановка условия:
Если придет Вася или Коля и мама разрешит, то пойду
гулять.
Обозначим :
| Приход Васи | A | |
| Приход Коли | B | |
| Разрешение мамы | C |
Запишем логическую функцию F = ( A V B )
& C
Составим таблицу истинности
| A | B | A V B | C | ( A V B ) & C |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 |
Создание таблицы истинности позволяет
рассмотреть все возможные ситуации и получить для каждого случая результирующее
значение логического выражения.
Пример 2
Постановка условия: Выбрать из массива нечетные положительные числа
Четное число A
Нечетное число ¬A
Положительное число B
| Четное число | A | |
| Нечетное число | ¬A | |
| Положительное число | B |
F = ¬A Λ B
Таблица истинности
| A | ¬A | B | ¬A Λ B |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
Пример 3
Постановка условия: Имеем массив
из N целых положительных чисел. Подсчитайте количество четных и нечетных.
Подсчитайте количество четных и нечетных.
Если X – четное
A
Если X – нечетное ¬A
Логическая функция F = A V ¬A
| A | ¬A | A V ¬A |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
И что же мы имеем? A V ¬A = 1
Дизъюнкция высказывания с инверсией всегда истинна.
И вправду, какими же еще могут быть целые положительные
числа?
Основные законы логики. В начало
Логические выражения могут быть равносильно преобразованы из одной формы в
другую согласно законам логики. Рассмотрим кратко основные из них.
1. Двойного отрицания:
А = ¬(¬A)
2. Переместительный (коммутативный) :
Переместительный (коммутативный) :
A V B = B V A
A & B = B & A
3. Сочетательный (ассоциативный):
(A V B) V C = A V (B V C)
(A&B) & C = A & (B & C)
4. Распределительный (дистрибутивный)
(A V B) & C = (A & C) V (B & C)
(A & B) V C = (A V C) & (B V C)
5. Закон общ. инверсии (законы де Моргана):
¬( A V B) = ¬A & ¬B
¬(A & B) = ¬A V ¬B
A à B = ¬A V B
¬(A à B) = A & ¬B
6. Закон идемпотентности
A V A = A
A & A = A
7. Законы исключения констант:
A V 1 = 1, A V 0 = A
A & 1 = A, A & 0 = 0
8.
Закон противоречия:
A & ¬A=
0.
9. Закон исключения третьего:
A V ¬A = 1.
10. Закон поглощения:
A V (A & B) = A;
A & (A V B) = A.
11. Закон исключения (склеивания):
(A&B) V (¬A & B) = B
(A V B) & (¬A V B) = B
Я не задерживался здесь подробно потому, что основные законы логики стройны и логичны. За подробными доказательствами и комментариями можно обратиться к литературе или проверить эти выкладки самостоятельно с использованием таблиц истинности.
Преобразование и упрощение
логических выражений. В начало
Как уже говорилось выше использование законов логики позволяет равносильно преобразовывать логические выражения, что зачастую приводит к их упрощению.
1. А V (┐А & В) = (A V ┐А) &
(AV B) = 1 & (AV B) = (1 &A) V (1 &B)
= A V B
— Выполняем дизъюнкцию с каждым из высказываний в скобках.
— Дизъюнкция A с
инверсией дает истину (1).
— Выполняем конъюнкцию с каждым из высказываний в скобках.
— Результатом конъюнкции высказывания с истиной является само
высказывание.
2. (А V В) & (┐A V B) & (С V┐B ) = B & (С V┐B ) = (B&С) V (B &┐B) = (B&┐С) V 0 =
(B V 0) & (C V 0) = B & C
— Согласно распределительному закону выводим B
за скобку из первой и второй дизъюнкций.
— Конъюнкция высказывания A
с его инверсией дают ложь.
— Дизъюнкция высказывания с ложью дает само высказывание.
— Выполняем конъюнкцию B с
каждым из высказываний в скобках.
— Конъюнкция B со своей
инверсией дают ложь.
— Дизъюнкция высказываний B и
C с ложью дают оригинальные
высказывания.
3. ┐((A v B) → ┐(B v C))
= A v B & ┐ ┐(B v C) = (A v B) & (B v C) = B v (A & C)
— Выполняем преобразование импликации согласно закону
де Моргана
— Двойная инверсия
пропадает, а высказывание
B, согласно распределительного закона выводим за скобку.
Решение логических задач. В начало
Логические задачи могут быть решены следующими способами.
1. С помощью рассуждений.
2. С помощью преобразований логических выражений.
3. Табличным способом.
Рассмотрим классическую задачу с разбитой вазой.
На звук разбившейся вазы прибежала мама. На вопрос мамы: кто это сделал, три мальчика ответили следующее.
— Саша сказал: Коля не разбивал, это Ваня.
— Вася ответил: Разбил Коля, Саша не играет в футбол.
— Коля сказал: Это не Ваня, а я еще уроки не выучил.
Как оказалось два мальчика сказали правду, а один солгал.
Метод рассуждений:
Саша: 1. Это не Коля. 2. Это Ваня.
Ваня: 1. Это Коля. 2. Это не Саша.
Коля: 1. Это не Ваня. – у Коли только одно высказывание.
Мальчиками, которые сказали правду, не могут быть одновременно Саша и Ваня, так как их высказывания противоречат друг другу.
Это не могут быть Саша и Коля – их высказывания противоречат друг другу.
Значит, правду сказали Ваня и Коля, а Саша солгал.
Значит, вазу разбил Коля.
Метод преобразования логических выражений.
C — вазу разбил Саша.
В – вазу разбил Ваня.
К – вазу разбил Коля.
Саша сказал: 1. ¬K 2. В
Ваня сказал: 1. К 2. ¬С
Коля сказал: 1. ¬В
Если Саша солгал, то выражение запишется: . ¬K = 0 В = 0
Если Саша сказал правду, ¬K = 1 В = 1
Рассмотрим предположения:
Коля солгал, а Саша и Ваня сказали правду.
¬K & В = 1 и К& ¬C =1 и B = 1
В результате имеем: ¬K & В & К & ¬C & B = 1
Но ¬K & К = 0 Значит ноль левой части равен единице правой.
Наше предположение неверно.
Предполагаем далее:
Ваня солгал, а Саша и Коля сказали правду.
Тогда имеем: ¬K & В = 1 и ¬K & C = 1 и ¬ В = 1
¬K & В & ¬K & C & ¬ В = 1
Учитывая что ¬B & B = 0 Левая и правая части выражения противоречат друг другу.
Предполагаем последний вариант:
Саша солгал, а Ваня и Коля сказали правду.
K & ¬ B = 1 и K & ¬C = 1 и ¬B = 1
K & ¬ B & K & ¬C & ¬B = 1 Упростим выражение, зная, что
K & K = K ¬B & ¬B = B
K & ¬B & ¬ C = 1
Результирующее выражение указывает на то, что наше предположение истинно и вазу разбил Коля.
Рассмотрим табличную форму решения логических задач.
Задача.
Джуди, Айрис и Линда живут в разных городах и имеют разные профессии. Нужно
определить их профессии и местожительства если известно:
— Джуди живет не в Париже, а Линда не в Риме.
— Парижанка не снимается в кино.
— Та, что живет в Риме, певица.
— Линда равнодушна к балету.
| Париж | Рим | Чикаго | Пение | Балет | Кино | |
| 0 | Джуди | 0 | ||||
| Айрис | 0 | |||||
| 0 | Линда | 0 | 0 | 1 |
Линда живет не в Риме, значит она
не певица, и равнодушна к балету, значит она актриса. А Айрис и Джуди актрисами
быть не могут.
А Айрис и Джуди актрисами
быть не могут.
| Париж | Рим | Чикаго | Пение | Балет | Кино | |
| 0 | Джуди | 0 | ||||
| 1 | Айрис | 0 | ||||
| 0 | 0 | 1 | Линда | 0 | 0 | 1 |
Парижанка не снимается в кино,
значит Линда не парижанка, а проживает в Чикаго. Теперь мы видим, что Джуди и
Линда не живут в Париже, значит там живет Айрис.
Теперь мы видим, что Джуди и
Линда не живут в Париже, значит там живет Айрис.
| Париж | Рим | Чикаго | Пение | Балет | Кино | |
| 0 | 1 | Джуди | 1 | 0 | ||
| 1 | Айрис | 1 | 0 | |||
| 0 | 0 | 1 | Линда | 0 | 0 | 1 |
Теперь получается, что Джуди
живет в Риме, а значит, она певица и Айрис остается быть балериной.
Основы компьютерной микросхематики. В начало
Основой всех компьютерных устройств, построенных по цифровому принципу, являются
логические элементы.
Логический элемент это электронное устройство, выполняющее соответствующую
логическую функцию.
Логический элемент И реализует конъюнкцию двух или более логических значений.
Таблица истинности схемы И
| X | Y | X&Y | |
| 0 | 0 | 0 | |
| 1 | 0 | 0 | |
| 0 | 1 | 0 | |
| 1 | 1 | 1 |
Логический элемент ИЛИ реализует дизъюнкцию двух или более
логических значений.
| X | Y | X V Y | |
| 0 | 0 | 0 | |
| 1 | 0 | 1 | |
| 0 | 1 | 1 | |
| 1 | 1 | 1 |
Логический элемент НЕ реализует логическую функцию инверсия.
| X | Y | |
| 0 | 1 | |
| 1 | 0 |
Реализация логических функций.
При помощи логических элементов в электронных
устройствах могут быть реализованы сложные логические функции. Рассмотрим
некоторые из них.
|
F = ¬ (
X V Y)
F = ( ¬X V Y)
F = ¬ ( ¬X & Y) | |
F = (X V Y) & ¬Y
F = (¬X & ¬Y) V Y
|
Элементы компьютерных схем.
Триггер
| Триггер — это электронная схема,
предназначенная для запоминания одного разряда двоичного кода. Триггер
имеет два устойчивых состояния, одно из которых соответствует двоичной
единице, а другое — двоичному нулю.S
– вход записи. R – сброс. Q – выход, хранимый бит. |
Сумматор
В целях максимального упрощения работы компьютера основная масса
математических операций сводится к сложению двоичных чисел. Поэтому главной
частью процессора является сумматор.
Поэтому главной
частью процессора является сумматор.
Сумматор — это электронно-логическая схема, выполняющая суммирование.
При сложении двоичных чисел образуется сумма в данном разряде, при этом возможен
перенос в старший разряд. Обозначим слагаемые (А, В), перенос (С) и сумму (S).
Построим таблицу сложения одноразрядных двоичных чисел с учетом переноса в
старший разряд.
Сложение одноразрядных двоичных чисел | |||
Слагаемые | Перенос | Сумма | |
| A | B | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Данная
схема называется полусумматором, так как выполняет суммирование
одноразрядных двоичных чисел без учета переноса из соседнего разряда.
|
P.S. На этом заканчивается вводный курс по основам логики. Как мы видим основные положения этой науки нашли свое широкое применение в компьютерных технологиях. Поэтому для серьезного использования компьютерной техники получение прочных знаний основ логики — обязательное условие.
Упрощение выражений с помощью карт
Карты позволяют упростить логические выражения. Главное при этом – сохранение истинностных значений исходной функции. Упрощение состоит в считывании функции с карты с применением основных логических правил (правило IV, табл. 2.14).
Для упрощения применяется определенный способ объединения ячеек, при котором формируются более крупные группы из ячеек карты.
Процедуру упрощения рассмотрим на примере. Возьмём в качестве исходной логическую функцию
(2.11.1).
Карта этой функции приведена на рис. 2.32.
| AB | ||||
| CD | 2,4 | |||
| 1,3,6 | ||||
| 6,7 | 1,2,5 | 1,2,3,4, 5,6,7 |
Рис. 2.32. Карта функции .
2.32. Карта функции .
Выпишем функции в каждой ячейке, следуя сверху вниз и слева направо. Получим функцию
(2.11.2).
Некоторые ячейки заполнялись более одного раза, например, угловая нижняя ячейка заполнялась семь раз, а считывается только один раз согласно правилу 1 табл. 2.14.
Полученная функция логически эквивалентна исходной, но слишком длинная и неудобная для использования.
Карта предоставляет возможности для упрощений. Для упрощений используется приём комбинирования любых двух соседних ячеек. Это приём называют также системой изменения одной переменной. Результатом комбинирования является сокращение букв, которые представлены одновременно и с отрицанием и без отрицания.
На рис. 2.33 представлен один из возможных вариантов попарного комбинирования ячеек.
В результате комбинирования получим функцию:
(2.11.3)
Ячейки верхней строки являются соседними ячейками нижней строки, а ячейки левого крайнего столбца являются соседними для ячеек правого крайнего столбца. Поэтому возможно комбинирование пар ячеек, расположенных в верхней и нижней строках, и в крайних левом и правом столбцах. Какой из вариантов комбинирования выбрать решает сам человек. (Решить задачу 4 из контрольных вопросов и задач).
Поэтому возможно комбинирование пар ячеек, расположенных в верхней и нижней строках, и в крайних левом и правом столбцах. Какой из вариантов комбинирования выбрать решает сам человек. (Решить задачу 4 из контрольных вопросов и задач).
| AB | ||||
| CD | ||||
| 1 | ||||
Рис. 2.33. Попарное комбинирование ячеек карты,
представленной на рис. 2.32
Поскольку в процедуре не участвуют незаполненные ячейки и участвуют все заполненные, то получаемые при любом комбинировании функции оказываются эквивалентными.
Попарное комбинирование позволяет уменьшить как число членов функции, так и длину каждого из них.
Попарное комбинирование основано на прямом применении правила IV таб. 2.14.
Можно выбирать комбинации из четырёх не пустых соседних ячеек. В принципе допускаются любые комбинации соседних ячеек, число которых составляет какую-либо степень двух.
На рис. 2.34 показан один из возможных вариантов комбинирования с комбинированием четырёх ячеек.
В результате проведенного комбинирования (объединения двух ячеек по две и четыре ячейки) получаем функцию:
. (2.11.4)
Рассмотреть другие варианты комбинирования ячеек по четыре (Решить задачи 5 и 6 из контрольных вопросов и задач).
| AB | ||||
| CD | ||||
| 1 | ||||
Рис. 2.34. Попарное комбинирование ячеек карты,
2.34. Попарное комбинирование ячеек карты,
представленной на рис. 2.32
Анализ задач с пятью и шестью переменными более сложен. Для тех, кому будет необходимо решать такие задачи, потребуется более глубокое изучение алгебры логики, для чего можно обратиться к следующим публикациям: Браун Д.Б., 1979;. Обухов В. Е., 1992; Шевелев Ю. П., 2000; Ерош, И. Л., 2001; Коледов Л. В., 2000; Валов, Г. М., 2000; Фридлендер, Б. И., 2005.
| AB | ||||
| CD | ||||
| 1 | ||||
Рис. 2.35. Попарное комбинирование ячеек карты,
2.35. Попарное комбинирование ячеек карты,
представленной на рис. 2.32
Конечно, сейчас редко кто строит и анализирует карты логических функций. На сегодняшний день имеется достаточное количество хорошо разработанных компьютерных программ и конечно при необходимости лучше привлечь к решению задачи специалистов в данной области.
В результате проведенного комбинирования (объединения двух ячеек по две и четырёх ячеек) получаем функцию:
. (2.11.4)
Рассмотреть другие варианты комбинирования ячеек по четыре (Решить задачи 5 и 6 из контрольных вопросов и задач).
Конечно, сейчас редко кто строит и анализирует карты логических функций. На сегодняшний день имеется достаточное количество хорошо разработанных компьютерных программ и конечно при необходимости лучше привлечь к решению задачи специалистов в данной области.
Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право. ..
..
Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все…
ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования…
Что будет с Землей, если ось ее сместится на 6666 км? Что будет с Землей? — задался я вопросом…
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Логика — документация по SymPy 1.11
Введение
Логический модуль для SymPy позволяет формировать и манипулировать логическими выражениями с использованием символьных и логических значений.
Формирование логических выражений
Вы можете создавать логические выражения с помощью стандартных операторов Python и .
( и ), | ( или ), ~ ( не ):
>>> из импорта sympy *
>>> х, у = символы ('х, у')
>>> у | (х и у)
у | (х и у)
>>> х | у
х | у
>>> ~х
~ х
Вы также можете формировать значения с помощью >> и << :
>>> х >> у Подразумевает (х, у) >>> х << у Подразумевает (у, х)
Как и большинство типов в SymPy, логические выражения наследуются от Basic :
>>> (y & x).subs({x: True, y: True}) Истинный >>> (х | у).атомы() {х, у}
Логический модуль также включает следующие функции для получения логических выражений. из их таблиц истинности:
- sympy.logic.boolalg.SOPform( переменных , minterms , dontcares=None )[источник]
Функция SOPform использует упрощенные_пары и избыточную группу- устранение алгоритма для преобразования списка всех входных комбинаций, которые сгенерируйте «1» (minterms) в виде наименьшей суммы продуктов.
Переменные должны быть указаны в качестве первого аргумента.
Возвращает логическую функцию
или(т. е. «сумма произведений» или форма «СОП»), которая дает желаемый результат. Если есть входы, которые могут игнорироваться, передать их также в виде списка.Результатом будет одна из (возможно, многих) функций, удовлетворяющих условия.
Примеры
>>> из sympy.logic импортировать SOPform >>> из символов импорта sympy >>> w, x, y, z = символы ('w x y z') >>> minterms = [[0, 0, 0, 1], [0, 0, 1, 1], . .. [0, 1, 1, 1], [1, 0, 1, 1], [1, 1, 1, 1]]
>>> не важно = [[0, 0, 0, 0], [0, 0, 1, 0], [0, 1, 0, 1]]
>>> SOPform([w, x, y, z], minterms, dontcares)
(у и я) | (~ ш и ~ х)
.. [0, 1, 1, 1], [1, 0, 1, 1], [1, 1, 1, 1]]
>>> не важно = [[0, 0, 0, 0], [0, 0, 1, 0], [0, 1, 0, 1]]
>>> SOPform([w, x, y, z], minterms, dontcares)
(у и я) | (~ ш и ~ х)
Термины также могут быть представлены целыми числами:
>>> minterms = [1, 3, 7, 11, 15] >>> наплевать = [0, 2, 5] >>> SOPform([w, x, y, z], minterms, dontcares) (у и я) | (~ ш и ~ х)
Их также можно указать с помощью словарей, которые не обязательно должны быть полностью указано:
>>> minterms = [{w: 0, x: 1}, {y: 1, z: 1, x: 0}] >>> SOPform([w, x, y, z], minterms) (х & ~ ш) | (у и г и ~ х)Или комбинация:
>>> minterms = [4, 7, 11, [1, 1, 1, 1]] >>> наплевать = [{w : 0, x : 0, y: 0}, 5] >>> SOPform([w, x, y, z], minterms, dontcares) (ш и у и г) | (~ш и ~у) | (х и г и ~ ш)Ссылки
[Р557]
https://en.wikipedia.org/wiki/Quine-McCluskey_algorithm
- sympy.
 logic.boolalg.POSform( переменные , minterms , dontcares=нет )[источник]
logic.boolalg.POSform( переменные , minterms , dontcares=нет )[источник] Функция POSform использует упрощенные_пары и избыточную группу устранение алгоритма для преобразования списка всех входных комбинаций которые генерируют «1» (minterms) в наименьшей форме произведения сумм.
Переменные должны быть указаны в качестве первого аргумента.
Возвращает логическую функцию
И(т. е. «произведение сумм» или форма «POS»), которая дает желаемый результат. Если есть входы, которые могут игнорироваться, передать их также в виде списка.Результатом будет одна из (возможно, многих) функций, удовлетворяющих условия.
Примеры
>>> из sympy.logic импортировать POSform >>> из символов импорта sympy >>> w, x, y, z = символы ('w x y z') >>> minterms = [[0, 0, 0, 1], [0, 0, 1, 1], [0, 1, 1, 1], ... [1, 0, 1, 1], [1, 1, 1, 1]] >>> не важно = [[0, 0, 0, 0], [0, 0, 1, 0], [0, 1, 0, 1]] >>> POSform([w, x, y, z], minterms, dontcares) г & (у | ~ ш)Термины также могут быть представлены целыми числами:
>>> minterms = [1, 3, 7, 11, 15] >>> наплевать = [0, 2, 5] >>> POSform([w, x, y, z], minterms, dontcares) г & (у | ~ ш)
Их также можно указать с помощью словарей, которые не обязательно должны быть полностью указано:
>>> minterms = [{w: 0, x: 1}, {y: 1, z: 1, x: 0}] >>> POSform([w, x, y, z], minterms) (x | y) & (x | z) & (~w | ~x)Или комбинация:
>>> minterms = [4, 7, 11, [1, 1, 1, 1]] >>> наплевать = [{w : 0, x : 0, y: 0}, 5] >>> POSform([w, x, y, z], minterms, dontcares) (w | x) & (y | ~w) & (z | ~y)Ссылки
[Р558]
https://en.
 wikipedia.org/wiki/Quine-McCluskey_algorithm
wikipedia.org/wiki/Quine-McCluskey_algorithm
- sympy.logic.boolalg.ANFform( переменных , истинные значения )[источник]
Функция ANFform преобразует список значений истинности в Алгебраическая нормальная форма (АНФ).
Переменные должны быть указаны в качестве первого аргумента.
Возврат True, False, логическая функция
и(т.е. «моном Жегалкина») или логическая функцияXor(т.е. «полином Жегалкина»). Когда правда и ложь представлены 1 и 0 соответственно, тоИ— это умножение, аXor— сложение.Формально произведением является «моном Жегалкина» (логический И) конечного набора различных переменных, включая пустое множество, произведение которого обозначается 1 (Истина). «Полином Жегалкина» — это сумма (логическое Xor) множество мономов Жегалкина, где пустое множество обозначается на 0 (ложь).
- Параметры:
переменные : список переменных
9(х и у)Ссылки
[Р559]
https://en.
 wikipedia.org/wiki/Zhegalkin_polynomial
wikipedia.org/wiki/Zhegalkin_polynomial
Логические функции
- класс sympy.logic.boolalg.Boolean ( *args ) [источник]
Логический объект — это объект, для которого логические операции имеют смысл.
- as_set()[источник]
Переписывает логическое выражение в терминах вещественных множеств.
Примеры
>>> из sympy import Symbol, Eq, Or, And >>> x = Символ('x', реальный=Истина) >>> Уравнение(х, 0).as_set() {0} >>> (х > 0).as_set() Интервал.открыть(0, оо) >>> И(-2 < х, х < 2).as_set() Интервал.открыть(-2, 2) >>> Или(х < -2, 2 < х).as_set() Союз(Интервал.открыть(-оо,-2), Интервал.открыть(2, оо))
- равно( другие )[источник]
Возвращает
True, если заданные формулы имеют одинаковую таблицу истинности. Чтобы две формулы были равны, они должны иметь одинаковые литералы.Примеры
>>> из sympy.
 abc импортировать A, B, C
>>> from sympy import И, Или, Не
>>> (A >> B).равно(~B >> ~A)
Истинный
>>> Не(И(А, В, С)).равно(И(Не(А), Не(В), Не(С)))
ЛОЖЬ
>>> Не(И(А, Не(А))).равно(Или(В, Не(В)))
ЛОЖЬ
abc импортировать A, B, C
>>> from sympy import И, Или, Не
>>> (A >> B).равно(~B >> ~A)
Истинный
>>> Не(И(А, В, С)).равно(И(Не(А), Не(В), Не(С)))
ЛОЖЬ
>>> Не(И(А, Не(А))).равно(Или(В, Не(В)))
ЛОЖЬ
- класс sympy.logic.boolalg.BooleanTrue[источник]
Версия SymPy
True, синглтон, к которому можно получить доступ черезS.true.Это версия SymPy
Trueдля использования в логическом модуле. Основное преимущество использованияtrueвместоTrueзаключается в том, что сокращенное логическое значение операции типа~и>>будет работать, как и ожидалось, в этом классе, тогда как с Правда они действуют побитно на 1. Функции в логическом модуле вернут это класс, когда они оцениваются как истинные.Примечания
Может возникнуть некоторая путаница в отношении того, когда
Trueследует использовать и когдаS.следует использовать в различных контекстах на протяжении всего SymPy. Важно помнить, что true
true sympify(True)возвращаетS.true. Это означает, что для большинства часть, вы можете просто использоватьTrueи он будет автоматически конвертирован доS.trueпри необходимости, подобно тому, как вы обычно можете использовать 1 вместоS.One.Эмпирическое правило:
«Если рассматриваемое логическое значение можно заменить произвольным
Boolean, напримерOr(x, y)илиx > 1, используйтеS.true. В противном случае используйтеTrue”Другими словами, используйте
S.trueтолько в тех контекстах, где boolean используется как символическое представление истины. Например, если объект попадает в.argsлюбого выражения, то это обязательно должно бытьS.trueвместоTrue, т. к.
элементы
к.
элементы .argsдолжны бытьBasic. С другой стороны,==не является символьной операцией в SymPy, так как она всегда возвращаетВерноилиЛожно, и делает это с точки зрения структурного равенства а не математический, поэтому он должен возвращатьПравда. Предположения система должна использоватьTrueиFalse. Помимо неудовлетворительного приведенное выше эмпирическое правило, система предположений использует трехзначную логику (True,False,None), тогда какS.trueиS.falseпредставляют двузначную логику. Если вы сомневаетесь, используйтеTrue.«
S.true == True is True».Пока “
S.true равно True” равноFalse, “S.true == True” равноTrue, поэтому, если есть какие-либо сомнения относительно того, является ли функция или выражение вернетS.или true
true True, просто используйте==вместобудетдля сравнения, и он будет работать в любом кейс. Наконец, для логических флагов лучше просто использовать, если x. вместо, если x равно True. Цитировать PEP 8:Не сравнивать логические значения с
ВерноилиЛожноиспользуя==.Примеры
>>> from sympy import sympify, true, false, или >>> Симптом (правда) Истинный >>> _ верно, _ верно (Ложная правда)
>>> Или(правда, ложь) Истинный >>> _ верно Истинный
оператора Python дают логический результат для истинного, но побитовый результат для True
>>> ~правда, ~правда (Неверно, -2) >>> правда >> правда, правда >> правда (Правда, 0)
оператора Python дают логический результат для истинного, но побитовый результат для True
>>> ~правда, ~правда (Неверно, -2) >>> правда >> правда, правда >> правда (Правда, 0)
См.
 также
такжеsympy.logic.boolalg.BooleanFalse- as_set()[источник]
Перепишите логические операторы и реляционные отношения в терминах реальных множеств.
Примеры
>>> из sympy import true >>> true.as_set() УниверсалСет
- класс sympy.logic.boolalg.BooleanFalse[источник]
SymPy версия
False, синглтона, к которому можно получить доступ черезS.false.Это версия SymPy
Falseдля использования в логическом модуле. основное преимущество использованияfalseвместоFalseэто сокращение Логические операции, такие как~и>>, будут работать в этом классе должным образом. тогда как сFalseони действуют побитно на 0. Функции в логическом модуле вернет этот класс, когда они оцениваются как ложные.Примечания
См.
 раздел примечаний в
раздел примечаний в sympy.logic.boolalg.BooleanTrueПримеры
>>> from sympy import sympify, true, false, или >>> Симпифицировать(Ложь) ЛОЖЬ >>> _ Ложь, _ Ложь (Ложная правда)
>>> Или(правда, ложь) Истинный >>> _ верно Истинный
Операторы Python дают логический результат для false, но побитовый результат для False
>>> ~ложь, ~ложь (Правда, -1) >>> ложь >> ложь, ложь >> ложь (Правда, 0)
См. также
sympy.logic.boolalg.BooleanTrue- as_set()[источник]
Перепишите логические операторы и отношения в терминах реальных множеств.
Примеры
>>> из импорта sympy false >>> false.as_set() Пустой набор
- класс sympy.logic.boolalg.And( *args )[источник]
Логическая функция И.
Он оценивает свои аргументы по порядку, немедленно возвращая false когда аргумент ложный и истинный, если они все истинны.

Примеры
>>> из sympy.abc импортировать x, y >>> из импорта sympy И >>> х и у х и у
Примечания
Оператор
ипредоставляется для удобства, но обратите внимание, что его использование здесь отличается от его обычного использования в Python, которое побитовое а также. Следовательно,А(а, б)иа и бдадут разные результаты, еслиииb— целые числа.>>> И(х, у).sub(х, 1) у
- класс sympy.logic.boolalg.Or( *args )[источник]
Логическая функция ИЛИ
Он оценивает свои аргументы по порядку, немедленно возвращая значение true когда аргумент истинен, и ложен, если все они ложны.
Примеры
>>> из sympy.abc импортировать x, y >>> из импорта sympy или >>> х | у х | у
Примечания
| Операторпредоставляется для удобства, но обратите внимание, что его использование здесь отличается от его обычного использования в Python, которое побитовое или же. Следовательно,
Следовательно, Or(a, b)иa | bвернет разные вещи, еслиaиb— целые числа.>>> Или(х, у).sub(х, 0) у
- класс sympy.logic.boolalg.Not( аргумент )[источник]
Логическая функция НЕ (отрицательная)
Возвращает
true, если утверждениеfalseилиFalse. Возвращаетfalse, если операторtrueилиTrue.Примеры
>>> from sympy import Не, И, Или >>> из sympy.abc импортировать x, A, B >>> Нет (правда) ЛОЖЬ >>> Нет (ложь) Истинный >>> Не(И(Верно, Ложь)) Истинный >>> Нет(Или(Верно, Ложь)) ЛОЖЬ >>> Не(И(И(Истина, х), Или(х, Ложь))) ~ х >>> ~х ~ х >>> Не(И(Или(А, В), Или(~А, ~В))) ~((А | В) и (~А | ~В))
Примечания
Оператор
~предоставляется для удобства, но обратите внимание, что его использование здесь отличается от его обычного использования в Python, которое побитовое нет. В частности,
В частности, ~aиNot(a)будут разными, еслиaбудет целое число. Кроме того, поскольку bool в подклассе Python отint,~Trueсовпадает с~1, который равен-2, который имеет логическое значение значение Истина. Чтобы избежать этой проблемы, используйте логические типы SymPy.истинаиложь.
>>> из импорта sympy true >>> ~ Верно -2 >>> ~правда ЛОЖЬ
- класс sympy.logic.boolalg.Xor( *args )[источник]
Логическая функция XOR (исключающее ИЛИ).
Возвращает True, если нечетное число аргументов имеет значение True, а остальные ЛОЖЬ.
Возвращает False, если четное число аргументов равно True, а остальные ЛОЖЬ. 9b и
Xor(a, b)будет отличаться, еслиaиb— целые числа.>>> Xor(x, y).
 sub(y, 0)
Икс
sub(y, 0)
Икс
- класс sympy.logic.boolalg.Nand( *args )[источник]
Логическая функция И-НЕ.
Он оценивает свои аргументы по порядку, немедленно возвращая True, если они есть. из них Ложь, и Ложь, если все они Истинны.
Возвращает True, если хотя бы один из аргументов имеет значение False. Возвращает False, если все аргументы имеют значение True
Примеры
>>> из sympy.logic.boolalg импорт Nand >>> из символов импорта sympy >>> х, у = символы ('х у') >>> Нанд(Ложь, Истина) Истинный >>> Нанд(Правда, Правда) ЛОЖЬ >>> N и (х, у) ~ (х и у)
- класс sympy.logic.boolalg.Nor( *args )[источник]
Логическая функция НЕ-ИЛИ.
Он оценивает свои аргументы по порядку, немедленно давая False, если они есть из них истинны, и истинны, если все они ложны.
Возвращает False, если какой-либо аргумент имеет значение True Возвращает True, если все аргументы имеют значение False
Примеры
>>> из sympy.
 logic.boolalg import Nor
>>> из символов импорта sympy
>>> х, у = символы ('х у')
logic.boolalg import Nor
>>> из символов импорта sympy
>>> х, у = символы ('х у')
>>> Нор(Верно, Ложь) ЛОЖЬ >>> Нор(Правда, Правда) ЛОЖЬ >>> Нор(Ложь, Истина) ЛОЖЬ >>> Нор(Ложь, Ложь) Истинный >>> Нор(х, у) ~(х | у)
- класс sympy.logic.boolalg.Xnor( *args )[источник]
Логическая функция XNOR.
Возвращает False, если нечетное число аргументов имеет значение True, а остальные ЛОЖЬ.
Возвращает True, если четное число аргументов имеет значение True, а остальные ЛОЖЬ.
Примеры
>>> из sympy.logic.boolalg импорт Xnor >>> из символов импорта sympy >>> х, у = символы ('х у') >>> Xnor(Истина, Ложь) ЛОЖЬ >>> Xnor(Правда, Правда) Истинный >>> Xnor(Верно, Ложь, Верно, Верно, Ложно) ЛОЖЬ >>> Xnor(Правда, Ложь, Правда, Ложь) Истинный
- класс sympy.logic.boolalg.Implies( *args )[источник]
Логическое следствие.

A означает, что B эквивалентно если A, то B. Математически это записывается как \(A \Rightarrow B\) и эквивалентно \(\neg A \vee B\) или
~A | Б.Принимает два логических аргумента; А и Б. Возвращает False, если A истинно, а B ложно В противном случае возвращает True.
Примеры
>>> из импорта sympy.logic.boolalg Подразумевается >>> из символов импорта sympy >>> х, у = символы ('х у')>>> Подразумевается (Истина, Ложь) ЛОЖЬ >>> Подразумевает(Ложь, Ложь) Истинный >>> Подразумевается (правда, правда) Истинный >>> Подразумевает (ложь, правда) Истинный >>> х >> у Подразумевает (х, у) >>> у << х Подразумевает (х, у)
Примечания
Операторы
>>и<<предоставляются для удобства, но обратите внимание что их использование здесь отличается от их обычного использования в Python, т.е. битовые сдвиги. Следовательно,подразумевает (a, b)иa >> bвернет разные вещи, еслиaиbявляются целыми числами. В частности, поскольку Python
считает
В частности, поскольку Python
считает TrueиFalseцелыми числами,True >> Trueбудет то же, что и1 >> 1, т. е. 0, истинность которого равна False. К чтобы избежать этой проблемы, используйте объекты SymPytrueиfalse.>>> из импорта sympy true, false >>> Верно >> Ложно 1 >>> правда >> ложь ЛОЖЬ
- класс sympy.logic.boolalg.Equivalent ( *args ) [источник]
Отношение эквивалентности.
Эквивалент(A, B)равно True, если оба A и B оба True или оба False.Возвращает True, если все аргументы логически эквивалентны. В противном случае возвращает False.
Для двух аргументов это эквивалентно
Xnor.Примеры
>>> from sympy.logic.boolalg import Equivalent, And >>> из sympy.abc импортировать x >>> Эквивалент(Ложь, Ложь, Ложь) Истинный >>> Эквивалент(Истина, Ложь, Ложь) ЛОЖЬ >>> Эквивалент(х, И(х, Истина)) Истинный
- класс sympy.
 logic.boolalg.ITE ( *args ) [источник]
logic.boolalg.ITE ( *args ) [источник] Предложение If-then-else.
ITE(A, B, C)оценивает и возвращает результат B, если A истинно иначе он возвращает результат C. Все аргументы должны быть логическими.С точки зрения логических элементов ITE соответствует мультиплексору 2-к-1, где A - сигнал выбора.
Примеры
>>> из sympy.logic.boolalg импортировать ITE, And, Xor, Or >>> из sympy.abc импортировать x, y, z >>> ИТЭ(Правда, Ложь, Правда) ЛОЖЬ >>> ITE(Or(True, False), And(True, True), Xor(True, True)) Истинный >>> ИТЭ(х, у, г) ИТЭ (х, у, г) >>> ИТЭ(Истина, х, у) Икс >>> ИТЭ(Ложь, х, у) у >>> ИТЭ(х, у, у) у
Попытка использовать нелогические аргументы вызовет TypeError:
>>> ИТЭ(Истина, [], ()) Traceback (последний последний вызов): ... TypeError: ожидается bool, Boolean или ITE, а не `[]`
- класс sympy.logic.boolalg.Exclusive( *args )[источник]
Истина, если истинен только один аргумент или ни один аргумент.

Exclusive(A, B, C)эквивалентно~(А и В) и ~(А и С) и ~(В и С).Для двух аргументов это эквивалентно
Xor.Примеры
>>> из импорта sympy.logic.boolalg Эксклюзив >>> Эксклюзив(Ложь, Ложь, Ложь) Истинный >>> Эксклюзив(Ложь, Правда, Ложь) Истинный >>> Эксклюзивный (ложь, правда, правда) ЛОЖЬ
Следующие функции могут использоваться для обработки алгебраических, конъюнктивных, Дизъюнктивные и отрицательные нормальные формы:
- sympy.logic.boolalg.to_anf( expr , deep=True )[источник]
Преобразует expr в алгебраическую нормальную форму (ANF).
ANF является канонической нормальной формой, что означает, что два эквивалентные формулы будут преобразованы в один и тот же АНФ.
Логическое выражение находится в ANF, если оно имеет форму
\[1 \oplus a \oplus b \oplus ab \oplus abc\]
- т.
 (~A & (Эквивалент(B, C)))
(~A & (Эквивалент(B, C)))
- т.
- sympy.logic.boolalg.to_cnf( выражение , упрощение=ложь , сила=ложь )[источник]
Преобразование пропозиционального логического предложения
exprв конъюнктивное нормальное форма:((A | ~B | ...) & (B | C | ...) & ...). ЕслиупроститьравноTrue,exprвычисляется до простейшей CNF. форма с использованием алгоритма Куайна-МакКласки; это может занять много времени время. Если переменных больше 8, то должен быть установлен флаг \(force`\) доTrueдля упрощения (по умолчаниюFalse).Примеры
>>> из sympy.logic.boolalg импортировать в_cnf >>> из sympy.abc импортировать A, B, D >>> to_cnf(~(A | B) | D) (D | ~A) и (D | ~B) >>> to_cnf((A | B) & (A | ~A), Истина) А | Б
- sympy.logic.boolalg.to_dnf( выражение , упрощение=ложь , сила=ложь )[источник]
Преобразовать пропозициональное логическое предложение
exprв дизъюнктивное нормальное форма:((A & ~B & .. Если ..) | (B & C & ...) | ...)
..) | (B & C & ...) | ...) упроститьравноTrue,exprпреобразуется в простейшую форму ДНФ с использованием алгоритм Куайна-МакКласки; это может занять много времени время. Если имеется более 8 переменных, флагforceдолжен быть установлен наTrueдля упрощения (по умолчаниюЛожь).Примеры
>>> из sympy.logic.boolalg импортировать в_dnf >>> из sympy.abc импортировать A, B, C >>> to_dnf(B & (A | C)) (А и Б) | (ДО Н.Э) >>> to_dnf((A и B) | (A и ~B) | (B и C) | (~B и C), True) А | С
- sympy.logic.boolalg.to_nnf( выражение , упрощение=Истина )[источник]
Преобразует
exprв нормальную форму отрицания (NNF).Логическое выражение находится в NNF, если оно содержит только
И,ИлииНе, аNotприменяется только к литералам. Если
Если упроститьравноTrue, результат не содержит лишних предложений.Примеры
>>> из sympy.abc импортировать A, B, C, D >>> from sympy.logic.boolalg import Not, Equivalent, to_nnf >>> to_nnf(Not((~A и ~B) | (C и D))) (А | В) и (~ С | ~ D) >>> to_nnf(Эквивалент(A >> B, B >> A)) (A | ~B | (A и ~B)) и (B | ~A | (B и ~A))
- sympy.logic.boolalg.is_anf ( выражение ) [источник]
Проверяет, находится ли
exprв алгебраической нормальной форме (ANF).Логическое выражение находится в ANF, если оно имеет форму
\[1 \oplus a \oplus b \oplus ab \oplus abc\]
т. е. чисто истинная, чисто ложная конъюнкция переменные или исключающая дизъюнкция. Эксклюзивный дизъюнкция может содержать только истину, переменные или соединение переменных. Никакие отрицания не допускаются.
Примеры
>>> from sympy.logic.boolalg import And, Not, Xor, true, is_anf >>> из sympy.
 abc импортировать A, B, C
>>> is_anf(истина)
Истинный
>>> is_anf(A)
Истинный
>>> is_anf(И(А,В,С))
Истинный
>>> is_anf(Xor(A, Not(B)))
ЛОЖЬ
abc импортировать A, B, C
>>> is_anf(истина)
Истинный
>>> is_anf(A)
Истинный
>>> is_anf(И(А,В,С))
Истинный
>>> is_anf(Xor(A, Not(B)))
ЛОЖЬ
- sympy.logic.boolalg.is_cnf ( выражение ) [источник]
Проверяет, находится ли выражение в конъюнктивной нормальной форме.
Примеры
>>> из sympy.logic.boolalg импортировать is_cnf >>> из sympy.abc импортировать A, B, C >>> is_cnf(A | B | C) Истинный >>> is_cnf(A и B и C) Истинный >>> is_cnf((A и B) | C) ЛОЖЬ
- sympy.logic.boolalg.is_dnf ( выражение ) [источник]
Проверяет, находится ли выражение в дизъюнктивной нормальной форме.
Примеры
>>> из sympy.logic.boolalg импортировать is_dnf >>> из sympy.abc импортировать A, B, C >>> is_dnf(A | B | C) Истинный >>> is_dnf(A и B и C) Истинный >>> is_dnf((A и B) | C) Истинный >>> is_dnf(A & (B | C)) ЛОЖЬ
- sympy.
 logic.boolalg.is_nnf ( expr , упрощенный = True ) [источник]
logic.boolalg.is_nnf ( expr , упрощенный = True ) [источник] Проверяет, если
exprнаходится в нормальной форме отрицания (NNF).Логическое выражение находится в NNF, если оно содержит только
И,ИлииНе, аNotприменяется только к литералам. ЕслиупрощенныйравенTrue, проверяется, не содержит ли результат избыточных предложений.Примеры
>>> из sympy.abc импортировать A, B, C >>> from sympy.logic.boolalg import Not, is_nnf >>> is_nnf(A и B | ~C) Истинный >>> is_nnf((A | ~A) & (B | C)) ЛОЖЬ >>> is_nnf((A | ~A) & (B | C), False) Истинный >>> is_nnf(Не(A и B) | C) ЛОЖЬ >>> is_nnf((А >> В) & (В >> А)) ЛОЖЬ
- sympy.logic.boolalg.gateinputcount( expr )[источник]
Возвращает общее количество входов для логических элементов, реализующих Логическое выражение.

- Возврат:
целое число
Количество входов ворот
Примечание
Не все логические функции считаются здесь воротами, только те, которые считаются стандартными воротами. Это:
и,Или,Xor,Не, иITE(мультиплексор).Нанд,Нор, иXnorбудет оцениваться какNot(And())и т. д.Примеры
>>> from sympy.logic import And, Or, Nand, Not, gateinputcount >>> из sympy.abc импортировать x, y, z >>> выражение = И(х, у) >>> gateinputcount(expr) 2 >>> gateinputcount(Или(expr, z)) 4
Обратите внимание, что
Nandавтоматически оценивается какNot(And()), поэтому>>> gateinputcount(Nand(x, y, z)) 4 >>> gateinputcount(Not(И(x, y, z))) 4
Хотя этого можно избежать, используя
Assessment=False>>> gateinputcount(Nand(x, y, z, оценка=ложь)) 3
Также обратите внимание, что сравнение будет считаться булевой переменной:
>>> gateinputcount(И(x > z, y >= 2)) 2
Как и символ: >>> количество ворот (x) 0
Упрощение и проверка эквивалентности
- sympy.
 logic.boolalg.simplify_logic( expr , form=None , deep=True , force=False )[источник]
logic.boolalg.simplify_logic( expr , form=None , deep=True , force=False )[источник] Эта функция упрощает логическую функцию до ее упрощенной версии в форме SOP или POS. Тип возвращаемого значения -
илиили Объектив SymPy.- Параметры:
выражение : Логическое выражение
форма : строка (
'cnf'или'dnf') илиНет(по умолчанию).Если
'cnf'или'dnf', простейшее выражение в соответствующем возвращается нормальная форма; еслиNone, возвращается ответ в соответствии с формой с наименьшим количеством аргументов (по умолчанию в CNF).глубокий : bool (по умолчанию
True)Указывает, следует ли рекурсивно упростить любой небулевы функции, содержащиеся во входных данных.

принудительно : bool (по умолчанию
False)Поскольку упрощения требуют экспоненциального времени в числе переменных, по умолчанию существует ограничение на выражения с 8 переменных. Когда выражение имеет более 8 переменных только символическое упрощение (управляется
глубокий) есть сделанный. УстановивforceнаTrue, это ограничение снимается. Быть известно, что это может привести к очень длительному времени упрощения.
Примеры
>>> из sympy.logic импорта simple_logic >>> из sympy.abc импортировать x, y, z >>> из sympy импорт S >>> b = (~x & ~y & ~z) | ( ~ х и ~ у и г) >>> упрощение_логики(б) ~ х и ~ у
>>> С(б) (г и ~ х и ~ у) | (~ х и ~ у и ~ г) >>> упрощение_логики(_) ~ х и ~ у
Функция SymPy
simple()также может использоваться для упрощения логических выражений до их простейшие формы.
- sympy.logic.boolalg.bool_map( bool1 , bool2 )[источник]
Вернуть упрощенную версию bool1 и отображение переменных что делает два выражения bool1 и bool2 представляют одно и то же логическое поведение для некоторого соответствия между переменными каждого. Если существует более одного отображения такого рода, одно из них возвращается.
Например,
И(х, у)логически эквивалентноИ(а, б)для отображение{x: a, y: b}или{x: b, y: a}. Если такого сопоставления не существует, вернутьFalse.Примеры
>>> from sympy import SOPform, bool_map, Or, And, Not, Xor >>> из sympy.abc импортировать w, x, y, z, a, b, c, d >>> function1 = SOPform([x, z, y], [[1, 0, 1], [0, 0, 1]]) >>> function2 = SOPform([a, b, c], [[1, 0, 1], [1, 0, 0]]) >>> bool_map (функция1, функция2) (у и ~ г, {у: а, г: б})Результаты не обязательно уникальны, но они каноничны.
 Здесь,
Здесь, (w, z)может быть(a, d)или(г, а):>>> eq = Или(И(Не(у), ш), И(Не(у), z), И(х, у)) >>> eq2 = Или(И(Не(с), а), И(Не(с), г), И(б, в)) >>> bool_map(eq,eq2) ((x & y) | (w & ~ y) | (z & ~ y), {w: a, x: b, y: c, z: d}) >>> eq = And(Xor(a, b), c, And(c,d)) >>> bool_map(eq, eq.subs(c, x)) (c & d & (a | b) & (~a | ~b), {a: a, b: b, c: d, d: x})
Управление выражениями
Для управления логическими выражениями можно использовать следующие функции:
- sympy.logic.boolalg.distribute_and_over_or ( выражение ) [источник]
Дано предложение
expr, состоящее из союзов и дизъюнкций литералов, вернуть эквивалентное предложение в CNF.Примеры
>>> from sympy.logic.boolalg import Distribute_and_over_or, И, Или, Не >>> из sympy.abc импортировать A, B, C >>> распределить_и_пере_или(Или(А, И(Не(Б), Не(С)))) (А | ~ В) и (А | ~ С)
- sympy.
 logic.boolalg.distribute_or_over_and ( выражение ) [источник]
logic.boolalg.distribute_or_over_and ( выражение ) [источник] Дано предложение
expr, состоящее из союзов и дизъюнкций литералов, вернуть эквивалентное предложение в DNF.Обратите внимание, что вывод НЕ упрощен.
Примеры
>>> from sympy.logic.boolalg import Distribute_or_over_and, И, Или, Не >>> из sympy.abc импортировать A, B, C >>> распределить_или_по_и(И(Или(Не(А), В), С)) (Б и С) | (С и ~А)
- sympy.logic.boolalg.distribute_xor_over_and ( выражение ) [источник]
Дано предложение
expr, состоящее из союза и эксклюзивные дизъюнкции литералов возвращают эквивалентная исключающая дизъюнкция.Обратите внимание, что вывод НЕ упрощен.
Примеры
>>> from sympy.logic.boolalg import Distribute_xor_over_and, And, Xor, Not >>> из sympy.abc импортировать A, B, C >>> Distributed_xor_over_and(И(Xor(Не(A), B), C)) (В и С) ^ (С и ~ А)
- sympy.
 logic.boolalg.eliminate_implications ( выражение ) [источник]
logic.boolalg.eliminate_implications ( выражение ) [источник] Изменение
ПодразумеваетиЭквивалентвИ,Или, иНе. То есть вернуть выражение, эквивалентноеexpr, но имеющее толькои,|и~как логические операторы.Примеры
>>> from sympy.logic.boolalg >>> из sympy.abc импортировать A, B, C >>> remove_implications (подразумевает (A, B)) Б | ~ А >>> remove_implications (эквивалент (A, B)) (А | ~ В) и (В | ~ А) >>> remove_implications (эквивалент (A, B, C)) (А | ~С) и (В | ~А) и (С | ~В)
Вывод
Этот модуль реализует некоторые процедуры вывода в пропозициональной логике.
Функция satisfiable проверит, является ли данное логическое выражение выполнимым, то есть вы можете присвоить значения переменным, чтобы сделать предложение
True.
Например, выражение
x & ~xневыполнимо, так как нет значения дляx, которые делают это предложениеПравда. С другой стороны,(x | y) & (x | ~y) & (~x | y)выполнимо, причем какx, так иyявляютсяПравда.>>> из sympy.logic.inference импорт выполним >>> из символа импорта sympy >>> х = Символ('х') >>> у = Символ('у') >>> выполнимо (х и ~ х) ЛОЖЬ >>> выполнимо((x | y) & (x | ~y) & (~x | y)) {х: Истина, у: Истина}Как видите, когда предложение выполнимо, оно возвращает модель, которая делает это предложение
True. Если это не выполнимо, он вернетFalse.- sympy.logic.inference.satisfiable( expr , алгоритм=Нет , all_models=False , минимальный=False )[источник]
Проверить выполнимость пропозиционального предложения. Возвращает модель в случае успеха.
 Возвращает {true: true} для тривиально истинных выражений.
Возвращает {true: true} для тривиально истинных выражений.При установке all_models в True, если заданное выражение выполнимо, тогда возвращает генератор моделей. Однако, если выражение невыполнимо затем возвращает генератор, содержащий единственный элемент False.
Примеры
>>> из sympy.abc импортировать A, B >>> из sympy.logic.inference импорт выполним >>> выполнимо(A и ~B) {А: Верно, Б: Ложь} >>> выполнимо(A и ~A) ЛОЖЬ >>> выполнимо (правда) {Правда правда} >>> следующий (выполнимый (A & ~ A, all_models = True)) ЛОЖЬ >>> models = satisfiable((A >> B) & B, all_models=True) >>> далее(модели) {А: Ложь, Б: Верно} >>> далее(модели) {А: верно, Б: верно} >>> def use_models (модели): ... для модели в моделях: ... если модель: ... # Сделайте что-нибудь с моделью. ... печать (модель) ... еще: ... # Данное выражение невыполнимо. ... печать("НЕСАТ") >>> use_models(satisfiable(A >> ~A, all_models=True)) {А: Ложь} >>> use_models(satisfiable(A ^ A, all_models=True)) UNSAT
Булевы функции (формы SOP, POS)
Схема
Представление булевых функций
Использование переключающих устройств, таких как транзисторы, порождает особый случай булевой алгебры, называемый алгеброй переключения.
 В алгебре переключения все переменные принимают одно из двух значений: 0 и 1.
В алгебре переключения все переменные принимают одно из двух значений: 0 и 1.[adsense1]
В булевой алгебре 0 используется для представления «открытого» или «ложного» состояния логического элемента. Точно так же 1 используется для представления «закрытого» состояния или «истинного» состояния логического элемента.
Логическое выражение — это выражение, состоящее из переменных, констант (0 — ложь и 1 — истина) и логических операторов, результатом которых является истина или ложь.
Булева функция — это алгебраическая форма логического выражения. Булева функция n-переменных представлена как f(x1, x2, x3….xn). Используя булевы законы и теоремы, мы можем упростить булевы функции цифровых схем. Краткое примечание о различных способах представления булевой функции показано ниже.
- Форма суммы продуктов (СОП)
- Суммарное произведение (POS) форма
- Канонические формы
Существует два типа канонических форм:
- Сумма минимальных членов или каноническая СОП
- Product-of-max terms или Canonical POS
Булевы функции могут быть представлены с помощью логических элементов И-НЕ, а также с использованием метода K-карты (карты Карно).
 Мы можем стандартизировать логические выражения, используя две стандартные формы.
Мы можем стандартизировать логические выражения, используя две стандартные формы.Форма СОП – Сумма произведений, форма
Форма POS – произведение сумм форма
Стандартизация логических уравнений сделает внедрение, развитие и упрощение более простым и систематическим.
Форма суммы произведений (SOP)
Форма суммы произведений (SOP) представляет собой метод (или форму) упрощения логических выражений логических вентилей. В этой SOP-форме представления булевой функции переменные обрабатываются по И (продукт) для формирования термина продукта, и все эти термины продукта объединяются по ИЛИ (суммируются или складываются) вместе, чтобы получить окончательную функцию.
[адсенс2]
Форма суммы произведений может быть сформирована путем сложения (или суммирования) двух или более членов произведения с использованием логической операции сложения. Здесь термины произведения определяются с помощью операции И, а термин суммы определяется с помощью операции ИЛИ.

Форма суммы произведений также называется дизъюнктивной нормальной формой, так как термины произведения объединяются вместе, а операция дизъюнкции является логическим ИЛИ. Форма суммы продуктов также называется стандартной СОП. Представление формы
SOP наиболее подходит для их использования в FPGA (программируемых вентильных матрицах).
Примеры
AB + ABC + CDE
(AB) ̅ + ABC + CD E ̅
Форма SOP может быть получена с помощью
- Запись И для каждой входной комбинации, которая дает ВЫСОКИЙ выход.
- Запись входных переменных, если значение равно 1, и запись дополнения переменной, если ее значение равно 0.
- ИЛИ условия И для получения выходной функции.
Пример: логическое выражение для функции большинства F = A’BC + AB’C + ABC ‘ + ABC
Таблица истинности:
Теперь запишите комбинацию входных переменных с высоким выходом. F = АВ + ВС + АС.
Проверка
По закону идемпотентности мы знаем, что
([ABC + ABC)] + ABC) = (ABC + ABC) = ABC
Теперь функция F = A'BC + AB'C + ABC ' + ABC
= A'BC + AB'C + ABC' + ([ABC + ABC)] + ABC)
= (ABC + ABC') + (ABC + AB'C) + (ABC + A' ВС)
= АВ (С + С') + А (В + В') С + (А + А') ВС
= АВ + ВС + АС.

Форма произведения сумм (POS)
Форма произведения сумм - это метод (или форма) упрощения логических выражений логических вентилей. В этой форме POS все переменные объединяются по ИЛИ, т. е. записываются как суммы для формирования суммирующих условий.
Все эти составляющие суммы объединяются (умножаются) вместе, чтобы получить форму произведения суммы. Эта форма прямо противоположна форме СОП. Так что это также можно назвать «двойной формой SOP».
Здесь условия суммы определяются с помощью операции ИЛИ, а условия произведения определяются с помощью операции И. Когда два или более членов суммы умножаются с помощью логической операции ИЛИ, результирующее выходное выражение будет иметь форму произведения сумм или форму POS.
Форма произведения сумм также называется конъюнктивной нормальной формой, поскольку члены суммы объединяются вместе, а операция конъюнкции является логическим И. Форма произведения сумм также называется стандартной POS.
Примеры
(A+B) * (A + B + C) * (C +D)
(A+B) ̅ * (C + D + E ̅)
Форма POS может быть получена по телефону
- Запись условия ИЛИ для каждой комбинации входов, которая дает НИЗКИЙ выходной сигнал.

- Запись входных переменных, если значение равно 0, и запись дополнения переменной, если ее значение равно 1.
- И условия ИЛИ для получения выходной функции.
Пример: логическое выражение для функции большинства F = (A + B + C) (A + B + C ') (A + B' + C) (A' + B + C)
Теперь запишите ввод комбинация переменных с высокой производительностью. F = АВ + ВС + АС.
Проверка
По закону идемпотентности мы знаем, что
[(A + B + C) (A + B + C)] (A + B + C) = [(A + B + C)] ( A + B + C) = (A + B + C)
Теперь функция
F = (А + В) (В + С) (А + С)
= (А + В + С) (А + В + С') (А + В' + С) (А' + В + В)
= [(А + В + С) (А + В + С)] (А + В + С) (А + В + С') (А + В' + С) (А' + В + В)
= [(А + В + С) (А + В + С')] [(А + В + С) (А' + В + С)] [(А + В + С) (А + Б' + В)]
= [(А + В) + (С * С')] [(В + С) + (А * А')] [(А + С) + (В * В')]
= [(A + B) + 0] [(B + C) + 0] [(A + C) + 0] = (A + B) (B + C) (A + C)
Каноническая форма (Стандартная форма SOP и POS)
Любая булева функция, которая выражается как сумма minterms или как произведение maxterms, называется «канонической формой».

В основном используется два логических термина: «minterms» и «maxterms».
Когда форма SOP логического выражения находится в канонической форме, каждый из его терминов продукта называется «minterm». Таким образом, каноническая форма функции суммы произведений также известна как «каноническая форма minterm», или «Sum-of-minterms», или стандартная каноническая форма SOP.
Аналогичным образом, когда POS-форма логического выражения находится в канонической форме, каждый из его суммирующих терминов называется «maxterm». Таким образом, каноническая форма функции произведения сумм также известна как «каноническая форма maxterm или произведение суммы или стандартная каноническая форма POS».
Минимальные термины
Минтерм определяется как произведение n переменных, в котором каждая из n переменных появляется один раз либо в дополненной, либо в недополненной форме. Минимальный член обозначается как mi, где i находится в диапазоне 0 ≤ i <2ⁿ.
Переменная находится в дополненной форме, если ее значение присвоено 0, и переменная находится в недополненной форме, если ее значение присвоено 1.

Для логической функции с 2 переменными (x и y) возможные минтермы:
x'y', x'y, xy' и xy.
Для булевой функции с 3 переменными (x, y и z) возможные minterms:
x'y'z', x'y'z, x'yz', x'yz, xy'z' , xy'z, xyz' и xyz.
- 1 – Minterms = minterms, для которых функция F = 1,
- 0 – Minterms = minterms, для которых функция F = 0.
Любая логическая функция может быть выражена как сумма (ИЛИ) ее 1-минутных членов. Представление уравнения будет
- F (список переменных) = Σ (список индексов 1-минутного члена)
Пример: F (x, y, z) = Σ (3, 5, 6, 7)
Обратная функция может быть выражена как сумма (ИЛИ) ее нулевых членов. Представление уравнения будет
- F (список переменных) = Σ (список индексов 0-минутного члена)
Пример: F' (x, y, z) = Σ (0,1, 2, 4)
Примеры канонической формы выражения суммы произведений (каноническая форма минимального члена):
i) Z = XY + XZ'
ii) F = XYZ' + X'YZ + X'YZ' + XY'Z + XYZ
В стандартной форме СОП максимально возможные условия произведения для n переменных задаются как 2ⁿ.
 Таким образом, для уравнений с 2 переменными произведение составляет 22 = 4. Аналогично, для уравнений с 3 переменными произведение составляет 23 = 8.
Таким образом, для уравнений с 2 переменными произведение составляет 22 = 4. Аналогично, для уравнений с 3 переменными произведение составляет 23 = 8.Максимальное число членов
Максимальный термин определяется как произведение n переменных в диапазоне 0 ≤ i < 2ⁿ. Максимальный член обозначается как Mi. В термине max каждая переменная дополняется, если ее значение равно 1, и каждая переменная не дополняется, если ее значение присваивается 0.
Для булевой функции с двумя переменными (x и y) возможное максимальное термины:
х + у, х + у', х' + у и х' + у'.
Для булевой функции с тремя переменными (x, y и z) возможные maxterms:
x + y + z, x + y + z', x + y' + z, x + y' + z ', x' + y + z, x' + y + z', x' + y' + z и x' + y' + z'.
- 1 – Максимальное число членов = максимальное число членов, для которых функция F = 1.
- 0 – максимальное число членов = максимальное число членов, для которых функция F = 0.
Любая логическая функция может быть выражена произведением (И) ее 0-макс.
 членов. Представление уравнения будет
членов. Представление уравнения будет- F (список переменных) = Π (список индексов 0-max)
Пример: F (x, y, z) = Π (0, 1, 2, 4)
Обратная функция может быть выражена как произведение (И) ее 1-макс. членов. Представление уравнения будет
- F(список переменных) = Π(список индексов 1-max)
Пример: F’ (x, y, z) = Π (3, 5, 6, 7)
Примеры канонической формы произведения выражений суммы (каноническая форма максимального члена):
i. Z = (X + Y) (X + Y′)
ii. F = (X′ + Y + Z′) (X′ + Y + Z) (X′ + Y′ + Z′)
В стандартной форме POS максимально возможные члены суммы для n переменных задаются как 2ⁿ . Итак, для уравнений с 2 переменными сумма членов равна 22 = 4. Аналогично, для уравнений с 3 переменными сумма членов равна 23 = 8,9.0005
Таблица для 2n минимальных членов и 2n максимальных членов
Следующая таблица поможет вам понять представление средних и максимальных членов 3 переменных.
Преобразование канонических форм
Мы можем представить одно каноническое сформированное уравнение в другой канонической форме, т.
 е. мы можем представить форму уравнения SOP в форме POS и уравнение формы POS в форме SOP. Чтобы преобразовать канонические уравнения, мы поменяем местами символы Σ и Π после перечисления порядковых номеров уравнений, которые исключены из исходной формы уравнения.
е. мы можем представить форму уравнения SOP в форме POS и уравнение формы POS в форме SOP. Чтобы преобразовать канонические уравнения, мы поменяем местами символы Σ и Π после перечисления порядковых номеров уравнений, которые исключены из исходной формы уравнения.Важно помнить о логических функциях, что формы SOP и POS дублируют друг друга. Чтобы преобразовать каноническую форму уравнений, необходимо выполнить 2 шага. Это
. Шаг 1: Поменяйте местами рабочие символы Σ и Π в уравнении.
Шаг 2: Примените принцип двойственности Де Моргана к порядковым номерам булевой функции или запишите индексы членов, которые не представлены в данной форме уравнения.
Преобразование формы SOP в форму POS
Чтобы преобразовать форму SOP в форму POS, сначала мы должны изменить Σ на Π, а затем записать числовые индексы отсутствующих переменных данной булевой функции.
Пример:
Функция SOP
F = ∑ A, B, C (0, 2, 3, 5, 7) = A' B' C' + A B' C' + A B' C + ABC ' + ABC записывается в форме POS как
Шаг 1: изменение операционного знака на Π
Шаг 2: запись недостающих индексов терминов, 001, 100 и 110.
 Теперь напишите форму суммы для этих отмеченных термов.
Теперь напишите форму суммы для этих отмеченных термов.001 = (A + B + C) 100 = (A + B' + C') 110 = (A + B' + C')
Запись нового уравнения в форме POS,
F = Π A, B, C (1, 4, 6) = (A + B + C) * (A + B' + C') * (A + B' + C')
Преобразование формы POS в SOP form
Чтобы преобразовать форму POS в форму SOP, сначала мы должны изменить Π на Σ, а затем написать числовые индексы отсутствующих переменных данной булевой функции.
Пример: Функция POS F = Π A, B, C (2, 3, 5) = A B’ C’ + A B’ C + ABC’ записывается в форме SOP как
Шаг 1: изменение знака операции на Σ
Шаг 2: запись отсутствующих индексов терминов 000, 001, 100, 110 и 111. Теперь напишите форму произведения для этих отмеченных термов.
000 = A' * B' * C' 001 = A' * B' * C 100 = A * B' * C'
110 = A * B* C' 111 = A * B * C
Запись вниз по новому уравнению в виде СОП,
F = Σ A, B, C (0, 1, 4, 6, 7) = (A' * B' * C') + (A' * B' * C) + (A * B' * C') + (A * B * C') + (A * B * C)
Преобразование формы СОП в стандартную форму СОП или форму канонической СОП
Мы можем включить все переменные в каждый член произведения уравнения формы СОП, в котором нет всех переменных, путем преобразования в стандартную форму СОП.
 Функцию нормальной формы SOP можно преобразовать в стандартную форму SOP, используя закон булевой алгебры (A + A’ = 1) и выполнив следующие шаги.
Функцию нормальной формы SOP можно преобразовать в стандартную форму SOP, используя закон булевой алгебры (A + A’ = 1) и выполнив следующие шаги.Шаг 1:
Путем умножения каждого нестандартного термина продукта на сумму его отсутствующей переменной и ее дополнения, что дает 2 термина продукта
Шаг 2:
Повторяя шаг 1, пока все результирующие термины продукта не будут содержать все переменные
Этими двумя шагами мы можем преобразовать функцию SOP в стандартную функцию SOP. В этом процессе для каждой отсутствующей переменной в функции количество терминов продукта будет удваиваться.
Пример:
Преобразование нестандартной SOP-функции F = x y + x z + y z
Sol:
F = x y + x z + y z
= x y (z + z') + x (y + y') г + (х + х') у г
= x y z + x y z' + x y z + x y' z + x y z + x' y z
= x y z + x y z' + x y' z + x' y z
Стандартная форма СОП: F = x y z + x y z' + x y' z + x' y z
Преобразование формы POS в стандартную форму POS или каноническую форму POS
Мы можем включить все переменные в каждый термин продукта уравнения формы POS, который не имеет всех переменные путем преобразования в стандартную форму POS.
 Обычную функцию формы POS можно преобразовать в стандартную форму POS, используя закон алгебры логики (A * A’ = 0) и выполнив следующие шаги.
Обычную функцию формы POS можно преобразовать в стандартную форму POS, используя закон алгебры логики (A * A’ = 0) и выполнив следующие шаги.Шаг 1:
Добавляя каждый нестандартный член суммы к произведению его отсутствующей переменной и ее дополнения, что дает 2 члена суммы
Шаг 2:
Применяя закон булевой алгебры, A + BC = (A + B) * (A + C)
Шаг 3:
Повторяя шаг 1, пока все результирующие члены суммы не будут содержать все переменные
Этими тремя шагами мы можем преобразовать функцию POS в стандартную функцию POS.
Пример:
F = (A’ + B + C) * (B’ + C + D’) * (A + B’ + C’ + D)
В первом члене переменная D или D’ отсутствует, поэтому мы добавляем к ней D*D’ = 1. Тогда
(A' + B + C + D*D') = (A' + B + C + D) * (A' + B + C + D')
Аналогично, во втором члене переменная A или A' отсутствует, поэтому мы добавляем к нему A*A' = 1. Тогда
(B' + C + D' + A*A') = (A + B' + C + D') * (A' + B' + C + D')
Третий член уже в стандартная форма, так как она имеет все переменные.
 Теперь стандартное уравнение формы POS функции
Теперь стандартное уравнение формы POS функцииF = (А' + В + С + D) * (А' + В + С + D') * (А + В' + С + D') * (А' + В' + С + D') * (A + B' + C' + D)
[Решено] Упрощение логических выражений важно для проектирования и реализации цифровых систем. Мы обсудили множество способов...
Получите больше от подписки*
- Доступ к более чем 100 миллионам учебных ресурсов по конкретным курсам
- Круглосуточная помощь опытных наставников по более чем 140 предметам
- Полный доступ к более чем 1 миллиону решений для учебников
*Вы можете изменить, приостановить или отменить в любое время
Упрощение логических выражений важно для
проектирование и внедрение цифровых систем. Мы обсудили множество способов выполнения задач по упрощению, начиная с правил булевой алгебры и переходя к специализированным методам, таким как карты Куайна-МакКласки и карты Карно.
 Мы также видели Multisim Logic Converter, автоматизированный инструмент для упрощения логики.
Мы также видели Multisim Logic Converter, автоматизированный инструмент для упрощения логики.Провести исследование преимуществ упрощения логики при проектировании и реализации цифровых систем.
Информатика Инженерная технология Программная инженерия ЭЛЕКТРОННЫЙ ЭЛД-302
Ответ и объяснение
Решено проверенным экспертом
Рейтинг Helpful
inia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur
Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Donec aliquetПолучите полный доступ к Course Hero
Изучите более 16 миллионов пошаговых ответов из нашей библиотеки
Подпишитесь, чтобы посмотреть ответ
am lacinia pulvinar tortor nec facilisis.
 Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus,
Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus,ctum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor
ongue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna.
 Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing
Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscinga molestie conequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Пелленте
исц.элит. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet.
 Nam risus ante, dapibus a molestie consequat,
Nam risus ante, dapibus a molestie consequat,Итур Лаореет. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac
Пошаговое объяснение
ce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molesti
pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis.
 Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur
Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficiturgue
Отзывы студентов
100% (2 оценки)
Подробное объяснение
"Большое спасибо"
Онлайн-минимизация булевых функций
Онлайн-минимизация булевых функцийГлавная японский английский Калькулятор дробей Твит
9 октября 2011 г. Повышение производительности! Уменьшите ошибки тайм-аута. Тяжелый пример
Галерея карт Карно
Введите логические функции
Обозначение 9B (циркумфлекс)
Введите таблицу истинности
Введите «0», «1» или «x».
Таблица истинности (2 входа) Выход 0 0 0 1 1 0 1 1 Таблица истинности (3 входа) Выход 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 Таблица истинности (4 входа) Выход 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 г.
0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 г.
1 Таблица истинности (5 входов) Выход 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 г.0 1 1 0 0 1 0 0 0 0 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 0 0 0 0 1 0 0 1 0 1 0 1 0 0 1 0 1 1 0 1 1 0 0 0 г.
1 1 0 1 0 1 1 1 0 0 1 1 1 1 1 0 0 0 0 1 0 0 0 1 1 0 0 1 0 1 0 0 1 1 1 0 1 0 0 1 0 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1 0 0 0 1 1 0 0 1 1 1 0 1 0 1 1 0 1 1 1 1 1 0 0 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 Таблица истинности (6 входов) г. 
Выход 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 1 1 0 0 0 0 1 1 1 0 0 1 0 0 0 0 0 1 0 0 1 0 0 1 0 1 0 0 0 1 0 1 1 0 0 1 1 0 0 0 0 1 1 0 1 0 0 1 1 1 0 0 0 1 1 1 1 0 1 0 0 0 0 0 1 0 0 0 1 0 1 0 0 1 0 0 1 0 0 1 1 0 1 0 1 0 0 0 1 0 1 0 1 0 1 0 1 1 0 0 1 0 1 1 1 0 1 1 0 0 0 0 1 г.
1 0 0 1 0 1 1 0 1 0 0 1 1 0 1 1 0 1 1 1 0 0 0 1 1 1 г.0 1 0 1 1 1 1 0 0 1 1 1 1 1 1 0 0 0 0 0 1 0 0 0 0 1 г.
1 0 0 0 1 0 1 0 0 0 1 1 1 0 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 1 1 0 1 0 0 0 1 0 1 0 0 1 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 1 0 0 1 0 1 1 0 1 1 0 1 1 1 0 1 0 1 1 1 1 1 1 0 0 0 0 1 1 0 0 0 1 1 1 0 0 1 0 г. 
1 1 0 0 1 1 1 1 0 1 0 0 1 1 0 1 0 1 1 1 0 1 1 0 1 г.1 0 1 1 1 1 1 1 0 0 0 1 1 1 0 0 1 1 1 1 0 1 0 1 1 1 г.
0 1 1 1 1 1 1 0 0 1 1 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 9№ Булева алгебра
- Изучив этот раздел, вы должны уметь:
- Описывать логические схемы, используя булевы уравнения.
- • Создание логических выражений для выходов промежуточных вентилей.
- • Используйте сложные логические уравнения для описания полных логических схем.
- Упростите логические уравнения, используя логические законы.
- • Коммутативный.

- • Ассоциативный.
- • Распределительный.
- • Личность.
- • Дополнение.
- • Двойственность.
- • Теорема де Моргана.
- Используйте теорему Де Моргана, чтобы преобразовать схемы с несколькими вентилями в универсальные вентили.
Булева алгебра
Модуль цифровой электроники 2.1 показал, что работу одного вентиля можно описать с помощью логического выражения. Например, работа одного вентиля И с входами A и B и выходом X может быть выражена как:
X = A•B
Примечание:
Символ • представляет логическое И, но поскольку использование специальных символов может быть неудобным в печатных материалах, символ И часто опускается, как в AB, или отделяется полной остановка, как в AB, используемая для обозначения умножения в стандартной алгебре. Символы умножения x и * также можно увидеть в некоторых текстах, потому что логическое И похоже на двоичное умножение (но не то же самое, когда используются числа, имеющие более одного бита).
 В модуле 2.2 показана взаимосвязь между таблицей истинности, описывающей работу схемы, и логическим уравнением, описывающим логику схемы.
В модуле 2.2 показана взаимосвязь между таблицей истинности, описывающей работу схемы, и логическим уравнением, описывающим логику схемы.Комбинационная логическая схема, показанная на рис. 2.3.1 (повторение рис. 2.2.2), описывается логическим уравнением:
X = (A•B) + (A•C) + (A •B•C)
Рис. 2.3.1 Трехвходовая схема с резервными вентилями
Это также можно записать (менее ясно) как «Выход X будет равен 1, когда A и B или A и C или A и B и C равно 1, иначе X будет равно 0".
Однако модуль 2.2 также показал, что, хотя логическое уравнение может дать точное описание логического процесса, описываемого таблицей истинности, оно может потребовать упрощения, прежде чем оно будет интерпретировано как реальная схема. Схема, показанная на рис. 2.3.1, была упрощена в модуле 2.2 путем тщательного изучения таблицы истинности для поиска избыточных вентилей. Однако с чем угодно, кроме самых простых схем, это может быть утомительно, и легко сделать ошибки.
Таким образом, этот модуль описывает методы прямого упрощения булевых уравнений с помощью булевой алгебры, а не с помощью таблиц истинности.

Упрощение схемы с использованием булевой алгебры
Алгебраический метод, используемый для упрощения цифровых схем, применяет ряд булевых законов для последовательного упрощения сложных уравнений. Выбранные законы и правила применяются шаг за шагом к исходному уравнению, чтобы в конечном итоге прийти к упрощенной версии, которую можно реализовать с меньшим количеством вентилей и, следовательно, привести к более простой схеме.
Булевы законы
Законы булевой алгебры в чем-то похожи на законы стандартной алгебры, но в некоторых случаях булевы законы уникальны. Это связано с тем, что когда логика применяется к цифровым схемам, любая переменная, такая как A, может иметь только два значения 1 или 0, тогда как в стандартной алгебре A может иметь много значений.
Коммутативные законы
В группе переменных, связанных операторами И или ИЛИ, порядок переменных не имеет значения.
1а. Логическое сложение (ИЛИ): A+B = B+A
1б. Логическое умножение (И): A•B = B•A
Ассоциативные законы
Порядок вычисления можно изменить, не влияя на результат (изменить условия в скобках или удалить скобки).
 Примечание. Это допустимо только в том случае, если все знаки (+ или •) совпадают.
Примечание. Это допустимо только в том случае, если все знаки (+ или •) совпадают.2а. Логическое сложение (ИЛИ): (A+B)+C = A+(B+C) = A+B+C
2b. Логическое умножение (И): (A•B)•C = A•(B•C) = A•B•C = ABC
Законы распределения
Тот же самый ответ получается при умножении (по И) переменной на группа переменных в квадратных скобках, объединенных (или) вместе, как если бы каждое умножение (И) выполнялось отдельно.
Закон 3а подобен разложению на множители в нормальной алгебре, но закон 3b уникален для булевой алгебры, потому что в отличие от нормальной алгебры, где A x A=A 2 , в булевой алгебре A•A = A
3a. А•(В+С) = А•В+А•С
3б. A+(B•C) = (A+B) • (A+C)
Identity Elements
В правиле 4a, когда переменная A объединяется по И с логической единицей (называется Identity Element для оператора AND). Переменная, объединенная AND с 1, сохраняет свою идентичность.
Правило 4b показывает, что элемент идентичности для оператора ИЛИ равен 0, и любая переменная (например, A), объединенная ИЛИ с 0, сохраняет свою идентичность.

4а. А•1 = А
4б. A+0 = A
5a и 5b показывают, как путем «приведения элемента идентичности» (в столбце B таблиц истинности) в состояния, противоположные тем, которые используются в 4a и 4b, получается выходной сигнал, который совпадает с Элемент идентификации.
5а. А•0 = 0
5б. A+1 = 1
6a и 6b показывают, что операция И или ИЛИ двух идентичных переменных дает результат, равный одной переменной, показывая, что одна из переменных является избыточной, полезное правило при упрощении булевых уравнений.
6а. А•А = А
6б. A+A = A
Дополнение Закона
7a. A + A = 1 Любая переменная, объединенная операцией ИЛИ с обратной, равна 1
7b. A • A = 0 Любая переменная, объединенная по И со своей обратной, равна 0
Сокращение
8a. Когда одна переменная (A) объединяется по И с самой собой ИЛИ со второй переменной (A+B), результат равен одной переменной.
8а А•(А+В) = А
8б. Когда одна переменная (A) объединяется по ИЛИ с самой собой И второй переменной (A•B), результат равен одной переменной.

8b А+(А•В) = А
8с. Когда одна переменная (A) объединяется с самой собой ИЛИ со второй переменной (A+B), единственная переменная исчезает.
8c А+(А+В) = (А+В)
8d. Когда одна переменная (A) объединяется И с самой собой И второй переменной (A•B), единственная переменная исчезает.
8d A•(A•B) = (A•B)
Правила двойственности
Можно получить дополнительные идентичности, получив двойственность идентичности. Это включает замену операторов И на ИЛИ и операторов ИЛИ на И. Кроме того, любые 0 заменяются на 1, а 1 на 0, как показано в таблице 2.3.2.
Правило двойственности можно использовать для замены логического выражения, содержащего элементы И и ИЛИ, на его эквивалентное двойственное выражение.
Таблица 2.3.3 показывает, что A•(B+C) совпадает с A+(B•C).
Упрощение логических уравнений
Минимизация сложных логических выражений до их простейшей формы с использованием логических законов и правил заключается в выборе наиболее подходящего закона или правила для пошагового сокращения выражения.
 Если результирующая минимизация верна, минимизированное уравнение и исходное уравнение должны давать идентичные выходные столбцы при сравнении таблиц истинности для исходной и минимизированной схем.
Если результирующая минимизация верна, минимизированное уравнение и исходное уравнение должны давать идентичные выходные столбцы при сравнении таблиц истинности для исходной и минимизированной схем.Эти булевы алгебраические методы обычно используются в логических схемах с несколькими логическими элементами и только двумя или тремя входами, поскольку этот метод упрощения становится более сложным и громоздким в использовании, когда задействовано больше логических элементов или входов.
Какие законы применяются для изменения уравнения и в каком порядке - это вопрос практики и интуиции. Этот метод включает в себя просмотр исходного сложного уравнения и выбор закона, который упростит конкретную часть, поэтому получение более простого уравнения, а затем выбор другого закона, который еще больше упростит уравнение, и так далее, пока уравнение больше нельзя будет упростить. .
Не существует простого алгоритма для определения порядка шагов, которые необходимо предпринять, и можно выбрать несколько путей для достижения цели упрощенной и идеально минимизированной схемы.

Является ли результат также минимально возможной схемой, можно судить только путем поиска любого возможного дальнейшего сокращения с использованием булевых законов.
На практике небольшие схемы с двумя или тремя входами очень часто можно упростить, просто взглянув на таблицу истинности и выбрав любые избыточные логические комбинации, как показано в таблице 2.2.2 в модуле 2.2 (Комбинационная логика), но логические упрощение полезно для более сложных схем.
Примеры логического упрощения
Пример 1
Предположим, доступ к кассе в магазине ограничен определенными сотрудниками, каждый из которых имеет ключ, который выдает логическую единицу на определенных входах схемы разблокировки.
Только директор магазина (М) может войти в одиночку. Помощник менеджера (A) и кассир (C) также имеют доступ, но только в сопровождении друг друга или менеджера магазина. Разработайте комбинационную логическую схему, которая разрешает доступ, создавая логическую единицу, когда выполняются вышеуказанные условия.

Таблица истинности
Условия, требующие выхода логической 1, могут быть организованы в виде таблицы истинности (таблица 2.3.4), и логические выражения могут быть получены из таблицы истинности для каждой комбинации входов, которая дает выход логической 1.
Пять логических выражений могут быть разделены операторами ИЛИ для формирования полного логического уравнения.
X = M + M•C + A•C + A•M + A•C•M
Рис. 2.3.2 Схема доступа к кассе
Это предполагает схему, подобную показанной на рис. 2.3.2, что потребовало бы четырех I.C:
1x 74HCT08 2 входа И (содержащий 4 вентиля).
1x 74HCT10 3 входа И (содержащий 3 вентиля).
1x 74HCT32 2 входа ИЛИ (содержат 4 вентиля).
1x 74HCT4075 3 входа ИЛИ (содержат 3 вентиля).
Однако, выбрав подходящие законы и правила из перечисленных выше, схему можно значительно упростить.
Начиная с уравнения, полученного из Таблицы 2.3.4:
Рис. 2.3.3 Упрощенная схема доступа к кассе
X = M + M•C + A•C + A•M + A•C•M
Поскольку M + M•C = M (правило приведения 8b)
X = M + A•C + A•M + A•C•M
И как M + A•C + A•M = M + A•M + A•C (Закон коммутативности 1a)
X = M + A•M + A•C + A• C•M
А так как M + A•M = M (правило редукции 8b)
X = M + A•C + A•C•M
А так как M + A•C + A•C•M = M + A•C•M + A•C (Закон перестановочности 1a)
X = M + A•C•M + A•C
А так как M + A•C•M = M (правило редукции 8b)
Х = М + А•С
Дальнейшее уменьшение невозможно.

Упрощенная схема показана на рис. 2.3.3, которая выполняет те же функции, что и на рис. 2.3.2. Это можно подтвердить, сравнив упрощенное уравнение X = M + A•C с исходным столбцом X в таблице 2.3.5.
Упрощенная схема на рис. 2.3.3 по-прежнему требует двух микросхем (И и ИЛИ) и теперь использует только один вентиль на микросхему. Если запасные ворота не будут использоваться где-то еще в другой части схемы, это все равно расточительно.
Рис. 2.3.4 Цепь доступа только к кассе
Лучшим вариантом может быть замена функций И и ИЛИ универсальными вентилями, такими как НЕ-ИЛИ или НЕ-И. Версия упрощенной схемы «только NAND» показана на рис. 2.3.4. В этой версии используются три вентиля вместо двух, но все вентили одинаковы и могут быть размещены в одной микросхеме 7400. Таким образом, исходная схема была сокращена с четырех ИС до одной.
Операция
Оба входа NAND 1 соединены вместе, что преобразует его в инвертор или логический элемент НЕ и, следовательно, создает выходной сигнал Mat.
 И-НЕ 2 работает как логический элемент И с инвертированным выходом, поэтому на выходе получается A•C. Логическое выражение для схемы, использующей логические элементы И-НЕ, теперь принимает следующий вид:
И-НЕ 2 работает как логический элемент И с инвертированным выходом, поэтому на выходе получается A•C. Логическое выражение для схемы, использующей логические элементы И-НЕ, теперь принимает следующий вид:X = M + A•C
Это связано с применением еще одного очень полезного закона булевой алгебры, теоремы Де Моргана. Прежде чем рассмотреть, как работает теорема, обратите внимание на разницу в использовании черточек инверсии в логических выражениях. Это важная особенность применения теоремы Де Моргана:
Непрерывная полоса A•B указывает на то, что входные данные (например, для логического элемента И) инвертированы, в то время как сплошная полоса A•B указывает на инвертированный выход.
Теорема Де Моргана
Рис. 2.3.5 Закон Де Моргана 1
Рис. 2.3.6 Закон Де Моргана 2
Август Де Морган сформулировал расширение алгебраической логики Джорджа Буля, которое стало очень важным в цифровой логике. Он используется не только для упрощения логических выражений, но также может использоваться для изменения функции логических вентилей, так что вентили НЕ-И (или вентили ИЛИ-НЕ) могут выполнять любые другие стандартные логические функции вентилей.
 Теорема состоит из двух законов, которые описывают, как инвертирование входных данных ворот меняет функцию ворот.
Теорема состоит из двух законов, которые описывают, как инвертирование входных данных ворот меняет функцию ворот.Закон 1.
A + B = A • B Инвертирование входов в вентиль ИЛИ меняет его функцию на НЕ-И.
Закон 2.
A • B = A + B Инвертирование входных сигналов логического элемента И меняет его функцию на НЕ-ИЛИ
Рассматривая эти два равенства в обратном порядке, A + B = A • B Теорема Де Моргана часто описывается как «Сломай планку и поменяй знак». Это означает, что при размещении или удалении черты над оператором И или ИЛИ (• или +) оператор инвертируется. Следовательно, дополнением функции И является ИЛИ.
Применение теоремы Де Моргана
Эти равенства, обычно называемые законами Де Моргана 1 и 2, проиллюстрированы на рис. 2.3.5 и рис. 2.3.6, поскольку они применимы к элементам И, ИЛИ, НЕ-И и ИЛИ. Однако обратите внимание, что когда теорема Де Моргана применяется к вентилям XOR и XNOR, функция вентиля не меняется.
Полезность теоремы Де Моргана применительно к схемам можно увидеть, сравнив рис.
 2.3.3 и рис. 2.3.4, где она сыграла важную роль в изменении функций логических элементов И и ИЛИ на рис. 2.3.3 для всех Элементы И-НЕ на рис. 2.3.4, поэтому схема может быть выполнена с использованием одной ИС вместо двух.
2.3.3 и рис. 2.3.4, где она сыграла важную роль в изменении функций логических элементов И и ИЛИ на рис. 2.3.3 для всех Элементы И-НЕ на рис. 2.3.4, поэтому схема может быть выполнена с использованием одной ИС вместо двух.Инвертирование входов
На рис. 2.3.4 в схеме появляется дополнительный вентиль НЕ-И 1, два входа которого соединены вместе, чтобы действовать как вентиль НЕ (проверьте это, взглянув на таблицу истинности для вентиля И-НЕ в Рис. 2.3.5), когда оба входа одинаковы (строка 1 и строка 4), выход (X) является инвертированной версией входов (A•B).
Этот дополнительный логический элемент на рис. 2.3.4 обеспечивает М на верхнем входе И-НЕ 3 вместо М, подаваемого на верхний вход вентиля ИЛИ на рис. 2.3.3.
И-НЕ 2 на рис. 2.3.4 заменяет логический элемент И на рис. 2.3.3, так что нижним входом в И-НЕ 3 теперь является A•C вместо A•C.
Следовательно, входы NAND 3 теперь M и M•C. Поэтому оба входа в И-НЕ 3 были инвертированы (без фактического использования каких-либо логических элементов НЕ), чтобы заставить И-НЕ 3 действовать, согласно теореме Де Моргана, как функцию ИЛИ, что дает правильный выход X = M + A•C.

Резюме
Булева алгебра дает более компактный способ описания комбинационной логической схемы, чем только таблицы истинности. Его также можно использовать для упрощения схем, однако это также может быть громоздким и подверженным ошибкам. Когда задействованы схемы с более чем двумя или тремя входами, лучшим методом сокращения схем, который хорошо работает со схемами, имеющими до четырех или шести входов, является карта Карно.
Обсуждение решения для наилучшего метода минимизации булевых функций – IJERT
Обсуждение решения для наилучшего метода минимизации булевых функций
R.Mohana Ranga Rao T. Santosh Kumar
Доцент Ассоциированный Профессор
Кафедра ECE Кафедра ECE
MLRIT, Дандигал MLRIT, Дандигал
РЕЗЮМЕ:
В этой статье обсуждается тематическое исследование методов минимизации булевых функций. Проблема минимизации булевых функций может быть старой, но в таких средах, как проектирование PLA, проектирование систем управления или проектирование встроенного оборудования для самотестирования (BIST), а также в разработке программного обеспечения
, проблемы с искусственным интеллектом и т.
 д., это оказывает значительное влияние. Очевидно, что необходимо обсудить эту булеву функцию, поскольку размер схемы, минимизация мощности и стоимости, оптимизация площади являются существенными факторами при проектировании цифровой схемы. Основная цель любого метода — устранение избыточных пар, которые помогают минимизировать размер логического выражения. В этой статье упоминается сравнение различных методов на основе их плюсов и минусов. Рассматриваются следующие методы: карта Карно [8] (K-карта), метод Куайна [6]-МакКласки [1] (QM) и методы минимизации булевых функций на основе M-терминов.
д., это оказывает значительное влияние. Очевидно, что необходимо обсудить эту булеву функцию, поскольку размер схемы, минимизация мощности и стоимости, оптимизация площади являются существенными факторами при проектировании цифровой схемы. Основная цель любого метода — устранение избыточных пар, которые помогают минимизировать размер логического выражения. В этой статье упоминается сравнение различных методов на основе их плюсов и минусов. Рассматриваются следующие методы: карта Карно [8] (K-карта), метод Куайна [6]-МакКласки [1] (QM) и методы минимизации булевых функций на основе M-терминов.Ключевые слова: Булевы функции, минимизация, K-Map, QM, M-Terms, Prime Implicants, литералы
ВВЕДЕНИЕ
Цифровые элементы (логические элементы) являются основными электронными компонентами любой цифровой схемы. Логический вентиль выполняет логическую операцию на основе одного или нескольких входов и выдает одно значение выходного напряжения (т. е. уровни высокого и низкого напряжения).
 Логически эти значения напряжения можно обозначить как 1 и 0, и они используются при разработке и анализе работы логических вентилей. Логический элемент представляет собой логическую функцию. Булева функция — это алгебраическое выражение, состоящее из логических переменных (со значениями «истина» или «1» и «ложь» или 0) и логических операторов (то есть ИЛИ, И и НЕ). Это может быть большое количество булевых алгебраических выражений, которые
Логически эти значения напряжения можно обозначить как 1 и 0, и они используются при разработке и анализе работы логических вентилей. Логический элемент представляет собой логическую функцию. Булева функция — это алгебраическое выражение, состоящее из логических переменных (со значениями «истина» или «1» и «ложь» или 0) и логических операторов (то есть ИЛИ, И и НЕ). Это может быть большое количество булевых алгебраических выражений, которыеуказать заданную логическую функцию. Поэтому важно найти самый простой.
Булева функция может быть представлена таблицей истинности. Таблица истинности представляет собой табличное представление всех взаимосвязей ввода-вывода цифровой схемы. Он отображает все возможные комбинации входных значений с соответствующими выходными значениями. Обычно логическое выражение может быть задано в двух формах: SOP и POS. Булевы выражения SOP могут быть легко сгенерированы из таблиц истинности путем формирования операции ИЛИ из И всех входных переменных (стандартных продуктов или минимальных терминов), для которых выход равен 1.
 Выражения POS основаны на 0 в таблице истинности и генерируются. наоборот, как SOP, взяв И ИЛИ всех входных переменных (стандартные суммы или максимальные члены).
Выражения POS основаны на 0 в таблице истинности и генерируются. наоборот, как SOP, взяв И ИЛИ всех входных переменных (стандартные суммы или максимальные члены).ИСТОРИЯ
Идея минимизации булевой функции впервые была предложена английским математиком и философом Джорджем Булем, который изобрел булеву алгебру в 1854 году, с помощью которой минимизация осуществляется путем минимизации числа литералов, позже К. Э. Шеннон [7] показал, как булеву алгебру можно использоваться при проектировании цифровых схем (Шеннон [7], 1938 г.). Цифровые вентили являются основным компонентом любой цифровой схемы. Булева логика — основная концепция, лежащая в основе всех современных электронных цифровых компьютеров. Используя булевы законы, можно минимизировать цифровые логические схемы за счет уменьшения исходного количества цифровых компонентов (вентилей), необходимых для реализации цифровых схем. Это уменьшит размер микросхемы, стоимость и увеличит скорость схемы. Законы, предложенные Булем, не являются систематическими и не пригодными для компьютерной реализации, более того, они требуют больше времени для упрощения.
 Позже было введено несколько алгоритмов, чтобы решить проблему реализации. Karnaugh [8] предложил методику для
Позже было введено несколько алгоритмов, чтобы решить проблему реализации. Karnaugh [8] предложил методику дляупрощает логические выражения с помощью элегантной визуальной техники, которая на самом деле представляет собой модифицированную таблицу истинности, предназначенную для получения выражений минимальной суммы произведений (SOP) и произведения сумм (POS) (Karnaugh [8], 1953). Техника, основанная на карте Карно [8] (K-Map), выходит за рамки шести переменных. Куайн [6] и МакКласки [1] предложили метод, основанный на алгоритмах, для упрощения функций булевой логики (МакКласки [1] - 1956, Куайн [6] - 1952). Новый метод [4] предложен Р. Мохана Ранга Рао [4]. 4], в котором минимизация выполняется с помощью М-терминов для упрощения функции с использованием десятичных значений.
ОПРЕДЕЛЕНИЯ
Сумма произведений (SOP): это наиболее распространенная форма логических выражений. Выражения реализованы как вентили И (произведения), питающие один вентиль ИЛИ (сумма).

Произведение сумм (POS): это менее часто используемая форма логических выражений. Выражения реализованы как вентили ИЛИ (суммы), вводимые в один вентиль И (произведение).
Номинальная стоимость: Перечислите степени двойки справа налево. Старт в 20; оцените его как «1», 21 как 2 и 22 как 4, аналогичным образом увеличьте показатель степени на единицу для каждой степени. Остановиться, когда количество элементов в списке равно количеству цифр в двоичном числе.
Примерный номер 10011011 состоит из восьми цифр, поэтому список до восьми элементов будет выглядеть так: 128, 64, 32, 16, 8, 4, 2, 1 эти элементы называются номиналами соответствующих элементов соответствующих позиции.
М-ТЕРМЫ: М-термы генерируются путем сложения/вычитания соответствующего минимального термина с его номиналами. На основе значения бита, т.е. сложения, если двоичное значение равно 0, вычитания, если двоичное значение равно 1.
Например: 5 - заданный минимальный срок
Minterm Двоичная нотация Номинальная стоимость M-terms 5 0 1 0 1 8 4 2 1 13 1 7 4
СПИСОК МИНТЕРМ:
Это набор минтерм, который можно комбинировать.

напр. (1, 5) и (0, 1, 2, 3) — список minterm.
ГЛАВНОЕ ИМПЛИКАНТ
Это список minterm, который нельзя комбинировать ни с каким другим списком minterm.
Карта Карно
Идея Карты Карно [8] (Карно [8], 1953) состоит в том, чтобы нарисовать таблицу истинности выражений в виде матрицы таким образом, чтобы каждая строка и каждый столбец матрицы ставили минтермы, отличающиеся значением одной переменной, рядом друг с другом. Затем, сгруппировав соседние ячейки матрицы, вы можете определить термины продукта, исключающие все дополняющие литералы, что приводит к минимизации версии выражения.
4.1 Преимущества K-Map
Это быстрый метод упрощения выражения до четырех переменных. Он дает визуальный метод упрощения логики. Можно визуально увидеть различные возможные комбинации и быстро выбрать необходимые. импликанты идентифицируются быстро. Этот принцип был распространен на очень крупномасштабную интеграцию путем включения его в метод проектирования логики проходного транзистора, и он подходит как для SOP, так и для POS форм сокращения.

К-карты не подходят, когда число задействованных переменных превышает четыре. С трудом может использоваться до пяти- и шестипеременных систем. Но за пределами «Шести переменных» k карт не могут быть физически визуализированы.
Не подходит для компьютерного сокращения, важным моментом является то, что упрощение k-map выполняется вручную, а процесс упрощения сильно зависит от способностей человека. Необходимо позаботиться о том, чтобы заполнить каждую ячейку соответствующей записью, такой как 0, 1 или безразличный термин. Ячейка, оставленная незаполненной, может быть ошибочно принята за неважный термин, что приведет к ошибочным результатам.
Метод Куайна-МакКласки (табличный метод)
Метод Куайна[6]-МакКласки [1] не зависит от визуальных паттернов, поскольку становится трудным, когда количество переменных больше, поэтому Q-M особенно полезен, когда логические функции имеют большое количество переменных, например, для более функции с пятью переменными.
 Алгоритм не может быть выполнен вручную из-за длительной процедуры, поэтому были разработаны компьютерные программы, использующие этот алгоритм с использованием различных плоских форм. Метод сводит функцию в стандартной форме суммы произведений к набору простых импликант, из которых исключается как можно больше переменных. Эти первичные импликанты затем проверяются, чтобы увидеть, не являются ли некоторые из них избыточными. Существенные импликанты простых чисел, которые не очевидны на k-карте, можно ясно увидеть в окончательных результатах с помощью диаграммы импликантов простых чисел.
Алгоритм не может быть выполнен вручную из-за длительной процедуры, поэтому были разработаны компьютерные программы, использующие этот алгоритм с использованием различных плоских форм. Метод сводит функцию в стандартной форме суммы произведений к набору простых импликант, из которых исключается как можно больше переменных. Эти первичные импликанты затем проверяются, чтобы увидеть, не являются ли некоторые из них избыточными. Существенные импликанты простых чисел, которые не очевидны на k-карте, можно ясно увидеть в окончательных результатах с помощью диаграммы импликантов простых чисел.Минусы:
Более длительная процедура, чем карта k, требующая нескольких группировок и шагов, по сравнению с картой k, она намного медленнее
Нет визуальной идентификации процесса восстановления
Метод QM по существу является МЕТОДОМ КОМПЬЮТЕРНОЙ ОБРАБОТКИ.
6. НОВАЯ ПРОЦЕДУРА УПРОЩЕНИЯ УПРОЩЕНИЕ НА ОСНОВЕ М-ТЕРМОВ
Основное преимущество предложенного метода перед обычными методами заключается в том, что все упрощение основано на десятичных значениях (например, М-термах), которые хорошо известны каждому и каждому дизайнеру, поэтому на практике этот метод легко реализовать для повышения производительности.

Представлена процедура упрощения на основе М-термов с использованием предложенного алгоритма: [4]
Преобразование данной логической операции в каноническую форму SOP и получение двоичной записи для каждого минтерма.
Теперь получите номиналы всех заданных минимальных членов. (Обычно это было бы одинаково для всех минимальных условий).
Вычислите M-термины для заданных минимальных терминов.
Сравните каждый M-термин с предоставленными входными данными (минимум терминов), чтобы идентифицировать соседние термины. Если M-термин эквивалентен любому минимальному термину предоставленных входных данных, тогда минимальный термин и M-термин должны быть сгруппированы вместе, чтобы создать пару (основная импликация). При группировании два термина следуют в порядке возрастания.
Повторяйте описанный выше шаг до тех пор, пока не станет невозможно сравнивать термины, и исключите все повторяющиеся пары.

Сравнить простые импликанты между собой так, чтобы разность между элементами простой импликанты была одинаковой и равнялась 2L , L=0,1,2..N. При сравнении убедитесь, что сравнение выполняется между одинаковыми элементами, то есть должны сравниваться первые элементы двух пар и вторые элементы двух пар. Как только найдутся два термина, отличающиеся на 2L, сгруппируйте две пары в один четырехугольник. Теперь повторите ту же процедуру для всех пар.
Поменять местами все объединенные термы, термы, которые вообще не объединялись, и простые импликанты, не входящие ни в одну четверку.
Теперь повторите шаги VI и VII, чтобы свести к минимуму заданную логическую функцию/минимальные члены до тех пор, пока не станет невозможно комбинировать члены.
Теперь устраните избыточные импликанты простых чисел, используя диаграмму импликантов простых чисел, как в методе Куайна [6]-МакКласки [1].
ЗАКЛЮЧЕНИЕ
В этой статье проводится сравнение трех методов и делается вывод о том, что новый метод минимизации на основе M-терминов может выдержать даже основные недостатки карты Карно [8] и карты Куайна [6]-МакКласки
[1] так как это просто, быстрее и позволяет сократить количество необходимых сравнений. Новый метод можно использовать даже при большем количестве переменных. На основании результатов таблицы 1 [9] уверенно можно рассматривать метод M-Term для булевой функции
Новый метод можно использовать даже при большем количестве переменных. На основании результатов таблицы 1 [9] уверенно можно рассматривать метод M-Term для булевой функцииупрощение. Еще одна причина, по которой следует использовать этот метод, заключается в том, что компьютерное сокращение возможно.
ТАБЛИЦА-1 [9]
№ переменной (n)
Всего сравнений в худшем случае
Метод управления качеством
Метод MQM
2
4
4
3
15
12
4
56
32
5
210
80
6
792
192
7
3003
448
8
11440
1024
ССЫЛКИ
McCluskey EJ, минимизация булевой функции, Bell system Tech.
 Журнал, т. 35, № 5, стр. 1417-1444, 1956.
Журнал, т. 35, № 5, стр. 1417-1444, 1956.С. П. Томашевески , Минимизация булевых функций на основе WWW, Международный журнал прикладной математики и компьютерных наук, том. 13, нет. 1, стр. 577-583, 2003.
Джайн Т.К., Кушваха Д.С., Мисра А.К., Оптимизация метода Куайна [6]-Маккласки для минимизации логических выражений, Международная конференция по автономным и автономным системам, (ICAS), 2008.
Р. Мохан Ранга Рао, Инновационная процедура минимизации булевой функции, Международный журнал передовых инженерных наук и технологий (IJAEST), том 3, выпуск № 1, стр. 012-014, 2011.
Аруначалам Солайраджу, Раджупиллай Периясами, Упрощение оптимальной булевой функции с помощью K-Map с использованием объектно-ориентированного алгоритма, Международный журнал компьютерных приложений (IJCA), том 15, выпуск № 7, стр. 28-32 февраля 2011 г.
Куайн В.В. (1952): Проблема упрощения таблиц истинности -
.





 – 116с.
– 116с.

 subs({x: True, y: True})
Истинный
>>> (х | у).атомы()
{х, у}
subs({x: True, y: True})
Истинный
>>> (х | у).атомы()
{х, у}
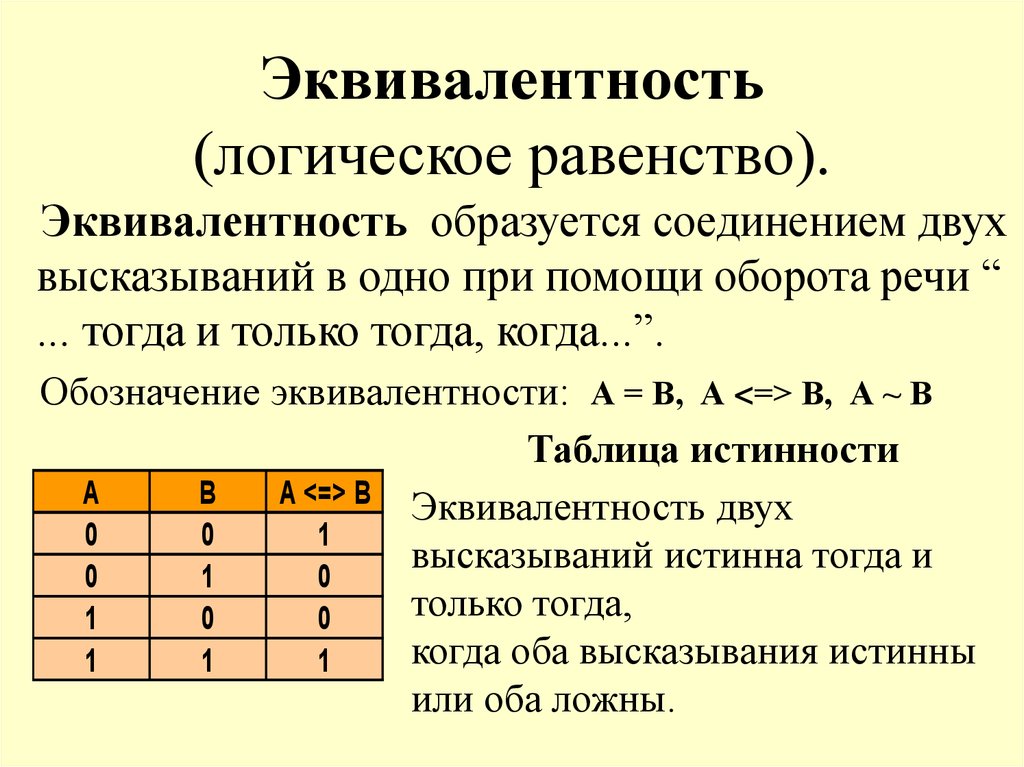 .. [0, 1, 1, 1], [1, 0, 1, 1], [1, 1, 1, 1]]
>>> не важно = [[0, 0, 0, 0], [0, 0, 1, 0], [0, 1, 0, 1]]
>>> SOPform([w, x, y, z], minterms, dontcares)
(у и я) | (~ ш и ~ х)
.. [0, 1, 1, 1], [1, 0, 1, 1], [1, 1, 1, 1]]
>>> не важно = [[0, 0, 0, 0], [0, 0, 1, 0], [0, 1, 0, 1]]
>>> SOPform([w, x, y, z], minterms, dontcares)
(у и я) | (~ ш и ~ х)
 logic.boolalg.POSform( переменные , minterms , dontcares=нет )[источник]
logic.boolalg.POSform( переменные , minterms , dontcares=нет )[источник] wikipedia.org/wiki/Quine-McCluskey_algorithm
wikipedia.org/wiki/Quine-McCluskey_algorithm wikipedia.org/wiki/Zhegalkin_polynomial
wikipedia.org/wiki/Zhegalkin_polynomial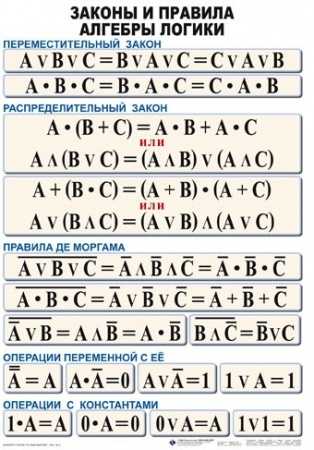 abc импортировать A, B, C
>>> from sympy import И, Или, Не
>>> (A >> B).равно(~B >> ~A)
Истинный
>>> Не(И(А, В, С)).равно(И(Не(А), Не(В), Не(С)))
ЛОЖЬ
>>> Не(И(А, Не(А))).равно(Или(В, Не(В)))
ЛОЖЬ
abc импортировать A, B, C
>>> from sympy import И, Или, Не
>>> (A >> B).равно(~B >> ~A)
Истинный
>>> Не(И(А, В, С)).равно(И(Не(А), Не(В), Не(С)))
ЛОЖЬ
>>> Не(И(А, Не(А))).равно(Или(В, Не(В)))
ЛОЖЬ
 true
true  к.
элементы
к.
элементы  true
true  также
также раздел примечаний в
раздел примечаний в 
 Следовательно,
Следовательно,  В частности,
В частности, 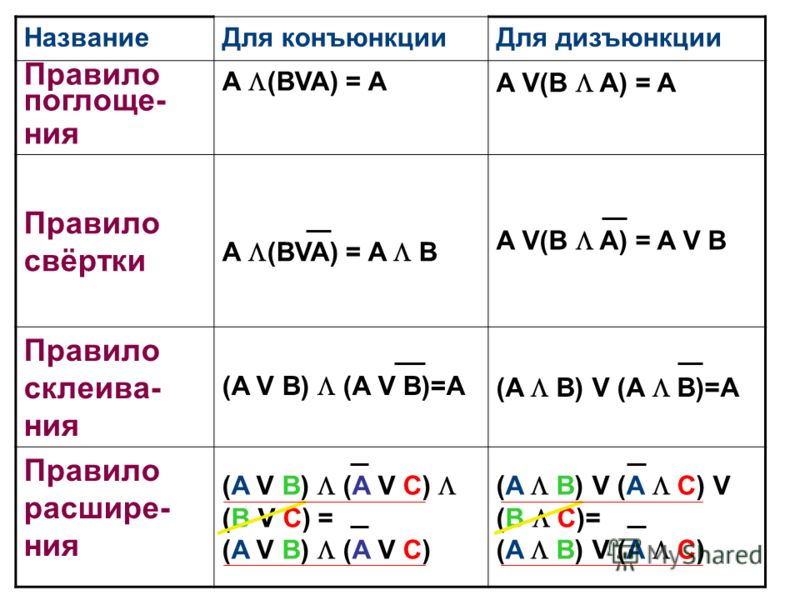 sub(y, 0)
Икс
sub(y, 0)
Икс
 logic.boolalg import Nor
>>> из символов импорта sympy
>>> х, у = символы ('х у')
logic.boolalg import Nor
>>> из символов импорта sympy
>>> х, у = символы ('х у')

 В частности, поскольку Python
считает
В частности, поскольку Python
считает  logic.boolalg.ITE ( *args ) [источник]
logic.boolalg.ITE ( *args ) [источник]
 (~A & (Эквивалент(B, C)))
(~A & (Эквивалент(B, C)))  ..) | (B & C & ...) | ...)
..) | (B & C & ...) | ...) 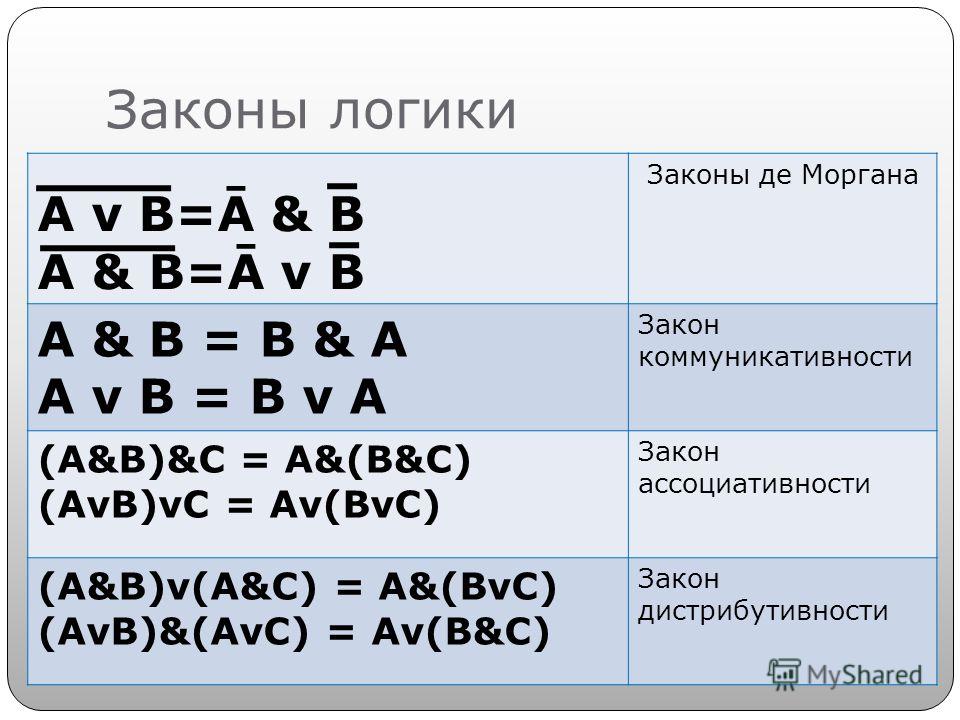 Если
Если  abc импортировать A, B, C
>>> is_anf(истина)
Истинный
>>> is_anf(A)
Истинный
>>> is_anf(И(А,В,С))
Истинный
>>> is_anf(Xor(A, Not(B)))
ЛОЖЬ
abc импортировать A, B, C
>>> is_anf(истина)
Истинный
>>> is_anf(A)
Истинный
>>> is_anf(И(А,В,С))
Истинный
>>> is_anf(Xor(A, Not(B)))
ЛОЖЬ
 logic.boolalg.is_nnf ( expr , упрощенный = True ) [источник]
logic.boolalg.is_nnf ( expr , упрощенный = True ) [источник]
 logic.boolalg.simplify_logic( expr , form=None , deep=True , force=False )[источник]
logic.boolalg.simplify_logic( expr , form=None , deep=True , force=False )[источник]
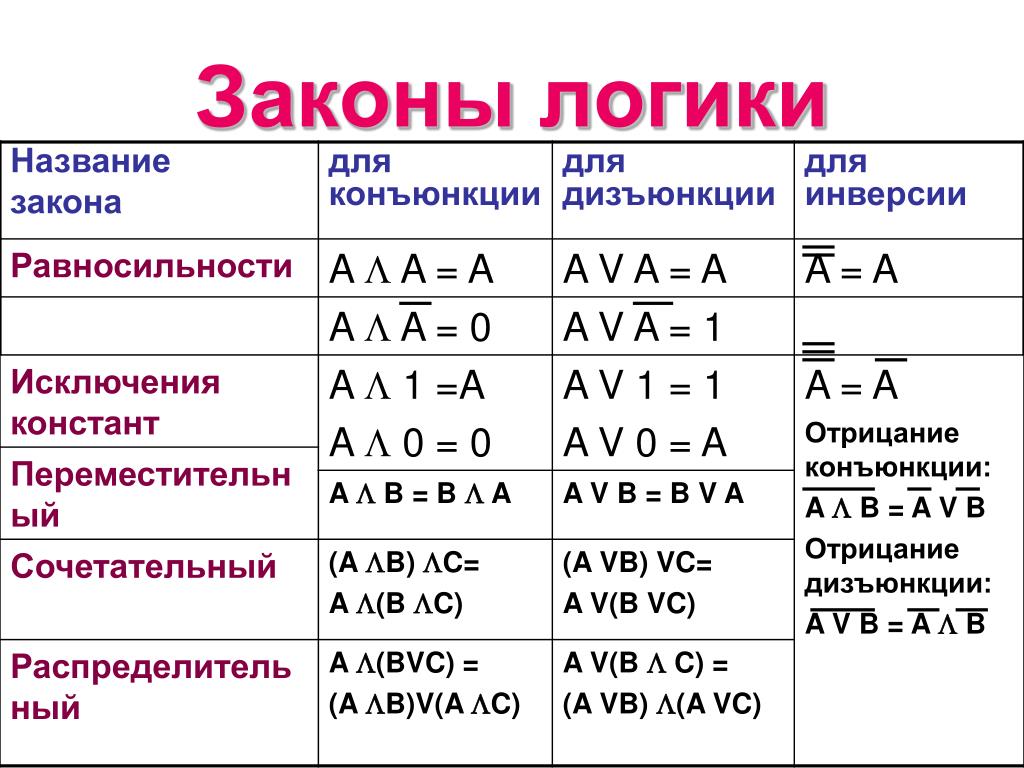
 Здесь,
Здесь, 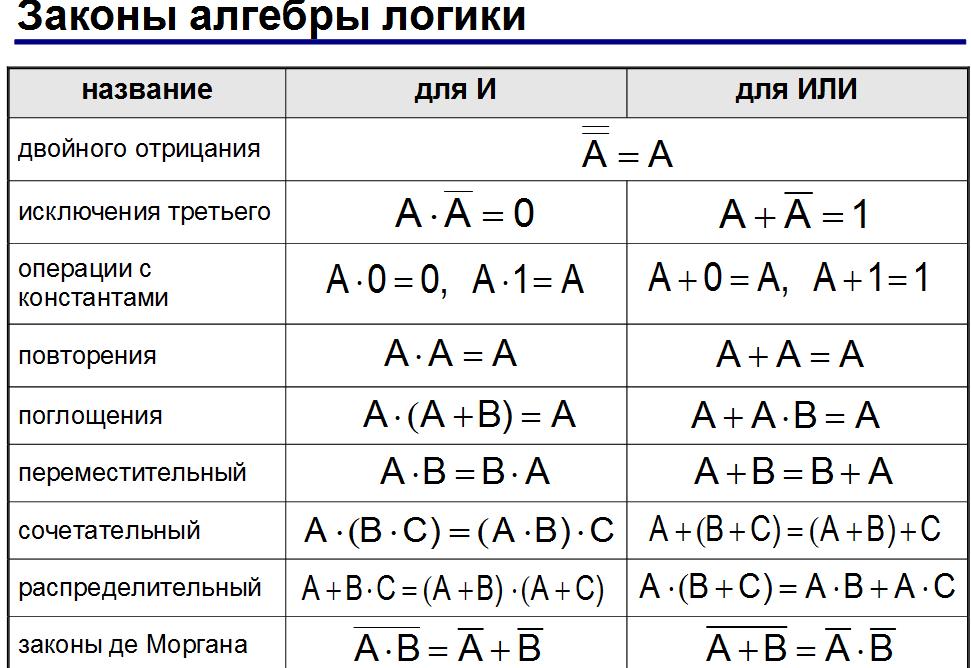 logic.boolalg.distribute_or_over_and ( выражение ) [источник]
logic.boolalg.distribute_or_over_and ( выражение ) [источник] logic.boolalg.eliminate_implications ( выражение ) [источник]
logic.boolalg.eliminate_implications ( выражение ) [источник]
 Возвращает {true: true} для тривиально истинных выражений.
Возвращает {true: true} для тривиально истинных выражений. В алгебре переключения все переменные принимают одно из двух значений: 0 и 1.
В алгебре переключения все переменные принимают одно из двух значений: 0 и 1. Мы можем стандартизировать логические выражения, используя две стандартные формы.
Мы можем стандартизировать логические выражения, используя две стандартные формы.




 Таким образом, для уравнений с 2 переменными произведение составляет 22 = 4. Аналогично, для уравнений с 3 переменными произведение составляет 23 = 8.
Таким образом, для уравнений с 2 переменными произведение составляет 22 = 4. Аналогично, для уравнений с 3 переменными произведение составляет 23 = 8. членов. Представление уравнения будет
членов. Представление уравнения будет е. мы можем представить форму уравнения SOP в форме POS и уравнение формы POS в форме SOP. Чтобы преобразовать канонические уравнения, мы поменяем местами символы Σ и Π после перечисления порядковых номеров уравнений, которые исключены из исходной формы уравнения.
е. мы можем представить форму уравнения SOP в форме POS и уравнение формы POS в форме SOP. Чтобы преобразовать канонические уравнения, мы поменяем местами символы Σ и Π после перечисления порядковых номеров уравнений, которые исключены из исходной формы уравнения. Теперь напишите форму суммы для этих отмеченных термов.
Теперь напишите форму суммы для этих отмеченных термов. Функцию нормальной формы SOP можно преобразовать в стандартную форму SOP, используя закон булевой алгебры (A + A’ = 1) и выполнив следующие шаги.
Функцию нормальной формы SOP можно преобразовать в стандартную форму SOP, используя закон булевой алгебры (A + A’ = 1) и выполнив следующие шаги. Обычную функцию формы POS можно преобразовать в стандартную форму POS, используя закон алгебры логики (A * A’ = 0) и выполнив следующие шаги.
Обычную функцию формы POS можно преобразовать в стандартную форму POS, используя закон алгебры логики (A * A’ = 0) и выполнив следующие шаги. Теперь стандартное уравнение формы POS функции
Теперь стандартное уравнение формы POS функции Мы также видели Multisim Logic Converter, автоматизированный инструмент для упрощения логики.
Мы также видели Multisim Logic Converter, автоматизированный инструмент для упрощения логики. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus,
Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing
Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing Nam risus ante, dapibus a molestie consequat,
Nam risus ante, dapibus a molestie consequat, Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur
Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur

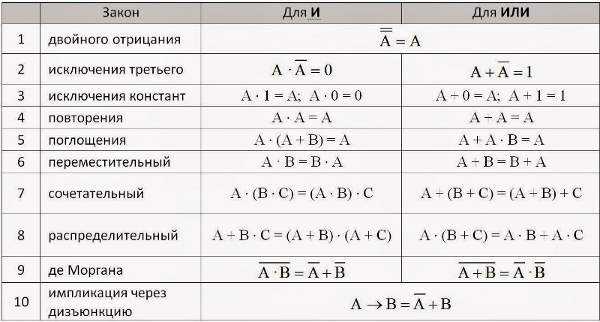
_8-500x500.jpg)

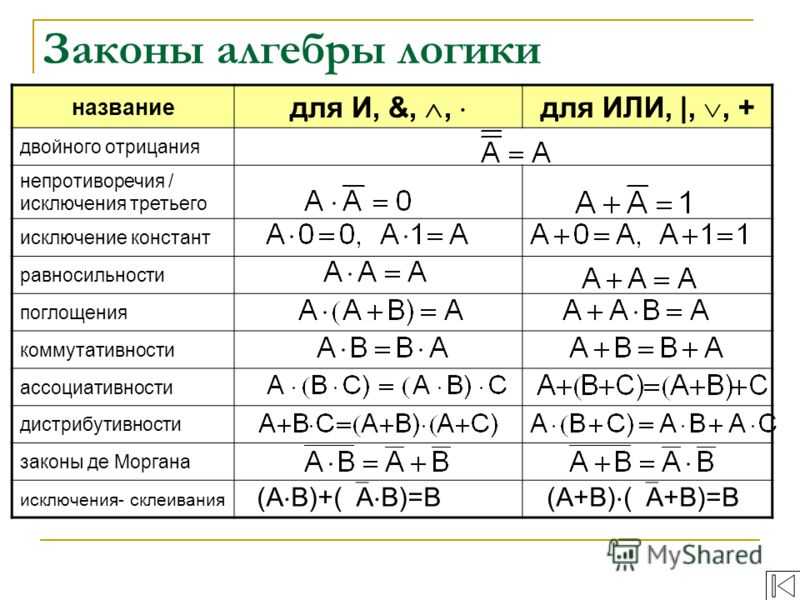



 В модуле 2.2 показана взаимосвязь между таблицей истинности, описывающей работу схемы, и логическим уравнением, описывающим логику схемы.
В модуле 2.2 показана взаимосвязь между таблицей истинности, описывающей работу схемы, и логическим уравнением, описывающим логику схемы.
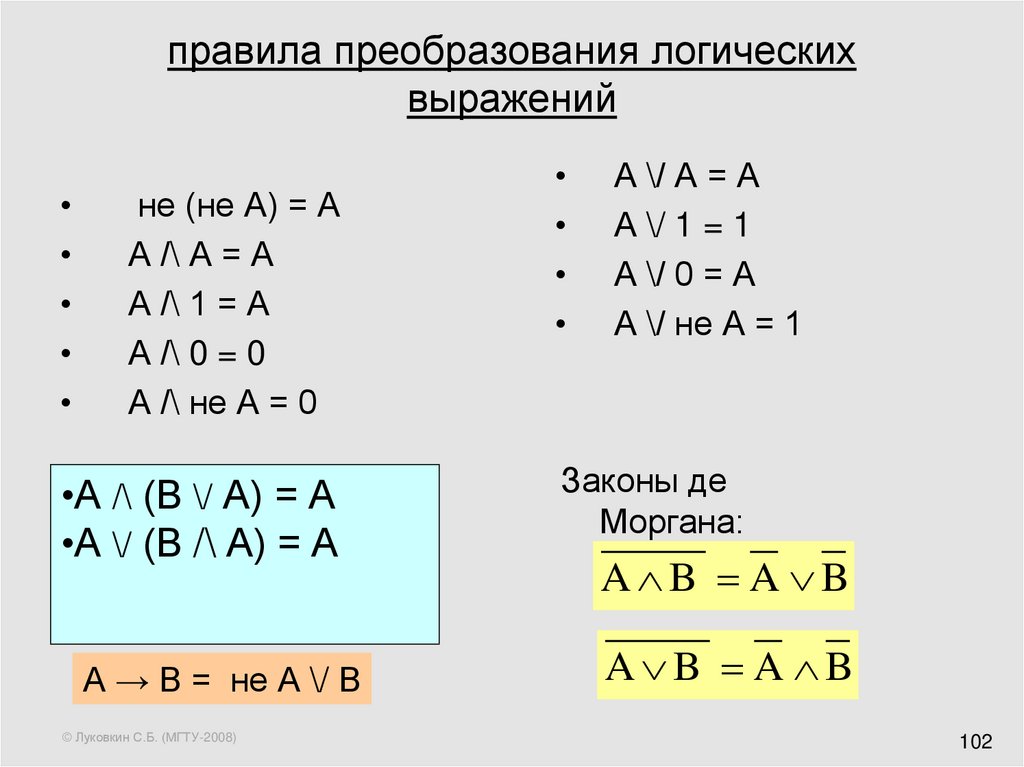 Примечание. Это допустимо только в том случае, если все знаки (+ или •) совпадают.
Примечание. Это допустимо только в том случае, если все знаки (+ или •) совпадают.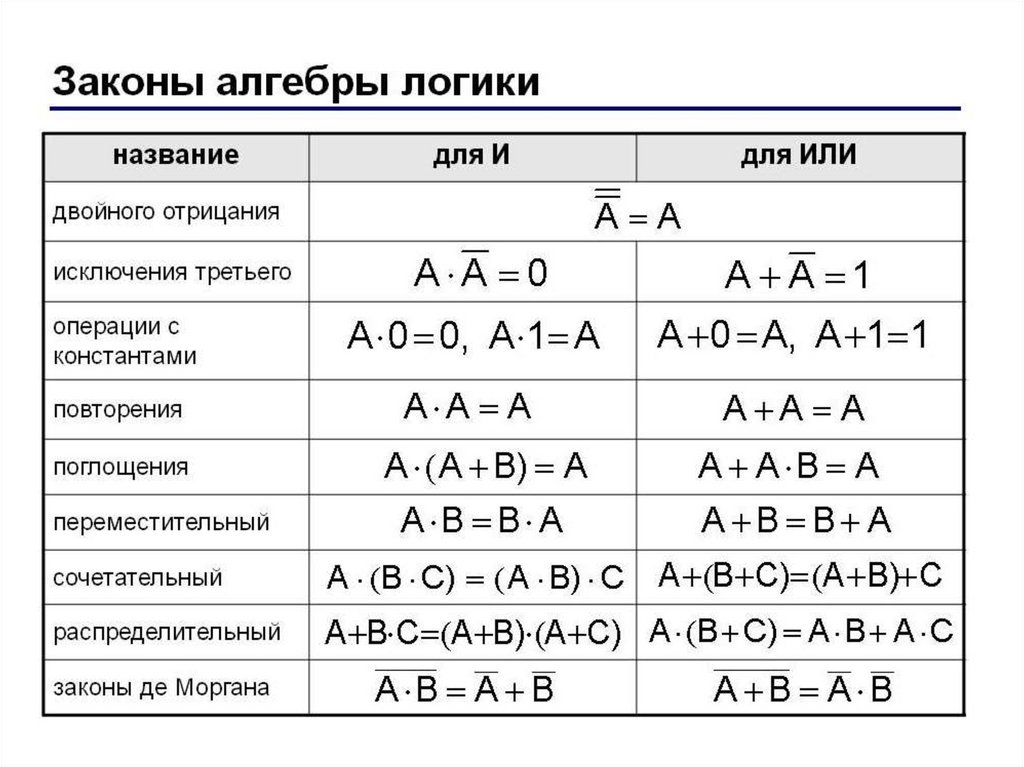

 Если результирующая минимизация верна, минимизированное уравнение и исходное уравнение должны давать идентичные выходные столбцы при сравнении таблиц истинности для исходной и минимизированной схем.
Если результирующая минимизация верна, минимизированное уравнение и исходное уравнение должны давать идентичные выходные столбцы при сравнении таблиц истинности для исходной и минимизированной схем.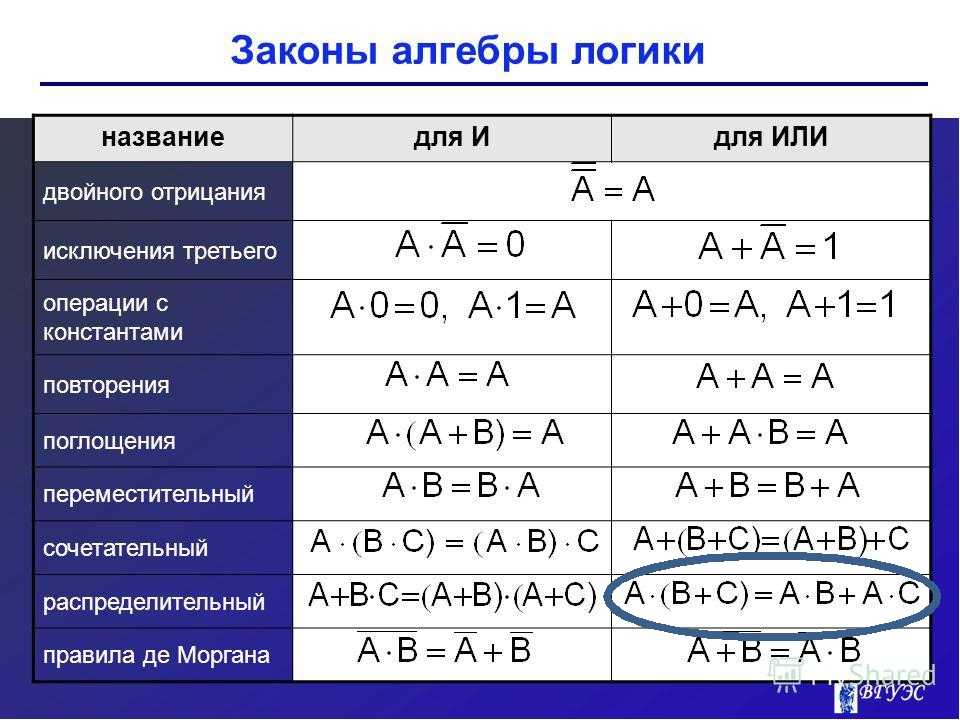


 И-НЕ 2 работает как логический элемент И с инвертированным выходом, поэтому на выходе получается A•C. Логическое выражение для схемы, использующей логические элементы И-НЕ, теперь принимает следующий вид:
И-НЕ 2 работает как логический элемент И с инвертированным выходом, поэтому на выходе получается A•C. Логическое выражение для схемы, использующей логические элементы И-НЕ, теперь принимает следующий вид: Теорема состоит из двух законов, которые описывают, как инвертирование входных данных ворот меняет функцию ворот.
Теорема состоит из двух законов, которые описывают, как инвертирование входных данных ворот меняет функцию ворот. 2.3.3 и рис. 2.3.4, где она сыграла важную роль в изменении функций логических элементов И и ИЛИ на рис. 2.3.3 для всех Элементы И-НЕ на рис. 2.3.4, поэтому схема может быть выполнена с использованием одной ИС вместо двух.
2.3.3 и рис. 2.3.4, где она сыграла важную роль в изменении функций логических элементов И и ИЛИ на рис. 2.3.3 для всех Элементы И-НЕ на рис. 2.3.4, поэтому схема может быть выполнена с использованием одной ИС вместо двух.
 д., это оказывает значительное влияние. Очевидно, что необходимо обсудить эту булеву функцию, поскольку размер схемы, минимизация мощности и стоимости, оптимизация площади являются существенными факторами при проектировании цифровой схемы. Основная цель любого метода — устранение избыточных пар, которые помогают минимизировать размер логического выражения. В этой статье упоминается сравнение различных методов на основе их плюсов и минусов. Рассматриваются следующие методы: карта Карно [8] (K-карта), метод Куайна [6]-МакКласки [1] (QM) и методы минимизации булевых функций на основе M-терминов.
д., это оказывает значительное влияние. Очевидно, что необходимо обсудить эту булеву функцию, поскольку размер схемы, минимизация мощности и стоимости, оптимизация площади являются существенными факторами при проектировании цифровой схемы. Основная цель любого метода — устранение избыточных пар, которые помогают минимизировать размер логического выражения. В этой статье упоминается сравнение различных методов на основе их плюсов и минусов. Рассматриваются следующие методы: карта Карно [8] (K-карта), метод Куайна [6]-МакКласки [1] (QM) и методы минимизации булевых функций на основе M-терминов. Логически эти значения напряжения можно обозначить как 1 и 0, и они используются при разработке и анализе работы логических вентилей. Логический элемент представляет собой логическую функцию. Булева функция — это алгебраическое выражение, состоящее из логических переменных (со значениями «истина» или «1» и «ложь» или 0) и логических операторов (то есть ИЛИ, И и НЕ). Это может быть большое количество булевых алгебраических выражений, которые
Логически эти значения напряжения можно обозначить как 1 и 0, и они используются при разработке и анализе работы логических вентилей. Логический элемент представляет собой логическую функцию. Булева функция — это алгебраическое выражение, состоящее из логических переменных (со значениями «истина» или «1» и «ложь» или 0) и логических операторов (то есть ИЛИ, И и НЕ). Это может быть большое количество булевых алгебраических выражений, которые Выражения POS основаны на 0 в таблице истинности и генерируются. наоборот, как SOP, взяв И ИЛИ всех входных переменных (стандартные суммы или максимальные члены).
Выражения POS основаны на 0 в таблице истинности и генерируются. наоборот, как SOP, взяв И ИЛИ всех входных переменных (стандартные суммы или максимальные члены). Позже было введено несколько алгоритмов, чтобы решить проблему реализации. Karnaugh [8] предложил методику для
Позже было введено несколько алгоритмов, чтобы решить проблему реализации. Karnaugh [8] предложил методику для
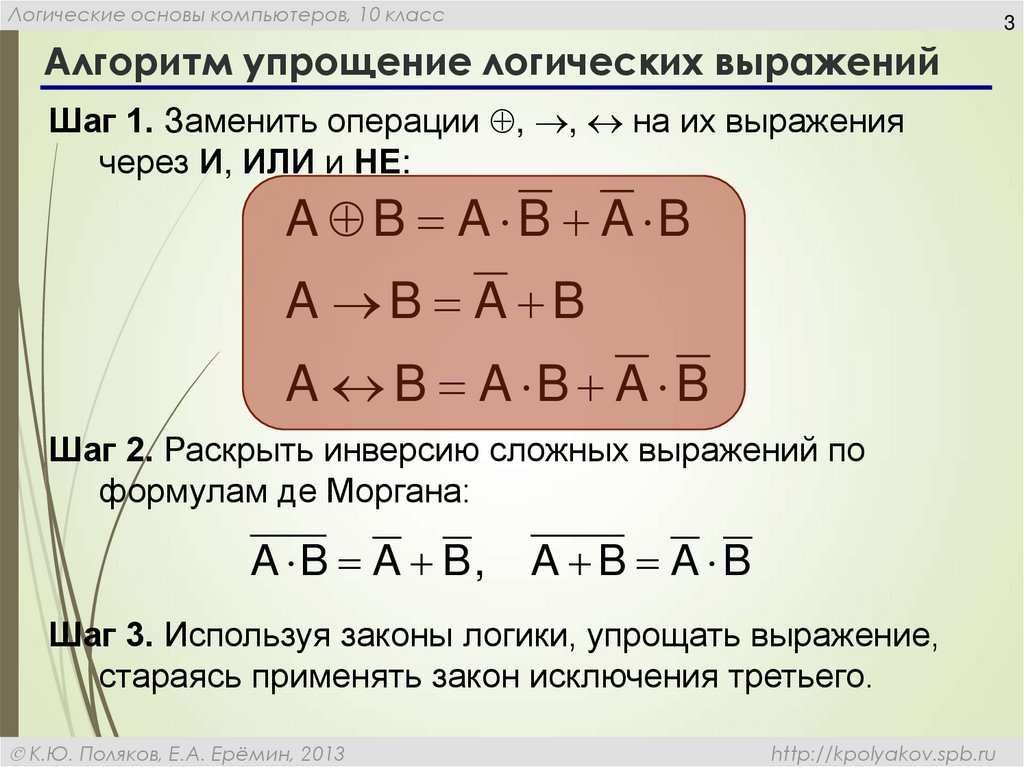

 Алгоритм не может быть выполнен вручную из-за длительной процедуры, поэтому были разработаны компьютерные программы, использующие этот алгоритм с использованием различных плоских форм. Метод сводит функцию в стандартной форме суммы произведений к набору простых импликант, из которых исключается как можно больше переменных. Эти первичные импликанты затем проверяются, чтобы увидеть, не являются ли некоторые из них избыточными. Существенные импликанты простых чисел, которые не очевидны на k-карте, можно ясно увидеть в окончательных результатах с помощью диаграммы импликантов простых чисел.
Алгоритм не может быть выполнен вручную из-за длительной процедуры, поэтому были разработаны компьютерные программы, использующие этот алгоритм с использованием различных плоских форм. Метод сводит функцию в стандартной форме суммы произведений к набору простых импликант, из которых исключается как можно больше переменных. Эти первичные импликанты затем проверяются, чтобы увидеть, не являются ли некоторые из них избыточными. Существенные импликанты простых чисел, которые не очевидны на k-карте, можно ясно увидеть в окончательных результатах с помощью диаграммы импликантов простых чисел.

 Новый метод можно использовать даже при большем количестве переменных. На основании результатов таблицы 1 [9] уверенно можно рассматривать метод M-Term для булевой функции
Новый метод можно использовать даже при большем количестве переменных. На основании результатов таблицы 1 [9] уверенно можно рассматривать метод M-Term для булевой функции Журнал, т. 35, № 5, стр. 1417-1444, 1956.
Журнал, т. 35, № 5, стр. 1417-1444, 1956.